Enhancing Wind Power Forecasting in the Spanish Market Through Transformer Neural Networks and Temporal Optimization

Abstract

The increasing penetration of renewable energy, and wind power in particular, requires accurate short-term forecasting to ensure grid stability, reduce operational uncertainty, and facilitate large-scale integration of intermittent resources. This study evaluates Transformer-based architectures for wind power forecasting using hourly generation data from Spain (2020–2024). Time series were segmented into input windows of 12, 24, and 36 h, and multiple model configurations were systematically tested. For benchmarking, LSTM and GRU models were trained under identical protocols. The results show that the Transformer consistently outperformed recurrent baselines across all horizons. The best configuration, using a 36 h input sequence with moderate dimensionality and shallow depth, achieved an RMSE of 370.71 MW, MAE of 258.77 MW, and MAPE of 4.92%, reducing error by a significant margin compared to LSTM and GRU models, whose best performances reached RMSEs above 395 MW and MAPEs above 5.7%. Beyond predictive accuracy, attention maps revealed that the Transformer effectively captured short-term fluctuations while also attending to longer-range dependencies, offering a transparent mechanism for interpreting the contribution of historical information to forecasts. These findings demonstrate the superior performance of Transformer-based models in short-term wind power forecasting, underscoring their capacity to deliver more accurate and interpretable predictions that support the reliable integration of renewable energy into modern power systems.

1. Introduction

Wind energy represents a cornerstone in the global transition toward sustainable and low-carbon power systems due to its environmental benefits, economic competitiveness, and capacity to mitigate greenhouse gas emissions. Over the past decades, installed wind power capacity has expanded rapidly worldwide, reflecting both technological progress and the urgency of reducing reliance on fossil fuels [1]. In Europe, wind power has become central to achieving climate and energy objectives through large-scale deployment and supportive policy frameworks such as the European Green Deal and the Fit for 55 package [2,3]. Spain ranks among the leading countries in this field, with production levels comparable to global benchmarks such as Germany and India. However, the inherent variability of wind resources poses persistent integration challenges, as forecasting errors can compromise grid stability, increase operational costs, and limit the sustainable deployment of renewable energy [4,5].

Accurate short-term wind power forecasting is therefore required for enabling reliable integration of renewables into modern power systems and supporting the development of sustainable smart grids. Despite significant progress, existing approaches still face difficulties in capturing the nonlinear and long-range temporal dependencies that characterize wind power generation. Traditional physical and statistical models, such as numerical simulations and Autoregressive Integrated Moving Average ARIMA-family methods, offered efficient short-horizon forecasts but were constrained by assumptions of linearity and stationarity, limiting their effectiveness in highly dynamic environments [4,6,7]. These limitations motivate the exploration of advanced data-driven approaches capable of delivering accurate and robust forecasts to enhance energy system sustainability.

Machine learning (ML) and deep learning (DL) methods have been increasingly explored for wind power forecasting, offering notable improvements over traditional statistical approaches. Random Forests, Gradient Boosting, and hybrid decomposition-based models have demonstrated competitive accuracy by learning from historical data without rigid assumptions [4,8]. Nevertheless, these methods face practical limitations, as their performance often depends on large, high-quality datasets and extensive feature engineering, while recurrent and convolutional networks, despite their advances, still struggle to fully capture long-range sequential dependencies critical for wind power dynamics [9,10]. Recent developments in attention mechanisms and Transformer architectures provide a promising alternative by explicitly modeling long-range temporal dependencies. Early applications in wind forecasting confirm their capacity to leverage complex temporal patterns, but most rely on high-frequency, turbine-level meteorological inputs [11]. This highlights a gap in the ability of streamlined forecasting frameworks based on aggregated historical generation to reflect realistic data availability in many national power systems. Addressing this gap is important to improve predictive performance while supporting the sustainable integration of wind energy into smart grids.

In light of the challenges discussed above, this study pursues two primary objectives. The first is to develop a Transformer-based architecture for short-term wind power forecasting using historical generation data as input. By leveraging the self-attention mechanism, the approach aims to capture long-range and multi-scale temporal dependencies inherent in aggregated power series, providing a data-efficient solution suitable for operational contexts with limited access to high-resolution meteorological variables. The second objective is to apply this framework to a case study of hourly wind power generation in Spain during the 2020–2024 period, using data reported by the European Network of Transmission System Operators for Electricity (ENTSO-E). The performance of the Transformer model is benchmarked against two widely adopted DL architectures, LSTM and GRU networks, in order to assess predictive accuracy and robustness under realistic system constraints. To guide this analysis, the following research questions (RQs) are formulated:

• RQ1: Can Transformer architectures achieve higher accuracy than recurrent models in short-term wind power forecasting when only historical generation data are available?
• RQ2: How do input sequence length and key architectural choices of the Transformer model affect forecasting performance?

The remainder of this paper is structured as follows. Section 2 provides a background on the Spanish wind power sector and reviews existing forecasting methodologies, highlighting the specific gaps this study addresses. Section 3 details the methodological design, including data preprocessing, model architecture, and training strategy. Section 4 reports the empirical results, focusing on the comparative performance of Transformer, LSTM, and GRU models under different input configurations. Finally, Section 5 summarizes the main findings, answers the research questions, and discusses avenues for future research in the context of sustainable energy systems.

2. Background of Forecasting in the Wind Power Sector

2.1. The Spanish Wind Power Sector

Spain has consolidated its position as one of Europe’s leading countries in wind energy deployment, with recent years marked by a steady expansion of renewable capacity. By the end of 2024, the national installed generation capacity reached approximately 129 GW, with wind accounting for 24.9% and solar photovoltaic slightly ahead at 25.1%. Together with other renewable sources, this expansion brought the share of renewables to nearly 66% of total capacity, reflecting a rapid acceleration in the country’s energy transition. The year 2024 alone witnessed an unprecedented addition of 7.3 GW in renewable capacity, much of it from newly commissioned wind installations [12,13]. In terms of actual generation, wind energy emerged as the leading source of electricity in 2024, contributing 23.2% of national supply, followed by nuclear (20%) and solar photovoltaic (17%) [12]. On average, between August 2024 and July 2025, more than 80% of Spain’s electricity was generated from low-carbon technologies, including wind, nuclear, solar, and hydropower, underscoring the central role of clean energy in shaping the country’s electricity mix [14].

Despite these achievements, the Spanish wind sector continues to face persistent challenges. The heterogeneous geographic distribution of wind farms, spanning coastal areas, central plateaus, and mountainous regions, results in high spatial and temporal variability, which complicates system operation and planning [15]. Furthermore, Spain’s electricity market operates under a day-ahead and intraday structure, where deviations between forecasted and realized generation translate directly into imbalance costs and risks for system reliability [16]. These market dynamics create a pressing need for accurate, robust, and adaptive short-term forecasting tools capable of supporting efficient dispatch decisions under increasingly tight operational margins. Taken together, these features, high wind penetration, regional climatic diversity, systemic relevance in the national energy mix, and dependence on short-term market mechanisms, make Spain an ideal testbed for evaluating advanced forecasting models. In this context, exploring the potential of Transformer-based architectures is not only relevant for addressing domestic operational challenges but also provides transferable insights for other power systems worldwide seeking to enhance the sustainable integration of renewable energy resources [17].

2.2. Forecasting Approaches for Wind Energy

Early forecasting approaches were primarily based on persistence models, physical simulations, and statistical techniques such as the ARIMA family. These methods provided short-term forecasts with reasonable accuracy under stable conditions but were constrained by assumptions of linearity and stationarity, limiting their ability to represent the highly volatile and nonlinear dynamics of wind power generation [4,6,7]. While physical models incorporated atmospheric physics and fluid dynamics [18], their effectiveness depended strongly on the quality of numerical weather predictions, often struggling to adapt to site-specific conditions and abrupt fluctuations. To overcome these limitations, ML methods have been increasingly explored for wind power forecasting. Algorithms such as Random Forests and Gradient Boosting demonstrated strong predictive performance by automatically learning from historical data without predefined assumptions [4]. In addition, hybrid approaches that combine ML with decomposition techniques, such as Empirical Mode Decomposition (EMD), achieved superior accuracy by isolating relevant temporal features [8]. Nevertheless, these methods face important constraints for large-scale deployment in sustainable energy systems; as their effectiveness depends heavily on access to large, high-quality datasets, they require extensive feature engineering, and they lack the capacity to explicitly capture sequential dependencies critical for time series forecasting.

DL techniques have emerged as powerful alternatives to address these challenges, offering the ability to model complex nonlinearities and temporal dependencies in large-scale datasets. Within this paradigm, Multilayer Perceptrons (MLPs) have been employed to capture nonlinear feature interactions [19], while Recurrent Neural Networks (RNNs), particularly Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) variants, are widely used for their ability to model sequential dependencies and dynamic temporal patterns [9,10]. Convolutional Neural Networks (CNNs), initially designed for spatial data, have also been adapted to extract local temporal features and spatial correlations from meteorological inputs. Furthermore, hybrid architectures such as CNN-LSTM have demonstrated strong performance in multi-step forecasting tasks, particularly in offshore or geographically diverse contexts where both spatial and temporal heterogeneity are pronounced [20,21]. Building on these advances, data-driven preprocessing methods have been proposed to improve the quality of training inputs for DL models. For instance, adversarial frameworks such as Wasserstein GAN with gradient penalty (WGAN-GP) have been used to mitigate biases and enhance data representativeness, leading to improved accuracy in short-term wind power forecasting [22].

More recently, attention mechanisms have been integrated into DL architectures to enhance their ability to identify and prioritize the most relevant parts of input sequences. By dynamically weighting temporal features, attention improves both predictive accuracy and interpretability, two aspects essential for operational adoption in energy systems. For example, Marulanda et al. [23] developed an LSTM-attention framework combined with seasonal decomposition and normalization techniques for the Spanish electricity market, showing substantial improvements over baseline DL models. Similarly, the AMC-LSTM model introduced by [24] demonstrated that incorporating attention layers enhances accuracy and provides interpretability benefits, which are increasingly valued in the decision-making processes of system operators. In addition, Belletreche et al. [25] proposed a hybrid Conv-Dual Attention LSTM (Conv-DA-LSTM) tailored for desert regions, which achieved high predictive accuracy and outperformed traditional models, underscoring the adaptability of attention-based approaches to challenging environments.

Beyond attention-augmented recurrent architectures, recent advances in sequence modeling have led to the application of Transformer-based models in wind forecasting. Originally developed for natural language processing, Transformers leverage self-attention to capture long-range dependencies, making them particularly suited to the nonlinear and multi-scale temporal patterns of wind generation data. Several studies have confirmed their effectiveness when using high-frequency meteorological variables, such as wind speed and direction at multiple altitudes, temperature, and atmospheric pressure, together with historical power output [11]. The Powerformer model, for instance, adapts the Transformer framework to wind forecasting, achieving competitive performance by enriching feature representations with turbine-level data. However, reliance on fine-grained exogenous variables often limits the operational applicability of these approaches. A recent comprehensive review by [26] reinforces these developments, highlighting the advantages of attention-based and Transformer models in handling long-range temporal dependencies, while also identifying open challenges such as data availability, interpretability, and the computational costs of large-scale implementations. In contrast, the present study addresses this gap by developing a streamlined Transformer-based forecasting framework trained on historical wind power generation aggregated at the national level. This methodology reflects realistic data availability in many power systems, where turbine-level or high-frequency meteorological data may not be accessible, and aims to provide an efficient and scalable solution that supports the sustainable integration of wind energy into modern smart grids.

3. Self-Attention and Transformer Models in Time Series Prediction

The Transformer architecture is a sequence modeling framework that eliminates the need for recurrence and convolution, relying exclusively on self-attention mechanisms to capture contextual dependencies. This design allows the model to effectively learn relationships between all elements within a sequence, independent of their position, and has proven highly scalable and effective across a wide range of sequence prediction tasks [27].

Formally, let $\mathbf{X}\in {\mathbb{R}}^{T\times d}$ denote an input sequence of length T, where each element is represented by a d-dimensional feature vector [28]. To compute self-attention, the input sequence is linearly projected into three distinct representations: the query matrix $\mathbf{Q}$, the key matrix $\mathbf{K}$, and the value matrix $\mathbf{V}$.

$$\mathbf{Q}=\mathbf{X}{\mathbf{W}}^Q,\mathbf{K}=\mathbf{X}{\mathbf{W}}^K,\mathbf{V}=\mathbf{X}{\mathbf{W}}^V,$$

(1)

where ${\mathbf{W}}^Q,{\mathbf{W}}^K,{\mathbf{W}}^V\in {\mathbb{R}}^{d\times d_k}$ are trainable parameters, and $d_k$ is the latent dimension. Scaled dot-product attention is then defined as follows:

$$\mathrm{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{softmax}\left({\displaystyle \frac{\mathbf{Q}{\mathbf{K}}^{\top }}{\sqrt{d_k}}}\right)\mathbf{V}.$$

(2)

This operation produces a weighted combination of the values, where weights reflect the learned relevance of each position in the sequence. The result is projected back into the original feature space:

$$\mathbf{Z}=\mathrm{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V}){\mathbf{W}}^O,$$

(3)

with ${\mathbf{W}}^O\in {\mathbb{R}}^{d_k\times d}$. This allows residual connections and normalization to be applied in subsequent layers. To further enrich the model’s representational capacity, the Transformer introduces the multi-head attention mechanism. In this case, instead of computing a single attention operation, the model projects the input into multiple subspaces and performs self-attention independently in each [29]. Specifically, for h attention heads, the input is transformed using h distinct sets of projection matrices:

$${\mathrm{head}}_i=\mathrm{Attention}(\mathbf{X}{\mathbf{W}}_i^Q,\mathbf{X}{\mathbf{W}}_i^K,\mathbf{X}{\mathbf{W}}_i^V),i=1,\dots ,h,$$

(4)

where each ${\mathbf{W}}_i^Q,{\mathbf{W}}_i^K,{\mathbf{W}}_i^V\in {\mathbb{R}}^{d\times d_k}$, with $d_k=d/h$. These heads capture different types of dependencies across the sequence. The outputs of all heads are then concatenated and linearly transformed:

$$\mathrm{MultiHead}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h){\mathbf{W}}^O,$$

(5)

where ${\mathbf{W}}^O\in {\mathbb{R}}^{d\times d}$ is another learnable matrix. This structure enables the model to jointly attend to information from diverse representation subspaces at different positions, increasing the expressiveness and flexibility of the attention mechanism without increasing its computational complexity. The use of multi-head attention has proven to capture complex, long-range patterns in sequences, particularly in tasks such as time series forecasting where both short-term fluctuations and long-term trends coexist [30].

For the present study, which focuses on single-step forecasting, only the encoder stack of the Transformer is employed. Each encoder layer consists of multi-head self-attention followed by a position-wise feed-forward network:

$$\mathbf{Z}=\mathrm{LayerNorm}\left(\mathbf{X}+\mathrm{MultiHead}(\mathbf{Q},\mathbf{K},\mathbf{V})\right),$$

(6)

$${\mathbf{X}}^{\prime }=\mathrm{LayerNorm}\left(\mathbf{Z}+\mathrm{FFN}\left(\mathbf{Z}\right)\right),$$

(7)

where $\mathrm{FFN}(·)$ is a two-layer feed-forward network with ReLU activation:

$$\mathrm{FFN}\left(\mathbf{z}\right)=max(0,\mathbf{z}{\mathbf{W}}_1+{\mathbf{b}}_1){\mathbf{W}}_2+{\mathbf{b}}_2.$$

(8)

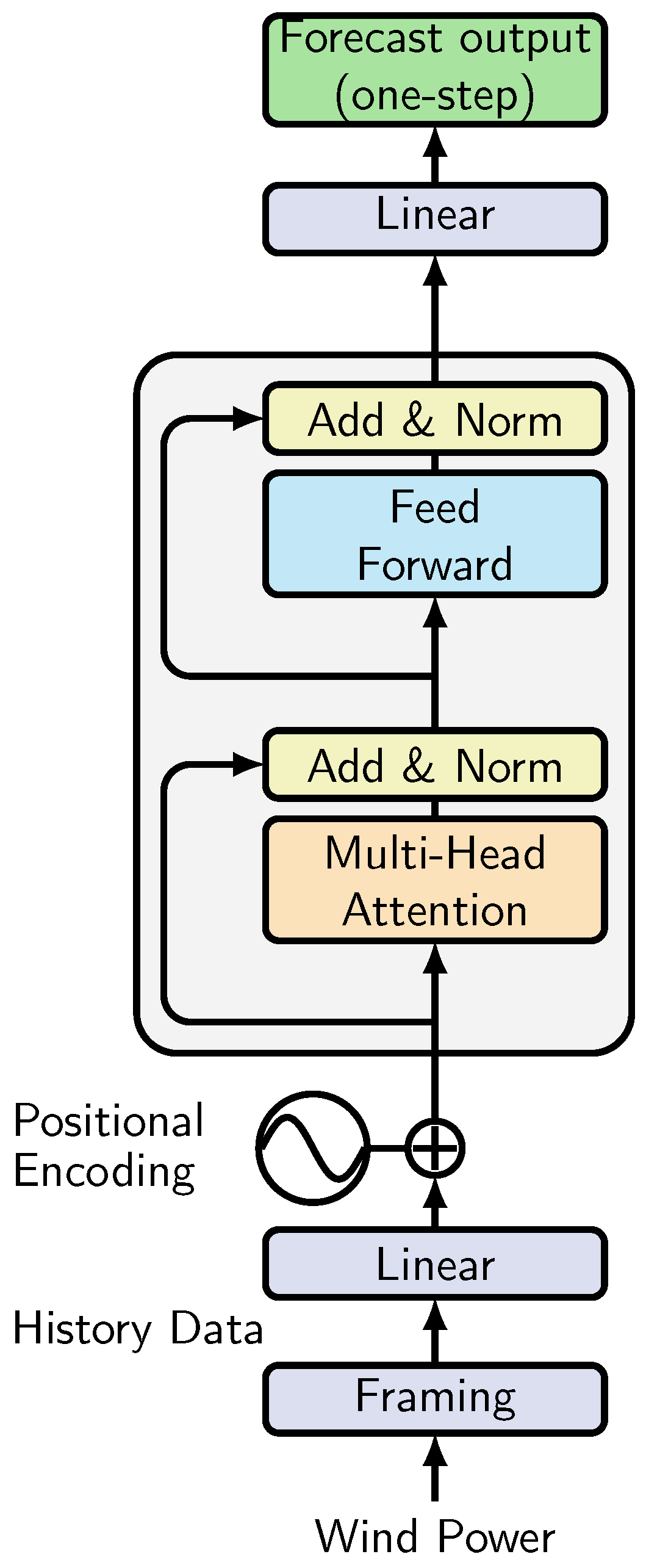
The final encoder output is aggregated and passed through a linear projection layer to produce the next value ${\widehat{y}}_{t+1}$. Unlike multi-step autoregressive decoding, this formulation avoids the need for a decoder with masked attention, reducing parameters and computation while aligning with the single-step prediction objective. The architecture adopted in this study, illustrated in Figure 1, is an encoder-only Transformer tailored for short-term wind power forecasting. By relying on self-attention, the model captures both short-term fluctuations and long-range temporal dependencies within the input window. Unlike language models, no sequence tokens (e.g., start-of-sequence or end-of-sequence markers) are required, since the task involves continuous numerical values. The representation of the historical window is directly mapped through a linear output layer to forecast the next observation, which simplifies the design while preserving the ability to model complex temporal patterns.

4. Methodological Framework for Transformer-Based Wind Power Forecasting

This section presents the methodological framework adopted to forecast wind power generation using a Transformer-based DL approach. The process is structured into four main components: data acquisition and preprocessing, formal definition of the forecasting problem, specification of the Transformer model architecture, and evaluation of predictive performance. Each component is designed to ensure temporal consistency and compatibility with the characteristics of time series forecasting. The aim is to provide a reproducible pipeline that allows for an objective comparison between the Transformer model and conventional DL baselines, such as LSTM and GRU networks. The following subsections detail the procedures and decisions adopted at each stage of the methodology.

4.1. Data Source and Preprocessing

The initial phase of the analysis involved the preparation of the historical wind power generation dataset. Raw data were obtained from the ENTSO-E, covering hourly records for Spain over the period from January 2020 to December 2024 [31]. These records were consolidated into a single, chronologically ordered time series to ensure temporal continuity and facilitate downstream analysis. Special attention was paid to maintaining uniform temporal granularity throughout the series. During inspection, it was observed that variations in data frequency emerged at specific intervals, potentially due to internal updates in the data provider’s reporting mechanisms. To ensure consistency with the majority of the dataset and compatibility with the Transformer-based forecasting framework, temporal harmonization procedures were applied. This included aligning all records to an hourly resolution. Furthermore, data integrity checks were implemented to identify and correct structural issues, such as duplicated or misaligned timestamps.

Missing values were also addressed during this stage. Anomalies were identified in correspondence with systemic calendar transitions, particularly daylight saving time changes, where certain hours were absent due to official time shifts. These gaps were not the result of sensor or transmission failures but instead stemmed from temporal discontinuities imposed by the civil time system. To preserve the temporal structure of the dataset and enable uninterrupted input sequences for model training, missing values were imputed using linear interpolation. This method provides a simple yet effective solution for estimating missing values based on their immediate temporal context, ensuring a smooth transition between known observations without introducing abrupt fluctuations. Following data preparation, an exploratory analysis was conducted to characterize the statistical properties and temporal dynamics of the wind power generation series.

4.2. Problem Formulation

The objective of this study is to forecast wind power generation using a univariate time series model based exclusively on historical values. Let ${\left\{y_t\right\}}_{t=1}^T$ denote the time series of observed wind power generation, sampled at hourly intervals. At each time step t, the model receives a fixed-length window of L past observations ${\mathbf{y}}_{t-L+1:t}=\{y_{t-L+1},\dots ,y_t\}$ and produces a prediction ${\widehat{y}}_{t+1}$ for the next time step:

$${\widehat{y}}_{t+1}=f_{\theta }\left({\mathbf{y}}_{t-L+1:t}\right)$$

(9)

where $f_{\theta }(·)$ is a nonlinear mapping function parameterized by $\theta$, implemented using a Transformer-based neural network. This single-step ahead forecast formulation is particularly relevant for real-time grid operation and energy dispatch scenarios, where accurate short-term predictions are required. Unlike multi-step forecasting approaches that propagate errors across horizons, this formulation avoids compounding uncertainty and allows for more stable model evaluation. It also enables the assessment of the model’s ability to capture short-term temporal dependencies, which is relevant for highly volatile processes such as wind power generation. The design leverages the Transformer’s self-attention mechanism to capture both local fluctuations and long-range patterns within the historical window, without relying on auxiliary or exogenous variables. In this study, the forecasting task is explicitly framed as a one-step ahead prediction problem on hourly data. The dataset was partitioned chronologically, with 70% of the data allocated to training, 15% reserved for validation, and the remaining 15% held out for testing. Standardization parameters for z-score normalization were computed exclusively on the training split and applied consistently across validation and test sets to preserve temporal consistency and avoid information leakage. Sliding windows were constructed independently within each split to ensure that no input–output pair crossed data boundaries.

4.3. Transformer Model Architecture

Following the theoretical foundations of the Transformer described in Section 3, the model was adapted to the task of one-step-ahead wind-power forecasting. The hourly time series was segmented into fixed-length windows (input length L) using a sliding window approach; each subsequence of length $L\in 12,24,36$ was employed to predict the immediate next observation. The dataset was partitioned chronologically into 70%/15%/15% splits for training, validation, and testing, respectively. Standardization parameters for z-score normalization (mean and standard deviation) were computed exclusively on the training split and subsequently applied to the validation and test sets. Sliding windows were constructed independently within each split to ensure that no input–output pair crossed the boundaries between training, validation, and testing.

The encoder-only Transformer architecture was implemented with an input projection, sinusoidal positional encoding, and a stack of $N\in 2,3$ encoder layers. Each encoder layer applied multi-head attention with $H\in 2,4,8$ heads and model dimension $d_{\mathrm{model}}\in 16,32,64$, with dropout rates of $0.1,0.2,0.3$ and batch sizes of $16,32,64$. Training was carried out using the Adam optimizer with a learning rate of ${10}^{-3}$ and mean squared error (MSE) loss [32,33]. Early stopping was applied on the validation loss with a patience of five epochs and a minimum improvement threshold of ${10}^{-4}$. Randomness was controlled by fixing the seed at 42, and all tensors were represented in torch.float32. All experiments were executed on CPU. The runs were performed on an Apple Silicon system (macOS/Darwin 23.4.0, ARM64, 14 physical cores / 14 logical threads, 36 GB RAM). All models were implemented in Python 3.11.7 (Python Software Foundation, Wilmington, DE, USA), using PyTorch 2.2.2 (Meta AI, Menlo Park, CA, USA) for deep learning, NumPy 1.26.4 and Pandas 2.3.2 for data processing, Scikit-learn 1.7.0 for auxiliary ML procedures, and Matplotlib 3.8.0 for visualization (all open-source).

4.4. Evaluation Metrics

To evaluate the performance of the proposed Transformer-based forecasting model, a comparative analysis is conducted against two widely used DL baselines: LSTM and GRU networks. These models are known for their ability to capture temporal dependencies and non-linear relationships in sequential data and have been extensively applied in wind power forecasting tasks. However, their reliance on sequential processing limits their efficiency in capturing long-range dependencies, particularly for extended input sequences [34]. In contrast, the Transformer architecture leverages self-attention mechanisms to model global dependencies in parallel, making it a compelling alternative for time series prediction. As a benchmark, a naïve baseline with a lag of 1 h (${\widehat{y}}^{\mathrm{naive}}t=yt-1$) was included, computed on the same aligned indices as the model predictions. This baseline provides a simple yet informative lower bound for assessing the added value of more complex forecasting models.

To objectively assess the predictive performance and generalization ability of the models, three standard error metrics are employed: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE). These metrics provide complementary perspectives on forecast accuracy, MAE offers a direct measure of average error magnitude, RMSE penalizes larger deviations more heavily, and MAPE evaluates relative error as a percentage of actual values. The MAE quantifies the average absolute difference between the predicted values ${\widehat{y}}_t$ and the actual observations $y_t$ and is computed as follows [35]:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{t=1}^n|{\widehat{y}}_t-y_t|.$$

(10)

The RMSE, which emphasizes larger errors due to the squaring operation, is defined as [36,37]:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{t=1}^n{({\widehat{y}}_t-y_t)}^2}.$$

(11)

Lastly, the MAPE expresses the forecast error as a percentage of the actual value, offering a scale-independent metric for evaluation [37,38]:

$$\mathrm{MAPE}={\displaystyle \frac{100\%}{n}}\sum _{t=1}^n\left|{\displaystyle \frac{y_t-{\widehat{y}}_t}{y_t}}\right|.$$

(12)

In addition to these three standard metrics, further indicators are incorporated to capture the final and relative and normalized performance. The normalized RMSE (nRMSE) expresses the RMSE as a percentage of the mean of the actual values, thus contextualizing the magnitude of the error with respect to the average generation level [39]:

$$\mathrm{nRMSE}={\displaystyle \frac{\mathrm{RMSE}}{\overline{y}}}\times 100,$$

(13)

where $\overline{y}$ denotes the mean of the actual values. The Mean Absolute Scaled Error (MASE) evaluates forecast accuracy relative to the 1 h naïve baseline, providing a scale-free comparison across models [40]:

$$\mathrm{MASE}={\displaystyle \frac{\mathrm{MAE}}{\frac{1}{n-1}{\sum }_{t=2}^n|y_t-y_{t-1}|}}.$$

(14)

Finally, the symmetric Mean Absolute Percentage Error (sMAPE) addresses the asymmetry of MAPE by normalizing forecast errors with respect to the average of predicted and actual values [41]:

$$\mathrm{sMAPE}={\displaystyle \frac{100\%}{n}}\sum _{t=1}^n{\displaystyle \frac{2|{\widehat{y}}_t-y_t|}{|{\widehat{y}}_t| + |y_t|}}.$$

(15)

5. Experimental Results

Before implementing the forecasting models, an exploratory analysis was conducted to characterize the statistical properties and temporal dynamics of wind power generation in Spain. The resulting dataset, composed of 43,848 hourly records spanning five years, is presented in

Table 1. Descriptive statistics of hourly wind power generation (in MW).

Statistic	Value
Count	43,848
Mean	6661.10
Standard Deviation	3867.57
Minimum	196
25th Percentile	3587.44
Median (50%)	5943
75th Percentile	9119
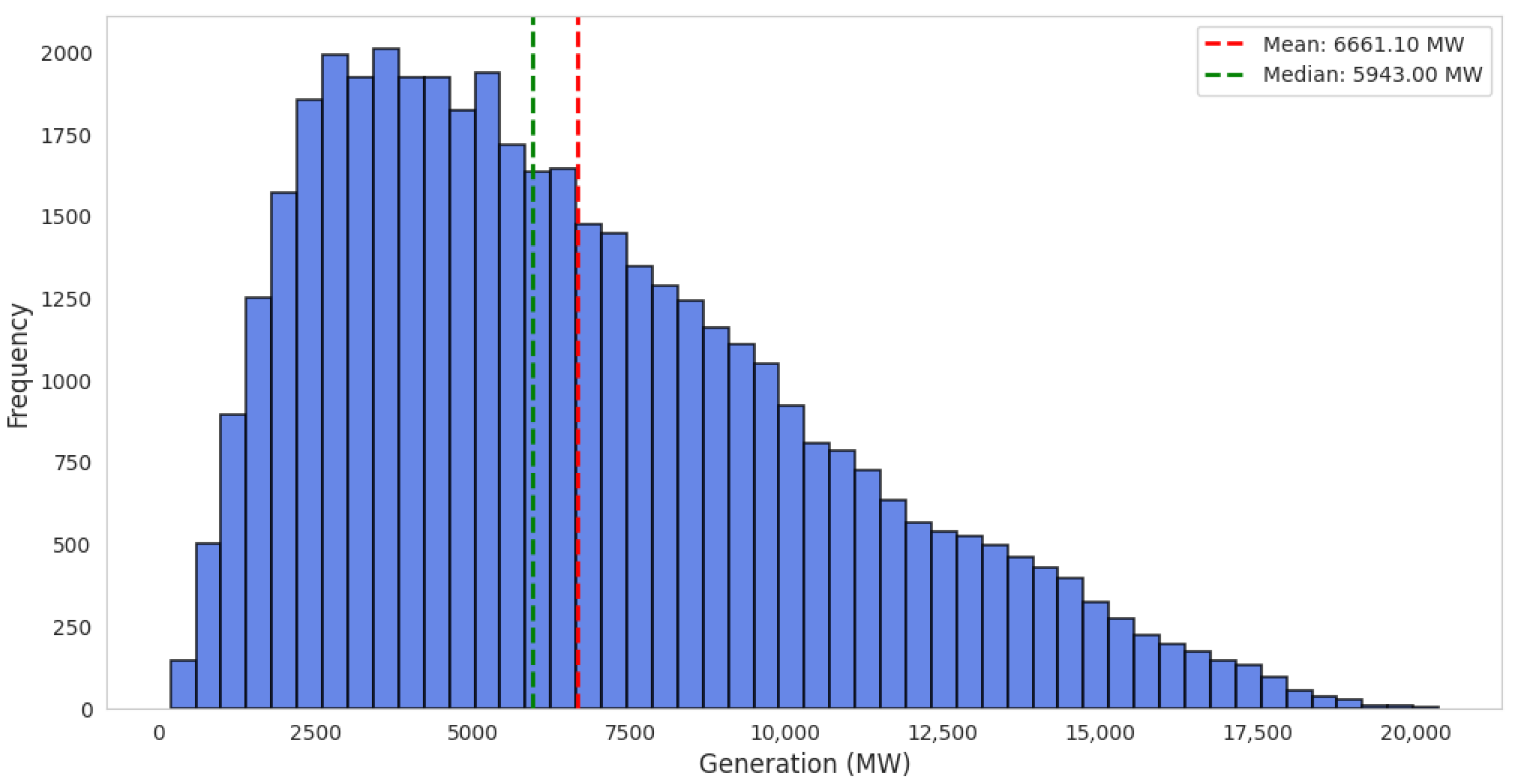
Maximum	20,321

. The average generation is approximately 6661 MW, with a standard deviation of 3867 MW, indicating substantial variability in wind power output. The distribution is positively skewed, as evidenced by the higher mean compared to the median (5943 MW), and values range from a minimum of 196 MW to a maximum of 20,321 MW. Figure 2 provides a histogram of wind power generation frequencies, further illustrating the right-skewed nature of the data. Most observations fall within the range of 2000 to 8000 MW, while extreme values are less frequent but relevant for understanding the volatility of the series.

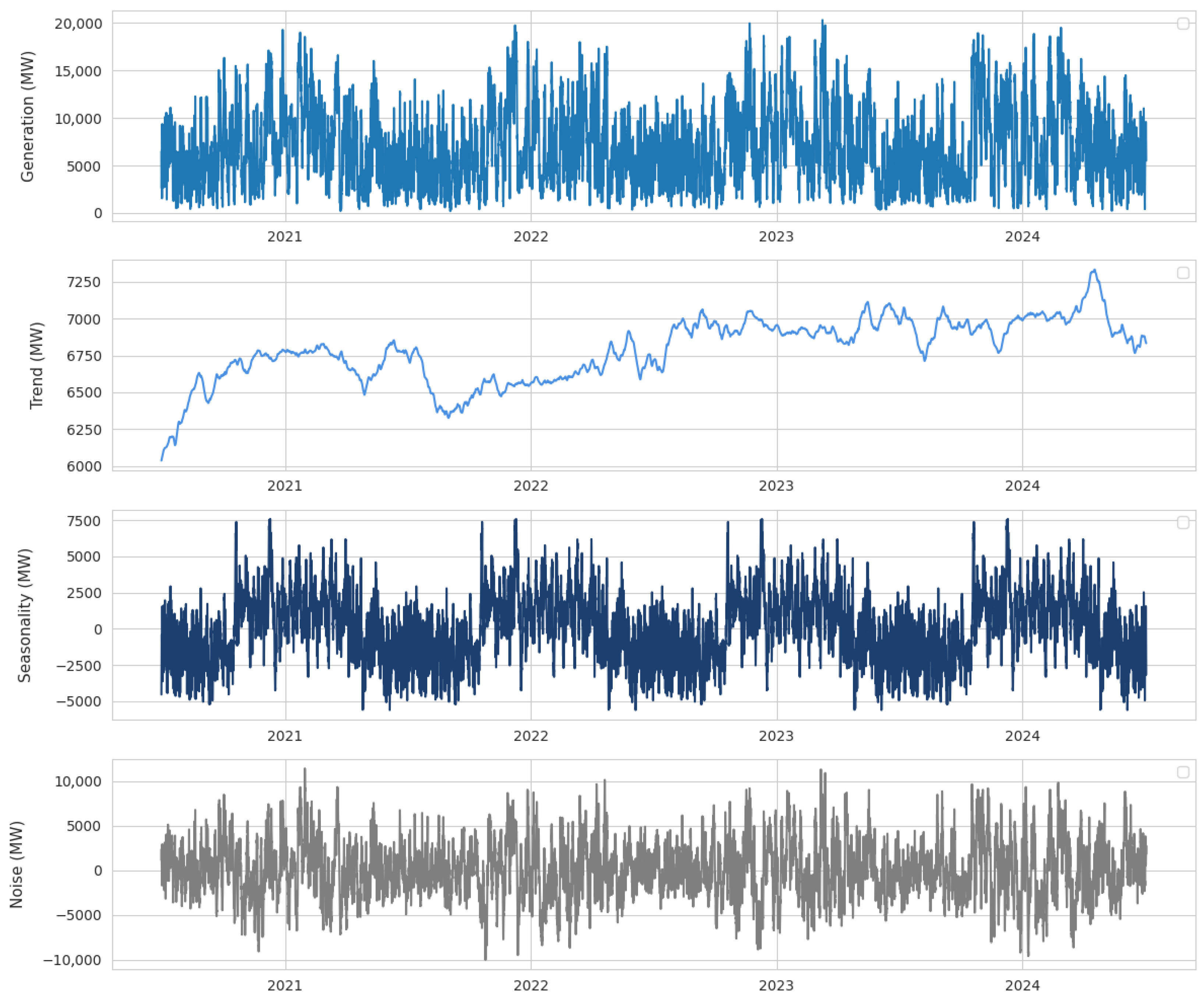
To gain deeper insights into the temporal structure of the series, Figure 3 presents a classical additive decomposition into trend, seasonal, and residual components, with an annual cycle specified on hourly data. The trend component shows a progressive increase in wind power generation over the years, reflecting broader structural changes in the energy mix. The seasonal component highlights recurrent annual cycles, indicating systematic variability linked to meteorological conditions. At the same time, the residual component captures high-frequency fluctuations and abrupt changes, pointing to short-term dependencies that characterize the volatility of wind generation. Together, these patterns confirm that the series exhibits both short-term and long-term dependencies, thereby justifying the adoption of a Transformer-based architecture capable of capturing temporal dynamics across multiple scales.

As described in Section 4, the forecasting pipeline was implemented by restructuring the hourly time series into overlapping input–output pairs using a sliding-window mechanism, thereby enabling temporal dependencies to be learned from fixed-length historical sequences. To preserve temporal consistency and prevent information leakage, the dataset was partitioned chronologically into training (70%), validation (15%), and testing (15%) subsets. Standardization was performed through z-score normalization, with mean and standard deviation computed exclusively on the training set and subsequently applied to validation and test data to ensure consistency. To investigate RQ2, the effect of input resolution and architectural choices on predictive accuracy, three sequence lengths (12, 24, and 36 h) were evaluated. For each forecasting horizon, the Transformer was trained across a grid of hyperparameter settings, including model dimensionality, number of attention heads, encoder depth, dropout rate, and batch size (see Section 4.3). Standard error metrics were employed to evaluate all configurations, and for each horizon (12 h, 24 h, and 36 h), the model with the lowest RMSE on the test set was selected as the best-performing configuration. While RMSE guided this selection due to its sensitivity to large deviations, the final benchmarking and comparative analysis also report complementary metrics, ensuring a comprehensive assessment of predictive accuracy across models. The results corresponding to the 12 h input configuration, where half-daily historical observations were employed to predict the subsequent value are presented first, with the five best-performing Transformer models on the test set reported in

Table 2. Top 5 Transformer models for 12 h input sequence, ranked by test RMSE. Metrics are reported for the train, validation, and test sets. The model highlighted in grey corresponds to the best performance on the test set in terms of RMSE.

Dim	Heads	Layers	Dropout	Batch	Set	RMSE	MAE	MAPE
16	2	3	0.1	16	Train	336.73	244.31	4.70
					Val	360.16	254.40	4.41
					Test	380.62	267.61	5.18
16	4	2	0.1	16	Train	337.41	245.25	4.77
					Val	361.26	255.71	4.50
					Test	380.92	268.71	5.23
32	4	3	0.1	16	Train	337.90	246.04	4.80
					Val	361.40	256.19	4.52
					Test	381.10	268.21	5.24
16	4	3	0.1	16	Train	337.43	244.50	4.68
					Val	361.24	254.35	4.38
					Test	381.56	267.79	5.17
32	4	3	0.1	32	Train	341.57	248.27	4.76
					Val	364.12	257.55	4.46
					Test	381.85	270.16	5.27

.

Among the evaluated configurations for the 12 h input horizon, the top-performing Transformer models achieved test RMSE values in the range of 380–382 MW, with corresponding MAE values between 267 and 270 MW and MAPE below 5.3%. The best-ranked configuration (Dim = 16, heads = 2, layers = 3, dropout = 0.1, and batch = 16) attained a test RMSE of 380.62 MW, with validation and training RMSE values of 360.16 MW and 336.73 MW, respectively. This relatively narrow gap across splits indicates stable generalization and limited overfitting. Other high-performing configurations, such as those with Dim = 32 and four attention heads, yielded comparable results, reinforcing that model capacity beyond a certain threshold does not necessarily translate into improved accuracy. Instead, consistent patterns emerged across the top-ranked models: dropout rates of 0.1, batch sizes of 16 or 32, and encoder depths of two to three layers. These findings suggest that moderate regularization and architectural depth are sufficient to achieve robust performance under the 12 h horizon. Importantly, increasing the number of attention heads did not produce systematic gains, indicating that additional attention diversity offers limited benefits for relatively short input sequences.

Following the analysis of the 12 h input configuration, the performance of Transformer models trained with a 24 h sequence length was subsequently examined. This setting allows the model to incorporate a full day of historical wind power generation when predicting the subsequent value, thereby potentially capturing daily periodicities and longer-term dependencies that shorter windows may overlook.

Table 3. Top 5 Transformer models for 24 h input sequence, ranked by test RMSE. Metrics are reported for the train, validation, and test sets. The model highlighted in grey corresponds to the best performance on the test set in terms of RMSE.

Dim	Heads	Layers	Dropout	Batch	Set	RMSE	MAE	MAPE
16	2	3	0.1	32	Train	334.24	242.49	4.66
					Val	360.05	253.97	4.39
					Test	375.75	263.02	5.08
16	4	3	0.1	32	Train	334.29	242.86	4.72
					Val	359.04	253.99	4.46
					Test	375.90	263.01	5.11
32	4	2	0.2	32	Train	338.03	245.95	4.75
					Val	361.82	256.63	4.49
					Test	376.74	264.82	5.14
32	4	2	0.1	32	Train	332.12	240.25	4.60
					Val	357.04	251.49	4.33
					Test	377.14	261.20	5.01
32	4	3	0.1	16	Train	335.55	245.06	4.80
					Val	359.88	256.51	4.56
					Test	377.29	264.31	5.20

presents the performance of the five best-performing configurations under this new temporal scope. As in the 12 h setup, each model reflects a distinct combination of the architectural hyperparameters introduced in Section 4.3, including dimensionality, number of attention heads, encoder depth, dropout rate, and batch size. This selection allows for a focused comparison of the most accurate configurations under the 24 h input scenario.

Among the tested configurations, the best performance for the 24 h input horizon was achieved by the model with a dimensionality of 16, two attention heads, three encoder layers, a dropout rate of 0.1, and a batch size of 32. This configuration yielded a test RMSE of 375.75, MAE of 263.02, and MAPE of 5.08, while also exhibiting balanced results across training and validation, thus indicating effective generalization. The remaining top-performing models followed a consistent pattern, relying on relatively compact architectures with either 16 or 32 dimensions, two to three encoder layers, and predominantly a dropout rate of 0.1. In terms of batch size, while the 12 h horizon favored configurations with 16, the 24 h setting showed a preference for 32, suggesting that slightly larger batches contribute to more stable training dynamics when longer input sequences are used. Interestingly, as in the 12 h horizon, the number of attention heads did not show a clear performance advantage beyond two or four, suggesting that increasing attention diversity does not necessarily translate into improved accuracy for short- to medium-range horizons.

Finally, the evaluation of Transformer models trained with a 36 h input sequence is presented in

Table 4. Top 5 Transformer models for 36 h input sequence, ranked by test RMSE. Metrics are reported for the train, validation, and test sets. The model highlighted in grey corresponds to the best performance on the test set in terms of RMSE.

Dim	Heads	Layers	Dropout	Batch	Set	RMSE	MAE	MAPE
32	4	2	0.1	16	Train	331.52	240.88	4.64
					Val	354.91	251.12	4.35
					Test	370.71	258.77	4.92
32	4	3	0.2	16	Train	333.74	243.08	4.73
					Val	357.74	253.73	4.45
					Test	372.49	261.47	5.12
32	2	2	0.1	16	Train	330.67	239.73	4.58
					Val	355.32	251.03	4.29
					Test	373.36	261.64	5.02
16	4	3	0.2	32	Train	333.39	242.43	4.71
					Val	357.29	253.26	4.45
					Test	374.64	262.39	5.12
32	2	2	0.1	32	Train	332.79	242.06	4.66
					Val	358.04	254.44	4.43
					Test	374.69	264.94	5.17

. This configuration provides the model with an extended temporal context, allowing the learning of broader temporal dependencies and delayed effects in wind generation patterns. However, longer input sequences may also introduce noise or redundant information, increasing the risk of overfitting if not adequately regularized. Therefore, assessing the performance under this extended horizon is relevant to determine whether the additional historical context leads to tangible improvements or diminishing returns compared to shorter input lengths. As in the previous cases, the top five performing configurations under this setting were identified and analyzed based on their predictive accuracy on the test set.

Among the 36 h input configurations, the best predictive performance was achieved by the model with a dimensionality of 32, four attention heads, two encoder layers, a dropout rate of 0.1, and a batch size of 16. This model reached an RMSE of 370.71, MAE of 258.77, and MAPE of 4.92% on the test set. Notably, the gap between training and test performance (RMSE: 331.52 vs. 371.71) remained narrow, indicating effective generalization and limited overfitting. Compared to the 12 h configuration, where smaller dimensionality (16) was generally favored, the results for the 36 h horizon suggest that larger model dimensionality (32) becomes beneficial when capturing longer temporal dependencies. Across the top-performing models, relatively shallow architectures with two encoder layers predominated, indicating that greater depth does not necessarily improve performance in extended horizons. Dropout values of 0.1 were consistently observed, highlighting the importance of regularization as the sequence length increases. Furthermore, smaller batch sizes (mostly 16) continued to be preferred, reinforcing the observation that reduced batch regimes promote stable convergence across horizons. In addition to its predictive accuracy, this configuration also demonstrated strong computational efficiency. Although the training schedule allowed for a maximum of 50 epochs, convergence was reached after only 11 epochs due to the application of early stopping, resulting in a total training time of 439.10 s, with a median epoch duration of 40.02 s. From a deployment perspective, the model further exhibited low-latency suitability, achieving an average inference time of 3.698 ms (p95 = 4.768 ms) when evaluated on batches of 16 sequences of length 36. These results show not only the accuracy of the architecture under extended input horizons but also its ability to achieve rapid convergence and efficient inference, reinforcing its practical viability for real-world forecasting applications.

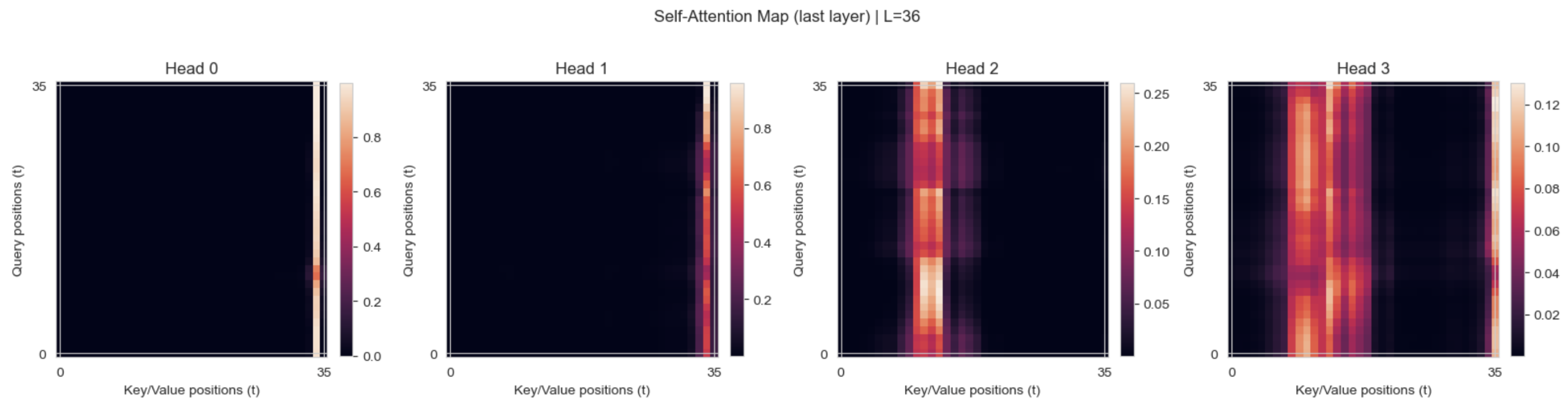
Importantly, the attention maps for the 36 h horizon revealed that most heads concentrated their weights on the most recent hours, highlighting the dominant role of short-term dynamics in wind power variability. Nevertheless, certain heads distributed attention more broadly across intermediate and even earlier positions within the input window, suggesting that the model simultaneously captured longer-range dependencies. This division of roles across attention heads indicates a complementary mechanism in which recent fluctuations are emphasized while broader temporal patterns are also considered (see Figure 4). Consequently, the 36 h input horizon demonstrated that extended context lengths enable the Transformer to leverage both short- and long-term information.

Complementary error stratification further validated the robustness of the 36 h configuration. As reported in

Table 5. Mean absolute ramp error across different horizons.

Horizon ($\mathbf{\Delta }\mathit{h}$)	N	MAE Ramp (MW)
1 h	6541	356.01
3 h	6539	363.05
6 h	6536	377.24

, mean absolute ramp errors increased moderately with the ramp horizon, from 356 MW at $\mathrm{\Delta }$1 h to 377 MW at $\mathrm{\Delta }$6 h. This progression indicates that, although absolute ramp prediction errors rise with longer intervals, the growth remains limited, which highlights that the model preserves a reasonable capacity to adapt to temporal ramps of larger magnitude. Under extreme conditions (

Table 6. Error metrics for strong ramps (|$\mathrm{\Delta }y$| > p90) and peak generation events ($y>p95$).

Event	Horizon ($\mathbf{\Delta }\mathit{h}$)	MAE (MW)	RMSE (MW)
Strong ramps	1 h	678.95	798.37
	3 h	383.92	511.27
	6 h	330.01	452.92
Peaks	–	375.81	525.73

), the model exhibited higher errors, particularly for strong ramps ($\left|\mathrm{\Delta }y\right|>p90$). The largest deviations occurred at short horizons ($\mathrm{\Delta }$1 h, MAE = 679 MW), reflecting the challenge of anticipating abrupt fluctuations. At longer horizons ($\mathrm{\Delta }$3 h and $\mathrm{\Delta }$6 h), both MAE and RMSE declined, showing that broader aggregation intervals mitigate the impact of short-term variability. Regarding peak generation events ($y>p95$), errors remained substantial (MAE = 376 MW, RMSE = 526 MW), confirming the intrinsic difficulty of accurately forecasting rare and highly volatile extreme values.

To establish a robust benchmark against the Transformer-based architectures, complementary experiments were conducted using recurrent neural networks, specifically LSTM and GRU models. Both architectures were implemented with a comparable design, consisting of stacked recurrent layers, followed by a fully connected output layer to produce point forecasts. The evaluation protocol was kept identical to that of the Transformer experiments: chronological data partitioning (70% training, 15% validation, and 15% testing); z-score normalization based exclusively on the training set; and input sequence lengths of 12, 24, and 36 h. Model selection was carried out through an exhaustive grid search across key hyperparameters, including the number of hidden units (16, 32, and 64), the number of recurrent layers (1, 2, and 3), dropout regularization levels (0.1, 0.2, and 0.3), and batch sizes (16, 32, and 64). Training was performed using the Adam optimizer with a learning rate of ${10}^{-3}$, and early stopping was applied on the validation loss with a patience of five epochs and a minimum improvement threshold of ${10}^{-4}$. This procedure ensured that model complexity, convergence dynamics, and generalization ability were systematically evaluated under conditions directly comparable to those of the Transformer models.

Table 7. Comparison of the best Transformer (36 h), LSTM, and GRU models across different horizons. Only error metrics are reported, and architectures are summarized by main hyperparameters. The model highlighted in grey corresponds to the best performance on the test set in terms of RMSE.

Model	Horizon	Architecture (Summary)	RMSE	MAE	MAPE (%)	nRMSE (%)	MASE	sMAPE (%)
Transformer	36 h	Dim = 32, Heads = 4, Layers = 2, Dropout = 0.1, Batch = 16	370.71	258.77	4.92	5.92	0.68	4.85
LSTM	12 h	Hidden = 32, Layers = 2, Dropout = 0.1, Batch = 32	412.80	304.11	6.12	6.59	0.80	6.04
LSTM	24 h	Hidden = 32, Layers = 1, Dropout = 0.2, Batch = 16	406.69	299.34	6.05	6.49	0.79	5.93
LSTM	36 h	Hidden = 32, Layers = 1, Dropout = 0.3, Batch = 32	397.59	292.37	5.92	6.35	0.77	5.83
GRU	12 h	Hidden = 32, Layers = 2, Dropout = 0.2, Batch = 32	412.35	304.60	6.22	6.58	0.80	6.09
GRU	24 h	Hidden = 16, Layers = 2, Dropout = 0.1, Batch = 16	404.95	298.51	6.09	6.46	0.79	5.95
GRU	36 h	Hidden = 32, Layers = 1, Dropout = 0.1, Batch = 16	395.47	289.11	5.78	6.32	0.76	5.71

summarizes the best-performing configurations of the Transformer, LSTM, and GRU architectures across the three input horizons. The Transformer model, trained with a 36 h input sequence, consistently outperformed the recurrent baselines, achieving an RMSE of 370.71 MW, MAE of 258.77 MW, and MAPE of 4.92%. These values represent a substantial improvement over the naïve 1 h lag benchmark, whose MAE ranged between 378.08 and 378.39 MW depending on the window length, thus confirming the ability of the model to capture temporal dependencies beyond short-term persistence. For the recurrent models, the best LSTM configuration (36h, hidden = 32, layers = 1, dropout = 0.3) reached an RMSE of 397.59 MW and MAE of 292.37 MW, while the best GRU (36h, hidden = 32, layers = 1, dropout = 0.1) slightly outperformed the LSTM, with an RMSE of 395.47 MW and MAE of 289.11 MW. Although both models reduced errors relative to the naïve baseline, their performance lagged behind the Transformer in all error measures, particularly in MAE and sMAPE, where reductions were less pronounced. The comparison of normalized errors provides further insights. While the LSTM and GRU achieved nRMSE values around 6.3–6.5%, the Transformer reduced this figure to 5.92%. Similarly, sMAPE decreased from 5.71–6.09% in the recurrent networks to 4.85% in the Transformer. These differences, though moderate in relative terms, are significant in operational contexts where small percentage improvements translate into large absolute reductions in forecast error. Overall, the results support RQ1 by demonstrating that the Transformer architecture generalizes better across horizons, improving not only absolute accuracy (RMSE, MAE, and MAPE) but also scale-independent and relative metrics (nRMSE, MASE, and sMAPE). The recurrent baselines exhibited performance gains when provided with extended input windows (36 h). However, even under their best-performing configurations, they consistently lagged behind the Transformer, underscoring the latter’s superior capacity to capture long-range dependencies and complex temporal dynamics.

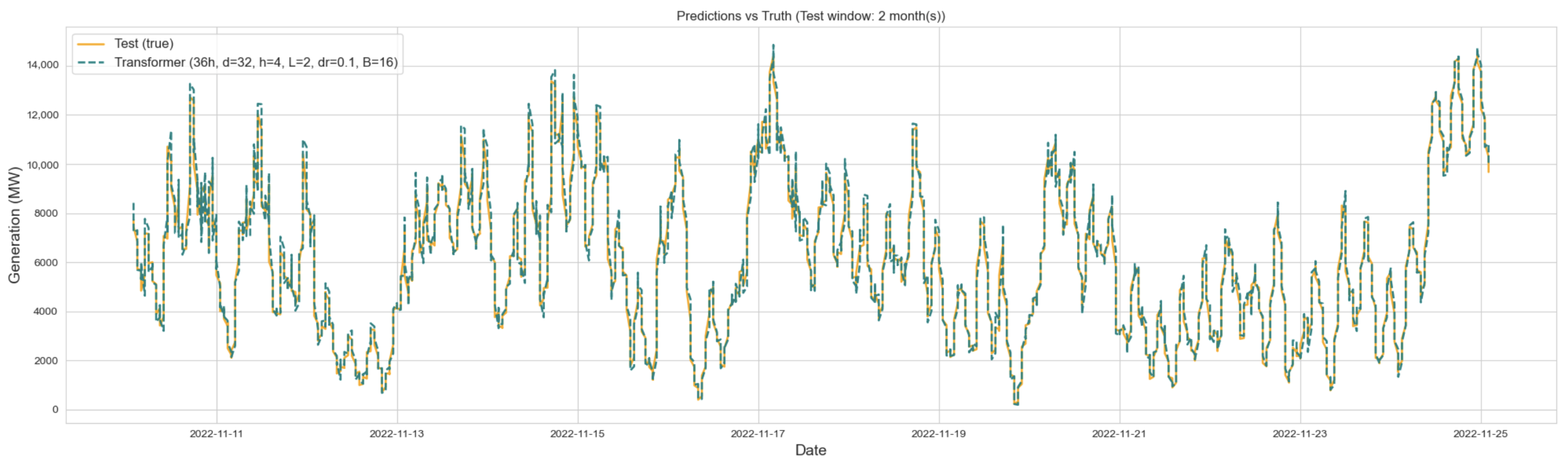
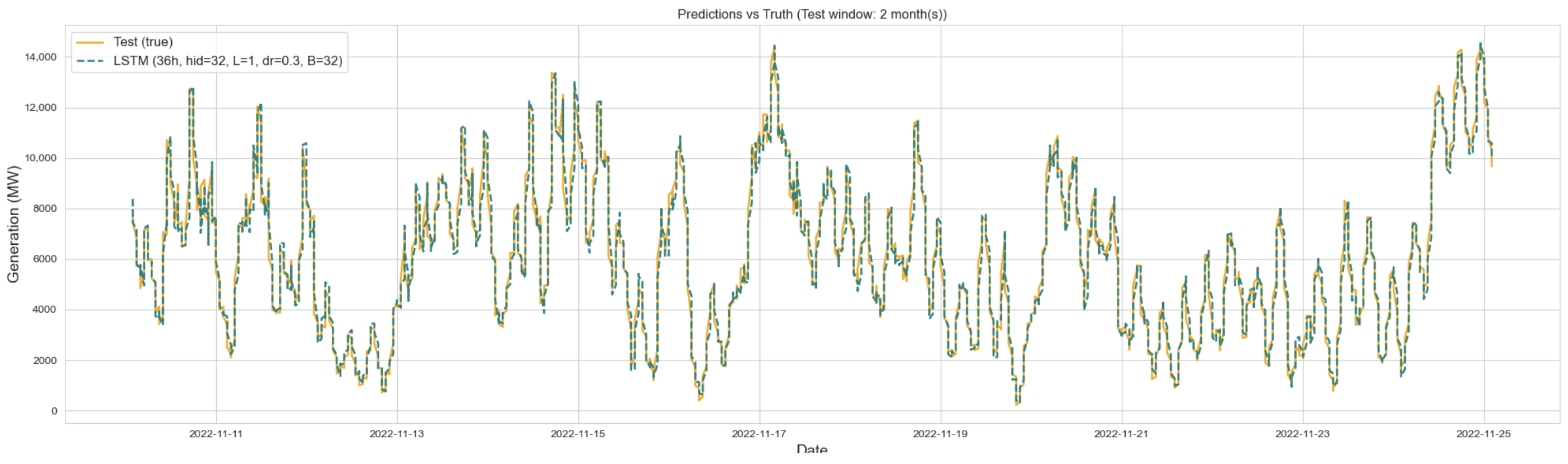
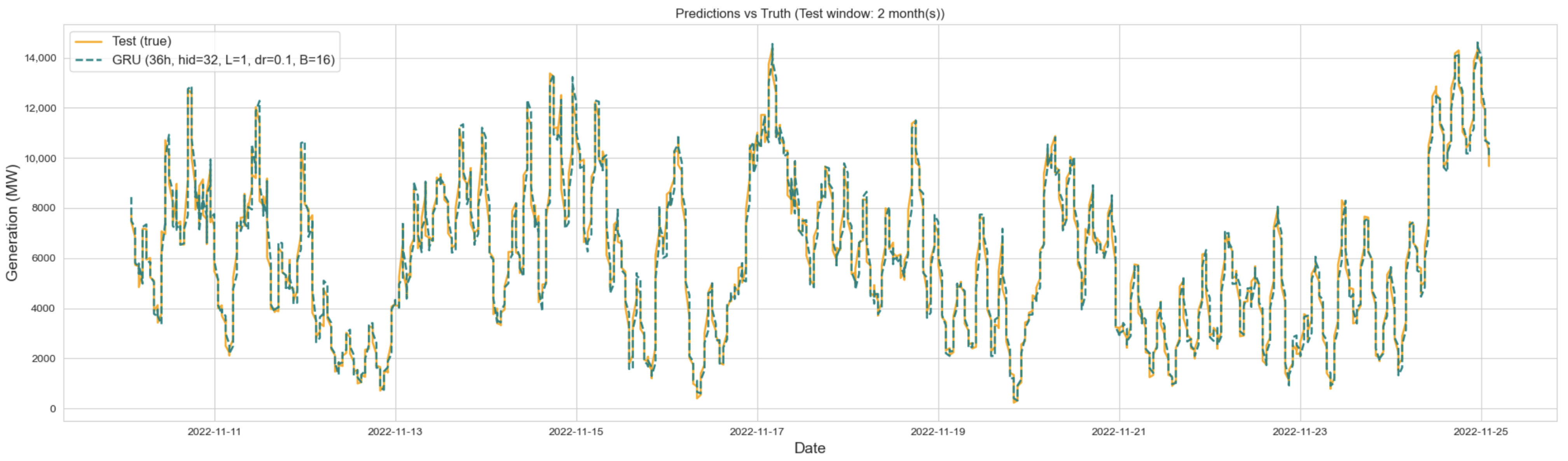
To complement the tabular results and provide further insight into model behavior, Figure 5, Figure 6 and Figure 7 illustrate the alignment between actual wind power generation and predictions from the best-performing configurations of Transformer, LSTM, and GRU over a two-month segment of the test set. The comparison highlights clear differences in the models’ ability to reproduce temporal variability, especially at peak values. The GRU model, while capable of capturing overall trends, systematically underpredicts sharp peaks and exhibits lagged responses to sudden ramps, which reflects the limitations of its simpler recurrent gating structure. In contrast, the LSTM model reacts more promptly to fluctuations and tracks moderate variations with reasonable accuracy. Nonetheless, its forecasts occasionally overshoot during rapid transitions, showing instability under highly volatile conditions. The Transformer model achieves the closest alignment with the ground truth across the full range of dynamics, successfully capturing both smooth transitions and abrupt surges in wind generation.

6. Discussion of Findings

The empirical results of this study demonstrate that Transformer-based architectures achieve superior predictive accuracy in short-term wind power forecasting compared to recurrent models. The best-performing configuration, trained with a 36 h input window and a compact architecture of two encoder layers, four attention heads, and moderate dropout (0.1), reached an RMSE of 370.71 MW, MAE of 258.77 MW, and MAPE of 4.92% on the test set. From a computational standpoint, the model converged efficiently, requiring only 11 epochs out of a maximum of 50 due to early stopping (total training time of 439.10 s and median epoch duration of 40.02 s), and exhibited low-latency suitability, with inference averaging 3.698 ms (p95 = 4.768 ms) for batches of 16 sequences. Attention maps showed that, while most heads concentrated on the most recent lags, others distributed weights across earlier positions, confirming that the Transformer simultaneously leverages short-term fluctuations and longer-range dependencies. These results show that performance gains do not stem from indiscriminate model complexity, but rather from balanced architectures with tuned hyperparameters that provide an advantageous trade-off between accuracy, and interpretability.

In contrast, the best LSTM and GRU models, both using 36 h input sequences, achieved higher errors. The LSTM configuration (hidden = 32, layers = 1, dropout = 0.3, and batch = 32) reached an RMSE of 397.59 MW and MAE of 292.37 MW, while the GRU (hidden = 32, layers = 1, dropout = 0.1, and batch = 16) slightly outperformed the LSTM with an RMSE of 395.47 MW and MAE of 289.11 MW. Although both recurrent models improved substantially over the naïve 1 h lag benchmark (MAE ≈ 378 MW), they lagged behind the Transformer in all metrics. Particularly, scale-independent measures such as nRMSE and sMAPE showed consistent advantages for the Transformer (5.92% and 4.85%, respectively) compared to the recurrent baselines (nRMSE ≈ 6.3–6.6% and sMAPE ≈ 5.7–6.1%). Visual inspections over a two-month segment of the test set further confirmed these results, with the GRU systematically underpredicting peaks and lagging during ramps, the LSTM tracking moderate fluctuations but occasionally overshooting in highly volatile conditions, while the Transformer provided the closest alignment across both gradual and abrupt dynamics.

Placed in the context of the existing literature, these results reinforce recent advances that highlight the benefits of attention mechanisms and hybrid designs [20,21,22,23,25]. Unlike prior work that relies on meteorological covariates or turbine-level signals, this study demonstrates that a Transformer trained exclusively on historical, aggregated generation data can achieve competitive performance. This has practical significance for the Spanish power system, where forecasting accuracy directly influences imbalance costs and operational reliability in day-ahead and intraday markets. The ability of a lightweight Transformer to deliver accurate forecasts under these constraints provides a scalable tool for system operators and market agents who may not have access to high-resolution meteorological data, thereby supporting grid stability and Spain’s broader sustainability objectives within the European energy transition.

Nevertheless, several limitations should be acknowledged. First, the analysis is restricted to deterministic forecasts at the national level, leaving open questions regarding regional variability and probabilistic forecasting. As highlighted by recent reviews [26], interpretability and uncertainty quantification remain pressing challenges for the deployment of DL models in energy forecasting. Future research could therefore extend this work by incorporating probabilistic frameworks, attention-based interpretability analyses, and cross-country validations to test generalization under different system conditions.

7. Conclusions

The increasing penetration of variable renewables, particularly wind power, underscores the need for accurate short-term forecasting to support system reliability and efficient market operation. Using high-resolution Spanish data, this study assessed a Transformer-based approach to one-step-ahead wind power forecasting and contrasted it against strong recurrent baselines (LSTM/GRU) under a common, chronologically consistent evaluation protocol.

Three main findings emerged. First, in response to RQ1, the Transformer consistently outperformed LSTM and GRU across absolute and scale-independent metrics. The best Transformer, trained within the 36 h context, achieved RMSE = 370.71 MW, MAE = 258.77 MW, and MAPE = 4.92 %, improving upon the 1 h naïve persistence baseline (test MAE_naive ≈ 378 MW) and surpassing the best LSTM/GRU configurations (RMSE ≈ 398/395 MW; MAE ≈ 292/289 MW). Normalized errors corroborate this advantage (nRMSE = 5.92 %, sMAPE = 4.85 % versus ≈ 6.3–6.6 % and 5.7–6.1 % for recurrent models). Second, addressing RQ2, input resolution, and architectural choices proved to be relevant. Extending the window to 36 h yielded the most accurate results, while shallow encoders with two layers, moderate dimensionality of 32, and dropout of 0.1 provided the best balance between capacity and regularization. Additional attention heads or deeper stacks did not result in systematic improvements. Third, attention maps revealed a division of labor across heads, where most emphasized the most recent hours, whereas some attended to intermediate or earlier lags. This indicates that the Transformer is capable of jointly capturing short-term fluctuations and longer-range patterns. Error stratification also showed a moderate increase in mean absolute ramp error with ramp horizon, rising from 356 MW at $\mathrm{\Delta }$1 h to 377 MW at $\mathrm{\Delta }$6 h, and highlighted larger errors for strong ramps and peaks, which reflects the intrinsic difficulty of forecasting rare and highly volatile events.

From an operational standpoint, the preferred Transformer proved computationally efficient. With a maximum budget of 50 epochs, early stopping led to convergence in 11 epochs (total 439.10 s, median per epoch 40.02 s), and inference was low-latency, with a mean of 3.698 ms and a p95 of 4.768 ms for batches of 16 sequences of length 36. These characteristics make the approach suitable for near-real-time deployment in market and system-operation workflows, where small percentage improvements imply large absolute reductions in forecast error. Future work should extend this framework to probabilistic and multi-step settings, incorporate exogenous meteorological signals and multi-resolution inputs, and explore uncertainty quantification and interpretability at finer spatial granularity. Cross-system validations would test external validity under diverse climatic regimes. Overall, the evidence supports the use of compact, well-tuned Transformers as a practical and scalable tool for short-term wind forecasting, contributing to grid stability and facilitating the integration of renewables in Spain’s energy transition.