Empirical Analysis of the Energy–Growth Nexus with Machine Learning and Panel Causality: Evidence from Disaggregated Energy Sources
Abstract
1. Introduction
1.1. Objectives and Contributions
- Disaggregated analysis of energy sources: By moving beyond aggregate indicators and employing source-level data, the heterogeneous growth effects of the eight primary energy sources coal, oil, natural gas, nuclear, hydro, wind, solar, and other renewables are explicitly identified.
- Comparative evaluation across country groups: By conducting a cross-group comparison, the study systematically evaluates how the nexus varies across different levels of development and structural heterogeneity, ranging from relatively homogeneous developed economies to diverse global samples.
- Comprehensive advanced methodological framework: By combining conventional linear econometric models, including the Dumitrescu–Hurlin panel causality test, with nonlinear ML approaches, while also testing conventional statistical linear models, specifically multiple linear regression as a benchmark for nonlinear prediction, the study provides a robust framework that captures both predictive accuracy and causal direction, extending prior work that typically relied on a single class of models.
- Is there evidence of unidirectional or bidirectional causality between energy consumption and GDP across different energy sources and country groups?
- How does the relationship between energy consumption and economic growth differ across country groups (OECD founding members, all OECD members, the G20, and the global sample) given structural and institutional heterogeneity?
- To what extent do ML approaches, particularly artificial neural networks, enhance the ability to capture complex patterns and improve predictive performance compared to conventional linear regression models in heterogeneous contexts, while also complementing econometric causality tests in understanding the energy–growth nexus?
1.2. Rationale for the Methodological Approach
1.3. Structure of the Study
2. Literature Review
3. Materials and Methods
3.1. Data Description
3.2. Descriptive Statistics and Correlation Analysis
3.3. Multilayer Perceptron Neural Network
3.4. Dumitrescu–Hurlin Panel Causality Test
4. Results and Discussion
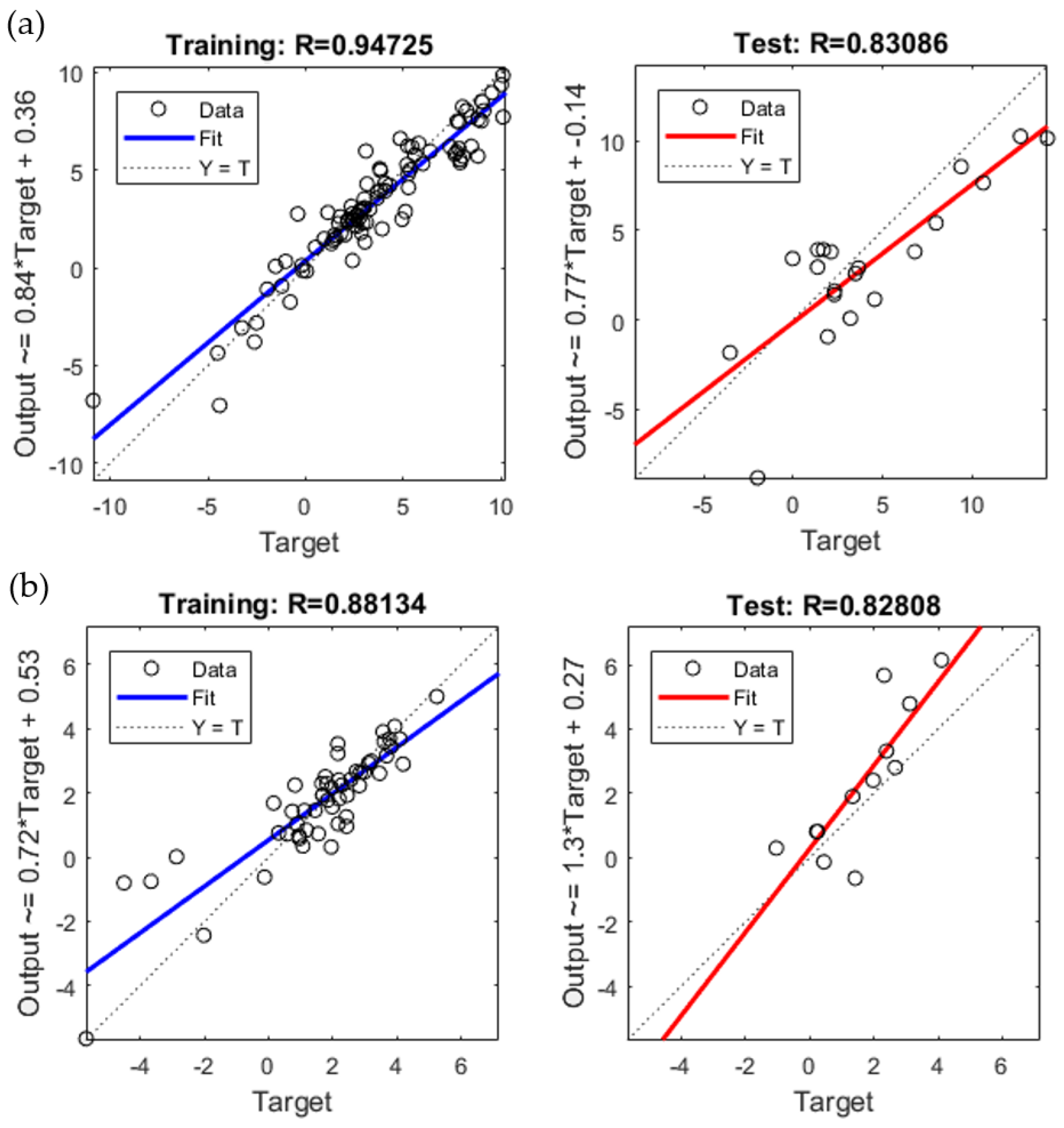
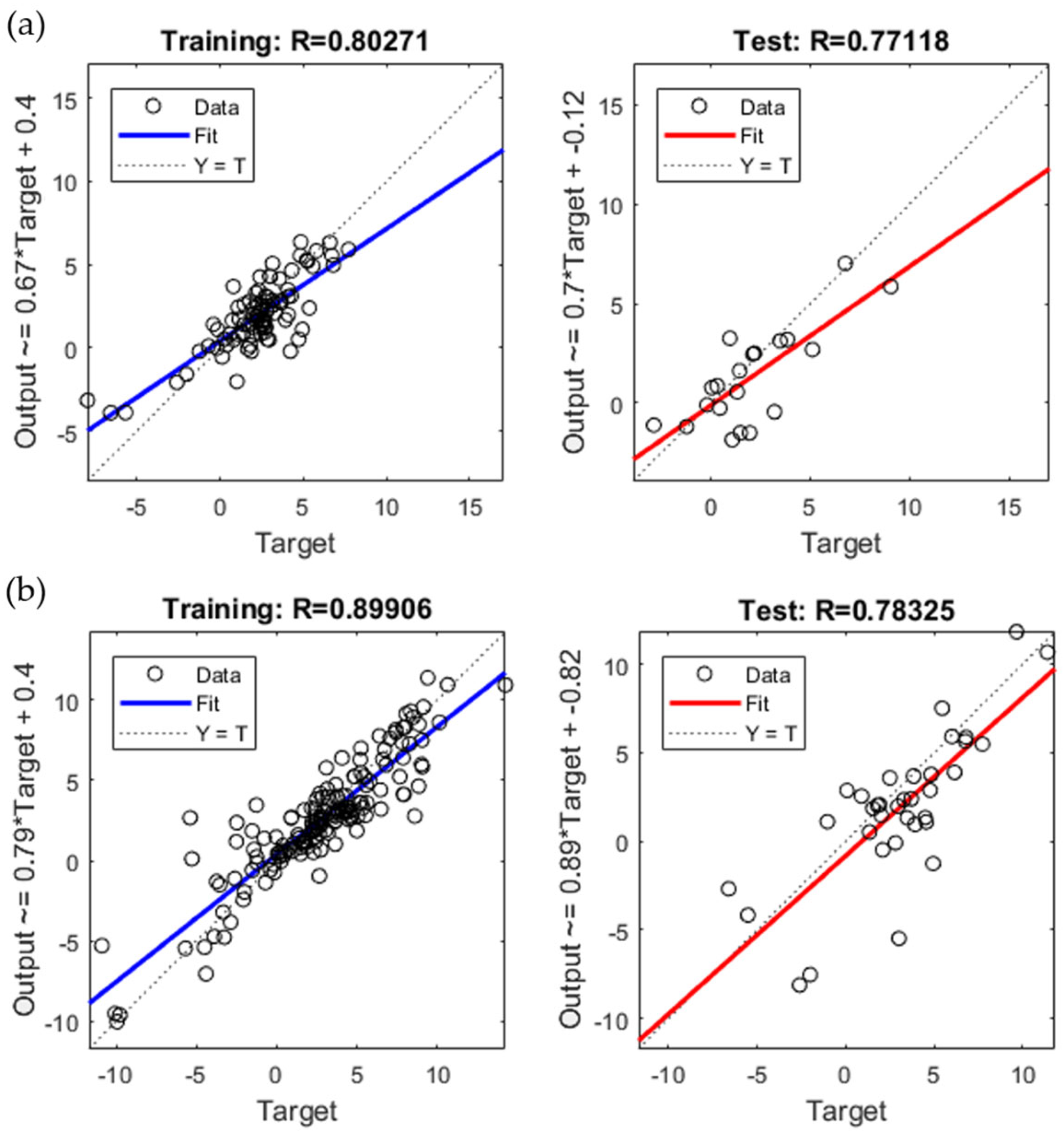
4.1. Machine Learning Analysis
4.2. Panel-Based Bidirectional Causality Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| ANN | Artificial Neural Network |
| MLP | Multilayer Feedforward Neural Network |
| GDP | Gross Domestic Product |
| Corr | Pearson’s correlation coefficient |
| ICC | Intraclass Correlation Coefficient |
| CI | Confidence Interval |
Appendix A
References
- Apergis, N.; Payne, J.E. On the causal dynamics between renewable and non-renewable energy consumption and economic growth in developed and developing countries. Energy Syst. 2011, 2, 299–312. [Google Scholar] [CrossRef]
- Salim, R.A.; Hassan, K.; Shafiei, S. Renewable and non-renewable energy consumption and economic activities: Further evidence from OECD Countries. Energy Econ. 2014, 44, 350–360. [Google Scholar] [CrossRef]
- Inglesi-Lotz, R. The impact of renewable energy consumption to economic growth: A panel data application. Energy Econ. 2016, 53, 58–63. [Google Scholar] [CrossRef]
- Kahia, M.; Aȉssa, M.S.B.; Lanouar, C. Renewable and non-renewable energy use-economic growth nexus: The case of MENA Net Oil Importing Countries. Renew. Sustain. Energy Rev. 2017, 71, 127–140. [Google Scholar] [CrossRef]
- Behera, J.; Mishra, A.K. Renewable and non-renewable energy consumption and economic growth in G7 Countries: Evidence from Panel Autoregressive Distributed Lag (P-ARDL) Model. Int. Econ. Econ. Policy 2020, 17, 241–258. [Google Scholar] [CrossRef]
- Romer, P.M. Increasing returns and long-run growth. J. Political Econ. 1986, 94, 1002–1037. [Google Scholar] [CrossRef]
- Lucas, R.E., Jr. On the mechanics of economic development. J. Monet. Econ. 1988, 22, 3–42. [Google Scholar] [CrossRef]
- Ntanos, S.; Skordoulis, M.; Kyriakopoulos, G.; Arabatzis, G.; Chalikias, M.; Galatsidas, S.; Batzios, A.; Katsarou, A. Renewable energy and economic growth: Evidence from European Countries. Sustainability 2018, 10, 2626. [Google Scholar] [CrossRef]
- Can, H.; Korkmaz, Ö. The relationship between renewable energy consumption and economic growth: The case of Bulgaria. Int. J. Energy Sect. Manag. 2020, 13, 573–589. [Google Scholar] [CrossRef]
- Bouyghrissi, S.; Berjaoui, A.; Niba, M. The nexus between renewable energy consumption and economic growth in Morocco. Environ. Sci. Pollut. Res. 2021, 28, 5693–5703. [Google Scholar] [CrossRef]
- Gyimah, J.; Yao, X.; Tachega, M.A.; Hayford, I.S.; Opoku-Mensah, E. Renewable energy consumption and economic growth: New evidence from Ghana. Energy 2022, 248, 123559. [Google Scholar] [CrossRef]
- Asiedu, B.A.; Hassan, A.A.; Bein, M.A. Renewable energy, non-renewable energy, and economic growth: Evidence from 26 European Countries. Environ. Sci. Pollut. Res. 2021, 28, 11119–11128. [Google Scholar] [CrossRef] [PubMed]
- Maji, I.K.; Sulaiman, C.; Abdul-Rahim, A.S. Renewable energy consumption and economic growth nexus: A fresh evidence from West Africa. Energy Rep. 2019, 5, 384–392. [Google Scholar] [CrossRef]
- Namahoro, J.P.; Wu, Q.; Xiao, H.; Zhou, N. The asymmetric nexus of renewable energy consumption and economic growth: New evidence from Rwanda. Renew. Energy 2021, 174, 336–346. [Google Scholar] [CrossRef]
- Mahalingam, B.; Orman, W.H. GDP and energy consumption: A panel analysis of the US. Appl. Energy 2018, 213, 208–218. [Google Scholar] [CrossRef]
- Smith, A. An Inquiry into the Nature and Causes of the Wealth of Nations; W. Strahan and T. Cadell: London, UK, 1776. [Google Scholar]
- Swan, T. Economic growth and capital accumulation. Econ. Rec. 1956, 32, 334–361. [Google Scholar] [CrossRef]
- Sen, D.; Tunç, K.M.M.; Günay, M.E. Forecasting electricity consumption of OECD countries: A global machine learning modeling approach. Util. Policy 2021, 70, 101222. [Google Scholar] [CrossRef]
- Kahia, M.; Moulahi, T.; Mahfoudhi, S.; Boubaker, S.; Omri, A. A machine learning process for examining the linkage among disaggregated energy consumption, economic growth, and environmental degradation. Resour. Policy 2022, 79, 103104. [Google Scholar] [CrossRef]
- Abd El-Aal, M.F.; Mahmoud, H.A.M.; Abdelsamiea, A.T.; Hegazy, M.S. Leveraging machine learning to assess the impact of energy consumption on global GDP growth: What actions should be taken globally toward environmental concerns? Int. J. Energy Econ. Policy 2024, 14, 108–115. [Google Scholar] [CrossRef]
- Zhang, L.; Padhan, H.; Singh, S.K.; Gupta, M. The impact of renewable energy on inflation in G7 economies: Evidence from artificial neural networks and machine learning methods. Energy Econ. 2024, 136, 107718. [Google Scholar] [CrossRef]
- Khan, A.M.; Wyrwa, A. Integrating machine learning and econometric models to uncover macroeconomic determinants of renewable energy production in the selected European countries. Energy 2025, 333, 137266. [Google Scholar] [CrossRef]
- Cogoljević, D.; Alizamir, M.; Piljan, I.; Piljan, T.; Prljić, K.; Zimonjić, S. A machine learning approach for predicting the relationship between energy resources and economic development. Phys. A Stat. Mech. Its Appl. 2018, 495, 211–214. [Google Scholar] [CrossRef]
- Kurniawan, R.; Managi, S. Forecasting annual energy consumption using machine learnings: Case of Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2019, 257, 012032. [Google Scholar] [CrossRef]
- Magazzino, C.; Mele, M.; Morelli, G. The relationship between renewable energy and economic growth in a time of COVID-19: A machine learning experiment on the Brazilian Economy. Sustainability 2021, 13, 1285. [Google Scholar] [CrossRef]
- Sah, H.K.; Sisodia, G.S.; Ahmed, G.; Rafiuddin, A.; Abidi, N. The role of energy consumption and economic growth on carbon emission: Application of artificial neural network. Int. J. Energy Econ. Policy 2023, 13, 591–596. [Google Scholar] [CrossRef]
- Lu, F.; Ma, F.; Hu, S. Does energy consumption play a key role? Re-evaluating the energy consumption-economic growth nexus from GDP growth rates forecasting. Energy Econ. 2024, 129, 107268. [Google Scholar] [CrossRef]
- Ricardo, D. On the Principles of Political Economy and Taxation; John Murray: London, UK, 1817. [Google Scholar]
- Solow, R.M. A contribution to the theory of economic growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Amri, F. The relationship amongst energy consumption (renewable and non-renewable), and GDP in Algeria. Renew. Sustain. Energy Rev. 2017, 76, 62–71. [Google Scholar] [CrossRef]
- Shakouri, B.; Yazdi, S.K. Causality between renewable energy, energy consumption, and economic growth. Energy Sources Part B Econ. Plan. Policy 2017, 12, 838–845. [Google Scholar] [CrossRef]
- Saad, W.; Taleb, A. The causal relationship between renewable energy consumption and economic growth: Evidence from Europe. Clean Technol. Environ. Policy 2018, 20, 127–136. [Google Scholar] [CrossRef]
- Rahman, M.M.; Velayutham, E. Renewable and non-renewable energy consumption-economic growth nexus: New evidence from South Asia. Renew. Energy 2020, 147 Part 1, 399–408. [Google Scholar] [CrossRef]
- Xie, P.; Zhu, Z.; Hu, G.; Huang, J. Renewable energy and economic growth hypothesis: Evidence from N-11 Countries. Econ. Res.-Ekon. Istražıvanja 2023, 36, 1–21. [Google Scholar] [CrossRef]
- Kilinc-Ata, N. Investigation of the impact of environmental degradation on the transition to clean energy: New evidence from Sultanate of Oman. Energies 2025, 18, 839–853. [Google Scholar] [CrossRef]
- Yuan, J.; Liu, S. A double machine learning model for measuring the impact of the made in China 2025 strategy on green economic growth. Sci. Rep. 2024, 14, 12026. [Google Scholar] [CrossRef] [PubMed]
- World Bank (n.d.). World Development Indicators: GDP Growth (Annual %). Available online: https://databank.worldbank.org/reports.aspx?source=2&series=NY.GDP.MKTP.KD.ZG&country=# (accessed on 14 February 2023).
- Our World in Data (n.d.). Primary Energy Consumption by Source and Country. Global Change Data Lab. Available online: https://ourworldindata.org/grapher/energy-consumption-by-source-and-country (accessed on 14 February 2023).
- Ozturk, I. A literature survey on energy–growth nexus. Energy Policy 2010, 38, 340–349. [Google Scholar] [CrossRef]
- Payne, J.E. Survey of the international evidence on the causal relationship between energy consumption and growth. J. Econ. Stud. 2010, 37, 53–95. [Google Scholar] [CrossRef]
- Stern, D.I. The role of energy in economic growth. Ann. N. Y. Acad. Sci. 2011, 1219, 26–51. [Google Scholar] [CrossRef]
- Apergis, N.; Payne, J.E. Renewable energy consumption and economic growth: Evidence from a panel of OECD countries. Energy Policy 2010, 38, 656–660. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Paramati, S.R.; Ozturk, I.; Bhattacharya, S. The effect of renewable energy consumption on economic growth: Evidence from top 38 countries. Appl. Energy 2016, 162, 733–741. [Google Scholar] [CrossRef]
- Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Christo, V.R.E.; Nehemiah, H.K.; Minu, B.; Kannan, A. Correlation-based ensemble feature selection using bioinspired algorithms and classification using backpropagation neural network. Comput. Math. Methods Med. 2019, 2019, 7398307. [Google Scholar] [CrossRef]
- Romo-Chavero, M.A.; Cantoral-Ceballos, J.A.; Pérez-Díaz, J.A.; Martinez-Cagnazzo, C. A hybrid model for BGP anomaly detection using median absolute deviation and machine learning. IEEE Open J. Commun. Soc. 2025, 6, 2102–2116. [Google Scholar] [CrossRef]
- Pasini, A. Artificial neural networks for small dataset analysis. J. Thorac. Dis. 2015, 7, 953–960. [Google Scholar]
- MATLAB R2017b, The MathWorks, Inc.: Natick, MA, USA, 2017.
- Wang, Z.; Fu, Y.; Huang, T.S. Signal Proccessing. In Computer Vision and Pattern Recognition; Wang, Z., Fu, Y., Huang, T.S., Eds.; USA Academic Press: San Diego, CA, USA, 2019; Volume: Deep learning through sparse and low-rank modeling, pp. 121–142. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley-Interscience: New York, NY, USA, 2000. [Google Scholar]
- Dumitrescu, E.I.; Hurlin, C. Testing for Granger non-causality in heterogeneous panels. Econ. Model. 2012, 29, 1450–1460. [Google Scholar] [CrossRef]
- Wanas, N.; Auda, G.; Kamel, M.S.; Karray, F. On the optimal number of hidden nodes in a neural network. In Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering (Cat. No. 98TH8341), Waterloo, ON, Canada, 25–28 May 1998; Volume 2, pp. 918–921. [Google Scholar]
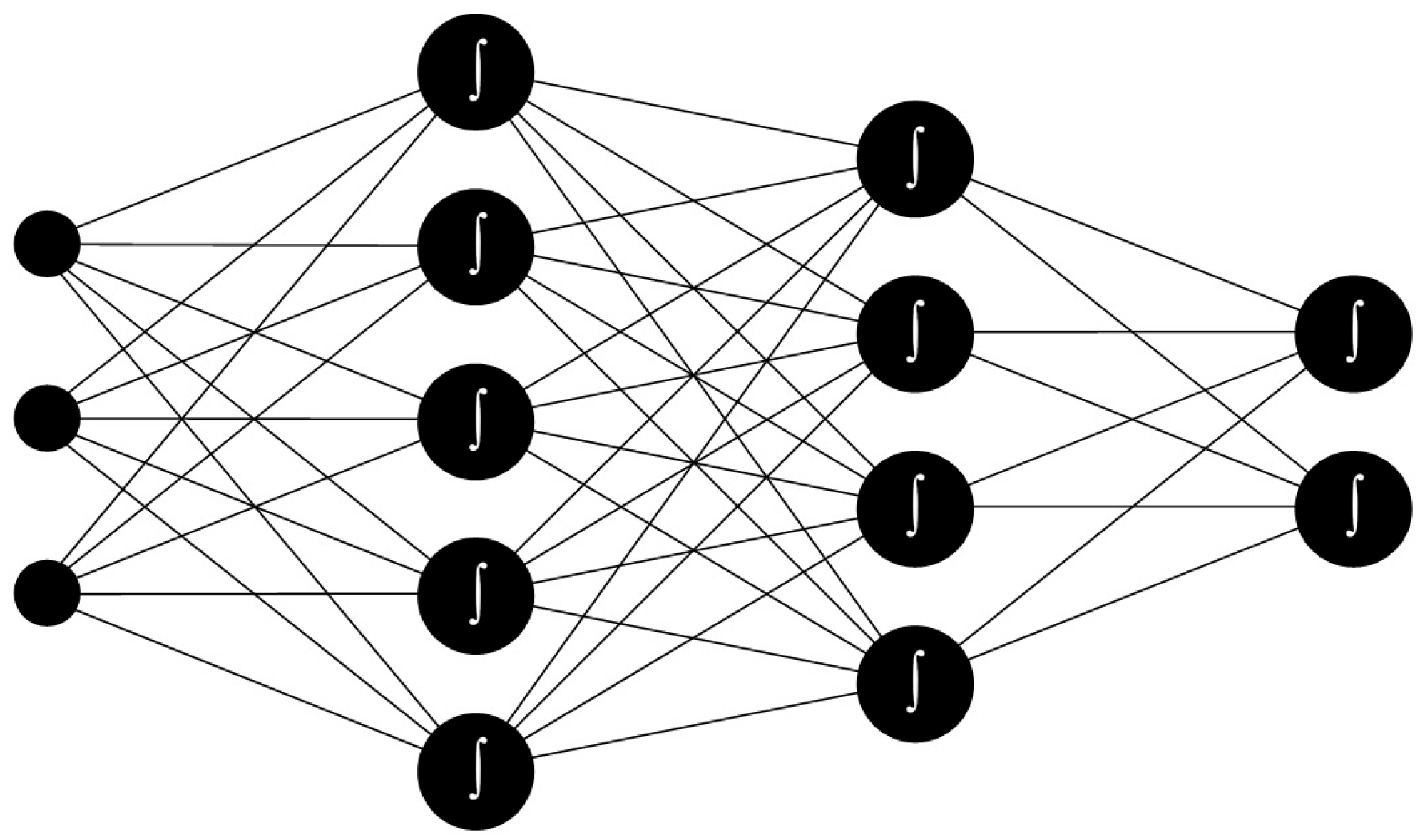
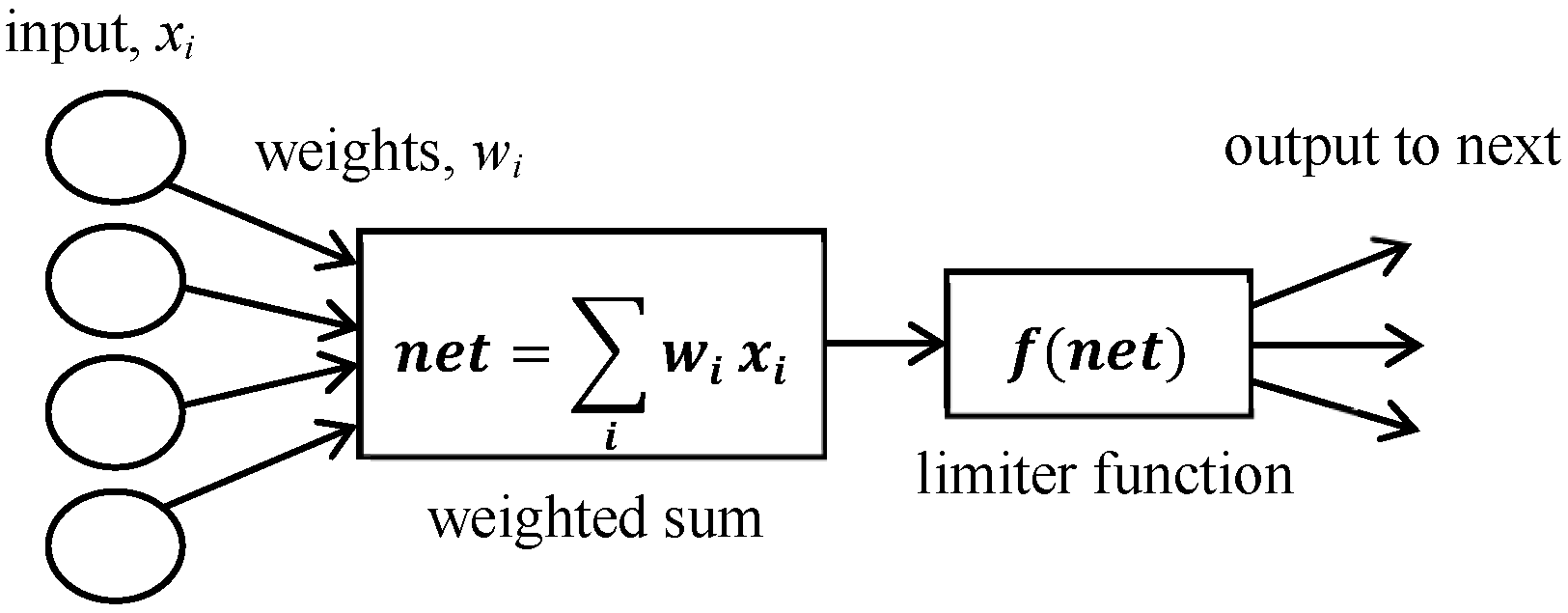
| Dependent Variable (%) | Independent Variables (kWh) |
|---|---|
| Growth Rate | Coal |
| Oil | |
| Gas | |
| Nuclear | |
| Hydro | |
| Wind | |
| Solar | |
| Other Renewables |
| Dataset | |
|---|---|
| OECDf | 440 |
| OECDa | 778 |
| G20 | 418 |
| World | 1715 |
| Variable | M | SD | Median | Q1 | Q3 | Min | Max |
|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) | 7900.000 | 7620.000 | 5720.000 | 1490.000 | 11,900.000 | 0.000 | 32,200.000 |
| Oil per capita (kWh) | 16,200.000 | 13,000.000 | 12,700.000 | 5880.000 | 23,800.000 | 1191.000 | 61,800.000 |
| Gas per capita (kWh) | 10,900.000 | 9530.000 | 9190.000 | 2000.000 | 15,100.000 | 195.000 | 32,700.000 |
| Nuclear per capita (kWh—equivalent) | 2930.000 | 4540.000 | 470.000 | 0.000 | 5230.000 | 0.000 | 20,600.000 |
| Hydro per capita (kWh—equivalent) | 3000.000 | 6510.000 | 1620.000 | 238.000 | 2410.000 | 0.000 | 34,400.000 |
| Wind per capita (kWh—equivalent) | 428.000 | 732.000 | 82.100 | 2.780 | 551.000 | 0.000 | 4160.000 |
| Solar per capita (kWh—equivalent) | 184.000 | 391.000 | 6.000 | 0.218 | 156.000 | 0.000 | 3150.000 |
| Other renewables per capita (kWh—equivalent) | 399.000 | 450.000 | 209.000 | 35.500 | 653.000 | 0.000 | 1980.000 |
| GDP growth | 2.890 | 3.730 | 2.730 | 1.240 | 5.030 | −11.000 | 14.200 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|---|---|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) (1) | 1 | 0.188 *** | 0.038 | 0.061 | −0.003 | 0.083 * | 0.145 *** | 0.100 ** | 0.059 |
| Oil per capita (kWh) (2) | 1 | 0.758 *** | 0.303 *** | 0.336 *** | 0.130 *** | 0.053 | 0.206 *** | −0.158 *** | |
| Gas per capita (kWh) (3) | 1 | 0.191 *** | 0.451 *** | 0.203 *** | 0.059 | 0.190 *** | −0.170 *** | ||
| Nuclear per capita (kWh—equivalent) (4) | 1 | 0.247 *** | 0.146 *** | −0.016 | 0.171 *** | −0.154 *** | |||
| Hydro per capita (kWh—equivalent) (5) | 1 | 0.160 *** | −0.053 | 0.279 *** | −0.075 | ||||
| Wind per capita (kWh—equivalent) (6) | 1 | 0.660 *** | 0.732 *** | −0.204 *** | |||||
| Solar per capita (kWh—equivalent) (7) | 1 | 0.570 *** | −0.196 *** | ||||||
| Other renewables per capita (kWh—equivalent) (8) | 1 | −0.299 *** | |||||||
| GDP growth (9) | 1 |
| Variable | M | SD | Median | Q1 | Q3 | Min | Max |
|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) | 7580.000 | 7400.000 | 5240.000 | 2430.000 | 10,300.000 | 0.000 | 38,200.000 |
| Oil per capita (kWh) | 19,200.000 | 11,400.000 | 17,200.000 | 11,700.000 | 23,800.000 | 2915.000 | 80,400.000 |
| Gas per capita (kWh) | 9320.000 | 6630.000 | 8040.000 | 4680.000 | 11,500.000 | 0.000 | 31,300.000 |
| Nuclear per capita (kWh—equivalent) | 3670.000 | 5100.000 | 225.000 | 0.000 | 7030.000 | 0.000 | 23,900.000 |
| Hydro per capita (kWh—equivalent) | 8540.000 | 19,800.000 | 1820.000 | 260.000 | 4920.000 | 0.000 | 112,000.000 |
| Wind per capita (kWh—equivalent) | 837.000 | 1290.000 | 215.000 | 26.200 | 1150.000 | 0.000 | 7360.000 |
| Solar per capita (kWh—equivalent) | 197.000 | 364.000 | 7.760 | 0.312 | 258.000 | 0.000 | 3150.000 |
| Other renewables per capita (kWh—equivalent) | 1850.000 | 5610.000 | 538.000 | 194.000 | 1250.000 | 0.000 | 43,200.000 |
| GDP growth | 2.310 | 3.410 | 2.420 | 1.070 | 3.960 | −14.600 | 24.400 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|---|---|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) (1) | 1 | −0.041 * | −0.150 *** | 0.163 *** | −0.054 ** | 0.052 ** | 0.110 *** | 0.015 | −0.022 |
| Oil per capita (kWh) (2) | 1 | 0.403 *** | 0.039 | 0.092 *** | 0.024 | 0.040 * | 0.085 *** | −0.014 | |
| Gas per capita (kWh) (3) | 1 | −0.081 *** | −0.078 *** | −0.077 *** | −0.026 | −0.078 *** | 0.072 *** | ||
| Nuclear per capita (kWh—equivalent) (4) | 1 | 0.068 *** | 0.125 *** | 0.105 *** | 0.053 ** | −0.112 *** | |||
| Hydro per capita (kWh—equivalent) (5) | 1 | 0.068 *** | −0.059 ** | 0.733 *** | −0.071 *** | ||||
| Wind per capita (kWh—equivalent) (6) | 1 | 0.392 *** | 0.080 *** | −0.131 *** | |||||
| Solar per capita (kWh—equivalent) (7) | 1 | 0.001 | −0.154 *** | ||||||
| Other renewables per capita (kWh—equivalent) (8) | 1 | −0.058 ** | |||||||
| GDP growth (9) | 1 |
| Variable | M | SD | Median | Q1 | Q3 | Min | Max |
|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) | 5040.000 | 4090.000 | 3880.000 | 2280.000 | 6410.000 | 0.000 | 22,300.000 |
| Oil per capita (kWh) | 23,100.000 | 12,500.000 | 19,400.000 | 15,700.000 | 29,900.000 | 5029.000 | 80,400.000 |
| Gas per capita (kWh) | 10,800.000 | 7950.000 | 9570.000 | 4670.000 | 14,600.000 | 0.000 | 31,300.000 |
| Nuclear per capita (kWh—equivalent) | 4040.000 | 5820.000 | 224.000 | 0.000 | 6820.000 | 0.000 | 23,900.000 |
| Hydro per capita (kWh—equivalent) | 12,900.000 | 25,200.000 | 1970.000 | 481.000 | 12,700.000 | 6.500 | 112,000.000 |
| Wind per capita (kWh—equivalent) | 1260.000 | 1510.000 | 683.000 | 157.000 | 1890.000 | 0.000 | 7360.000 |
| Solar per capita (kWh—equivalent) | 227.000 | 359.000 | 12.800 | 1.020 | 342.000 | 0.000 | 1710.000 |
| Other renewables per capita (kWh—equivalent) | 2430.000 | 7240.000 | 680.000 | 292.000 | 1360.000 | 0.000 | 43,200.000 |
| GDP growth | 1.910 | 3.370 | 1.990 | 0.823 | 3.250 | −11.300 | 24.400 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|---|---|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) (1) | 1 | −0.041 * | −0.150 *** | 0.163 *** | −0.054 ** | 0.052 ** | 0.110 *** | 0.015 | −0.022 |
| Oil per capita (kWh) (2) | 1 | 0.403 *** | 0.039 | 0.092 *** | 0.024 | 0.040 * | 0.085 *** | −0.014 | |
| Gas per capita (kWh) (3) | 1 | −0.081 *** | −0.078 *** | −0.077 *** | −0.026 | −0.078 *** | 0.072 *** | ||
| Nuclear per capita (kWh—equivalent) (4) | 1 | 0.068 *** | 0.125 *** | 0.105 *** | 0.053 ** | −0.112 *** | |||
| Hydro per capita (kWh—equivalent) (5) | 1 | 0.068 *** | −0.059 ** | 0.733 *** | −0.071 *** | ||||
| Wind per capita (kWh—equivalent) (6) | 1 | 0.392 *** | 0.080 *** | −0.131 *** | |||||
| Solar per capita (kWh—equivalent) (7) | 1 | 0.001 | −0.154 *** | ||||||
| Other renewables per capita (kWh—equivalent) (8) | 1 | −0.058 ** | |||||||
| GDP growth (9) | 1 |
| Variable | M | SD | Median | Q1 | Q3 | Min | Max |
|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) | 7580.000 | 7400.000 | 5240.000 | 2430.000 | 10,300.000 | 0.000 | 38,200.000 |
| Oil per capita (kWh) | 19,200.000 | 11,400.000 | 17,200.000 | 11,700.000 | 23,800.000 | 2915.000 | 80,400.000 |
| Gas per capita (kWh) | 9320.000 | 6630.000 | 8040.000 | 4680.000 | 11,500.000 | 0.000 | 31,300.000 |
| Nuclear per capita (kWh—equivalent) | 3670.000 | 5100.000 | 225.000 | 0.000 | 7030.000 | 0.000 | 23,900.000 |
| Hydro per capita (kWh—equivalent) | 8540.000 | 19,800.000 | 1820.000 | 260.000 | 4920.000 | 0.000 | 112,000.000 |
| Wind per capita (kWh—equivalent) | 837.000 | 1290.000 | 215.000 | 26.200 | 1150.000 | 0.000 | 7360.000 |
| Solar per capita (kWh—equivalent) | 197.000 | 364.000 | 7.760 | 0.312 | 258.000 | 0.000 | 3150.000 |
| Other renewables per capita (kWh—equivalent) | 1850.000 | 5610.000 | 538.000 | 194.000 | 1250.000 | 0.000 | 43,200.000 |
| GDP growth | 2.310 | 3.410 | 2.420 | 1.070 | 3.960 | −14.600 | 24.400 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|---|---|---|---|---|---|---|---|---|---|
| Coal per capita (kWh) (1) | 1 | 0.123 *** | 0.368 *** | −0.007 | −0.187 *** | −0.079 * | −0.134 *** | −0.099 ** | 0.05 |
| Oil per capita (kWh) (2) | 1 | 0.606 *** | −0.011 | 0.121 ** | −0.247 *** | −0.140 *** | 0.094 ** | 0.077 | |
| Gas per capita (kWh) (3) | 1 | −0.042 | −0.229 *** | −0.101 ** | 0.029 | −0.303 *** | −0.006 | ||
| Nuclear per capita (kWh—equivalent) (4) | 1 | −0.096 ** | −0.106 ** | −0.081 * | −0.119 ** | −0.021 | |||
| Hydro per capita (kWh—equivalent) (5) | 1 | −0.184 *** | −0.245 *** | 0.721 *** | 0.021 | ||||
| Wind per capita (kWh—equivalent) (6) | 1 | 0.342 *** | −0.111 ** | −0.031 | |||||
| Solar per capita (kWh—equivalent) (7) | 1 | −0.112 ** | −0.159 *** | ||||||
| Other renewables per capita (kWh—equivalent) (8) | 1 | 0.017 | |||||||
| GDP growth (9) | 1 |
| Data | Train | Test | ||||
|---|---|---|---|---|---|---|
| 95% CI | 95% CI | |||||
| G20 | 0.94 | 0.97 | 0.95–0.98 | 0.83 | 0.91 | 0.76–0.97 |
| OECDf | 0.88 | 0.93 | 0.87–0.96 | 0.82 | 0.90 | 0.62–0.97 |
| OECDa | 0.80 | 0.88 | 0.82–0.92 | 0.77 | 0.87 | 0.65–0.95 |
| World | 0.89 | 0.95 | 0.93–0.96 | 0.78 | 0.87 | 0.75–0.94 |
| Null Hypothesis | W-Stat. | Zbar-Stat. | p | Decision |
|---|---|---|---|---|
| Coal does not cause GDP growth | 1.544 | −0.993 | 0.321 | Fail to reject |
| GDP growth does not cause Coal | 7.733 *** | 12.494 | 0.000 | Reject |
| Oil does not cause GDP growth | 1.162 * | −1.826 | 0.068 | Reject |
| GDP growth does not cause Oil | 4.055 *** | 4.478 | 0.000 | Reject |
| Gas does not cause GDP growth | 1.914 | −0.187 | 0.852 | Fail to reject |
| GDP growth does not cause Gas | 2.961 ** | 2.094 | 0.036 | Reject |
| Nuclear does not cause GDP growth | 0.899 ** | −2.400 | 0.016 | Reject |
| GDP growth does not cause Nuclear | 3.904 *** | 4.149 | 0.000 | Reject |
| Hydro does not cause GDP growth | 1.147 * | −1.860 | 0.063 | Reject |
| GDP growth does not cause Hydro | 3.384 *** | 3.017 | 0.003 | Reject |
| Wind does not cause GDP growth | 1.306 | −1.512 | 0.131 | Fail to reject |
| GDP growth does not cause Wind | 6.907 *** | 10.695 | 0.000 | Reject |
| Solar does not cause GDP growth | 1.318 | −1.486 | 0.137 | Fail to reject |
| GDP growth does not cause Solar | 6.703 *** | 10.249 | 0.000 | Reject |
| Other renewables does not cause GDP growth | 1.851 | −0.325 | 0.745 | Fail to reject |
| GDP growth does not cause Other renewables | 2.774 * | 1.687 | 0.092 | Reject |
| Null Hypothesis | W-Stat. | Zbar-Stat. | p | Decision |
|---|---|---|---|---|
| Coal does not cause GDP growth | 1.102 *** | −2.693 | 0.007 | Reject |
| GDP growth does not cause Coal | 3.126 *** | 3.379 | 0.001 | Reject |
| Oil does not cause GDP growth | 1.111 *** | −2.667 | 0.008 | Reject |
| GDP growth does not cause Oil | 3.064 *** | 3.191 | 0.001 | Reject |
| Gas does not cause GDP growth | 1.037 *** | −2.889 | 0.004 | Reject |
| GDP growth does not cause Gas | 2.050 | 0.149 | 0.881 | Fail to reject |
| Nuclear does not cause GDP growth | 0.437 *** | −4.689 | 0.000 | Reject |
| GDP growth does not cause Nuclear | 2.384 | 1.152 | 0.249 | Fail to reject |
| Hydro does not cause GDP growth | 0.961 *** | −3.117 | 0.002 | Reject |
| GDP growth does not cause Hydro | 2.066 | 0.197 | 0.844 | Fail to reject |
| Wind does not cause GDP growth | 1.165 ** | −2.506 | 0.012 | Reject |
| GDP growth does not cause Wind | 3.319 *** | 3.958 | 0.000 | Reject |
| Solar does not cause GDP growth | 2.341 | 1.024 | 0.306 | Fail to reject |
| GDP growth does not cause Solar | 4.869 *** | 8.608 | 0.000 | Reject |
| Other renewables does not cause GDP growth | 1.089 *** | −2.734 | 0.006 | Reject |
| GDP growth does not cause Other renewables | 2.088 | 0.265 | 0.791 | Fail to reject |
| Null Hypothesis | W-Stat. | Zbar-Stat. | p | Decision |
|---|---|---|---|---|
| Coal does not cause GDP growth | 0.923 ** | −2.408 | 0.016 | Reject |
| GDP growth does not cause Coal | 4.069 *** | 4.627 | 0.000 | Reject |
| Oil does not cause GDP growth | 0.614 *** | −3.099 | 0.002 | Reject |
| GDP growth does not cause Oil | 2.879 ** | 1.965 | 0.049 | Reject |
| Gas does not cause GDP growth | 0.618 *** | −3.091 | 0.002 | Reject |
| GDP growth does not cause Gas | 2.071 | 0.159 | 0.874 | Fail to reject |
| Nuclear does not cause GDP growth | 0.442 *** | −3.483 | 0.001 | Reject |
| GDP growth does not cause Nuclear | 2.751 * | 1.680 | 0.093 | Reject |
| Hydro does not cause GDP growth | 0.780 *** | −2.727 | 0.006 | Reject |
| GDP growth does not cause Hydro | 2.692 | 1.547 | 0.122 | Fail to reject |
| Wind does not cause GDP growth | 0.617 *** | −3.092 | 0.002 | Reject |
| GDP growth does not cause Wind | 4.974 *** | 6.649 | 0.000 | Reject |
| Solar does not cause GDP growth | 0.710 *** | −2.885 | 0.004 | Reject |
| GDP growth does not cause Solar | 6.481 *** | 10.020 | 0.000 | Reject |
| Other renewables does not cause GDP growth | 1.087 ** | −2.041 | 0.041 | Reject |
| GDP growth does not cause Other renewables | 2.748 * | 1.673 | 0.094 | Reject |
| Null Hypothesis | W-Stat. | Zbar-Stat. | p | Decision |
|---|---|---|---|---|
| Coal does not cause GDP growth | 1.210 *** | −3.534 | 0.000 | Reject |
| GDP growth does not cause Coal | 3.691 *** | 7.561 | 0.000 | Reject |
| Oil does not cause GDP growth | 1.024 *** | −4.363 | 0.000 | Reject |
| GDP growth does not cause Oil | 2.657 *** | 2.938 | 0.003 | Reject |
| Gas does not cause GDP growth | 1.191 *** | −3.617 | 0.000 | Reject |
| GDP growth does not cause Gas | 2.237 | 1.059 | 0.290 | Fail to reject |
| Nuclear does not cause GDP growth | 0.641 *** | −6.079 | 0.000 | Reject |
| GDP growth does not cause Nuclear | 2.019 | 0.085 | 0.933 | Fail to reject |
| Hydro does not cause GDP growth | 0.886 *** | −4.982 | 0.000 | Reject |
| GDP growth does not cause Hydro | 2.108 | 0.484 | 0.629 | Fail to reject |
| Wind does not cause GDP growth | 1.126 *** | −3.910 | 0.000 | Reject |
| GDP growth does not cause Wind | 3.756 *** | 7.853 | 0.000 | Reject |
| Solar does not cause GDP growth | 1.431 ** | −2.545 | 0.011 | Reject |
| GDP growth does not cause Solar | 4.878 *** | 12.873 | 0.000 | Reject |
| Other renewables does not cause GDP growth | 1.205 *** | −3.555 | 0.000 | Reject |
| GDP growth does not cause Other renewables | 2.420 * | 1.878 | 0.060 | Reject |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ersöz Kaya, I.; Korkmaz, S. Empirical Analysis of the Energy–Growth Nexus with Machine Learning and Panel Causality: Evidence from Disaggregated Energy Sources. Sustainability 2025, 17, 8627. https://doi.org/10.3390/su17198627
Ersöz Kaya I, Korkmaz S. Empirical Analysis of the Energy–Growth Nexus with Machine Learning and Panel Causality: Evidence from Disaggregated Energy Sources. Sustainability. 2025; 17(19):8627. https://doi.org/10.3390/su17198627
Chicago/Turabian StyleErsöz Kaya, Irem, and Suna Korkmaz. 2025. "Empirical Analysis of the Energy–Growth Nexus with Machine Learning and Panel Causality: Evidence from Disaggregated Energy Sources" Sustainability 17, no. 19: 8627. https://doi.org/10.3390/su17198627
APA StyleErsöz Kaya, I., & Korkmaz, S. (2025). Empirical Analysis of the Energy–Growth Nexus with Machine Learning and Panel Causality: Evidence from Disaggregated Energy Sources. Sustainability, 17(19), 8627. https://doi.org/10.3390/su17198627





