Resilience Assessment and Sustainability Enhancement of Gas and CO2 Utilization via Carbon–Hydrogen–Oxygen Symbiosis Networks
Abstract
1. Introduction
2. Proposed Approach
2.1. Problem Statement
2.2. Mathematical Formulation of the Synthesis
2.3. Resilience Assessment
2.3.1. Perspective
2.3.2. Flow Dependency
2.3.3. Propagation Mechanism
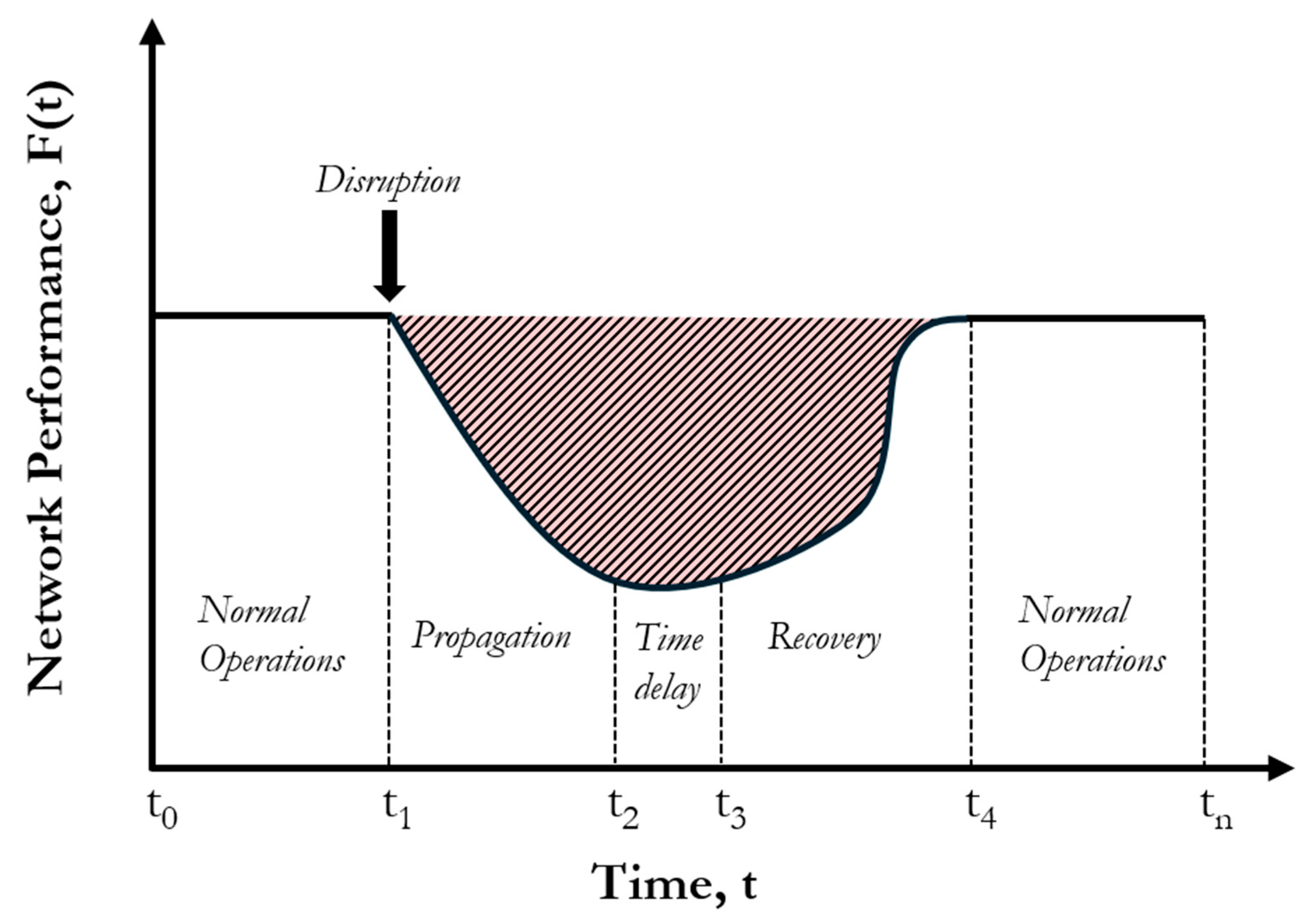
2.3.4. Resilience Quantification
3. Case Study
Proposed Industrial Cluster
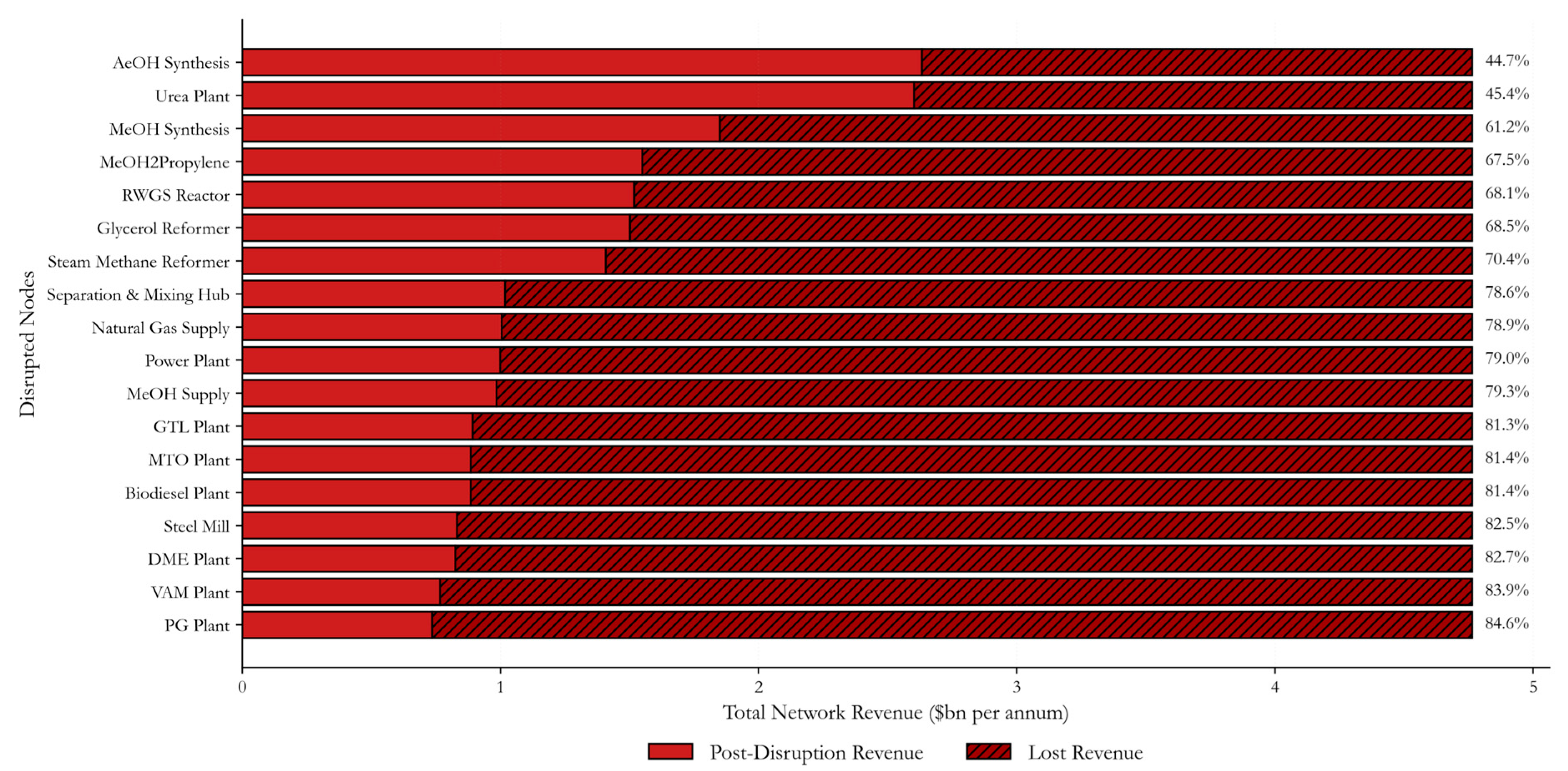
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| CHOSYN | Carbon–hydrogen–oxygen symbiosis network |
| GHG | Greenhouse gases |
| SDG | Sustainable development goals |
| IE | Industrial ecology |
| IS | Industrial symbiosis |
| ISN | Industrial Symbiosis network |
| EIP | Eco-industrial parks |
| PSE | Process systems engineering |
| GTL | Gas-to-liquid |
| MTO | Methanol-to-olefins |
| PG | Propylene glycol |
| DME | Dimethyl ether |
| BD | Biodiesel |
| VAM | Vinyl acetate monomer |
| MeOH | Methanol |
| AeOH | Acetic acid |
| RWGS | Reverse water-gas shit reaction |
| MILP | Mixed integer linear programming |
| Set of all plants | |
| Set of all internal sources | |
| Set of all chemical species | |
| Set of all external sources | |
| Set of all dischargeable sources | |
| Set of all interceptors | |
| Net atomic flow of carbon | |
| Net atomic flow of hydrogen | |
| Net atomic flow of oxygen | |
| Coefficient of carbon atom in species s | |
| Coefficient of hydrogen atom in species s | |
| Coefficient of oxygen atom in species s | |
| Molar flowrate of species s supplied by plant p as an internal source | |
| Molar flowrate of species s demanded by plant p | |
| Molar flowrate of purchased raw material s | |
| Molar flowrate of discharged species s | |
| Upper bound on demand | |
| Upper bound on discharge | |
| Stoichiometric coefficient of species s in reaction j | |
| Flowrate assigned to interceptor j | |
| Binary variable denoting the selection of interceptor j | |
| Flowrate of species s targeted for utilization in plant p | |
| Separation efficiency for species s | |
| Cost of purchasing and discharging species s | |
| Cost of interceptor j | |
| Upstream emissions from procurement of species s | |
| Direct process emissions from interceptor j | |
| Processing steps in interceptor j | |
| Flow dependency of node v on node u | |
| Lower bound on flow dependency | |
| Upper bound on flow dependency | |
| Criticality factor | |
| Flowrate from node u to node v | |
| Edge survival | |
| Node functionality | |
| Resilience score |
References
- Thiel, G.P.; Stark, A.K. To Decarbonize Industry, We Must Decarbonize Heat. Joule 2021, 5, 531–550. [Google Scholar] [CrossRef]
- Rogelj, J.; Popp, A.; Calvin, K.V.; Luderer, G.; Emmerling, J.; Gernaat, D.; Fujimori, S.; Strefler, J.; Hasegawa, T.; Marangoni, G.; et al. Scenarios towards Limiting Global Mean Temperature Increase below 1.5 °C. Nat. Clim. Change 2018, 8, 325–332. [Google Scholar] [CrossRef]
- Zanon-Zotin, M.; Baptista, L.B.; Rochedo, P.R.R.; Szklo, A.; Schaeffer, R. Industrial Sector Pathways to a Well-below 2 °C World: A Global Integrated Assessment Perspective. Appl. Energy 2025, 381, 125173. [Google Scholar] [CrossRef]
- Gabrielli, P.; Rosa, L.; Gazzani, M.; Meys, R.; Bardow, A.; Mazzotti, M.; Sansavini, G. Net-Zero Emissions Chemical Industry in a World of Limited Resources. One Earth 2023, 6, 682–704. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Daehn, K.; Basuhi, R.; Gregory, J.; Berlinger, M.; Somjit, V.; Olivetti, E.A. Innovations to Decarbonize Materials Industries. Nat. Rev. Mater. 2022, 7, 275–294. [Google Scholar] [CrossRef]
- Siemon, L.; Dickel, K.; Mennenga, M. Collaborative Energy Transformation Measures for Industrial Decarbonization: A System of Systems Engineering Challenge. In Proceedings of the 2025 20th Annual System of Systems Engineering Conference (SoSE), Tirana, Albania, 8–11 June 2025; pp. 1–6. [Google Scholar]
- Pauliuk, S.; Heeren, N.; Berrill, P.; Fishman, T.; Nistad, A.; Tu, Q.; Wolfram, P.; Hertwich, E.G. Global Scenarios of Resource and Emission Savings from Material Efficiency in Residential Buildings and Cars. Nat. Commun. 2021, 12, 5097. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Liu, X.; Li, S.; Zhang, C.; Yang, S. A Review on Recent Progress, Challenges and Perspective of Battery Thermal Management System. Int. J. Heat Mass Transf. 2021, 167, 120834. [Google Scholar] [CrossRef]
- den Hond, F. Industrial Ecology. In International Encyclopedia of the Social & Behavioral Sciences; Smelser, N.J., Baltes, P.B., Eds.; Pergamon: Oxford, UK, 2001; pp. 7320–7326. ISBN 978-0-08-043076-8. [Google Scholar]
- Chertow, M.R. INDUSTRIAL SYMBIOSIS: Literature and Taxonomy. Annu. Rev. Energy Environ. 2000, 25, 313–337. [Google Scholar] [CrossRef]
- Perrucci, D.V.; Aktaş, C.B.; Sorentino, J.; Akanbi, H.; Curabba, J. A Review of International Eco-Industrial Parks for Implementation Success in the United States. City Environ. Interact. 2022, 16, 100086. [Google Scholar] [CrossRef]
- Andiappan, V.; Wan, Y.K.; Ng, D.K.S. Process Systems Engineering for Decarbonisation Strategies and Systems. Process Integr. Optim. Sustain. 2021, 5, 173–174. [Google Scholar] [CrossRef]
- Noureldin, M.M.B.; El-Halwagi, M.M. Synthesis of C-H-O Symbiosis Networks. AIChE J. 2015, 61, 1242–1262. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. A Shortcut Approach to the Multi-Scale Atomic Targeting and Design of C–H–O Symbiosis Networks. Process Integr. Optim. Sustain. 2017, 1, 3–13. [Google Scholar] [CrossRef]
- Topolski, K.; Noureldin, M.M.B.; Eljack, F.T.; El-Halwagi, M.M. An Anchor-Tenant Approach to the Synthesis of Carbon-Hydrogen-Oxygen Symbiosis Networks. Comput. Chem. Eng. 2018, 116, 80–90. [Google Scholar] [CrossRef]
- Topolski, K.; Lira-Barragán, L.F.; Panu, M.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Integrating Mass and Energy through the Anchor-Tenant Approach for the Synthesis of Carbon-Hydrogen-Oxygen Symbiosis Networks. Ind. Eng. Chem. Res. 2019, 58, 16761–16776. [Google Scholar] [CrossRef]
- Al-Fadhli, F.M.; Mukherjee, R.; Wang, W.; El-Halwagi, M.M. Design of Multiperiod C–H–O Symbiosis Networks. ACS Sustain. Chem. Eng. 2018, 6, 9130–9136. [Google Scholar] [CrossRef]
- Goh, Q.H.; Farouk, A.A.; Lee, J.-Y.; Chew, I.M.L. Synthesis of a Multiperiod C–H–O Symbiosis Network for the Potential Valorization of Glycerol to PHA Production. Ind. Eng. Chem. Res. 2022, 61, 16368–16382. [Google Scholar] [CrossRef]
- Mukherjee, R.; El-Halwagi, M.M. Reliability of C-H-O Symbiosis Networks under Source Streams Uncertainty. Smart Sustain. Manuf. Syst. 2018, 2, 132–153. [Google Scholar] [CrossRef]
- Juárez-García, M.; Ponce-Ortega, J.M.; El-Halwagi, M.M. A Disjunctive Programming Approach for Optimizing Carbon, Hydrogen, and Oxygen Symbiosis Networks. Process Integr. Optim. Sustain. 2019, 3, 199–212. [Google Scholar] [CrossRef]
- Panu, M.; Topolski, K.; Abrash, S.; El-Halwagi, M.M. CO2 Footprint Reduction via the Optimal Design of Carbon-Hydrogen-Oxygen SYmbiosis Networks (CHOSYNs). Chem. Eng. Sci. 2019, 203, 1–11. [Google Scholar] [CrossRef]
- Farouk, A.A.; El-Halwagi, M.M.; Foo, D.C.Y.; Chew, I.M.L. Development of a C–H–O Symbiosis Network during Conceptual Design via Economic, Sustainability, and Safety Metrics. ACS Sustain. Chem. Eng. 2021, 9, 3735–3749. [Google Scholar] [CrossRef]
- Juárez-García, M.; El-Halwagi, M.M.; Ponce-Ortega, J.M. Systematic Approach for Synthesizing Carbon–Hydrogen–Oxygen Networks Involving Detailed Process Simulations. Ind. Eng. Chem. Res. 2021, 60, 16378–16393. [Google Scholar] [CrossRef]
- Juárez-García, M.; Segovia-Hernández, J.G.; Ponce-Ortega, J.M.; Contreras-Zarazúa, G. Controllability Evaluation of the Separation Zones of a Carbon-Hydrogen-Oxygen Symbiosis Network through the SVD Technique: Conventional and Intensified Options. Chem. Eng. Process- Process Intensif. 2024, 197, 109695. [Google Scholar] [CrossRef]
- Lei, Z.; Yang, Y.; Hui, W.; Liu, G. Modular Design Approach of Chemical Processes Based on Carbon-Hydrogen-Oxygen Symbiosis Networks. Energy 2025, 331, 137022. [Google Scholar] [CrossRef]
- El-Halwagi, M.M.; Sengupta, D.; Pistikopoulos, E.N.; Sammons, J.; Eljack, F.; Kazi, M.-K. Disaster-Resilient Design of Manufacturing Facilities Through Process Integration: Principal Strategies, Perspectives, and Research Challenges. Front. Sustain. 2020, 1, 595961. [Google Scholar] [CrossRef]
- Gross, S.; Stelzenmüller, C. Europe’s Messy Russian Gas Divorce; The Brookings Institution: Washington, DC, USA, 2024. [Google Scholar]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A Review of Definitions and Measures of System Resilience. Reliab. Eng. Syst. Saf. 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Ayyub, B.M. Systems Resilience for Multihazard Environments: Definition, Metrics, and Valuation for Decision Making. Risk Anal. 2014, 34, 340–355. [Google Scholar] [CrossRef]
- Newman, M.E.J. The Structure and Function of Complex Networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective Dynamics of ‘Small-World’ Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Ruth, M. Exploring the Resilience of Industrial Ecosystems. J. Environ. Manag. 2013, 122, 65–75. [Google Scholar] [CrossRef]
- Zeng, Y.; Xiao, R.; Li, X. A Resilience Approach to Symbiosis Networks of Ecoindustrial Parks Based on Cascading Failure Model. Math. Probl. Eng. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Chopra, S.S.; Khanna, V. Understanding Resilience in Industrial Symbiosis Networks: Insights from Network Analysis. J. Environ. Manag. 2014, 141, 86–94. [Google Scholar] [CrossRef]
- Li, Y.; Shi, L. The Resilience of Interdependent Industrial Symbiosis Networks: A Case of Yixing Economic and Technological Development Zone. J. Ind. Ecol. 2015, 19, 264–273. [Google Scholar] [CrossRef]
- Xiao, Z.; Cao, B.; Sun, J.; Zhou, G. Culture of the Stability in an Eco-Industrial System Centered on Complex Network Theory. J. Clean. Prod. 2016, 113, 730–742. [Google Scholar] [CrossRef]
- Fraccascia, L.; Giannoccaro, I.; Albino, V. Rethinking Resilience in Industrial Symbiosis: Conceptualization and Measurements. Ecol. Econ. 2017, 137, 148–162. [Google Scholar] [CrossRef]
- Li, X.; Xiao, R. Analyzing Network Topological Characteristics of Eco-Industrial Parks from the Perspective of Resilience: A Case Study. Ecol. Indic. 2017, 74, 403–413. [Google Scholar] [CrossRef]
- Liu, K.; Wang, X.; Yan, Y. Network Analysis of Industrial Symbiosis in Chemical Industrial Parks: A Case Study of Nanjing Jiangbei New Materials High-Tech Park. Sustainability 2022, 14, 1381. [Google Scholar] [CrossRef]
- Valenzuela-Venegas, G.; Henríquez-Henríquez, F.; Boix, M.; Montastruc, L.; Arenas-Araya, F.; Miranda-Pérez, J.; Díaz-Alvarado, F.A. A Resilience Indicator for Eco-Industrial Parks. J. Clean. Prod. 2018, 174, 807–820. [Google Scholar] [CrossRef]
- Valenzuela-Venegas, G.; Vera-Hofmann, G.; Díaz-Alvarado, F.A. Design of Sustainable and Resilient Eco-Industrial Parks: Planning the Flows Integration Network through Multi-Objective Optimization. J. Clean. Prod. 2020, 243, 118610. [Google Scholar] [CrossRef]
- Thun, S.Q.; Chew, I.M.L. Resilience Evaluation of Active and Passive Redundancy Using Carbon-Hydrogen-Oxygen Symbiosis Network—An Integrated and Post-Design Analysis. J. Clean. Prod. 2024, 476, 143736. [Google Scholar] [CrossRef]
- Gopalakrishnan, M.; Ponce-Ortega, J.M.; El-Halwagi, M.M. A Systems Approach for Process Simplification through Process Integration. Chem. Eng. Technol. 2012, 35, 1262–1272. [Google Scholar] [CrossRef]
- Zhang, C.; El-Halwagi, M.M. Chemical Engineering Progress; American Institute of Chemical Engineers: New York, NY, USA, 2017; pp. 28–32. [Google Scholar]
- Mavrotas, G. Effective Implementation of the ε-Constraint Method in Multi-Objective Mathematical Programming Problems. Appl. Math. Comput. 2009, 213, 455–465. [Google Scholar] [CrossRef]
- Hosseini, S.; Ivanov, D.; Dolgui, A. Review of Quantitative Methods for Supply Chain Resilience Analysis. Transp. Res. PART E-Logist. Transp. Rev. 2019, 125, 285–307. [Google Scholar] [CrossRef]
- Chrisandina, N.J.; Vedant, S.; Iakovou, E.; Pistikopoulos, E.N.; El-Halwagi, M.M. Metrics and Methods for Resilience-Aware Design of Process Systems: Advances and Challenges. Curr. Opin. Chem. Eng. 2024, 43, 100984. [Google Scholar] [CrossRef]
- Gong, J.; You, F. Resilient Design and Operations of Process Systems: Nonlinear Adaptive Robust Optimization Model and Algorithm for Resilience Analysis and Enhancement. Comput. Chem. Eng. 2018, 116, 231–252. [Google Scholar] [CrossRef]
- Farouk, A.A.; Chew, I.M.L. Development of a Simultaneous Mass-Water Carbon-Hydrogen-Oxygen Symbiosis Network. Sustain. Prod. Consum. 2021, 28, 419–435. [Google Scholar] [CrossRef]
- De Klerk, A. Fischer-Tropsch Synthesis. In Fischer-Tropsch Refining; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 73–103. ISBN 978-3-527-63560-3. [Google Scholar]
- Stöcker, M. Methanol-to-Hydrocarbons: Catalytic Materials and Their Behavior1. Microporous Mesoporous Mater. 1999, 29, 3–48. [Google Scholar] [CrossRef]
- Medrano-García, J.D.; Ruiz-Femenia, R.; Caballero, J.A. Revisiting Classic Acetic Acid Synthesis: Optimal Hydrogen Consumption and Carbon Dioxide Utilization. In Computer Aided Chemical Engineering, Proceedings of the 29 European Symposium on Computer Aided Process Engineering, Eindhoven, The Netherlands, 16–19 June 2019; Kiss, A.A., Zondervan, E., Lakerveld, R., Özkan, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 46, pp. 145–150. [Google Scholar]
- Cuevas-Castillo, G.A.; Michailos, S.; Akram, M.; Hughes, K.; Ingham, D.; Pourkashanian, M. Techno Economic and Life Cycle Assessment of Olefin Production through CO2 Hydrogenation within the Power-to-X Concept. J. Clean. Prod. 2024, 469, 143143. [Google Scholar] [CrossRef]
- Medrano-García, J.D.; Calvo-Serrano, R.; Tian, H.; Guillén-Gosálbez, G. Win–Win More Sustainable Routes for Acetic Acid Synthesis. ACS Sustain. Chem. Eng. 2025, 13, 1522–1531. [Google Scholar] [CrossRef]
- Almaraz, O.; Riley, J.; Palanki, S. Technoeconomic Analysis of Microwave-Assisted Dry Reforming Integrated with Chemical Looping for Production of Methanol. Ind. Eng. Chem. Res. 2025, 64, 12074–12086. [Google Scholar] [CrossRef]
- Rosner, F.; Papadias, D.; Brooks, K.; Yoro, K.; Ahluwalia, R.; Autrey, T.; Breunig, H. Green Steel: Design and Cost Analysis of Hydrogen-Based Direct Iron Reduction. Energy Environ. Sci. 2023, 16, 4121–4134. [Google Scholar] [CrossRef]
- Awani, K.; Khallaghi, N.; Kumar, V.; Nabavi, S.A. Techno-Economic Assessment of an Integrated GTL Facility for Urea Production. J. CO2 Util. 2025, 99, 103157. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Hsieh, W.; Chang, H.; Ho, C.-D. Design and Economic Analysis of Industrial-Scale Methanol-to-Olefins Plants. J. Taiwan Inst. Chem. Eng. 2022, 130, 103893. [Google Scholar] [CrossRef]
- Devkota, S.; Karmacharya, P.; Maharjan, S.; Khatiwada, D.; Uprety, B. Decarbonizing Urea: Techno-Economic and Environmental Analysis of a Model Hydroelectricity and Carbon Capture Based Green Urea Production. Appl. Energy 2024, 372, 123789. [Google Scholar] [CrossRef]
- Jiménez, R.X.; Young, A.F.; Fernandes, H.L.S. Propylene Glycol from Glycerol: Process Evaluation and Break-Even Price Determination. Renew. Energy 2020, 158, 181–191. [Google Scholar] [CrossRef]
- Apostolakou, A.A.; Kookos, I.K.; Marazioti, C.; Angelopoulos, K.C. Techno-Economic Analysis of a Biodiesel Production Process from Vegetable Oils. Fuel Process. Technol. 2009, 90, 1023–1031. [Google Scholar] [CrossRef]
- Kofler, R.; Campion, N.; Hillestad, M.; Meesenburg, W.; Clausen, L.R. Techno-Economic Analysis of Dimethyl Ether Production from Different Biomass Resources and Off-Grid Renewable Electricity. Energy Fuels 2024, 38, 8777–8803. [Google Scholar] [CrossRef]
- Mavrotas, G.; Florios, K. An Improved Version of the Augmented ε-Constraint Method (AUGMECON2) for Finding the Exact Pareto Set in Multi-Objective Integer Programming Problems. Appl. Math. Comput. 2013, 219, 9652–9669. [Google Scholar] [CrossRef]
- Nikas, A.; Fountoulakis, A.; Forouli, A.; Doukas, H. A Robust Augmented ε-Constraint Method (AUGMECON-R) for Finding Exact Solutions of Multi-Objective Linear Programming Problems. Oper. Res. Int. J. 2022, 22, 1291–1332. [Google Scholar] [CrossRef]
- Bles, W.; Paterakis, N.; van Oers, Y.; Torres, D. Pyaugmecon: 1.0.8; Zenodo: Geneva, Switzerland, 2024. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Houston, TX, USA, 2025. [Google Scholar]
- Bynum, M.L.; Hackebeil, G.A.; Hart, W.E.; Laird, C.D.; Nicholson, B.L.; Siirola, J.D.; Watson, J.-P.; Woodruff, D.L. Pyomo—Optimization Modeling in Python; Springer Optimization and Its Applications; Springer International Publishing: Cham, Switzerland, 2021; Volume 67, ISBN 978-3-030-68927-8. [Google Scholar]
- Hart, W.E.; Watson, J.-P.; Woodruff, D.L. Pyomo: Modeling and Solving Mathematical Programs in Python. Math. Prog. Comp. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function Using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; Varoquaux, G., Vaught, T., Millman, J., Eds.; SciPy Organizers: Pasadena, CA, USA, 2008; pp. 11–15. [Google Scholar]

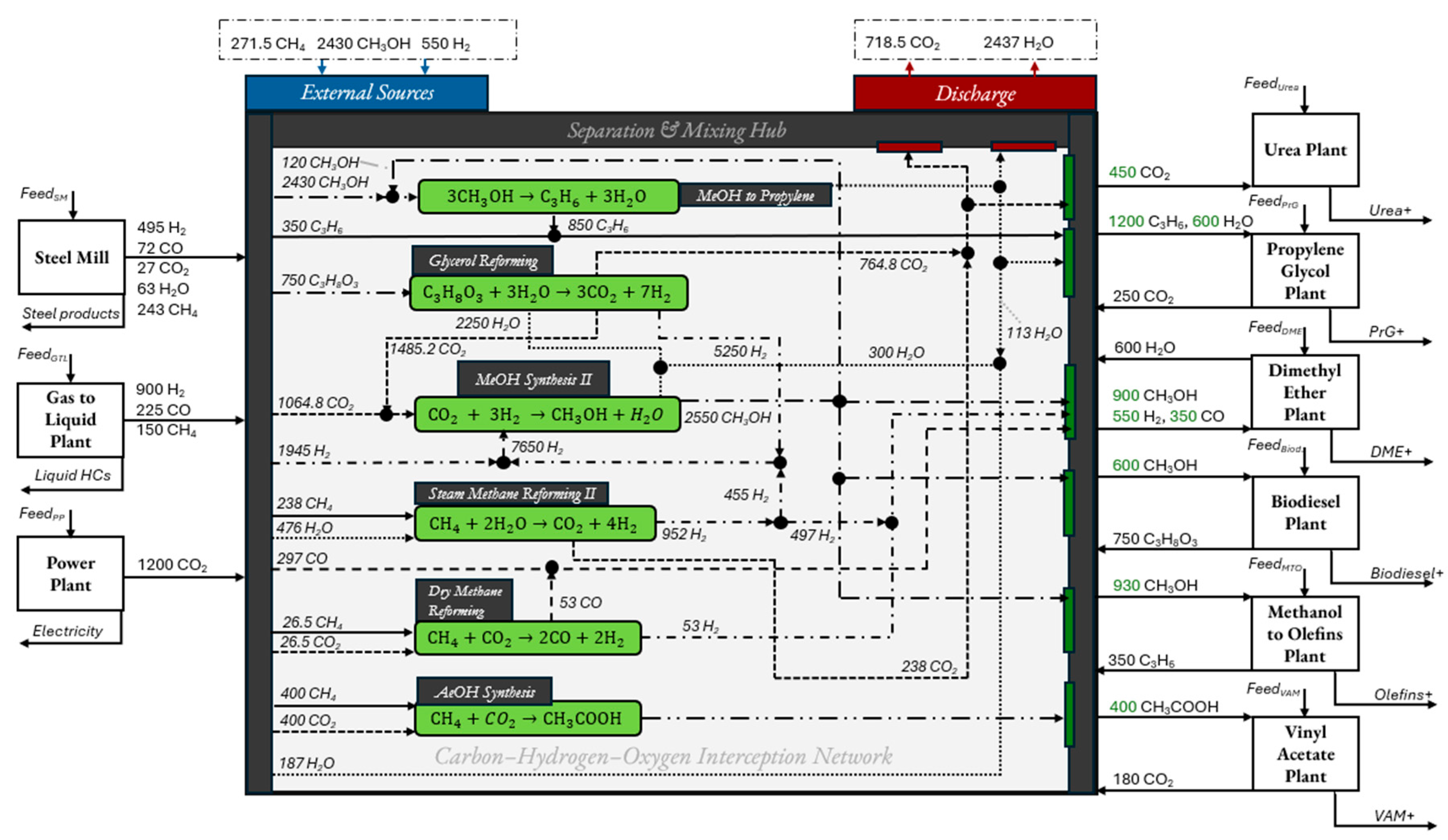

| Plants | Raw Material | Product | Governing Chemical Reaction |
|---|---|---|---|
| Power | Natural gas | Electricity | |
| Steel Mill | Iron ore/Coal | Steel products | |
| GTL | Natural gas | Syngas | The Fischer-Tropsch synthesis reactions |
| MTO | Methanol | Olefins | |
| PG | Propylene | Propylene glycol | |
| DME | Syn gas/Methanol | Dimethyl ether | |
| BD | Palm oil and methanol | Biodiesel | |
| VAM | Ethylene/acetic acid | VAM | |
| Urea | Ammonia | Urea |
| Power Plant | Steel Mill | GTL | MTO | PG | DME | BD | VAM | |
|---|---|---|---|---|---|---|---|---|
| Flow (kmol/h) | 1200 | 900 | 1395 | 470 | 250 | 600 | 750 | 180 |
| Component Composition (mol%) | ||||||||
| H2 | 55 | 65 | ||||||
| CO | 8 | 16 | ||||||
| CO2 | 100 | 3 | 180 | |||||
| H2O | 7 | 600 | ||||||
| CH4 | 27 | 11 | ||||||
| C2H4 | 9 | 120 | ||||||
| C3H6 | 350 | 250 | ||||||
| C3H8O3 | 750 | |||||||
| Demand In | MTO | Urea | BD | VAM | PG | DME |
|---|---|---|---|---|---|---|
| Flow (kmol/h) | ||||||
| H2 | 550 | |||||
| CO | 350 | |||||
| CO2 | 450 | |||||
| H2O | 600 | |||||
| C2H4 | 400 | |||||
| C3H6 | 1200 | |||||
| CH3OH | 930 | 600 | 900 | |||
| CH3COOH | 400 |
| j | Description | Stoichiometric Formula | Cost a | Steps a | Emissions a |
|---|---|---|---|---|---|
| 1 | Methanol Synthesis I | 0.92 | 6 | 0.224 | |
| 2 | Methanol Synthesis II | 1.50 | 5 | 0.224 | |
| 3 | Methanol Synthesis III b | 1.00 | 5 | 0.400 | |
| 4 | Acetic Acid Synthesis I | 0.39 | 6 | 2.556 | |
| 5 | Acetic Acid Synthesis II | 0.39 | 2 | 2.045 | |
| 6 | Acetic Acid Synthesis III | 0.60 | 5 | 2.045 | |
| 7 | Steam Methane Reforming I | 0.95 | 4 | 0.425 | |
| 8 | Steam Methane Reforming II | 0.95 | 4 | 0.425 | |
| 9 | Dry Reforming of Methane | 1.33 | 4 | 0.300 | |
| 10 | Forward Water-Gas Shift Reaction b | 0.20 | 2 | 0.400 | |
| 11 | Reverse Water-Gas Shift Reaction b | 0.20 | 2 | 0.400 | |
| 12 | Glycerol Reforming | 3.25 | 5 | 1.307 | |
| 13 | Methanol to Propylene | 1.44 | 4 | 4.660 |
| Commodity | Price |
|---|---|
| Electricity a | $0.3 per kWh |
| Finished steel products | $600 per ton |
| Liquid hydrocarbons | $750 per ton |
| Olefins | $800 per ton |
| Urea | $300 per ton |
| Propylene glycol | $900 per ton |
| Biodiesel | $1200 per ton |
| Vinyl acetate monomer a | $1200 per ton |
| Dimethyl ether | $900 per ton |
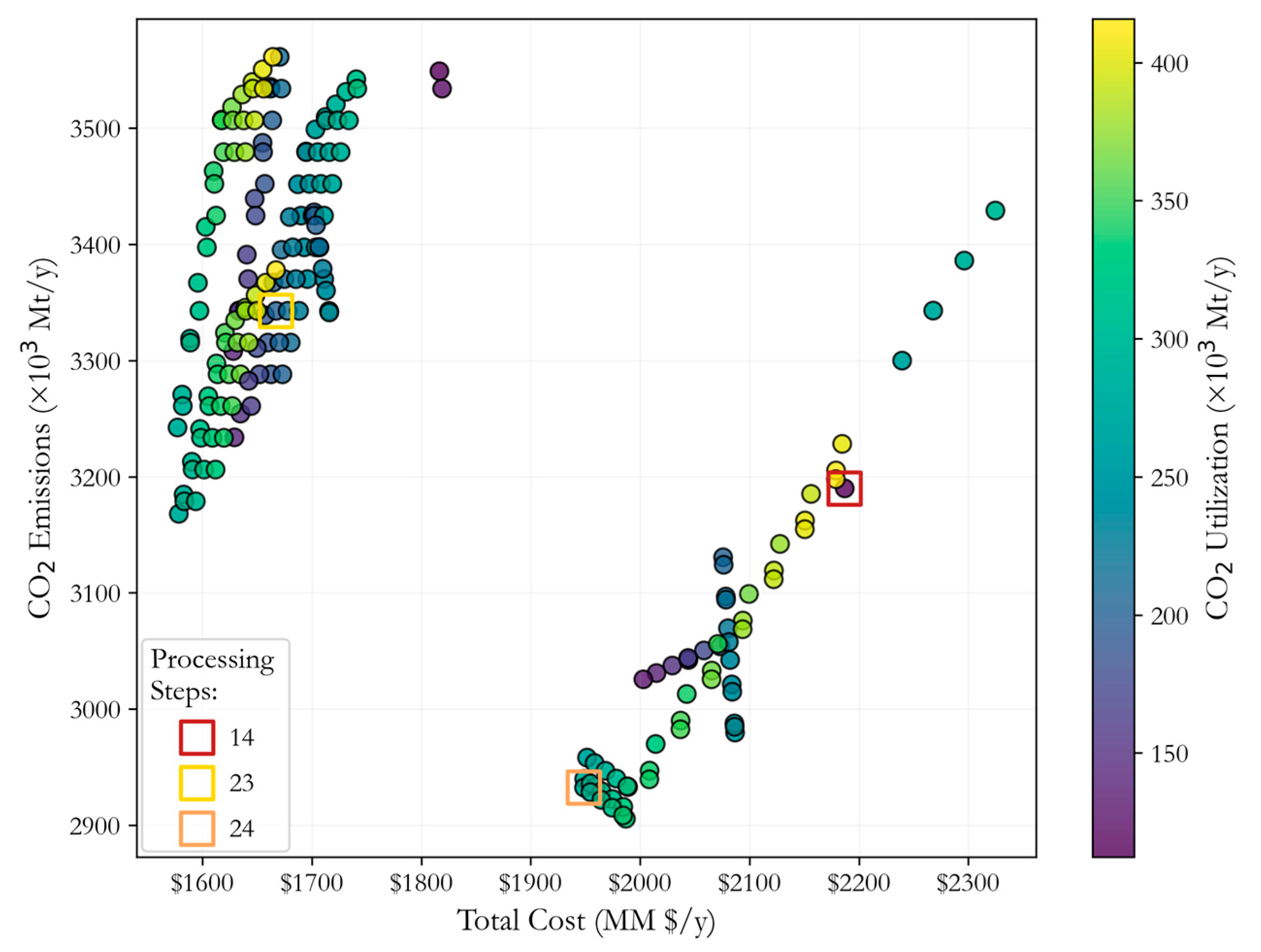
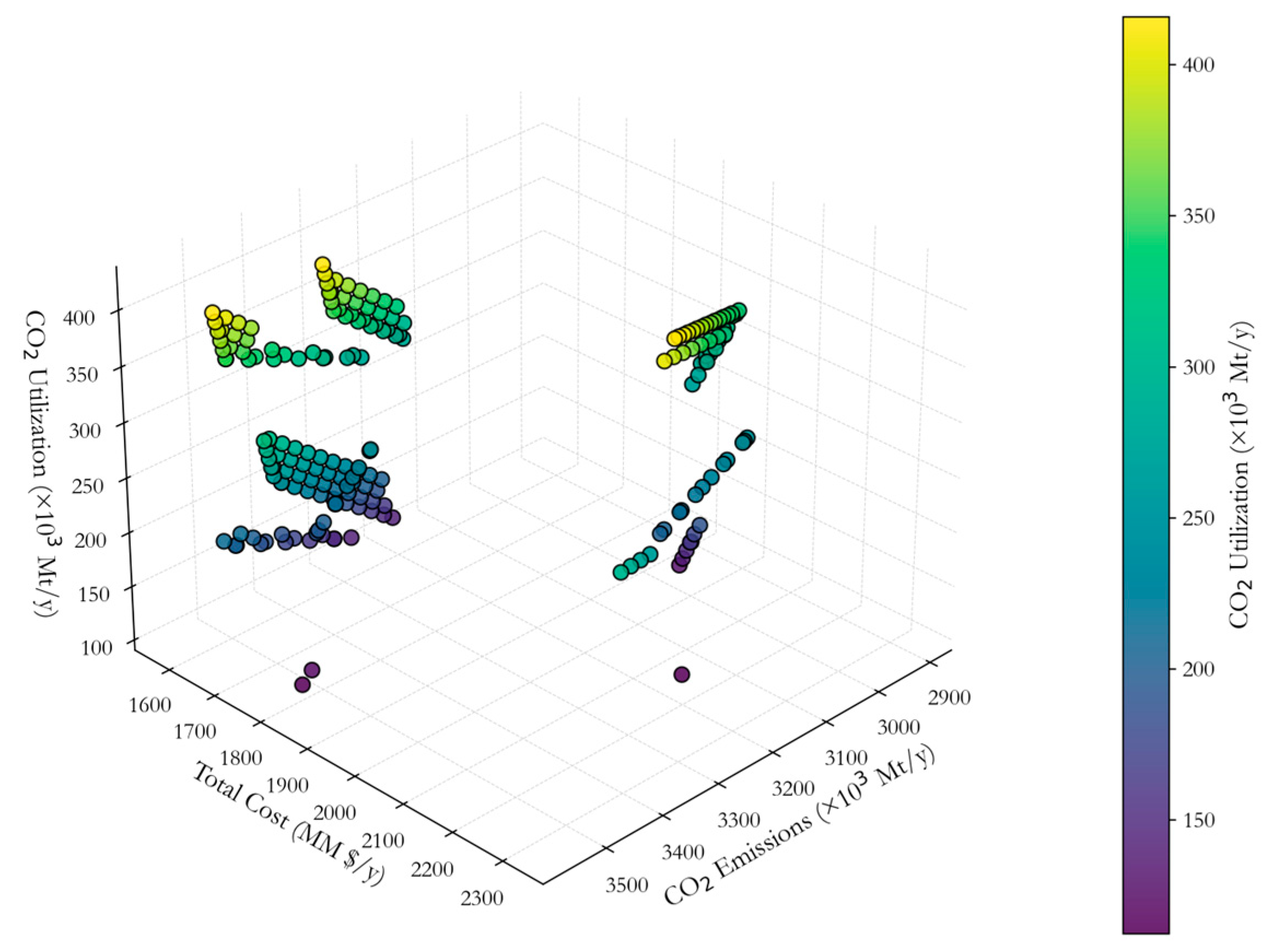
| Cost a | CO2-eq Emissions a | CO2 Utilization a | Processing Steps | |
|---|---|---|---|---|
| Min Cost | $1577 | 3,242,285 | 281,952 | 23 |
| Min CO2-eq Emissions | $1987 | 2,905,573 | 330,352 | 24 |
| Max CO2 Utilization | $1664 | 3,561,255 | 415,829 | 23 |
| Min Processing Steps | $2187 | 3,189,890 | 112,389 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aldawsari, M.; El-Halwagi, M.M. Resilience Assessment and Sustainability Enhancement of Gas and CO2 Utilization via Carbon–Hydrogen–Oxygen Symbiosis Networks. Sustainability 2025, 17, 8622. https://doi.org/10.3390/su17198622
Aldawsari M, El-Halwagi MM. Resilience Assessment and Sustainability Enhancement of Gas and CO2 Utilization via Carbon–Hydrogen–Oxygen Symbiosis Networks. Sustainability. 2025; 17(19):8622. https://doi.org/10.3390/su17198622
Chicago/Turabian StyleAldawsari, Meshal, and Mahmoud M. El-Halwagi. 2025. "Resilience Assessment and Sustainability Enhancement of Gas and CO2 Utilization via Carbon–Hydrogen–Oxygen Symbiosis Networks" Sustainability 17, no. 19: 8622. https://doi.org/10.3390/su17198622
APA StyleAldawsari, M., & El-Halwagi, M. M. (2025). Resilience Assessment and Sustainability Enhancement of Gas and CO2 Utilization via Carbon–Hydrogen–Oxygen Symbiosis Networks. Sustainability, 17(19), 8622. https://doi.org/10.3390/su17198622







