Identification of Microplastic Accumulation Zones in a Tidal River: A Case Study of the Fraser River, British Columbia, Canada
Abstract
1. Introduction
2. Methodology
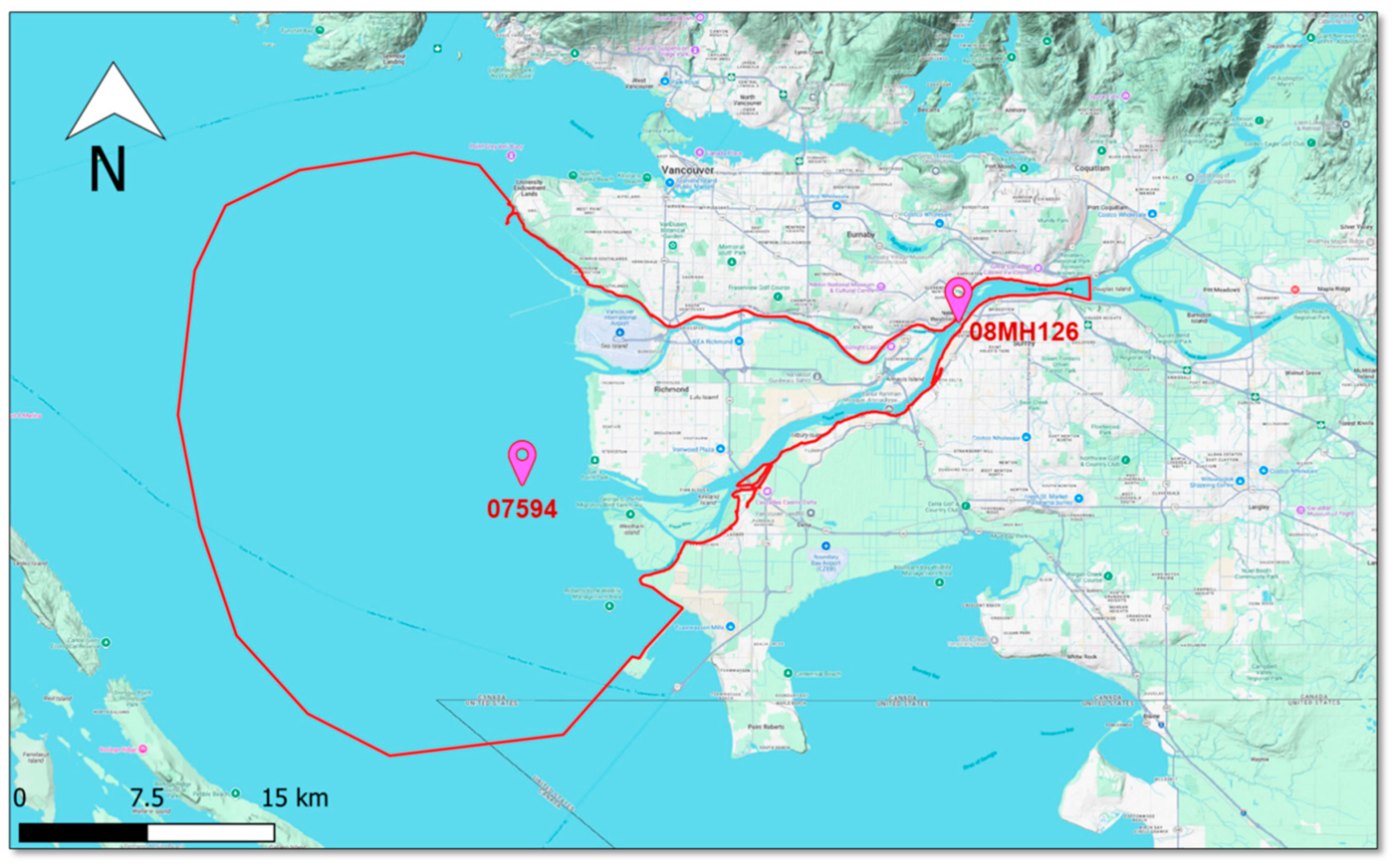
2.1. Study Area
2.2. Hydrodynamic Model
2.3. Particle Tracking Model
2.4. Clustering Algorithm
2.5. Source Identification and Release Scenarios
3. Results and Discussion
3.1. Grid Sensitivity Analysis and Mesh Selection
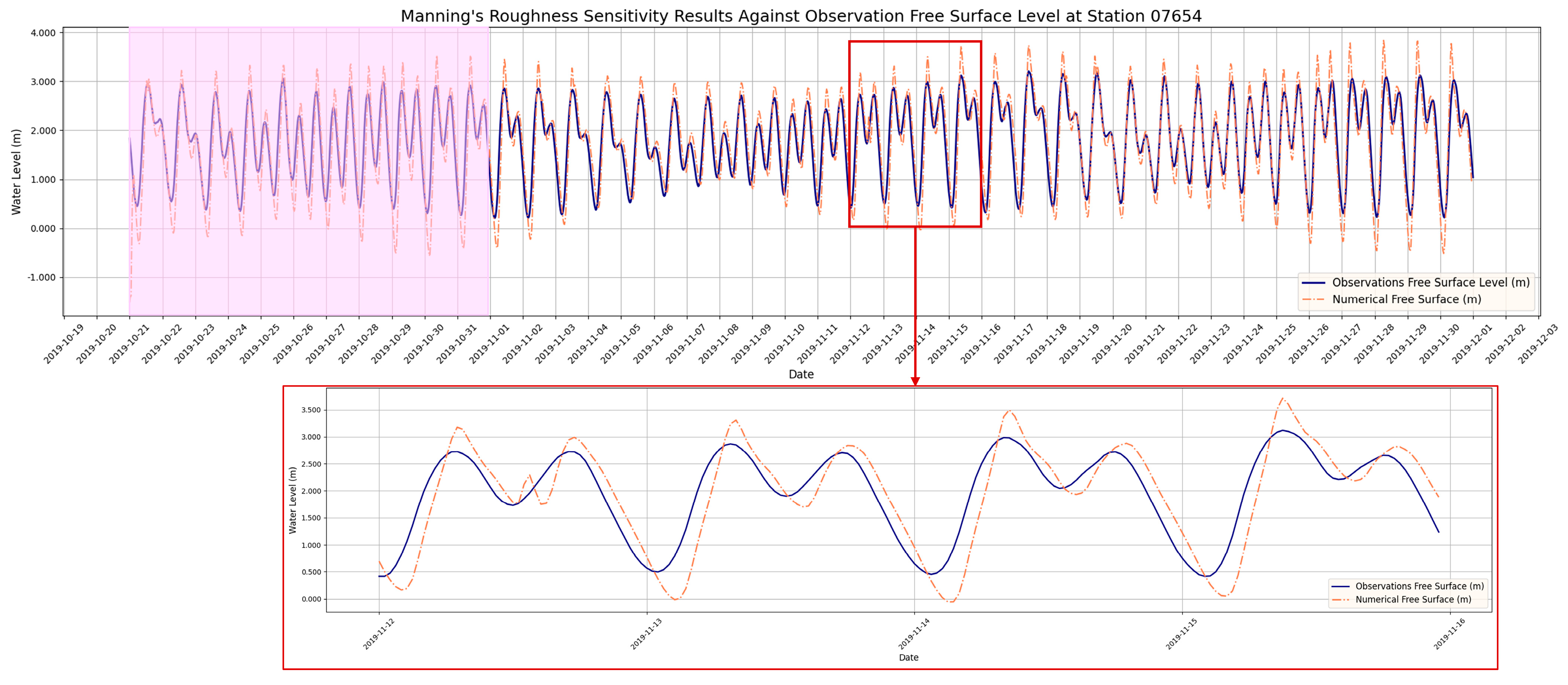
3.2. Hydrodynamic Model Calibration
3.3. Particle Tracking Model Results
4. Conclusions
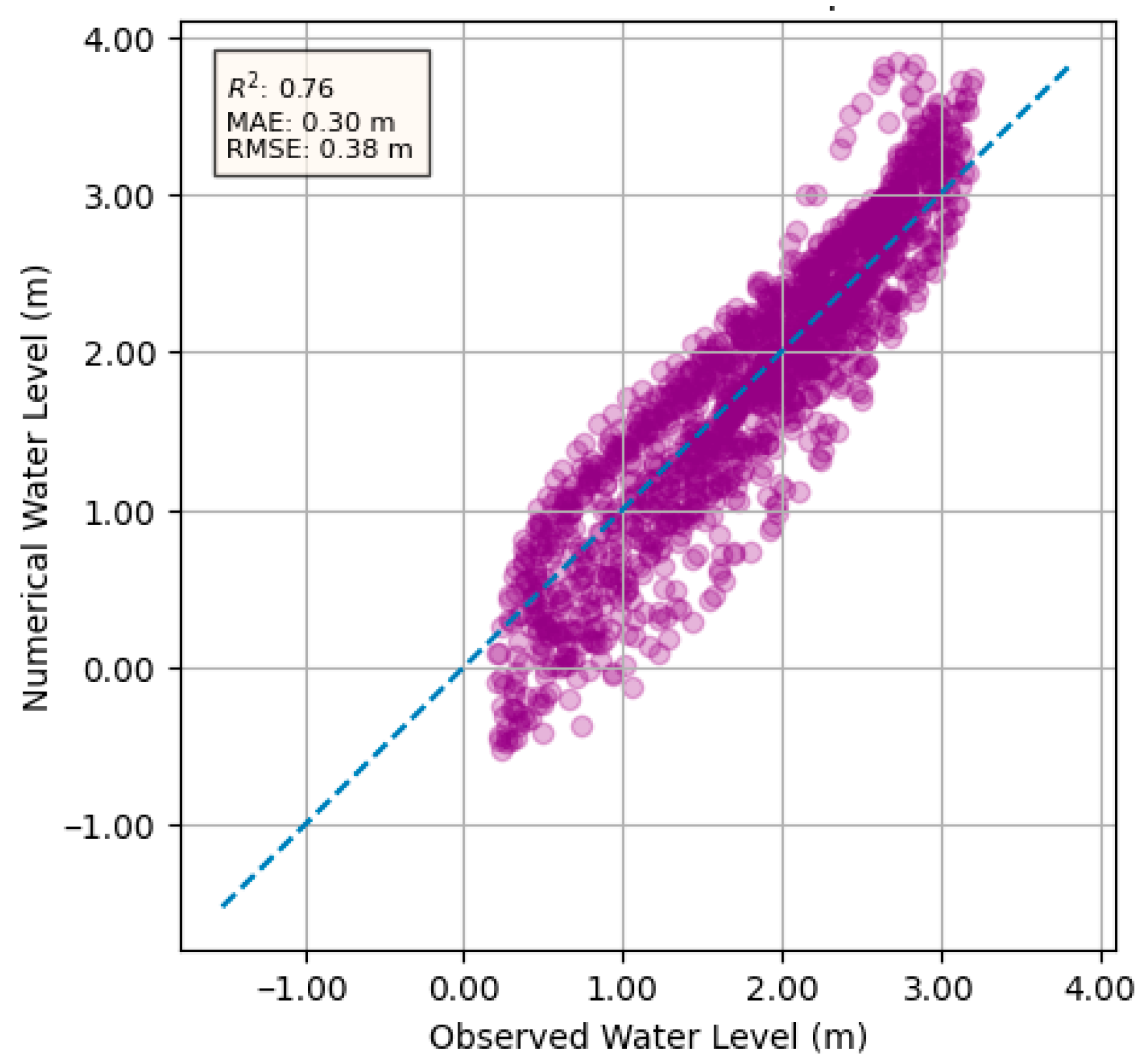
- The hydrodynamic model demonstrated its capability to simulate water levels and velocity fields with acceptable accuracy, validated against observed data with an RMSE of 0.38 m, an MAE of 0.3 m, and an R2 value of 76%. Sensitivity analysis of Manning’s roughness coefficient confirmed that provided the optimal balance between accuracy and error minimization, ensuring reliable simulations and alignment with established practices in riverine modeling.
- The clustering results showed that the detected locations of the accumulation zones were perfectly consistent across all release scenarios, regardless of the number of released microplastic particles at the CSO and WWTP sources.
- The use of OPTICS as part of this methodology proved to be novel and effective, offering a reliable and parameter-flexible approach for identifying density-based microplastic accumulation zones.
- Although the present simulations were carried out for a single hydrodynamic condition, the Fraser River is characterized by pronounced seasonal variation in flow magnitude. High flows during the freshet period may enhance downstream flushing of particles, whereas lower-flow periods may favor localized retention and accumulation. Future modeling work should incorporate seasonal variability to assess how hydrodynamic changes influence the stability and persistence of accumulation zones.
- Future research may also expand on this methodology by integrating additional clustering techniques to trace the sources and receptors of particles in accumulation zones or by exploring the influence of particle interactions in high-density regions. Further extensions may also incorporate external forcing such as wind in the hydrodynamic model, variable particle density, and time-varying release scenarios to better represent the complexity of microplastic transport processes. Additionally, shoreline beaching and wash-off processes, which may influence the long-term retention and re-entrainment of microplastics near riverbanks, were not included in this study but represent valuable areas for future investigation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CaMPSim-3D | Three-dimensional Canadian Microplastic Simulation Model |
| CSO | Combined Sewer Overflow |
| WWTP | Wastewater Treatment Plant |
| OPTICS | Ordering Points to Identify the Clustering Structure |
| HEC-RAS | Hydrologic Engineering Center’s River Analysis System |
| TUFLOW | Two-dimensional Unsteady Flow Software |
| IDW | Inverse Distance Weighting |
| UTM | Universal Transverse Mercator |
| QGIS | Quantum Geographic Information System |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
References
- Masura, J.; Baker, J.; Foster, G.; Arthur, C. Laboratory Methods for the Analysis of Microplastics in the Marine Environment: Recommendations for Quantifying Synthetic Particles in Waters and Sediments; NOAA Technical Memorandum NOS-OR&R-48; NOAA: Silver Spring, MD, USA, 2015. [Google Scholar]
- Petersen, F.; Hubbart, J.A. The occurrence and transport of microplastics: The state of the science. Sci. Total Environ. 2021, 758, 143936. [Google Scholar] [CrossRef]
- Van Melkebeke, M.; Janssen, C.; De Meester, S. Characteristics and Sinking Behavior of Typical Microplastics Including the Potential Effect of Biofouling: Implications for Remediation. Environ. Sci. Technol. 2020, 54, 8668–8680. [Google Scholar] [CrossRef] [PubMed]
- Chubarenko, I.; Bagaev, A.; Zobkov, M.; Esiukova, E. On some physical and dynamical properties of microplastic particles in marine environment. Mar. Pollut. Bull. 2016, 108, 105–112. [Google Scholar] [CrossRef]
- Skalska, K.; Ockelford, A.; Ebdon, J.E.; Cundy, A.B. Riverine microplastics: Behaviour, spatio-temporal variability, and recommendations for standardised sampling and monitoring. J. Water Process Eng. 2020, 38, 101600. [Google Scholar] [CrossRef]
- Li, L.; Li, M.; Deng, H.; Cai, L.; Cai, H.; Yan, B.; Hu, J.; Shi, H. A straightforward method for measuring the range of apparent density of microplastics. Sci. Total Environ. 2018, 639, 367–373. [Google Scholar] [CrossRef]
- Mercogliano, R.; Avio, C.G.; Regoli, F.; Anastasio, A.; Colavita, G.; Santonicola, S. Occurrence of Microplastics in Commercial Seafood under the Perspective of the Human Food Chain. A Review. J. Agric. Food Chem. 2020, 68, 5296–5301. [Google Scholar] [CrossRef]
- Marcharla, E.; Vinayagam, S.; Gnanasekaran, L.; Soto-Moscoso, M.; Chen, W.-H.; Thanigaivel, S.; Ganesan, S. Microplastics in marine ecosystems: A comprehensive review of biological and ecological implications and its mitigation approach using nanotechnology for the sustainable environment. Environ. Res. 2024, 256, 119181. [Google Scholar] [CrossRef]
- Inwati, P.; Verma, D.K.; Harinkhede, H. Impact of Microplastic in Marine Environment and Human Health. Int. J. Sci. Res. Sci. Technol. 2024, 11, 221–231. [Google Scholar]
- Liubartseva, S.; Coppini, G.; Lecci, R.; Creti, S. Regional approach to modeling the transport of floating plastic debris in the Adriatic Sea. Mar. Pollut. Bull. 2016, 103, 115–127. [Google Scholar] [CrossRef]
- Parizi, A.H. Urban Discharge and Fate of Microplastics: Characterizing the Role of Combined Sewer Overflows and Microplastics in the Fraser River in British Columbia. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2022. [Google Scholar] [CrossRef]
- DHI. MIKE 11—A Modeling System for Rivers and Channels; Danish Hydraulic Institute (DHI): Hørsholm, Denmark, 2020. [Google Scholar]
- US Army Corps of Engineers. HEC-RAS River Analysis System—User’s Manual Version 6.0; Hydrologic Engineering Center: Davis, CA, USA, 2020. [Google Scholar]
- Consortium Open℡EMAC-MASCARET. TELEMAC-2D v8p5 User Manual; EDF R&D, Laboratoire National d’Hydraulique et Environnement: Chatou Cedex, France, 2023; 8p. [Google Scholar]
- DHI. MIKE 21—A Two-Dimensional Free-Surface Flow Modeling System; Danish Hydraulic Institute (DHI): Hørsholm, Denmark, 2020. [Google Scholar]
- BMT Group. TUFLOW User Manual—Build 2020-01-AB; BMT: London, UK, 2020. [Google Scholar]
- EDF R&D, Laboratoire National d’Hydraulique et Environnement (LNHE). TELEMAC-3D User Manual, Version 8p5; EDF R&D: Chatou, France, 2024.
- Deltares. Delft3D Flexible Mesh Suite; Deltares: Delft, The Netherlands, 2021. [Google Scholar]
- Flow Science, Inc. FLOW-3D User Manual; Flow Science: Santa Fe, NM, USA, 2022. [Google Scholar]
- Yin, L.; Nie, X.; Deng, G.; Tian, J.; Xiang, Z.; Abbasi, S.; Chen, H.; Zhang, W.; Xiao, R.; Gan, C.; et al. Hydrodynamic driven microplastics in Dongting Lake, China: Quantification of the flux and transportation. J. Hazard. Mater. 2024, 480, 136049. [Google Scholar] [CrossRef]
- Bondelind, M.; Sokolova, E.; Nguyen, A.; Karlsson, D.; Karlsson, A.; Björklund, K. Hydrodynamic modelling of traffic-related microplastics discharged with stormwater into the Göta River in Sweden. Environ. Sci. Pollut. Res. 2020, 27, 24218–24230. [Google Scholar] [CrossRef]
- Institute of Hydraulic Engineering and Water Resources Management, RWTH Aachen University. PELETS-2D: Particle Tracking in Hydrodynamic Models; RWTH Aachen University: Aachen, Germany, 2020. [Google Scholar]
- Ghazizadeh, M.; Rey, A.; Pilechi, A.; Burcher, R.; Drouin, S.S.-O.; Lamontagne, P. A high-performance ray tracing particle tracking model for the simulation of microplastics in inland and coastal aquatic environments. Comput. Phys. Commun. 2025, 307, 109423. [Google Scholar] [CrossRef]
- Ghazizadeh, M.; Pilechi, A.; Lamontagne, P. Numerical simulation of microplastics transport in Saguenay Fjord using ray tracing particle tracking model. In Proceedings of the Canadian Society for Civil Engineering Annual Conference; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. SIGMOD Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD’96: Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Mishra, A.; Siht, E.; Väli, G.; Liblik, T.; Buhhalko, N.; Lips, U. Mapping microplastic pathways and accumulation zones in the Gulf of Finland, Baltic Sea—Insights from modeling. Front. Mar. Sci. 2025, 11, 1524585. [Google Scholar] [CrossRef]
- Thomson, R.E. (Ed.) Oceanography of the British Columbia Coast; Canadian Special Publication of Fisheries and Aquatic Sciences: Ottawa, ON, Canada, 1981; ISBN 0-660-10978-6. [Google Scholar]
- Northwest Hydraulic Consultants (nhc). Fraser River Hydraulic Model Update: Final Report; BC Ministry of Environment: Surrey, BC, Canada; Northwest Hydraulic Consultants: North Vancouver, BC, Canada, 2008. [Google Scholar]
- Masoom, S.; Gu, L. 3D Hydrodynamic Modeling of Lower Fraser River. In Proceedings of the Salish Sea Ecosystem Conference; University Archives, Heritage Resources, Western Libraries; Western Washington University: Seattle, WA, USA, 2018. [Google Scholar]
- Kostaschuk, R.A.; Atwood, L.A. River discharge and tidal controls on salt-wedge position and implications for channel shoaling: Fraser River, British Columbia. Can. J. Civ. Eng. 1990, 17, 452–459. [Google Scholar] [CrossRef]
- Bourdages, M.; Ehrenbrink, B.P.E.; Marsh, S.J.; Gillies, S.L.; Paine, J.K.; Bogaerts, P.; Strangway, A.; Robertson, K.; Groeneweg, A. Presence of Microplastics in the Fraser River, British Columbia. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2017; Volume 2017, p. H31H-1609. [Google Scholar]
- Gillies, S.L.; Chauhan, J.; Brunner, K. Microplastics Found in Lower Fraser River Sediments. In Proceedings of the International Conference on Environmental Science and Technology, Paris, France, 19–20 February 2024. [Google Scholar]
- Babajamaaty, G. Numerical Simulation of Microplastics Transport in a Part of Fraser River and Detection of Accumulation Zones Based on Clustering Methods. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2023. [Google Scholar] [CrossRef]
- Gessler, D.; Hall, B.; Spasojevic, M.; Holly, F.; Pourtaheri, H.; Raphelt, N. Application of 3D Mobile Bed, Hydrodynamic Model. J. Hydraul. Eng. 1999, 125, 737–749. [Google Scholar] [CrossRef]
- Roberts, K.J.; Pringle, W.J.; Westerink, J.J. OceanMesh2D: An Unstructured Mesh Generator for Coastal and Ocean Modeling. Geosci. Model. Dev. 2025, 12, 1847–1868. [Google Scholar] [CrossRef]
- Government of British Columbia Official Shapefiles and Bathymetry Data. 2023. Available online: https://www2.gov.bc.ca/gov/content/data/geographic-data-services (accessed on 29 November 2024).
- Kvale, E.P. The origin of neap–spring tidal cycles. Mar. Geol. 2006, 235, 5–18. [Google Scholar] [CrossRef]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill: Columbus, OH, USA, 1959. [Google Scholar]
- Rodi, W. Turbulence Models and Their Application in Hydraulics: A State-of-the-Art Review, 3rd ed.; Rodi, W., Ed.; Routledge: London, UK, 2017; ISBN 978-0-203-73489-6. [Google Scholar]
- Stacey, M.T.; Monismith, S.G.; Burau, J.R. Observations of Turbulence in a Partially Stratified Estuary. J. Phys. Oceanogr. 1999, 29, 1950–1970. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Tsz Yeung Leung, A.; Stronach, J.; Matthieu, J. Modelling Behaviour of the Salt Wedge in the Fraser River and Its Relationship with Climate and Man-Made Changes. JMSE 2018, 6, 130. [Google Scholar] [CrossRef]
- Government of Canada Historical Hydrometric Data. Available online: https://wateroffice.ec.gc.ca/mainmenu/historical_data_index_e.html (accessed on 29 November 2024).
- Government of Canada Tides, Currents, and Water Levels Stations. Available online: https://www.tides.gc.ca/en/tides-currents-and-water-levels (accessed on 29 November 2024).
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation Project: Beaverton, OR, USA, 2023; Available online: https://qgis.org (accessed on 16 September 2025).
- Jalón-Rojas, I.; Wang, X.H.; Fredj, E. A 3D numerical model to Track Marine Plastic Debris (TrackMPD): Sensitivity of microplastic trajectories and fates to particle dynamical properties and physical processes. Mar. Pollut. Bull. 2019, 141, 256–272. [Google Scholar] [CrossRef]
- Soto-Navarro, J.; Jordá, G.; Deudero, S.; Alomar, C.; Amores, Á.; Compa, M. 3D hotspots of marine litter in the Mediterranean: A modeling study. Mar. Pollut. Bull. 2020, 155, 111159. [Google Scholar] [CrossRef]
- Mansui, J.; Darmon, G.; Ballerini, T.; Van Canneyt, O.; Ourmieres, Y.; Miaud, C. Predicting marine litter accumulation patterns in the Mediterranean basin: Spatio-temporal variability and comparison with empirical data. Prog. Oceanogr. 2020, 182, 102268. [Google Scholar] [CrossRef]
- Pilechi, A.; Mohammadian, A.; Murphy, E. A numerical framework for modeling fate and transport of microplastics in inland and coastal waters. Mar. Pollut. Bull. 2022, 184, 114119. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inform. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics; Le Cam, L.M., Neyman, J., Eds.; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Metro Vancouver. Fraser River Environmental Monitoring Programs Comprehensive Review 2014–2019: Summary Report; Metro Vancouver: Burnaby, BC, Canada, 2019. [Google Scholar]
- Smart, I. (Ed.) Fraser River Protection: An Initial Assessment of the Legal Failure for Cumulative Impacts; Environmental Law Centre: Edmonton, AB, Canada, 2024. [Google Scholar]
- Landos, M. From Pristine to Polluted: How Chemicals and Pollutants Drive Fishery Decline sand Ecosystem Collapse; International Pollutants Elimination Network: Fraser River, BC, Canada, 2024. [Google Scholar]
- McHugh, N. Investigating the Spatial and Temporal Distribution of Microplastics in the Fraser River and Burrard Inlet (British Columbia, Canada). Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2025. [Google Scholar]
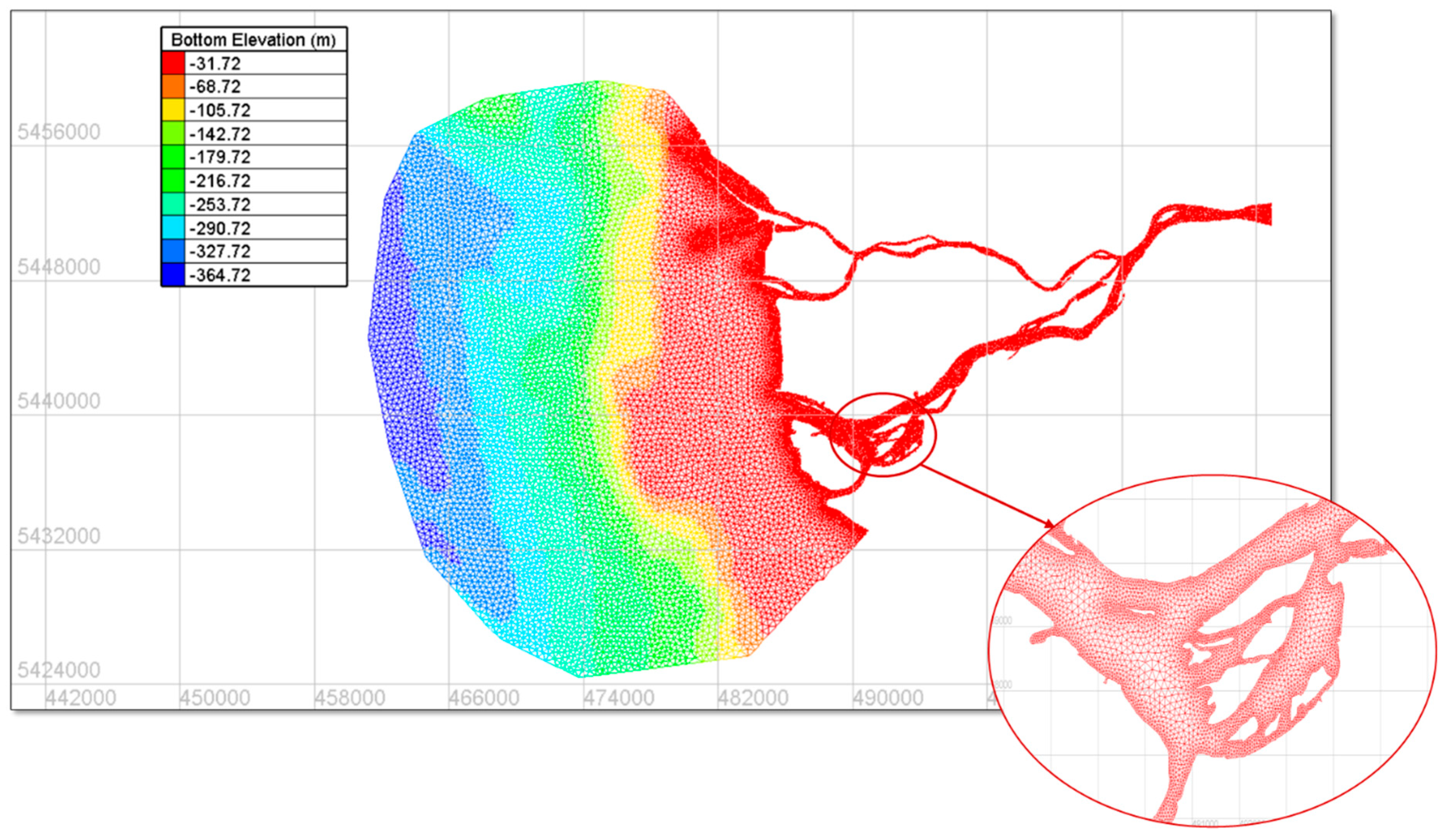



| Mesh Candidate | Minimum Element Size (m) | Maximum Element Size (m) | Maximum Element Size Near Shores (m) | Mesh Gradation | Node Count | Element Count |
|---|---|---|---|---|---|---|
| 1 | 35 | 300 | 25 | 0.13 | 463,245 | 834,480 |
| 2 | 34 | 350 | 20 | 0.1 | 532,710 | 970,800 |
| 3 | 40 | 400 | 25 | 0.1 | 422,730 | 765,150 |
| Manning’s Coefficient | R2 (%) | RMSE (m) | MAE (m) |
|---|---|---|---|
| 0.02 | 73 | 0.4 | 0.31 |
| 0.025 | 75 | 0.38 | 0.3 |
| 0.03 | 76 | 0.38 | 0.3 |
| 0.035 | 76 | 0.38 | 0.3 |
| 0.04 | 74 | 0.39 | 0.31 |
| Particle Count of Release at Each CSO and WWTP Source | Minimum Cluster Size (Percent of Particle Population) | Minimum Number of Samples | Maximum Neighborhood Distance (m) | Cluster Steepness Threshold |
|---|---|---|---|---|
| 30,000 | 0.02 | 400 | 400 | 0.0005 |
| 40,000 | 0.019 | 400 | 500 | 0.0005 |
| 50,000 | 0.024 | 700 | 500 | 0.0005 |
| 60,000 | 0.024 | 700 | 500 | 0.0005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamidiaala, S.; Babajamaaty, G.; Mohammadian, A.; Pilechi, A.; Ghazizadeh, M. Identification of Microplastic Accumulation Zones in a Tidal River: A Case Study of the Fraser River, British Columbia, Canada. Sustainability 2025, 17, 8591. https://doi.org/10.3390/su17198591
Hamidiaala S, Babajamaaty G, Mohammadian A, Pilechi A, Ghazizadeh M. Identification of Microplastic Accumulation Zones in a Tidal River: A Case Study of the Fraser River, British Columbia, Canada. Sustainability. 2025; 17(19):8591. https://doi.org/10.3390/su17198591
Chicago/Turabian StyleHamidiaala, Shahrzad, Golnoosh Babajamaaty, Abdolmajid Mohammadian, Abolghasem Pilechi, and Mohammad Ghazizadeh. 2025. "Identification of Microplastic Accumulation Zones in a Tidal River: A Case Study of the Fraser River, British Columbia, Canada" Sustainability 17, no. 19: 8591. https://doi.org/10.3390/su17198591
APA StyleHamidiaala, S., Babajamaaty, G., Mohammadian, A., Pilechi, A., & Ghazizadeh, M. (2025). Identification of Microplastic Accumulation Zones in a Tidal River: A Case Study of the Fraser River, British Columbia, Canada. Sustainability, 17(19), 8591. https://doi.org/10.3390/su17198591







