Assessing Human Vulnerability to Urban Flood in Southern Sardinia (IT)

Abstract

The increasing frequency and magnitude of flood-related disasters has led to adopting advanced flood models to provide a better understanding of flood vulnerability, particularly for human lives. Human flood vulnerability assessment is a primary objective when planning and designing in urban areas. Results of a numerical model in the coastal hamlet of Solanas (Sardinia, IT), in terms of water velocity and depth, have been processed using the empirical method of the regional legislation (RAS), as suggested by the National Network for Environmental Protection. Vulnerability maps and statistical parameters were compared and benchmarked with the DEFRA method, which is largely used in the UK and is regarded as a state-of-the-art empirical approach. The main findings from the benchmark results between the DEFRA and RAS methods suggest that the applicability threshold of the RAS method can significantly underestimate the pedestrian vulnerability to urban flood in Solanas, and this paper suggests a preliminary step in improving that method could be a tentative threshold value of 0.10 m depth to assure a more realistic evaluation of human vulnerability in Solanas.

1. Introduction

Under climate change and urbanization, flood risk management has become a major issue for many urban areas [1]. Flood mapping is a central element of flood risk management [2], producing flood hazard maps which show the extent of flooded areas for various scenarios as requested by the European Flood Directive 2007/60.

Some small ungauged basins are those where rainfall is assumed to be spatially uniform and measurements of flood peak discharges are not available [3]. In small ungauged basins, theoretical statistical distributions of flood frequency cannot be applied as they require calibration, and the preferred models are the conceptual ones that reproduce, in a simplified form, the hydrologic and hydraulic mechanisms governing the formation of the design hydrograph. The basic, simplified assumption and the lack of a calibration/validation phase make conceptual models low in reliability for flood mapping. Recently, several simple conceptual rainfall–runoff models have been proposed [4].

The combination of hydrologic and hydraulic models for flood mapping has various levels of complexity in small ungauged basins, e.g., hydrodynamic models ranging from 1D or 2D models to advanced, more rare, 3D models [5]. The 1D hydraulic models, for steady and unsteady flow analysis [6,7], do not provide the properties’ flow field (i.e., velocity and direction), which is crucial to assess vulnerabilities in urban areas in the existing or planned configuration [8]. Although advanced 2D hydraulic approaches are more computationally expensive than 1D models, requiring long processing times that limit their spatial and temporal scope [9], they are recommended for detailed local spatial scale areas and complex urban settings where the 1D hypothesis is often not applicable [10]. Examples of 2D hydrodynamic models are DELFT3D, HEC-RAS, MIKE21, and TELEMAC, and they are based on the numerical solution to the 2D shallow water equations (SWEs) on a grid to produce accurate flow fields in flooded urban areas [11]. Nevertheless, large inherent uncertainties in model structure, model parameters, boundary conditions, or input data still limit the accuracy of 2D models in small urban and ungauged basins [12]. Quantification of model uncertainty in an urban basin is currently an active and attractive area of research [13].

Several studies on urban flood risk have focused on vulnerability in terms of concept, definition, and quantification [14]. Physical and social aspects are the key components of urban flood vulnerability, mainly carrying, on a technical ground, the relationship between Urbs and Civitas, city and citizenship. In addition to the vulnerability of buildings and infrastructures in the form of economic damage from depth–damage relationships, vulnerability of Urbs includes human life, which is sometimes disproportionately exposed in disadvantaged and marginalized communities [15]. In a future marked by a rapid acceleration in urbanization processes [16] and significant increase in both the frequency and intensity of flash floods in coming decades [17], managing human vulnerability to floods that rapidly occur in populated areas is crucial for future sustainable Civitas, as identified in Sustainable Development Goal 11 [18] of the United Nations. Many urban areas have experienced the severe consequences and damage to their ecosystems from the construction of large gray infrastructures to protect against flash floods [19]. Sustainable Drainage Systems (SuDS) [20] can provide a revolutionary change in this field, improving the sustainability of those urban areas where human vulnerability requires the adoption of measures to reduce both the flow volume and celerity of floods [21].

This paper proposes a flood depth-velocity-damage function (FDVDF) fed by simulation results from the MIKE+ 2D Overland [22] application in a small coastal urbanized basin in Southern Sardinia (Italy). These analyses are motivated by the problems of flood vulnerability characterization for small, rapidly urbanizing watersheds. Specifically, the FDVDF maps were used to evaluate the flood vulnerability in the hamlet of Solanas, as a key indicator to support the plan and design of flood adaptation measures in urban public spaces. The results highlight the complexities of urban flood response in terms of vulnerability indexes and their sensitivity to function parameters.

2. Materials and Methods

2.1. Mapping Urban Flood Vulnerability

The representation of the flooding phenomenon of the hamlet of Solanas uses the application of two-dimensional (2D) models in urban areas from Article 8 of the Implementation Rules of the PAI, introduced with the resolution of the Institutional Committee no. 1 on 27 February 2018. However, this study is not exhaustive with respect to the requirements of implementing rules and only develops the aspects of greatest interest for some specific goals. The paragraph summarizes some aspects of the model and the main results useful for the enhancement of the urban development and environmental enhancement of Solanas.

The development and application of the modeling tools in the so-called residual basins, defined as a part of the territory not directly affected by the hydrographic network, is growing in interest. This modeling is different from that aimed at determining the hydraulic risk in the territories adjacent to the main hydrographic network, where the water current, associated with flooding and with high return times (greater than 50 years), in the river network can often be represented by means of a linear hydraulic model (1D) to determine the average velocity and the water depth.

Modeling of the flood phenomenon in urban areas is distinguished by the following:

• Shorter return times (frequent and rapid phenomena);
• Different spatial representation (larger scale on limited map);
• The presence of obstacles and complex elevation trends do not allow a prevailing direction of flow.

The purpose of the modeling is to quantify the frequency of occurrence, intensity, and magnitude of urban floods. Specifically, flood characteristics include flood depth, velocity, and extent of specified return periods [23], and they are mapped in the entire residual basin. Here, vulnerability is defined as the extent of harm to which the urban area is susceptible to floods and to its exposure to a specific level of hazard. In general terms, exposure can include values such as people, property, economic activities, and cultural and natural heritages, located in hazard-prone areas. One of the fundamental aspects of flood risk management is to assess the vulnerability of inhabitants to floods in urban areas [24]. Human vulnerability is primarily related to the loss of life; non-fatal injuries (blunt trauma, contusions, lacerations, and animal bites [25,26]) are considered. Anyway, it is notable that flooding events resulting in non-fatal damage are seven times more likely to occur than those resulting in death [27]. In addition, sources of flood fatalities include pedestrian crossings, basement drownings, vehicular deaths, collapsed buildings, and electrocution [28]. Pedestrians walking in flooded urban areas is one of the major causes of death associated with flood events, as pedestrians tend to underestimate the impact that flood flow can have on the human body [29]. Experimental activities showed that the predominant failure mechanism was sliding [30], and a good descriptor of the sliding mechanism is the product of depth (h) and velocity (v) [31,32]. To overcome the limitations of experimental activities involving people, ref. [33,34] have proposed the following conceptual modeling techniques:

• Toppling mechanism;
• Complex velocity profile and forces acting on the human body;
• Bed slope conditions;
• Body shape characteristics;
• Bias of controlled laboratory conditions.

The authors in [29] conducted an extensive and rigorous investigation, including a comparison and benchmark of five methods (four used by government organizations, and the fifth being regarded as a state-of-the-art empirical approach). In Italy, the guidelines of the National Network for Environmental Protection (ISPRA) [35] indicate the conceptual method proposed by [36] and adopted by the Department for Environment, Food and Rural Affairs (DEFRA) to quantify the human vulnerability (V_p) in the UK in the following Equation (1):

$$V_p=h\left(v+0.5\right)+DF,$$

(1)

where h is the water depth in meters and v is the water velocity in meters per second, and DF is the debris factor, the value of which depends on the probability that debris would lead to a significantly greater vulnerability in pedestrians. Considering urban as the dominant land use, guidelines suggest the following:

if h < 0.25 m then DF = 0,

otherwise DF = 1.

The hydrogeological management plan (PAI) [37] in Sardinia significantly modified the ISPRA method both in the DF value and type of threshold. Specifically, the RAS method assumes the following mathematical form:

$$V_p=h\left(v+0.5\right)+0.25$$

(2)

if h < 0.25 m then V_p = 0,

(3)

$$\mathrm{otherwise} V_p=h\left(v+0.5\right)+0.25$$

(4)

if V_p > 1 then V_p = 1.

(5)

The Municipalities can produce local studies with 2D-modeling analysis for urban areas and identify those parts of the territory in which V_p assumes a value of less than or equal to 0.75 for all return periods (from 50 to 500 years) as critical areas (Hi*). In Hi* areas, no hazard mapping is required and no restrictions on land use are imposed.

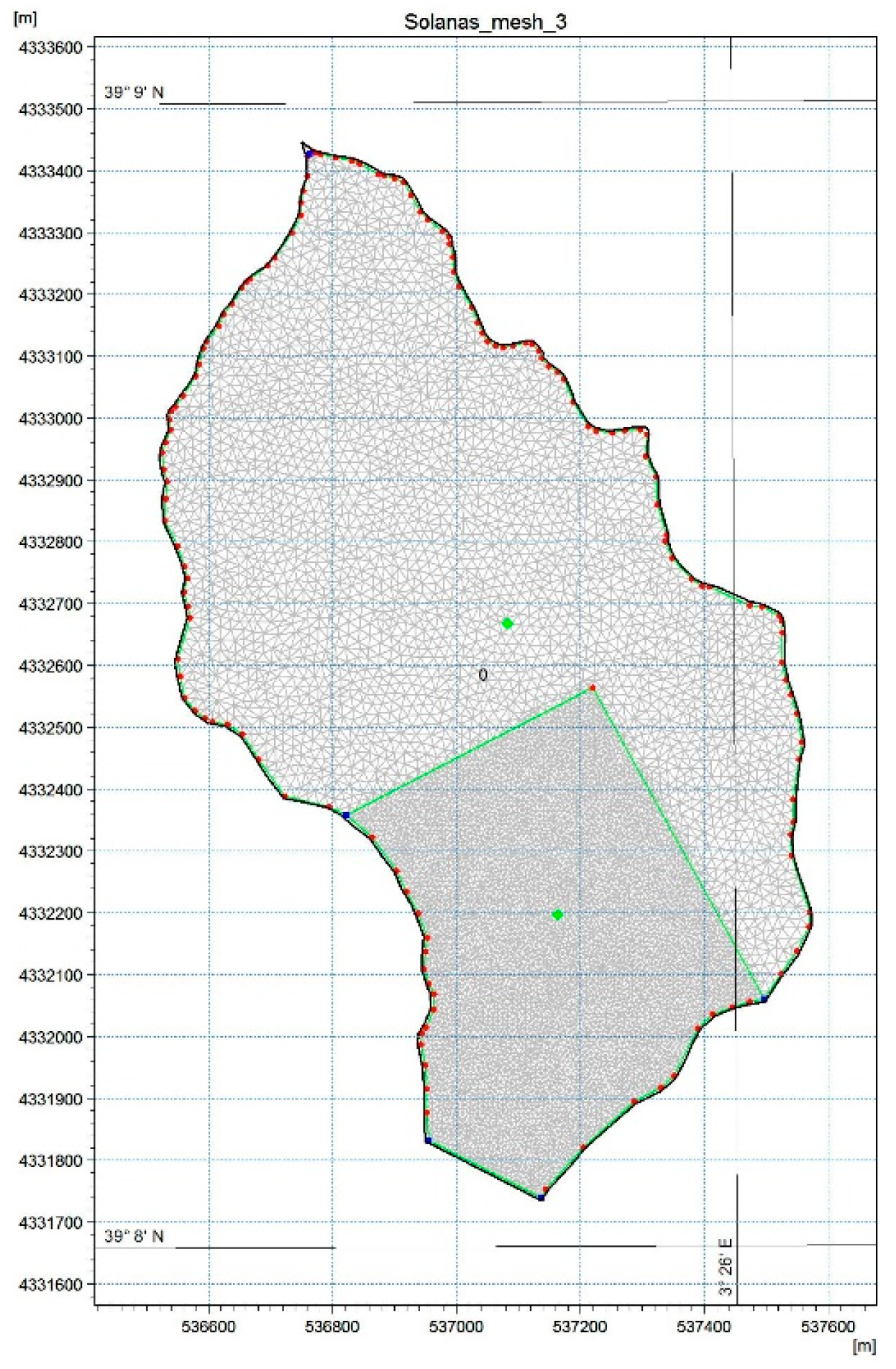
2.2. Area of Study

Solanas is situated in the south-eastern area of Sardinia, IT, which is the second biggest island in the Mediterranean Sea. Solanas is the seaside hamlet of Sinnai, the geographical coordinates of which are approximately 39.3053° N latitude and 9.2045° E longitude. The administrative area of Solanas has an area of approximately 26.7 km². The town of Solanas is located within a residual hydrographic basin (Figure 1), i.e., not characterized by a main hydrographic network. The surface area of this basin is equal to 1.3 km², with an average altitude of 350 m on a range from mean sea level to an altitude of 550 m.

This residual basin is part of the main basin of Rio Solanas with an estimated length of 13.4 km and a drainage area of 34 km². The Solanas basin shows mainly late Paleozoic plutonites and related phylonian complexes, some strips of Tertiary conglomerate deposits, and extensive layers of Quaternary deposits. On a physiographic level, the greater importance of the piedmont valley sector is clear, where the riverbed is not confined but expands within a vast alluvial area. Along this stretch the stream shows a clear wandering attitude within robust terraced Holocene alluviums. The mouth is perennial with a tendency to open onto the southeast edge of Solanas beach.

Solanas beach is of the pocket-beach type and is closed by two rocky headlands, limiting the littoral cell, which is seaward of the upper limit of the Posidonia oceanica meadow and the morphostructures of the geological basement. The beach and coastal dunes in Solanas have always supplied sand for a wide range of uses, and, initially, the extracted volumes were limited to buckets, wheelbarrows, or small pickup truck loads. However, starting post-World War II, and thanks to the urban development, the coastal and river sand has been extracted at an accelerated rate exceeding the natural replenishment rate of sand in this physiographic unit [38]. Due to the extractive character, this mining was an extremely pervasive and damaging activity that destroyed a large part of the coastal environment of Solanas. With an average available area by user of 9 m²/person, the physical carrying capacity [39] is equal to 4500 tourists in the summer season, without considering eventual trends in sea state parameters.

Sardinian coastal areas have been subject to significant anthropogenic pressure and urbanization processes over the past 60 years. The urbanization of Solanas developed extremely rapidly from the 1980s to the end of last century (Figure 2). In 2004, the “save coasts” law was approved, which imposed, as a safeguard measure, the non-buildability of territories within 2 km from the shoreline. However, urban drainage facilities have not upgraded (e.g., larger diameter pipes or storage facilities) consistently with the rapid urbanization growth, resulting in frequent flooding events in Solanas in recent years (Figure 3).

2.3. Numerical Model Application to Solanas Flood

Referring to the scientific literature of the sector for further information, the methodology developed consists of two phases:

• Hydrological model of inflow–runoff transformation for the determination of runoff (net rainfall hyetograph with leak assessment) for reference rainfall events (gross rainfall from rainfall probability curves or historical rainfall grams);
• Hydraulic model for the study of surface current propagation by solving two-dimensional equations characterizing shallow water equation model—SWE—flow for underground and surface drainage.

Rainfall is a key driver of urban flood response and flood peak distributions in small-scale urban watersheds [40]. For the determination of the design hyetogram used for the estimation of the flood hydrograph, please refer to the ADIS Guidelines (Guidelines and operational guidelines for the hydraulic modeling of flooding phenomena in residual urban basins), which indicate the use of a Chicago hyetograph. Based on two analytical equations for rainfall intensity over time from an IDF (intensity–duration–frequency) analytical expression, the “Chicago Design Storm” [41] calculates design rainfalls of urban storm water infrastructures, preserving the volumes of all rainfall intensities. IDF is calculated for the cumulative precipitation height over any duration within the rainfall time using the two-component extreme value (TCEV) distribution. The indication of the duration is provided by the time of concentration of the basin with the position of the peak equal to 0.4 of the duration and a return time of 25 years.

The present study employs the MIKE+ hydrodynamic model [22] that offers a strong foundation for analyzing flood dynamics, especially in difficult terrains. MIKE+ 2D uses a 2D-modeling system that solves the two-dimensional St. Venant (dynamic flow) equations using a cell-centered finite volume method. The time integration is performed using an explicit scheme and the numerical solution uses a self-adapting time step for optimizing stability and simulation times. The two-dimensional grid can be a normal rectangular grid or a mesh. Comparative studies between different hydrodynamic models have been presented in order to identify the most effective flood simulation model, evaluating the impact of hydrological and hydraulic factors and the influence of GPS topographic mapping in urbanized areas [42]. Ref. [43] shows that, although MIKE and HEC-RAS models simulate the maximum flood volume on the same day, HEC-RAS underestimated the total flood volume (−8.3%). In [44], model accuracy is validated against historical flood data, revealing that MIKE effectively addresses challenges related to grid resolution and flood delineation.

In this paper, MIKE+ 2D was used to simulate surface floods from surcharging collection system networks, reproducing the behavior of a fluid propagating on a locally complex topography, such as the urban one in Solanas.

To properly reproduce that complex-surface micro topography, MIKE+ requires the following input data:

• Technical cartography in digital format with adequate resolution;
• The digital terrain model (DTM) (Figure 4);
• The digital model of roads and buildings (Figure 4).

The most sensitive input affecting the 2D flood inundation simulation attributes (depth, extent, and velocity) is the digital terrain model (DTM); thus, this places higher requirements on the quality and resolution of DEMs [45,46]. The results of [43] indicate that flood characteristic simulations exhibit noticeable stepwise changes as DTM resolution varies and the resolution should, preferably, be better than 5 m, as this directly affects the accuracy of flood depth simulation. In this work, a high-resolution DTM with a grid of 1 m from a Laser Scanning LIDAR https://www.sardegnageoportale.it/webgis2/sardegnamappe/?map=download_raster (accessed on 23 January 2025) was selected as the most promising in terms of balance between simulation accuracy and computational times. In the Sardinia region, residual basins are GIS elements contained in the latest update of the information layer of the Regional Geo-topographic database at 1:1000 scale (Figure 5).

The numerical method, used for the solution of the equations of the 2D problem, uses the implicit finite volume algorithm that allows for larger time steps than explicit methods and for an increase in stability compared to traditional finite difference or finite element methods. To properly model 2D free-surface flows for flood analysis in the pluvial environment of Solanas basin, the 2D Overland module in MIKE+ was activated and coupled with MIKE 21. The domain was represented in the unstructured calculation mesh of Figure 6, with a maximum element area of 10 m² and a building from the DTM excluded from the mesh.

The 2D model simulation time and accuracy were controlled by specifying the two-stage explicit second-order Runge–Kutta scheme. Drying and wet depths were set to 5 and 10 mm. Solver used fluid properties for clear water, as no sediment transport was considered in the simulations, e.g., high concentration of debris or mud during severe floods. Surface roughness was applied to the model, as a Manning number varying in each triangular element of the domain, based on a background layer of the Corine Landcover and MIKE+ predefined roughness values in the “Material table”. Constant eddy viscosity was supposed to be equal to 1.5 m²/s and uniformly distributed in the domain. All boundaries of the domain were assigned as closed, meaning that water will not enter or leave the domain across the perimeter, except for the southern side where the coastline (straight line in Figure 6) has a water level that is equal to 1.8 m, and it is constant in time and space, as required by the ADIS Guidelines. In this application, no local sources and sinks were defined within the domain.

3. Results

Figure 7 and Figure 8 show the results of the numerical model in terms of the water depth and current velocity fields in the flooded portions (wet cells of the hydraulic model) from the surface runoff formed in the Solanas residual basin. The analysis allows us to clearly identify the main characteristics of the urban flood. Comparing the fields of depth (h > 0.1 m) and velocity (v > 0.1 m/s), the latter is significantly wider (+72%), showing that a large part of the flooded area has a current velocity with very low depth; in about half of these cells, the current velocity is higher than 0.5 m/s. The flood propagation is clearly defined along a NW-SE direction in two approximately parallel paths, and the western in the urban area runs along the main street of Solanas, hitting the buildings on both sides with a speed largely exceeding 1.5 m/s, and the eastern crossing a rural area with lower velocities (v < 0.5 m/s) and higher depth causes flooding in a depressed area of the countryside. Maximum values of depth and velocity in the entire residual basin are d_max = 0.97 m and v_max = 1.90 m/s.

The rural area shows a higher flooding rate compared to the urban area, which may be attributed to differences in topography and drainage capacity, with the latter mainly due to soil sealing from agricultural land use practices. Both flooding paths originate outside the urban area along deep incised canals that collect the outflows of the upstream portion of the basin. These flows cross the SP 17 at high speed where the drains of the artificial drainage network are undersized and poorly maintained. While these results enhance our understanding of the flooding dynamics in Solanas, the complex patterns of depth and velocity need to be combined to properly develop targeted mitigation measures to reduce the vulnerability of future flooding events.

Flood Vulnerability Index Comparison

The results of the benchmark analysis for the RAS and DEFRA methods highlight the significant sensibility of the vulnerability predictions to model structure and parameters.

From the comparisons, it can be seen that the RAS model, rather than the DEFRA model, produces a significantly lower extension of the areas with an extreme FHR. The RAS model defines an application threshold of depth below which the vulnerability is not assessed. This is equivalent to establishing that pedestrians are not vulnerable to any flooding conditions when h < 0.25 m, regardless of the velocity of the current. The portion of the residual basin, in which this threshold is equaled or exceeded (area in

Table 1. Statistical summaries of vulnerability index comparison between RAS and DEFRA methods. Area is the extension of territory where the indicator is evaluated as being water depth above the predefined threshold; vulnerable area is the extension of territory where vulnerability indicator is different from zero; statistical indicators (max, average, standard deviation—std dev) are calculated in the area with vulnerability.

	RAS	DEFRA
Area [m2] (A)	14,925 (1.5%)	1,020,100 (100%)
Vulnerable Area [m2] (AV)	14,925 (1.5%)	723,475 (70.9%)
Max Vulnerability (MV)	0.81	1.61
Std Dev Vulnerability (SDV)	0.08	0.15
Average Vulnerability (AV)	0.45	0.03

), is equal to 14,925 m², or only 1.5% of the residual basin. On the contrary, the DEFRA model assesses the vulnerability throughout the flooded territory (area equal to 100% of the residual basin in Table 1). The DEFRA model uses the same depth value (h = 0.25 m), not as the threshold of applicability but as the threshold below which the probability that debris would lead to a significantly greater vulnerability to pedestrians is negligible. Therefore, for d < 0.25 m, the debris factor is zero (DF = 0) (1). As a result, in the entire portion of the basin where the RAS model is applied, there is a vulnerability (A = AV = 14,925 m²) against 70.9% by the DEFRA model. The second consequence concerns the statistics of the first (specifically the average vulnerability—AV—value) and the second order (the standard deviation—SDV—value). The applicability threshold of the RAS model (h = 0.25 m) results in a reduced map of 597 vulnerability values higher than the minimum value from Equation (4) which is equal to 0.375 for h equal to the threshold and current velocity equal to zero (hydrostatic conditions of the current), as opposed to the DEFRA model which provides an extended map of 40,804 vulnerability values where the minimum value is zero. This results, in a greater dispersion, of the vulnerability data sample in the DEDRA model are (SDV = 0.15) than in the RAS model (SDV = 0.08), while the average vulnerability value of the RAS model is significantly higher (AV = 0.45) than in the DEFRA model (AV = 0.03). The maximum vulnerability value estimated by the DEFRA method (MV = 1.61) is significantly higher (+99%) than the value by the RAS method (MV = 0.81). This difference can be explained, in part (76%), by the different coefficient of the two equations (DF = 1 for DEFRA, and 0.25 for RAS) and, in part (24%), by the different combination of d and v that maximizes vulnerability in the two methods. This last aspect highlights how the RAS and DEFRA models, in addition to producing significantly different vulnerability values and their statistics, generate vulnerability maps with different spatial distributions, e.g., the urban area with maximum vulnerability from the two models is different.

The comparison between the spatial distributions of vulnerability values assumes a planned significance when associated with the following classes developed by [38,39] (

Table 2. Vulnerability classification in DEFRA and RAS approaches.

Vp	DEFRA Class	RAS Class
<0.75	low	low
0.75–1.0	moderate	high
1.0–1.25
1.25–2.5	significant
>2.5	extreme

). The RAS classification uses a threshold of V_p equal to 0.75 and the municipalities shall introduce restrictions on building rights only in those parts of the urban and peri-urban (H_i*) areas in which V_p is higher than 0.75 (high in Table 2). In the DEFRA classification, three classes of vulnerability are defined above the V_p threshold of 0.75, each for a different group of people effectively at risk (i.e., for some (children) for most, and for all).

Figure 9 and Figure 10 clearly show that there are no significant urban and peri-urban areas with high vulnerability for the RAS method, while the DEFRA method shows areas of moderate and significant vulnerabilities in the terminal stretch of the two flood propagation paths along a NW-SE direction. In particular, while the RAS method does not highlight the need to introduce urban planning restrictions in Solanas, the DEFRA method identifies the roundabout of the main street (western path) and the depressed area of the countryside (eastern path) as project areas for vulnerability reduction interventions.

4. Discussion

The comparison between the results of the two methods highlights the limitations of the RAS approach in representing the conditions of vulnerability for pedestrians in urban flooding conditions. The RAS method does not highlight significant portions of urban and peri-urban areas with vulnerability to depth and velocity for events with a return time of 25 years. In contrast, those conditions result in moderate and significant vulnerability in two areas of Solanas by the DEFRA method. Furthermore, these benchmark results confirm the caution needed in an empirical method alone [47]. While the authors acknowledge that rigorous validation and comparison of empirical methods is difficult to assess, and largely beyond the scope of this paper, some of the inconsistencies between the different empirical methods are worthy of being used to support the planning and design of flood mitigation measures in urban and peri-urban spaces such as Solanas. Both methods are based on the product of the depth and velocity and are largely inconsistent with an analysis of the hydrodynamic forces on a stationary body. This inconsistency is expected to be considerably high when the velocity is in excess of 1 m/s, as is generally the case for extreme flood events, as that simulated in Solanas with a 25 year-return period.

As explained through the paper, the main difference in the predictions is thought to be due to the use of depth threshold. In both methods, the threshold is set at 0.25m. While in the RAS method it is a threshold of the applicability of the method, in the DEFRA method it indicates the threshold below in which the impact of debris flow in the conditions of pedestrian stability is negligible. The use of the RAS method applicability threshold indicates that below 0.25 m there is no pedestrian vulnerability. This aspect appears to be linked to the definition of vulnerability as the possibility of loss of human life due to slipping and consequent drowning, but it appears to be aimed at adult males in good physical condition. The DEFRA method indicates how fragile people (e.g., children, the elderly, or people with reduced mobility) can lose their stability even in conditions of depth below the threshold. Details of forces acting on a flooded human body, for sliding and toppling instabilities, are provided by mechanics-based human behavior models [48].

The main findings from the benchmark results between the DEFRA and RAS methods suggest that the meaning of the adopted threshold (i.e., threshold applicability of the method in RAS or threshold for fragile people stability in DEFRA) can significantly affect the map of pedestrian vulnerability to urban flood in Solanas. While the definition of a new method is largely beyond the aim of this paper, a preliminary step in improving that method could consider a tentative threshold value of 0.10 m depth to assure a more realistic evaluation [49]. While preliminary, this step would allow us to maintain the methodological approach referred to in the regional planning legislation in Sardinia (Equations (2–5) and

Table 3. Statistical summaries of vulnerability index comparison between RAS method and its modified version (RAS_MOD). Results highlight the RAS method sensibility to the d threshold (3) of zero vulnerability.

	RAS	RAS_MOD
Area [m2]	14,925 (1.5%)	97,825 (9.6%)
Area with vulnerability [m2]	14,925 (1.5%)	97,825 (9.6%)
Max Vulnerability	0.81	0.81
Std Dev Vulnerability	0.08	0.09
Average Vulnerability	0.45	0.33

) but extend the vulnerability assessment to different combinations of depth and velocity in portions of the territory currently not under analysis.

Preserving the original methodological approach, in the entire portion of the basin where the modified RAS model (RAS_MOD) is applied, there is a vulnerability (A = AV = 97,825 m²). The area in which conditions of vulnerability for the person arise increases significantly by 655%. Therefore, in the face of a substantial invariance of the values of maximum vulnerability and standard deviation, the average value of vulnerability decreases by about 27%. The fact that the area with vulnerability increases sixfold appears in Figure 11, where both NW-SE routes present vulnerabilities in a large part of their development while the terminal areas (the roundabout in the urban area and the depressed area in the peri-urban area) occupy significant portions of the territory, defining those areas as unsafe for pedestrians.

5. Conclusions

Although urban vulnerability highlights a complexity that the human component alone cannot describe, the assessment of the vulnerability of pedestrians to flooding in urban areas is a priority tool in urban center planning. The paper shows that the currently applied method (RAS method) could significantly affect the map of pedestrian vulnerability to urban floods in Solanas. This is mainly due to the adopted threshold of the RAS method, which regards threshold applicability, meaning that below the value of 0.25 m the method is not applied, and the vulnerability is set equal to 0. Comparison of RAS and DEFRA methods partially supports this preliminary conclusion. A first tentative of reduction of this gap and assessment of the RAS method sensitivity to the threshold value is presented through the paper. Conclusions should highlight the need for further research in the evaluation of the stability of fragile people during floods and the impact of sediment transport, particularly mud, during floods in the urban area of Solanas. In the case of Solanas, the vulnerability analysis presented in this paper can be an opportunity to rethink the public space and the capability of connecting and giving new order to individual settlements and agglomerations of second homes without a center. The two paths of the flood in urban and peri-urban areas require interventions in the form of SuDS (e.g., lamination park and permeable pavements), with a vision of adaptation to the natural phenomenon and urban redevelopment in which these interventions define new public spaces.