Forecasting Global Solar Energy Consumption Using Conformable Fractional Incomplete Gamma Grey Model

Abstract

Solar energy has become the core driver of global energy transformation. To achieve a more accurate prediction of the global solar energy consumption, this study presents a novel conformable fractional incomplete gamma grey model (denoted as CFIGGM). In this new model, the conformable fractional-order accumulation operator is introduced to fully mine the information of small samples and reduce the dependence on data distribution. Meanwhile, the Whale Optimization Algorithm is also utilized to solve the optimal value of nonlinear parameters in the newly proposed model to enhance its prediction performance. Moreover, numerical experiments are carried out on five sequences to verify the performance of the new model. The experiments’ results show that the proposed model has better prediction performance than the comparative models. Then, the new model is applied to forecast the global solar energy consumption. The fitting MAPE of the newly proposed model is 0.07% on the training set, and the prediction MAPE is 0.78% on the test set. As an application, the trend in global solar energy consumption is predicted by using the proposed model. Its result shows that the global solar energy consumption is projected to maintain a strong growth momentum, but the growth rate will slow down in the future. The results can serve as strong supporting data for relevant departments and enterprises.

1. Introduction

As a clean and renewable energy form, solar energy plays an increasingly central role in the global energy transformation, sustainable development, and tackling global climate change challenges. Since the 21st century, the decline in the cost of solar photovoltaic technology has driven its installed capacity to grow exponentially. Solar energy and wind energy are complementary to the diversification of energy structures. Compared with the geographical limitations of wind energy, solar energy has a wider applicability, especially in low-latitude areas. In 2024, the proportion of generation from wind and solar in the global generation had increased from 13% to 15%. In the past decade, their total production has increased fourfold, with wind energy accounting for 55% and solar energy accounting for 45% [1]. The global solar energy consumption has reached 7.7177 Exajoules. The average growth rate in solar energy consumption stands at 25.8% over the past decade, and the growth rate in 2024 reached 27.5% [1].

Due to the comprehensive impact of uneven regional development, dynamic policy adjustments, and technological iteration updates, global solar energy consumption shows significant nonlinear fluctuations and phased evolution characteristics, posing significant challenges for accurate prediction. It is worth noting that, as the country with the largest solar energy installation and consumption in the world, China’s solar energy consumption accounts for 43.2% of the global total in 2024. The dynamic evolution of its trend plays an undeniable role in shaping the global solar energy consumption pattern. The dynamic characteristics of China’s solar energy consumption are deeply dependent on the phased adjustment of relevant domestic systems, and its development trajectory is highly consistent with the key institutional nodes. The Renewable Energy Law was officially promulgated in 2006, which directly promoted the photovoltaic industry from its initial stage to large-scale development [2]. It directly drove the rapid increase in domestic solar energy consumption, reaching 142.19 Petajoules by 2015. In 2014, the “Energy Development Strategy Action Plan (2014–2020)” was issued [3], which clarified the direction of “accelerating the development of solar power generation” and set quantitative goals. It proposed that the installed capacity of photovoltaics should reach about 100 million kilowatts by 2020, which laid a clear path for the growth of solar energy consumption and further consolidated the upward consumption trend. After the clear goal of “peak carbon emissions and carbon neutrality” was proposed in 2020, relevant supporting policies were gradually implemented to strengthen the non-linear growth trend of solar energy consumption [4]. China’s solar energy consumption increased from 940.07 Petajoules in 2020 to 3020.69 Petajoules in 2024. The release of the “14th Five-Year Plan” in 2021 not only continues the direction of “accelerating the development of renewable energy” but also emphasizes the promotion of the proportion of non-fossil energy, such as solar energy and wind energy [5]. It sets a long-term goal of non-fossil energy accounting for 25% of primary energy consumption by 2030, providing institutional guarantees for the sustained growth of solar energy consumption. Driven by these policy systems, not only has it gradually formed the core evolution law of China’s solar energy consumption, but it has also become one of the key sources of the “non-linear” characteristics of global solar energy consumption.

The accurate prediction of energy consumption plays an indispensable core significance in policy formulation, energy market planning, and the implementation of sustainable development strategies. To attain superior predictive performance, numerous time series methods and machine learning approaches have been widely employed in the field of energy consumption. Nevertheless, these approaches generally necessitate an adequate volume of training data. In scenarios with incomplete information or a few samples, grey models tend to exhibit more favorable predictive performance.

The grey model (GM) is specifically formulated to combat the issue of “limited data and poor information” [6]. It does not necessitate a large amount of raw data and does not require data to follow a specific distribution. It performs outstandingly in scenarios where data is scarce and information is incomplete, and is applied in short-term economic forecasting, small-scale production planning, disaster early warning, and so on. However, the classical grey model doesn’t have sufficient prediction accuracy and adaptability. Therefore, many scholars have made improvements in terms of model structure [7,8], data pre-processing [9,10], optimization of background values [11,12,13], optimization of models’ parameters [14], and other aspects to enhance the grey model’s prediction performance and adaptability. One of the main methods involves improving grey prediction models by using appropriate grey accumulation operators. In the past decades, many grey accumulation generation operators have been proposed. To finely regulate the sequence’s randomness and avoid “over-smoothing” or “insufficient smoothing”, a Fractional-order Accumulation Generation Operator (FAGO) was firstly designed to establish the FGM(1,1) based on the operator [15]. It is naturally derived from an integer-order operator and can effectively reflect the characteristics of new information priority in the raw sequence. Subsequently, scholars proposed other new grey fractional order accumulation operators or improved them to enrich the grey prediction theory. By introducing the fractional Hausdorff derivative [16] into grey prediction theory, the fractional Hausdorff grey model (FHGM) was established [17]. In response to the issue of ill-condition in the grey model, the weakened fractional order accumulation operator is designed to address the issue and improve the performance of the conventional model [18]. In order to mine more valid grey information, the probabilistic accumulation generation operator (PAGO) is designed to construct the PGM(1,1) model [19]. In response to the computational complexity of the traditional FAGO operator, the theory of conformable fractional accumulation generation operator (CFAGO) and the inverse CFAGO based on conformable fractional-order derivative is established. Based on this theory, CFGM(1,1) is constructed, which markedly enhances performance in the prediction of non-smooth time series compared to classical models [20]. A previous study comparing CFGM(1,1) with the Caputo fractional grey model found that CFGM(1,1) yields more accurate predictions on certain real-world datasets [21]. Accordingly, numerous scholars have employed the CFAGO operator to extend grey theory and boost the efficiency of the grey model. Reference [22] incorporated the grey CFAGO operator into the logical grey model to boost its stability. To further enhance the multivariate grey prediction model, an improved CFAGO operator was developed and applied to establish the CFDNGBM (r, N) model [23]. Using the ability of the CFAGO operator in handling the non-linear data sequence, the variable structural conformable fractional unbiased grey model was constructed, which can automatically adjust its structure according to the characteristics of the raw sequence [24]. Considering the existence of time-delay in real-world data sequences, the classical grey model was extended to the CFGTM model by integrating the time-delay rule and the CFAGO operator. It has higher effectiveness and flexibility in the prediction of electric power generation than those of other models [25]. To utilize the super adaptability of the CFAGO operator, the CFGM($\varphi$,1,$t^r$) model was designed by innovating CFAGO in the conventional model, and has better performance than other competing models [26]. Reference [27] incorporated the inverse accumulation operator and CFAGO operator into the classical grey model, and applied the CFGOM(1,1) model to predict electricity consumption in Shandong, Fujian, and Beijing, China. It is obvious that the CFAGO operator can effectively improve the grey models and expand their application fields. Optimizing the grey action quantity constitutes another critical approach to improve grey models. Many studies adopt the linear grey action quantity to replace the constant grey quantity of grey models [28,29]. Addressing the data sequences that approximately follow a pattern combining partial exponential and partial linear characteristics, lots of scholars utilize the grey quantity with time power term to optimize the grey models [30,31]. Moreover, other types of grey action quantity which can reflect the system’s external non-linear effects are likewise widely employed in refining grey models [32,33]. Adopting appropriate grey action quantity as external inputs for grey prediction systems serves to effectively enhance the predictive performance and adaptability of grey models. As a result of the outstanding performance in predicting the sequence with small samples or incomplete information, grey models have been commonly employed to forecast the energy generation, energy consumption, or installed capacity. Aimed at the non-linearity, seasonality, and growth characteristics of energy data sequences, the structural adaptive seasonal grey Bernoulli model was established and applied to forecast natural gas production [34]. Addressing the absence of reasonable and effective multivariate forecasting methods in natural gas consumption prediction, the AGMPM($\gamma$,N) model based on the FAGO operator was developed to forecast China’s natural gas consumption [35]. In addition, numerous scholars have applied grey prediction theory to forecasting oil production [36], oil consumption [37], solar power generation [38], solar energy consumption [39], solar energy installed capacity [40], wind energy installed capacity [41], and other such factors. In summary, grey prediction theory is very effective in predicting energy consumption, generation, and installed capacity with small samples.

However, solar energy consumption exhibits significant non-linear characteristics and phased growth trends, primarily due to fluctuations in policy support intensity and the iterative advancement of core technologies (e.g., photovoltaics). Accurate prediction of such consumption patterns has emerged as a critical imperative for supporting the optimization of global energy layouts and advancing the transformation of energy structures. To address this challenge, the academic community has developed a range of energy consumption forecasting techniques, encompassing physical models, statistical econometric models, and machine learning models. Nevertheless, the reliable predictive accuracy of these models is highly dependent on large-scale, high-integrity historical datasets. They can only exhibit limited effectiveness in scenarios with sufficient data. Furthermore, for medium- to long-term solar energy consumption forecasting at the global scale, or in underdeveloped regions with inadequate accumulation of solar energy-related data, existing models often struggle to deliver satisfactory predictive performance. This shortfall stems from two key constraints: insufficient data volume, and the inherent difficulty in capturing non-linear variations across different regions—both of which undermine the models’ ability to adapt to complex, data-scarce scenarios. Because the grey model is not limited by the size of the sample and the distribution form of the data, it has a natural advantage in handling “small sample, poor information” energy prediction problems. Many scholars have thus turned to using the grey model for solar energy consumption prediction at regional or local scales. However, most grey models currently use the traditional integer-order accumulation generation, which has obvious deficiencies when applied to solar energy consumption prediction. On the one hand, the traditional integer-order accumulation generation operator gives the same weight to all data points, making it difficult to effectively eliminate the interference of random factors (such as short-term policy fluctuations, extreme climate). On the other hand, the constant grey action quantity of the traditional grey model is difficult to depict the dynamic changes of the impact of unknown factors (such as sudden technological breakthroughs, cross-regional energy collaboration) on the system. At the same time, current research on solar energy consumption prediction mostly focuses on a single national or regional scale, and research based on grey models for global solar energy consumption prediction is still relatively scarce. Therefore, this study proposed a Conformable Fractional-order Incomplete Gamma Grey Model (CFIGGM) by integrating the conformable fractional-order accumulation operator and incomplete gamma grey action quantity into the traditional grey model. This model effectively overcomes the core dual defects of the traditional grey model, namely the “over accumulation fuzzy consumption law” and the “difficulty in characterizing the dynamic impact of constant grey action quantity”. On the one hand, the conformable fractional-order accumulation operator can avoid the masking of the inherent consumption law by over accumulation. On the other hand, the incomplete gamma grey action quantity can dynamically capture the impact of unknown factors (such as sudden technological breakthroughs or regional policy adjustments) on the system. It significantly improves the prediction accuracy of global solar energy consumption, especially in the medium- and long-term prediction dimensions, as well as in scenarios of underdeveloped regions with scarce data. Generally, the principal contributions stemming from this study are as follows.

(1)

A Novel Conformable Fractional Incomplete Gamma Grey Model (CFIGGM) is established. The conformable fractional operator is incorporated into the traditional model to mitigate the randomness of the raw sequence. The new model can easily obtain superior simulation performance.

(2)

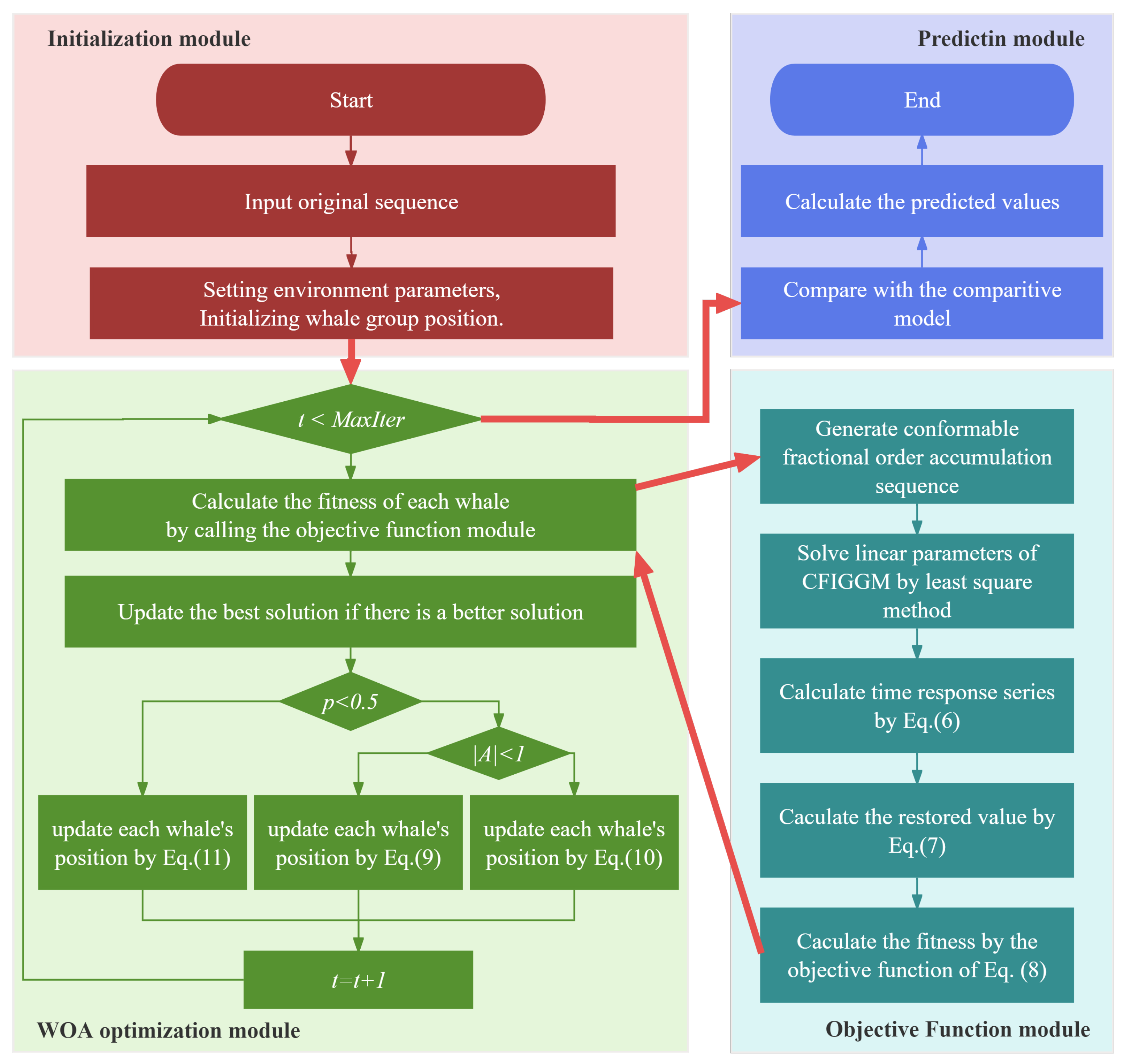
The Whale Optimization Algorithm is employed to search for the optimal order $\alpha$ and non-linear parameter $\mu$ of the proposed model. It makes the model obtain lower simulation error and better prediction performance.

(3)

The newly proposed model is applied to forecasting the global solar energy consumption, which significantly outperforms the comparison models in terms of fitting accuracy and predictive performance. Using the CFIGGM model, it is found that global solar energy consumption will maintain a strong growth, but with a slower growth rate. The result can provide evidence-based decision support for the layout of renewable energy under the carbon neutrality goal and energy structure adjustment.

The rest of this paper is structured as follows. In Section 2, the theory of the classical grey model and the conformable fractional incomplete gamma grey model is introduced. In Section 3, four validation experiments are conducted to verify the new model’s performance. Section 4 introduces the application in forecasting solar energy consumption. At last, the conclusion is presented in Section 5.

2. Methodology

2.1. The Conformable Fractional Incomplete Gamma Grey Model

The traditional grey model (GM(1,1)) serves as the cornerstone of grey models. It utilizes the integer order Accumulation Generation Operator (AGO) to preprocess the original sequence, thereby enhancing data regularity and reducing randomness [6]. In recent years, a lot of work on the extension of grey accumulation operators has been performeed. Lots of accumulation operators have been proposed and employed to develop numerous new grey prediction models. Conformable Fractional Accumulation Generation Operator (CFAGO) ranks among the most widely adopted operators in grey theory. It has been widely utilized to improve grey models, which are applied in the prediction of energy, economy, environment, and so on [42,43,44,45,46]. The definition of CFAGO is described as follows.

Definition 1

([20]). For the original ${\mathit{\text{sequences}}}^{\left(0\right)}=\{s_1^{\left(0\right)},s_2^{\left(0\right)},\dots ,s_n^{\left(0\right)}\}$, the α-order conformal fractional sequence of $s^{\left(0\right)}$ is

$$s^{\left(\alpha \right)}=\{s_1^{\left(\alpha \right)},s_2^{\left(\alpha \right)},\dots ,s_n^{\left(\alpha \right)}\}.$$

(1)

The Conformable Factional Accumulation Generation Operator (CFAGO) is defined as

$$s_k^{\left(\alpha \right)}=\left\{\begin{array}{c}\sum _{j=1}^k{\displaystyle \frac{s_j^{\left(0\right)}}{j^{\lceil \alpha \rceil -\alpha }}},\alpha \in (0,1];\hfill \\ \sum _{j=1}^k{s}_j^{(\alpha -1)},\alpha \in (1,+\infty ),\hfill \end{array}\right.$$

(2)

where α is the order of the operator.

Based on the CFAGO operator, the Conformable Fractional Grey Model (CFGM(1,1)) is developed to enhance the ability of the grey model [20]. However, the grey action quantity of CFGM(1,1) is also an invariant, which reflects that the external factor of the system is unchanging. When the external factor of the system varies linearly, the CFNGM(1,1,k,c) model is constructed [47]. Regarding the external influences with non-linear changes in the system, we establish a novel conformable fractional-order grey prediction model with the incomplete gamma function. The theory of the new model is described as follows.

Definition 2.

Given the sequence $s^{\left(\alpha \right)}$ as defined in Definition 1, the equation

$$s_{k+1}^{\left(\alpha \right)}-s_k^{\left(\alpha \right)}+0.5{\beta }_1(s_{k+1}^{\left(\alpha \right)}+s_k^{\left(\alpha \right)})=0.5{\beta }_2(\gamma (\mu ,k+1)+\gamma (\mu ,k))+{\beta }_0$$

(3)

is the Conformable Fractional Incomplete Gamma Grey Model (CFIGGM). The whitening equation of the CFIGGM model is defined as

$${\displaystyle \frac{\mathrm{d}{s}_t^{\left(\alpha \right)}}{\mathrm{d}t}}+{\beta }_1{s}_t^{\left(\alpha \right)}={\beta }_2\gamma (\mu ,t)+{\beta }_0$$

(4)

where, the constant ${\beta }_1$ and the term ${\beta }_2\gamma (\mu ,t)+{\beta }_0$ are its development coefficient and grey quantity respectively.

The optimal parameters $\left[\widehat{{\beta }_1},\widehat{{\beta }_2},\widehat{{\beta }_0}\right]$ of CFIGGM can be solved by Theorem 1.

Theorem 1.

The parameters $\widehat{\beta }=\left[\widehat{{\beta }_1},\widehat{{\beta }_2},\widehat{{\beta }_0}\right]$ of CFIGGM are

$$\widehat{\beta }={\left({\mathsf{\Phi }}^T\mathsf{\Phi }\right)}^{-1}{\mathsf{\Phi }}^T{\rm Y},$$

(5)

where ${\rm Y}=\left[\begin{array}{c}{\upsilon }_2\\ {\upsilon }_3\\ ⋮\\ {\upsilon }_n\end{array}\right],\mathsf{\Phi }=\left[\begin{array}{ccc}{\varphi }_2& {\gamma }_2& 1\\ {\varphi }_3& {\gamma }_3& 1\\ ⋮& ⋮& ⋮\\ {\varphi }_n& {\gamma }_n& 1\end{array}\right],{\upsilon }_i=s_i^{\left(\alpha \right)}-s_{i-1}^{\left(\alpha \right)},{\varphi }_i=-0.5(s_{i-1}^{\left(\alpha \right)}+s_i^{\left(\alpha \right)}),$${\gamma }_i=0.5(\gamma (\mu ,i-1)+\gamma (\mu ,i)).$

Proof of Theorem 1.

The detailed proof is provided in Appendix A. □

Through substituting the optimal parameters $\widehat{\beta }$ into the Equation (4) and then solving it, the time response sequence of CFIGGM can be obtained.

Theorem 2.

When the optimal parameters of CFIGGM are $\left[\widehat{{\beta }_1},\widehat{{\beta }_2},\widehat{{\beta }_0}\right]$, the time response sequence of CFIGGM is

$${\widehat{s}}_k^{\left(\alpha \right)}=s_1^{\left(\alpha \right)}{e}^{-{\widehat{\beta }}_1(k-1)}+\sum _{i=2}^{k}0.5(({\widehat{\beta }}_2\gamma (\mu ,i)+{\widehat{\beta }}_2\gamma (\mu ,i-1)+2{\widehat{\beta }}_0)e^{-{\widehat{\beta }}_1(k-i+0.5)}).$$

(6)

The k-$th$ predicted value is

$${\widehat{s}}_k^{\left(0\right)}=k^{\lceil \alpha \rceil -\alpha }\sum _{i=1}^k{(-1)}^{k-i}\left(\begin{array}{c}\lceil \alpha \rceil \\ k-i\end{array}\right){\widehat{s}}_i^{\left(\alpha \right)}.$$

(7)

Proof of Theorem 2.

The detailed proof is provided in Appendix B. □

2.2. Optimization of Nonlinear Parameters in CFIGGM

The appropriate parameters of CFIGGM can improve the fitting and prediction performance significantly. To achieve the optimal model, it is imperative to select an appropriate fractional order $\alpha$ of the CFAGO operator and the fine-tune parameter $\mu$ in the incomplete gamma grey quantity. So, we construct an optimization model (8), whose objective function is to minimize the simulation error, to obtain the optimal parameters $\alpha$ and $\mu$. The optimization model is

$$\begin{array}{cc}\hfill & minf(\alpha ,\mu )={\displaystyle \frac{1}{n-1}}\sum _{k=2}^n\left|{\displaystyle \frac{{\widehat{s}}_k^{\left(0\right)}-s_k^{\left(0\right)}}{s_k^{\left(0\right)}}}\right|\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}\widehat{\beta }={\left({\mathsf{\Phi }}^T\mathsf{\Phi }\right)}^{-1}{\mathsf{\Phi }}^T{\rm Y},\hfill \\ {\rm Y}={\left[{\upsilon }_2,{\upsilon }_3,\dots ,{\upsilon }_n\right]}^T,{\upsilon }_i=s_i^{\left(\alpha \right)}-s_{i-1}^{\left(\alpha \right)},\hfill \\ \mathsf{\Phi }=\left[\begin{array}{ccc}{\varphi }_2& {\gamma }_2& 1\\ {\varphi }_3& {\gamma }_3& 1\\ ⋮& ⋮& ⋮\\ {\varphi }_n& {\gamma }_n& 1\end{array}\right],{\varphi }_i=-0.5(s_{i-1}^{\left(\alpha \right)}+s_i^{\left(\alpha \right)}),{\gamma }_i=0.5(\gamma (\mu ,i-1)+\gamma (\mu ,i)),\hfill \\ {\widehat{s}}_k^{\left(\alpha \right)}=s_t^{\left(\alpha \right)}{e}^{-{\beta }_1(k-1)}+\sum _{i=2}^{k}0.5\left(e^{-{\beta }_1(k-i+0.5)}({\beta }_2\gamma (\mu ,i)+{\beta }_2\gamma (\mu ,i-1)+2{\beta }_0)\right),\hfill \\ {\widehat{s}}_k^{\left(0\right)}=k^{\lceil \alpha \rceil -\alpha }\sum _{i=1}^k{(-1)}^{k-i}\left(\begin{array}{c}\lceil \alpha \rceil \\ k-i\end{array}\right){\widehat{s}}_i^{\left(\alpha \right)},k>2,\hfill \\ {\widehat{s}}_1^{\left(1\right)}={\widehat{s}}_1^{\left(0\right)}=s_1^{\left(0\right)},\hfill & \gamma (\mu ,t)={\int }_0^t{\tau }^{\mu -1}{e}^{-\tau }d\tau ,\hfill & \alpha \in (0,20),\mu \in (0,30).\hfill \end{array}\right..\hfill \end{array}$$

(8)

Due to its outstanding optimization capability [48] and extensive practical applications [49,50], the Whale Optimization Algorithm (WOA) is employed to solve the parameter optimization problem (8) of the CFIGGM model. WOA is an optimization algorithm inspired by the prey behavior of humpback whales. It achieves global optimization through three strategies. In encircling prey [48], the $t+1$ step’s position of each whale can be calculated as

$${\chi }_{t+1}={\chi }_t^{*}-A·D,$$

(9)

where, $D=\left|C{\chi }_t^{*}-{\chi }_t\right|,C=2r_1,A=2a{r}_2-a$. D is the distance between the current whale and the one at optimal position, in which C is the random coefficient vector used to enhance search flexibility. $r_1$ and $r_2$ are random values between 0 and 1. a exhibits a linear decrease from 2 to 0. In bubble-net attacking [48], the position can be updated by

$${\chi }_{t+1}=D^{\prime }{e}^{bl}cos\left(2\pi l\right)+{\chi }_t^{*},$$

(10)

where, $D^{\prime }=\left|{\chi }_t^{*}-{\chi }_t\right|$, $e^{bl}cos\left(2\pi l\right)$ is used to generate the spiral path around the optimal solution, b controls the tightness of the spiral path, and l is the random value in $[-1,1]$. In the random search [48], the position can be updated by

$${\chi }_{t+1}={\chi }_{\mathrm{rand}}-A·D_{\mathrm{rand}}$$

(11)

where, $D_{\mathrm{rand}}=\left|C{\chi }_{\mathrm{rand}}-{\chi }_t\right|$, ${\chi }_{\mathrm{rand}}$ is a random individual in the population.

As shown in Figure 1, the prediction process of CFIGGM consists of the Initialization Module, WOA Optimization Module, Objective Function Module, and Prediction Module.

3. Validation of the CFIGGM Model

3.1. Evaluation Metrics and Comparative Models

In this study, we primarily employ the Signed Relative Percentage Error (SRPE) and Mean Absolute Percentage Error (MAPE) to evaluate models. The formula of SRPE is

$$SRP{E}_k={\displaystyle \frac{{\widehat{s}}_k^{\left(0\right)}-s_k^{\left(0\right)}}{s_k^{\left(0\right)}}}\times 100\%,$$

(12)

where, $s_k^{\left(0\right)}$ is the k-th real value of original sequence, and ${\widehat{s}}_k^{\left(0\right)}$ is the corresponding k-th predicted value. The formula for MAPE is given by

$$MAPE={\displaystyle \frac{1}{n}}\sum _{k=1}^n\left|SRP{E}_k\right|\times 100\%,$$

(13)

where, n is the size of raw sequence.

For a dataset with n samples, it is usually divided into two subset. One subset with p samples is used to construct the models. The other subset with $n-p$ samples is used to validate these models. Then, the simulation error is described as

$${MAPE}_{sim}={\displaystyle \frac{1}{p}}\sum _{k=1}^p\left|SRP{E}_k\right|\times 100\%.$$

(14)

The prediction error is described as

$${MAPE}_{pred}={\displaystyle \frac{1}{n-p}}\sum _{k=p+1}^n\left|SRP{E}_k\right|\times 100\%.$$

(15)

${MAPE}_{sim}$ is used to evaluate the fitting ability of grey models, while ${MAPE}_{pred}$ is used for verifying these models’ prediction performance. To verify the effectiveness of CFIGGM, four models, including GM(1,1), IGGM, CFGM, and CFNGM, are selected as comparative models redwhich are presented in

Table 1. Comparative grey models.

No.	Name	Grey Model
1	GM(1,1)	${\displaystyle \frac{\mathrm{d}{s}_t^{\left(1\right)}}{\mathrm{d}t}}+{\beta }_1{s}_t^{\left(1\right)}={\beta }_0$
2	IGGM	${\displaystyle \frac{\mathrm{d}{s}_t^{\left(1\right)}}{\mathrm{d}t}}+{\beta }_1{s}_t^{\left(1\right)}={\beta }_2\gamma (\mu ,t)+{\beta }_0$
3	CFGM(1,1)	${\displaystyle \frac{\mathrm{d}{s}_t^{\left(\alpha \right)}}{\mathrm{d}t}}+{\beta }_1{s}_t^{\left(\alpha \right)}={\beta }_0$
4	CFNGM	${\displaystyle \frac{\mathrm{d}{s}_t^{\left(\alpha \right)}}{\mathrm{d}t}}+{\beta }_1{s}_t^{\left(\alpha \right)}={\beta }_{2}t+{\beta }_0$

. Meanwhile, the machine learning methods such as Back-Propagation (BP) neural network and Support Vector Regression (SVR) are also compared with the CFIGGM model.

3.2. Datasets for Validation

To validate the efficacy of the proposed model, we utilized five real-world datasets encompassing energy consumption and generation for experimental verification. Each dataset comprises 13 data points, whose detailed specifications are presented in

Table 2. The original sequences in Examples 1–5.

Example	Raw Sequence	Type	Region	Source
1	[1080.24, 1341.07, 1497.00, 1705.30, 1870.63, 1931.75, 2078.06, 2393.69, 2817.09, 3059.68, 3339.89, 3772.96, 3746.95], (unit: Billion cubic meters)	natural gas consumption	China	[51]
2	[330, 339, 354, 367, 378, 406, 416, 433, 444, 458, 463, 484, 482], (unit: Kilogram)	oil consumption per capita	China	[51]
3	[21,971.37, 24,940.32, 28,587.97, 32,711.81, 34,541.35, 37,032.14, 41,934.49, 47,000.88, 49,762.64, 54,203.41, 56,383.69, 58,019.97, 61,297.09], (unit: Trillion kWh)	electricity consumption	China	[52]
4	[349,008.26, 388,961.1, 411,726.90, 424,425.94, 413,633.00, 399,834.00, 388,820.00, 391,403.00, 397,452.00, 401,915.00, 404,860.00, 429,576.00, 448,246.00], (unit: Ten thousand tons)	coal consumption	China	[51]
5	[14.84, 15.97, 17.99, 18.96, 18.39, 21.80, 20.76, 23.07, 23.45, 26.10, 28.51, 29.21, 30.27], (unit: Terawatt-hours)	renewable generation	Denmark	[1]

.

To ensure experimental consistency and objectivity, a uniform dataset partitioning strategy was applied across all datasets. The first 10 data points of each dataset were allocated to the trainset for training models and parameter optimization, while the remaining 3 data points constituted the testset for evaluating model generalization capability. After determining the optimal model parameters and deriving the optimized model, both fitting errors on the trainset and prediction errors on the testset were calculated, serving as core metrics for assessing model fitting accuracy and predictive performance.

3.3. Numerical Validation Experiments

In order to comprehensively verify the performance of the proposed model, five examples were designed to validate the model’s ability in fitting, predicting, processing non-linear data, and generalization through these sequences. In Examples 1–3, we mainly validated the model’s fitting, prediction, and comprehensive capabilities. In Example 4, we validated the model’s ability to handle non-linear sequences. In Example 5, we validated the generalization ability of the model.

3.3.1. Example 1: Validation of CFIGGM Model’s Performance on Natural Gas Consumption

In this subsection, the original sequence listed in Table 2 is used to validate the performance of the CFIGGM model. It represents the annual natural gas consumption in China over the period 2010–2022. Through the trainset and WOA algorithm, the optimal parameters of the different grey models are filled in

Table 3. The optimal parameters of different grey models in Example 1.

Model	Optimal Parameters
GM(1,1)	${\beta }_0=1150.0350,{\beta }_1=-0.1025$
IGGM	${\beta }_0=1084.5613,{\beta }_1=-0.1537,{\beta }_2=-9.3248,\mu =5.83007$
CFGM	${\beta }_0=1150.0148,{\beta }_1=-0.1025,\alpha =2.8388$
CFNGM	${\beta }_0=1121.7022,{\beta }_1=-0.3365,{\beta }_2=-365.1571,\alpha =0.7442$
CFIGGM	${\beta }_0=981.3880,{\beta }_1=0.1169,{\beta }_2=0.0024,\mu =9.9483,\alpha =0.2961$

. The predicted values of CFIGGM and the comparative models are shown in

Table A1. Simulation and prediction values of different models in Example 1 (unit: billion cubic meters).

No.	Raw Data	GM(1,1)	IGGM	CFGM(1,1)	BP	SVR	CFNGM	CFIGGM
1	1080.24	1080.24	1080.24	1080.24	1080.24	1080.24	1080.24	1080.24
2	1341.07	1327.59	1341.06	1327.58	1178.07	1322.91	1345.23	1313.77
3	1497.00	1470.84	1520.34	1470.84	1462.10	1579.50	1514.24	1555.62
4	1705.37	1629.55	1674.39	1629.55	1631.90	1732.89	1663.02	1702.99
5	1870.63	1805.39	1809.55	1805.39	1858.81	1937.86	1809.83	1809.47
6	1931.75	2000.20	1954.00	2000.20	2038.76	2100.43	1968.29	1931.90
7	2078.06	2216.03	2137.83	2216.04	2105.32	2160.56	2152.38	2119.64
8	2393.69	2455.16	2382.25	2455.16	2264.64	2304.48	2379.17	2393.69
9	2817.09	2720.08	2699.30	2720.08	2608.35	2614.97	2671.26	2737.45
10	3059.68	3013.59	3095.99	3013.59	3069.41	3031.48	3059.68	3105.94
11	3339.89	3338.78	3578.35	3338.77	3333.58	3270.12	3587.73	3445.66
12	3772.96	3699.05	4154.05	3699.04	3631.84	3545.76	4316.30	3712.63
13	3746.95	4098.20	4833.61	4098.19	3956.63	3971.78	5331.34	3881.96

. The comparison of all models is shown in Figure 2. Their errors of simulation and prediction are listed in

Table 4. Errors of different models in Examples 1–5.

Example	Type	GM(1,1)	IGGM	CFGM(1,1)	BP	SVR	CFNGM	CFIGGM
1	$MAP{E}_{sim}$	2.84	1.65	2.84	2.90	3.66	1.84	1.57
	$MAP{E}_{pred}$	3.79	15.41	3.79	3.83	4.70	21.37	2.78
2	$MAP{E}_{sim}$	0.76	0.44	0.64	0.96	0.91	0.49	0.36
	$MAP{E}_{pred}$	4.91	1.57	4.09	1.44	2.36	1.36	1.04
3	$MAP{E}_{sim}$	1.69	1.13	1.23	3.92	2.12	1.16	0.99
	$MAP{E}_{pred}$	12.95	11.00	8.84	3.50	3.06	7.04	2.50
4	$MAP{E}_{sim}$	2.03	0.62	1.98	2.90	1.67	0.73	0.47
	$MAP{E}_{pred}$	7.69	6.59	13.43	3.83	5.13	1.59	1.34
5	$MAP{E}_{sim}$	3.14	2.66	2.94	4.94	5.16	2.31	2.27
	$MAP{E}_{pred}$	2.95	5.66	6.80	5.98	3.62	3.91	2.00

. The fitting MAPE of CFIGGM is 1.57%, which is the lowest fitting error among these models. It shows that it has the best fitting performance. By comparing with the testset, the predicted MAPE error of CFIGGM is 2.78%, which is also the lowest among these models. It shows that CFIGGM has better prediction accuracy than the comparative models in forecasting the natural gas consumption of China.

3.3.2. Example 2: Validation of CFIGGM Model’s Performance on Oil Consumption

In this example, the original sequence listed in Table 2 is the oil consumption per capita from 2010 to 2022, which is employed to verify the performance of the proposed model. By parameter optimization and estimation, the optimal parameters of all grey models are filled in

Table 5. The optimal parameters of different grey models in Example 2.

Model	Optimal Parameters
GM(1,1)	${\beta }_0=322.2994,{\beta }_1=-0.0381$
IGGM	${\beta }_0=324.9571,{\beta }_1=-0.0258,{\beta }_2=1.8021,\mu =4.9345$
CFGM	${\beta }_0=316.3334,{\beta }_1=-0.0332,\alpha =0.6382$
CFNGM	${\beta }_0=362.6191,{\beta }_1=0.7944,{\beta }_2=195.3618,\alpha =0.7301$
CFIGGM	${\beta }_0=306.1618,{\beta }_1=0.0211,{\beta }_2=-112.4631,\mu =1.8594,\alpha =0.5405$

. The computed values filled in

Table A3. Simulation and prediction values of different models in Example 3 (unit: Kilogram).

No.	Raw Data	GM(1,1)	IGGM	CFGM(1,1)	BP	SVR	CFNGM	CFIGGM
1	330.00	330.00	330.00	330.00	330.00	330.00	330.00	330.00
2	339.00	341.32	339.00	339.00	339.02	343.80	338.06	338.84
3	354.00	354.57	351.62	354.26	348.20	352.92	351.77	354.00
4	367.00	368.34	367.29	369.04	363.50	368.12	367.77	366.86
5	378.00	382.64	384.39	383.78	376.76	381.29	384.66	382.60
6	406.00	397.49	401.22	398.67	387.98	392.43	401.24	399.78
7	416.00	412.92	416.92	413.83	416.54	420.80	416.96	416.63
8	433.00	428.95	431.40	429.33	426.73	430.93	431.64	432.15
9	444.00	445.60	444.93	445.22	444.07	448.16	445.29	445.96
10	458.00	462.89	457.89	461.55	455.29	459.30	458.00	458.00
11	463.00	480.86	470.61	478.35	469.57	473.48	469.87	468.38
12	484.00	499.53	483.31	495.65	481.38	478.55	481.01	477.25
13	482.00	518.92	496.15	513.49	493.42	499.83	491.50	484.77

are obtained by these optimal models. The comparison of all models is shown in Figure 3. The MAPEs of all models are presented in Table 4. Obviously, CFIGGM has the best fitting performance, which denotes that it has the best ability to capture the characteristics of small samples. The predicted MAPE of CFIGGM is also the lowest. It shows that CFIGGM has the best prediction performance in forecasting China’s oil consumption per capita.

3.3.3. Example 3: Validation of CFIGGM Model’s Performance on Electricity Consumption

In this example, we utilized annual electricity consumption from 2010 to 2022 listed in Table 2 to validate the CFIGGM model’s performance. The first 10 data samples of the sequence are employed to build CFIGGM and the comparative grey models. The optimal parameters of the models are filled in

Table 6. The optimal parameters of different grey models in Example 3.

Model	Optimal Parameters
GM(1,1)	${\beta }_0=22,899.6218,{\beta }_1=-0.0927$
IGGM	${\beta }_0=17,910.0917,{\beta }_1=-0.0880,{\beta }_2=6887.3948,\mu =1.2793$
CFGM	${\beta }_0=20,413.5157,{\beta }_1=-0.0676,\alpha =1.2282$
CFNGM	${\beta }_0=9811.1007,{\beta }_1=-0.0788,{\beta }_2=21,637.9030,\alpha =1.9225$
CFIGGM	${\beta }_0=19,441.4058,{\beta }_1=0.0738,{\beta }_2=1.3165,\mu =8.2286,\alpha =0.4622$

. The calculated values of all models are filled in

Table A4. Simulation and prediction values of different models in Example 4 (unit: trillion kWh).

No.	Raw Data	GM(1,1)	IGGM	CFGM(1,1)	BP	SVR	CFNGM	CFIGGM
1	21,971.37	21,971.37	21,971.37	21,971.37	21,971.37	21,971.37	21,971.37	21,971.37
2	24,940.32	26,130.14	24,990.51	25,034.99	23,227.48	25,369.56	24,774.99	24,940.32
3	28,587.97	28,669.35	28,602.46	28,397.06	26,366.05	28,402.77	28,709.10	28,896.93
4	32,711.81	31,455.31	31,787.32	31,668.28	30,222.08	32,129.37	31,839.51	31,778.30
5	34,541.35	34,511.99	34,934.89	34,989.24	34,581.51	36,342.47	34,974.23	34,564.36
6	37,032.14	37,865.70	38,237.11	38,431.60	36,515.57	38,211.61	38,363.14	37,907.11
7	41,934.49	41,545.32	41,789.61	42,041.54	39,148.65	40,756.31	42,035.10	41,934.45
8	47,000.88	45,582.50	45,648.06	45,854.04	44,331.07	45,764.77	45,941.73	46,292.48
9	49,762.64	50,012.00	49,853.46	49,898.85	49,686.89	50,940.82	50,017.65	50,412.94
10	54,203.41	54,871.93	54,442.72	54,203.29	52,606.43	53,762.36	54,203.42	53,791.31
11	56,383.69	60,204.14	59,453.09	58,793.79	57,300.89	58,299.24	58,452.27	56,137.03
12	58,019.97	66,054.50	64,924.04	63,696.80	60,575.33	60,526.71	62,730.19	57,387.63
13	61,297.09	72,473.37	70,898.24	68,939.39	64,036.83	62,198.41	67,013.76	57,645.18

. The comparison of the fitting and prediction values is presented in Figure 4. The fitting MAPE of CFIGGM is 0.99%, which indicates that the CFIGGM model demonstrates the optimal fitting effect. Its prediction MAPE is 2.50%. It shows that CFIGGM has the best performance in forecasting annual electricity consumption.

3.3.4. Example 4: Validation of CFIGGM Model’s Capability in Handling Non-Linear Sequences

In this subsection, we validate the ability of the CFIGGM model to handle non-linear sequences on the raw sequence, which is China’s coal consumption from 2010 to 2022, and listed in Table 2. The sequence has typical nonlinear characteristics, which can be clearly seen from Figure 5. The optimal parameters of CFIGGM and the comparative models are determined via the WOA or trainset. The optimal parameters of the grey models are presented in

Table 7. The optimal parameters of different grey models in Example 4.

Model	Optimal Parameters
GM(1,1)	${\beta }_0=409,337.3496,{\beta }_1=0.0034$
IGGM	${\beta }_0=351,213.6297,{\beta }_1=-0.0767,{\beta }_2=-1767.9210,\mu =6.1161$
CFGM	${\beta }_0=367,100.2414,{\beta }_1=0.0379,\alpha =1.9788$
CFNGM	${\beta }_0=352,691.4023,{\beta }_1=0.3379,{\beta }_2=18,118.7154,\alpha =0.2084$
CFIGGM	${\beta }_0=329,687.6060,{\beta }_1=-0.0189,{\beta }_2=-5980.2756,\mu =4.9887,\alpha =0.7864$

. The fitting and predicted values are presented in

Table A2. Simulation and prediction values of different models in Example 2 (unit: 10,000 tons).

No.	Raw Data	GM(1,1)	IGGM	CFGM(1,1)	BP	SVR	CFNGM	CFIGGM
1	349,008.26	349,008.26	349,008.26	349,008.26	349,008.26	349,008.26	349,008.26	349,008.26
2	388,961.10	407,470.41	390,744.75	392,685.30	353,422.76	387,222.00	385,494.10	388,960.99
3	411,726.90	406,096.75	411,727.28	406,275.24	393,880.78	398,501.69	415,700.49	415,819.17
4	424,425.94	404,727.72	419,542.12	411,639.81	416,934.44	404,929.06	418,397.29	419,984.32
5	413,633.00	403,363.30	414,058.62	412,325.09	429,794.06	408,514.32	411,048.80	411,204.45
6	399,834.00	402,003.49	401,975.43	410,029.97	418,864.65	405,467.20	402,205.16	399,834.01
7	388,820.00	400,648.26	391,284.01	405,714.04	404,891.17	401,571.39	395,850.49	392,326.71
8	391,403.00	399,297.60	387,370.60	399,977.11	393,737.90	398,461.86	393,563.97	390,894.37
9	397,452.00	397,951.49	392,323.68	393,220.68	396,353.56	399,191.10	395,678.02	395,153.03
10	401,915.00	396,609.92	405,955.57	385,727.00	402,479.05	400,898.89	401,915.16	403,731.45
11	404,860.00	395,272.87	427,063.39	377,701.80	406,998.48	402,158.91	411,737.69	415,209.19
12	429,576.00	393,940.33	454,293.65	369,299.23	412,146.24	402,990.36	424,535.08	428,482.17
13	448,246.00	392,612.28	486,553.72	360,637.26	417,359.08	409,968.31	439,719.07	442,812.19

. A comparison of all models is presented in Figure 5. Compared with the comparative models, CFIGGM has the lowest fitting MAPE and prediction MAPE, which are 0.47% and 1.34%, respectively. From Figure 5, it can also be easily observed that the CFIGGM model has the best fitting and predictive performance. It shows that CFIGGM can effectively capture and model the inherent laws and patterns hidden in the non-linear sequence.

3.3.5. Example 5: Validation of CFIGGM Model’s Generalization Ability

In this section, we validate the performance of the newly proposed model by predicting renewable power generation in Denmark, which is listed in Table 2. The optimal parameters of all grey models are presented in

Table 8. The optimal parameters of different grey models in Example 5.

Model	Optimal Parameters
GM(1,1)	${\beta }_0=15.2346,{\beta }_1=-0.0545$
IGGM	${\beta }_0=14.0602,{\beta }_1=-0.0939,{\beta }_2=-0.0280,\mu =6.3929$
CFGM	${\beta }_0=13.9109,{\beta }_1=-0.0302,\alpha =2.9407$
CFNGM	${\beta }_0=14.6444,{\beta }_1=0.4393,{\beta }_2=1.0771,\alpha =0.0010$
CFIGGM	${\beta }_0=11.5788,{\beta }_1=-0.0216,{\beta }_2=-1.2912,\mu =3.6368,\alpha =0.5267$

. The fitted values and predicted results calculated by these models are provided in

Table A5. Simulation and prediction values of different models in Example 5 (unit: Terawatt-hours).

No.	Raw Data	GM(1,1)	IGGM	CFGM(1,1)	BP	SVR	CFNGM	CFIGGM
1	14.84	14.84	14.84	14.84	14.84	14.84	14.84	14.84
2	15.97	16.49	16.16	15.97	16.01	16.52	15.82	15.89
3	17.99	17.41	17.55	17.36	17.10	17.53	17.90	17.99
4	18.96	18.39	18.72	18.58	19.05	19.35	18.86	18.90
5	18.39	19.42	19.65	19.72	19.98	20.22	19.54	19.51
6	21.80	20.51	20.46	20.82	19.43	19.71	20.33	20.27
7	20.76	21.66	21.36	21.90	22.72	22.77	21.38	21.33
8	23.07	22.87	22.50	22.97	21.71	21.83	22.70	22.65
9	23.45	24.16	23.99	24.04	23.94	23.91	24.29	24.16
10	26.10	25.51	25.83	25.12	24.30	24.25	26.09	25.78
11	28.51	26.94	28.04	26.22	26.86	26.63	28.06	27.47
12	29.21	28.45	30.59	27.33	27.58	28.79	30.16	29.21
13	30.27	30.05	33.48	28.47	28.28	29.42	32.36	30.98

. The fitting MAPE of the CFIGGM model is 2.27%. The prediction MAPE of the CFIGGM model is 2.00%. They are lower than the fitting MAPEs and prediction MAPEs of the comparative models. From Table A5 and Figure 6, it can be concluded that our model outperforms the comparative model in Denmark’s renewable power generation prediction. At the same time, it also reflects that the CFIGGM model is suitable for small-sample time series in different fields of other countries.

3.4. Analysis of Validation

In this section, we provide a comprehensive analysis of the verification experiment results. The fitting MAPE and prediction MAPE of the CFIGGM model and comparative models in Examples 1–5 are shown in Table 4. In Example 1, the fitting errors of CFIGGM, IGGM, and CFNGM models are similar, but the prediction error of CFIGGM is only 2.78%, far lower than the 15.41% of IGGM and 21.37% of CFNGM. It indicates that it significantly improves the predictive ability of classical grey models by integrating conformable fractional-order and incomplete gamma grey action quantity. In Example 2, all models have a fitting error of less than 1%, and the CFIGGM model has the lowest fitting error of 0.36%. Its predictive performance is better than that of other models. In particular, the CFIGGM model has significant advantages compared to GM(1,1) and CFGM(1,1). In Example 3, the predictive performance of CFIGGM also far exceeds other comparative grey models. Based on the three examples, it can be seen that CFIGGM has outstanding advantages in both fitting and prediction performance. In Example 4, the CFIGGM model still achieved the lowest fitting and prediction errors when it is used to handle the typical non-linear sequence. This indicates that it has strong non-linear data processing capability. In Example 5, unlike the previous four examples of China’s energy consumption data, Denmark’s renewable energy generation data were used to validate the CFIGGM model. It still showed better fitting and prediction performance, verifying its good generalization ability. Compared to machine learning methods such as BP and SVR, the new model is easier to obtain the optimal model through training. In addition, due to the clear mathematical and physical meanings of the parameters in the new model, its interpretability is significantly better than machine learning models, where the parameters are mostly “black box” in nature. In summary, the new model has excellent comprehensive performance. Therefore, we will apply this model to research on predicting global solar energy consumption in the next section.

4. Application of the CFIGGM Model to Global Solar Energy Consumption Prediction

In recent decades, with the acceleration of industrialization, the large-scale consumption of fossil fuels has led to a rapid increase in carbon dioxide, which has resulted in multiple environmental crises such as air pollution, the intensification of the greenhouse effect, and ecosystem degradation. It poses a severe challenge to the global ecological security and the sustainable development of human society. In this context, the international community has gradually formed a policy paradigm of collaborative governance of environment and development. Many countries are stepping up efforts to research, develop, and apply renewable energy technologies through technological innovation and institutional change, aiming to break through the dependence on the traditional high-carbon development model. Solar energy stands among the most abundant and extensively distributed renewable energy sources worldwide. Through the systematic integration of the development and utilization of solar energy resources and environmental protection, it can not only effectively reduce the pollutant emissions of energy consumption, but also promote the formation of a new industrial system and consumption mode characterized by low-carbon.

The precise consumption prediction of solar energy is closely associated with environmental protection and sustainable development, which can effectively support investment decision making in the energy industry, and help policy formulation and market mechanism improvement. In order to obtain accurate prediction results, we have collected the history dataset of solar energy consumption of the period 2016–2024 from the Energy Institute Statistical Review of World Energy 2025 [1]. The raw data sequence $s^0$ is [1265.18 1695.08 2161.05 2645.99 3182.15 3889.78 4854.82 6038.51 7717.72 3] (unit: Petajoule). The sequence from 2016 to 2022 is used to construct the models, and the rest is used to verify their prediction performance. The parameters of GM(1,1) are ${\beta }_0=1294.9$ and ${\beta }_1=-0.2030$. The nonlinear parameters of IGGM, CFGM(1,1), CFNGM, and CFIGGM are obtained via WOA. The optimal values of the parameters are ${\beta }_0=-104.2402,$${\beta }_1=-0.2019,{\beta }_2=350.2161,\mu =0.2229$ in IGGM. The optimal parameters of CFGM(1,1) are ${\beta }_0=1214.4525,{\beta }_1=-0.1839,\alpha =0.9178$. The optimal parameters of CFNGM are ${\beta }_0=1145.4743,{\beta }_1=-0.3686,{\beta }_2=-404.8571,\alpha =0.5331$. The optimal parameters of CFIGGM are ${\beta }_0=1131.4703,{\beta }_1=-0.0713,{\beta }_2=0.0054,\mu =10.1188,\alpha =0.5790$. The optimal BP model is trained by minimizing the fitting error while avoiding overfitting. The hyper-parameters of the optimal SVR model is obtained by the Grid Search method. According to the optimal grey models and machine learning methods, the fitting values and predicted values calculated by each model are shown in

Table 9. Simulation and prediction values of CFIGGM and comparative models on the global solar energy consumption (unit: Petajoule).

Year	Raw Data	GM(1,1)	IGGM	CFGM(1,1)	CFNGM	SVR	BP	CFIGGM
2016	1265.18	1265.18	1265.18	1265.18	1265.18	1265.18	1265.18	1265.18
2017	1695.08	1724.02	1695.08	1695.08	1699.47	1888.45	1550.74	1695.08
2018	2161.05	2115.26	2118.06	2116.02	2151.30	2342.65	2076.73	2161.16
2019	2645.99	2595.30	2602.77	2612.58	2622.01	2834.97	2646.84	2636.69
2020	3182.15	3184.26	3188.23	3206.27	3168.97	3347.33	3240.17	3183.33
2021	3889.78	3906.89	3902.55	3919.88	3858.33	3913.81	3896.16	3889.78
2022	4854.82	4793.51	4776.07	4779.73	4779.79	4661.45	4761.94	4849.42
$MAP{E}_{sim}$		1.07	0.82	0.92	0.63	5.25	2.34	0.07
2023	6038.51	5881.33	5844.84	5816.98	6062.08	5681.06	5942.67	6120.04
2024	7717.72	7216.03	7152.70	7068.90	7893.72	6931.69	7273.66	7700.87
$MAP{E}_{pred}$		4.55	5.26	6.04	1.34	8.05	3.67	0.78

. The computed values of all models are in close agreement with the real values, as shown in Figure 7. The fitting MAPE of CFIGGM is the lowest, though the fitting MAPEs of all models are close to 1%. Meanwhile, the prediction of the newly proposed model is 0.78% which is also the lowest. The MAPEs of different models are shown in Table 9. It shows that CFIGGM has the best fitting and prediction ability. Therefore, we utilize CFIGGM to forecast the global consumption of solar energy. The predicted values from 2025 to 2029 are 9540.81 Petajoules, 11,566.17 Petajoules, 13,709.22 Petajoules, 15,925.51 Petajoules, and 18,198.36 Petajoules. It is evident that global solar energy consumption will reach 18,198.36 Petajoules in 2029, indicating a sustained growth trend in the future. In general, global solar energy consumption shows a sustained and significant growth trend. However, the year-on-year growth rate will drop from 23.89% in 2024 to 14.27% in 2029. The main reason is that the current solar energy consumption base has reached a high level, and the growth rate naturally falls with the improvement of market maturity. However, the growth rate of solar energy consumption remains higher than the global average rate of energy consumption, showing the resilience and sustainability of solar energy growth.

5. Conclusions

As a clean and renewable energy source, solar energy has broad development prospects. With the technological advances and the ongoing cost reductions, the share of solar energy in the worldwide energy structure will continue to increase, making an important contribution to the realization of sustainable development goals. Forecasting solar energy consumption can serve as a scientific foundation for stabilizing the energy system, the sound development of the energy industry, the precise implementation of policies, the realization of environmental protection goals, and energy security. In this study, we propose a novel Conformable Fractional Incomplete Gamma Grey Model, denoted as CFIGGM, to forecast global solar energy consumption via improving the traditional grey model. In the new model, the CFAGO operator replaces the integer-order Accumulation Generation Operator (AGO) in IGGM, thereby mining the hidden characteristics of the original sequence. The CFAGO can break through the rigid limit of traditional integer-order AGO through continuously adjustable order regulation and historical memory characteristics, so that the CFIGGM can capture the patterns of nonlinear, non-stationary, and small-sample data with higher accuracy. From the five case studies in Section 3, it is observed that the prediction accuracy of the new model outperforms that of other comparative models. Thus, we employ the new proposed model for forecasting the global solar energy consumption, with $MAP{E}_{sim}$ of 0.07% and $MAP{E}_{pred}$ of 0.78%, which are lower than those of other comparison models. Subsequently, the new model is employed to forecast global solar energy consumption. The predicted global solar energy consumption from 2025 to 2029 are 9540.81 Petajoules, 11,566.17 Petajoules, 13,709.22 Petajoules, 15,925.51 Petajoules, and 18,198.36 Petajoules. The results indicate that the global solar energy consumption will continue to grow, albeit with a declining growth rate. According to the historical records (2016–2024) and the predicted values (2025–2029), the solar energy consumption will sustain its historical upward trajectory in the next years. Specifically, the consumption is projected to rise gradually from 9540.81 Petajoules in 2025 to 18,198.36 Petajoules in 2029, achieving a 1.91-fold total growth over five years. It is worth noting that the compound annual growth rate of global solar energy consumption is expected to drop to 17.5% between 2025 and 2029, lower than the historical 25.3% from 2016 to 2024. On the one hand, the relative growth rate has moderately slowed down with the continuous expansion of the solar energy consumption base. On the other hand, the absolute growth of solar energy consumption will remain strong during the period 2025–2029. For example, it is expected that the annual absolute increment in 2028–2029 will reach 2272.85 Petajoules, an increase of 35.4% from the recorded 1679.21 Petajoules in 2023–2024. The global solar energy consumption in 2029 will be 14.38 times that of 2016. This indicates that solar energy is about to transform from a traditional “supplementary energy” to the “core pillar” of the global energy supply system. The predicted results can provide a quantitative reference for policy formulation—specifically, for guiding decisions in areas such as photovoltaic installed capacity planning and cross-regional power grid investment optimization. Simultaneously, they also offer targeted data support for energy market entities to adjust their capacity allocation strategies.

The core advantage of the CFIGGM model lies in its precise depiction and predictive ability for “non-linear small sample time series”. This methodological characteristic gives it the potential to be applied in multiple fields. Specifically, its potential application directions can be summarized as the following three categories. First, it can be extended to prediction scenarios for other types of renewable energy, such as wind energy production and hydropower consumption. The sequences of these energy sources exhibit significant non-linear characteristics. And the historical data accumulation in some regions or new projects is limited. Second, it is applicable to cross-regional energy demand prediction, especially for developing countries with limited historical data. Third, it can be extended to non-energy fields characterized by small sample data, such as regional GDP, industrial output value of emerging industries, etc. Moreover, the practicability of the proposed model in complex scenarios can be improved through structural optimization, interdisciplinary integration, standardized evaluation, and other methods, and then provide reliable tools for problem solving in more fields. For example, the new model is a univariate model, which struggles to deal with complex systems affected by multiple factors. In future research, it is necessary to break through the univariate framework and build a multivariable conformable fractional order incomplete gamma grey model. Meanwhile, the new model can be integrated into the energy management, economic early warning, and other decision support systems. The parameters can be dynamically updated through real-time data input to achieve a closed-loop between forecasting and decision-making.