Impact of Sub-Cloud Evaporation on Precipitation in Tropical Monsoon Islands
Abstract
1. Introduction
2. Materials and Methods
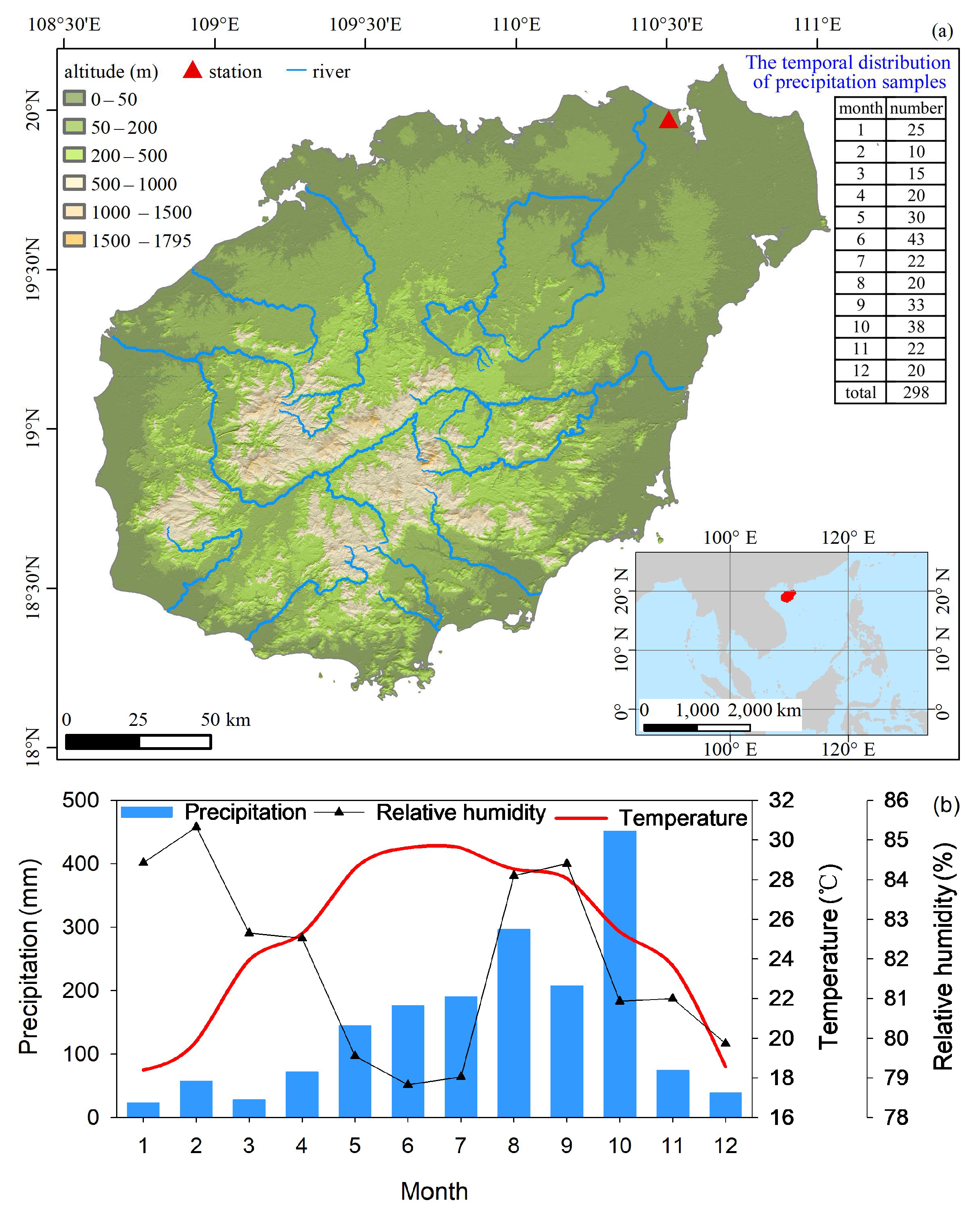
2.1. Study Area
2.2. Datasets
2.2.1. Precipitation Isotope Data
2.2.2. Meteorological Data
2.3. Methods
2.3.1. The Slope of the Theoretical Local Meteoric Water Line (LMWL) and Theoretical Local Evaporation Line (LEVL)
- (1)
- The slope of the theoretical LMWL
- (2)
- The slope of the theoretical LEVL
2.3.2. Calculation of the Sub-Cloud Evaporation
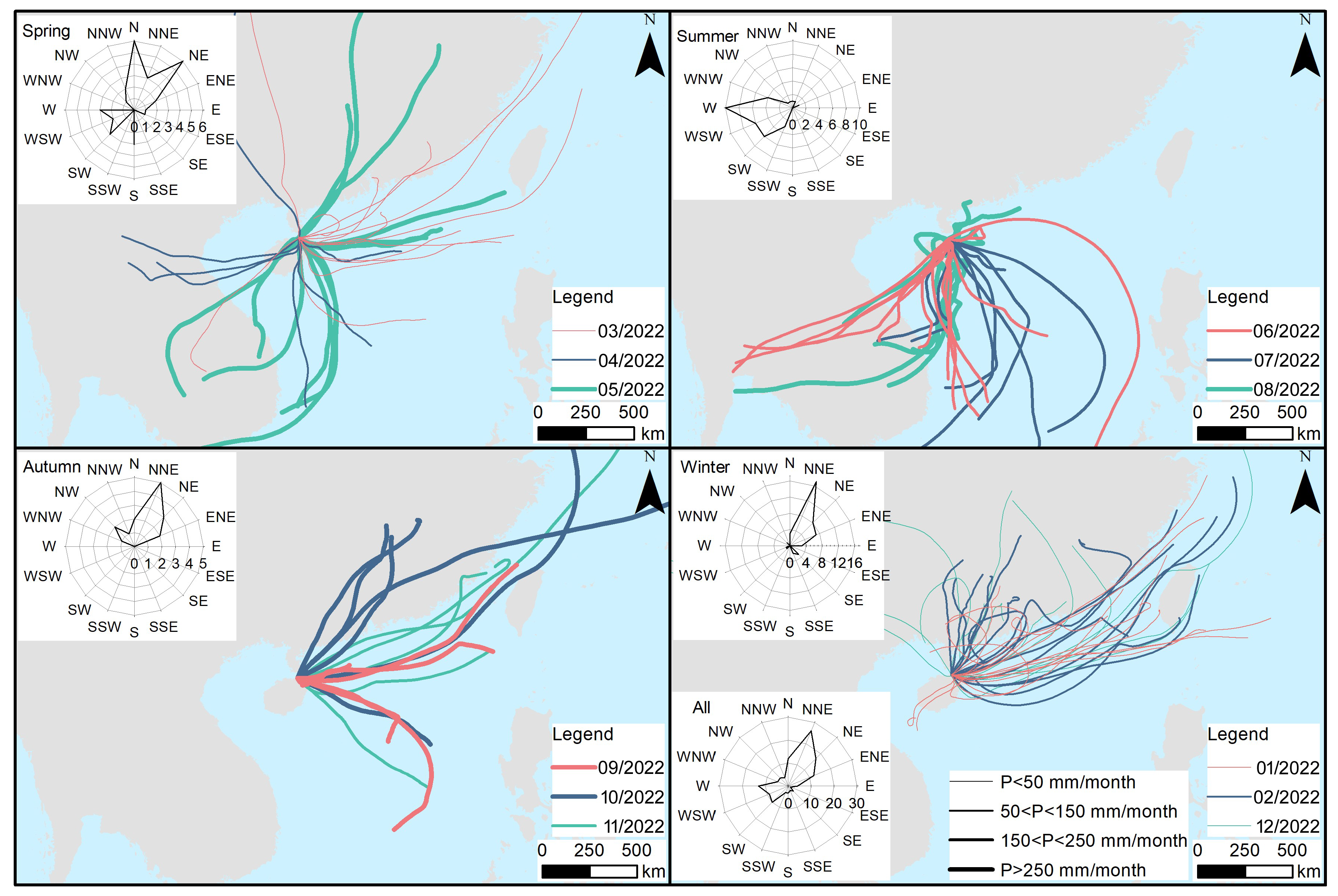
2.3.3. Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) Model
2.3.4. Assessment of Uncertainty
3. Results
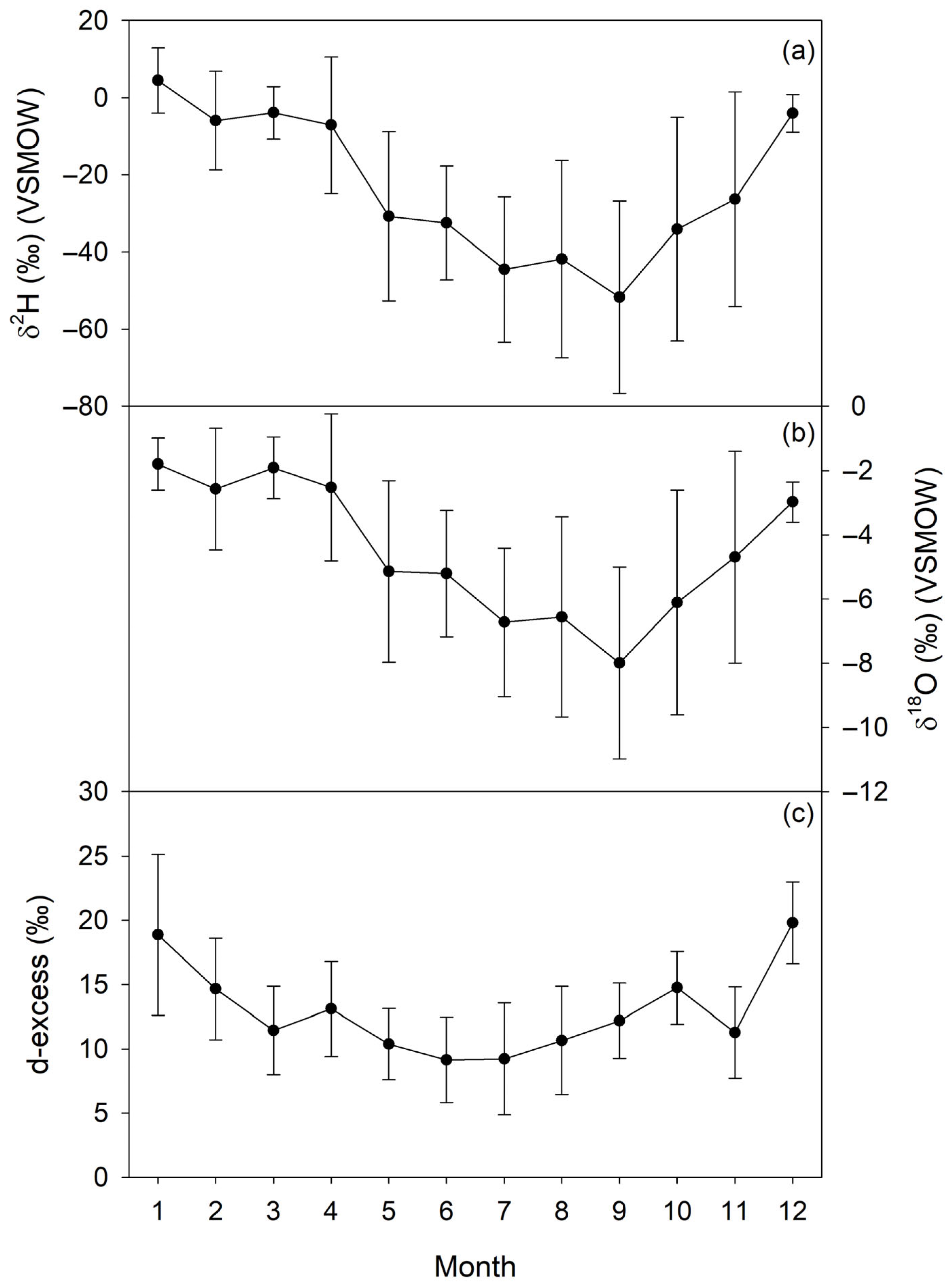
3.1. Temporal Variation in Precipitation Isotopes
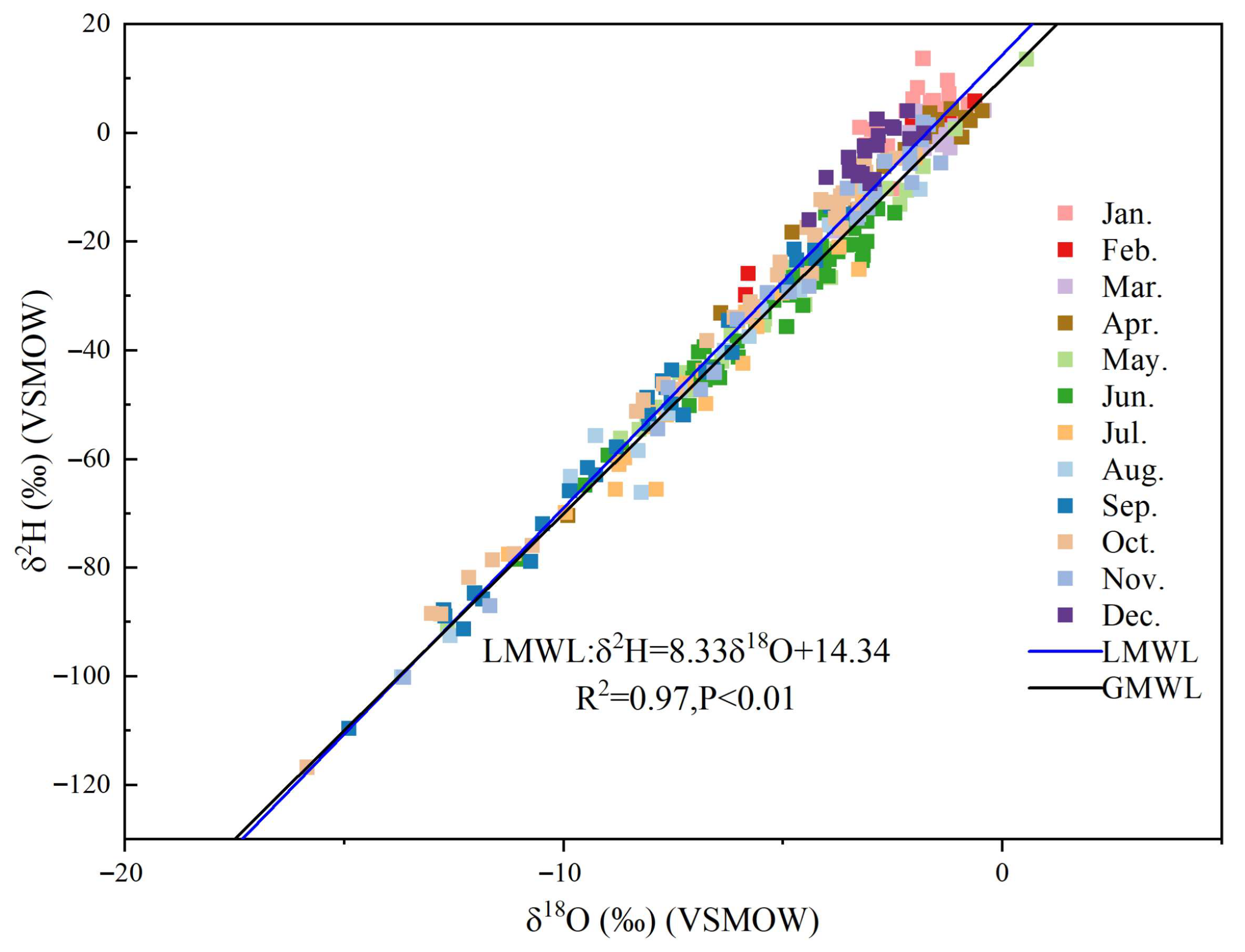
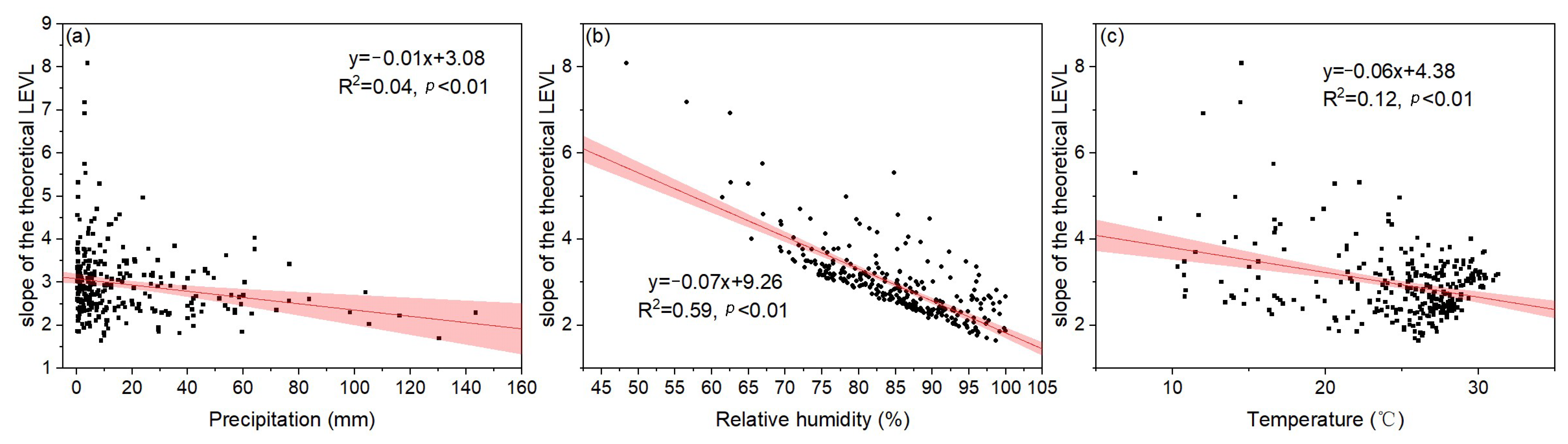
3.2. Slopes of the Theoretical LMWL and LEVL
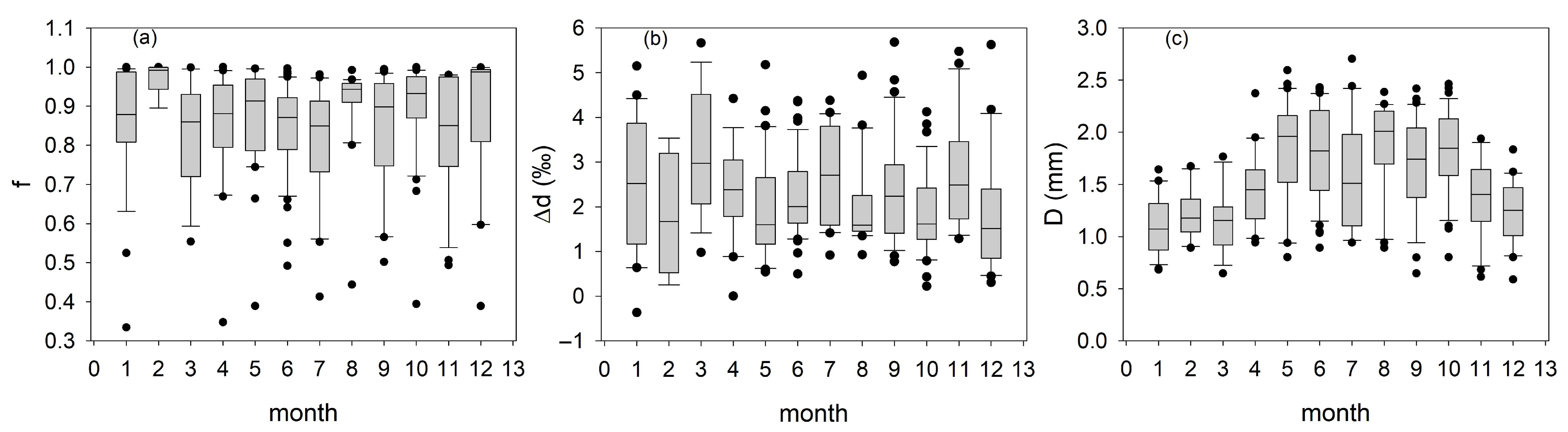
3.3. Sub-Cloud Evaporation
4. Discussion
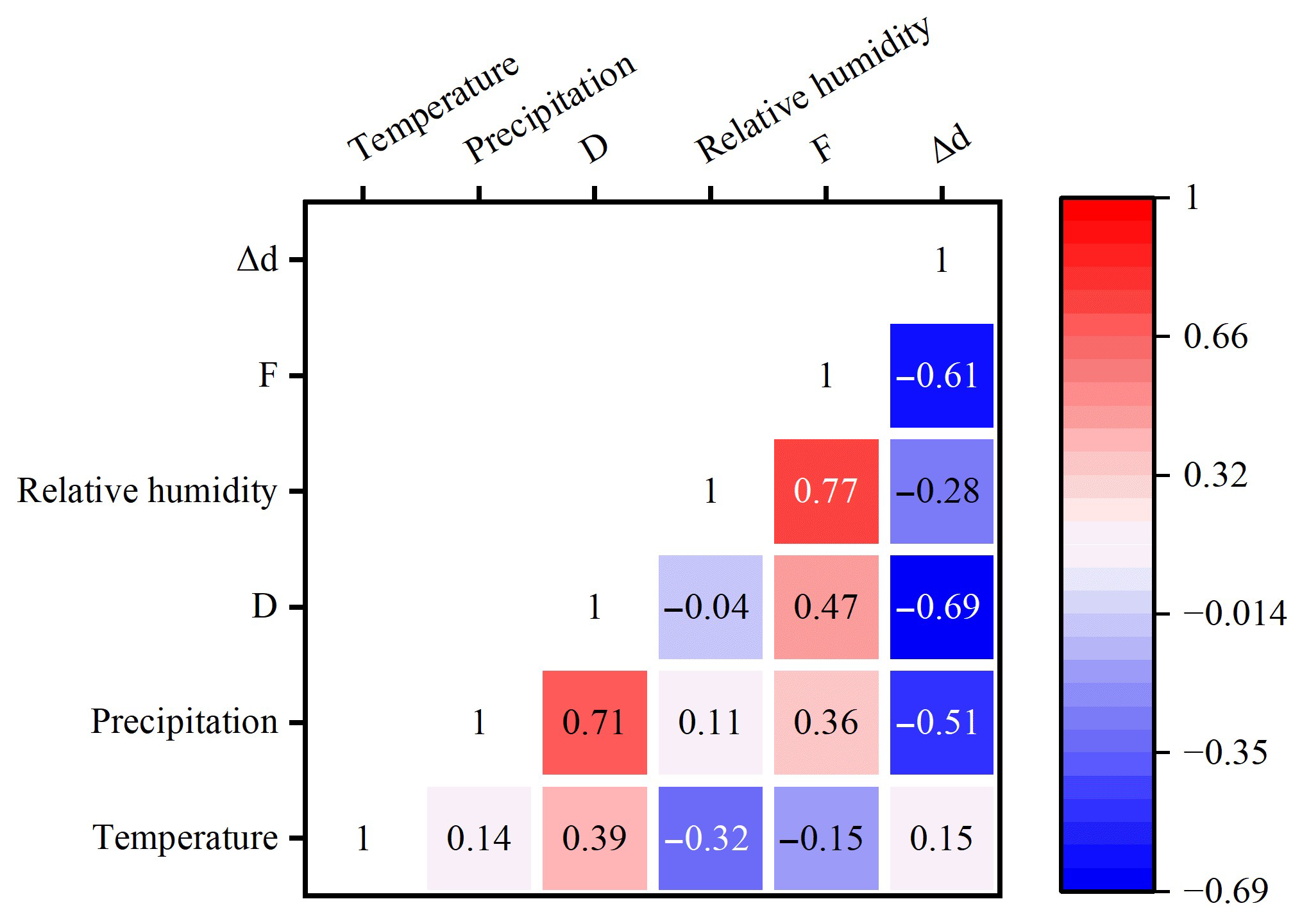
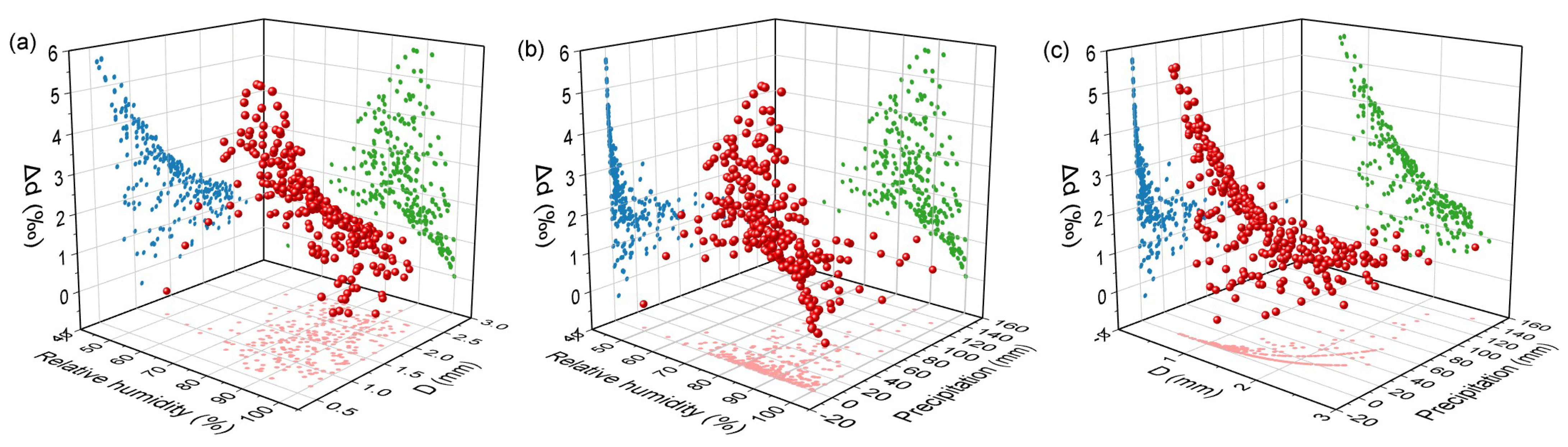
4.1. Influencing Factors of Sub-Cloud Evaporation: Temperature, Relative Humidity and Precipitation
4.2. Uncertainty Analysis
5. Conclusions
- (1)
- Influenced by below-cloud evaporation, the slope of the LMWL (δ2H = 8.33δ18O + 14.33) is slightly lower than the average slope of the theoretical LMWL (8.48). There is no significant seasonal variation trend in Δd and f due to the effect of complex water vapor sources.
- (2)
- On the one hand, the sub-cloud evaporation of precipitation is most sensitive to changes in relative humidity; on the other hand, it is difficult to use a single meteorological factor to explain the sub-cloud evaporation of precipitation in the study area as the humid and hot environmental conditions could reduce the impact of sub-cloud evaporation on precipitation isotopes.
- (3)
- The exchange of precipitation isotopes with large amounts of recirculating water vapor results in changes in the isotopic composition of precipitation, which is an important source of uncertainty in sub-cloud evaporation simulations. In addition, the relatively strict assumption of the Stewart model that raindrops at the cloud base have reached isotopic equilibrium with the surrounding water vapor is also a potential source of uncertainty in below-cloud evaporation simulations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Messié, M.; Petrenko, A.; Doglioli, A.M.; Martinez, E.; Alvain, S. Basin-scale biogeochemical and ecological impacts of islands in the tropical Pacific Ocean. Nat. Geosci. 2022, 15, 469–474. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Chen, W.-T.; Wu, C.-M. Novel perspectives on multiple-peak diurnal convection over a tropical mountainous island from idealized large-eddy simulations. Npj Clim. Atmos. Sci. 2024, 7, 325. [Google Scholar] [CrossRef]
- Boyle, M.J.W.; Bonebrake, T.C.; Dias da Silva, K.; Dongmo, M.A.K.; Machado França, F.; Gregory, N.; Kitching, R.L.; Ledger, M.J.; Lewis, O.T.; Sharp, A.C.; et al. Causes and consequences of insect decline in tropical forests. Nat. Rev. Biodivers. 2025, 1, 315–331. [Google Scholar] [CrossRef]
- Good, P.; Chadwick, R.; Holloway, C.E.; Kennedy, J.; Lowe, J.A.; Roehrig, R.; Rushley, S.S. High sensitivity of tropical precipitation to local sea surface temperature. Nature 2021, 589, 408–414. [Google Scholar] [CrossRef]
- Song, F.; Dong, H.; Wu, L.; Leung, L.R.; Lu, J.; Dong, L.; Wu, P.; Zhou, T. Hot season gets hotter due to rainfall delay over tropical land in a warming climate. Nat. Commun. 2025, 16, 2188. [Google Scholar] [CrossRef]
- Shiogama, H.; Watanabe, M.; Kim, H.; Hirota, N. Emergent constraints on future precipitation changes. Nature 2022, 602, 612–616. [Google Scholar] [CrossRef]
- Kathayat, G.; Sinha, A.; Tanoue, M.; Yoshimura, K.; Li, H.; Zhang, H.; Cheng, H. Interannual oxygen isotope variability in Indian summer monsoon precipitation reflects changes in moisture sources. Commun. Earth Environ. 2021, 2, 96. [Google Scholar] [CrossRef]
- Sha, L.; Tian, L.; Sha, L.; Li, Y.; Wang, X.; Hu, P.; Liang, Q.; Zong, B.; Duan, P.; Cheng, H. Triple oxygen isotope compositions reveal transitions in the moisture source of West China Autumn Precipitation. Commun. Earth Environ. 2024, 5, 188. [Google Scholar] [CrossRef]
- Cui, Y.; Tian, L.; Cai, Z.; Wang, S. Spatially inhomogeneous response of precipitation δ18O in China to ENSO cycles. Npj Clim. Atmos. Sci. 2025, 8, 164. [Google Scholar] [CrossRef]
- Thirumalai, K.; Clemens, S.C.; Rosenthal, Y.; Conde, S.; Bu, K.; Desprat, S.; Erb, M.; Vetter, L.; Franks, M.; Cheng, J.; et al. Extreme Indian summer monsoon states stifled Bay of Bengal productivity across the last deglaciation. Nat. Geosci. 2025, 18, 443–449. [Google Scholar] [CrossRef]
- Xia, Z.; Surma, J.; Winnick, M.J. The response and sensitivity of deuterium and 17O excess parameters in precipitation to hydroclimate processes. Earth-Sci. Rev. 2023, 242, 104432. [Google Scholar] [CrossRef]
- Liang, Q.; Sha, L.; Li, J.; Zhang, J.; Wang, X.; Zhou, S.; Lin, F.; Xue, Y.; Duan, R.; He, Y.; et al. Seasonal Variations and Controls on Triple Oxygen and Hydrogen Isotopes in Precipitation-A Case Study From Monitoring in Southwest China. J. Geophys. Res.-Atmos. 2024, 129, e2023JD040654. [Google Scholar] [CrossRef]
- Koppa, A.; Rains, D.; Hulsman, P.; Poyatos, R.; Miralles, D.G. A deep learning-based hybrid model of global terrestrial evaporation. Nat. Commun. 2022, 13, 1912. [Google Scholar] [CrossRef]
- Sun, C.; Tian, L.; Shanahan, T.M.; Partin, J.W.; Gao, Y.; Piatrunia, N.; Banner, J. Isotopic variability in tropical cyclone precipitation is controlled by Rayleigh distillation and cloud microphysics. Commun. Earth Environ. 2022, 3, 50. [Google Scholar] [CrossRef]
- Da Silva, N.A.; Haerter, J.O. Super-Clausius–Clapeyron scaling of extreme precipitation explained by shift from stratiform to convective rain type. Nat. Geosci. 2025, 18, 382–388. [Google Scholar] [CrossRef]
- Jackson, L.S.; Birch, C.E.; Chagnaud, G.; Marsham, J.H.; Taylor, C.M. Daily rainfall variability controls humid heatwaves in the global tropics and subtropics. Nat. Commun. 2025, 16, 3461. [Google Scholar] [CrossRef] [PubMed]
- Conroy, J.; Noone, D.; Cobb, K.; Moerman, J.; Konecky, B. Paired stable isotopologues in precipitation and vapor: A case study of the amount effect within western tropical Pacific storms. J. Geophys. Res.-Atmos. 2016, 121, 3290–3303. [Google Scholar] [CrossRef]
- Torri, G.; Nugent, A.; Popp, R. The Isotopic Composition of Rainfall on a Subtropical Mountainous Island. J. Hydrometeorol. 2023, 24, 761–781. [Google Scholar] [CrossRef]
- Sánchez-Murillo, R.; Herrera, D.; Farrick, K.; Esquivel-Hernández, G.; Sánchez-Gutiérrez, R.; Barberena-Moncada, J.; Guatemala-Herrera, J.; Flores-Meza, Y.; Cerón-Pineda, R.; Gil-Urrutia, L.; et al. Stable isotope tempestology of tropical cyclones across the North Atlantic and Eastern Pacific Ocean basins. Ann. N. Y. Acad. Sci. 2025, 1543, 145–165. [Google Scholar] [CrossRef] [PubMed]
- Kurita, N.; Ichiyanagi, K.; Matsumoto, J.; Yamanaka, M.; Ohata, T. The relationship between the isotopic content of precipitation and the precipitation amount in tropical regions. J. Geochem. Explor. 2009, 102, 113–122. [Google Scholar] [CrossRef]
- Wei, Z.; Lee, X.; Liu, Z.; Seeboonruang, U.; Koike, M.; Yoshimura, K. Influences of large-scale convection and moisture source on monthly precipitation isotope ratios observed in Thailand, Southeast Asia. Earth Planet. Sci. Lett. 2018, 488, 181–192. [Google Scholar] [CrossRef]
- Vimeux, F.; Risi, C.; Barthe, C.; François, S.; Cauquoin, A.; Jossoud, O.; Metzger, J.; Cattani, O.; Minster, B.; Werner, M. Is the Isotopic Composition of Precipitation a Robust Indicator for Reconstructions of Past Tropical Cyclones Frequency? A Case Study on Réunion Island From Rain and Water Vapor Isotopic Observations. J. Geophys. Res.-Atmos. 2024, 129, e2023JD039794. [Google Scholar] [CrossRef]
- He, S.; Jackisch, D.; Samanta, D.; Yi, P.; Liu, G.; Wang, X.; Goodkin, N. Understanding Tropical Convection Through Triple Oxygen Isotopes of Precipitation From the Maritime Continent. J. Geophys. Res.-Atmos. 2021, 126, e2020JD033418. [Google Scholar] [CrossRef]
- Schmitt, S.; Riveros-Iregui, D.; Hu, J. The role of fog, orography, and seasonality on precipitation in a semiarid, tropical island. Hydrol. Process. 2018, 32, 2792–2805. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Wee, B.; LeGrande, A.; Wang, J.; Goodkin, N.; Wang, X. Precipitation 17O-Excess Altered During Tropical Convection: Evidence From Monsoon Cold Surges in Singapore. J. Geophys. Res.-Atmos. 2024, 129, e2023JD040437. [Google Scholar] [CrossRef]
- Salamalikis, V.; Argiriou, A.A.; Dotsika, E. Isotopic modeling of the sub-cloud evaporation effect in precipitation. Sci. Total Environ. 2016, 544, 1059–1072. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Zhang, M.; Gao, Y.; Ge, J. Different responses of extreme and mean precipitation to land use and land cover changes. Npj Clim. Atmos. Sci. 2025, 8, 175. [Google Scholar] [CrossRef]
- Cheng, L.-W.; Yu, C.-K.; Chen, S.-P. Identifying mechanisms of tropical cyclone generated orographic precipitation with Doppler radar and rain gauge observations. Npj Clim. Atmos. Sci. 2025, 8, 35. [Google Scholar] [CrossRef]
- Wang, S.; Shi, Y.; Xing, M.; Wu, H.; Pang, H.; Lei, S.; Wang, L.; Zhang, M. Quantifying the below-cloud evaporation of raindrops using near-surface water vapour isotopes: Applications in humid and arid climates in East Asia. J. Hydrol. 2024, 638, 131561. [Google Scholar] [CrossRef]
- Wang, S.J.; Zhang, M.J.; Che, Y.J.; Zhu, X.F.; Liu, X.M. Influence of Below-Cloud Evaporation on Deuterium Excess in Precipitation of Arid Central Asia and Its Meteorological Controls. J. Hydrometeorol. 2016, 17, 1973–1984. [Google Scholar] [CrossRef]
- Chen, F.; Chen, J.; Wang, S.; Wu, X.; Zhang, Q.; Gao, M.; Kang, X.; Pu, Z.; Zhang, D. Below-cloud evaporation effect on stable water isotopes in precipitation at the eastern margin of Qinghai-Tibet Plateau. Hydrol. Process. 2022, 36, e14699. [Google Scholar] [CrossRef]
- Ye, L.; Zhu, G.; Chen, L.; Qiu, D.; Jiao, Y.; Li, R.; Lu, S.; Yang, J. Influence of below-cloud evaporation on stable isotopes of precipitation in the Yellow River source region. Hydrol. Process. 2024, 38, e15064. [Google Scholar] [CrossRef]
- Zhou, X.; Xu, K.; Ashok, K.; Shi, J.; Zhang, L.; Yu, J.-Y.; Liu, B.; Tam, C.-Y.; Xu, H.; Wang, W. Compound marine heatwaves and tropical cyclones delay the onset of the Bay of Bengal summer monsoon. Npj Clim. Atmos. Sci. 2025, 8, 162. [Google Scholar] [CrossRef]
- Utsumi, N.; Kim, H. Observed influence of anthropogenic climate change on tropical cyclone heavy rainfall. Nat. Clim. Change 2022, 12, 436–440. [Google Scholar] [CrossRef]
- Craig, H. Standard for Reporting Concentrations of Deuterium and Oxygen-18 in Natural Waters. Science 1961, 133, 1833–1834. [Google Scholar] [CrossRef]
- Criss, R.E. Principles of Stable Isotope Distribution; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Majoube, M. Fractionnement en oxygène 18 et en deutérium entre l’eau et sa vapeur. J. De Chim. Phys. 1971, 68, 1423–1436. [Google Scholar] [CrossRef]
- Skrzypek, G.; Mydlowski, A.; Dogramaci, S.; Hedley, P.; Gibson, J.J.; Grierson, P.F. Estimation of evaporative loss based on the stable isotope composition of water using Hydrocalculator. J. Hydrol. 2015, 523, 781–789. [Google Scholar] [CrossRef]
- Gibson, J.J.; Birks, S.J.; Jeffries, D.; Yi, Y. Regional trends in evaporation loss and water yield based on stable isotope mass balance of lakes: The Ontario Precambrian Shield surveys. J. Hydrol. 2017, 544, 500–510. [Google Scholar] [CrossRef]
- Bam, E.K.P.; Ireson, A.M. Quantifying the wetland water balance: A new isotope-based approach that includes precipitation and infiltration. J. Hydrol. 2019, 570, 185–200. [Google Scholar] [CrossRef]
- Zhu, G.F.; Guo, H.W.; Qin, D.H.; Pan, H.X.; Zhang, Y.; Jia, W.X.; Ma, X.G. Contribution of recycled moisture to precipitation in the monsoon marginal zone: Estimate based on stable isotope data. J. Hydrol. 2019, 569, 423–435. [Google Scholar] [CrossRef]
- Craig, H.; Gordon, L.I. Deuterium and oxygen 18 variations in the ocean and marine atmosphere. In Stable Isotopes in Oceanographic Studies and Paleotemperature; Consiglio Nazionale Delle Ricerche, Laboratorio Di Geologia Necleare: Spoleto, Italy, 1956. [Google Scholar]
- Gonfiantini, R. Environmental isotopes in lake studies. In Handbook of Environmental Isotope Geochemistry; Springer: Berlin, Germany, 1986. [Google Scholar]
- Gat, J.R.; Mook, W.G.; Meijer, H.J. Stable isotopes processes in the water cycle. In Environmental isotopes in the Hydrological Cycle (Principles and Applications); Atmospheric Water; UNESCO and IAEA: Paris, France, 2001; pp. 17–40. [Google Scholar]
- Merlivat, L. Molecular Diffusivities Of (H2o)-O-1 6 Hd16o, And (H2o)-O-18 In Gases. J. Chem. Phys. 1978, 69, 2864–2871. [Google Scholar] [CrossRef]
- Stewart, M.K. Stable Isotope Fractionation Due to Evaporation And Isotopic-Exchange of Falling Waterdrops—Applications to Atmospheric Processes and Evaporation Of Lakes. J. Geophys. Res. 1975, 80, 1133–1146. [Google Scholar] [CrossRef]
- Pruppacher, H.; Klett, J.; Wang, P. Microphysics of Clouds and Precipitation. Aerosol Sci. Technol. 1998, 28, 381–382. [Google Scholar] [CrossRef]
- Yang, J. Physics of Clouds and Precipitation; China Meteorological Press: Beijing, China, 2011. [Google Scholar]
- Best, A.C. The size distribution of raindrops. Q. J. R. Meteorol. Soc. 1950, 76, 16–36. [Google Scholar] [CrossRef]
- Kinzer, G.D.; Gunn, R. The Evaporation, Temperature And Thermal Relaxation-Time Of Freely Falling Waterdrops. J. Meteorol. 1951, 8, 71–83. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Li, D.; Li, W.; Yang, Y. Identifying water vapor sources of precipitation in forest and grassland in the north slope of the Tianshan Mountains, Central Asia. J. Arid. Land 2022, 14, 297–309. [Google Scholar] [CrossRef]
- Xing, M.; Liu, W.G.; Hu, J.; Wang, Z. A set of methods to evaluate the below-cloud evaporation effect on local precipitation isotopic composition: A case study for Xi’an, China. Atmos. Chem. Phys. 2023, 23, 9123–9136. [Google Scholar] [CrossRef]
- Craig, H. Isotopic Variations In Meteoric Waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef]
- Clark, I.; Fritz, P. Environmental Isotopes in Hydrogeology; Lewis Publishers: New York, NY, USA, 1997. [Google Scholar]
- Araguas-Araguas, L.; Froehlich, K.; Rozanski, K. Stable isotope composition of precipitation over southeast Asia. J. Geophys. Res.-Atmos. 1998, 103, 28721–28742. [Google Scholar] [CrossRef]
- Peng, H.; Mayer, B.; Harris, S.; Krouse, H.R. The influence of below-cloud secondary effects on the stable isotope composition of hydrogen and oxygen in precipitation at Calgary, Alberta, Canada. Tellus Ser. B-Chem. Phys. Meteorol. 2007, 59, 698–704. [Google Scholar] [CrossRef]
- Graf, P.; Wernli, H.; Pfahl, S.; Sodemann, H. A new interpretative framework for below-cloud effects on stable water isotopes in vapour and rain. Atmos. Chem. Phys. 2019, 19, 747–765. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, M.; Wang, S.; Ma, Q.; Zhu, X.; Dong, L. Relationship between sub-cloud secondary evaporation and stable isotopes in precipitation of Lanzhou and surrounding area. Quat. Int. 2015, 380, 68–74. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Li, D.; Li, W. Effect of sub-cloud evaporation on precipitation in the Tianshan Mountains (Central Asia) under the influence of global warming. Hydrol. Process. 2020, 34, 5557–5566. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, Z.; Guo, H.; Zhang, Y.; Yong, L.; Wan, Q.; Sun, Z.; Ma, H. Below-Cloud Evaporation of Precipitation Isotopes over Mountains, Oases, and Deserts in Arid Areas. J. Hydrometeorol. 2021, 22, 2533–2545. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, M.; Zhang, Y.; Huang, Z.; Yao, X.; Wang, J.; Han, T.; Su, P. Sub-Cloud Secondary Evaporation in Precipitation Stable Isotopes Based on the Stewart Model in Yangtze River Basin. Atmosphere 2021, 12, 575. [Google Scholar] [CrossRef]
- Wang, S.; Jiao, R.; Zhang, M.; Crawford, J.; Hughes, C.E.; Chen, F. Changes in Below-Cloud Evaporation Affect Precipitation Isotopes During Five Decades of Warming Across China. J. Geophys. Res.-Atmos. 2021, 126, e2020JD033075. [Google Scholar] [CrossRef]
- Sarkar, M.; Bailey, A.; Blossey, P.; de Szoeke, S.; Noone, D.; Meléndez, E.; Leandro, M.; Chuang, P. Sub-cloud rain evaporation in the North Atlantic winter trade winds derived by pairing isotopic data with a bin-resolved microphysical model. Atmos. Chem. Phys. 2023, 23, 12671–12690. [Google Scholar] [CrossRef]
- He, S.; Jackisch, D.; Feng, L.; Samanta, D.; Wang, X.; Goodkin, N. Uncovering Below Cloud Rain-Vapor Interactions During Tropical Rain Events Through Simultaneous and Continuous Real-Time Monitoring of Rain and Vapor Isotopes. J. Geophys. Res.-Atmos. 2024, 129, e2023JD040084. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Zhang, M.; Duan, L.; Xia, Y. An hourly-scale assessment of sub-cloud evaporation effect on precipitation isotopes in a rainshadow oasis of northwest China. Atmos. Res. 2022, 274, 106202. [Google Scholar] [CrossRef]
- Kong, Y.; Pang, Z.; Froehlich, K. Quantifying recycled moisture fraction in precipitation of an arid region using deuterium excess. Tellus Ser. B-Chem. Phys. Meteorol. 2013, 65, 19251. [Google Scholar] [CrossRef]
- Sun, C.; Chen, W.; Chen, Y.; Cai, Z. Stable isotopes of atmospheric precipitation and its environmental drivers in the Eastern Chinese Loess Plateau, China. J. Hydrol. 2020, 58, 124404. [Google Scholar] [CrossRef]
- Friedman, I.; Machta, L.; Soller, R. Water vapor exchange between a water droplet and its environment. Journ. Aeophys Res. 1962, 67, 2761–2770. [Google Scholar] [CrossRef]
- Froehlich, K.; Kralik, M.; Papesch, W.; Rank, D.; Scheifinger, H.; Stichler, W. Deuterium excess in precipitation of Alpine regions—Moisture recycling. Isot. Environ. Health Stud. 2008, 44, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Crawford, J.; Hollins, S.E.; Meredith, K.T.; Hughes, C.E. Precipitation stable isotope variability and subcloud evaporation processes in a semi-arid region. Hydrol. Process. 2017, 31, 20–34. [Google Scholar] [CrossRef]
- Gat, J.R. Oxygen and hydrogen isotopes in the hydrologic cycle. Annu. Rev. Earth Planet. Sci. 1996, 24, 225–262. [Google Scholar] [CrossRef]

| Month | Slope of the LMWL | Slope of the Theoretical LMWL | Slope of the Theoretical LEVL |
|---|---|---|---|
| 1 | 7.05 | 8.88 | 3.85 |
| 2 | 6.57 | 8.80 | 2.75 |
| 3 | 6.34 | 8.54 | 3.04 |
| 4 | 7.57 | 8.51 | 3.11 |
| 5 | 7.69 | 8.41 | 2.84 |
| 6 | 7.36 | 8.31 | 2.86 |
| 7 | 7.97 | 8.31 | 2.84 |
| 8 | 8.11 | 8.35 | 2.56 |
| 9 | 8.32 | 8.36 | 2.71 |
| 10 | 8.26 | 8.44 | 2.81 |
| 11 | 8.39 | 8.48 | 2.98 |
| 12 | 6.25 | 8.82 | 3.33 |
| mean | 8.33 | 8.48 | 2.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Li, D.; Zhuang, L.; Zhao, M. Impact of Sub-Cloud Evaporation on Precipitation in Tropical Monsoon Islands. Sustainability 2025, 17, 8161. https://doi.org/10.3390/su17188161
Chen H, Li D, Zhuang L, Zhao M. Impact of Sub-Cloud Evaporation on Precipitation in Tropical Monsoon Islands. Sustainability. 2025; 17(18):8161. https://doi.org/10.3390/su17188161
Chicago/Turabian StyleChen, Haiyan, Dalong Li, Lin Zhuang, and Min Zhao. 2025. "Impact of Sub-Cloud Evaporation on Precipitation in Tropical Monsoon Islands" Sustainability 17, no. 18: 8161. https://doi.org/10.3390/su17188161
APA StyleChen, H., Li, D., Zhuang, L., & Zhao, M. (2025). Impact of Sub-Cloud Evaporation on Precipitation in Tropical Monsoon Islands. Sustainability, 17(18), 8161. https://doi.org/10.3390/su17188161







