Coordination in Energy Platforms: How Fairness Concerns and Market Power Shape Pricing and Profitability
Abstract
1. Introduction
1.1. Research Background
- The existence or absence of coordination between platforms;
- Competition and market power asymmetries across platforms;
- Consumers’ fairness concerns, i.e., their sensitivity to price differences between two platforms.
1.2. Related Literature
- How do fairness concerns affect customer choices and pricing decisions of the platform? Can the emergence of fairness concerns improve the unfair conditions between platforms?
- In different models, how does market power influence the pricing strategies? What are the implications for price levels and profit distribution when one platform takes the lead?
- How does coordination through power dispatch change the pricing strategies? In what ways do coordinate and non-coordinate modes lead to different outcomes in pricing decisions?
1.3. Contribution
- We fill a literature gap by analyzing how fairness considerations and market power together shape platform pricing strategies. Prior research typically focuses on one or the other, but rarely both simultaneously.
- We introduce consumer heterogeneity by distinguishing between green consumers and traditional non-green consumers, and model their platform selection based on individual rationality and incentive-compatibility constraints.
- We extend the framework in [41] by allowing platform collaboration via power dispatch, offering fresh insights into the pricing and market dynamics resulting from inter-platform cooperation.
2. Research Method
2.1. Game Theoretic Modeling
2.2. Customer Choice Modeling
2.3. Platform Coordination Modeling
3. Model Setup and Equilibrium Analysis
3.1. Platform’s Pricing Strategy Under Fairness Concern and Power Dispatch (Model CW)
3.1.1. Stackelberg Game Model (F, CW)
3.1.2. Nash Model of Simultaneous Pricing (T, CW)
3.2. Platform’s Pricing Strategy Without Fairness Concern but with Power Dispatch (Model NW)
3.2.1. Stackelberg Game Model (F, NW)
3.2.2. Nash Model of Simultaneous Pricing (T, NW)
3.3. Platform’s Pricing Strategy with Fairness Concern but Without Power Dispatch (Model CO)
3.3.1. Stackelberg Game Model (F, CO)
3.3.2. Nash Model of Simultaneous Pricing (T, CO)
3.4. Platform’s Pricing Strategy Without Fairness Concern or Power Dispatch (Model NO)
3.4.1. Stackelberg Game Model (F, NO)
3.4.2. Nash Model of Simultaneous Pricing (T, NO)
4. Numerical Analysis
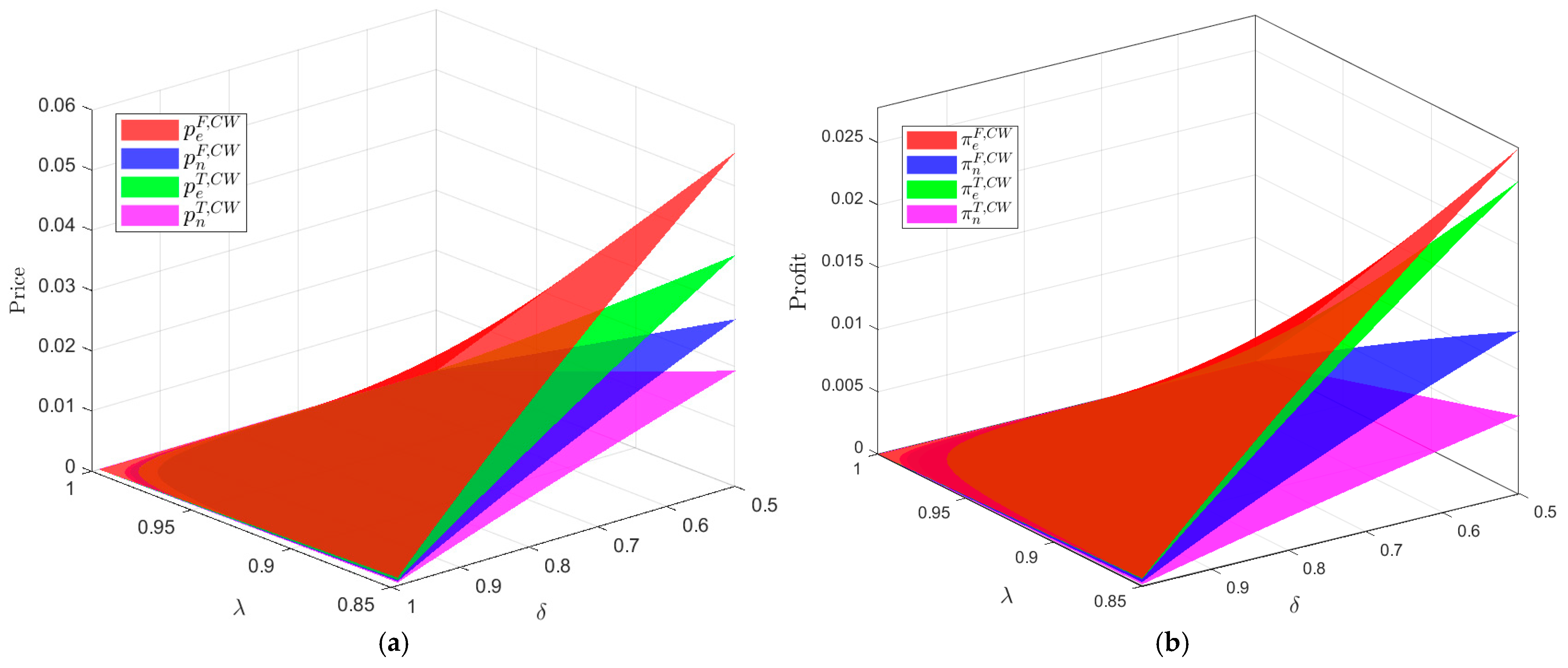
4.1. Impact of Market Power on the Optimal Solution
4.2. Impact of Fairness Concern on the Optimal Solution
4.3. Impact of Energy Dispatch Coordination on the Optimal Solution
4.4. Differential Impact of Fairness Concerns on Platform Profitability
5. Discussion
5.1. Discussion of Findings
- (1)
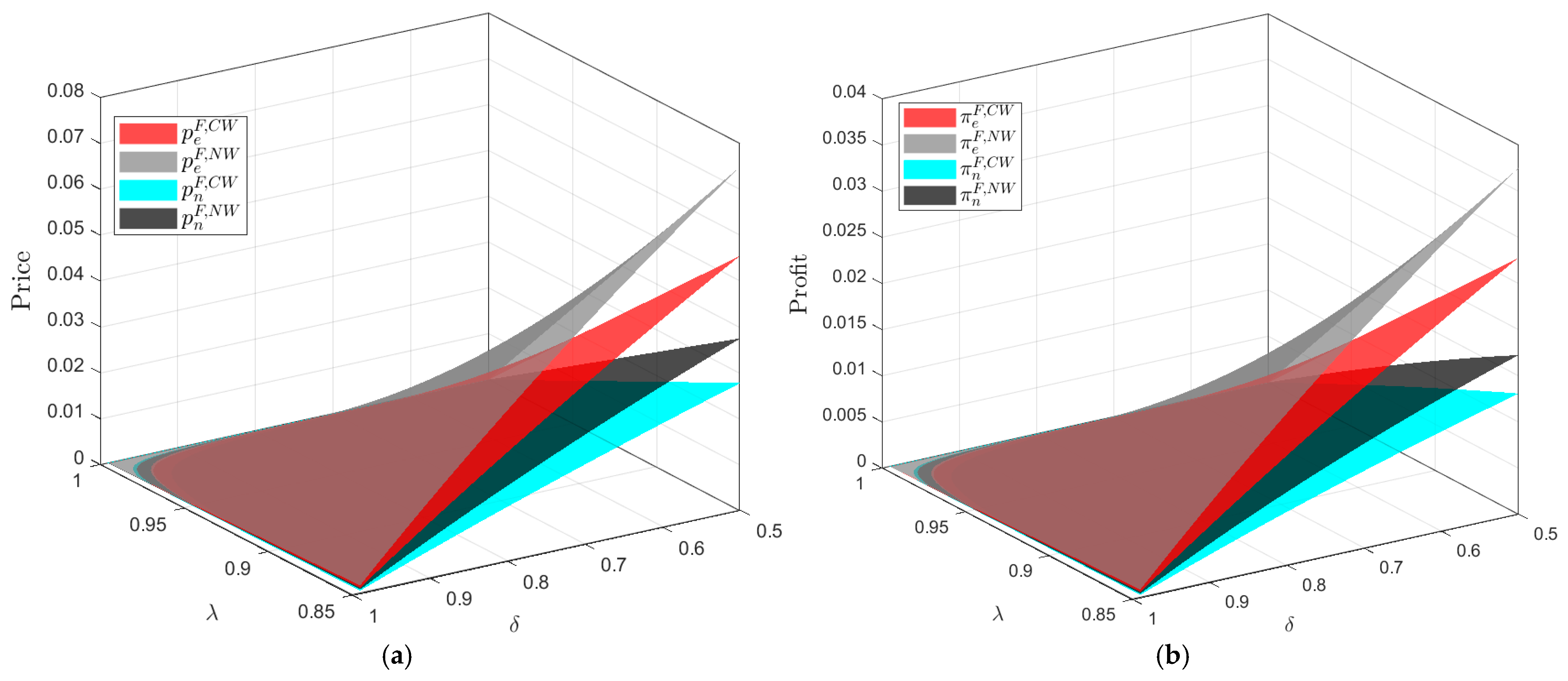
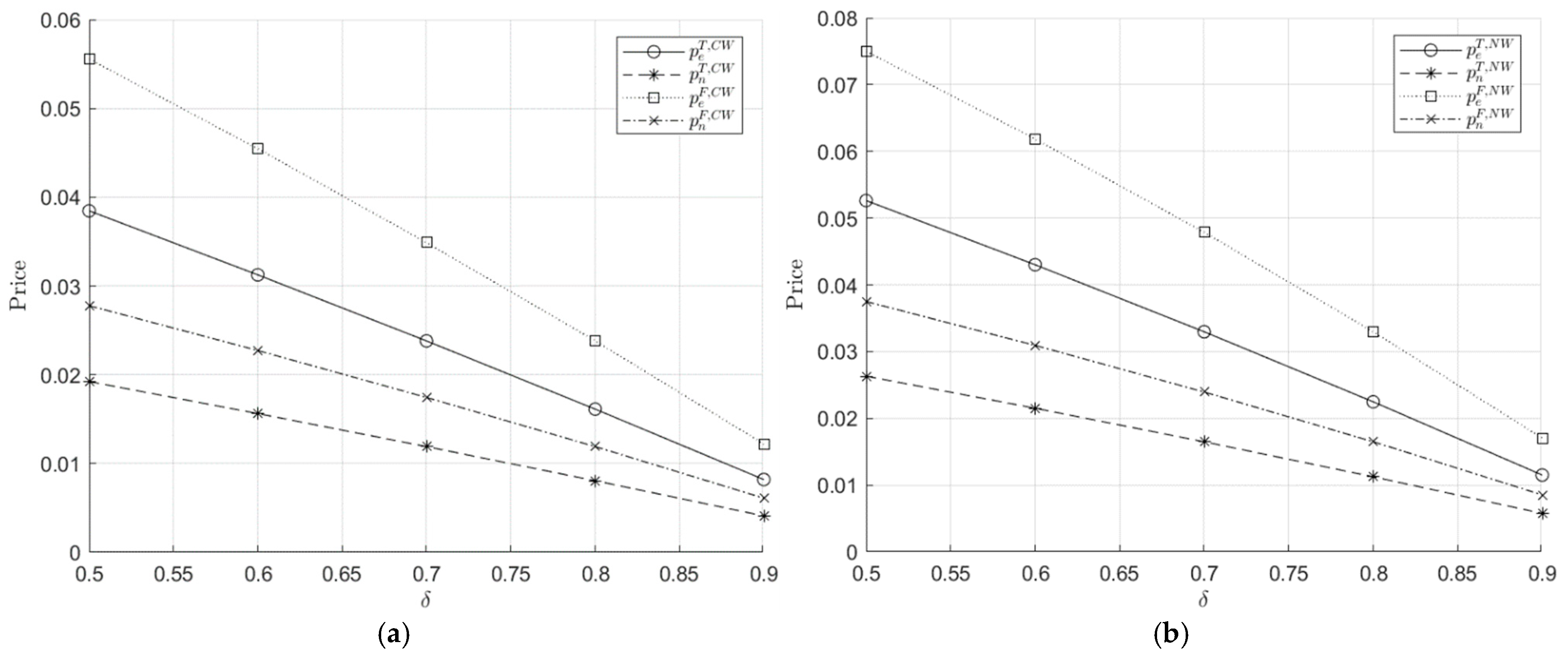
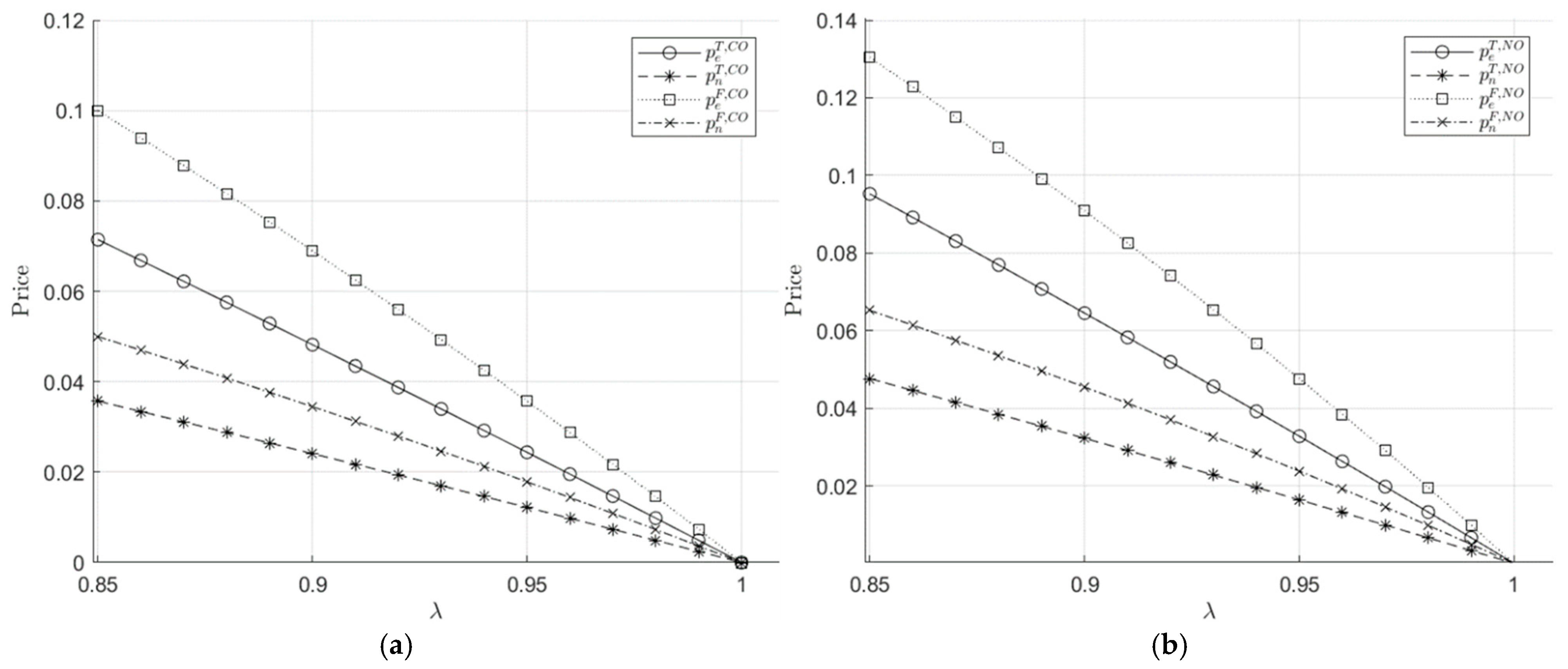
- By analyzing the equilibrium solutions shows that, ceteris paribus, prices under fairness concerns are lower than those without. When comparing CW with NW in Figure 7, or comparing CO with NO in Figure 8, the results suggest that when fairness concerns exist, platforms compensate users economically by offering lower prices.
- (2)
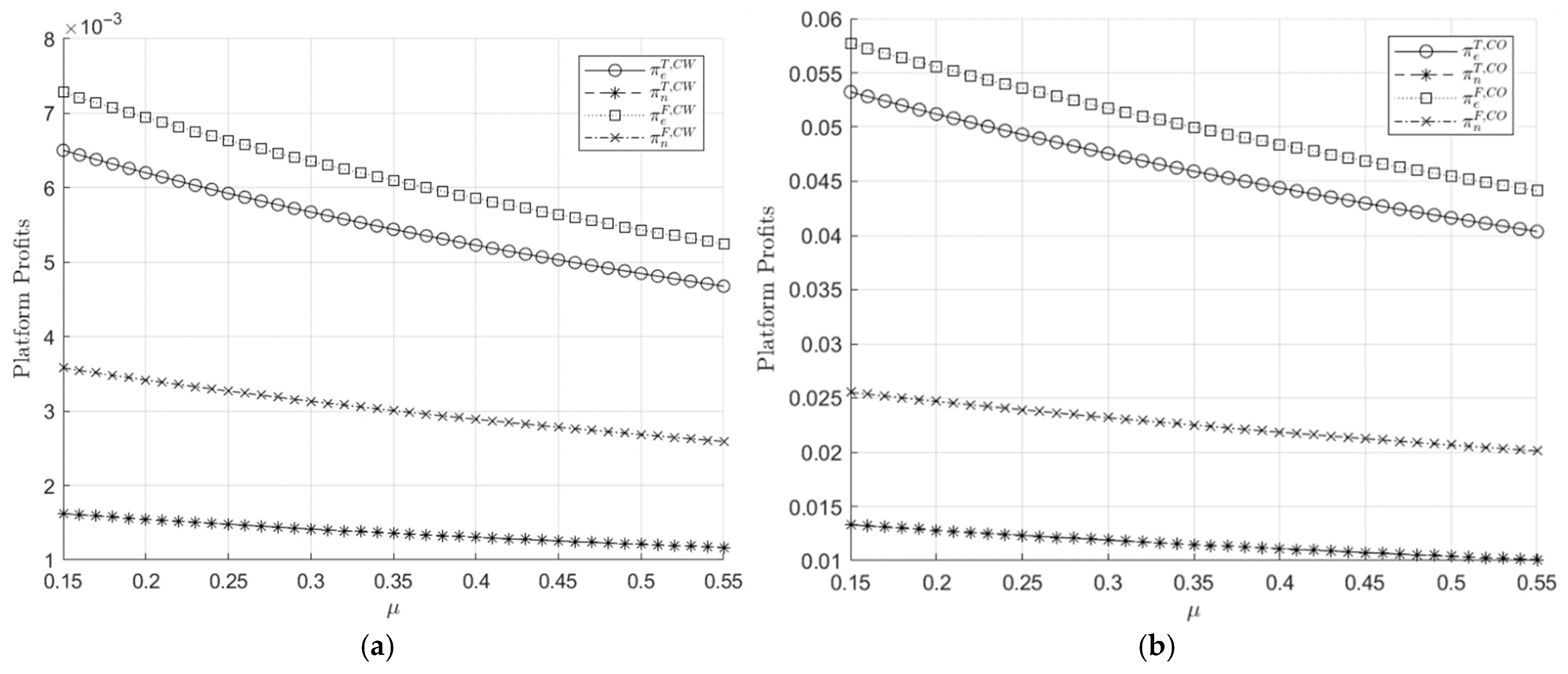
- According to Figure 9, in the presence of dispatch coordination (CW), both platforms’ prices and profits are lower than in the absence of coordination (CO). When coordination exists between platforms, if combined with a higher economic preference factor and a higher loss-adjusted factor, the comparative advantage of thermal power declines and competition intensifies, leading to lower electricity prices. Therefore, the profits under the coordination case are also lower.
- (3)
- As shown in Figure 9a, under the scenario where electricity dispatch exists, the profit of e-platform is always greater than that of n-platform, and . Given the same platform, the profit from simultaneous pricing by a platform is always lower than the profit of e-platform when it has a first-mover advantage, and .
- (4)
- Without considering resource dispatch, changes in the fairness concern coefficient have a similar impact on platform profits. The numerical simulations in Figure 9b also show that under the absence of resource dispatch, the profit of e-platform remains higher than that of n-platform, and . Given the same platform, the profit from simultaneous pricing by both platforms is always lower than the profit of e-platform when it holds a first-mover advantage, and . The intuitive results align with the findings of [41].
5.2. Managerial Implications
5.3. Research Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CW | Considering fairness concern and with power dispatch |
| CO | Considering fairness concern, excluding power dispatch |
| NW | No fairness concern and with power dispatch |
| NO | No fairness concern, excluding power dispatch |
Appendix A
Appendix B
Appendix C
Appendix D
Appendix E
References
- United Nations. The 17 Goals. Available online: https://sdgs.un.org/goals (accessed on 8 August 2025).
- Cheng, X.; Liu, P.; Zhu, L. The Impact of Electricity Market Reform on Renewable Energy Production. Energy Policy 2024, 194, 114306. [Google Scholar] [CrossRef]
- Zeng, M.; Yang, Y.; Wang, L.; Zhang, X. The Power Industry Reform in China 2015: Policies, Evaluations and Solutions. Renew. Sustain. Energy Rev. 2016, 57, 94–110. [Google Scholar] [CrossRef]
- Kong, L.; Lu, K.; Xie, J.; Zhu, Z. Competitive strategies for differentiated services of power trading platforms under the situation of release of electricity selling market. Comput. Ind. Eng. 2025, 203, 110956. [Google Scholar] [CrossRef]
- Zeng, Y.; Wei, X.; Yao, Y.; Xu, Y.; Sun, H.; Chan, W.; Feng, W. Determining the pricing and deployment strategy for virtual power plants of peer-to-peer prosumers: A game-theoretic approach. Appl. Energy 2023, 345, 121349. [Google Scholar] [CrossRef]
- Steadman, S.; Bennato, A.R.; Giulietti, M. Would you like to trade your energy? A comparative survey experiment on energy trading platforms. Energy J. 2024, 45, 1–24. [Google Scholar] [CrossRef]
- Guo, S.; Feng, T. Blockchain-based smart trading mechanism for renewable energy power consumption vouchers and green certificates: Platform design and simulation. Appl. Energy 2024, 369, 123351. [Google Scholar] [CrossRef]
- Menzel, T.; Teubner, T. Green Energy Platform Economics—Understanding Platformization and Sustainabilization in the Energy Sector. Int. J. Energy Sect. Manag. 2021, 15, 456–475. [Google Scholar] [CrossRef]
- Kufeoglu, S.; Liu, G.; Anaya, K.; Pollitt, M. Digitalisation and New Business Models in Energy Sector; Cambridge Working Papers in Economics; Cambridge University: Cambridge, UK, 2019; Available online: https://www.jstor.org/stable/pdf/resrep30431.pdf (accessed on 8 August 2025).
- Kowalska-Pyzalska, A. An Empirical Analysis of Green Electricity Adoption among Residential Consumers in Poland. Sustainability 2018, 10, 2281. [Google Scholar] [CrossRef]
- Ambec, S.; Crampes, C. Electricity Provision with Intermittent Sources of Energy. Resour. Energy Econ. 2012, 34, 319–336. [Google Scholar] [CrossRef]
- Dorsey-Palmateer, R. Effects of Wind Power Intermittency on Generation and Emissions. Electr. J. 2019, 32, 25–30. [Google Scholar] [CrossRef]
- Reguant, M. The Efficiency and Sectoral Distributional Impacts of Large-Scale Renewable Energy Policies. J. Assoc. Environ. Resour. Econ. 2019, 6, 129–168. [Google Scholar] [CrossRef]
- Wang, C.; Chen, H.; Wang, Z.; Gao, Y.; Zhang, G. Economic Assessment and Grid Parity Analysis of Photovoltaic Power Generation Considering Tradable Green Certificate. Appl. Energy 2025, 382, 125282. [Google Scholar] [CrossRef]
- Motalleb, M.; Siano, P.; Ghorbani, R. Networked Stackelberg Competition in a Demand Response Market. Appl. Energy 2019, 239, 680–691. [Google Scholar] [CrossRef]
- Yin, S.; Ai, Q.; Li, Z.; Zhang, Y.; Lu, T. Energy Management for Aggregate Prosumers in a Virtual Power Plant: A Robust Stackelberg Game Approach. Int. J. Electr. Power Energy Syst. 2020, 117, 105605. [Google Scholar] [CrossRef]
- Ambec, S.; Crampes, C. Decarbonizing Electricity Generation with Intermittent Sources of Energy. J. Assoc. Environ. Resour. Econ. 2019, 6, 1105–1134. [Google Scholar] [CrossRef]
- Hotaling, C.; Bird, S.; Heintzelman, M.D. Willingness to Pay for Microgrids to Enhance Community Resilience. Energy Policy 2021, 154, 112248. [Google Scholar] [CrossRef]
- Mazur, Ł.; Cieślik, S.; Czapp, S. Trends in Locally Balanced Energy Systems without the Use of Fossil Fuels: A Review. Energies 2023, 16, 4551. [Google Scholar] [CrossRef]
- Weitemeyer, S.; Kleinhans, D.; Vogt, T.; Agert, C. Integration of Renewable Energy Sources in Future Power Systems: The Role of Storage. Renew. Energy 2015, 75, 14–20. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer Energy Trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
- Crampes, C.; von Der Fehr, N.H.M. Decentralised cross-border interconnection. Energy J. 2023, 44, 147–169. [Google Scholar] [CrossRef]
- Park, D.; Kaffine, D.T. Do competitive markets clean up the US electricity sector?: Evidence from the Southwest Power Pool. Energy J. 2025, 46, 99–125. [Google Scholar] [CrossRef]
- Das, U.; Nandi, C.; Mandal, S.; Bhattacharjee, S. A systematic literature review on hybrid energy systems. Energy Environ. 2023, 34, 3417–3449. [Google Scholar] [CrossRef]
- Al-Awami, A.T.; El-Sharkawi, M.A. Coordinated Trading of Wind and Thermal Energy. IEEE Trans. Sustain. Energy 2011, 2, 277–287. [Google Scholar] [CrossRef]
- Zeng, M.; Yang, Y.; Fan, Q.; Liu, Y.; Zou, Z. Coordination between Clean Energy Generation and Thermal Power Generation under the Policy of “Direct Power-Purchase for Large Users” in China. Util. Policy 2015, 33, 10–22. [Google Scholar] [CrossRef]
- Gautier, A.; Jacqmin, J.; Poudou, J.C. The Prosumers and the Grid. J. Regul. Econ. 2018, 53, 100–126. [Google Scholar] [CrossRef]
- Gautier, A.; Jacqmin, J.; Poudou, J.C. The Energy Community and the Grid. Resour. Energy Econ. 2025, 82, 101480. [Google Scholar] [CrossRef]
- Martín-Utrilla, F.D.; Chaves-Ávila, J.P.; Cossent, R. Decision Framework for Selecting Flexibility Mechanisms in Distribution Grids. Econ. Energy Environ. Policy 2022, 11, 71–92. [Google Scholar] [CrossRef]
- Yang, Z.; Fu, X.; Gao, P.; Chen, Y. Fairness Regulation of Prices in Competitive Markets. Manuf. Serv. Oper. Manag. 2024, 26, 1897–1917. [Google Scholar] [CrossRef]
- Schittekatte, T.; Meeus, L. Least-Cost Distribution Network Tariff Design in Theory and Practice. Energy J. 2020, 41, 119–156. [Google Scholar] [CrossRef]
- Soares, J.; Lezama, F.; Faia, R.; Limmer, S.; Dietrich, M.; Rodemann, T.; Ramos, S.; Vale, Z. Review on Fairness in Local Energy Systems. Appl. Energy 2024, 374, 123933. [Google Scholar] [CrossRef]
- Gasca, M.V.; Rigo-Mariani, R.; Debusschere, V.; Sidqi, Y. Fairness in Energy Communities: Centralized and Decentralized Frameworks. Renew. Sustain. Energy Rev. 2025, 208, 115054. [Google Scholar] [CrossRef]
- Dynge, M.F.; Cali, U. Distributive energy justice in local electricity markets: Assessing the performance of fairness indicators. Appl. Energy 2025, 384, 125463. [Google Scholar] [CrossRef]
- Rios-Ocampo, M.A.; Romero, J.C.; Centeno, E.; Mora, S. A just energy transition is not just a transition: Framing energy justice for a quantitative assessment. Energy Res. Soc. Sci. 2025, 119, 103900. [Google Scholar] [CrossRef]
- Musilek, P.; Hussain, A. Equity-oriented power sharing and demand response for enhancing green energy access in mixed communities. Energy Build. 2024, 308, 114029. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Zeng, L.; Jiang, J.; Zhu, X.; Peng, J. Logistics Service Decision for E-Commerce Supply Chain with Fairness Concern under Uncertain Environment. Int. J. Gen. Syst. 2024, 54, 1–36. [Google Scholar] [CrossRef]
- Müsgens, F. Quantifying Market Power in the German Wholesale Electricity Market Using a Dynamic Multi-Regional Dispatch Model. J. Ind. Econ. 2006, 54, 471–498. [Google Scholar] [CrossRef]
- Borenstein, S.; Bushnell, J.B.; Wolak, F.A. Measuring Market Inefficiencies in California’s Restructured Wholesale Electricity Market. Am. Econ. Rev. 2002, 92, 1376–1405. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.; Wu, C. A Stackelberg Game Approach for Heterogeneous Energy Market in Integrated Energy System. Int. J. Energy Res. 2021, 45, 1038–1054. [Google Scholar] [CrossRef]
- Zhou, C.; Li, X.; Ren, Y.; Yu, J. How Do Fairness Concern and Power Structure Affect Competition between E-Platforms and Third-Party Sellers? IEEE Trans. Eng. Manag. 2023, 71, 7479–7495. [Google Scholar] [CrossRef]
- Crowley, B.; Kazempour, J.; Mitridati, L. How Can Energy Communities Provide Grid Services? A Dynamic Pricing Mechanism with Budget Balance, Individual Rationality, and Fair Allocation. Appl. Energy 2025, 382, 125154. [Google Scholar] [CrossRef]
- Ansarin, M.; Ghiassi-Farrokhfal, Y.; Ketter, W.; Collins, J. A Review of Equity in Electricity Tariffs in the Renewable Energy Era. Renew. Sustain. Energy Rev. 2022, 161, 112333. [Google Scholar] [CrossRef]
- Chandra, R.; Banerjee, S.; Radhakrishnan, K.K.; Panda, S.K. Transactive Energy Market Framework for Decentralized Coordination of Demand Side Management within a Cluster of Buildings. IEEE Trans. Ind. Appl. 2021, 57, 3385–3395. [Google Scholar] [CrossRef]
- Sun, T.; Feng, Y.; Zanocco, C.; Flora, J.; Majumdar, A.; Rajagopal, R. Solar and battery can reduce energy costs and provide affordable outage backup for US households. Nat. Energy 2025, 10, 1025–1040. [Google Scholar] [CrossRef]
- Yun, G.; Zheng, Q.P.; Bai, L.; Pasiliao, E.L. Robust Pricing for Demand Response under Bounded Rationality in Residential Electricity Distribution. Eur. J. Oper. Res. 2025, 324, 654–668. [Google Scholar] [CrossRef]
- Deng, Z.; Shaharudin, M.R.; Shariff, S.; Tseng, M. Optimal Decisions in an Authorized Remanufacturing Closed-Loop Supply Chain under Dual-Fairness Concerns. Sustainability 2024, 16, 7609. [Google Scholar] [CrossRef]
- Chen, Z.; Khalilpour, K.; Yao, Q. Coordinating Risk Aversion and Pricing Strategies in Green Supply Chains: A Study of Manufacturer Competition. Sustainability 2024, 16, 11284. [Google Scholar] [CrossRef]



| References | Dispatch Coordination | Market Power | Fairness Concern | Platform Competition Modelling |
|---|---|---|---|---|
| [22,23,26] | √ | |||
| [29] | √ | |||
| [30] | √ | √ | ||
| [32] | √ | |||
| [33] | √ | |||
| [38] | √ | √ | ||
| [39] | √ | |||
| [41] | √ | √ | ||
| This paper | √ | √ | √ | √ |
| With Power Dispatch | Without Power Dispatch | |
|---|---|---|
| Fairness concern | (Yes, Yes) | (Yes, No) |
| Fairness neutral | (No, Yes) | (No, No) |
| Notation | Description | |
|---|---|---|
| Subscript | means thermal “electricity” platform and “new” green platform, separately | |
| Superscript | T denotes simultaneous pricing, whereas F means the presence of the first-mover advantage | |
| Parameter | The reservation value of the buyer when joining either of the platforms | |
| The economic preference factor, proxied as the probability of a consumer successfully purchasing electricity from a green platform | ||
| The loss-adjusted coefficient for the consumer when switching to the thermal platform | ||
| Fairness concerns the sensitivity of consumers when joining a thermal platform | ||
| Utility Function | The utility of consumers “choosing” platform or | |
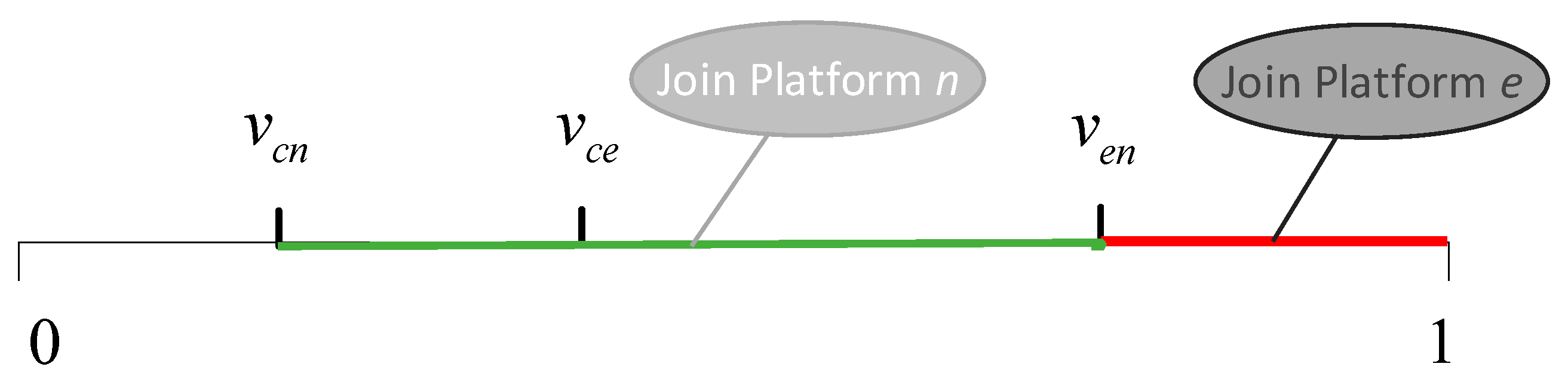
| and are the critical points for consumers “choosing” platform or under IR; represents the indifference point between choosing or under IC | ||
| Decision variables | The user base for joining the platform or | |
| Electricity price in platform and | ||
| Profit function in platform and |
| Equilibrium | Model CW | Model NW | Model CO | Model NO |
|---|---|---|---|---|
| Stackelberg pricing of e-platform | ||||
| Stackelberg pricing of n-platform | ||||
| Nash pricing of e-platform | ||||
| Nash pricing of n-platform | ||||
| e-platform profit under Stackelberg | ||||
| n-platform profit under Stackelberg | ||||
| e-platform profit under Nash | ||||
| n-platform profit under Nash |
| Parameters | Meaning | Value Ranges |
|---|---|---|
| The economic preference factor, proxied as the probability of a consumer successfully purchasing electricity from a green platform | >0.8 | |
| The consumer loss-adjusted coefficient accounts for the residual part of the value after considering the losses | >0.5 | |
| Fairness concern | (0, 1), with 0.35 used in some cases |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Wang, A. Coordination in Energy Platforms: How Fairness Concerns and Market Power Shape Pricing and Profitability. Sustainability 2025, 17, 8144. https://doi.org/10.3390/su17188144
Kong L, Wang A. Coordination in Energy Platforms: How Fairness Concerns and Market Power Shape Pricing and Profitability. Sustainability. 2025; 17(18):8144. https://doi.org/10.3390/su17188144
Chicago/Turabian StyleKong, Lingcheng, and Ao Wang. 2025. "Coordination in Energy Platforms: How Fairness Concerns and Market Power Shape Pricing and Profitability" Sustainability 17, no. 18: 8144. https://doi.org/10.3390/su17188144
APA StyleKong, L., & Wang, A. (2025). Coordination in Energy Platforms: How Fairness Concerns and Market Power Shape Pricing and Profitability. Sustainability, 17(18), 8144. https://doi.org/10.3390/su17188144






