Next Article in Journal
The Moderating Effect of Size on the Relationship Between Liquidity Management and Sustainable Profitability: Evidence from BRICS Financial Firms
Previous Article in Journal
Segmental Calibration of Soil–Tool Contact Models for Sustainable Tillage Using Discrete Element Method
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 17
Issue 18
10.3390/su17188127
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Impact of Earthquake on Rainfall Thresholds for Sustainable Geo-Hazard Warnings: A Case Study of Luding Earthquake

by
Qun Zhang
1,2,
Junfeng Li
3,4,5,*,
Shengjie Jin
1,*,
Yanhui Liu
3,
Shikang Liu
1,
Zhuo Wang
1,
Lei Zhang
1 and
Zeyi Song
1
1
Sichuan Institute of Land and Space Ecological Restoration and Geological Hazard Prevention, Chengdu 610036, China
2
College of Environment and Civil Engineering, Chengdu University of Technology, Chengdu 610059, China
3
Technology Innovation Center for Geohazard Monitoring and Risk Early Warning, Ministry of Natural Resources, Beijing 100081, China
4
School of Civil Engineering, Shenyang Jianzhu University, Shenyang 110168, China
5
China Institute of Geo-Environment Monitoring, Beijing 100081, China
*
Authors to whom correspondence should be addressed.
Sustainability 2025, 17(18), 8127; https://doi.org/10.3390/su17188127
Submission received: 8 July 2025 / Revised: 27 August 2025 / Accepted: 4 September 2025 / Published: 9 September 2025
(This article belongs to the Special Issue A Research on Sustainable Prevention and Management of Geological Disasters in Engineering)
Browse Figures
Versions Notes

Abstract

This study explores the impact of the 2022 Mw 6.8 Luding Earthquake on various geo-hazards and their corresponding rainfall thresholds. Focusing on the seismic intensity VI zone in Sichuan Province, China, we analyzed 1979 geo-hazard records and hourly precipitation data from 475 stations between 2010 and 2024. Empirical ID (intensity–duration) and AC (accumulated rainfall–continuous rainfall duration) rainfall threshold models are established based on these datasets. By comparing pre- and post-earthquake data, this study assesses changes in the spatial distribution and triggering rainfall thresholds of landslides, rockfalls, and debris flows. The results indicate a significant increase in geo-hazard risks post-earthquake, particularly near the Xianshuihe Fault, with rockfall risks exhibiting the most pronounced rise. Statistical analysis reveals that the rainfall thresholds required to trigger geo-hazards decreased notably after the earthquake: ID models indicate a decrease of approximately 20%, while AC models show a reduction of about 20% in the western zone and 10% in the eastern zone. A four-level early warning system is developed using empirical rainfall threshold models, offering tailored hazard alerts for different regions and geo-hazard types. The variation in threshold values between the east and west zones highlights the influence of differing topographic and climatic conditions. These findings provide critical insights for post-seismic hazard assessment and inform more effective, sustainable early warnings, thereby supporting more reliable and sustainable disaster risk management in earthquake-affected regions.

1. Introduction

Meteorological conditions, especially different types of precipitation, are the primary natural triggers of sudden geo-disasters. Experts and scholars began studying the relationship between rainfall and geo-hazards at an early stage [1,2,3,4]. When rainwater infiltrates the soil, it increases the pore water pressure and reduces matric suction, which makes rocks and soil more prone to sliding [5,6]. Therefore, weather forecasts predicting potential rainfall in vulnerable areas play a vital role in geo-hazard prevention and sustainable disaster management.
A rainfall threshold model, physical or empirical, is a cost-effective tool in early warning systems for various types of geo-hazards [7,8,9]. It defines a critical amount of rainfall, beyond which it is highly likely that a specific geo-hazard is likely to occur. While the empirical method can be widely applied over large regions by investigating statistical functional relationships between rainfall values and landslide occurrences [10,11,12], the physical method is more suitable for small areas where detailed information is available [10,11]. In 1956, Caine [4] introduced the rainfall intensity and duration threshold model, which laid the foundation for debris flow early warning. Wilson & Wieczorek [13] later improved the traditional model by incorporating the Antecedent Precipitation Index, enhancing the model’s adaptability to real-world rainfall processes. As research in this area continues to develop, four main types of models are frequently used to characterize rainfall thresholds: (1) rainfall intensity and rainfall duration [14,15]; (2) short-term rainfall and previous effective rainfall amounts [16,17]; (3) cumulative rainfall and duration [18]; and (4) cumulative rainfall and rainfall intensity [19]. In recent years, advancements in statistical methods have been used in the field of rainfall thresholds, including incorporating detailed hydrogeological and geomorphological information in study areas [20,21,22]; using geostatistical techniques to deal with rainfall data distribution and other geological information [23,24]; applying black-box models and machine learning for predictive analysis [25,26,27]; and improving the resolution of precipitation and geospatial data [28,29]. These methodologies enhanced the accuracy of geo-hazard forecasts and contributed to more effective and sustainable risk assessment frameworks.
Earthquakes are one of the most recurrent and destructive natural disasters, often causing substantial human casualties and significant geo-hazards [30,31,32]. On a global scale, an earthquake of magnitude (Mw) greater than 7 occurs at least once a month, leading to around 37,000 deaths each year [33]. These coseismic and following geo-hazards exacerbate the overall impact of earthquakes, particularly in mountainous regions [34]. For instance, the 2008 Mw 7.9 Wenchuan earthquake in China triggered approximately 200,000 landslides, resulting in an estimated USD 30 billion in economic losses and contributing to 30% of total deaths [35,36]. In addition to human casualties, landslides often block critical infrastructure, impeding rescue efforts and prolonging the suffering of survivors [37]. As a result, earthquakes set off a chain of devastating effects, with geo-hazards being a major contributor to the compounding and following destruction [38,39,40].
During and after earthquakes, liquefaction results in loss of cohesion and increasing pore pressure in the sediments accumulated on slopes [41]. External factors such as aftershocks, rainfall, snowmelt, or anthropogenic disturbances can further destabilize these materials, leading to the reactivation of geo-hazards and posing ongoing threats in post-seismic areas [42,43]. Over time, as geological stresses adjust and ecosystems gradually regenerate, geo-hazard activity typically stabilizes to pre-earthquake levels [44,45]. In this process, the effect of earthquakes on geo-hazard rainfall thresholds and warning systems is an important and urgent research direction. It is crucial for preventing secondary disasters and ensuring the success of sustainable post-earthquake recovery and reconstruction [46].
By focusing on establishing rainfall threshold levels using empirical models, this study aims to address the research gaps and meet the practical needs of disaster prevention by examining the impact of earthquakes on warnings for rainfall-induced geo-hazards. The seismic intensity VI zone of the 9.5 Luding Earthquake was chosen to be the study area, and the study process includes three aspects: First, we analyzed the number of geo-hazards and the distance between them and the seismic fault zone to examine the effect of the earthquake on the distribution of geo-hazards. Second, we compared the triggered rainfall associated with geo-hazards before and after the earthquake, based on two empirical rainfall threshold models. Third, we established a four-level warning system by calculating the envelope curves of the rainfall thresholds, providing a cost-effective and long-term sustainable warning system.

2. Materials and Methods

2.1. Information About Luding Earthquake and Data Collection

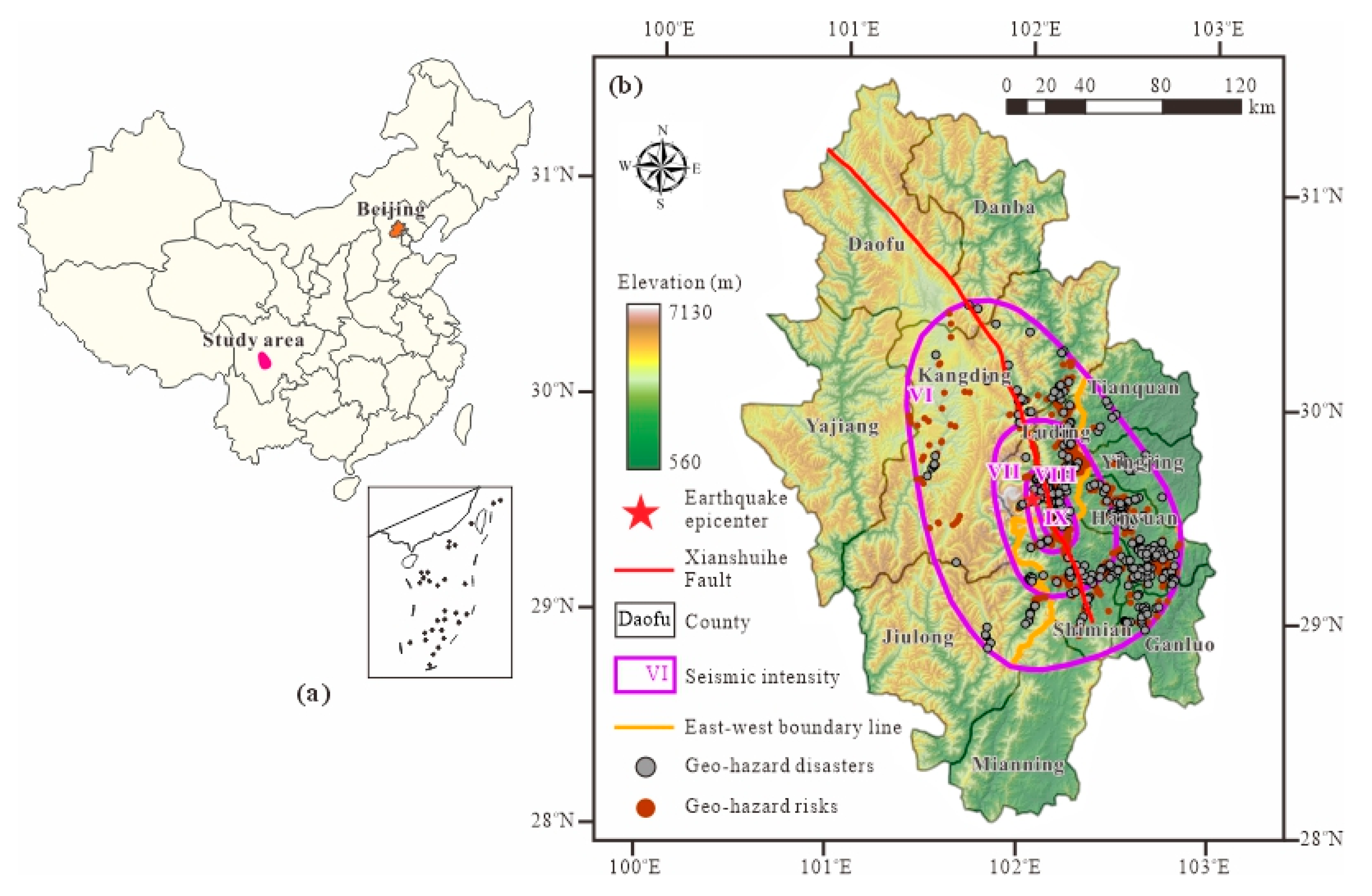
On 5 September 2022, a Mw 6.8 earthquake occurred in Luding County, Ganzi City, China, with a focal depth of 16 km. The maximum seismic intensity reached level IX, and the epicenter was located at latitude 29.5° N, longitude 102.08° E (Figure 1). This earthquake is classified as a mainshock–aftershock and is considered an event with high-angle geo-hazard development [47,48]. The triggering fault has been identified as the Xianshuihe Fault, which extends over 170 km from Kangding to Shimian (Figure 1). This earthquake caused 93 fatalities, injured more than 400, and resulted in the relocation of 50,000 people. Field investigations indicated that the earthquake triggered numerous geo-hazards, damaging buildings and roads in the affected area, especially in the seismic intensity VI zone. Consequently, this study mainly focuses on said zone.
The seismic intensity VI zone of the 2022 Luding Earthquake is situated in the southwest of Sichuan Province, in southwest China, across 11 counties, with a total area of approximately 19,110 km2. Based on the geologic information of Sichuan Province [49,50,51], the study area can be divided into two sub-zones: the west zone and east zone (Figure 1). The west zone is part of the Western Sichuan Plateau region, with an overall elevation of over 3000 m and more arid meteorological conditions. In this zone, rivers flow between mountains, with strong river incision creating dangerous rapids and deep valleys. The landscape exhibits significant elevation differences ranging from 1000 to 3000 m. River valley slopes range from 40° to 80°, creating high potential for various types of geo-hazards [50,51,52,53]. In contrast, the east zone belongs to the Eastern Sichuan Hills region, with an elevation below 3000 m, primarily consisting of low to medium-sized hills and mountains. This area exhibits gentler topography compared to the west zone, and due to its abundant rainfall, geo-disasters occur frequently [49,50,51,54]. Therefore, the rainfall thresholds were calculated for the west and east zones separately.
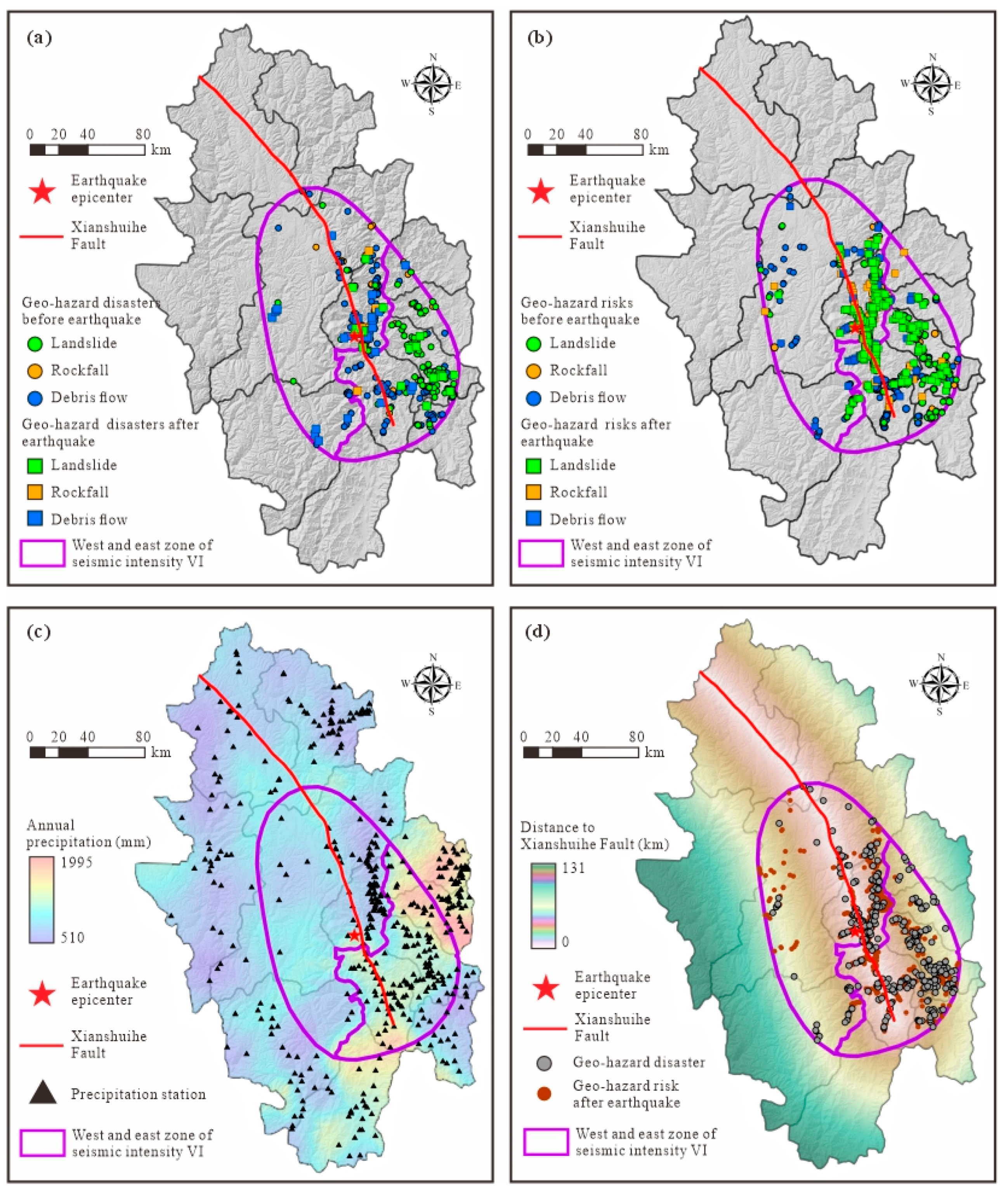
We collected a total of 1979 geo-hazard data in the study area from 2010 to 2024, including 428 rainfall-induced disasters and 1551 risks (Figure 1). Geo-hazard disaster refers to a geo-hazard event that has already occurred (Figure 2a); the occurrence time and triggered factors were recorded in detail by local engineers or residents, and only rainfall-triggered disasters were selected for this study. Meanwhile, geo-hazard risk refers to a developed but currently inactive geo-hazard that has been documented and may be triggered in the future (Figure 2b). Table 1 shows the number of different geo-hazards in the study area. Analysis of the disaster data reveals distinct spatial patterns between the two sub-zones. In the west zone, the mountainous gully terrain contributed to a high frequency of debris flows. In contrast, in the east zone, abundant rainfall combined with hilly terrain triggered more landslides. Additionally, the west zone developed more geo-hazard risks, while fewer occurred. This discrepancy is likely due to the higher precipitation levels in the east zone, which increase the likelihood of geo-hazard activation.
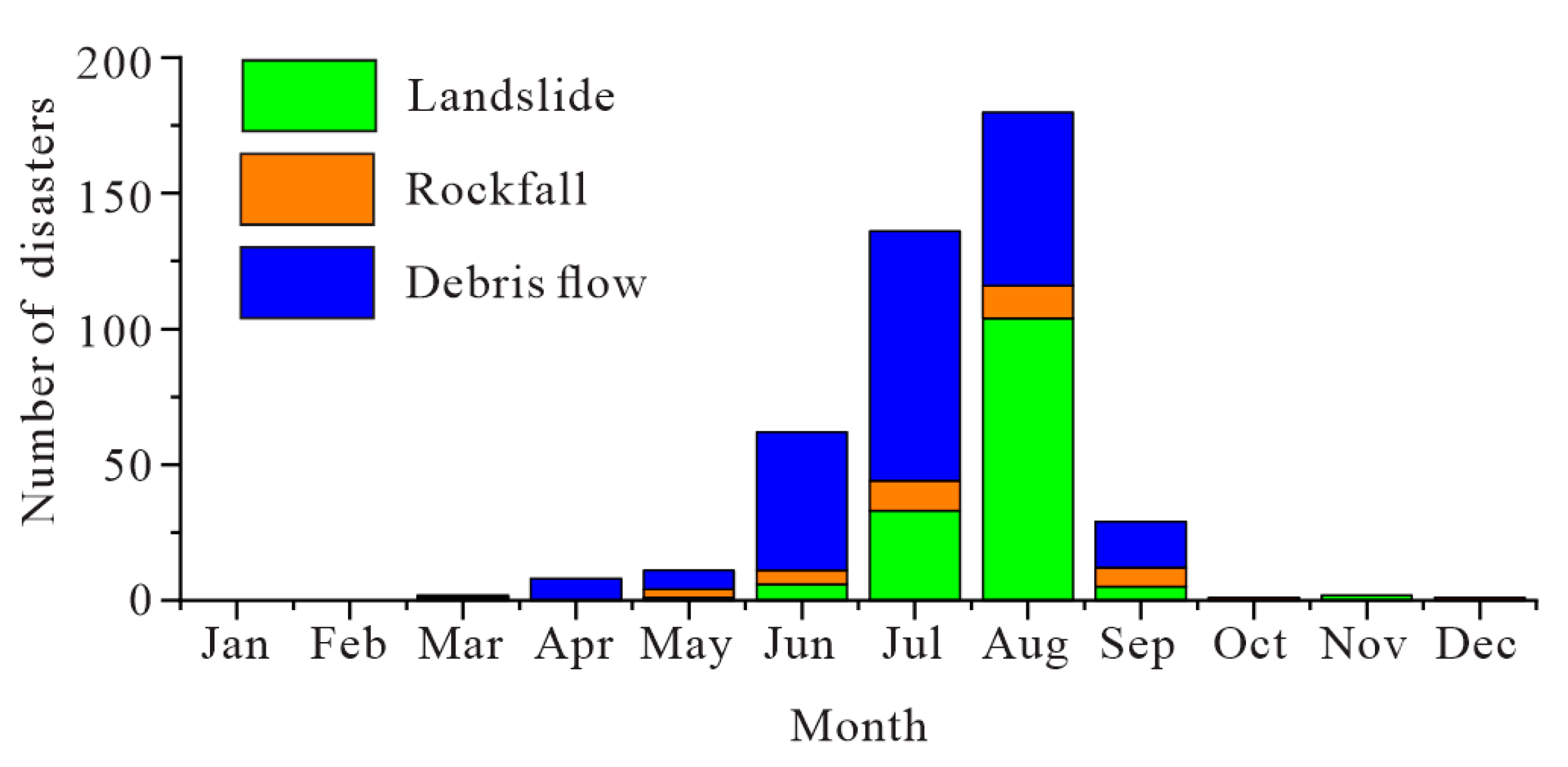
Rainfall data were collected from 475 precipitation stations, recorded hourly (Figure 2c). The annual precipitation distribution reveals a more humid condition in the east zone compared to the west zone, while the occurrence of geo-hazard disasters shows a strong correlation with precipitation levels. Figure 3 shows that more than 85% of disasters occurred between June and August, coinciding with the rainy season in the study area. In order to more accurately assess the rainfall associated with each geo-hazard disaster, precipitation stations outside of the seismic intensity VI region are also used in the calculation.

2.2. Rainfall Parameters of Geo-Hazard Disasters

We calculated the rainfall parameters of each geo-hazard disaster based on the data from the relevant precipitation stations. However, there is currently no consensus on the most appropriate method of selecting the best stations [12]. Following a methodology similar to that used in previous studies [24,26,55], we computed the rainfall data from the five nearest precipitation stations. The multiple rainfall parameters for each disaster were determined through the distance-weighted mean of precipitation collected from the stations (see Equation (1)).
P h = ∑ i = 1 n t i P i ∑ i = 1 n t i , t i = 1 S i + 0.5
Ph is the hourly precipitation of a geo-hazard disaster; Pi is the rainfall data from the ith precipitation station; Si is the distance between the landslide and the ith precipitation station; and ti is the weight calculated from Si.
Based on the hourly rainfall data of each geo-hazard disaster, the nearest rainfall event preceding each occurrence was identified. A rainfall event is defined as a continuous period of precipitation, separated by gaps of 3 consecutive hours with 0 mm of rainfall, or 6 h with less than 5 mm of rainfall [9] (a sensitivity test of rainfall event gaps is displayed in Text S1). Then, the duration (D) and intensity (I) of this nearest rainfall event can be obtained.
To take into account the long-term effect of rainfall, parameters were also extracted from daily rainfall data. Antecedent rainfall (A) was calculated by summing the daily rainfall prior to the disaster event. This parameter reflects the rainfall infiltration, groundwater variation, and moisture content in the soil and rock mass [18,19,56]. Since the amount of retained groundwater decreases over time due to evaporation and drainage, a decay factor was applied to reduce the impact of precipitation occurring several days before the event (Equation (2)). Intraday rainfall or current rainfall (C) is defined as the precipitation at the disaster occurrence day.
A = ∑ d = 1 n y d P d
where d is the number of days prior to disaster occurrence; Pd is the daily precipitation measured on the dth day prior to the occurrence, P d   =   ∑ h   =   1 24 P h ; n is the number of days considered; y is the decay factor; and yd denotes y to the power of d. We considered y = 0.84, as the same value was used in previous studies around our study area [16,17,24]; a sensitivity test of y is displayed in Text S1. To determine n, we used correlation analysis between the antecedent rainfall of a specific number of days and the antecedent rainfall of 30 days [16,17,18]. Then, we defined that n is the number of days on which the correlation coefficient is higher than 0.95. The analysis results indicate that in the east zone, n = 5 for all types of geo-hazards; in the west zone, n = 5 for landslides and rockfalls, and n = 4 for debris flows.

2.3. Establishment of Rainfall Threshold Models

In this study, we considered two rainfall threshold models. The rainfall intensity–duration (ID) model plots the I and D of a disaster-triggered rainfall event onto a double logarithmic coordinate system [4,9]. Then, a fitted curve is obtained based on data from all geo-hazards (Equation (3)). The ID model focuses on the most recent rainfall event and is suitable for warning of geo-hazards induced by short-term heavy rainfall conditions. Additionally, the antecedent-intraday rainfall (AC) model utilizes a fitting line to fit the A and C data from geo-hazard disasters (Equation (4)) [16,17]. This model considers precipitation several days prior to the disaster occurrence, making it suitable for assessing long-term rainfall conditions. Due to the different meteorological conditions, these rainfall thresholds were applied separately for the west and east zones. Furthermore, due to the limited data on rockfalls and the similar triggering mechanisms of rockfalls and landslides, we combined rockfalls and landslides into one group to build the threshold models.
I = b D − a
C = u A + v
a and b are the slope and intercept on a log-log coordinate system in the ID model, and u and v are the slope and intercept in the AC model.
After defining these models, a leveling geo-hazard warning system can be established by determining envelopes. The blue warning envelope (the lowest-ranking warning) encompasses all data; the yellow warning envelope encompasses the largest 80% of the sample data; the orange warning envelope encompasses the largest 50% of the sample data; and the red warning envelope (the highest-ranking warning) encompasses the largest 20% of the sample data. These warning levels provide a reference for disaster emergency response.

3. Analysis of Earthquake Effect

In this section, the effect of the Luding Earthquake on the geo-hazards was studied by comparing data from before and after the earthquake. Three aspects were analyzed: (1) the number of geo-hazard disasters and risks; (2) the distance between geo-hazards and the Xianshuihe Fault; and (3) rainfall threshold models.

3.1. Number of Geo-Hazards

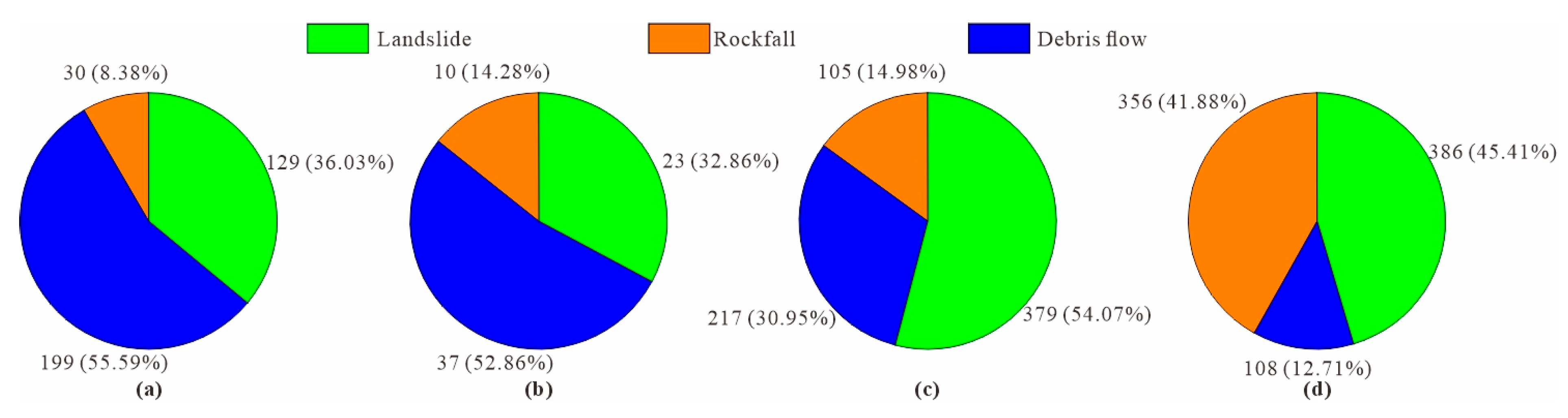
We can see from the geo-hazard disaster statistics (Figure 4a,b) that the percentage of various geo-hazard types differs greatly between pre-earthquake and post-earthquake. The earthquake does not strongly change the disaster-triggering factors, such as lithology, geomorphology, and precipitation. Thus, the proportion of different disaster types was only limitedly influenced by the earthquake. Geo-hazard risk statistics (Figure 4c,d) show that the number of post-earthquake risks recorded from September 2022 to December 2024 is larger than that of post-earthquake risks recorded over 12 years. This indicates that seismic shaking results in the formation of numerous geo-hazards. Furthermore, the proportion of rockfall has increased significantly (from 14.98% to 41.98%), suggesting that the shaking effect contributes to the fracturing of hard rocks and the formation of dangerous rock masses.

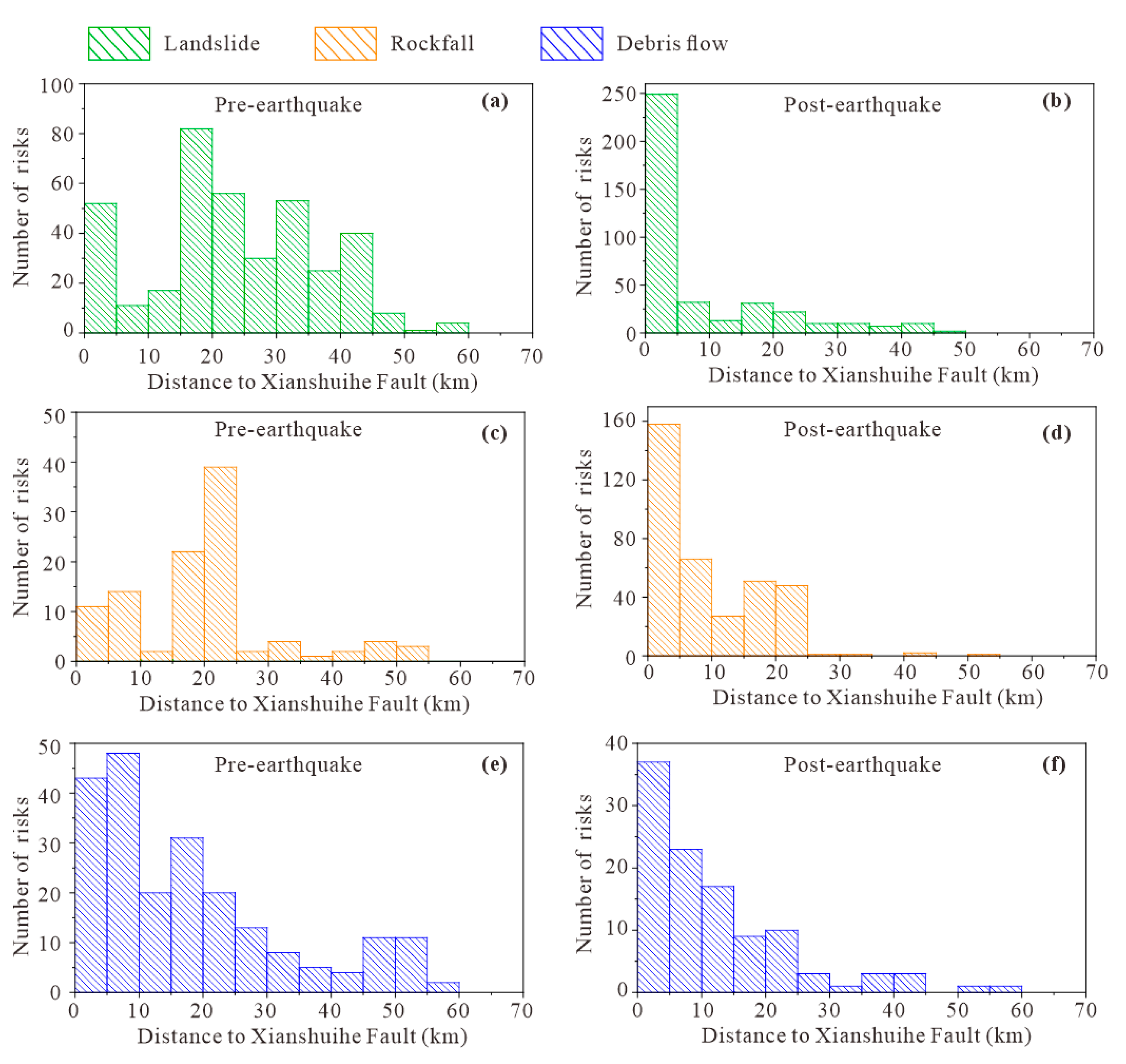
3.2. Distance to the Xianshuihe Fault

The Xianshuihe Fault is the main seismogenic fault zone responsible for the Luding Earthquake, and the seismic vibrations primarily propagate along it. The distance between geo-hazards and the fault reflects the influence of the earthquake on the development of these hazards (Figure 2d) [57,58]. Statistical analysis of geo-hazard disasters reveals that most landslides occur between 30 and 40 km from the Xianshuihe Fault (Figure 5a), whereas rockfalls and debris flows are predominantly concentrated within 10 km of the fault (Figure 5c,e), suggesting that rockfalls and debris flows are more susceptible to the effects of fractured rock and soil masses near the fault zone. After the earthquake, geo-hazard occurrence concentrates around the Xianshuihe Fault (Figure 5b,d,f). The proportion of landslides within a 10 km range increases by more than 20%, rockfalls have risen by 30%, and debris flows by 5% (Table 2). These changes in geo-hazard distribution highlight the significant impact of the earthquake on the spatial patterns of such disasters. The kernel density hotspot maps of geo-hazards also show a similar result: more geo-hazards concentrate around the Xianshuihe Fault (Figure S1).
A similar pattern is evident in the analysis of geo-hazard risks (Figure 6). Before the earthquake, the majority of landslides and rockfalls were developed beyond 20 km from the fault. However, after the earthquake, these geo-hazard risks developed in the vicinity of the Xianshuihe Fault. Notably, the number of landslides within 10 km of the fault increased by more than 50%, and rockfalls rose by nearly 40% (Table 2). These findings indicate that the Luding Earthquake significantly reshaped the spatial distribution of geo-hazard risks. Therefore, it is essential that post-earthquake geo-hazard early warning systems prioritize areas in close proximity to fault zones. Enhanced disaster monitoring and thorough field investigations in these regions are critical for effective risk mitigation and future hazard preparedness.

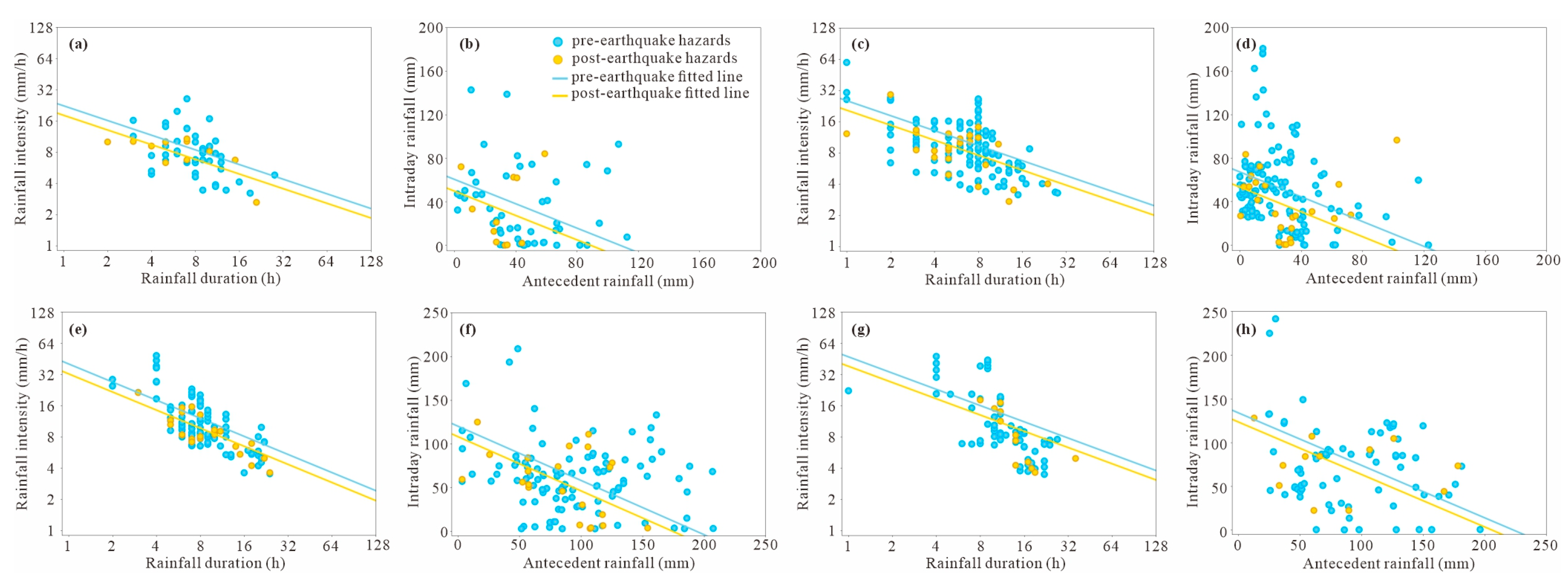
3.3. Rainfall Threshold Models

Precipitation is the major factor triggering disasters in the study area [59,60]. Seismic vibrations caused by earthquakes can weaken the stability of rock and soil masses, thereby affecting the triggering conditions of geo-hazards. Comparing the rainfall thresholds for geo-hazards before and after the earthquake allows for quantification of the earthquake’s impact. Figure 7 and Table 3 present the results of threshold models. Generally, both landslide–rockfall events and debris flows show lower fitted curves after the earthquake in both the east and west zones. In the ID models, seismic activity leads to a 17~20% reduction in the intercept values for both types of disasters across two zones. In the AC models, a nearly 20% decrease in the intercept is observed in the west zone, while the east zone shows a decrease of around 10%. Overall, both ID and AC models exhibit lower curves after the earthquake. This reduction is attributed to soil and rock weakening, crack propagation, and changes in hydrological conductivity caused by the main earthquake and subsequent aftershocks.

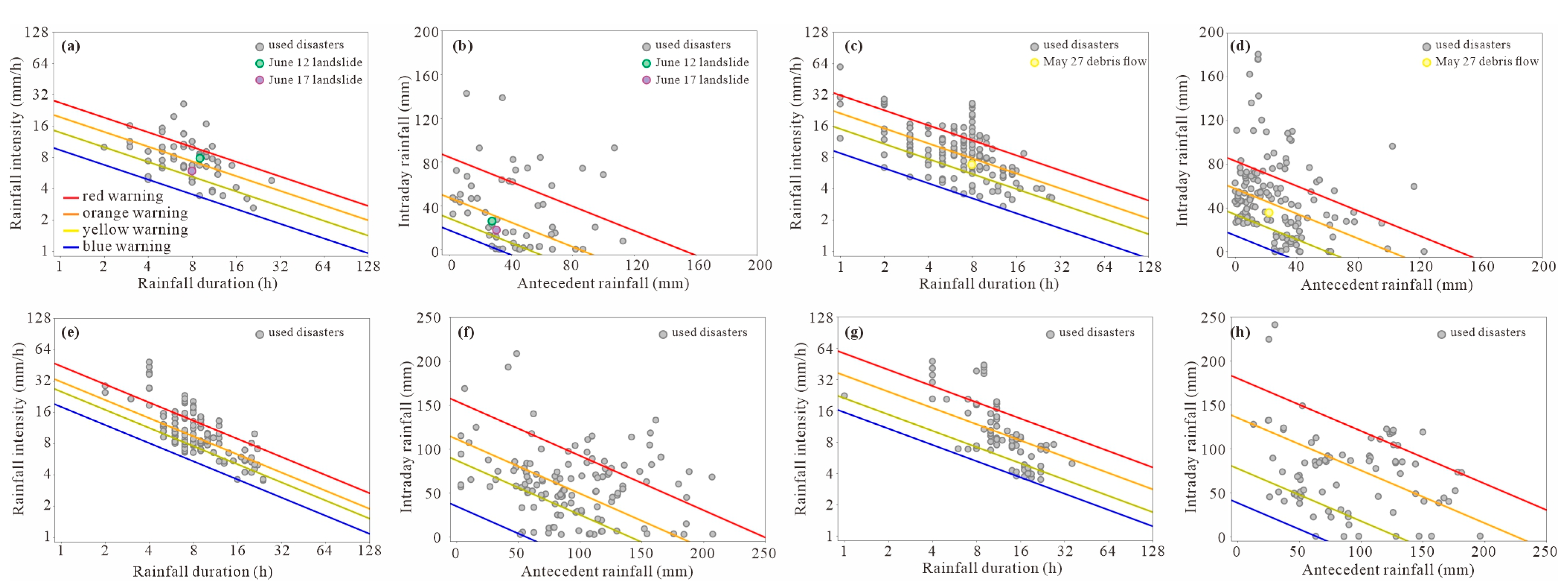
4. Rainfall Threshold Warning System

Four-level warning systems were established based on the threshold models. Due to the data scarcity in the post-earthquake group, it is difficult to establish a dependent post-earthquake warning system. Additionally, since the recovery of the geo-environment after an earthquake is gradual [34], it is reasonable to integrate pre- and post-earthquake data into one warning system. Therefore, we combined all data to build the warning system, while still distinguishing between types of geo-hazards and the east–west zones. Figure 8 and Table 4 present the results of the four-level early warning systems, and the equations of all point data, R2, and confidence bands are displayed in Texts S1 and S2. The rainfall thresholds in the east zone are significantly higher than the west zone, likely due to the greater precipitation in the east (Figure 2c). Furthermore, the thresholds of debris flow are generally higher than landslide and rockfall. The occurrence of debris flow depends on the material accumulation and failure of mountainous valleys, justifying a higher rainfall threshold.
By defining these warning levels, regional geo-hazard prediction and response efforts can be carried out in a more systematic and sustainable manner. In general, the response to a blue warning involves notifying local governments to strengthen emergency duty arrangements; the response to yellow warning entails informing relevant local departments to enhance monitoring and patrols of geo-hazard risks within the affected areas; orange warnings notify potentially affected residents and inform local emergency rescue teams; and a red warning requires the immediate evacuation of potentially affected residents [61].
The validation of the warning system requires the input of a large number of new geo-hazard disasters. At present, the availability of such data is limited, which constrains the completeness of the model validation. Full validation can therefore only be achieved in the future as more data becomes available. Nevertheless, we collected data on three new geo-hazard events in 2025 to test the performance of the warning system: (1) a landslide that occurred in Kangding County (Figure 1) on 12 June; (2) a landslide in Kangding County on 17 June; and (3) a debris flow in Jiulong County on 27 May. These three geo-hazard disasters were of small-scale magnitude and did not cause any harm to the local residents or damage public infrastructure. We calculated the parameters of three events and applied them to test the ID and AC warning models in the west zone. The results show that the 12th June landslide constitutes orange and yellow warning levels in the ID and AC models, respectively; the 17 June landslide is counted as a yellow warning in both the ID and AC models; and the 27 May debris flow also constituted a yellow warning in both the ID and AC models (Figure 8). Overall, the three events were basically captured by the four-level warning system, demonstrating the preliminary applicability of the proposed approach and strong potential for operational use in early warning practice.

5. Discussion

This study developed an empirical rainfall threshold warning system and discussed pre- and post-earthquake situations. The application potential of these thresholds to the current disaster management plans of Sichuan needs to be stressed. The results in Section 3 show a significant reduction in the rainfall thresholds required to trigger geo-hazards following the earthquake, particularly in the west zone. When lowering the thresholds for early warnings, resource limitations must be considered. The regions with higher thresholds (east zone) may require more frequent monitoring and response systems, potentially straining local resources. Moreover, targeted communication strategies are necessary to prevent warning fatigue, particularly in areas where thresholds have been reduced post-earthquake. Additionally, social equity and resilience should be integrated into the sustainability approach. A differentiated approach based on geographical risk exposure, such as areas more sensitive and closer to fault zones, would help to prevent overburdening vulnerable populations with excessive warnings while ensuring that high-risk zones receive timely and actionable alerts. It is important to note that the derived thresholds are subject to inherent uncertainties, and error margins may vary across regions due to differences in rainfall records and local geological conditions. Explicitly acknowledging these margins enhances the credibility of the findings and provides more reliable guidance for disaster management planning. Therefore, incorporating updated geo-hazard thresholds is essential for a sustainable disaster risk reduction framework that minimizes environmental impact and ensures the long-term protection of vulnerable populations.
Machine learning (ML) methods, such as random forests and neural networks, are other strong approaches to calculate rainfall thresholds, though not used in this study. ML’s major strength lies in its ability to capture complex, non-linear relationships between environmental variables and hazard occurrences without relying on explicit physical assumptions; it absolutely performs better than empirical methods in predictive accuracy. However, these benefits come with challenges: ML models require extensive datasets, preprocessing, feature engineering, and hyperparameter tuning to avoid overfitting and ensure generalizability. Issues such as data scarcity, missing records, or biased sampling can hinder applicability. Additionally, although interpretability techniques such as SHAP values and feature importance ranking have been developed, the inherent “black-box” nature of many ML algorithms raises concerns for operational adoption in early warning systems, where transparency and accountability are essential for decision-makers and communities. In contrast, empirical methods provide clear interpretability and are grounded in geological processes, making them useful for operational early warning systems, especially in regions with limited geological resources. Therefore, while ML offers powerful predictive capabilities, the empirical threshold approach remains advantageous in contexts demanding transparency, adaptability, and lower data and resource demands.
The findings of this study on the impact of the Luding Earthquake on rainfall thresholds for geo-hazards offer valuable insights that could be generalized to other tectonically active mountainous regions, such as the Himalayas or Central America. The observed reduction in rainfall thresholds post-earthquake, particularly near fault zones, is likely applicable to areas with similar seismic and climatic conditions, where earthquakes destabilize slopes and increase susceptibility to landslides, rockfalls, and debris flows. Some other factors may also be considered for a different study area; for instance, the establishment of threshold models in the Himalayas may focus on varying elevation and complex precipitation patterns. In addition, local factors such as lithology, vegetation cover, and human activity may influence the exact magnitude of threshold changes. The four-level warning system developed in the study could serve as a template for other regions, though it should be calibrated to local data, and the number of levels and specific thresholds may differ. Further validation with regional datasets would be necessary to ensure accuracy and relevance.

6. Conclusions

This study examines the impact of the Luding Earthquake on the spatial distribution of geo-hazards and the corresponding rainfall thresholds. The research focuses on the seismic intensity VI zone of the Luding Earthquake. We systemically analyzed hourly precipitation data from 475 rainfall stations and geo-hazard information from 1979 records. A comparative assessment was then carried out to evaluate the differences in geo-hazard characteristics before and after the earthquake. Based on these findings, we developed four-level early warning systems for various types of geo-hazards across both the east and west zones. These systems aim to promote sustainable risk reduction and long-term resilience in earthquake-prone regions. The key findings and contributions of this study are as follows:
(1) The Luding Earthquake caused more geo-hazard risks in the study area, especially increasing rockfall risks. However, the proportion of various geo-hazard disaster events is not substantially influenced by the earthquake.
(2) Both post-earthquake geo-hazard disasters and risks exhibit a denser spatial distribution along the seismogenic fault zone compared to the pre-earthquake geo-hazards. This observation highlights critical areas that require prioritized and sustainable disaster monitoring following seismic events.
(3) The rainfall threshold analysis reveals that post-earthquake geo-hazards are triggered by relatively lower rainfall levels, especially in the west zone, which exhibited a more than 20% decrease in threshold values.
(4) The east zone, characterized by more humid meteorological conditions, demonstrates higher rainfall thresholds than the west zone. Among the different types of geo-hazards, debris flows require higher rainfall thresholds to be triggered compared to landslides and rockfalls.
(5) The advantage of empirical models lies in their simplicity and broad applicability, while they may also involve considerable uncertainty. When sufficient data and supporting conditions, such as hydrological information, are available, machine learning or more advanced statistical models are recommended for developing the warning system.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su17188127/s1, Table S1: ID model with different rainfall event gaps; Table S2: AC model with different decay factors; Table S3: R2 of different threshold models; Figure S1: Kernel-density hotspot maps of: (a) pre-earthquake geohazards and (b) post-earthquake geohazards; Figure S2: Confidence bands of different threshold models. (a) ID model of landslide-rockfall in the West zone; (b) AC model of landslide-rockfall in the West zone; (c) ID model of debris flow in the West zone; (d) AC model of debris flow in the West zone; (e) ID model of landslide-rockfall in the East zone; (f) AC model of landslide-rockfall in the East zone; (g) ID model of debris flow in the East zone; (h) AC model of debris flow in the East zone.

Author Contributions

Conceptualization, Q.Z. and S.J.; methodology, Q.Z. and S.J.; software, Q.Z.; validation, J.L. and Z.W.; formal analysis, J.L. and Q.Z.; investigation, Q.Z. and Z.S.; resources, S.J. and J.L.; data curation, L.Z. and Y.L.; writing—original draft preparation, Q.Z.; writing—review and editing, J.L. and S.J.; visualization, S.L.; supervision, J.L. and S.J.; project administration, S.J.; funding acquisition, Q.Z. and S.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by the Open Fund of Technology Innovation Center for Geohazard Monitoring and Risk Early Warning, Ministry of Natural Resources (No.TICGM-2024-08); the Natural Science Foundation of Sichuan Province (No. 24JBGS0060); the Sichuan Science and Technology Program (No.2024YFFK0108); research funds from Department of Natural Resources of Sichuan Province (No.N5100012024000900 and No.N5100012024000981); the Science Foundation of Yan’an City (No.N5118012023000092); and research funds from the Sichuan Institute of Land and Space Ecological Restoration and Geological Hazard Prevention (No.KYL202204-0084 and No.KYL202407-0109).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data is available upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
  2. Catani, F.; Casagli, N.; Ermini, L.; Righini, G.; Menduni, G. Landslide hazard and risk mapping at catchment scale in the Arno River basin. Landslides 2005, 2, 329–342. [Google Scholar] [CrossRef]
  3. Guzzetti, F.; Cardinali, M.; Reichenbach, P.; Cipolla, F.; Sebastiani, C.; Galli, M.; Salvati, P. Landslide striggered by the 23 November 2000 rainfall event in the Imperia Province, Western Liguria, Italy. Eng. Geol. 2004, 73, 229–245. [Google Scholar]
  4. Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A Phys. Geogr. 2017, 38, 23–27. [Google Scholar]
  5. Offenthaler, I.; Felderer, A.; Formayer, H.; Glas, N.; Leidinger, D.; Leopold, P.; Schmidt, A.; Lexer, M.J. Threshold or limit? precipitation dependency of Austrian landslides, an ongoing challenge for hazard mapping under climate change. Sustainability 2020, 12, 6182. [Google Scholar] [CrossRef]
  6. Calvello, M.; Papa, M.N.; Pratschke, J.; Crescenzo, M.N. Landslide risk perception: A case study in Southern Italy. Landslides 2016, 13, 349–360. [Google Scholar]
  7. Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
  8. Zhang, S.; Xu, C.; Wei, F.; Hu, K.; Xu, H.; Zhao, L.; Zhang, G. A physics-based model to derive rainfall intensity-duration threshold for debris flow. Geomorphology 2020, 351, 106930. [Google Scholar]
  9. Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar]
  10. Marin, R.J. Physically based and distributed rainfall intensity and duration thresholds for shallow landslides. Landslides 2020, 17, 2907–2917. [Google Scholar] [CrossRef]
  11. Sheng, Y.; Li, Y.; Xi, G.; Li, Z. Threshold assessment of rainfall-induced landslides in Sangzhi County: Statistical analysis and physical model. Bull. Eng. Geol. Environ. 2022, 81, 388. [Google Scholar] [CrossRef]
  12. Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
  13. Wilson, R.C.; Wieczorek, G.F. Rainfall thresholds for the initiation of debris flows at La Honda, California. Environ. Eng. Geosci. 1995, 1, 11–27. [Google Scholar] [CrossRef]
  14. Lazzari, M.; Piccarreta, M.; Capolongo, D. Landslide triggering and local rainfall thresholds in Bradanic Foredeep, Basilicata region (Southern Italy). Landslide Sci. Pract. 2013, 2, 671–677. [Google Scholar]
  15. Rosi, A.; Peternel, T.; Jemec-Auflič, M.; Komac, M.; Segoni, S.; Casagli, N. Rainfall thresholds for rainfall-induced landslides in Slovenia. Landslides 2016, 13, 1571–1577. [Google Scholar] [CrossRef]
  16. Guo, X.; Cui, P.; Li, Y. Debris flow warning threshold based on antecedent rainfall: A case study in Jiangjia Ravine, Yunnan, China. J. Mt. Sci.-Engl. 2013, 10, 305–314. [Google Scholar]
  17. Yang, H.; Wei, F.; Ma, Z.; Guo, H.; Su, P.; Zhang, S. Rainfall threshold for landslide activity in Dazhou, southwest China. Landslides 2020, 17, 61–77. [Google Scholar]
  18. Peruccacci, S.; Brunetti, M.T.; Gariano, S.L.; Melillo, M.; Rossi, M.; Guzzetti, F. Rainfall thresholds for possible landslide occurrence in Italy. Geomorphology 2017, 290, 39–57. [Google Scholar] [CrossRef]
  19. Hong, Y.; Hiura, H.; Shino, K.; Suemine, A.; Fukuoka, H.; Wang, G. The influence of intense rainfall on the activity of large-scale crystalline schist landslides in Shikoku Island, Janpan. Landslides 2005, 2, 97–105. [Google Scholar]
  20. Zhao, B.; Dai, Q.; Han, D.; Zhang, J.; Zhuo, L.; Berti, M. Application of hydrological model simulations in landslide predictions. Landslides 2020, 17, 877–891. [Google Scholar]
  21. Zhuang, J.; Peng, J.; Wang, G.; Iqbal, J.; Wang, Y.; Li, W.; Xu, Q.; Zhu, X. Prediction of rainfall-induced shallow landslides in the Loess Plateau, Yan’an, China, using the TRIGRS model. Earth Surf. Proc. Land. 2016, 42, 915–927. [Google Scholar] [CrossRef]
  22. Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Vennari, C.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
  23. Vessia, G.; Curzio, D.D.; Chiaudani, A.; Rusi, S. Regional rainfall threshold maps drawn through multivariate geostatistical techniques for shallow landslide hazard zonation. Sci. Total. Environ. 2020, 705, 135815. [Google Scholar] [CrossRef]
  24. Xu, Z.; Xiao, Z.; Zhao, X.; Ma, Z.; Zhang, Q.; Zeng, P.; Zhang, X. Derivation of landslide rainfall thresholds by geostatistical methods in Southwest China. Sustainability 2024, 16, 4044. [Google Scholar] [CrossRef]
  25. Steger, S.; Moreno, M.; Crespi, A.; Zellner, P.J.; Gariano, S.L.; Brunetti, M.T.; Melillo, M.; Peruccacci, S.; Marra, F.; Kohrs, R.; et al. Deciphering seasonal effects of triggering and preparatory precipitation for improved shallow landslide prediction using generalized additive mixed models. Nat. Hazards Earth Syst. Sci. 2023, 23, 1483–1506. [Google Scholar] [CrossRef]
  26. Peres, D.J.; Cancelliere, A. Comparing methods for determining landslide early warning thresholds: Potential use of non-triggering rainfall for locations with scarce landslide data availability. Landslides 2021, 18, 3135–3147. [Google Scholar] [CrossRef]
  27. Zhang, S.; Pecoraro, G.; Jiang, Q.; Calvello, M. A probabilistic procedure to define multidimensional rainfall thresholds for territorial landslide warning models. Landslides 2025, 22, 1773–1787. [Google Scholar] [CrossRef]
  28. Leonarduzzi, E.; Molnar, P. Deriving rainfall thresholds for landsliding at the regional scale: Daily and hourly resolutions, normalisation, and antecedent rainfall. Nat. Hazards Earth Syst. Sci. 2020, 20, 2905–2929. [Google Scholar] [CrossRef]
  29. Gariano, S.L.; Melillo, M.; Peruccacci, S.; Brunetti, M.T. How much does the rainfall temporal resolution affect rainfall thresholds for landslide triggering? Nat. Hazards 2020, 100, 655–670. [Google Scholar] [CrossRef]
  30. Bradley, K.; Mallick, R.; Andikagumi, H.; Hubbard, J.; Meilianda, E.; Switzer, A.; Du, N.; Brocard, G.; Alfian, D.; Benazir, B.; et al. Earthquake-triggered 2018 Palu Valley landslides enabled by wet rice cultivation. Nat. Geosci. 2019, 12, 935–939. [Google Scholar] [CrossRef]
  31. Keefer, D.K. Landslides caused by earthquakes. Geol. Soc. Am. Bull. 1984, 95, 406–421. [Google Scholar] [CrossRef]
  32. Marano, K.D.; Wald, D.J.; Allen, T.I. Global earthquake casualties due to secondary effects: A quantitative analysis for improving rapid loss analyses. Nat. Hazards 2010, 52, 319–328. [Google Scholar] [CrossRef]
  33. USGS. Earthquake Hazards Program. Available online: https://www.usgs.gov/programs/earthquake-hazards (accessed on 1 January 2025).
  34. Huang, R.; Fan, X. The landslide story. Nat. Geosci. 2013, 6, 325–326. [Google Scholar] [CrossRef]
  35. Xu, C.; Xu, X.; Yao, X.; Dai, F. Three (nearly) complete inventories of landslides triggered by the May 12, 2008 Wenchuan Mw 7.9 earthquake of China and their spatial distribution statistical analysis. Landslides 2014, 11, 441–461. [Google Scholar] [CrossRef]
  36. Yin, Y.; Wang, F.; Sun, P. Landslide hazards triggered by the 2008 Wenchuan earthquake, Sichuan, China. Landslides 2009, 6, 139–152. [Google Scholar] [CrossRef]
  37. Zhang, L.; Liu, X.; Li, Y.; Liu, Z.; Lin, J.; Shen, J.; Tang, X.; Zhang, Y.; Liang, W. Emergency medical rescue efforts after a major earthquake: Lessons from the 2008 Wenchuan earthquake. Lancet 2012, 379, 853–861. [Google Scholar] [CrossRef] [PubMed]
  38. Bertrand, E.; Duval, A.M.; Régnier, J.; Azzara, R.M.; Bergamaschi, F.; Bordoni, P.; Cara, F.; Cultrera, G.; Di Giulio, G.; Milana, G.; et al. Site effects of the Roio basin, L’Aquila. Bull. Earthq. Eng. 2011, 9, 809–823. [Google Scholar] [CrossRef]
  39. Cetin, K.O.; Papadimitriou, A.G.; Altun, S.; Pelekis, P.; Unutmaz, B.; Rovithis, E.; Akgun, M.; Klimis, N.; Askan, A.; Ziotopoulou, K.; et al. The role of site effects on elevated seismic demands and corollary structural damage during the October 30, 2020, M7.0 Samos Island (Aegean Sea) Earthquake. Bull. Earthq. Eng. 2021, 20, 7763–7792. [Google Scholar] [CrossRef]
  40. Shinohara, Y.; Kume, T. Changes in the factors contributing to the reduction of landslide fatalities between 1945 and 2019 in Japan. Sci. Total. Environ. 2022, 827, 154392. [Google Scholar] [CrossRef]
  41. Hu, W.; Scaringi, G.; Xu, Q.; Huang, R. Internal erosion controls failure and runout of loose granular deposits: Evidence from flume tests and implications for postseismic slope healing. Geophys. Res. Lett. 2011, 45, 5518–5527. [Google Scholar] [CrossRef]
  42. Fan, X.; Scaringi, G.; Domènech, G.; Yang, F.; Guo, X.; Dai, L.; He, C.; Xu, Q.; Huang, R. Two multi-temporal datasets that track the enhanced landsliding after the 2008 Wenchuan earthquake. Earth. Syst. Sci. Data 2019, 11, 35–55. [Google Scholar] [CrossRef]
  43. LaHusen, S.R.; Duvall, A.R.; Booth, A.M.; Grant, A.; Mishkin, B.A.; Montgomery, D.R.; Roering, J.J.; Wartman, J. Rainfall triggers more deep-seated landslides than Cascadia earthquakes in the Oregon Coast Range, USA. Sci. Aav. 2020, 6, eaba6790. [Google Scholar] [CrossRef] [PubMed]
  44. Marc, O.; Hovius, N.; Meunier, P.; Uchida, T.; Hayashi, S. Transient changes of landslide rates after earthquakes. Geology 2015, 43, 883–886. [Google Scholar] [CrossRef]
  45. Tanyaş, H.; Kirschbaum, D.; Görüm, T.; van Westen, C.J.; Tang, C.; Lombardo, L. A closer look at factors governing landslide recovery time in post-seismic periods. Geomorphology 2021, 391, 107912. [Google Scholar] [CrossRef]
  46. Wang, X.; Fan, X.; Fang, C.; Dai, L.; Zhang, W.; Zheng, H.; Xu, Q. Long-Term Landslide Evolution and Restoration After the Wenchuan Earthquake Revealed by Time-Series Remote Sensing Images. Geophys. Res. Lett. 2024, 51, e2023GL106422. [Google Scholar] [CrossRef]
  47. Li, W.; Chen, J.; Lu, H.; Shan, Y.; Li, Z.; Chen, B.; Wu, L.; Xu, Z.; Li, W.; Zhang, P.; et al. Emergency analysis of the impact of the Luding Ms 6.8 earthquake on Hailuogou glacier. Geomat. Inf. Sci. Wuhan Univ. 2023, 48, 47–57. (In Chinese) [Google Scholar]
  48. Lu, Y.; Yang, Y.; Zeng, L.; Xu, W.; Song, J.; Li, X. Research on the Surface Deformation, Fault Rupture, and Coseismic Geohazard of the 2022 Luding Mw 6.8 Earthquake. Sensors 2023, 23, 9875. [Google Scholar] [CrossRef]
  49. Liu, S.; Yang, Y.; Deng, B.; Zhong, Y.; Wen, L.; Sun, W.; Li, Z.; Jansa, L.; Li, J.; Song, J.; et al. Tectonic evolution of the Sichuan Basin, Southwest China. Earth-Sci. Rev. 2021, 213, 103470. [Google Scholar] [CrossRef]
  50. Yang, F.; Xu, S. Regional Geological Background of Sichuan Basin. In Sedimentation and Reservoirs of Marine Shale in South China; Springer Nature: Berlin/Heidelberg, Germany, 2024; pp. 9–16. [Google Scholar]
  51. Sichuan Institute of Geological Survey. Regional Geology of China—Sichuan; Geology Press: Beijing, China, 2023. (In Chinese) [Google Scholar]
  52. Zhang, P. A review on active tectonics and deep crustal processes of the Western Sichuan region, eastern margin of the Tibetan Plateau. Tectonophysics 2013, 584, 7–22. [Google Scholar] [CrossRef]
  53. Qu, Y.; Jin, X. Geological hazards susceptibility evaluation based on multi-year spatial–temporal evolution of assessment factors in Luding area, Sichuan Province, China. Geol. J. 2024, 59, 1520–1538. [Google Scholar] [CrossRef]
  54. Xu, S.; Zhou, X. Spatiotemporal Evolution Characteristics of Hanyuan Landslide in Sichuan Province, China, on 21 August 2020. Appl. Sci. 2025, 15, 3872. [Google Scholar] [CrossRef]
  55. Marin, R.J.; Velásquez, M.F.; García, E.F.; Alvioli, M.; Aristizábal, E. Assessing two methods of defining rainfall intensity and duration thresholds for shallow landslides in data-scarce catchments of the Colombian Andean Mountains. Catena 2021, 206, 105563. [Google Scholar] [CrossRef]
  56. Yang, Z.; Cai, H.; Shao, W.; Huang, D.; Uchimura, T.; Lei, X.; Tian, H.; Qiao, J. Clarifying the hydrological mechanisms and thresholds for rainfall-induced landslide: In situ monitoring of big data to unsaturated slope stability analysis. Bull. Eng. Geol. Environ. 2018, 78, 2139–2150. [Google Scholar] [CrossRef]
  57. Fan, X.; Wang, X.; Fang, C.; Jansen, J.D.; Dai, L.; Tanyas, H.; Zang, N.; Tang, R.; Xu, Q.; Huang, R. Deep learning can predict global earthquake-triggered landslides. Natl. Sci. Rev. 2025, 12, nwaf179. [Google Scholar] [CrossRef] [PubMed]
  58. Djukem, D.L.W.; Fan, X.; Braun, A.; Chevalier, M.; Wang, X.; Dai, L.; Fang, C.; Zhang, X.; Gorum, T.; Xu, Q.; et al. Traditional and modified Newmark displacement methods after the 2022 Ms 6.8 Luding earthquake (Eastern Tibetan Plateau). Landslides 2024, 21, 807–828. [Google Scholar] [CrossRef]
  59. Zho, H.; Mu, C.; Yang, B.; Huang, G.; Hong, J. Evaluating Landslide Hazard in Western Sichuan: Integrating Rainfall and Geospatial Factors Using a Coupled Information Value–Geographic Logistic Regression Model. Sustainability 2025, 17, 1485. [Google Scholar] [CrossRef]
  60. Xiao, T.; Wang, Y.; Zhao, Y.; Jing, F.; Zhan, Z.; Wang, L.; Fan, J.; Gan, W.; Yang, X.; Fang, Y. The hazard risk assessment of regional heavy rainfall over Sichuan Basin of China. Nat. Hazards 2017, 88, 1155–1168. [Google Scholar] [CrossRef]
  61. GB/T 40112-2021; State Administration for Market Regulation. Specifications for Risk Assessment of Geological Hazard. Standards Press of China: Beijing, China, 2021. (In Chinese)
Sustainability 17 08127 g001
Figure 1. Study area information: (a) geographic location of the study area; (b) detailed characteristics of the study area, including elevation, distribution of geo-hazards, seismic intensity, earthquake epicenter, and the Xianshuihe Fault.
Figure 1. Study area information: (a) geographic location of the study area; (b) detailed characteristics of the study area, including elevation, distribution of geo-hazards, seismic intensity, earthquake epicenter, and the Xianshuihe Fault.
Sustainability 17 08127 g001
Sustainability 17 08127 g002
Figure 2. (a) Distribution of geo-hazard disasters; (b) distribution of geo-hazard risks; (c) distribution of precipitation stations and annual precipitation; (d) geo-hazards and distance to the Xianshuihe Fault.
Figure 2. (a) Distribution of geo-hazard disasters; (b) distribution of geo-hazard risks; (c) distribution of precipitation stations and annual precipitation; (d) geo-hazards and distance to the Xianshuihe Fault.
Sustainability 17 08127 g002
Sustainability 17 08127 g003
Figure 3. The number of geo-hazard disasters occurring each month.
Figure 3. The number of geo-hazard disasters occurring each month.
Sustainability 17 08127 g003
Sustainability 17 08127 g004
Figure 4. The number of geo-hazards before and after the Luding Earthquake. (a) Pre-earthquake geo-hazard disasters; (b) post-earthquake geo-hazard disasters; (c) pre-earthquake geo-hazard risks; (d) post-earthquake geo-hazard risks.
Figure 4. The number of geo-hazards before and after the Luding Earthquake. (a) Pre-earthquake geo-hazard disasters; (b) post-earthquake geo-hazard disasters; (c) pre-earthquake geo-hazard risks; (d) post-earthquake geo-hazard risks.
Sustainability 17 08127 g004
Sustainability 17 08127 g005
Figure 5. Distance to the Xianshuihe Fault for geo-hazard disasters. (a,c,e) are plots for geo-hazards before the earthquake; and (b,d,f) are plots for geo-hazards after the earthquake.
Figure 5. Distance to the Xianshuihe Fault for geo-hazard disasters. (a,c,e) are plots for geo-hazards before the earthquake; and (b,d,f) are plots for geo-hazards after the earthquake.
Sustainability 17 08127 g005
Sustainability 17 08127 g006
Figure 6. Distance to the Xianshuihe Fault for geo-hazard risks. (a,c,e) are plots for geo-hazards before the earthquake; and (b,d,f) are plots for geo-hazards after the earthquake.
Figure 6. Distance to the Xianshuihe Fault for geo-hazard risks. (a,c,e) are plots for geo-hazards before the earthquake; and (b,d,f) are plots for geo-hazards after the earthquake.
Sustainability 17 08127 g006
Sustainability 17 08127 g007
Figure 7. The comparison of threshold models pre- and post-earthquake. (a) ID model of landslide–rockfall in the west zone; (b) AC model of landslide–rockfall in the west zone; (c) ID model of debris flow in the west zone; (d) AC model of debris flow in the west zone; (e) ID model of landslide–rockfall in the east zone; (f) AC model of landslide–rockfall in the east zone; (g) ID model of debris flow in the east zone; (h) AC model of debris flow in the east zone.
Figure 7. The comparison of threshold models pre- and post-earthquake. (a) ID model of landslide–rockfall in the west zone; (b) AC model of landslide–rockfall in the west zone; (c) ID model of debris flow in the west zone; (d) AC model of debris flow in the west zone; (e) ID model of landslide–rockfall in the east zone; (f) AC model of landslide–rockfall in the east zone; (g) ID model of debris flow in the east zone; (h) AC model of debris flow in the east zone.
Sustainability 17 08127 g007
Sustainability 17 08127 g008
Figure 8. Four-level early warning envelopes of rainfall threshold models and test results. (a) ID model of landslide–rockfall in the west zone; (b) AC model of landslide–rockfall in the west zone; (c) ID model of debris flow in the west zone; (d) AC model of debris flow in the west zone; (e) ID model of landslide–rockfall in the east zone; (f) AC model of landslide–rockfall in the east zone; (g) ID model of debris flow in the east zone; (h) AC model of debris flow in the east zone.
Figure 8. Four-level early warning envelopes of rainfall threshold models and test results. (a) ID model of landslide–rockfall in the west zone; (b) AC model of landslide–rockfall in the west zone; (c) ID model of debris flow in the west zone; (d) AC model of debris flow in the west zone; (e) ID model of landslide–rockfall in the east zone; (f) AC model of landslide–rockfall in the east zone; (g) ID model of debris flow in the east zone; (h) AC model of debris flow in the east zone.
Sustainability 17 08127 g008
Table 1. Number of geo-hazards in the study area.
Table 1. Number of geo-hazards in the study area.
Geo-Hazard TypeGeo-Hazard DisasterGeo-Hazard Risk
WestEastWestEast
Landslide31121450315
Rockfall182240061
Debris flow14294189136
Table 2. The proportion of geo-hazards located around the Xianshuihe Fault.
Table 2. The proportion of geo-hazards located around the Xianshuihe Fault.
Geo-Hazard TypeBefore EarthquakeAfter Earthquake
≤5 km≤10 km≤5 km≤10 km
Landslide disaster10%14%39%39%
Rockfall disaster23%30%40%60%
Debris flow disaster24%44%35%48%
Landslide risk14%16%64%73%
Rockfall risk11%25%44%63%
Debris flow risk19%42%34%46%
Table 3. Rainfall threshold models before and after earthquake.
Table 3. Rainfall threshold models before and after earthquake.
ZoneGeo-Hazard TypeID ModelAC Model
Pre-EarthquakePost-EarthquakePre-EarthquakePost-Earthquake
WestLandslide–rockfallI = 22.33D−0.47I = 18.09D−0.47C = −0.56A + 60.53C = −0.56A + 49.76
Debris flowI = 24.46D−0.48I = 20.61D−0.48C = −0.57A + 67.25C = −0.57A + 53.34
EastLandslide–rockfallI = 40.42D−0.58I = 32.41D−0.48C = −0.62A + 120.25C = −0.62A + 108.32
Debris flowI = 47.35D−0.52I = 38.40D−0.52C = −0.60A + 133.97C = −0.60A + 123.52
Table 4. Four-level early warning envelopes of rainfall threshold models.
Table 4. Four-level early warning envelopes of rainfall threshold models.
ZoneGeo-Hazard TypeWarning LevelID ModelAC Model
WestLandslide–rockfallBlueI = 9.40D−0.47C = −0.56A + 17.25
YellowI = 13.88D−0.47C = −0.56A + 28.15
OrangeI = 19.49D−0.47C = −0.56A + 47.04
RedI = 26.78D−0.47C = −0.56A + 74.58
Debris flowBlueI = 8.80D−0.48C = −0.57A + 14.79
YellowI = 15.07D−0.48C = −0.57A + 34.06
OrangeI = 21.27D−0.48C = −0.57A + 54.24
RedI = 31.73D−0.48C = −0.57A + 79.78
EastLandslide–rockfallBlueI = 18.00D−0.58C = −0.62A + 35.02
YellowI = 25.22D−0.58C = −0.62A + 87.23
OrangeI = 31.54D−0.58C = −0.62A + 112.44
RedI = 45.66D−0.58C = −0.62A + 159.51
Debris flowBlueI = 15.44D−0.52C = −0.60A + 38.41
YellowI = 21.11D−0.52C = −0.60A + 77.60
OrangeI = 35.01D−0.52C = −0.60A + 135.35
RedI = 56.90D−0.52C = −0.60A + 180.33
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, Q.; Li, J.; Jin, S.; Liu, Y.; Liu, S.; Wang, Z.; Zhang, L.; Song, Z. Impact of Earthquake on Rainfall Thresholds for Sustainable Geo-Hazard Warnings: A Case Study of Luding Earthquake. Sustainability 2025, 17, 8127. https://doi.org/10.3390/su17188127

AMA Style

Zhang Q, Li J, Jin S, Liu Y, Liu S, Wang Z, Zhang L, Song Z. Impact of Earthquake on Rainfall Thresholds for Sustainable Geo-Hazard Warnings: A Case Study of Luding Earthquake. Sustainability. 2025; 17(18):8127. https://doi.org/10.3390/su17188127

Chicago/Turabian Style

Zhang, Qun, Junfeng Li, Shengjie Jin, Yanhui Liu, Shikang Liu, Zhuo Wang, Lei Zhang, and Zeyi Song. 2025. "Impact of Earthquake on Rainfall Thresholds for Sustainable Geo-Hazard Warnings: A Case Study of Luding Earthquake" Sustainability 17, no. 18: 8127. https://doi.org/10.3390/su17188127

APA Style

Zhang, Q., Li, J., Jin, S., Liu, Y., Liu, S., Wang, Z., Zhang, L., & Song, Z. (2025). Impact of Earthquake on Rainfall Thresholds for Sustainable Geo-Hazard Warnings: A Case Study of Luding Earthquake. Sustainability, 17(18), 8127. https://doi.org/10.3390/su17188127

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop