Segmental Calibration of Soil–Tool Contact Models for Sustainable Tillage Using Discrete Element Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Material
- (1)
- Materials in the calibration experiment
- (2)
- Verification of the materials in the experiment
2.2. Test Methods
2.2.1. Calibration of Soil Interparticle Parameters
- (1)
- Selection of interparticle contact model in discrete element method
- (2)
- Physical experiment on accumulation angle for soil particles
- (3)
- Multi-factor simulation experiment for calibration of interparticle contact parameters in discrete element method
2.2.2. Calibration of Contact Parameters Between Black Soil and Soil-Engaging Components
- (1)
- Physical accumulation angle experiment for soil-engaging component–soil particle interactions
2.3. Validation Experiment
3. Results
3.1. The Results and Analysis of the Calibration Test of Contact Parameters Between Soil Particles
3.1.1. Interaction Effect of Contact Parameters Between Soil Particles
- (1)
- The interaction between JKR surface energy and static friction coefficient
- (2)
- The interaction between JKR surface energy and rolling friction coefficient
3.1.2. Optimal Combination Optimization and Verification of Contact Parameters Between Soil Particles
3.2. Calibration Test Results and Analysis of Contact Parameters Between Black Soil and Soil-Engaging Components
3.2.1. Interaction Effects of Contact Parameters at Soil–Implement Interface
- (1)
- Interaction between JKR surface energy and static friction coefficient
- (2)
- Interaction between JKR surface energy and rolling friction coefficient
3.2.2. Optimization and Validation of Optimal Contact Parameters Between Soil and Soil-Engaging Components
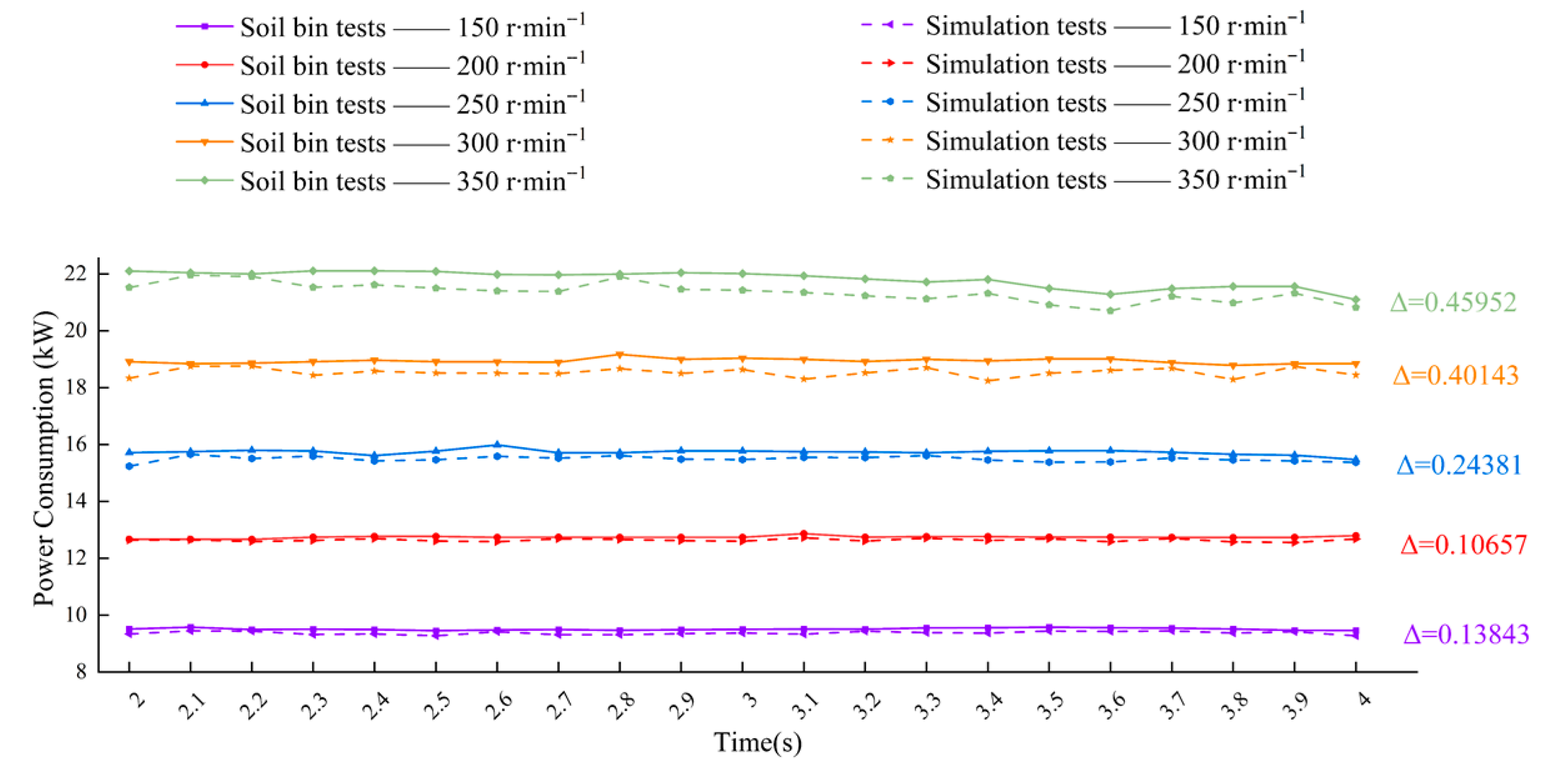
3.3. Analysis of Validation Test Results
4. Discussion
4.1. Segmented Calibration Framework for Accurate Soil–Machine Modeling
4.2. Advancing Sustainable Machinery Design Through Virtual Simulation
4.3. Influence of Soil Moisture and Soil Type on Model Accuracy
4.4. Comparison of the JKR Model with Other Contact Models
5. Conclusions
- (1)
- Using the soil accumulation angle as the evaluation index, optimized soil particle parameters were obtained—a JKR surface energy of 0.46 J·m−2, collision restitution coefficient of 0.51, static friction coefficient of 0.65, and rolling friction coefficient of 0.13. Simulation results showed high consistency with experimental observations, confirming the accuracy and reliability of the soil–soil parameter calibration.
- (2)
- Based on the optimized soil–soil parameters, the interaction parameters between black soil and 65Mn steel were calibrated, yielding a JKR surface energy of 0.29 J·m−2, collision restitution coefficient of 0.55, static friction coefficient of 0.64, and rolling friction coefficient of 0.07. The comparison of simulated and experimental soil accumulation angles validated that these parameters accurately captured the mechanical behavior between soil and machine components.
- (3)
- Validation through rotary tillage tests showed that across blade rotation speeds of 150–350 r·min−1, the errors between DEM-simulated and measured power consumption remained below 0.5 kW, while the differences in ground surface flatness ranged from 0.2 to 4.2 mm, decreasing overall with increasing speed. These results demonstrate that the segmented calibration method is highly accurate and robust, reliably predicting soil–tool interactions and operational performance. The calibrated parameters provide a solid foundation for the virtual simulation and optimization of agricultural machinery, supporting efficient, high-quality, and sustainable field operations.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, X.; Luo, Z.; Hao, Z.; Zheng, E.; Yao, H.; Zhu, Y.; Wang, X. Investigation on tillage resistance and soil disturbance in wet adhesive soil using discrete element method with three-layer soil-plough coupling model. Powder Technol. 2024, 436, 119463. [Google Scholar] [CrossRef]
- Long, S.; Xu, S.; Zhang, Y.; Li, B.; Sun, L.; Wang, Y.; Wang, J. Method of soil-elastoplastic DEM parameter calibration based on recurrent neural network. Powder Technol. 2023, 416, 118222. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Hu, C.; Li, Z.; Tang, J.; Mao, K.; Wang, X. Calibration of wet sand and gravel particles based on JKR contact model. Powder Technol. 2022, 397, 117005. [Google Scholar] [CrossRef]
- Li, J.; Tong, J.; Hu, B.; Wang, H.; Mao, C.; Ma, Y. Calibration of parameters of interaction between clayey black soil with different moisture content and soil-engaging component in northeast China. Trans. Chin. Soc. Agric. Eng. 2019, 35, 130–140. [Google Scholar]
- Tamás, K.; Jóri, I.J.; Mouazen, A.M. Modelling soil–sweep interaction with discrete element method. Soil Tillage Res. 2013, 134, 223–231. [Google Scholar] [CrossRef]
- Aikins, K.A.; Ucgul, M.; Barr, J.B.; Jensen, T.A.; Antille, D.L.; Desbiolles, J.M.A. Determination of discrete element model parameters for a cohesive soil and validation through narrow point opener performance analysis. Soil Tillage Res. 2021, 213, 105123. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Validation of a hysteretic spring (plastic) contact model for a sweep tool operating in a cohesionless soil. Soil Tillage Res. 2014, 144, 220–227. [Google Scholar] [CrossRef]
- Shi, L.; Zhao, W.; Sun, W. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method. Trans. Chin. Soc. Agric. Eng. 2017, 33, 181–187. [Google Scholar]
- Wu, T.; Huang, W.; Chen, X.; Ma, X.; Han, Z.; Pan, T. Calibration of discrete element model parameters for cohesive soil considering the cohesion between particles. J. South China Agric. Univ. 2017, 38, 93–98. [Google Scholar]
- Wang, W.; Cai, D.; Xie, J.; Zhang, C.; Liu, L.; Chen, L. Parameters Calibration of discrete element model for corn stalk powder compression simulation. Trans. Chin. Soc. Agric. Mach. 2021, 52, 127–134. [Google Scholar]
- Wen, X.; Yuan, H.; Wang, G.; Jia, H. Calibration Method of Friction coefficient of granular fertilizer by discrete element simulation. Trans. Chin. Soc. Agric. Mach. 2020, 51, 115–122+142. [Google Scholar]
- Xiang, W.; Wu, M.; Lv, J.; Quan, W.; Ma, L.; Liu, J. Calibration of simulation physical parameters of clay loam based on soil accumulation test. Trans. Chin. Soc. Agric. Eng. 2019, 35, 116–123. [Google Scholar]
- Peng, F.; Wang, H.; Fang, F.; Liu, Y. Calibration of discrete element model parameters for pellet feed based on injected section method. Trans. Chin. Soc. Agric. Mach. 2018, 49, 140–147. [Google Scholar]
- Zhang, R.; Han, D.; Ji, Q.; He, Y.; Li, J. Calibration methods of sandy soil parameters in simulation of discrete element method. Trans. Chin. Soc. Agric. Mach. 2017, 48, 49–56. [Google Scholar]
- Xia, G.; Yang, X.; Wan, Z.; Liu, W.; Li, D. Research status of wear and surface modification of soil contact parts of agricultural machinery. Jiangsu Agric. Sci. 2020, 48, 46–51. [Google Scholar]
- ASTM D2216-19; Standard Test Methods for Laboratory Determination of Water (Moisture) Content of Soil and Rock by Mass. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM D3080/D3080M-11; Standard Test Method for Direct Shear Test of Soils Under Consolidated Drained Conditions. ASTM International: West Conshohocken, PA, USA, 2011.
- ISO 17892-2:2014; Geotechnical Investigation and Testing—Laboratory Testing of Soil—Part 2: Determination of Bulk Density. International Organization for Standardization: Geneva, Switzerland, 2014.
- ASTM D4767-11; Standard Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils. ASTM International: West Conshohocken, PA, USA, 2011.
- Sun, J.; Liu, Q.; Yang, F.; Liu, Z.; Wang, Z. Calibration of discrete element simulation parameters of sloping soil on loess plateau and its interaction with rotary tillage components. Trans. Chin. Soc. Agric. Mach. 2022, 53, 63–73. [Google Scholar]
- Tian, X.; Cong, X.; Qi, J.; Guo, H.; Li, M.; Fan, X. Parameter calibration of discrete element model for corn straw-soil mixture in black soil areas. Trans. Chin. Soc. Agric. Mach. 2021, 52, 100–108+242. [Google Scholar]
- Ma, Y.; Wang, Z.; Shi, L.; Zhao, W.; Sun, B.; Dai, F.; Li, H. Determination the intrinsic parameters and calibration of contact parameters for wheat seed particles. J. China Agric. Univ. 2025, 30, 175–184. [Google Scholar]
- GB/T 225-2006; Steel—Determination of Nitrogen Content—Stehlmann’s Reduction Method. Standardization Administration of China: Beijing, China, 2006.
- Wang, H.; Ding, K.; Xia, J.; Zhang, G.; Wang, Y.; Kang, Q. Calibration of disturbed-saturated paddy soil discrete element parameters based on slump test. Trans. Chin. Soc. Agric. Mach. 2024, 55, 222–230. [Google Scholar]
- Zhou, H.; Che, H.; Geng, D.; Chen, M.; Zhang, Y. Discrete element modeling and parameter calibration of typical soil in maize field tillage layer. Trans. Chin. Soc. Agric. Mach. 2023, 54, 49–60+113. [Google Scholar]
- Dai, F.; Song, X.; Zhao, W.; Zhang, F.; Ma, H.; Ma, M. Simulative Calibration on Contact Parameters of Discrete Elements for Covering Soil on Whole Plastic Film Mulching on Double Ridges. Trans. Chin. Soc. Agric. Mach. 2019, 50, 49–56+77. [Google Scholar]

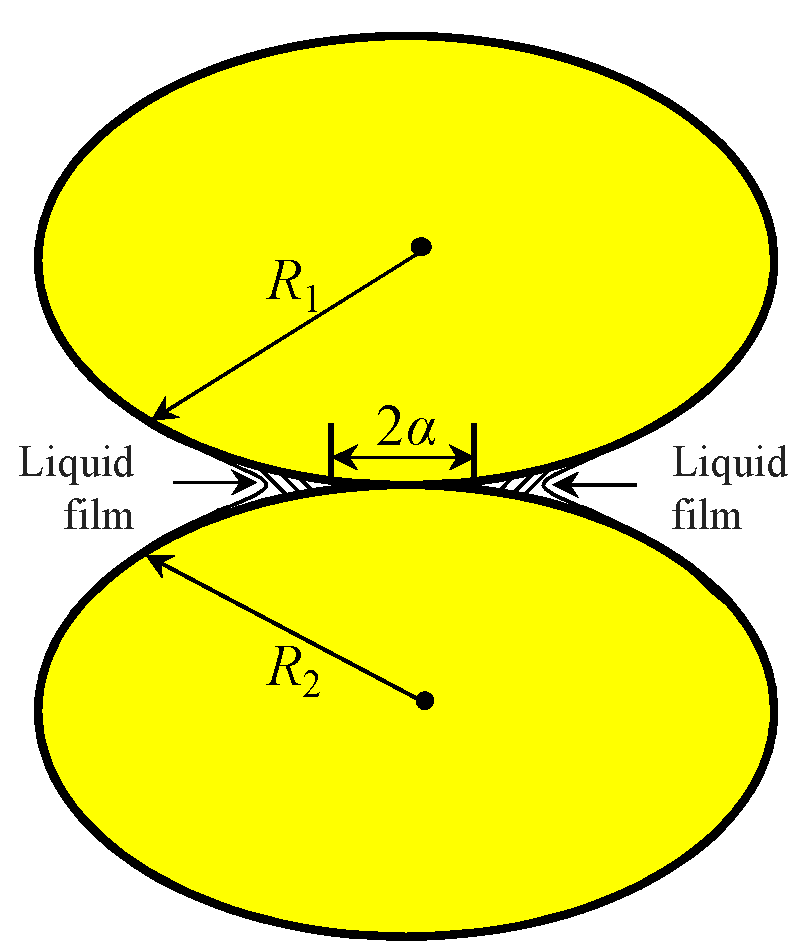





| Parameter | Value |
| Power | 44.1–55.1 kW |
| Dimensions (L × W × H) | 1850 × 800 × 850 mm |
| Number of blades installed | 36 |
| Working width | 160 cm |
| Level | JKR Surface Energy x1/(J·m−2) | Collision Recovery Coefficient x2 | Static Friction Coefficient x3 | Rolling Friction Coefficient x4 |
|---|---|---|---|---|
| High level (+1) | 1 | 0.9 | 1.0 | 0.50 |
| Center level (0) | 0.7 | 0.6 | 0.6 | 0.28 |
| Low level (−1) | 0.4 | 0.3 | 0.2 | 0.05 |
| Level | JKR Surface Energy x5/(J·m−2) | Collision Recovery Coefficient x6 | Static Friction Coefficient x7 | Rolling Friction Coefficient x8 |
|---|---|---|---|---|
| High level (+1) | 0.8 | 0.90 | 0.80 | 0.05 |
| Center level (0) | 0.5 | 0.55 | 0.55 | 0.15 |
| Low level (−1) | 0.2 | 0.20 | 0.30 | 0.25 |
| Test No. | JKR Surface Energy x1/(J·m−2) | Collision Recovery Coefficient x2 | Static Friction Coefficient x3 | Rolling Friction Coefficient x4 | Accumulation Angle/(°) |
|---|---|---|---|---|---|
| 1 | 0.40 | 0.30 | 0.60 | 0.28 | 36.5 ± 0.2 |
| 2 | 1.00 | 0.30 | 0.60 | 0.28 | 42.2 ± 0.3 |
| 3 | 0.40 | 0.90 | 0.60 | 0.28 | 37.6 ± 0.1 |
| 4 | 1.00 | 0.90 | 0.60 | 0.28 | 39.3 ± 0.4 |
| 5 | 0.70 | 0.60 | 0.20 | 0.05 | 34.7 ± 0.2 |
| 6 | 0.70 | 0.60 | 1.00 | 0.05 | 37.1 ± 0.3 |
| 7 | 0.70 | 0.60 | 0.20 | 0.50 | 32.8 ± 0.3 |
| 8 | 0.70 | 0.60 | 1.00 | 0.50 | 39.0 ± 0.2 |
| 9 | 0.40 | 0.60 | 0.60 | 0.05 | 32.3 ± 0.2 |
| 10 | 1.00 | 0.60 | 0.60 | 0.05 | 38.2 ± 0.3 |
| 11 | 0.40 | 0.60 | 0.60 | 0.50 | 38.5 ± 0.1 |
| 12 | 1.00 | 0.60 | 0.60 | 0.50 | 37.4 ± 0.4 |
| 13 | 0.70 | 0.30 | 0.20 | 0.28 | 38.6 ± 0.4 |
| 14 | 0.70 | 0.90 | 0.20 | 0.28 | 33.2 ± 0.2 |
| 15 | 0.70 | 0.30 | 1.00 | 0.28 | 40.4 ± 0.3 |
| 16 | 0.70 | 0.90 | 1.00 | 0.28 | 37.9 ± 0.2 |
| 17 | 0.40 | 0.60 | 0.20 | 0.28 | 33.0 ± 0.2 |
| 18 | 1.00 | 0.60 | 0.20 | 0.28 | 41.2 ± 0.1 |
| 19 | 0.40 | 0.60 | 1.00 | 0.28 | 42.1 ± 0.4 |
| 20 | 1.00 | 0.60 | 1.00 | 0.28 | 40.8 ± 0.2 |
| 21 | 0.70 | 0.30 | 0.60 | 0.05 | 36.7 ± 0.2 |
| 22 | 0.70 | 0.90 | 0.60 | 0.05 | 34.8 ± 0.3 |
| 23 | 0.70 | 0.30 | 0.60 | 0.50 | 39.1 ± 0.3 |
| 24 | 0.70 | 0.90 | 0.60 | 0.50 | 36.6 ± 0.4 |
| 25 | 0.70 | 0.60 | 0.60 | 0.28 | 36.1 ± 0.2 |
| 26 | 0.70 | 0.60 | 0.60 | 0.28 | 38.5 ± 0.2 |
| 27 | 0.70 | 0.60 | 0.60 | 0.28 | 37.4 ± 0.3 |
| 28 | 0.70 | 0.60 | 0.60 | 0.28 | 37.6 ± 0.2 |
| 29 | 0.70 | 0.60 | 0.60 | 0.28 | 37.1 ± 0.3 |
| Kolmogorov–Smirnov | Shapiro–Wilk | |||||
|---|---|---|---|---|---|---|
| Statistic | Degree of Freedom | p | Statistic | Degree of Freedom | p | |
| black soil accumulation angle | 0.115 | 29 | 0.200 | 0.962 | 29 | 0.376 |
| Source of Variance | Sum of Squares | Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 178.54 | 14 | 12.75 | 10.28 | <0.0001 |
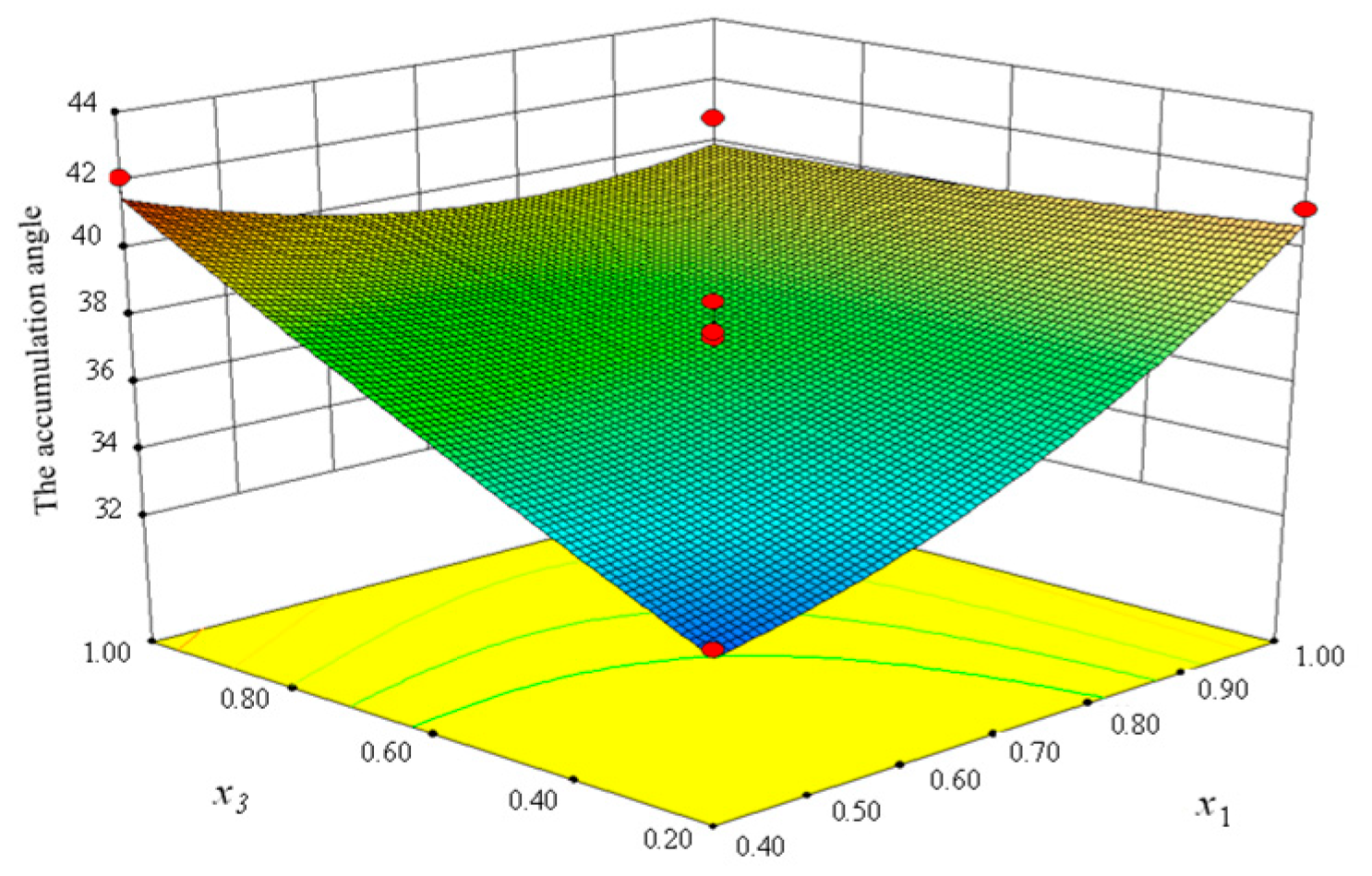
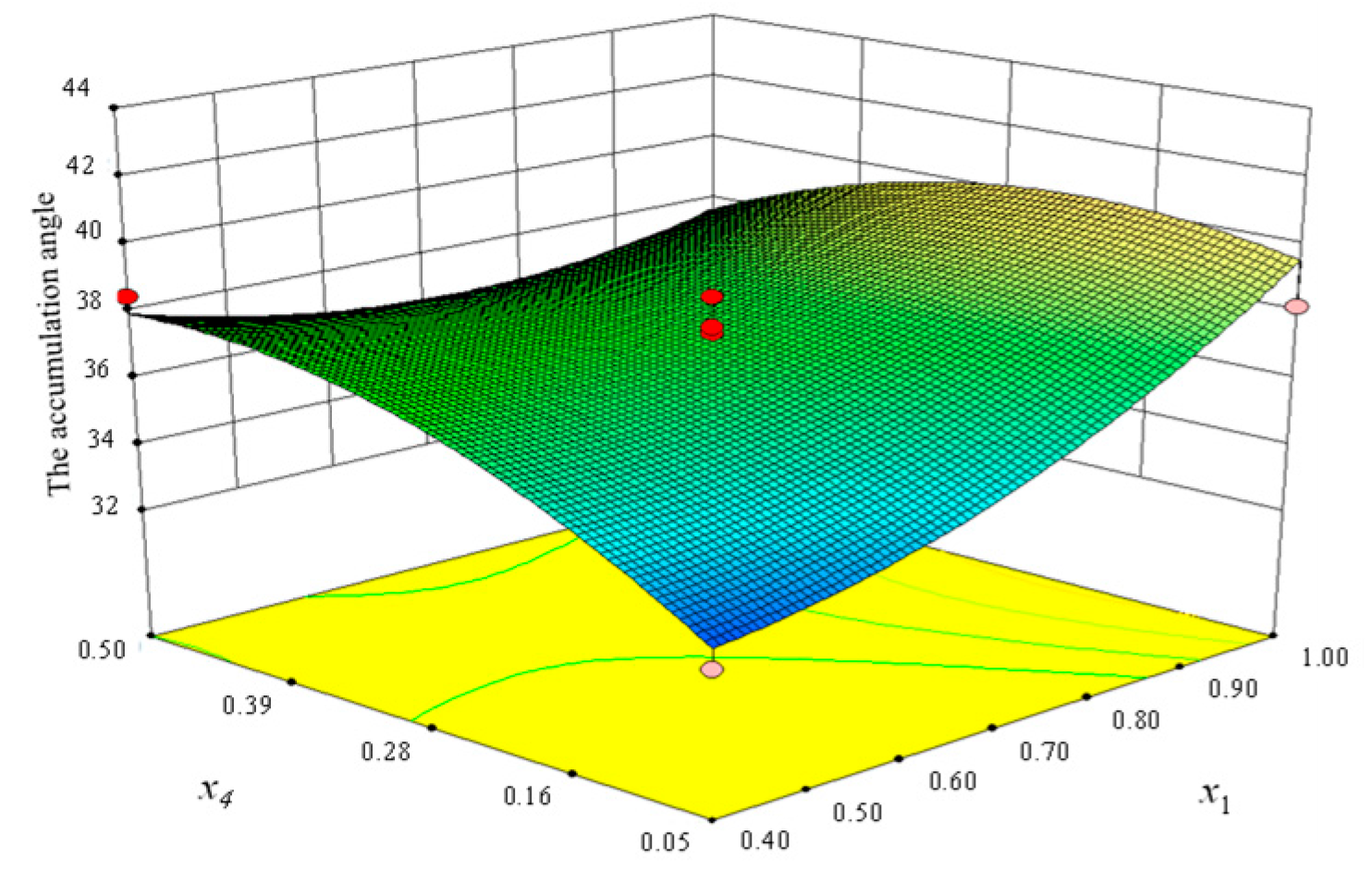
| x1 | 30.4 | 1 | 30.4 | 24.51 | 0.0002 |
| x2 | 16.57 | 1 | 16.57 | 13.36 | 0.0026 |
| x3 | 47.2 | 1 | 47.2 | 38.06 | <0.0001 |
| x4 | 7.68 | 1 | 7.68 | 6.19 | 0.0260 |
| x1 x2 | 4 | 1 | 4 | 3.23 | 0.0941 |
| x1 x3 | 22.56 | 1 | 22.56 | 18.19 | 0.0008 |
| x1 x4 | 12.25 | 1 | 12.25 | 9.88 | 0.0072 |
| x2 x3 | 2.1 | 1 | 2.1 | 1.7 | 0.2139 |
| x2 x4 | 0.09 | 1 | 0.09 | 0.073 | 0.7916 |
| x3 x4 | 3.61 | 1 | 3.61 | 2.91 | 0.1101 |
| 9.61 | 1 | 9.61 | 7.75 | 0.0146 | |
| 1.27 | 1 | 1.27 | 1.02 | 0.3287 | |
| 0.21 | 1 | 0.21 | 0.17 | 0.6868 | |
| 14.99 | 1 | 14.99 | 12.08 | 0.0037 | |
| Lack-of-fit term | 14.35 | 10 | 1.44 | 1.91 | 0.2797 |
| Pure error | 3.01 | 4 | 0.75 | ||
| Sum | 195.90 | 28 |
| Test No. | JKR Surface Energy x5/(J·m−2) | Collision Recovery Coefficient x6 | Static Friction Coefficient x7 | Rolling Friction Coefficient x8 | Accumulation Angle/(°) |
|---|---|---|---|---|---|
| 1 | 0.20 | 0.20 | 0.55 | 0.15 | 34.3 ± 0.2 |
| 2 | 0.80 | 0.20 | 0.55 | 0.15 | 40.0 ± 0.1 |
| 3 | 0.20 | 0.90 | 0.55 | 0.15 | 35.4 ± 0.3 |
| 4 | 0.80 | 0.90 | 0.55 | 0.15 | 37.2 ± 0.2 |
| 5 | 0.50 | 0.55 | 0.30 | 0.05 | 32.2 ± 0.3 |
| 6 | 0.50 | 0.55 | 0.80 | 0.05 | 34.5 ± 0.4 |
| 7 | 0.50 | 0.55 | 0.30 | 0.25 | 30.6 ± 0.1 |
| 8 | 0.50 | 0.55 | 0.80 | 0.25 | 36.9 ± 0.2 |
| 9 | 0.20 | 0.55 | 0.55 | 0.05 | 30.1 ± 0.4 |
| 10 | 0.80 | 0.55 | 0.55 | 0.05 | 36.1 ± 0.3 |
| 11 | 0.20 | 0.55 | 0.55 | 0.25 | 36.3 ± 0.4 |
| 12 | 0.80 | 0.55 | 0.55 | 0.25 | 35.2 ± 0.2 |
| 13 | 0.50 | 0.20 | 0.30 | 0.15 | 36.4 ± 0.3 |
| 14 | 0.50 | 0.90 | 0.30 | 0.15 | 31.1 ± 0.3 |
| 15 | 0.50 | 0.20 | 0.80 | 0.15 | 38.2 ± 0.4 |
| 16 | 0.50 | 0.90 | 0.80 | 0.15 | 35.8 ± 0.2 |
| 17 | 0.20 | 0.55 | 0.30 | 0.15 | 30.9 ± 0.3 |
| 18 | 0.80 | 0.55 | 0.30 | 0.15 | 39.1 ± 0.1 |
| 19 | 0.20 | 0.55 | 0.80 | 0.15 | 39.9 ± 0.2 |
| 20 | 0.80 | 0.55 | 0.80 | 0.15 | 38.7 ± 0.2 |
| 21 | 0.50 | 0.20 | 0.55 | 0.05 | 33.1 ± 0.4 |
| 22 | 0.50 | 0.90 | 0.55 | 0.05 | 31.6 ± 0.2 |
| 23 | 0.50 | 0.20 | 0.55 | 0.25 | 37.7 ± 0.3 |
| 24 | 0.50 | 0.90 | 0.55 | 0.25 | 33.8 ± 0.2 |
| 25 | 0.50 | 0.55 | 0.55 | 0.15 | 33.9 ± 0.1 |
| 26 | 0.50 | 0.55 | 0.55 | 0.15 | 36.4 ± 0.2 |
| 27 | 0.50 | 0.55 | 0.55 | 0.15 | 35.2 ± 0.2 |
| 28 | 0.50 | 0.55 | 0.55 | 0.15 | 35.4 ± 0.3 |
| 29 | 0.50 | 0.55 | 0.55 | 0.15 | 34.9 ± 0.1 |
| Kolmogorov–Smirnov | Shapiro–Wilk | |||||
|---|---|---|---|---|---|---|
| Statistic | Degree of Freedom | p | Statistic | Degree of Freedom | p | |
| black soil with soil-engaging accumulation angle | 0.086 | 29 | 0.200 | 0.969 | 29 | 0.535 |
| Source of Variance | Sum of Squares | Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Model | 197.53 | 14 | 14.11 | 12.03 | <0.0001 |
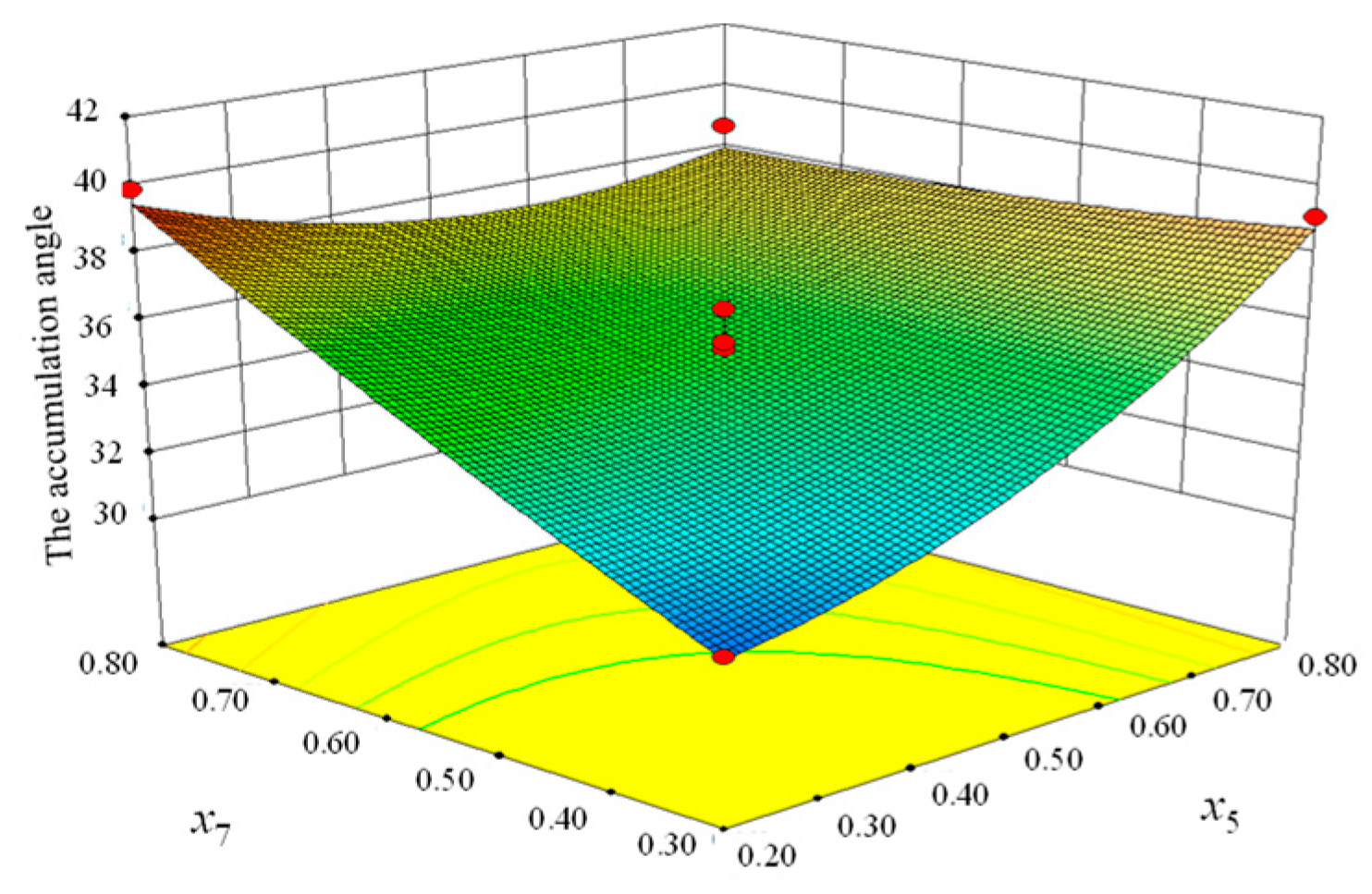
| x5 | 31.36 | 1 | 31.36 | 26.74 | 0.0001 |
| x6 | 18.25 | 1 | 18.25 | 15.56 | 0.0015 |
| x7 | 46.81 | 1 | 46.81 | 39.9 | <0.0001 |
| x8 | 13.87 | 1 | 13.87 | 11.82 | 0.004 |
| x5 x6 | 3.8 | 1 | 3.8 | 3.24 | 0.0934 |
| x5 x7 | 22.09 | 1 | 22.09 | 18.83 | 0.0007 |
| x5 x8 | 12.6 | 1 | 12.6 | 10.74 | 0.0055 |
| x6 x7 | 2.1 | 1 | 2.1 | 1.79 | 0.202 |
| x6 x8 | 1.44 | 1 | 1.44 | 1.23 | 0.2866 |
| x7 x8 | 4 | 1 | 4 | 3.41 | 0.0861 |
| 11.95 | 1 | 11.95 | 10.19 | 0.0065 | |
| 0.52 | 1 | 0.52 | 0.44 | 0.5173 | |
| 0.39 | 1 | 0.39 | 0.33 | 0.5737 | |
| 20.55 | 1 | 20.55 | 17.52 | 0.0009 | |
| Lack-of-Fit Term | 13.17 | 10 | 1.32 | 1.68 | 0.3392 |
| Pure error | 3.25 | 4 | 0.81 | ||
| Sum | 213.95 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, B.; Guo, S.; Gao, Y.; Ye, M.; Xie, C.; Zhang, A.; Wu, Y.; Feng, X. Segmental Calibration of Soil–Tool Contact Models for Sustainable Tillage Using Discrete Element Method. Sustainability 2025, 17, 8126. https://doi.org/10.3390/su17188126
Qi B, Guo S, Gao Y, Ye M, Xie C, Zhang A, Wu Y, Feng X. Segmental Calibration of Soil–Tool Contact Models for Sustainable Tillage Using Discrete Element Method. Sustainability. 2025; 17(18):8126. https://doi.org/10.3390/su17188126
Chicago/Turabian StyleQi, Bendi, Shunchang Guo, Yunpeng Gao, Mingming Ye, Chenggong Xie, Aitong Zhang, Yuhan Wu, and Xin Feng. 2025. "Segmental Calibration of Soil–Tool Contact Models for Sustainable Tillage Using Discrete Element Method" Sustainability 17, no. 18: 8126. https://doi.org/10.3390/su17188126
APA StyleQi, B., Guo, S., Gao, Y., Ye, M., Xie, C., Zhang, A., Wu, Y., & Feng, X. (2025). Segmental Calibration of Soil–Tool Contact Models for Sustainable Tillage Using Discrete Element Method. Sustainability, 17(18), 8126. https://doi.org/10.3390/su17188126







