Genetic Algorithm Based Band Relevance Selection in Hyperspectral Imaging for Plastic Waste Material Discrimination
Abstract
1. Introduction
- Impact of initialization scheme
- Impact of the classifier type on the resulting band selection
- Optimization approach to increase efficiency with advanced classifiers
- Impact of the width of the band response
- Method for steering band selection towards a more balanced accuracy between multiple classes.
2. Materials and Methods
2.1. Sample Materials
2.2. Hyperspectral Imaging Setup
2.3. Genetic Algorithm Method for Band Selection
2.3.1. Representation of the Solution Domain
2.3.2. Initialization of GA Population
2.3.3. Selection of Individuals According to Fitness Function
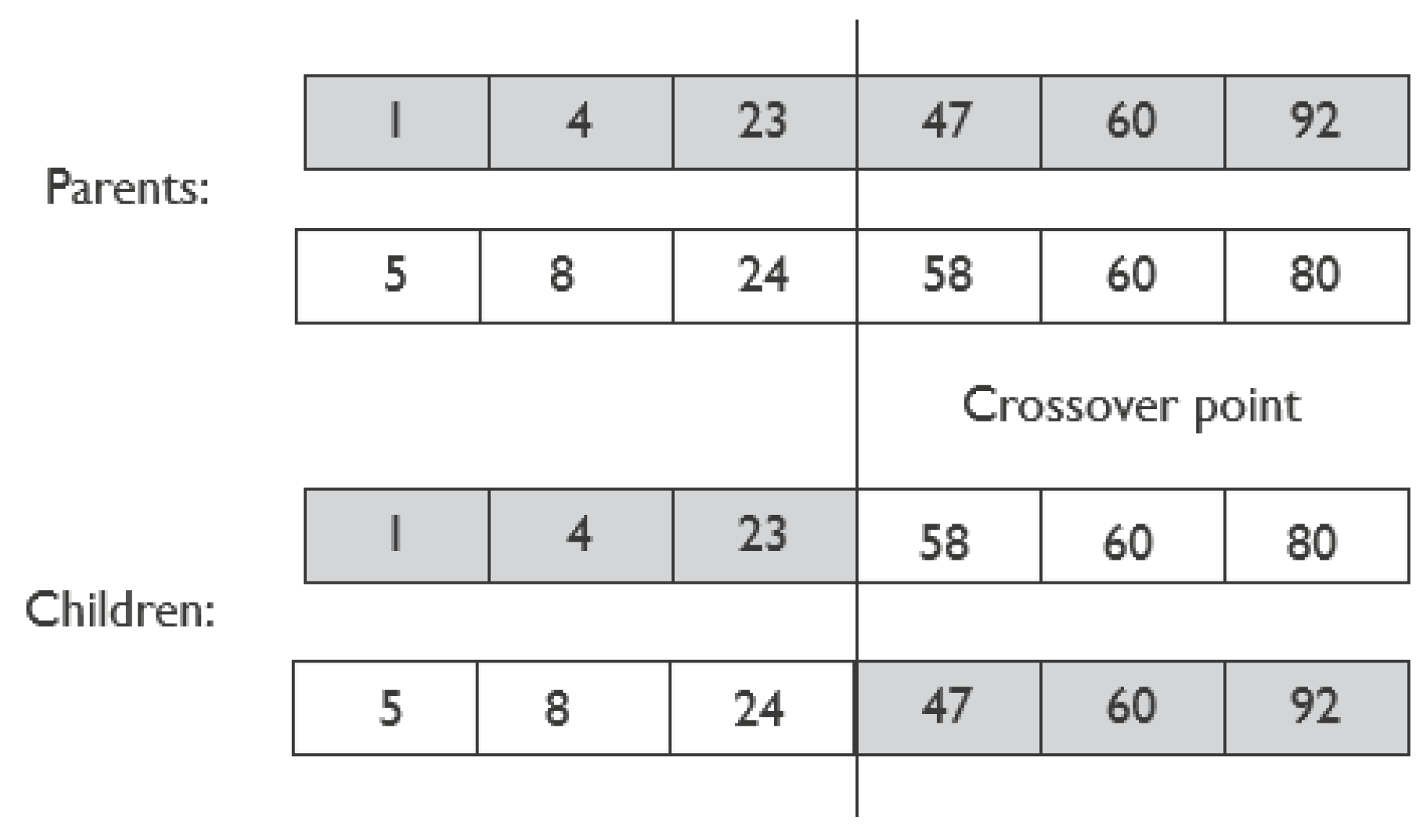
2.3.4. Evolution: Crossover and Mutation
2.3.5. Parameter Selection for Genetic Algorithm
2.3.6. Fitness Function Modification for Multiclass Cases
- Default scheme:The fitness function computation is the mean classification accuracy for all material classes.
- Penalization scheme:This approach introduces a second term in the fitness computation to penalize the potential lack of equity in class accuracy caused by band selection. The first term in Equation (3) corresponds to the mean pixel accuracy per class (identical to Equation (2)), while the second term is the difference between the highest and lowest class classification accuracies, which is subtracted from the mean class accuracy. Both terms are divided by the total number of classes, N. Therefore, for any band subset , the fitness is computed as:
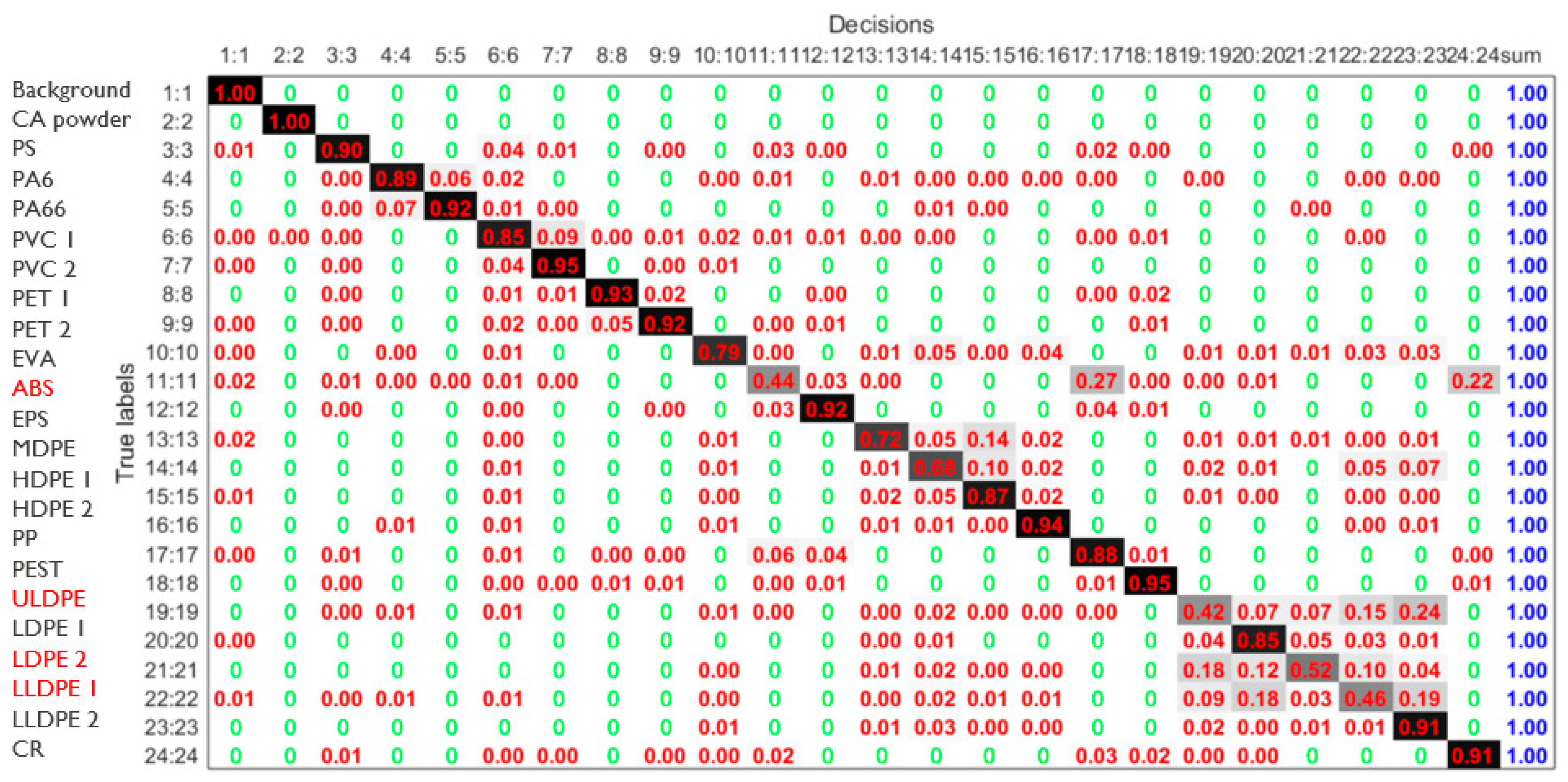
- Weight-based/prioritization scheme:Analysis shows that materials ABS, MDPE, ULDPE, LLDPE1, and LDPE2 (classes 11, 13, 19, 21, and 22) are the hardest to classify. About half of all materials reach high accuracy (>80%), but these five often fall below 50% when fewer bands are used. To improve performance, the fitness function assigns a weight of 1 to these challenging classes and 1/10 to others. The mean classification accuracy is then computed using Equation (4) by weighting the accuracy of all class materials by their corresponding class weight, W(k).
- Subset-based fitness computation 1:The band selection fitness is calculated using the classification accuracy for challenging materials ABS, MDPE, ULDPE, LLDPE1, and LDPE2 (classes 11, 13, 19, 21, and 22), as shown in Equation (5). This approach prioritizes accurate identification of these materials, while the classifier is still trained on all material classes.
- Subset-based fitness computation 2:The band subset fitness is computed as the classification accuracy of the challenging materials, as given by Equation (5). The difference is that in this approach, the classifier model is only trained for these challenging classes.
2.3.7. Simulation of Broader Band Responses
2.3.8. Benchmarking with Respect to State-of-the-Art Successive Projection Algorithm
3. Results and Discussion
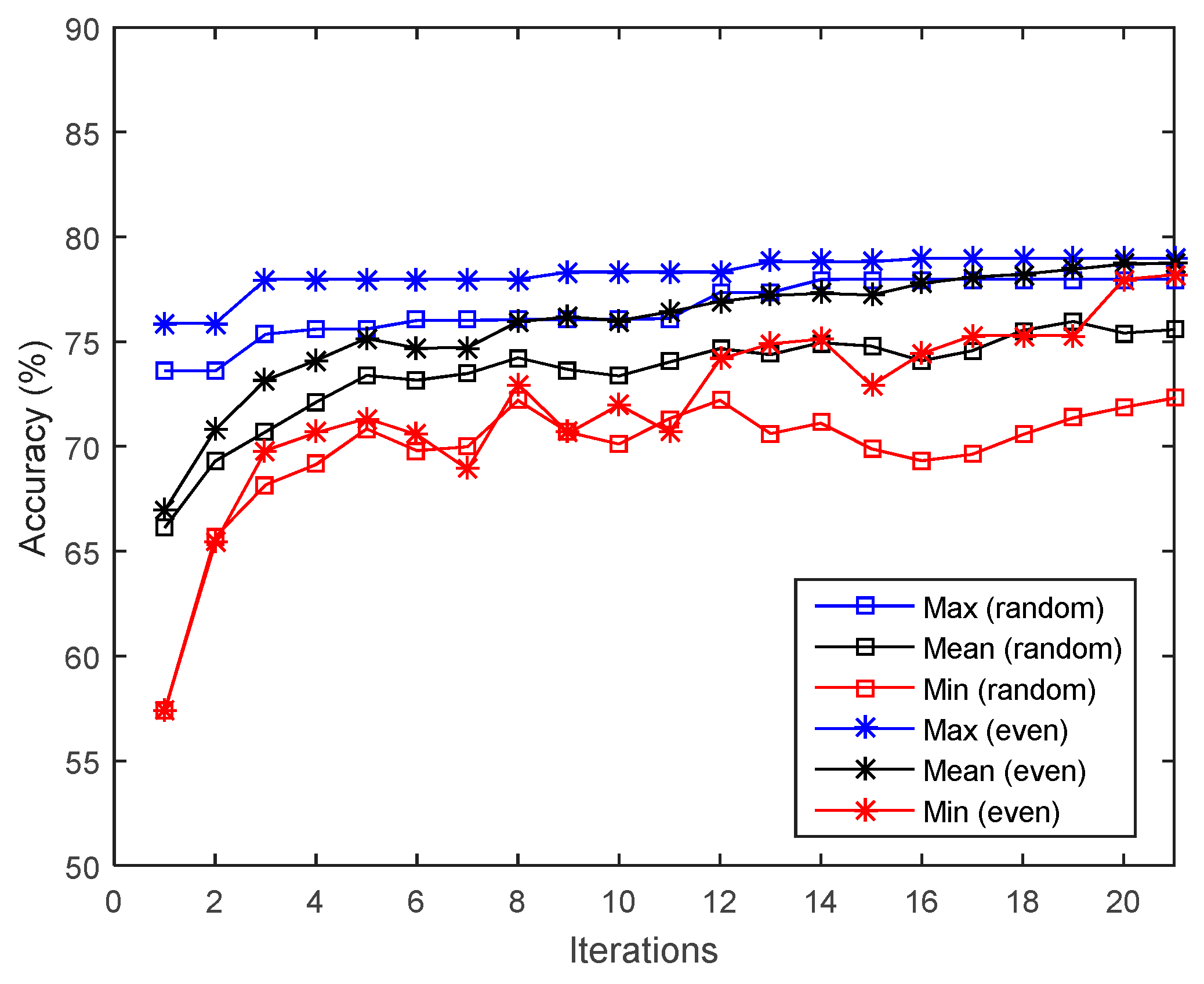
3.1. Impact of Initialization with Even Distribution
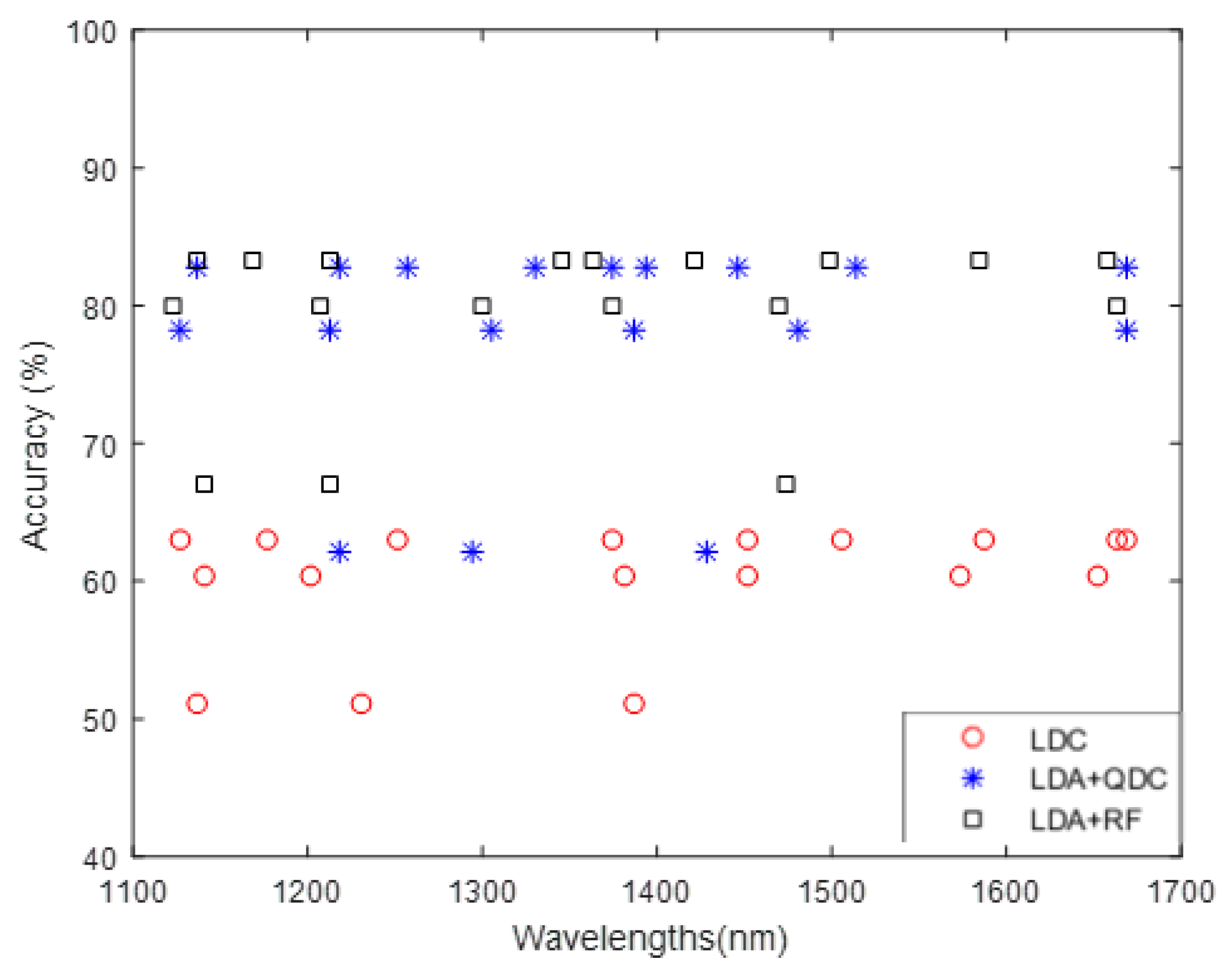
3.2. Impact of Classifier Method on Band Selection
- Band subsets generated by a particular classifier (LDC, QDC, or RF) tended to perform best when evaluated using the same classifier, as reflected by the highest classification accuracy (shown in bold).
- Band subsets selected using a quadratic classifier (QDC) yield higher accuracy for RF models than those selected by a linear discriminant classifier (LDC), likely because QDC better captures the non-linearity of RF. In some cases, QDC-selected bands even outperform or match the performance of band subsets generated specifically for RF.
3.3. Impact of Neighboring Band Selection
3.4. Impact of Width of Band Responses
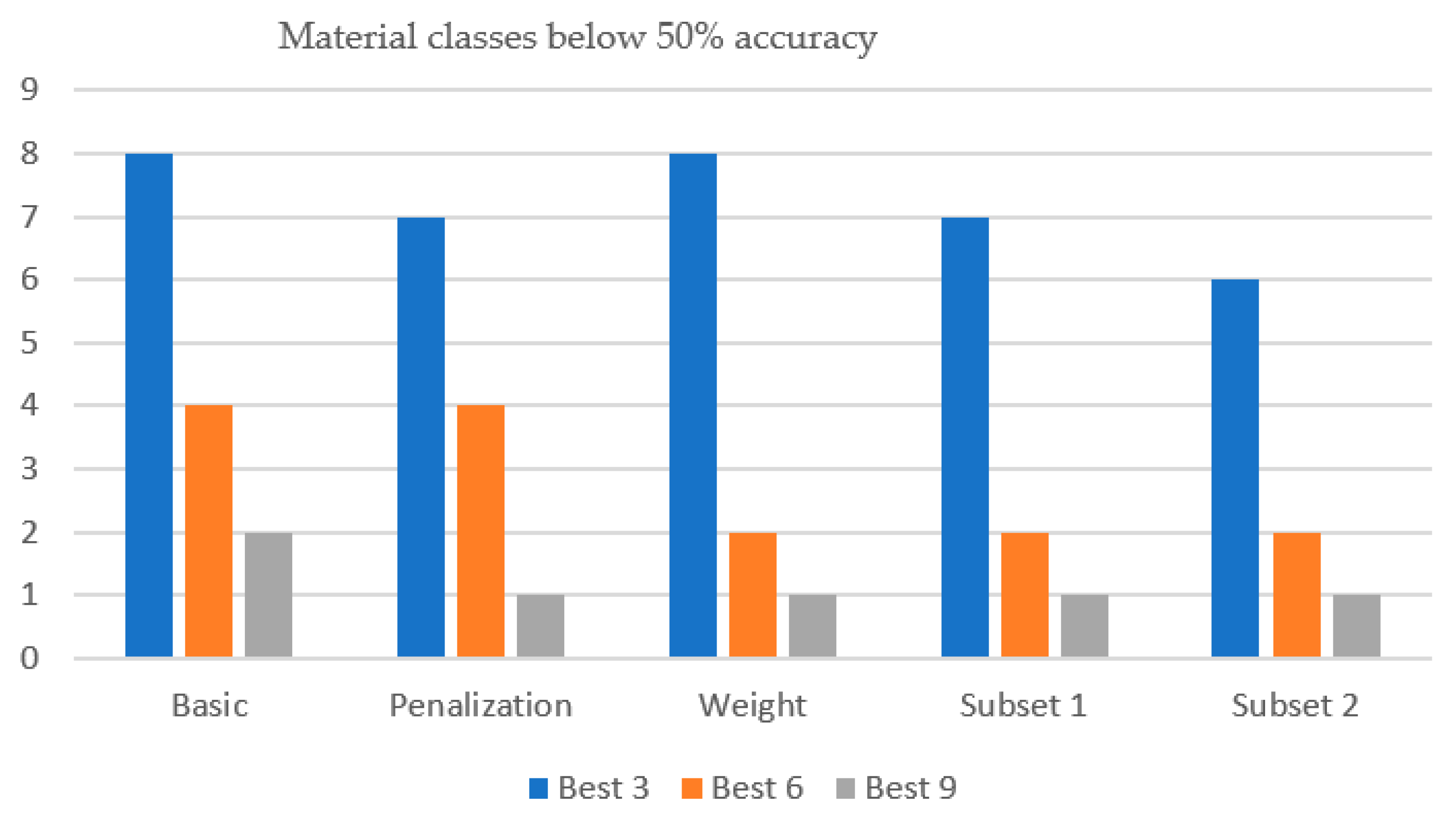
3.5. Impact of Prioritization Scheme to Steer Band Selection Towards More Balanced Multiclass Discrimination
3.6. Benchmarking with Successive Projection Algorithm (SPA)
4. Conclusions and Outlook
- The proposed algorithm consistently outperforms the state-of-the-art benchmarked SPA algorithm, finding a subset between 6 and 9 bands with a classification accuracy above 80% for a set of 22 microplastic materials.
- The proposed initialization scheme with an even band distribution improves the convergence of genetic algorithms for band selection.
- Optimal band selection varies per classifier, with quadratic classifiers yielding better band selection results across different classifier models.
- Combining classifiers across algorithm phases can achieve better quality and efficiency trade-offs than a single advanced classifier.
- Replacing the optimal band subset with bands more than 10 nm away consistently reduces the classification accuracy, especially for subsets of only three or four bands.
- Similar band selection results were obtained from narrow or broader (up to 25 nm) band assumptions, although selections from narrower sets translated more easily to broader ranges.
- Our modified fitness computation scheme ensures a more balanced accuracy across material classes, thereby increasing the applicability of the algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HSI | Hypers-Spectral Imaging |
| GA | Genetic Algorithm |
| LDA | Linear Discriminant Analysis |
| LDC | Linear Discriminant Classifier |
| QDC | Quadratic Discriminant Classifier |
| RF | Random Forest |
| SWIR | Short Wavelength Infra-Red |
| SPA | Successive Projection Algorithm |
References
- Sustainable Production and Consumption. 2020. Available online: https://ec.europa.eu/jrc/en/research-topic/sustainable-production-and-consumption (accessed on 1 July 2024).
- The World’s Plastic Pollution Crisis, Explained. Available online: https://www.nationalgeographic.com/environment/article/plastic-pollution (accessed on 1 July 2024).
- Tomaselli, D. Automated Recycling System Using Computer Vision. ECE-498 Capstone Des. Proj. Advis. Prof. Cotter 2019. [Google Scholar]
- Wang, Z.; Li, H.; Yang, X. Vision-based robotic system for on-site construction and demolition waste sorting and recycling. J. Build. Eng. 2020, 32, 101769. [Google Scholar] [CrossRef]
- Thornton Hampton, L.M.; Bouwmeester, H.; Brander, S.M.; Coffin, S.; Cole, M.; Hermabessiere, L.; Mehinto, A.C.; Miller, E.; Rochman, C.M.; Weisberg, S.B. Research recommendations to better understand the potential health impacts of microplastics to humans and aquatic ecosystems. Microplast. Nanoplast. 2022, 2, 18. [Google Scholar] [CrossRef]
- Mapping Exposure-Induced Immune Effects: Connecting the Exposome and the Immunome|EXIMIOUS Project|Fact Sheet|H2020|CORDIS|European Commission. Available online: https://cordis.europa.eu/project/id/874707 (accessed on 7 July 2024).
- Tirkey, A.; Sheo, L.; Upadhyay, B. Microplastics: An overview on separation, identification and characterization of microplastics. Mar. Pollut. Bull. 2021, 170, 112604. [Google Scholar] [CrossRef]
- Eduard, W.; Weinbruch, S.; Skogstad, A.; Skare, Ø.; Nordby, K.C.; Notø, H. Content of clinker and other materials in personal thoracic aerosol samples from cement plants estimated by scanning electron microscopy and energy-dispersive X-ray microanalysis. Ann. Work. Expo. Health 2023, 67, 990–1003. [Google Scholar] [CrossRef]
- Primpke, S.; Christiansen, S.H.; Cowger, W.; De Frond, H.; Deshpande, A.; Fischer, M.; Holland, E.B.; Meyns, M.; O’Donnell, B.A.; Ossmann, B.E.; et al. Critical Assessment of Analytical Methods for the Harmonized and Cost-Efficient Analysis of Microplastics. Appl. Spectrosc. 2020, 74, 1012–1047. [Google Scholar] [CrossRef]
- Sim, W.; Song, S.W.; Park, S.; Jang, J.I.; Kim, J.H.; Cho, Y.M.; Kim, H.M. Unveiling microplastics with hyperspectral Raman imaging: From macroscale observations to real-world applications. J. Hazard. Mater. 2024, 463, 132861. [Google Scholar] [CrossRef]
- Meyers, N.; Catarino, A.I.; Declercq, A.M.; Brenan, A.; Devriese, L.; Vandegehuchte, M.; De Witte, B.; Janssen, C.; Everaert, G. Microplastic detection and identification by Nile red staining: Towards a semi-automated, cost-and time-effective technique. Sci. Total Environ. 2022, 823, 153441. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; ElMasry, G.; Sun, D.W.; Allen, P. Non-destructive prediction and visualization of chemical composition in lamb meat using NIR hyperspectral imaging and multivariate regression. Innov. Food Sci. Emerg. Technol. 2012, 16, 218–226. [Google Scholar] [CrossRef]
- Gonzalez, P.; Pichette, J.; Vereecke, B.; Masschelein, B.; Krasovitski, L.; Bikov, L.; Lambrechts, A. An extremely compact and high-speed line-scan hyperspectral imager covering the SWIR range. In Image Sensing Technologies: Materials, Devices, Systems, and Applications V; SPIE: Bellingham, WA, USA, 2018; Volume 10656, p. 106560L. [Google Scholar] [CrossRef]
- Blanch-Perez-del-Notario, C.; Luthman, S.; Lefrant, R.; Gonzalez, P.; Lambrechts, A. Compact high-speed snapshot hyperspectral imager in the SWIR range (1.1–1.65 nm) and its potential in sorting/recycling industry. In Algorithms, Technologies, and Applications for Multispectral and Hyperspectral Imaging XXVIII; SPIE: Bellingham, WA, USA, 2022; Volume 12094, pp. 47–55. [Google Scholar]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern trends in hyperspectral image analysis: A review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Serranti, S.; Fiore, L.; Bonifazi, G.; Takeshima, A.; Takeuchi, H.; Kashiwada, S. Microplastics characterization by hyperspectral imaging in the SWIR range. SPIE Future Sens. Technol. 2019, 11197, 134–140. [Google Scholar]
- Faltynkova, A.; Wagner, M. Developing and testing a workflow to identify microplastics using near infrared hyperspectral imaging. Chemosphere 2023, 336, 139186. [Google Scholar] [CrossRef]
- Faltynkova, A.; Johnsen, G.; Wagner, M. Hyperspectral imaging as an emerging tool to analyze microplastics: A systematic review and recommendations for future development. Microplast. Nanoplast. 2021, 1, 13. [Google Scholar] [CrossRef]
- Alboody, A.; Vandenbroucke, N.; Porebski, A.; Sawan, R.; Viudes, F.; Doyen, P.; Amara, R. A New Remote Hyperspectral Imaging System Embedded on an Unmanned Aquatic Drone for the Detection and Identification of Floating Plastic Litter Using Machine Learning. Remote Sens. 2023, 15, 3455. [Google Scholar] [CrossRef]
- Tamin, O.; Moung, E.G.; Dargham, J.A.; Yahya, F.; Omatu, S. A review of hyperspectral imaging-based plastic waste detection state-of-the-arts. Int. J. Electr. Comput. Eng. 2023, 13, 3407–3419. [Google Scholar] [CrossRef]
- Rogers, M.; Blanc-Talon, J.; Urschler, M.; Delmas, P. Wavelength and texture feature selection for hyperspectral imaging: A systematic literature review. Food Meas. 2023, 17, 6039–6064. [Google Scholar] [CrossRef]
- Mahieu, B.; Qannari, E.M.; Jaillais, B. Extension and significance testing of Variable Importance in Projection (VIP) indices in Partial Least Squares regression and Principal Components Analysis. Chemom. Intell. Lab. Syst. 2023, 242, 104986. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Robin Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Araújo, M.C.U.; Saldanha, T.C.B.; Galvão, R.K.H.; Yoneyama, T.; Chame, H.C.; Visani, V. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis. Chemom. Intell. Lab. Syst. 2001, 57, 65–73. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Saqui, D.; Saito, J.H.; Jorge, L.A.D.C.; Ferreira, E.J.; Lima, D.C.; Herrera, J.P. Methodology for Band Selection of Hyperspectral Images Using Genetic Algorithms and Gaussian Maximum Likelihood Classifier. In Proceedings of the 2016 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2016; pp. 733–738. [Google Scholar] [CrossRef]
- Nagasubramanian, K.; Jones, S.; Sarkar, S.; Singh, A.K.; Singh, A.; Ganapathysubramanian, B. Hyperspectral band selection using genetic algorithm and support vector machines for early identification of charcoal rot disease in soybean stems. Plant Methods 2018, 14, 86. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Bruzzone, L.; Guan, R.; Zhou, F.; Yang, C. Spectral-Spatial Genetic Algorithm-Based Unsupervised Band Selection for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9616–9632. [Google Scholar] [CrossRef]
- Tschannerl, J.; Ren, J.; Zabalza, J.; Marshall, S. Segmented Autoencoders for Unsupervised Embedded Hyperspectral Band Selection. In Proceedings of the 2018 7th European Workshop on Visual Information Processing (EUVIP), Tampere, Finland, 26–28 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Moharram, M.A.; Sundaram, D.M. Adaptive feature selection for hyperspectral image classification based on Improved Unsupervised Mayfly Optimization Algorithm. Earth Sci. Inform. 2024, 17, 4145–4159. [Google Scholar] [CrossRef]
- Ayna, C.O.; Mdrafi, R.; Du, Q.; Gurbuz, A.C. Learning-Based Optimization of Hyperspectral Band Selection for Classification. Remote Sens. 2023, 15, 4460. [Google Scholar] [CrossRef]
- Feng, J.; Gao, Q.; Shang, R.; Cao, X.; Bai, G.; Zhang, X.; Jiao, L. Multi-agent deep reinforcement learning for hyperspectral band selection with hybrid teacher guide. Knowl.-Based Syst. 2024, 299, 112044. [Google Scholar] [CrossRef]
- Rahman, M.; Teng, S.W.; Murshed, M.; Paul, M.; Brennan, D. BSDR: A Data-Efficient Deep Learning-Based Hyperspectral Band Selection Algorithm Using Discrete Relaxation. Sensors 2024, 24, 7771. [Google Scholar] [CrossRef]
- Mou, L.; Saha, S.; Hua, Y.; Bovolo, F.; Bruzzone, L.; Zhu, X.X. Deep reinforcement learning for band selection in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Blanch-Perez-del-Notario, C.; Azari, A.; Jayapala, M.; Lambrechts, A. Microplastic discrimination with hyperspectral imaging. In Proceedings of the 14th IEEE GRSS Workshop on Hyperspectral Image and Signal Processing, (WHISPERS), Helsinki, Finland, 9–11 December 2024; pp. 1–5. [Google Scholar] [CrossRef]
- MS-200-SHORT-RV|SEIWA Optical. Available online: https://www.seiwaamerica.com/product/camera-tube/ms-200-twl/ms-200-short-rv (accessed on 21 August 2025).
- Matlab. The Mathworks, Natick. 2019. Available online: https://mathworks.com (accessed on 20 June 2020).
- PerClass BV 2008–2022, Delft, NL. Available online: http://perclass.com/perclass-toolbox/product (accessed on 15 January 2018).
- Naes, T.; Isaksson, T.; Fearn, T.; Davies, T. A User-Friendly Guide to Multivariate Calibration and Classification; NIR Publications: Chichester, UK, 2004. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice-Hall: Eaglewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Holland, J. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Blanch-Perez-del-Notario, C.; Baert, R.; D’Hondt, M. Multi-objective genetic algorithm for task assignment on heterogeneous nodes. Int. J. Digit. Multimed. Broadcast. 2012, 2012, 716780. [Google Scholar]
- Camelo, M.; Donoso, Y.; Castro, H. MAGS—An approach using multi-objective evolutionary algorithms for grid task scheduling. Int. J. Appl. Math. Inform. 2011, 5, 117–126. [Google Scholar]
- Iosifidis, Y.; Mallik, A.; Mamagkakis, S.; De Greef, E.; Bartzas, A.; Soudris, D.; Catthoor, F. A framework for automatic parallelization, static and dynamic memory optimization in MPSoC platforms. In Proceedings of the 47th Design Automation Conference, (DAC ’10), Anaheim, CA, USA, 13–18 June 2010; pp. 549–554. [Google Scholar]
- Zomaya, A.Y.; Ward, C.; Macey, B. Genetic scheduling for parallel processor systems: Comparative studies and performance issues. IEEE Trans. Parallel Distrib. Syst. 1999, 10, 795–812. [Google Scholar] [CrossRef]
- Han, M. Successive Projections Algorithm (SPA) for Variable Selection. 2024. Available online: https://mingqianghan.github.io/posts/2024/10/variable-selection-spa%20/ (accessed on 9 July 2025).
- Tasseron, P.; Van Emmerik, T.; Peller, J.; Schreyers, L.; Biermann, L. Advancing floating macroplastic detection from space using experimental hyperspectral imagery. Remote Sens. 2021, 13, 2335. [Google Scholar] [CrossRef]
- Chen, W.; Zhi, X.; Hu, J.; Yu, L.; Han, Q.; Zhang, W. Genetic Algorithm-Based Weighted Constraint Target Band Selection for Hyperspectral Target Detection. Remote Sens. 2025, 17, 673. [Google Scholar]



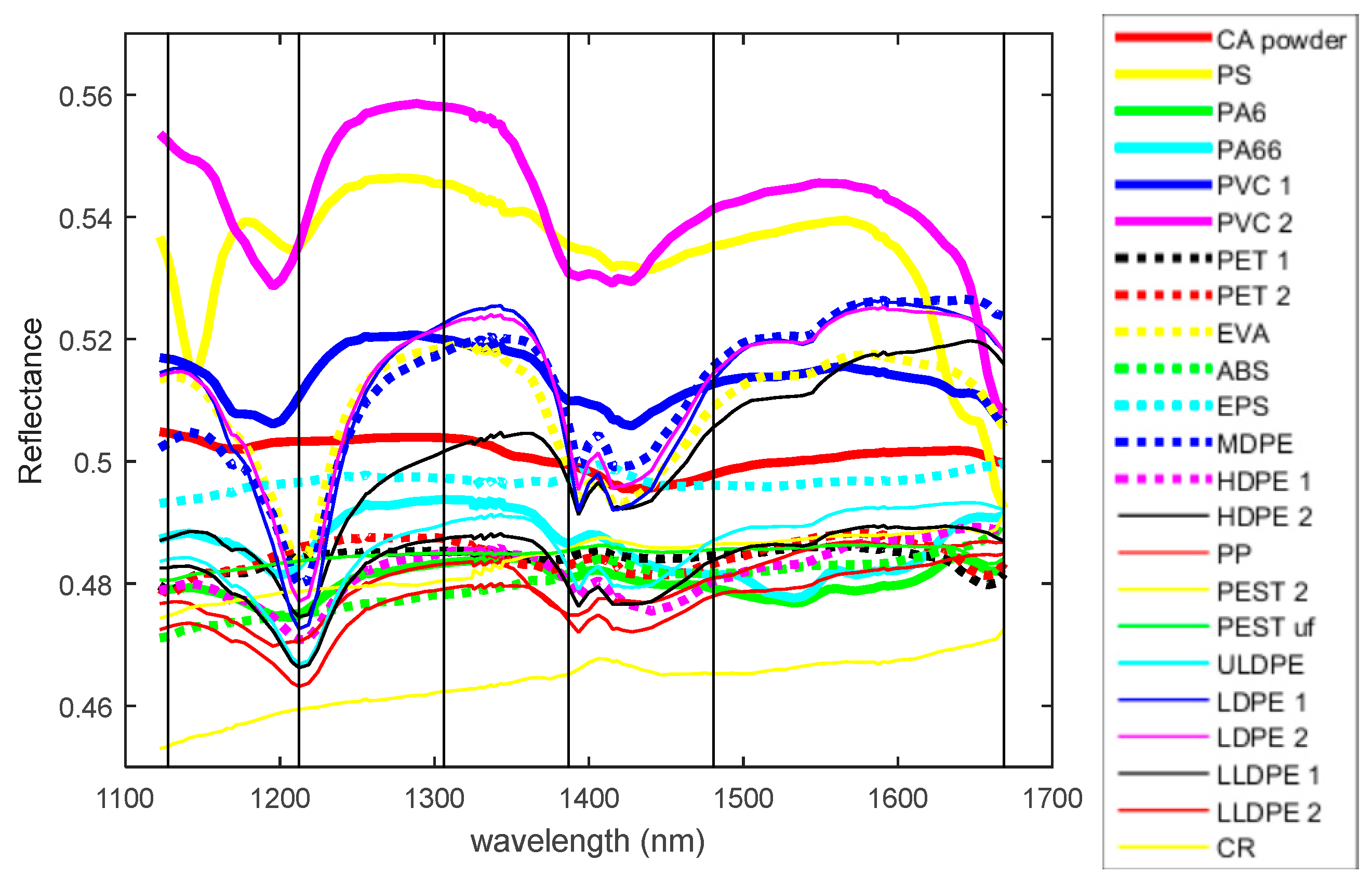
| Sample | Material | Form | Sample | Material | Form |
|---|---|---|---|---|---|
| ULDPE | Ultra low-density polyethylene | Pellet | EVA | 20% Ethylene-vinyl acetate | Pellet |
| LDPE.1, LDPE.2 | Low-density polyethylene | Pellet | ABS | Acrylonitrile-Butadiene-Styrene | Pellet |
| PP | Polypropylene | Pellet | EPS | Expanded polystyrene foam | Beads |
| LLDPE.1 | Linear low-density polyethylene | Pellet | PS | Polystyrene | Pellet |
| LLDPE.2 | Linear low-density polyethylene made with metallocene catalyst | Pellet | PA6 | Nylon 6 | Pellet |
| MDPE | Medium-density polyethylene | Pellet | PA66b | Nylon 6.6 | Pellet |
| HDPE.1, HDPE.2 | High-density polyethylene | Pellet | PVC.1 | Polyvinyl chloride | Pellet |
| PEST | Polyester | Fabric | PVC.2 | Polyvinyl chloride with phthalates | Pellet (flex) |
| PET.1 | Polyethylene terephthalate | Pellet | CR | Crumb rubber from used tires | Particles |
| PET.2 | Recycled polyethylene terephthalate | Pellet | CA | Cellulose acetate | Powder |
| Crossover rate | 0.8 |
| Mutation rate | 0.6 |
| Population size | 10/20 |
| Max generations | 15–20 |
| To 5 nm Set F’ (101 Bands) | To 15 nm Set F’ (33 Bands) | To 25 nm Set F’ (20 Bands) | |
|---|---|---|---|
| From 5 nm set F | F’= F | F’ = F/3 | F’ = F/5 |
| From 15 nm set F | F’ = 3 * F | F’ = F | F’ = ((3 * F) − 1)/5 |
| From 25 nm set F | F’ = (5 * F) − 2 | F’ = ((5 * F) − 2)/3 | F’ = F |
| Pop 10 | Random init. | Distributed init. |
|---|---|---|
| Best three bands | 61.5% | 62.3% |
| Best six bands | 78.1% | 78.2% |
| Best nine bands | 81.4% | 82.9% |
| Pop 20 | Random init. | Distributed init. |
| Best three bands | 61.6% | 61.6% |
| Best six bands | 76.1% | 78.3% |
| Best nine bands | 82.4% | 83.5% |
| Best Bands | LDC Model | LDA + QDC Model | LDA + RF Model | |
|---|---|---|---|---|
| Best three bands | LDC generated | 51.0% | 59.2% | 63.7% |
| LDA + QDC generated | 47.4% | 62.1% | 64.1% | |
| LDA + RF generated | 49.5% | 60.5% | 66.3% | |
| Best four bands | LDC generated | 55.8% | 66.8% | 68.3% |
| LDA + QDC generated | 54.7% | 69.5% | 73.9% | |
| LDA + RF generated | 54.9% | 68.0% | 71.9% | |
| Best six bands | LDC generated | 60.4% | 76.7% | 80.5% |
| LDA + QDC generated | 59.4% | 78.2% | 81.1% | |
| LDA + RF generated | 58.5% | 76.8% | 80.0% | |
| Best nine bands | LDC generated | 62.9% | 81.0% | 78.9% |
| LDA + QDC generated | 62.0% | 82.8% | 83.1% | |
| LDA + RF generated | 60.4% | 82.3% | 83.2% | |
| Best 16 bands | LDC generated | 66.3% | 84.8% | 78.7% |
| LDA + QDC generated | 62.7% | 87.6% | 83.3% | |
| LDA + RF generated | 64.1% | 85.2% | 84.2% | |
| LDC (15it) | LDA + QDC (15it) | LDA + RF (15 it) | LDA + QDC (10it + 5it) | LDA + RF (10it + 5it) | |
|---|---|---|---|---|---|
| Best three bands | 51.0% | 62.1% | 66.3% | 60.6% | 68.2% |
| Best four bands | 55.8% | 68.2% | 74.3% | 69.5% | 76.2% |
| Best six bands | 60.4% | 78.2% | 80.0% | 76.2% | 81.5% |
| Best nine bands | 62.9% | 82.8% | 83.2% | 81.7% | 82.4% |
| Best 16 bands | 66.3% | 87.6% | 84.2% | 87.0% | 82.4% |
| Variation over Mean Pixel Accuracy (%) for LDA+QDC Classifier | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| B | B + 1 | B − 1 | B + 2 | B − 2 | B + 3 | B − 3 | B + 4 | B − 4 | |
| Best three bands | 62.1% | +0.26 | −1.52 | −0.92 | −3.08 | −2.66 | −5.36 | −4.59 | −7.43 |
| Best four bands | 68.2% | +0.17 | +0.23 | −1.48 | −0.44 | −3.83 | −2.69 | −5.94 | −5.12 |
| Best six bands | 78.2% | −0.93 | −1.32 | −2.11 | −1.86 | −3.33 | −2.42 | −5.42 | −3.13 |
| Best nine bands | 82.8% | +0.45 | −0.72 | −1.19 | −1.60 | −1.94 | −2.44 | −1.81 | −3.32 |
| Best 16 bands | 87.6% | +0.33 | −0.57 | −1.05 | −0.74 | −0.85 | −0.52 | −1.86 | −1.43 |
| Accuracy on 5 nm Width | Accuracy on 15 nm Width | Accuracy on 25 nm Width | ||
|---|---|---|---|---|
| Best three bands | Selection from width = 5 nm | 61.6% | 64.3% | 65.7% |
| Selection from width = 15 nm | 60.9% | 64.3% | 65.7% | |
| Selection from width = 25 nm | 61.9% | 63.8% | 65.7% | |
| Best six bands | Selection from width = 5 nm | 78.9% | 80.5% | 81.5% |
| Selection from width = 15 nm | 76.6% | 80.0% | 82.4% | |
| Selection from width = 25 nm | 76.0% | 79.4% | 81.8% | |
| Best nine bands | Selection from width = 5 nm | 83.5% | 86.4% | 88.0% |
| Selection from width = 15 nm | 82.3% | 86.3% | 88.2% | |
| Selection from width = 25 nm | 82.8% | 86.4% | 88.8% | |
| Original Bands | Best Three Bands | Best Six Bands | Best Nine Bands |
|---|---|---|---|
| 101 bands of 5 nm | 19-32-56 | 3-19-33-50-76-99 | 3-10-14-19-32-50-61-82-98 |
| 33 bands of 15 nm | 7-11-19 | 5-7-11-19-25-33 | 2-4-7-13-17-21-23-28-33 |
| 20 bands of 25 nm | 4-7-12 | 3-4-7-11-14-20 | 1-3-4-5-8-12-13-17-20 |
| Basic | Penalization | Weight | Subset 1 | Subset 2 | ||
|---|---|---|---|---|---|---|
| Best nine bands | Mean accuracy | 83.3/45.5% | 83.0/45.3% | 82.5/46.1% | 82.4/39.5% | 81.8/44.2% |
| Worst-4 accur | 50.0% | 50.3% | 53.4% | 51.0% | 51.0% | |
| Materials < 50% | (2) abs, uldpe | (1) abs | (1) uldpe | (1) uldpe | (1) uldpe | |
| Best six bands | Mean accuracy | 78.4/34.0% | 78.6/37.2% | 77.2/34.2% | 76.8/34.2% | 76.1/28.8% |
| Worst-4 accur | 39.9% | 41.77% | 47.12% | 47.1% | 43.3% | |
| Materials < 50% | (4) lldpe1, abs, uldpe, ldpe2 | (4) lldpe1, abs, uldpe, ldpe2 | (2) uldpe, abs | (2) uldpe, abs | (2) uldpe, abs | |
| Best three bands | Mean accuracy | 60.8/8.8% | 60.6/8.9% | 60.7/9.3% | 60.4/9.4% | 59.6/12.7% |
| Worst-4 accur | 18.6% | 19.6% | 17.6% | 17.3% | 22.6% | |
| Materials < 50% | (8) | (7) | (8) | (7) | (6) |
| Method | LDC | LDA + QDC | LDA + RF | Band Number | |
|---|---|---|---|---|---|
| Best three bands | SPA | 41.9% | 53.4% | 56.7% | 19-50-101 |
| GA-SPA | 45.0% | 60.1% | 60.3% | 18-32-101 | |
| GA | 47.4% | 62.1% | 64.1% | 19-32-59 | |
| Best four bands | SPA | 48.9% | 66.7% | 67.5% | 19-42-50-101 |
| GA-SPA | 51.1% | 66.7% | 70.0% | 18-32-71-101 | |
| GA | 54.7% | 69.5% | 73.9% | 2-19-72-100 | |
| Best six bands | SPA | 54.0% | 74.7% | 76.8% | 2-19-42-50-97-101 |
| GA-SPA | 52.3% | 71.9% | 72.0% | 18-32-42-71-96-101 | |
| GA | 59.4% | 78.2% | 81.1% | 2-18-34-51-67-101 | |
| Best nine bands | SPA | 60.0% | 81.5% | 79.9% | 2-19-42-50-57-59-85-97-101 |
| GA-SPA | 58.1% | 80.9% | 80.6% | 2-4-18-32-42-59-71-96-101 | |
| GA | 62.0% | 82.8% | 83.1% | 4-19-26-39-49-52-62-72-101 | |
| Best 16 bands | SPA | 62.5% | 86.3% | 80.8% | 2-4-12-14-19-32-40-42-50-57-59-60-85-97-99-101 |
| GA-SPA | 63.2% | 86.6% | 81.8% | 2-4-9-13-15-18-32-42-46-54-59-71-85-96-99-101 | |
| GA | 62.7% | 87.6% | 83.3% | 1-9-15-19-21-32-38-44-50-56-62-68-71-89-95-101 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blanch-Perez-del-Notario, C.; Jayapala, M. Genetic Algorithm Based Band Relevance Selection in Hyperspectral Imaging for Plastic Waste Material Discrimination. Sustainability 2025, 17, 8123. https://doi.org/10.3390/su17188123
Blanch-Perez-del-Notario C, Jayapala M. Genetic Algorithm Based Band Relevance Selection in Hyperspectral Imaging for Plastic Waste Material Discrimination. Sustainability. 2025; 17(18):8123. https://doi.org/10.3390/su17188123
Chicago/Turabian StyleBlanch-Perez-del-Notario, Carolina, and Murali Jayapala. 2025. "Genetic Algorithm Based Band Relevance Selection in Hyperspectral Imaging for Plastic Waste Material Discrimination" Sustainability 17, no. 18: 8123. https://doi.org/10.3390/su17188123
APA StyleBlanch-Perez-del-Notario, C., & Jayapala, M. (2025). Genetic Algorithm Based Band Relevance Selection in Hyperspectral Imaging for Plastic Waste Material Discrimination. Sustainability, 17(18), 8123. https://doi.org/10.3390/su17188123







