Dynamic Facility Location and Allocation Optimization for Sustainable Product-Service Delivery Using Co-Evolutionary Adaptive Genetic Algorithms
Abstract
1. Introduction
2. State-of-the-Art Reviews
2.1. Service Facility Location and Allocation
2.2. Supply Chain Network Design for Sustainable Service Delivery
3. Model Formulation
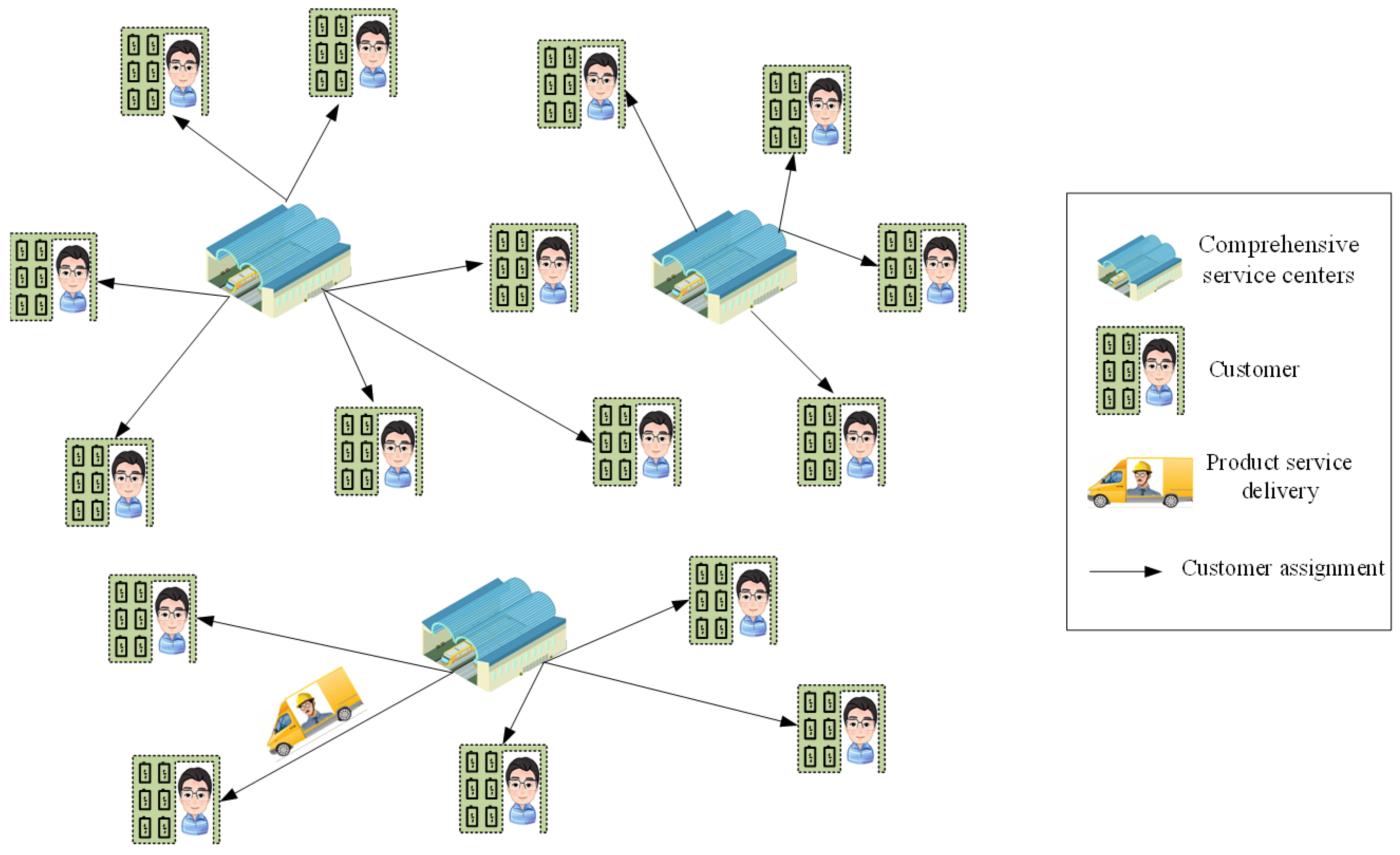
3.1. Problem Description
- A customer is only served by one CSC in a time period [41].
- Once a CSC is opened, it shouldn’t be closed.
- The total number of the CSCs is not predetermined.
3.2. Parameters and Decision Variables
- set of customers.
- set of CSC.
- set of periods.
- distance between customer j and i.
- : added product sales in customer i in the time period compared with period .
- service demand of customer i in the time period .
- index indicating the extent of the product servitization in the time period t, (0,1].
- average profit of a completed servitized product.
- fixed cost for opening a CSC in customer i.
- average annual operation cost of a completed servitized product in customer i.
- : maximum service capacity of CSC.
- maximum allowable distance between customer i and CSC.
- : total number of CSCs in the time period t.
- : 1 if an opened CSC is in customer I at the beginning of period , 0 otherwise.
- 1 if the customer i is assigned to CSC j at the beginning of period , 0 otherwise.
3.3. Objective Functions and Constraints
4. Proposed Algorithm: A Co-Evolutionary-Based Adaptive Multi-Objective Genetic Algorithms
4.1. Chromosome Representation
4.2. Adaptive Strategy
4.2.1. Adaptive Objective Functions
4.2.2. Adaptive Fitness Function
4.2.3. Adaptive Crossover and Mutation Probabilities
4.3. Genetic Operators with Gene Repair
4.3.1. Crossover Operator
4.3.2. Mutation Operator
4.4. Buffer-Based Elite Trans-Generation Migration
4.5. The Procedure of the Proposed Algorithm
- If g x × y, go to Step 3. x is the interval between the migrations. y is a positive integer.
- If g x × y, carry out the elite migration and update the individuals in the buffer. And then, go to Step 3.
5. Case Study
5.1. Problem Statement
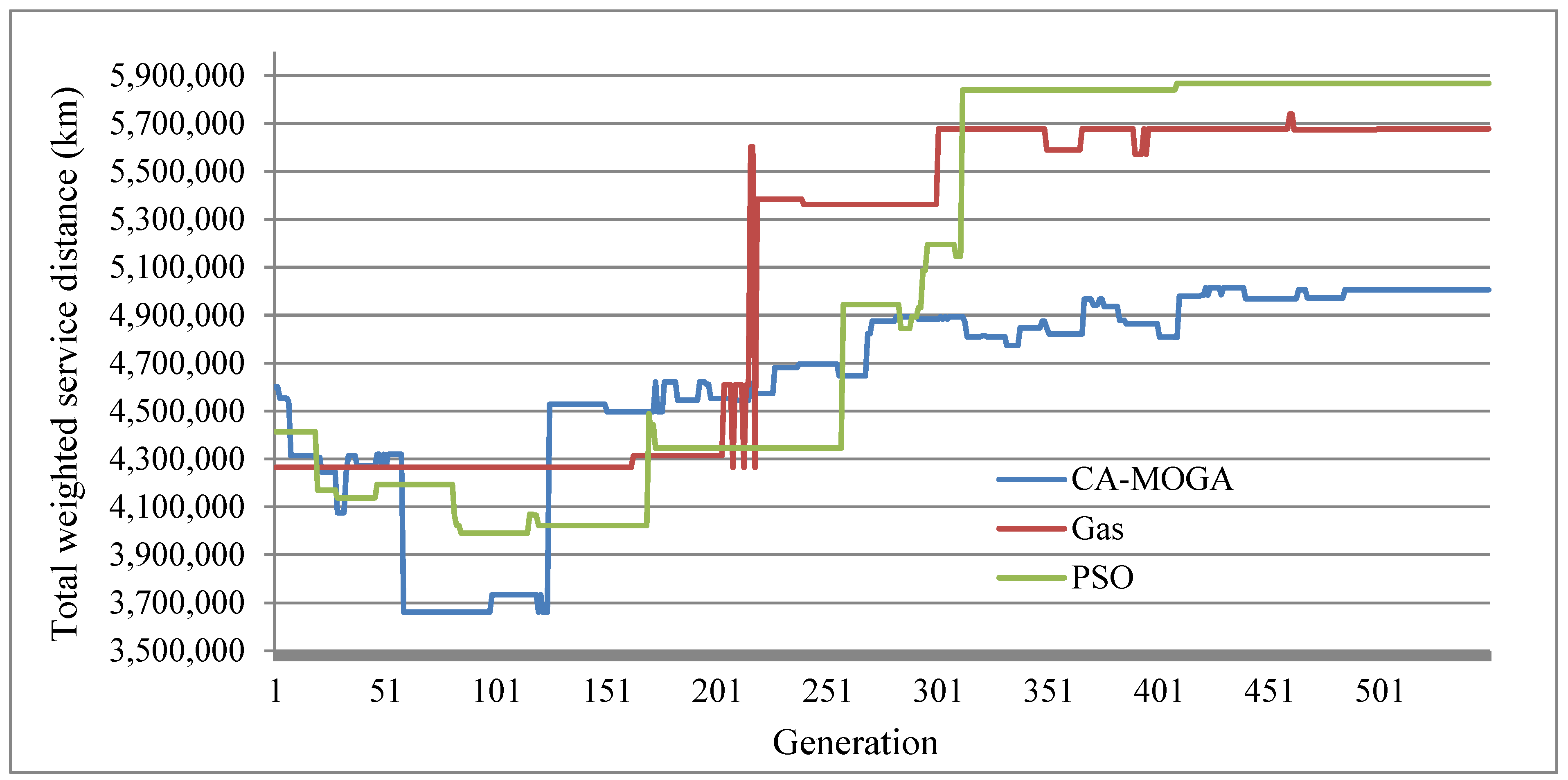
5.2. Computational Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, K.; Lin, K.-Y.; Wang, J.; Ma, Y.; Li, H.; Zhang, L.; Liu, K.; Feng, L. UNISON framework for user requirement elicitation and classification of smart product-service system. Adv. Eng. Inform. 2023, 57, 101996. [Google Scholar] [CrossRef]
- Murata, H.; Kobayashi, H. A Needs-Based Design Method for Product–Service Systems to Enhance Social Sustainability. Sustainability 2025, 17, 3619. [Google Scholar] [CrossRef]
- Yuan, W.; Chang, D.; Han, T. A context-aware smart product-service system development approach and application case. Comput. Ind. Eng. 2023, 183, 109468. [Google Scholar] [CrossRef]
- Canfield Petrecca, A.C.; Vezzoli, C.; Ceschin, F. Personal Data Management in Smart Product-Service Systems: Preliminary Design Strategies to Avoid User Manipulation in Democratic Processes. Sustainability 2024, 16, 10110. [Google Scholar] [CrossRef]
- Giglio, D.; Paolucci, M.; Roshani, A. Integrated lot sizing and energy-efficient job shop scheduling problem in manufacturing/remanufacturing systems. J. Clean. Prod. 2017, 148, 624–641. [Google Scholar] [CrossRef]
- Schroeder, A.; Naik, P.; Ziaee Bigdeli, A.; Baines, T. Digitally enabled advanced services: A socio-technical perspective on the role of the internet of things (IoT). Int. J. Oper. Prod. Manag. 2020, 40, 1243–1268. [Google Scholar] [CrossRef]
- Xu, Z.; Elomri, A.; Zhang, Q.; Liu, C.; Shi, L. Status review and research strategies on product-service supply chain. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2020, 234, 1075–1086. [Google Scholar] [CrossRef]
- Henriques, R.; Figueiredo, F.; Nunes, J. Product-Services for a Resource-Efficient and Circular Economy: An Updated Review. Sustainability 2023, 15, 12077. [Google Scholar] [CrossRef]
- Kohlbeck, E.; Cauchick-Miguel, P.A.; Mendes, G.H.; Zomer, T.T. A Longitudinal History-Based Review of the Product-Service System: Past, Present, and Future. Sustainability 2023, 15, 11922. [Google Scholar] [CrossRef]
- Meier, H.; Roy, R.; Seliger, G. Industrial product-service systems—IPS2. CIRP Ann. 2010, 59, 607–627. [Google Scholar] [CrossRef]
- Chen, C.-W. Guidance on the Conceptual Design of Sustainable Product–Service Systems. Sustainability 2018, 10, 2452. [Google Scholar] [CrossRef]
- Vahedi-Nouri, B.; Rohaninejad, M.; Hanzálek, Z.; Foumani, M. A batch production scheduling problem in a reconfigurable hybrid manufacturing-remanufacturing system. Comput. Ind. Eng. 2025, 204, 111099. [Google Scholar] [CrossRef]
- Pasandideh, S.H.R.; Niaki, S.T.A. Genetic application in a facility location problem with random demand within queuing framework. J. Intell. Manuf. 2012, 23, 651–659. [Google Scholar] [CrossRef]
- Daskin, M. Network and Discrete Location: Models, Algorithms, and Applications, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Seuring, S.; Müller, M. From a literature review to a conceptual framework for sustainable supply chain management. J. Clean. Prod. 2008, 16, 1699–1710. [Google Scholar] [CrossRef]
- Weber, A. Alfred Weber’s Theory of the Location of Industries; The University of Chicago Press: Chicago, IL, USA, 1929. [Google Scholar]
- Turkoglu, D.C.; Genevois, M.E. A comparative survey of service facility location problems. Ann. Oper. Res. 2020, 292, 399–468. [Google Scholar] [CrossRef]
- Zhang, Q.L.; Mao, H.J. An Integrated Method for Locating Logistic Centers in a Rural Area. Sustainability 2022, 14, 5563. [Google Scholar] [CrossRef]
- Ahmadi, Z.; Ghezavati, V. Developing a new model for a competitive facility location problem considering sustainability using Markov chains. J. Clean. Prod. 2020, 273, 16. [Google Scholar] [CrossRef]
- López, C.C.; Crama, Y.; Pironet, T.; Semet, F. Multi-period distribution networks with purchase commitment contracts. Eur. J. Oper. Res. 2024, 312, 556–572. [Google Scholar] [CrossRef]
- Zhang, G.; Jianping, Z.; Bisheng, H.; Ruiqing, Z.; Zou, X. An optimisation model of hierarchical facility location problem for urban last-mile delivery with drones. Transp. A Transp. Sci. 2024, 1–29. [Google Scholar] [CrossRef]
- Yang, Y.; Bui, H.T.; Loxton, R. SDP-based Benders decomposition for solving p-median quadratic facility location problems. Comput. Oper. Res. 2025, 182, 107119. [Google Scholar] [CrossRef]
- Kale, A.; Upadhyay, A.; Anbanandam, R. A hierarchical facility location-allocation model for sustainable municipal solid waste management in urban cities. Socio-Econ. Plan. Sci. 2025, 101, 102259. [Google Scholar] [CrossRef]
- He, D.; Tian, Q.; Lin, Y.H.; Yu, Y. Bilevel competitive facility location and design under a nested logit model. Comput. Oper. Res. 2025, 183, 107146. [Google Scholar] [CrossRef]
- Hu, H.; Tang, J.; Li, J. Robust facility location and fortification considering fortification failure probability. Omega 2025, 137, 103357. [Google Scholar] [CrossRef]
- Abbasi, S.; Saboury, A.; Jabalameli, M.S. Reliable supply chain network design for 3PL providers using consolidation hubs under disruption risks considering product perishability: An application to a pharmaceutical distribution network. Comput. Ind. Eng. 2021, 152, 17. [Google Scholar] [CrossRef]
- Joneghani, N.M.; Zarrinpoor, N.; Eghtesadifard, M. A mathematical model for designing a network of sustainable medical waste management under uncertainty. Comput. Ind. Eng. 2022, 171, 19. [Google Scholar] [CrossRef]
- Punyim, P.; Karoonsoontawong, A.; Unnikrishnan, A.; Ratanavaraha, V. A Heuristic for the Two-Echelon Multi-Period Multi-Product Location-Inventory Problem with Partial Facility Closing and Reopening. Sustainability 2022, 14, 32. [Google Scholar] [CrossRef]
- Tang, L.H.; Wu, D.X. Enhanced capacitated facility location problem for mental accounting management using partial resource concentration. Ann. Oper. Res. 2023, 335, 385–424. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.M.; Cheng, C.; Qi, M.Y. A multi-objective fuzzy facility location problem with congestion and priority for drone-based emergency deliveries. Comput. Ind. Eng. 2023, 179, 15. [Google Scholar] [CrossRef]
- Mishra, S.; Singh, S.P. Designing dynamic reverse logistics network for post-sale service. Ann. Oper. Res. 2022, 310, 89–118. [Google Scholar] [CrossRef]
- Medrano-Gómez, X.D.; Ferreira, D.; Toso, E.A.V.; Ibarra-Rojas, O.J. Using the maximal covering location problem to design a sustainable recycling network. J. Clean. Prod. 2020, 275, 124020. [Google Scholar] [CrossRef]
- Shi, J.M.; Wang, R.; Chen, W.Y.; Xing, L.N.; Jin, M.Z. Bi-objective design of household E-waste collection with public advertising and competition from informal sectors. Waste Manag. 2020, 102, 65–75. [Google Scholar] [CrossRef]
- Gharibi, K.; Abdollahzadeh, S. A mixed-integer linear programming approach for circular economy-led closed-loop supply chains in green reverse logistics network design under uncertainty. J. Enterp. Inf. Manag. 2025, 38, 1–31. [Google Scholar] [CrossRef]
- Altekin, F.T.; Ayli, E.; Sahin, G. After-sales services network design of a household appliances manufacturer. J. Oper. Res. Soc. 2017, 68, 1056–1067. [Google Scholar] [CrossRef]
- Xiang, X.; Fang, T.; Liu, C.; Pei, Z. Robust service network design problem under uncertain demand. Comput. Ind. Eng. 2022, 172, 108615. [Google Scholar] [CrossRef]
- Momenitabar, M.; Dehdari Ebrahimi, Z.; Arani, M.; Mattson, J. Robust possibilistic programming to design a closed-loop blood supply chain network considering service-level maximization and lateral resupply. Ann. Oper. Res. 2023, 328, 859–901. [Google Scholar] [CrossRef]
- Wang, C.; Yankui, L.; Yang, G. Modeling a robust 2-service community healthcare network design problem with central hospital congestion. Int. J. Gen. Syst. 2024, 53, 1073–1102. [Google Scholar] [CrossRef]
- Zang, Y.; Wang, M.; Liu, H.; Qi, M. Moment-based distributionally robust joint chance constrained optimization for service network design under demand uncertainty. Optim. Eng. 2024, 25, 1631–1683. [Google Scholar] [CrossRef]
- Mirzaei, E.; Nikbakhsh, E.; Kashan, A.H. Accelerated Benders decomposition algorithm for the reliable service network design problem under disruption. Comput. Ind. Eng. 2025, 207, 111234. [Google Scholar] [CrossRef]
- Hall, J.; Porteus, E. Customer service competition in capacitated systems. Manuf. Serv. Oper. Manag. 2000, 2, 144–165. [Google Scholar] [CrossRef]
- Lei, D. Co-evolutionary genetic algorithm for fuzzy flexible job shop scheduling. Appl. Soft Comput. 2012, 12, 2237–2245. [Google Scholar] [CrossRef]
- Joines, J.A.; Houck, C.R. On the Use of Non-Stationary Penalty Functions to Solve Nonlinear Constrained Optimization Problems with GA’s, Evolutionary Computation. In Proceedings of the First IEEE Conference on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; pp. 579–584. [Google Scholar]
- López-Ibáñez, M.; Knowles, J.; Laumanns, M. On sequential online archiving of objective vectors. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Mansouri, S.A. Coordination of set-ups between two stages of a supply chain using multi-objective genetic algorithms. Int. J. Prod. Res. 2005, 43, 3163–3180. [Google Scholar] [CrossRef]
- Karafotias, G.; Hoogendoorn, M.; Eiben, A.E. Parameter Control in Evolutionary Algorithms: Trends and Challenges. IEEE Trans. Evol. Comput. 2015, 19, 167–187. [Google Scholar] [CrossRef]
- Kim, H.; Liou, M.-S. New fitness sharing approach for multi-objective genetic algorithms. J. Glob. Optim. 2012, 55, 579–595. [Google Scholar] [CrossRef]
- Wang, C.; Ma, B.; Sun, J. A co-evolutionary genetic algorithm with knowledge transfer for multi-objective capacitated vehicle routing problems. Appl. Soft Comput. 2023, 148, 110913. [Google Scholar] [CrossRef]






| Number | Customers | Location | Product Demand in the Planning Horizon | Cost (Thousand CNY) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Longitude | Latitude | ||||||||
| 1 | Shenzhen | 114.09 | 22.55 | 1407 | 59 | 44 | 30 | 6000 | 100 |
| 2 | Nanning | 108.31 | 22.83 | 1415 | 75 | 56 | 88 | 4000 | 67 |
| 3 | Guangzhou | 113.24 | 23.13 | 2340 | 81 | 61 | 41 | 6000 | 100 |
| 4 | Xiamen | 118.08 | 24.45 | 512 | 21 | 16 | 11 | 5000 | 83 |
| … | |||||||||
| 36 | Beijing | 116.5 | 39.9 | 1261 | 70 | 53 | 39 | 6000 | 100 |
| 37 | Huhehaote | 111.65 | 40.81 | 613 | 60 | 45 | 59 | 3000 | 50 |
| 38 | Luoyang | 112.27 | 34.41 | 650 | 57 | 43 | 69 | 3000 | 50 |
| 39 | Dongguan | 113.45 | 23.02 | 790 | 37 | 28 | 40 | 4000 | 67 |
| Parameter | t = 0 | t = 1 | t = 2 | t = 3 |
|---|---|---|---|---|
| 0.2 | 0.6 | 0.8 | 0.9 | |
| CNY 150 thousand | ||||
| km | ||||
| Customers | Solution 1 | Solution 2 | Solution 3 | Solution 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t = 1 | t = 2 | t = 3 | t = 1 | t = 2 | t = 3 | t = 1 | t = 2 | t = 3 | t = 1 | t = 2 | t = 3 | |
| 1 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 |
| 2 | 39 | 39 | 39→6 | 39 | 39 | 39→6 | 39 | 39 | 39→6 | 39 | 39 | 39→6 |
| 3 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 | 39 |
| … | ||||||||||||
| 10 | 9 | 9 | 9→13 | 8 | 8 | 8→13 | 8 | 8 | 8→13 | 9 | 9 | 5 |
| … | ||||||||||||
| 23 | 22 | 22→18 | 22→18 | 22 | 22→18 | 22→18 | 22 | 22→18 | 22→18 | 22 | 22→18 | 22→18 |
| 24 | 26 | 26→28 | 26→28 | 26 | 26→28 | 26→28 | 26 | 26→28 | 26→28 | 26 | 26→28 | 26→28 |
| … | ||||||||||||
| 32 | 36 | 36 | 36→30 | 36 | 36 | 36→30 | 34 | 34 | 34→30 | 34 | 34 | 34→30 |
| … | ||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, W.; Xu, Z. Dynamic Facility Location and Allocation Optimization for Sustainable Product-Service Delivery Using Co-Evolutionary Adaptive Genetic Algorithms. Sustainability 2025, 17, 8000. https://doi.org/10.3390/su17178000
Ye W, Xu Z. Dynamic Facility Location and Allocation Optimization for Sustainable Product-Service Delivery Using Co-Evolutionary Adaptive Genetic Algorithms. Sustainability. 2025; 17(17):8000. https://doi.org/10.3390/su17178000
Chicago/Turabian StyleYe, Wei, and Zhitao Xu. 2025. "Dynamic Facility Location and Allocation Optimization for Sustainable Product-Service Delivery Using Co-Evolutionary Adaptive Genetic Algorithms" Sustainability 17, no. 17: 8000. https://doi.org/10.3390/su17178000
APA StyleYe, W., & Xu, Z. (2025). Dynamic Facility Location and Allocation Optimization for Sustainable Product-Service Delivery Using Co-Evolutionary Adaptive Genetic Algorithms. Sustainability, 17(17), 8000. https://doi.org/10.3390/su17178000







