Resolving the Classic Resource Allocation Conflict in On-Ramp Merging: A Regionally Coordinated Nash-Advantage Decomposition Deep Q-Network Approach for Connected and Automated Vehicles

Abstract

To improve the traffic efficiency of connected and automated vehicles (CAVs) in on-ramp merging areas, this study proposes a novel region-level multi-agent reinforcement learning framework, Regionally Coordinated Nash-Advantage Decomposition Deep Q-Network with Conflict-Aware Q Fusion (RC-NashAD-DQN). Unlike existing vehicle-level control methods, which suffer from high computational overhead and poor scalability, our approach abstracts on-ramp and main road areas as region-level control agents, achieving coordinated yet independent decision-making while maintaining control precision and merging efficiency comparable to fine-grained vehicle-level approaches. Each agent adopts a value–advantage decomposition architecture to enhance policy stability and distinguish action values, while sharing state–action information to improve inter-agent awareness. A Nash equilibrium solver is applied to derive joint strategies, and a conflict-aware Q-fusion mechanism is introduced as a regularization term rather than a direct action-selection tool, enabling the system to resolve local conflicts—particularly at region boundaries—without compromising global coordination. This design reduces training complexity, accelerates convergence, and improves robustness against communication imperfections. The framework is evaluated using the SUMO simulator at the Taishan Road interchange on the S1 Yongtaiwen Expressway under heterogeneous traffic conditions involving both passenger cars and container trucks, and is compared with baseline models including C-DRL-VSL and MADDPG. Extensive simulations demonstrate that RC-NashAD-DQN significantly improves average traffic speed by 17.07% and reduces average delay by 12.68 s, outperforming all baselines in efficiency metrics while maintaining robust convergence performance. These improvements enhance cooperation and merging efficiency among vehicles, contributing to sustainable urban mobility and the advancement of intelligent transportation systems.

1. Introduction

In real-world traffic management, diverse engineering and management strategies have been applied to improve traffic flow organization in urban and freeway networks. Common measures include modifying road markings and installing or replacing existing traffic signs to better guide vehicle movements, as well as dynamically adjusting control measures such as speed limits, signal timings, and lane assignments based on real-time traffic conditions. In certain cases, changes to traffic regulations—such as prioritizing specific vehicle types or imposing time-based restrictions on large and heavy vehicles—have been implemented to enhance merging efficiency and reduce safety risks. Transportation agencies have also explored utilizing underused road segments or auxiliary lanes during peak hours, and in some complex interchanges, partial manual traffic management has been employed to alleviate severe congestion. These approaches, while often effective in localized contexts, face challenges in maintaining long-term adaptability and scalability under fluctuating traffic demands.

In addition, diverse sources of information—such as congestion onset patterns, bottleneck incidents, and site-specific geometric constraints—are frequently used to tailor traffic management strategies to local conditions. For example, in signalized intersections, Xie et al. [1] propose synthetic delay for signalized intersections based on traffic dynamics to improve the efficiency of the network under various conditions. In freeway bottleneck management, Han et al. [2] proposed an IPMATD3-based ITC approach for a large freeway corridor in mixed traffic to improve freeway traffic efficiency, mobility, safety, and environmental sustainability. In ramp merging scenarios, He et al. [3] integrated variable speed limit and ramp metering to enhance vehicle group safety and efficiency in a mixed traffic environment. On the empirical side, in lane-changing behavior analysis, Yasir Ali et al. [4] propose a wavelet-transform-based method combined with a case–control design to correctly identify lane-changing decision points and balance lane-changing/non-lane-changing samples, enabling fair and accurate calibration of lane-changing decision models and revealing optimal analysis settings.

Current studies have shown that the frequent lane changes and speed adjustments in merging areas often lead to traffic congestion and accidents [5,6,7]. Recognizing that appropriate ramp control can effectively improve traffic safety and alleviate congestion, researchers have designed various ramp control strategies over the years, such as fixed-time ramp control from the 1960s, traffic-responsive control methods like ALINEA proposed by Papageorgiou [8], predictive control proposed by Gomes et al. [9], and coordinated multi-ramp control like HERO proposed by Papamichail et al. [10]. However, these conventional control methodologies exhibit inherent limitations when handling dynamic traffic scenarios with heterogeneous vehicle composition, revealing the inadequacy of relying solely on fixed-time, responsive, and coordinated controls to handle complex traffic scenarios [11,12].

With the development of vehicle automation and communication technologies, the introduction of CAVs has provided a new solution to ramp control challenges [13,14]. CAVs, through intelligent perception, precise control, and vehicle-to-vehicle (V2V) communication, overcome the limitations of traditional ramp control. First, CAVs exhibit millisecond-level responsiveness to dynamic traffic fluctuations through their integrated perception-control systems without relying solely on signal control or predictive models, making them more efficient in sudden traffic flow changes. Second, CAVs can reduce lane changes and speed differences in merging areas through cooperative driving, avoiding vehicle conflicts and congestion seen in traditional ramp controls. Lastly, CAVs can optimize traffic flow through shared data, especially in complex environments, achieving more refined and globalized control. Recent studies (2020–2024) have extensively explored CAV ramp control methods across more than 15 countries [15], with such methods broadly categorized into rule-based, data-driven, and model-based methods.

Rule-based methods rely on predefined rules or logic to control vehicle behavior. Wang et al. [16] studied a cooperative control method that prioritizes special vehicles’ passage in centralized CAV control scenarios at typical Y-shaped ramp merging areas. Yang et al. [17] proposed an adaptive control system to prevent queue overflow at downstream ramps through ramp queue estimation and adaptive signal operations on the mainline. Rule-based ramp control applies fixed rules based on different traffic scenarios, offering simplicity and directness but lacking flexibility and adaptability in dynamic traffic conditions.

Data-driven methods leverage large amounts of real-time data collected from traffic systems to optimize ramp merging control using machine learning and deep learning techniques [18,19]. For instance, Wang et al. [20] developed a DQN-based intelligent vehicle merging model using a real dataset, which improved traffic efficiency in merging areas. Lin et al. [21] utilized deep reinforcement learning to propose an urban expressway ramp coordination control method based on vehicle identification (AVI) data, effectively using OD information to alleviate congestion. Gu et al. [22] established a roadside data collection platform and employed algorithms based on Random Forest (RF) and Deep Q-Networks (DQN) to improve merging area efficiency and merging success rates. While data-driven methods excel in handling high-dimensional and complex data, they often rely heavily on high-quality datasets. Moreover, such methods can act like black boxes, failing to capture intricate interactions between vehicles adequately.

Model-based methods construct mathematical models of traffic flow to accurately represent behaviors in complex traffic environments. For instance, to reflect cooperative behaviors among vehicles, cooperative driving models are applied to ramp merging control. Chen et al. [23] proposed a distributed cooperative control strategy for CAVs in merging scenarios based on rotation, which reduces gaps within the merging control area while suppressing traffic oscillations. Xue et al. [24] divided CAVs on the mainline and ramp into multiple local platoons based on spacing and speed and designed a distributed cooperative control strategy, significantly improving average travel speed, traffic efficiency, and total travel time. Furthermore, game theory has become an effective tool for understanding and optimizing complex interactions during ramp merging. Liu et al. [25] proposed a cooperative game-based vehicle control method for merging areas, reducing vehicle conflicts and improving comfort and efficiency in merging acceleration lanes. Qu et al. [26] deeply analyzed the dynamic interactive game characteristics of vehicle lane changing and merging, and the lane-changing cut-out behavior of mainline vehicles in trajectory data is analyzed and defined from the perspectives of game decision-making and cost. Jiang et al. [27] proposed a game theory-based on-ramp merging controller for connected automated vehicles (CAVs) in mixed traffic flow. However, model-based methods struggle to handle high-dimensional data and often require extensive data for model calibration to extract representative behavioral parameters. Combining data-driven and model-based approaches is thus necessary.

Although previous studies have explored the integration of game-theoretic concepts into deep reinforcement learning frameworks, the original Nash-DQN still suffers from structural and coordination limitations [28]. It relies on a single Q-network, which tends to overestimate action values, and lacks value–advantage decomposition, reducing its ability to distinguish between actions. In contrast, Nash Double Q-learning introduces two separate Q-networks to mitigate overestimation, and Dueling DDQN decomposes Q-values to enhance action differentiation. For instance, Li et al. [29] proposed a Nash Double Q-learning-based merging strategy that improves coordination between ramp and mainline vehicles. Shi et al. [30] demonstrated that a Dueling DDQN with single-step momentum updates achieves faster convergence and higher decision success rates than standard DQN and DDQN in highway scenarios.

However, existing approaches such as Li et al. [29], while effective in handling pairwise interactions between ramp and mainline vehicles, often simplify the scenario by considering only one ramp vehicle at a time. Such fine-grained vehicle-level control may struggle to scale efficiently in dense multi-agent environments and may often overlook the broader coordination required among multiple traffic streams. Moreover, as the number of agents increases, the joint state–action space grows exponentially, leading to significant computational overhead and demanding more samples and training time to converge toward effective policies. This issue becomes particularly severe when each vehicle is treated as an individual agent, resulting in a dramatic increase in the dimensionality of the learning space. In high-density merging areas, these scalability and coordination limitations are compounded by the fact that main road and on-ramp traffic streams compete for limited road space, forming a classic resource allocation conflict analogous to the “tragedy of the commons”. Without proper coordination, each vehicle’s pursuit of its own travel efficiency can lead to overall congestion, reduced safety, and inefficient space–time utilization. This study adopts the working hypothesis that coordinated decision-making among connected and automated vehicles (CAVs), guided by game-theoretic principles and reinforcement learning, can resolve this conflict by achieving equilibrium strategies that balance individual and system-level benefits.

The key assumptions underlying this hypothesis are: (1) all CAVs are equipped with vehicle-to-vehicle (V2V) communication and precise control capabilities; (2) heterogeneous vehicle types are considered, reflecting differences in dynamic performance; and (3) environmental factors such as weather or non-CAV driver unpredictability are beyond the scope of this study. The main limitation is that the proposed framework is validated through simulation rather than large-scale field deployment. This focus on resolving the merging-area resource allocation problem under controlled conditions forms one of the core contributions and novelties of this paper, which is reflected in its title. Our proposed Regionally Coordinated Nash-Advantage Decomposition Deep Q-Network (RC-NashAD-DQN) abstracts the traffic flow at each on-ramp and main road segment as a control unit, enabling regional cooperation. By treating each unit as an agent and incorporating game-theoretic decision-making with Q-value decomposition, the model significantly reduces computational complexity and improves scalability when managing dense multi-agent traffic flows.

Although the Nash equilibrium provides effective coordination among regions by balancing macro traffic strategies, it does not explicitly guarantee fine-grained action-level coordination at the boundaries between neighboring control regions. This gap can trigger residual conflicts during vehicle-level execution at merging points. Residual conflicts are local action-level clashes that emerge at inter-regional boundaries even after achieving Nash equilibrium at the regional level. These conflicts stem from decentralized Q-value estimation, which fails to align expected action values along the borders of the joint Q-matrix. In high-density merging areas, such discrepancies may cause misaligned vehicle behaviors, such as simultaneous merging attempts or erratic deceleration. To bridge this gap, a conflict-aware Q-fusion mechanism is proposed to harmonize Q-values across neighboring agents—particularly at matrix boundaries—thereby enhancing local action coordination while preserving global equilibrium, which supports sustainable traffic coordination in high-density merging areas.

The main contributions of this paper are as follows:

(1)

Unlike Nash-Q, Nash DQN, QMix, and MADDPG, the proposed RC-NashAD-DQN introduces a region-based coordination mechanism that treats ramp–main road interaction areas as unified decision regions, enabling consistent yet independent policy execution. A conflict-aware Q-fusion term is embedded into the loss function to resolve inter-regional action conflicts while preserving local autonomy. Furthermore, an advantage decomposition structure is integrated into the Nash equilibrium computation to enhance policy stability and joint value estimation, providing a more robust and coordinated control framework for complex traffic interactions.

(2)

Unlike existing methods that typically target single vehicle types, this study considers mixed traffic environments with both passenger cars and container trucks. By modeling heterogeneous vehicle interactions, the proposed method improves the realism and practical applicability of merging control strategies.

The remaining sections are organized as follows: Section 2 introduces the problem definition. Section 3 describes the modeling approach. Section 4 presents a typical case study with numerical simulations. Section 5 concludes the paper and provides future research directions.

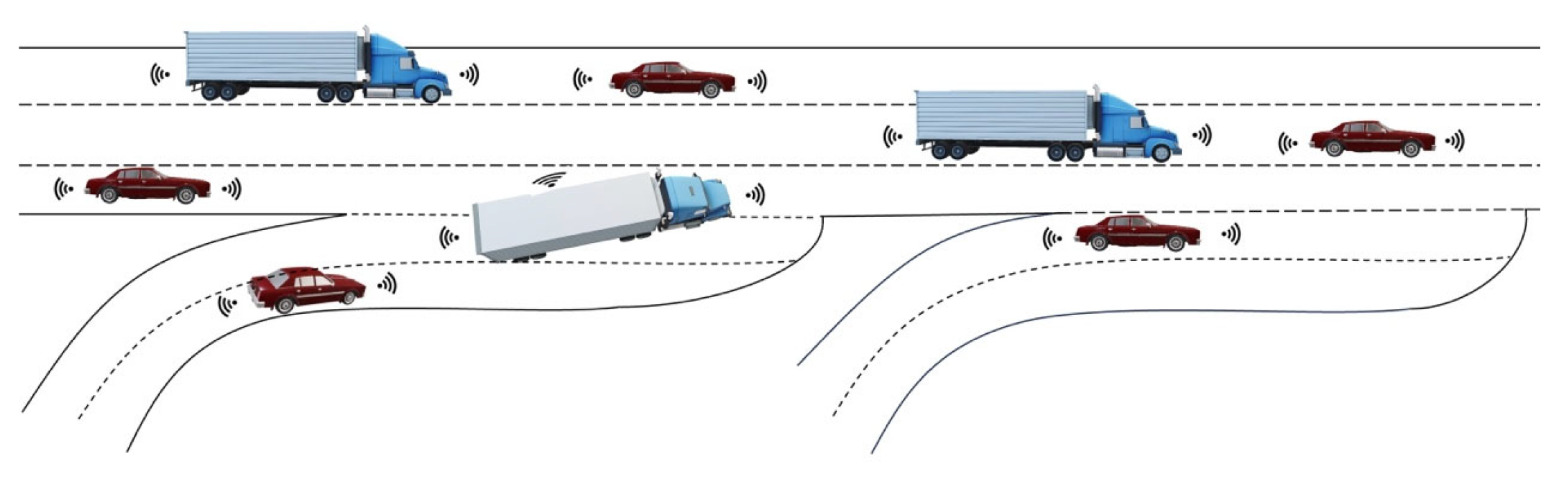
2. Problem Description

In expressways, there exist traffic scenarios where multiple consecutive on-ramps merge within a relatively short spatial range. Such scenarios typically consist of two or more on-ramp merging areas. An on-ramp merging area is composed of several components, including on-ramps, main road segments, acceleration lanes, taper sections, and diverging facilities (Figure 1). The design speed for on-ramps is generally 40 km/h, while the design speed for the main road is typically 120 km/h.

All vehicles discussed in this study are connected and automated vehicles (CAVs), categorized into two types: passenger cars and container trucks (Figure 2). Passenger cars are smaller, have faster driving speeds, can accelerate and decelerate more quickly, and are able to maintain shorter following distances. In contrast, container trucks are larger in size and mass, which results in lower maximum speed limits, weaker acceleration, and poorer braking performance. Consequently, container trucks require larger following distances. As shown in Figure 3, all four possible car–truck following combinations (CC, CT, TC, TT) are illustrated, where “C” represents passenger cars and “T” represents container trucks.

In the context of connected and automated driving, the traffic flow of the main road and each on-ramp is managed by a control unit. Each control unit functions as an intelligent agent equipped with V2X communication, radar, and IMU and GPS sensors, enabling information exchange among the agents. Furthermore, the traffic flows on the main road and the on-ramps exhibit both cooperative and competitive behaviors. For instance, on-ramp traffic may accelerate to merge into gaps in the main road traffic as quickly as possible, while main road traffic may aim to maintain its speed and lane position to minimize disruption caused by merging on-ramp vehicles. This dynamic interaction forms a game-theoretic relationship.

3. Methodology

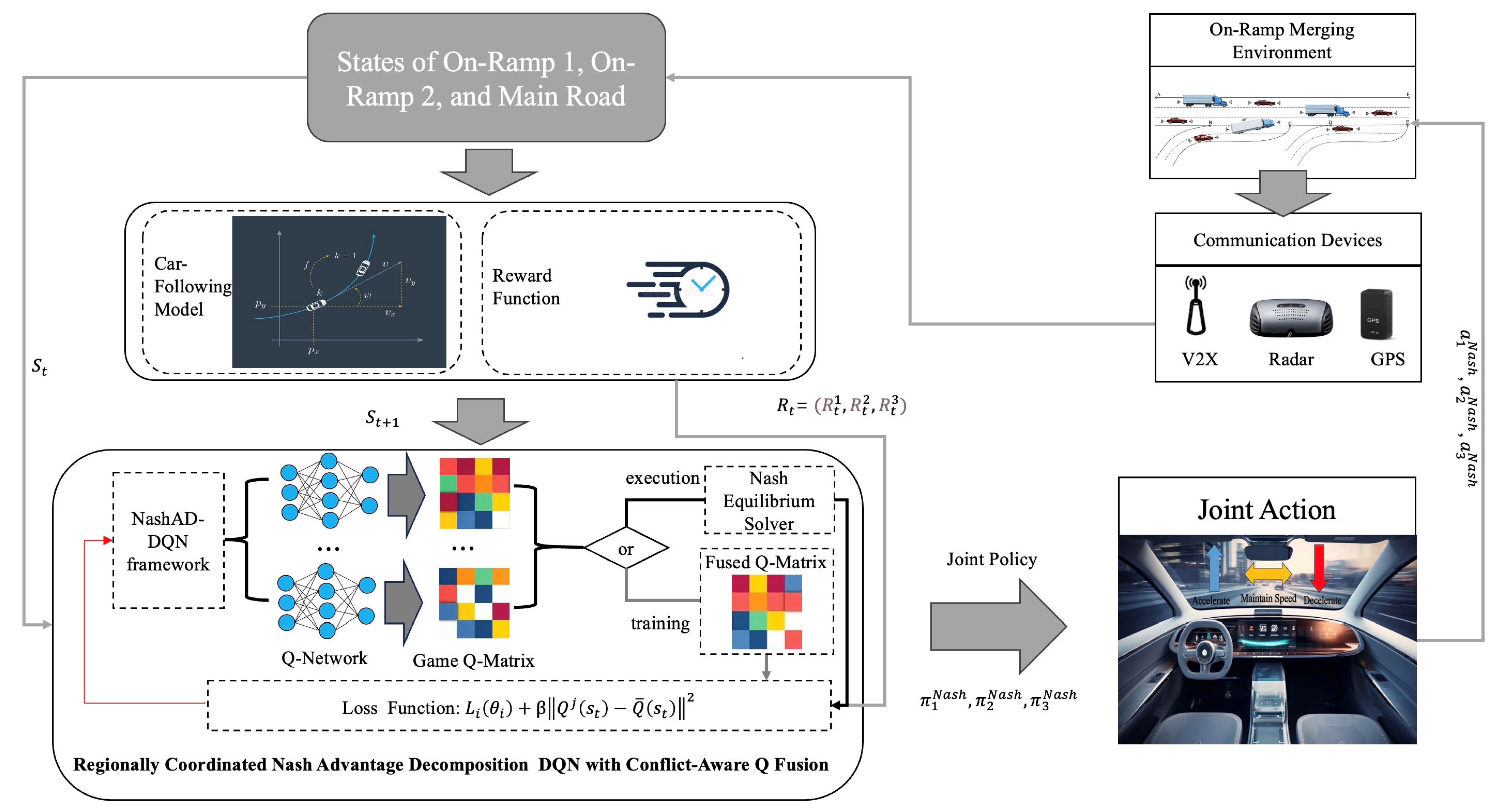
3.1. Model Overview

As shown in Figure 4, the overall framework of the model is presented. First, real-time traffic flow states are collected through a combination of communication devices and data acquisition techniques, including Vehicle-to-Everything (V2X) communication modules, roadside units (RSUs), vehicle-mounted On-Board Units (OBUs), radar sensors, loop detectors, video detection systems, LiDAR sensors, and GPS-based trajectory tracking. Such devices enable continuous monitoring of vehicle positions, speeds, and traffic density, providing reliable inputs for the proposed control model. Next, joint decisions are made using the Regionally Coordinated Nash Advantage Decomposition Deep Q-Network with Conflict-Aware Q Fusion (RC-NashAD-DQN) to achieve cooperative and competitive control of traffic flows in the on-ramps and main road. Finally, by updating states every second and using reward feedback to enhance flow efficiency, the merging area’s traffic efficiency is continuously improved.

In the event of a partial or complete failure of components within the proposed intelligent traffic management system—such as communication breakdowns, sensor malfunctions, or decision module errors—the control authority is designed to revert to a predefined fallback strategy governed by the higher-level regional transport management center. This strategy prioritizes safety by reverting CAVs to conservative car-following and lane-changing behaviors, using onboard perception and local decision-making without relying on centralized coordination. From a macro-control perspective, prolonged downtime could lead to temporary degradation in merging efficiency and increased congestion in affected regions, with severity depending on traffic demand levels and system configuration. In high-demand scenarios, the absence of coordinated merging may cause local queue spillbacks and reduced space–time utilization. Therefore, the design also specifies a maximum allowable control latency for remotely managed or autonomous vehicles (e.g., under 500 ms) to ensure responsiveness in mixed traffic. These considerations ensure that even under degraded conditions, the system maintains basic operational safety while minimizing the regional traffic performance loss until normal operations are restored.

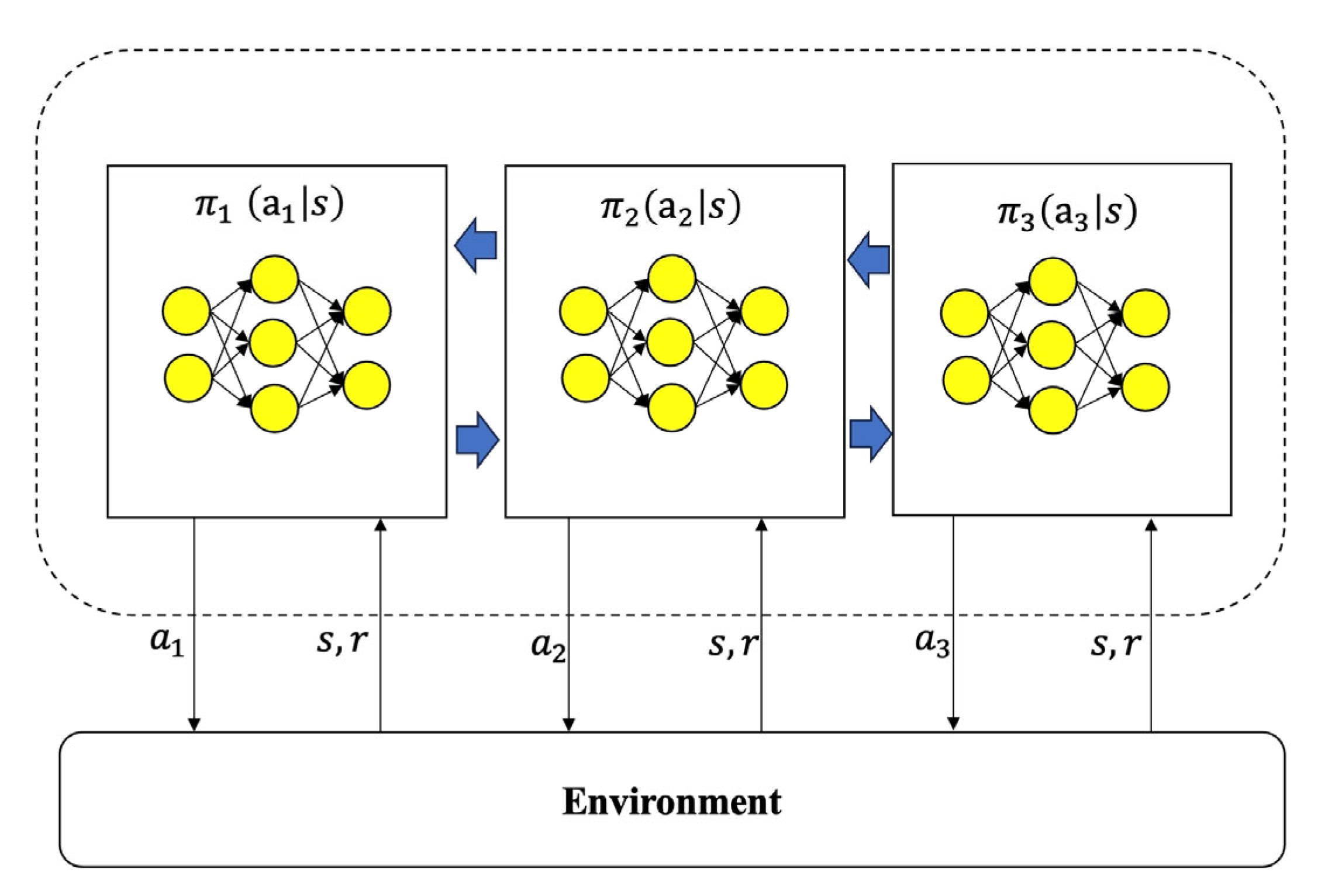
3.2. Multi-Agent Reinforcement Learning

In this study, we extend the Deep Q-Network (DQN) framework to a multi-agent scenario by integrating NashAD-DQN, which addresses both the instability of Q-value estimation and the strategic interdependence between agents. Unlike standard DQN that operates in a single-agent setting, our approach abstracts each control unit as an agent with two Q-networks to mitigate the overestimation bias and support equilibrium learning.

Let the environment state be $s$, joint action space be $A=A_1\times A_2\times A_3$, and the network parameters for the $i$-th agent be ${\theta }_i$. For each agent i, two Q-networks, ${\widehat{Q}}_i$ and ${\tilde{Q}}_i$, are maintained. The estimated Q-value is given by:

$$Q_i\left(s,\overrightarrow{a};{\widehat{\theta }}_i\right)\approx {\widehat{Q}}_i\left(s,\overrightarrow{a}\right)$$

(1)

where $\overrightarrow{a}=\left(a_1,a_2,a_3\right)$ is the joint action of all agents. During training, we first construct a joint Q matrix for each agent and then solve for the Nash equilibrium over the joint strategy space. The resulting equilibrium joint action is used both for environment interaction and for computing the target value in the loss function.

This method allows each agent to not only consider its own Q-value but also respond to the strategies of other agents, leading to a more stable and cooperative control policy under competitive traffic scenarios (Figure 5). In the proposed multi-agent system, Agent 1, Agent 2, and Agent 3 are responsible for controlling the traffic flows on on-ramp 1, on-ramp 2, and the main road, respectively. Each agent makes decisions independently based on local observations using deep neural networks. The environment provides traffic flow states (e.g., speed, flow rate, density) and reward signals. By sharing partial observations and interacting through a joint Q-learning framework, the agents coordinate their strategies to optimize merging behavior under a partially observable and non-stationary environment.

The algorithm (Algorithm 1) is added to illustrate the regional coordination process, including traffic state acquisition, dynamic region partitioning, inter-agent communication, Nash-based decision-making, and feedback execution, providing a clear overview of how RC-NashAD-DQN balances global coordination and local adaptability. Lines 5–6 make explicit how regional partitions and overlap zones are formed each tick; lines 8–15 show message exchange with TTL/retry and stale-drop; lines 17–25 detail how regional Q-values incorporate neighbor context and how overlap conflicts are scored; lines 27–31 show the Nash equilibrium action selection and feedback execution. This directly addresses the reviewer’s request for a clear algorithm describing regional interaction, communication management, dynamic partitioning, and coordination-zone overlaps.

Algorithm 1 Pseudocode of regional coordination per control interval, Δt.

Inputs: · Sensors: RSU/OBU, radar/loop/video/LiDAR, GNSS · Communication Manager: TTL τ, one retry, drop-stale policy · Action set $A_i$ for each region $i$ (e.g., ${VSL}_i$, ${ramp\text{\_}rate}_i$, ${platoon\text{\_}setpoints}_i$) 1: Traffic state acquisition 2: $Z_t$ ← read_all_sensors ( )         # raw detections 3: $S_t$ ← aggregate_features ($Z_t$)      # speed, density, flow, gap, type mix 4: Dynamic region partitioning + overlap detection 5: R ← partition_roadway ($S_t$; method = density/conflict clustering) 6: O ← compute_overlaps (R)       # O = $\{O_{ij}$| regions $i,j$ share a merging boundary window} 7: Neighbor communication (bounded delay/loss) 8: for each region $i$ ∈ R do 9:    ${msg}_i$ ← ⟨${state\text{\_}summary}_i$ $(S_t$|$R_i$), ${boundary\text{\_}intent}_i$ ($S_t$|${\partial }_{R_i}$)⟩ 10:  CommManager.broadcast (${msg}_i$) 11: end for 12: M ← CommManager.collect (TTL = τ, retry = 1)     # receive neighbor summaries; discard stale/duplicates 13: for any missing neighbor $j$ do           # partial observability handling 14:  use last_known (j) with time-decay weighting 15: end for 16: Regional Q-value construction with advantage decomposition 17: for each region $i$ ∈ R do 18:  $S_i$ ← compose_local_joint_state $(S_t$|$R_i$, M|N(i)) # include neighbors’ summaries near boundaries 19:  build $Q_i(s,a)$ = $V_i\left(s\right)$ + $A_i(s,a)$ − ${\displaystyle \frac{1}{\left|A\right|}}{\displaystyle {\sum }_{a^{\prime }}}A\left(s,a^{\prime }\right)$ 20: end for 21: Overlap-aware conflict scoring (short-horizon rollout on overlaps only) 22: for each overlap $O_{ij}$ ∈ O do 23:  $c_{ij}$ ← conflict_score $(s_i$, $s_j$, horizon H, $safety\text{\_}threshold$ $d_{min}$) 24: end for 25: C ← $\{c_{ij}$}                    # used as weights for boundary actions 26: Nash-based decision (per-step equilibrium over joint actions) 27: a * (* The superscript “*” denotes the optimal solution (Nash equilibrium action)) ← solve_nash_equilibrium ({$Q_i$}, overlaps = C) # joint action $(a_{1^{*}}$, …, $a_{{\left|R\right|}^{*}}$) 28: U ← map_actions_to_controls (a *)         # $\{{VSL}_i$, ${ramp\text{\_}rate}_i$, ${platoon\text{\_}setpoints}_i$} 29: Feedback execution and logging 30: apply_controls (U)                 # actuators/V2X commands 31: log_transition $(S_t$, $a *, {reward}_t$, $S_{t+\Delta t}$)       # for offline analysis/training 32: t ← t + Δt

3.2.1. State Space Considering Vehicle Heterogeneity

In this study, the state space includes speed, flow rate, and density. To capture the key characteristics of heterogeneous traffic flows involving cars and trucks, the Optimal Velocity (OV) car-following model proposed by Bando [31] is extended into a heterogeneous form:

$$\left\{\begin{array}{c}{\displaystyle \frac{d^2{x}_n\left(t\right)}{d{t}^2}} = a_n\left\{f\left(\Delta x_n\left(t\right)\right) -{\displaystyle \frac{d{x}_n\left(t\right)}{dt}}\right\}\\ f\left(\Delta x_n\left(t\right)\right) =\left({\displaystyle \frac{V_n^{max}}{2}}\right)\left[tanh\left(\Delta x_n\left(t\right)-d_s\right) + tanh\left(d_s\right)\right]\end{array}\right.$$

(2)

Here, $x_n\left(t\right)$ is the position of vehicle $n$ at time $t$, $a_n$ is the sensitivity coefficient, and $V_n^{max}$ is the maximum speed depending on the vehicle type. Their values depend on the characteristics of different car–truck following combinations, specifically: $a_n$ has four options ($a_{cc}$, $a_{ct}$, $a_{tc}$, $a_{tt}$), while $V_n^{max}$ has two options ($V_c^{max}$, $V_t^{max}$). $\Delta {\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)$ represents the spacing of vehicle $n$, given by: $\Delta {\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right) = {\mathrm{x}}_{\mathrm{n}-1}\left(\mathrm{t}\right) - {\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)$, $\mathrm{f}\left(\Delta {\mathrm{x}}_{\mathrm{n}}\left(\mathrm{t}\right)\right)$ is the optimal velocity function defined according to Ge’s formula [32], and $d_s$ is the safe distance.

The macroscopic traffic flow speed $V_{\mathit{macro}}$ on the on-ramps or the main road is given by the following:

$$V_{\mathit{macro}}={\displaystyle \frac{1}{N_i}}{\sum }_{n=1}^{N_i}f\left(\Delta x_n\left(t\right)\right)$$

(3)

where $N_i$ represents the number of vehicles in the on-ramp or main road traffic flow.

Building upon this, we define the regional reward function $R_{i,t}$ as follows:

$$R_{i,t}=\lambda ·V_{\mathit{macro}}$$

(4)

Here, λ is a positive scaling coefficient that adjusts the sensitivity of the reward signal to changes in regional average speed, ensuring stable training and appropriately balancing the influence of speed-based efficiency within the overall learning process.

To extend beyond the traditional car-following abstraction, this study incorporates additional region-level state features that reflect the spatial structure and behavioral interactions within each control unit:

The full state vector $s_i\left(t\right)$ includes the following:

• Macroscopic traffic flow indicators:
  ${\overline{v}}_i\left(t\right)$: average speed of vehicles in region $i$
  ${\rho }_i\left(t\right)$: vehicle density
  $q_i\left(t\right)$: traffic flow (veh/time)
• Behavioral statistics:
  ${\sigma }_v^i\left(t\right)$: speed variance, reflecting flow stability
  $h_i\left(t\right)$: average headway
  ${\gamma }_i^{car}$, ${\gamma }_i^{truck}$: vehicle type ratios
• Inter-agent interaction context:

Relative distance/speed to neighboring regions

Predicted arrival rates from upstream zones

Agents exchange state–action information with adjacent regions to estimate the relative merging intensity and temporal gap availability. This enriched state design allows agents to infer not only their internal traffic state, but also the latent behavioral dynamics of merging, yielding, and competitive driving across zones. Such an extended state space provides a stronger foundation for learning coordinated strategies that balance local efficiency and inter-agent safety.

3.2.2. Deep Network Structure

As illustrated in Figure 6, the proposed deep hierarchical architecture is designed to extract spatiotemporal features and generate region-level control policies for multiple traffic flow zones (on-ramp 1, on-ramp 2, and the main road). It consists of four main components: the input layer, convolutional layer, fully connected layers, and output layer.

The input layer encodes regional macroscopic traffic state features, including average speed, vehicle density, average spacing, and available merging gap. These features collectively describe the current aggregate traffic conditions in each control region and form a structured spatiotemporal input matrix. To capture spatial correlations and temporal transitions across regions, the model applies two convolutional layers using 4 × 4 kernels with ReLU activation. The convolutional encoder transforms the raw macroscopic state features into a shared latent representation that captures interaction-relevant spatial patterns. This shared representation is then passed into three parallel decision branches, each corresponding to a control region. Each branch employs multi-layer perceptrons (MLPs) to output region-specific macro control commands, such as adjusting average acceleration or modifying the vehicle insertion or merging rate. This design supports modular multi-agent decision-making while preserving global consistency through the shared encoder.

To further improve policy robustness and interpretability, the architecture integrates a dueling Q-network structure, as proposed by Wang et al. (2016) in “Dueling Network Architectures for Deep Reinforcement Learning” [33]. The value stream V(s) estimates the overall importance of the current regional traffic state, while the advantage stream A(s,a) quantifies the relative benefit of taking action a in state s. These two components are combined to compute the final Q-value via the following:

$$\mathrm{Q}\left(\mathrm{s},\mathrm{a}\right)=\mathrm{V}\left(\mathrm{s}\right)+\left(\mathrm{A}\left(\mathrm{s},\mathrm{a}\right)-{\displaystyle \frac{1}{\left|\mathrm{A}\right|}}{\sum }_{a^{\prime }}A\left(s,a^{\prime }\right)\right)$$

(5)

where ∣A∣ is the total number of available actions. This decomposition enables the network to better distinguish the relative merits of different actions under the same state.

In addition, a hierarchical decision mechanism is employed, where the upper-level network produces high-level semantic decisions (e.g., facilitate merging, hold position, or slow down), and each region-specific lower-level module translates the selected policy into concrete macroscopic control signals based on real-time flow characteristics. This hierarchical-dueling structure enhances both the coordination and stability of control strategies across traffic regions in a learning-based multi-agent setting.

To validate the necessity of the advantage decomposition, we performed an ablation experiment in which the RC-NashAD-DQN was modified to use a single shared Q-function without decomposition. As shown in Figure 7, the simplified model exhibited slower convergence and lower final performance, confirming that the decomposition enhances both learning stability and policy effectiveness. Although the advantage decomposition shares a similar mathematical form with the Dueling DQN, the motivation and implementation differ: in RC-NashAD-DQN, the state-value function represents the regionally coordinated joint value derived from multi-agent Nash-based interactions, while the advantage function focuses on distinguishing the utility of individual actions within the joint strategy space. This design allows the model to capture inter-agent dependencies and resolve high-conflict situations more effectively, which a standard dueling structure does not address. These results empirically justify the integration of the advantage decomposition into our framework.

3.2.3. Nash-Advantage Decomposition Deep Q-Network Design and Training

Building upon the NashAD-DQN architecture introduced in Section 3.2.3, this section presents the joint strategy optimization process across agents in the merging area. While the online Q-network estimates the value of each local action under decentralized observations, the target Q-network leverages the full Q-matrix to compute a Nash equilibrium over the joint action space (Figure 8). This equilibrium guides the coordinated update of each agent’s policy, ensuring both local optimality and global consistency across heterogeneous vehicle flows. Compared to conventional Nash Double Q-learning, the proposed NashAD-DQN not only separates target estimation and action selection through dual networks but also enhances policy differentiation via value-advantage decomposition and improves coordination by embedding regional Nash equilibrium constraints.

The Nash equilibrium condition is defined as follows: for each agent $i$, its Nash equilibrium strategy ${\mathsf{\pi }}_i^{\mathit{Nash}}$ satisfies the condition that, given the strategies of all other agents ${\mathsf{\pi }}_{-i}^{\mathit{Nash}}$, no agent can achieve a higher reward by unilaterally changing its own strategy:

$$Q_i({\mathsf{\pi }}_i^{\mathit{Nash}},{\mathsf{\pi }}_{-i}^{\mathit{Nash}}) \ge Q_i({\mathsf{\pi }}_i,{\mathsf{\pi }}_{-i}^{\mathit{Nash}})\mathsf{\forall }{\pi }_i \mathsf{\in } {\Pi }_i$$

(6)

where ${\mathsf{\pi }}_i^{\mathit{Nash}}$ is the Nash equilibrium strategy of agent $i$ is the combination of strategies of all other agents except $i$; and ${\mathsf{\pi }}_{-i}^{\mathit{Nash}}$ represents the set of all possible strategies for the traffic flow.

For three traffic flows, when they all execute Nash equilibrium strategies ${\mathrm{\pi }}^{\mathrm{Nash}}$ = $\left({\mathrm{\pi }}_1^{\mathrm{Nash}},{\mathrm{\pi }}_2^{\mathrm{Nash}},{\mathrm{\pi }}_3^{\mathrm{Nash}}\right)$, the Q-value in NashAD-DQN is defined as the sum of the current reward and the expected future return:

$$Q_i^{\mathit{Nash}}\left(s,a_1,a_2,a_3\right)= \mathrm{E}\left[\left.R_{i,t}^{{\mathsf{\pi }}^{\mathit{Nash}}}\right| S_t,a_{1,t},a_{2,t},a_{3,t}\right]$$

(7)

To train the Q-network, driving samples are collected through interaction with the traffic environment and other traffic flows, as shown in the pseudocode in Algorithm 1. Every time all agents execute a joint action ($a_1^j$, $a_2^j$, $a_3^j$), a driving sample is generated and stored in the experience replay buffer:

$$M = {\left\{S_t^j,a_1^j, a_2^j, a_3^j,S_{t+1}^j,R_1^j,R_2^j,R_3^j\right\}}_{j\mathsf{ϵ}N}$$

(8)

where $j$ represents one sample transition recorded for all agents, and $N$ is the maximum capacity of the replay buffer.

To update the Q-network, a mini-batch of transitions is sampled from the buffer. An ϵ-greedy strategy is used to balance exploration and exploitation. As training proceeds, the probability of selecting random actions decreases to a lower bound (e.g., 10%), with the remaining actions selected via learned Nash strategies. For each sampled transition j, the target value is defined as follows:

$$y_i^j=R_i^j+\mathsf{\gamma }{{\tilde{Q}}_i}^{\mathit{nash}}\left(S_{t+1}^j,a_i^j;{\tilde{\theta }}_i\right)$$

(9)

The loss function for training is given by the following equation:

$$\begin{gathered} L_i\left({\mathsf{\theta }}_i\right)={\displaystyle \frac{1}{M}}{\displaystyle \sum _j^M}{\left({\widehat{Q}}_i\left(S_{t+1}^j,a_i^j;{\widehat{\theta }}_i\right)-y_i^j\right)}^2\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\displaystyle \frac{1}{M}}{\displaystyle {\sum }_j^M}{\left({\widehat{Q}}_i\left(S_{t+1}^j,a_i^j;{\widehat{\theta }}_i\right)-R_i^j-\gamma {{\tilde{Q}}_i}^{nash}\left(S_{t+1}^j,a_i^j;{\tilde{\theta }}_i\right)\right)}^2 \end{gathered}$$

(10)

Here, ${\widehat{Q}}_i$ denotes the online Q-network, and ${{\widehat{Q}}_i}^{nash}$ is computed using the online network with parameters ${\widehat{\theta }}_i$. The use of separate online and target networks prevents training instability caused by simultaneous updates. The target network parameters ${\tilde{\theta }}_i$ are periodically updated with those of the target network ${\tilde{Q}}_i$ to stabilize learning and ensure convergence toward Nash equilibrium policies.

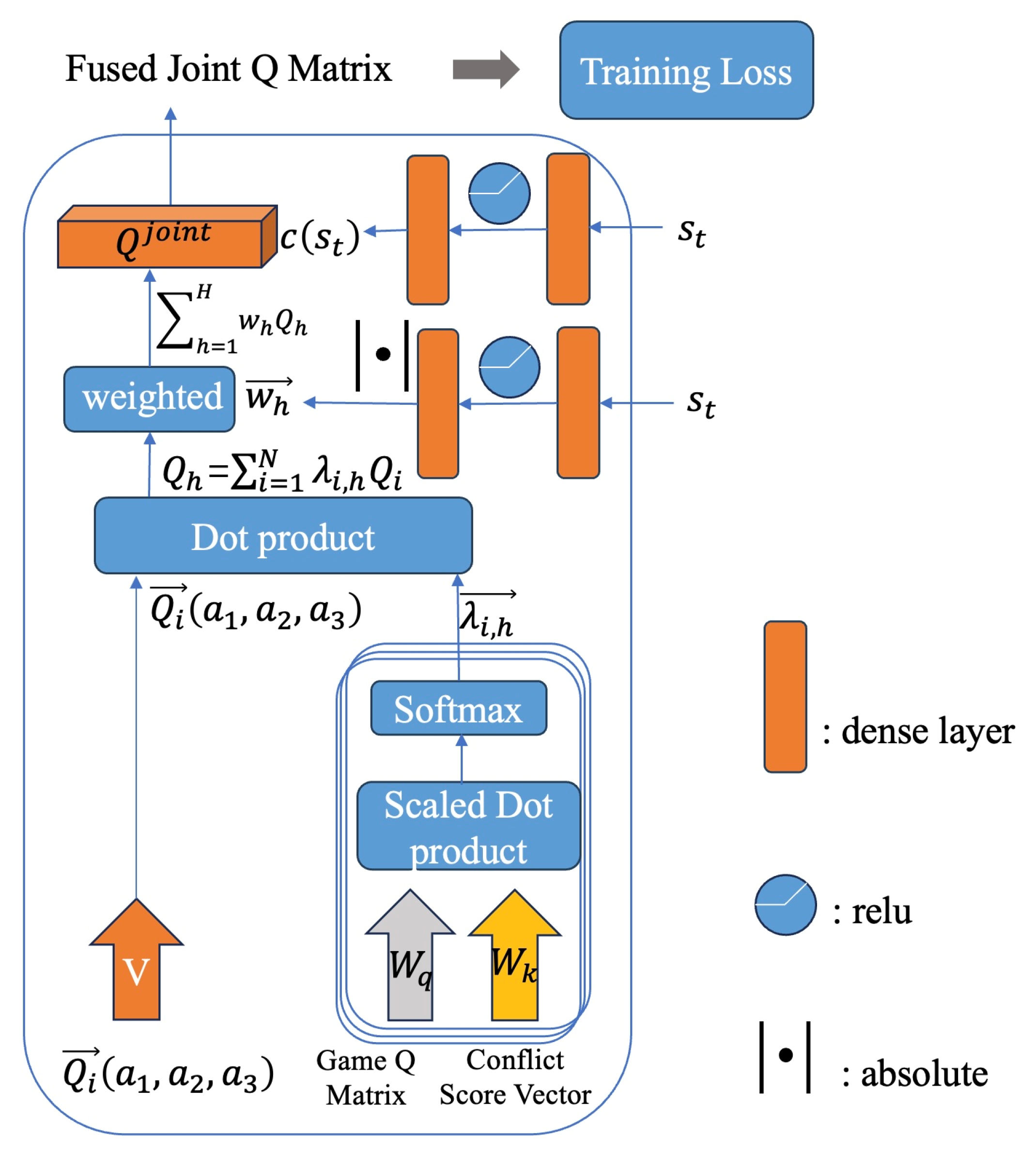
3.3. Conflict-Aware Q-Value Fusion Module and New Loss Function Design

While the NashAD-DQN framework introduced in Section 3.2 enables high-level coordination among agents by solving for joint equilibrium strategies, it primarily focuses on macro-level policy alignment across control regions (e.g., on-ramp 1, on-ramp 2, and the main road). However, such regional coordination may not adequately address local conflicts that emerge at the boundaries between agents where individual vehicles interact directly during merging. These localized conflicts are often critical to overall traffic efficiency and safety, especially in dense or competitive scenarios.

To tackle this limitation, we introduce a Conflict-Aware Q Fusion module, which explicitly models and mitigates the conflict potential between agents at the micro-level (Figure 9). By integrating attention-weighted Q-value fusion across agents, this module refines the joint action evaluation, allowing the system to account for inter-agent edge conflicts that are not fully captured by Nash equilibrium strategies alone. This fine-grained adjustment enhances both the stability and effectiveness of the learned policy.

3.3.1. Fusion Process

Given the individual Q-value matrix for each agent $i \mathsf{\in } N$, we first flatten it into a vector:

$${\overrightarrow{Q}}_i\left(a\right)\in {\mathbb{R}}^{\left|A_1\right|\times \left|A_2\right|\times \left|A_3\right|}$$

(11)

We then introduce a spatiotemporal conflict score vector $\overrightarrow{V}\in {\mathbb{R}}^{\left|A_1\times A_2\times A_3\right|}$, which encodes the degree of agent interaction conflict across joint actions. This vector encodes the level of interaction conflict across all possible joint actions $\overrightarrow{a}=\left(a_1, a_2,a_3\right),$ and is constructed as follows.

(1)

Trajectory Rollout

For each joint action a, we simulate the future T seconds of movement for all agents using a predefined vehicle dynamics model. The predicted trajectory of agent i under action $a_i$ is as follows:

$${Trajectory}_i\left(a_i\right)=\left\{\left[x_i^{\left(n\right)}\left(t\right),v_i^{\left(n\right)}\left(t\right)\right]|n\in {\mathcal{V}}_i, t=1\dots T\right\}$$

(12)

where $x_i^{\left(n\right)}$ and $v_i^{\left(n\right)}$ denote the position and velocity at time t, respectively. Vᵢ denotes the set of all vehicles within the control region of agent i.

(2)

Spatiotemporal Conflict Detection

For each pair of agents (i, j), we evaluate the trajectory overlap under the given joint action. A conflict is detected when the predicted distance between agents falls below a safety threshold $d_{safe}$. The conflict score between two agents is defined as follows:

$$conflict\left(i,j|a_i,a_j\right)={\displaystyle {\sum }_{n\in {\mathcal{V}}_i}}{\displaystyle {\sum }_{m\in {\mathcal{V}}_i}}{\displaystyle {\sum }_{t=1}^T}1\left(\left|{x_t}^{\left(n\right)}-{x_t}^{\left(m\right)}\right|<d_{safe}\right)$$

(13)

The total conflict score of the joint action a is then computed as follows:

$$V\left(a\right)={\displaystyle {\sum }_i}{\sum }_{j\ne i}Conflict\left(i,j|a_{i,}{a}_j\right)$$

(14)

(3)

Conflict Score Vector Construction

Traversing the entire joint action space $a\in A_1\times A_2\times A_3$, we obtain the conflict score vector:

$$\overrightarrow{V}=\left[V\left(a^{\left(1\right)}\right),V\left(a^{\left(2\right)}\right),\dots ,V\left(a^{\left(\left|A\right|\right)}\right)\right]$$

(15)

This vector is then used to compute the scaled dot-product attention weights that guide the fusion of multi-agent Q-values.

(4)

Attention-Based Q Fusion

Using trainable projection matrices $W_q$ and $W_k$, we compute attention weights across heads $h=1,\dots ,H$ as follows:

$${\lambda }_{i,h}=Softmax\left({\displaystyle \frac{{\left(W_q{\overrightarrow{Q}}_i\right)}^T\left(W_k\overrightarrow{V}\right)}{\sqrt{d}}}\right)$$

(16)

Here, $W_q$ and $W_k$ are trainable parameters, and ${\lambda }_{i,h}$ measures the attention of agent i to the $h$-th fusion head.

For each head h $\in \left\{1, \dots ,H\right\}$, we obtain an intermediate fused Q:

$$Q_h= {\displaystyle {\sum }_{i=1}^N}{\lambda }_{i,h}·Q_i, N=3$$

(17)

Next, we apply a context-aware weight $w_h$, generated via a neural network:

$$c\left(s_t\right)= ReLU\left(Dense\left(ReLU\left(Dense\left(s_t\right)\right)\right)\right)$$

(18)

$$w_h={\displaystyle \frac{exp\left(-‖c\left(s_t\right)-Q_h‖\right)}{{\sum }_{h^{\prime }=1}^{H}exp\left(-‖c\left(s_t\right)-Q_{h^{\prime }}‖\right)}}$$

(19)

The final fused joint Q-matrix is as follows:

$$Q^{joint}={\displaystyle {\sum }_{h=1}^H}{w}_h·Q_h$$

(20)

3.3.2. New Loss Function Design

The overall loss function for each agent i is composed of two parts: standard temporal-difference (TD) loss and a fusion regularization term:

$${L_i\left({\theta }_i\right)}^{\prime }=L_i\left({\mathsf{\theta }}_i\right)+\beta ·{‖Q^{joint}\left(s_t\right)-\overline{Q}\left(s_t\right)‖}^2$$

(21)

where $\overline{Q}\left(s_t\right)$ = ${\displaystyle {\sum }_{i=1}^N}{Q}_i\left(s_t\right)$, N = 3, and β is a hyperparameter balancing coordination and convergence. As shown in Algorithm 2,

Training Phase: The fused Q matrix $Q^{joint}$ is used only to construct a regularization term in the loss function, helping to align agent policies.

Execution Phase: Each agent uses its independent $Q_i$ to solve a Nash equilibrium game and select its action accordingly. Fused Q is not used at inference.

As illustrated in Figure 10, the RC-NashAD-DQN model demonstrates faster convergence performance (a) and a more flexible response to conflict scenarios through smoother policy fusion guided by conflict scores (c). Although it exhibits slightly higher policy variation (b), this variability may result from its adaptive adjustment to regional conflicts. Regarding speed distribution (d), RC-NashAD-DQN achieves a more balanced traffic state, preventing overly aggressive behavior and ensuring smoother merging flows.

Algorithm 2 Pseudocode of NashAD-DQN with conflict-aware Q fusion.

Initialize: · replay buffer: M · For each agent i, initialize online network $\widehat{Q_i}$(S), target network $\widetilde{Q_i}$(S), and parameters ${\widehat{\theta }}_i$, ${\tilde{\theta }}_i$ 1: for episode = 1 to M do: 2:  Initialize environment 3:  for time step t = 1 to T do 4:    for each agent i ∈ N do 5:      Sample joint actions $\left(a_{1,t},a_{2,t},a_{3,t}\right)$ based on Nash equilibrium $Q_i^{\mathit{Nash}}$ and strategy ${\mathsf{\pi }}_i^{\mathit{Nash}}$ 6:    end for 7:    Execute joint actions $\left(a_{1,t},a_{2,t},a_{3,t}\right)$ and observe next state and rewards $\left(R_{1,t},R_{2,t},R_{3,t}\right)$ 8:    Store experience $(S_t$,$a_{1,t},a_{2,t},a_{3,t}$, $S_{t+1}$, $R_{1,t},R_{2,t},R_{3,t})$ in replay buffer M 9:    Update $t\leftarrow t+1$, $k\leftarrow k+1$, $S_t\leftarrow S_{t+1}$ 10:    if t = T then 11:     Reset S0 and t 12:    end if 13:  end for

14:  if $k>\left|M\right|$ then 15:     Sample batch M from buffer: ${(S}_t^j$, $a_{1,t}^j,a_{2,t}^j,a_{3,t}^j$, $S_{t+1}^j$, $R_{1,t}^j, R_{2,t}^j, R_{3,t}^j$) 16:     Use target network to compute target value $\widetilde{Q_i}\left(S\right)$ = target network $\left(S_{t+1}^j;{\tilde{\theta }}_i\right)$ 17:     Compute Nash equilibrium value ${\widetilde{Q_i}}^{\mathit{Nash}}$ and strategy ${\mathsf{\pi }}_i^{\mathit{Nash}}$ 18:     if j is terminal then 19:      $Q_{i,j}^{*}$ = $R_i^{j+1}$ 20:     else 21:      $Q_{i,j}^{*}$ = $R_i^{j+1}+\mathsf{\gamma }{\widetilde{Q_i}}^{\mathit{Nash}}\left(S_{t+1}^j;a_i^j\right)$ 22:   end if 23:  end if Conflict-aware Q-fusion (training only) 24: for each agent i: 25:  Flatten $Q_i$ into ${\overrightarrow{Q}}_i$ 26:  Compute conflict score vector V 27:  for h in $\left\{1, \dots ,H\right\}$ do 28:    for each agent i do 29:       ${\lambda }_{i,h}=Softmax\left({\displaystyle \frac{{\left(W_q{\overrightarrow{Q}}_i\right)}^T\left(W_k\overrightarrow{V}\right)}{\sqrt{d}}}\right)$ 30:    end for 31:    $Q_h$ = ${\displaystyle {\sum }_{i=1}^3}{\lambda }_{i,h}·Q_i$ 32:    end for 33:    $c\left(s_t\right)$ = $\mathrm{ReLU}\left(Dense\left(ReLU\left(Dense\left(s_t\right)\right)\right)\right)$ 34:    for h do: 35:      $w_h={\displaystyle \frac{exp\left(-‖c\left(s_t\right)-Q_h‖\right)}{{\sum }_{h^{\prime }=1}^{H}exp\left(-‖c\left(s_t\right)-Q_{h^{\prime }}‖\right)}}$ 36:    end for 37:    $Q^{joint}$ = ${\displaystyle {\sum }_{h =1}^H}{w_{h }· Q}_h$ 38:    $\overline{Q}$ = ${\displaystyle {\sum }_{i=1}^3}{Q}_i$ 39: end for Total loss for each agent 40: for each agent i do 41:  TD loss: ${\displaystyle \frac{1}{M}}{\displaystyle {\sum }_j^M}{\left({\widehat{Q}}_i\left(S_{t+1}^j,a_i^j;{\widehat{\theta }}_i\right)-R_i^j-\gamma {{\tilde{Q}}_i}^{nash}\left(S_{t+1}^j,a_i^j;{\tilde{\theta }}_i\right)\right)}^2$ 42:  Fusion regularization: $\beta ·{‖Q^{joint}-\overline{Q}‖}^2$ 43:  Total loss: TD loss + Fusion regularization 44:  Update ${\widehat{\theta }}_i$ using gradient descent

45:  Every C steps, update target network: ${\tilde{\theta }}_i\leftarrow {\widehat{\theta }}_i$. 46: end for

4. Numerical Settings

4.1. Experimental Process

Table 1. Parameter descriptions.

Parameter	Description	Value
ALPHA	Learning rate	0.1
GAMMA	Discount factor	0.99
EPSILON_START	Initial exploration rate	0.5
EPSILON_END	Final exploration rate	0.01
DECAY_RATE	Exploration rate decay	0.995
N_ACTIONS	Number of actions	3
MEMORY_SIZE	Experience replay buffer size	2000
BATCH_SIZE	Mini-batch size for training	64
TAU	Target network soft update parameter	0.1
SYNC_TARGET_STEPS	Target network synchronization interval	200
UPDATE_STEPS	Model update interval	4

lists the parameters related to the training and optimization of the reinforcement learning model. The values for parameters such as the learning rate (ALPHA), discount factor (GAMMA), and exploration rate (EPSILON_START) are based on established practices in reinforcement learning, particularly in traffic control and multi-agent systems. These values are consistent with those found in similar studies, such as Wang et al. [16] and Lin et al. [21], where these parameters were shown to yield effective results. Furthermore, these parameters were fine-tuned through preliminary experimentation to ensure optimal performance in the specific traffic scenarios modeled in this study.

To evaluate the robustness and generality of the proposed model, we designed a ramp merging scenario characterized by high traffic density, mixed vehicle types (cars and trucks), and two interacting on-ramps. This configuration was intentionally selected to introduce substantial complexity and variability, closely reflecting typical highway merging conditions in practice. While additional traffic layouts, such as weaving areas or intersections, were not included in the current study due to maintaining a focused scope, the selected setup provides a realistic and challenging testbed for assessing model performance.

This study selected the north-to-south merging area of the Taishan Road Interchange on the S1 Yongtaiwen Expressway in Ningbo, China, for simulation. The main road is a two-lane segment in each direction, with two on-ramps merging into the southbound section. Each merging zone is approximately 250 m in length, followed by a downstream section of 550 m. The simulation duration was set to 1000 s. The main road flow on the S1 Expressway runs in a north-south direction and carries a high traffic volume of 890 veh/h. The on-ramp primarily serves vehicles entering the S1 Expressway from Taishan Road, with a traffic volume of 1086 veh/h. The merging area’s traffic density is particularly high, reaching 1976 veh/h during peak hours. The vehicle composition was 60% passenger cars (max speed 40 m/s) and 40% container trucks (max speed 30 m/s).

To input realistic traffic flow scenarios for on-ramp merging areas, the simulation extracted from OSM sets the through traffic factor for cars to 5 and the count to 12; for trucks, the through traffic factor is set to 5 and the count is set to 8. In the simulation interface, the traffic scaling factor is set to 15. The initial positions of the CAVs were set randomly within the traffic environment, ensuring realistic initial traffic conditions. SUMO is highly suitable for simulating heterogeneous traffic flows that include both heavy trucks and passenger cars. First, we extracted realistic simulation scenarios from OSM. Next, through SUMO’s TraCI interface, Python 3.9.18 was used for secondary development (Figure 11). Finally, TensorFlow, an open-source deep learning framework, was employed to build and train machine learning models. The experiments were conducted on a Windows system equipped with a GPU 2080 Ti.

To highlight the advantages of the proposed Regionally Coordinated Multi-Agent Deep Reinforcement Learning Control Model with Conflict-Aware Q Fusion, we selected a baseline model employing deep Q-learning for ramp merging, where variable speed limits are optimized under a vehicle-to-infrastructure (V2I) environment using spatiotemporal traffic conditions and MPC-based prediction. This baseline integrates METANET-based flow forecasting and uses a compound reward structure involving speed, delay, and throughput to train the DQN controller [34], hereinafter referred to as C-DRL-VSL. We did not adopt the Nash Double Q-learning model as the baseline because their control scenario considers only one ramp vehicle agent.

4.2. Experimental Results

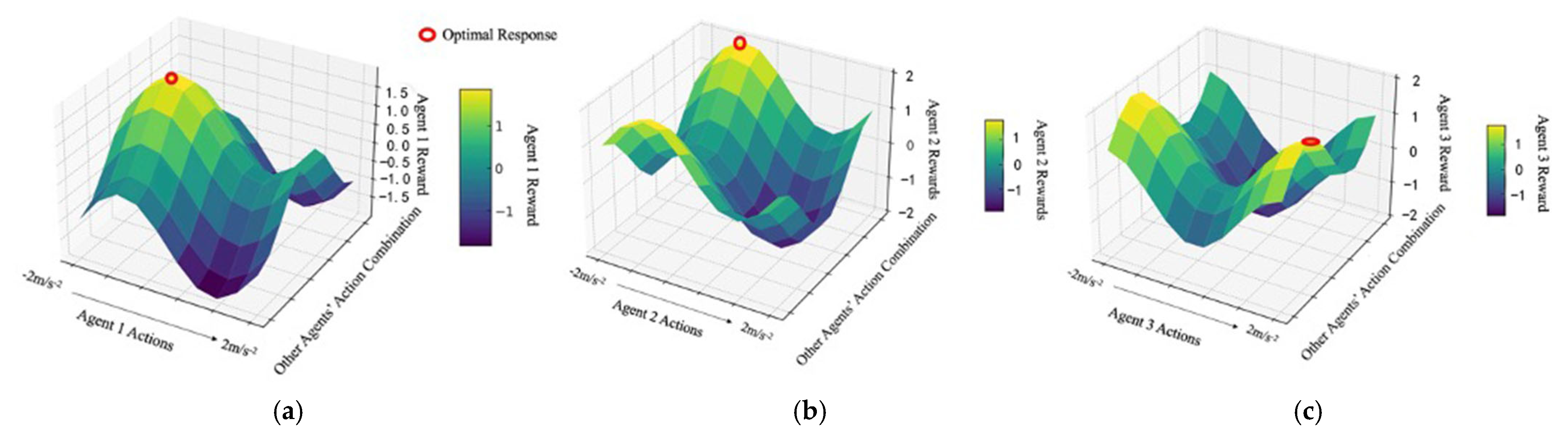
4.2.1. Nash Equilibrium State

During the execution stage, the action spaces and reward functions of the three agents are defined. Given the fixed actions of the other two agents, each agent determines its best response by maximizing its expected reward. The joint action profile in which all agents’ actions are mutual best responses constitutes a Nash equilibrium. By solving this equilibrium, the optimal interactive strategies among traffic flows in the merging game are obtained (Figure 12).

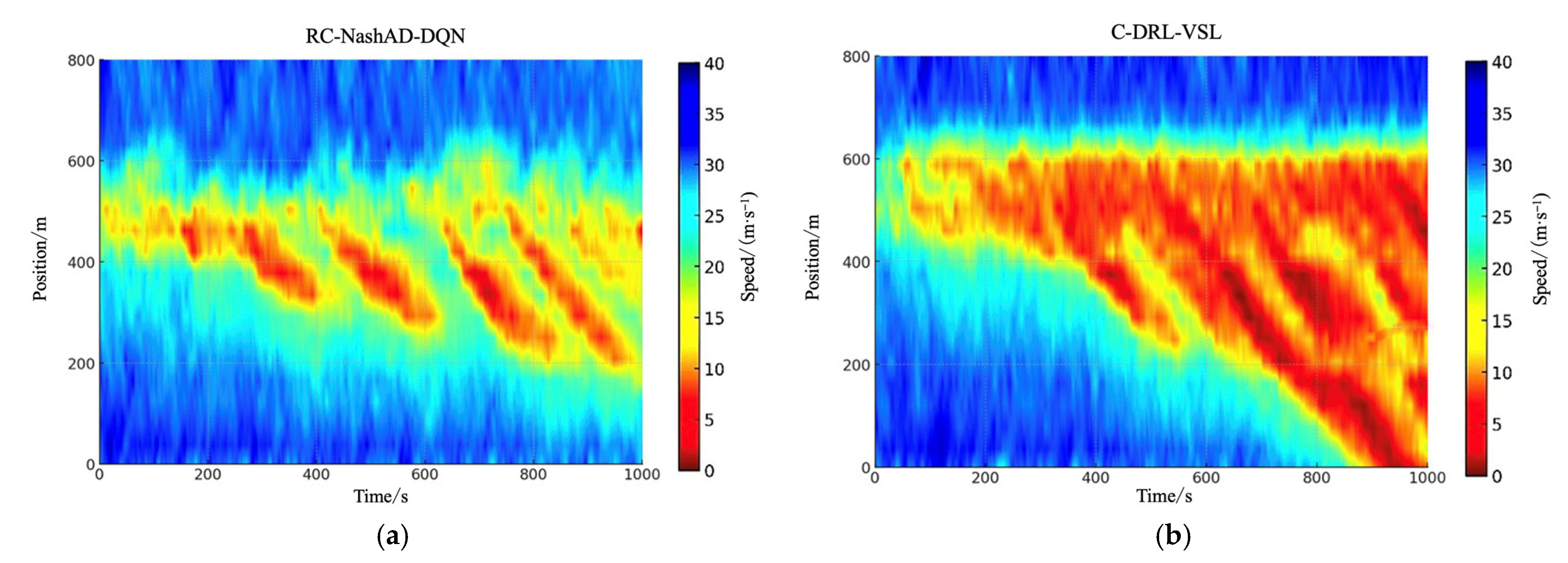
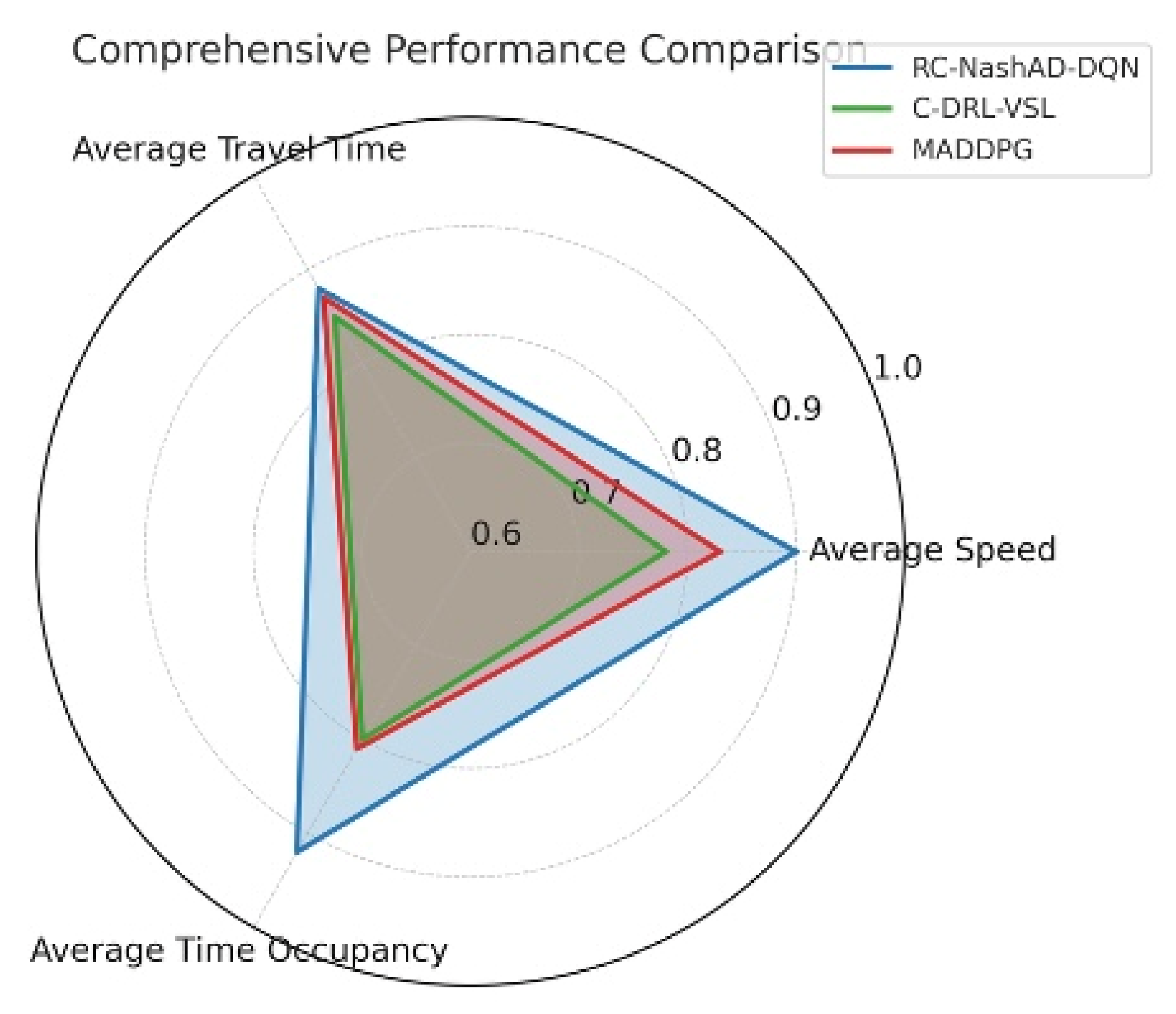
4.2.2. Average Speed

From the comparison of boxplots in Figure 13 and Figure 14, it can be seen that under the RC-NashAD-DQN model, the speed distribution of vehicles, whether on the main road or the two on-ramps, is broader. This indicates that vehicles can achieve higher speeds, and the overall mean speed is also higher. In contrast, under the C-DRL-VSL model, the median and maximum speeds are significantly lower than those under the RC-NashAD-DQN model. Vehicle speeds are clearly constrained, reflecting the poor performance of the C-DRL-VSL model in addressing vehicle acceleration and on-ramp merging issues.

By collecting the average real-time segment speed across the entire 800 m length of the highway main road, heatmaps of average segment speeds over time were obtained under both the C-DRL-VSL model and the RC-NashAD-DQN model (Figure 15). Segment average speeds were calculated every 200 m, starting from the upstream point of the main road, taking the average instantaneous speeds of all vehicles within each segment, resulting in four segments across the 800 m stretch. In Figure 15, the vertical axis represents the relative position from the upstream starting point, the horizontal axis represents simulation time, and the color represents the segment’s average speed, with transitions from red to blue indicating increasing average speeds.

From Figure 15, it can be observed that at 200 s into the simulation, the average segment speed starts to decrease slightly within the 400–600 m downstream segment of the main road. As the simulation progresses, traffic congestion on the main road gradually spreads upstream until severe congestion is observed across the 600 m stretch from the starting point. Comparing the heatmaps of average segment speeds under the C-DRL-VSL model and the RC-NashAD-DQN model, it can be found that under the C-DRL-VSL model, traffic congestion spreads upstream over time, and by approximately 800 s into the simulation, severe congestion is prevalent within the 600 m stretch from the upstream starting point, with average speeds generally below 10 m/s. In contrast, under the RC-NashAD-DQN model, traffic congestion also spreads upstream over time, but even by the end of the simulation, only mild congestion is observed within the 800 m stretch from the starting point, with average speeds remaining above 10 m/s.

Quantitative analysis reveals that the RC-NashAD-DQN framework achieves a 23.4% higher congestion dissipation rate (p < 0.05, t-test) compared to the C-DRL-VSL model, slows the upstream spread of congestion, and maintains higher average speeds over the same simulation time. In contrast, the C-DRL-VSL model results in longer congestion segments and lower average speeds on the main road.

4.2.3. Average Travel Time

From Figure 16 and Figure 17, it is evident that RC-NashAD-DQN consistently outperforms the baseline C-DRL-VSL in optimizing travel time for both passenger cars and container trucks. Specifically, for passenger cars, RC-NashAD-DQN achieves a more compact and uniform travel time distribution, effectively reducing extreme cases of delay and eliminating the long-tail phenomenon observed in the baseline.

For container trucks, the performance advantage is even more pronounced. This is primarily due to the inherent differences in following behavior—container trucks require longer headways and have lower acceleration capabilities, making them more sensitive to control strategies. RC-NashAD-DQN incorporates a value-advantage decomposition architecture, which enables the model to better distinguish the action value differences under the same state. This mechanism is particularly beneficial for vehicles with limited maneuverability, such as trucks, as it enhances the model’s ability to learn fine-grained, adaptive control strategies. By decomposing the Q-value into a shared state value and action-specific advantages, the model can more precisely evaluate when cautious actions (e.g., maintaining distance or gentle acceleration) are truly advantageous. Coupled with the regionally coordinated framework, the model facilitates safer and more efficient integration of heavy vehicles, especially under high-density and conflict-prone merging scenarios.

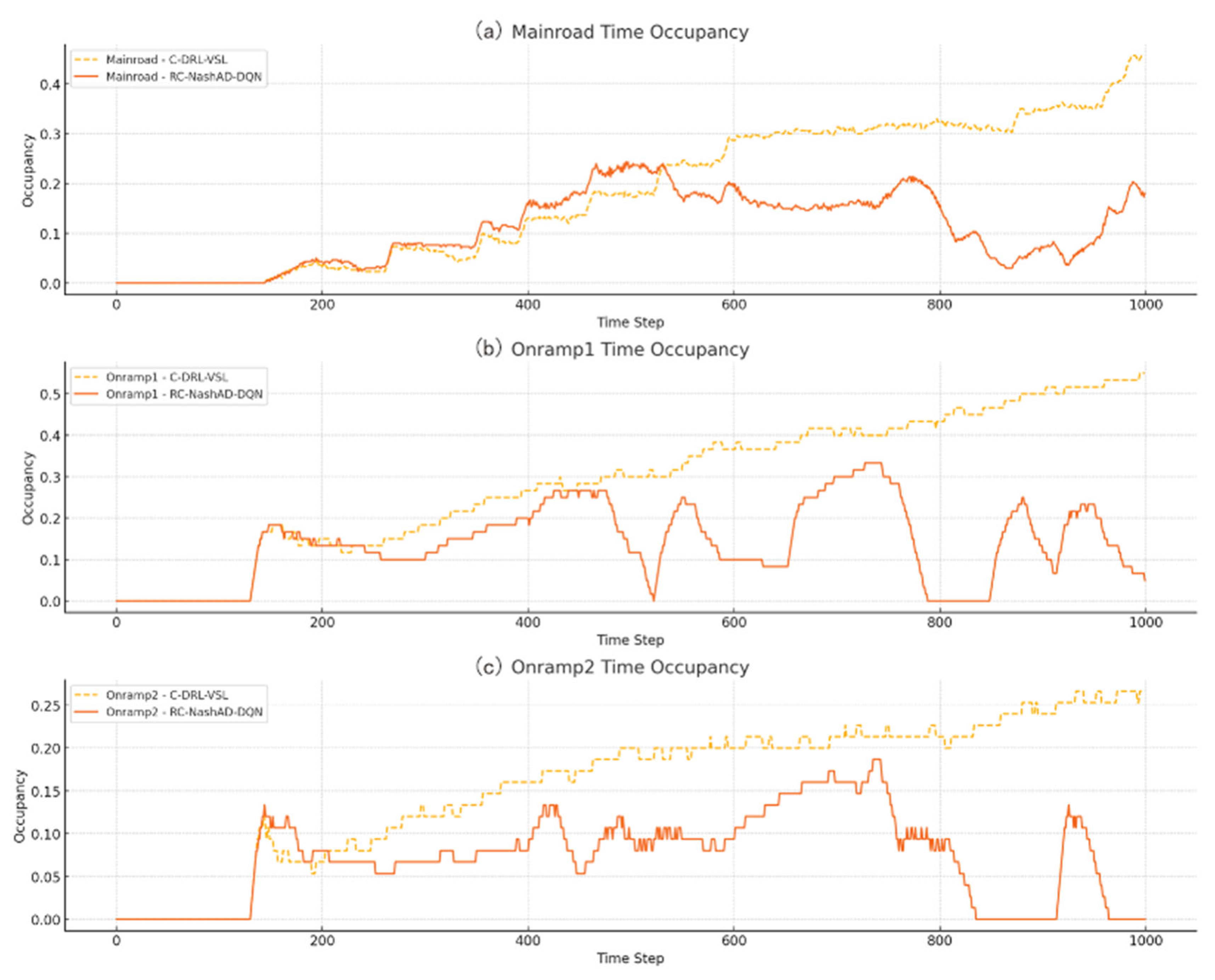
4.2.4. Time Occupancy

The average time occupancy describes the proportion of time a road segment is occupied by vehicles during the observation period. From Figure 18, it can be observed that RC-NashAD-DQN is more flexible in adjusting time occupancy, demonstrating strong adaptability and dynamic control capabilities. It effectively reduces occupancy rates during peak periods, thus lowering the likelihood of congestion. In contrast, C-DRL-VSL generally exhibits higher time occupancy rates and lacks sufficient adjustment capabilities across different road segments, resulting in more severe traffic congestion. This analysis indicates that RC-NashAD-DQN has greater advantages in complex traffic management scenarios, effectively improving traffic efficiency and reducing traffic flow pressure.

4.3. Computational Cost and Robustness

In Section 4.2, the proposed framework was first compared with C-DRL-VSL to directly assess the improvements over a DQN-based baseline. In Section 4.3, we extend the comparison to also include MADDPG [35], which represents a different class of multi-agent reinforcement learning methods (policy gradient approaches). This allows us to demonstrate that the advantages of Nash coordination and Q-fusion are not limited to DQN-based settings but generalize to broader MARL paradigms. To keep the evaluation focused and comparable, broader baselines such as QMIX or VDN are not included.

4.3.1. Computational Cost

In addition to performance metrics, we compared the computational cost and convergence time among all models. Figure 19 and Figure 20 report the average convergence time and the average training duration per episode for the proposed model and the baseline methods. These results provide a clear view of the trade-off between performance gains and computational requirements.

In Figure 19, the x-axis represents the number of training episodes, and the y-axis denotes the average cumulative reward per episode. The solid blue line corresponds to RC-NashAD-DQN, the solid orange line to C-DRL-VSL, and the solid green line to MADDPG. RC-NashAD-DQN not only outperforms in terms of convergence speed but also achieves a significantly higher final return than the other two methods, indicating its advantages in strategy stability and long-term rewards.

Figure 20 highlights the trade-off between performance and computational cost: RC-NashAD-DQN sacrifices some per-episode training speed but achieves much faster convergence, leading to superior overall efficiency compared to the baseline models.

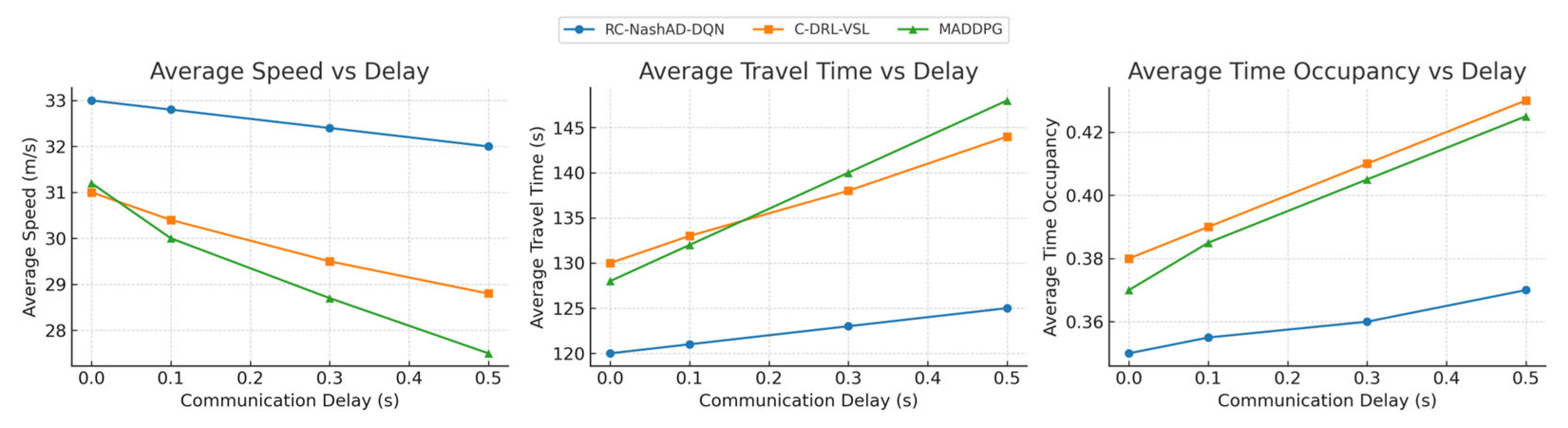
4.3.2. Robustness

To evaluate the transferability of RC-NashAD-DQN, we further tested the model under increased agent density (1.5× baseline) in the ramp merging scenario. The results indicate that the proposed framework maintains stable performance in terms of equilibrium strategy convergence, average travel time, and time occupancy, demonstrating robustness to higher traffic demand. While this study focuses on ramp merging, the region-level coordination design is adaptable to other highway configurations (e.g., weaving sections, roundabouts) with minimal modification to the region partitioning and communication modules, suggesting good potential for broader application.

This radar chart (Figure 21) compares the normalized comprehensive performance of RC-NashAD-DQN, C-DRL-VSL (a DQN variant), and MADDPG across average speed, average travel time, and average time occupancy, showing that RC-NashAD-DQN consistently achieves the best results in all metrics, followed by MADDPG, while C-DRL-VSL performs the worst, highlighting the superior efficiency and coordination capability of RC-NashAD-DQN in high-density traffic scenarios.

In the baseline setting, we assume that agents can fully observe the required states of neighboring CAVs within their region without noise or delay. This assumption facilitates the evaluation of the proposed algorithm under idealized conditions, enabling clearer analysis of the core decision-making mechanism. However, in real-world CAV deployments, communication channels are subject to latency, packet loss, and partial observability. To investigate the robustness of our method, we conducted a supplementary experiment introducing random communication delays (uniformly distributed between 0.1 s and 0.5 s) and packet loss rates up to 10%. Results show that RC-NashAD-DQN maintained superior performance compared with baseline methods, with only moderate degradation in average speed and travel time (Figure 22). This demonstrates that our framework can tolerate moderate communication imperfections, although future work will further explore robust policy learning techniques to address more severe communication constraints.

5. Conclusions

This study focuses on traffic control in on-ramp merging scenarios and proposes a multi-agent deep reinforcement learning model based on NashAD-DQN and conflict-aware Q fusion for connected and automated vehicles (CAVs), aiming to address traffic congestion and delay issues in on-ramp merging areas and to support the development of sustainable transportation systems.

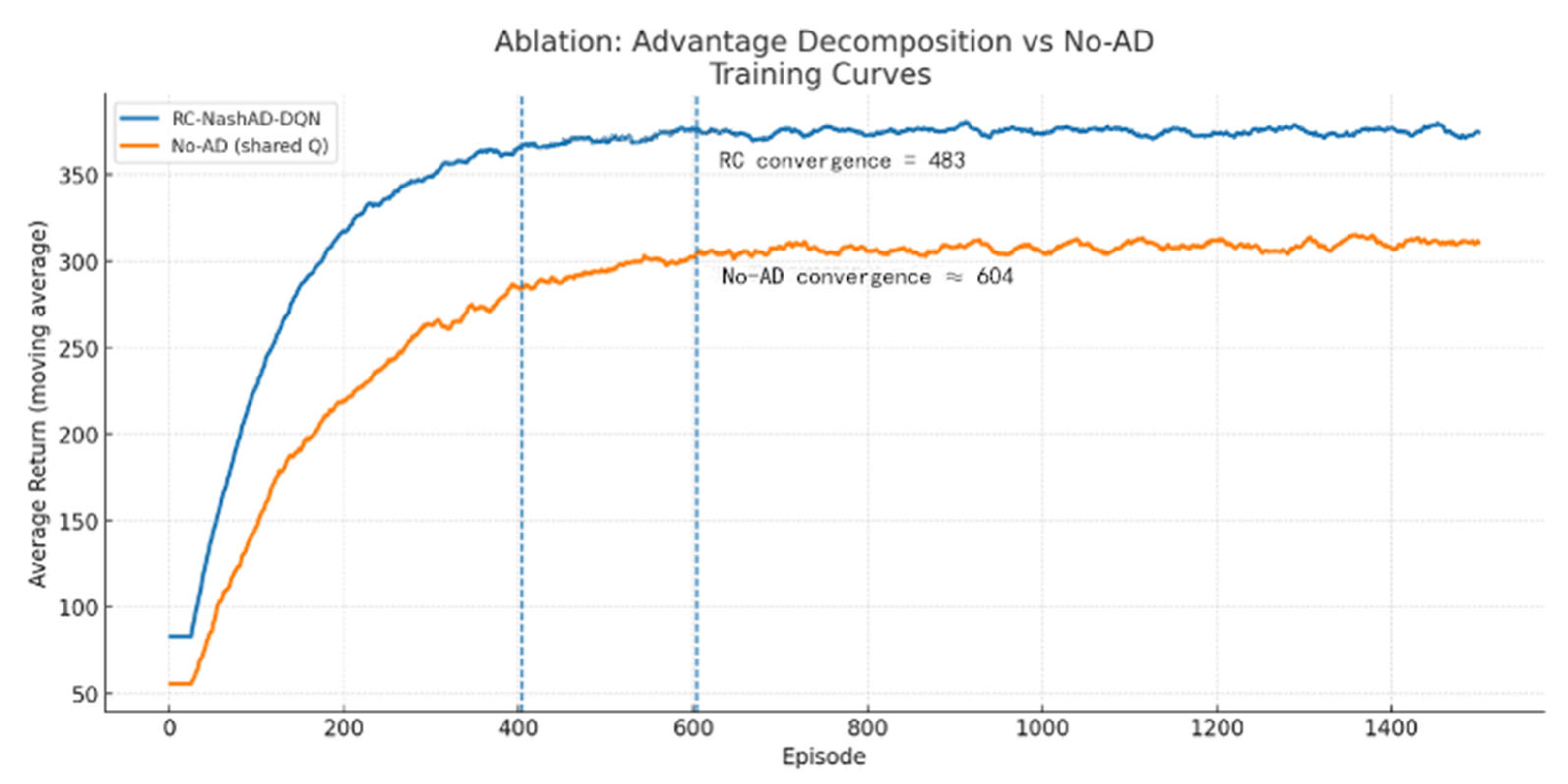
• The proposed framework addresses two major limitations in existing multi-agent reinforcement learning traffic control models: instability in equilibrium strategy learning and the lack of fine-grained conflict resolution across regions. By embedding a conflict-aware Q-fusion mechanism into the Nash Advantage Decomposition Deep Q-Network, the model effectively balances global coordination with local adaptability, achieving higher strategy stability and reduced solution overhead. Moreover, the region-level control design supports scalable deployment in complex traffic networks.
• Simulation experiments conducted on real-world highway merging settings show that the proposed approach significantly improves average speed, reduces time occupancy, and lowers travel time compared to the C-DRL-VSL baseline. These results demonstrate the effectiveness of embedding spatio-temporal conflict resolution into Nash-based learning and underscore the practical value of region-level coordination in balancing local interactions and global traffic efficiency.

Future research can be extended and deepened in the following directions:

• Precisely simulating individual vehicle behavior, such as lane-changing, acceleration, and deceleration, by setting ramp merging rules and main road traffic rules in the model to accurately capture the interaction processes among vehicles.
• Developing adaptive traffic control strategies for mixed traffic flows, where CAVs coexist with human-driven vehicles.
• Exploring more complex and multi-layered traffic management architectures to further enhance the cooperation and competition capabilities of CAVs, contributing to sustainable intelligent transportation development.
• Future work will extend the evaluation to more diverse traffic configurations, enabling a broader validation of the proposed approach across different roadway geometries and operational conditions.