Spatiotemporal Responses and Threshold Mechanisms of Urban Landscape Patterns to Ecosystem Service Supply–Demand Dynamics in Central Shenyang, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Preprocessing
2.3. Methods
2.3.1. The Landscape Index
2.3.2. Assessment of Ecosystem Service Supply and Demand
- (1)
- WR
- (2)
- FR
- (3)
- AP
- (4)
- CS
- (5)
- HQ
- (6)
- Ecological supply–demand ratio (ESDR)
2.3.3. Spatial Variation Trend
2.3.4. Driving Forces and Threshold Analysis Methods
- (1)
- Screening of potential landscape characteristic factors
- (2)
- Driving Force Analysis Based on XGBoost-SHAP
- (3)
- Threshold Analysis
3. Results
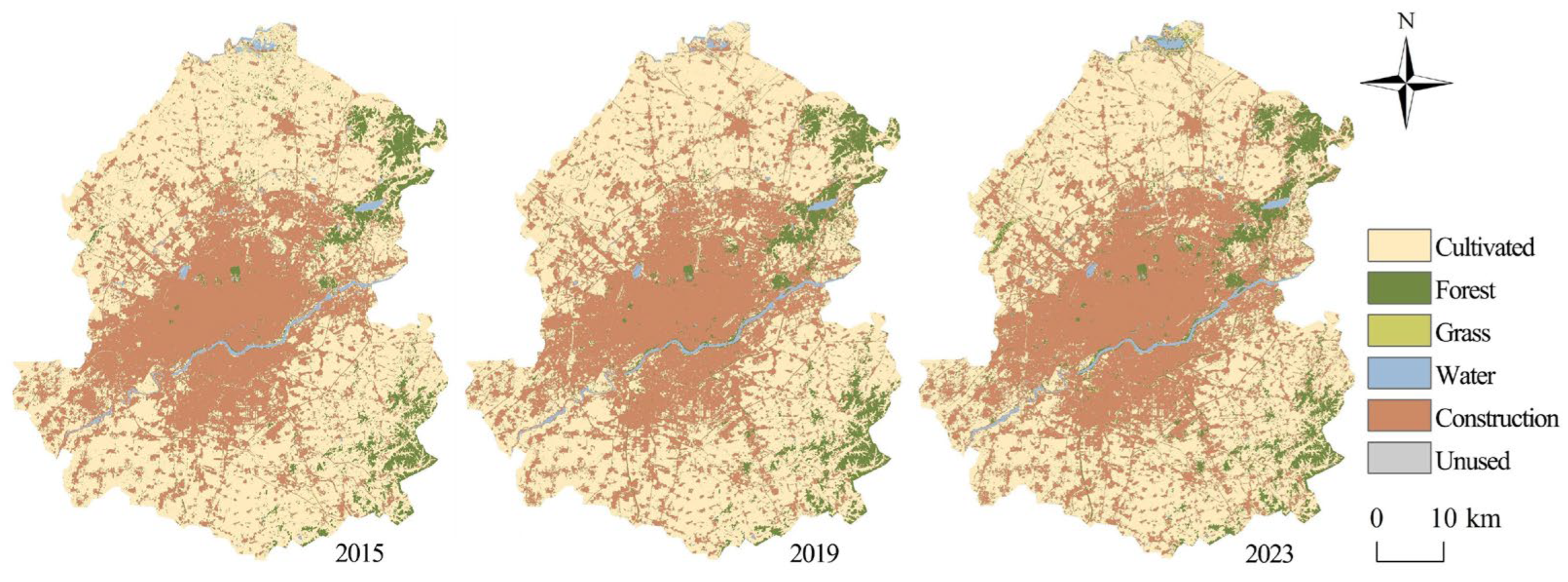
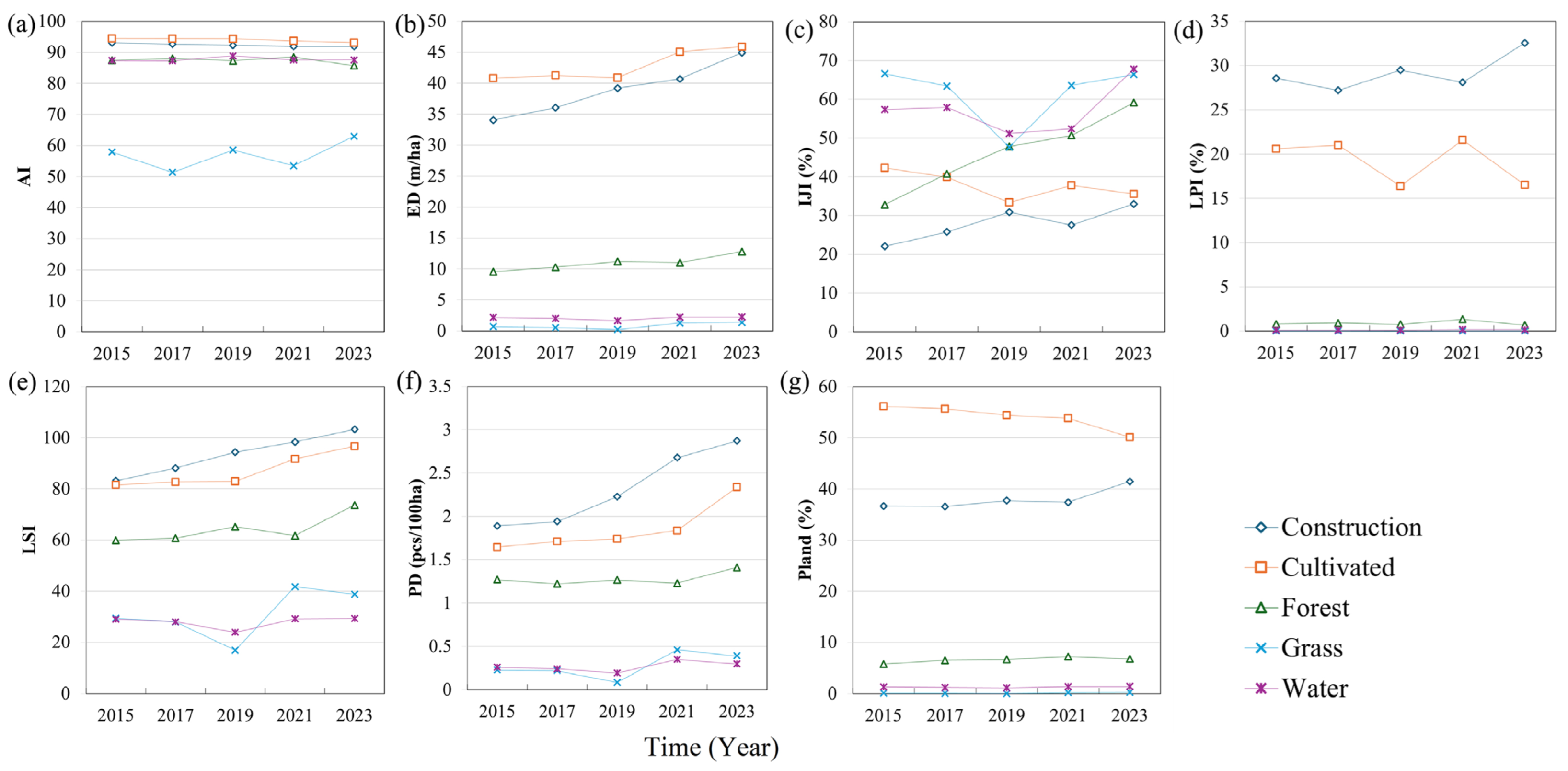
3.1. Spatiotemporal Differentiation Characteristics of Landscape Patterns
3.1.1. Temporal Differentiation Characteristics
3.1.2. Spatial Differentiation Characteristics
3.2. Spatiotemporal Differentiation Characteristics of ES Supply and Demand
3.2.1. Spatiotemporal Differentiation Characteristics of Supply
3.2.2. Spatiotemporal Differentiation Characteristics of Demand
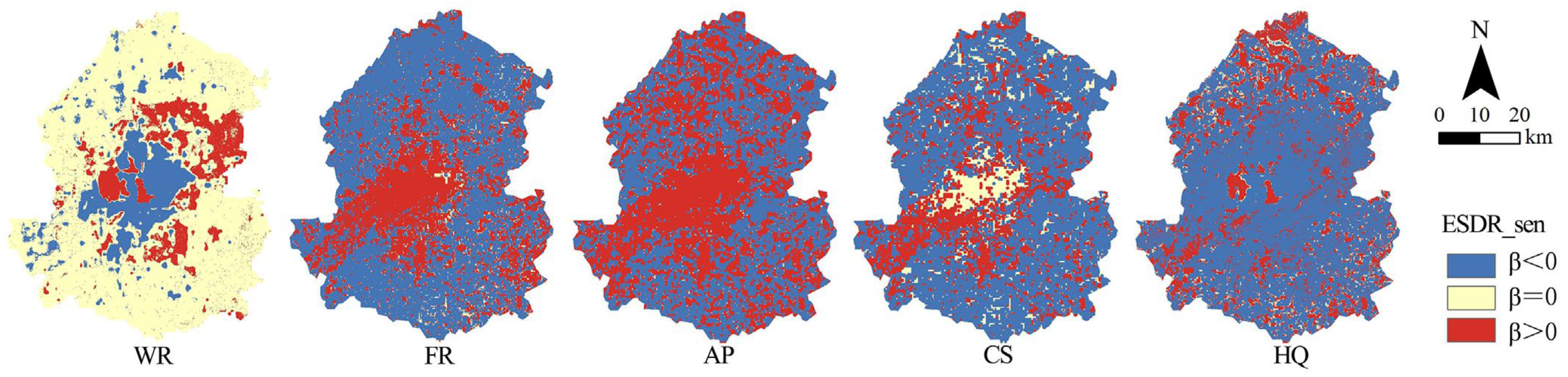
3.2.3. Spatiotemporal Differentiation Characteristics of ESDR
3.3. Results of Driving Mechanism Analysis
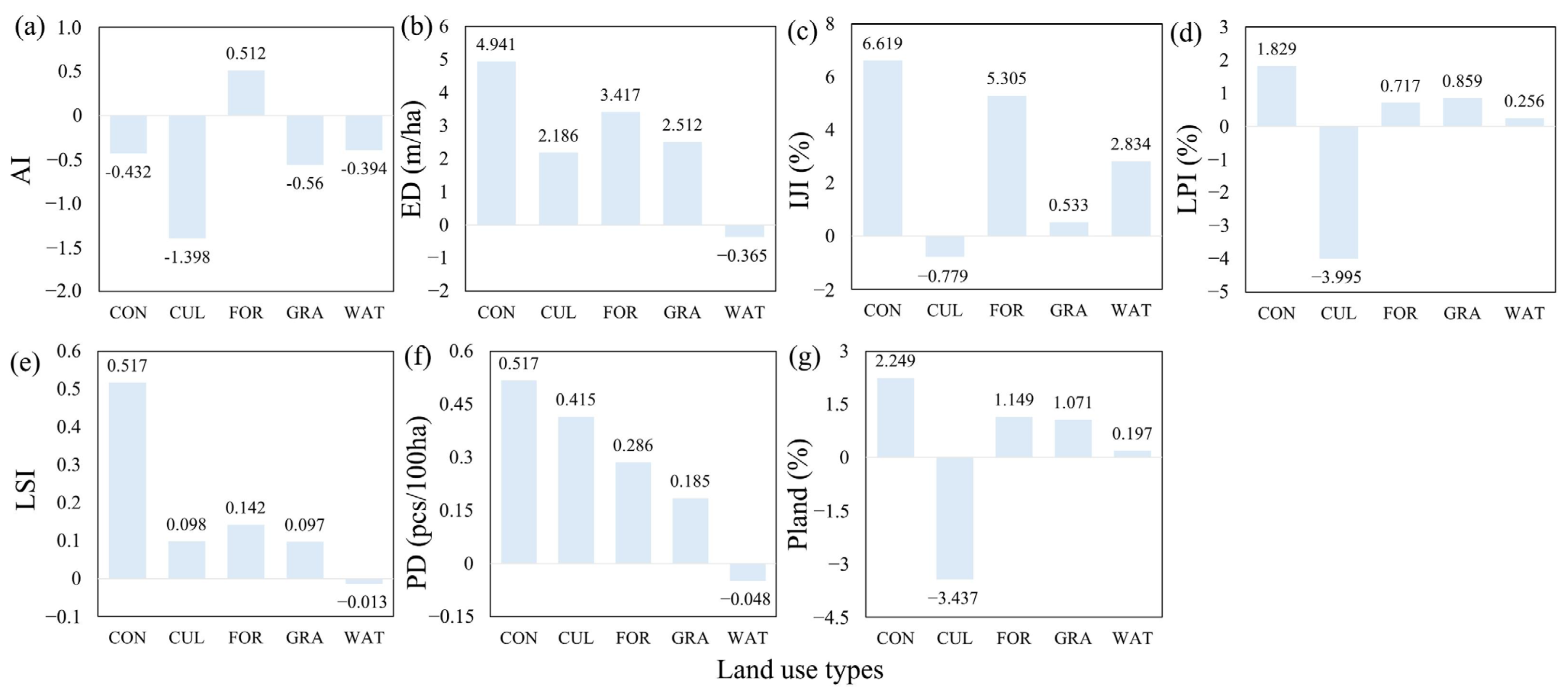
3.3.1. Screening of Landscape Characteristic Factors
3.3.2. Correlation Between Landscape Characteristic Factors and ESs
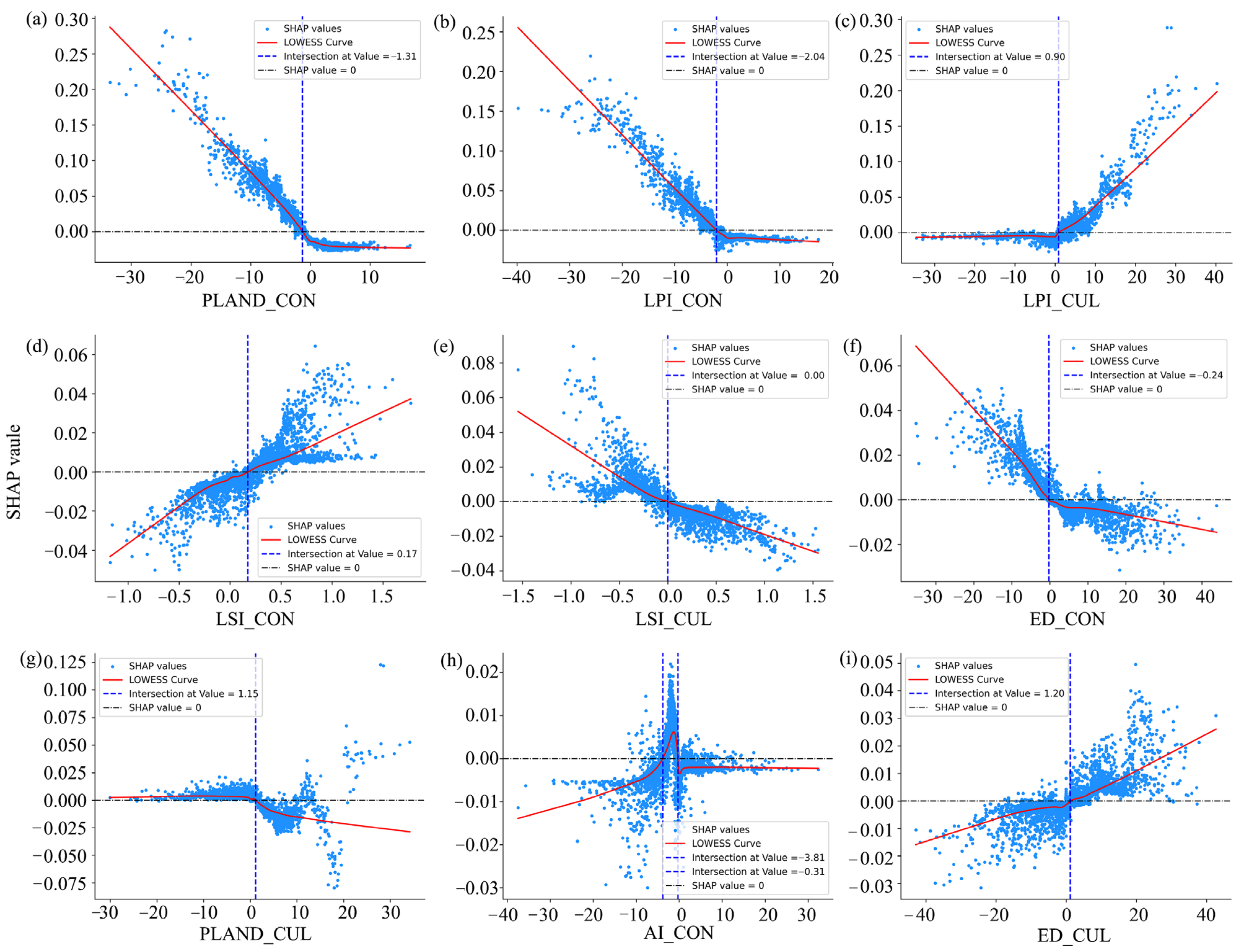
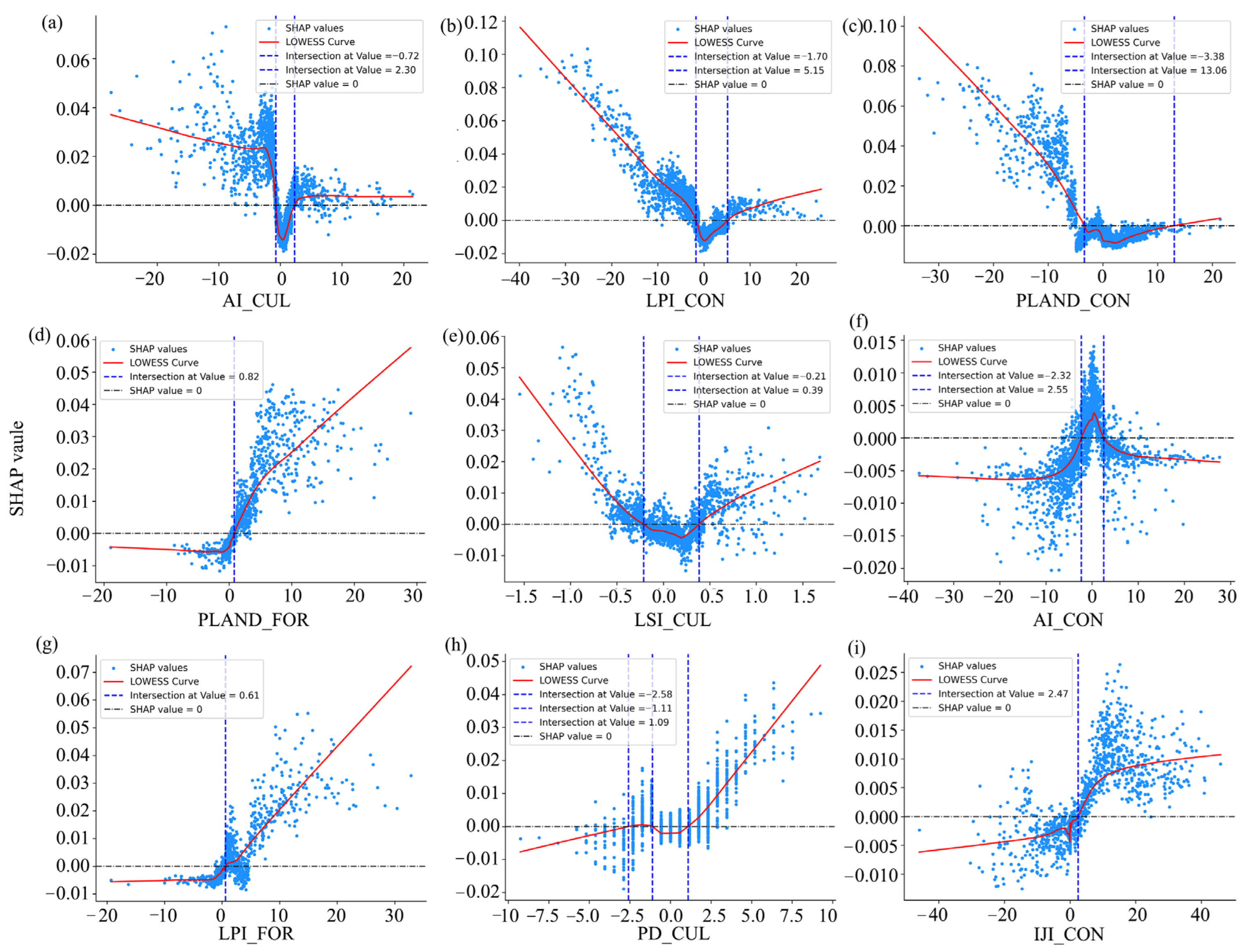
3.3.3. Threshold Effect of Landscape Characteristic Factors
4. Discussion
4.1. Interactive Relationship Between Landscape Pattern Indices and Supply–Demand of ESs
4.2. Driving Mechanism and Threshold Analysis
4.3. Development Suggestions
4.4. Limitations and Prospects
5. Conclusions
- (1)
- The spatiotemporal distribution of landscape pattern indices at the patch-type level reveals significant differences across land types. Over time, the annual fluctuations of these indices vary by land category: construction land and forest areas have generally exhibited upward trends, while cultivated land has shown a consistent decline. Water bodies have remained relatively stable, whereas grassland has experienced the most pronounced fluctuations. In terms of spatial distribution, variations in the landscape indices are also evident due to the differing geographic locations of each land type, resulting in diverse patterns of change across the study area.
- (2)
- The supply, demand, and supply–demand relationships of different ESs exhibit significant spatial variation. Established urban areas typically experience a supply deficit but show strong potential for positive development. In contrast, emerging urban areas often demonstrate a supply surplus; however, they are trending toward unfavorable development. The proportions of favorable development zones for the supply–demand relationships of water regulation (WR), AP, FR, CS, and HQ are 14.5%, 35.8%, 50.2%, 25.6%, and 25.3%, respectively.
- (3)
- The influence of landscape pattern characteristics on ESs is distinctly non-linear, with each index exerting a unique effect and exhibiting clear threshold intervals. Among these factors, area-related indices, specifically PLAND and LPI, emerge as the primary drivers influencing the favorable development of ES supply–demand relationships. The shape index (LSI) ranks second in importance when determining target values. Other indices, such as AI, IJI, ED, and PD, show varying effects across different types of ESs, underscoring the complexity and context-specific nature of their impacts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form |
| ESs | Ecosystem services |
| WR | Water retention |
| FR | Flood regulation |
| AP | Air purification |
| CS | Carbon sequestration |
| HQ | Habitat quality |
| ESDR | Ecological supply–demand ratio |
| ESDR_WR | Ecological supply–demand ratio of water retention |
| ESDR_FR | Ecological supply–demand ratio of flood regulation |
| ESDR_AP | Ecological supply–demand ratio of air purification |
| ESDR_CS | Ecological supply–demand ratio of carbon sequestration |
| ESDR_HQ | Ecological supply–demand ratio of habitat quality |
| AI_CON | Aggregation Index for construction |
| AI_CUL | Aggregation Index for cultivated |
| AI_FOR | Aggregation Index for forest |
| AI_GRA | Aggregation Index for grassland |
| AI_WAT | Aggregation Index for water |
| ED_CON | Edge density for construction |
| ED_CUL | Edge density for cultivated |
| ED_FOR | Edge density for forest |
| ED_GRA | Edge density for grassland |
| ED_WAT | Edge density for water |
| IJI_CON | Interspersion and juxtaposition index for construction |
| IJI_CUL | Interspersion and juxtaposition index for cultivated |
| IJI_FOR | Interspersion and juxtaposition index for forest |
| IJI_GRA | Interspersion and juxtaposition index for grassland |
| IJI_WAT | Interspersion and juxtaposition index for water |
| LPI_CON | Largest patch index for construction |
| LPI_CUL | Largest patch index for cultivated |
| LPI_FOR | Largest patch index for forest |
| LPI_GRA | Largest patch index for grassland |
| LPI_WAT | Largest patch index for water |
| LSI_CON | Landscape shape index for construction |
| LSI_CUL | Landscape shape index for cultivated |
| LSI_FOR | Landscape shape index for forest |
| LSI_GRA | Landscape shape index for grassland |
| LSI_WAT | Landscape shape index for water |
| PD_CON | Patch density for construction |
| PD_CUL | Patch density for cultivated |
| PD_FOR | Patch density index for forest |
| PD_GRA | Patch density index for grassland |
| PD_WAT | Patch density index for water |
| PLAND_CON | Percentage of landscape for construction |
| PLAND_CUL | Percentage of landscape for cultivated |
| PLAND_FOR | Percentage of landscape for forest |
| PLAND_GRA | Percentage of landscape for grassland |
| PLAND_WAT | Percentage of landscape for water |
References
- Wang, W.J.; Wang, G.Y.; Yang, M.L.; Mu, X.H.; Zhu, Z.W. Strategies of Critical Areas of Ecological Space in High-density Urban Areas from the Perspective of Ecosystem Supply and Demand, A Case Study of Guilin. Chin. Landsc. Archit. 2024, 40, 15–21. [Google Scholar]
- Costanza, R.; d’Arge, R.; de Groot, R.; Belt, M. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Su, C.; Fu, B.J. Discussion on Links Among Landscape Pattern, Ecological Process, and Ecosystem Services. Chin. J. Nat. 2012, 34, 277–283. [Google Scholar]
- Castro, A.J.; Verburg, P.H.; Martín-López, B.; Garcia-Llorente, M.; Cabello, J.; Vaughn, C.C.; López, E. Ecosystem service trade-offs from supply to social demand: A landscape-scale spatial analysis. Landsc. Urban Plan. 2014, 132, 102–110. [Google Scholar] [CrossRef]
- Baró, F.; Haase, D.; Gómez-Baggethun, E.; Frantzeskaki, N. Mismatches between ecosystem services supply and demand in urban areas: A quantitative assessment in five European cities. Ecol. Indic. 2015, 55, 146–158. [Google Scholar] [CrossRef]
- Choumert, J. An empirical investigation of public choices for green spaces. Land Use Policy 2010, 27, 1123–1131. [Google Scholar] [CrossRef]
- Cheng, C.N.; Hu, Y.; Zhao, M. Progress and prospect of the spatiotemporal change and ecosystem services evaluation of urban green space pattern. Prog. Geogr. 2020, 39, 1770–1782. [Google Scholar] [CrossRef]
- Shao, M.; Li, F.Z.; Li, X. Evaluation of Supply and Demand of Green Space Ecosystem Service Function in Chengdu-Chongqing Urban Agglomeration Based on Multi-source Data. Landsc. Archit. 2021, 28, 60–66. [Google Scholar]
- Liu, X.; Wang, K.; Qi, Z.X.; Li, T.; Li, S. Urban green space layout optimization based on ecosystem service supply and demand. J. Hunan Ecol. Sci. 2022, 9, 8–17. [Google Scholar]
- Liu, Y.T.; Qin, M.L.; Ouyang, H.T. The optimization of territorial spatial resources allocation based on the balance of supply and demand of ecosystem services. J. Nat. Resour. 2024, 39, 1358–1383. [Google Scholar] [CrossRef]
- Wang, X.K.; Su, Y.B.; Ren, Y.F.; Zhang, H.X.; Sun, X.; Ouyang, Z.Y. Urban ecosystem: Highly spatial heterogeneity. Acta Ecol. Sin. 2020, 40, 5103–5112. [Google Scholar]
- Kirwan, M.L.; Megonigal, J.P. Tidal wetland stability in the face of human impacts and sea-level rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef]
- Yang, W.Q.; Yang, P.; Sun, X.; Han, B.L. Changes of landscape patter and its impacts on multiple ecosystem services in Beijing. Acta Ecol. Sin. 2022, 42, 6487–6498. [Google Scholar]
- Su, S.L.; Xiao, R.; Jiang, Z.L.; Zhang, Y. Characterizing landscape pattern and ecosystem service value changes for urbanization impacts at an eco-regional scale. Appl. Geogr. 2012, 34, 295–305. [Google Scholar] [CrossRef]
- Liang, Y.J.; Liu, L.J. Integration of ecosystem services and landscape pattern: A review. Acta Ecol. Sin. 2018, 38, 7159–7167. [Google Scholar] [CrossRef]
- Ayinuer, Y.; Zhang, F.; Yu, H.Y.; Kung, H. Quantifying the spatial correlations between landscape pattern and ecosystem service value: A case study in Ebinur Lake Basin, Xinjiang, China. Ecol. Eng. 2018, 113, 94–104. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Tong, Z.M.; Zhang, L.T.; Liu, Y.L. Nonlinear effects of landscape patter on ecosystem services and threshold regulation; a case study of eco-efficient synergistic zone in Fujian Province. Acta Ecol. Sin. 2024, 44, 9535–9551. [Google Scholar]
- Wu, X.; Zhou, Z.X. Spatial relationship belween supply and demand of ecosystem services through urban green infrastructure: Case of Xi’ an Cily. Acta Ecol. Sin. 2019, 39, 9211–9221. [Google Scholar]
- Xu, C.; Meng, N.; Lu, F. Research on Urban Green Infrastructure Management in Macao from the Perspective of Ecosystem Service Demand. Chin. Landsc. Archit. 2020, 36, 104–109. [Google Scholar]
- Meerow, S.; Newell, J.P. Spatial planning for multifunctional green infrastructure: Growing resilience in Detroit. Landsc. Urban Plan. 2017, 159, 62–75. [Google Scholar] [CrossRef]
- Gu, K.K.; Cheng, F.; Yang, Q.Q. Analysis of multifunctional urban green infrastructure using a GISP model. Acta Ecol. Sin. 2018, 38, 7113–7119. [Google Scholar] [CrossRef]
- Li, J.Y.; Yang, D.D.; Yang, F.; Zhang, Y.; Wang, H.C. Influence of landscape pattern on ecosystem service supply-demand mismatch in Tianjin within the context of urbanization. Acta Ecol. Sin. 2024, 44, 4987–5002. [Google Scholar]
- Grêt-Regamey, A.; Bebi, P.; Bishop, I.D.; Schmid, W.A. Linking GIS-based models to value ecosystem services in an Alpine region. J. Environ. Manag. 2008, 89, 197–208. [Google Scholar] [CrossRef]
- Inkoom, J.N.; Frank, S.; Greve, K.; Walz, U.; Fürst, C. Suitability of Different Landscape Metrics for the Assessments of Patchy Landscapes in West Africa. Ecol. Indic. 2018, 85, 117–127. [Google Scholar] [CrossRef]
- Qi, Y.X.; Shen, P.X.; Ren, S.; Chen, T.Y.; Hu, Y.D. Coupling effect of landscape patterns on the spatial and temporal distribution of ecosystem services: A case study in Harbin City, Northeast China. Sci. Rep. 2025, 15, 4606. [Google Scholar] [CrossRef]
- Eziz, M.; Yimit, H.; Tursun, Z.; Rusuli, Y. Variations in Ecosystem Service Value in Response to Oasis Land-use Change in Keriya Oasis, Tarim Basin, China. Nat. Areas J. 2014, 34, 353–364. [Google Scholar] [CrossRef]
- Yang, N.; Tan, X.W.; You, Z.X. Strategies and Practice of Ecological Restoration Planning for National Land and Space in the New Era, Shenyang. Planners 2020, 36, 34–38+45. [Google Scholar]
- Wu, Y.; Shi, K.; Chen, Z.; Liu, S.; Chang, Z. An improved time-series DMSP-OLS-like data (1992–2023) in China by integrating DMSP-OLS and SNPP-VIIRS. In Harvard Dataverse; Harvard University: Cambridge, MA, USA, 2021; Volume 5. [Google Scholar] [CrossRef]
- Wu, J.G. Chapter 1 Basic Concepts in Landscape Ecology. Landscape Ecology: Pattern, Process, Scale and Hierarchy, 2nd ed.; Higher Education Press: Beijing, China, 2007; pp. 2–24. [Google Scholar]
- Li, D.K.; Ding, S.Y.; Liang, G.F.; Zhao, Q.H.; Tang, Q.; Kong, L.H. Landscape heterogeneity of mountainous and hilly area in the wester Henan Province based on moving window method. Acta Ecol. Sin. 2014, 34, 3414–3424. [Google Scholar]
- Zhou, D.M.; Chen, C.Y.; Wang, M.J.; Luo, Z.W.; Kang, L.T.; Wu, S. Gradient and Directional Differentiation in Landscape Patter Characteristics of Urban Ecological Space Based on Optimal Spaltial Scale: A Case Study in Changsha City, China. J. Ecol. Rural. Environ. 2022, 38, 566–577. [Google Scholar]
- Wang, B.; Shu, X.B.; Liao, F.Q.; Li, Y.; Wan, Z.W. Spatitemporal of Land Use Conflicts and Multi-Scenario Simulation in Poyang Lake Area Based on Optimal Landscape Scale. Res. Soil Water Conserv. 2024, 31, 336–347. [Google Scholar]
- Zhang, C.S.; Fan, N.; Liu, C.L.; Xie, G.D. Spatio-temporal pattern and evolution of ecosystem water conservation in China from from 1990 to 2023. Acta Ecol. Sin. 2023, 43, 5536–5545. [Google Scholar]
- Zhang, C.S.; Xie, G.D.; Liu, C.L.; Fan, N.; Wang, X.K. Evaluation of water conservation of China s ecosystems based on benchmark. Acta Ecol. Sin. 2022, 42, 9250–9260. [Google Scholar]
- Jiang, B.; Bai, Y.; Chen, J.; Alatalo, J.M.; Xu, X.; Liu, G.; Wang, Q. Land management to reconcile ecosystem services supply and demand mismatches—A case study in Shanghai municipality, China. Land Degrad. Dev. 2020, 31, 2684–2699. [Google Scholar] [CrossRef]
- Kong, L.Q.; Wang, Y.Q.; Zheng, H.; Xiao, Y.; Xu, W.H.; Zhang, L.; Xiao, Y.; Ouyang, Z.Y. A method for evaluating ecological space and ecological conservation redlines in river basins: A case of the Yangtze River Basin. Acta Ecol. Sin. 2019, 39, 835–843. [Google Scholar] [CrossRef]
- Kang, D.; Ye, Q. Study on evaluation and decomposition of volume capture ratio of annual rainfall in sponge city. China Water Wastewater 2015, 31, 4. [Google Scholar]
- Monthly Report on Urban Air Quality Status. Available online: https://www.mee.gov.cn/hjzl/dqhj/cskqzlzkyb/ (accessed on 4 March 2025).
- Li, C.H.; Hu, M.L.; Yong, X.Q. Upply-demand matching of ecosystem services in xuzhou. J. Hunan Ecol. Sci. 2022, 9, 10. [Google Scholar]
- Landuyt, D.; Broekx, S.; Engelen, G.; Uljee, I.; Van der Meulen, M.; Goethals, P.L.M. The importance of uncertainties in scenario analyses—A study on future ecosystem service delivery in Flanders. Sci. Total Environ. 2016, 553, 504–518. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, B.; Bai, Y.; Xu, X.B.; Alatalo, J.M. Quantifying ecosystem services supply and demand shortfalls and mismatches for management optimization. Sci. Total Environ. 2019, 650, 1426–1439. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Huang, Y.; Wang, R.; Mei, J. Dependence of air pollutants concentration on mixing height in Tongling City. Environ. Sci. Technol. 2018, 41, 63–70. [Google Scholar]
- Zhu, L.Y.; Hu, K.; Sun, S. Research on the Spatiotemporal Variation of Carbon Storage in the Coastal Zone of Liaoning Province Based on InVEST Model. GEOSCIENCE 2022, 36, 96–104. [Google Scholar]
- Qu, C.; Li, W.; Xu, J.; Shang, Y.H. Potential impact of black land conservation and utilization on carbon storage in Heilongjiang Province. J. Northwest For. Univ. 2023, 38, 194–203. [Google Scholar]
- Xu, L.; He, N.P.; Yu, G.R. A dataset of carbon density in Chinese terrestrial ecosystems (2010s). China Sci. Data 2019, 4, 1–7. [Google Scholar] [CrossRef]
- Li, Z.Y.; Zhu, X.S.; Yang, L.; Wang, X.Y.; Tian, H. Spatial temporal Evolution Characteristics and Influencing Factors of Carbon Emissions in Yunnan Province Based on Land Use Changes. Bull. Soil Water Conserv. 2023, 43, 297–303. [Google Scholar]
- Meng, X.Y.; Wu, Y.X. Supply-demand bundles and ecological function management of urban ecosystem services: Taking central urban area of Qiqihar as an example. Chin. J. Appl. Ecol. 2023, 34, 3393–3403. [Google Scholar]
- Gao, Y.; Ma, L.; Liu, J.X.; Zhuang, Z.Z.; Huang, Q.H.; Li, M.C. Constructing Ecological Networks Based on Habitat Quality Assessment: A Case Study of Changzhou, China. Sci. Rep. 2017, 7, 46073. [Google Scholar] [CrossRef]
- Yang, Z.P.; Xu, J.W.; Feng, X.H.; Guo, M.; Jin, Y.H.; Gao, X.J. Effects of land use change on habitat based on InVEST model in Northeast China. Ecol. Sci. 2018, 37, 139–147. [Google Scholar]
- Zhang, D.H.; Wang, Y.; Yao, N. Urbanization and ecological effect in mid-southern Liaoning urban agglomeration, China. Chin. J. Appl. Ecol. 2022, 33, 2521–2529. [Google Scholar]
- Wang, J.; Zhai, T.L.; Lin, Y.F.; Kong, X.S.; He, T. Spatial imbalance and changes in supply and demand of ecosystem services in China. Sci. Total Environ. 2019, 657, 781–791. [Google Scholar] [CrossRef]
- Young, J.; Watt, A.; Nowicki, P.; Alard, D.; Clitherow, J.; Henle, K.; Johnson, R.; Laczko, E.; McCracken, D.; Matouch, S.; et al. Towards sustainable land use: Identifying and managing the conflicts between human activities and biodiversity conservation in Europe. Biodivers. Conserv. 2005, 14, 1641–1661. [Google Scholar] [CrossRef]
- Falcucci, A.; Maiorano, L.; Boitani, L. Changes in land-use/land-cover patterns in Italy and their implications for biodiversity conservation. Landsc. Ecol. 2007, 22, 617–631. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, X.M.; Huang, L.Y.; Zhu, C.M.; Shahtahmassebi, A.R.; Zhang, J.; Shen, S.Z.; Peng, R.; Deng, J.S.; Wang, K.; et al. Fine-scale mapping of urban ecosystem service demand in a metropolitan context: A population-income-environmental perspective. Sci. Total Environ. 2021, 781, 146784. [Google Scholar] [CrossRef]
- Wang, X.F.; Yao, W.J.; Feng, X.M.; Jia, Z.X.; Zhang, X.R.; Ma, J.H.; Zhou, J.T.; Tu, Y.; Sun, Z.C. Changes and driving factors of ecosystem services supply and demand on the Tibetan plateau. Acta Ecol. Sin. 2023, 43, 6968–6982. [Google Scholar]
- Birkes, D.; Dodge, Y. 6.3 Estimating the Regression Line. In Alternative Methods of Regression; Wiley Series in Probability and Statistics; Wiley-Interscience: Hoboken, NJ, USA, 1993; pp. 113–118. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Pang, J.; He, L.; He, Z.; Zeng, W.; Yuan, Y.; Bai, W.; Zhao, J. Interactions and Driving Force of Land Cover and Ecosystem Service Before and After the Earthquake in Wenchuan County. Sustainability 2025, 17, 3094. [Google Scholar] [CrossRef]
- Gong, D.C.; Du, N.; Wang, L.; Zhang, X.Y.; Li, L.; Zhang, H.F. Estimation of near-surface ozone concentration in the Beijing-Tianjin-Hebei region based on XGBoost-LME model. Environ. Sci. 2024, 45, 3815–3827. [Google Scholar]
- Huang, Q.; Tan, C.; Yang, B. Research on the evaluation method of ecotourism suitability in Subtropical Regions based on XGBoost algorithm. J. Geo-Inf. Sci. 2024, 26, 303–317. [Google Scholar]
- Yang, D.F.; Wang, X.M.; Han, R.N. Nonlinear and synergistic effects of the built environment on street vitality: The case of Shenyang. Urban Plan. Forum 2023, 5, 93–102. [Google Scholar]
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, J.; Cheng, Y.; Zheng, H.; Zhang, J. Evaluation of the Impact of Land Use Evolution on Water Conservation Capacity in Xinbin County, Upper Reaches of Hun River. Res. Soil Water Conserv. 2023, 30, 169176. [Google Scholar]
- Huang, J.; Fan, J.H.; He, X.R. InVest-Model Based Evaluation of Water Conservation Function in Zhangjiakou Area, China. Mt. Res. 2021, 39, 327–337. [Google Scholar]
- Ji, K.Y.; Li, X.M.; Gao, J.; Xu, J.Y.; Gao, Y.Q. Assessment of urban vulnerability to heavy rain and flood disasters. Adv. Sci. Technol. Water Resour. 2024, 44, 13–20. [Google Scholar]
- Yan, S.H.; Hong, B. PM2.5 Concentration Distribution Characteristics in Different Landscape Spaces and Influencing Factors in Urban Park. Landsc. Archit. 2019, 26, 101–106. [Google Scholar]
- Interpretation of the notice of the Office of the People’s Government of Shenyang City on the issuance of the work program of greening urban areas in Shenyang City. Available online: https://www.shenyang.gov.cn/zwgk/zcwj/zcjd/wzjd/202112/t20211201_1700038.html (accessed on 26 June 2025).
- Li, X.Y.; Kuang, W.H. Urban land use/cover change and its impact on urban flood regulation ecosystem service in Beijing. Acta Ecol. Sin. 2020, 40, 5525–5533. [Google Scholar]
- Shi, T.M.; Gao, Y.; Wang, D. Research on the path of carbon fixation and carbon sink in urban space under dual carbon target. J. Shenyang Jianzhu Univ. (Nat. Sci.) 2024, 40, 193–202. [Google Scholar]
- Chen, L.; Hao, J.M.; Wang, F.; Yin, Y.Y.; Gao, Y.; Duan, W.K.; Yang, J. Carbon sequestration function of cultivated land use system based on the carbon cycle for the Huang-Huai-Hai Plain. Resour. Sci. 2016, 38, 1039–1053. [Google Scholar]
- Sala, O.E.; Chapin, F.S., III; Armesto, J.J.; Berlow, E.; Bloomfield, J.; Dirzo, R.; Huber-Sanwald, E.; Huenneke, L.F.; Jackson, R.B.; Kinzig, A.; et al. Global biodiversity scenarios for the year 2100. Science 2000, 287, 1770–1774. [Google Scholar] [CrossRef] [PubMed]
- Jun, W.; Xi, G.; Qing, Z.; Guo, J.X.; Han, Y.; Zhong, L.; Liu, S.Y. Threshold effects and supply-demand ratios should be considered in the mechanisms driving ecosystem services. Ecol. Indic. 2022, 142, 109281. [Google Scholar] [CrossRef]
- Pan, Z.; He, J.; Liu, D.; Wang, J.; Guo, X. Ecosystem health assessment based on ecological integrity and ecosystem services demand in the Middle Reaches of the Yangtze River Economic Belt, China. Sci. Total Environ. 2021, 774, 144837. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, Y.; Pu, J.; Tao, J.; Chen, Y.; Huang, P.; Shi, X.; Ran, Y.; Gu, Z. Achieving the supply-demand balance of ecosystem services through zoning regulation based on land use thresholds. Land Use. Polic. 2024, 139, 107056. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Sun, X.Y.; Zhang, H.; Deng, C.N.; Zhao, K.; Jin, Y.Y.; Chen, D.L. Supply-Demand Balance of Ecosystem Services in the Middle Reaches of the Yangtze River Based on Land Use Change. J. Soiland Water Conserv. 2024, 38, 227–238. [Google Scholar]
- He, J.; Shi, X. Detection of social-ecological drivers and impact thresholds of ecological degradation and ecological restoration in the last three decades. J. Environ. Manag. 2022, 318, 115513. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, L.; Zhu, G. Effects of transport infrastructures and climate change on ecosystem services in the integrated transport corridor region of the Qinghai-Tibet Plateau. Sci. Total Environ. 2023, 885, 163961. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Zhao, T.; Ding, S. Research on territorial spatial planning based on the theory of ecosystem service network. Acta Ecol. Sin. 2023, 43, 4868–4875. [Google Scholar] [CrossRef]
- Shen, J.; Li, S.; Liang, Z.; Liu, L.; Li, D.; Wu, S. Exploring the heterogeneity and nonlinearity of trade-offs and synergies among ecosystem services bundles in the Beijing-Tianjin-Hebei urban agglomeration. Ecosyst. Serv. 2020, 43, 101103. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Z.Q.; Xu, C.L.; Yu, Y.Q.; Lu, G.J.; Li, H.R.; Li, H.L. Effects of fertility improvement measures on soil quality and maize yield in horizontal terraced fields of black soil hilly region. Bull. Soil Water Conserv. 2022, 42, 190–196+222. [Google Scholar]
- Bodnaruk, E.W.; Kroll, C.N.; Yang, Y.; Hirabayashi, S.; Nowak, D.J.; Endreny, T.A. Where to plant urban trees? A spatially explicit methodology to explore ecosystem service tradeoffs. Landsc. Urban Plan. 2017, 157, 457–467. [Google Scholar] [CrossRef]
- Zhao, H.B.; Gu, T.S.; Tang, J.Q.; Gong, Z.Y.; Zhao, P.J. Urban flood risk differentiation under land use scenario simulation. iScience 2023, 26, 106479. [Google Scholar] [CrossRef]
- Chen, M.; Dai, F.; Yang, B.; Zhu, S.W. Effects of neighborhood green space on PM2.5 mitigation Evidence from five megacities in China. Build. Environ. 2019, 156, 33–45. [Google Scholar] [CrossRef]
- Wang, S.; Wu, M.; Hu, M.; Fan, C.; Wang, T.; Xia, B. Promoting landscape connectivity of highly urbanized area: An ecological network approach. Ecol. Indic. 2021, 125, 107487. [Google Scholar] [CrossRef]
- Hong, G.; Wu, X.F.; Cai, R.H. Influence of Urban Green Infrastructure Landscape Pattern on Carbon Sequestration Performance at the Optimal Grid Unit. Chin. Landsc. Archit. 2023, 39, 138–144. [Google Scholar]
- Wang, Q.N.; Wei, Q.L.; Xie, Y.S.; Luo, Y.Y. Coupling Analysis of the Spatial Pattern Evolution of Green Space and Road Network in the Central City of Chengdu. Chin. Landsc. Archit. 2022, 38, 90–95. [Google Scholar]









| Data Name | Data Source | Data Type | Resolution |
|---|---|---|---|
| Administrative Boundaries | National Platform for Common Geospatial Information Services (www.tianditu.gov.cn, accessed on 10 January 2025) | Shpfile | / |
| Remote Sensing Data | Landsat8-9 OLI_TIRS Satellite Imagery | Raster | 30 m |
| DEM | Geospatial Data Cloud (https://www.gscloud.cn, accessed on 11 January 2025) | Raster | 30 m |
| Precipitation, Annual Average Evapotranspiration, Soil Data, and PM2.5 | National Tibetan Plateau Scientific Data Center (https://data.tpdc.ac.cn, accessed on 28 January 2025) | Raster | 1000 m |
| Population Density | LandScan (https://landscan.ornl.gov, accessed on 1 February 2025) | Raster | 1000 m |
| GDP | Geographical Remote Sensing Ecology Network Platform (gisrs.cn, accessed on 1 February 2025) | Raster | 1000 m |
| Water Consumption Data | Liaoning Province Water Resources Bulletin | Text | / |
| Night Light Index | Harvard Dataverse [28] | Raster | 1000 m |
| Landscape Index | Abbreviation | Meaning | Calculation Formula |
|---|---|---|---|
| Aggregation Index | AI | AI examines the connectivity between patches of each landscape type. A smaller value indicates a more discrete landscape. | represents the number of similar adjacent patches of the corresponding landscape type, 0 < AI ≤ 100. |
| Edge density | ED | The length of patch boundaries per unit area directly characterizes the overall complexity of the landscape. | E is the total length of patch boundaries in the landscape; A is the total landscape area; ED ≥ 0, unbounded, m/ha. |
| Interspersion and juxtaposition index | IJI | A measure of landscape isolation and patch mixing. A larger index indicates more obvious patterns of alternating different patches and higher patch dispersion. | is the total edge length between patches i and k, E is the total edge length in the entire landscape (excluding the background), and m is the number of patch types, 0 < IJI ≤ 100,%. |
| Largest patch index | LPI | Identifies the dominant patch type in the landscape. The index value helps determine the dominant patch type and indirectly reflects the direction and intensity of human activity interference. | is the area of the largest patch; A is the total landscape area; 0 ≤ LPI ≤ 100,%. |
| Landscape shape index | LSI | The value increases as the landscape shape becomes more irregular or deviates further from a square. | E is the total length of all patch boundaries in the landscape; A is the total landscape area. LSI ≥ 1, unbounded. |
| Patch density | PD | The degree of patch aggregation within a specific range. Within a particular study area, a higher density indicates a larger total number of patches. | N is the total number of patches in the landscape; A is the total landscape area; PD > 0, pcs/100 ha, unbounded. |
| Percentage of landscape | PLAND | When the patch area percentage approaches zero, it indicates a decrease in the occurrence of that patch type. A value of 100 means the entire landscape consists of only one patch type. | aij is the area of the j-th patch in the i-th landscape type; A is the total landscape area,%. |
| Land Use Type | Catchment Type | Target Value of Annual Runoff Control Rate (%) | Rainfall-Runoff Coefficient | |
|---|---|---|---|---|
| Cultivated | Green Space | 85 | 0.15 | |
| Forest | Green Space | 85 | 0.15 | |
| Grass | Green Space | 85 | 0.15 | |
| Water | Water Surface | 100 | 1.0 | |
| Construction | Hard Roof, Roads and Squares | 75 | 0.9 | |
| Unused | Unpaved Dirt Roads | 45 | 0.3 | |
| Total Control Rate | 2015 | - | 82 | - |
| 2019 | 81 | |||
| 2023 | 81 | |||
| Land Use Type | Carbon Densities | Carbon Emission (Absorption) Coefficients | |||
|---|---|---|---|---|---|
| Cultivated | 4.75 | 8.12 | 33.51 | 0 | 0.461 |
| Forest | 60.08 | 30.06 | 160.97 | 2.21 | −0.581 |
| Grass | 31.71 | 23.66 | 55.13 | 29.03 | −0.021 |
| Water | 3.325 | 0.6125 | 168.335 | 0.3875 | −0.253 |
| Construction | 5.777 | 2.90 | 8.497 | 0.77 | 159.38 |
| Unused | 2.26 | 9.03 | 14.66 | 0 | −0.005 |
| Case | Supply | Demand | Coincident Conditions |
|---|---|---|---|
| 1 | + | + | S+ > D |
| 2 | + | Unchanged | None |
| 3 | + | − | None |
| 4 | Unchanged | − | None |
| 5 | − | − | S− < D− |
| Ecosystem Service | Land Use | AI | ED | IJI | LPI | LSI | PD | PLAND |
|---|---|---|---|---|---|---|---|---|
| WR | Construction | −0.026 | −0.100 ** | −0.089 ** | −0.134 ** | −0.069 ** | −0.061 | −0.161 ** |
| Cultivated | 0.121 ** | −0.005 | 0.014 | 0.148 ** | −0.061 | −0.073 ** | 0.173 ** | |
| Forest | −0.004 | −0.041 | −0.046 | −0.045 | −0.029 | 0.002 | −0.053 | |
| Grass | −0.001 | 0.004 | −0.01 | −0.006 | 0.002 | 0.007 | −0.004 | |
| Water | 0.068 ** | 0.027 | 0.060 | 0.013 | −0.009 | −0.007 | 0.02 | |
| FR | Construction | −0.209 ** | 0.112 ** | −0.047 ** | −0.678 ** | 0.253 ** | 0.156 ** | −0.671 ** |
| Cultivated | 0.164 ** | 0.156 ** | −0.030 | 0.508 ** | −0.047 ** | −0.094 ** | 0.529 ** | |
| Forest | 0.015 | 0.066 ** | −0.003 | 0.052 ** | 0.034 | 0.018 | 0.064 ** | |
| Grass | 0.007 | 0.012 | −0.030 | 0.01 | 0.011 | −0.002 | 0.01 | |
| Water | −0.014 | −0.067 ** | −0.022 | −0.02 | −0.042 ** | −0.012 | −0.027 | |
| AP | Construction | −0.199 ** | 0.071 ** | −0.01 | −0.736 ** | 0.218 ** | 0.151 ** | −0.745 ** |
| Cultivated | 0.163 ** | 0.102 ** | 0.008 | 0.500 ** | −0.074 ** | −0.101 ** | 0.533 ** | |
| Forest | 0.033 ** | 0.096 ** | 0.002 | 0.092 ** | 0.054 ** | 0.021 | 0.112 ** | |
| Grass | 0.01 | 0.012 | −0.023 | 0.001 | 0.013 | 0.004 | 0.008 | |
| Water | 0.004 | −0.040 ** | −0.023 | 0.017 | −0.032 ** | −0.009 | 0.013 | |
| CS | Construction | −0.302 ** | −0.023 | −0.055 ** | −0.747 ** | 0.289 ** | 0.216 ** | −0.762 ** |
| Cultivated | 0.221 ** | 0.118 ** | 0.011 | 0.543 ** | −0.116 ** | −0.158 ** | 0.570 ** | |
| Forest | 0.026 | 0.03 | 0.021 | 0.041 | −0.008 | −0.013 | 0.041 | |
| Grass | 0.008 | 0.004 | −0.031 | −0.002 | 0 | −0.007 | 0 | |
| Water | 0.016 | 0.01 | −0.027 | 0.120 ** | −0.029 | −0.021 | 0.121 ** | |
| HQ | Construction | −0.083 ** | 0.079 ** | 0.175 ** | −0.300 ** | 0.120 ** | 0.081 ** | −0.291 ** |
| Cultivated | −0.080 ** | 0.027 | 0.044 | 0.002 | 0.059 ** | 0.067 ** | −0.011 | |
| Forest | 0.104 ** | 0.275 ** | 0.096 ** | 0.276 ** | 0.184 ** | 0.041 | 0.308 ** | |
| Grass | −0.006 | 0.063 ** | −0.01 | 0.047 ** | 0.056 ** | 0.040 | 0.053 ** | |
| Water | 0.017 | 0.03 | 0.02 | 0.099 ** | −0.006 | 0.009 | 0.104 ** |
| Ecosystem Service | WR | FR | AP | CS | HQ | |
|---|---|---|---|---|---|---|
| Model Evaluation Metrics | ||||||
| R2 | 0.478 | 0.598 | 0.728 | 0.703 | 0.355 | |
| MAE | 0.007 | 0.011 | 0.026 | 0.042 | 0.048 | |
| MSE | 0.0003 | 0.0003 | 0.002 | 0.004 | 0.006 | |
| RMSE | 0.017 | 0.018 | 0.045 | 0.065 | 0.07 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Hu, Z.; Wang, R.; Zhu, L. Spatiotemporal Responses and Threshold Mechanisms of Urban Landscape Patterns to Ecosystem Service Supply–Demand Dynamics in Central Shenyang, China. Sustainability 2025, 17, 7419. https://doi.org/10.3390/su17167419
Yang M, Hu Z, Wang R, Zhu L. Spatiotemporal Responses and Threshold Mechanisms of Urban Landscape Patterns to Ecosystem Service Supply–Demand Dynamics in Central Shenyang, China. Sustainability. 2025; 17(16):7419. https://doi.org/10.3390/su17167419
Chicago/Turabian StyleYang, Mengqiu, Zhenguo Hu, Rui Wang, and Ling Zhu. 2025. "Spatiotemporal Responses and Threshold Mechanisms of Urban Landscape Patterns to Ecosystem Service Supply–Demand Dynamics in Central Shenyang, China" Sustainability 17, no. 16: 7419. https://doi.org/10.3390/su17167419
APA StyleYang, M., Hu, Z., Wang, R., & Zhu, L. (2025). Spatiotemporal Responses and Threshold Mechanisms of Urban Landscape Patterns to Ecosystem Service Supply–Demand Dynamics in Central Shenyang, China. Sustainability, 17(16), 7419. https://doi.org/10.3390/su17167419








