A Multi-Temporal Regulation Strategy for EV Aggregators Enabling Bi-Directional Energy Interactions in Ancillary Service Markets for Sustainable Grid Operation
Abstract
1. Introduction
- To transcend the limitations of conventional approaches that are typically confined to single-market frameworks, this study pioneers a market-coupled and temporally layered scheduling paradigm for electric vehicle aggregator (EVA) participation in ancillary service markets. This innovative framework enables multi-temporal coordination and cross-market synergy, thereby significantly improving the spatiotemporal orchestration of distributed energy flexibility resources while promoting sustainable grid operation through reduced reliance on carbon-intensive peaking plants and enhanced integration of clean transportation systems.
- Existing models often inadequately capture the coupling between power and energy constraints during EV charging and discharging. This paper introduces a systematic derivation of individual EV power–energy-feasible regions, yielding closed-form boundary expressions. These formulations serve as analytically tractable yet physically accurate constraints, enhancing the realism and precision of the dispatch optimization model while maximizing energy utilization efficiency and supporting sustainable energy management practices through optimized EV resource deployment.
- Recognizing the stochastic and heterogeneous nature of user participation, this study incorporates user response willingness via utility-driven functions and probabilistic response modeling. This behaviorally enriched framework enables adaptive scheduling that is both robust and cost-effective under uncertain and dynamic user engagement, marking a substantive advancement over deterministic or fully controllable EV models while fostering widespread adoption of clean transportation technologies through user-centric incentive mechanisms that align economic benefits with environmental sustainability goals.
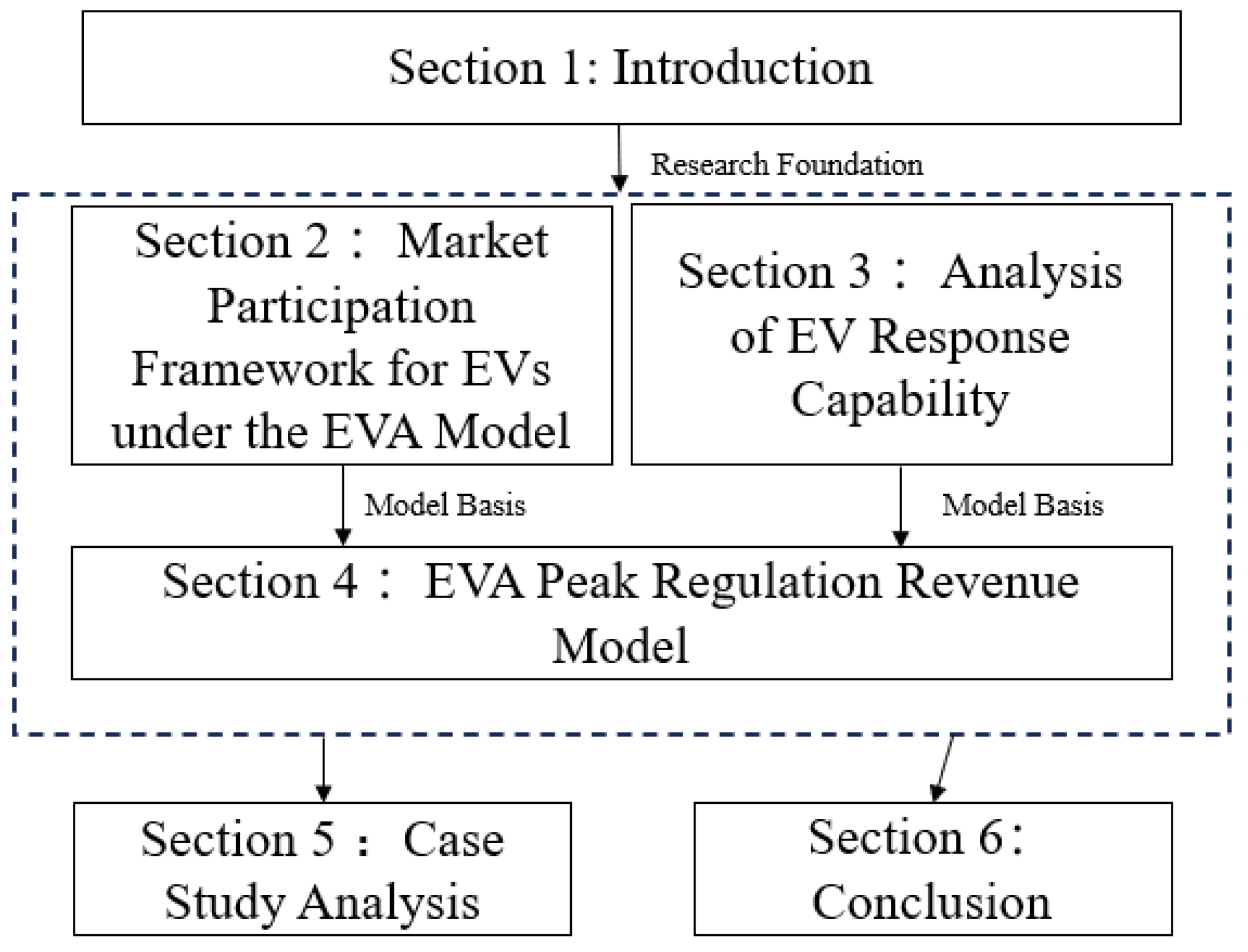
2. Market Participation Framework for EVs in the EVA Model
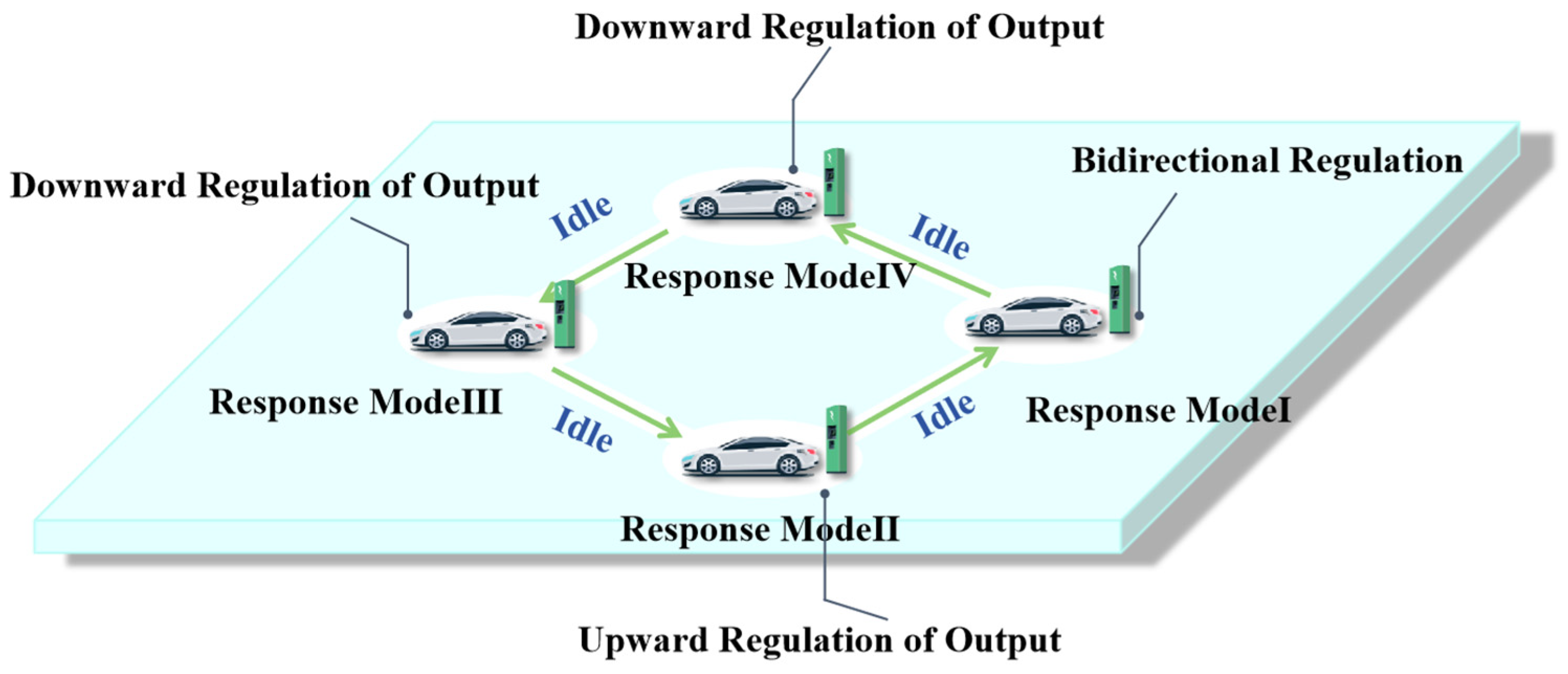
3. Analysis of EV Response Capability
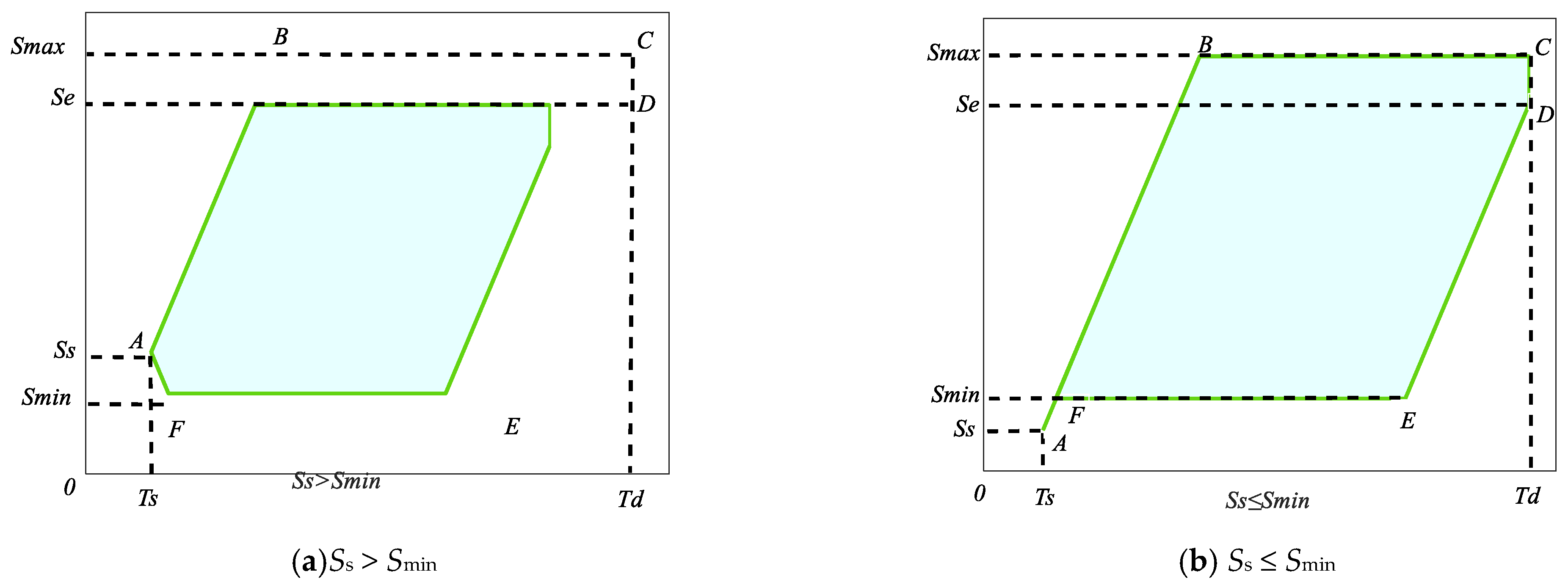
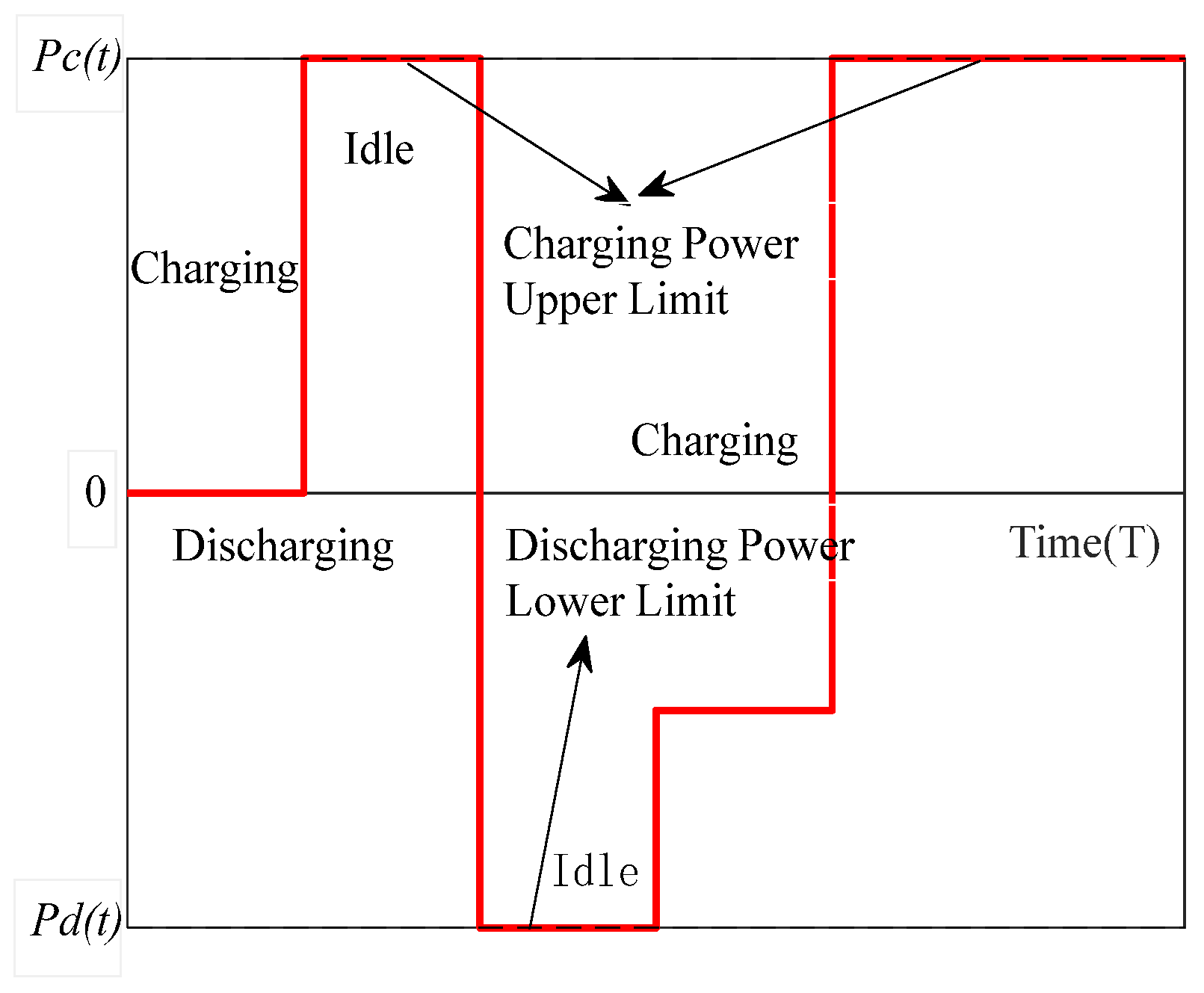
3.1. Feasible Dispatch Region of EVs
3.2. Analysis of EV Response Boundaries
- (1)
- Analysis of Individual EV Response Boundaries
- (2)
- Response Boundaries of EV Aggregation
- (a)
- According to the probabilistic models of relevant parameters outlined in Section 3.2 on EV uncertainty analysis and modeling, the charging power, SOC capacity, and charging energy of individual EVs are determined, and their charging/discharging status is identified;
- (b)
- Based on the individual EV response boundaries, the energy boundaries of each EV are calculated using Equations (4) and (5);
- (c)
- Steps (a)–(b) are iteratively executed until the predefined EV sample size is reached, and the feasible boundaries of energy and power for the EV aggregation are determined based on Equation (6).
3.3. Modeling of EV User Willingness
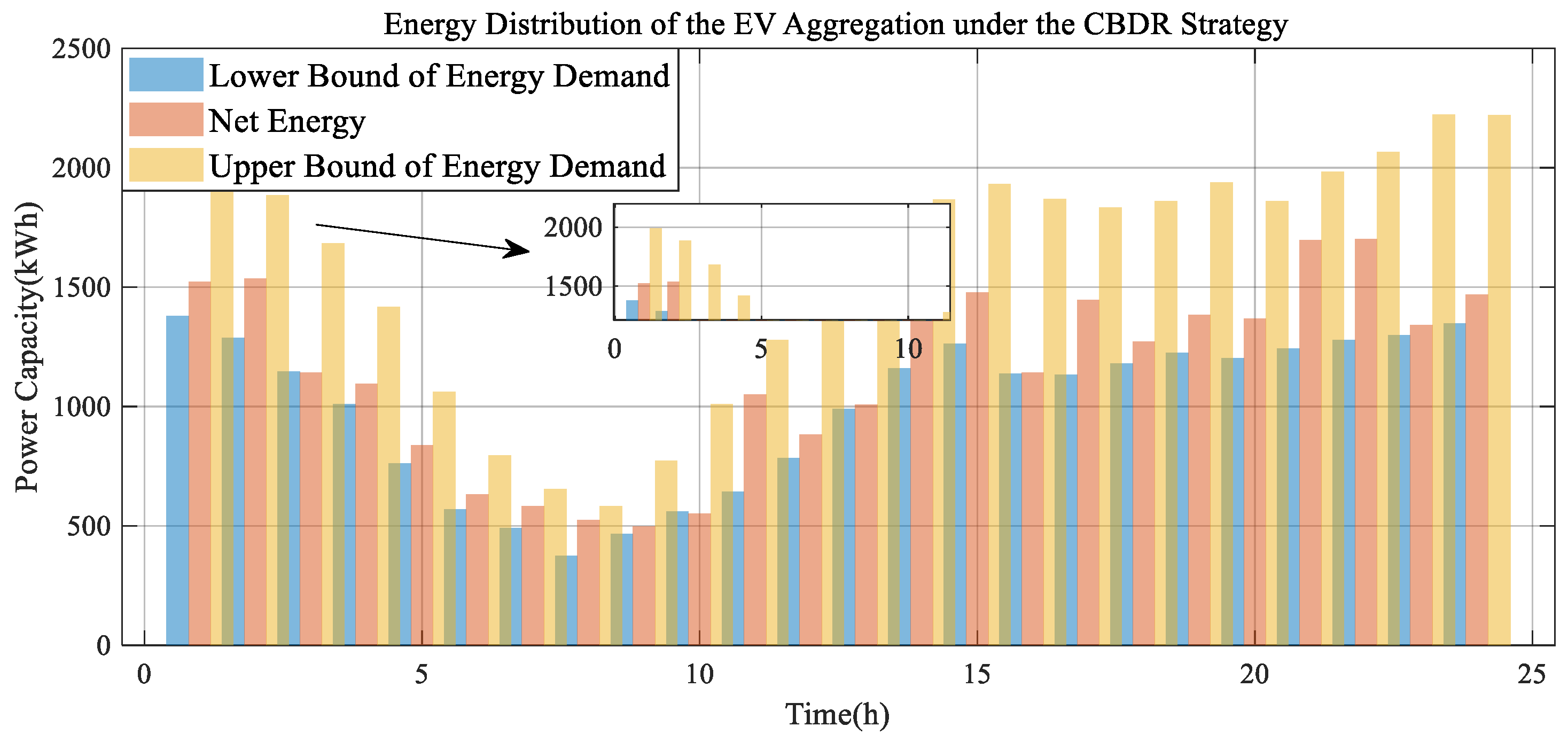
3.4. Charging-Based Demand Response Strategy (CBDR)
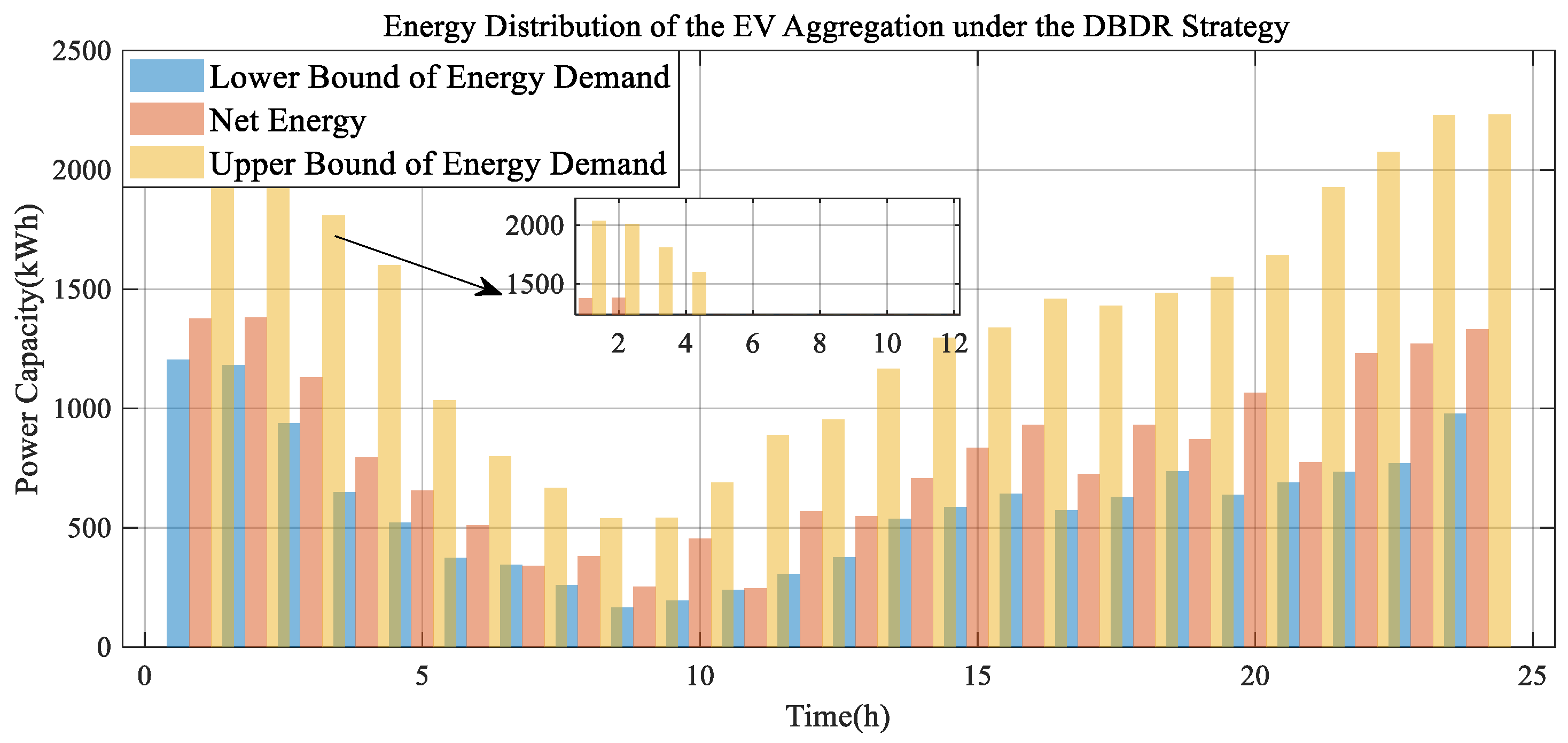
3.5. Discharging-Based Demand Response Strategy (DBDR)
4. EVA Peak Regulation Revenue Model
4.1. EVA Operating Costs
4.2. EVA Compensation Revenue
4.3. Objective Function and Constraints
- (a)
- EVA Constraints
- (b)
- Energy Boundary Constraints
- (c)
- EV Quantity Constraint
- (d)
- Battery State Constraint
- (e)
- Power Constraint
5. Case Study Analysis
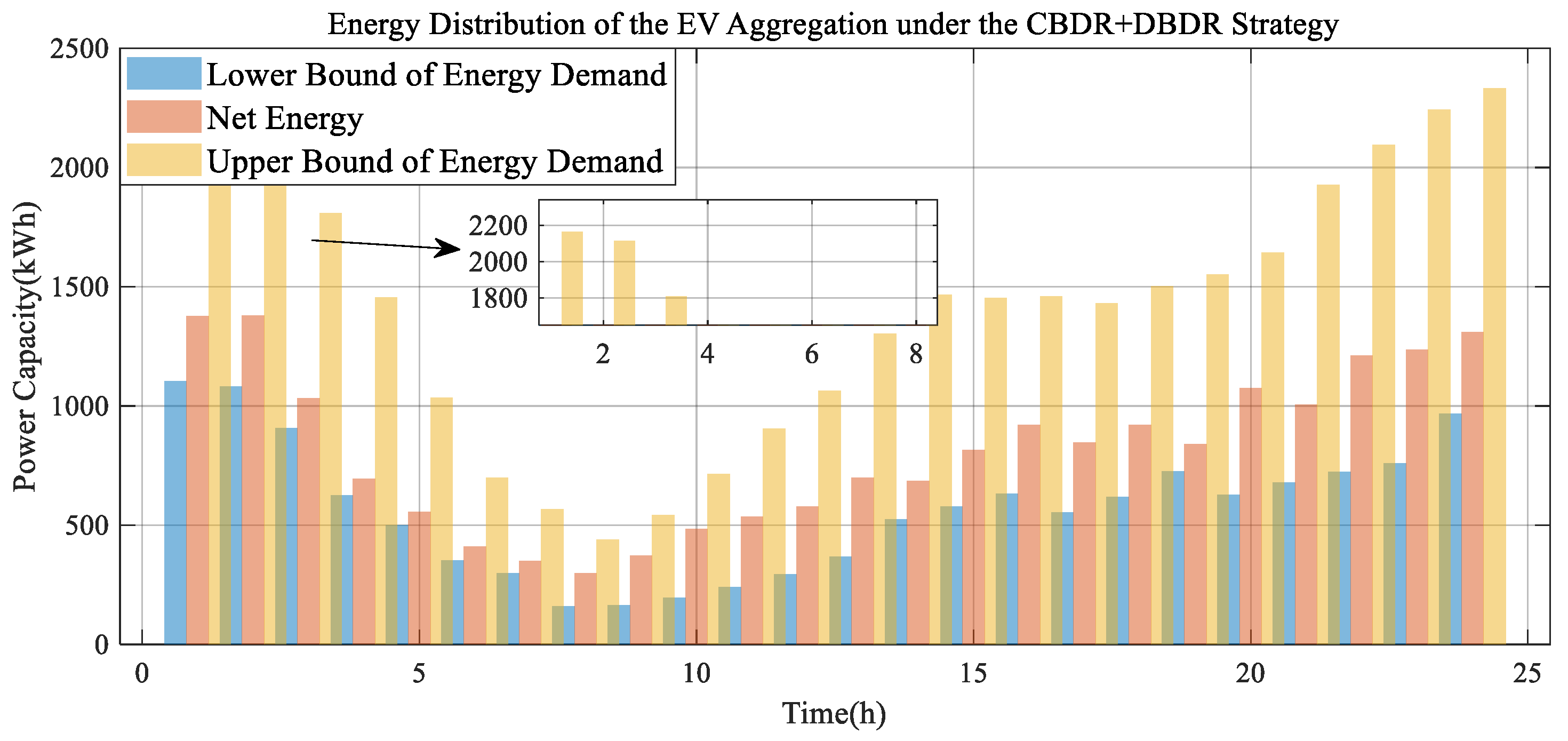
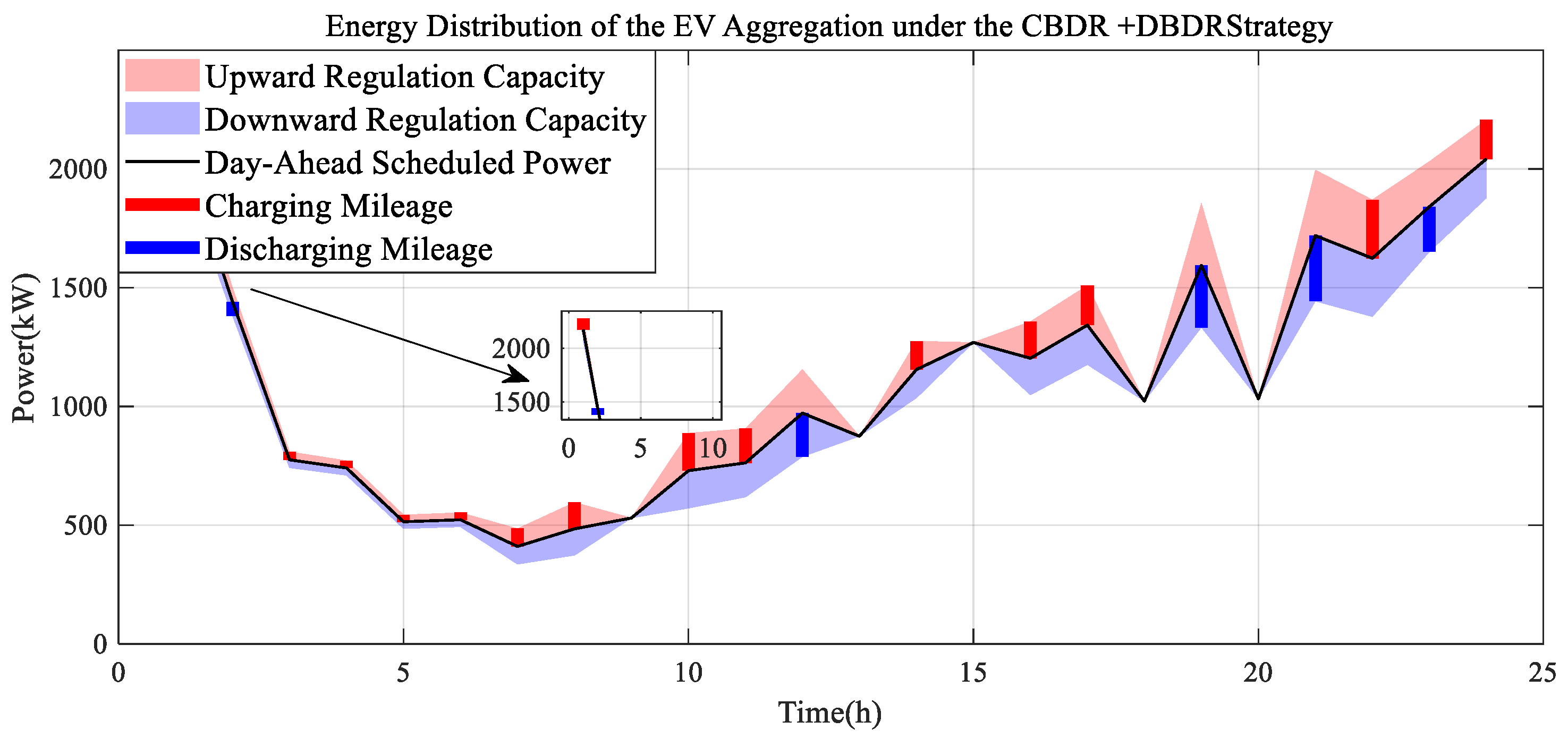
5.1. Multi-Period Real-Time Energy Regulation Analysis of an EVA
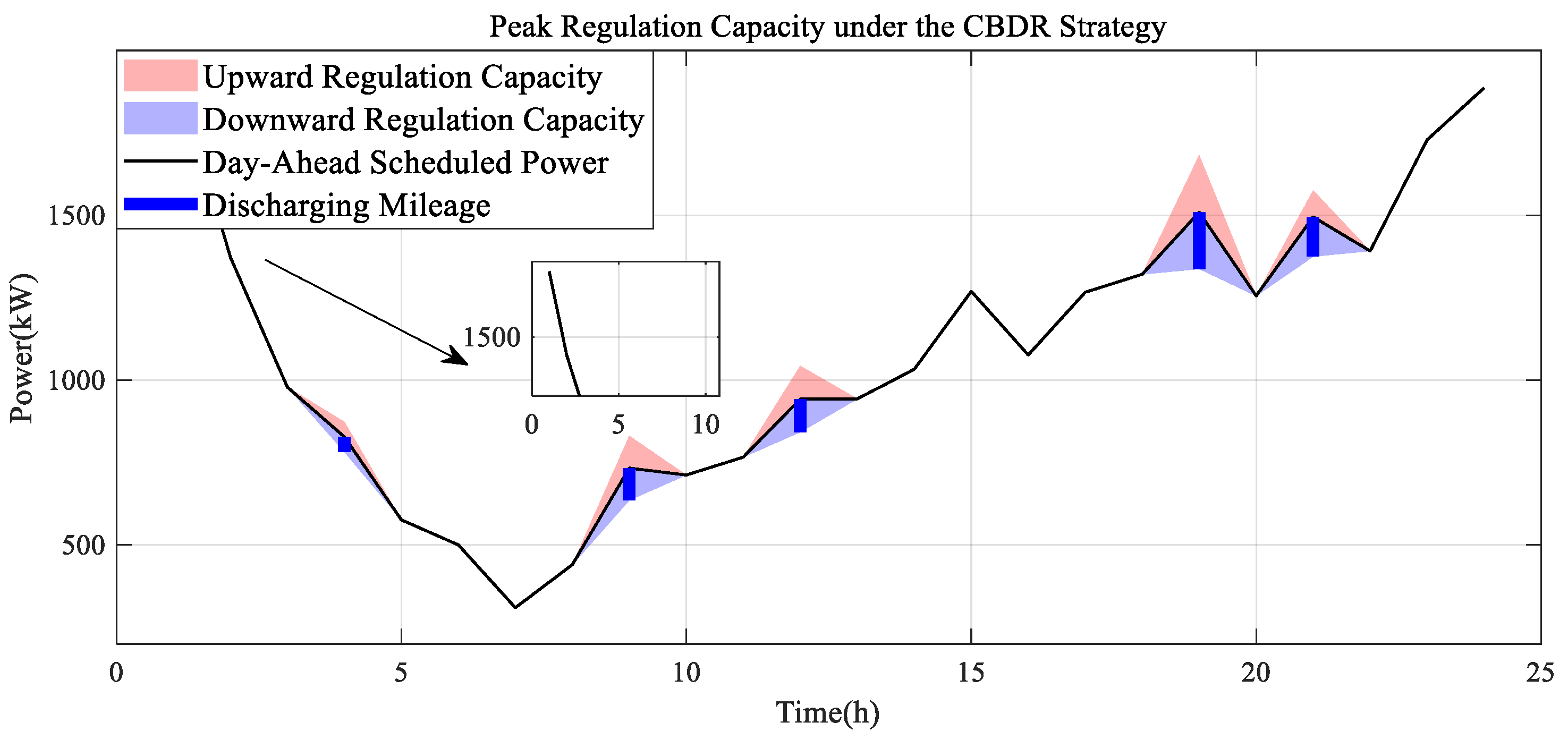
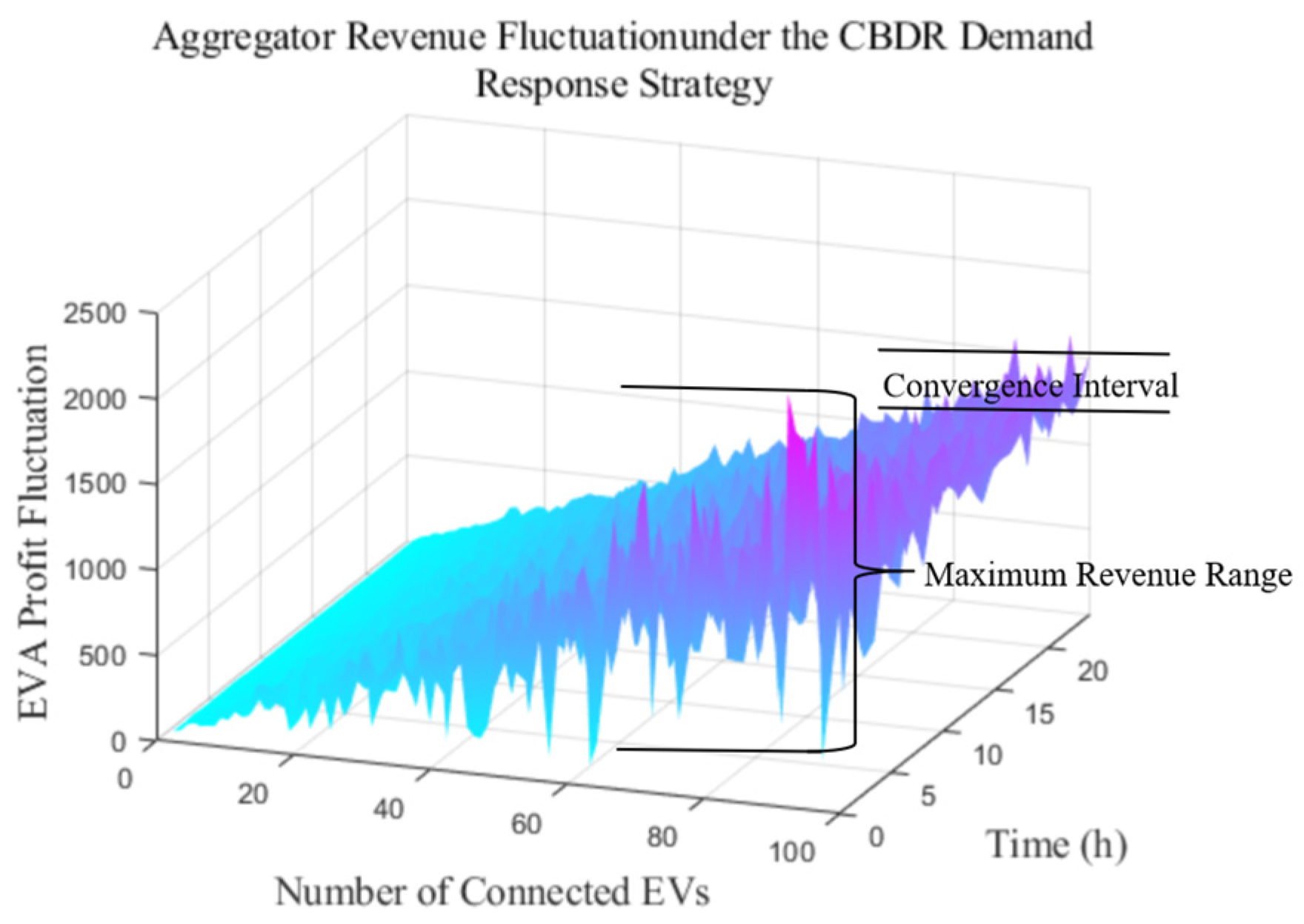
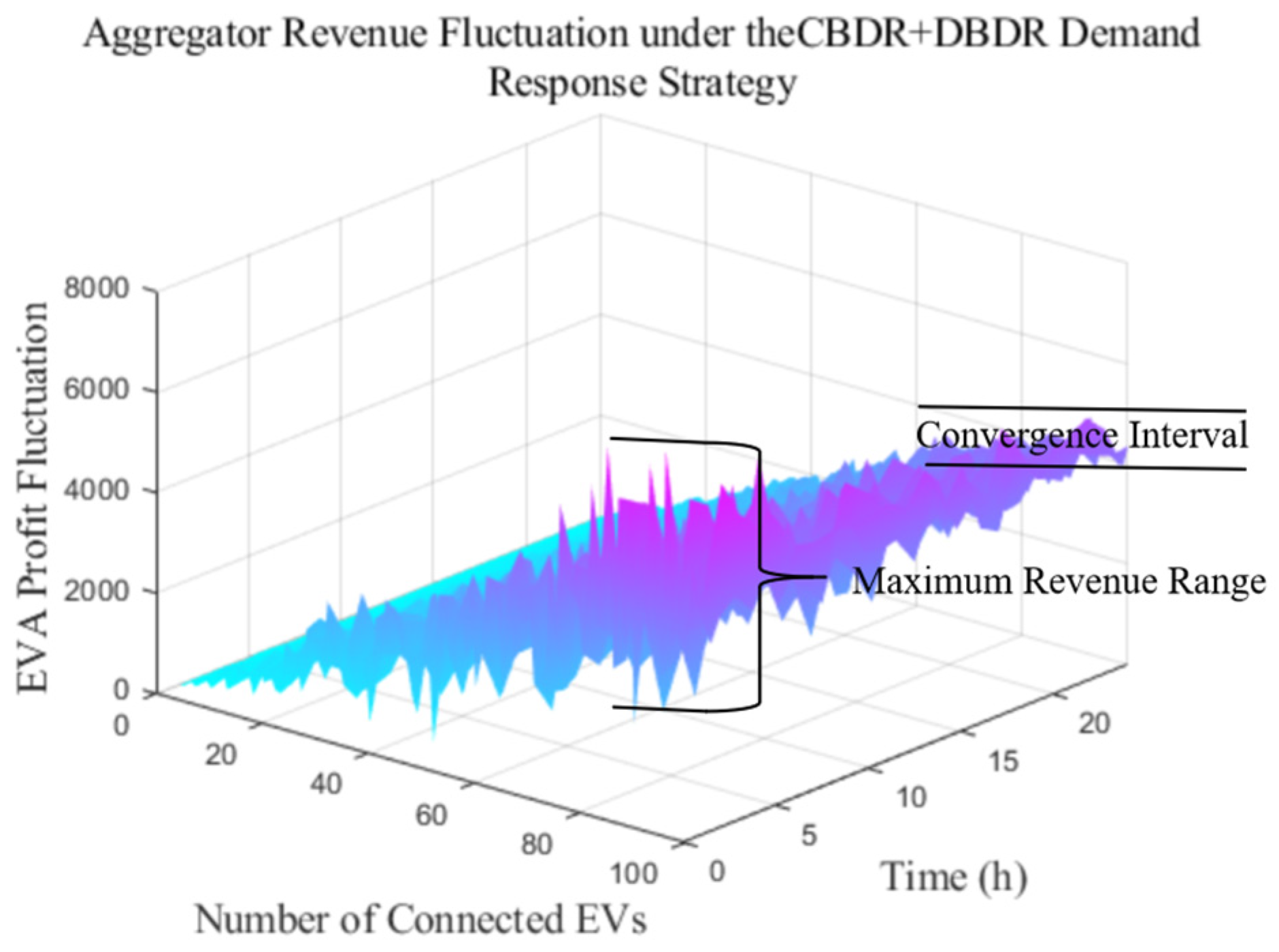
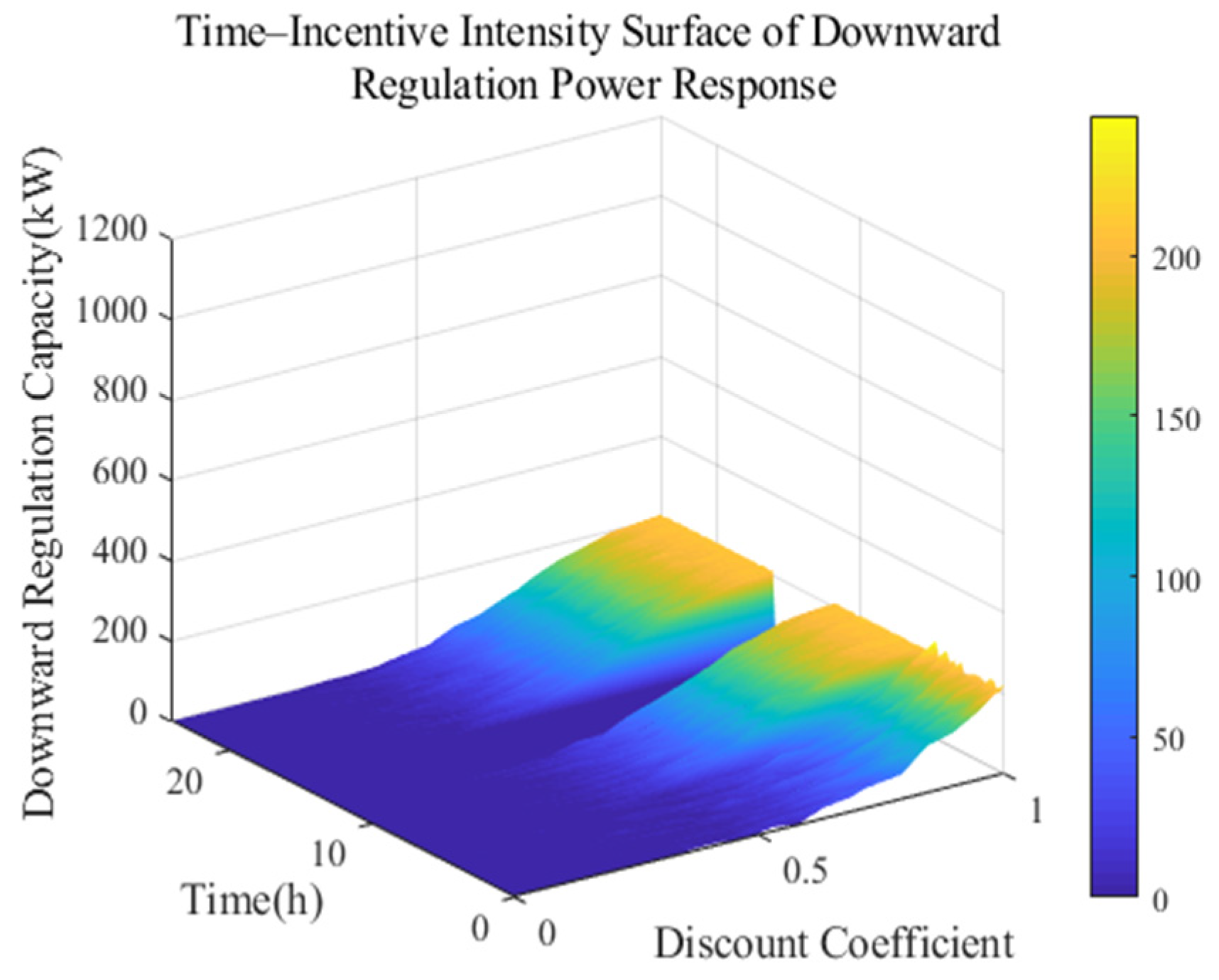
5.2. Real-Time Peak Regulation Margin and Revenue Analysis of the EVA
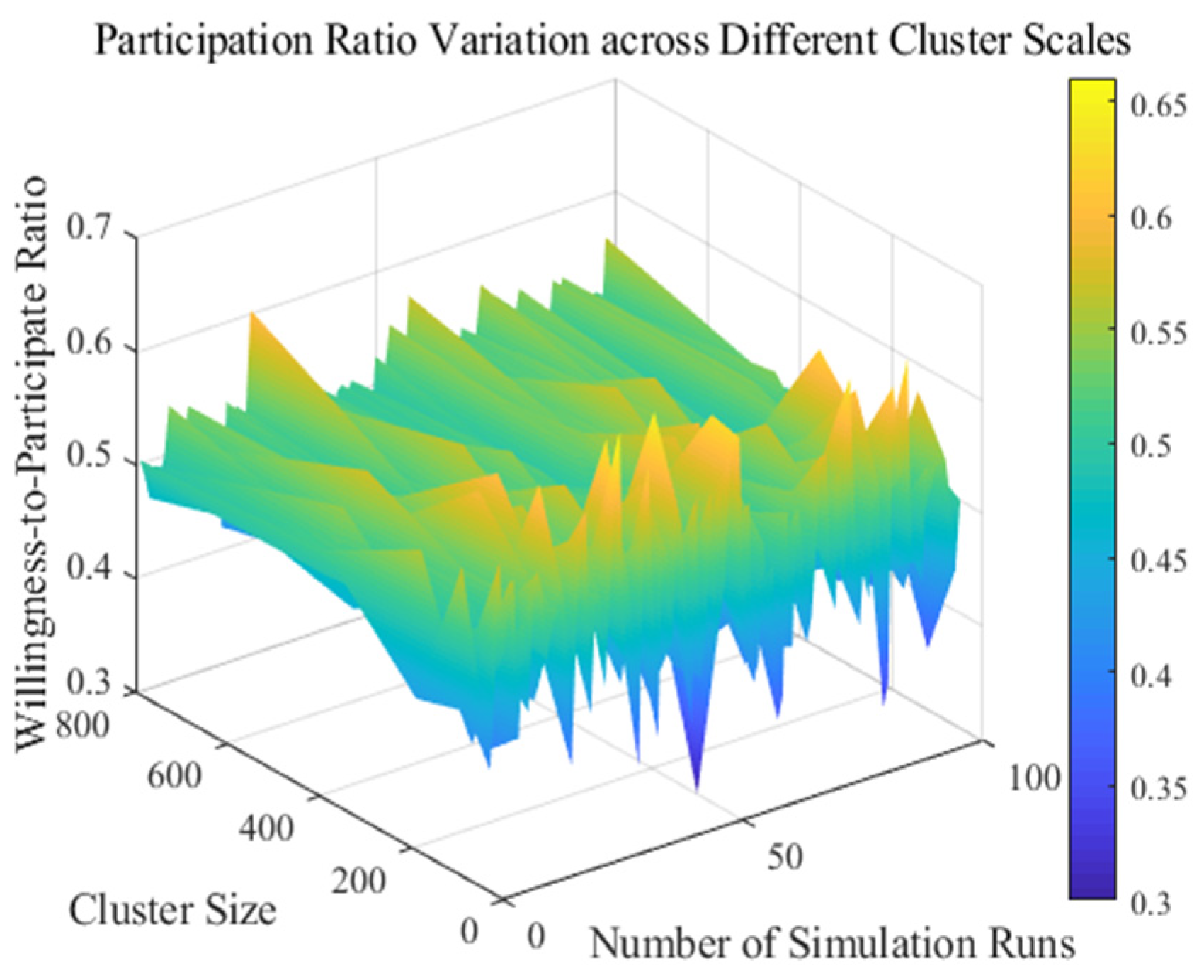
5.3. Analysis of EV User Willingness
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohiti, M.; Monsef, H.; Lesani, H. A decentralized robust model for coordinated operation of smart distribution network and electric vehicle aggregators. Int. J. Electr. Power Energy Syst. 2019, 104, 853–867. [Google Scholar] [CrossRef]
- Nie, X.P.; Mansouri, S.A.; Jordehi, A.R.; Tostado-Véliz, M. A two-stage optimal mechanism for managing energy and ancillary services markets in renewable-based transmission and distribution networks by participating electric vehicle and demand response aggregators. Int. J. Electr. Power Energy Syst. 2024, 158, 109917. [Google Scholar] [CrossRef]
- Ireshika, M.A.S.T.; Kepplinger, P. Uncertainties in model predictive control for decentralized autonomous demand side management of electric vehicles. J. Energy Storage 2024, 83, 110194. [Google Scholar] [CrossRef]
- Aljohani, T.; Mohamed, M.A.; Mohammed, O. Tri-level hierarchical coordinated control of large-scale EVs charging based on multi-layer optimization framework. Electr. Power Syst. Res. 2024, 226, 109923. [Google Scholar] [CrossRef]
- Shern, S.J.; Sarker, M.T.; Haram, M.H.S.M.; Ramasamy, G.; Thiagarajah, S.P.; Al Farid, F. Artificial intelligence optimization for user prediction and efficient energy distribution in electric vehicle smart charging systems. Energies 2024, 17, 5772. [Google Scholar] [CrossRef]
- Liu, Z.-F.; Liu, Y.-Y.; Jia, H.-J.; Jin, X.-L.; Liu, T.-H.; Wu, Y.-Z. Bi-level energy co-optimization of regional integrated energy system with electric vehicle to generalized-energy conversion framework and flexible hydrogen-blended gas strategy. Appl. Energy 2025, 390, 125868. [Google Scholar] [CrossRef]
- Daneshzand, F.; Coker, P.J.; Potter, B.; Smith, S.T. Ev smart charging: How tariff selection influences grid stress and carbon reduction. Appl. Energy 2023, 348, 121482. [Google Scholar] [CrossRef]
- Yong, J.Y.; Tan, W.S.; Khorasany, M.; Razzaghi, R. Electric vehicles destination charging: An overview of charging tariffs, business models and coordination strategies. Renew. Sustain. Energy Rev. 2023, 184, 113534. [Google Scholar] [CrossRef]
- Lin, H.; Zhou, Y.; Li, Y.; Zheng, H. Aggregator pricing and electric vehicles charging strategy based on a two-layer deep learning model. Electr. Power Syst. Res. 2024, 227, 109971. [Google Scholar] [CrossRef]
- Banda, P.; Bhuiyan, M.A.; Hasan, K.N.; Zhang, K. Assessment of hybrid transfer learning method for forecasting EV profile and system voltage using limited EV charging data. Sustain. Energy Grids Netw. 2023, 36, 101191. [Google Scholar] [CrossRef]
- Yadav, K.; Singh, M. Implementation of DC net metering scheme in off-board EV charging systems with a time of usage capability. Electr. Power Syst. Res. 2023, 224, 109690. [Google Scholar] [CrossRef]
- Rezaei, N.; Khazali, A.; Mazidi, M.; Ahmadi, A. Economic energy and reserve management of renewable-based microgrids in the presence of electric vehicle aggregators: A robust optimization approach. Energy 2020, 201, 117629. [Google Scholar] [CrossRef]
- Gao, X.; Chan, K.W.; Xia, S.; Zhou, B.; Lu, X.; Xu, D. Risk-constrained offering strategy for a hybrid power plant consisting of wind power producer and electric vehicle aggregator. Energy 2019, 177, 183–191. [Google Scholar] [CrossRef]
- Alipour, M.; Mohammadi-Ivatloo, B.; Moradi-Dalvand, M.; Zare, K. Stochastic scheduling of aggregators of plug-in electric vehicles for participation in energy and ancillary service markets. Energy 2017, 118, 1168–1179. [Google Scholar] [CrossRef]
- Park, S.-W.; Cho, K.-S.; Hoefter, G.; Son, S.-Y. Electric vehicle charging management using location-based incentives for reducing renewable energy curtailment considering the distribution system. Appl. Energy 2022, 305, 117680. [Google Scholar] [CrossRef]
- Li, F.; Gao, Y.; Wu, Y.; Xia, Y.; Wang, C.; Hu, J.; Huang, Z. Incentive learning-based energy management for hybrid energy storage system in electric vehicles. Energy Convers. Manag. 2023, 293, 117480. [Google Scholar] [CrossRef]
- Anqi, W. Economic efficiency of high-performance electric vehicle operation based on neural network algorithm. Comput. Electr. Eng. 2023, 112, 109026. [Google Scholar] [CrossRef]
- He, Z.; Hou, H.; Hou, T.; Fang, R.; Tang, J.; Xie, C. Multi-objective optimization for improving EV users’ adhesion with hybrid demand response strategy. Energy Rep. 2023, 9, 316–322. [Google Scholar] [CrossRef]
- Dokuchaev, N.; Zolotarevich, V. Optimal energy storing and selling in continuous time stochastic multi-battery setting. Sustain. Energy Grids Netw. 2020, 22, 100340. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, X.; Liu, H.; Ji, Z.; Li, F. Optimal dispatching strategy for residential demand response considering load participation. Glob. Energy Interconnect. 2024, 7, 38–47. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, A.; Wang, F.; Yan, X.; Li, Y.; Duić, N.; Shafie-Khah, M.; Catalão, J.P. Optimal scheduling of an EV aggregator for demand response considering triple level benefits of three-parties. Int. J. Electr. Power Energy Syst. 2021, 125, 106447. [Google Scholar] [CrossRef]
- Golmohamadi, H.; Keypour, R.; Bak-Jensen, B.; Pillai, J.R. A multi-agent based optimization of residential and industrial demand response aggregators. Int. J. Electr. Power Energy Syst. 2019, 107, 472–485. [Google Scholar] [CrossRef]
- Li, K.; Wang, F.; Mi, Z.; Fotuhi-Firuzabad, M.; Duić, N.; Wang, T. Capacity and output power estimation approach of individual behind-the-meter distributed photovoltaic system for demand response baseline estimation. Appl. Energy 2019, 253, 113595. [Google Scholar] [CrossRef]
- Shafie-Khah, M.; Heydarian-Forushani, E.; Golshan, M.E.H.; Siano, P.; Moghaddam, M.; Sheikh-El-Eslami, M.; Catalão, J. Optimal trading of plug-in electric vehicle aggregation agents in a market environment for sustainability. Appl. Energy 2016, 162, 601–612. [Google Scholar] [CrossRef]
- Lu, X.; Li, K.; Xu, H.; Wang, F.; Zhou, Z.; Zhang, Y. Fundamentals and business model for resource aggregator of demand response in electricity markets. Energy 2020, 204, 117885. [Google Scholar] [CrossRef]
- Cavus, M.; Allahham, A. Spatio-Temporal Attention-Based Deep Learning for Smart Grid Demand Prediction. Electronics 2025, 14, 2514. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Ma, J.; Li, D.; Zhang, W. Distributionally robust optimal dispatching method of integrated electricity and heating system based on improved Wasserstein metric. Int. J. Electr. Power Energy Syst. 2023, 151, 109120. [Google Scholar] [CrossRef]
- Mazidi, M.; Monsef, H.; Siano, P. Robust day-ahead scheduling of smart distribution networks considering demand response programs. Appl. Energy 2016, 178, 929–942. [Google Scholar] [CrossRef]
- Mohiti, M.; Monsef, H.; Anvari-Moghaddam, A.; Lesani, H. Two-Stage Robust Optimization for Resilient Operation of Microgrids Considering Hierarchical Frequency Control Structure. IEEE Trans. Ind. Electron. 2019, 67, 9439–9449. [Google Scholar] [CrossRef]
- Zheng, Y.; Niu, S.; Shang, Y.; Shao, Z.; Jian, L. Integrating plug-in electric vehicles into power grids: A comprehensive review on power interaction mode, scheduling methodology and mathematical foundation. Renew. Sustain. Energy Rev. 2019, 112, 424–439. [Google Scholar] [CrossRef]
- Yi, Z.; Scoffield, D.; Smart, J.; Meintz, A.; Jun, M.; Mohanpurkar, M.; Medam, A. A highly efficient control framework for centralized residential charging coordination of large electric vehicle populations. Int. J. Electr. Power Energy Syst. 2020, 117, 105661. [Google Scholar] [CrossRef]
- Jian, L.; Zheng, Y.; Shao, Z. High efficient valley-filling strategy for centralized coordinated charging of large-scale electric vehicles. Appl. Energy 2017, 186 Pt 1, 46–55. [Google Scholar] [CrossRef]
- Flores, R.J.; Shaffer, B.P.; Brouwer, J. Electricity costs for an electric vehicle fueling station with Level 3 charging. Appl. Energy 2016, 169, 813–830. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.; Li, J. A fast LP-based approach for robust dynamic economic dispatch problem: A feasible region projection method. IEEE Trans. Power Syst. 2020, 35, 4116–4119. [Google Scholar] [CrossRef]
- Li, S.; Gu, C.; Zeng, X.; Zhao, P.; Pei, X.; Cheng, S. Vehicle-to-grid management for multi-time scale grid power balancing. Energy 2021, 234, 121201. [Google Scholar] [CrossRef]
- Jiang, Y.; Dong, J.; Huang, H. Optimal bidding strategy for the price-maker virtual power plant in the day-ahead market based on multi-agent twin delayed deep deterministic policy gradient algorithm. Energy 2024, 306, 132388. [Google Scholar] [CrossRef]
- Wang, M.; Mu, Y.; Jiang, T.; Jia, H.; Li, X.; Hou, K.; Wang, T. Load curve smoothing strategy based on unified state model of different demand side resources. J. Mod. Power Syst. Clean Energy 2018, 6, 540–554. [Google Scholar] [CrossRef]
- Deng, R.; Xiang, Y.; Huo, D.; Liu, Y.; Huang, Y.; Huang, C.; Liu, J. Exploring flexibility of electric vehicle aggregators as energy reserve. Electr. Power Syst. Res. 2020, 184, 106305. [Google Scholar] [CrossRef]
- Lu, C.; Gu, N.; Jiang, W.; Wu, C. Sample-adaptive robust economic dispatch with statistically feasible guarantees. IEEE Trans. Power Syst. 2023, 39, 779–793. [Google Scholar] [CrossRef]
- Song, M.; Amelin, M. Purchase bidding strategy for a retailer with flexible demands in day-ahead electricity market. IEEE Trans. Power Syst. 2016, 32, 1839–1850. [Google Scholar] [CrossRef]
- Fang, D.; Tang, H.; Hatziargyriou, N.; Zhang, T.; Chen, W.; Zhang, Q. Dual-center control scheme and FF-DHRL-based collaborative optimization for charging stations under intra-day peak-shaving demand. Appl. Energy 2024, 368, 123453. [Google Scholar] [CrossRef]
- Ali, M.U.; Zafar, A.; Nengroo, S.H.; Hussain, S.; Alvi, M.J.; Kim, H.-J. Towards a smarter battery management system for electric vehicle applications: A critical review of lithium-ion battery state of charge estimation. Energies 2019, 12, 446. [Google Scholar] [CrossRef]
- Shi, Q.; Chen, C.F.; Mammoli, A.; Li, F. Estimating the profile of incentive-based demand response (IBDR) by integrating technical models and social-behavioral factors. IEEE Trans. Smart Grid 2019, 11, 171–183. [Google Scholar] [CrossRef]
- Watson, D.; Hastie, C.; Rodgers, M. Comparing different regulation offerings from a battery in a wind R&D park. IEEE Trans. Power Syst. 2017, 33, 2331–2338. [Google Scholar] [CrossRef]
- Guo, S.; Li, P.; Ma, K.; Yang, B.; Yang, J. Robust energy management for industrial microgrid considering charging and discharging pressure of electric vehicles. Appl. Energy 2022, 325, 119846. [Google Scholar] [CrossRef]








| No. | Methodology | Core Techniques/Models | Key Features and Advantages | Limitations and Challenges | Representative References |
|---|---|---|---|---|---|
| 1 | Dynamic Time-of-Use Pricing | Time-segmented pricing, price response models | Facilitates valley filling and peak clipping, significantly reduces user energy costs | Assumes full user compliance with price signals, neglects behavioral autonomy | [4,5] |
| 2 | Bi-level Deep Learning Framework | Deep Reinforcement Learning (DRL), Deep Q-Networks (DQNs) | Joint optimization of aggregator pricing and EV charging strategies, enhances intelligent charging decisions | Complex training, requires extensive data | [6] |
| 3 | Hybrid Transfer Learning Model | Transfer learning, time-series forecasting | Addresses data scarcity, improves accuracy of EV charging demand prediction | Heavily dependent on model generalization capability | [7] |
| 4 | Flexibility-Driven Dynamic Pricing Model | Decentralized response strategies, flexibility modeling | Reduces supply–demand mismatch, considers EV autonomy, improves response precision | Requires accurate characterization of individual flexibility | [8] |
| 5 | Robust Microgrid Energy Management Model | Robust optimization, uncertainty modeling | Balances technical, economic, and environmental performance; enhances dispatch reliability | Computationally intensive, uncertainty in parameters remains | [9] |
| 6 | Info-gap Decision Theory and Bi-level Stochastic Optimization | Info-gap theory, bi-level stochastic programming | Enhances dispatch resilience and profit maximization under uncertainty | High model complexity and solving difficulty | [10,11] |
| 7 | Stochastic Response Models | Demand elasticity and price sensitivity modeling | Reduces user energy costs, improves economic responsiveness | Often neglects user heterogeneity and bidirectional uncertainty | [12,13,14] |
| 8 | User Behavior Modeling and Charging Habit Analysis | Willingness-aware demand response (PSDR, IBDR) | Increases user participation while preserving comfort and autonomy | Complex behavioral modeling, high data requirements | [15,16,17,18,19,20] |
| 9 | Multi-agent Uncertainty-Integrated Aggregator Cost Modeling | Multi-agent game theory, integrated market and system uncertainty | Realistically reflects EVA profitability considering multi-level interactions | Requires precise multi-layer uncertainty modeling | [21,22,23] |
| 10 | Robust Optimization and Mixed-Integer Linear Programming (MILP) | Robust optimization, MILP formulation | Ensures near-global optimality and computational feasibility | High computational demand for large-scale problems | [24,25] |
| 11 | Demand Forecasting and Deep Learning | ST-CALNet, CNN + LSTM + attention | Spatiotemporal capture; better accuracy, interpretability | Regional bias; opaque LSTM; high complexity | [26] |
| 12 | Peak Shaving, Vehicle-to-Grid (V2G) Scheduling and Coordinated Dispatch Strategies | Grid–EV interaction, virtual power plant dispatch | Enhances system stability, reduces operating costs, promotes tightly coupled grid–EV ecosystems | Requires complex coordination mechanisms, challenges in real-time dispatch | [27,28,29,30,31,32] |
| Abbreviation | Full Name |
|---|---|
| EVA | Electric Vehicle Aggregator |
| EV | Electric Vehicle |
| CBDR | Charging-Based Demand Response |
| DBDR | Discharging-Based Demand Response |
| DR | Demand Response |
| V2G | Vehicle-to-Grid |
| SOC | State of Charge |
| AS Market | Ancillary Services Market |
| R_DA | Day-Ahead Market Price |
| R_up/R_down | Regulation Prices |
| Scenario | Response Strategy |
|---|---|
| Scenario 1 | Only the effect of the CBDR is considered. The EVA sets charging incentive discounts, and EVs responding to the CBDR are controlled by the EVA to participate in ancillary service peak regulation. |
| Scenario 2 | Only the effect of the DBDR is considered. The EVA sets appropriate discharging subsidies, and EVs responding to the DBDR are controlled by the EVA to participate in ancillary service peak regulation. |
| Scenario 3 | Both CBDR and DBDR effects are considered. The EVA simultaneously sets charging incentive discounts and discharging subsidies. EVs respond to CBDR and DBDR across multiple time periods and are coordinated by the EVA to participate in ancillary service peak regulation. |
| Item | CBDR | DBDR | CBDR + DBDR |
|---|---|---|---|
| Subsidy Cost | – | 1410.58584 | 2279.02056 |
| Electricity Purchase Cost | 1260.98458 | 1153.63228 | 1350.06435 |
| Peak Regulation Cost | 800.54838 | 702.05845 | 1003.54826 |
| Energy Revenue | 2287.26843 | 3202.97581 | 6587.89309 |
| Capacity Revenue | 1260.97757 | 1630.61758 | 2700.11592 |
| Total Operating Revenue | 1486.71304 | 1567.31682 | 4655.37584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Liu, Y.; Tian, C.; Peng, B. A Multi-Temporal Regulation Strategy for EV Aggregators Enabling Bi-Directional Energy Interactions in Ancillary Service Markets for Sustainable Grid Operation. Sustainability 2025, 17, 7315. https://doi.org/10.3390/su17167315
Ma X, Liu Y, Tian C, Peng B. A Multi-Temporal Regulation Strategy for EV Aggregators Enabling Bi-Directional Energy Interactions in Ancillary Service Markets for Sustainable Grid Operation. Sustainability. 2025; 17(16):7315. https://doi.org/10.3390/su17167315
Chicago/Turabian StyleMa, Xin, Yubing Liu, Chongyi Tian, and Bo Peng. 2025. "A Multi-Temporal Regulation Strategy for EV Aggregators Enabling Bi-Directional Energy Interactions in Ancillary Service Markets for Sustainable Grid Operation" Sustainability 17, no. 16: 7315. https://doi.org/10.3390/su17167315
APA StyleMa, X., Liu, Y., Tian, C., & Peng, B. (2025). A Multi-Temporal Regulation Strategy for EV Aggregators Enabling Bi-Directional Energy Interactions in Ancillary Service Markets for Sustainable Grid Operation. Sustainability, 17(16), 7315. https://doi.org/10.3390/su17167315






