Spatiotemporal-Imbalance-Aware Risk Prediction Framework for Lightning-Caused Distribution Grid Failures
Abstract
1. Introduction
- (1)
- Analytical methods based on electrical characteristics or probabilistic statistics. For example, Zhang et al. [12] developed an electrical geometry model to simultaneously compute fault rates on photovoltaic systems and tripping rates on distribution lines, while Alessio et al. [13,14,15] proposed a probabilistic statistical framework to quantify risks associated with lightning protection equipment failures.
- (2)
- Data sparsity: The sparse nature of lightning strike data in distribution networks leads to the neglect of low-frequency, high-hazard events, resulting in underestimation of extreme risks.
- Poor generalization: Due to the long-tail distribution of lightning faults, traditional machine learning models exhibit unstable performance in predicting rare high-hazard events.
- Low interpretability: Black-box models lack transparency, hindering their utility in operational decision-making.
2. Model Frame
3. Data Entry and Preprocessing
4. Criteria Optimization Model for Association Rule Discovery
4.1. Preliminary
4.2. Database
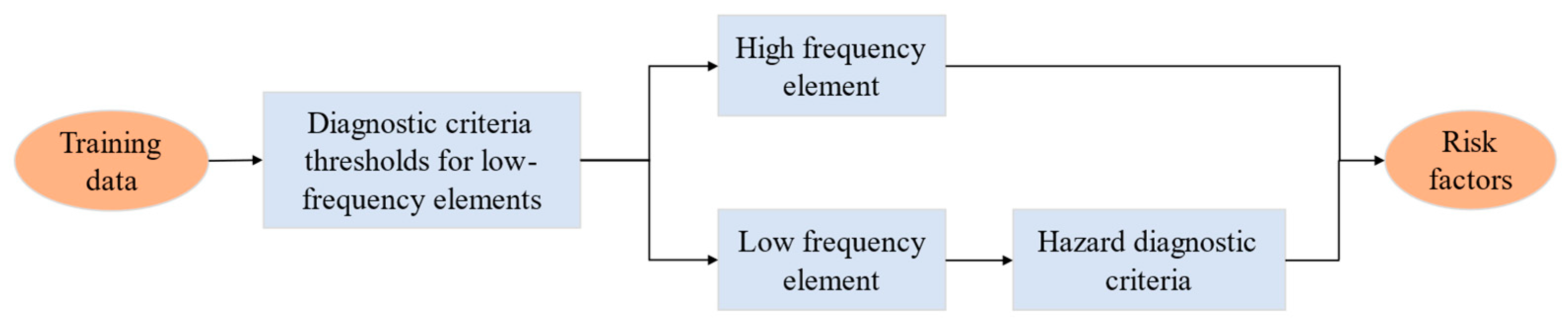
4.3. Development of Diagnostic Thresholds for Low-Frequency Element Analysis
4.4. Calculation of Diagnostic Criteria for Hazard
4.5. Implementation Process of CS-ARM Prediction Model
5. Association Rule Mining with Adaptive Weight Adjustment
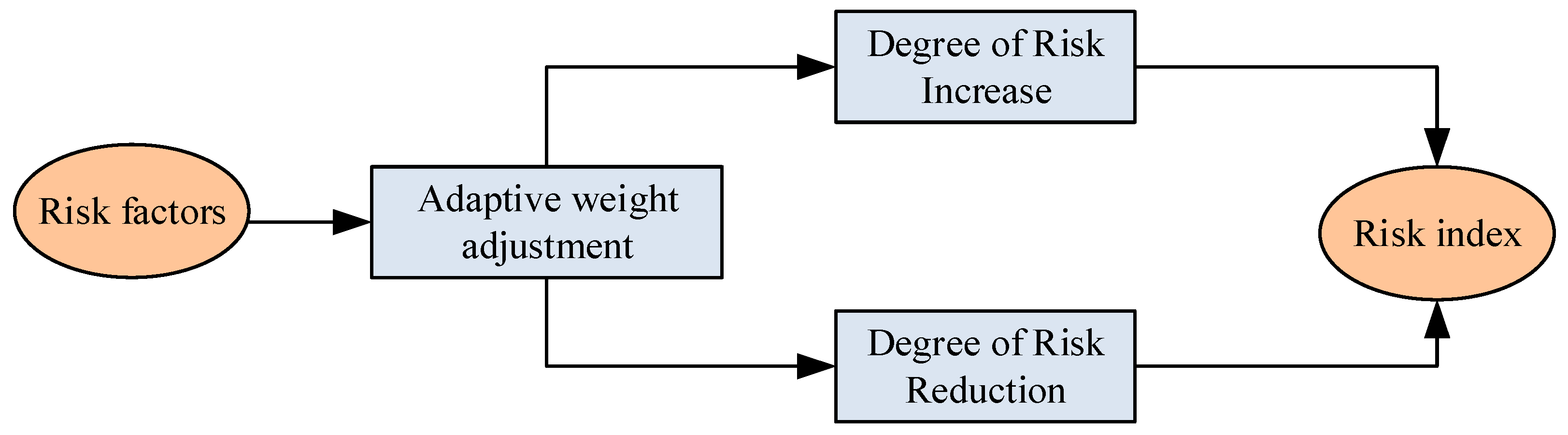
5.1. Construction of the Adaptive Weight Adjustment Model
5.2. Implementation Process of WA-ARM
| Algorithm 1 Adaptive Weight Adjustment Input | |
| 1: | Initialize |
| 2: | for each environmental feature in environmental features do: |
| 3: | |
| 4: | for each element in do: |
| 5: | |
| 6: | end for |
| 7: | for each element in do: |
| 8: | |
| 9: | |
| 10: | |
| 11: | end for |
| 12: | |
| 13: | end for |
| 14: | |
| 15: | return |
- For a given environmental element : Use Equation (15) to calculate the high-frequency element’s risk influence on it. Use Equations (18)–(20) to calculate the low-frequency element’s risk influence on it.
- Use Equation (14) to compute the comprehensive risk score of the individual element .
- Repeat Steps 1–2 to determine the risk score for each element.
- Calculate the predicted failure risk level for each fault record and normalize it (0 → 1: impossible to occur → certain to occur).
6. Results and Discussion
6.1. The Correlation Between Feature Factors and Lightning Strike Faults
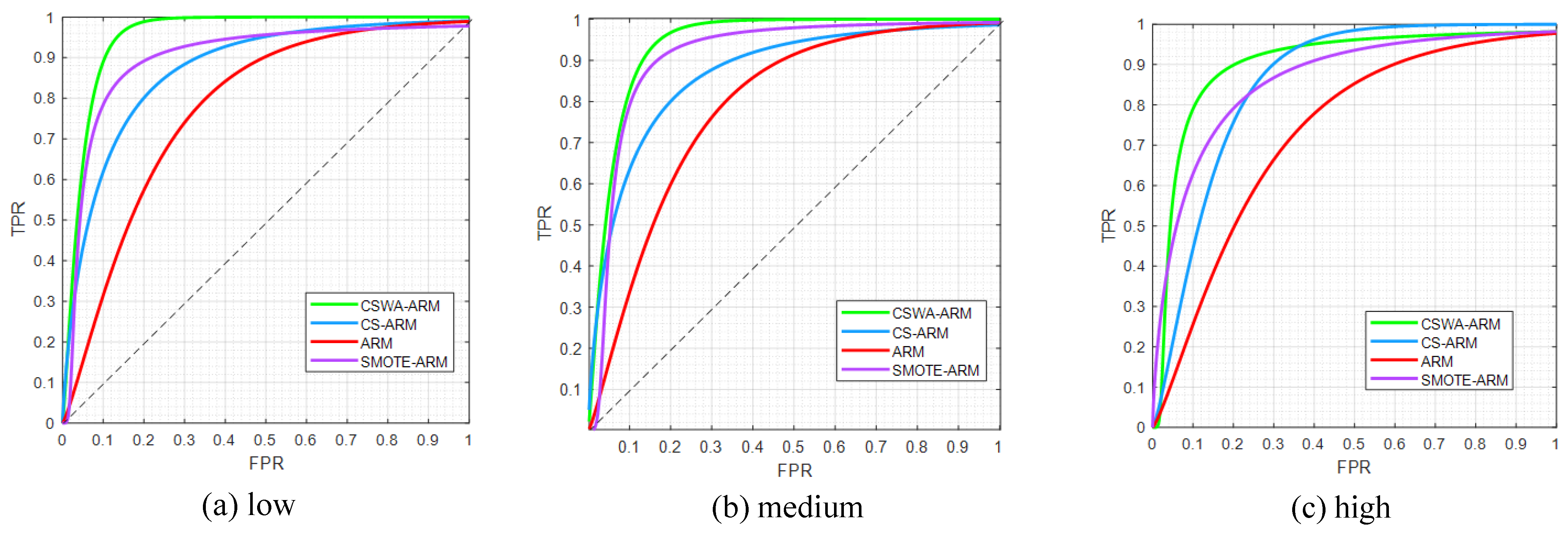
6.2. Evaluation of Prediction Performance
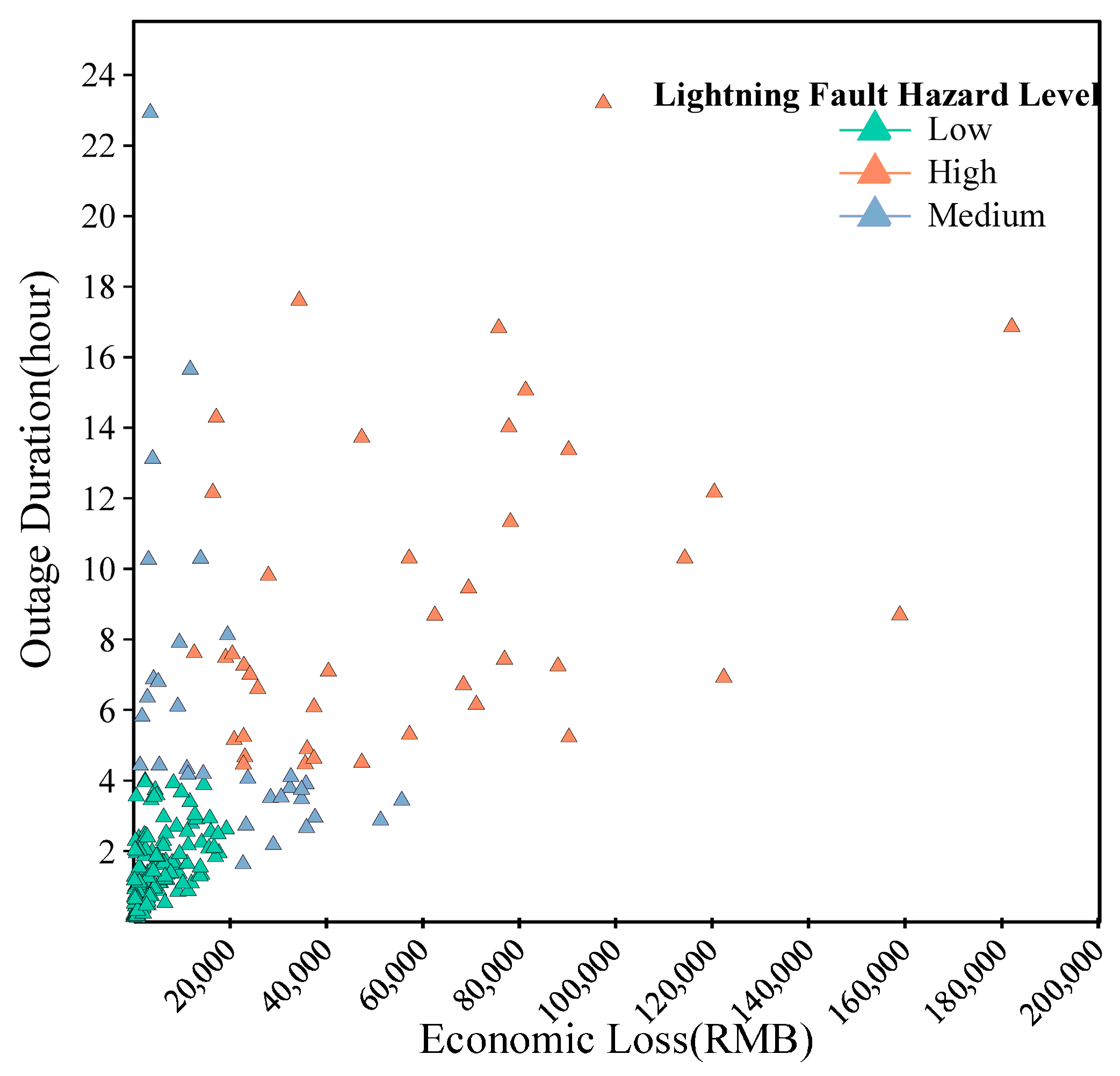
6.3. Lightning Failure Risk Hazard Test
7. Conclusions
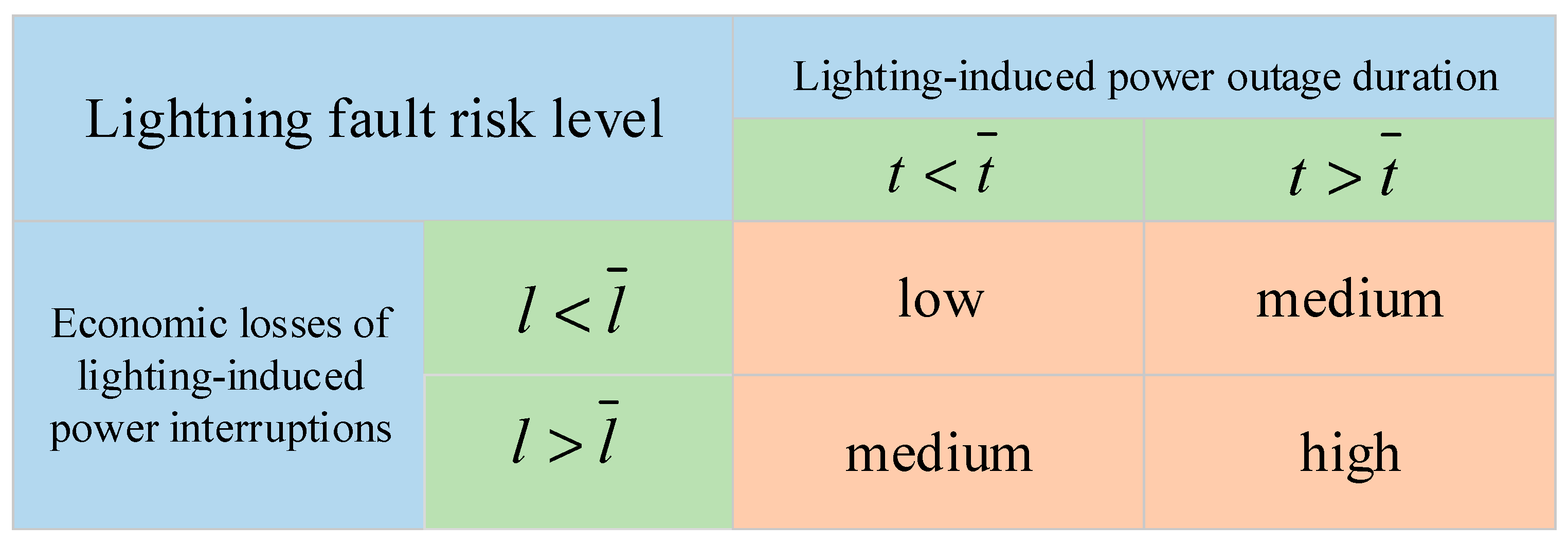
- Inspired by risk matrix theory, we designed a lightning strike hazard-level matrix. This matrix demonstrates strong specificity in evaluating lightning strike risk, comprehensively considers economic loss factors, and simplifies the assessment process. These advantages enable it to better meet risk assessment requirements in specific application scenarios.
- We proposed a diagnostic threshold-setting method for low-frequency elements and a calculation approach for hazard diagnostic criteria. This method incorporates previously neglected low-frequency elements into the analysis and identifies low-frequency, high-hazard factors. It addresses data imbalance issues from both temporal and spatial dimensions.
- An adaptive weight adjustment model was developed. By assigning different relative weights, this model determines the varying impacts of environmental factors on overall system reliability, thereby further improving prediction accuracy.
- Research Limitations
- (1)
- Data Dependency: The model requires all 14 feature fields listed in Table 1; due to dataset limitations, comprehensive model testing under extreme weather conditions could not be conducted.
- (2)
- Implementation Constraints: Actual system integration and field deployment tests have not been conducted due to current research limitations, primarily because real-time deployment requires multi-source data integration with SCADA and lightning monitoring systems, and hardware architecture adaptation for different grid companies’ needs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.; Tong, C.; Xiang, M.; Wang, T.; Xu, J.; Zheng, J. Lightning risk estimation and preventive control method for power distribution networks referring to the indeterminacy of wind power and photovoltaic. Electr. Power Syst. Res. 2023, 214 Pt A, 108896. [Google Scholar] [CrossRef]
- Chinese National Energy Administration (NEA) and China Electricity Council (CEC). National Electric Reliability Annual Report. 2020. Available online: https://prpq.nea.gov.cn/uploads/file1/20250331/67ea4fb889529.pdf (accessed on 3 August 2025).
- Tang, Y.; He, K.; Shu, H.; Wang, K.; Lou, W.; Qin, Z.; Han, Y.; Dai, Y. Reliability and Safety Assessment of Distribution Networks in Mountainous Plateau Areas Subject to Low-amplitude Lightning. Reliab. Eng. Syst. Saf. 2025, 264, 111305. [Google Scholar] [CrossRef]
- Yang, J.; An, Y.; Hu, Y.; Yao, S.; Pang, Z.; Qi, Y.; Sha, X.; Wang, Q.; Qu, L. Analysis of influencing factors of lightning strike damage of optical fiber composite overhead ground wire in distribution network. Electr. Power Syst. Res. 2025, 241, 111346. [Google Scholar] [CrossRef]
- Snodgrass, J.; Xie, L. Overvoltage analysis and protection of lightning arresters in distribution systems with distributed generation. Int. J. Electr. Power Energy Syst. 2020, 123, 106209. [Google Scholar] [CrossRef]
- Huang, J.; Lu, H.; Du, M. Coordinated development of digital economy and ecological resilience in China: Spatial—Temporal evolution and convergence. Environ. Dev. Sustain. 2025, 1–29. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, L.; Wei, R.; Wang, D. A Novel Lightning Overvoltage Protection Scheme Using Magnetic Rings for Transmission Line Systems. IEEE Trans. Ind. Electron. 2023, 70, 12872–12882. [Google Scholar] [CrossRef]
- Xie, P.; Fang, Z. Lightning Performance of Unshielded 220 kV Transmission Lines Equipped With Metal Oxide Arresters. IEEE Trans. Electromagn. Compat. 2022, 64, 795–804. [Google Scholar] [CrossRef]
- Kuang, F.; Li, X.; Zhong, X.; Xu, Z.; Zhou, L. Classification of lightning strike risk for distribution line tower terrain in mountainous area. J. Electr. Power Sci. Technol. 2021, 36, 66–72. [Google Scholar]
- Zhang, H.; Deng, Y.; Wang, Y.; He, X.; Lan, L.; Wen, X. Joint diagnosis and validation of lightning risk for transmission lines by using multisource data. Electr. Power Syst. Res. 2024, 236, 110878. [Google Scholar] [CrossRef]
- Liu, H.; Han, Y.; Chen, C.; Chen, Y.; Cheng, Z.; Li, L. Research on lightning trip rate calculation and differentiated lightning protection of distribution line. Insul. Surge Arresters 2020, 296, 7–12. [Google Scholar]
- Zhang, M.; Liu, J.; Liu, Y.; Xia, L.; Chai, C.; Li, P. Lightning risk assessment of active distribution network with distributed photovoltaic system. Energy Rep. 2024, 12, 3711–3717. [Google Scholar] [CrossRef]
- Misuri, A.; Antonioni, G.; Cozzani, V. Quantitative risk assessment of domino effect in Natech scenarios triggered by lightning. J. Loss Prev. Process Ind. 2020, 64, 104095. [Google Scholar] [CrossRef]
- Piparo, G.B.L.; Maccioni, M.; Kisielewicz, T.; Mazzetti, C. Probability of Damage of Apparatus Powered by an HV/LV Transformer due to Lightning to a Structure Protected by a Lightning Protection System. In Proceedings of the 2023 International Symposium on Lightning Protection (XVII SIPDA), Suzhou, China, 9–13 October 2023; pp. 1–6. [Google Scholar]
- Souto, L.; Taylor, P.C.; Wilkinson, J. Probabilistic impact assessment of lightning strikes on power systems incorporating lightning protection design and asset condition. Int. J. Electr. Power Energy Syst. 2023, 148, 108974. [Google Scholar] [CrossRef]
- Wang, J.; Gao, S.; Yu, L.; Zhang, D.; Xie, C.; Chen, K.; Kou, L. Data-driven lightning-related failure risk prediction of overhead contact lines based on Bayesian network with spatiotemporal fragility model. Reliab. Eng. Syst. Saf. 2023, 231, 109016. [Google Scholar] [CrossRef]
- Zhou, Q.; Ye, J.; Yang, G.; Huang, R.; Zhao, Y.; Gu, Y.; Bian, X. Lightning risk assessment of offshore wind farms by semi-supervised learning. Eng. Appl. Artif. Intell. 2023, 126 Pt C, 107050. [Google Scholar] [CrossRef]
- Fister, I., Jr.; Fister, I.; Fister, D.; Podgorelec, V.; Salcedo-Sanz, S. A comprehensive review of visualization methods for association rule mining: Taxonomy, challenges, open problems and future ideas. Expert Syst. Appl. 2023, 233, 120901. [Google Scholar] [CrossRef]
- Veerappa, M.; Anneken, M.; Burkart, N.; Huber, M.F. Chapter 9—Explaining CNN classifier using association rule mining methods on time-series. In Explainable Deep Learning AI; Benois-Pineau, J., Bourqui, R., Petkovic, D., Quénot, G., Eds.; Academic Press: San Diego, CA, USA, 2023; pp. 173–189. [Google Scholar]
- Wu, W.; Wang, S.; Liu, B.; Shao, Y.; Xie, W. A novel software defect prediction approach via weighted classification based on association rule mining. Eng. Appl. Artif. Intelligence. 2024, 129, 107622. [Google Scholar] [CrossRef]
- Jia, P.; Zhang, J.; Zhao, B.; Li, H.; Liu, X. Privacy-preserving association rule mining via multi-key fully homomorphic encryption. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 641–650. [Google Scholar] [CrossRef]
- Nadakinamani, R.G.; Reyana, A.; Gupta, Y.; Kautish, S.; Ghorashi, S.; Jamjoom, M.M.; Mohamed, A.W. High-performance association rule mining: Mortality prediction model for cardiovascular patients with COVID-19 patterns. Alex. Eng. J. 2023, 71, 347–354. [Google Scholar] [CrossRef]
- Tandan, M.; Acharya, Y.; Pokharel, S.; Timilsina, M. Discovering symptom patterns of COVID-19 patients using association rule mining. Comput. Biol. Med. 2021, 131, 104249. [Google Scholar] [CrossRef]
- Ibrahim, N.A.; Alwi, S.R.W.; Manan, Z.A.; Mustaffa, A.A.; Kidam, K. Risk matrix approach of extreme temperature and precipitation for renewable energy systems in Malaysia. Energy 2022, 254 Pt C, 124471. [Google Scholar] [CrossRef]
- Pang, K.; Li, S.; Lu, Y.; Kang, N.; Zou, L.; Lu, M. Association rule mining with fuzzy linguistic information based on attribute partial ordered structure. Soft Comput. 2023, 27, 17447–17472. [Google Scholar] [CrossRef]
- Liu, W.; Wang, X.; Ye, P.; Jiang, L.; Feng, R. Safety accident analysis of power transmission and substation projects based on association rule mining. Environ. Sci. Pollut. Res. 2023, 1–12. [Google Scholar] [CrossRef]
- Huang, J.; Chen, C.; Sun, C.; Cao, Y.; An, Y. An integrated risk assessment model for the multi-perspective vulnerability of distribution networks under multi-source heterogeneous data distributions. Int. J. Electr. Power Energy Syst. 2023, 153, 109397. [Google Scholar] [CrossRef]
- Jiang, W.; Ma, S.; Zhang, Z.; Xu, Y. Study on Key Causal Factors and Pathways of Fire and Explosion Accidents in Hazardous Chemical Storage Tank Area. J. Loss Prev. Process Ind. 2025, 97, 105704. [Google Scholar] [CrossRef]
- Tu, X.; Fu, L.; Wang, Q. Carbon price prediction based on multidimensional association rules and optimized multi-factor LSTM model. Energy 2025, 329, 136768. [Google Scholar] [CrossRef]
- Nam, H.; Yun, U.; Yoon, E.; Lin, J.C.-W. Efficient approach for incremental weighted erasable pattern mining with list structure. Expert Syst. Appl. 2020, 143, 113087. [Google Scholar] [CrossRef]
- Lee, G.; Yun, U.; Ryu, K.H. Mining frequent weighted itemsets without storing transaction ids and generating candidates. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2017, 25, 111–144. [Google Scholar] [CrossRef]
- Lee, G.; Yun, U.; Ryang, H.; Kim, D. Erasable itemset mining over incremental databases with weight conditions. Eng. Appl. Artif. Intell. 2016, 52, 213–234. [Google Scholar] [CrossRef]
- Rönkä, S.; Konttinen, H.; Kriikku, P.; Hakkarainen, P.; Häkkinen, M.; Karjalainen, K. Exploring the risk matrix of drug overdose deaths of young people: Drug use patterns, individual characteristics, circumstances, and environment. Drug Alcohol Depend. 2025, 274, 112757. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Bai, J.; Wang, H.; Luan, L.; Zhu, W.; Wang, J.; Liu, Z. Lightning risk assessment method for overhead transmission lines based on multi-dimensional association information fusion. J. Electr. Eng. 2018, 38, 6233–6244. [Google Scholar]
- Phillips, G.; Teixeira, H.; Kelly, M.G.; Herrero, F.S.; Várbíró, G.; Solheim, A.L.; Kolada, A.; Free, G.; Poikane, S. Setting nutrient boundaries to protect aquatic communities: The importance of comparing observed and predicted classifications using measures derived from a confusion matrix. Sci. Total Environ. 2024, 912, 168872. [Google Scholar] [CrossRef] [PubMed]


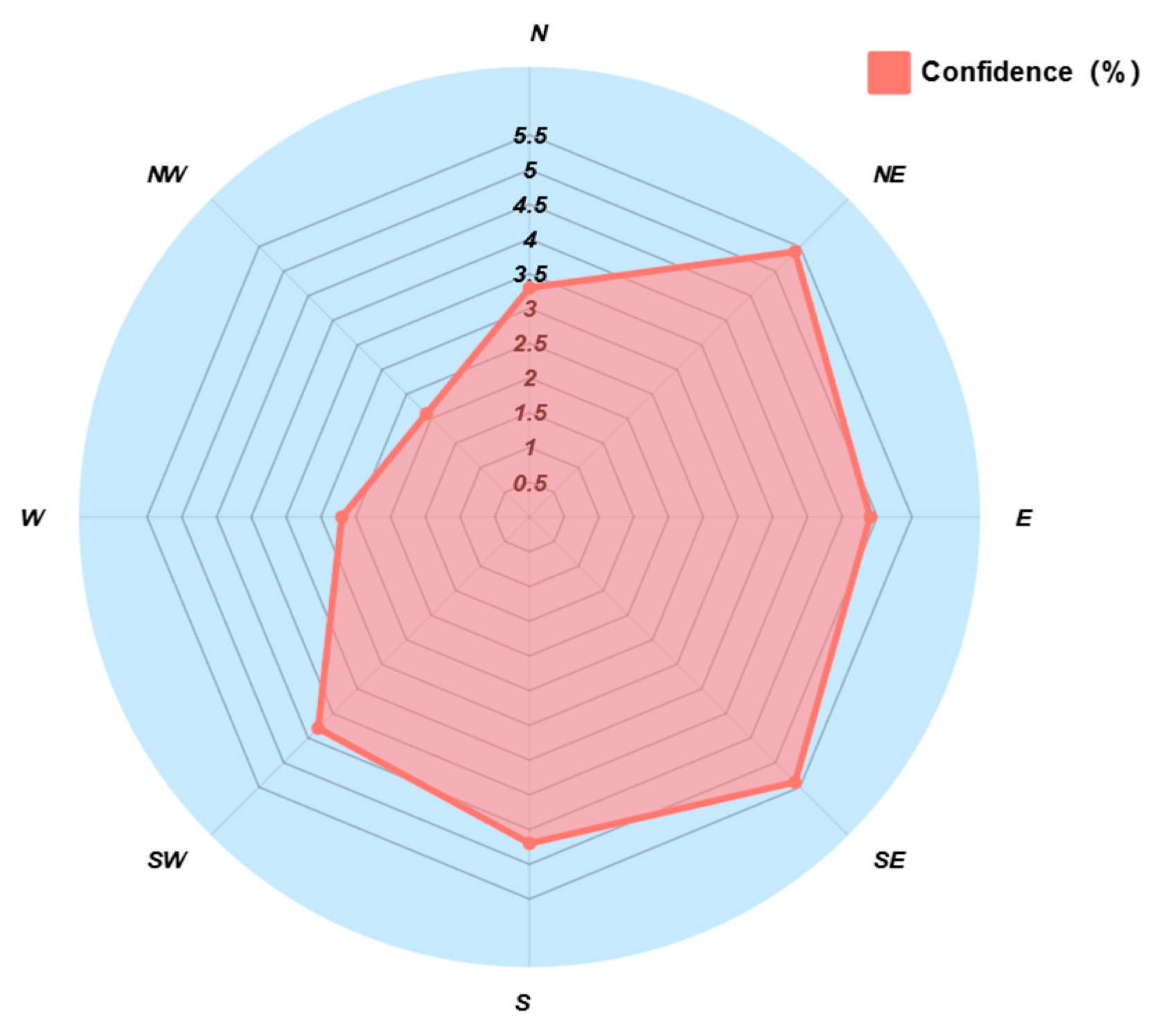
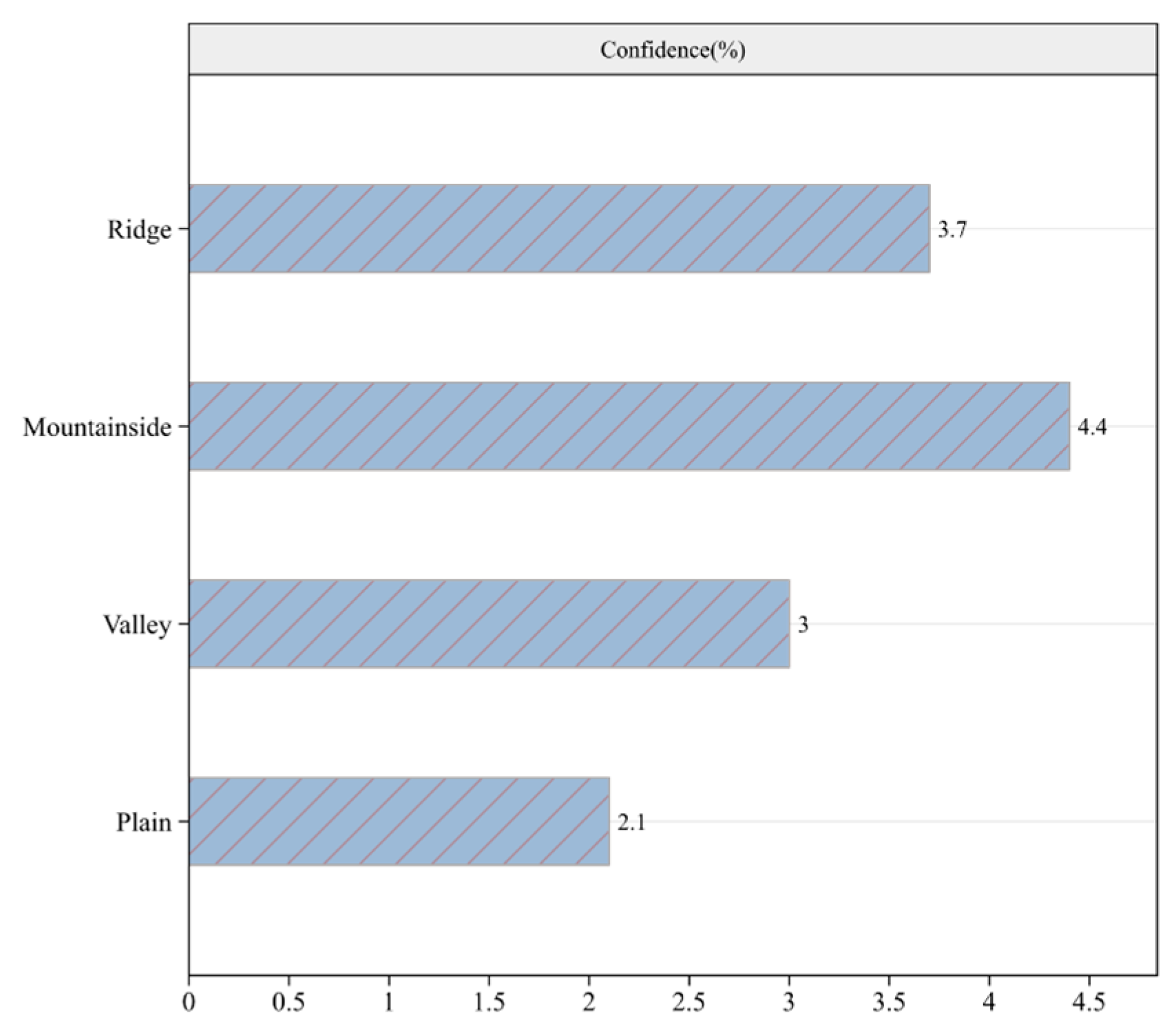
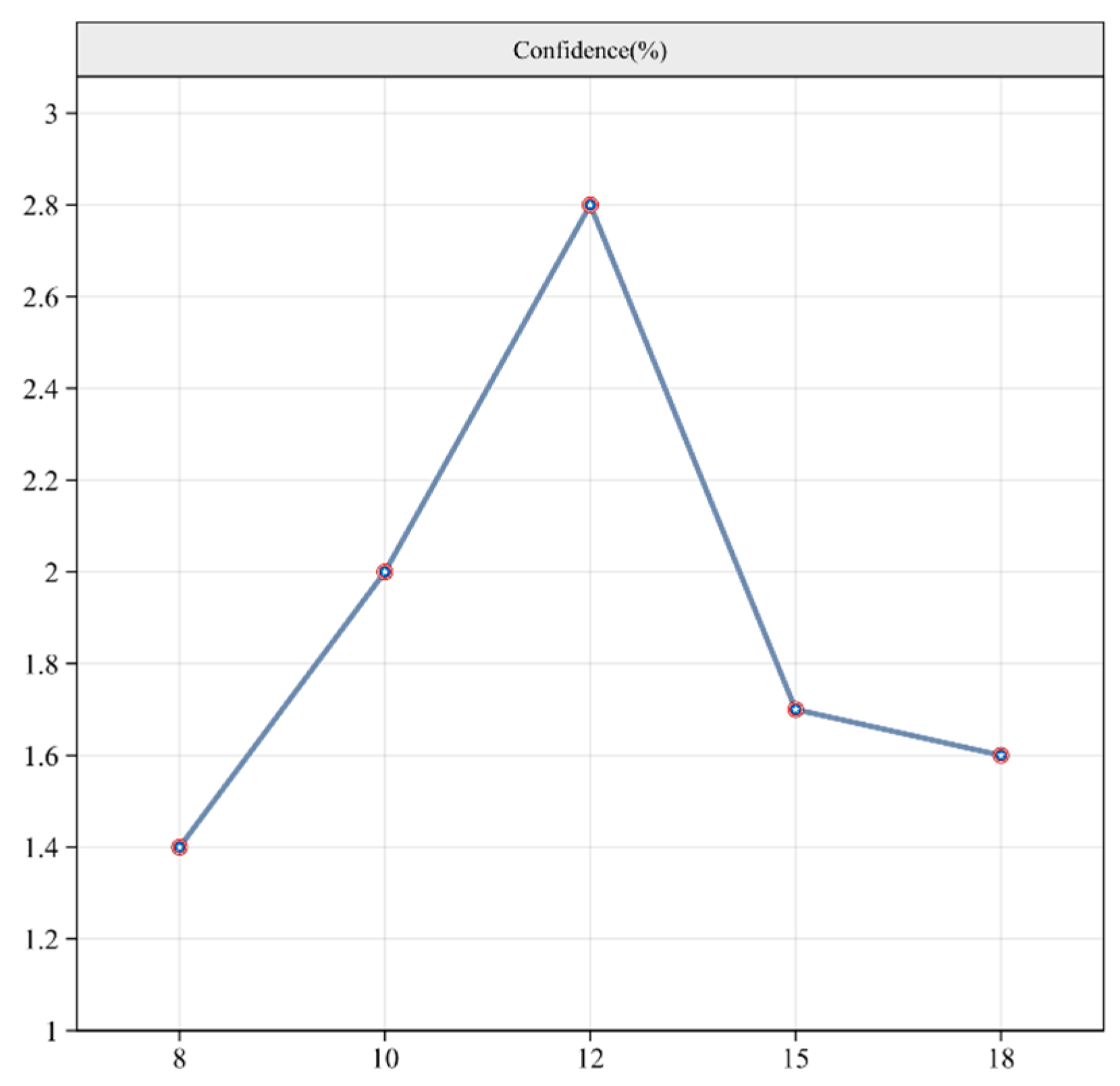
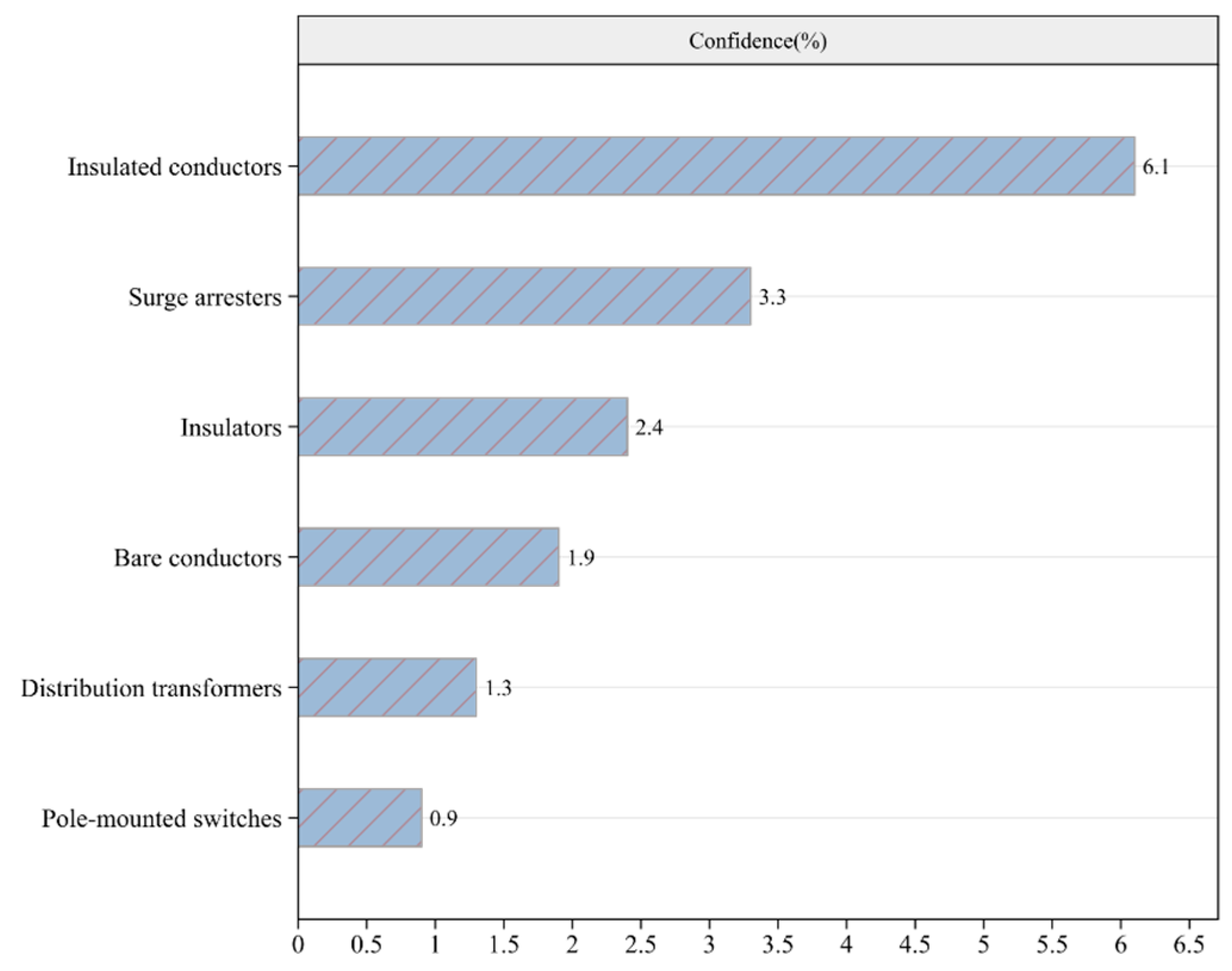



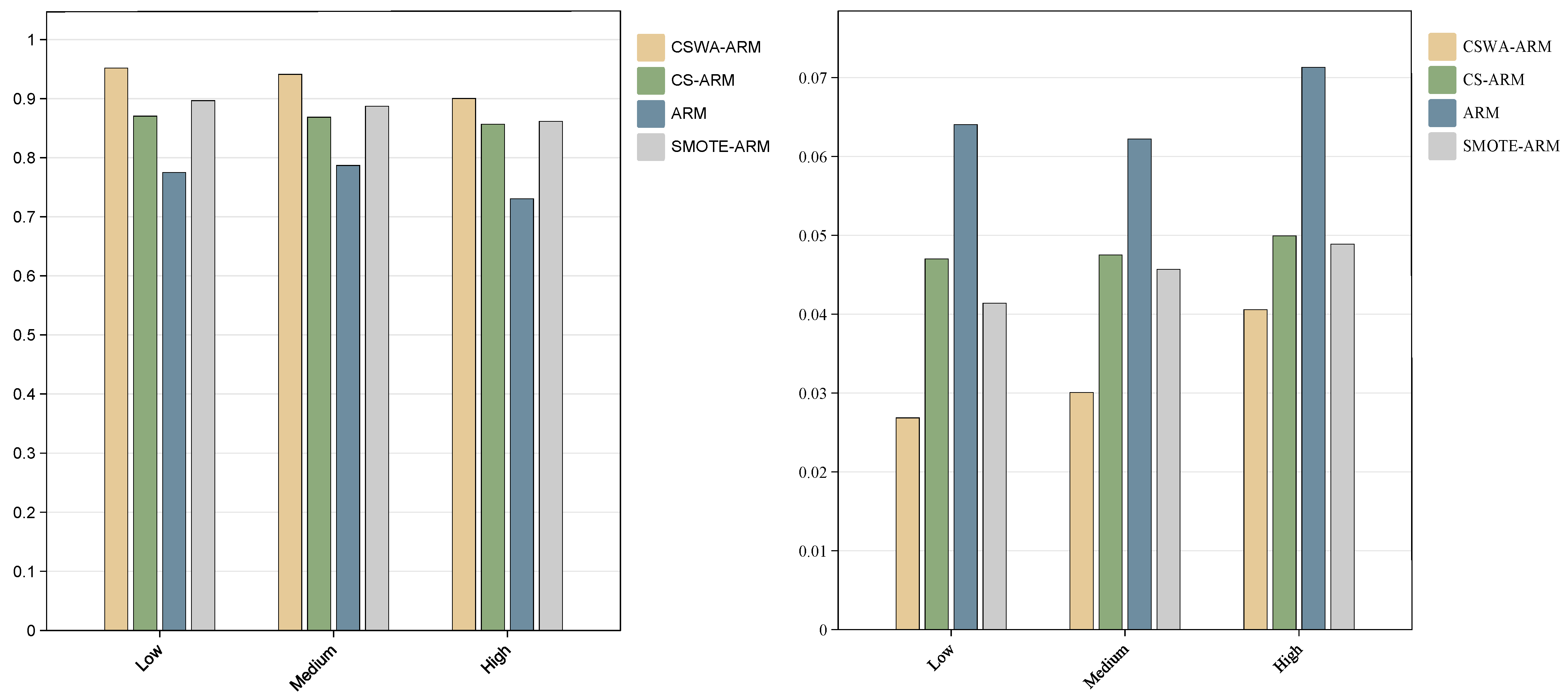
| Attribute Character | Element |
|---|---|
| Voltage | 10 kV, 35 kV |
| Transmission tower height (m) | 8, 10, 12, 15, 18 |
| Circuit number | Single circuit, double circuit |
| Faulty equipment | Insulators, distribution transformers, bare conductors, pole-mounted switches |
| Month | 1–12 |
| Day | 1–30 |
| Moment (h) | 1–24 |
| Slope position | Ridge, mountainside, valley, plain |
| Weather | Sunny, overcast, cloudy, rainy, sleet, stormy |
| Temperature (°C) | ≤6, 7–12, 13–18, 18–24, ≥24 |
| Air pressure (hPa) | Average |
| Wind speed (m/s) | Average |
| Aspect | E, N, S, W, NE, NW, SE, SW |
| Lightning failure hazard level | Low, medium, high |
| Attribute Character | Element |
|---|---|
| Voltage | 35 kV |
| Transmission tower height (m) | 10, 15 |
| Circuit number | triple circuit |
| Faulty equipment | Distribution transformers |
| Month | 1, 2, 9, 10, 11, 12 |
| Day | 1–30 |
| Moment (h) | 1–24 |
| Slope position | Valley, plain |
| Weather | Sunny, overcast, sleet, stormy |
| Temperature (°C) | ≤6, 7–12, 13–18 |
| Air pressure (hPa) | Average |
| Wind speed (m/s) | Average |
| Aspect | N, W, NW, SW |
| CSWA-ARM | AUC | SE | CI |
| Low | 0.93640 | 0.03137 | 0.87492–0.95789 |
| Medium | 0.91862 | 0.03609 | 0.84789–0.98935 |
| High | 0.87956 | 0.04518 | 0.79100–0.96811 |
| CS-ARM | AUC | SE | CI |
| Low | 0.85847 | 0.04955 | 0.76–0.0.92558 |
| Medium | 0.83764 | 0.05355 | 0.73267–0.94260 |
| High | 0.80995 | 0.05846 | 0.69538–0.92453 |
| ARM | AUC | SE | CI |
| Low | 0.75703 | 0.06665 | 0.62641–0.88765 |
| Medium | 0.70598 | 0.07322 | 0.56248–0.84948 |
| High | 0.69632 | 0.07433 | 0.5504–0.84191 |
| SMOTE-ARM | AUC | SE | CI |
| Low | 0.89662 | 0.04139 | 0.81550–0.97774 |
| Medium | 0.88701 | 0.0457 | 0.80143–0.96733 |
| High | 0.86168 | 0.0489 | 0.76583–0.95763 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, S.; Yang, X.; Huang, J.; Hu, J.; Zuo, J.; Li, S. Spatiotemporal-Imbalance-Aware Risk Prediction Framework for Lightning-Caused Distribution Grid Failures. Sustainability 2025, 17, 7228. https://doi.org/10.3390/su17167228
Tang S, Yang X, Huang J, Hu J, Zuo J, Li S. Spatiotemporal-Imbalance-Aware Risk Prediction Framework for Lightning-Caused Distribution Grid Failures. Sustainability. 2025; 17(16):7228. https://doi.org/10.3390/su17167228
Chicago/Turabian StyleTang, Shenqin, Xin Yang, Jie Huang, Junyao Hu, Jiawu Zuo, and Shuo Li. 2025. "Spatiotemporal-Imbalance-Aware Risk Prediction Framework for Lightning-Caused Distribution Grid Failures" Sustainability 17, no. 16: 7228. https://doi.org/10.3390/su17167228
APA StyleTang, S., Yang, X., Huang, J., Hu, J., Zuo, J., & Li, S. (2025). Spatiotemporal-Imbalance-Aware Risk Prediction Framework for Lightning-Caused Distribution Grid Failures. Sustainability, 17(16), 7228. https://doi.org/10.3390/su17167228







