Joint Training Method for Assessing the Thermal Aging Health Condition of Oil-Immersed Power Transformers

Abstract

Transformer health assessment enables predictive maintenance strategies that extend equipment lifespan, minimize resource consumption, and support sustainable power system operations. However, traditional methods often rely on simple health indicators, which fail to effectively capture the complex relationships within transformer health data. To address this issue, this article proposes a joint training method based on a wide and deep model, enhanced with Bayesian inference and Markov chain Monte Carlo (MCMC) techniques. The model combines a wide component, which uses linear regression to identify global patterns in transformer health parameters, and a deep neural network that learns complex nonlinear relationships, such as those in thermal aging data. Bayesian inference is integrated to quantify uncertainties in the predictions, while MCMC is employed for robust parameter estimation during training. This combination enables a more accurate, interpretable, and comprehensive assessment of transformer conditions. Experimental results on realistic datasets show that the proposed method significantly improves prediction accuracy and reliability compared to existing approaches. Specifically, the joint wide and deep model outperforms traditional methods by 6.6% in classification accuracy, demonstrating its potential for application in smart grid systems. This research contributes to sustainable power system management by enabling more efficient resource utilization and supporting the transition to sustainable energy systems.

1. Introduction

Power transformers are indispensable assets in electrical power systems, responsible for voltage conversion and enabling efficient transmission and distribution of electricity. Among various types, oil-immersed transformers are predominantly used in high-voltage and high-capacity scenarios due to their superior insulation and thermal characteristics. Over their service life, transformers are subjected to thermal, electrical, and mechanical stresses that lead to degradation of internal components—particularly the oil–paper insulation system. Common health-related conditions include thermal aging, moisture ingress, oil acidification, sludge formation, and partial discharges. If unaddressed, these conditions can degrade performance, increase the risk of in-service failure, and potentially lead to power outages or cascading failures. Therefore, accurate health condition assessment is essential for ensuring system reliability and supporting the shift from time-based maintenance to predictive, condition-based strategies.

Improving transformer performance is closely tied to understanding their health condition, which is crucial for enhancing reliability and making informed asset management decisions [1]. Unlike traditional condition monitoring, the health index (HI) is a helpful tool that combines condition information about transformers to provide a single quantitative indicator that represents their general health [2]. Although the HI does not represent the state of any specific transformer component, it effectively reflects the overall aging and degradation level of the equipment over time. This study focuses on the development of data-driven approaches for evaluating the health condition of oil-immersed power transformers based on HI modeling and classification techniques.

Existing transformer health assessment methods include the linear weighted sum method [3,4,5], fuzzy inference systems [6,7,8], and artificial intelligence techniques [9,10,11]. The linear weighted sum method assigns scores and weights to various condition indicators, typically based on expert judgment, to compute a composite health index [5]. However, this approach is highly subjective, as the assigned weights may vary between experts, leading to inconsistent or biased results. Furthermore, diagnostic thresholds often overlap across categories, creating ambiguity in classification. Fuzzy logic offers a partial solution by mapping inputs to outputs using rule-based inference systems [12,13,14], thereby reducing dependence on precise numerical thresholds. Nonetheless, designing effective fuzzy systems still requires substantial expert knowledge, particularly in defining membership functions and crafting appropriate inference rules that accurately reflect the underlying physical phenomena.

Artificial intelligence (AI) algorithms have become increasingly popular in transformer health condition assessment due to their ability to analyze large datasets and uncover complex patterns. These methods can generally be categorized as either interpretable or non-interpretable models [15,16]. Interpretable models, such as logistic regression [17], decision trees [18], and K-nearest neighbors (KNNs) [19], are conceptually straightforward and easier for stakeholders to understand, thereby enhancing their trust and acceptance. However, such models may underperform when applied to complex, high-dimensional data, as they often fail to capture intricate nonlinear relationships. In contrast, non-interpretable models—including support vector machines [20], random forests [21], and deep learning techniques [22]—offer greater predictive power but lack transparency. These models are also more sensitive to noise and data anomalies, which may affect the consistency of their predictions.

Beyond individual methods, hybrid approaches have been proposed to leverage the complementary strengths of different algorithms, aiming to improve both the accuracy and robustness of transformer health condition assessment [23]. For example, Badawi et al. [24] integrated multiple dissolved gas analysis (DGA) techniques using rule-based logic to enhance fault diagnosis performance. However, such rule-based models may fall short when faced with complex nonlinear data. Similarly, Zeinoddini-Meymand, H. et al. utilized a combination of linear regression and nonlinear models, such as ANN and ANFIS, to analyze diverse data patterns for transformer HI evaluation [25], but these combinations sometimes lack the ability to deeply model complex interactions between features. Zhang, H. et al. proposed a combined deep neural network approach, which weights outputs from multiple models based on prediction accuracy to enhance reliability [26]. Although this enhances prediction accuracy, the lack of interpretability in deep learning approaches can impact user trust. Additionally, Abdo, A. et al. developed a hybrid model that integrates machine learning techniques, including the multi-feature clustering method, cluster set, and multi-class support vector machine, with HI calculations and fault mechanism analysis to refine transformer fault classification [27]. Despite its excellence in integration, this method demands high standards in data quality and algorithm tuning due to its complex feature engineering processes. Building on these approaches, the wide and deep predictive modeling framework offers a novel hybrid solution. Initially developed for the recommendation field [28]. This model has been effectively adapted for transformer health condition assessment [29]. The wide component captures feature co-occurrence patterns, while the deep component identifies complex, nonlinear relationships in the data, allowing the model to generalize across new feature combinations. This combined approach enables a balance between interpretability and prediction accuracy.

Based on the above background, this article proposes a novel hybrid approach for transformer health condition classification. The proposed model integrates a wide component using multivariate linear regression (MLR) and a deep component consisting of a deep neural network (DNN), incorporating Markov chain Monte Carlo (MCMC) methods for parameter optimization. The main contributions of this work include the following:

(1)

A wide and deep model is proposed for transformer health condition assessment, employing joint training and unified optimization to enhance the learning capabilities of both components.

(2)

The joint training mechanism, facilitated by MCMC, optimizes the parameters of both the wide and deep components. This integration not only ensures efficient learning of global feature interactions but also enhances complex feature learning capabilities.

(3)

The model offers the following specific advantages:

(a)

The wide component effectively memorizes global interrelationships, while the deep neural network component, optimized through MCMC, exhibits a strong generalization ability, enabling it to recognize intricate health patterns across different transformer conditions.

(b)

The joint training of both components results in a significant improvement in the overall accuracy of transformer thermal aging health assessments, offering a more reliable and robust tool for predictive maintenance and informed operational decision making.

The remainder of the article is organized as follows. Section 2 describes the framework and methodology, including the wide and deep model components. Section 3 presents experimental results and analysis. Section 4 compares the proposed method with other approaches. Finally, Section 5 concludes the article with a summary and suggestions for future research.

2. Framework and Method

The analytical process is structured as follows: Section 2.1 describes the input selection, Section 2.2 introduces the wide and deep framework, Section 2.3 focuses on the wide model component, Section 2.4 details the deep model component, and Section 2.5 explains the integration of the wide and deep components.

2.1. Input Selection

Power transformers comprise multiple components, including the iron core, windings, oil–paper insulation, and auxiliary devices, all of which are susceptible to the aging caused by thermal, electrical, and mechanical stresses. Although dissolved gas analysis (DGA) is a widely used indicator of thermal aging, it can sometimes provide misleading information due to the generation of gases during normal operation. Therefore, to more accurately assess the health of a transformer, it is essential to consider a broader range of parameters, including chemical, electrical, and mechanical factors, in addition to DGA. By integrating these additional health condition parameters with DGA, the overall accuracy of transformer health assessments can be significantly improved.

(1)

Water dynamics:

(a)

Solubility and migration: As temperature increases, the solubility of water in transformer oil rises, disrupting the equilibrium of water distribution between the oil and the paper insulation. Initially, this may lead to a reduction in water content in the paper insulation as moisture migrates into the oil. However, over time, water accumulates in the oil, diminishing its insulating properties and ultimately compromising the overall effectiveness of both the oil and paper insulation.

(b)

Aging acceleration: At lower temperatures, the solubility of water in oil decreases, driving water back into the paper insulation. This accelerates the aging process of the insulation material and may elevate the risk of localized electrical discharges.

(2)

Acidification:

Oxidative acceleration: Elevated temperatures boost oxidative reactions in both oil and paper, leading to the production of acidic compounds. These acids compromise the chemical stability of the oil and degrade insulation performance by corroding metal parts and accelerating paper insulation breakdown.

(3)

Furfural formation:

Operating transformers at elevated temperatures accelerates the aging of paper insulation, which is reflected in increased furfural production. High temperatures promote the decomposition of cellulose in the paper insulation, leading to a rise in furfural levels. This increase serves as an indicator of insulation degradation, signaling a deterioration in the integrity of the insulating material.

(4)

Direct electrical property impacts:

(a)

Dielectric breakdown voltage (DBV): Temperature increase reduces oil viscosity, impacting its insulating properties and lowering DBV. Additionally, elevated temperatures enhance the solubility of water in the oil and accelerate its acidification, both of which contribute to a reduction in the oil’s dielectric strength, thereby increasing the risk of electrical breakdown.

(b)

Dissipation factor (DF): Higher temperatures improve oil’s electrical conductivity and modify polarization processes, elevating the dissipation factor. This signifies more energy loss in alternating electric fields, with elevated temperatures also speeding up chemical reactions that produce polar molecules, further degrading insulation quality.

This detailed analysis demonstrates how temperature directly affects the physical and chemical properties of transformer oil and indirectly influences the water and acidity dynamics within the oil–paper insulation system. These changes significantly impact the system electrical performance. Therefore, effective temperature control, along with regular monitoring of the oil electrical properties, acidity, and water content, is essential for ensuring optimal transformer performance and extending its service life.

In this article, a quantitative assessment based on total dissolved combustible gases (TDCG) and other additional measurements, including oil characterization parameters, such as DBV, DF, furan, water content, and acidity, is presented. The six features considered are listed in

Table 1. Thermal aging health condition assessment label type.

Number	Parameter
1	Water/ppm
2	Acidity/(mgKOH/g)
3	DBV/kV
4	DF/%
5	TDCG/ppm
6	Furan/ppm

.

2.2. Wide and Deep Framework

As illustrated in Figure 1, the model framework utilized in this study combines a Bayesian multivariate linear regression component, termed the wide component, with a deep Bayesian probabilistic neural network component. The wide component employs Bayesian methods to model linear combinations of features, estimating the posterior distributions of parameters to quantify their uncertainties. In contrast, the deep component integrates deep learning with Bayesian inference, using neural network architectures to identify complex patterns in the data and quantify uncertainties in the predictions. This hybrid approach enables a comprehensive analysis of the data and enhances the accuracy of predictive outcomes. The following section will provide a detailed description of these components.

According to Bayes’ theorem, the posterior distribution is proportional to the likelihood function and the prior distribution. Direct computation of the posterior is often challenging; therefore, MCMC methods are used to sample from it. This process is crucial for the accurate estimation of model parameters. It is essential to carefully select the number of iterations and the burn-in period to ensure that the sampling process converges to the appropriate distribution.

2.3. Wide Part

In the wide model part, Bayesian Cauchy MLR can be employed to robustly handle datasets with continuous response variables that may include extreme values or outliers. When we consider categorizing health indices into several ordered conditions, such as very good (VG), good (G), moderate (M), bad (B), and very bad (VB), we can use integers to label these conditions for use in an ordered regression model. Specifically, these categories can be marked with different k values according to their order, as follows:

• k = 1 corresponds to VG.
• k = 2 corresponds to G.
• k = 3 corresponds to M.
• k = 4 corresponds to B.
• k = 5 corresponds to VB.

For a particular categorization level k, the ordered regression model can express the conditional probability of that level as follows [30]:

$$p(y=k|\mu ,\sigma ,\{{\theta }_j\})$$

(1)

where σ is the standard deviation and μ is the model’s linear predictor part, representing the response variable’s mean. {θ_j} is a set of thresholds used to convert continuous probabilities into probabilities for ordered categories. μ is determined by the following linear equation:

$$\mu ={\beta }_0+{{\displaystyle \sum }}_{i=1}^n{\beta }_i{x}_i+\epsilon$$

(2)

where β₀ is the intercept term, the constant component of the linear part of the model. x_i is an independent variable. β_i are the regression coefficients associated with x_i, indicating the average impact of x_i on μ. ε is the error term, representing the portion of the variation in the dependent variable that the model does not explain.

Within the framework of an ordered regression model, selecting the appropriate probability distribution curve and its corresponding thresholds is crucial for quantifying the probabilities of ordinal classification outcomes, which can be chosen based on the actual data’s distribution characteristics. A schematic diagram, as shown in Figure 2, represents the probability of each outcome with vertical bars, where the height of each bar directly corresponds to the probability value. The thresholds determine the position of these bars, and in the figure, they are represented by vertical dashed lines, which divide the continuous probability distribution curve into adjacent intervals corresponding to each ordinal category. The thresholds determine the position of these bars. By calculating the area under the probability distribution curve between two thresholds, we can precisely determine the probability of each ordinal outcome. Unlike traditional approaches that typically adopt the normal distribution [29,30], this study employs a Cauchy–normal distribution. This distribution combines the heavy tails of the Cauchy distribution—enabling robust handling of outliers—with the general properties of the normal distribution, resulting in a more resilient and effective statistical model for ordinal classification tasks.

The expression for the conditional probability in this case is as follows:

$$p(y=k|\mu ,\sigma ,\{{\theta }_j\})=F_{\text{Cauchy}}\left({\displaystyle \frac{{\theta }_k-\mu }{\sigma }}\right)-F_{\text{Cauchy}}\left({\displaystyle \frac{{\theta }_{k-1}-\mu }{\sigma }}\right)$$

(3)

where y represents the health condition of the transformer, while F_Cauchy denotes the cumulative distribution function (CDF) of the Cauchy distribution, defined for any real number k as follows:

$$F_{\text{Cauchy}}(k)={\displaystyle \frac{1}{\pi }}\mathit{arctan}(k)+{\displaystyle \frac{1}{2}}$$

(4)

Applying this definition to the probability calculation yields the following Equation (5):

$$p(y=k|\mu ,\sigma ,\{{\theta }_j\})=\left({\displaystyle \frac{1}{\pi }}\mathit{arctan}\left({\displaystyle \frac{{\theta }_k-\mu }{\sigma }}\right)+{\displaystyle \frac{1}{2}}\right)-\left({\displaystyle \frac{1}{\pi }}\mathit{arctan}\left({\displaystyle \frac{{\theta }_{k-1}-\mu }{\sigma }}\right)+{\displaystyle \frac{1}{2}}\right)$$

(5)

The conditional probability for each specific ordered response category can be calculated in an ordered regression model that utilizes the CDF of the Cauchy–normal distribution.

For the smallest ordered value, y = 1, as follows:

$$p(y=1|\mu ,\sigma ,\{{\theta }_j\})=F_{\text{Cauchy}}\left({\displaystyle \frac{{\theta }_1-\mu }{\sigma }}\right)-F_{\text{Cauchy}}\left(-\infty \right)$$

(6)

Since F_Cauchy (−∞) = 0, it follows that Equation (7) is a follows:

$$p(y=1|\mu ,\sigma ,\{{\theta }_j\})=F_{\text{Cauchy}}\left({\displaystyle \frac{{\theta }_1-\mu }{\sigma }}\right)$$

(7)

For the largest ordered value, y = k, as in the following Equation (8):

$$p(y=5|\mu ,\sigma ,\{{\theta }_j\})=F_{\text{Cauchy}}\left(+\infty \right)-F_{\text{Cauchy}}\left({\displaystyle \frac{{\theta }_{K-1}-\mu }{\sigma }}\right)$$

(8)

Since F_Cauchy (+∞) = 1, it follows that Equation (9) is as follows:

$$p(y=5|\mu ,\sigma ,\{{\theta }_j\})=1-F_{\text{Cauchy}}\left({\displaystyle \frac{{\theta }_{K-1}-\mu }{\sigma }}\right)$$

(9)

To assess the transformer health condition using the Bayesian Cauchy MLR model, the following steps are performed:

(1) Model framework setup: Response variable y from 1 (VG condition) to 5 (VB condition). Predictor variables x_j: water, acidity, DBV, DF, TDCG, and furan.

(2) Constructing the linear component: Construct the linear predictor model using μ = β₀ + β₁·Water + β₂·Acidity + β₃·DBV + β₄·DF + β₅·TDCG + β₆·Furan.

(3) Thresholds, distribution parameters, and prior distribution selection: choose appropriate thresholds {θ_j} to segment different levels of transformer health condition. Assume the metric measure of health condition follows a normal distribution, where predictor variables determine μ, and σ is the standard deviation. Select suitable prior distributions for the regression coefficients β₀, β₁, …, β₆, threshold parameters θ_j, and standard deviation σ. Normal priors could be set for the regression coefficients, ordered normal priors could be set for the thresholds, and a half-Cauchy prior could be set for the standard deviation.

(4) MCMC sampling: Employ MCMC methods to sample from the posterior distribution to estimate model parameters. Set appropriate iterations and burn-in periods to ensure convergence of the sampling.

(5) Posterior analysis: Analyze the posterior distributions of regression coefficients and threshold parameters to understand the impact of each predictor variable on a transformer health condition.

2.4. Deep Part

A deep Bayesian neural network is applied in the deep part. In addition, it incorporates Bayesian inference based on the deep neural network structure. The model utilizes the advantages of DNN in dealing with complex data and employs a Bayesian approach to deal with the uncertainty of the network parameters, providing a more comprehensive prediction.

First, the input layer is the first layer of the deep neural network and is used to receive the raw data x. This layer performs no computation and only transfers the data to the next network layer.

The hidden layers, or pattern layers, are the core of DNN, responsible for processing input data and feature extraction. In these layers, we employ the Leaky ReLU activation function, mathematically expressed as follows:

$$\text{Leaky ReLU}(\mathit{x})=\max (\alpha \mathit{x},\mathit{x})$$

(10)

where α is a small positive constant. x is the input. Compared to traditional ReLU, this activation function provides a non-zero gradient for negative inputs, enhancing network training efficiency and performance. The output of each hidden layer can be represented as follows:

$${\mathit{h}}^{(l)}=\text{Leaky ReLU}({\mathit{W}}^{(l)}{\mathit{h}}^{(l-1)}+{\mathit{b}}^{(l)})$$

(11)

where h^(l) represents the weighted input of the lth layer, and W^(l) and b^(l) are the weight and bias of the layer, respectively.

Finally, the output layer generates the final predictions based on the task, such as classification or regression. The output layer formula in a deep neural network is expressed as follows:

$$y=\text{softmax}({\mathit{W}}^{\mathrm{out}}{\mathit{h}}^{(L)}+{\mathit{b}}^{\mathrm{out}})$$

(12)

where softmax is the activation function, W^out is the weight matrix of the output layer. h^(L) is the output of the penultimate layer in the network. b^out is the bias of the output layer.

In the described model, the Bayesian approach is reflected in how network weights and biases are defined using prior distributions. Each neuron’s weight and bias are not fixed values but are random variables following Gaussian distributions.

To utilize the deep Bayesian neural network regression model for assessing the transformer health condition, the following steps can be followed:

(1) Model framework setup: Response variable y is similar to the Bayesian ordinal regression model described above.

(2) Input layer: Receives the transformer parameters data, water, acidity, DBV, DF, TDCG, and furan.

(3) Hidden layer: The hidden layers are organized into 3 tiers, each containing 20 units. For each neuron in the first hidden layer, the weighted sum is calculated as follows:

$$h_{1,i}=w_{1,i,1}\cdot \text{Water}+w_{1,i,2}\cdot \text{Acidity}+w_{1,i,3}\cdot \text{DBV}+w_{1,i,4}\cdot \mathit{DF}+w_{1,i,5}\cdot \text{TDCG}+w_{1,i,6}\cdot \text{Furan}+b_{1,i}$$

(13)

The activation function is as follows:

$$h_{1,i,\mathit{activated}}=\max (\alpha \cdot h_{1,i},h_{1,i})$$

(14)

Hidden layer 2 is as follows:

$$h_{2,i}={\displaystyle \sum }_{j=1}^{20}{w}_{2,i,j}\cdot h_{2,j,\mathit{activated}}+b_{2,i}$$

(15)

The activation function is as follows:

$$h_{2,i,\mathit{activated}}=\max (\alpha \cdot h_{2,i},h_{2,i})$$

(16)

Hidden layer 3: The weighted sum in the third hidden layer is as follows:

$$h_{3,i}={\displaystyle \sum }_{j=1}^{20}{w}_{3,i,j}\cdot h_{3,j,\mathit{activated}}+b_{3,i}$$

(17)

The activation function is as follows:

$$h_{3,i,\mathit{activated}}=\max (\alpha \cdot h_{3,i},h_{3,i})$$

(18)

(4) Output layer: The output layer generates predictions for the transformer’s health condition based on the output from hidden layer 3, as follows:

$$y_{pred}=\mathit{\text{Softmax}}({\displaystyle \sum }_{i=1}^{20}{w}_{o,i}\cdot h_{3,i,\mathit{activated}}+b_o)$$

(19)

(5) Application of the Bayesian method: Network weights and biases are treated as random variables following Gaussian or other appropriate prior distributions. Specifically, each weight and bias is considered to be drawn from a prior distribution, which can be chosen based on prior knowledge or experience. This enables us to account for the uncertainty of parameters during the training process and update our confidence in the parameters in subsequent inference.

(6) MCMC sampling: Estimating network parameters’ posterior distribution using MCMC methods.

(7) Posterior analysis: Analyzing the posterior distribution to assess the impact of predictor variables on transformer health condition.

From the above description, it can be seen that the hidden layer is focused on processing higher-level abstract features rather than directly handling raw input data. Therefore, variables, such as water, acidity, etc., do not directly appear in the formulas for hidden layer 2. These original variables are processed in the earlier layers of the network (such as the input layer and hidden layer 1), while hidden layer 2 concentrates on extracting deeper-level features from this processed data.

2.5. Wide and Deep Model Uses a Joint Method

The wide and deep model joins the outputs of the two parts to obtain a final condition prediction. This model considers the wide and deep components’ outputs as two independent information streams. To integrate the information from both parts, a weighted fusion strategy is adopted. This strategy is controlled by a fusion weight, α, which is treated as a learnable parameter and estimated during the MCMC joint training process. This allows the model to provide a data-driven determination of the importance of the wide component relative to the deep component in the final prediction. The fused output of the model is defined as follows:

$$P(y|k)=\alpha \cdot P_{\text{wide}}(y|k)+(1-\alpha )\cdot P_{\text{deep}}(y|k)$$

(20)

where P(y|k) represents the probability of predicting class y given input x, while P_wide(y|k) and P_deep(y|k) are the predicted probabilities from the wide and deep components, respectively.

To effectively train this model, a joint loss function was designed to simultaneously optimize the predictive accuracy of both the wide and deep components. This loss function joins the loss from the wide component L_wide and the loss from the deep component L_deep, along with a regularization term for controlling the fusion weights α, thereby preventing an excessive bias towards either component, as follows:

$$L=L_{\text{wide}}(W_{\text{wide}})+L_{\text{deep}}(W_{\text{deep}})+\lambda \cdot R(\alpha )$$

(21)

where L_wide and L_deep represent the losses from the wide and deep components, respectively, R(α) is the regularization term for the fusion weights α, and λ is a hyperparameter that controls the strength of regularization.

Establishing the foundational framework of the wide and deep models is a prerequisite to integrating wide and deep models while employing MCMC techniques for parameter estimation. This approach emphasizes adopting an integrated training strategy to achieve the optimal combination of parameters for both wide and deep models, thereby maximizing the model’s predictive performance. Details on the specific configuration of MCMC parameters will be elaborated in the subsequent sections of the article.

3. Experiment Design and Results

This section presents the experimental results. Section 3.1 describes the data preprocessing process, Section 3.2 outlines the experimental settings, and Section 3.3 summarizes the joint prediction results.

3.1. Data Preprocessing

(1)

Raw electricity consumption data:

This study is conducted on a real dataset of transformer condition measurements provided by a professional asset management and health assessment consultancy company, referred to here as the asset management and health assessment (AMHA) consulting company. AMHA calculated a HI for each transformer belonging to their clients. Specifically, AMHA carried out oil sample collection and testing on 90 oil-immersed transformers. The tests covered 11 categories of data, including water content, acidity, DBV, TDCG, furan content, DF, and total solids, amounting to 990 tests in total. The health condition of a transformer is represented by a continuous value ranging from 0 to 1, where 0 indicates the best health condition, and 1 indicates the worst. The closer this value is to 0, the better the condition of the transformer; conversely, the closer it is to 1, the more deteriorated the transformer’s health. These tests aimed to ensure the provided data’s accuracy and reliability. It is important to note that the collected data has been identified as a benchmark dataset and used to develop and compare various transformer HI analysis models. For more information, please refer to references [31].

To provide a clearer view of the dataset structure and parameters used in the HI calculation,

Table 2. Diagnostic test results.

No.	Water	Acidity	TDCG	Furan	DBV	DF	HI	Label
1	21.7	0.024	483	0.86	32.5	0.075	0.377	G
2	26.9	0.098	254	0.65	40.5	0.894	0.334	G
3	14.5	0.033	78	0.26	58	0.14	0.29	G
4	21.2	0.226	215	5.53	48.7	0.424	0.7	B
5	10	0.01	126	0.06	75	0.111	0.102	VG
6	15.5	0.075	38	0.53	71	0.143	0.274	G

presents sample data from five representative oil-immersed transformers. These anonymized records include key condition indicators used in this study.

Although the transformers were installed some time ago, the underlying aging mechanisms—such as insulation degradation, moisture ingress, and oil oxidation—remain relevant for modern units. Moreover, our data-driven model is generalizable and can be applied to newer datasets with similar condition indicators, making the dataset still useful for current power system applications.

(2)

Data augmentation:

The augmented dataset utilized in this study was derived from the source described in [31], and the corresponding labels were assigned according to the approach outlined in [32]. An expansion of the dataset is implemented to ensure the accuracy of the analyses. The dataset is generated from the original dataset using the data augmentation method, which assumes that the original parameter values are modified by randomly adding or subtracting a certain percentage of standard deviation. The standard deviation for the random perturbations was set to 5% of the standard deviation of each corresponding feature in the original dataset. This value was chosen to ensure that augmented data points remain physically plausible while providing sufficient diversity to enhance model training and generalization. The original dataset is assumed to consist of eigenvectors x = (x₁, x₂, x₃, …, x_n) and a target value y, and the eigenvalues in the augmented data are guaranteed to remain non-negative. The data enhancement generates new samples x′ and y′, where for each feature x_i, the expression for generating a new feature $x_i^{\prime }$ is as follows:

$$x_i^{\prime }=\max (x_i+ϵ,0)$$

(22)

where ϵ∼N(0, σ²) is a random perturbation taken from a normal distribution with a mean of 0 and a variance of σ².

It should be noted that while this process does not perfectly balance the classes, the use of a Bayesian framework for modeling provides inherent robustness to class imbalance by quantifying uncertainty in the parameter estimates. A total of 200 samples are generated and shuffled with the original dataset to eliminate any potential order bias. Figure 3 illustrates the distribution of the data. The original dataset comprised 30 samples, which were derived from condition records of 90 power transformers. These 30 real samples were reserved exclusively as a fixed hold-out test set, ensuring that final model evaluation was conducted on completely unseen, non-augmented data.

After the sample data were collected, we applied a wide and deep model to assess the health condition of transformers. Considering the algorithm’s sensitivity to the diversity of data, the MAX-MIN scaling method was selected for data normalization. This method was implemented in the following manner:

$$f(x_i)={\displaystyle \frac{x_i-\min (\mathit{x})}{\max (\mathit{x})-\min (\mathit{x})}}$$

(23)

where x_i represents the original data point, min(x) represents the minimum value of that indicator in the dataset, and max(x) represents the maximum value of that indicator in the dataset.

3.2. Experimental Settings

In the presented research setup, we employ an MCMC sampling approach using the Metropolis algorithm within a probabilistic model. The following key aspects characterize this approach:

(1) Metropolis sampling: The Metropolis sampler is chosen due to its effectiveness in scenarios where gradient-based samplers are not applicable. This makes it suitable for complex distributions and models with non-differentiable components.

(2) Sampling configuration: The sampling process is configured to include 30,000 draws and an additional 4000 tuning steps. This tuning phase helps achieve a stable condition before the actual sampling begins. While using a single chain, the setup facilitates parallelization to enhance computational efficiency.

(3) Burn-in and thinning: A burn-in period of 3000 is set to discard initial samples that may not represent the stationary distribution. Thinning reduces autocorrelation within the samples, thus enhancing sample independence.

(4) Effective sample extraction: Following burn-in and thinning, effective samples are extracted for subsequent analysis.

(5) Prediction on test data: The setup is prepared for prediction on test data, aligning the model for assessment against unknown data.

(6) Posterior predictive checks: We conduct posterior predictive checks by generating 1000 samples from the posterior predictive distribution using the model and the extracted traces. This essential step serves to validate the predictive accuracy of the model.

The advantages of this setup include the ability to handle complex and non-differentiable models, thorough exploration of the posterior distribution through the Metropolis sampler, and enhanced sample independence through burn-in and thinning. Additionally, posterior predictive checks allow for a comprehensive assessment of the model’s performance on unseen data, ensuring the robustness and reliability of the model’s predictions.

The experiments were conducted on a workstation equipped with an Intel Core i9-10850K CPU (10 cores, 20 threads) and 64 GB of RAM. All computations were performed on the CPU, and no GPU acceleration was used.

3.3. Joint Prediction Results

(1)

Joint weight determinations:

As shown in Figure 4, the joint training process assigns a weight of 0.8 to the wide model, indicating its dominant role in the final prediction. This suggests that the wide model is particularly effective in capturing linear feature relationships, memorizing interactions, and extracting rule-based patterns.

Despite its lower weight, the deep model remains essential for identifying complex nonlinear dependencies and high-level interactions that the wide model may overlook. Its contribution, though smaller, enhances the model’s overall predictive capability by capturing nuanced patterns in the data.

(2)

Case analysis and prediction accuracy:

First, we visualized the probability distribution of each health condition category for the transformer using the box plots in Figure 5a. The central line in these plots shows the median for each category. At the same time, the edges of the box mark the quartiles, briefly revealing the bulk of the data distribution. Scatter plots complement this by displaying the exact probability values for each data point, helping us to closely observe the probabilities’ specific distribution.

Regarding the distribution and probability levels across categories, VG has a median close to 1.0, indicating that most individuals are in excellent health. The G category displays more dispersed data points with a slightly lower median, suggesting generally good but variable health conditions. The M category has fewer points, with a median at a moderate level. Both the B and VB categories show extremely low medians, especially VB, where nearly all data points cluster at very low probability levels, indicating poor health conditions. Ultimately, the prediction of the thermal aging health condition for the transformer suggests that it is in VG condition.

The confusion matrix provides insights into the model’s classification performance across the five predefined health condition categories. As shown in Figure 5b, the diagonal elements indicate correctly classified instances, with the model demonstrating strong performance for extreme categories, such as VG and VB. However, misclassifications are observed, particularly between adjacent categories like M and B, as evidenced by the presence of non-zero values in the off-diagonal cells.

4. Comparative Analysis

In this section, a comprehensive comparative analysis is presented. The performance of the proposed joint wide and deep model is evaluated against its individual components, which represent standalone traditional linear and deep learning methods. First, the performance is compared with existing methods in Section 4.1, followed by an evaluation of the proposed wide and deep model in Section 4.2. In Section 4.3 and Section 4.4, the performance metrics for transformer health classification are discussed, and in Section 4.5, the evaluation using ROC curve analysis is presented.

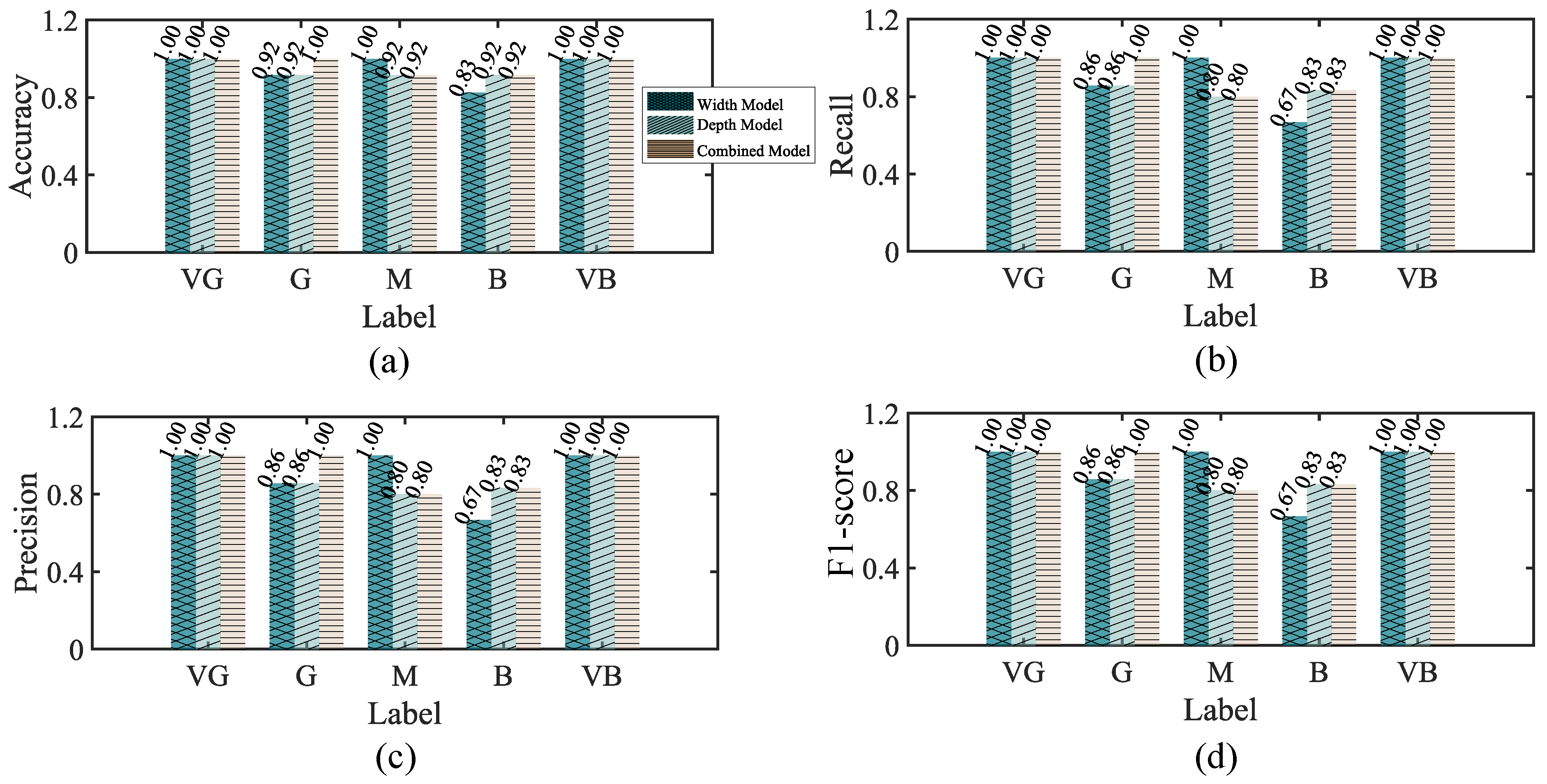
4.1. Performance Comparison of Independent Wide and Deep Models

In the performance analysis of the wide model, as shown in Figure 6a, the wide model incorrectly classifies one transformer in the G condition as M. This misclassification indicates that the wide model is not sufficiently accurate in distinguishing categories with similar features. Also, confusion between the B and M conditions, where two B conditions are misclassified as M, suggests that the model underperforms when dealing with more complex or similarly featured categories. Therefore, despite the wide model performing well in some categories, there is significant room for improvement in enhancing its precision in classifying similar conditions.

The confusion matrix for the deep model, as depicted in Figure 6b, demonstrates the model’s superiority in distinguishing complex feature categories. However, it also shows some misclassification between the G and M categories, such as misclassifying the G condition as M and the M condition as B. These misclassifications might be due to the deep model’s excessive sensitivity in extracting nuanced features. Compared to the wide model, the deep model performs slightly better in distinguishing the G and M categories with similar features, but there are still misclassifications. Both models distinguish extreme categories, such as VG and VB.

4.2. Advantages of the Joint Wide and Deep Model

Compared to its individual components, the joint wide and deep model demonstrates several notable improvements, including the following:

Improved classification accuracy: The joint model significantly reduces misclassification rates, particularly in intermediate categories, such as G and M.

Greater stability: It achieves perfect classification for extreme categories VG, G, and VB and outperforms standalone models in handling borderline cases.

Overall enhanced performance: By combining the memorization strength of the wide model and the generalization capability of the deep model, the joint approach delivers more comprehensive and reliable classification results.

4.3. Detailed Confusion Matrix Analysis

To further support the classification performance of the proposed model, we conducted a comparative analysis of the confusion matrices for the wide model, deep model, and the joint wide and deep model. As shown in the respective confusion matrices, all three models correctly identified most samples in the extreme categories, such as VG and VB, reflecting their effectiveness in handling clearly distinguishable cases.

However, the wide model exhibited notable misclassifications between neighboring categories, especially between G and moderate M, as well as between M and B, indicating limitations in capturing complex feature interactions. The deep model improved slightly in these areas but still showed some confusion in the middle categories due to potential overfitting to subtle variations.

In contrast, the joint wide and deep model significantly reduced misclassification rates across all categories, particularly in the intermediate ones. It achieved higher accuracy and stability by effectively combining the memorization capability of the wide model with the generalization power of the deep model. The diagonal dominance in its confusion matrix demonstrates its superior ability to distinguish between all five health condition classes more reliably than the individual models.

These results confirm the advantage of joint training in leveraging both linear and nonlinear patterns, leading to more accurate and robust transformer health assessments.

4.4. Performance Metrics

The performance assessment of transformer health condition classification models focuses on accurately categorizing each instance into these specific categories. The variables within the standard performance metrics formulas are defined as follows:

True positives (TPs): The number of transformers that are correctly identified as having a specific health condition.

True negatives (TNs): The number of transformers that are correctly identified as not having a specific health condition.

False positives (FPs): The number of transformers that are incorrectly classified as having a specific health condition.

False negatives (FNs): The number of transformers with a specific health condition that has not been identified as such.

Key metrics include the following:

(1) Model accuracy: This measures the model’s overall performance across all categories, calculated as the ratio of correctly predicted observations to total observations. It is calculated using the following formula:

$$\text{Accuracy}={\displaystyle \frac{\mathit{TP}+\mathit{TN}}{\mathit{TP}+\mathit{TN}+\mathit{FP}+\mathit{FN}}}$$

(24)

(2) Recall (sensitivity): This evaluates the proportion of actual positive cases (e.g., transformers with anomalies) that are correctly identified, which is crucial for preventing equipment failure due to missed anomalies, and is calculated as follows:

$$\text{Recall}={\displaystyle \frac{\mathit{TP}}{\mathit{TP}+\mathit{FN}}}$$

(25)

(3) Precision (positive predictive value): This assesses the percentage of correctly identified positive cases using the following formula:

$$\text{Precision}={\displaystyle \frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}}$$

(26)

(4) F1-Score: The harmonic mean of precision and recall, it balances these two metrics and is useful for comparing multiple models; it is given by the following formula:

$$\text{F1-score}={\displaystyle \frac{2\times \text{Precision}\times \text{Recall}}{\text{Precision}+\text{Recall}}}$$

(27)

The charts in Figure 7 compare the performance of the wide, deep, and joint models across different health condition categories. The specific numerical comparison results are shown in the bar charts. As observed from the bar charts, the joint model outperforms or at least equals the individual wide and deep models across all assessment metrics. Particularly in the G and B health condition categories, the joint model significantly surpasses the other two, demonstrating its advantage in handling complex data distributions.

4.5. Performance Evaluation Using ROC Curve Analysis

The receiver ROC curve illustrates the diagnostic ability at various thresholds, with a higher area under the curve (AUC) indicating better differentiation between healthy and abnormal conditions. These metrics provide a comprehensive framework for assessing the model’s performance in differentiating transformers’ various health conditions.

As shown in Figure 8, the ROC curves of the joint model indicate strong discriminative performance. The AUC values for VG, G, B, and VB are close to the ideal score of 1.00, reflecting excellent sensitivity and specificity in classification. The AUC for the M category is slightly lower at 0.98, suggesting slightly reduced separability in this intermediate class. Overall, the model shows robust classification capabilities, particularly for clearly distinguishable health categories.

The overlap in classification for the middle categories, particularly the slightly lower AUC of 0.98 for Class M, suggests a need for a more nuanced examination of the feature space and potential adjustment of decision thresholds to refine the model’s accuracy. This reduced performance likely stems from two factors—the inherent ambiguity and feature overlap between adjacent health states G, M, and B, and the smaller number of training samples for this intermediate category. The results demonstrate high predictive accuracy overall, though there is room for improvement in classifying these borderline cases. Future work could aim to collect more data for these intermediate conditions or explore advanced feature engineering techniques to create more separable class boundaries.

Figure 9 illustrates the ROC curves for individual models. The wide model performs well, particularly in the VG, G, B, and VB categories, with AUC values 1.00. It is only slightly weaker in the M category, with an AUC of 0.97. While performing well in the VG, B, and VB categories with AUC values of 1.00, the deep model is weaker in the G and M categories, with AUC values of 0.88 and 0.86, respectively.

Overall, the joint model has AUC values that are higher than or equal to those of the joint models across all categories, demonstrating more robust classification capability and stability. In particular, the joint model shows higher accuracy in the G and M categories, highlighting its advantage in handling complex data distributions. This improvement in predictive performance underscores its superior ability to handle imbalanced samples while also reflecting the advantages of joint training.

5. Conclusions

This article proposed a novel wide and deep joint model for assessing the thermal aging health condition of oil-immersed power transformers, contributing to more sustainable power system operations. The main contributions are as follows:

Model architecture: We developed a hybrid model that combines a Bayesian linear “wide” component for interpretability with a “deep” neural network for capturing complex patterns. The integration of MCMC-based joint training enables both accurate predictions and uncertainty quantification.

Performance improvement: Experimental results on 30 real-world transformers showed that the joint model achieved a 6.6% improvement in classification accuracy compared to traditional methods, with particularly strong performance for ambiguous intermediate health conditions.

Key advantages: The model provides robust and reliable assessments with quantified uncertainty, enabling risk-aware decision making in transformer asset management. The joint training approach effectively leverages the complementary strengths of both components.

The proposed method offers a practical solution for transformer health monitoring, contributing to improved maintenance planning and reduced unexpected failures in power systems. Future work will focus on expanding the dataset, incorporating temporal dynamics, and extending the framework to other power system assets.