Temporal and Spatial Evolution of Grey Water Footprint in the Huai River Basin and Its Influencing Factors
Abstract
1. Introduction
2. Overview of the Study Area
3. Research Methodology and Data Sources
3.1. Agricultural Grey Water Footprint
3.1.1. Grey Water Footprint of Planting Industry
3.1.2. Grey Water Footprint of Livestock and Poultry Farming
3.2. Industrial Grey Water Footprint
3.3. Domestic Grey Water Footprint
3.4. Regional Grey Water Footprint and Footprint Intensity
3.5. Spatial Autocorrelation Analysis
3.6. Construction of Grey Water Footprint Decoupling Model
3.7. Geographic Detector
3.8. STIRPAT Model
3.9. Data Sources
4. Results
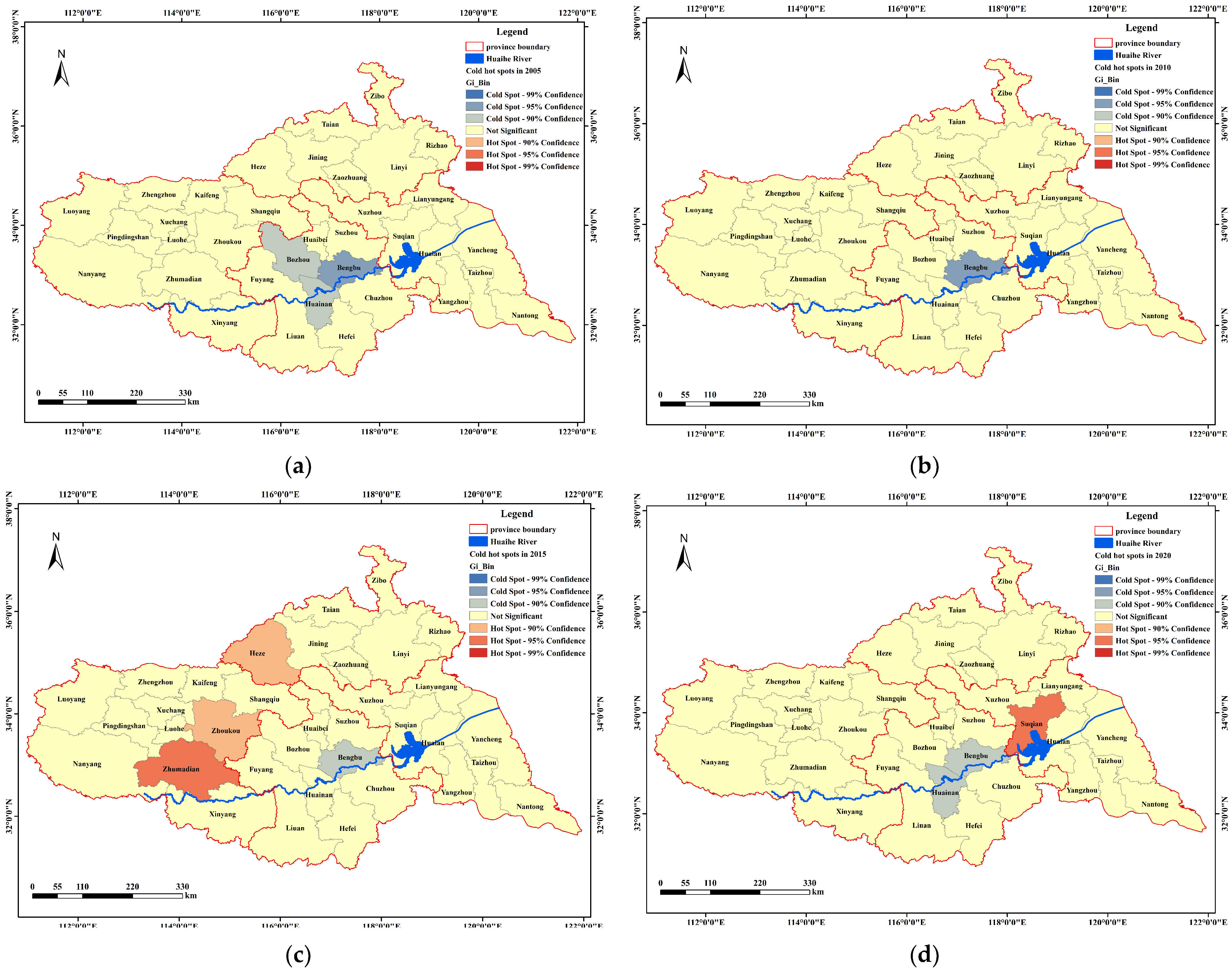
4.1. Spatial Autocorrelation Analysis of Grey Water Footprint
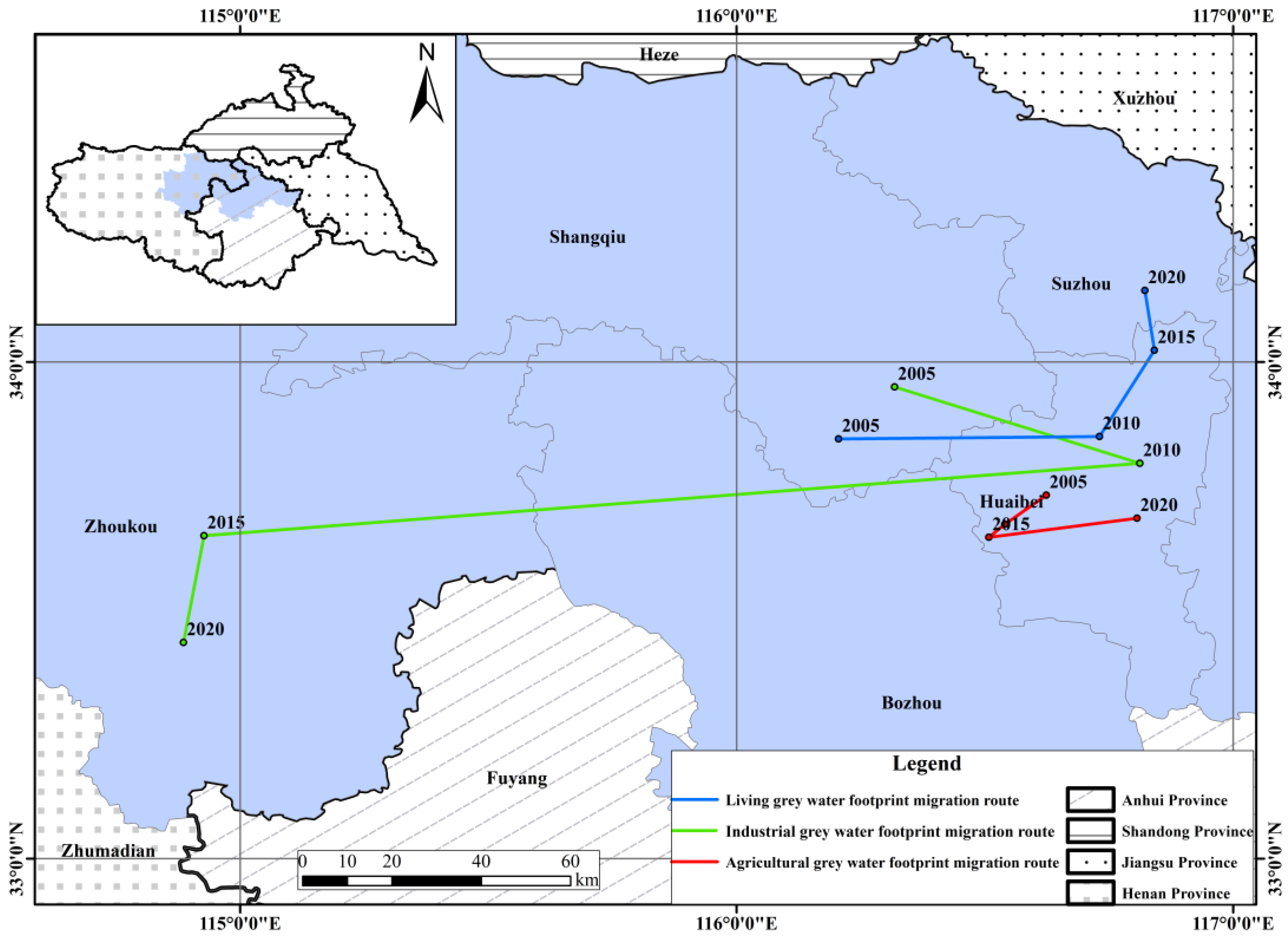
4.2. Spatial Differences of Grey Water Footprint
4.3. Grey Water Footprint Decoupling Analysis
4.4. Spatial Geographic Detection of Influencing Factors of Grey Water Footprint
4.4.1. Factor Detector
4.4.2. Factor Interactive Detection
4.5. Influencing Factors of Grey Water Footprint
4.5.1. Multiple Regression Analysis
4.5.2. Ridge Regression Analysis
5. Discussion
6. Conclusions
- (1)
- The GWF in the Huai River Basin shows no significant global spatial agglomeration yet presents a distinct pattern of “higher in the east and west, lower in the north and south”. High-value areas are stably distributed in southern Henan, including Nanyang, Xinyang, and Zhoukou, and northern Jiangsu, including Xuzhou and Yancheng, whereas most cities in Anhui Province remain at low GWF levels. This spatial pattern necessitates regionally differentiated governance strategies. For high-value areas in Henan and Jiangsu, stricter measures for agricultural non-point source pollution control are required, such as reducing chemical fertilizer and pesticide application and promoting ecological farming. For low-value areas in Anhui and Shandong, cross-regional ecological compensation mechanisms should be explored to encourage upstream water source protection.
- (2)
- The Huai River Basin achieved a critical transition from “weak decoupling” to “strong decoupling” around 2015. The proportion of cities in strong decoupling increased from 31.4% in 2005–2010 to 85.7% in 2015–2020. Huaibei City exhibited an extremely low decoupling elasticity of −0.99, verifying the effectiveness of its circular economy model. However, five cities failed to achieve strong decoupling. Continuous monitoring and early warning systems are essential for cities at risk of recessive or weak negative decoupling, such as Tai’an and Zaozhuang, to promote cleaner industrial transformation.
- (3)
- Geographical detector analysis demonstrates that the interaction between economic factors, A1 and A2, and technological factors, namely T, serves as the dominant driver of grey water footprint variations in the Huai River Basin. Their interaction q-values range from 0.84 to 0.93, significantly exceeding the explanatory power of single factors. The STIRPAT model further quantifies seven significant influencing factors, ranked by importance as T, G, U, P, A2, A1, and W. These factors collectively explain 90.2% of GWF variations in the basin. These results imply that mitigating grey water footprint in the Huai River Basin requires synergistic regulation of economic structure and technological progress, with priority given to factors ranked by importance, such as reducing T and optimizing G, to achieve targeted control.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GWF | Grey water footprint |
| A1 | Primary industry production value |
| A2 | Secondary sector production value |
| A3 | Tertiary sector production value |
| P | Population |
| U | Urbanization rate |
| G | The total sown area of crops |
| W | Discharge volume of industrial wastewater |
| T | Intensity of grey water footprint |
References
- Li, H.; Zheng, W.; Liu, G. Critical Review and Methodological Improvements of Grey Water Footprint. Chin. J. Environ. Manag. 2024, 16, 127–135. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, G.; Wang, L. Spatial-temporal distribution and driving models of agricultural grey water footprint efficiency in the Huai River Basin. Water Resour. Prot. 2020, 36, 60–66+85. [Google Scholar] [CrossRef]
- Gan, R.; Li, Y.; Guo, L.; Tang, H. Comprehensive Evaluation of Sustainable Water Resources Utilization in Nine Provinces of the Yellow River Basin Based on Water Footprint. Yellow River 2024, 46, 93–99+106. [Google Scholar] [CrossRef]
- Perry, C. Water footprints: Path to enlightenment, or false trail? Agric. Water Manag. 2014, 134, 119–125. [Google Scholar] [CrossRef]
- Hoekstra, A.; Hung, P. Virtual Water Trade: A Quantification of Virtual Water Flows Between Nations in Relation to International Crop Trade; Value of Water Research Report Series No. 11; UNESCO-IHE Institute for Water Education: Delft, The Netherlands, 2002; Available online: http://www.waterfootprint.org/Reports/Report11.pdf (accessed on 29 May 2025).
- Sun, S.; Xu, L.; Chen, J. A Study on the Decoupling Relationship Between Agricultural Grey Water Footprint and Agricultural Economic Growth: Based on the Empirical Analysis of 11 Provinces and Cities in the Yangtze River Economic Belt. Water Sav. Irrig. 2022, 48, 17–23. [Google Scholar]
- Ma, X.; Yang, D.; Shen, X.; Zhai, Y.; Zhang, R.; Hong, J. How much water is required for coal power generation: An analysis of gray and blue water footprints. Sci. Total Environ. 2018, 636, 547–557. [Google Scholar] [CrossRef]
- Zhan, X.; Lu, J.; Xue, Y. Ecological efficiency study of different rice planting patterns—Based on gray water footprint model and SBM-Undesirable model. Agric. Econ. 2023, 43, 29–31. [Google Scholar]
- Wang, D.; Li, J.; Ye, Y.; Tan, F. An Improved Calculation Method of Grey Water Footprint. J. Nat. Resour. 2015, 30, 2120–2130. [Google Scholar] [CrossRef]
- Li, W.; Li, B.; Ma, W. Prediction of agricultural grey water footprint in Henan Province based on GM(1,N)-BP neural network. Environ. Ecol. Stat. 2023, 30, 335–354. [Google Scholar] [CrossRef]
- Meng, X.; Lu, J.; Wu, J.; Zhang, Z.; Chen, L. Quantification and Evaluation of Grey Water Footprint in Yantai. Water 2022, 14, 1893. [Google Scholar] [CrossRef]
- Du, H.; Wang, G.; Ran, G.; Lyu, M. Agricultural gray water footprint in the Tarim River Basin using SDGs analysise. Arid Zone Res. 2023, 40, 1184–1193. [Google Scholar] [CrossRef]
- Yapicioğlu, P.; Yeşilnacar, M. Grey water footprint assessment of geothermal water resources in the southeastern Anatolia region. Turk. J. Earth Sci. 2021, 30, 1200–1207. [Google Scholar] [CrossRef]
- Yin, M.; Zhu, H.; Hu, Y.; Li, Z.; Zhang, J. Analysis of various characteristics and driving factors of gray water footprint in Gansu Province. Arid Zone Res. 2022, 39, 1810–1818. [Google Scholar] [CrossRef]
- Cheng, P.; Sun, D.; Song, X. Study on the Spatial and Temporal Dynamic Evolution and Driving Factors of Grey Water Footprint in China. Ecol. Environ. Sci. 2024, 33, 745–756. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, R.; Wang, Z.; Yang, F. Spatial Heterogeneity of the Impact Factors on Gray Water Footprint Intensity in China. Sustainability 2020, 12, 865. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Y. Trends and Consumption Structures of China’s Blue and Grey Water Footprint. Water 2018, 10, 494. [Google Scholar] [CrossRef]
- Liu, P.; Yi, X.; Feng, Y.; Shang, M.; Bao, Z. Water Environment Carrying Capacity Assessment of Yangtze River Economic Belt Using Grey Water Footprint Model. Water Supply 2021, 21, 4003–4014. [Google Scholar] [CrossRef]
- Xu, Z.; Hu, D.; Shu, T.; Peng, F.; Yan, F. Research on the Evaluation Model of Nitrogen and Phosphorus Atmospheric Deposition Pollution Based on Grey Water Footprint. Mod. Bus. Trade Ind. 2025, 12, 247–249. [Google Scholar] [CrossRef]
- Shu, T.; Xiao, S.; Peng, F.; Yan, F. Research on an Improved Copper Slag Water Footprint Evaluation Model Based on Bioamplification Effects. Mod. Bus. Trade Ind. 2025, 12, 250–252. [Google Scholar] [CrossRef]
- Yan, F.; Li, N.; Wu, R. Grey water footprint model of heavy metal based on the hazard quotient. Ecol. Indic. 2024, 162, 112052. [Google Scholar] [CrossRef]
- Liu, H.; Liu, X.; Zhang, T.; Du, X.; Zhao, Y.; Luo, J.; Qiu, W.; Wu, S.; Liu, H. Nitrogen and Gray Water Footprints of Various Cropping Systems in Irrigation Districts: A Case from Ningxia, China. Water 2025, 17, 717. [Google Scholar] [CrossRef]
- Aldaya, M.; Chapagain, A.; Hoekstra, A.; Mekonnen, M. The Water Footprint Assessment Manual: Setting the Global Standard, 1st ed.; Routledge: London, UK, 2011; pp. 1–192. [Google Scholar]
- He, Z.; Xiang, P. An Analysis of the Variations and Driving Factors of Grey Water Footprint in Hunan Province. China Rural Water Hydropower 2018, 10, 19–26. [Google Scholar]
- Bao, X.; Zhu, X. Countermeasures on water environment governance in Huai River Basin. J. Econ. Water Resour. 2021, 39, 35–40+78–79. [Google Scholar] [CrossRef]
- Feng, Q.; Bi, Z.; Liu, J. Spatial and temporal evolution of water footprints of main crops in Huai River Basin and analysis of influencing factors. J. Water Resour. Water Eng. 2022, 33, 213–219. [Google Scholar] [CrossRef]
- Liu, Q. Distribution and Environmental Risk Assessment of Fertilizer Application on Farmland in Huai River Basin. Ecol. Environ. Sci. 2015, 24, 1512–1518. [Google Scholar] [CrossRef]
- Chen, B.; Ren, Z. A Spatio-temporal Study on the Economic Growth, FDI and the Industrial Pollution Emission in Huai River Basin. J. Jiaxing Univ. 2017, 29, 119–127. [Google Scholar] [CrossRef]
- Huang, W.; Yan, B.; Ji, J. A Review of researches on the gray water footprint. Environ. Eng. 2017, 35, 149–153. [Google Scholar] [CrossRef]
- Wang, S.; Lin, Y. Spatial Evolution and its Drivers of Regional Agro-ecological Efficiency in China’s from the Perspective of Water Footprint and Gray Water Footprint. Geogr. Sci. 2021, 41, 290–301. [Google Scholar] [CrossRef]
- Gai, L.; Xie, G.; Li, S.; Zhang, C.; Chen, L. A Study on Production Water Footprint of Winter-Wheat and Maize in the North China Plain. Resour. Sci. 2010, 32, 2066–2071. [Google Scholar]
- Liu, C. Evaluation on Utilization of Water Resources of Food Production in China. J. Huazhong Agric. Univ. Soc. Sci. Ed. 2017, 16, 22–29+146. [Google Scholar] [CrossRef]
- Han, Q.; Sun, C.; Zou, W. Grey water footprint efficiency measure and its driving pattern analysis on provincial scale in China from 1998 to 2012. Resour. Sci. 2016, 38, 1179–1191. [Google Scholar] [CrossRef]
- GB 3838-2002; Environmental Quality Standards for Surface Water. State Environmental Protection Administration (SEPA): Beijing, China, 2002.
- Han, Y.; Jia, D.; Huang, H.; Wang, C.; Qu, C. Water footprint of winter wheat and its influencing factors in Haihe River Basin based on path analysis. Water Resour. Prot. 2019, 35, 8. [Google Scholar] [CrossRef]
- Han, Q. The Research of Grey Water Footprint in China. Master’s Thesis, Liaoning Normal University, Dalian, China, 2016. [Google Scholar]
- Wang, C.; Yin, S.; Yu, S.; Wei, J.; Gu, X.; Gong, M.; Zhang, R. A 2013-based Atmospheric Ammonia Emission Inventory and Its Characteristic of Spatial Distribution in Henan Province. Chin. J. Environ. Sci. 2018, 39, 1023–1030. [Google Scholar] [CrossRef]
- Sun, Y. Research on the Spatial and Temporal Pattern Evolution and Driving Factors of Gray Water Footprint in Yangtze River Economic Belt. J. Lanzhou Univ. Financ. Econ. 2022, 38, 1–15. [Google Scholar]
- Wang, X.; Huang, K.; Yang, S.; Wang, Z.; Hu, T. Temporal Variability and Influencing Factors of Sectoral Water Footprint in China. J. Nat. Resour. 2014, 29, 2114–2126. [Google Scholar] [CrossRef]
- Liu, H.; Chen, M.; Tang, Z. Study on Ecological Compensation Standards of Water Resources Based on Grey Water Footprint: A Case of the Yangtze River Economic Belt. Resour. Environ. Yangtze Val. 2019, 28, 2553–2563. [Google Scholar] [CrossRef]
- Ding, Q.; Liu, G.; Fu, H. Research on the integrated spatial connection of ports in the Yangtze River delta based on Gravity models and spatial autocorrelation. J. Ningbo Univ. Nat. Sci. Eng. Ed. 2024, 37, 1–8. [Google Scholar] [CrossRef]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Fu, K.; Yin, W.; Song, Y.; Du, Y.; Qi, F.; Yang, C.; Li, Q.; Huang, D. Resource allocation efficiency and spatial autocorrelation analysis of China’s elderly care institutions in 2021. Mod. Prev. Med. 2024, 51, 1249–1254. [Google Scholar] [CrossRef]
- Tapio, P. Towards a theory of decoupling: Degrees of decoupling in the EU and case of road traffic in Finland between 1970 and 2001. Transp. Policy 2005, 12, 137–151. [Google Scholar] [CrossRef]
- OECD. Modeling the Impact of Agricultural Policies on Farm Investments Under Uncertainty: The Case of the Cap Arable Crop Regime; OECD Publishing: Paris, France, 2006; Volume 5, pp. 1–35. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Christakos, G.; Liao, Y.; Gu, X.; Zheng, X. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Fu, B. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Niu, L.; Zhang, L.; Xi, F.; Wang, J. Influencing factors and scenario forecasting of carbon emissions in Liaoning Province, China. Chin. J. Appl. Ecol. 2023, 34, 499–509. [Google Scholar] [CrossRef]
- Dietz, T.; Rosa, E. Rethinking the environmental impacts of population affluence and technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar]
- Tai’an Ecology and Environment Bureau. Available online: https://sthjj.taian.gov.cn/ (accessed on 30 April 2024).
- Dong, J.; Liu, X.; Li, Z. Assessment of sustainability of water resource utilization on the northern slope of Tianshan Mountains based on grey water footprint. South-North Water Transf. Water Sci. Technol. 2025, 23, 69–78. [Google Scholar] [CrossRef]
- Du, Q.; Sun, X.; Tang, L. Analysis of the Changes in Greywater Footprint and Its Driving Factors in Yinchuan City. Water Resour. Dev. Manag. 2024, 44, 61–68+73. [Google Scholar] [CrossRef]
- Han, X. Analysis of The Spatial Association Network Structure of Water-Intensive Utilization Efficiency and Its Driving Factors in the Yellow River Basin. Master’s Thesis, Northwest A&F University, Yangling, China, 2024. [Google Scholar]
- Xu, R.; Shi, J.; Hao, D.; Ding, Y.; Gao, J. Research on Temporal and Spatial Differentiation and Impact Paths of Agricultural Grey Water Footprints in the Yellow River Basin. Water 2022, 14, 2759. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, J.; Zhang, S. Study on water footprint and water efficiency of cereal production in the Huai River basin. J. Agric. Resour. Environ. 2024, 41, 371–382. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, J.; Liang, T.; Shao, Q. Impact of water projects on River Flood Regime and Water Quality in Huai River Basin. Water Resour. Manag. 2010, 24, 889–908. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, K. Index system of water system connectivity and its application. Shuili Xuebao 2020, 51, 1080–1088+1100. [Google Scholar] [CrossRef]
- Zuo, Q.; Cui, G. Quantitative evaluation of human activities affecting an interconnected river system network. ACTA Geogr. Sin. 2020, 75, 1483–1493. [Google Scholar] [CrossRef]
- Zhang, L.; Che, L.; Wang, Z.; Hao, L. Study on evolution and driving factors of relationship between water pollution and economic decoupling in Yangtze River Economic Zone. Water Resour. Hydropower Eng. 2021, 52, 47–59. [Google Scholar] [CrossRef]
- Yue, L.; Song, Y.; Jiang, L. National energy efficiency of countries in the “Belt and Road” region and its decoupling from economic growth. Resour. Sci. 2019, 41, 834–846. [Google Scholar] [CrossRef]
- Tian, C.; Li, P.; Shao, H.; Li, M.; Zheng, Y. Analysis of Driving Forces of Energy Consumptionin Rural Areas of China’s Henan Province Based on the STIRPAT Model and Ridge Regression. Pol. J. Environ. Stud. 2020, 29, 1391–1398. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Zhang, L.; Wang, Z.; Ji, S. Research on Determining the Critical Influencing Factors of Carbon Emission Integrating GRA with an Improved STIRPAT Model: Taking the Yangtze River Delta as an Example. Int. J. Environ. Res. Public Health 2022, 19, 8791. [Google Scholar] [CrossRef]
- Dai, H.; Sun, T.; Zhang, K.; Guo, W. Research on Rural Nonpoint Source Pollution in the Process of Urban-Rural Integration in the Economically-Developed Area in China Based on the Improved STIRPAT Model. Sustainability 2015, 7, 782–793. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. ACTA Geogr. Sin. 2017, 72, 19. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, Y. Government institutional trust and sustainable environment: Evidence from BRICS economies. Econ. Res.-Ekon. Istraživanja 2023, 36, 1–20. [Google Scholar] [CrossRef]
- Wang, S.; Xu, H.; Gao, C.; Xu, M. Water Balance Response of the Climatic Change Based on SWAT Model in the Upper-Middle Reach of Huaihe River Basin. Progress. Inquisitiones Mutat. Clim. 2015, 11, 402–411. [Google Scholar] [CrossRef]
- Ahmad, K.; Iqbal, M.; Tariq, M.; Khan, A.; Nadeem, A.; Chen, J.; Usanova, K.; Almujibah, H.; Alyami, H.; Abid, M. Exploring alternate coupling inputs of a data-driven model for optimum daily streamflow prediction in calibrated SWAT-BiLSTM rainfall-runoff modeling. Front. Water 2025, 7, 1558218. [Google Scholar] [CrossRef]






| Livestock and Poultry Category | Feces/(kg/d) | Urine (kg/d) | Raising Cycle/d | Excrement Recovery Rate |
|---|---|---|---|---|
| hog | 2 | 3.3 | 199 | 0.3 |
| cattle | 20 | 10 | 365 | 0.2 |
| sheep | 2.6 | - | 365 | 0.2 |
| fowl | 0.125 | - | 210 | 0.5 |
| Livestock and Poultry Category | Fecaluria | Contaminant Content (kg/t) | Pollution Flow Loss Coefficient | ||||
|---|---|---|---|---|---|---|---|
| COD | Ammonia Nitrogen | Total Nitrogen | COD | Ammonia Nitrogen | Total Nitrogen | ||
| hog | feces | 52.00 | 3.08 | 5.88 | 0.0558 | 0.0304 | 0.0534 |
| urine | 9.00 | 1.43 | 3.30 | 0.5000 | 0.5000 | 0.5000 | |
| cattle | feces | 31.00 | 1.71 | 4.37 | 0.0616 | 0.0222 | 0.0568 |
| urine | 6.00 | 3.47 | 8.00 | 0.5000 | 0.5000 | 0.5000 | |
| sheep | feces | 4.63 | 0.80 | 7.50 | 0.0550 | 0.0410 | 0.0530 |
| fowl | feces | 45.65 | 2.79 | 10.42 | 0.0859 | 0.0415 | 0.0847 |
| State | The Meaning of Status | ΔGWF | ΔGDP | Decoupling Elasticity | |
|---|---|---|---|---|---|
| Connection | Expansion connection (EC) | Economic growth boosts environmental stress, with pollution rising as fast as or faster than the economy. | >0 | >0 | 0.8 ≤ e ≤ 1.2 |
| Recessionary connection (RC) | Economic downturn reduces environmental stress, with pollution falling as fast as the shrinking economy. | <0 | <0 | 0.8 ≤ e ≤ 1.2 | |
| Decoupling | Weak decoupling (WD) | Economic growth raises environmental stress, yet pollution rises much slower than the economy. | >0 | >0 | 0 ≤ e < 0.8 |
| Strong decoupling (SD) | Economic growth coincides with declining environmental stress. | <0 | >0 | e < 0 | |
| Recessionary decoupling (RD) | Economic decline reduces environmental stress, with pollution dropping far faster than the economy. | <0 | <0 | e > 1.2 | |
| Negative decoupling | Weak negative decoupling (WND) | Economic downturn reduces environmental stress, but pollution declines slightly slower than the economy. | <0 | <0 | 0 ≤ e < 0.8 |
| Strong negative decoupling (SND) | Economic decline, yet environmental stress rises. | >0 | <0 | e < 0 | |
| Expansionary negative decoupling (END) | Economic growth sparks a surge in environmental stress. | >0 | >0 | e > 1.2 | |
| Time | Moran’s Index | Expected Index | z-Score | p-Value |
|---|---|---|---|---|
| 2005 | −0.002954 | −0.029412 | 0.225038 | 0.821950 |
| 2010 | 0.006507 | −0.029412 | 0.303598 | 0.761434 |
| 2015 | 0.090452 | −0.029412 | 1.002787 | 0.315964 |
| 2020 | 0.019359 | −0.029412 | 0.411006 | 0.681068 |
| Model | R | R2 | After the Adjustment of R2 | Model Error | Durbin–Watson |
|---|---|---|---|---|---|
| Numeric value | 0.957 | 0.917 | 0.911 | 0.1826 | 1.554 |
| Variable | Unstandardized Coefficients | Standardization Coefficient | t | Significance | Collinearity Statistics | |
|---|---|---|---|---|---|---|
| Tolerance | VIF | |||||
| Constant | −3.698 | −4.521 | 0.000 | |||
| A1 | 0.069 | 0.084 | 1.125 | 0.263 | 0.115 | 8.714 |
| A2 | 0.203 | 0.322 | 3.848 | 0.000 | 0.091 | 10.989 |
| A3 | 0.053 | 0.098 | 1.255 | 0.212 | 0.104 | 9.606 |
| P | 0.339 | 0.236 | 4.890 | 0.000 | 0.274 | 3.650 |
| U | 0.777 | 0.389 | 7.006 | 0.000 | 0.207 | 4.834 |
| G | 0.386 | 0.362 | 5.669 | 0.000 | 0.156 | 6.399 |
| W | 0.091 | 0.101 | 3.241 | 0.002 | 0.654 | 1.530 |
| T | 0.635 | 1.037 | 17.777 | 0.000 | 0.187 | 5.336 |
| K = 0.06 | Non-Standardized Coefficients | Standardization Coefficient | t | P | VIF Value | R2 | Adjust R2 | F | |
|---|---|---|---|---|---|---|---|---|---|
| B | Standard Error | Beta | |||||||
| Constant | −1.461 | 0.668 | - | −2.187 | 0.030 * | - | 0.902 | 0.896 | 150.807 (0.000 **) |
| lnT | 0.482 | 0.026 | 0.786 | 18.246 | 0.000 ** | 2.485 | |||
| lnA1 | 0.139 | 0.034 | 0.170 | 4.063 | 0.000 ** | 2.349 | |||
| lnA2 | 0.129 | 0.030 | 0.204 | 4.291 | 0.000 ** | 3.034 | |||
| lnA3 | 0.008 | 0.026 | 0.014 | 0.304 | 0.761 | 3.037 | |||
| lnP | 0.357 | 0.053 | 0.248 | 6.773 | 0.000 ** | 1.797 | |||
| lnU | 0.563 | 0.084 | 0.282 | 6.708 | 0.000 ** | 2.356 | |||
| lnG | 0.352 | 0.045 | 0.330 | 7.837 | 0.000 ** | 2.369 | |||
| lnW | 0.115 | 0.026 | 0.128 | 4.479 | 0.000 ** | 1.089 | |||
| dependent variable: lnGW | |||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, Y.; Wang, Q.; Xu, J.; Xie, F.; Xu, W. Temporal and Spatial Evolution of Grey Water Footprint in the Huai River Basin and Its Influencing Factors. Sustainability 2025, 17, 7157. https://doi.org/10.3390/su17157157
Wang X, Zhang Y, Wang Q, Xu J, Xie F, Xu W. Temporal and Spatial Evolution of Grey Water Footprint in the Huai River Basin and Its Influencing Factors. Sustainability. 2025; 17(15):7157. https://doi.org/10.3390/su17157157
Chicago/Turabian StyleWang, Xi, Yushuo Zhang, Qi Wang, Jing Xu, Fuju Xie, and Weiying Xu. 2025. "Temporal and Spatial Evolution of Grey Water Footprint in the Huai River Basin and Its Influencing Factors" Sustainability 17, no. 15: 7157. https://doi.org/10.3390/su17157157
APA StyleWang, X., Zhang, Y., Wang, Q., Xu, J., Xie, F., & Xu, W. (2025). Temporal and Spatial Evolution of Grey Water Footprint in the Huai River Basin and Its Influencing Factors. Sustainability, 17(15), 7157. https://doi.org/10.3390/su17157157






