Abstract
The development of urban underground space is a necessary way to realize the sustainable development of the city, and it is also an essential means to solve urban environmental problems such as traffic congestion and resource shortage. Scientific suitability evaluation is the prerequisite for the rational planning and development of underground space. Previous studies have encountered problems such as an imperfect index system, a single weighting method, and loss of membership degrees in fuzzy evaluation, which have led to unreasonable evaluation results. Taking the northern coastal cities of Weifang as the research area, the evaluation index system is established, and the index weights are calculated by the improved structural CRITIC. An improved fuzzy mathematical evaluation model based on the weighted summation method is proposed to carry out the suitability evaluation of underground space development in the research area. The results show that: (1) The proposed method of combination weight and improved fuzzy mathematics evaluation takes into account the scientific weight and avoids the subjective bias, and also corrects the issue of membership degree loss in the membership matrix of comprehensive evaluation. (2) When the area of the grid unit is 0.02% of the area of the research area, the size of the evaluation unit is more reasonable. (3) The area that is very suitable for underground space development accounts for 8.69%, and the more suitable area accounts for 25.55%, mainly located in the northwest and central–southern regions of the research area. It can provide a reference for the suitability evaluation of underground space development.
1. Introduction
With the rapid development of economy and society, the process of urbanization is constantly advancing, and the relationship between population and land supply is increasingly tense [1,2,3], resulting in a series of social problems such as traffic congestion, building density and resource shortage. As an important part of urban land, underground space has a huge scale of space resources [4,5,6]. Scientific and rational development of urban underground space is an important way to solve social problems and realize sustainable development of the city [7]. However, the process of underground space development is irreversible, and blind development will lead to many problems such as resource waste, environmental damage and even geological disasters [8]. Scientific suitability evaluation is the primary premise of urban underground space development, which can greatly reduce the later operating costs such as environmental restoration, engineering maintenance and risk avoidance caused by blind development [9]. As a relatively developed area in our country, coastal cities have more urgent demand for underground space, and the influencing factors in the process of development and utilization are more complex [10].
In recent years, many scholars have conducted numerous studies on the suitability evaluation of underground space development considering the evaluation index system, the index weighting method and the evaluation model. The evaluation index system is the cornerstone of evaluating the suitability of underground space development, and different regions have different geological, hydrological and environmental characteristics [11,12]. On the basis of engineering geology, hydrogeology and environmental conditions, a comprehensive evaluation index system including 11 indexes such as seawater erosion and existing underground engineering was established by considering the factors of human engineering activities [13]. In the evaluation system proposed by Jia et al. [14] for coastal plain cities, the basic geology includes engineering geology, hydrogeology and other factors, and the binding geological conditions include sand liquefaction and fault zones and other factors. Social and economic factors, including population density, per capita GDP and land price, were considered by Peng et al. [15] in consideration of the impact of the cost and benefit of underground space development, an evaluation index system with social and economic factors in an important position was constructed. These index systems were established according to the different geological characteristics of the study areas. Therefore, it is scientific and necessary to establish a targeted evaluation index system by considering the characteristics of the study area.
In the process of comprehensive evaluation, the scientific and rational weight of the index occupies an important position, which is one of the key steps of comprehensive evaluation. In many cases of suitability evaluation of underground space development, the single weighting methods such as the analytic hierarchy process (AHP) or the entropy weight method were often used. The AHP was adopted by Yan et al. [16] to assign weight to the impact factors in the evaluation index system of underground space development in Dezhou City, which accurately reflected the suitability of geological environment. The entropy weight method and variable fuzzy set were adopted by Jiang et al. [17] to evaluate the quality of underground space resources in Beijing CBD, which can effectively reduce subjectivity. The AHP was used to determine the weights of geological environmental indicators, and the group judgment matrix approach was applied to assign weights to the socio-economic factors [18]. However, these single weighting methods are either subjective like the AHP with expert experience judgment, or objective like the entropy weight method only considers the information of indicators themselves and ignores the correlation between indicators. Therefore, these traditional single weighting methods have limitations and cannot meet the evaluation model based on scientific and reasonable criteria.
In addition to the traditional single subjective weighting method and the objective weighting method, many scholars prefer the combined weighting method that integrates both subjective and objective approaches, because it can not only consider the different influence degrees of evaluation indicators, but also avoid the bias resulting from overly subjective evaluations. The improved AHP and CRITIC methods were used to assign weights to key geological indicators [19], addressing both subjective and objective uncertainty. The game theory combination weighting was adopted by Feng et al. [20] to determine the weight of the evaluation index, and combined with the index linkage function to make a scientific and effective evaluation of the instability risk of landfill. Based on the principle of minimum discrimination information, the subjective IAHP method and the objective CRITIC method were combined by Jin et al. [21] to make the combined weight as close as possible to the subjective weight and the objective weight. The Lagrange multiplier method was used by Zhou et al. [22] for the linear optimization combination of the AHP and the entropy method to assess the risk of water inrush from coal seam roofs. Based on the evaluation index system of intelligent lane-changing and obstacle avoidance functions of vehicles, the multiplicative synthesis normalization method was used by Zhan Qi et al. [23] to the combined weight calculation of improve the G1 method and the CRITIC method. The current combined weighting methods have solved the disadvantages of single weighting to a certain extent, but most of them adopt linear optimization and other combinatorial methods, and lack of fusion at the principle level.
In addition, the choice of evaluation model will also affect the scientificity, operability and accuracy of evaluation results. The fuzzy comprehensive evaluation method was adopted by Sun et al. [24] to evaluate the geological suitability of underground space in the core urban area of Beijing. The BP neural network topology model was constructed by Fan et al. [25] based on the entropy method to evaluate the suitability of sponge city construction. Dou et al. [26] optimized the TOSIS model using grey relational analysis based on a combination weighting methods of the AHP and CRITIC. Zhu et al. [27] established the matter-element extension evaluation model of game theory combinatorial weighting, and proved that the model was basically consistent with the actual situation and feasible. The 3D modeling and grey relational analysis were utilized for decision making, and the underground space development was evaluated through attribute modeling [28]. The automated constraint identification and hybrid analysis were used by Deng et al. [29] to evaluate the development potential and priorities of underground spaces.
The above studies and theories enrich and improve the evaluation system model of underground space development suitability, but there are some problems. For instance, the BP neural network models have the characteristics of extremely difficult to obtain data samples, unrepresentative, and difficult to control the fitting speed. In the matter-element extension model, it is impossible to calculate the comprehensive correlation degree when the matter-element to be evaluated exceeds the node domain [30]. In the fuzzy comprehensive evaluation model, the suitability level of evaluation indexes determined based on the principle of maximum membership degree is not consistent with the objective facts. Furthermore, different sizes of evaluation units will have an impact on the results. The excessively large evaluation units may lead to overly coarse results, while the excessively small ones can result in significant workload and low efficiency.
Therefore, taking the northern coastal area of Weifang City as the research area, an evaluation indicator system for the suitability of underground space development in coastal cities is constructed considering five aspects: topography, engineering geology, hydrogeology, environmental geology, and socio-economic factors. A subjective and objective combined weighting method named improved structural CRITIC is used for the weighting of evaluation indicators. To correct the issue of membership degree loss in the comprehensive evaluation, on the basis of obtaining the traditional fuzzy comprehensive evaluation results, a grade score matrix is multiplied to comprehensively consider the degree of belonging to each evaluation grade. The above-mentioned combined weighting method and the improved fuzzy evaluation method are used to evaluate the suitability of underground space development and utilization in Weifang coastal area. Meanwhile, four fuzzy mathematics evaluation models under different grid unit sizes are constructed, and the influences of different grid unit sizes on the evaluation results of the development suitability for underground space are compared and analyzed. This study will provide a reference for the theory, method and application demonstration of suitability evaluation of urban underground space development.
2. Research Area Background
The research area is located in the coastal city in the north of Weifang City, Shandong Province, which includes three administrative regions: Shouguang City, Hanting District, and Changyi City, with a total area of 4615.62 km2, as shown in Figure 1. It is connected with Qingdao and Yantai in the east, Zibo and Dongying in the west, Linyi and Rizhao in the south, and the Bohai Sea in the north. It spans from 118°59′ E to 120°01′ E in longitude and from 36°25′ N to 37°22′ N in latitude. The research area presents a trend of higher elevation in the south and lower elevation in the north, transitioning from hills in the south to alluvial plains in the north. It belongs to the warm temperate continental monsoon climate zone. There are Weihe River, Mi River, Bailang River and other rivers distributed in the research area, which flow into Laizhou Bay of Bohai Sea from south to north.
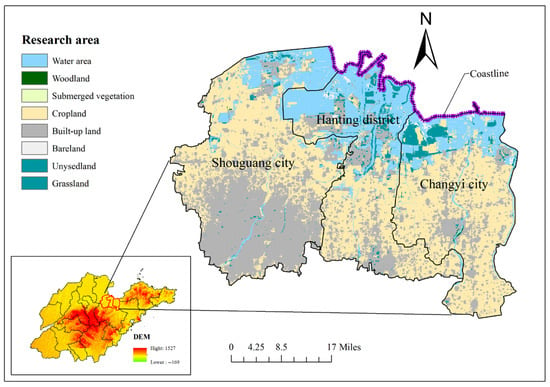
Figure 1.
Geographical location map of the research area.
The alluvial deposits such as quaternary soil, sand and gravel are distributed in the upper part of Weibei Plain. The Quaternary Pleistocene-Holocene alluvial, marine, and fluvio-marine deposits have a total thickness of over 400 m, gradually increasing from south to north. The Quaternary strata includes nine formations: the Weibei Formation, the Xukou Formation, the Linyi Formation, the Yihe Formation, the Huanghe Formation, the Heituhu Formation, and the Hanting Formation. The geological structure of Weibei Plain is mainly faulted structure. The Shandong section of Tancheng–Lujiang fault zone (Yishu fault zone) runs north–south through the middle of Weifang City. The east is Jiaoliao Uplift, and the west is divided into the Luxi Uplift and the North China Depression by the east–west trending Qihe–Guangrao fault.
Under the influence of geological structure, three marine layers were formed through three marine movements in the study area. After a long time of underground water burial, 3–4 layers of closed natural brine aquifers with a total thickness of approximately 15–50 m were formed. There was shallow fresh water in the upper layer of the southern part of the study area, which formed a three-layer structure of fresh–salty–fresh, the middle part was generally a two-layer structure of salty–fresh, and the northern part was mostly a three-layer structure of salty–fresh–salty. The freshwater area, from top to bottom along the stratigraphy, can be divided into the phreatic-microconfined aquifer layer, middle-deep confined aquifer and deep confined aquifer, which were mainly distributed in the Houzhen, Nancun, Gudi and Xinhe line. In addition, due to the unreasonable development of groundwater, Madian funnel, Liulu funnel, Weihan Funnel and Changyi Funnel were gradually formed in the northern part of the study area. It also induced a series of environmental geological problems such as land subsidence and seawater intrusion. Taking into account the geographical location, hydrogeology, engineering geology, environmental geology, social economy and other factors of the coastal city of Weifang, the selected research area has the common geological and urban characteristics of coastal cities. The research methods proposed based on this background have general applicability, and the research results have reference value for similar coastal cities.
3. Evaluation Theories and Methods
The theories and methods for evaluating the suitability of underground space development in coastal cities can be introduced considering three aspects: the construction of the evaluation indicator system, the calculation of combined subjective and objective weights, and the improved fuzzy mathematical evaluation model.
3.1. The Evaluation Indicator System
Taking the suitability of underground space development of coastal cities as the target layer of the evaluation system, the criterion layer of the evaluation system is constructed considering five aspects: engineering geology, hydrogeology, environmental geology, topography and landform, social economy. Then, taking into account both the vertical geological dimension and the horizontal social dimension, the evaluation system’s indicator layer is further composed of 14 indicators: topographic slope, fracture structure, soil ununiformity, soil bearing capacity, groundwater abundance, groundwater level depth, permeability of rock and soil layers, seawater intrusion, land subsidence, coastal erosion, traffic accessibility, land use status, population density, and building density. The three-dimensional evaluation indicator system finally constructed is shown in Figure 2.
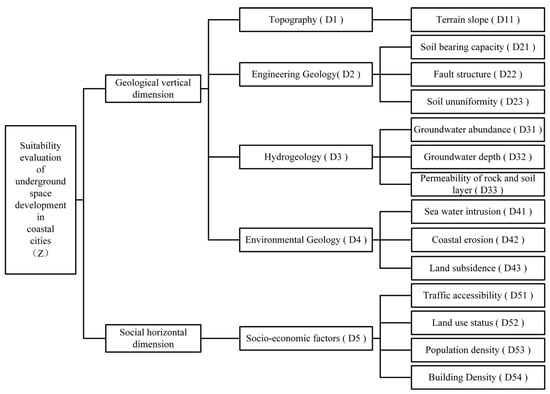
Figure 2.
Evaluation indicator system for the suitability of underground space development in coastal cities.
3.2. Combined Subjective and Objective Weight
The combined subjective and objective weight method proposed in this paper includes theories and methods related to subjective weight, objective weight, and the combination of subjective and objective weight.
The analytic hierarchy process (AHP) [31] is a kind of subjective weight method proposed by Saaty in the 1970s. It can convert qualitative problems into quantitative ones, thereby simplifying complex issues, and has the advantage of solving multi-objective and multi-level problems. The main calculation steps are as follows:
- 1.
- Experts are invited to make pairwise comparison of evaluation indicators by using the 1–9 scale method [32], and the judgment matrixes of the criterion layer and the indicator layer are constructed, respectively.
- 2.
- The consistency test of each judgment matrix C is carried out, respectively, to eliminate the possible errors in the construction process of the judgment matrix. The formulas for the consistency test are as follows:

Table 1.
The values of the average random consistency index.
- 3.
- Based on the judgment matrix C that passed the consistency test, the geometric average method is used to construct the comprehensive judgment matrix S. Then, the maximum eigenvalue λmax and the eigenvector W of the comprehensive judgment matrix S are solved, and the calculation formula is as follows:
Similarly, the consistency test is carried out on matrix S. If CR < 0.1, it indicates that the comprehensive judgment matrix S meets the consistency requirements, and the corresponding eigenvector W is the subjective weight of the evaluation indicator system.
The CRITIC method [33] is an approach to measure the objective weights of indicators by considering both their contrast intensities and conflicts among indicators, taking into account not only their own variability but also their correlation with other indicators. If the information provided by the indicator is independent and valuable, the weights of the indicators should be higher, and if the corresponding indicators are highly correlated and provide similar information, the weights should be lower. The calculation steps are as follows:
- 4.
- Assuming that the research area is divided into m evaluation units and n evaluation indicators are established, an evaluation matrix X is established, and the data are normalized according to the positive or negative Formula (5) to avoid the influence of dimensions, and the normalized matrix is shown in Formula (6).
- 5.
- The correlation coefficient and conflict indicator Sj between the indicators are calculated using the following formula.
- 6.
- Formula (9) is used to calculate the comprehensive information bearing capacity Cj of the evaluation indicators [34], and the combined subjective and objective weights are obtained by normalizing them using Formula (10).
3.3. Improved Fuzzy Mathematics Evaluation
Fuzzy mathematical theory is used to deal with uncertainty and fuzziness of data in the basic principles of fuzzy comprehensive evaluation [35]. The trapezoidal distribution in the fuzzy distribution method is used to construct the membership function Mi = M(ki) of the evaluation indicators, and the ki is the ith evaluation indicator. If the evaluation grade is divided into t grades, the interval values of the corresponding grades of each evaluation indicator are a1, a2, ai, … at, then the corresponding membership function is shown in Formulas (11)–(13).
In the formula, 1 < i < t, and the value of ai is determined by the measured data of each indicator combined with the evaluation grade.
For each evaluation unit, based on the measured data of each evaluation indicator in the research area, the membership function Mi = M(ki) is applied to obtain the membership degree matrix D of the evaluation indicators with respect to the evaluation object, as shown in Formula (14) below.
where Dij is the membership degree of the ith indicator to the jth evaluation grade.
The fuzzy comprehensive evaluation result B of each evaluation unit can be obtained by multiplying the combined subjective and objective combination weight ωj and membership matrix D, as shown below.
In the formula, Bj refers to the degree of each evaluation unit belonging to the jth evaluation grade by considering all evaluation indicators, and then the evaluation level of each unit can be determined according to the principle of maximum membership degree.
However, the principle of maximum membership emphasizes that the evaluation results belong to the level with the highest membership degree, but often ignores the degree of evaluation results belonging to other levels. For example, in a fuzzy comprehensive evaluation divided into five grades, the calculated result is [0.3, 0.29, 0.14, 0.14, 0.13], and according to the principle of maximum membership degree, the evaluation result should be the first grade corresponding to 0.3. Obviously, the degree belonging to the second grade is 0.29, which is very close to the degree belonging to the first grade, resulting in the evaluation results are biased.
Therefore, on the basis of obtaining the traditional fuzzy comprehensive evaluation results, the method of multiplying by a grade score matrix is proposed in this paper, as shown in Formula (16), in order to eliminate the membership degree loss of the maximum membership principle.
Among them, Si is the score value assigned to the ith grade, and the more appropriate the grade of development, the higher the corresponding score. A represents the final evaluation grade obtained for an evaluation unit. Then, the same method is used to obtain the evaluation results of all evaluation units. All comprehensive evaluation results are converted into the CSV format and connected with the evaluation unit grid attributes of ArcGIS, and the results are finally presented visually in GIS platform.
4. Evaluation Calculation
The evaluation theories and methods proposed above are adopted to carry out the evaluation of underground space development suitability based on the background of the research area. According to the relevant geological exploration data of the research area, 10 experts in related fields are invited to score the criterion layer and the indicator layer, and a judgment matrix of the criterion layer and 4 judgment matrixes of the indicator layer are constructed through pairwise comparison of indicators. Furthermore, the judgment matrices constructed by the 10 experts are used for consistency checks adopting Formulas (1) and (2).
The judgment matrices that have passed the consistency check are combined using the geometric average method, and the Formula (4) is used to calculate the contribution degrees of the criterion layer to the target layer and the indicator layer to the criterion layer, respectively. The subjective weights of the evaluation index system are finally obtained, as shown in Table 2.

Table 2.
The subjective weights of the evaluation indicator system.
Based on the evaluation indicator data in the research area, the Formula (5) is used to normalize each evaluation indicator, and the Formula (6) is used to establish a normalization matrix. Then, the correlation coefficient and conflict indicator between the indicators are calculated using the Formulas (7) and (8). Formulas (9) and (10) are used to calculate the combined subjective and objective weights of evaluation indicators, as shown in Table 3.

Table 3.
The combined subjective and objective weight of the evaluation indicator system.
As can be seen from Table 3, on the basis of considering the experience of experts, a certain degree of subjectivity can be eliminated by considering the objective correlation between the indicator data themselves, making the combined weights more scientific and reasonable. Among them, the combined subjective and objective weights of the evaluation indicators such as terrain slope, fault structure, groundwater depth, permeability of rock and soil layer, sea saltwater intrusion, traffic accessibility, land use status, population density and building density have increased to varying degrees compared to the subjective weights, while the combined subjective and objective weights of the evaluation indicators such as soil bearing capacity, rock and soil species uniformity, groundwater abundance, coastal erosion and land subsidence have shown a slight decrease compared to their subjective weights.
To further reflect the scientificity and rationality of combined subjective and objective weights, the comparison of the subjective weights, objective weights, and combined weights of the evaluation indicators are presented in Figure 3. It can be seen that the overall trend of the subjective weights is consistent with that of the combined weights except for a slight difference, while there is a significant difference in the objective weights. The reasons for the difference can be understood from Formulas (9) and (10). The combined weights are obtained by normalizing the product of the subjective weight and the conflict among indicators, while the objective weights are derived by normalizing the product of the standard deviation of the data and the conflict among indicators. The subjective weights result in relatively significant differences in the weights among the indicators, while the standard deviations between adjacent indicators are relatively small. Consequently, the combined weights and subjective weights demonstrate similar patterns of change. It also shows that simply relying on the objective weights of evaluation indicators cannot scientifically measure the suitability of underground space development of coastal cities. Therefore, it is the most scientific and reasonable weight calculation method to obtain optimized subjective-objective combined weights by combining subjective weights with objective correlation analysis of indicator data.
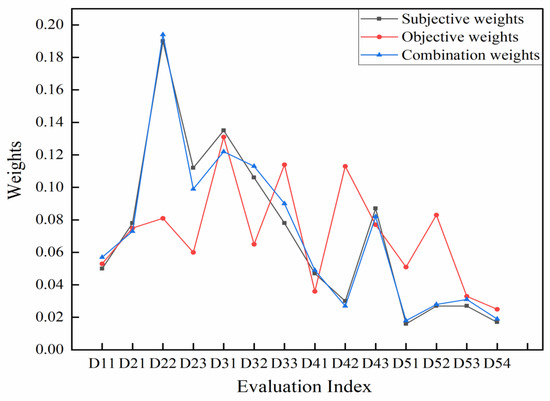
Figure 3.
Comparison of weights based on different calculation methods.
The data of the top four evaluation indicators ranked by combined subjective and objective weights, namely fault structure, groundwater abundance, groundwater depth, and soil uniformity, are separately extracted to analyze their distribution characteristics in the research area. Based on the data of sampling points obtained through methods such as drilling investigations and experimental tests, interpolation processing is conducted using the kriging tool within the spatial analyst tools, and the data of four evaluation indicators are shown in Figure 4. As can be seen from the figure, there are the north–south trending Tancheng–Lujiang fault zone and Shangwujing fault zone, as well as the east–west trending Qihe–Guangrao fault zone in the research area, which are basically evenly distributed in the three administrative regions. As evident from the water abundance distribution of the strata, extensive brine resources are distributed across the coastal plain area in the northern part of the research region, with the single-well brine yield generally ranging between 500 and 1000 m3/d. Loose rock pore water is distributed in the southwest of Shouguang City, the south of Hanting District and the middle of Changyi City, and the maximum water inflow of single well can reach 2000–3000 m3/d.
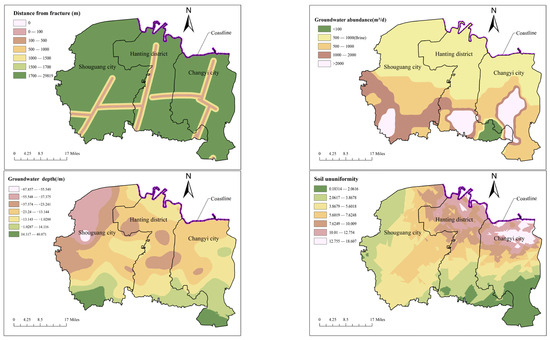
Figure 4.
Data chart of the top four evaluation indicators in terms of combined subjective and objective weights.
Regarding the evaluation indicator of groundwater level, based on the groundwater level within 60 m below the ground surface in June 2016, an obvious groundwater funnel is observed at the junction of Yingli Town, Taitou Town, and Shuangwangcheng Ecological Economic Park Management Committee in Shouguang City, with the maximum water level reaching over −80 m. Meanwhile, groundwater funnels are also present in Dajiawa Subdistrict, Yangzi Subdistrict, and Gudi Subdistrict of Hanting District, with water table depths ranging approximately from −20 m to −30 m. Additionally, a small-scale groundwater depression cone is observed near Kuiju Subdistrict in Changyi City, where the water table depth similarly ranges from approximately −20 m to −30 m. Weighted processing is conducted on the ununiformity of soil types within a 20 m depth range of geological drill holes in the research area. The richer the variety of soil types, the higher the value, indicating greater non-uniformity. As shown in the figure, the soil ununiformity in the coastal area of the research zone is relatively high, and the soil types are quite diverse. These areas are predominantly distributed with medium-coarse sand, silt, and silty clay formed by Quaternary alluvial–proluvial processes, as well as silty-fine sand, loamy sand, and loam formed by alluvial-marine deposition. In the southeast of the research area, the types of soil masses are relatively simple, mainly distributed as sandy soil and rock types.
The suitability of underground space development in coastal cities is divided into five grades: very suitable, more suitable, general suitable, less suitable and unsuitable. The research area is divided into 2063 evaluation units with the size of 1.5 km × 1.5 km, and the fuzzy mathematics comprehensive evaluation is carried out by using the above evaluation methods. Formulas (11)–(13) are used to establish the membership function of all evaluation indexes. Among them, taking the land subsidence as an example, the cumulative land subsidence in the research area from 2006 to 2021 is shown in Figure 5. As can be seen from the figure, there is a land subsidence funnel at the junction of Yangjiazhuangzi Village in Yingli Town, Shouguang City and Dajiawa Subdistrict, Hanting District, with an area of 471.52 km2. The subsidence center is located in Yangjiazhuangzi Village, Yingli Town, Shouguang City, and the cumulative subsidence from 2006 to 2021 is 1469 mm. Meanwhile, there is another small land subsidence funnel near Caojiazhuang Village, Wenjia Subdistrict, Shouguang City, with a cumulative subsidence of 874 mm. In addition, there is also a land subsidence zone in the area from Cuijiayangzi Village to Dongxiaying Town at the junction of Hanting District and Changyi City, with an area of 310.22 km2. The subsidence center is located in Cuijiayangzi Village, and the cumulative subsidence amount is 847 mm. Overall, the land subsidence trend in the research area gradually weakens from north to south.
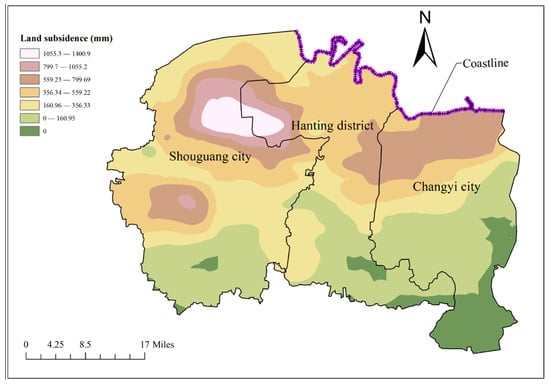
Figure 5.
The cumulative land subsidence in the research area from 2006 to 2021.
Considering the land subsidence characteristics in the research area, the values of the five grades are set as 200 mm, 300 mm, 500 mm, 800 mm and 1000 mm, respectively, and the membership function is constructed as shown in the following formula.
Five evaluation units numbered 1, 328, 649, 710, 2061 are randomly selected from the 2062 evaluation units, and their land subsidence data are = 0, = 277.70, = 494.9, = 645.14, and = 254.25, respectively. The five groups of data are, respectively, brought into the land subsidence membership function, and the membership degrees of the land subsidence belonging to the five evaluation levels in the five evaluation units are = [1, 0, 0, 0, 0], = [0.22, 0.78, 0, 0, 0], = [0, 0.03, 0.97, 0, 0], = [0, 0, 0.52, 0.48, 0], and = [0.46, 0.54, 0, 0, 0], respectively.
Among them, taking the evaluation unit numbered 328 as an example, the membership degree of other evaluation indicators is obtained by using similar calculation methods, and the membership matrix of this unit containing all evaluation indicators is obtained as shown below. Then, the Formula (15) is used to multiply the combined subjective and objective weights obtained above with the membership matrix of all evaluation indicators, and the fuzzy comprehensive evaluation results of underground space development suitability in the research area are obtained as = {0.284, 0.193, 0.374, 0.149, 0}.
Furthermore, the five levels are assigned scores of 5, 4, 3, 2, and 1 respectively, and the Formula (16) is used to eliminate the membership loss of evaluation levels. Finally, the improved fuzzy comprehensive evaluation score of evaluation unit numbered 328 is = 3.613.
To analyze the impact of changes in the weights of different evaluation indicators on the overall evaluation results, four evaluation units with numbered 1, 328, 649, and 710 are randomly selected from all the evaluation units. The sensitivity analyses of the indicator weights are carried out using the improved fuzzy comprehensive evaluation method mentioned above, and the results are shown in Figure 6. Analysis shows that as the weights of the indicators increase, different units exhibit similar patterns of change, that is, the evaluation scores increase linearly along with the increase in the weight of the indicators. This is because when the weight of a single indicator increases, the total weight must remain at 1, which leads to a consistent rate of change for all indicators. Meanwhile, the absolute values of the slopes in each indicator reflect their sensitivity to the results. It can be seen that the several indicators with higher sensitivity are fault structure, groundwater depth, groundwater abundance, and soil ununiformity, which are generally consistent with the calculation results of the combined weights. Furthermore, the final evaluation results of the 4 evaluation units remained within the range of original evaluation grade and did not change with the increase in the weight of the indicators, indicating the scientificity and stability of the combined weighting methods proposed.
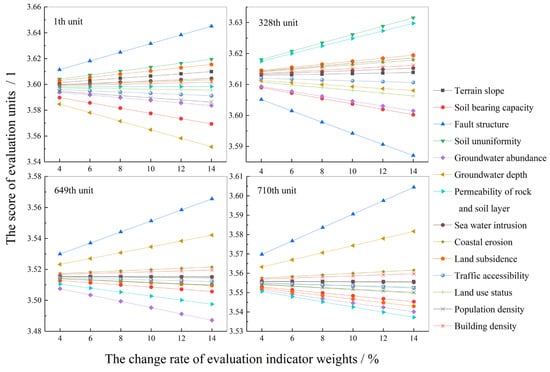
Figure 6.
Sensitivity analysis of evaluation indicator weights.
5. Results Analysis
The same methods are used to calculate all other evaluation units, and the improved fuzzy comprehensive evaluation scores of all units are visualized on the ArcGIS platform. The evaluation result is obtained as shown in Figure 7.
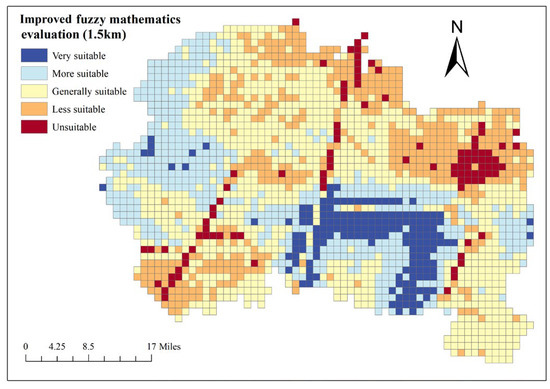
Figure 7.
Evaluation results based on combined weights and improved fuzzy mathematics.
As can be seen from Figure 7, the areas that are very suitable for underground space development in the research area are mainly distributed in the central and southern part of Hanting District and the southwest part of Changyi City. The areas unsuitable for underground space development are mainly concentrated in Wujing fault, Tancheng–Lujiang fault, Qihe–Guangrao fault, southwest of Shouguang City and northeast of Changyi City. In addition, in the east and southeast areas of Shouguang City and the northeast area of Changyi City, there are some areas that are less suitable for underground space development because of the shallow groundwater depth and high water abundance. According to the statistical data, the underground space development areas of very suitable, more suitable, general suitable, less suitable and unsuitable area are 393.77 km2, 1098.53 km2, 1879.36 km2, 1015.75 km2 and 228.21 km2, respectively, accounting for 8.53%, 23.8%, 40.72%, 22% and 4.94% of the total research area, respectively.
To clarify the impact of different weighting methods on the final evaluation results, the evaluation results based on the CIRTIC objective weighting method are compared and analyzed, as shown in Figure 8. Analysis shows that the area marked as “a” in the figure is approximately 22.5 km2, located near Yangkou Beach in the coastal area of the Bohai Sea. Compared to the inland areas, this region has environmental geological problems such as coastal erosion, seawater intrusion, and uneven soil quality. Moreover, this area has a relatively sparse population and few buildings, with a large amount of water bodies. However, the evaluation results of many units are “More suitable”, which are obviously unreasonable when compared with the actual situation. The areas marked as “b” and “c” in the figure are located at the center of the fault zones in the Hengli Road-Hebei Lingzi Village and Lijiatai Village-Yangjiawuzi Village, respectively, with areas of 11.25 km2 and 24.75 km2. However, the zoning results obtained through objective calculations are “Very suitable” or “More suitable”, which are obviously unreasonable.
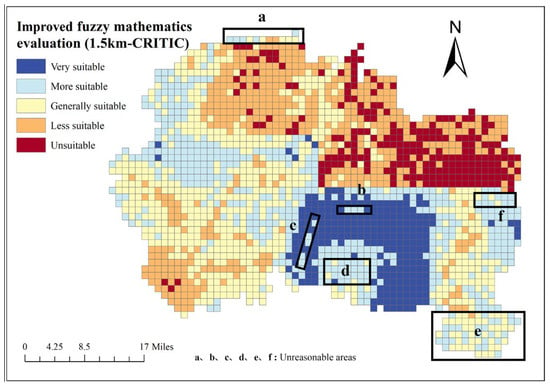
Figure 8.
Evaluation results based on objective weights (CRITIC) and improved fuzzy mathematics.
The areas marked as “d” and “e” in the figure are located in the Cuijiaguanzhuang Village area and the Mengjiawa Village-Xixiaotong Village area, respectively, with areas of 58.5 km2 and 67.5 km2. These regions have relatively high groundwater abundance and relatively shallow groundwater depth, resulting in significant difficulties in underground development. Similarly, the area marked as “f” in the figure is located in the area between Beixinxing Village and Caojiadian Village, with an area of approximately 58.5 km2. This region has a relatively shallow groundwater depth and strong groundwater abundance, coupled with low population density and building density. Therefore, it can be concluded that the evaluation results obtained using a single objective weighting method are obviously unreasonable.
To further analyze the suitability of underground space development in different administrative regions, the land areas of different suitability grades for underground space development in three administrative regions are extracted, as shown in Figure 9. It can be seen that the suitability of underground space development in the three administrative regions all follow a normal distribution law. Generally, the areas with general suitability for underground space development are the largest, while the areas with very high suitability and those with unsuitability are relatively the small. Among them, the areas that are very suitable and more suitable for underground space development in Shouguang City are 26.85 km2 and 630.93 km2, respectively, and the less suitable and unsuitable areas are 402.72 km2 and 64.88 km2, respectively. The areas that are very suitable and more suitable for underground space development in Hanting District are 219.26 km2 and 223.73 km2, respectively, and the less suitable and unsuitable areas are 250.58 km2 and 62.65 km2, respectively. The areas that are very suitable and more suitable for underground space development in Changyi City are 147.66 km2 and 243.87 km2, respectively, and the less suitable and unsuitable areas are 362.45 km2 and 100.68 km2, respectively.
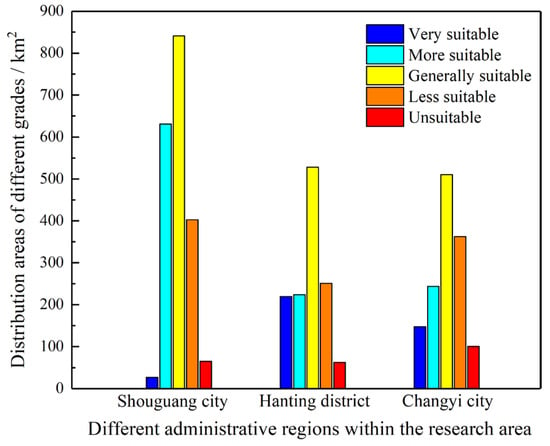
Figure 9.
Statistics of suitable zoning area for underground space development in different administrative regions.
The evaluation results obtained above are based on the grid division with evaluation units of 1.5 km × 1.5 km, and the size of the evaluation units may have an impact on the evaluation results of the study area. Therefore, the evaluation units are further divided into other three cases: 0.5 km × 0.5 km, 1.0 km × 1.0 km and 2.0 km × 2.0 km, and the evaluation results under different cases are calculated and compared based on the aforementioned evaluation methods and processes. Figure 10 shows the comparison of evaluation results in four cases where the evaluation grid units are 0.5 km × 0.5 km, 1.0 km × 1.0 km, 1.5 km × 1.5 km and 2.0 km × 2.0 km, respectively.
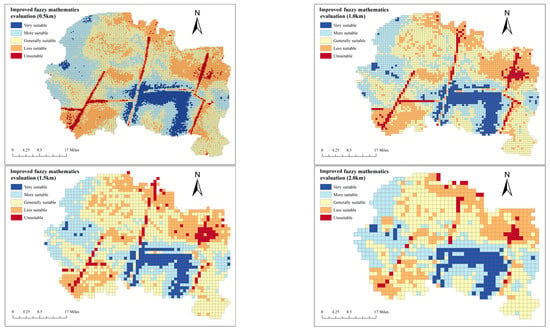
Figure 10.
Comparison of evaluation results based on different grid units.
It can be seen from Figure 10 that the evaluation results of underground space development suitability in the study area corresponding to different evaluation unit sizes are generally consistent, and the areas that are very suitable for development are still basically concentrated in the central and southern part of Hanting District and the southwest part of Changyi City. And the areas unsuitable for development are mainly concentrated in the vicinity of several fault structures and the northeast area of Changyi City. However, due to the differences in grid unit size, there are still some degrees of variation in the final evaluation results in some local areas. For example, in the evaluation results with the grid unit of 2.0 km × 2.0 km, the distribution of both suitable and unsuitable development areas is relatively discrete, and regions with different evaluation levels cross each other and are discontinuous. The main reason for this result is that the large grid unit size can mask the geological characteristics and related data in some areas. With the refinement of mesh unit size, the suitability partition gradually becomes smooth. Obviously, the evaluation results are basically the same when the grid unit sizes are 1.0 km × 1.0 km and 0.5 km × 0.5 km, and the distribution characteristics and laws of suitable and unsuitable underground space development areas are basically the same.
To analyze the influence of grid unit size on the evaluation results, the areas of different evaluation levels in four different cases are extracted, as shown in Figure 11. The results show that in the evaluation model with the grid unit size of 0.5 km × 0.5 km, the areas of very suitable, more suitable, generally suitable, less suitable and unsuitable are 400.98 km2, 1179.42 km2, 1786.26 km2, 1096.62 km2 and 152.34 km2, respectively, accounting for 8.69%, 25.55%, 38.7%, 23.76% and 3.3% of the total area. Similarly, in the evaluation model with the grid unit size of 1.0 km × 1.0 km, the areas of very suitable, more suitable, generally suitable, less suitable and unsuitable are 446.74 km2, 1157.32 km2, 1711.28 km2, 1083.74 km2 and 216.54 km2, respectively, accounting for 9.68%, 25.07%, 37.08%, 23.48% and 4.69% of the total area. However, the evaluation results of the grid unit size of 2.0 km × 2.0 km are slightly different, and the areas of very suitable, more suitable, generally suitable, less suitable and unsuitable are 462.36 km2, 1239.6 km2, 1721.89 km2, 1040.31 km2 and 151.46 km2, respectively, accounting for 10.02%, 26.86%, 37.31%, 22.54% and 3.28% of the total area. The comparison shows that the evaluation results obtained by the evaluation model with the grid unit size of 0.5 km × 0.5 km are basically consistent with those obtained by the evaluation model with grid unit size 1.0 km × 1.0 km.
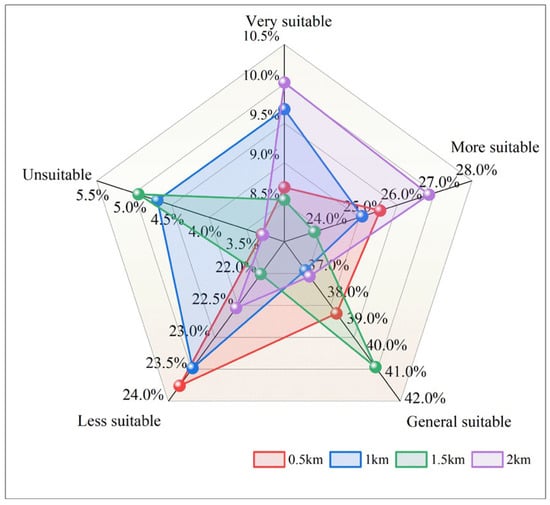
Figure 11.
Areas comparison of evaluation grade partition under different grid unit sizes.
To further analyze the influence of different grid unit sizes on the suitable zoning area for underground space development in different administrative regions, the suitable zoning areas for underground space development corresponding to different grid unit sizes in different administrative regions are extracted, as shown in Figure 12. Analysis shows that the suitability grades of underground space development in different administrative regions under different grid unit sizes still follow a normal distribution pattern on the whole. Although different grid unit sizes may lead to slight differences in the suitable zoning areas, overall, grid unit sizes have no significant impact on the values of the suitable area for underground space development in different administrative regions. Meanwhile, by combining the comparison diagrams of suitability zoning under different grid unit sizes, it can be seen that the grid accuracy has a greater impact on the distribution range and characteristics of different suitability grades, and has a relatively small influence on the quantity such as the area and its proportion.
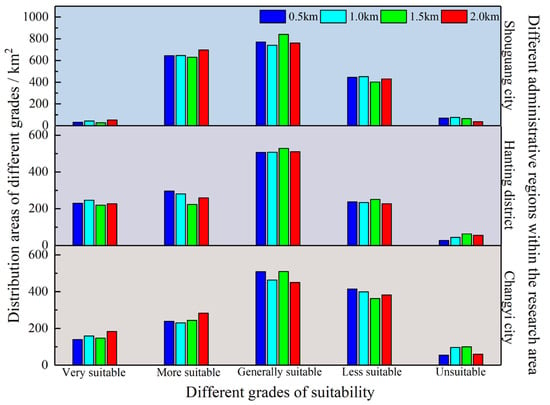
Figure 12.
Statistics of the suitable zoning area for underground space development in the research area under different grid units.
In summary, although the evaluation model with a larger grid size can reflect the suitability zoning of underground space development in general, the evaluation results are still rough because the larger grid size will ignore the evaluation index data of some areas. As the grid size becomes finer, the evaluation results tend to be more consistent, but the required evaluation index data and workload will also increase in an exponential pattern. Based on the above analysis results, it can be concluded that the evaluation model with a grid size of 1.0 km × 1.0 km is more reasonable and accurate. At the same time, taking into account the varying sizes of different research areas, it can be calculated that when the grid size is 0.02% of the research area, the size of the evaluation unit is more reasonable. It can provide a reference for the future research on the suitability evaluation zoning of underground space development in other research areas, and reduce the workload as far as possible on the premise of obtaining scientific and reasonable conclusions.
6. Discussion
- (1)
- The improved fuzzy mathematical evaluation model proposed in this paper can better reflect the situation that some qualitative evaluation indexes are in the transition region, and the method of grade assignment weighting is adopted to solve the problem of membership loss. In the specific calculation process, the values of the five grades are 5, 4, 3, 2 and 1, respectively. Of course, other scores can also be assigned, such as 10, 8, 6, 4 and 2. The influence of different values on the evaluation results will be further discussed in the future.
- (2)
- In the future, other evaluation models and methods, such as the matter-element extension model, neural network and machine learning, can be adopted to carry out the evaluation of the suitability of underground space development in coastal cities. However, there are differences in the adjustment mechanisms of weights between machine learning algorithms such as neural networks and traditional evaluation models like fuzzy mathematics. How to coordinate the relationship between these two weighting approaches, enhance the convergence and stability of machine learning models, and optimize the parameters of neural network models will be crucial directions for future research.
7. Conclusions
- (1)
- The proposed theoretical methods of combining subjective and objective weights and improving fuzzy mathematical evaluation can make the weight distribution of evaluation indicators more scientific and reasonable, and the problem of membership loss of each evaluation level in the fuzzy comprehensive evaluation process can also be solved well. The practice proves that it can be well applied in the evaluation of the suitability of underground space development of coastal cities.
- (2)
- When the size of evaluation unit size is approximately 0.02% of the area of the research area, it is a more scientific and reasonable evaluation model size. At this scale, it is possible to obtain a relatively accurate evaluation and zoning results of the suitability for underground space development in the research area. At the same time, it can also reduce a lot of workload in the evaluation index data acquisition and calculation process.
- (3)
- The area within the research region that is very suitable for underground space development is 400.98 km2, accounting for 8.69%, mainly distributed in the central–southern parts of the research area. The area that is more suitable for development is 1179.42 km2, accounting for 25.55%, mainly distributed in the central and northwestern regions of the research area. The area unsuitable for underground space development accounts for 3.3%, primarily influenced by factors such as fault structures, groundwater depth, and groundwater abundance.
Author Contributions
Conceptualization, S.D.; methodology, S.D.; validation, Y.L.; formal analysis, S.D. and Y.L.; resources, J.D.; data curation, C.H. and Y.Y.; writing, S.D. and Y.L.; visualization, Y.L.; project administration, Z.W. and M.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Open Fund of the Key Laboratory of Geological Safety of Coastal Urban Underground Space, Ministry of Natural Resources, grant number BHKF2022Z05, and the Open Fund of Key Laboratory of Geological Disaster Risk Prevention and Control of Shandong Provincial Emergency Management Department, grant number 801KF2024-DZ07.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy and confidentiality concerns.
Acknowledgments
We would like to express our sincere gratitude to all the participants who contributed to this research. We also appreciate the valuable feedback and insights provided by colleagues and experts, which greatly enhanced the quality of this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, K.; Chen, J.; Xu, F.; He, Y.; Li, J. Evaluation model of comprehensive potential of underground space development in coastal cities. Chin. J. Undergr. Space Eng. 2023, 19, 1412–1421. [Google Scholar]
- Peng, F.; Qiao, Y.; Sabri, S.; Atazadeh, B.; Rajabifard, A. A collaborative approach for urban underground space development toward sustainable development goals: Critical dimensions and future directions. Front. Struct. Civ. Eng. 2021, 15, 20–45. [Google Scholar] [CrossRef]
- Lai, Y.; Wang, Y.; Cheng, J.; Chen, X.; Liu, Q. Review of constraints and critical success factors of developing urban underground space. Undergr. Space 2023, 12, 137–155. [Google Scholar] [CrossRef]
- Peng, F.; Qiao, Y.; Dong, Y.; Yan, Z.; Zhu, H. Development strategy for urban underground space in the new development stage. Strateg. Study CAE 2024, 26, 176–185. [Google Scholar] [CrossRef]
- Tann, L.V.D.; Sterling, R.; Zhou, Y.; Metje, N. Systems approaches to urban underground space planning and management—A review. Undergr. Space 2020, 5, 144–166. [Google Scholar] [CrossRef]
- Admiraal, H.; Cornaro, A. Why underground space should be included in urban planning policy—And how this will enhance an urban underground future. Tunn. Undergr. Space Technol. 2016, 55, 214–220. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, J.; Liu, H.; Zhang, Z. Present status and development trends of underground space in Chinese cities: Evaluation and analysis. Tunn. Undergr. Space Technol. 2018, 71, 253–270. [Google Scholar] [CrossRef]
- Tan, F.; Wang, J.; Jiao, Y.; Ma, B.; He, L. Suitability evaluation of underground space based on finite interval cloud model and genetic algorithm combination weighting. Tunn. Undergr. Space Technol. 2021, 108, 103743. [Google Scholar] [CrossRef]
- Bobylev, N. Comparative analysis of environmental impacts of selected underground construction technologies using the analytic network process. Autom. Constr. 2011, 20, 1030–1040. [Google Scholar] [CrossRef]
- Yu, P.; Liu, H.; Wang, Z.; Fu, J.; Zhang, H.; Wang, J.; Yang, Q. Development of Urban Underground Space in Coastal Cities in China: A Review. Deep Undergr. Sci. Eng. 2023, 2, 148–172. [Google Scholar] [CrossRef]
- Hao, M.; Ren, W.; Xia, W.; Fu, J.; Zhu, H.; Sun, P.; Wang, K.; Xu, M. Suitability Evaluation of Urban Underground Space Development: A Case Study of Qingdao City. Appl. Sci. 2024, 14, 6617. [Google Scholar] [CrossRef]
- Chen, H.; Tan, X.; Zhang, Y.; Hu, B.; Xu, S.; Dai, Z.; Zhang, Z.; Xiong, H.; Song, X.; Luo, D. The Application of Variable Weight Theory on the Suitability Evaluation of Urban Underground Space Development and Utilization for Urban Resilience and Sustainability. Buildings 2025, 15, 387. [Google Scholar] [CrossRef]
- Wang, M.; Wang, H.; Feng, Y.; He, Y.; Han, Z.; Zhang, B. Investigating Urban Underground Space Suitability Evaluation Using Fuzzy C-Mean Clustering Algorithm—A Case Study of Huancui District, Weihai City. Appl. Sci. 2022, 12, 12113. [Google Scholar] [CrossRef]
- Jia, W.; Li, Z.; Liu, K.; Yan, J.; Zhu, W.; Guo, B.; Yang, P. Evaluation of geological suitability of underground space in typical coastal plain cities. Geol. Explor. 2024, 60, 0367–0376. [Google Scholar]
- Peng, Z.; Zhang, Y.; Tan, F.; Lv, J.; Li, L. Variable-Weight Suitability Evaluation of Underground Space Development Considering Socioeconomic Factors. Sustainability 2023, 15, 3574. [Google Scholar] [CrossRef]
- Yan, C.; Kang, F.; Han, J.; Yang, X. Suitability evaluation of geological environment for underground space development in Dezhou City. Geol. Rev. 2021, 67, 43–44. [Google Scholar]
- Jiang, Y.; Wu, L.; Che, D. Integrated Entropy Weight and Variable Fuzzy Sets Evaluation Approach for Underground Space Resource Quality Problem. J. China Univ. Min. Technol. 2009, 38, 872–878. [Google Scholar]
- Ye, W.; Huang, J.; Xu, P.; Yuan, J.; Zeng, L.; Zhang, Y.; Wang, Y.; Wang, S.; Xu, X.; Guo, Z.; et al. Suitability Evaluation of Underground Space Development by Considering Socio-Economic Factors—An Empirical Study from Longgang Region of China. Sustainability 2025, 17, 2788. [Google Scholar] [CrossRef]
- Mo, J.; Zhu, L.; Liu, W.; Wen, P.; Xie, Z.; Li, R.; Ji, C.; Cheng, W.; Zhang, Y.; Chen, C.; et al. 3D-CWC: A Method to Evaluate the Geological Suitability for Layered Development and Utilization of Urban Underground Space. Land 2025, 14, 551. [Google Scholar] [CrossRef]
- Feng, S.; Xu, Y.; Yang, J.; Zheng, Q.; Zhang, X. Risk assessment of landfill instability based on set pair-combination weighting. Rock Soil Mech. 2024, 45, 2129–2139. [Google Scholar]
- Jin, R.; Wang, L.; Zhang, T.; Li, Q. Bridge Construction Quality Evaluation Based on Combination Weighting Method—Technique for Order Preference by Similarity to an Ideal Solution Theory. Appl. Sci. 2023, 13, 12018. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, H.; Jiao, Y.; Yu, B.; Guo, J. Evaluation of the risk of water inrush from coal roof based on combination weighting method. Sci. Technol. Eng. 2022, 22, 3497–3503. [Google Scholar]
- Zhan, Q.; Zhou, W.; Li, W.; Zhang, X.; Liu, Z. Fuzzy Comprehensive Evaluation on Vehicle Intelligent Obstacle Avoidance Function by Lane Changing Based on Combination Weighting. J. Highw. Transp. Res. Dev. 2023, 40, 236–244. [Google Scholar] [CrossRef]
- Sun, W.; Yang, W.; Deng, Y.; Li, W. Geological Suitability Evaluation of Underground Space in Beijing Urban Area Based on Fuzzy Mathematics. Acta Geosci. Sin. 2024, 45, 73–79. [Google Scholar]
- Fan, J.; Xu, J.; Hu, H. Research on Construction Suitability Evaluation of Sponge City Based on Back Propagation Neural Network Model: A Case of Changting, China. Ecol. Econ. 2019, 35, 222–229. [Google Scholar]
- Dou, F.; Xing, H.; Li, X.; Yuan, F.; Lu, Z.; Li, X.; Ge, W. 3D Geological Suitability Evaluation for Urban Underground Space Development Based on Combined Weighting and Improved TOPSIS. Nat. Resour. Res. 2022, 31, 693–711. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, S.; Lin, L.; Xu, X.; Shi, Z. Based on the Combination of Game Theory and Weighted Matter—Element Extension Model Study on Waterlogging Resilience Assessment of Metro Stations. J. Catastrophol. 2023, 38, 1–6. [Google Scholar] [CrossRef]
- Ni, X.; Li, J.; Xu, J.; Shen, Y.; Liu, X. Grey relation analysis and multiple criteria decision analysis method model for suitability evaluation of underground space development. Eng. Geol. 2024, 338, 107608. [Google Scholar] [CrossRef]
- Deng, F.; Cheng, T.; Huang, Y.; Chen, Z.; Han, Q. Evaluation of urban underground space via automated constraint identification and hybrid analysis. Tunn. Undergr. Space Technol. 2024, 153, 106005. [Google Scholar] [CrossRef]
- Fu, L.; Fan, J.; Shi, X.; Zhu, S.; Wei, X.; Tian, H. Concealed morphology construction and stability evaluation of two butted-well horizontal salt caverns gas storage. Energy 2025, 317, 134499. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Xie, M.; Peng, Y.; Yang, J.; Kang, W. The AHP (1–9 value scale) level method to analyze the development of logistics under the perspective of low-carbon environmental protection: Taking Shandong province, China, as an example. Wirel. Commun. Mob. Comput. 2022, 2022, 3707002. [Google Scholar] [CrossRef]
- Choo, E.U.; Schoner, B.T.; Wedley, W.C. Interpretation of criteria weights in multicriteria decision making. Comput. Ind. Eng. 1999, 37, 527–541. [Google Scholar] [CrossRef]
- Wu, L.; Zhao, G. Structural CRITIC-based Weighting Method for Academic Journals Evaluation Index and Comparison. Stat. Decis. 2024, 40, 56–62. [Google Scholar] [CrossRef]
- Tong, D.; Tan, F.; Ma, B.; Jiao, Y.; Wang, J. A Suitability Evaluation Method of Urban Underground Space Based on Rough Set Theory and Conditional Entropy: A Case Study in Wuhan Changjiang New Town. Appl. Sci. 2022, 12, 1347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).