Spatiotemporal Dengue Forecasting for Sustainable Public Health in Bandung, Indonesia: A Comparative Study of Classical, Machine Learning, and Bayesian Models
Abstract
1. Introduction
2. Overview of Forecasting Approaches
3. Application: Monthly Dengue Incidences in Bandung, Indonesia
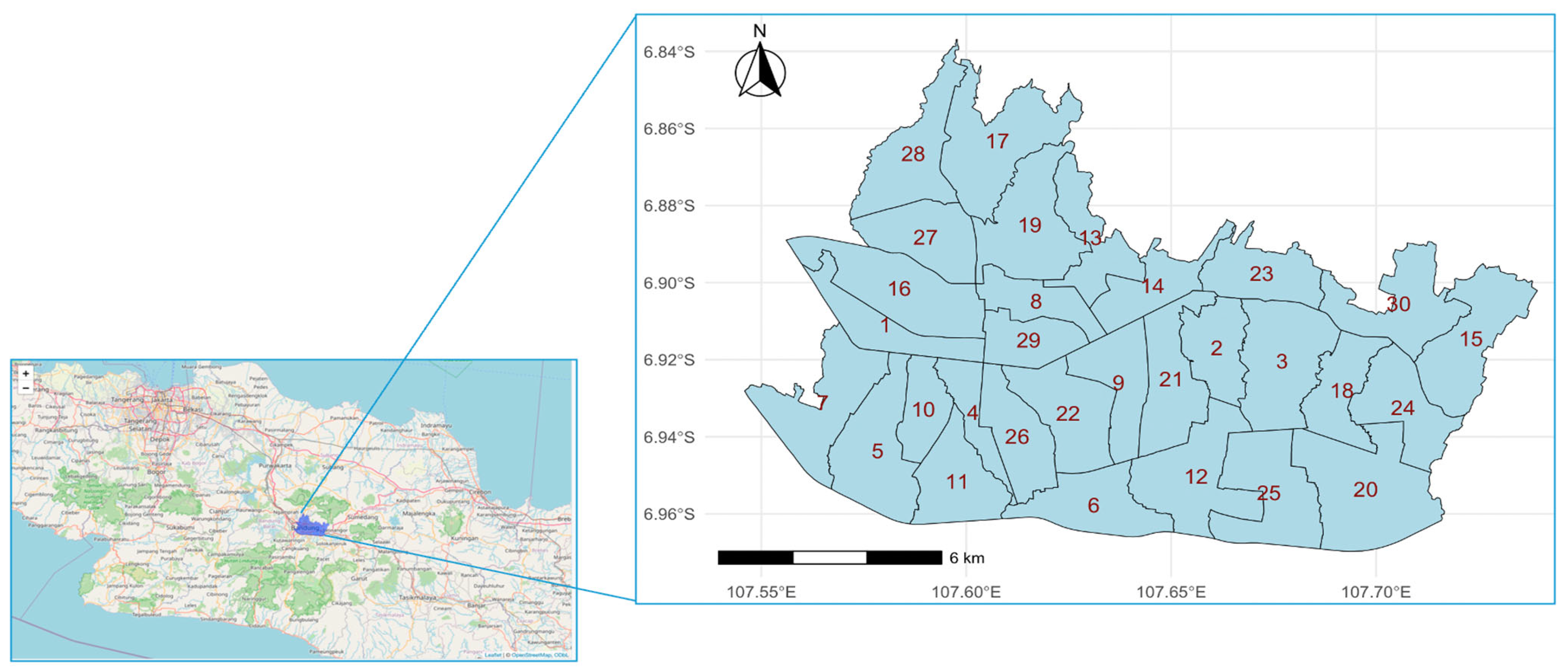
3.1. Study Area
3.2. Data
3.3. Model Estimation
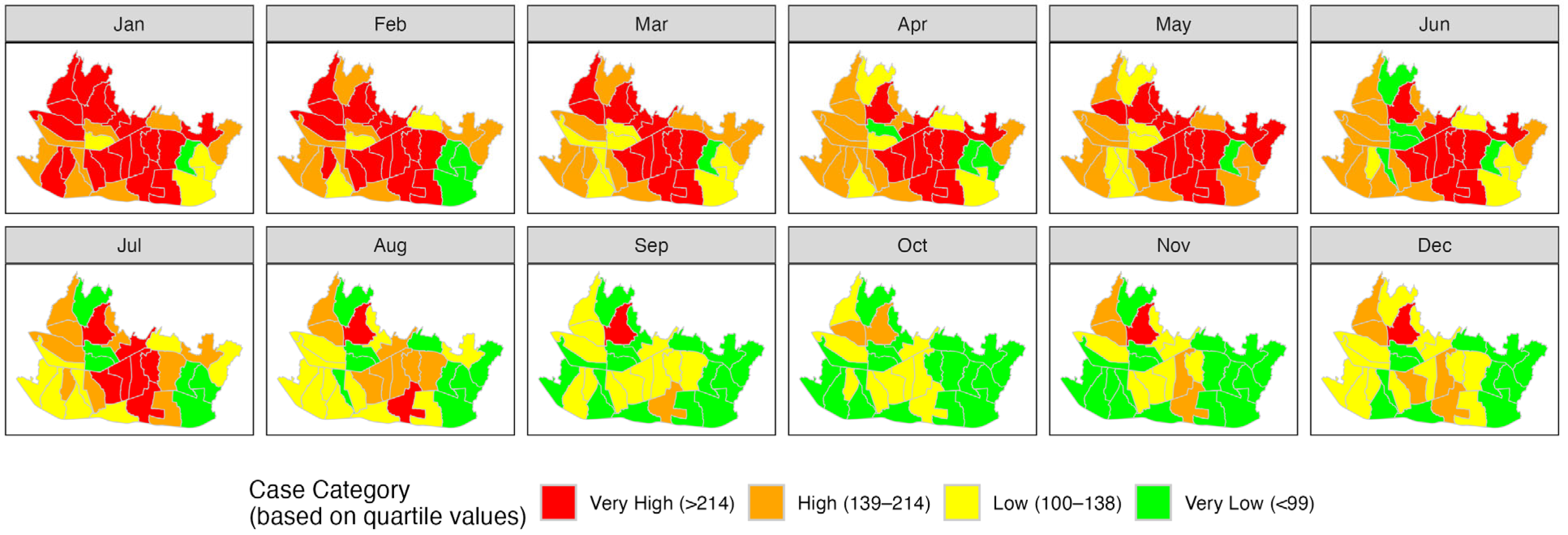
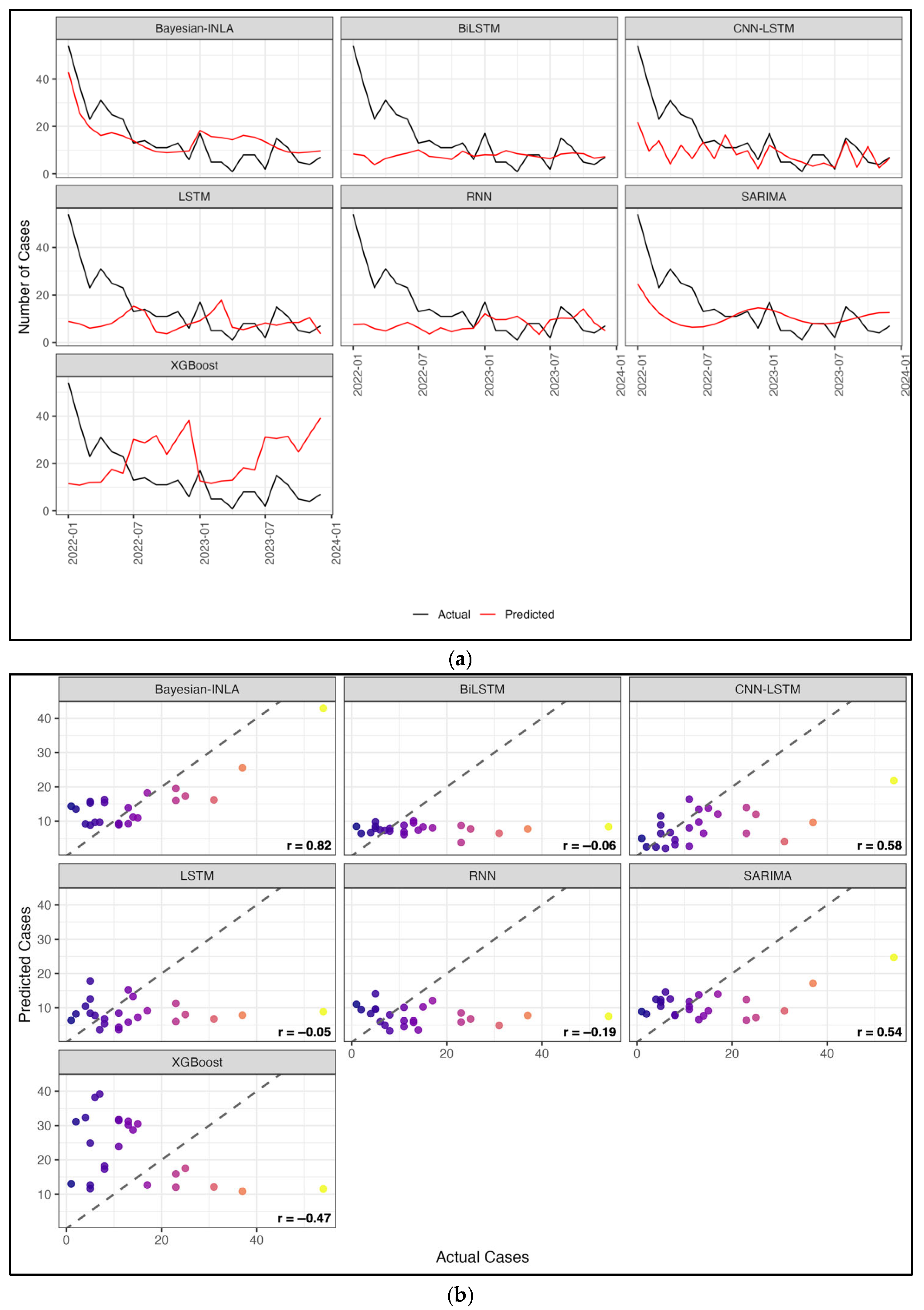
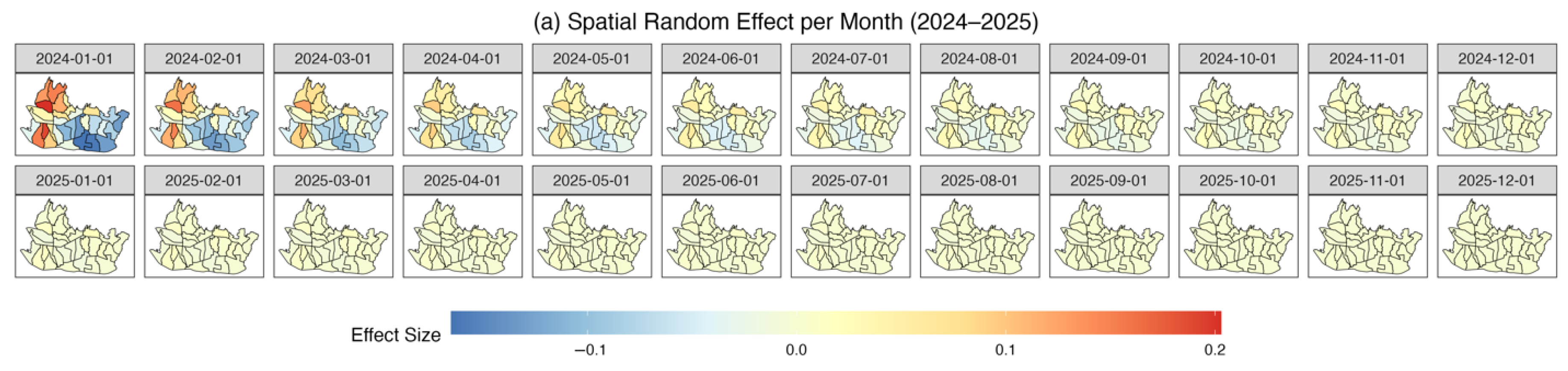
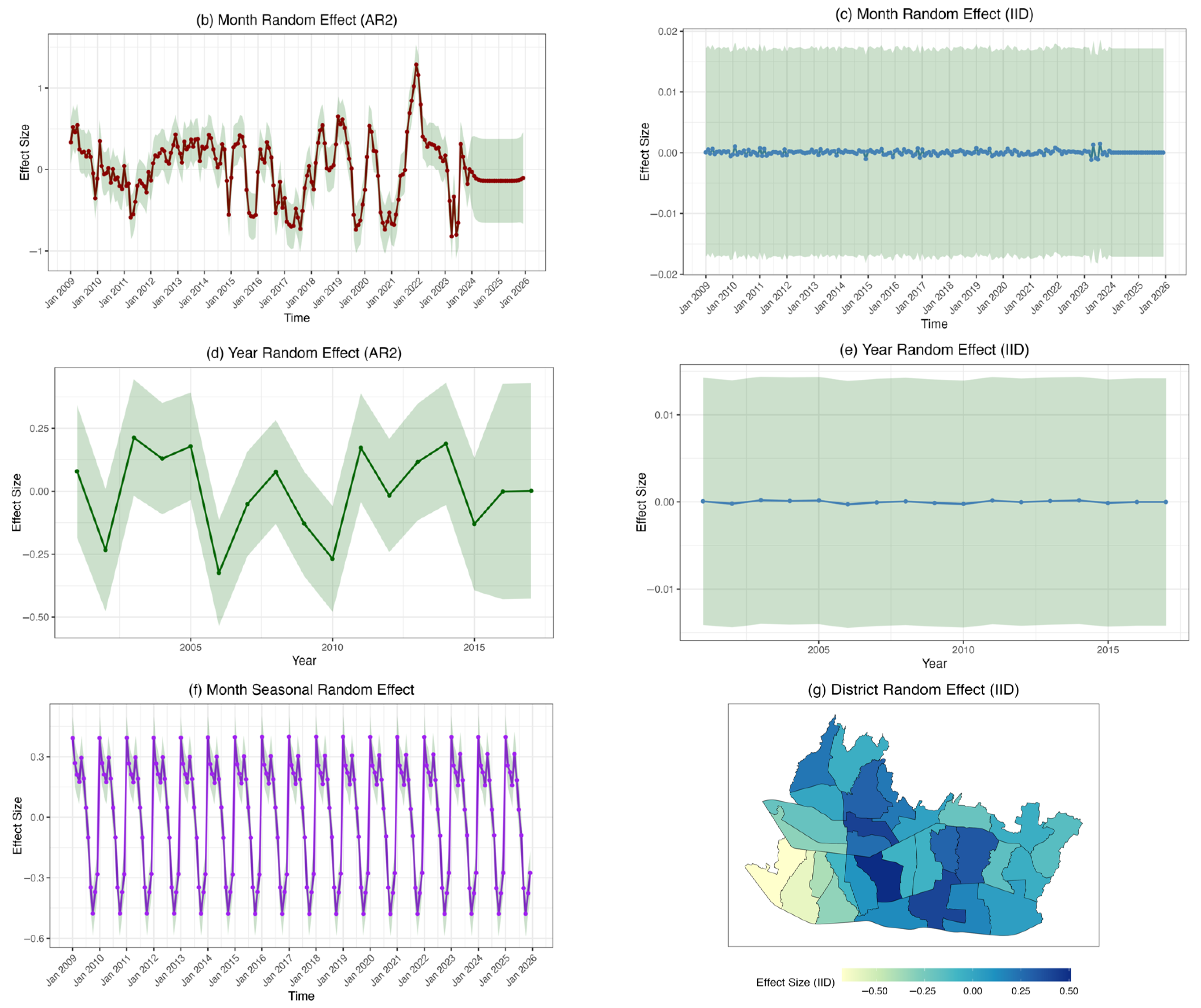
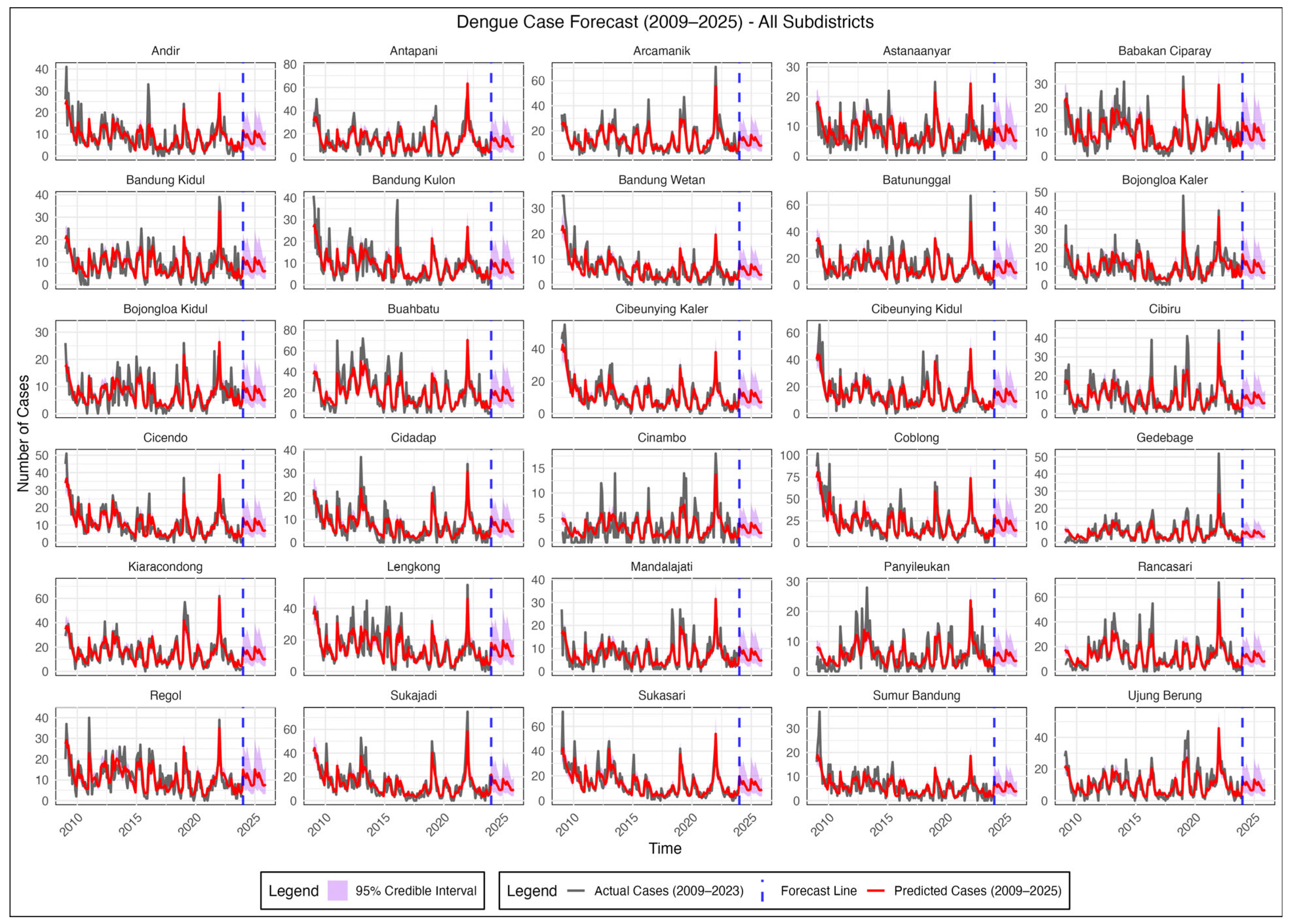
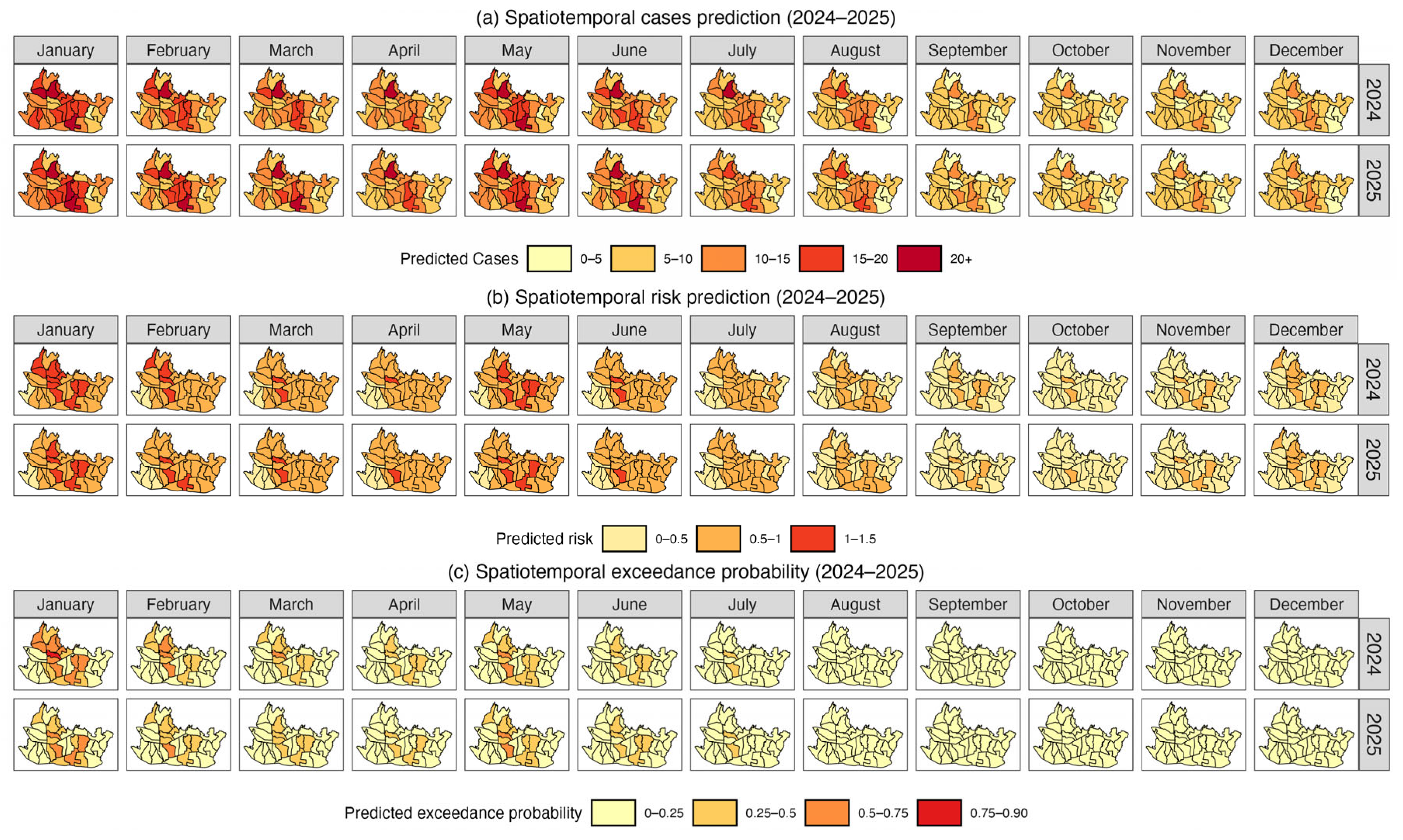
3.4. Result and Model Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Classical, Machine Learning, and Bayesian Forecasting Models
Appendix A.1. The Seasonal Autoregressive Integrated Moving Average (SARIMA)
Appendix A.2. Extreme Gradient Boosting (XGBoost)
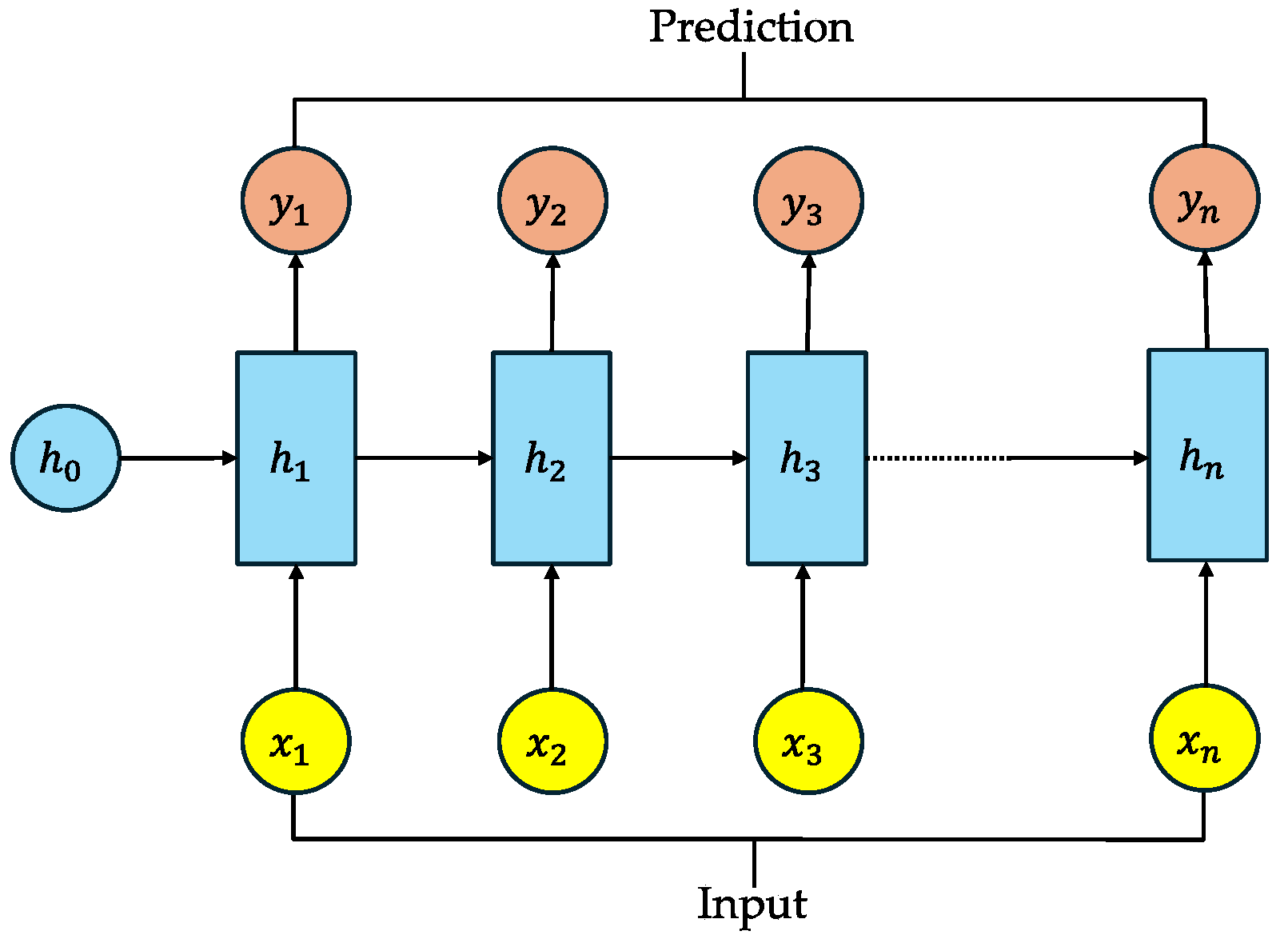
Appendix A.3. Recurrent Neural Networks (RNNs)
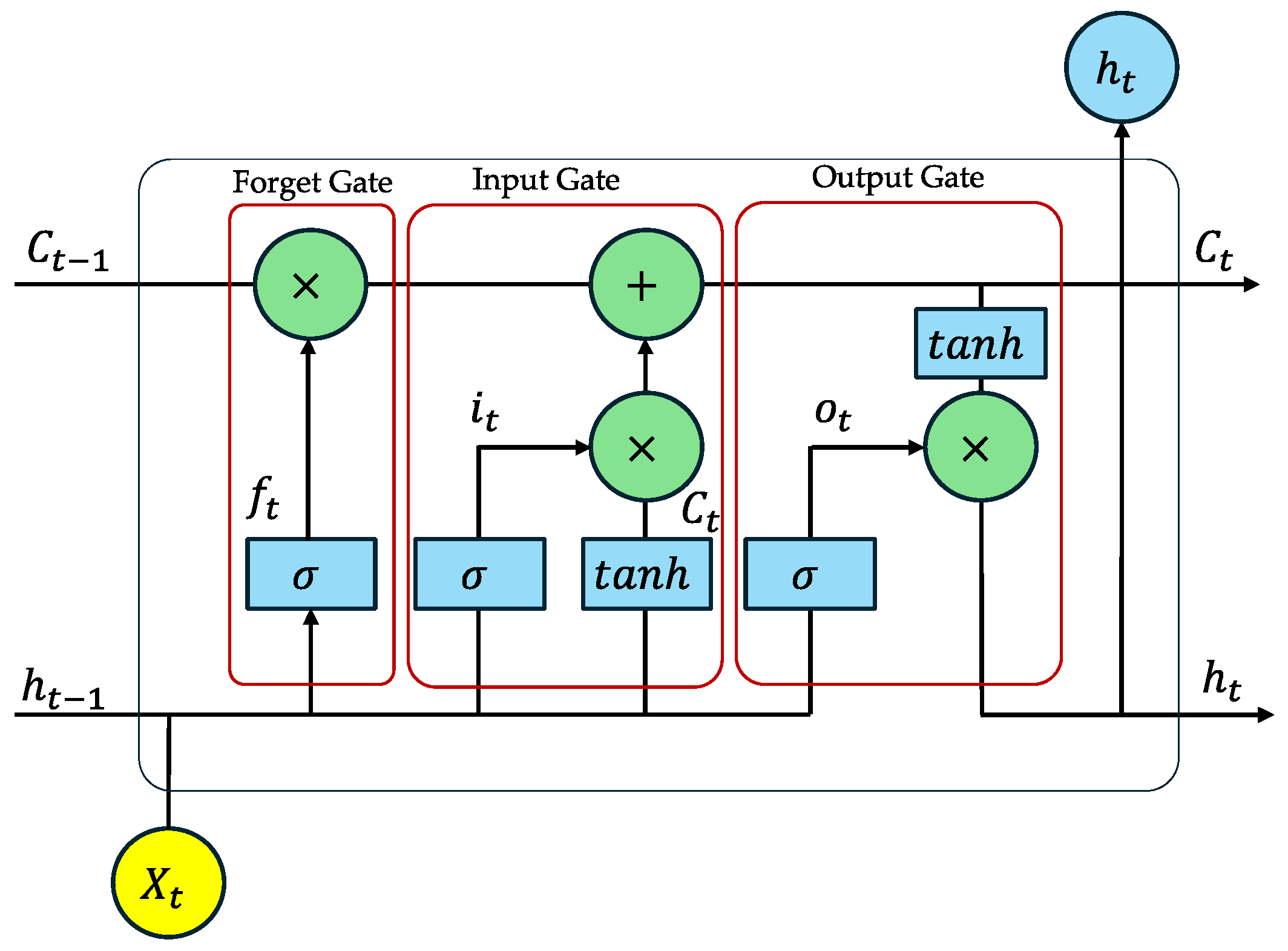
Appendix A.4. Long Short-Term Memory (LSTM)
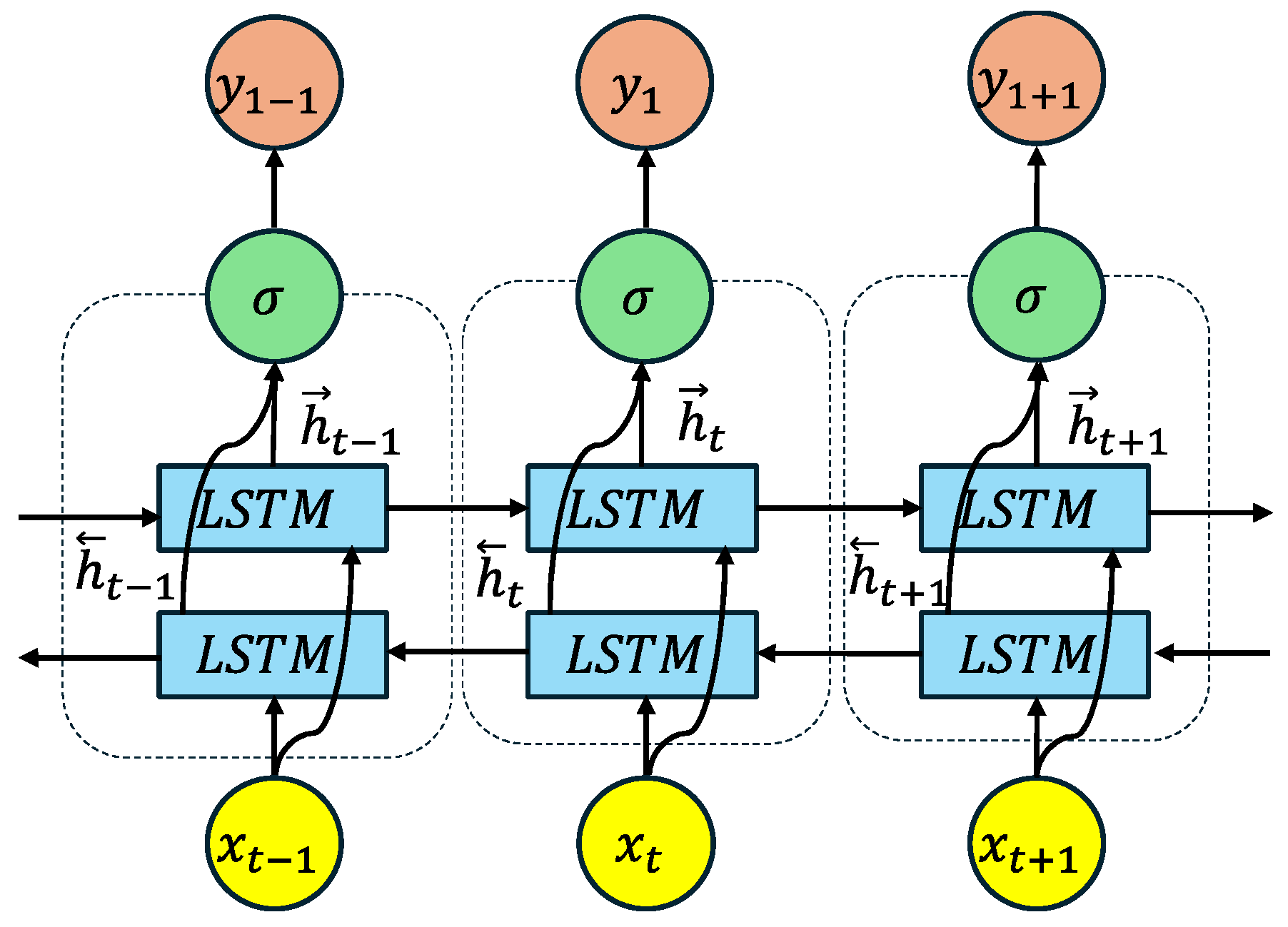
Appendix A.5. Bidirectional Long Short-Term Memory (BiLSTM)
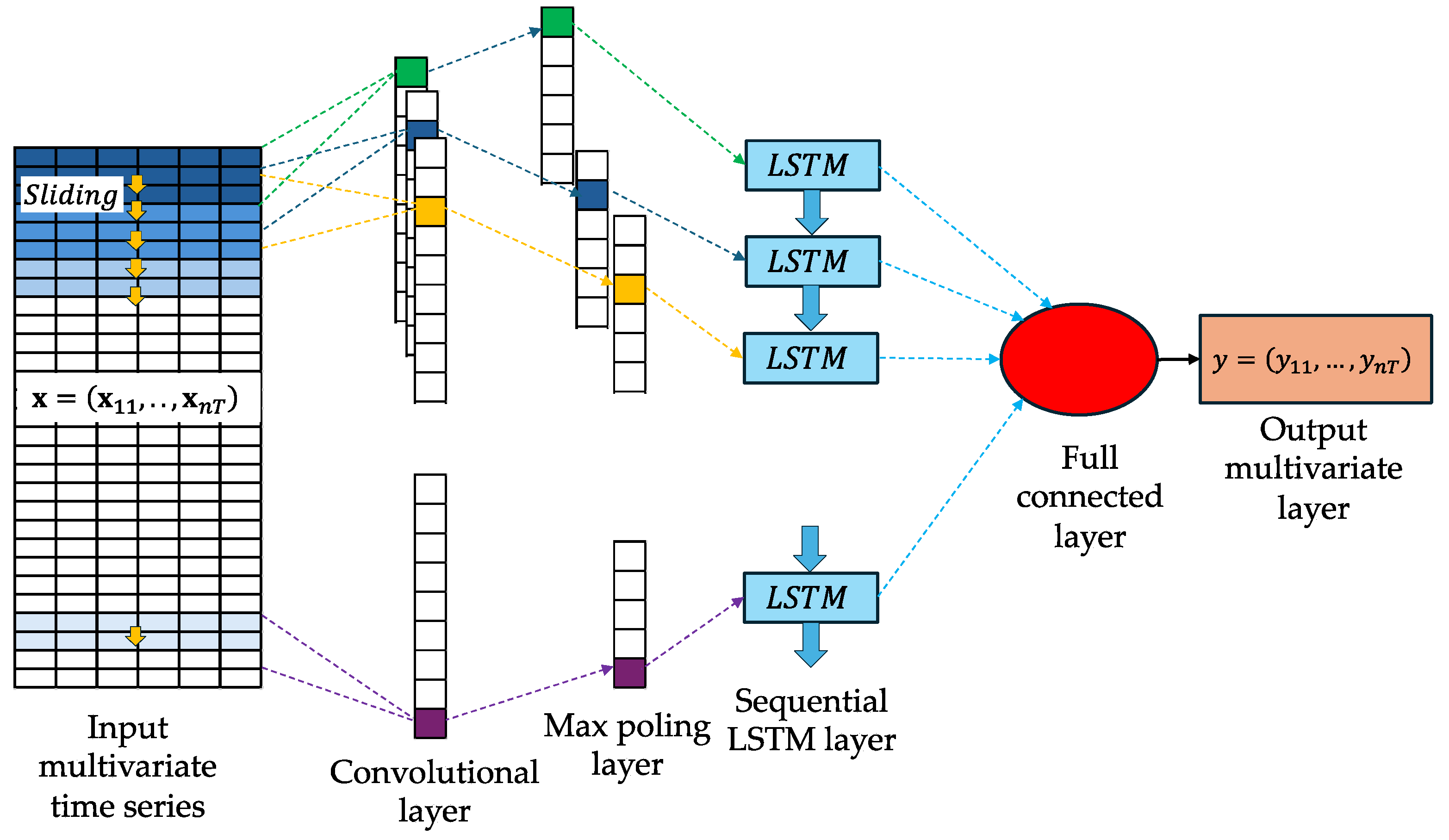
Appendix A.6. Convolutional Neural Network (CNN)
Appendix A.7. Bayesian Spatiotemporal
| Component | Prior | |
|---|---|---|
| ) | ||
| : | ||
| Interaction effect | ~Type IV: | is contingent upon in both spatial and temporal dimensions. The spatially structured effect follows Leroux CAR model: denotes an ) otherwise. The temporally structure is defined as follows: |
Appendix B. District ID and Coordinates
| ID | District | Coordinates | |
|---|---|---|---|
| Longitude | Latitude | ||
| 1 | Andir | 107.5804 | −6.9108 |
| 2 | Antapani | 107.6612 | −6.9169 |
| 3 | Arcamanik | 107.6771 | −6.9203 |
| 4 | Astanaanyar | 107.6017 | −6.9337 |
| 5 | Babakan Ciparay | 107.5784 | −6.9435 |
| 6 | Bandung Kidul | 107.6312 | −6.9577 |
| 7 | Bandung Kulon | 107.5650 | −6.9310 |
| 8 | Bandung Wetan | 107.6172 | −6.9048 |
| 9 | Batununggal | 107.6372 | −6.9258 |
| 10 | Bojongloa Kaler | 107.5895 | −6.9328 |
| 11 | Bojongloa Kidul | 107.5978 | −6.9516 |
| 12 | Buahbatu | 107.6561 | −6.9502 |
| 13 | Cibeunying Kaler | 107.6303 | −6.8883 |
| 14 | Cibeunying Kidul | 107.6455 | −6.9007 |
| 15 | Cibiru | 107.7232 | −6.9145 |
| 16 | Cicendo | 107.5836 | −6.9015 |
| 17 | Cidadap | 107.6076 | −6.8632 |
| 18 | Cinambo | 107.6917 | −6.9279 |
| 19 | Coblong | 107.6155 | −6.8849 |
| 20 | Gedebage | 107.6975 | −6.9536 |
| 21 | Kiaracondong | 107.6501 | −6.9250 |
| 22 | Lengkong | 107.6249 | −6.9339 |
| 23 | Mandalajati | 107.6722 | −6.8976 |
| 24 | Panyileukan | 107.7067 | −6.9324 |
| 25 | Rancasari | 107.6739 | −6.9545 |
| 26 | Regol | 107.6125 | −6.9398 |
| 27 | Sukajadi | 107.5902 | −6.8882 |
| 28 | Sukasari | 107.5871 | −6.8665 |
| 29 | Sumur Bandung | 107.6153 | −6.9149 |
| 30 | Ujung Berung | 107.7056 | −6.9055 |
References
- Jaya, I.G.N.M.; Folmer, H. Bayesian spatiotemporal forecasting and mapping of COVID-19 risk with application to West Java Province, Indonesia. J. Reg. Sci. 2021, 61, 849–881. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Dengue and Severe Dengue. Available online: https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 16 May 2025).
- Kularatne, S.A.; Dalugama, C. Dengue infection: Global importance, immunopathology and management. Clin. Med. 2022, 22, 9–13. [Google Scholar] [CrossRef]
- Soneja, S.; Tsarouchi, G.; Lumbroso, D.; Tung, D.K. A Review of Dengue’s Historical and Future Health Risk from a Changing Climate. Curr. Environ. Health Rep. 2021, 8, 245–265. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Health Republic of Indonesia (Kemenkes RI). Waspada Penyakit di Musim Hujan. Available online: https://kemkes.go.id/id/waspada-penyakit-di-musim-hujan (accessed on 16 May 2025).
- Shepard, D.S.; Undurraga, E.A.; Halasa, Y.A.; Stanaway, J.D. The global economic burden of dengue: A systematic analysis. Lancet Infect. Dis. 2016, 16, 935–941. [Google Scholar] [CrossRef] [PubMed]
- Bandung City Health Office. Bandung Health Profile 2010–2024; Bandung City Health Office: Bandung, Indonesia, 2024. [Google Scholar]
- Morin, C.W.; Comrie, A.C.; Ernst, K. Climate and Dengue Transmission: Evidence and Implications. Environ. Health Perspect. 2013, 121, 1264–1272. [Google Scholar] [CrossRef]
- Alahmari, A.A.; Almuzaini, Y.; Alamri, F.; Alenzi, R.; Khan, A.A. Strengthening global health security through health early warning systems: A literature review and case study. J. Infect. Public Health 2024, 17, 85–95. [Google Scholar] [CrossRef]
- Degallier, N.; Favier, C.; Menkes, C.; Lengaigne, M.; Ramalho, W.M.; Souza, R.; Servain, J.; Boulanger, J.-P. Toward an early warning system for dengue prevention: Modeling climate impact on dengue transmission. Clim. Change 2010, 98, 581–592. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H. Spatiotemporal forecasting models with and without a confounded covariate. J. Geogr. Syst. 2025, 27, 113–146. [Google Scholar] [CrossRef]
- Osei, F.B.; Stein, A.; Ofosu, A. Poisson-Gamma Mixture Spatially Varying Coefficient Modeling of Small-Area Intestinal Parasites Infection. Int. J. Environ. Res. Public Health 2019, 16, 339. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H. Bayesian spatiotemporal mapping of relative dengue disease risk in Bandung, Indonesia. J. Geogr. Syst. 2020, 22, 104–152. [Google Scholar] [CrossRef]
- Hasan, P.; Khan, T.D.; Alam, I.; Haque, M.E. Dengue in Tomorrow: Predictive Insights from ARIMA and SARIMA Models in Bangladesh: A Time Series Analysis. Health Sci. Rep. 2024, 7, e70276. [Google Scholar] [CrossRef]
- Tian, N.; Zheng, J.-X.; Li, L.-H.; Xue, J.-B.; Xia, S.; Lv, S.; Zhou, X.-N. Precision Prediction for Dengue Fever in Singapore: A Machine Learning Approach Incorporating Meteorological Data. Trop. Med. Infect. Dis. 2024, 9, 72. [Google Scholar] [CrossRef]
- Majeed, M.A.; Shafri, H.Z.M.; Zulkafli, Z.; Wayayok, A. A Deep Learning Approach for Dengue Fever Prediction in Malaysia Using LSTM with Spatial Attention. Int. J. Environ. Res. Public Health 2023, 20, 4130. [Google Scholar] [CrossRef] [PubMed]
- Chou-Chen, S.W.; Barboza, L.A.; Vásquez, P.; García, Y.E.; Calvo, J.G.; Hidalgo, H.G. Bayesian spatio-temporal model with INLA for dengue fever risk prediction in Costa Rica. Environ. Ecol. Stat. 2023, 30, 687–713. [Google Scholar] [CrossRef]
- Methiyothin, T.; Ahn, I. Forecasting Dengue Fever in France and Thailand using XGBoost. In Proceedings of the APSIPA ASC 2022, Chiang Mai, Thailand, 7–10 November 2022. [Google Scholar]
- Frifra, A.; Maanan, M.; Maanan, M.; Rhinane, H. Harnessing LSTM and XGBoost Algorithms for Storm Prediction. Sci. Rep. 2024, 14, 11381. [Google Scholar] [CrossRef]
- Cruz-Victoria, J.C.; Netzahuatl-Muñoz, A.R.; Cristiani-Urbina, E. Long Short-Term Memory and Bidirectional Long Short-Term Memory Modeling and Prediction of Hexavalent and Total Chromium Removal Capacity Kinetics of Cupressus lusitanica Bark. Int. J. Environ. Res. Public Health 2024, 16, 2874. [Google Scholar] [CrossRef]
- Chen, X.; Moraga, P. Forecasting dengue across Brazil with LSTM neural networks and SHAP-driven lagged climate and spatial effects. BMC Public Health 2025, 25, 973. [Google Scholar] [CrossRef]
- Bounoua, I.; Saidi, Y.; Yaagoubi, R.; Bouziani, M. Deep Learning Approaches for Water Stress Forecasting in Arboriculture Using Time Series of Remote Sensing Images: Comparative Study between ConvLSTM and CNN-LSTM Models. Technologies 2024, 12, 77. [Google Scholar] [CrossRef]
- Sebastianelli, A.; Spiller, D.; Carmo, R.; Wheeler, J.; Nowakowski, A.; Jacobson, L.V.; Kim, D.; Barlevi, H.; Cordero, Z.E.R.; Colón-González, F.J.; et al. A reproducible ensemble machine learning approach to forecast dengue outbreaks. Sci. Rep. 2024, 14, 3807. [Google Scholar] [CrossRef]
- Song, C.; Yang, X.; Shi, X.; Bo, Y.; Wang, J. Estimating missing values in China’s official socioeconomic statistics using progressive spatiotemporal Bayesian hierarchical modeling. Sci. Rep. 2018, 8, 10055. [Google Scholar] [CrossRef]
- Salim, M.F.; Satoto, T.B.T.; Danardono. Predicting Spatiotemporal Dynamics of Dengue Using INLA in Yogyakarta, Indonesia. BMC Public Health 2025, 25, 1321. [Google Scholar] [CrossRef] [PubMed]
- Westergaard, G.; Erden, U.; Mateo, O.A.; Lampo, S.M.; Akinci, T.C.; Topsakal, O. Time Series Forecasting Utilizing Automated Machine Learning (AutoML): A Comparative Analysis Study on Diverse Datasets. Information 2024, 15, 39. [Google Scholar] [CrossRef]
- Baharom, M.; Ahmad, N.; Hod, R.; Manaf, M.R.A. Dengue Early Warning System as Outbreak Prediction Tool: A Systematic Review. Risk Manag. Healthc. Policy 2022, 15, 871–886. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Vargas, W.; Ríos-Tapias, P.A.; Marin-Velásquez, K.; Giraldo-Gallo, E.; Segura-Cardona, A.; Arboleda, M. Density of Aedes aegypti and Dengue Risk in Northwestern Antioquia, Colombia. PLoS ONE 2024, 19, e0295317. [Google Scholar] [CrossRef]
- Lim, J.T.; Dickens, B.S.; Haoyang, S.; Ching, N.L.; Cook, A.R. Inference on Dengue Epidemics with Bayesian Regime Switching Models. PLoS Comput. Biol. 2020, 16, e1007839. [Google Scholar] [CrossRef]
- Sylvestre, E.; Joachim, C.; Cecilia-Joseph, E.; Bouzillé, G.; Campillo-Gimenez, B.; Cuggia, M.; Cabié, A.; Santos, V.S. Data-Driven Methods for Dengue Prediction Using Real-World and Big Data: A Systematic Review. PLoS Negl. Trop. Dis. 2022, 16, e0010056. [Google Scholar] [CrossRef]
- Aswi, A.; Cramb, S.; Moraga, P.; Mengersen, K. Bayesian Spatial and Spatio-Temporal Approaches to Modelling Dengue Fever: A Systematic Review. Epidemiol. Infect. 2018, 147, e33. [Google Scholar] [CrossRef]
- Blangiardo, M.; Cameletti, M. Spatial and Spatio-Temporal Bayesian Models with R-INLA; Wiley: Chennai, India, 2015. [Google Scholar]
- Alam, N.M.; Mitra, S.; Pandey, S.K.; Jana, C.; Ray, M.; Ghosh, S.; Mazumdar, S.P.; Shankar, S.V.; Saha, R.; Kar, G. Enhanced Spatio-Temporal Modeling for Rainfall Forecasting: A High-Resolution Grid Analysis. Water 2024, 16, 1891. [Google Scholar] [CrossRef]
- Ravenda, F.; Cesarini, M.; Peluso, S.; Mira, A. A Probabilistic Spatio-Temporal Neural Network to Forecast COVID-19 Counts. Int. J. Data Sci. Anal. 2024, 1, 1–8. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks for Traffic Forecasting. In Proceedings of the IJCAI 2018, Stockholm, Sweden, 13–19 July 2018. [Google Scholar]
- Adin, A.; Goicoa, T.; Hodges, J.S.; Schnell, P.M.; Ugarte, M.D. Alleviating Confounding in Spatio-Temporal Areal Models with Application to Crimes Against Women in India. Stat. Model. 2023, 23, 9–30. [Google Scholar] [CrossRef]
- Gu, W.; Guo, B.; Zhang, Z.; Lu, H. Civil Aviation Passenger Traffic Forecasting: SARIMA vs. Neural Network. Sustainability 2024, 16, 4110. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Almuflih, A.S. Extreme Gradient Boosting-Based Approach for Green Building Cost Prediction. Sustainability 2022, 14, 6651. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Mienye, I.D.; Swart, T.G.; Obaido, G. Recurrent Neural Networks: A Review of Architectures and Applications. Information 2024, 15, 517. [Google Scholar] [CrossRef]
- Aseeri, A.O. RNN-Based Forecasting Methodology for Short-Term Power Load Forecasts. J. Comput. Sci. 2023, 68, 101984. [Google Scholar] [CrossRef]
- Guo, D.; Duan, P.; Yang, Z.; Zhang, X.; Su, Y. CNN-BiLSTM Attention-Based Prediction of Silica Powder Warehouse Movement. Energies 2024, 17, 3757. [Google Scholar] [CrossRef]
- Bekkar, A.; Hssina, B.; Douzi, S.; Douzi, K. Air-Pollution Prediction in Smart Cities: Deep Learning Approach. J. Big Data 2021, 8, 161. [Google Scholar] [CrossRef]
- Syed, M.A.B.; Ahmed, I. A CNN-LSTM Architecture for Vessel Track Association Using AIS Data. Sensors 2023, 23, 6400. [Google Scholar] [CrossRef]
- Gelman, A.; Jakulin, A.; Pittau, M.G.; Su, Y.S. A Weakly Informative Default Prior for Logistic and Other Regression Models. Ann. Appl. Stat. 2008, 2, 1360–1383. [Google Scholar] [CrossRef]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]

| Approach | Description | Pros | Cons |
|---|---|---|---|
| SARIMA [14] | Seasonal ARIMA; traditional time series model for univariate data with seasonal patterns |
|
|
| Machine Learning (XGBoost) [18] | Ensemble ML method combining decision trees for strong nonlinear prediction |
|
|
| Deep Learning (RNN, LSTM, BiLSTM) [21] | Recurrent Neural Networks for time series with sequential dependency |
|
|
| CNN–LSTM [23] | Combines CNN for spatial features and LSTM for temporal sequence |
|
|
| Bayesian Spatiotemporal Model [17,25] | Statistical model with explicit spatial and temporal structure and uncertainty quantification |
|
|
| Model | Architecture/Structure | Training Epochs | Batch Size | Optimizer/Learning Rate | Regularization Method | Description/Notes |
|---|---|---|---|---|---|---|
| SARIMA | Not applicable | N/A | N/A | N/A | N/A | Classical time series ARIMA model with seasonal differencing |
| XGBoost | Gradient Boosted Decision Trees | 300 | N/A | eta = 0.05 | max_depth = 6, subsample = 0.8, colsample = 0.8 | Includes calendar features (sin/cos month), district, and month as categorical input |
| RNN | Simple RNN (64, return_seq) → Dropout (0.2) → RNN (32) → Dropout (0.2) → Dense (1) | 200 | 16 | Adam (lr = 0.001) | Dropout (0.2) | Sequence-to-one model using 12-month time windows |
| LSTM | LSTM (64) → Dropout (0.3) → Dense (1) | 100 | 16 | Adam (lr = 0.001) | Dropout (0.3) | Temporal modeling with LSTM; 12-month lag window |
| BiLSTM | BiLSTM (128, return_seq) → Dropout (0.3) → BiLSTM (64) → Dropout (0.3) → Dense (1) | 200 | 16 | Adam (lr = 0.001) | Dropout (0.3) | Bidirectional LSTM for learning past and future context |
| CNN–LSTM | ConvLSTM2D (64) → BatchNorm → Dropout (0.2) → Dense (256, relu) → Dropout (0.2) → Dense (1) | 200 | 1 | Adam (lr = 0.001) | Dropout (0.2) | Incorporates raw and spatial lag inputs; reshaped to 2D for convolution |
| Bayesian–INLA | Bayesian hierarchical model (latent Gaussian) | N/A | N/A | INLA approximation (Bayesian) | Half-Cauchy prior on precision | Spatiotemporal random effects: IID, AR (2), seasonal, spatial (Leroux CAR) |
| Month | Min | Max | Mean | Median | Boxplot |
|---|---|---|---|---|---|
| January | 0 | 72 | 11 | 9 |  |
| February | 0 | 54 | 10 | 6 |  |
| March | 0 | 75 | 13 | 9 |  |
| April | 0 | 51 | 10 | 8 |  |
| May | 0 | 34 | 8 | 7 |  |
| June | 0 | 48 | 9 | 6 |  |
| July | 0 | 69 | 11 | 8 |  |
| August | 0 | 52 | 9 | 6 |  |
| September | 0 | 67 | 13 | 9 |  |
| October | 0 | 55 | 10 | 8 |  |
| November | 0 | 27 | 7 | 6 |  |
| December | 0 | 67 | 10 | 7 | 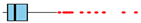 |
| Model | MAE | sMAPE | RMSE | Correlation (R) | ||||
|---|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | Training | Testing | |
| SARIMA | 4.435 | 5.830 | 48.722 | 64.290 | 6.607 | 8.702 | 0.765 | 0.588 |
| XGBoost | 2.635 | 9.330 | 30.938 | 81.592 | 4.085 | 12.865 | 0.926 | −0.011 |
| RNN | 5.878 | 7.110 | 63.300 | 74.136 | 8.816 | 11.311 | 0.411 | −0.054 |
| LSTM | 5.887 | 6.878 | 62.847 | 72.452 | 8.774 | 10.737 | 0.399 | 0.125 |
| BiLSTM | 5.830 | 6.749 | 62.684 | 71.784 | 8.676 | 10.906 | 0.424 | −0.001 |
| CNN–LSTM | 5.433 | 6.805 | 55.016 | 71.098 | 8.641 | 10.438 | 0.577 | 0.260 |
| Bayesian Spatiotemporal | 3.289 | 5.543 | 39.034 | 62.137 | 4.723 | 7.482 | 0.890 | 0.723 |
| Parameter | Mean | SD | q (0.025) | q (0.975) |
|---|---|---|---|---|
| Intercept coefficient | 0.098 | 0.133 | –0.163 | 0.360 |
| Annual time trend coefficient | –0.040 | 0.015 | –0.071 | –0.01 |
| Hyperparameter | Mean | SD | q (0.025) | q (0.975) | Total Variance (%) |
|---|---|---|---|---|---|
| Overdispersion | 12.7432 | 0.8125 | 11.2359 | 14.4199 | |
| 0.7753 | 0.0422 | 0.6835 | 0.8482 | ||
| −0.1836 | 0.0885 | −0.3541 | −0.0080 | ||
| −0.0142 | 0.1026 | −0.2188 | 0.1820 | ||
| −0.0440 | 0.0921 | −0.2420 | 0.1141 | ||
| 0.9786 | 0.0115 | 0.9500 | 0.9937 | ||
| 0.9441 | 0.0096 | 0.9230 | 0.9605 | ||
| −0.3342 | 0.0784 | −0.4800 | −0.1735 | ||
| 0.2914 | 0.0369 | 0.2265 | 0.3711 | 23.962 | |
| 0.0074 | 0.0022 | 0.0040 | 0.0127 | 0.821 | |
| 0.3832 | 0.0340 | 0.3215 | 0.4547 | 29.359 | |
| 0.2532 | 0.0571 | 0.1610 | 0.3841 | 24.803 | |
| 0.0087 | 0.0038 | 0.0037 | 0.0183 | 1.182 | |
| 0.0061 | 0.0017 | 0.0035 | 0.0102 | 0.662 | |
| 0.2698 | 0.0134 | 0.2450 | 0.2975 | 19.211 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaya, I.G.N.M.; Andriyana, Y.; Tantular, B.; Pangastuti, S.S.; Kristiani, F. Spatiotemporal Dengue Forecasting for Sustainable Public Health in Bandung, Indonesia: A Comparative Study of Classical, Machine Learning, and Bayesian Models. Sustainability 2025, 17, 6777. https://doi.org/10.3390/su17156777
Jaya IGNM, Andriyana Y, Tantular B, Pangastuti SS, Kristiani F. Spatiotemporal Dengue Forecasting for Sustainable Public Health in Bandung, Indonesia: A Comparative Study of Classical, Machine Learning, and Bayesian Models. Sustainability. 2025; 17(15):6777. https://doi.org/10.3390/su17156777
Chicago/Turabian StyleJaya, I Gede Nyoman Mindra, Yudhie Andriyana, Bertho Tantular, Sinta Septi Pangastuti, and Farah Kristiani. 2025. "Spatiotemporal Dengue Forecasting for Sustainable Public Health in Bandung, Indonesia: A Comparative Study of Classical, Machine Learning, and Bayesian Models" Sustainability 17, no. 15: 6777. https://doi.org/10.3390/su17156777
APA StyleJaya, I. G. N. M., Andriyana, Y., Tantular, B., Pangastuti, S. S., & Kristiani, F. (2025). Spatiotemporal Dengue Forecasting for Sustainable Public Health in Bandung, Indonesia: A Comparative Study of Classical, Machine Learning, and Bayesian Models. Sustainability, 17(15), 6777. https://doi.org/10.3390/su17156777







