Converter-Based Power Line Emulators for Testing Grid-Forming Converters Under Various Grid Strength Conditions
Abstract
1. Introduction
2. Modeling of the Converter-Based Power Line Emulator
2.1. Bergeron Transmission Line Model in Converter-Based Power Line Emulation
2.1.1. Fundamental Theory of the Bergeron Model
- L is the transmission line inductance per unit length (H/m);
- C is the transmission line capacitance per unit length (F/m);
- R is the series resistance per unit length (/m);
- G is the shunt conductance per unit length (S/m);
- and are the distributed voltage and current, respectively.
2.1.2. Norton Equivalent Representation in the Bergeron Model
2.2. A Framework and Algorithm of the Power Converter-Based Line Emulation Model
2.2.1. Thévenin Equivalent Model and Inductance Determination in Grid Emulation
| Algorithm 1: Single-Phase Current Injection Algorithm Based on Ideal Bergeron Model. |
 |
2.2.2. Practical Implementation of Converter-Based Power Line Emulation
- = Traveling time delay [s];
- N= Buffer size (number of stored data points);
- = Sampling time per step [s].
2.2.3. Determination of Characteristic Impedance Based on Short-Circuit Ratio
2.2.4. Thévenin Equivalent Representation in Grid Emulation
- is the short-circuit capacity at the PCC [VA];
- is the rated power of the converter [VA].
2.2.5. Determination of Characteristic Impedance with Fixed Propagation Delay
2.3. Power Converter-Based Line Emulation Model Validation with Simple Test Case
2.3.1. Ideal Model
2.3.2. Non-Ideal Model
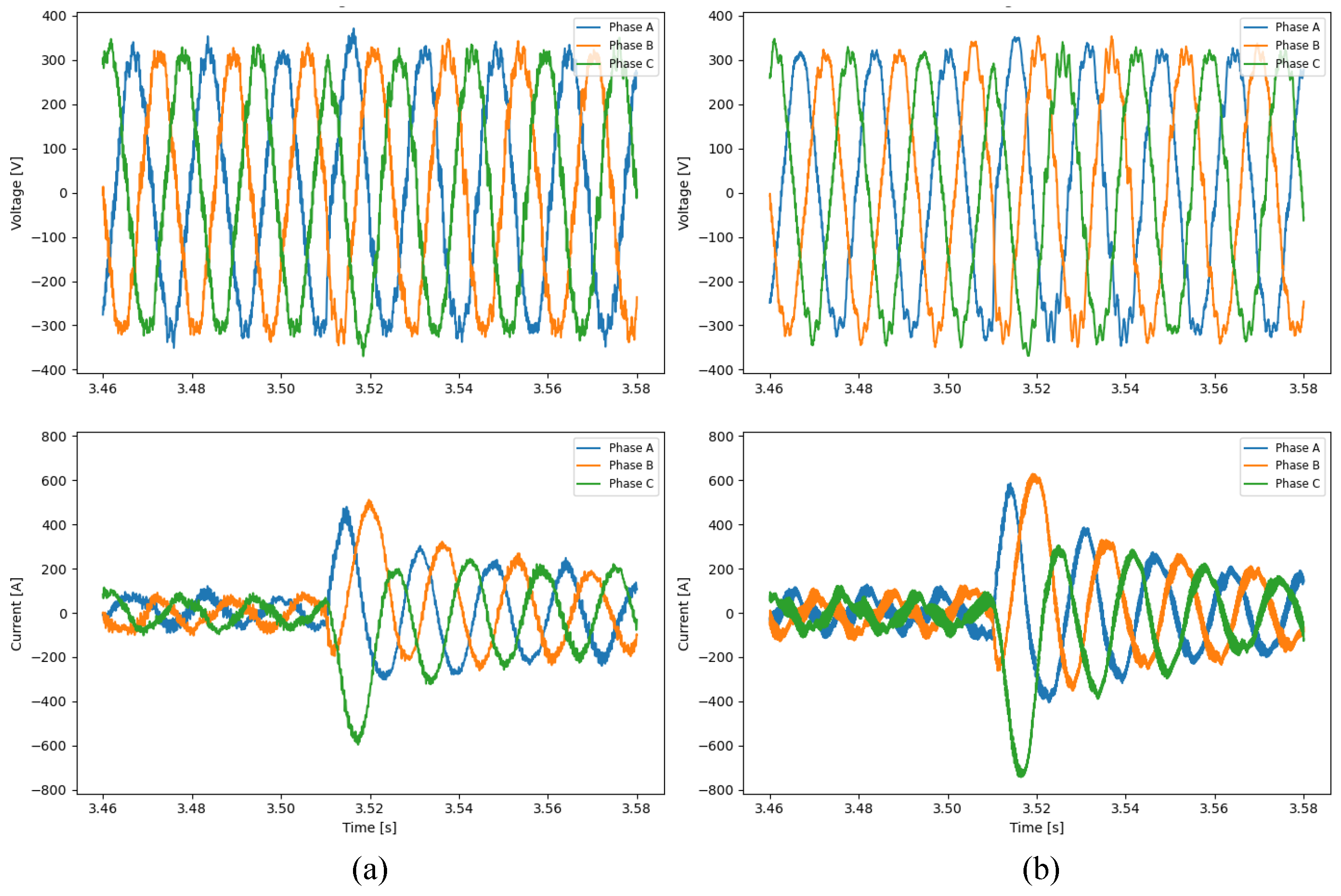
3. Grid-Forming Converter Test with Proposed Power Converter-Based Line Emulation Model: Phase Jump Test
3.1. Simulation Conditions
3.2. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matevosyan, J.; Badrzadeh, B.; Prevost, T.; Quitmann, E.; Ramasubramanian, D.; Urdal, H.; Achilles, S.; MacDowell, J.; Huang, S.H.; Vital, V.; et al. Grid-Forming Inverters: Are They the Key for High Renewable Penetration? IEEE Power Energy Mag. 2019, 17, 89–98. [Google Scholar] [CrossRef]
- Al-Shetwi, A.Q.; Hannan, M.; Jern, K.P.; Mansur, M.; Mahlia, T. Grid-connected renewable energy sources: Review of the recent integration requirements and control methods. J. Clean. Prod. 2020, 253, 119831. [Google Scholar] [CrossRef]
- California Independent System Operator. What the Duck Curve Tells Us About Managing a Green Grid; California Independent System Operator: Folsom, CA, USA, 2016. [Google Scholar][Green Version]
- ISO New England. Solar Power in New England: Concentration and Impact; ISO New England: Holyoke, MA, USA, 2017. [Google Scholar][Green Version]
- Wilkinson, S.; Maticka, M.J.; Liu, Y.; John, M. The duck curve in a drying pond: The impact of rooftop PV on the Western Australian electricity market transition. Util. Policy 2021, 71, 101232. [Google Scholar] [CrossRef]
- Hou, Q.; Zhang, N.; Du, E.; Miao, M.; Peng, F.; Kang, C. Probabilistic duck curve in high PV penetration power system: Concept, modeling, and empirical analysis in China. Appl. Energy 2019, 242, 205–215. [Google Scholar] [CrossRef]
- Lew, D.; Asano, M.; Boemer, J.; Ching, C.; Focken, U.; Hydzik, R.; Lange, M.; Motley, A. The power of small: The effects of distributed energy resources on system reliability. IEEE Power Energy Mag. 2017, 15, 50–60. [Google Scholar] [CrossRef]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef]
- Notton, G.; Nivet, M.-L.; Voyant, C.; Paoli, C.; Darras, C.; Motte, F.; Fouilloy, A. Intermittent and stochastic character of renewable energy sources: Consequences, cost of intermittence and benefit of forecasting. Renew. Sustain. Energy Rev. 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.M.; Hannegan, B. Achieving a 100% Renewable Grid: Operating Electric Power Systems with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Australian Energy Market Operator (AEMO). Technical Integration of Distributed Energy Resources; Technical Report; AEMO: Melbourne, Australia, 2019. [Google Scholar][Green Version]
- Kim, J.K.; Lee, S.; Kim, J.S.; Choi, H. The Need for Modeling the Impact of Behind-the-Meter Generation Trip on Primary Frequency Response Through Operational Experiences in Korea Power System. IEEE Trans. Power Syst. 2022, 37, 1661–1664. [Google Scholar] [CrossRef]
- Kim, S.; Lee, H.; Kim, H.; Jang, D.H.; Kim, H.J.; Hur, J.; Cho, Y.S.; Hur, K. Improvement in policy and proactive interconnection procedure for renewable energy expansion in South Korea. Renew. Sustain. Energy Rev. 2018, 98, 150–162. [Google Scholar] [CrossRef]
- Kim, J.K.; Kang, J.; Shim, J.W.; Kim, H.; Shin, J.; Kang, C.; Hur, K. Dynamic performance modeling and analysis of power grids with high levels of stochastic and power electronic interfaced resources. Proc. IEEE 2023, 111, 854–872. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.; Chung, Y.H.; Yoo, D.W.; Kim, C.K.; Hur, K. Operating region of modular multilevel converter for HVDC with controlled second-order harmonic circulating current: Elaborating PQ capability. IEEE Trans. Power Deliv. 2015, 31, 493–502. [Google Scholar] [CrossRef]
- Kim, H.; Kang, J.; Shim, J.W.; Beerten, J.; Van Hertem, D.; Jung, H.J.; Kim, C.K.; Hur, K. Exploiting redundant energy of MMC–HVDC to enhance frequency response of low inertia AC grid. IEEE Access 2019, 7, 138485–138494. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.K.; Song, J.; Lee, J.; Han, K.; Shin, J.; Kim, T.; Hur, K. Smart and green substation: Shaping the electric power grid of Korea. IEEE Power Energy Mag. 2019, 17, 24–34. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbič, G.; Kim, H.; Hur, K. On droop control of energy-constrained battery energy storage systems for grid frequency regulation. IEEE Access 2019, 7, 166353–166364. [Google Scholar] [CrossRef]
- Xu, B.; Gao, C.; Zhang, J.; Yang, J.; Xia, B.; He, Z. A Novel DC Chopper Topology for VSC-Based Offshore Wind Farm Connection. IEEE Trans. Power Electron. 2021, 36, 3017–3027. [Google Scholar] [CrossRef]
- Erlich, I.; Shewarega, F.; Engelhardt, S.; Kretschmann, J.; Fortmann, J.; Koch, F. Effect of wind turbine output current during faults on grid voltage and the transient stability of wind parks. In Proceedings of the 2009 IEEE Power and Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Christensen, P.; Andersen, G.K.; Seidel, M.; Bolik, S.; Engelken, S.; Knueppel, T.; Krontiris, A.; Wuerflinger, K.; Bülo, T.; Jahn, J.; et al. High Penetration of Power Electronic Interfaced Power Sources and the Potential Contribution of Grid Forming Converters; University of Strathclyde: Glasgow, UK, 2020. [Google Scholar]
- Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-Forming Inverters: A Critical Asset for the Power Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
- Denis, G.; Prevost, T.; Debry, M.; Xavier, F.; Guillaud, X.; Menze, A. The Migrate project: The challenges of operating a transmission grid with only inverter-based generation. A grid-forming control improvement with transient current-limiting control. IET Renew. Power Gener. 2018, 12, 523–529. [Google Scholar] [CrossRef]
- IEEE 2800-2022; IEEE Standard for Interconnection and Interoperability of Inverter-Based Resources (IBRs) Interconnecting with Associated Transmission Electric Power Systems. IEEE: Piscataway, NJ, USA, 2022.
- 50Hertz; Ampiron; TenneT; TransnetBW. 4-TSO Paper on Requirements for Grid-Forming Converters. 2022. Available online: https://www.netztransparenz.de/xspproxy/api/staticfiles/ntp-relaunch/dokumente/zuordnung_unklar/grundlegende-anforderungen-an-netzbildende-umrichter/220504_-_4-tso_paper_on_requirements_for_grid-forming_converters.pdf (accessed on 30 May 2024).
- FinGrid. Grid Code Specifications for Grid Energy Storage Systems SJV2019; FinGrid: Helsinki, Finland, 2020. [Google Scholar]
- IEC 61400-21-2:2023; Wind Energy Generation Systems—Part 21-4: Wind Turbine Components and Subsystems. International Electrotechnical Commission: Geneva, Switzerland, 2023.
- ENTSO-E; Wind Europe; Solar Power Europe; T&D Europe. High Penetration of Power Electronic Interfaced Power Sources (HPoPEIPS). 2017. Available online: https://consultations.entsoe.eu/system-development/entso-e-connection-codes-implementation-guidance-d-3/user_uploads/igd-high-penetration-of-power-electronic-interfaced-power-sources.pdf (accessed on 30 May 2024).
- Australian Energy Market Operator. Voluntary Specification for Grid-Forming Inverters. 2023. Available online: https://aemo.com.au/-/media/files/initiatives/primary-frequency-response/2023/gfm-voluntary-spec.pdf (accessed on 30 May 2024).
- Australian Energy Market Operator. Voluntary Specification for Grid-Forming Inverters: Core Requirements Test Framework. 2024. Available online: https://aemo.com.au/-/media/files/initiatives/engineering-framework/2023/grid-forming-inverters-jan-2024.pdf?la=en&hash=7778A2249D8C29A95A2FADCD9AAA509D (accessed on 15 October 2024).
- National Grid ESO. Stability Pathfinder Oct 2019, Draft Grid CODE Grid Forming and Request for Information Feedback. 2019. Available online: https://www.neso.energy/document/185306/download (accessed on 30 May 2024).
- GC0137; Minimum Specification Required for Provision of GB Grid Forming (GBGF) Capability (Formerly Virtual Synchronous Machine/VSM Capability). National Grid ESO: Wokingham, UK, 2021.
- National Grid ESO. Great Britain Grid Forming Best Practice Guide. 2023. Available online: https://www.studocu.com/pt-br/document/escola-universitaria-universidade-federal-do-rio-de-janeiro/ciencias/great-britain-grid-forming-best-practices-guide-april-2023/92650440 (accessed on 30 May 2024).
- National Grid ESO. System Oscillation Assessment of Inverter Based Resources (IBRs). 2024. Available online: https://www.neso.energy/document/301686/download (accessed on 30 May 2024).
- Aljarrah, R.; Fawaz, B.B.; Salem, Q.; Karimi, M.; Marzooghi, H.; Azizipanah-Abarghooee, R. Issues and Challenges of Grid-Following Converters Interfacing Renewable Energy Sources in Low Inertia Systems: A Review. IEEE Access 2024, 12, 5534–5561. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Pryor, S.C. Climate Change Mitigation Potential of Wind Energy. Climate 2021, 9, 136. [Google Scholar] [CrossRef]
- Curran, O.; Guerreiro, G.M.G.; Azarian, S.; Martin, F.; Dreyer, T. WTG Manufacturer’s Experience with Subsystem and Component Validation for Wind Turbines. In Proceedings of the 21st Wind & Solar Integration Conference, The Hague, The Netherlands, 12–14 October 2022; pp. 458–465. [Google Scholar]
- Expert Group: Advanced Capabilities for Grids with a High Share of Power Park Modules. 2023. Available online: https://eepublicdownloads.blob.core.windows.net/public-cdn-container/clean-documents/Network%20codes%20documents/GC%20ESC/GC%20ESC%20MEETING%20DOCS/2023/ACCPM_Report_Draft_0.9_.pdf (accessed on 30 May 2024).
- Energinet. Classification: Public Technical Regulation 3.2.5 for Wind Power Plants Above 11 kW. 2016. Available online: https://en.energinet.dk/media/5pbflmly/technical-regulation-325-for-wind-power-plants-above-11-kw-revision-4.pdf (accessed on 30 May 2024).
- Electric Power Research Institute. Grid Forming Inverters: EPRI Tutorial. 2023. Available online: https://www.epri.com/research/products/000000003002028090 (accessed on 30 May 2024).
- Energy Systems Integration Group. Grid-Forming Technology in Energy Systems Integration, High Share of Inverter-Based Generation Task Force. 2022. Available online: https://www.esig.energy/wp-content/uploads/2022/03/ESIG-GFM-report-2022.pdf (accessed on 30 May 2024).
- FinGrid. Specific Study Requirements for Grid Energy Storage Systems; FinGrid: Helsinki, Finland, 2023. [Google Scholar]
- Gevorgian, V.; Koralewicz, P.; Shah, S.; Yan, W.; Wallen, R.; Mendiola, E. Testing GFM and GFL Inverters Operating with Synchronous Condensers. In Proceedings of the 2023 IEEE Power and Energy Society General Meeting, Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Ghime, S.; Amico, G.; Kkuni, K.V.; Guerreiro, G.M.G.; Jensen, K.H.; Yang, G. Enabling Islanding and Re-Synchronization of Grid-Forming Offshore Wind Turbine Generators. In Proceedings of the 22nd Wind and Solar Integration Workshop, Helsinki, Finland, 8–11 October 2024. [Google Scholar]
- Gomes Guerreiro, G.M.; Sharma, R.; Martin, F.; Ghimire, P.; Yang, G. Concerning Short-Circuit Current Contribution Challenges of Large-Scale Full-Converter Based Wind Power Plants. IEEE Access 2023, 11, 64141–64159. [Google Scholar] [CrossRef]
- Gomes Guerreiro, G.M.; Martin, F.; Dreyer, T.; Yang, G.; Andresen, B. Advancements on Grid Compliance in Wind Power: Component & Subsystem Testing, Software-/Hardware-in-the-Loop, and Digital Twins. IEEE Access 2024, 12, 25949–25966. [Google Scholar] [CrossRef]
- Hans, F.; Curioni, G.; Jersch, T.; Quistorf, G.; Ruben, M.; Müller, A.; Wessels, C.; Fenselau, C.; Prima, I.; Lehmann, J. Towards Full Electrical Certification of Wind Turbines on Test Benches—Experiences Gained from the HiL-GridCoP Project. In Proceedings of the 21st Wind & Solar Integration Workshop, The Hague, The Netherlands, 12–14 October 2022; pp. 122–129. [Google Scholar] [CrossRef]
- Hans, F.; Quistorf, G.; Jersch, T.; Chekavskyy, G.; Bujak, G.; Sobanski, P.; Eckerle, J. Mobil-Grid-CoP—A New Approach for Grid Compliance Testing on Multimegawatt Wind Turbines in Field. In Proceedings of the 22nd Wind & Solar Integration Workshop, Copenhagen, Denmark, 26–28 September 2023. [Google Scholar]
- InterOPERA Consortium. Grid-Forming Functional Requirements for HVDC Converter Stations and DC-Connected PPMs in Multi-Terminal Multi-Vendor HVDC Systems. 2024. Available online: https://interopera.eu/wp-content/uploads/files/deliverables/InterOPERA-D2.2-GFM-functional-requirements-202401.pdf (accessed on 30 May 2024).
- Johansen, K. Grid Codes: Recommendations for Connection of Offshore Wind Power Energinet; Energinet Associated Activities: Fredericia, Denmark, 2020. [Google Scholar]
- Li, Z.; Wang, X.; Zhao, F.; Munk-Nielsen, S.; Geske, M.; Grune, R.; Andersen, D.B.R.; Rodriguez, M.G. Power-Hardware Design and Topologies of Converter-Based Grid Emulators for Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 5001–5017. [Google Scholar] [CrossRef]
- Lyu, X.; Groß, D. Grid Forming Fast Frequency Response for PMSG-Based Wind Turbines. IEEE Trans. Sustain. Energy 2024, 15, 23–38. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and Challenges of Low-Inertia Systems (Invited Paper). In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar] [CrossRef]
- Musca, R.; Vasile, A.; Zizzo, G. Grid-forming converters. A critical review of pilot projects and demonstrators. Renew. Sustain. Energy Rev. 2022, 165, 112551. [Google Scholar] [CrossRef]
- National Grid. Onshore vs. Offshore Wind Energy. 2023. Available online: https://www.nationalgrid.com/stories/energy-explained/onshore-vs-offshore-wind-energy (accessed on 30 May 2024).
- North American Electric Reliability Corporation. Grid Forming Technology: Bulk Power System Reliability Considerations. 2021. Available online: https://www.nerc.com/comm/RSTC_Reliability_Guidelines/White_Paper_Grid_Forming_Technology.pdf (accessed on 30 May 2024).
- North American Electric Reliability Corporation. White Paper: Grid Forming Functional Specifications for BPS-Connected Battery Energy Storage Systems. 2023. Available online: https://www.nerc.com/comm/RSTC_Reliability_Guidelines/White_Paper_GFM_Functional_Specification.pdf (accessed on 30 May 2024).
- Neshati, M.; Azarian, S.; Curran, O.; Pillai, R.; Due, J.; Guest, E.; Freire, N.; Dreyer, T.; Martin, F. Grid Connection Testing of Wind Energy Converters with Medium Voltage Generator- and Grid Emulation on a Multi-Megawatt Power-Hardware-in-the-Loop Test Rig. In Proceedings of the 22nd Wind & Solar Integration Workshop, Copenhagen, Denmark, 26–28 September 2023. [Google Scholar] [CrossRef]
- OSMOSE. D3.3 Analysis of the Synchronisation Capabilities of BESS Power Converters. 2021. Available online: https://www.osmose-h2020.eu/wp-content/uploads/2022/04/D3.3-Analysis-of-the-synchronisation-capabilities-of-BESS-power-converters.pdf (accessed on 30 May 2024).
- Pattabiraman, D.; Lasseter, R.H.; Jahns, T.M. Comparison of Grid Following and Grid Forming Control for a High Inverter Penetration Power System. In Proceedings of the 2018 IEEE Power and Energy Society General Meeting, Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Rokrok, E.; Qoria, T.; Bruyere, A.; Francois, B.; Guillaud, X. Integration of a storage device to the DC bus of a grid-forming controlled HVDC interconnection. Electr. Power Syst. Res. 2022, 212, 108601. [Google Scholar] [CrossRef]
- TenneT. Grid Connection Requirements for DC Connected PPMs, System Needs and Functions, Annex C.2.300. 2023. Available online: https://www.tennet.eu/de/strommarkt/kunden-deutschland/netzkunden/netzanschlussregeln (accessed on 30 May 2024).
- UNIFI Consortium. UNIFI Specifications for Grid-Forming Inverter-Based Resources—Version 2, UNIFI-2024-2-1. 2022. Available online: https://docs.nrel.gov/docs/fy24osti/89269.pdf (accessed on 30 March 2024).
- U.S. Energy Information Administration. Table 1.1. Net Generation by Energy Source: Total (All Sectors). 2023. Available online: https://www.eia.gov/electricity/annual/html/epa_01_01.html (accessed on 18 March 2024).
- VDE FNN. FNN Guideline: Grid Forming Behavior of HVDC Systems and DC-Connected PPMs. 2020. Available online: https://www.vde.com/en/fnn/dokumente-en (accessed on 30 May 2024).
- Tamura, Y.; Dan, E.; Morie, I.; Nakanishi, Y.; Yokokawa, S. Development of Power System Simulator for Research and Education. IEEE Trans. Power Syst. 1990, 5, 492–499. [Google Scholar] [CrossRef]
- Parizad, A.; Mohamadian, S.; Iranian, M.E.; Guerrero, J.M. Power System Real-Time Emulation: A Practical Virtual Instrumentation to Complete Electric Power System Modelling. IEEE Trans. Power Electron. 2023, 15, 889–900. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, B.; Zheng, S.; Ma, Y.; Wang, F.; Tolbert, L.M. Development of a Converter-Based Transmission Line Emulator with Three-Phase Short-Circuit Fault Emulation Capability. IEEE Trans. Power Electron. 2018, 33, 10215–10228. [Google Scholar] [CrossRef]
- Dommel, H.W. Digital computer solution of electromagnetic transients in single- and multi-phase networks. IEEE Trans. Power Appar. Syst. 1969, 88, 734–741. [Google Scholar] [CrossRef]
- Watson, N.; Arrillaga, J. Power Systems Electromagnetic Transients Simulation; Institution of Engineering and Technology (IET): Stevenage, UK, 2003. [Google Scholar]
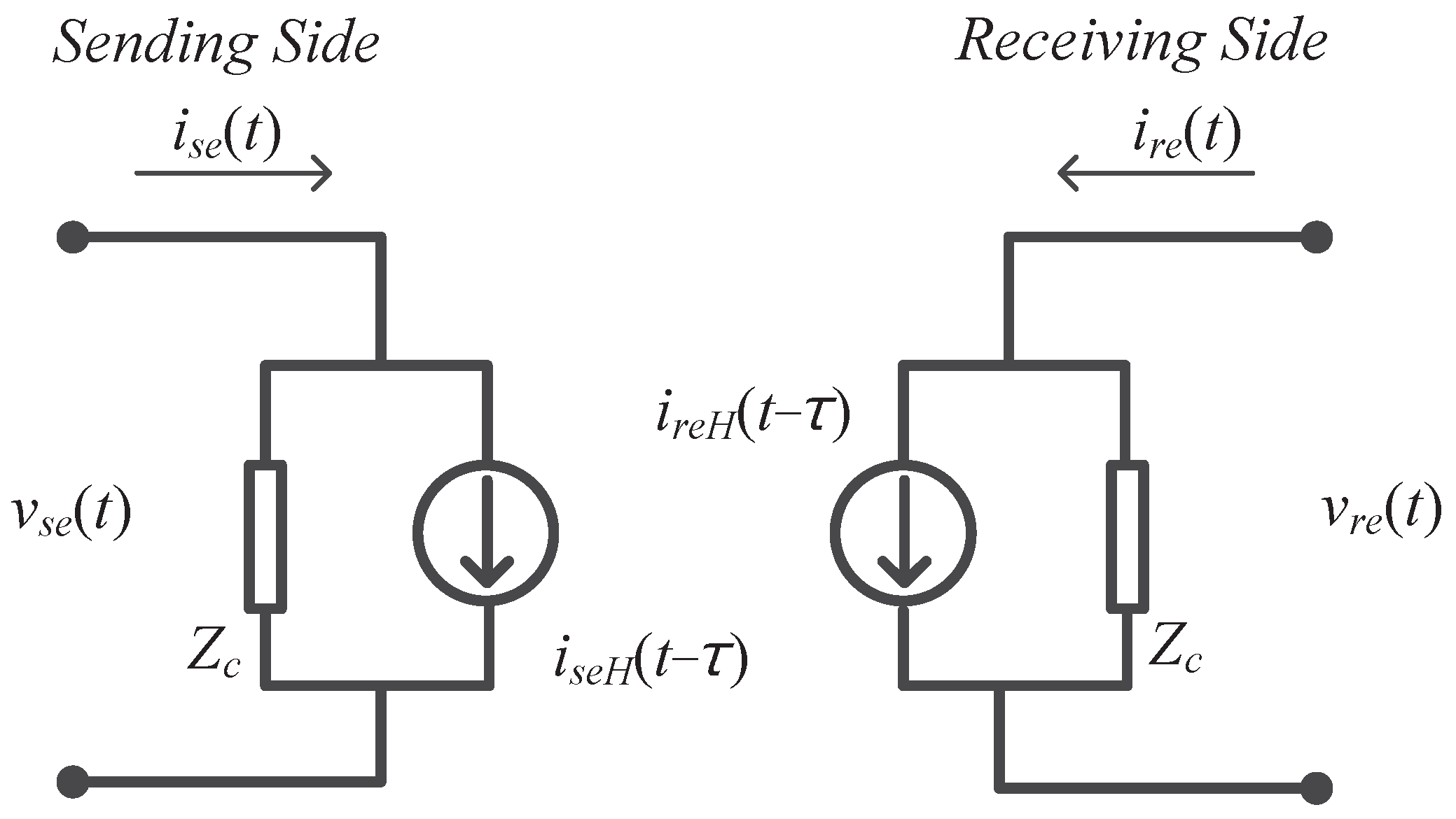


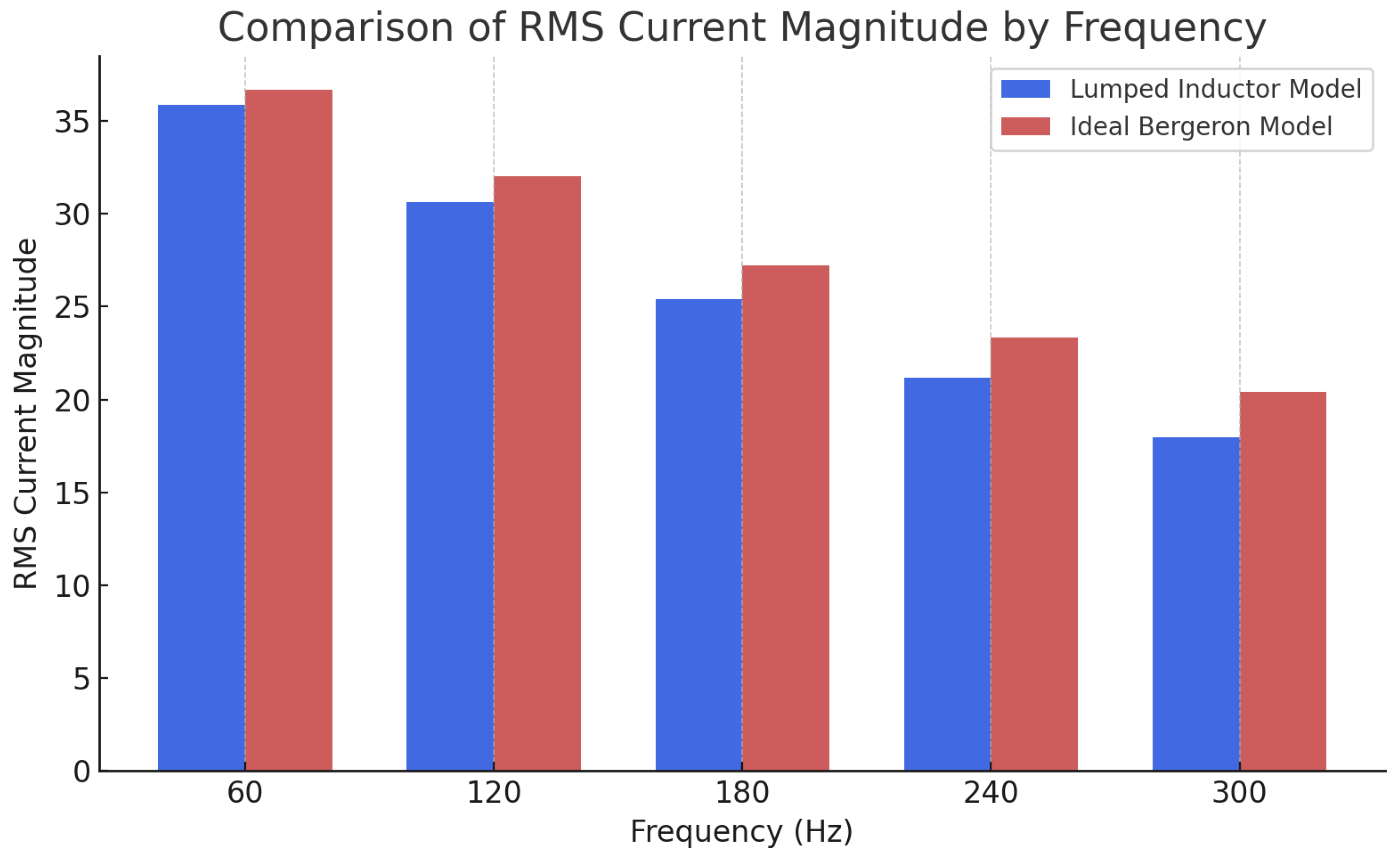
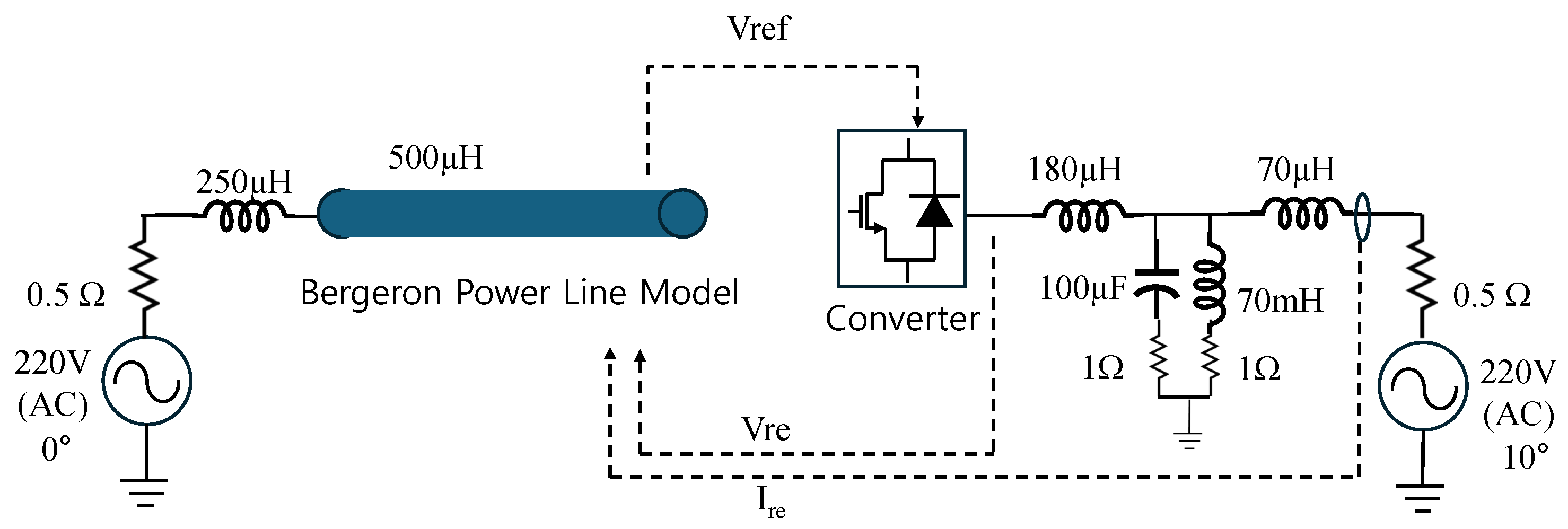

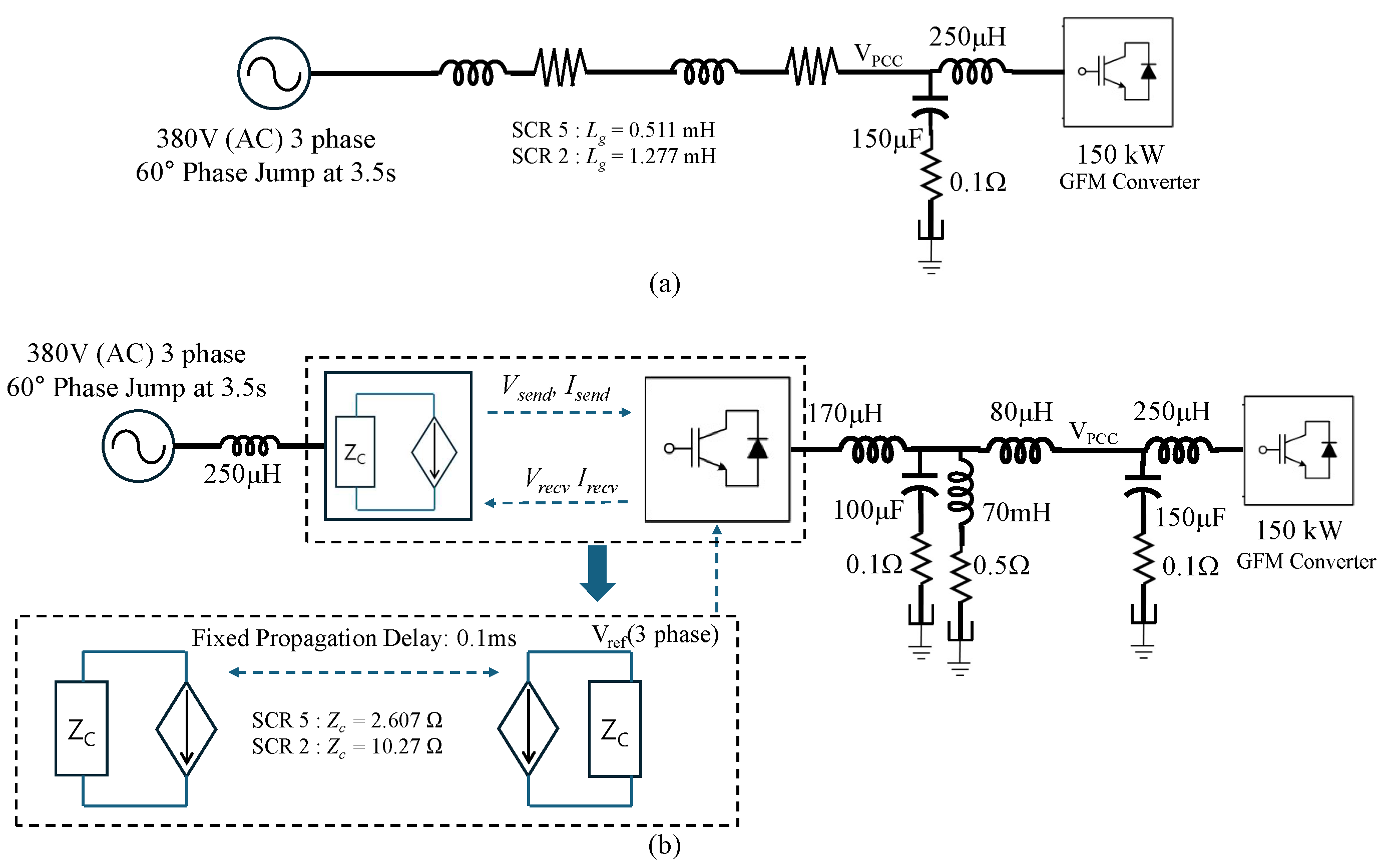

| Frequency | Lumped Inductor | Bergeron Line Model | Deviation |
|---|---|---|---|
| (Hz) | RMS Current (A) | RMS Current (A) | (%) |
| 60 | 35.8833 | 36.6934 | 2.258 |
| 120 | 30.6201 | 32.0532 | 4.680 |
| 180 | 25.4019 | 27.2410 | 7.240 |
| 240 | 21.1939 | 23.3330 | 10.093 |
| 300 | 17.9720 | 20.3979 | 13.498 |
| Converter Parameters | Value |
|---|---|
| Converter-side inductor | 180 [H] |
| Grid-side inductor | 70 [H] |
| Converter filter capacitor | 100 [F] |
| Converter shunt inductor | 70 [mH] |
| Characteristic impedance () | 5 [] |
| Traveling time () | 0.1 [ms] |
| Converter Parameters | Value |
|---|---|
| Converter-Side Inductor | 250 [H] |
| Converter Filter Capacitor | 150 [F] |
| Switching Frequency | 4 [kHz] |
| Control Time Period | 125 [s] |
| P Droop | 5% |
| Q Droop | 20% |
| DC Voltage | 750 [V] |
| Converter Parameters | Value |
|---|---|
| Converter-Side Inductor | 180 [H] |
| Grid-Side Inductor | 70 [H] |
| Converter Filter Capacitor | 100 [F] |
| Converter Shunt Inductor | 70 [mH] |
| Switching Frequency | 20 [kHz] |
| Control Time Period | 10 [s] |
| DC Voltage | 1000 [V] |
| Parameter | SCR = 2 | SCR = 5 |
|---|---|---|
| Grid Impedance () | 0.48133 | 0.192533 |
| Grid Inductance () | 1.277 mH | 0.511 mH |
| Power Line Inductance () | 1.027 mH | 0.261 mH |
| Characteristic Impedance () | 10.2677 | 2.607 |
| Propagation Delay () | 0.1 ms | 0.1 ms |
| Sampling Time () | 10 s | 10 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, C.-S.; Youn, Y.-W.; Choi, H.-K.; Kim, T.-J. Converter-Based Power Line Emulators for Testing Grid-Forming Converters Under Various Grid Strength Conditions. Sustainability 2025, 17, 6690. https://doi.org/10.3390/su17156690
Hwang C-S, Youn Y-W, Choi H-K, Kim T-J. Converter-Based Power Line Emulators for Testing Grid-Forming Converters Under Various Grid Strength Conditions. Sustainability. 2025; 17(15):6690. https://doi.org/10.3390/su17156690
Chicago/Turabian StyleHwang, Chul-Sang, Young-Woo Youn, Heung-Kwan Choi, and Tae-Jin Kim. 2025. "Converter-Based Power Line Emulators for Testing Grid-Forming Converters Under Various Grid Strength Conditions" Sustainability 17, no. 15: 6690. https://doi.org/10.3390/su17156690
APA StyleHwang, C.-S., Youn, Y.-W., Choi, H.-K., & Kim, T.-J. (2025). Converter-Based Power Line Emulators for Testing Grid-Forming Converters Under Various Grid Strength Conditions. Sustainability, 17(15), 6690. https://doi.org/10.3390/su17156690








