1. Introduction
The crucial function performed by commercial banks in supporting the economic activities, growth, and development of their nations, all the while serving the interests of their multiple stakeholders, cannot be overstated [
1,
2,
3,
4,
5]. As principally risk-taking institutions, in the conduct of their business they constantly assume and manage several conventional banking risks such as market, operational, liquidity, and credit risks, thereby creating sustainable value for their primary stakeholders, which typically comprise depositors, borrowers, creditors, investors, governments, as well as the general public [
3,
5,
6]. This mainstream sustainable value-creation perspective to commercial banks’ raison d’être is broadly perceived to be underpinned by the managerial approach to financial sustainability, which for the most part derives from value maximisation theory (see, for example, the study by Zabolotnyy and Wasilewski [
7]), although in the finance and economic literature it has frequently been linked to several other related theoretical constructs of corporate governance and business ethics, such as (enlightened) stakeholder theory, social entity theory, trusteeship theory, plurastic theory, as well as the associated concept of corporate social responsibility [
3,
8,
9].
At the same time, however, as a sector, commercial banks also fulfil a significant purpose in terms of maintaining the financial stability of the economies within which they operate, primarily by facilitating economic activities as well as contributing to economic growth [
1,
10,
11,
12,
13,
14]. These latter roles have, within the context of contemporary finance and economic literature, been predominantly underscored by the preeminent economic theories of financial intermediation, fractional reserve, credit creation, and interdependency [
12,
13,
15,
16,
17]. Thus, the long-term financial sustainability of commercial financial institutions carries a broader societal impact, influencing not only key stakeholders but also the wider community and global efforts to achieve the United Nations’ Sustainable Development Goals (SDGs) [
1,
3,
4,
5,
18].
Despite the construct of long-term financial sustainability, arguably only gaining an ever-increasing prominence in recent years, it remains, in essence, a deep-rooted notion that is closely aligned with the long-established “going concern” principle, which reflects an entity’s ability to maintain viability, continuity, and sustained operations over time. Originating as early as the 17th century [
19], this principle is underpinned by the representational theory of measurement (see, for example, the study by Musvoto and Gouws [
20]) and broadly signifies a company’s capacity to operate without facing imminent liquidation. Such assessments typically consider core internal factors such as profitability, liquidity, and investor sentiment [
21]. Within the context of commercial banking, long-term financial sustainability rests on the premise that institutions must remain operationally and financially viable, exhibiting minimal deviation from expected performance norms [
21]. This perspective further underscores the imperative of responsible financial management, one that balances current performance with the safeguarding of future financial success, including intergenerational equity [
22]. Accordingly, the central tenet of financial sustainability for banks lies in their ability to consistently generate earnings, support steady growth, meet ongoing payment and funding obligations to stakeholders, as well as sustain operations through resilient and self-sufficient business models [
22,
23,
24].
Prominent scholars in this field, such as Gleißner, Günther and Walkshäus [
22], have in recent years posited that, to be relevant to stakeholder’s economic decisions, the nature and orientation of a company’s financial sustainability information should be consistent with a long-term, future-oriented value creation and preservation perspective. They maintain that its meaning is such that it is inherently an ex-ante and forward-looking phenomenon, and that, in the truest sense, proprietary future- and forward-looking information regarding a company’s plans as well as related risks might, strictly speaking, be best suited to making an assessment about its financial sustainability. Conversely, it has also been suggested that, in the absence of insider information, its measurement can be based on observable historical data, which is based on the presumption that the evaluated past information is representative of the future, unless there are plausible explanations for why those relationships are no longer valid (see, for example the studies by Ziegler et al. [
25] and Günther, Gleißner and Walkshäusl [
24]). The abovementioned perspective indicates that the scope of financial sustainability simultaneously covers several financial variables that form the relationship framework linking value and continuity of business [
7]. Within this framework, financial sustainability has been conceptualised as a quantitatively measurable construct, characterised by a positive real growth rate, a high probability of survival (i.e., low insolvency risk), limited earnings volatility, and a risk–return profile that renders the entity an attractive investment for its shareholders [
22].
Over the past few decades, several scholars within the fields of banking, finance, and economics have sought to investigate credit-related determinants of commercial banks’ long-term financial sustainability. Although many of these scholars have traditionally sought to direct their attention to studying their long-term financial sustainability in terms of a narrow a perspective emphasizing mainly internal conditions (see, for example [
22]), recently there has been a shift towards a more holistic approach that takes into account internal company-specific conditions as well as external environmental conditions [
26,
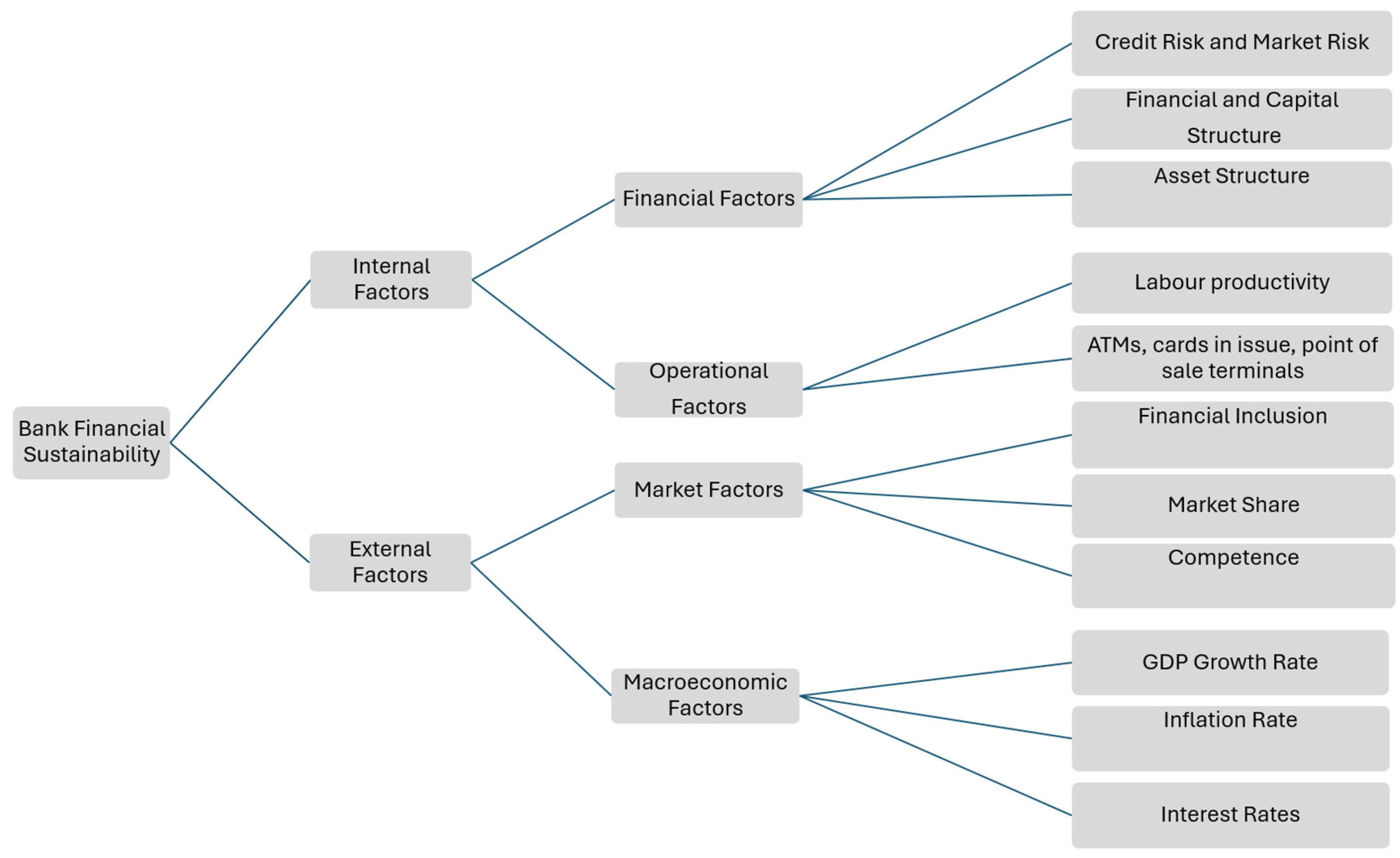
27]. A related taxonomy consistent with this perspective is presented in
Figure 1 below. In terms of this representation, internal factors can typically be regarded as bank-specific, reflecting characteristics inherent to each institution’s governance, strategic orientation, and risk culture; whereas external factors may be attributed to market and macro-economic conditions (see, for example the study by Basha and Tejesh [
5]). In this regard, commercial banks’ long-term financial sustainability can be determined by a confluence of internal bank-specific and external macro-economic or macro-financial factors [
5,
26].
On the other hand, the peculiarity of commercial banks’ value proposition in terms of credit creation implies that their long-term success, survival, and financial sustainability is inherently linked to credit risk and its effective management [
10,
28,
29,
30,
31,
32]. Moreover, the previously mentioned interdependencies between the banks themselves, as well as their banking sector and the real economies, compounds their sustainability and survival risk; which implies that the collapse of one bank may often have catastrophic ripple-effects that could trigger severe systemic repercussions that could potentially culminate in sector-wide-collapse and the destabilisation of the entire financial system, as highlighted during the recent global financial crisis of 2008–2010 [
15,
16,
17,
33,
34]. In this regard, it has been suggested that commercial banks’ long term financial sustainability may have significant implications for the sustainable growth and development of the global economy [
18]. This rationale highlights the cruciality of examining the effect of credit risk-related factors on the long-term financial sustainability and resilience of commercial banks.
1.1. Literature Review
1.1.1. Theoretical Framework
Four foundational and interconnected theoretical frameworks are arguably the most pertinent to the study of the relationships between bank-specific credit risk factors and long-term financial sustainability of commercial banks, namely the resource-based view (RBV) theory, institutional theory, industrial organisation (IO) theory, and the dynamic capabilities framework. Perhaps an appropriate perspective on the analysis of these frameworks is to position them into two segments on the basis of their nature. Thus, on the one hand, the resource-based view theory emphasises the importance of a company’s internal resources and capabilities to determine its long-term viability and survival [
35]. It is founded upon the proposition that possessing valuable, rare, inimitable, non-substitutable, and organised (VRIN-O) resources and capabilities gives companies a competitive advantage and helps maintain sustainable performance [
36,
37,
38]. Given this underpinning, unique company-level resources and capabilities represent a source of competitive advantage based on the proposition that companies are heterogeneous, that their heterogeneity is the result of their strategic choices, and that their resource commitments over time will ultimately determine their performance and sustainability [
35].
Moreover, since differences in the performance of companies across time can primarily be explained by their unique resources and capabilities rather than the industry structural characteristics, superior returns can also be enhanced through effective management of resources and capabilities [
39]. In this vein, as “special” institutions (see, for example the study by Fama [
40]), commercial banks possess unique resources and capabilities that they can develop to enhance their ability to adapt to a fast-changing competitive environment and also improve their survival prospects [
35]. A vast and a growing body of empirical literature has demonstrated the relevance of RBV theory in examining how commercial banks create and sustain their competitive advantage (see, for example, the studies by Donnellan and Routledge, 2019 [
39], Ristyawan, Putro and Siallagan [
41], Esteve-Pérez and Mañez-Castillejo [
35], and Paolone et al. [
42]). However, a few scholars such as Bhandari, Rana, Paul and Salo [
36] have suggested that RBT may be insufficient to independently explain sustainable performance.
On the other hand, the second category of related theories, namely institutional theory, industrial organisation theory, and the external dynamic capabilities framework not only focus on internal capabilities of long-term sustainability, but external capabilities as well [
35]. The first—institutional theory—considers banks as “institutions”. According to Scott [
43], institutions comprise cognitive, normative, and regulative structures and activities that provide stability and meaning to social behaviour. At the heart of the concept of institutional theory is legitimacy, which ensures companies’ credibility with stakeholders. Companies can achieve legitimacy and long-term sustainability by adopting the institutional norms, behaviours, and beliefs that are created by society, government, and public opinion [
44]. This means that as institutions, banks are expected to adapt their strategic behaviours when responding to formal and informal institutional pressures [
45]. This form of institutional disposition could alternatively be seen in the light of a “rational egoist profit maximisers, who obey laws and regulations only when it is in the company’s best economic interest, which serves particular stakeholders who are critical to the existence of the company such as regulators and shareholders” [
46]. Consistent with this perspective, commercial banks are likely to exhibit isomorphic responses to institutional pressures as a strategic means of preserving organisational legitimacy [
47]. Notably, both resource-based view theory and institutional theory could be considered closely aligned with the CAMELS (Capital adequacy, Asset quality, Management quality, Earnings, Liquidity and Sensitivity to market risk) framework often used to study bank survival in the fields of economics, finance, and organisational studies [
48,
49]. They are also consistent with the previously mentioned hypotheses of value maximization, credit creation, and the representational theory of measurement [
50,
51,
52,
53,
54].
Similarly to the previously mentioned institutional theory perspective, industrial organisation theory can also be used to understand company behaviour and industry performance. It predicts that industry or market performance is determined by the conduct of the companies within that market, and in turn that company behaviour and performance is determined by various market structure variables [
55]. Various studies have validated the applicability of this framework in the banking sector, such as Neuberger [
56], Gunji and Miyazaki [
57], and VanHoose [
58].
Lastly, the dynamic capabilities framework, often credited to Teece, Pisano and Sheen [
59], focuses on how a company’s capabilities allow it to achieve and sustain a competitive ability and performance. In this context, capabilities are regarded as a set of learned processes and activities that enable an organisation to produce a particular outcome [
59,
60,
61]. The framework analyses the sources and methods of wealth creation, based on the proposition that by constantly integrating, building, and reconfiguring both internal and external competencies, a company can sustain its competitive advantage and performance under rapidly changing circumstances [
59]. Consequently, the dynamic capabilities framework could perhaps be largely considered a variation of resource-based view and industrial organisation theories [
62]. Several recent studies provide support for the applicability of this framework within the banking and financial services sector (see, for example the studies by Ristyawan, Putro and Siallagan [
61], Rohani, Shahrasbi and Gregoire [
63], and Cavusgil and Deligonul [
60]).
1.1.2. Review of the Empirical Literature
Although numerous scholars such as Ristyawan, Putro and Siallagan [
61], Haris, Yao and Fatima [
64], Kwashie, Tawiah and Kojo [
65] and Lawrence, Babatunde, Doorasamy and Sarpong [
66] have sought to analyse credit risk and the financial sustainability of commercial banks in recent years, there remains a lack of clarity about the key variables of interest, their interrelationships, and their significance due to the problematic state of current evidence which has remained somewhat mixed. Nevertheless, two distinct schools of thought seem to have emerged from this body of literature: one suggests that credit risk negatively affects the long-term financial sustainability of commercial banks, whereas the second contradicts this perspective.
Shair et al. [
67] investigated the effects of liquidity risk, credit risk, and competition on the profitability of Pakistani banks during a ten-year period from 2007 to 2017. Their results demonstrated that credit risk, as measured by the ratio of loan loss provision to total loans, had a negative and significant effect on the profitability of Pakistani banks. Similarly, Shaheen et al. [
68], in an attempt to examine the impact of market competition on efficiency and profitability in the Pakistani banking sector during the 2006–2016 period, reported that the impact of credit risk on banks’ profitability and efficiency was significant and negative. Buchory [
69] examined the effects of banking intermediation, secondary reserves, operational efficiency, and credit risk on banking profitability using empirical data obtained from a sample of 22 Indonesian regional development banks during the 2019–2022 period. The author measured credit risk using NPLs and profitability, which was proxied using a ratio of return on assets (ROA). He found that NPLs ratios have a negative and significant effect on ROA. Along the same lines, Haris, Yao and Fatima [
64] also attempted to examine the effects of credit risk and liquidity on banking profitability, using a sample of 37 Pakistani banks during the COVID-19 pandemic. The researchers defined credit risk as ratio of loan loss provisions to total gross loans, and profitability using three proxies used to measure profitability, namely return on assets (ROA), return on equity (ROE), and net interest margin (NIM). Utilising ordinary least squares (OLS), as well as fixed and random effects regression analysis techniques, the researchers observed that credit risk had a negative and significant relationship to return on assets, return on equity, and net interest margin (NIM). Tomak [
70] examined the effect of credit risk when evaluating the effect of capital structure on the banking performance of 20 private deposit banks in Turkey during a 10 year period from 2012 to 2023, yielding 240 observations. The researcher utilised the NPLs and the ratio of cost to income to measure credit risk, debt ratios to measure capital structure, and the return on assets to measure sustainability. He found that NPLs and credit risk negatively affected bank sustainability.
Mohanty and Sarkar [
71] investigated the relationship between various internal bank-specific and external factors and profitability in public sector banks of India and further assessed the extent of their impact on financial performance. Bank-specific determinants were classified into five broad categories; that is, liquidity risk, credit risk, operational efficiency, capital efficiency, and bank size. The authors defined credit risk as a ratio of loan loss provision as a percentage of total assets and NPLs as a percentage of total assets, whereas the return on assets and return on net worth ratios were used as dependent measures of bank sustainability. Utilising secondary data obtained from the annual reports of selected banks and financial data for a sample of 21 public sector banks for a period of five years, they reported an association between credit risk and bank sustainability. The abovementioned results were similar to those of the study by Căpraru and Ihnatov [
72], who also found that cost-to-income ratio of banks, bank size, credit risk, and market concentration negatively influenced bank profitability of commercial banks in the EU15 banking systems during the period 2001 to 2015.
Conversely, some studies have found that banks with higher levels of credit risk have higher or increased profitability. For example, Sufian [
73], examining the determinants of bank performance of 77 commercial banks operating in three South Asian Association for Regional Cooperation (SAARC) member countries during the 1997 to 2008 period, found a positive and significant effect of credit risk and capitalization on bank performance. In this study, the researcher measured credit risk using the ratio of loan loss provisions to total loans (LLP/TL), and capitalisation using the book value of shareholders’ equity as a fraction of total assets. Similarly, Cheng et al. [
74] investigated the influence of the effect of credit risk and other bank-specific dynamics on bank profitability. The authors stated their observations comprised of data from a sample of 54 banks listed on the Johannesburg Stock Exchange (JSE) for the period 2012–2018. Credit risk was defined using the ratios of NPLs, capital adequacy, and cost per loan whereas bank sustainability was defined using the ratios of return on assets, return on equity, and net interest margin. Using Partial Least Squares Structural Equation Modeling, the authors observed that credit risk had a significant positive association with bank sustainability. In a similar vein, Naceur, Ben, and Omran [
75] observed that bank capitalisation and credit risk have a positive and significant impact on banks’ net interest margin, cost efficiency, and sustainability in their study of the effect of the influence of bank regulation, concentration, and financial and institutional development on commercial bank margins and profitability across a broad selection of Middle East and North Africa (MENA) countries.
Despite extensive research into the internal and external factors influencing the financial sustainability of commercial credit-lending institutions, a definitive consensus remains elusive. Moreover, while significant scholarly attention has been given to the role of non-performing loans, there has been comparatively limited investigation into their interaction with other credit loss variables—such as expected losses, capitalization, and leverage. This gap in the literature has resulted in a lack of comprehensive evidence regarding the aggregate effect of these credit risk variables on banks’ financial performance. Such an oversight is particularly problematic, as prior studies in related fields have demonstrated that characterizing aggregate effects can be highly complex due to various interdependent factors (see, for example the study by Bagade, Banerjee and Gupta [
76]). In light of the preceding discussion, the primary aim of the current study was to examine the effect of credit-risk related factors on the long-term financial sustainability and resilience of commercial banks. This was done by developing a model that functionally relates commercial banks’ long-term performance to expected credit losses, impairment gains or losses, NPLs, and CET1 and leverage variables which were collectively specified as proxies for portfolio credit risk after controlling for growth, as well as economic disturbances such as the global financial crisis and the COVID-19 pandemic, as well as changes in the regulatory framework implemented during the study period. Various statistical, mathematical, and econometric methods were applied to panel data observations of listed South African banks to achieve the empirical aspects of the overall research objectives. The originality of the current study lies in the holistic approach of gauging all five bank-specific credit risk variables (expected credit losses, impairment gains and losses, NPLs, CET1, and leverage) in evaluating the impact of credit risk on commercial banks’ long-term financial sustainability. Thus, the primary contribution of this study is that it finally posits a working model that makes it possible to comprehensibly evaluate the effects of bank-specific credit risk on the financial sustainability of commercial banks.
2. Materials and Methods, Data Collection and Preparation
As outlined earlier, the central objective of this study was to evaluate the impact of bank-specific credit risk factors on the long-term financial sustainability of commercial banks, controlling for growth dynamics, as well as major exogenous shocks such as the global financial crisis and the COVID-19 pandemic, as well as regulatory framework reforms.
Table 1 presents the definitions, computation formulas, and functional roles of the key variables used in the empirical analysis, structured to align with established methodologies in prior empirical research.
To achieve the research objectives, a quantitative research design was employed, driven by the need for evidence-based empirical analysis on the subject. This approach ensures methodological rigour in examining the relationships among key financial variables. Consequently, a comprehensive suite of statistical, mathematical, and econometric techniques was applied to panel data observations of listed South African banks. In banking and finance research panel data approaches are widely recognised for their ability to capture both cross-sectional and temporal dimensions, consists of empirical observations collected over multiple periods for either identical or distinct cross-sections (see, among others for example the study by Rastogi, Gupte and Meenakshi [
77]). This methodological framework enhances the robustness of the analysis by enabling the examination of heterogeneity across entities and dynamic relationships over time, allowing for more precise inferences regarding financial performance and risk dynamics. The selection of panel data models in this study, as opposed to time-series or cross-sectional approaches, was driven by their distinct methodological advantages. Panel models offer several key benefits: (i) they facilitate the estimation of unbiased and efficient estimators, (ii) they provide a higher number of degrees of freedom, which mitigates small sample issues inherent in linear regression estimation due to the time dimension of the data, and (iii) they effectively address common econometric challenges, including autocorrelation, multicollinearity, heteroscedasticity, and omitted variable bias [
78,
79].
Moreover, in the context of non-stationary variables, panel data models exhibit lower estimation bias compared to time-series models, even before implementing corrective measures for cross-sectional and time-series dependence [
80,
81]. This methodological advantage enhances the robustness of empirical findings, making panel data a preferred framework for analyzing dynamic financial relationships over time.
Thus, to be included in the research sample, banks were required to be listed on the Johannesburg Stock Exchange (JSE) and have continuous data availability in the IRESS database for the most recent twenty-four-year period (2006–2023). The selection of this timeframe was driven by the necessity of ensuring data consistency across all banks, thereby enabling a balanced panel structure. A balanced panel approach was adopted to mitigate the challenges associated with missing values across time observations, ensuring that all variables were consistently observed over the study period, thereby reducing heterogeneity. Although survivorship bias remained a consideration, a balanced panel offers significant advantages over its unbalanced counterpart, primarily by minimising the risk of biased or inefficient estimates [
82].
Applying these selection criteria, the final study sample comprised empirical observations from six of South Africa’s largest banks, covering the period 2006–2023. The selection of panel dimensions—specifically the number of cross-sectional units (N) and time periods (T)—is a critical methodological consideration in panel econometrics, particularly when employing a Panel Error Correction Model (PECM). In this study, a balanced panel comprising six listed South African banks (N = 6) over a 18 year period (T = 18) yields 108 observations, offering a sound empirical foundation for dynamic estimation and inference.
This dimensional configuration strikes a pragmatic balance between methodological rigor and sector-specific data constraints. Although modest in size, the panel provides sufficient degrees of freedom to support robust statistical testing, enhance estimator efficiency, and reduce standard errors [
83]. Importantly, panel structures enable the model to address unobserved heterogeneity across banks—such as risk culture, management philosophy, or strategic orientation [
84,
85,
86]—which, if uncontrolled, can introduce omitted variable bias [
87]. The use of fixed effects or related estimators allows for reliable control over such latent, time-invariant characteristics.
The temporal span of 18 years was considered as particularly well-suited to the selected PECM framework, which is designed to disentangle short-term dynamics from long-term equilibrium relationships. While large-T asymptotics are ideal in theory (see for example the study by Pesaran and Shin [
88]), prior empirical studies confirm that moderate time spans—especially those exceeding a decade—are sufficient to identify adjustment speeds, equilibrium error terms, and temporal convergence patterns, provided the underlying relationships are not excessively slow-moving. Moreover, the “macro-panel” nature of this dataset (small N, moderate T) aligns with established practice in financial stability and bank-level studies, where the focus is often on deep, within-unit variation across time. Here, 18 annual observations per institution afford ample within-bank variation to reliably estimate dynamic parameters and capture institutional responses to regulatory framework reforms and exogenous economic shocks. Methodologies that accommodate slope heterogeneity [
89] also remain applicable in this structure. Consequently, the current study’s N = 6, T = 18 configuration was considered methodologically robust, empirically sufficient, and theoretically defensible for analysing the dynamic credit risk–sustainability nexus in South Africa’s commercial banking sector.
The empirical observations were extracted from the IRESS Database, which is a proprietary financial database that hosts information on publicly listed companies, including detailed financial statements, market data, and corporate actions for banking institutions [
90]. The database provides extensive coverage of financial institutions’ performance metrics, making it suitable for analysing the banking sector’s dynamics across various time periods. The initial data extraction process involved collecting information based on each bank’s establishment date, resulting in an unbalanced panel due to the varying inception years among the sampled institutions. To address this temporal heterogeneity and ensure methodological consistency, the dataset underwent several cleansing procedures to create a balanced panel structure [
87].
Following preliminary examination, the starting period was standardised to 2006 across all banking institutions to eliminate temporal gaps and create a consistent time series. This approach aligns with the recommendations by Wooldridge [
91], whose work emphasises the importance of balanced panels in achieving robust econometric estimations. Additionally, dummy variables were computed to capture dichotomous events that significantly impacted the banking sector during the study period. These included (a) economic disturbances, mainly the global financial crisis and COVID-19 pandemic, and (b) regulatory framework reforms, particularly the 2018 transition by the banks from International Accounting Standard 32 (IAS 32) [
92] to International Financial Reporting Standard 9 (IFRS 9) [
93]. This approach of incorporating structural breaks through dummy variables is consistent with methodologies employed by Beck et al. [
94]. This approach also facilitates the isolation of exogenous effects on banking performance indicators that could distort the empirical results.
2.1. Preliminary Data Analysis
2.1.1. Cross-Sectional Dependence Testing
Before model specification, the study conducted tests for cross-sectional dependence, which is critical in panel data analysis as it determines the appropriate estimation techniques [
95]. Cross-sectional dependence occurs when unobserved common factors simultaneously affect all cross-sectional units, resulting in correlation across entities within the panel [
96,
97]. Testing for cross-sectional dependence is particularly important in banking sector studies, considering the interconnected nature of financial institutions and their susceptibility to common macroeconomic shocks [
98]. The presence of cross-sectional dependence, if unaddressed, can lead to inefficient estimators and invalid inferences due to biased standard errors [
99]. The Pesaran cross-section dependence (CD) test was employed. This test examines the correlation of residuals across entities and is robust to structural breaks and non-stationary factors [
100]. The results indicated significant cross-sectional dependence in the panel data, necessitating error correction mechanisms in the empirical model to account for serial correlation across cross-sections.
2.1.2. Multicollinearity Assessment
The examination of multicollinearity was conducted using correlation plot analysis and variance inflation factors (VIF) according to the principles outlined by O’Brien [
101]. The initial diagnostics revealed that two variables exhibited severe multicollinearity, which could potentially lead to inflated standard errors and unstable coefficient estimates [
102]. Rather than employing Principal Component Analysis (PCA), which combines collinear variables into composite indices [
103], this study opted for mean-centering of the collinear variables. While PCA effectively reduces dimensions and addresses multicollinearity, it often complicates interpretation as the resulting components represent combinations of original variables rather than the variables themselves [
104]. The mean-centering approach followed the mathematical specification:
where:
represents the centered variable,
is the original variable, and
is the mean of the original variable.
This technique reduces the correlation between variables by subtracting the mean from each observation, thereby diminishing the dimension effect while preserving the original scale and interpretability of the variables [
105]. Unlike ridge regression, which introduces a penalty parameter that may bias coefficient estimates, or PCA, which alters the interpretation of variables, mean-centering preserves the original meaning of variables while reducing their collinearity [
106]. The effectiveness of this approach was confirmed through post-transformation correlation analysis and VIF calculations, which demonstrated a significant reduction in multicollinearity while maintaining the fundamental characteristics of the original variables [
107]. This satisfied the assumption of no multicollinearity in the classical linear regression model.
2.1.3. Panel Unit Root and Cointegration Testing
Unit Root Tests
The analysis was performed using R-Studio [
108] data analysis and statistical computing package (R-Studio Version 4.4.2). To examine the stationarity properties of the variables, the study employed multiple panel unit root tests, including Levin-Lin-Chu (LLC), Im-Pesaran-Shin (IPS), and Panel Augmented Dickey-Fuller (ADF) tests [
109,
110]. These complementary tests were selected to provide robust verification of the integration order of the variables [
111]. The results indicated varying orders of integration among the variables, with some series being stationary at level (I(0)) while others required first-differencing to achieve stationarity (I(1)). This mixed order of integration guided the selection of an appropriate cointegration testing approach and subsequent model specification [
112].
Cointegration Analysis
Considering the order of integration, the study employed the Combined Johansen–Fisher panel cointegration test to examine the existence of long-run relationships among the variables [
113]. This approach extends Johansen’s cointegration methodology to panel settings by combining
p-values from individual cross-section cointegration tests and offers superior power compared to alternative tests when dealing with mixed-order integration [
114].
The Johansen–Fisher panel cointegration test is based on the following vector error correction model (VECM) specification:
where:
is a vector of variables for cross-section i at time t,
represents fixed effects,
is the long-run multiplier matrix,
are short-run coefficient matrices, and
is the error term.
The test examines the rank of
to determine the number of cointegrating vectors (see, for example the study by Johansen [
115]). The Fisher statistic aggregates the
p-values from individual Johansen tests using the formula:
where
pi is the
p-value from the cointegration test for cross-section I; this statistic follows a chi-square distribution with 2N degrees of freedom [
110]. The results revealed the presence of cointegrating vectors among the variables, confirming long-run equilibrium relationships and justifying the use of an error correction model [
116].
2.2. Model Specification and Estimation
2.2.1. Panel Error Correction Model, Model Selection, and Justification
Based on the established cointegration relationship, a panel error correction model was specified with random effects assumptions, aligning with the methodology proposed by Pesaran et al. [
88]. The selection of the Panel Error Correction Model (PECM) as the primary analytical framework in this study is grounded in both theoretical considerations and empirical validation through preliminary diagnostic tests. The model selection process began with a rigorous assessment of the time series properties of the variables, employing unit root and cointegration tests to establish the presence of long-run equilibrium relationships.
A key justification for adopting the PECM lies in the confirmed cointegration relationships among the variables. Empirical testing demonstrated that, while individual series exhibit non-stationary behavior, linear combinations exhibit stationary properties, thus validating the existence of long-term equilibrium dynamics [
117]. These findings necessitate an error correction framework capable of capturing both long-run equilibrium relationships and short-run adjustment mechanisms. The presence of cointegration implies that deviations from equilibrium are transitory, with variables inherently converging toward their long-run path over time. Ignoring these relationships would result in model misspecification and potentially spurious regression results, particularly given the non-stationary nature of the individual series [
118].
2.2.2. Comparison of PECM and Alternative Approaches
This section presents a comparative evaluation of the study’s preferred Panel Error Correction Model (PECM) against alternative estimation techniques, including the Vector Error Correction Model (VECM), the Fixed Effects (FE) model, and the Generalised Method of Moments (GMM) estimator—specifically System GMM. The discussion concludes with a justification for the selection of the PECM as the most suitable empirical strategy for this study.
PECM vs. VECM
While the Vector Error Correction Model (VECM) offers an alternative approach for modeling cointegrated variables, it was deemed less suitable due to methodological limitations. Specifically:
The VECM treats all variables as endogenous and estimates a system of equations, which is computationally intensive and may suffer from dimensionality constraints in large datasets [
119].
More importantly, VECM does not allow for a focused distinction between the dependent and explanatory variables, limiting its ability to explicitly examine the short-run and long-run dynamics of the key dependent variable (FIN_SUST).
The PECM, by contrast, preserves a clear structural distinction between dependent and independent variables while incorporating the error correction mechanism to adjust deviations from long-run equilibrium [
120].
PECM vs. Fixed Effects (FE) Model
A comparison between PECM and the fixed effects (FE) model highlights key theoretical limitations of the latter:
Fixed effects estimation assumes stationarity, requiring first differencing to eliminate non-stationarity. However, when variables are cointegrated, differencing destroys long-run equilibrium relationships, resulting in misspecified estimations [
121].
The FE model fails to account for cointegration, leading to inefficient parameter estimates and misleading statistical inferences (see, for example the study by Pesaran and Smith [
122]).
Furthermore, fixed effects models do not incorporate an error correction mechanism, which is critical for modeling equilibrium adjustments in banking research, where understanding market resilience is key.
Superiority of PECM over FE Models
The PECM, implemented via the PMG estimator, offers a more flexible and theoretically sound approach, allowing short-run dynamics and error variances to vary across cross-sections while maintaining homogeneous long-run coefficients [
88]. Additionally, using Driscoll–Kraay standard errors enhanced robustness by effectively managing cross-sectional and temporal dependencies—a significant advantage for financial panel data analysis [
123].
PECM vs. GMM and SGMM
The Generalized Method of Moments (GMM) estimator, particularly the Arellano–Bond [
124] difference GMM and Blundell–Bond [
125] system GMM, is widely used in dynamic panel modelling. However, these approaches were deemed inappropriate for this study due to key theoretical and practical limitations:
Final Model Selection Verdict
The PECM was chosen as the most methodologically sound framework, aligning with the study’s objectives of examining both short-run and long-run relationships. The ability to decompose short-run fluctuations while maintaining equilibrium distinguishes it from conventional panel models, particularly fixed effects and GMM-based approaches. Robust standard error estimation further ensures statistical validity, strengthening model reliability despite heteroskedasticity in the panel dataset.
By explicitly integrating error correction, PECM provides a comprehensive framework for investigating equilibrium dynamics, institutional resilience, and market efficiency—offering superior theoretical consistency and empirical robustness over alternative modelling approaches.
2.2.3. Selection of the Random Effects Specification
The random effects specification was deemed appropriate given two key assumptions: (a) the sampled banking institutions represented a broader population of financial entities rather than constituting the entire population [
127], and (b) the unobserved heterogeneity across banks was uncorrelated with the included regressors [
128]. The long-run model was estimated using the “pooling” estimator modified using the pooled-mean group (PMG) estimators within the plm (panel linear model) library framework in RStudio Version 4.4.2 (see, for example the study by Croissant and Millo [
129]). The rationale for employing the PMG estimator principle lies in its ability to constrain long-run coefficients to be homogeneous across cross-sections while allowing short-run dynamics and error variances to differ, providing a balanced approach between fully heterogeneous and entirely homogeneous panel estimations [
88]. The initial diagnostic tests revealed the presence of both heteroskedasticity and serial correlation in the estimated model, necessitating further refinements to the estimation procedure. The long-run model followed the model specification:
2.2.4. Robust Standard Error Estimation
To address heteroskedasticity and serial correlation, the study employed Driscoll–Kraay robust standard errors for coefficient estimation [
123]. This approach yields consistent standard error estimates that are robust to various forms of spatial and temporal dependence, particularly valuable in finance and banking studies where cross-sectional correlation is prevalent [
130]. The Driscoll–Kraay estimator modifies the standard nonparametric time series covariance matrix estimator to account for spatial dependence, making it particularly suitable for panels with a large number of time periods (T) relative to the number of cross-sections (N) [
123]. This time technique has been effectively employed in numerous banking studies, including those by Berger et al. [
131] and Dell’Ariccia et al. [
132], that examined similar financial dynamics across institutions.
2.2.5. Short-Run Dynamics Estimation
The estimation of short-run coefficients presented computational challenges due to the creation of lags and first differences, which initially resulted in significant data loss. To overcome this limitation, a structured sequential approach was adopted. First, lags were computed individually for each cross-sectional unit to account for unit-specific dynamics. An empty list was then initialised to store these lagged values. Subsequently, first differences and short-run coefficients were calculated and integrated into the dataset to reconstruct a balanced and complete panel. This methodical process ensured the preservation of a sufficient number of observations for robust estimation while maintaining the integrity of the panel structure [
126].
The final model incorporated both long-run and short-run components, with the error correction term (representing the speed of adjustment) expected to be negative and statistically significant, confirming model convergence [
120]. This negative coefficient indicates the speed at which deviations from long-run equilibrium are corrected in each period, with larger absolute values suggesting faster adjustment [
117]. As emphasised by Demetriades and Hussein [
133], a statistically significant and negative error correction term provides evidence of a stable long-run relationship. It confirms the appropriateness of the error correction specification. This rigorous process resulted in the following empirical model specification:
2.2.6. Post-Estimation Diagnostics
The final panel error correction model underwent rigorous diagnostic testing to ensure compliance with the assumptions of a classical linear regression model. Residual plots were examined for normality and homoskedasticity, and additional tests confirmed the absence of serial correlation after correction [
134]. These diagnostics validated the model’s statistical integrity and suitability for inferential analysis.
3. Results
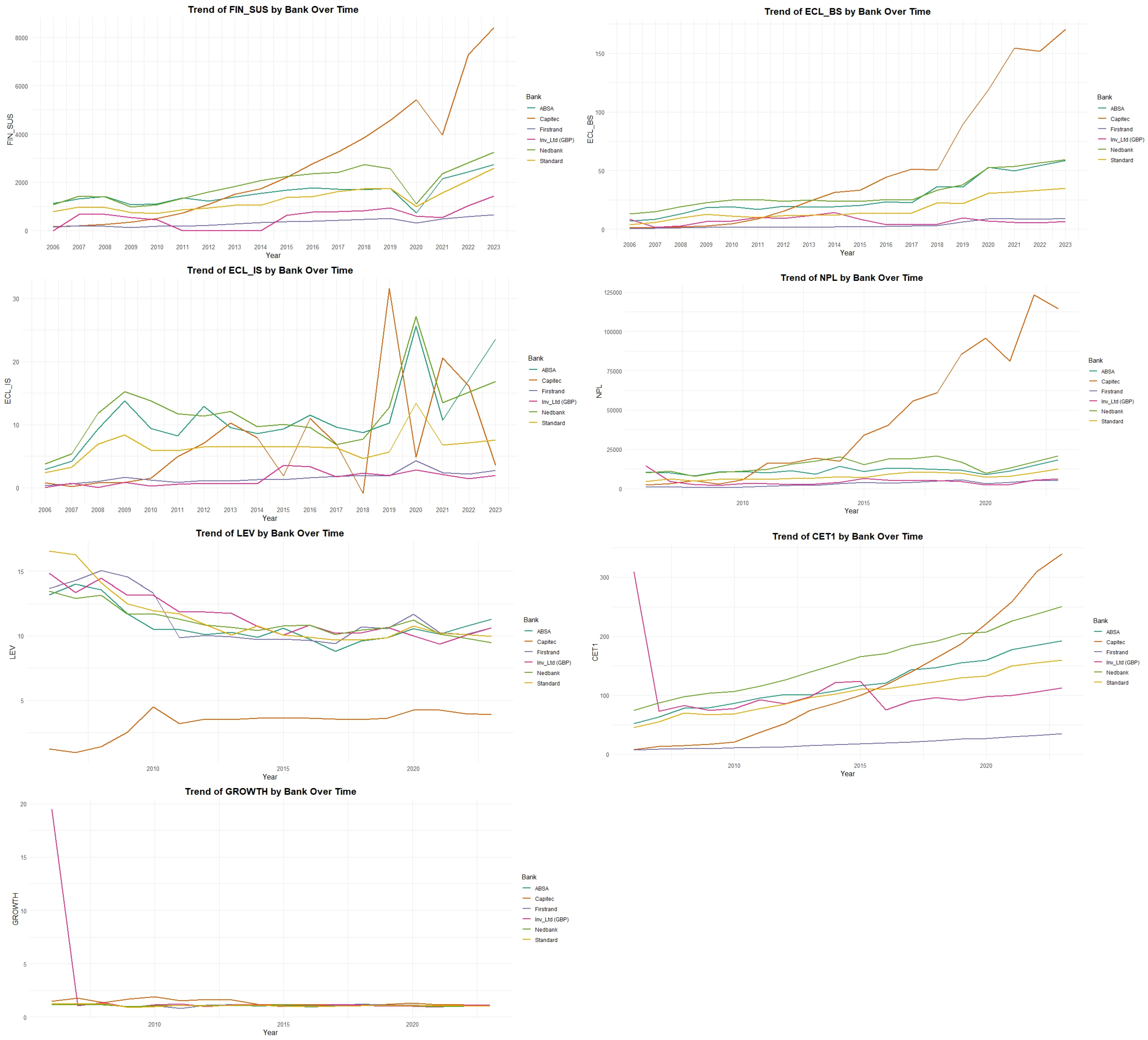
Figure 2 provides a composite visualization of the temporal evolution of the dependent and independent variables for the six sampled banks over the 2006–2023 study period. The first panel depicts financial sustainability (FIN_SUST), proxied by headline earnings per share. Capitec exhibits a notably steep and accelerating growth trajectory—particularly post-2010—suggesting increasingly robust per-share profitability. Nedbank follows with a sustained upward trend, while ABSA and Standard Bank reflect moderate, steady gains. In contrast, FNB’s performance appears relatively stable with minor fluctuations, and Investec reveals a volatile path marked by an early surge, subsequent decline, and eventual recovery. These heterogeneous trends underscore material differences in long-term earnings resilience and profitability dynamics across institutions.
The second panel illustrates expected credit losses (ECL_BS), revealing pronounced volatility and interbank variation. ABSA and FirstRand both show subdued ECL_BS values prior to 2020, followed by sharp post-pandemic spikes—peaking in 2023—likely reflecting elevated credit impairment due to COVID-19-related economic disruptions [
135]. Capitec, by contrast, begins with the lowest ECL_BS level, increasing steadily—particularly after 2018—potentially indicative of portfolio expansion or evolving risk appetite. Nedbank shows a more tempered increase, suggesting conservative credit provisioning. Investec’s profile is largely stable until an abrupt escalation in 2023. Overall, these trends suggest both systemic and idiosyncratic factors shaping banks’ credit risk exposure.
The third panel, which captures impairment gains and losses (ECL_IS), reveals significantly higher short-term volatility relative to ECL_BS—highlighting its sensitivity to transitory shocks and earnings fluctuations. Notably, ECL_IS volatility intensifies post-2018, peaking during 2019–2020 in line with the pandemic’s onset. Capitec maintains consistently low ECL_IS levels, reinforcing perceptions of stable credit management. The broader sectoral volatility reflects heightened provisioning adjustments and earnings compression during stress periods.
The fourth panel examines non-performing loans (NPLs), further elucidating bank-level credit risk. Capitec diverges sharply from its peers post-2013, with a sustained and steep rise in NPLs—suggestive of structural portfolio risk or aggressive loan book expansion. ABSA, Standard Bank, and Nedbank display more gradual increases, while FNB and Investec consistently maintain the lowest NPL levels. These findings emphasise significant asymmetries in credit quality and exposure across the sector.
The fifth panel focuses on leverage (LEV), highlighting a common trajectory among most banks. ABSA, FNB, Nedbank, Standard Bank, and Investec all demonstrated elevated leverage during the pre-2009 period, with visible deleveraging post-crisis—indicative of sector-wide adjustments to risk appetite and regulatory capital requirements. Capitec, operating from a consistently lower leverage base, appears structurally distinct—likely due to its business model or capital efficiency strategies.
The sixth panel displays common equity tier 1 capital (CET1), used here as a proxy for scaled equity reserves. Capitec again distinguishes itself, registering a steep and persistent rise in CET1—particularly after 2010—reflecting a strengthening capital buffer relative to balance sheet scale. ABSA and Nedbank also show material increases, albeit more gradual. FNB and Standard Bank trend upward modestly, while Investec displays greater variability. The overall trend suggests a sectoral emphasis on enhanced capitalization in response to evolving prudential standards.
Finally, the seventh panel tracks asset growth. Investec shows a period of rapid expansion in the mid-2000s—possibly driven by acquisition strategies or portfolio diversification—before reverting to more stable growth, converging with its peers. Other institutions (ABSA, Capitec, FNB, Nedbank, Standard Bank) exhibit more modest and stable growth rates, mostly within a 0–2% range. This convergence reflects a mature and competitively constrained banking landscape in South Africa, where organic growth opportunities are increasingly limited.
Collectively, the trends in
Figure 2 reveal substantial variations across banks in financial sustainability, credit risk exposure, capital structure, and growth trajectories. These disparities underscore the need for nuanced, institution-specific credit risk analysis to effectively assess the long-term financial sustainability of South African banks.
3.1. Pre-Modelling Investigation
3.1.1. Correlation Analysis
This section presents the correlation analysis of the variables. The correlation was examined using the Persons Correlation technique, and the findings are presented using the correlation plot. In addition, the multicollinearity variance inflation factors (VIF) were also used to examine the strength of the relationship between the explanatory variables; this was to ensure that the variables are not perfectly collinear with each other and do not violate the assumption of the classical linear regression model (CLRM).
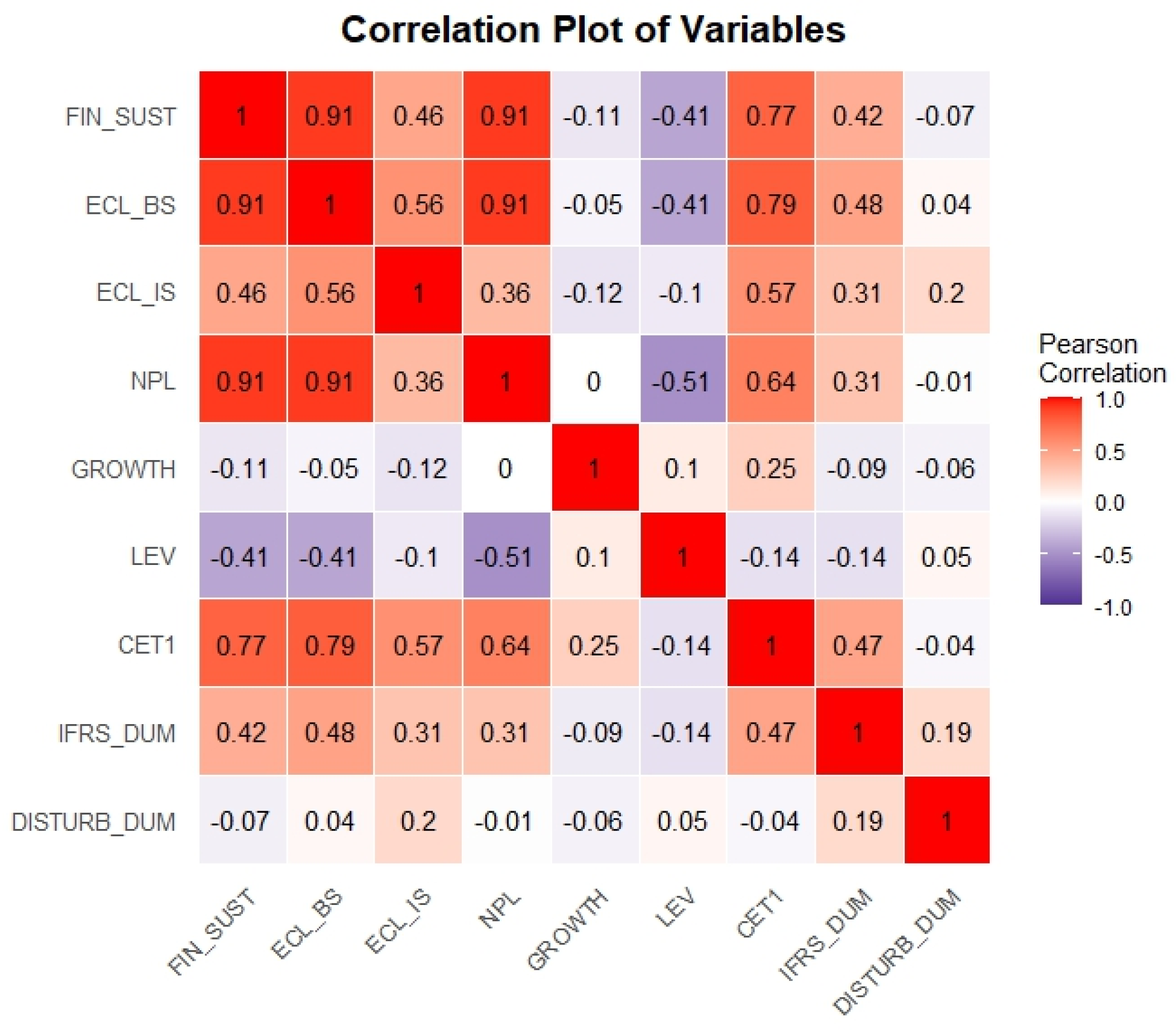
The findings presented in
Table 2 and
Figure 3 cumulatively show a degree of correlation between the variables. Therefore, this study used a mathematical technique to lower the dimensionality of the correlated variables by centering the variables around their long-run mean. This was an efficient and preferred method over the principal component analysis (PCA) method, which was used to construct a single index capturing the dynamics of the collinear variables, or another technique of dropping collinear variables based on their significance to this study. Thus, careful consideration and care went into preserving these variables and modelling them all without affecting the findings’ quality.
3.1.2. Stationarity Tests
To ensure the reliability of the empirical analysis, it is crucial to examine the stationarity properties of the variables. Unit root tests determine whether a time series variable is stationary or non-stationary. The stationarity tests’ findings indicate a shared order of integration among the variables; some variables are stationary at levels and others at 1st difference, indicating a varying order of integration among the variables.
Table 3 presents the unit root tests.
3.1.3. Cointegration
The study conducted the Pedroni [
136] cointegration test to examine for the presence of long-run relationships between the variables; in addition, the crux of utilising the Pedroni cointegration test is that the test is specifically designed to accommodate heterogeneous data panel series. Therefore, it fits the panel data structure of this study, where banks are the cross-sectional units. The results of the Pedroni cointegration tests presented in
Table 4 below revealed cointegration among the variables in a panel data series; as validated by the probability value that is significant at least at both the 5% level for both the Modified Phillips–Perron and the Augmented Dickey–Fuller statistics as well as at the 10% significance level for the Phillips-Perron statistic. Hence, the study failed to reject the null hypothesis of no cointegration. The study utilised the Newey–West [
137] lag operator to increase the Pedroni cointegration test’s robustness and validate the study’s findings.
3.2. The Panel Error Correction Model
Because the study established the presence of cointegrating vectors among the variables, the next step was to conduct a panel error correction model to correct for the short-run deviation among the variables. Thus, the panel error correction model was performed based on the model’s assumptions and data artefact sections.
Table 5 presents the findings.
4. Results Discussion
As stated in the introduction, this study aims to examine the explanatory power of the impact of credit risk on banks’ performance after controlling for growth dynamics, regulatory framework reforms, as well as exogeneous economic disturbances relating to the global financial crises and the COVID-19 pandemic. This study was predetermined at the 5% significance level; this is the t-statistic of +/−1.95 (where at least the t-stat is close to or greater than 2).
Table 5 shows the empirical findings of credit risk’s short-run and long-run impact on banks’ performance for 2006–2023. The model results show that the model is correctly specified. This is confirmed by the error correction term (ECT), which is negative and statistically significant at the 5% significance level. The ECT ϕ coefficient value of −0.7363047 indicates that at least 74 per cent deviation in the short run is corrected in the long run. In addition, the negative value also shows a stable relationship between cointegrating vectors and a convergence to a long-term equilibrium in the opposite direction [
138].
The findings from the PECM provide insights into the impact of credit risk on bank performance. When examining the t-values of the estimated variables, starting with the short run, the findings from the short-run coefficient estimates indicate that expected credit loss (ECL_BS) is statistically significant at the 5% significance level. This is because the t-value of the coefficient is greater than 2. The t-statistic shows that a standard unit change of ECL_BS resulted in a 3.21 negative impact on bank performance in the short run. This finding reflects the importance of internal credit risk management capabilities, aligning with the previously mentioned resource-based view (RBV), which regards risk analytics and provisioning frameworks as strategic resources that shape company performance. The findings show that ECL_IS is statistically significant in the short run; this is evident in the p-value that is less than the 0.05 benchmark statistical significance level, p < 0.05. Similarly, the t-value shows that impairment gains and losses (ECL_IS) are significant, as a single standard unit change on ECL_IS caused a negative impact of 19.94 on the dependent variable. NPLs, however, yield a positive short-run effect of 12.65. Consequently, ECL_BS has the highest absolute effect on bank performance other than credit risk variables. Taken together, the above metrices suggest South African commercial banks may be pricing risk effectively, a perspective aligned with industrial organisation (IO) theory, which emphasises strategic behavior in competitive markets.
Surprisingly, the control variable, GROWTH, has a negative and statistically significant impact on the dependent variable. The t-stat value associated with the control variable is greater than the benchmark of +/−1.95, and the associated p-value is less than 0.05. The t-stat value of −16.5887 indicates that the variable had a single standard unit change in the GROWTH variable and accounts for at least a 16.59 change in the dependent variable in standard units. Leverage (LEV) showed a similar explanatory relationship with the GROWTH variable regarding statistical significance and the nature of the relationship with the dependent variable. However, the variable has less explanatory power than the GROWTH variable in absolute terms. The results of these two indicators may be seen to reflect structural constraints in the banking sector, supporting IO theory’s emphasis on market maturity and diminishing returns in saturated industries.
On the other hand, regarding the CET1 variable, the results show that it is positively and statistically significantly associated with bank performance. This is validated by the t-statistic value (2.3744) of the coefficient, which is greater than the benchmark +/−1.95. When scoping, the findings suggest that a single standard unit change in CET1 resulted in a positive 2.4 impact on bank performance. The study controlled for the regulatory framework reforms as well as exogenous economic shocks related to the global financial crisis and COVID-19 pandemic. However, both variables are statistically insignificant at the 5% significance level. In addition, these variables exhibited a negative association with the dependent variable, with varying degrees of influence in absolute terms. The above findings align with the RBV as they emphasise capital adequacy as a valuable resource. Moreover, they are also consistent with the dynamic capabilities framework, as CET1 is considered to reflect banks’ capacity to reconfigure and adapt financial buffers in response to shocks. Neither the IFRS accounting standard dummy nor the economic disturbance dummy is statistically significant in the short run. However, from an institutional theory standpoint, their inclusion captures how regulatory framework reforms and external disruptions may influence performance expectations, even if their immediate effects are limited.
The study was interested in the long-run relationship of the variables, mainly credit risk variables, on banks’ performance. Hence, the PECM model was used to ensure that the findings capture both the short-run and long-run dynamic of the variables’ behaviour, accounting for time frequency and variation in the data series to ensure that the findings are reliable. As mentioned in the previous section, the study focuses on the impact of credit risk on banks’ performance. As such, the focus of is on credit risk variables, ECL_IS, ECL_BS, and NPL. The study accounts for growth, CET1, economic disturbance, and accounting regulation framework. The model presents the accounting regulation framework and economic disturbances as dichotomous variables in the empirical model.
The long-run findings indicate that all variables, except the IFRS_DUM, are statistically significant in terms of their explanatory power for bank performance in the long run. The value of the t-statistic shows that a standard unit change of ECL_BS resulted in a 3.18 negative impact on bank performance in the long run. The findings show that ECL_IS is statistically significant in the long run; this is evident in the p-value that is less than the 0.05 benchmark statistical significance level, p < 0.05. The value of the t-statistic shows that a single standard unit change in ECL_IS caused a negative impact of 4.18 on the dependent variable. When examining ECL_BS and ECL_IS, this study shows that ECL_IS caused the most impact in absolute terms compared to ECL_BS, with a marginal difference. Both of these measures underscore the enduring relevance of credit risk management over time, a central tenet in both the previously mentioned RBV and dynamic capabilities theoretical frameworks.
Scoping to other credit risk variables, the findings show that NPL is statistically significant at a 5% significance level in the long run; the explanatory power that the variable has on the dependent variable is 11.9522. Further examination indicates that a single unit change caused a positive 11.92 impact on bank performance. NPL has the highest absolute effect on bank performance than other credit risk variables. This may be seen as reflecting structural pricing advantages or dominant market positions, as interpreted through the IO lens. The control variable GROWTH negatively and statistically significantly impacts the dependent variable. The value of the t-statistic of the control variable is greater than the benchmark of +/−1.95, and the associated p-value is less than 0.05. The t-stat value of −7.6800 indicates that the variable had a single standard unit change in the GROWTH variable, and has caused a 7.68 change in the dependent variable in standard units. At the same time, LEV reverses direction, showing a positive effect (2.06), while CET1 again exhibits a strong positive impact (6.93), reinforcing its role as a resilience-enhancing mechanism. Together, these three statistics (GROWTH, LEV, and CET1) support the argument that adaptive financial structuring and capital management represent dynamic capabilities that banks deploy to maintain long-term viability.
As previously mentioned, the analysis controlled for regulatory framework changes and economic disturbances; however, only the economic disturbance dummy (DISTURB_DUM) was statistically insignificant at the 5% significance level. The IFRS_DUM was positive and statistically significantly associated with bank performance. The t-statistic of the variable is recorded at 2.5720, indicating that a single standard unit deviation in the variable influenced the dependent variable by 2.5720 units in the long run. The latter suggests that institutional conformity to global reporting standards enhances legitimacy and investor confidence in line with the key pillars of institutional theory. On an absolute value comparison, the PECM model indicates that the economic disturbance dummy (DISTURB_DUM) variable had the least impact on bank performance, with a marginal difference separating the two variables.
Taken together, the results confirm a stable long-run equilibrium, as indicated by the significantly negative error correction term (ECT = −0.736), affirming convergence toward equilibrium at a 74% adjustment speed. This rapid convergence reflects dynamic capability in action, reflecting the distinctive capacity of the South African commercial banking sector to correct disequilibria and realign performance through internal and external adaptation mechanisms.
4.1. Post-Modelling Diagnostics
4.1.1. Heteroskedasticity
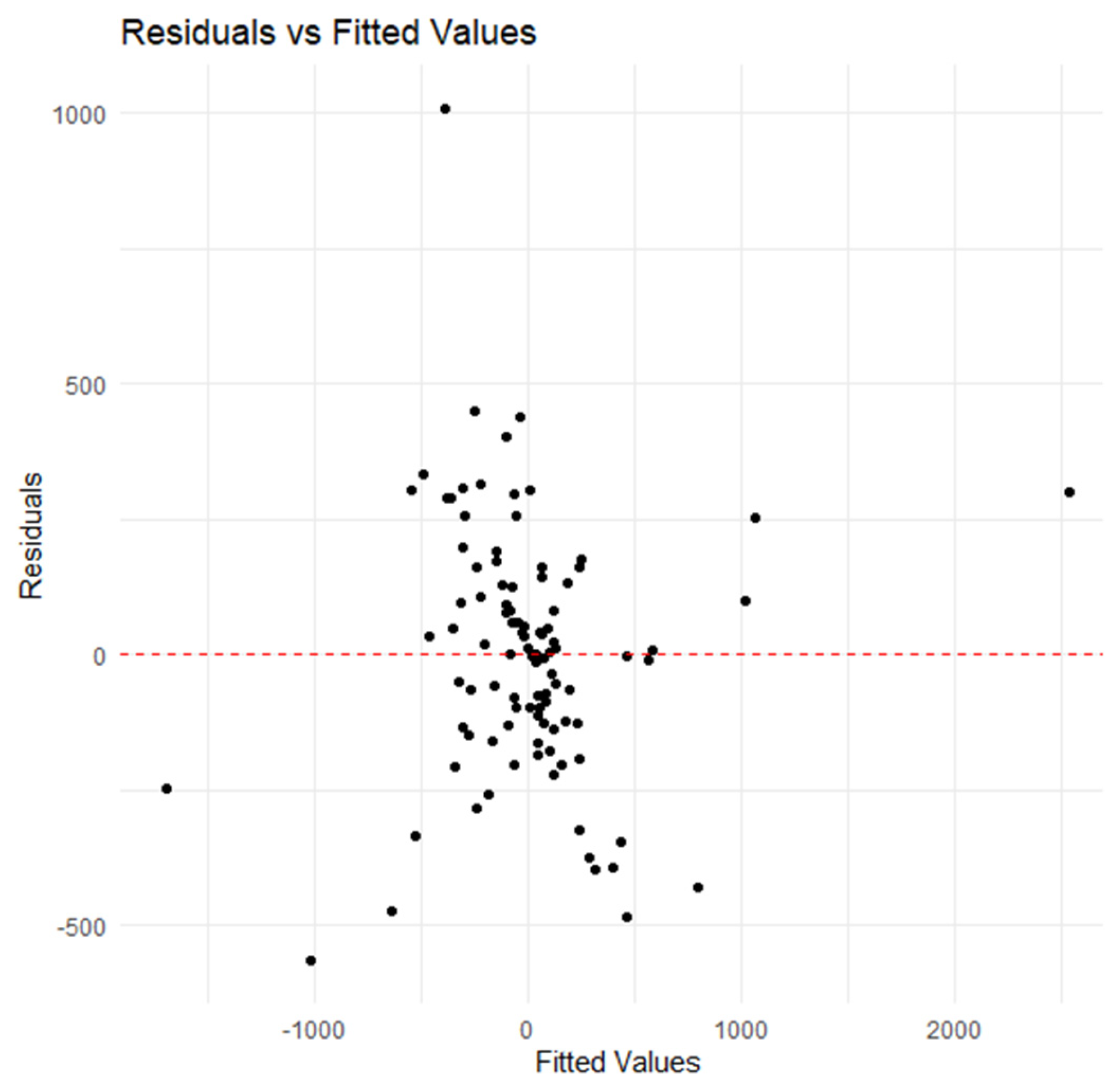
This section presents the results of homoskedasticity. This study utilised both the formal and informal approaches to detecting heteroskedasticity in the PECM model’s idiosyncratic errors. In this regard,
Figure 4 presents the informal approach, while
Table 6 presents the formal approach. The results in
Figure 4 show the predicted (fitted) values of the dependent variable from the model, the residuals (the difference between predicted values and actual values), and the line where Y = 0. This line presents a region where the residuals should randomly scatter around. From visual inspection, it can be observed that the spread of the residuals appears to be relatively consistent across the range of fitted values. In addition, the residuals appear to be randomly scattered around the zero line and there is no clear pattern of the speed increasing or decreasing as predicted values increase.
Table 6 presents the findings of the Breusch–Pagan homoskedasticity test. The test was used to examine the nature of variance among the residuals. The findings show that there is not enough evidence to conclude that the model’s residuals are not equal. Thus, this study failed to reject the test’s null hypothesis that the residuals are Homoskedastic, thus the conclusion is that there is no presence of heteroskedasticity among the residuals.
4.1.2. Serial Correlation
The next post-model diagnostic process was examining the serial correlation among the residuals. Testing for this is vital because serial correlation causes ordinary least squares (OLS) to no longer be a minimum variance estimator. In addition, it biases the estimated variances of the regression coefficients, making the t-statistic appear more significant than it is. As a result, the Wooldridge test for serial correlation was utilised to detect whether the residuals are correlated, and the findings are presented in
Table 7.
The findings presented in
Table 7 suggest insufficient statistical evidence to conclude that there is serial correlation in the idiosyncratic errors of the estimated PECM model. This is because the
p-value (0.1392) is greater than 0.05. Thus, the null hypothesis of the Wooldridge test could not be rejected.
5. Conclusions
This study investigated how bank-specific credit risk factors influence the short- and long-term financial sustainability and resilience of commercial banks, drawing on empirical data from listed South African commercial banks over an uninterrupted eighteen-year period (2006 to 2023). By integrating five key credit risk proxies comprising expected credit losses, impairment gains or losses, non-performing loans (NPLs), capital adequacy (CET1), and leverage, the study employed a comprehensive panel data framework to isolate the distinct effects of credit risk on long-term financial sustainability. This analysis controlled for growth dynamics, exogenous macroeconomic disruptions such as the COVID-19 pandemic and the global financial crisis, as well as regulatory framework reforms.
A central contribution of this study lies in its methodological rigour, particularly the formulation of a holistic model that captures the complex, multidimensional nature of credit risk and its bearing on the long-term financial sustainability of commercial banks. The application of robust statistical and econometric techniques not only ensured the integrity of the results, but also enabled the identification of significant, and in several cases theoretically consistent and intuitive, relationships between the explanatory variables and financial sustainability. In particular, expected credit losses (ECL_BS) and impairment-related measures (ECL_IS) were found to have negative and statistically significant effects, while CET1 and NPLs displayed positive associations, consistent with the theoretical role of capital buffers in enhancing resilience and the risk-pricing potential of NPLs in credit markets. These findings affirm the relevance of multiple theoretical perspectives—including the resource-based view, institutional theory, industrial organisation, and the dynamic capabilities framework—in explaining commercial bank resilience over time. Ultimately, this study contributes a replicable empirical model that provides a robust foundation for future research on the interplay between credit risk and financial sustainability in banking systems.
Future research could expand the scope of this study by conducting cross-country analyses in other emerging market economies, particularly within the BRICS bloc or the SADC region. Such comparative investigations would provide deeper insights into regional banking dynamics, structural differences, and institutional responses to credit risk. Moreover, integrating environmental, social, and governance (ESG) factors into the analytical framework would offer a more holistic perspective on how non-financial sustainability dimensions interact with credit risk and influence long-term financial sustainability. Finally, longitudinal studies examining the impact of major regulatory framework shifts as recommended in the current study would further enrich our understanding of policy efficacy and institutional resilience over time.