Optimization of a Cooperative Truck–Drone Delivery System in Rural China: A Sustainable Logistics Approach for Diverse Terrain Conditions

Abstract

Driven by the rapid expansion of e-commerce in China, there is a growing demand for high-efficiency, sustainability-oriented logistics solutions in rural regions, particularly for the time-sensitive distribution of perishable agricultural commodities. Traditional logistics systems face considerable challenges in these geographically complex regions due to limited infrastructure and extended travel distances. To address these issues, this study proposes an intelligent cooperative delivery system that integrates automated drones with conventional trucks, aiming to enhance both operational efficiency and environmental sustainability. A mixed-integer linear programming (MILP) model is developed to account for the diverse terrain characteristics of rural China, including forest, lake, and mountain regions. To optimize distribution strategies, the model incorporates an improved Fuzzy C-Means (FCM) algorithm combined with a hybrid genetic simulated annealing algorithm. The performance of three transportation modes, namely truck-only, drone-only, and truck–drone integrated delivery, was evaluated and compared. Sustainability-related externalities, such as carbon emission costs and delivery delay penalties, are quantitatively integrated into the total transportation cost objective function. Simulation results indicate that the cooperative delivery model is especially effective in lake regions, significantly reducing overall costs while improving environmental performance and service quality. This research offers practical insights into the development of sustainable intelligent transportation systems tailored to the unique challenges of rural logistics.

1. Introduction

In recent years, China’s express delivery industry has experienced remarkable growth. Since the market was liberalized in the late 1980s, the annual delivery volume has surged, reaching 40 billion items by 2017, with an average annual growth rate of 42.0%, consistently ranking first globally. The widespread adoption of information and communication technologies (ICT), including big data, cloud computing, and the Internet of Things, has significantly enhanced the timeliness, accuracy, and intelligence of logistics services. As a result, demand-driven and technology-enabled intelligent distribution systems have emerged to meet increasingly diversified customer expectations [1].

Amid this transformation, the rise of rural e-commerce has played a pivotal role in reshaping logistics service demand. The coverage and service quality of rural express delivery have steadily improved, benefiting nearly 600 million rural residents. In 2023, China’s rural online retail sales reached 2.5 trillion CNY—a 12.9% year-on-year increase and a thirteenfold increase compared to 2014 [2,3]. National initiatives such as the “E-commerce into Rural Areas” project, jointly promoted by the Ministry of Commerce and other departments, have further strengthened rural logistics infrastructure.

However, the logistics distribution of agricultural products in rural areas faces significant challenges. These products are highly perishable and time-sensitive, while rural regions are often characterized by sparse populations, rugged terrain, and inadequate transportation infrastructure. Consequently, conventional logistics models struggle to meet service requirements with respect to cost efficiency, reliability, and coverage.

To overcome these limitations, drones have recently emerged as a promising solution to enhance last-mile delivery in remote rural areas. A two-stage cooperative distribution model—integrating conventional trucks and drones—has shown potential in improving both temporal and spatial efficiency [4,5]. This intelligent cooperative system leverages the strengths of each mode: drones provide speed and accessibility in hard-to-reach locations, while trucks offer stability and larger load capacities over long distances.

Considering the unique characteristics of agricultural products in logistics and distribution, this study focuses on the distribution of agricultural products and explores how to optimize the logistics routes for rural agricultural products through the combined distribution system of trucks and drones. The focus of this study is on last-mile delivery to rural user locations, rather than the collection of bulk agricultural products from farms. The modeled scenario reflects the growing demand for small-parcel delivery driven by rural e-commerce, precision agriculture support, and the supply of time-sensitive agricultural inputs. Researchers both domestically and internationally have examined the potential applications of drones in urban and certain rural areas by developing various models. Recent studies have explored truck–drone coordination under complex delivery conditions, such as dynamic synchronization with uncertain travel times to improve reliability and efficiency [6], and use VNS to utilized to optimize the truck–drone collaborative delivery, supporting multi-site access and take-off and landing of non-customer nodes [7]. Scholars such as Li and Bi [8,9] separately, proposed urban logistics distribution models based on drones, focusing on evaluating the distribution efficiency of drones in urban environments.

Unlike prior studies that typically assume flat terrain or urban infrastructure, our work incorporates heterogeneous rural terrain features—specifically mountainous, lake, and forest areas—into the optimization process. Furthermore, this study extends existing models by comparing multiple delivery modes (truck-only, drone-only, and combined truck–drone systems) under varying environmental constraints, thereby providing a more comprehensive analysis of multi-modal delivery performance in geographically diverse rural regions. However, due to the complex terrain in rural areas of China and the significant variations in natural conditions, such as mountainous, lake, and forest regions, selecting an appropriate distribution mode based on local conditions remains a pressing research challenge. The terrain in rural China varies greatly, with notable differences in climate, road conditions, and farmland distribution across different regions. These factors make the selection and optimization of distribution methods more complex and challenging.

Therefore, conducting precise research on distribution models tailored to the geographical characteristics of rural areas in China has become an urgent issue. In particular, how to optimally select the combination of trucks and drones based on the varying road conditions across different regions to achieve the lowest cost and maximize customer satisfaction has not been fully explored in the existing literature.

Representative mountainous, lake, and forest terrains were selected from three major regions in southern, northern, and central China, and a mixed-integer linear programming (MILP) model was developed. Combining an improved Fuzzy C-Means (FCM) clustering algorithm with a genetic simulated annealing (GA-SA) algorithm, three distribution modes were compared and analyzed: truck-only delivery, drone-only delivery, and combined truck–drone delivery. The inclusion of time delay and carbon emission penalty factors aims to provide a balanced solution that optimizes both efficiency and sustainability for the “last mile” in rural areas.

The three selected terrains—mountainous, lake, and forest areas—exhibit typical geographical features and effectively represent the diverse and complex conditions found in rural areas of China [10,11]. In mountainous areas, roads are often narrow and uneven, which can significantly limit the effectiveness of truck-only delivery. In lake areas, slippery terrain and poor accessibility in certain areas make drones a more suitable option for investigation. Forest areas are characterized by complex road networks and relatively low population density, where the integration of trucks and drones can help compensate for the limitations of each mode. Therefore, selecting these three terrains for comparative analysis enables a more comprehensive assessment of the applicability of different distribution methods.

Taking terrain impact into account, this study compares three distribution modes: truck-only delivery, drone-only delivery, and combined truck–drone delivery. Truck delivery is more suitable for areas with favorable road conditions, while drone delivery effectively addresses the last-mile challenges in remote and hard-to-reach locations. The integrated truck–drone mode combines the strengths of both systems, enhancing efficiency in complex terrains. Given the geographical diversity of China’s rural areas, this study systematically examines the practical performance of different delivery strategies using modeling and simulation analyses. In contrast to previous studies, this research introduces an optimization model that incorporates the truck–drone combination across mountainous, lake, and forest terrains, while also accounting for delivery delay time and carbon emission penalties. This approach contributes valuable theoretical insights and practical guidance for optimizing last-mile logistics in rural areas.

2. Literature Review

In recent years, drone delivery has become a prominent topic in global smart logistics research due to its flexibility, rapid response capabilities, and low operating costs. Research on rural logistics and drone delivery, both domestically and internationally, has been steadily increasing. However, the majority of existing studies still primarily focus on urban and suburban delivery scenarios. International scholars have largely examined the effectiveness of drone technology in urban last-mile delivery, such as using drones for small-package distribution to alleviate traffic congestion and reduce labor costs. In contrast, the issue of drone delivery in rural areas, which presents complex geographical conditions, has received relatively limited attention.

Although domestic research has recently begun to shift focus toward rural logistics systems in recent years, much of it remains centered on enhancing the efficiency of traditional truck transportation or piloting drone technology in specific locations. There remains a notable lack of systematic route optimization and comprehensive model comparisons. Meanwhile, the development of the low-altitude economy has provided both policy and technological support for the commercialization of drones in rural areas. In particular, the two-stage distribution system, in which trucks transport drones to designated front-end nodes and drones complete the final leg of delivery, has gradually emerged as a key focus in current research initiatives [12,13].

As e-commerce continues to expand into penetrate rural areas, the importance of “last-mile” delivery in rural logistics is becoming increasingly evident. While drones have been widely adopted in urban environments, their feasibility and optimization strategies in the context of vast rural areas, with inconvenient transportation and complex terrain, remain underexplored. This is particularly relevant in China, where rural areas exhibit significant geographical diversity. Developing an efficient, low-carbon, and intelligent collaborative distribution model that integrates drones with traditional truck transportation has become a pressing and practical challenge.

Currently, most studies, both domestic and international, remain limited to analyzing single-mode distribution systems. Few have conducted comprehensive comparisons of the adaptability and efficiency of manual labor, trucks, drones, and their combinations across different terrains and resource conditions. This lack of multi-mode system evaluations, especially under the complex geographical constraints of rural areas, hinders the broader application and optimization of drone-based delivery solutions in diverse real-world scenarios.

Table 1. Research comparisons of drone delivery from 2015 to 2024.

Reference	Vehicles-Drones	Objectives	Time Windows	Consideration Factor 1	Consideration Factor 2	Combination Mode
Murray and Chu (2015) [14]	1-1	Minimum return time	No	Multitasking	Truck capacity	PDSTSP FSTSP
Ha et al. (2018) [15]	1-1	Minimum cost	No	Drones are retrieved from different locations	Cost of waiting for punishment	Series transportation
Kitjacharoenchai et al. (2019) [16]	m-u	Minimize time	No	Truck capacity and customer demand are not considered	Drone launch and recovery times at nodes were ignored	The drone launched from and returned to a nearby truck
Roberti et al. (2020) [17]	1-m	Minimum service time	No	Dynamic programming recursion models several variants of TSP-D	Strictly limit the set of feasible solutions	The Traveling Salesman Problem with Drones (TSP-D)
Chuan Wang et al. (2021) [18]	1-m	Optimal delivery cost	No	Trucks are responsible for transporting goods and drones to the station	Truck costs and drone delivery costs, including fixed parking fees	m-TSP-LAP
Moshref-Javadi et al. (2020) [19]	1-m	Minimum waiting time and cost	Yes	Each drone is delivered only once per shipment	A combination of trucks and drones in urban environments	STRP, trucks serve as mobile warehouses for drones
Yunqiang Yin et al. (2024) [20]	m-m	Minimum distribution negative utility	Yes	When parked at the mobile warehouse, the vehicle’s drone can be dispatched simultaneously	The optimal allocation of hospital cluster centers and the optimal collaborative path	VDCDRP-BP
Felix Tamke (2021) [21]	m-m	Minimum time	No	Restrictions on the flight range of drones	The truck cannot wait to retrieve the drone	Series transportation
Wang and Sheu (2019) [22]	m-m	Minimum cost	No	Flight range	Loading limit	Drones can dock at the docking nodes
Nawin Yanpirat (2023) [23]	1-m	Minimum service time	No	Deliver and collect packages simultaneously	Different loading capacities of drones	FSTSP-DR-MP
Zhiliang Bi et al. (2023) [4]	1-m	Minimize the waiting time	No	Trucks provide services for drones	Determine the driving path of the truck in a random environment	TSP
Schermer et al. (2019) [24]	m-m	Minimum completion time	No	Drones are deployed and retrieved at designated vertices and along arcs	/	VRPDERO
Konstantin Kloster et al. (2022) [25]	m-m	Minimum completion time	No	The drone station operates drones independently	/	mTSP-ds
Mo Elsayed (2020) [26]	/-1	The carbon emissions of unmanned aircraft	No	Three types of distribution methods	All-day parcel delivery operations in both urban and rural areas	/
Shuangxi Tian et al. (2023) [27]	1-m	Minimum the total cost	No	The large-scale target surveillance problem	The energy consumption model of the drone	Two-echelon routing problem (2E-RP)
Zhi Pei et al. (2024) [28]	/-2	Minimum delivery time	No	Battery capacity of drones	Urban delivery environment	/
Hossain et al. (2022) [29]	1-1	Analysis of the impact of drone performance	/	Four indicators predict the performance of drones	/	Trucks, drones only, and truck–drone combinations
Jeng-Shyang Pan et al. (2020) [30]	/-m	Minimum cost	No	Factors such as traffic and size around the village	The drones only deliver goods to the edge of the village	Unmanned logistics centers are combined with drones
Mohamed Salama (2020) [31]	1-m	Minimum cost/time	No	Cluster focus	All decisions involved in the model’s joint optimization	Allows multiple drones to be delivered in a cluster
Our study	1-1	Minimum cost and minimum delayed delivery time	Yes	Carbon emissions and delay costs	Comparison of three different terrains	Truck-and-Drone Coordinated Routing Problem with Time Windows and Environmental Costs (TDRP-TW-EC)

systematically organizes and compares the main studies from 2015 to 2024, providing a detailed comparison with the research presented in this study. A total of 19 relevant studies from the past decade were selected for comprehensive comparative analysis. Since Murray and Chu (2015) [14] pioneered the representative literature of the PDSTSP model, a large number of subsequent studies have focused on the application of the Mixed Integer Programming (MILP) model in path optimization (such as Ha et al., 2018 [15]; Kitjacharoenchai et al., 2019 [16]; Roberti et al., 2020 [17]; (Chuan Wang et al., 2021 [18]), and with minimizing the total cost, service time, completion time or customer waiting time as the main optimization goals, it shows a high degree of attention to scheduling efficiency and logistics cost.

In terms of model constraints, different studies have set up multiple extension factors in combination with actual distribution scenarios. Most studies do not consider the time window, but a few, such as Moshref-Javadi et al. (2020) [19] and YunqiangYin et al. (2024) [20], introduce time constraints to enhance the practical adaptability of the model. Felix Tamke (2021) [21] and Wang and Sheu (2019) [22] particularly emphasized flight range limitations, while Yanpirat (2020) [23] and Bi et al. (2023) [4] considered the diversity of drone payload and energy consumption management issues. In terms of the recycling mechanism, Ha et al. (2018) [15] explored the path changes brought about by recycling at different locations. Schermer et al. (2019) [24] and Kloster et al. (2022) [25] extended to the flexible mechanism of in-transit operation and delivery at transfer nodes. Mo Elsayed (2020) [26] simulated the operation of daily parcel delivery in urban and rural contexts.

In terms of the distribution combination mode, almost all studies adopt the truck–drone joint distribution mode, and most of them are configured with one vehicle and multiple drones, such as Momeni (2023) [27], Bi (2023) [4], and Pei (2024) [28]. There is also Yin, (2024) [20], whose hospital cluster model considers more complex transfer and collaboration scenarios. Furthermore, Hossain et al. (2022) [29] introduced the Bayesian network method to reason and analyze the influencing factors of drone performance, expanding the modeling boundary of traditional path optimization research. Pan et al. (2020) [30] set delivery restrictions based on the traffic conditions in rural scenarios and proposed a setting in which drone delivery does not enter villages, demonstrating the importance of practical constraints in rural environments.

In terms of algorithms, in addition to traditional exact algorithms, an increasing number of studies tend to integrate meta-heuristic algorithms (such as GRASP, VNS, and TS), intelligent optimization algorithms (such as Improved Cuckle Search and DQN), and machine learning methods (Salama, 2020 [31]) to enhance the solution efficiency and scalability. For instance, Kloster (2022) [25] proposed a multi-stage algorithm for scheduling autonomous drone stations, and Yin (2024) [20] combined the Benders decomposition and pricing algorithm to solve complex distributed routing problems.

Overall, the existing research can be roughly divided into four categories. The first includes studies focusing on single-truck delivery that explore route optimization and cost-efficiency in traditional ground-based logistics, particularly in rural and suburban areas with established road networks [32]. The second category focuses on the single drone mode, which is mostly used for short-distance delivery and point-to-point services [33]. The third type of research focuses on multi-mode combined systems, especially truck–drone cooperative models for path optimization and synchronized dispatch [34,35]. The fourth category attempts to explore the influence of geographical environment differences on distribution strategies and route selection [36]. This four-layer classification framework provides a more comprehensive theoretical basis for the comparative analysis in this study.

Most of these studies adopt methods such as mixed integer programming, dynamic programming, or intelligent algorithms to construct models and evaluate their efficiency and feasibility using simulation. However, it is important to note that a systematic comparison of the adaptability and optimization performance of different models under complex rural terrain conditions remains largely absent in the current literature.

Although existing research has made significant progress in model design, constraint setting, and algorithm solutions, there are still three main deficiencies: (1) Most studies fail to incorporate real-world environmental constraints, such as carbon emission costs and delay penalties; (2) Few studies systematically integrate topographical factors (such as mountainous, lake, and forest areas) into modeling to simulate the impact of terrain on speed, path selection, and costs; (3) There is a notable lack of comparative analysis on the adaptability of the three modes—trucks, drones, and their combinations—under different terrain conditions.

In response to the identified gaps, this study proposes a MILP optimization model that integrates both minimum total cost and minimum delay time objectives. The model incorporates carbon emission penalties and delivery delay costs into the objective function and introduces a terrain penalty coefficient to simulate the impact of terrain complexity on speed and route selection. To improve computational efficiency for large-scale problems and enhance the quality of the global optimal solution, this study adopts an improved Fuzzy C-Means (FCM) algorithm for clustering distribution tasks and integrates the genetic algorithm-simulated annealing (GA-SA) algorithm for global path optimization. Using three representative rural terrains—forest areas in Fujian, mountainous regions in Shanxi, and lake areas in Hubei—the study systematically compares the differences in cost, delivery time, and carbon emissions associated with three distribution modes: truck-only delivery, drone-only delivery, and truck–drone collaborative delivery. The findings offer both theoretical insights and practical guidance for optimizing rural e-commerce logistics systems under diverse geographical conditions.

3. Typical Rural Terrain

China’s rural areas are vast, with complex and diverse topography and landforms, resulting in significant spatial variations. This diversity in geographical and climatic conditions not only profoundly affects agricultural production models and resource utilization methods but also leads to notable differences in logistics demands, transportation accessibility, and infrastructure development across various regions. According to Zhou Yang’s analysis of the regional types of rural areas in China [37], rural areas in China can be roughly divided into the developed areas along the eastern coast and the underdeveloped areas in the central and western regions. The former includes some rural areas in the “Yangtze River Delta”, “Pearl River Delta”, and “Beijing-Tianjin-Tangshan” urban agglomerations and coastal provinces such as Shandong, Liaoning, and Fujian. Villages in the eastern regions exhibit a high degree of differentiation, with relatively advanced industrial integration and development. In contrast, the central and western regions are predominantly composed of traditional agricultural villages, characterized by low differentiation. Agriculture plays a central role in these areas, which are currently key focal points for rural revitalization and the optimization of logistics systems.

In this context, with careful consideration of natural geographical conditions, the typical landforms in rural areas of the central and western regions can be categorized into mountainous areas, lake areas, and forest areas. Mountainous areas are primarily characterized by undulating hills and winding roads, which limit transportation accessibility. However, these regions are well-suited for developing high-value-added industries such as forestry, fruit production, and ecological agriculture. Lake areas feature flat terrain and a dense network of water systems, making them ideal for aquaculture and grain crop cultivation. The agricultural products from these areas are typically bulk and perishable, leading to concentrated logistics demand with strong timeliness requirements. Forest areas, rich in forest resources, play a key role in forestry development and ecological protection. In these areas, logistics and distribution systems must balance both environmental protection and efficiency.

Based on the classification above, this study selects three representative provinces—Fujian (forest area), Shanxi (mountainous area), and Hubei (lake area)—as typical sample areas for a comparative analysis of differentiated logistics models. The forest areas of Fujian Province are known for their abundant mountains and dense forests, providing favorable conditions for ecological forestry and green distribution. The mountainous regions of Shanxi Province, characterized by significant terrain undulations and complex transportation conditions, present higher demands for multi-modal transport and route optimization. The lake area of Hubei Province, with its intricate network of waterways, is well-suited for exploring combined water and land distribution models or high-frequency, short-cycle distribution strategies. To comprehensively evaluate distribution efficiency and costs under different terrain conditions, this study designs and simulates three primary logistics models: truck delivery, drone delivery, and truck–drone collaborative delivery. Using empirical comparisons across various landforms, the study analyzes the performance differences of each model in terms of transportation costs, distribution time, carbon emissions, and other factors. Ultimately, the findings provide practical insights and decision-making references for the development of an intelligent and sustainable last-mile logistics system in rural areas.

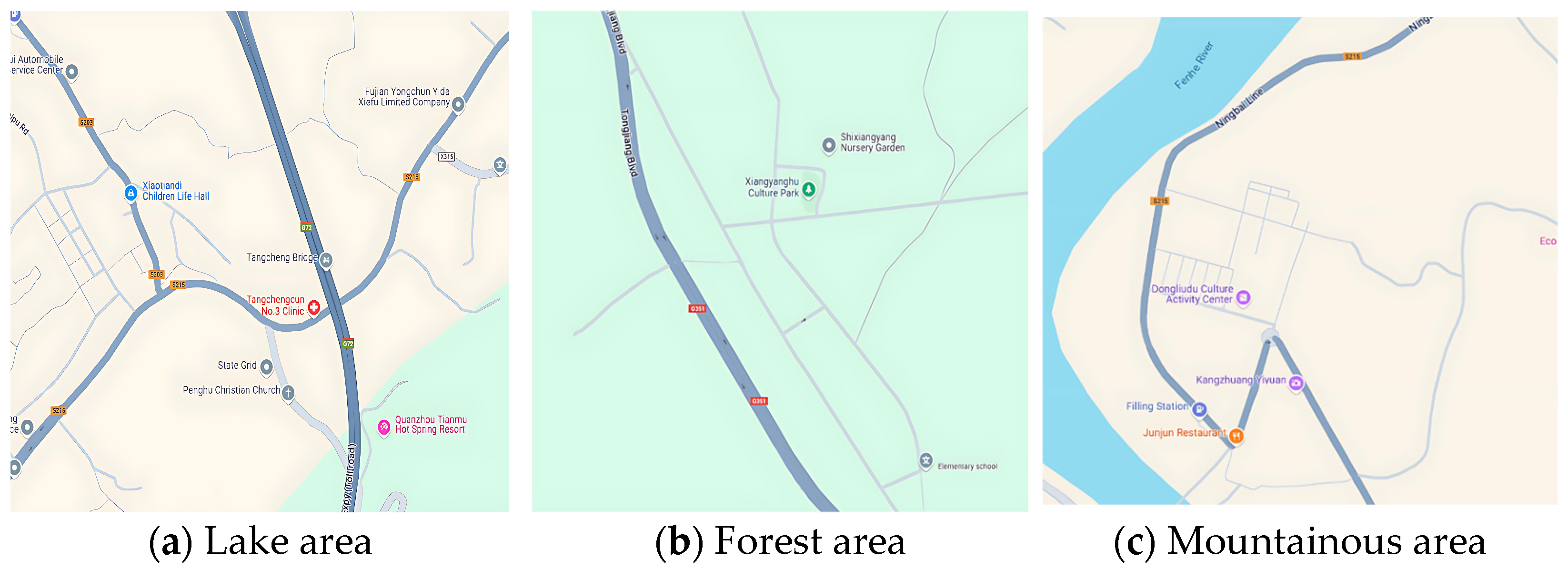
In conclusion, dividing rural areas in China into three major regions, including forest areas, lake areas, and mountainous areas, not only helps to provide precise rural development strategies based on geographical, climatic, and resource conditions but also promotes the differentiated implementation of rural revitalization policies and enhances the overall development level of the rural economy. This study, based on the road imaging service provided by Google Maps and combined with the road extraction service provided by Planning Cloud, derives the three major topographic maps used for simulation and emulation.

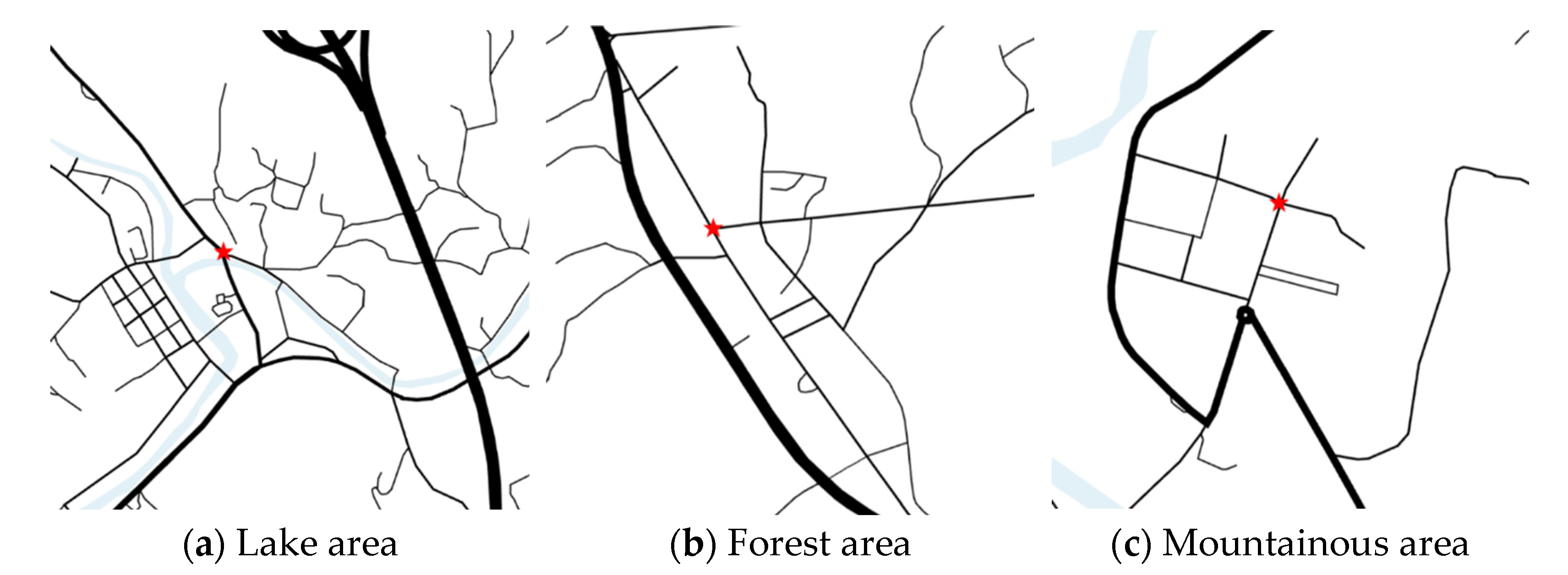
The representative terrain areas of forest, lake, and mountainous regions were selected as Meizhong Village in Penghu Town, Yongchun County, Quanzhou City, Fujian Province; Guojiawan Village in Xian’an District, Xianning City, Hubei Province; and Dongliudu Village in Luofan County, Taiyuan City, Shanxi Province, respectively. In these areas, the red five-pointed star denotes the local postal center, which also serves as the township center. The selected map and the road distribution diagram are presented in Figure 1 and Figure 2.

4. Problem Description and Model Assumptions

4.1. Problem Hypothesis

Based on the branch query service provided by the China Post website, the branch is used as the departure point for trucks or drones, serving as the distribution center. In the truck-only distribution mode, all distribution tasks are carried out solely by trucks. The trucks depart from the distribution center and deliver goods to each user point via the road network. For user points that are not accessible by road, manual distribution is used, and the corresponding delay time is factored in as a penalty cost. This mode aims to evaluate the benefits of single-truck distribution and serves as the comparison benchmark for the truck–drone combination. In the drone-only delivery mode, all tasks are handled entirely by drones. This study does not aim to compare the absolute efficiency of trucks and drones in isolation, but rather to investigate the performance improvements achievable through their coordinated use in rural logistics scenarios. The drones depart from the distribution center and fly directly to each user point for delivery. This mode assesses the performance of a single drone, focusing particularly on the feasibility of independent operation under favorable geographical conditions. The truck–drone combined delivery mode involves a two-stage delivery process. In the first stage, trucks transport drones from the distribution center to suitable parking positions. In the second stage, drones depart from the trucks and fly to various user points to complete the last-mile delivery. This mode aims to explore the comprehensive effects of truck–drone combined delivery in real rural terrains.

To minimize the total cost, we integrate factors such as fuel cost, labor cost, and maintenance cost into two main cost components, including the purchase cost and the fuel cost, which are closely tied to driving distance. Given the unique nature of agricultural products, delay time may lead to a decline in quality, and the environmental burden of carbon emissions impacts the sustainability of the logistics system. Therefore, this study incorporates delay time and carbon emissions as penalty factors in the total transportation cost calculation. Finally, the total distribution cost and total distribution time are used to evaluate the efficiency of each distribution mode. To simplify the problem, we make the following assumptions in the model design:

(1)

It is assumed that the transportation capacity and performance of trucks and drones remain stable, but the issue of drone endurance is not considered. While in practical applications, factors such as weather and load changes may affect the performance of trucks and drones, this study assumes constant performance for both vehicles throughout the entire distribution process to maintain the simplicity and operability of the model.

(2)

It is assumed that the flight speed and altitude of the drone are fixed, while the truck follows actual road conditions in its route planning. Since the flight speed and altitude of drones are typically constrained by technical standards or regulations, these parameters are assumed to be constant. The truck’s route planning is based on the actual road network in rural areas to ensure geographical accuracy. Simplifying the drone’s flight path to a straight line reduces model complexity and aids in the comparative analysis of different delivery modes.

(3)

It is assumed that each user point is served by a single drone, and each user point receives only one delivery task. Distribution tasks in rural areas are typically independent, with clear demand at each user point. By assigning a single drone to each user point, this assumption aligns with real-world operations and simplifies the model. It eliminates the complexity of multiple drones serving the same point, thus enabling a clearer evaluation of the optimization effects when combining drones and trucks.

(4)

It is assumed that all user points are accessible to drones in static planning, and dynamic real-time obstacle avoidance or drone charging limitations are not considered. To simplify the model, each delivery point is assumed to be directly reachable by a drone under the influence of pre-evaluated terrain resistance factors. Environmental factors such as forest density, water barriers, and mountain slopes are indirectly accounted for in the clustering and path planning stages, while in-flight obstacle detection and energy management are beyond the scope of this study.

(5)

It is assumed that each delivery task is carried out by a combination of one truck and one drone from each distribution center. While multiple vehicles and drones may be used in practice, this assumption simplifies the analysis and allows for a clearer understanding of how the combination of trucks and drones affects distribution efficiency and cost across different terrains.

(6)

Different terrains impact the transportation speed and capacity of trucks and drones in varying ways. Considering the diversity of rural terrains, the speeds of trucks and drones will be adjusted based on the characteristics of mountainous, forest, and lake regions. Mountainous areas are likely to negatively affect truck speeds, and the flight speed of drones may also be influenced by the undulating terrain. In forest and lake areas, the impact on the speeds of both trucks and drones will differ according to the specific terrain features. By incorporating these adjustments, the model will more accurately reflect logistics transportation efficiency in various terrains, thereby providing valuable support for subsequent logistics optimization efforts. In the modeling process, terrain correction coefficients are introduced to adjust the default speeds of trucks and drones, thereby reflecting the impact of different geographies on actual travel times.

(7)

It is assumed that the demand for agricultural products at each distribution point is fixed, and the maximum package weight does not exceed the minimum load capacity of a single package that can be carried. In other words, the demand at each distribution point remains constant throughout the distribution process, with a focus on the delivery of small- and medium-sized agricultural products.

4.2. Parameter Setting

Considering the approximate area of rural regions, square areas are selected for analysis. Each rural area covers 144 square kilometers. Assuming that the minimum distance between user points is approximately 500 m, and each household occupies 500 square meters, the distribution situation of 100 user points is analyzed. The parameter settings used in this study are outlined in

Table 2. Symbol and parameter settings.

Type	Variable	Definition
Assembles	C	The aggregated set of N distribution points, $C=\{c_1,c_2\cdots c_n\}$
	N	The set of M user points, $N=\{n_1,n_2\cdots n_m\}$
	V	The collection of distribution points and user points, $V=C\cup N$
	D	A collection of distribution centers, delivery points, and users, $D=\left\{\right(x_0,y_0\}\cup C\cup N$
	T	A collection of K trucks, $T=\{t_1,t_2\cdots t_k\}$
	W	The assembly of D drones, $W=\{w_1,w_2\cdots w_d\}$
Parameters	$P_i$	The priority of user point $i$
	$V_t$	The average driving speed of the truck
	$V_d$	The average traveling speed of drones
	$\widehat{T_i}$	The time when the truck provides service for user point $i$
	$T_i$	The time when the drone provides service to user point $i$
	$L_t$	The maximum mileage of the truck
	$L_d$	The maximum driving range of the drone
	$(x_i,y_i)$	The point coordinates of user $i$
	$C_t^1$	The purchase cost of each truck
	$C_d^1$	The purchase cost of each drone
	$C_t$	The unit operating cost of the truck
	$C_d$	The unit operating cost of the truck
	$Q_t$	The maximum load capacity of the truck
	$Q_d$	The maximum load capacity of the drone
	$\phi$	The unit weight of the goods
	$\mu$	The unit weight of a drone
	$q_i$	The demand quantity of user point $i$
	$f_{ijk}$	The loading capacity of the truck when passing through $(i,j)$
	$f_{ijd}$	The loading capacity of the drone when passing through $(i,j)$
	$[A_i,B_i]$	The expected time window of user $i$
	$\widehat{a_i}$	The point in time when the truck arrives at cluster center $i$
	$a_i$	The time point when the drone arrives at cluster center $i$
Decision variable	$a_i$	The time point when the drone arrives at cluster center $i$
	$b_d$	$\left\{\begin{array}{c}1,including drones\\ 0,\mathrm{otherwise}\end{array}\right.$
	$b_t$	$\left\{\begin{array}{c}1,including trucks\\ 0,\mathrm{otherwise}\end{array}\right.$
	$x_{ijk}$	$\left\{\begin{array}{c}1,the truck is driving from i to j\\ 0,\mathrm{otherwise}\end{array}\right.\forall i,j\in N,k\in T$
	$x_{ijd}$	$\left\{\begin{array}{c}1,the drone flies from i to j\\ 0,\mathrm{otherwise}\end{array}\forall i,j\in N,d\in W\right.$

below.

Considering the current practical conditions of trucks and drones, we select vehicles and drones suitable for rural areas as the data reference for the two-stage distribution system. The truck parameters are based on the Jiefang J6F light-medium truck, while the drone parameters are based on the JDX-500 VTOL. The parameters for both trucks and drones in this study are shown in

Table 3. Parameter settings of trucks and drones.

Parameters	Numerical Value/Unit	Parameters	Numerical Value/Unit
The maximum load capacity of the truck $Q_t$	2000 kg	The maximum load capacity of the drone $Q_d$	10 kg
The maximum driving distance of the truck $L_t$	300 km	The maximum traveling distance of drones $L_d$	30 km
The average speed of trucks $V_t$	50 km/h	The average speed of drones $V_d$	70 km/h
The unit operating cost of the truck $C_t$	0.7 CNY/km	The unit operating cost of drones $C_d$	0.3 CNY/km
The purchase cost of each truck $C_t^1$	20 CNY	The purchase cost of each drone $C_d^1$	10 CNY
The unit carbon emission cost of trucks $C_t^2$	0.3 CNY/km	The unit carbon emission cost of drones $C_d^2$	0.1 CNY/km
Truck unit service rate ${\beta }_t$	1.2	Unit service rate of drones ${\beta }_d$	1.4
Package unit weight $\phi$	2 kg	Self-weight of a single drone $\mu$	65 kg
User expectation time window $[A_i,B_i]$	[9:00, 17:00]	Penalty cost per unit time $P$	100 CNY/h

. Although there is a significant difference between the payload capacities of the truck and the drone, the two vehicles serve complementary roles in the joint delivery model. Each user point is assumed to require the delivery of a single small parcel, and the drone can serve up to five user points in a single dispatch. Moreover, while the truck can transport larger volumes, its speed and terrain adaptability are limited compared to the drone. These assumptions are made to reflect realistic rural delivery scenarios and emphasize the synergy between trucks and drones rather than a direct comparison of their standalone efficiency.

4.3. Modelling

Based on the problem description and parameter design, this is a two-objective mixed integer programming problem. A comprehensive MILP model is established.

The objective function (1) aims to minimize the total cost, which includes the combined operating costs of both the truck and the drone. This total cost encompasses factors such as fuel, labor, maintenance, and other relevant expenses.

The objective function (2) seeks to minimize the total delayed delivery time. The last moment when all user requirements are completed is taken as the delivery completion time, and the goal is to minimize the cumulative delayed delivery times for all tasks.

$$Min C=\sum _{d\in W}\sum _{i\in N}\sum _{j\in N}{x}_{ijd}{(C}_d+C_d^2)d_{ij}{b}_d+\sum _{k\in T}\sum _{i\in N}\sum _{j\in N}{x}_{ijk}\widehat{d_{ij}}(C_t+C_t^2)b_t+C_d^1{b}_d+C_t^1{b}_t+DT\ast P$$

(1)

$$Min DT=\sum _{i\in N}\mathit{max}\left(a_i-B_i,0\right)$$

(2)

Constraint (3) ensures consistency between the modeling assumptions and the cost-time calculations. We introduced terrain-specific correction coefficients that reflect the varying travel conditions across forest, lake, and mountainous areas. These coefficients are applied to both trucks and drones to adjust their nominal speeds and provide more realistic estimations of travel time. The correction factors $a_t$ were determined based on average terrain roughness, infrastructure limitations, and operational drone mobility under different environments. Specifically, the terrain correction coefficients are set as follows. For trucks, the coefficients are 0.70 in forest areas, 0.80 in lake areas, and 0.60 in mountainous areas. For drones, the coefficients are 0.75, 0.85, and 0.70, respectively.

Constraint (4) ensures that the time window for user point $i$ is at least greater than the sum of the fastest possible arrival time and the service time of the drone. This means that the drone must arrive within the allowed time window and provide the service before the window expires.

$$T_i={\displaystyle \frac{d_{ij}}{v{a}_t}}$$

(3)

$${\displaystyle \frac{d_{ij}}{v_d}}+T_i\le B_i-A_i$$

(4)

Constraints (5) and (6) indicate that the service time of the drone or truck at user point $i$ is proportional to its demand. This means that the time required for the drone or truck to complete the delivery at each user point is directly related to the amount of agricultural product being delivered. The larger the demand at a user point is, the longer the service time required for delivery.

$$T_i={\beta }_d{q}_i, {\beta }_{d}b>1$$

(5)

$$\widehat{T_i}={\beta }_t{q}_i,{\beta }_t>1$$

(6)

Constraint (7) indicates that the expected earliest arrival time window of user point $i$ is at least greater than the fastest possible arrival time of the drone. This ensures that the drone does not arrive at the user point earlier than the defined earliest permissible time window, preventing premature deliveries that may not align with the user’s preferred or acceptable delivery time.

$$A_i\ge \left\{\begin{array}{c}{\displaystyle \frac{d_{0i}}{v_d}}{x}_{0id}b,d_{0i}\le Q_d,\\ {\displaystyle \frac{\widehat{d_{0j}}}{v_t}}+{\displaystyle \frac{d_{ji}}{v_d}}{x}_{jid}b,d_{0j}>Q_d\end{array}\forall i\in N,j\in C\right.$$

(7)

Constraint (8) represents the straight-line path distance of the drone between two nodes. This constraint ensures that the drone’s flight path is calculated based on the shortest possible straight-line distance between two points, simplifying the model and reflecting the drone’s most efficient route under ideal conditions, without considering any detours or obstacles. Equation (7) defines the baseline Euclidean distance between delivery points. Subsequent calculations incorporate terrain correction factors as described in Equation (23) in Section 5, which adjust the baseline distance to reflect real-world terrain effects.

$$d_{ij}=\sqrt{{\left(x_j-x_i\right)}^2+{\left(y_j-y_i\right)}^2}$$

(8)

Constraints (9) and (10) indicate that each user point $i$ is served only once by one drone. These constraints ensure that the delivery task for each user point is assigned to a single drone, avoiding multiple drones servicing the same point and ensuring that the logistics system remains efficient and realistic by adhering to the assumption of exclusive service for each user point.

$$\sum _{d\in W}\sum _{j\in D}{x}_{ijd}=1,\forall i\in N$$

(9)

$$\sum _{d\in W}\sum _{i\in D}{x}_{ijd}=1,\forall j\in N$$

(10)

Constraint (11) indicates that for each distribution center, the truck can only leave and return once. It ensures that the truck performs a single round trip for the distribution task, avoiding multiple trips, which could lead to inefficiencies and increased costs.

Constraint (12) indicates that each drone can only leave the current distribution point once and return once. It ensures that the drone performs a single flight from the distribution center to the user point and returns once the delivery is completed, maintaining a clear and efficient operational flow.

$$\sum _{i\in C}{x}_{0ik}=\sum _{i\in C}{x}_{i0k}=1,\forall k\in T$$

(11)

$$\sum _{j\in N}{x}_{ijd}=\sum _{j\in N}{x}_{jid}=1,\forall i\in C,d\in W$$

(12)

Constraint (13) ensures that the total load carried by the truck at any time does not exceed its maximum load capacity. This prevents overloading, which could lead to unsafe conditions and inefficiencies during the transportation process.

Constraint (14) ensures that the total supply (i.e., the load) assigned to the drone along any path does not exceed its maximum payload capacity. This is crucial for maintaining operational efficiency and safety, as overloading could compromise the drone’s ability to complete the delivery successfully.

$$\sum _{i\in D}\sum _{j\in D}(x_{ijk}{q}_i\phi +x_{ijd}{q}_i\phi )+\mu d\le Q_t,\forall k\in T,d\in W$$

(13)

$$\sum _{i\in D}\sum _{j\in D}{x}_{ijd}{q}_{i}b\le Q_d,\forall d\in W$$

(14)

Constraint (15) ensures that the total transportation capacity provided by all trucks and drones is sufficient to meet the total demand of all user points. This ensures that the logistics system is capable of fulfilling the delivery requirements, avoiding any situation where demand exceeds the available transportation capacity, thus ensuring complete service coverage for all delivery tasks.

$$Q_{t}k+Q_{d}db\ge \sum _{i\in N}{q}_i$$

(15)

Constraint (16) ensures that the loading volume of trucks changes as they pick up and drop off goods at various user points. This constraint tracks the change in load from the distribution center to the user points and back, accounting for the deliveries made by the truck.

Constraint (17) handles the changes in the loading volume of drones as they pick up and drop off packages at different user points. It ensures that the drone’s load is updated correctly based on the deliveries it completes.

$$q_j{x}_{ijk}\le f_{ijk}\le \left(Q_t-q_i\right)x_{ijk},\forall i,j\in N,k\in T$$

(16)

$$q_j{x}_{ijd}\le f_{ijd}b\le \left(Q_d-q_i\right)x_{ijd}b,\forall i,j\in N,k\in T$$

(17)

Constraints (18) and (19) ensure that the total distance traveled by each truck and drone does not exceed their respective maximum mileage limits.

$$\sum _{i\in D}\sum _{j\in D}{x}_{ijd}{d}_{ij}b\le L_d,d\in W$$

(18)

$$\sum _{i\in D}\sum _{j\in D}{x}_{ijk}\widehat{d_{ij}}\le L_t,k\in T$$

(19)

Constraint (20) ensures that for the truck–drone combined transportation, the truck can directly deliver goods to the next user point and pick up the drone at the appropriate user point.

$$\widehat{a_j}\ge \sum _{i\in V}\sum _{j\in N}{x}_{ijd}{d}_{ij}b+\sum _{i\in V}\sum _{j\in N}{T}_j{x}_{ijd}b,\forall d\in W,j\in C$$

(20)

Constraint (21) indicates that the demand of user point $i$ is met by the drone.

$$x_{ijd}b(\sum _{j\in N}{f}_{jid}-\sum _{j\in N}{f}_{ijd})=q_i,\forall i\in N,d\in W$$

(21)

5. Algorithm Introduction

To address the logistics optimization problem for agricultural product delivery in complex rural terrains, this study is guided by the following research questions: First, how do terrain differences—specifically forest, lake, and mountainous regions—affect delivery efficiency and cost? Second, what is the comparative performance of truck-only, drone-only, and combined truck–drone delivery modes under different terrain constraints?

To answer these questions, a structured modeling and analysis framework was developed. First, an improved Fuzzy C-Means (FCM) algorithm was applied to cluster rural customer locations based on geographical features and demand patterns. Next, a mixed integer linear programming (MILP) model was formulated to optimize delivery routes, taking into account vehicle capacities, delivery time windows, and carbon emission penalties. To solve the model efficiently, we employed a hybrid genetic algorithm-simulated annealing (GA-SA) approach. Finally, simulation experiments were conducted across three representative rural terrain types to compare the performance of different delivery modes in terms of total cost, delivery time, and environmental impact.

5.1. Improved FCM Algorithm

5.1.1. Fuzzy C-Means Clustering Algorithm Based on Terrain Constraints

The Fuzzy C-Means (FCM) algorithm is employed to cluster distribution points effectively, aiming to optimize the truck–drone cooperative transportation mode [38]. However, traditional FCM might struggle to adapt to the varying terrain conditions. To address this issue, the study integrates terrain factors into the FCM clustering process, enhancing the model’s adaptability and improving the clustering’s relevance to different terrain characteristics.

5.1.2. Terrain Factors Guide the Initialization of Cluster Centers

In the traditional FCM initialization process, cluster centers are usually determined randomly or based on Euclidean distance. However, in this study, we modified the initialization strategy of cluster centers to better align with different rural terrain characteristics.

Due to the low road density in forest areas and the influence of tree occlusion on drones, cluster centers should be located as close as possible to the intersection points of main roads. In lake areas, water barriers limit truck routes, so cluster centers are allocated to regions more suitable for drone access to reduce cross-water transport costs. In mountainous terrain, elevation fluctuates greatly, and cluster centers are distributed in areas with gentler slopes and proximity to truck-accessible roads to enhance delivery feasibility.

After clustering, each user node is assigned a terrain label (forest, lake, or mountain) based on its cluster center’s geographical classification. These labels are retained and passed as input to the GA-SA algorithm. In the route optimization phase, terrain labels are used to apply terrain-based speed correction coefficients to the travel time calculations for both trucks and drones. For example, in mountainous areas, trucks are significantly slower due to steep slopes, while in lake areas, drones gain a relative advantage. The correction coefficients—0.70, 0.80, and 0.60 for trucks and 0.75, 0.85, and 0.70 for drones in forest, lake, and mountain areas, respectively—are embedded in the fitness evaluation function to ensure that terrain effects are quantitatively reflected in both route planning and cost estimation.

5.1.3. Adjustment of the Fuzzy Membership Degree Matrix Adapted to the Terrain

Under different terrains, the distribution of delivery points for trucks and drones is affected by terrain features. Therefore, when using the Fuzzy C-Means (FCM) algorithm for delivery point clustering, terrain factors need to be introduced to optimize the clustering results. The membership degree $u_{ij}$ from the data point $x_i$ to the cluster center $v_j$ calculated using the traditional FCM algorithm is mainly based on the Euclidean distance:

$$u_{ij}={\displaystyle \frac{1}{{\sum }_{k=1}^c{(\frac{d_{ij}}{d_{ik}})}^{\frac{2}{m-1}}}}$$

(22)

$d_{ij}$ is the distance from the data point $x_i$ to the cluster center $v_j$, and $m$ is the ambiguity coefficient.

In this study, considering the influence of terrain, the calculation formula of membership degree is adjusted as follows. Building upon the baseline distances from Equation (7) in Section 4, Equation (23) applies terrain resistance weights to adjust the effective travel distances used in clustering and route optimization.

$$d_{ij}=\propto d_{ij}^r+\beta d_{ij}^t$$

(23)

$d_{ij}^r$ is the Euclidean distance, $d_{ij}^t$ is the terrain resistance distance, including forest density, lake crossing limit, and the influence of mountain slope, $\propto ,\beta$ is the weighted parameter determined by the terrain features. With this optimization adjustment formula, the clustering effect of distribution points can be optimized under different terrains, and the efficiency of truck–drone cooperative transportation can be improved [39].

Although Hypothesis 4 indicates that dynamic obstacle avoidance is not considered, this refers to the absence of real-time rerouting or obstacle detection mechanisms during drone flight. However, environmental constraints are pre-integrated into the route design via the terrain resistance term $d_{ij}^t$, which reflects static barriers such as tree density, water areas, and slope steepness. This ensures that drones avoid infeasible paths during the clustering and scheduling stages. Thus, the simplification in Hypothesis 4 is consistent with the static modeling approach used in the algorithm.

5.2. Genetic Annealing Optimization Algorithm Combined with Terrain Factors

The genetic algorithm-simulated annealing (GA-SA) approach combines the global search ability of the genetic algorithm and the local optimization ability of the simulated annealing algorithm. In this study, when optimizing the path with the GA-SA algorithm, the fitness function, mutation operator, and temperature attenuation strategy were adjusted for different terrains. When optimizing the truck–drone cooperative path, different fitness evaluation indicators and constraints were introduced for different terrains to improve the adaptability of the algorithm [40,41].

5.2.1. Fitness Function Optimization

When optimizing the truck–drone path, the fitness function mainly considers the total transportation cost $C$ as follows:

$$C=C_t+C_d+C_p$$

(24)

Here, $C_t$ is the transportation cost of trucks, which is affected by road conditions, and $C_d$ is the transportation cost of drones, which is affected by flight energy consumption. Considering the influence of tree density on the flight time of drones, a correction factor for the flight speed of drones is introduced; $C_p$ is the penalty term related to terrain. In forest areas, drones are blocked by trees, and the flight time penalty is increased. Regarding $C_f$ in lake areas, restrictions on truck cross-lake transportation increase the penalty $C_l$ for route adjustment. The slope of mountainous areas affects the speed of trucks and increases the energy consumption penalty $C_m$.

$$C_p={{\omega }_{1}C}_f+{\omega }_2{C}_l+{{\omega }_{3}C}_m$$

(25)

Here, ${\omega }_1,{\omega }_2,\mathrm{a}\mathrm{n}\mathrm{d}{\omega }_3$ are the weighting factors, which are adjusted according to the experiment [42,43].

5.2.2. Terrain Adaptive Mutation Operator

The mutation operator of the genetic algorithm is used to escape from the local optimal solution. Under different terrains, we adopt different mutation strategies. When optimizing the path of drones in forest areas, high-density forest zones are avoided to reduce navigation difficulty and energy consumption. In lake areas, path adjustments account for water barriers, ensuring drone rerouting avoids long detours over non-traversable surfaces. In mountainous regions, slope constraints are introduced to avoid steep, energy-intensive segments. The adjustment formula of the mutation operator is as follows:

$$P_m=P_b+\gamma D_t$$

(26)

$D_t$ represents the terrain complexity, and $\gamma$ is the adjustment coefficient [44].

In addition to terrain-guided mutation, this study applies the terrain-corrected travel time formula (see Equation (3)) when evaluating each candidate solution. After a new path is generated through mutation, the travel time between nodes is computed using terrain-adjusted speeds based on their assigned cluster type. This ensures that cost, delay, and emission assessments reflect actual geographical constraints.

5.2.3. Annealing Temperature Attenuation Strategy

The simulated annealing algorithm adopts an exponential attenuation strategy as follows:

$$T_{k+1}=\lambda T_k$$

(27)

Here, $\lambda$ is the temperature attenuation rate.

In this study, different attenuation strategies are set for different terrains. For complex terrains (mountainous areas, forest areas), slow down attenuation and allow for longer exploration periods. For relatively gentle terrain (lake area), accelerate attenuation and increase convergence speed. The adjustment formula is as follows:

$$\lambda ={\lambda }_b+\delta D_t$$

(28)

Here, $\delta$ is the moderating parameter [45].

5.3. Algorithm Flow

We adopted a method combining the improved Fuzzy C-Means clustering (FCM) and the genetic annealing algorithm (GSA) to optimize the combined distribution route of trucks and drones. This algorithm first clusters the distribution demand points to distinguish the distribution ranges of trucks and drones, and on this basis, uses the improved GSA algorithm to solve the optimal path. Specifically, the algorithm process includes four main steps: data preprocessing, demand point clustering, task allocation, and path optimization.

• Data preprocessing and modeling

First, the research area of this study is the two-dimensional plane of $[X_{min},X_{max}]$ and $[Y_{min},Y_{max}]$. The distribution center $\left(\mathrm{0,0}\right)$ is at the red five-pointed star in the figure. The coordinates of all user points are expressed as the set $U=\left\{\left(x_i,y_i\right)\right|i=1,2,\dots ,N\}$. The truck can only travel along the road, and the maximum mileage is $L_t$. The drone takes off from the truck parking point, and the maximum range is $D_d$. Based on these constraints, the path optimization models for trucks and drones are established as follows:

$$minZ=\sum _{(i,j)\in T}{c}_{ij}{x}_{ij}+\sum _{(k,l)ϵD}{d}_{kl}{y}_{kl}$$

(29)

Here, $x_{ij}$ and $y_{kl}$ represent the binary decision variables in the truck and drone paths, respectively, and $c_{ij}$ and $d_{kl}$ represent the unit transportation costs (such as time or fuel consumption) of the two, respectively.

2.

Demand point clustering based on FCM

Due to the different influences of various terrain conditions on the transportation mode, we use the FCM clustering algorithm to classify the demand points to determine the users are suitable for direct truck delivery and those requiring drone delivery. The goal of the FCM algorithm is to minimize the objective function of fuzzy classification:

$$J_m=\sum _{i=1}^N\sum _{j=1}^C{u}_{ij}^m{‖x_i-c_j‖}^2\lambda ={\lambda }_b+\delta D_t$$

(30)

Here, $u_{ij}$ is the membership degree of cluster $j$ to which user point $i$ belongs, $c_j$ is the center of the $j$ th cluster, and $m$ is the ambiguity coefficient. Usually, $m=2$ is taken to balance the ambiguity degree of clustering. During the clustering process, we classified the blue user points close to the road as truck-accessible areas, while the green user points far from the road were assigned to drones.

3.

Task Allocation and Path Optimization

After the clustering is completed, we use the genetic annealing algorithm (GSA) to optimize the paths. GSA combines the global search ability of the genetic algorithm (GA) and the local search ability of simulated annealing (SA) to avoid falling into the local optimum. The specific steps are as follows. First, generate the initial population. By combining random generation with heuristic algorithms, generate multiple feasible path sequences as the initial solutions. Then, define and calculate the fitness function based on distribution cost, time constraints, and carbon emissions [46]. The fitness function is expressed as follows:

$$F\left(x\right)={\omega }_1\sum c_{ij}+{\omega }_2\sum d_{kl}+{\omega }_3\sum P_e$$

(31)

$P_e$ represents the carbon emission volume, and ${\omega }_1,{\omega }_2,{\omega }_3$ are the weighting coefficients are used to balance different optimization objectives.

Second, partial mapping crossover (PMX) and inversion mutation are adopted to enhance population diversity. During the iterative process of the genetic algorithm, after each update, the simulated annealing method is used to accept a poor solution with a certain probability of escaping the local optimum as follows:

$$P=e^{{\displaystyle \raisebox{1ex}{$-\Delta F$}\!\left/ \!\raisebox{-1ex}{$T$}\right.}}$$

(32)

Here, $\Delta F$ is the fitness difference between the current solution and the new solution, and $T$ is the annealing temperature, which gradually decreases to converge to the global optimum.

4.

Path generation and visualization

Finally, the truck–drone joint distribution path is generated based on the optimization results and mapped to the study area to verify the impact of different terrains on distribution efficiency. In this section, for the three different terrains of forest areas, lake areas, and mountainous areas, the FCM and GA-SA algorithms have been improved to make them more adaptable to the collaborative transportation requirements of trucks and drones in different terrains.

6. Simulation Results and Discussion

6.1. Simulation Settings

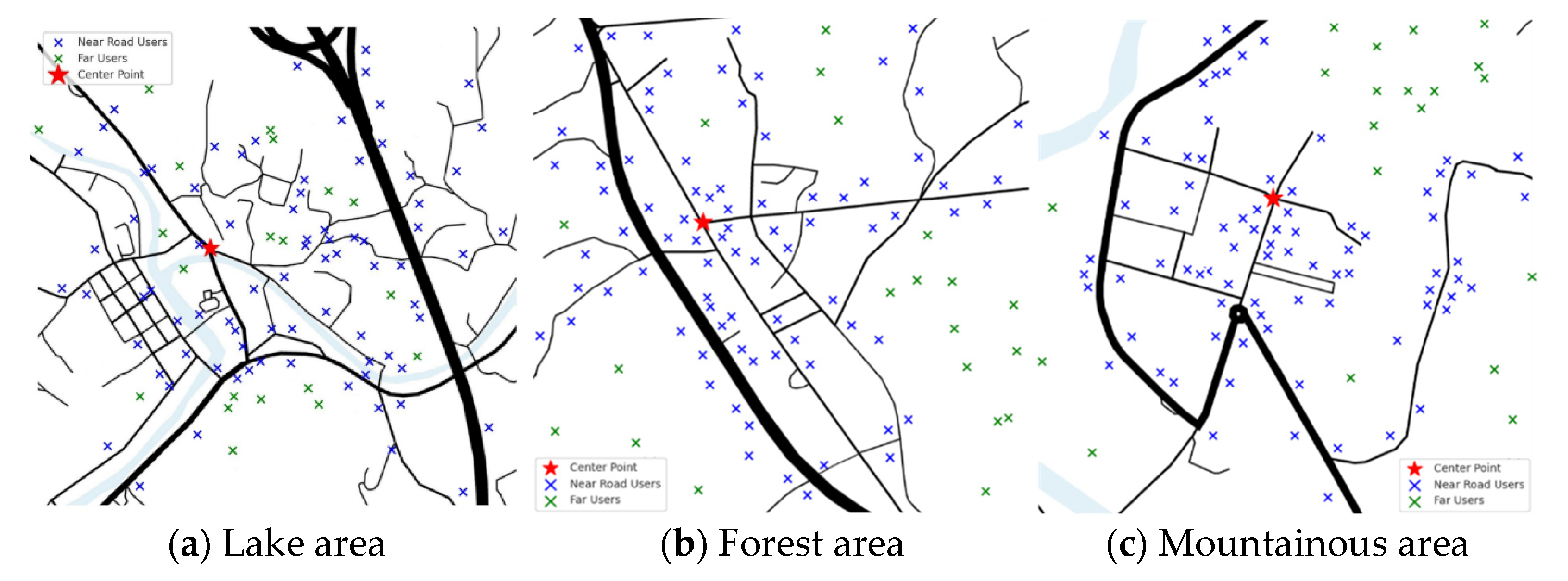
In addition to the postal centers indicated on the map, the remaining user points are randomly generated with a probability distribution, where 80% of the points are located near roads, and 20% are situated further away from road networks. Figure 3 illustrates the distribution of user points across forest, lake, and mountainous regions, reflecting real-world conditions. Simulation analyses are performed for three modes of delivery: truck-only, drone-only, and a combined truck–drone system. For clarity in representation, the truck’s path is depicted by straight lines with arrows indicating the sequence of transportation. In practice, the truck follows the actual road network, while the drone’s flight path is assumed to be a direct straight line. The user points’ distances from the transportation center are sequentially numbered, with points closer to the center assigned smaller numbers. The corresponding schematic diagram of these user numbers is shown in Figure 4, facilitating the subsequent explanation of the transportation sequence.

In order to mitigate the influence of stochastic fluctuations and random disturbances inherent in simulation experiments, each scenario was run multiple times. The reported results correspond to the median values of these runs rather than simple averages. This choice enhances the robustness of the conclusions by reducing sensitivity to extreme values and ensuring that the presented results reflect typical model behavior.

Additionally, Figure 5, Figure 6 and Figure 7 depict the schematic diagrams of the combined truck and drone transportation and distribution system. In these figures, blue numbers represent the user points served by drones, and black numbers represent the user points served by the truck. The sequence from left to right shows the order of joint delivery under the truck–drone mode. Connecting lines indicate the timing of drone takeoff and landing from the truck.

6.2. Formatting of Mathematical Components

This study systematically compares the effectiveness of various distribution models based on two key performance indicators: total distribution cost and total distribution time. The total distribution cost measures the overall economic expense incurred under each model, encompassing truck fuel costs, drone energy consumption, and labor costs for manual delivery. This indicator serves as a metric for evaluating the economic efficiency of each model, helping to determine which approach minimizes costs while maintaining effective service delivery. The total distribution time, on the other hand, represents the cumulative time required to deliver goods to each user point from the distribution center. This includes truck travel time, drone flight time, and any potential waiting periods. The total delivery time is a critical indicator of timeliness, which is especially important in rural agricultural product distribution, as it significantly impacts customer satisfaction.

Under the initial assumption of identical distribution demand points, both the comprehensive delay time penalty and the carbon emission penalty are incorporated into the total distribution cost. This study compares and analyzes the performance of three transportation modes—truck-only, drone-only, and truck–drone combination—across various dimensions, including distribution cost, distribution time, delay time penalty, and carbon emission penalty, within three distinct terrains, including forest areas, lake areas, and mountainous areas. The simulation results, which assess the combined advantages and applicability of coordinated truck–drone transportation in the context of complex rural terrain, are presented in

Table 4. Comparison of simulation results of different terrains for three transportation modes.

Category	Total Distribution Cost/CNY			Total Delivery Time/hour			Delay Time Penalty/CNY			Carbon Emission Penalty/CNY
	(a)	(b)	(c)	(a)	(b)	(c)	(a)	(b)	(c)	(a)	(b)	(c)
Trucks	425.26	402.08	441.73	10.42	10.38	11.02	242	238	302	54.98	49.22	41.92
Drones	453.24	518.91	465.93	12.14	10.95	11.24	314	295	325	34.81	111.96	35.23
Truck–Drones	267.39	217.3	304.78	9.29	8.75	9.63	129	75	163	30.73	38.42	38.11
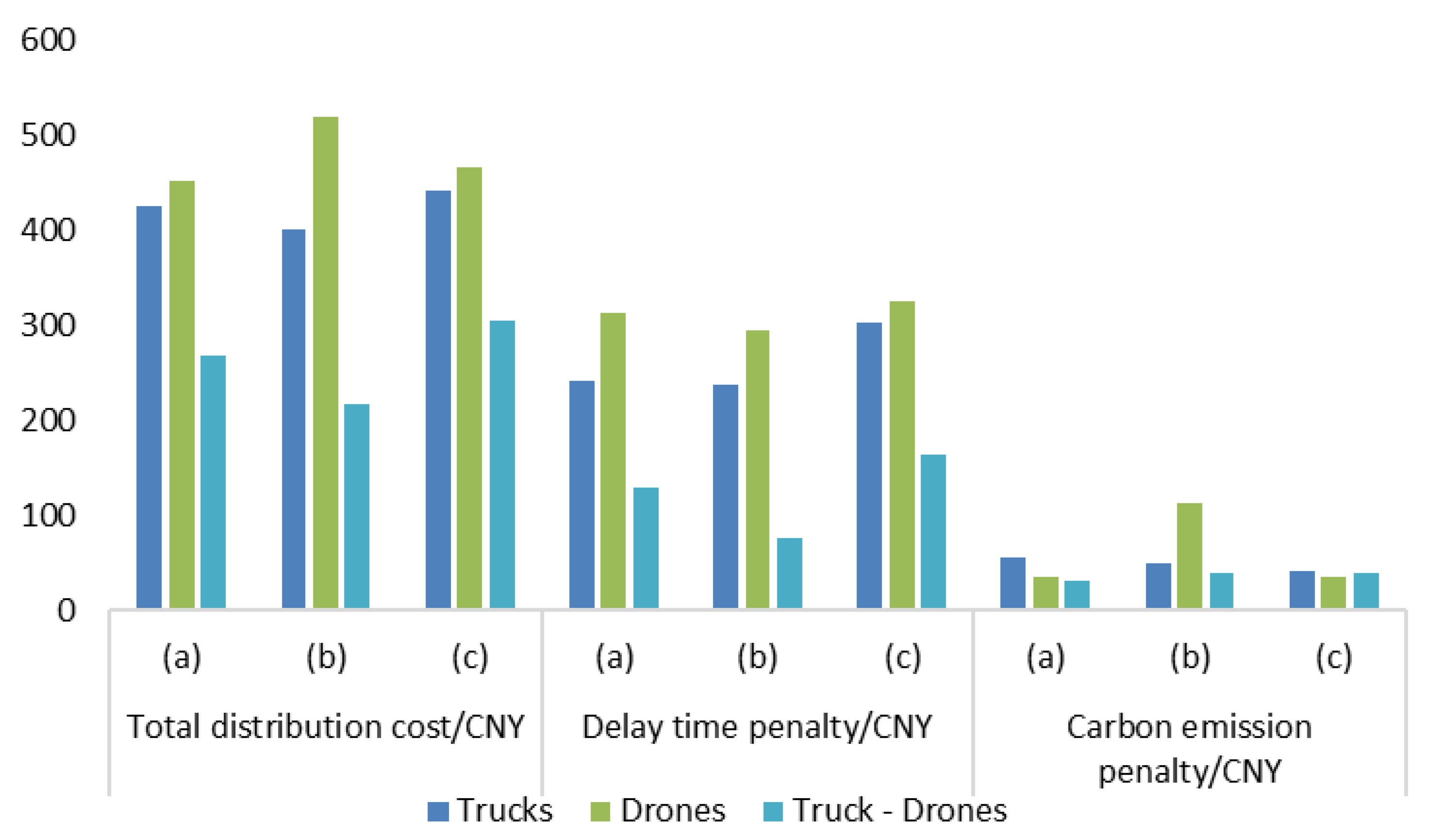
Efficiency savings	39.06%	52.04%	32.80%	1.99	1.92	1.5	52.81%	71.53%	47.94%	27.91%	43.81%	4.57%

. Category (a) corresponds to the lake area, category (b) to the forest area, and category (c) to the mountainous area.

The experimental results demonstrate that the proposed algorithm significantly enhances distribution efficiency in forest areas, lake areas, and mountainous areas. Compared to traditional path planning methods, it reduces costs by an average of 41.3 percent and saves 1.8 h. To provide a clearer comparison, a line graph is used to illustrate the two key indicators: distribution cost and delayed delivery time for each mode. Additionally, the results for different rural terrains (forest areas, lake areas, and mountainous areas) are shown to highlight the impact of the distribution mode on both time and cost. 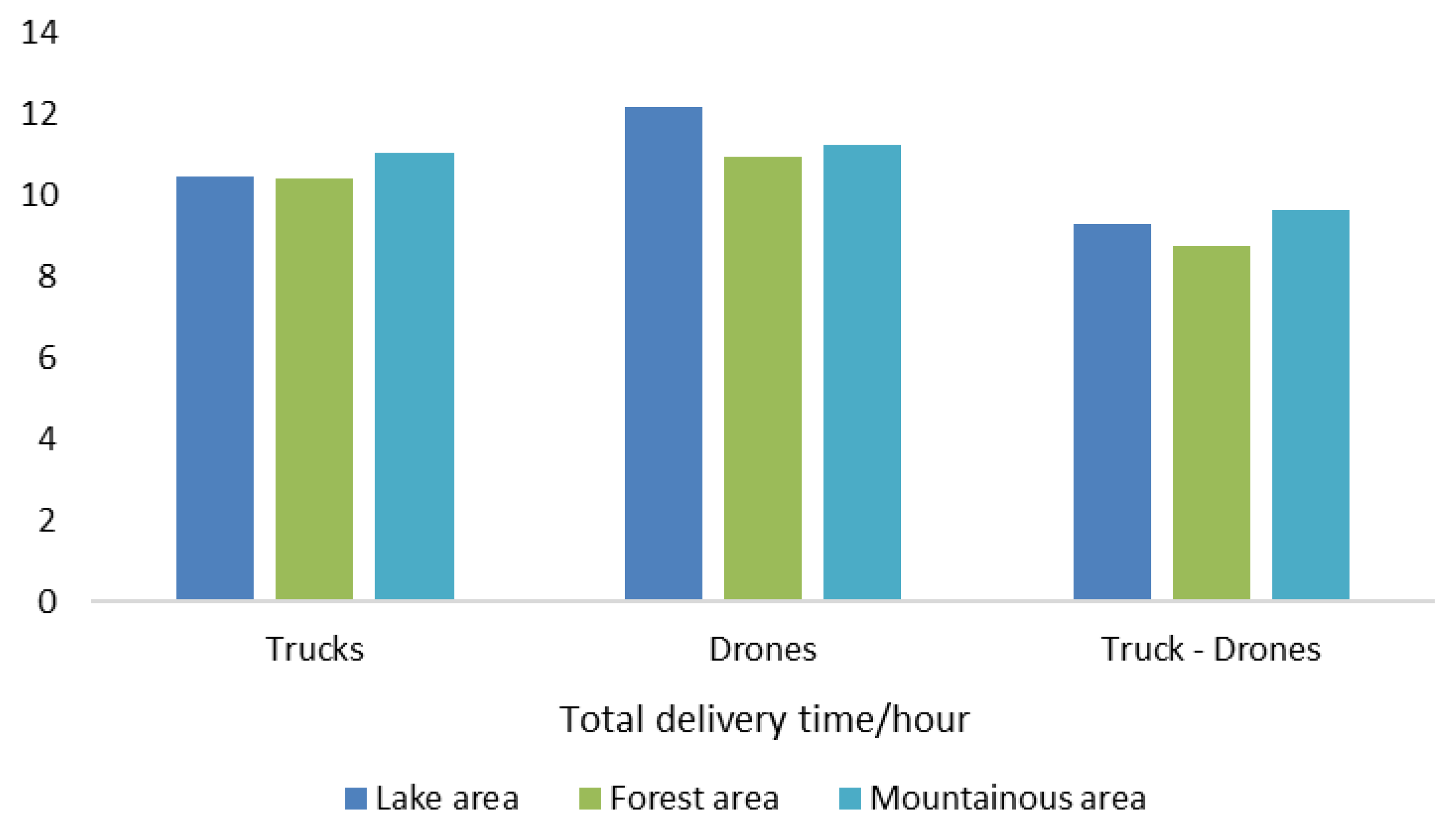The cost performance of each distribution mode across various rural terrains is presented in Figure 8, while the total delivery time is shown in Figure 9.

From the perspective of distribution costs, the truck–drone combined transportation mode consistently outperforms the single transportation modes across all three terrain types. Specifically, in forest, lake, and mountainous areas, the total costs were 267.39 CNY, 217.30 CNY, and 304.78 CNY, respectively, representing savings of 39.06%, 52.04%, and 32.80% compared to the truck-only mode. These results underscore the cost-effectiveness of leveraging drones for straight-line delivery in areas with complex terrain and limited road accessibility.

While drone-only delivery theoretically reduces labor requirements and route length, it incurs significantly higher costs than the combined mode in all three regions. This is likely due to the operational inefficiencies such as limited battery life, low payload capacity, and frequent take-offs and landings. In particular, in the lake area, the total cost of drone-only delivery reaches as high as 518.91 CNY, highlighting the cost disadvantage of relying solely on aerial delivery.

In terms of delivery delay time, the combined transportation mode also demonstrated the best performance. The total delivery times were 9.29, 8.75, and 9.63 h, respectively, reducing delivery time by 1.99, 1.92, and 1.50 h compared to the truck-only mode. This improvement is attributed to the drones’ ability to fly in direct paths while operating in parallel with the truck, thereby significantly shortening the total travel distance and improving delivery efficiency.

With regard to delay time penalties, the combined mode achieves notable reductions across all terrains. In the lake area, the delay cost under the combined mode is only 75 CNY, which is 71.53% lower than that of the truck-only mode. Similarly, in mountainous regions—where winding roads and steep elevation changes create logistical challenges—the delay costs for truck-only and drone-only modes reach 302 CNY and 325 CNY, respectively. In contrast, the combined mode reduces this to 163 CNY, achieving nearly 50% cost savings. These findings illustrate the importance of collaborative scheduling in topographically complex regions.

Carbon emission penalties are also generally lower for the combined mode. In forest and lake areas, the penalties are 30.73 CNY and 38.42 CNY, reflecting reductions of 27.91% and 43.81%, respectively, compared to the truck-only mode. This can be attributed to the increased use of drones for short-distance deliveries, which generate lower emissions. However, in mountainous areas, the emission penalty for the combined mode (38.11 CNY) reflects only a modest reduction of 4.57%. This suggests that complex elevation changes and flight path restrictions limit the emission benefits, indicating a need for further optimization through more intelligent drone task allocation, real-time path planning, and multi-drone coordination.

7. Summary

This study proposes and validates a sustainable truck–drone cooperative distribution model designed for rural regions in China, with a particular emphasis on addressing logistical challenges in forested, lake, and mountainous terrains. Compared to conventional single-mode transport systems, the integrated truck–drone approach significantly reduces total distribution costs, mitigates delivery delays, and lowers carbon emission penalties, thereby advancing both operational efficiency and environmental sustainability.

A key innovation of this research lies in its terrain-sensitive optimization framework. By analyzing performance across three representative terrain types, the study demonstrates how environmental characteristics directly impact the suitability and efficiency of different delivery modes. For instance, in forest, lake, and mountainous areas, the combined delivery mode reduced total distribution cost savings of 39.06%, 52.04%, and 32.80% compared to truck-only delivery. Drone-only delivery, despite its theoretical advantages in routing, resulted in the highest costs due to limited payload capacity, low dispatch efficiency, and multiple take-offs and landings. In terms of delivery efficiency, the combined mode achieved the shortest total delivery times, and the corresponding delay penalties were also significantly reduced.

In contrast to prior studies that focused on single-mode systems or simplified environments, this research integrates realistic terrain diversity, mode coordination, and emission penalties into a unified decision-making framework. In comparison with similar studies [15,21], this model offers improved flexibility, stronger ecological validity, and enhanced insight into rural last-mile delivery. Previous research has primarily focused on comparisons of single transportation modes [25], with limited attention to the application of combined modes in real-world terrains and complex environments. Therefore, the novelty of this study not only contributes new insights into drone delivery technology but also offers a richer theoretical foundation for optimizing rural logistics. The combined delivery model proposed here is highly innovative both in terms of its theoretical framework and its practical application.

In conclusion, the truck–drone collaborative model effectively addresses rural logistics challenges related to cost, efficiency, and sustainability. It consistently outperforms single-mode systems, particularly in terrains with difficult road conditions or dispersed demand. These findings confirm the importance of terrain-adaptive, multi-modal delivery strategies. Future research should incorporate stochastic demand, real-time data, and intelligent dispatch algorithms to further generalize and strengthen the model’s applicability. As supportive technologies and policies continue to evolve, the truck–drone systems are well-positioned to become a mainstream solution for sustainable, intelligent last-mile logistics in rural regions.

This study is based on fixed delivery scenarios in representative terrains and does not consider variations in demand, weather conditions, or temporal changes. As a result, the conclusions are illustrative rather than definitive. In addition, the absence of a baseline scenario for truck–drone coordination without algorithmic optimization makes it difficult to isolate the algorithm’s contribution. Future studies should introduce control experiments and incorporate stochastic demands and real-time data to enhance model robustness.

Furthermore, while carbon emissions are considered during the operational phase, the model does not account for long-term environmental impacts such as drone battery degradation, vehicle production energy, or e-waste from decommissioning. A more comprehensive life-cycle assessment is needed to evaluate environmental sustainability.

Finally, simplified assumptions—such as constant drone performance and the exclusion of obstacle avoidance—may reduce the model’s applicability in real-world settings. Future work should address these aspects to improve realism and adaptability.