A Combined Energy Management Strategy for Heavy-Duty Trucks Based on Global Traffic Information Optimization
Abstract
1. Introduction
- An optimization framework for the A-ECMS equivalent factor based on global traffic information and the NOA is designed, enabling the rapid acquisition of a high-quality equivalent factor.
- The CD-CS strategy is combined with the A-ECMS as a combined strategy, addressing the negative impacts caused by the inability to use the A-ECMS during the equivalent factor optimization phase.
2. Hybrid Electric Heavy-Duty Truck Model
2.1. Powertrain Structure and Operating Modes
| AMT Gear | Gear Ratio | Efficiency |
|---|---|---|
| Gear 1 | 12.10 | 96.6% |
| Gear 2 | 9.41 | 96.9% |
| Gear 3 | 7.31 | 97.0% |
| Gear 4 | 5.71 | 97.1% |
| Gear 5 | 4.46 | 98.3% |
| Gear 6 | 3.48 | 97.1% |
| Gear 7 | 2.71 | 98.4% |
| Gear 8 | 2.11 | 98.2% |
| Gear 9 | 1.64 | 98.4% |
| Gear 10 | 1.28 | 98.6% |
| Gear 11 | 1.00 | 99.6% |
| Gear 12 | 0.78 | 98.4% |
2.2. Transmission System and Vehicle Longitudinal Dynamic Model
2.3. Engine, ISG Motor, and Battery Models
3. EMS Based on Traffic Information
3.1. CD-CS in the Absence of Traffic Information
3.2. A-ECMS Based on Global Traffic Information
3.3. Combined Strategy of CD-CS and A-ECMS
4. Optimization Framework for A-ECMS Equivalent Factor Based on NOA
5. Results and Discussion
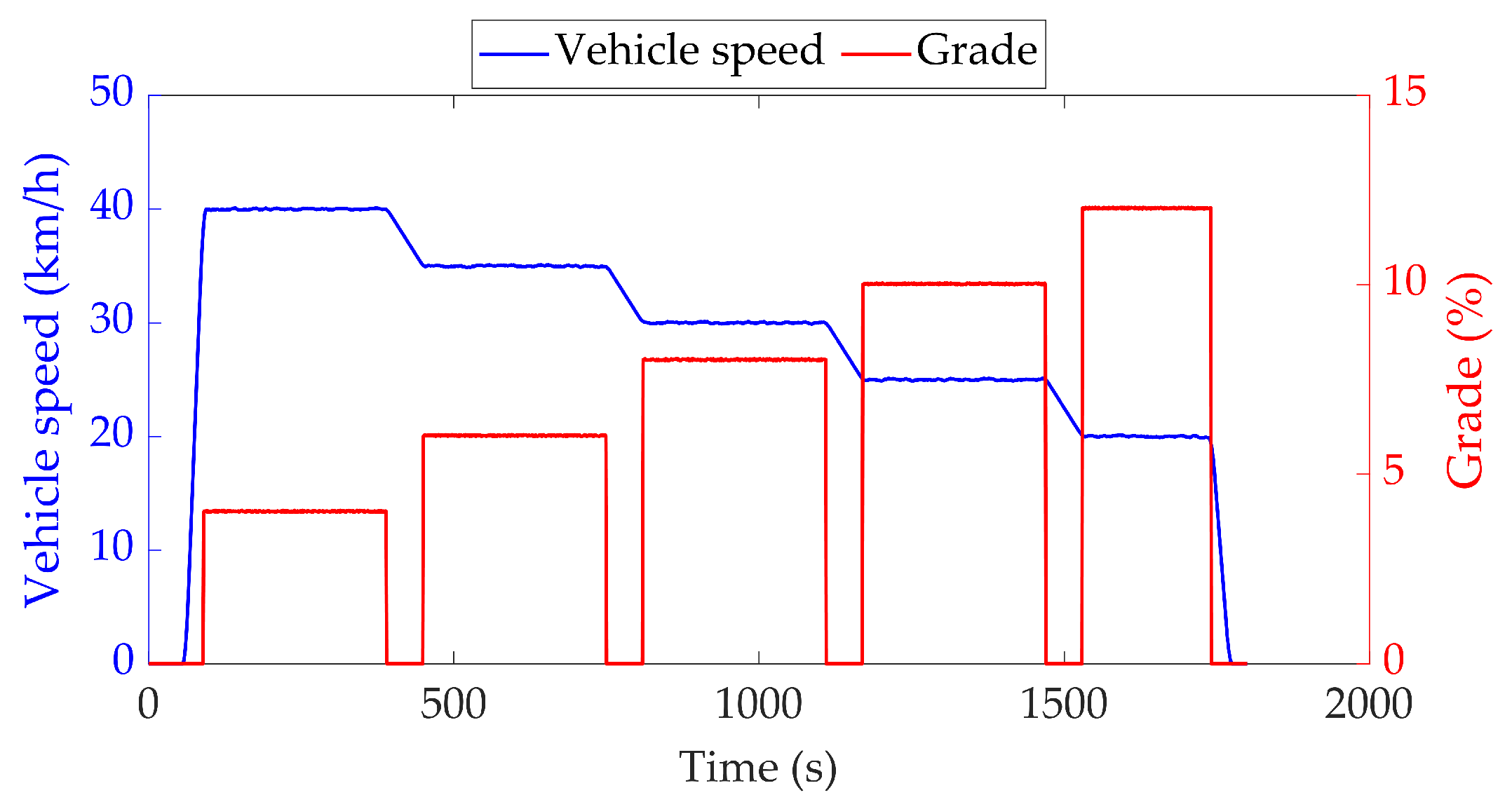
5.1. Verification of CD-CS Strategy
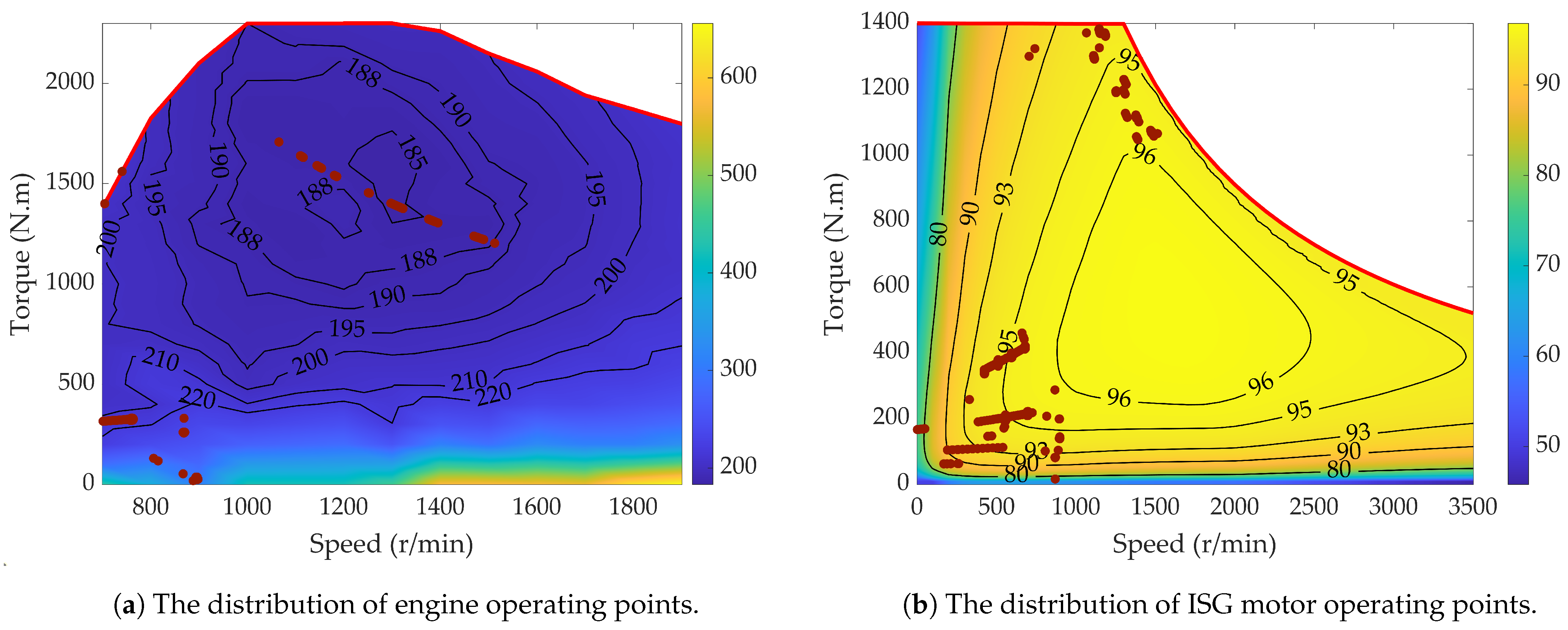
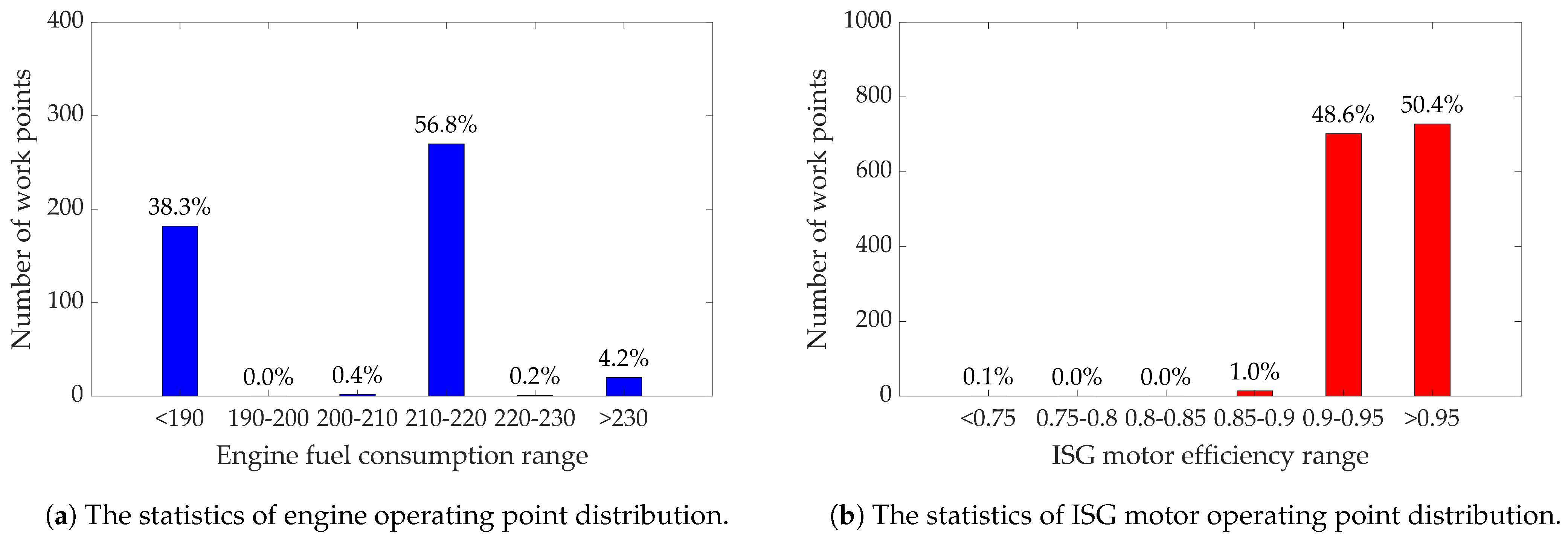
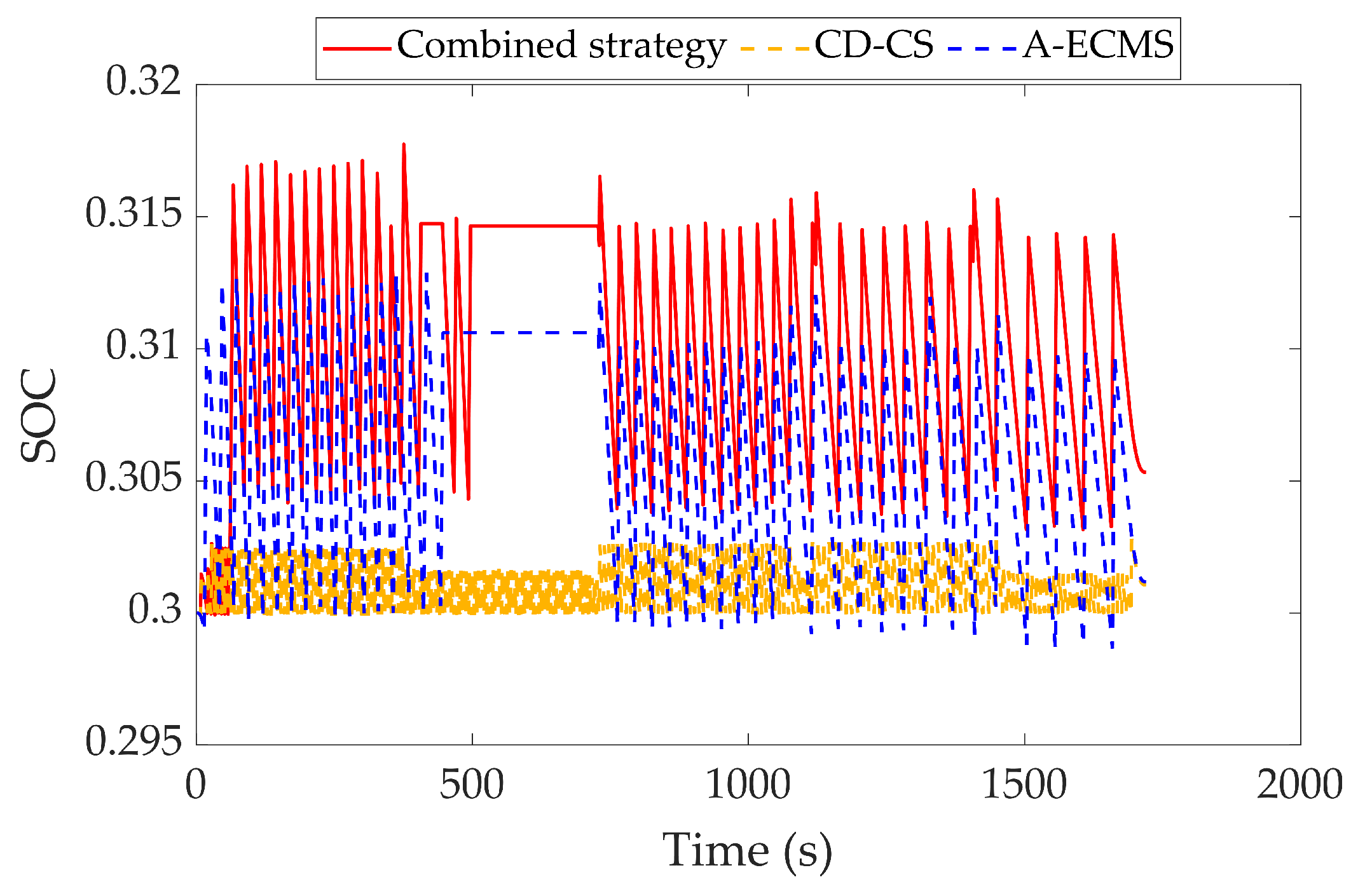
5.2. Verification of Combined Strategy
5.3. Validation of Robustness of Combined Strategy
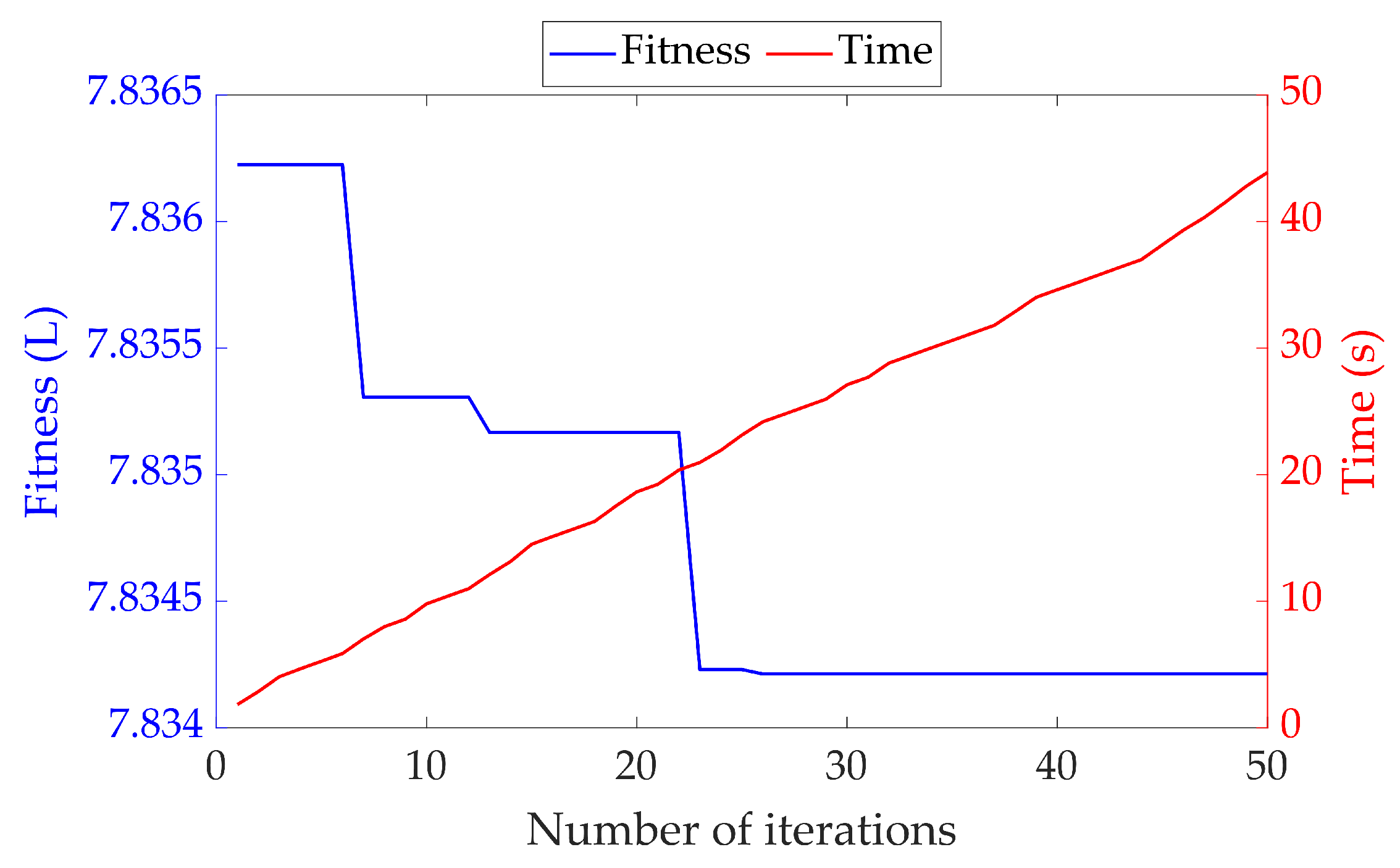
5.4. Verification of Rationality of NOA Operational Parameter Settings
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| HEV | Hybrid electric vehicle |
| EMS | Energy management strategy |
| CD-CS strategy | Charge depleting–charge sustaining strategy |
| ECMS | Equivalent consumption minimization strategy |
| SOC | State of charge |
| V2X | Vehicle-to-Everything |
| NOA | Nutcracker Optimization Algorithm |
| m | Vehicle mass |
| g | Acceleration due to gravity |
| Rolling resistance coefficient | |
| A | Windward area |
| Air resistance coefficient | |
| Rotational mass conversion factor | |
| Tire radius | |
| AMT gear ratio | |
| Final drive gear ratio | |
| Battery open-circuit voltage | |
| Battery internal resistance | |
| Q | Battery capacity |
| v | Vehicle speed |
| Engine speed | |
| Total drive torque | |
| Engine output torque | |
| Efficiency of clutch | |
| ISG motor output torque | |
| Efficiency of AMT | |
| Efficiency of the final drive and differential | |
| Grade angle | |
| Air density | |
| a | Vehicle acceleration |
| Engine fuel consumption rate | |
| ISG motor efficiency | |
| ISG motor speed | |
| I | Battery current |
| Battery output power | |
| Fuel consumption of CD-CS | |
| k | Stage number divided by time |
| Fuel consumption of A-ECMS | |
| Equivalent factor | |
| Battery output power | |
| H | Calorific value of gasoline |
| Initial equivalent factor | |
| Fitness function for equivalent factor optimization | |
| Adaptive component of fitness function | |
| Adaptive factor |
References
- Ehsani, M.; Singh, K.V.; Bansal, H.O.; Mehrjardi, R.T. State of the Art and Trends in Electric and Hybrid Electric Vehicles. Proc. IEEE 2021, 109, 967–984. [Google Scholar] [CrossRef]
- Tran, D.D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, L.; Coskun, S.; Pang, H.; Cui, Y.; Xi, J. Energy Management Strategies for Hybrid Electric Vehicles: Review, Classification, Comparison, and Outlook. Energies 2020, 13, 3352. [Google Scholar] [CrossRef]
- Mohammed, A.S.; Atnaw, S.M.; Salau, A.O.; Eneh, J.N. Review of optimal sizing and power management strategies for fuel cell/battery/super capacitor hybrid electric vehicles. Energy Rep. 2023, 9, 2213–2228. [Google Scholar] [CrossRef]
- Lian, R.; Peng, J.; Wu, Y.; Tan, H.; Zhang, H. Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle. Energy 2020, 197, 117297. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Z.; Huang, D.; Lin, T. Model Prediction and Rule Based Energy Management Strategy for a Plug-in Hybrid Electric Vehicle With Hybrid Energy Storage System. IEEE Trans. Power Electron. 2021, 36, 5926–5940. [Google Scholar] [CrossRef]
- Fan, L.; Wang, Y.; Wei, H.; Zhang, Y.; Zheng, P.; Huang, T.; Li, W. A GA-based online real-time optimized energy management strategy for plug-in hybrid electric vehicles. Energy 2022, 241, 122811. [Google Scholar] [CrossRef]
- Xin, W.; Xu, E.; Zheng, W.; Feng, H.; Qin, J. Optimal energy management of fuel cell hybrid electric vehicle based on model predictive control and on-line mass estimation. Energy Rep. 2022, 8, 4964–4974. [Google Scholar] [CrossRef]
- Wang, W.; Guo, X.; Yang, C.; Zhang, Y.; Zhao, Y.; Huang, D.; Xiang, C. A multi-objective optimization energy management strategy for power split HEV based on velocity prediction. Energy 2022, 238, 121714. [Google Scholar] [CrossRef]
- Guo, L.; Liu, H.; Han, L.; Yang, N.; Liu, R.; Xiang, C. Predictive energy management strategy of dual-mode hybrid electric vehicles combining dynamic coordination control and simultaneous power distribution. Energy 2023, 263, 125598. [Google Scholar] [CrossRef]
- Jui, J.J.; Ahmad, M.A.; Molla, M.I.; Rashid, M.I.M. Optimal energy management strategies for hybrid electric vehicles: A recent survey of machine learning approaches. J. Eng. Res. 2024, 12, 454–467. [Google Scholar] [CrossRef]
- Urooj, A.; Nasir, A. Review of intelligent energy management techniques for hybrid electric vehicles. J. Energy Storage 2024, 92, 112132. [Google Scholar] [CrossRef]
- Yan, F.; Wang, J.; Du, C.; Hua, M. Multi-Objective Energy Management Strategy for Hybrid Electric Vehicles Based on TD3 with Non-Parametric Reward Function. Energies 2023, 16, 74. [Google Scholar] [CrossRef]
- Guo, D.; Lei, G.; Zhao, H.; Yang, F.; Zhang, Q. Quadruple Deep Q-Network-Based Energy Management Strategy for Plug-In Hybrid Electric Vehicles. Energies 2024, 17, 6298. [Google Scholar] [CrossRef]
- Shuai, B.; Hua, M.; Li, Y.; Shuai, S.; Xu, H.; Zhou, Q. Optimal Energy Management of Plug-in Hybrid Electric Vehicles Through Ensemble Reinforcement Learning With Exploration-to-Exploitation Ratio Control. IEEE Trans. Intell. Veh. 2024, 8, 1–11. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Ruan, J.; Liang, Z.; Liu, K. Rule and optimization combined real-time energy management strategy for minimizing cost of fuel cell hybrid electric vehicles. Energy 2023, 285, 129442. [Google Scholar] [CrossRef]
- Chang, C.; Zhao, W.; Wang, C.; Song, Y. A Novel Energy Management Strategy Integrating Deep Reinforcement Learning and Rule Based on Condition Identification. IEEE Trans. Veh. Technol. 2023, 72, 1674–1688. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Zhang, Y.; Lei, Z.; Chen, Z.; Li, G. A neural network-based ECMS for optimized energy management of plug-in hybrid electric vehicles. Energy 2022, 243, 122727. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected HEVs and PHEVs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Hu, X.; Liu, T.; Qi, X.; Barth, M. Reinforcement Learning for Hybrid and Plug-In Hybrid Electric Vehicle Energy Management: Recent Advances and Prospects. IEEE Ind. Electron. Mag. 2019, 13, 16–25. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, F.; Zhang, C.; Sun, C. Stochastically predictive co-optimization of the speed planning and powertrain controls for electric vehicles driving in random traffic environment safely and efficiently. J. Power Sources 2022, 528, 231200. [Google Scholar] [CrossRef]
- Cui, W.; Cui, N.; Li, T.; Cui, Z.; Du, Y.; Zhang, C. An efficient multi-objective hierarchical energy management strategy for plug-in hybrid electric vehicle in connected scenario. Energy 2022, 257, 124690. [Google Scholar] [CrossRef]
- Sun, X.; Cao, Y.; Jin, Z.; Tian, X.; Xue, M. An Adaptive ECMS Based on Traffic Information for Plug-in Hybrid Electric Buses. IEEE Trans. Ind. Electron. 2023, 70, 9248–9259. [Google Scholar] [CrossRef]
- Hou, Z.; Guo, J.; Li, J.; Hu, J.; Sun, W.; Zhang, Y. Exploration the pathways of connected electric vehicle design: A vehicle-environment cooperation energy management strategy. Energy 2023, 271, 127081. [Google Scholar] [CrossRef]
- Ha, S.; Lee, H. Energy Management Strategy Based on V2X Communications and Road Information for a Connected PHEV and Its Evaluation Using an IDHIL Simulator. Appl. Sci. 2023, 13, 9208. [Google Scholar] [CrossRef]
- Liu, H.; Lei, Y.; Sun, W.; Chang, C.; Jiang, W.; Liu, Y.; Hu, J. Research on approximate optimal energy management and multi-objective optimization of connected automated range-extended electric vehicle. Energy 2024, 306, 132368. [Google Scholar] [CrossRef]
- Niu, Z.; He, H. A data-driven solution for intelligent power allocation of connected hybrid electric vehicles inspired by offline deep reinforcement learning in V2X scenario. Appl. Energy 2024, 372, 123861. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, F.; Xie, S.; Zhang, T.; Chen, Y.; Peng, G. Co-optimization of speed planning and energy management for connected plug-in hybrid electric vehicles on slippery roads. Energy 2025, 324, 135835. [Google Scholar] [CrossRef]
- Miao, Y.; Tian, Y.; Zhang, Y.; Ma, L. Parameter Optimization and Energy Management for a Dual-Motor Powertrain in Battery Electric Heavy Trucks. In Proceedings of the 2024 IEEE 22nd International Conference on Industrial Informatics (INDIN), Beijing, China, 18–20 August 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Jameel, M.; Abouhawwash, M. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl.-Based Syst. 2023, 262, 110248. [Google Scholar] [CrossRef]
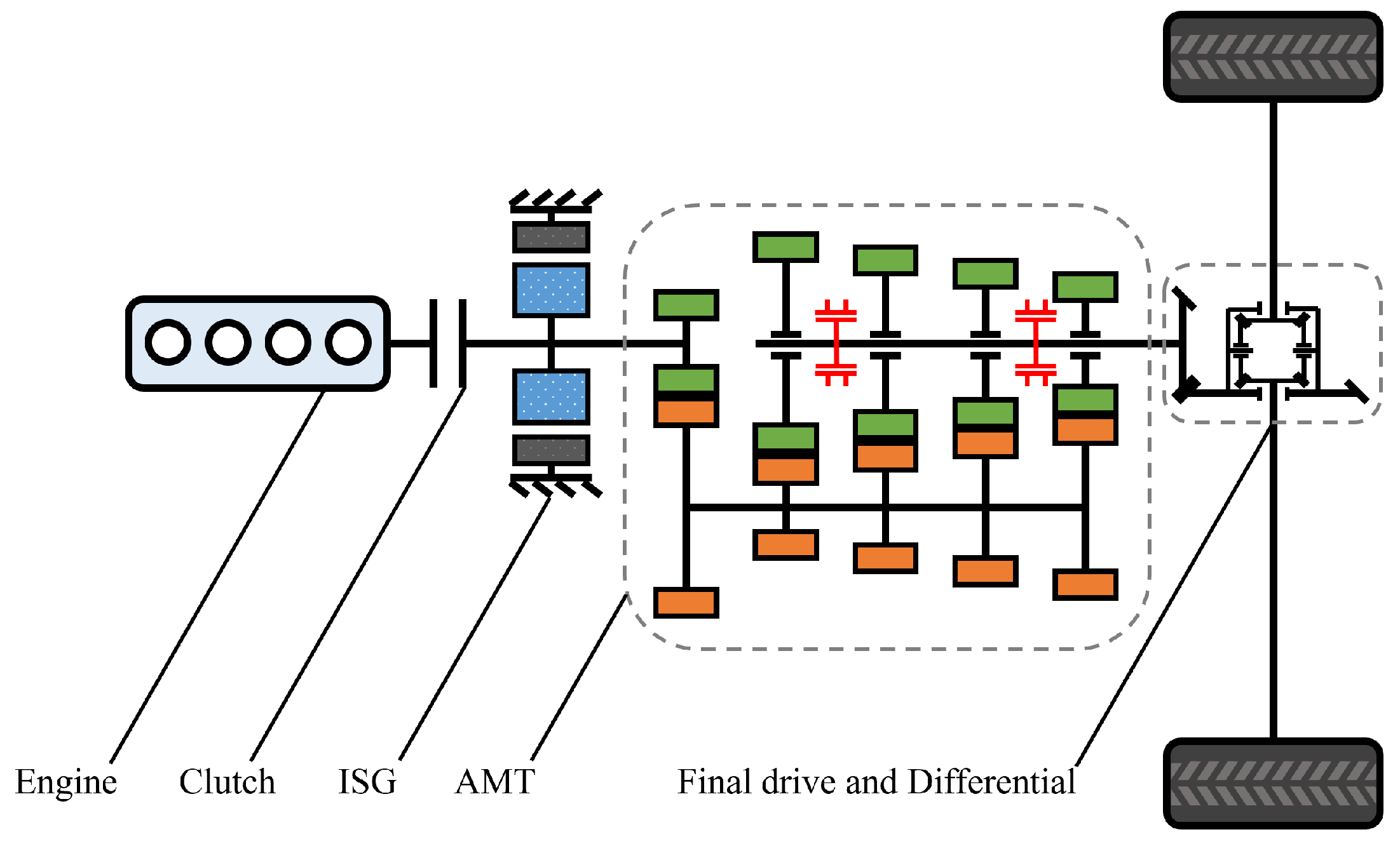
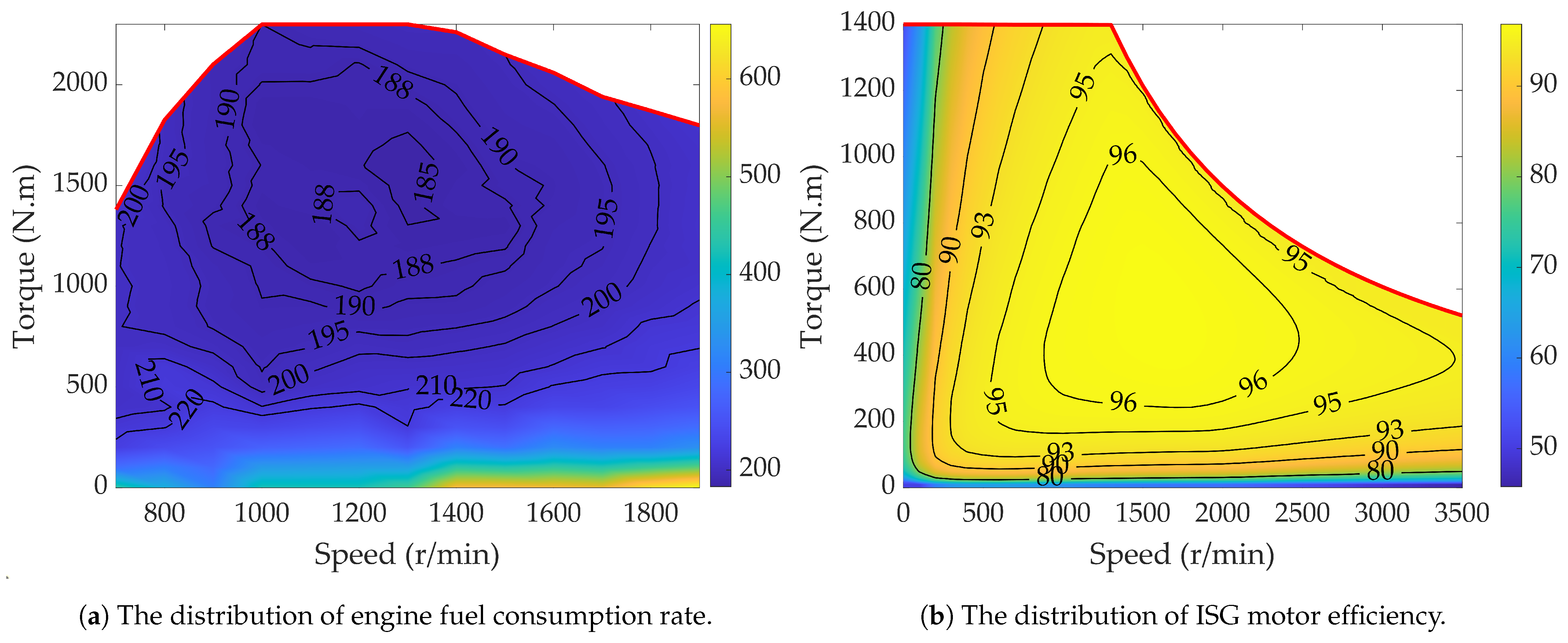

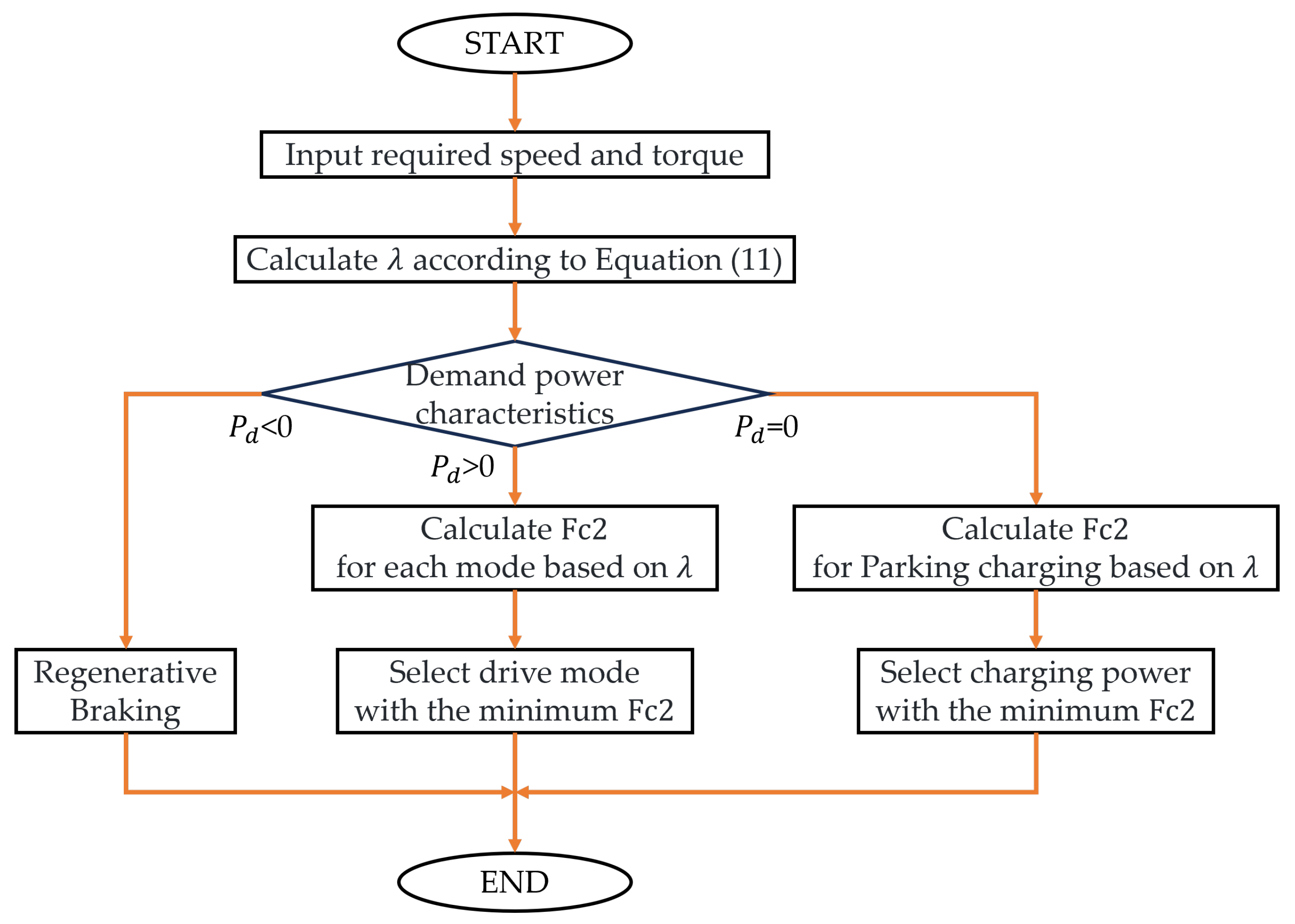
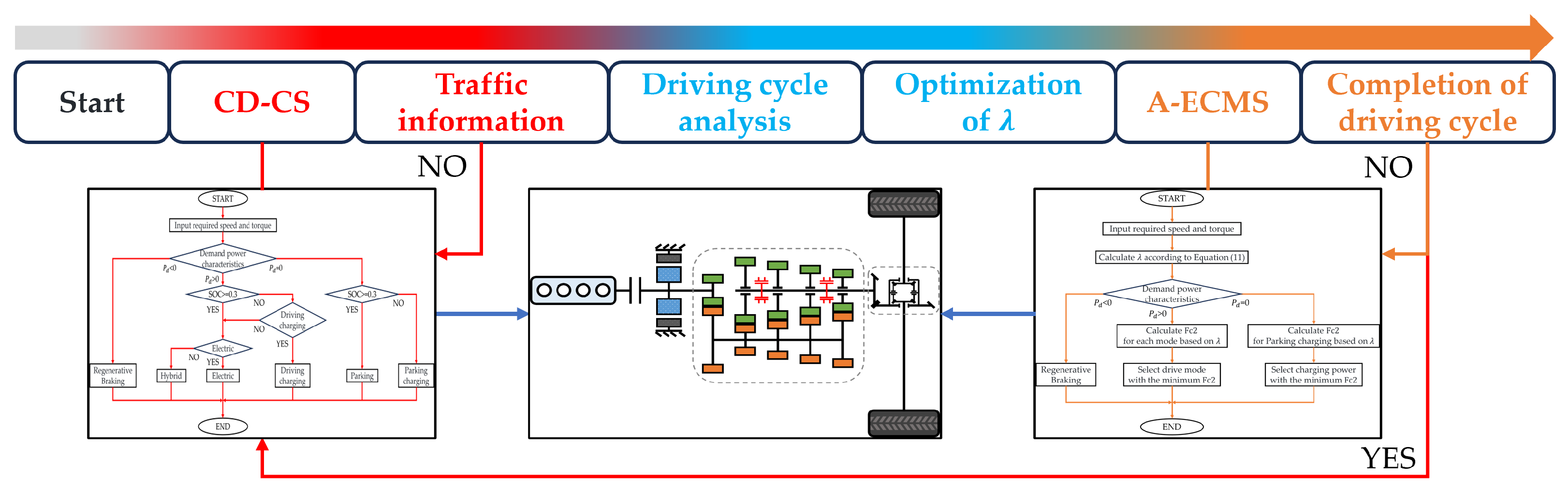

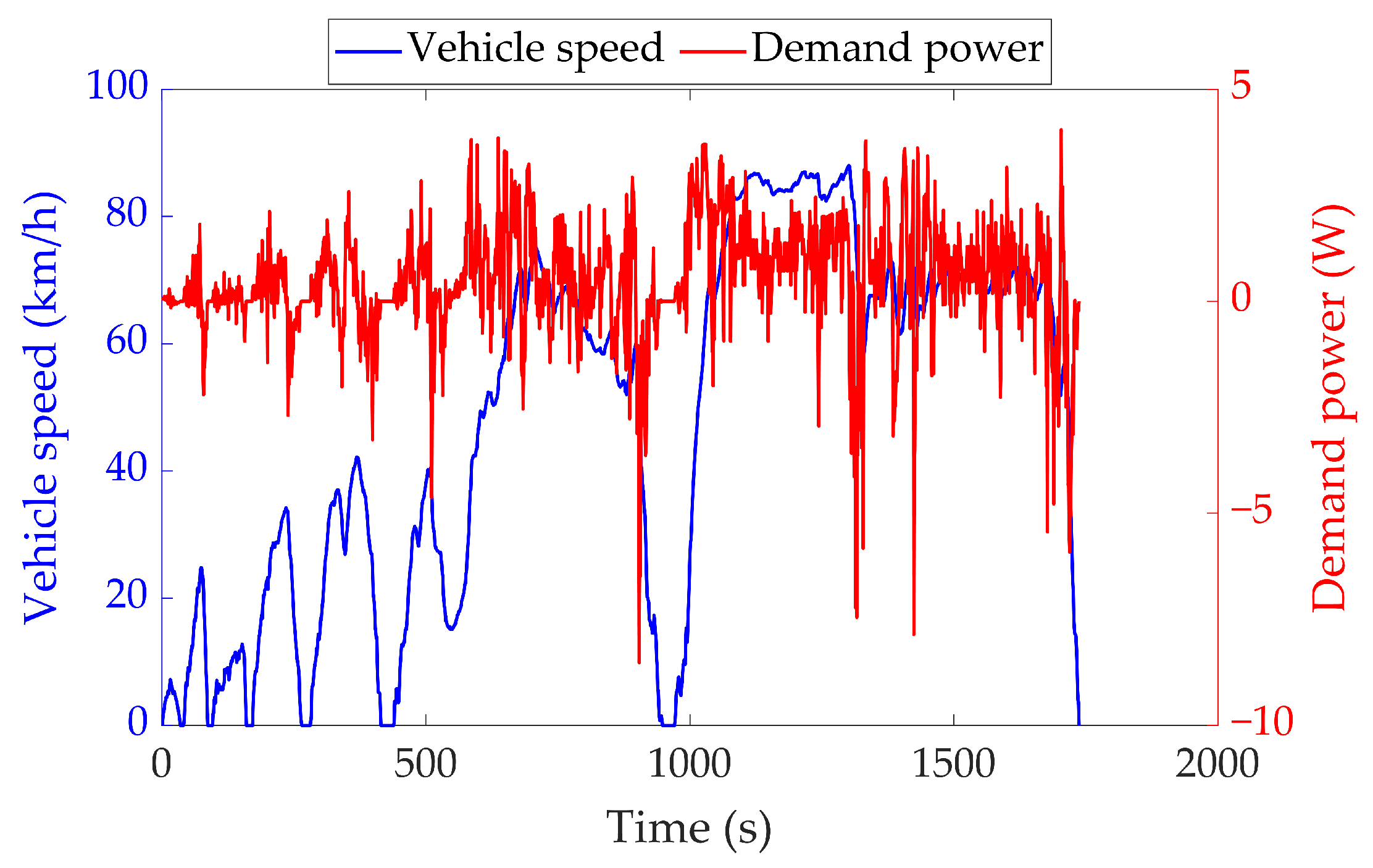
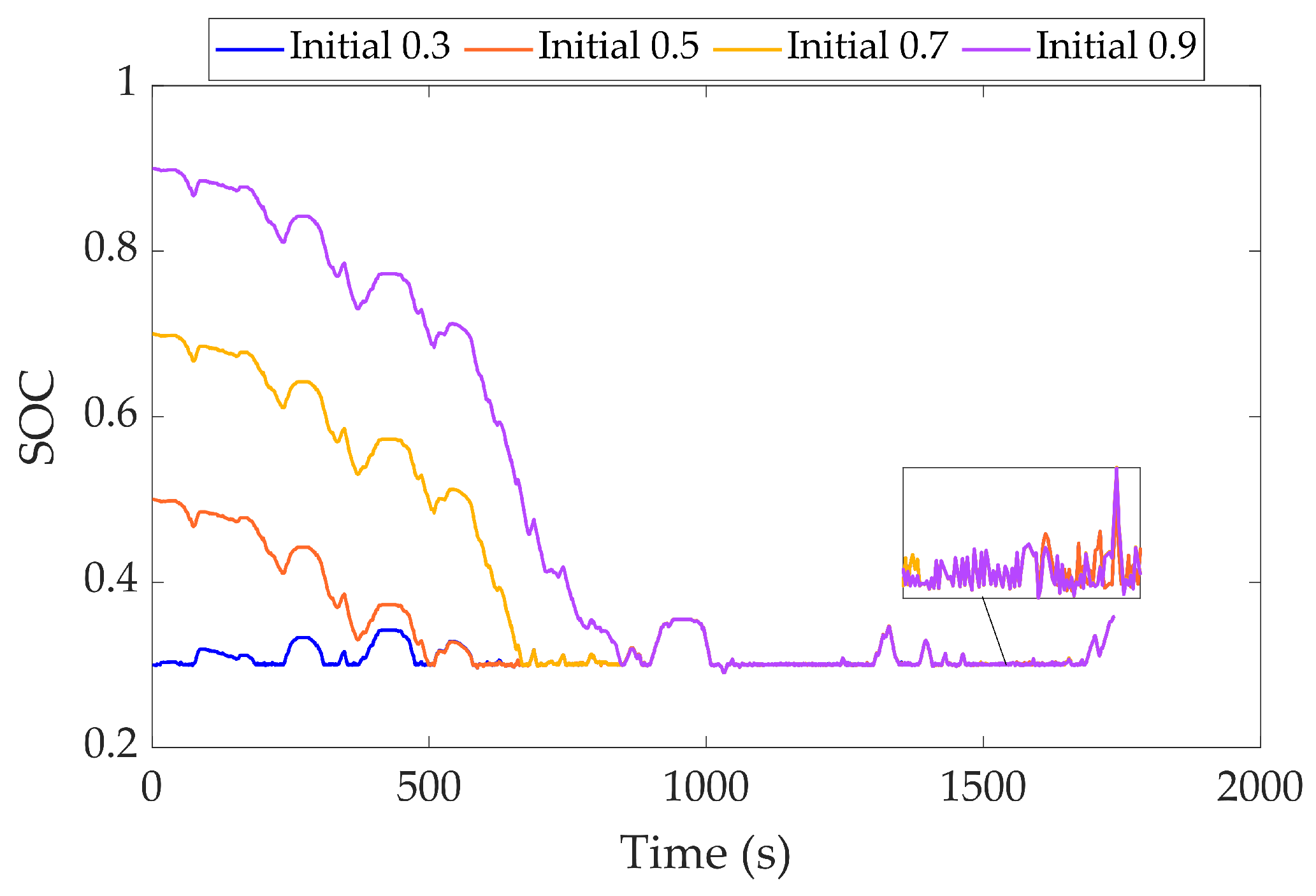
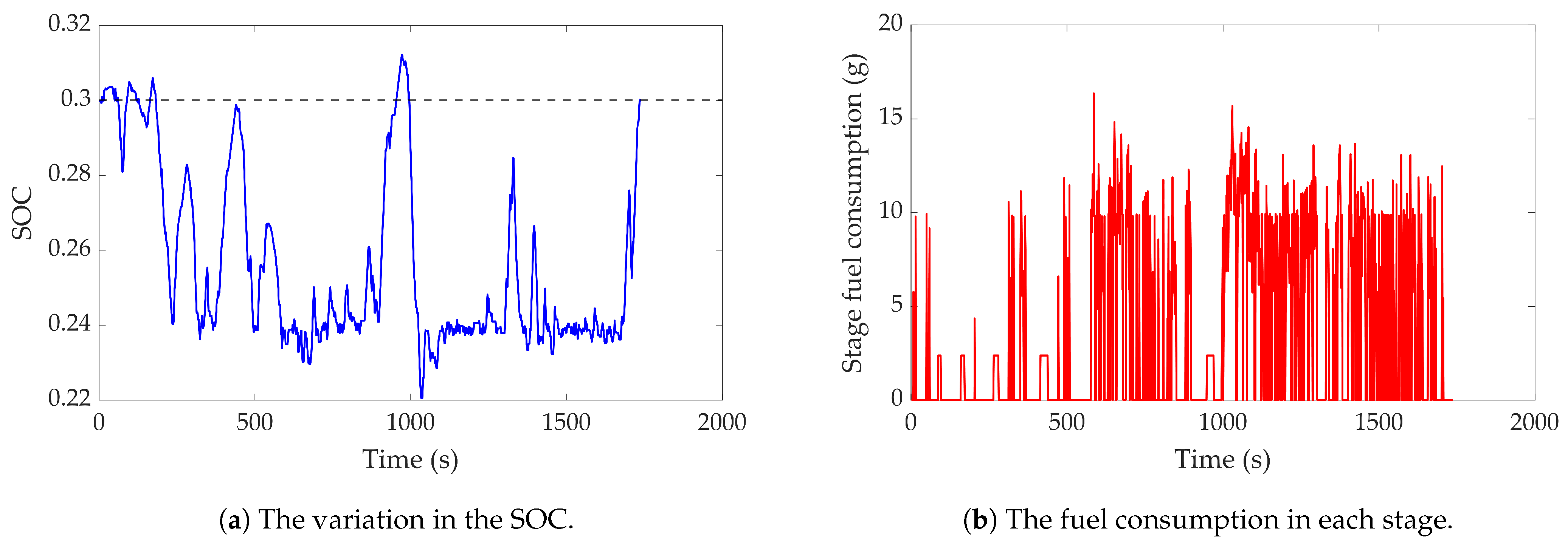
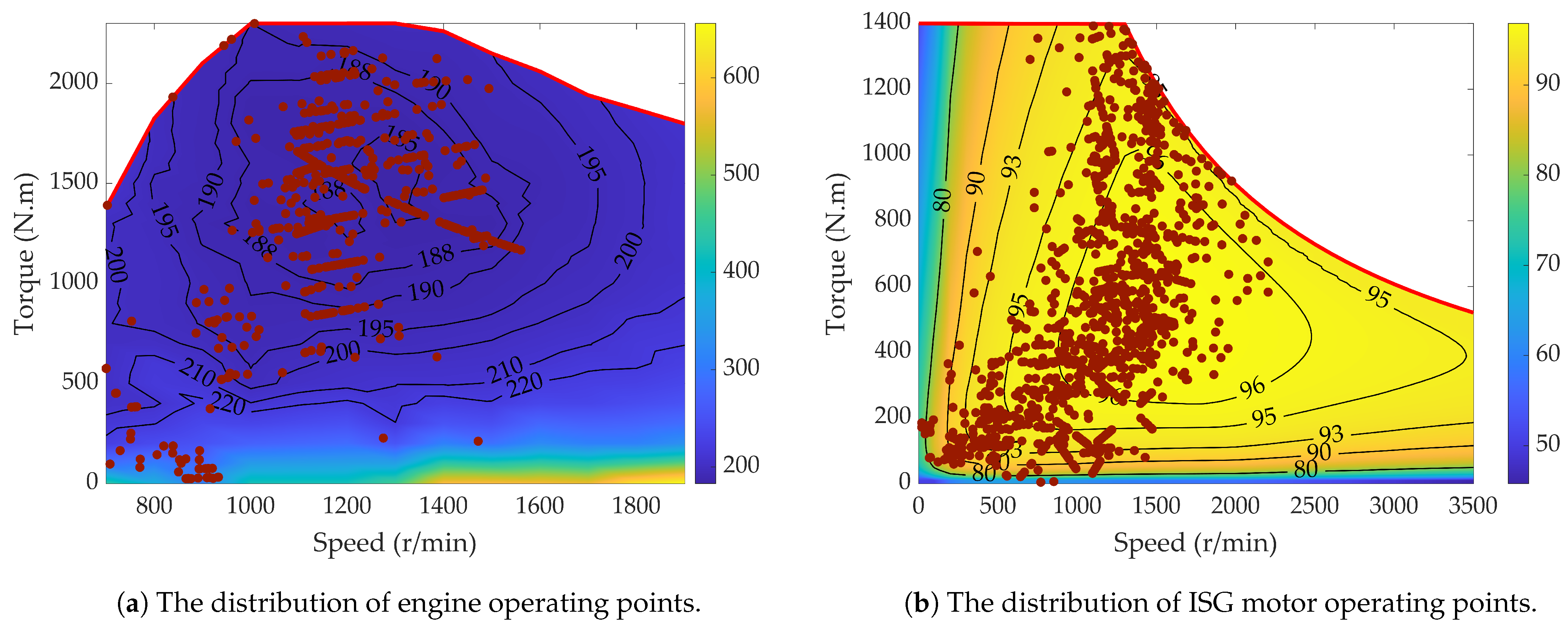
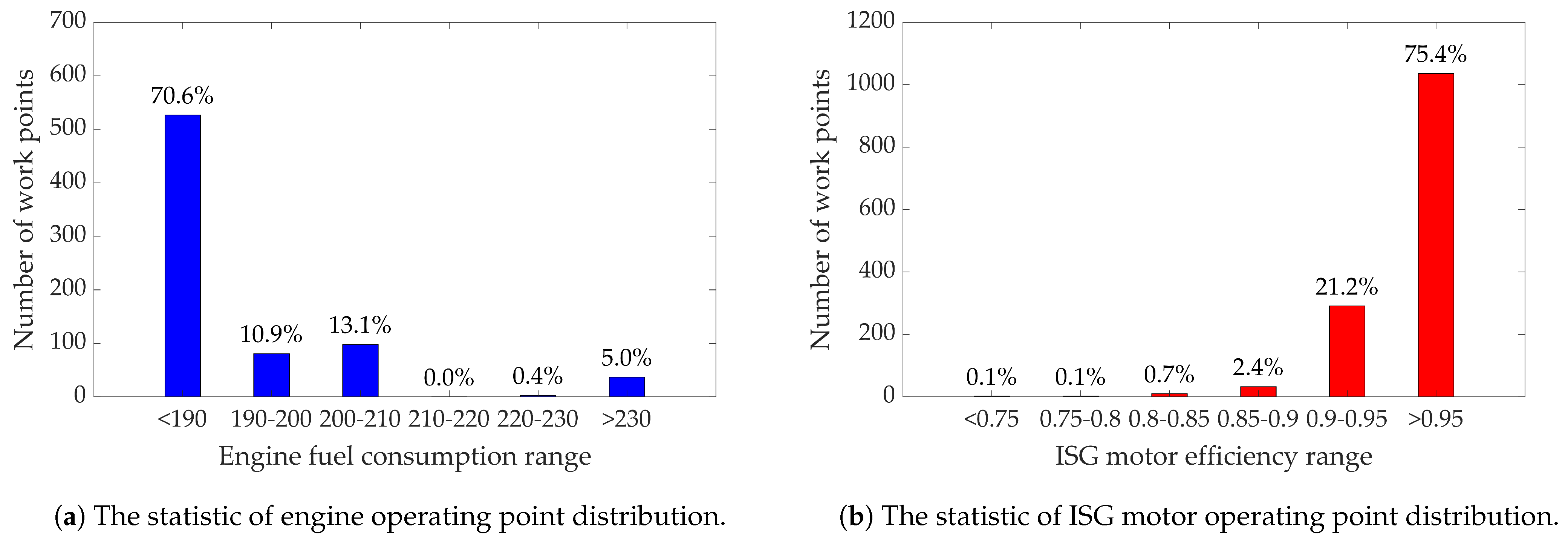
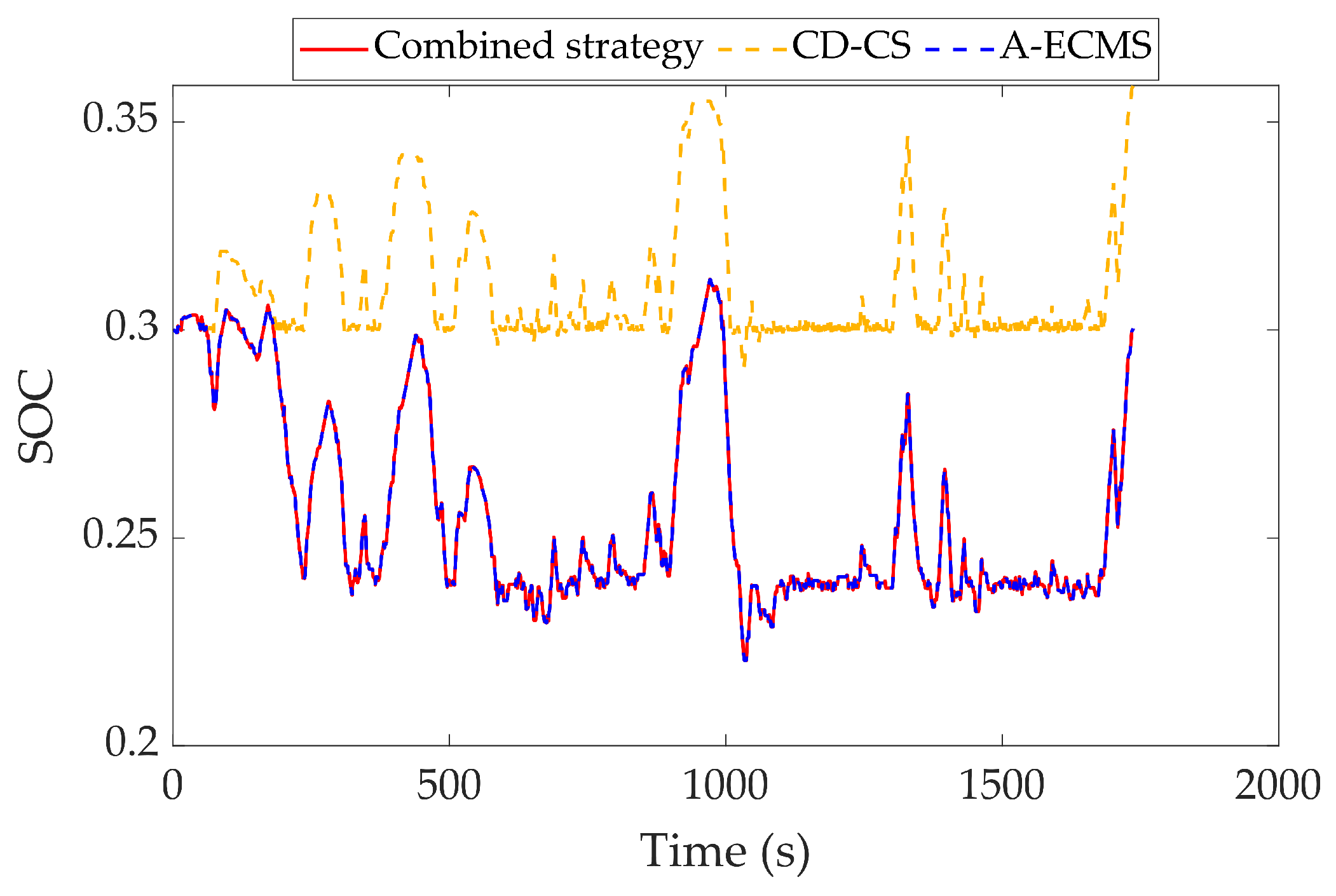
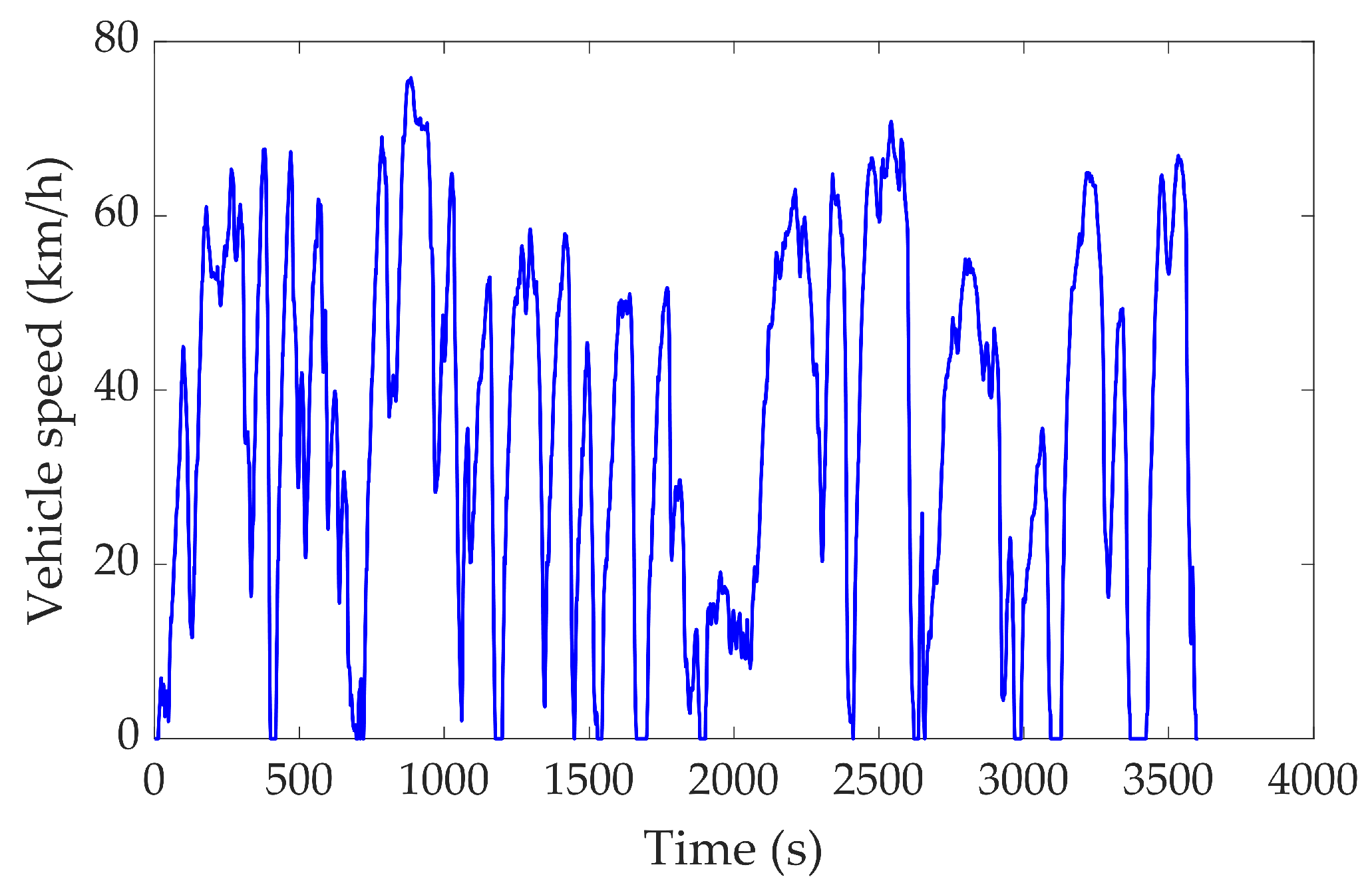
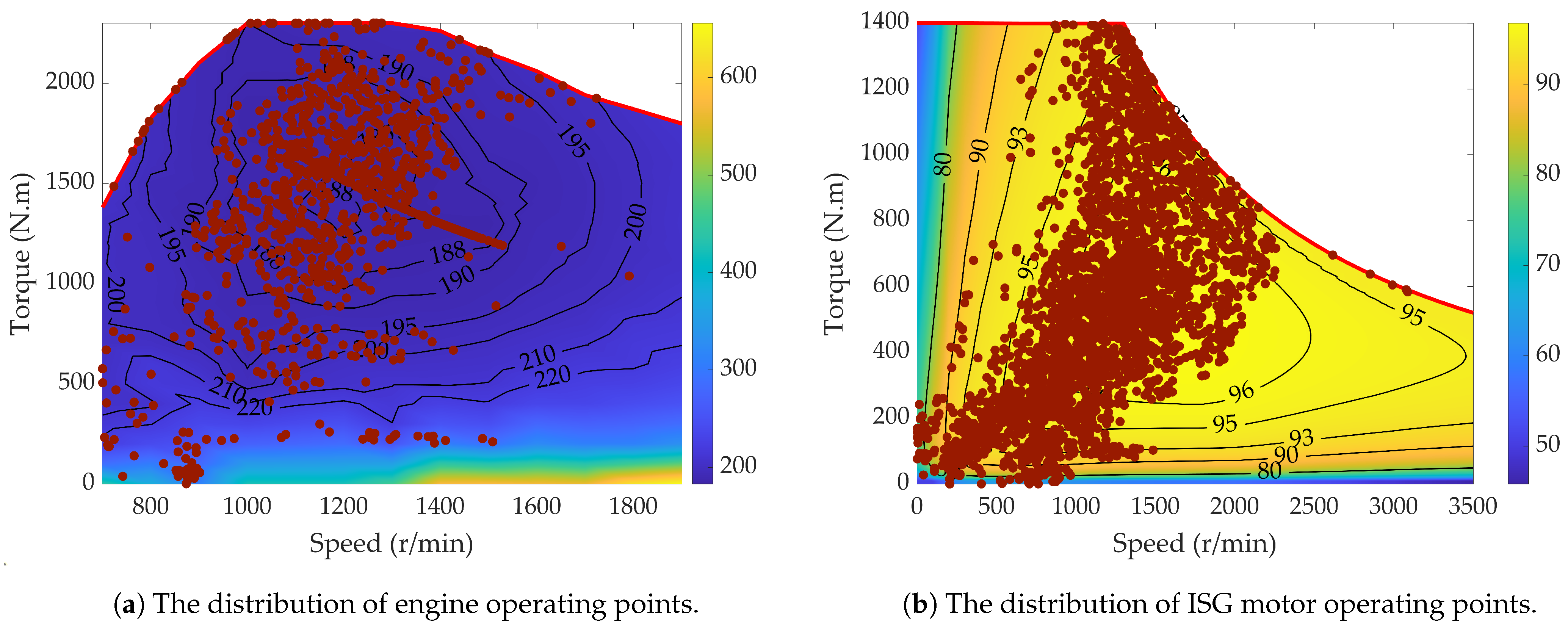



| Mode | Engine | Clutch | ISG Motor | AMT |
|---|---|---|---|---|
| Electric mode | Off | Off | On | On |
| Engine mode | On | On | Off | On |
| Hybrid mode | On | On | On | On |
| Driving charging | On | On | On | On |
| Parking charging | On | On | On | Off |
| Regenerative braking | Off | Off | On | On |
| Parameter | Symbol | Value |
|---|---|---|
| Vehicle mass | m | 49,000 |
| Acceleration due to gravity | g | 9.8 |
| Rolling resistance coefficient | Equation (4) | |
| Windward area | A | 6.163 |
| Air resistance coefficient | 0.7 | |
| Rotational mass conversion factor | 1.1 | |
| Tire radius | 0.526 | |
| AMT gear ratio | Table 3 | |
| Final drive gear ratio | 3.364 | |
| Battery open-circuit voltage | 540 | |
| Battery internal resistance | 0.157 | |
| Battery capacity | Q | 27.6 Ah |
| Allowed SOC range | SOC | 0.2–1.0 |
| Initial SOC | Final SOC | Fuel Consumption | RMS Error for CS Phase SOC |
|---|---|---|---|
| 0.3 | 0.3588 | 8.3332 L | 0.0179 |
| 0.5 | 0.3588 | 7.5321 L | 0.0174 |
| 0.7 | 0.3588 | 6.8140 L | 0.0180 |
| 0.9 | 0.3587 | 6.0639 L | 0.0195 |
| EMS | Final SOC | Fuel Consumption | Difference from A-ECMS | Difference from CD-CS Strategy |
|---|---|---|---|---|
| Combined strategy | 0.3004 | 7.8457 L | 0.15% | −5.85% |
| CD-CS strategy | 0.3588 | 8.3332 L | 6.37% | - |
| A-ECMS | 0.3094 | 7.8342 L | - | −5.99% |
| EMS | Final SOC | Fuel Consumption | Difference from A-ECMS | Difference from CD-CS Strategy |
|---|---|---|---|---|
| Combined strategy | 0.3003 | 14.2498 L | 0.13% | −4.69% |
| CD-CS strategy | 0.3536 | 14.9512 L | 5.06% | - |
| A-ECMS | 0.3003 | 14.2309 L | - | −4.82% |
| EMS | Final SOC | Fuel Consumption | Difference from A-ECMS | Difference from CD-CS Strategy |
|---|---|---|---|---|
| Combined strategy | 0.3053 | 2.9504 L | 0.08% | −3.99% |
| CD-CS strategy | 0.3011 | 3.0729 L | 4.23% | - |
| A-ECMS | 0.3012 | 2.9481 L | - | −4.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Li, L.; Wang, X. A Combined Energy Management Strategy for Heavy-Duty Trucks Based on Global Traffic Information Optimization. Sustainability 2025, 17, 6361. https://doi.org/10.3390/su17146361
Wu H, Li L, Wang X. A Combined Energy Management Strategy for Heavy-Duty Trucks Based on Global Traffic Information Optimization. Sustainability. 2025; 17(14):6361. https://doi.org/10.3390/su17146361
Chicago/Turabian StyleWu, Haishan, Liang Li, and Xiangyu Wang. 2025. "A Combined Energy Management Strategy for Heavy-Duty Trucks Based on Global Traffic Information Optimization" Sustainability 17, no. 14: 6361. https://doi.org/10.3390/su17146361
APA StyleWu, H., Li, L., & Wang, X. (2025). A Combined Energy Management Strategy for Heavy-Duty Trucks Based on Global Traffic Information Optimization. Sustainability, 17(14), 6361. https://doi.org/10.3390/su17146361






