Promoting Freight Modal Shift to High-Speed Rail for CO2 Emission Reduction: A Bi-Level Multi-Objective Optimization Approach
Abstract
1. Introduction
2. Literature Review
3. Methodology
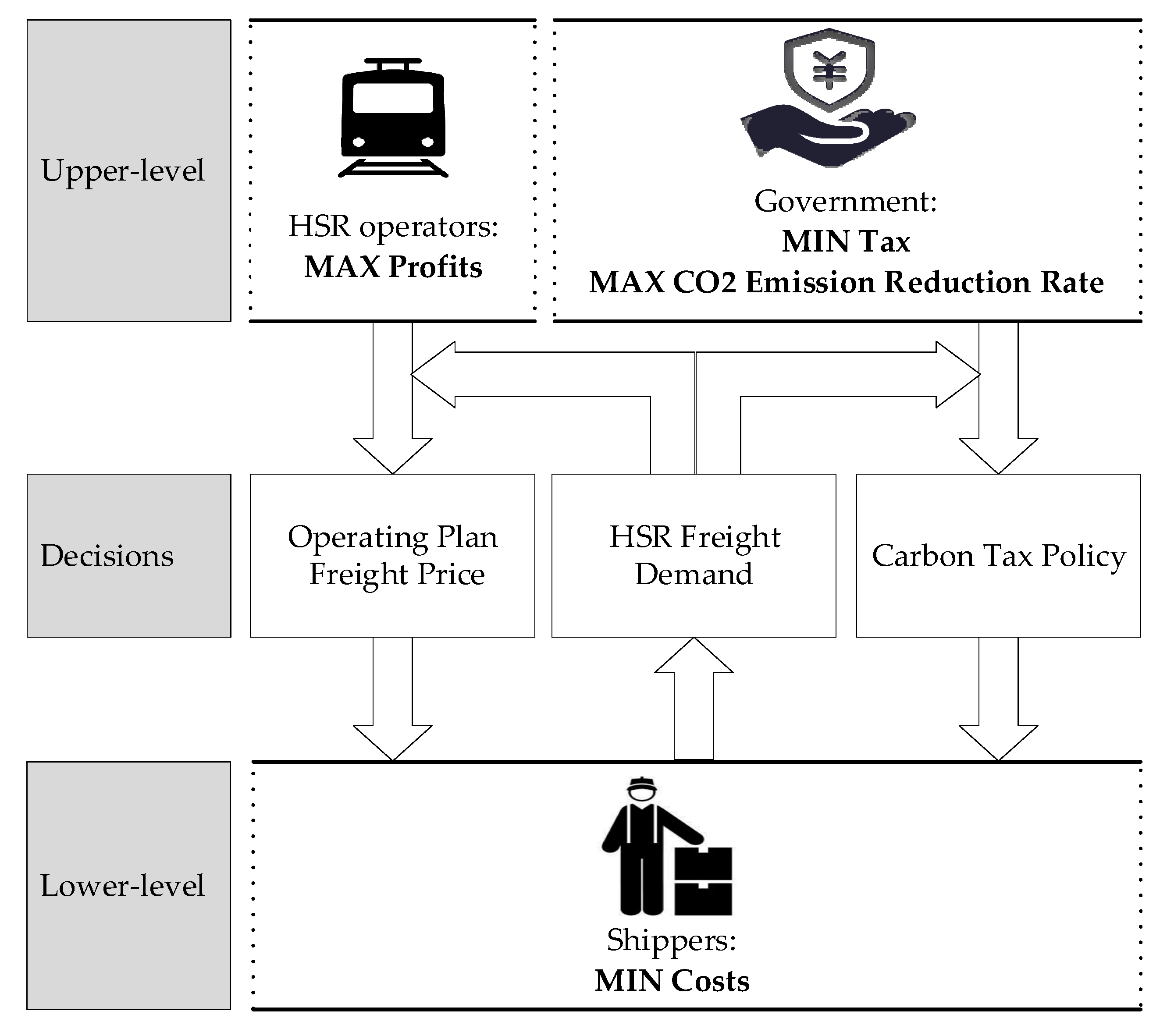
3.1. Problem Description
3.2. Upper Level: Decision-Making of the Government and HSR Operators
- (i)
- Constraints on timeliness
- (ii)
- Constraints on service frequency
- (iii)
- Constraints on the passing capacity of railway arcs
- (iv)
- Constraints on cargo flow and train flow
- (v)
- Constraints on decision variables
3.3. Lower-Level: Network Equilibrium Model
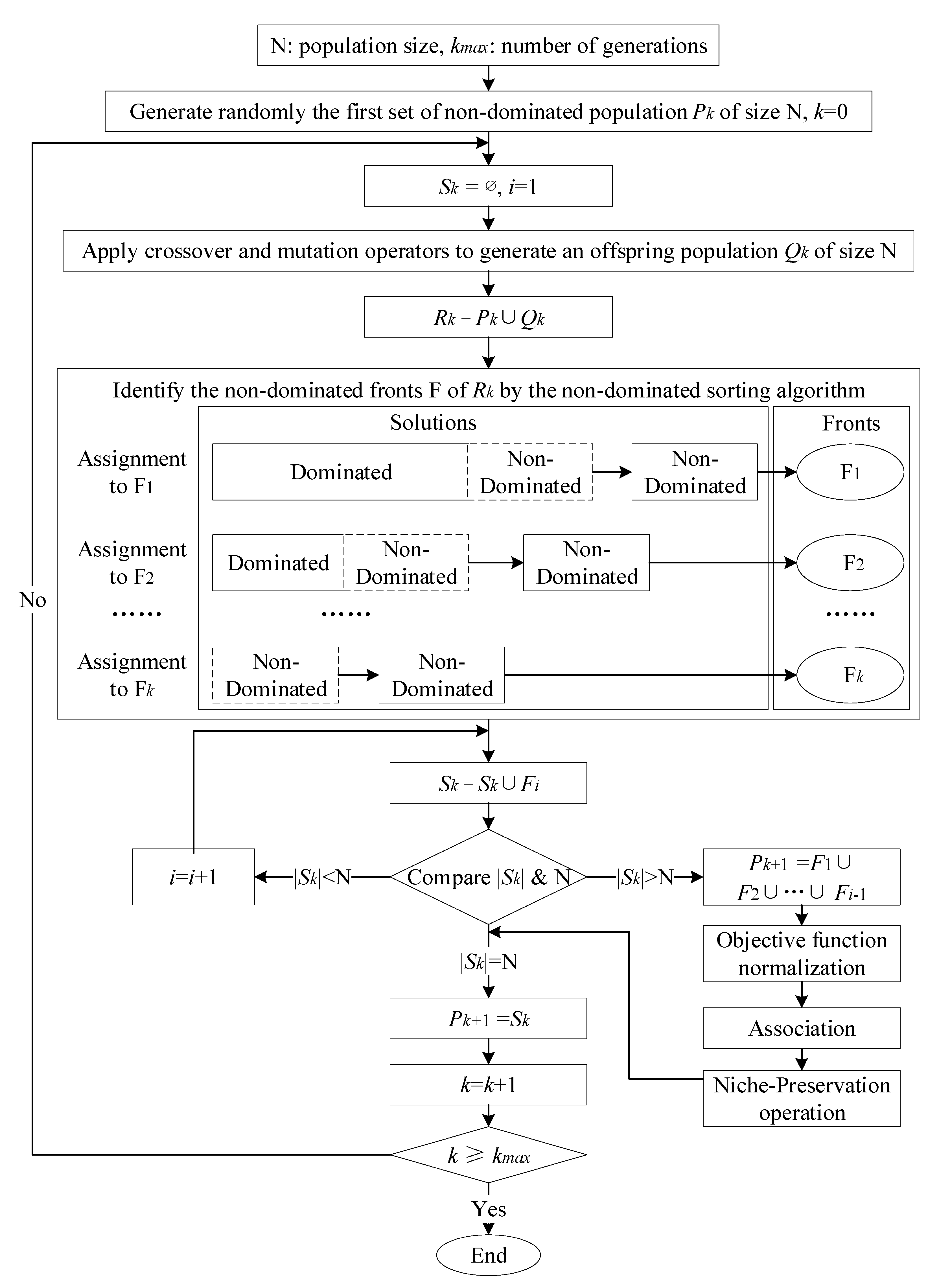
3.4. Algorithm Design
| Algorithm 1. Pricing, planning, and taxing (PPT) algorithm. |
| 1: Initialize 2: Set initial parameters: HSR freight rate , carbon tax rate 3: Set relative error threshold err, maximum number of iterations 4: Set iteration counter ite ← 0 5: Repeat 6: Input into lower-level model 7: Solve lower-level model to obtain equilibrium freight demand 8: Update ite ← ite + 1 9: Find the response function between the freight demand and utility attributes 10: Substitute into upper-level model 11: Solve upper-level model to get updated decision variables: 12: Until or 13: Return optimal solution |
- (1)
- Solving the lower-level model
- (2)
- Acquiring the reaction function
- (3)
- Solving the upper-level model
4. Case Study
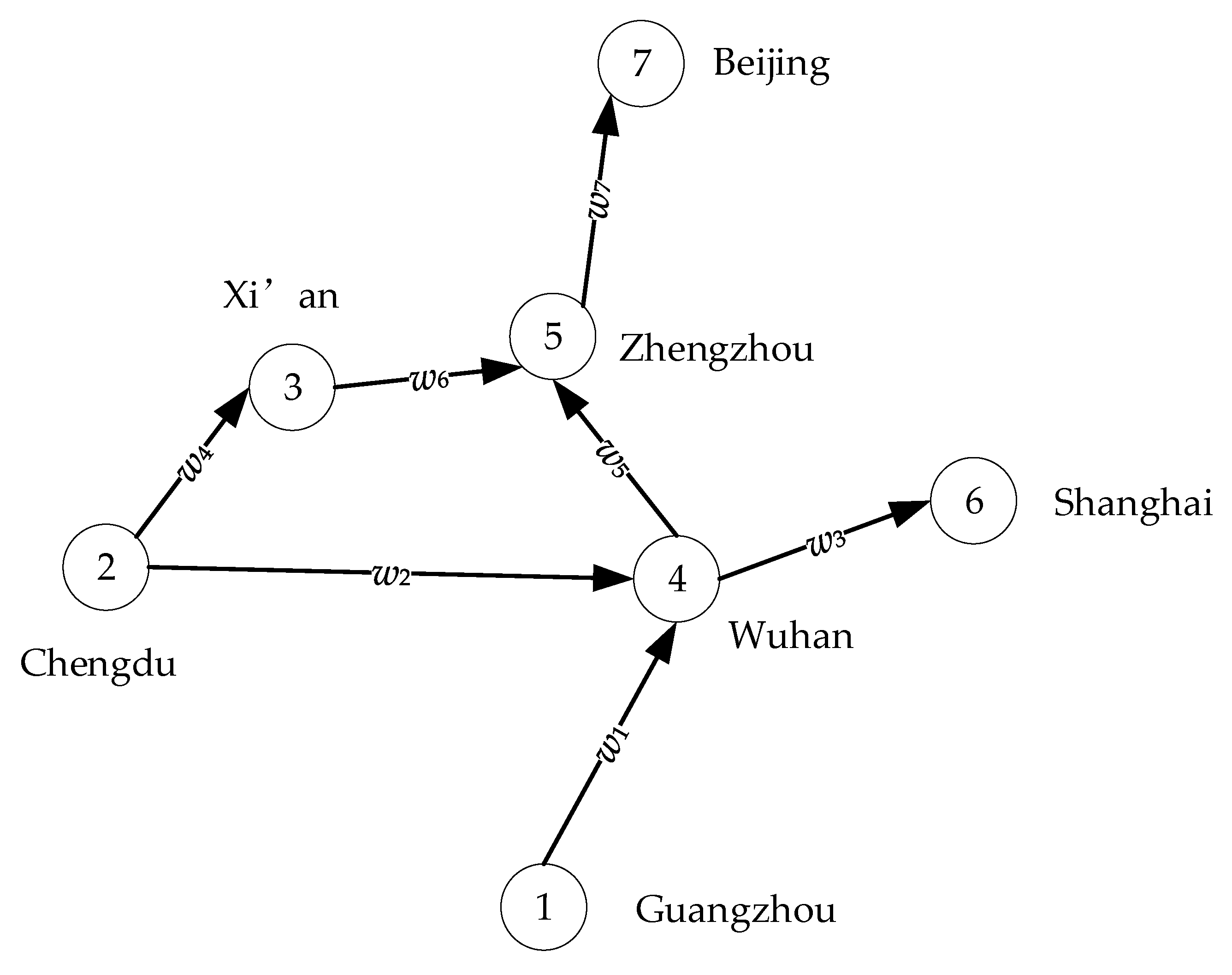
4.1. The Input Data
4.2. Results and Discussion
- Scenario #0: Reference
- Scenario #1: Optimizing HSR freight operation plans and rates
- Scenario #2: Tax policy added
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pathak, D.K.; Thakur, L.S.; Rahman, S. Performance evaluation framework for sustainable freight transportation systems. Int. J. Prod. Res. 2019, 57, 6202–6222. [Google Scholar] [CrossRef]
- Marcucci, E.; Gatta, V.; Le Pira, M.; Elias, W. Modal shift, emission reductions and behavioral change: Transport policies and innovations to tackle climate change. Res. Transp. Econ. 2019, 73, 1–3. [Google Scholar] [CrossRef]
- Kaack, L.H.; Vaishnav, P.; Morgan, M.G.; Azevedo, I.L.; Rai, S. Decarbonizing intraregional freight systems with a focus on modal shift. Environ. Res. Lett. 2018, 13, 083001. [Google Scholar] [CrossRef]
- Raza, Z.; Svanberg, M.; Wiegmans, B. Modal shift from road haulage to short sea shipping: A systematic literature review and research directions. Transp. Rev. 2020, 40, 382–406. [Google Scholar] [CrossRef]
- Islam, D.M.Z.; Ricci, S.; Nelldal, B.-L. How to make modal shift from road to rail possible in the European transport market, as aspired to in the EU Transport White Paper 2011. Eur. Transp. Res. Rev. 2016, 8, 18. [Google Scholar] [CrossRef]
- Salvucci, R.; Gargiulo, M.; Karlsson, K. The role of modal shift in decarbonising the Scandinavian transport sector: Applying substitution elasticities in TIMES-Nordic. Appl. Energy 2019, 253, 113593. [Google Scholar] [CrossRef]
- Mizutani, J.; Fukuda, S. Issues on modal shift of freight from road to rail in Japan: Review of rail track ownership, investment and access charges after the National Railway restructuring. Res. Transp. Bus. Manag. 2020, 35, 100484. [Google Scholar] [CrossRef]
- Bickford, E.; Holloway, T.; Karambelas, A.; Johnston, M.; Adams, T.; Janssen, M.; Moberg, C. Emissions and Air Quality Impacts of Truck-to-Rail Freight Modal Shifts in the Midwestern United States. Environ. Sci. Technol. 2014, 48, 446–454. [Google Scholar] [CrossRef]
- Chen, S.; Wu, J.; Zong, Y. The Impact of the Freight Transport Modal Shift Policy on China’s Carbon Emissions Reduction. Sustainability 2020, 12, 583. [Google Scholar] [CrossRef]
- Choi, B.; Park, S.-i.; Lee, K.-D. A System Dynamics Model of the Modal Shift from Road to Rail: Containerization and Imposition of Taxes. J. Adv. Transp. 2019, 2019, 7232710. [Google Scholar] [CrossRef]
- Chandra, S.; Christiansen, M.; Fagerholt, K. Analysing the modal shift from road-based to coastal shipping-based distribution—A case study of outbound automotive logistics in India. Marit. Policy Manag. 2020, 47, 273–286. [Google Scholar] [CrossRef]
- To, W.M. Greenhouse gases emissions from the logistics sector: The case of Hong Kong, China. J. Clean. Prod. 2015, 103, 658–664. [Google Scholar] [CrossRef]
- Chai, J.; Zhou, Y.; Zhou, X.; Wang, S.; Zhang, Z.G.; Liu, Z. Analysis on shock effect of China’s high-speed railway on aviation transport. Transp. Res. Part A-Policy Pract. 2018, 108, 35–44. [Google Scholar] [CrossRef]
- Bi, M.; He, S.; Xu, W. Express delivery with high-speed railway: Definitely feasible or just a publicity stunt. Transp. Res. Part A-Policy Pract. 2019, 120, 165–187. [Google Scholar] [CrossRef]
- Jia, X.; He, R.; Chai, H. Optimizing the Number of Express Freight Trains on a High-speed Railway Corridor by the Departure Period. IEEE Access 2020, 8, 100058–100072. [Google Scholar] [CrossRef]
- Regmi, M.B.; Hanaoka, S. Assessment of Modal Shift and Emissions along a Freight Transport Corridor Between Laos and Thailand. Int. J. Sustain. Transp. 2015, 9, 192–202. [Google Scholar] [CrossRef]
- Wang, M.; Liu, K.; Choi, T.-M.; Yue, X. Effects of Carbon Emission Taxes on Transportation Mode Selections and Social Welfare. IEEE Trans. Syst. Man Cybern.—Syst. 2015, 45, 1413–1423. [Google Scholar] [CrossRef]
- Bouchery, Y.; Ghaffari, A.; Jemai, Z.; Fransoo, J. Sustainable transportation and order quantity: Insights from multiobjective optimization. Flex. Serv. Manuf. J. 2016, 28, 367–396. [Google Scholar] [CrossRef]
- Lin, B.; Liu, C.; Wang, H.; Lin, R. Modeling the railway network design problem: A novel approach to considering carbon emissions reduction. Transport. Res. Part D-Transport. Environ. 2017, 56, 95–109. [Google Scholar] [CrossRef]
- Tao, X.; Wu, Q.; Zhu, L. Mitigation potential of CO2 emissions from modal shift induced by subsidy in hinterland container transport. Energy Policy 2017, 101, 265–273. [Google Scholar] [CrossRef]
- Kundu, T.; Sheu, J.-B. Analyzing the effect of government subsidy on shippers’ mode switching behavior in the Belt and Road strategic context. Transp. Res. Part E-Logist. Transp. Rev. 2019, 129, 175–202. [Google Scholar] [CrossRef]
- Chen, K.; Xin, X.; Niu, X.; Zeng, Q. Coastal transportation system joint taxation-subsidy emission reduction policy optimization problem. J. Clean. Prod. 2020, 247, 119096. [Google Scholar] [CrossRef]
- Nassar, R.F.; Ghisolfi, V.; Annema, J.A.; van Binsbergen, A.; Tavasszy, L.A. A system dynamics model for analyzing modal shift policies towards decarbonization in freight transportation. Res. Transp. Bus. Manag. 2023, 48, 100966. [Google Scholar] [CrossRef]
- Masone, A.; Marzano, V.; Simonelli, F.; Sterle, C. Exact and heuristic approaches for the Modal Shift Incentive Problem. Socio-Econ. Plan. Sci. 2024, 93, 101874. [Google Scholar] [CrossRef]
- Takman, J.; Gonzalez-Aregall, M. Public policy instruments to promote freight modal shift in Europe: Evidence from evaluations. Transp. Rev. 2024, 44, 612–633. [Google Scholar] [CrossRef]
- Liu, S.; Jia, G.Z. Promoting the modal shift of freight from road to rail in China: An evolutionary game and simulation study. PLoS ONE 2025, 20, e0320880. [Google Scholar] [CrossRef]
- Qu, C.; Wang, G.W.Y.; Zeng, Q. Modelling port subsidy policies considering pricing decisions of feeder carriers. Transp. Res. Part E-Logist. Transp. Rev. 2017, 99, 115–133. [Google Scholar] [CrossRef]
- Jiang, Y.; Sheu, J.-B.; Peng, Z.; Yu, B. Hinterland patterns of China Railway (CR) express in China under the Belt and Road Initiative: A preliminary analysis. Transp. Res. Part E-Logist. Transp. Rev. 2018, 119, 189–201. [Google Scholar] [CrossRef]
- Zhou, Y.; Fang, W.; Li, M.; Liu, W. Exploring the impacts of a low-carbon policy instrument: A case of carbon tax on transportation in China. Resour. Conserv. Recycl. 2018, 139, 307–314. [Google Scholar] [CrossRef]
- Qiu, R.; Xu, J.; Xie, H.; Zeng, Z.; Lv, C. Carbon tax incentive policy towards air passenger transport carbon emissions reduction. Transport. Res. Part D-Transport. Environ. 2020, 85, 102441. [Google Scholar] [CrossRef]
- Xia, W.; Zhang, A. High-speed rail and air transport competition and cooperation: A vertical differentiation approach. Transp. Res. Part B-Methodol. 2016, 94, 456–481. [Google Scholar] [CrossRef]
- Pazour, J.A.; Meller, R.D.; Pohl, L.M. A model to design a national high-speed rail network for freight distribution. Transp. Res. Part A-Policy Pract. 2010, 44, 119–135. [Google Scholar] [CrossRef]
- Hoffrichter, A.; Silmon, J.; Iwnicki, S.; Hillmansen, S.; Roberts, C. Rail freight in 2035-traction energy analysis for high-performance freight trains. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2012, 226, 568–574. [Google Scholar] [CrossRef]
- Liang, X.-H.; Tan, K.-H. Market potential and approaches of parcels and mail by high speed rail in China. Case Stud. Transp. Policy 2019, 7, 583–597. [Google Scholar] [CrossRef]
- Liang, X.-H.; Tan, K.-H.; Whiteing, A.; Nash, C.; Johnson, D. Parcels and mail by high speed rail—A comparative analysis of Germany, France and China. J. Rail Transp. Plan. Manag. 2016, 6, 77–88. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Hu, R.; Chen, R.T.; Cai, D.L.; Jiang, C.M. Competition in cargo and passenger between high-speed rail and airlines-considering the vertical structure of transportation. Transp. Policy 2024, 151, 120–133. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, F.-R.; Ao, W.K.; Guo, Z.-H.; Chen, Z.-W. Optimization of cargo distribution for high-speed freight trains to overcome strong wind conditions. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2434008. [Google Scholar] [CrossRef]
- Yu, X.; Lang, M.; Gao, Y.; Wang, K.; Su, C.-H.; Tsai, S.-B.; Huo, M.; Yu, X.; Li, S. An Empirical Study on the Design of China High-Speed Rail Express Train Operation Plan-From a Sustainable Transport Perspective. Sustainability 2018, 10, 2478. [Google Scholar] [CrossRef]
- Yu, X.; Lang, M.; Zhang, W.; Li, S.; Zhang, M.; Yu, X. An Empirical Study on the Comprehensive Optimization Method of a Train Diagram of the China High Speed Railway Express. Sustainability 2019, 11, 2141. [Google Scholar] [CrossRef]
- Li, S.; Zuo, D.; Li, W.; Zhang, Y.; Shi, L. Freight train line planning for large-scale high-speed rail network: An integer Benders decomposition-based branch-and-cut algorithm. Transp. Res. Part E-Logist. Transp. Rev. 2024, 192, 103750. [Google Scholar] [CrossRef]
- Wang, X.; Zhen, L.; Wang, S. Optimizing an express delivery mode based on high-speed railway and crowd-couriers. Transp. Policy 2024, 159, 157–177. [Google Scholar] [CrossRef]
- Li, S.; Chen, X.; Lang, M. A hybrid heuristic algorithm for high-speed rail line planning problem with multiple transport organization modes. Res. Transp. Bus. Manag. 2025, 60, 01949969. [Google Scholar] [CrossRef]
- Kolak, O.I.; Feyzioglu, O.; Noyan, N. Bi-level multi-objective traffic network optimisation with sustainability perspective. Expert Syst. Appl. 2018, 104, 294–306. [Google Scholar] [CrossRef]
- Owais, M.; Osman, M.K. Complete hierarchical multi-objective genetic algorithm for transit network design problem. Expert Syst. Appl. 2018, 114, 143–154. [Google Scholar] [CrossRef]
- Huang, W.; Xu, G.; Lo, H.K. Pareto-Optimal Sustainable Transportation Network Design under Spatial Queuing. Netw. Spat. Econ. 2020, 20, 637–673. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Sheffi, Y. Urban Transportation Networks: Equilibrium Analysis with Mathematical Programming Methods; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Chao, C.-C. Assessment of carbon emission costs for air cargo transportation. Transport. Res. Part D-Transport. Environ. 2014, 33, 186–195. [Google Scholar] [CrossRef]
- Chang, X.; Wu, J.; Li, T.; Fan, T.-J. The joint tax-subsidy mechanism incorporating extended producer responsibility in a manufacturing-recycling system. J. Clean. Prod. 2019, 210, 821–836. [Google Scholar] [CrossRef]

| Feature | HSR | Air |
|---|---|---|
| CO2 Emissions | Low | High |
| Speed | High | Highest |
| Cost | Moderate | High |
| Safety | High | High |
| Capacity | Large | Limited |
| Punctuality | High | High |
| Reference | Modal Shift | Measures |
|---|---|---|
| Regmi and Hanaoka [16] | Road to rail | Develop a dry port |
| Wang et al. [17] | Road to intermodal rail transport | Impose a carbon tax on shippers |
| Bouchery et al. [18] | Road to rail | Control total carbon emissions |
| Lin et al. [19] | Road to rail | Railway network design |
| Tao et al. [20] | Road to road–rail combined transport | Fix subsidy to road–rail transport users |
| Choi, et al. [10] | Road to rail | Containerization and taxation |
| Kundu and Sheu [21] | Maritime to rail | Subsidy to shippers |
| Chen et al. [22] | Road to water | Tax subsidy joint policy and regulatory price for water transport |
| Nassar et al. [23] | Road to rail and water | Infrastructure projects, pricing measures, and stakeholders’ decisions |
| Masone et al. [24] | Road to rail | Incentives |
| Takman and Gonzalez-Aregall [25] | Road to rail and water | Subsidies and regulations |
| Liu and Jia [26] | Road to rail | Subsidy to shippers |
| This study | Air to HSR | Carbon tax and HSR service optimization |
| Sets: | |
|---|---|
| Set of stations in the freight network | |
| Set of arcs in the freight network | |
| Set of HSR trains | |
| Set of express freight transportation mode | |
| Set of OD pairs with timeliness requirements , where represents the OD pair from origin to destination with a timeliness requirement t | |
| Parameters: | |
| Unit CO2 emissions of freight mode (tCO2/kg-km) | |
| Transporting distance of to be transported by freight mode (km) | |
| Transporting distance of train (km) | |
| Transporting distance of to be transported by train (km) | |
| Total express freight demands of (kg) | |
| Fixed operating cost of train (CNY) | |
| Distance-related cost of train (CNY/km) | |
| The average speed of transportation mode (km/h) | |
| Total transportation time for to be transported by train (h) | |
| In-route transportation time for to be transported by train (h) | |
| Operation time of the train at one intermediate station (h) | |
| The total number of intermediate station(s) passed by train | |
| In-route transportation time for to be transported by air freight (h) | |
| Station-to-door delivery time for to be transported by mode (h) | |
| Waiting time for to be transported by mode (h) | |
| if is transported by train and goes through the arc , otherwise | |
| The load capacity of train (kg) | |
| Load factor of HSR trains | |
| if the train occupies the transport arc , otherwise | |
| The passing capacity of the transport arc | |
| Finite constants that denote lower ( ) and upper ( ) bounds for the HSR freight rate of (CNY/kg) | |
| Finite constants that denote lower ( ) and upper ( ) bounds for the carbon tax rate (CNY/tCO2) | |
| Generalized cost of to be transported by mode | |
| Perceived utility of to be transported by mode | |
| if can be met by train , otherwise | |
| Respective weights of the four attributes of freight rate, carbon tax, transportation time, and reliability | |
| Decision variables: | |
| Carbon tax rate (CNY/tCO2) | |
| Freight volume of that is transported by mode (kg) | |
| HSR freight rate of (CNY/kg) | |
| Freight volume of that is allocated to train (kg) | |
| Service frequency of train | |
| Train | Route and Stop | Fixed Operating Costs (CNY) | Variable Costs (CNY) |
|---|---|---|---|
| K1 | 1-4-5-7 | 420,000 | 1,309,800 |
| K2 | 1-(4)-5-7 | 470,000 | 1,309,800 |
| K3 | 1-4-(5)-7 | 470,000 | 1,309,800 |
| K4 | 1-(4)-(5)-7 | 520,000 | 1,309,800 |
| K5 | 2-3-5-7 | 435,000 | 1,357,800 |
| K6 | 2-(3)-5-7 | 485,000 | 1,357,800 |
| K7 | 2-3-(5)-7 | 485,000 | 1,357,800 |
| K8 | 2-(3)-(5)-7 | 535,000 | 1,357,800 |
| K9 | 2-4-6 | 379,000 | 1,181,400 |
| K10 | 2-(4)-6 | 429,000 | 1,181,400 |
| Parameters | Numerical Value |
|---|---|
| 120 tons | |
| 20 train | |
| 60% | |
| CNY 600/km | |
| [250, 600] km/h | |
| 0.5 h | |
| [1.5, 1.5] h | |
| [95%, 76.7%] | |
| [0.0265, 0.6424] kg/ton-km |
| Total Demand (ton) | Average Transit Time (h) | Total Demand (ton) | Average Transit Time (h) | Air Freight Distance (km) | ||||
|---|---|---|---|---|---|---|---|---|
| HSR | Air | HSR | Air | |||||
| (1–4, 12) | 183 | 8 | 4 | (1–4,24) | 221 | 18 | 14 | 873 |
| (1–5, 12) | 165 | 10 | 5 | (1–5,24) | 192 | 20 | 15 | 1389 |
| (1–7, 12) | 439 | 12 | 6 | (1–7,24) | 472 | 22 | 16 | 1967 |
| (4–5, 12) | 119 | 5 | 4 | (4–5,24) | 103 | 15 | 14 | 500 |
| (4–7, 12) | 277 | 8 | 5 | (4–7,24) | 288 | 18 | 15 | 1133 |
| (5–7, 12) | 178 | 6 | 4 | (5–7,24) | 194 | 16 | 14 | 690 |
| (2–3, 12) | 63 | 6 | 4 | (2–3,24) | 93 | 16 | 14 | 606 |
| (2–4, 12) | 126 | 8 | 5 | (2–4,24) | 120 | 18 | 15 | 1047 |
| (2–5, 12) | 119 | 9 | 5 | (2–5,24) | 98 | 19 | 15 | 1039 |
| (2–6, 12) | 239 | 11 | 6 | (2–6,24) | 317 | 21 | 16 | 1782 |
| (2–7, 12) | 241 | 12 | 6 | (2–7,24) | 313 | 22 | 16 | 1697 |
| (3–5, 12) | 62 | 6 | 4 | (3–5,24) | 71 | 16 | 14 | 600 |
| (3–7, 12) | 178 | 8 | 5 | (3–7,24) | 162 | 18 | 15 | 936 |
| (4–6, 12) | 295 | 7 | 4 | (4–6,24) | 242 | 17 | 14 | 761 |
| Scenario | Objective(s) of the Upper-Level Model | Attributes in the Lower-Level Model |
|---|---|---|
| #0 | — | Price, time, reliability |
| #1 | Price, time, reliability | |
| #2 | Price, carbon tax, time, reliability |
| No. | Carbon Tax (CNY) | CO2 Emission Reduction Rate | HSR Profits (CNY) |
|---|---|---|---|
| 1 | 55,156 | 57.080% | 6,441,192 |
| 2 | 55,159 | 57.171% | 6,463,972 |
| 3 | 55,341 | 57.008% | 6,465,112 |
| 4 | 55,358 | 57.046% | 6,479,734 |
| 5 | 55,633 | 57.051% | 6,464,437 |
| 6 | 55,976 | 57.077% | 6,466,347 |
| 7 | 56,025 | 56.973% | 6,482,218 |
| 8 | 56,139 | 57.084% | 6,464,309 |
| 9 | 56,337 | 57.063% | 6,471,531 |
| Scenario | Scenario | ||||||
|---|---|---|---|---|---|---|---|
| #0 | #1 | #2 | #0 | #1 | #2 | ||
| (1–4,12) | 25 | 17.55 | 15.84 | (1–4,24) | 10 | 7.71 | 7.25 |
| (1–5,12) | 25 | 17.71 | 17.30 | (1–5,24) | 14 | 11.11 | 11.41 |
| (1–7,12) | 25 | 17.78 | 18.41 | (1–7,24) | 14 | 10.20 | 9.34 |
| (4–5,12) | 25 | 17.86 | 20.23 | (4–5,24) | 10 | 7.64 | 8.34 |
| (4–7,12) | 25 | 19.42 | 19.76 | (4–7,24) | 10 | 8.65 | 8.62 |
| (5–7,12) | 25 | 17.04 | 17.48 | (5–7,24) | 10 | 8.16 | 7.66 |
| (2–3,12) | 25 | 19.13 | 18.36 | (2–3,24) | 10 | 7.71 | 7.45 |
| (2–4,12) | 25 | 17.56 | 17.84 | (2–4,24) | 10 | 8.14 | 7.07 |
| (2–5,12) | 25 | 18.60 | 18.66 | (2–5,24) | 14 | 10.46 | 9.05 |
| (2–6,12) | 25 | 17.98 | 16.46 | (2–6,24) | 14 | 10.00 | 7.59 |
| (2–7,12) | 25 | 17.03 | 14.15 | (2–7,24) | 14 | 8.45 | 7.92 |
| (3–5,12) | 25 | 19.57 | 19.84 | (3–5,24) | 10 | 6.95 | 8.30 |
| (3–7,12) | 25 | 17.99 | 17.84 | (3–7,24) | 10 | 7.68 | 7.32 |
| (4–6,12) | 25 | 21.23 | 18.63 | (4–6,24) | 10 | 8.18 | 7.63 |
| Average | 25 | 18.32 | 17.91 | Average | 11.43 | 8.65 | 8.21 |
| Train | Scenario #1 | Scenario #2 | ||||
|---|---|---|---|---|---|---|
| Frequency (per Day) | Freight Volume (ton) | Load Factor (%) | Frequency (per Day) | Freight Volume (ton) | Load Factor (%) | |
| K1 | 1 | 116.107 | 96.76 | 1 | 118.744 | 98.95 |
| K2 | 3 | 557.724 | 99.42 | 3 | 524.448 | 99.24 |
| K3 | 2 | 293.776 | 99.67 | 2 | 304.135 | 99.57 |
| K4 | 3 | 467.809 | 99.86 | 3 | 536.967 | 99.89 |
| K5 | 1 | 117.479 | 97.90 | 1 | 107.840 | 89.87 |
| K6 | 2 | 304.223 | 91.17 | 2 | 321.312 | 96.21 |
| K7 | 1 | 222.118 | 91.43 | 1 | 248.530 | 98.15 |
| K8 | 2 | 376.613 | 97.63 | 2 | 393.424 | 99.51 |
| K9 | 2 | 212.580 | 88.58 | 2 | 235.905 | 98.29 |
| K10 | 3 | 522.777 | 99.36 | 4 | 653.674 | 99.76 |
| Scenario | Scenario | ||||||
|---|---|---|---|---|---|---|---|
| #0 | #1 | #2 | #0 | #1 | #2 | ||
| (1–4,12) | 24.03 | 61.12 | 69.49 | (1–4,24) | 46.58 | 69.51 | 73.69 |
| (1–5,12) | 20.60 | 56.11 | 58.33 | (1–5,24) | 11.91 | 33.17 | 30.52 |
| (1–7,12) | 19.98 | 51.21 | 48.26 | (1–7,24) | 12.96 | 40.97 | 49.46 |
| (4–5,12) | 34.50 | 72.28 | 60.42 | (4–5,24) | 53.22 | 77.03 | 70.83 |
| (4–7,12) | 28.29 | 55.43 | 53.77 | (4–7,24) | 48.75 | 62.27 | 62.70 |
| (5–7,12) | 31.14 | 71.49 | 69.53 | (5–7,24) | 50.86 | 69.52 | 73.88 |
| (2–3,12) | 29.28 | 62.64 | 66.89 | (2–3,24) | 50.93 | 74.88 | 77.28 |
| (2–4,12) | 26.74 | 65.69 | 64.33 | (2–4,24) | 48.63 | 68.59 | 78.13 |
| (2–5,12) | 23.09 | 55.94 | 55.62 | (2–5,24) | 11.44 | 41.13 | 57.13 |
| (2–6,12) | 21.45 | 54.51 | 62.25 | (2–6,24) | 13.06 | 44.61 | 68.33 |
| (2–7,12) | 18.58 | 55.17 | 69.27 | (2–7,24) | 12.02 | 58.16 | 63.46 |
| (3–5,12) | 29.25 | 60.15 | 58.67 | (3–5,24) | 50.95 | 81.79 | 69.91 |
| (3–7,12) | 27.43 | 63.06 | 63.85 | (3–7,24) | 48.67 | 72.20 | 75.49 |
| (4–6,12) | 28.41 | 46.27 | 59.38 | (4–6,24) | 48.72 | 66.97 | 71.99 |
| Average | 25.91 | 59.36 | 61.43 | Average | 36.34 | 61.49 | 65.92 |
| Results | Scenario #0 | Scenario #1 | Scenario #2 |
|---|---|---|---|
| Carbon tax rate (CNY/tCO2) | — | — | 29.11 |
| CO2 emissions (tons) | 3437.940 | 2158.955 | 1924.742 |
| Average freight rate of HSR (CNY/kg) | 18.21 | 13.48 | 13.06 |
| Average market share of HSR freight | 31.12% | 60.42% | 63.67% |
| Modal shift (compare with Scenario #0) | — | 29.30% | 32.55% |
| Carbon tax (CNY) | — | — | 56,025 |
| CO2 emission reduction rate (compare with air-only) | 23.15% | 51.74% | 56.97% |
| HSR profits (CNY) | — | 7,140,620 | 6,482,218 |
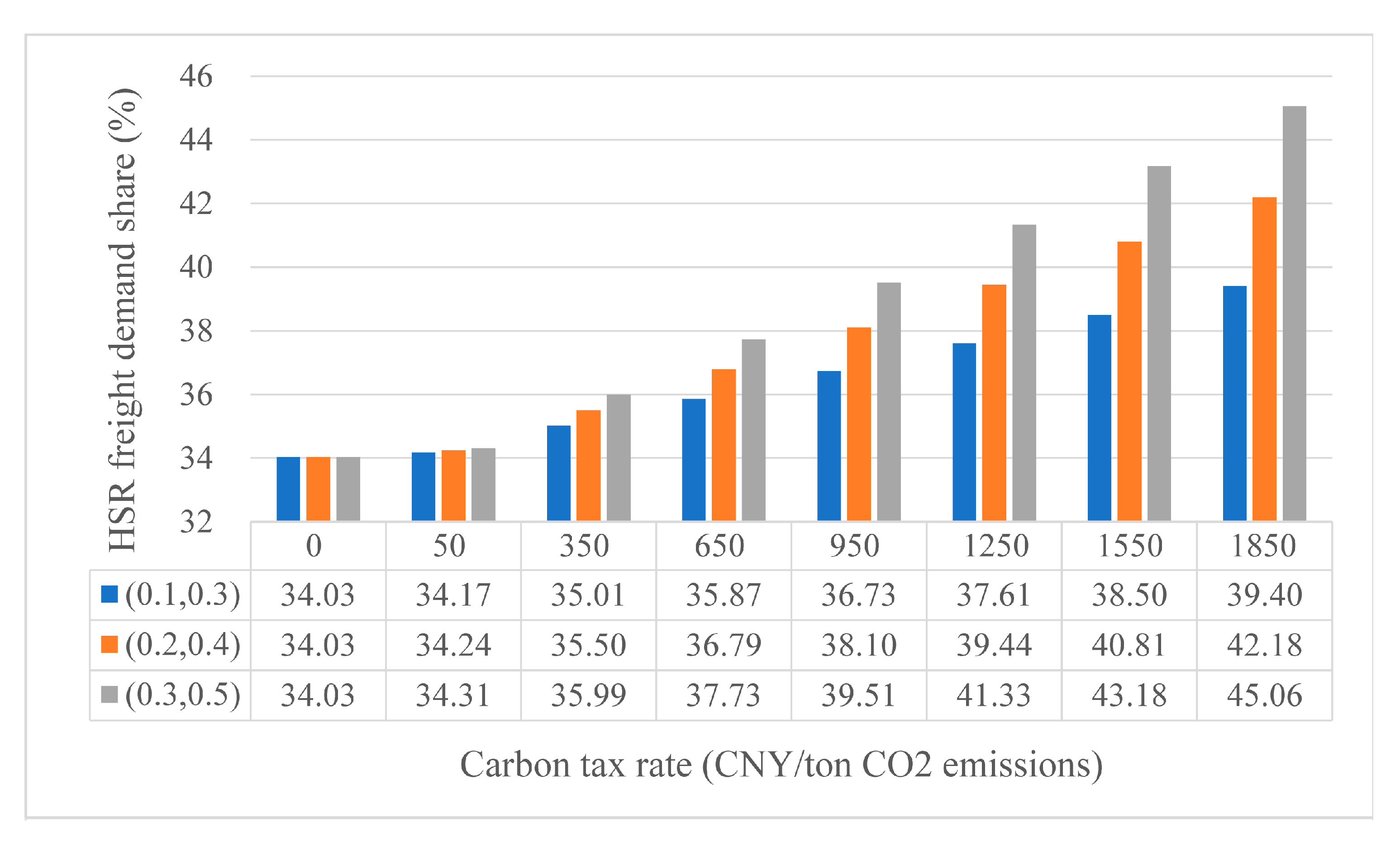
| Item | Results | ||
|---|---|---|---|
| (0, 100) | (1800, 1900) | (1800, 1900) | |
| (0.3, 0.5) | (0.1, 0.3) | (0.3, 0.5) | |
| Carbon tax rate (CNY/tCO2) | 20.67 | 1844.81 | 1850.65 |
| CO2 emissions (ton) | 1941.106 | 1668.259 | 1407.869 |
| Average freight rate of HSR (CNY/kg) | 12.92 | 13.44 | 13.10 |
| Average market share of HSR freight | 64.06% | 66.51% | 73.41% |
| Modal shift (compare with Scenario #0 in Section 4.2) | 32.94% | 35.39% | 42.29% |
| Carbon tax (CNY) | 40,116 | 3,077,627 | 2,605,473 |
| CO2 reduction rate (compare with air-only) | 56.61% | 62.71% | 68.53% |
| HSR profits (CNY) | 6,687,611 | 6,786,794 | 6,644,680 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L. Promoting Freight Modal Shift to High-Speed Rail for CO2 Emission Reduction: A Bi-Level Multi-Objective Optimization Approach. Sustainability 2025, 17, 6310. https://doi.org/10.3390/su17146310
Li L. Promoting Freight Modal Shift to High-Speed Rail for CO2 Emission Reduction: A Bi-Level Multi-Objective Optimization Approach. Sustainability. 2025; 17(14):6310. https://doi.org/10.3390/su17146310
Chicago/Turabian StyleLi, Lin. 2025. "Promoting Freight Modal Shift to High-Speed Rail for CO2 Emission Reduction: A Bi-Level Multi-Objective Optimization Approach" Sustainability 17, no. 14: 6310. https://doi.org/10.3390/su17146310
APA StyleLi, L. (2025). Promoting Freight Modal Shift to High-Speed Rail for CO2 Emission Reduction: A Bi-Level Multi-Objective Optimization Approach. Sustainability, 17(14), 6310. https://doi.org/10.3390/su17146310






