Optimal Strategies in a Manufacturer-Led Supply Chain Under Hybrid Carbon Policies and Retailer’s Fairness Concerns

Abstract

Implementing hybrid carbon policies is crucial for supply chains’ low-carbon transition. However, the downstream retailer is often passive in low-carbon strategies, leading to fair issues that may influence the decision-making of channel members. Therefore, this study integrates green technology, remanufacturing, retailer’s fairness concerns, low-carbon preference, and hybrid carbon policies into a manufacturer-led supply chain through differential game theory. Then, the equilibrium solutions for each member are analyzed under the centralized case and decentralized case involving a cost-sharing contract for low-carbon promotion. Our results show that centralized decision-making can optimize both the economic and environmental performances of channel members; retailer’s fairness concerns can enhance low-carbon promotional efforts and the cost-sharing ratio for such initiatives, but do not impact low-carbon production efforts. Additionally, a threshold exists on the relationship between retailer’s fairness concerns and the cost-sharing ratio; increased low-carbon preference motivates more efforts in low-carbon production and promotion. Moreover, stricter carbon policies motivate the manufacturer to increase low-carbon efforts, but the retailer tailors its low-carbon promotional strategy according to the unit carbon emissions of products to maintain an adequate level of low-carbon goodwill.

1. Introduction

The environment and ecological stability are facing a significant threat from global warming. A primary contributor to global warming is the significant greenhouse gas (GHG) emissions from human activities, especially CO₂ [1]. Since the industrial and transportation sectors are the biggest emitters of GHG emissions, major global carbon emissions stem from supply chain operations including manufacturing, inventory storage, freight transportation, logistics, and warehousing [2]. Therefore, it is urgent to promote the low-carbon transformation of supply chains.

Consequently, governments worldwide have implemented carbon-control policies such as carbon taxes and cap-and-trade systems. As a market-driven approach to reducing industrial and supply chain emissions, cap-and-trade systems have been widely adopted by major economies, including the European Union (EU Emissions Trading System), China (national ETS), and select U.S. states (e.g., California’s CAT program). Specifically, the cap-and-trade mechanism sets a cap on carbon emissions for different industries and allocates allowances to designated firms. Firms that emit less than their allocated allowances can sell surplus credits to those exceeding their limits [3,4]. Therefore, firms are spurred to reduce emissions through the market-driven pricing of carbon allowances that link environmental performance with financial outcomes [5]. Moreover, the government can adjust the cap and the price of carbon permits to influence corporate behavior, helping to effectively control and reduce overall emissions [6,7]. However, since the cap is fixed rather than the price, enterprises may encounter disruptions to their consistent operations owing to fluctuations in the carbon permit market influenced by weather and economic factors [8,9]. In contrast, a carbon tax would set a fixed price for carbon emissions, reducing uncertainty and encouraging operational adjustments [10]. Therefore, a mix of a carbon tax mechanism and a carbon emissions trading system would further incentivize companies to cut emissions [11]. In fact, hybrid carbon policies that concurrently implement cap-and-trade systems and carbon taxes have been adopted by several jurisdictions in the world, such as Switzerland, France, and Canada [12]. These empirical cases collectively demonstrate a unified policy paradigm: under well-designed regulatory boundaries, carbon markets and carbon taxes can function as complementary instruments, generating synergistic effects to optimize emission mitigation outcomes.

Green products tend to command a premium price from consumers with a low-carbon preference [13,14]. The “2024 China Sustainable Consumption Report” reveals that over 87% of respondents have incorporated low-carbon practices into their daily lives, prioritizing product performance, including responsible sourcing, low-carbon features, recycling systems, and resource circulation (Source: https://www.jiemian.com/article/12138572.html, accessed on 23 December 2024). As demand for low-carbon products rises, firms’ profits, production methods, and low-carbon strategies are increasingly impacted [15]. Additionally, improving products’ low-carbon goodwill (the reputation of products among consumers with a low-carbon preference) relies on the effectiveness of minimizing carbon emissions and mitigating environmental pollution [16]. To meet carbon regulations and market demand, channel members have to implement low-carbon operations, including green technology and eco-friendly materials [17]. Additionally, recycling and remanufacturing are crucial for a circular economy, reducing pressure on resources, the environment, and economic benefits [18,19]. Specifically, a potential method to reduce emissions is to implement the “resource–production–consumption–recycling–reproduction–reconsumption” mode in the supply chain [20]. Therefore, green technology and remanufacturing must be integrated into manufacturing for supply chains to undergo a low-carbon transition. For example, JD.com is committed to becoming a leader in energy conservation and emissions reduction by using eco-friendly technologies in its logistics and warehouse operations, such as automation and smart delivery systems. Additionally, its Green Logistics initiative also promotes the recycling and reuse of packaging in e-commerce and express delivery (Source: https://www.jdl.com/green, accessed on 25 December 2024). Similarly, BYD, a leading Chinese automaker specializing in electric vehicles (EVs) and hybrid cars, focuses on minimizing carbon emissions and energy consumption. The company also emphasizes battery recycling and repurposing, reducing waste by reusing valuable components in new products or processes (Source: https://www.bydglobal.com/cn/OurFuture.html, accessed on 5 January 2025). Retailers, too, can influence profitability through effective promotional strategies [21]. JD.com, for instance, has launched “Green Shopping Festivals” to promote energy-efficient products from brands like Haier, Midea, and BYD, offering discounts and trade-in programs to encourage consumers to buy sustainable products (Source: https://sw.wuhan.gov.cn/xwdt/gzdt/202407/t20240722_2431644.shtml, accessed on 5 January 2025).

While collaboration between partners can drive environmental improvements within the supply chain [22], retailers are often hesitant to engage in low-carbon marketing due to their general exemption from emissions regulation. As a result, a low-carbon promotion cost-sharing contract is commonly used for coordination [23]. In reality, manufacturers with market dominance often influence the low-carbon practices of businesses [24]. For example, the first “fluorine-free variable-frequency air conditioning low-carbon industrial chain” was created in 2010 by Haier in collaboration with eight vendors. Similarly, Coca-Cola collaborates with upstream companies to promote eco-friendly technologies and materials that reduce carbon emissions. Manufacturers, especially those in dominant positions, typically make decisions that favor their interests. Conversely, downstream retailers, as followers, often accept these decisions passively. In some cases, manufacturers may increase the wholesale prices of green products or impose high costs on retailers for carbon emissions reduction, leading to perceptions of unfairness that can negatively affect the development of manufacturers in the long term. Therefore, addressing fairness concerns in decision-making helps equitably distribute the benefits of channel members and promotes a successful low-carbon transition [25]. Consequently, the following retailer, at a disadvantaged position, should consider the fairness of its own profit compared to the leading manufacturer in the decision-making.

Many existing studies focus on the emissions reduction strategies in the supply chain under cap-and-trade regulation or carbon tax policy. There is some literature that has investigated how hybrid carbon policies influence the supply chain members’ emissions reduction decisions [26,27,28]. Additionally, there are also some studies about the impact of fairness concerns on the decisions and coordination in the supply chain [23,29,30,31]. However, none of them have considered fairness concerns and hybrid carbon policies within a common framework to analyze the decision-making in the supply chain.

Based on the above factors, this study integrates green technology, remanufacturing, retailer’s fairness concerns, low-carbon preference, and hybrid carbon policies into a manufacturer-led supply chain through differential game theory (given that the formation of low-carbon goodwill is a dynamic and long-term process, it is practical to apply the differential game theory). Then, two-stage Stackelberg models are established to answer the following questions:

(1)

What is the optimal strategy for the manufacturer’s efforts in green technology and remanufacturing, as well as the retailer’s effort in low-carbon promotion, considering low-carbon preference, hybrid carbon policies, and retailer’s fairness concerns?

(2)

How do hybrid carbon policies, retailer’s fairness concerns, and low-carbon preference influence the optimal strategies utilized by supply chain participants?

(3)

How can the downstream retailer with fairness concerns collaborate more effectively with the leading manufacturer to promote low-carbon initiatives?

The key contributions of this study comprise three points. First, we originally employ the differential game theory to analyze the optimal strategies on low-carbon operations, including green technology, remanufacturing, and promotion under hybrid carbon policies and retailer’s fairness concerns. Second, we analyze the influence of hybrid carbon policies, retailer’s fairness concerns, and low-carbon preference on the decision-making in the supply chain. Third, we propose a cost-sharing contract for promoting low-carbon products to better coordinate a manufacturer-led supply chain and analyze effective collaboration between channel members. The conclusions and research idea of this paper can provide a supplement and expand the prior research and lay a basis for the low-carbon transformation of the supply chain. Additionally, the managerial insights give feasible suggestions for the government and supply chain businesses to achieve the goal of emissions reduction.

The subsequent outline delineates the structure of this study: Section 2 reviews the literature on green technology and remanufacturing under carbon policies, as well as fairness concerns. Section 3 outlines the real problem that we study and presents the key assumptions. Section 4 introduces the differential game model and analyzes the equilibrium solutions in both decentralized and centralized scenarios. Section 5 conducts the comparative and sensitivity analyses. Section 6 presents a numerical analysis that highlights the main findings. Finally, Section 7 concludes the study, offering managerial insights and discussing research limitations. All proofs of the proposition and corollary are offered in Appendix A.

2. Literature Review

Carbon tax and cap-and-trade policies are the subject of this research, and the key literature on them are reviewed. First, we examine the relevant research on low-carbon operations, including green technology and remanufacturing, as well as fairness concerns. We then compare our study with previous research to highlight its necessity and significance.

The implementation of carbon policies requires channel members to adjust their operations to meet emission standards and significantly affects their decision-making [26]. Due to carbon regulations, the companies’ emissions reduction objectives rely on low-carbon operations, including green technology and remanufacturing [6,27,32,33,34]. For instance, Krass et al. [35] developed a profit-maximizing model for a monopolistic enterprise that selects green technologies based on price-dependent demand under environmental taxes. They found that while an initial increase in carbon taxes can encourage firms to adopt more sustainable technologies, further increases beyond a certain threshold may push firms to implement less sustainable options. Luo et al. [36] examined optimal manufacturing and remanufacturing strategies in a closed-loop supply chain under carbon tax, using four game-theoretic models. Their findings suggest that while carbon taxes effectively motivate the application of low-carbon technology and remanufacturing, excessively high taxes hinder remanufacturing unless carefully designed. Other studies have also investigated these strategies under cap-and-trade policy. For example, Yang et al. [37] analyzed the optimal collection mode for remanufacturing under cap-and-trade policy, evaluating how cost savings from remanufacturing, carbon emission factors, and collection mode choices impact emissions reduction and profits. Under cap-and-trade policy, Li et al. [23] investigated impacts that government subsidies have on investments in green technology and marketing strategies for supply chains and found that, although the effectiveness of fixed-cost and emission-reduction subsidies vary, both types improve supply chain coordination and incentive investments in green technologies. Moreover, Cheng et al. [27] established an optimization model for an economically constrained closed-loop supply chain network involving both low- and high-emission manufacturers under a mix of carbon tax and cap-and-trade regulation, and indicate that emission constraints can incentivize green investment, and reverse channels enhance resource utilization but reduce profits. Zhu et al. [26] examined the influences of different coordination contracts on collaborative emissions reduction strategies considering mixed carbon policies. They found that noncooperation results in inefficiency, and improving coordination and reducing carbon emissions can be attained most effectively through a bilateral cost-sharing contract.

Most studies rely on the “homo economicus” assumption, which asserts that individuals making decisions are rational and driven by self-interest. However, this assumption often leads to a gap between the optimal theoretical decisions of a company and its actual decisions [38]. Additionally, research has shown that decision-makers also consider fairness concerns [39,40,41]. Fairness concerns across the supply chain have been extensively researched, including pricing strategies [29] and green product production [30,42]. Recent research has focused on supply chain coordination to promote low-carbon transition, with particular emphasis on fairness in cost-sharing contracts [24,31,43]. Zhou et al. [24] showed that under certain cases, retailers’ fairness concerns affect the efficacy of promotions and cost-sharing collaborations for emissions reduction. Wang et al. [31] investigated coordination in a low-carbon supply chain led by a retailer with altruistic preferences and proposed that cost-sharing contracts considering altruistic preferences are conducible to fostering collaboration in emissions reduction. Yang et al. [43] evaluated the impact of retailer’s fairness concerns on strategies for green products in a pre-sale model, emphasizing the importance of fairness concerns and the pre-sale model for effective green product promotion and coordination.

Table 1. Summary of some relevant research.

Authors	Type of Carbon Policy		Structure of the Supply Chain	Fairness Concerns	Remanufacturing	Differential Game
	Cap-and-Trade	Carbon Tax
Zhou et al. [24]	×	×	a manufacturer, a retailer	√	×	×
Xu et al. [34]	√	×	a manufacturer, a retailer	×	×	×
Li et al. [29]	×	√	a manufacturer, a supplier	√	×	√
Yang et al. [37]	√	×	a manufacturer, a retailer or a third party	×	√	×
Li et al. [23]	√	×	a manufacturer, a retailer	√	×	×
Luo et al. [36]	×	√	a manufacturer, a retailer	×	√	×
Cheng et al. [27]	√	√	a manufacturer, a retailer	×	√	×
Xia et al. [30]	×	×	a manufacturer, a retailer	√	×	√
Yang et al. [43]	×	×	a manufacturer, a retailer	√	×	×
Cai et al. [6]	√	×	a manufacturer, a supplier	×	×	√
Zhu et al. [26]	√	√	a manufacturer, a retailer	×	√	√
This paper	√	√	a manufacturer, a retailer	√	√	√

positions our study within the current literature and highlights existing research gaps. First, most studies focused on the effects of individual carbon policy on the low-carbon strategies of channel members. While some research considered fairness concerns, remanufacturing or carbon policies for emissions reduction were not included. In contrast, our study integrates hybrid carbon policies and retailer’s fairness concerns, as well as remanufacturing, into a differential game model. Second, we propose that consumers with a low-carbon preference motivate low-carbon production, and the leading manufacturer is prepared to use a cost-sharing contract for low-carbon marketing. Third, we investigate the optimal strategies for green technology, remanufacturing, and promotion in a long-term dynamic way. Additionally, we examine the impact of hybrid carbon policies, retailer’s fairness concerns, and low-carbon preferences on the optimal strategies of channel members.

3. Problem Description

This study identifies the manufacturer as the leader, responsible for key decisions such as low-carbon operations and wholesale pricing. Then, the downstream retailer determines promotion efforts and sales strategies according to the manufacturer’s strategies [43,44]. Under hybrid carbon policies, there is a carbon tax (s) on unit carbon emissions of the manufacturer’s products. Additionally, if the allocated carbon emissions rights (E) for the manufacturer are in surplus or deficit, they can be traded at the market price (g) for sale or purchase. Driven by these policies, the manufacturer has to use green technology in production and recycle discarded products for remanufacturing. As consumers’ demand for low-carbon products rises, the manufacturer is incentivized to enhance efforts in low-carbon production. Then, the downstream retailer purchases these products at a wholesale price. During sales, the retailer can enhance product demand by marketing its low-carbon products through promotional strategies. Therefore, the manufacturer has an incentive to subsidize part of the retailer’s low-carbon promotional costs for securing a large market share. However, the low-carbon marketing and cost-sharing strategies are influenced by the retailer’s concerns on the fairness of its own profit compared to the manufacturer. Figure 1 illustrates the framework of the supply chain.

To develop a differential game model, we define notations for the variables and clarify important assumptions. Specifically, the decision variables for the manufacturer involve the emissions reduction from the green technology effort and recycling effort for remanufacturing, while the retailer’s decision variable includes the low-carbon promotional effort. Then, we treat the low-carbon goodwill as a state variable.

Table 2. Variables and their descriptions.

Parameters	Implication
D(t)	Market demand of products
Dr(t)	Recycling quantity of products
ES(t)	Carbon emission surplus
Cm, Cr	Unit production cost of new/remanufactured product
P	Retail price per unit of products
W	Wholesale price per unit of products
s, g	Unit carbon tax price/carbon emissions rights trading price
Em, Er	Unit carbon emissions of new/remanufactured products
E	Allocated carbon emissions rights
Q	Market size of products
k, l, f	Investment cost coefficient of green technology/recycling/low-carbon promotion
a, b	Influence coefficient of retail price/low-carbon good will
h	Influence coefficient of recycling effort
μ, γ	Influence coefficient of carbon emissions surplus/low-carbon promotional effort
δ	Decay rate of low-carbon goodwill
ρ	Discount factor
σ	Fairness concerns of the retailer
θ	Cost-sharing ratio for low-carbon promotion
Decision Variables
em(t)	Emissions reduction from green technology effort
τ(t)	Recycling effort for remanufacturing
u(t)	Low-carbon promotional effort
State Variable
G(t)	Low-carbon goodwill
Notations
Jm, Jr, Jsc	Objective function of the manufacturer/retailer/entire supply chain
Vm, Vr, Vsc	Value function of the manufacturer/retailer/entire supply chain
Superscripts
D	Decentralized decision-making
C	Centralized decision-making

summarizes the relevant parameters and variables.

Five key assumptions are given below.

Assumption 1.

For the manufacturer, costs are incurred from utilizing green technology and recycling used products for remanufacturing. For the retailer, the primary cost is the low-carbon promotion effort. Following previous research [45,46], the cost functions at time t, which include these costs, can be expressed as follows:

$$C_{{\mathrm{e}}_m(t)}={\displaystyle \frac{k{e}_m^2(t)}{2}},C_{\tau (t)}={\displaystyle \frac{l{\tau }^2(t)}{2}},C_{u(t)}={\displaystyle \frac{f{u}^2(t)}{2}}$$

(1)

where k > 0 means the investment cost coefficient of green technology; l > 0 means the investment cost coefficient of recycling; and f > 0 means the investment cost coefficient of low-carbon promotion.

Assumption 2.

Recycled products can be remanufactured into new products. Similar to Cheng et al. [27], as new and remanufactured products are considered the same quality, they share the same prices in the market demand. Since remanufactured products save significant energy and new materials [47], we have C_m > C_r and E_m > E_r. Moreover, the unit production costs, involving the carbon tax for new or remanufactured products, are defined as follows:

$$C_m+s{E}_m and C_r+s{E}_r$$

(2)

where C_m represents the unit production cost of new products; C_r represents the unit production cost of remanufactured products; sE_m represents the unit carbon tax cost of new products; and sE_r represents the unit carbon tax cost of remanufactured products. For calculation, the C_m and C_r are assigned as 0, because the unit production cost of brand-new products and remanufactured products still satisfies sE_m > sE_r which can represent the cost-saving characteristics of remanufacturing [26]. Furthermore, following the framework established by Govindan and Popiuc [48], the recycling function is defined as follows:

$$D_r(t)=A_0+h\tau (t)$$

(3)

where A₀ is the initial value of recycling, and the influence coefficient of the recycling effort is represented by h, where h > 0. In order to simplify the calculation, we assume that A₀ = 0 and the new product demand quantity is much greater than the remanufactured product demand quantity.

Assumption 3.

Since the rise in product demand correlates directly with the total growth in carbon emissions [49], the carbon emissions surplus through efforts in green technology and remanufacturing can be defined as follows:

$$ES(t)=\underset{allocated carbon emission rights}{\underbrace{E}}-\left[\underset{\begin{array}{l}total emissions without\\ emission reduction\end{array}}{\underbrace{E_{m}D(t)}}-\underset{\begin{array}{l}emission reduction\\ from green technology\end{array}}{\underbrace{e_m(t)}}-\underset{\begin{array}{l}emission reduction\\ from remanufacturing\end{array}}{\underbrace{\mathsf{\Delta }{D}_r(t)}}\right]$$

(4)

where ES(t) means the carbon emissions surplus; E means the allocated carbon emissions rights for the manufacturer; D(t) represents the product demand in the market; and $\mathsf{\Delta }=E_m-E_r>0$ denotes the amount of carbon emissions saved per product through remanufacturing. To simplify the calculation, e_m(t) is treated as a decision variable, representing the emissions reduction from the green technology effort [28]. Additionally, the low-carbon reputation of products is positively influenced by promotions [50,51]. According to Nerlove and Arrow [52], the evolution of low-carbon goodwill can be described as follows:

$$\stackrel{·}{G(t)}=\mu ES(t)+\gamma u(t)-\delta G(t)=\mu \left[E-E_{m}D(t)+e_m(t)+\mathsf{\Delta }{D}_r(t)\right]+\gamma u(t)-\delta G(t)$$

(5)

where μ > 0 means the impact coefficient of the carbon emissions surplus; γ > 0 means the impact coefficient of low-carbon promotion; δ > 0 means the decay rate of low-carbon goodwill; and $G(0)=G_0>0$ means the initial value of low-carbon goodwill.

Assumption 4.

Due to the complexity of the equilibrium solution, we adopt the assumption from prior research that the wholesale price and sale price of products are fixed parameters [24,26,30,31,53,54]. Additionally, consumer purchasing decisions are influenced by sales prices and the low-carbon goodwill of products. According to Ouardighi and Pasin [55], the product demand function is defined as follows:

$$D(t)=bG(t)(Q-aP)$$

(6)

where a means the influence coefficient of the sale price of products; b means the influence coefficient of the low-carbon goodwill of products; and Q denotesthe market size of products. Additionally, b reflects the level of low-carbon preference.

Assumption 5.

To improve product demand, the manufacturer chooses to cover a share of the retailer’s expenses on low-carbon promotion, denoted by θ, where 0 < θ < 1. In addition, the downstream retailer always considers the fairness of its own profit compared to the upstream manufacturer in decision-making.

Letting J_M be the profit function of the manufacturer, letting J_R be the profit function of the retailer, letting U_R be the retailer’s fair utility function, and σ be the coefficient of fairness concerns, the retailer’s utility function is expressed as follows:

$$U_R=J_R-\sigma (J_M-J_R),where \sigma \ge 0.$$

(7)

The manufacturer and the retailer’s profit functions are outlined below:

$$J_M=D(t)W-D(t)s{E}_m+s\left[e_m(t)+\mathsf{\Delta }{D}_r(t)\right]+gES(t)-C_{e_m(t)}-C_{\tau (t)}-\theta C_{u(t)}$$

(8)

$$J_R=D(t)(P-W)-(1-\theta )C_{u(t)}$$

(9)

4. Model and Results

4.1. Case D: Decentralized Decision-Making

In Case D, which incorporates a cost-sharing contract for low-carbon promotion, each channel member collaborates in emissions reduction. Specifically, the manufacturer initially establishes optimal strategies in green technology and remanufacturing, along with the cost-sharing for low-carbon marketing. Then, the retailer evaluates the fairness of its own profit compared to the manufacturer and decides the level of promotional efforts to optimize its utility. Assuming ρ represents the discount factor, the objective functions for the manufacturer and the retailer over an infinite time horizon are expressed below:

$$\underset{e_m,\tau ,\theta }{max}{J}_M^{*}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{D(t)W-D(t)s{E}_m+s\left[e_m(t)+\mathsf{\Delta }{D}_r(t)\right]+gES(t)-C_{e_m(t)}-C_{\tau (t)}-\theta C_{u(t)}\right\}dt$$

(10)

$$\underset{u}{max}{U}_R^{*}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{J_R-\sigma (J_M-J_R)\right\}dt$$

(11)

Substituting Equation (8) and Equation (9) into Equation (11) and arranging them yields the following:

$$\underset{u}{max}{U}_R^{*}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}\left\{D(t)(P-W)-(1-\theta )C_{u(t)}-\sigma \left[D(t)(2W-P)-D(t)s{E}_m+s{e}_m(t)+s\mathsf{\Delta }{D}_r(t)+gES(t)-C_{e_m(t)}-C_{\tau (t)}+(1-2\theta )C_{u(t)}\right]\right\}}dt$$

(12)

According to optimal control theory, each member in the game encounters the same situation at any given period in an infinite time horizon. Because deriving the equilibrium solution of dynamic parameters is complex, we omit the time variable t when writing the relevant parameters below. For convenience, we denote V_M and V_R as the value functions of the manufacturer and the retailer, respectively. Therefore, the corresponding Hamiltonian–Jacobi–Bellman (HJB) equations can be expressed as follows:

$$\begin{array}{l}\rho V_M=\underset{e_m,\tau ,\theta }{max}\left\{bG(Q-aP)(W-s{E}_m)+s(e_m+\mathsf{\Delta }h\tau )+gES(t)-{\displaystyle \frac{k{e}_m^2}{2}}-{\displaystyle \frac{l{\tau }^2}{2}}-{\displaystyle \frac{\theta f{u}^2}{2}}\right.\\ \left.\hspace{1em}\hspace{1em}+{\displaystyle \frac{\mathsf{\partial }{V}_M}{\mathsf{\partial }G}}\left[\mu (E-T)+\right.\gamma u\left.-\delta G\right]\right\}\end{array}$$

(13)

$$\begin{array}{l}\rho V_R=\underset{u}{max}\left\{bG(Q-aP)(P-W)-{\displaystyle \frac{(1-\theta )f{u}^2}{2}}\right.-\sigma \left[bG(Q-aP)(2W-P-s{E}_m\right.)+s(e_m+\mathsf{\Delta }h\tau )\\ \hspace{1em}\hspace{1em}+gES(t)-{\displaystyle \frac{k{e}_m^2}{2}}-{\displaystyle \frac{l{\tau }^2}{2}}+{\displaystyle \frac{(1-2\theta )f{u}^2}{2}}]\left.+{\displaystyle \frac{\mathsf{\partial }{V}_R}{\mathsf{\partial }G}}\left[\mu (E-T)+\right.\gamma u\left.-\delta G\right]\right\}\end{array}$$

(14)

We use the inverse induction method to obtain the optimal strategies of channel members in Case D, which are presented in Proposition 1 (proofs are listed in Appendix A).

Proposition 1.

The equilibrium solutions of channel members in Case D, with a low-carbon promotion cost-sharing contract, are delineated from a long-term and dynamic viewpoint as follows:

(1) The equilibrium solution for channel members is outlined below:

$${\tau }^{*}={\displaystyle \frac{\mathsf{\Delta }h\left[(\rho +\delta )(g+s)+b\mu W(Q-aP)\right]}{l(\rho +\delta +Qb\mu E_m-aPb\mu E_m)}}$$

(15)

$${\theta }^{*}={\displaystyle \frac{(\sigma +1)\left[3W-P-(2+5\sigma )(g+s)E_m+(6W-P)\sigma \right]}{(2\sigma +1)\left[P+W-(2+3\sigma )(g+s)E_m+(P+2W)\sigma \right]}}$$

(16)

$$u^{*}={\displaystyle \frac{b\gamma (Q-aP)\left[P+W-(2+3\sigma )(g+s)E_m+(P+2W)\sigma \right]}{2f(\sigma +1)(\rho +\delta +Qb\mu E_m-apb\mu E_m)}}$$

(17)

(2) The trajectory of the optimal low-carbon goodwill state can be outlined below:

$$G(t)=G_{\infty }^{*}+e^{-At}(G_0-G_{\infty }^{*})$$

(18)

where $A=Qb\mu E_m-aPb\mu E_m+\delta >0$, and $G_{\infty }^{*}={\displaystyle \frac{\mu (E+e_m^{*}+\mathsf{\Delta }h{\tau }^{*})+\gamma u^{*}}{A}}$;

(3) The channel members’ optimal utilities are as follows:

$$J_M^{*}=m_1\ast G_{\infty }^{\ast }+n_1,U_R^{*}=m_2\ast G_{\infty }^{*}+n_2$$

(19)

The values of m₁, m₂, n₁, and n₂ are as follows:

$$m_1={\displaystyle \frac{b(Q-aP)\left[W-(g+s)E_m\right]}{\delta +\rho +(Q-aP)b\mu E_m}}$$

(20)

$$m_2={\displaystyle \frac{b(Q-aP)\left[P-W+(P-2W)\sigma +(g+s)\sigma E_m\right]}{\delta +\rho +(Q-aP)b\mu E_m}}$$

(21)

$$n_1={\displaystyle \frac{(l+k{\mathsf{\Delta }}^2{h}^2){(\mu m_1+g+s)}^2}{2kl\rho }}+{\displaystyle \frac{(g+\mu m_1)E}{\rho }}+{\displaystyle \frac{{\gamma }^2{\left[m_2+m_1(2+4\sigma )\right]}^2}{8f\rho (\sigma +1)(2\sigma +1)}}$$

(22)

$$n_2={\displaystyle \frac{\left[\mu (\sigma m_1+2m_2)-(g+s)\sigma \right](l+k{\mathsf{\Delta }}^2{h}^2)(\mu m_1+g+s)}{2kl\rho }}+{\displaystyle \frac{(\mu m_2-g\sigma )E}{\rho }}+{\displaystyle \frac{{\gamma }^2{m}_2\left[m_2+m_1(4\sigma +2)\right]}{4f\rho (\sigma +1)}}$$

(23)

Specific conditions must be satisfied for ${\theta }^{*}\in (0,{\displaystyle \frac{\sigma +1}{2\sigma +1}})$, specifically: $\sigma <{\displaystyle \frac{P-W}{2W-P-(g+s)E_m}}$, $2W>P+(g+s)E_m$, and $P>W>(g+s)E_m$. The significance of these conditions will be further discussed in the inference section.

4.2. Case C: Centralized Decision-Making

In Case C, the entire chain’s enhancements in environmental and economic outcomes can be realized via the amalgamation of channel members. Additionally, retailer’s fairness concerns do not influence decisions made by channel members in Case C, because only decisions involving the distribution of income among channel members are subject to fairness concerns [30]. According to Equation (8) and Equation (9), to maximize the chain’s long-term and dynamic profits, the manufacturer focuses on green technology and remanufacturing, while the retailer put efforts in promoting low-carbon products. Assuming uniformity in the discount factor ρ (where ρ > 0) for each channel member, the entire chain’s objective function over an infinite time horizon can be expressed below:

$$\underset{e_m,\tau ,u}{max}{J}_{SC}^{C^{*}}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{D(t)P-D(t)s{E}_m\right.+s\left[e_m(t)+\mathsf{\Delta }{D}_r(t)\right]+gES(t)-C_{e_m(t)}-C_{\tau (t)}\left.-C_{u(t)}\right\}dt$$

(24)

The time variable t is omitted for simplicity, aligning with Case C. The variable V_SC represents the entire chain’s value function in Case C, indicating the profits generated during the planned period. Therefore, the corresponding HJB equation can be expressed below:

$$\begin{array}{l}\rho V_{SC}=\underset{e_m,\tau ,u}{max}\left\{bG(Q-aP)(P-s{E}_m)\right.+s(e_m+\mathsf{\Delta }h\tau )+gES(t)-{\displaystyle \frac{k{e}_m^2}{2}}-{\displaystyle \frac{l{\tau }^2}{2}}-{\displaystyle \frac{f{u}^2}{2}}\\ \hspace{1em}\hspace{1em}+{\displaystyle \frac{\mathsf{\partial }{V}_{SC}}{\mathsf{\partial }G}}[\mu ES(t)+\gamma u-\delta G\left.]\right\}\end{array}$$

(25)

The inverse induction approach is employed to solve the optimal strategies of channel members in Case C, which are outlined in Proposition 2 (see proofs in Appendix A).

Proposition 2.

The equilibrium solutions of channel members from a long-term and dynamic viewpoint in Case C can be delineated as follows:

(1) The optimal solution of channel members is listed below:

$$e_m^{C^{*}}={\displaystyle \frac{(\rho +\delta )(g+s)+b\mu P(Q-aP)}{k(\rho +\delta +Qb\mu E_m-aPb\mu E_m)}}$$

(26)

$${\tau }^{C^{*}}={\displaystyle \frac{\mathsf{\Delta }h\left[(\rho +\delta )(g+s)+b\mu P(Q-aP)\right]}{l(\rho +\delta +Qb\mu E_m-aPb\mu E_m)}}$$

(27)

$$u^{C^{*}}={\displaystyle \frac{b\gamma (Q-aP)\left[P-(g+s)E_m\right]}{f(\rho +\delta +Qb\mu E_m-aPb\mu E_m)}}$$

(28)

(2) The trajectory of the optimal low-carbon goodwill state can be listed below:

$$G^C(t)=G_{\infty }^{C^{*}}+e^{-At}(G_0-G_{\infty }^{C^{*}})$$

(29)

where $A=Qb\mu E_m-aPb\mu E_m+\delta >0$, and $G_{\infty }^{C^{*}}={\displaystyle \frac{\mu (E+e_m^{C^{*}}+\mathsf{\Delta }h{\tau }^{C^{*}})+\gamma u^{C^{*}}}{A}}$;

(3) The supply chain’s optimal profit is as follows:

$$J_{SC}^{C^{*}}=m_3\ast G_{\infty }^{C^{*}}+n_3$$

(30)

The values of m₃ and n₃ are as follows:

$$m_3={\displaystyle \frac{b(Q-aP)\left[P-(g+s)E_m\right]}{\delta +\rho +(Q-aP)b\mu E_m}}$$

(31)

$$n_3={\displaystyle \frac{(l+k{\mathsf{\Delta }}^2{h}^2){(\mu m_3+g+s)}^2}{2kl\rho }}+{\displaystyle \frac{(g+\mu m_3)E}{\rho }}+{\displaystyle \frac{{(\gamma m_3)}^2}{2f\rho }}$$

(32)

5. Comparative Analysis

First, the cost-sharing ratio for promoting low-carbon products and the correlation between it and retailer’s fairness concerns are both analyzed. Then, we compare the equilibrium solutions in Propositions 1 and 2 and examine the influences of hybrid carbon policies and low-carbon preference (denoted as s, g, and b) on green technology, remanufacturing, and low-carbon goodwill. Finally, we analyze and compare the profits in Case D and Case C.

Corollary 1.

Cost-sharing ratio for low-carbon promotion

(1) The equilibrium solution for the cost-sharing ratio for low-carbon promotion shows that, as the wholesale marginal profit increases, the manufacturer will be responsible for a larger portion of the low-carbon advertising expenses. In contrast, the cost-sharing ratio for low-carbon promotion will decrease as the retail price increases. Specifically, when $W>{\displaystyle \frac{(\sigma +1)P+(2+5\sigma )(g+s)E_m}{3(2\sigma +1)}}$, ${\theta }^{*}>0$, the manufacturer is prepared to bear the expenses of retailer’s low-carbon initiatives.

(2) The prior equilibrium solution demonstrates that manufacturer’s low-carbon endeavors remain uninfluenced by retailer’s fairness concerns. However, the retailer’s efforts in low-carbon promotional initiatives and the cost-sharing ratio for such initiatives are affected by its fairness concerns. Additionally, the relationship between the cost-sharing ratio for low-carbon promotion and retailer’s fairness concerns depends on specific values: $P^2{(\sigma +1)}^2+2PW(\sigma +1)(2\sigma +1)$ and $3W^2{(2\sigma +1)}^2+E_m^2{(g+s)}^2(7{\sigma }^2+4\sigma )+2E_m(g+s)$·$\left.\left[P(\sigma +1)\right.(3\sigma +2)+W(2\sigma +1)(5\sigma +2)\right]$ If the former value is higher, the ratio of cost-sharing for low-carbon marketing will persist in increasing due to retailer’s growing fairness concerns. It occurs as the retailer seeks to enhance profits, hence expressing greater concerns over fairness to the upstream manufacturer and increasing the cost-sharing ratio. Conversely, if the former value is lower, the cost-sharing ratio for low-carbon initiatives will remain constant, even as the retailer’s fairness concerns rise.

Corollary 2.

Comparison of the equilibrium solutions in Cases D and C

(1) The total decrease in carbon emissions through green technology and recycling efforts is detailed as follows: $e_m^{*}<e_m^{C^{*}}$, ${\tau }^{*}<{\tau }^{C^{*}}$;

(2) The downstream retailer’s low-carbon promotional effort is satisfied as follows: $u^{*}<u^{C^{*}}$, when $(\sigma +1)P>(2\sigma +1)W+(g+s)\sigma E_m$;

(3) The low-carbon goodwill obtained from low-carbon operations by both the manufacturer and retailer is satisfied as follows: $G_{\infty }^{*}<G_{\infty }^{C^{*}}$;

(4) The product demand is satisfied as follows: $D^{*}<D^{C^{*}}$.

This corollary indicates that in Case C, the manufacturer makes more effort to allocate resources towards environmentally friendly production practices and low-carbon initiatives, in contrast to Case D. Additionally, the level of the retailer’s low-carbon promotional effort depends on the values of $(\sigma +1)P$ and $(2\sigma +1)W+(g+s)\sigma E_m$. When the former is larger, the retailer will be incentivized to implement low-carbon initiatives in Case C. Conversely, if the latter is larger, the retailer will have less of an incentive to promote low-carbon products in Case C. Moreover, the increased low-carbon goodwill results in a higher demand for products as a whole because of the positive correlation between the two variables. Therefore, centralized decision-making is more effective to promote the achievement of emissions reduction objectives and support the supply chain towards low-carbon transition.

Corollary 3.

Sensitivity analysis of major parameters

In Case D, we have ${\displaystyle \frac{\mathsf{\partial }{e}_m^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{e}_m^{*}}{\mathsf{\partial }g}}>0$, ${\displaystyle \frac{\mathsf{\partial }{\tau }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{\tau }^{*}}{\mathsf{\partial }g}}>0$, ${\displaystyle \frac{\mathsf{\partial }{u}^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{u}^{*}}{\mathsf{\partial }g}}<0$, ${\displaystyle \frac{\mathsf{\partial }{\theta }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{\theta }^{*}}{\mathsf{\partial }g}}<0$, ${\displaystyle \frac{\mathsf{\partial }{e}_m^{*}}{\mathsf{\partial }b}}>0$, ${\displaystyle \frac{\mathsf{\partial }{\tau }^{*}}{\mathsf{\partial }b}}>0$, ${\displaystyle \frac{\mathsf{\partial }{u}^{*}}{\mathsf{\partial }b}}>0$, ${\displaystyle \frac{\mathsf{\partial }{u}^{*}}{\mathsf{\partial }\sigma }}>0$;

In Case C, we have ${\displaystyle \frac{\mathsf{\partial }{e}_m^{C^{*}}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{e}_m^{C^{*}}}{\mathsf{\partial }g}}>0$, ${\displaystyle \frac{\mathsf{\partial }{\tau }^{C^{*}}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{\tau }^{C^{*}}}{\mathsf{\partial }g}}>0$, ${\displaystyle \frac{\mathsf{\partial }{u}^{C^{*}}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{u}^{C^{*}}}{\mathsf{\partial }g}}<0$, ${\displaystyle \frac{\mathsf{\partial }{e}_m^{C^{*}}}{\mathsf{\partial }b}}>0$, ${\displaystyle \frac{\mathsf{\partial }{\tau }^{C^{*}}}{\mathsf{\partial }b}}>0$, ${\displaystyle \frac{\mathsf{\partial }{u}^{C^{*}}}{\mathsf{\partial }b}}>0$.

Corollary 3 demonstrates that the retailer’s fairness concerns are a driving force of its low-carbon promotional efforts in Case D. Specifically, with retailer’s fairness concerns rising, a more proactive stance will be adopted to promote low-carbon products and increase consumers’ low-carbon preference. Subsequently, demand for such products will increase. However, this increased demand requires the manufacturer to put more efforts in low-carbon operations, which negatively impacts its profits but creates a chance to satisfy the retailer’s perspective on an acceptable revenue.

Both Case D and Case C reveal that the increased s or g motivates the manufacturer to intensify efforts in low-carbon operations, including green technology and remanufacturing. However, the retailer is expected to reduce its low-carbon promotional efforts in response to stricter hybrid carbon policies. If the retailer persists in increasing its low-carbon promotion efforts, the manufacturer will face substantial costs due to carbon emissions rights trading and carbon taxes resulting from the increased demand, leading to a decrease in the entire chain’s profits. Therefore, as hybrid carbon policies tighten, the retailer decreases low-carbon promotional efforts to maintain an adequate level of low-carbon goodwill and sustain product demand. Additionally, the increased b related to low-carbon goodwill will encourage the manufacturer to intensify low-carbon efforts and the retailer to actively engage in promoting low-carbon products. Therefore, collaborative decision-making on emissions reduction to increase low-carbon goodwill is essential for every member of the channel to achieve the goal of boosting overall profits.

Corollary 4.

Impacts of major parameters on low-carbon goodwill

In Case D, if $0<E_m<{\displaystyle \frac{2f\mu ({\mathsf{\Delta }}^2{h}^{2}k+l)(\delta +\rho )(\sigma +1)}{bkl{\gamma }^2(Q-aP)(3\sigma +2)}}$, we have ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }g}}>0$, ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{C^{*}}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{C^{*}}}{\mathsf{\partial }g}}>0$; If $E_m>{\displaystyle \frac{2f\mu ({\mathsf{\Delta }}^2{h}^{2}k+l)(\delta +\rho )(\sigma +1)}{bkl{\gamma }^2(Q-aP)(3\sigma +2)}}$, we have ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }g}}<0$, ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{C^{*}}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{C^{*}}}{\mathsf{\partial }g}}<0$.

In Case C, if $0<E_m<{\displaystyle \frac{f\mu ({\mathsf{\Delta }}^2{h}^{2}k+l)(\delta +\rho )}{bkl{\gamma }^2(Q-aP)}}$, we have ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }g}}>0$, ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }g}}>0$; If $E_m>$${\displaystyle \frac{f\mu ({\mathsf{\Delta }}^2{h}^{2}k+l)(\delta +\rho )}{bkl{\gamma }^2(Q-aP)}}$, we have ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{*}}{\mathsf{\partial }g}}<0$, ${\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{C^{*}}}{\mathsf{\partial }s}}={\displaystyle \frac{\mathsf{\partial }{G}_{\infty }^{C^{*}}}{\mathsf{\partial }g}}<0$.

Corollary 4 demonstrates that carbon emissions per unit of product (E_m) determine how hybrid carbon regulations affect low-carbon goodwill. Specifically, when E_m is low, an increase in either s or g will enhance the product’s low-carbon goodwill. When E_m is high, an increase in s or g will decrease the product’s low-carbon goodwill. For products with high carbon emissions, because of the declined low-carbon goodwill, the decrease in demand for low-carbon goods allows the producer to save money on carbon emissions rights and cut down on carbon taxes. However, if there is no decline in low-carbon goodwill, the manufacturer will encounter challenges in effectively managing the rising expenses of carbon tax and carbon emissions rights trading.

Consistent with Corollary 3, the retailer uniformly implements identical adjustment strategies in response to the stricter carbon policies in Cases D and C. Therefore, low-carbon promotion by the retailer is the principal factor influencing the varying trends in low-carbon goodwill. Consistent with Zhu et al. [26], this discovery emphasizes the importance of the retailer as a moderator in a product’s low-carbon goodwill. Moreover, the manufacturer is supposed to attach great importance to the unit carbon emissions of products when planning strategies, and the retailer should tailor its low-carbon promotional strategies in accordance with E_m to maintain an adequate level of low-carbon goodwill.

Corollary 5.

Comparison of profits in two cases

From the standpoint of the complete supply chain, $J_{SC}^{C^{*}}>J_M^{*}+J_R^{*}$.

This corollary demonstrates that the aggregate profits in the supply chain of Case C surpass those of Case D. Additionally, the allocation of augmented profits is influenced by the position and bargaining power of each channel member; in Case C, the revenue gains of channel members surpass those in Case D. Therefore, it is essential to establish appropriate constraint mechanisms to encourage the producer and the retailer to accept centralized decision-making.

In summary, the manufacturer’s efforts in low-carbon operations in Case C surpass those in Case D, leading to higher profits in Case C. Specifically, improved carbon emissions reduction and better low-carbon goodwill can be achieved through the manufacturer’s low-carbon efforts in Case C, leading to optimization from both the economic and environmental viewpoints. Moreover, implementing certain constraints is essential to guarantee that both the manufacturer and the retailer are equipped to engage. These constraints can be represented as follows: $\mathsf{\Delta }{J}_R^{*}=J_R^{C^{*}}-J_R^{*}>0$.

6. Numerical Analysis

This part employs MATLAB R2021b to simulate the system, with an emphasis on the Case C and Case D products’ low-carbon goodwill trajectories. Our next step is to analyze how hybrid carbon policies and low-carbon preference affect low-carbon goodwill. Finally, we investigate the influence of retailer’s fairness concerns on low-carbon promotional efforts and the cost-sharing ratio for these initiatives. Data for this study were obtained from a survey conducted by an air conditioning manufacturer, as referenced in Zhu et al. [26]. The parameters used in the simulation include the following: P = 10, W = 6, E_m = 0.2, E_r = 0.05, h = 10, k = 40, l = 20, f = 13, a = 0.9, Q = 10, μ = 0.7, γ = 10, ρ = 0.8, b = 0.4, δ = 0.5, Δ = 0.15, s = 1, E = 20, and g = 6. Under the decentralized decision-making, we set σ = 0.7.

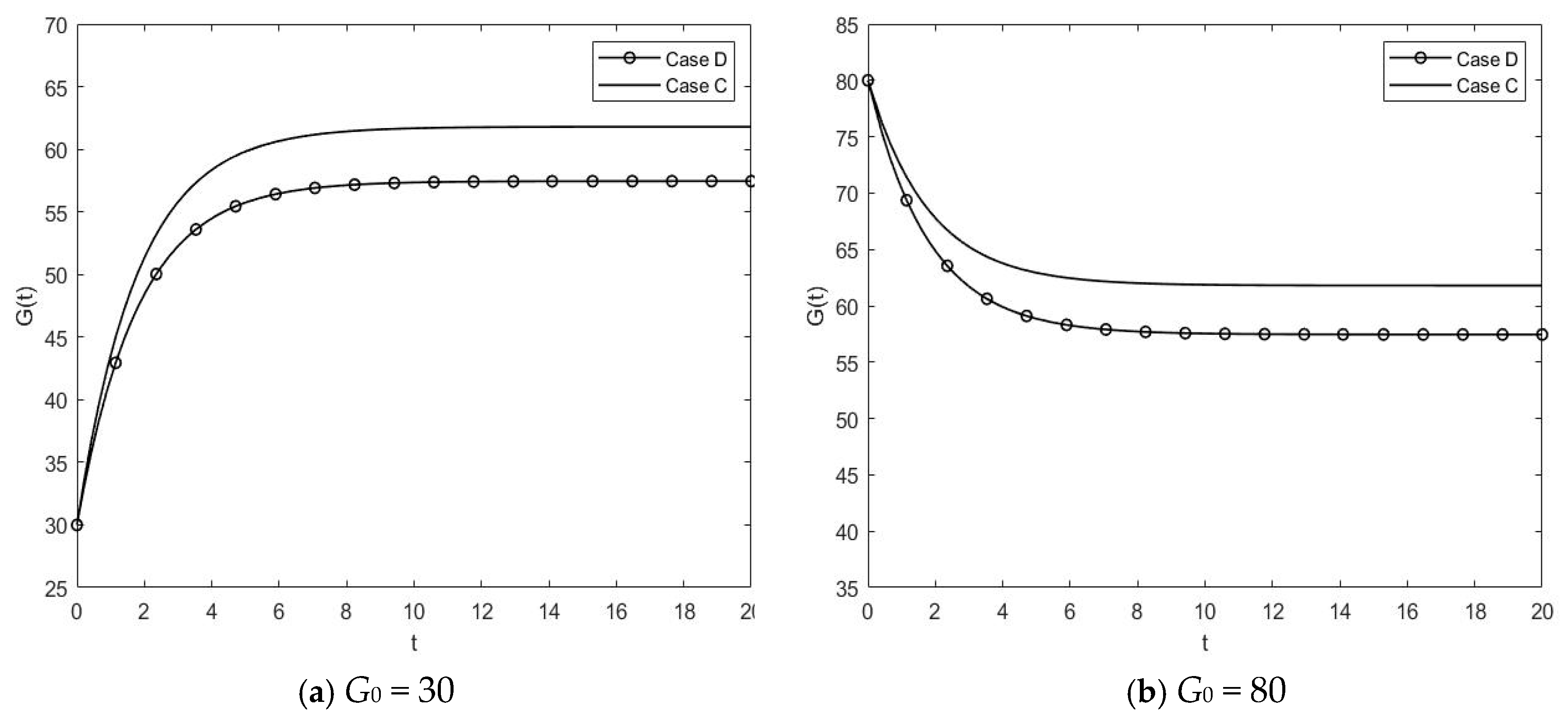
6.1. Trajectories of Low-Carbon Goodwill

Figure 2 depicts the trajectories of low-carbon goodwill, represented as G(t). In each scenario, G(t) is dictated by the beginning value G₀. At a lower G₀ level, low-carbon goodwill will increase and stabilize over time, as seen in Figure 2a. In contrast, when G₀ is high, a considerable decline in low-carbon goodwill occurs, as seen in Figure 2b. As is illustrated by the relationship $G_{\infty }^{C^{*}}>G_{\infty }^{*}$, a higher level of low-carbon goodwill occurs in Case C than Case D. Thus, the stable-condition value of low-carbon goodwill is contingent upon the specific decision-making case rather than the initial condition.

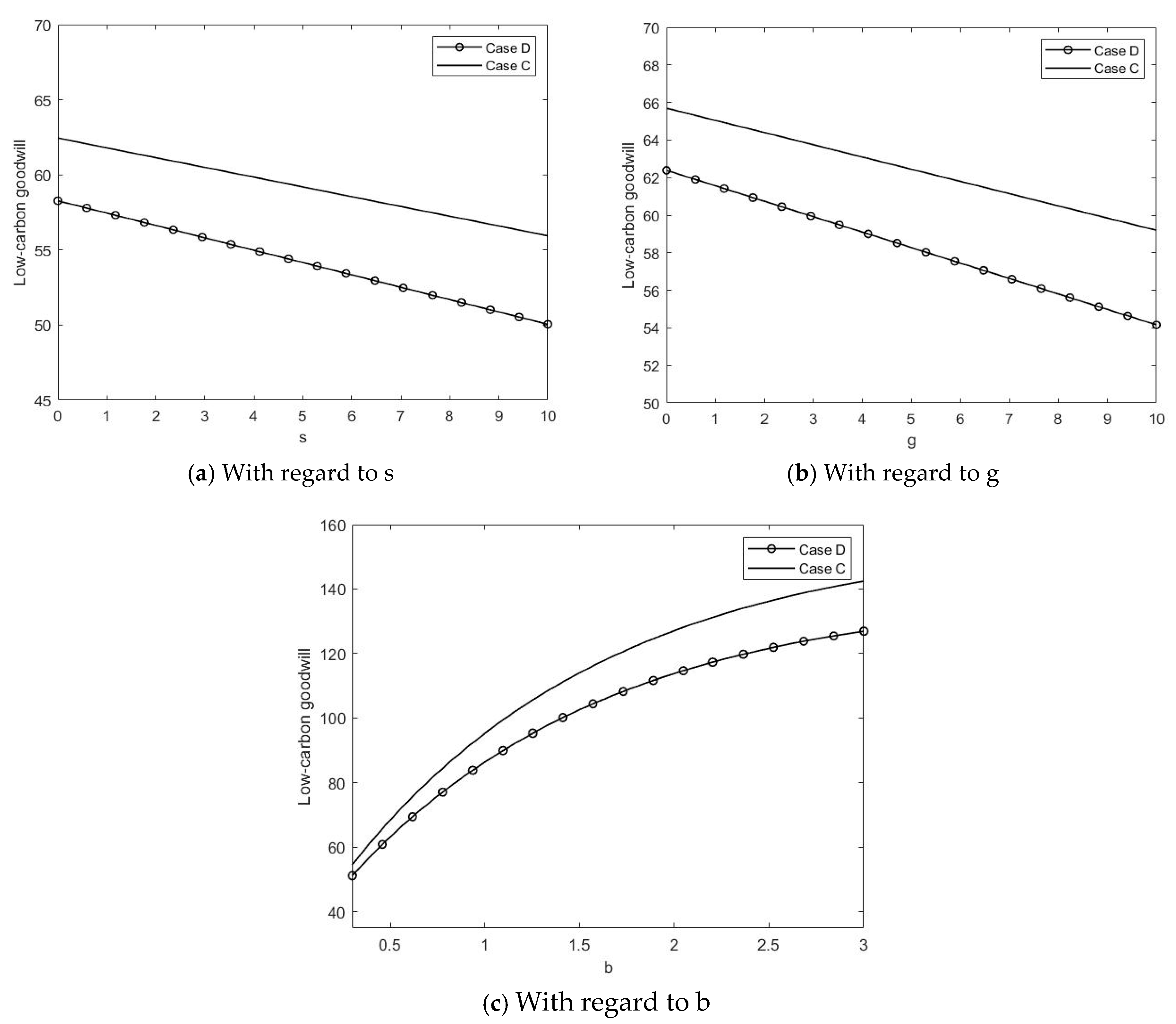
6.2. Impacts of Major Parameters on Low-Carbon Goodwill

Figure 3 demonstrates that the value of low-carbon goodwill in a stable condition is affected by hybrid carbon policies and low-carbon preference. First, we calculate the value of E_m from the dataset. Because of $E_m>{\displaystyle \frac{f\mu ({\mathsf{\Delta }}^2{h}^{2}k+l)(\delta +\rho )}{bkl{\gamma }^2(Q-aP)}}$, Figure 3a,b indicates that low-carbon goodwill decreases as s or g rises in both Case D and Case C. Meanwhile, the retailer as a moderator has an important impact on managing low-carbon goodwill. Then, as Figure 3c indicates, an increased low-carbon preference encourages channel members to put more efforts in low-carbon production and promotion, fostering strong low-carbon goodwill. Therefore, these results valid the findings in Corollary 4 and underscore the importance of collaboration between supply chain members to improve low-carbon goodwill.

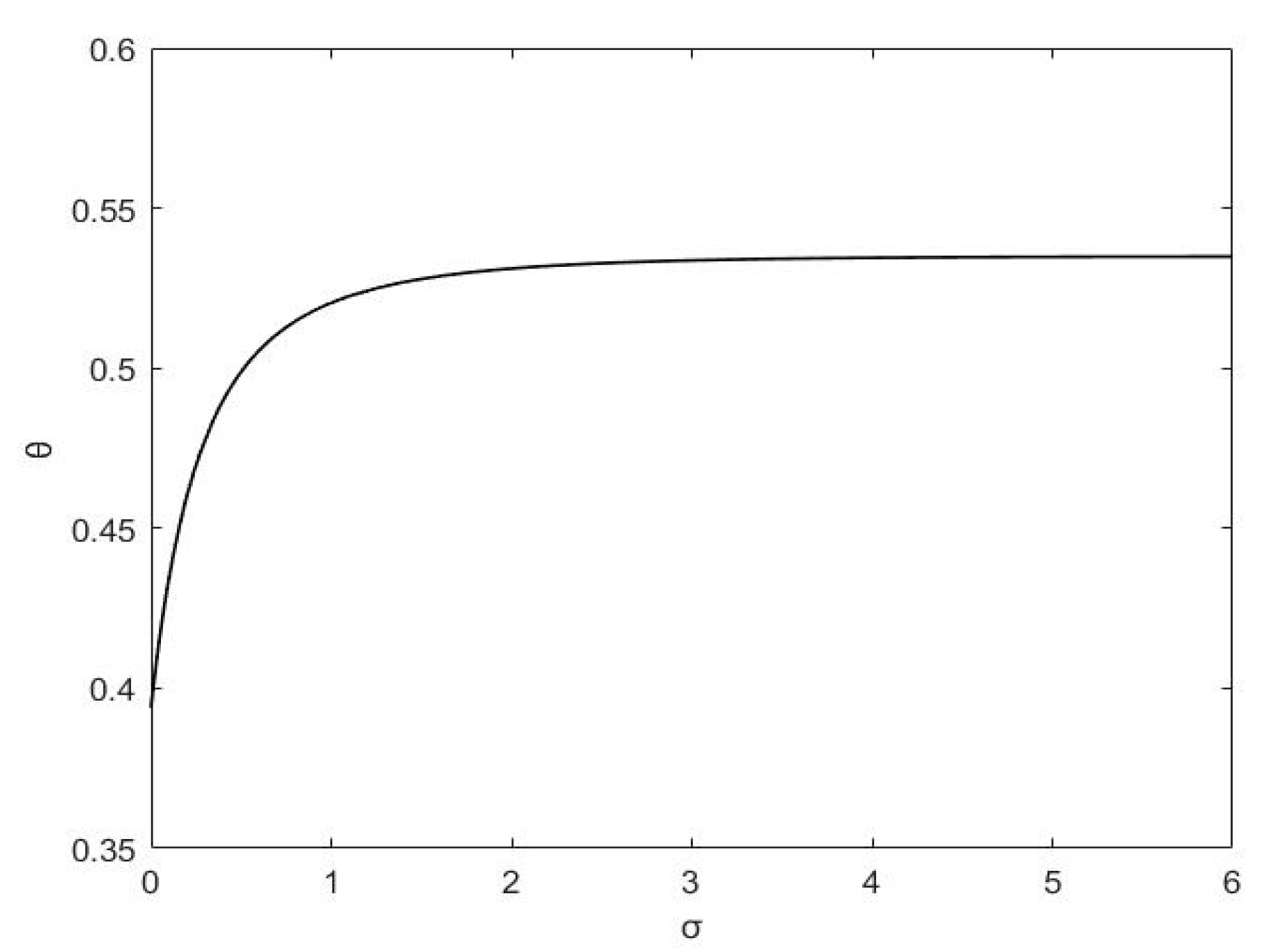
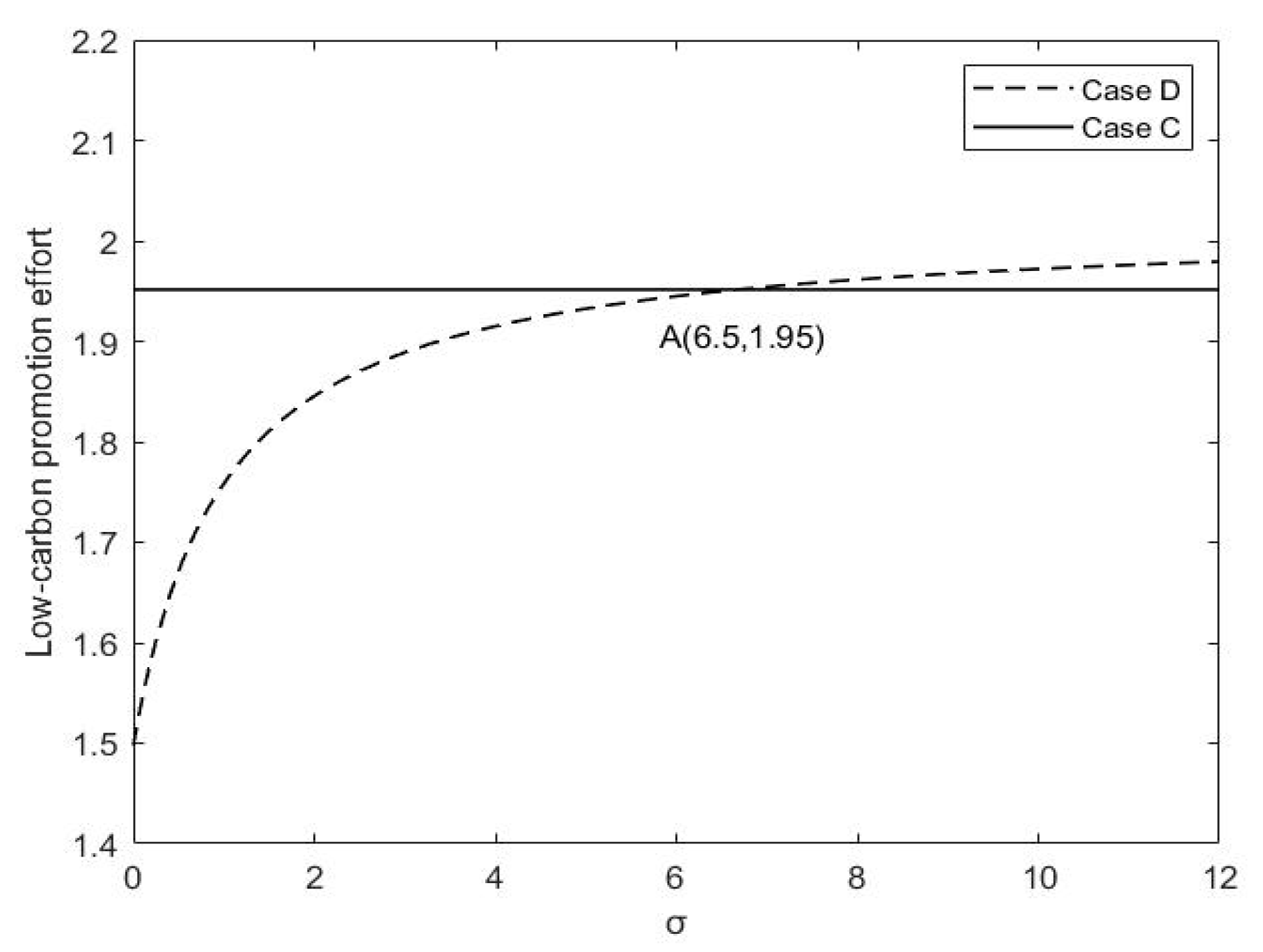
6.3. Influences of Retailer’s Fairness Concerns on Promotion and Cost-Sharing

This analysis examines the influences of retailer’s fairness concerns on retailer’s low-carbon promotional efforts and the cost-sharing ratio for such initiatives. From Figure 4 and Figure 5, the following findings are listed below:

(1) When retailer’s fairness concerns fall below three, there is a rapid increase in the cost-sharing ratio for low-carbon promotions as the retailer’s fairness concerns rise. Specifically, the retailer conveys this information to the upstream manufacturer, prompting it to contribute to low-carbon promotion costs. Additionally, this results in higher profits for each channel member. However, the cost-sharing ratio for low-carbon marketing remains constant after retailer’s fairness concerns surpass three. Consequently, excessive concerns about fairness do not substantially influence the manufacturer’s willingness to share costs for low-carbon activities.

(2) In Case C, the retailer’s low-carbon promotional effort is uninfluenced by fairness concerns. In contrast, in Case D, the retailer’s low-carbon promotional effort increases as its fairness concerns grow. Specifically, if the retailer’s concerns over fairness are below 6.5, Case C will exhibit a greater number of low-carbon promotional activities compared to Case D. Conversely, if the retailer’s fairness concerns surpass 6.5, Case D will exhibit a greater number of low-carbon promotional activities compared to Case C.

7. Discussion

7.1. Main Conclusions

This study analyzes the equilibrium solutions of each manufacturer-led supply chain member through a differential game method. Specifically, the analysis incorporates hybrid carbon policies, low-carbon operations including green technology and remanufacturing, retailer’s fairness concerns, and low-carbon preference under the centralized method and decentralized method, involving a cost-sharing contract for low-carbon promotional initiatives. Based on comparative and numerical analyses, the primary conclusions derived from the differential game approach are outlined below:

(1)

Under the centralized case, the chain’s overall profits and low-carbon goodwill are higher than those under the decentralized case. Therefore, adopting centralized decision-making can optimize both the economic and environmental performances of channel members.

(2)

The manufacturer’s low-carbon efforts remain uninfluenced by retailer’s fairness concerns, but they do augment the retailer’s initiatives in low-carbon advocacy. Additionally, when retailer’s fairness concerns fall below three, the cost-sharing ratio for low-carbon marketing will rise swiftly in response to an increase in fairness concerns. However, when retailer’s fairness concerns surpass three, the cost-sharing ratio stabilizes. Therefore, in order to raise the low-carbon advertising cost-sharing ratio, the retailer should address fairness issues within an ideal range and express these concerns effectively to the manufacturer.

(3)

The increased low-carbon preference is driving supply chain participants to put more efforts in low-carbon operations and marketing. Moreover, regardless of the decentralized or centralized method, the producer persists in intensifying efforts towards low-carbon operations as hybrid carbon policies become increasingly stringent. However, the retailer is expected to reduce its low-carbon promotional efforts in response to stricter hybrid carbon policies and serve as a moderator in maintaining an adequate low-carbon goodwill and sustain the supply chain’s low-carbon transition. Therefore, this partnership is essential for cultivating increased low-carbon goodwill, boosting product demand, and ultimately improving profits in the supply chain.

7.2. Managerial Insights

Our findings yield the following significant managerial insights:

(1)

Improve low-carbon awareness: Governments and corporations should intensify efforts to promote education on low-carbon knowledge. Specifically, governments can institute inclusive finance policies to incentivize the purchasing of low-carbon products. Additionally, a well-targeted low-carbon promotion subsidy policy can significantly contribute to low-carbon initiatives, thereby increasing consumer awareness about low-carbon options.

(2)

Pay attention to fairness concerns in promotion cost-sharing: Downstream retailers ought to evaluate the implications of fairness concerns and proactively convey this information to upstream manufacturers during negotiations. Moreover, formulating and establishing open and equitable cost-sharing agreements that balance the interests of manufacturers and retailers can incentivize retailers to participate more actively in low-carbon marketing initiatives.

(3)

Leverage different carbon policies effectively: Governments should take proactive steps to enhance existing carbon policies and leverage the complementary aspects of various carbon strategies to accelerate the transition to low-carbon operations. A coordinated approach can amplify the impacts of these policies on environmental and economic outcomes.

7.3. Research Limitations

This study has certain limitations that warrant further investigation.

First, it examines a limited scope of carbon policies. This study only examines a mix of carbon tax and cap-and-trade policies. Future research could explore the synergies between these policies and other existing carbon reduction strategies to provide a more comprehensive understanding of policy effectiveness.

Second, it does not consider the influence of recycling policies. While this study considers remanufacturing operations, it does not investigate the influence of recycling policies on low-carbon operations. Future studies could investigate the effects of recycling rules and incentives on supply chain sustainability as a whole.

Third, the effect of retailer rivalry on low-carbon promotion was not considered. Although we investigate the consequences of retailers’ fairness concerns in a manufacturer-led supply chain, the influence of retailer competition on low-carbon promotional initiatives is not taken into account in this study. Therefore, investigating how competition between retailers influences their low-carbon promotional initiatives could provide further insights into optimizing promotional strategies in competitive markets.