Adaptive Pendulum-Tuned Mass Damper Based on Adjustable-Length Cable for Skyscraper Vibration Control

Abstract

The dynamic control of vibrations in skyscrapers is a critical consideration in sustainable building design, particularly in response to environmental excitations such as wind impact or seismic activity. Effective vibration neutralisation plays a crucial role in providing the safety of high-rise buildings. This research introduces an innovative concept for an active vibration damper that operates based on fluid dynamic transport to adaptively alter a skyscraper’s natural frequency, thereby counteracting resonant vibrations. A distinctive feature of this system is an adjustable-length cable mechanism, allowing for the dynamic modification of the pendulum’s effective length in real time. The structure, based on cable length adjustment, enables the PTMD to precisely tune its natural frequency to variable excitation conditions, thereby improving damping during transient or resonance phenomena of the building’s dynamic behaviour. A comprehensive mathematical model based on Lagrangian mechanics outlines the governing equations for this system, capturing the interactions between pendulum motion, fluid flow, and the damping forces necessary to maintain stability. Simulation analyses examine the role of initial excitation frequency and variable damping coefficients, revealing critical insights into optimal damper performance under varied structural conditions. The findings indicate that the proposed pendulum damper effectively mitigates resonance risks, paving the way for sustainable skyscraper design through enhanced structural adaptability and resilience. This adaptive PTMD, featuring an adjustable-length cable, provides a solution for creating safe and energy-efficient skyscraper designs, aligning with sustainable architectural practices and advancing future trends in vibration management technology. The study presented in this article supports the development of modern skyscraper design, with a focus on dynamic vibration control for sustainability and structural safety. It combines advanced numerical modelling, data-driven control algorithms, and experimental validation. From a sustainability perspective, the proposed PTMD system reduces the need for oversized structural components by providing adaptive, efficient damping, thereby lowering material consumption and embedded carbon. Through dynamically retuning structural stiffness and mass, the proposed PTMD enhances resilience and energy efficiency in skyscrapers, lowers lifetime energy use associated with passive damping devices, and enhances occupant comfort. This aligns with global sustainability objectives and new-generation building standards.

1. Introduction

Interest in studying the dynamic response of civilian structures to environmental excitations such as wind and seismic activity has grown considerably in recent years [1,2,3,4]. Vibrations caused by such phenomena can pose a serious threat to the structural integrity of tall buildings and bridges [5,6]. To mitigate these risks, modern structures increasingly incorporate vibration control systems [7,8,9].

Well-documented real-world examples underscore the importance of vibration mitigation in tall buildings. The Taipei 101 skyscraper is equipped with a 660-ton tuned mass damper, which enhances structural stability and occupant comfort during typhoons and seismic events. Although passive, this system illustrates the importance of vibration control on a large scale in high-rise design. Similarly, the Citicorp Center in New York revealed a critical risk of dynamic instability due to underestimated wind loads, which necessitated urgent reinforcement of structural connections to prevent potential failure. These cases illustrate the increasing demand for damping systems that can respond in real time to changing environmental conditions.

Traditional tuned mass dampers (TMDs), while widely used and effective under steady-state conditions, suffer from fundamental limitations—primarily their fixed natural frequency and inability to adapt to varying dynamic loads. Passive TMDs are typically optimised for a single dominant excitation frequency, which limits their performance during transient or broadband excitations. To address this issue, the present study proposes an adaptive pendulum-tuned mass damper (PTMD) that enables real-time tuning by adjusting the effective pendulum length. This is achieved by shifting liquid within the pendulum body, thereby modifying the center of mass along a flexible suspension cable. Unlike systems that rely on variable mass or stiffness, the proposed design modifies its natural frequency through geometric adaptation. This study aims to explore the feasibility of this approach through conceptual design, dynamic modelling, and preliminary experimental validation.

In the context of vibration mitigation, both passive and active systems have been developed and analysed extensively [10,11,12]. Passive systems, such as tuned mass dampers (TMDs), are widely used due to their simplicity and reliability [13,14,15], though they often lack adaptability in real-time conditions [16,17]. Active and semi-active systems have been introduced to overcome these limitations, offering adjustable responses to dynamic changes [18,19,20]. Traditional TMD systems, although effective, suffer from key limitations, including fixed tuning and a lack of adaptability to changing dynamic conditions. The present study addresses these limitations by introducing a novel mechanism that dynamically adjusts the damper’s effective mass via fluid redistribution. This enables real-time tuning to external excitations, significantly improving performance under resonance-inducing conditions.

Recent studies have also explored more complex and innovative approaches to structural control, including the use of fluid-based mass systems and adaptive pendulum mechanisms [6,21,22]. These concepts aim to provide higher levels of tuning flexibility, especially for high-rise buildings exposed to varying dynamic loads. The present research introduces a novel active vibration control concept based on the controlled transportation of liquid mass between two reservoirs [23,24,25]. The goal is to develop a dynamic vibration eliminator that actively adjusts the structure’s natural frequency by shifting the liquid mass, enabling it to avoid resonance. This approach builds on previous active damper studies [26,27,28] and incorporates fluid dynamics for intelligent mass redistribution [29,30,31].

In this concept, a large water tank serves as the primary mass element, with a secondary liquid reservoir suspended beneath it like a pendulum. When resonance is detected through acceleration measurements, the system activates pumps to transfer fluid to a lower position, altering the mass distribution and thereby modifying the dynamic behaviour of the structure. If dangerous excitation reoccurs, the liquid is returned to the upper tank, allowing the process to repeat and create an adaptive feedback loop.

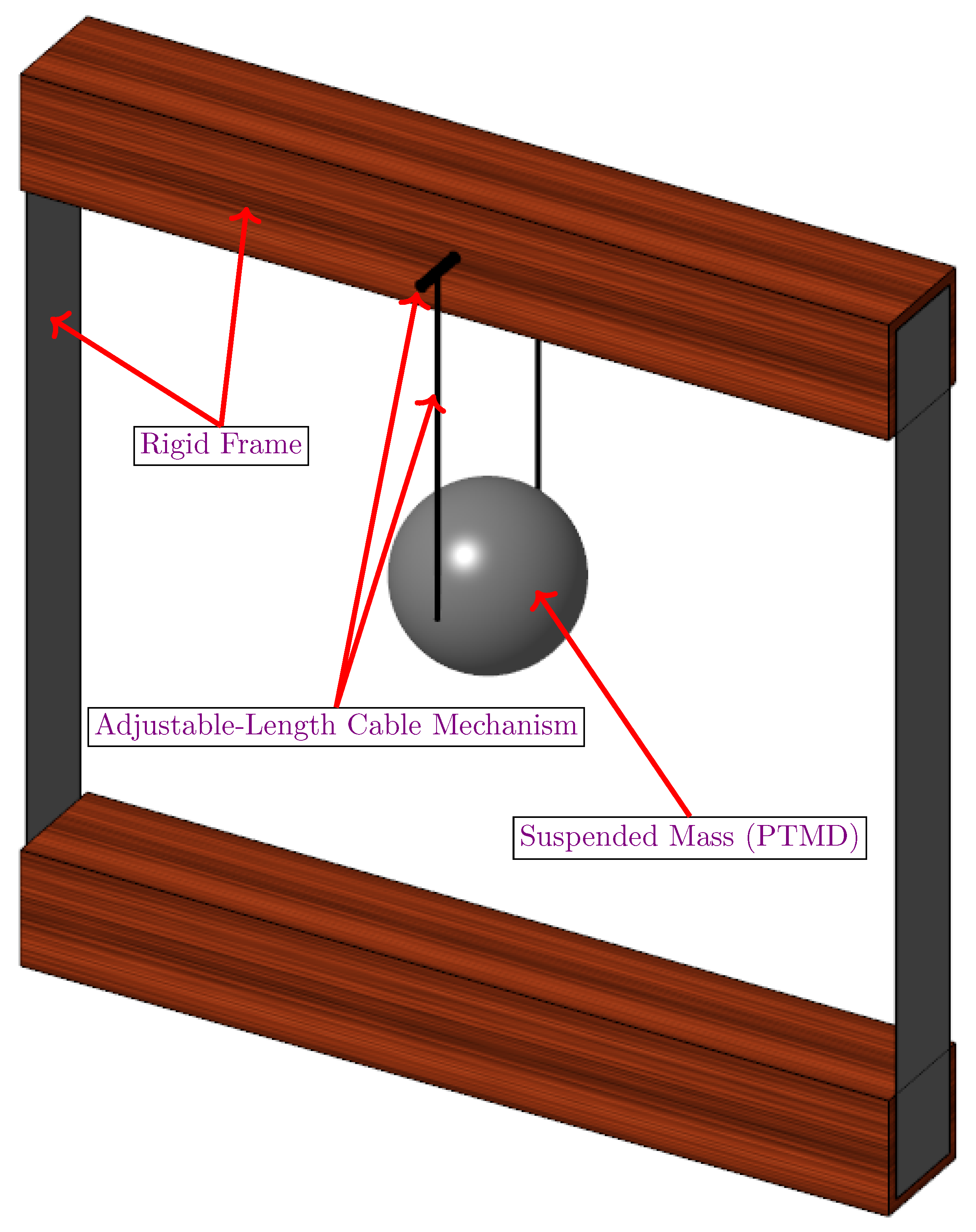
To explore the feasibility of this concept, a physical experimental model has been designed. For simplification, components of the structure are treated as rigid bodies, avoiding complications related to internal flexural modes. A CAD model of the test setup is shown in Figure 1. It features a rigid support frame, a suspended mass, and an adjustable-length cable to fine-tune dynamic response. The system is designed to simulate real-world damping conditions and validate analytical predictions. It is also established that during the test, mass will be transported from the upper to the lower tank based on the assumed flow characteristic obtained experimentally and then approximated by a mathematical function.

Modern design processes increasingly rely on numerical modelling and simulation to evaluate complex structural behaviours [32]. With the growing power of computational tools, it is now possible to simulate phenomena such as wind and earthquake loads using accurate mathematical functions. This allows for high-quality predictive analysis with minimal cost and time investment.

To avoid dependence on expensive commercial software, many engineering teams develop their own simulation tools based on open-source libraries [33,34,35,36,37,38]. Among the most commonly used are Python-based libraries for symbolic computation and data analysis, including SymPy and Pandas [39,40].

In this study, a custom simulation environment was created using such libraries to model the behaviour of the proposed fluid-based tuned mass damper. The simulation employs the Rayleigh damping model to replicate realistic structural damping conditions and determine optimal control parameters for the proposed system.

This work introduces an active vibration control system for high-rise buildings, grounded in the principles of fluid dynamic transport. The system adaptively transfers fluid between connected tanks. A change in mass is considered, which directly affects the effective length of the pendulum damper (PTMD). This results in an adaptive vibration absorber effect, allowing the tuning frequency to be adjusted to the operating conditions by adapting the building’s effective natural frequency in real time. The control mechanism is actuated by acceleration signals, enabling highly responsive damping that prevents resonance under environmental excitations such as wind or seismic activity.

2. Modelling of the Investigated System

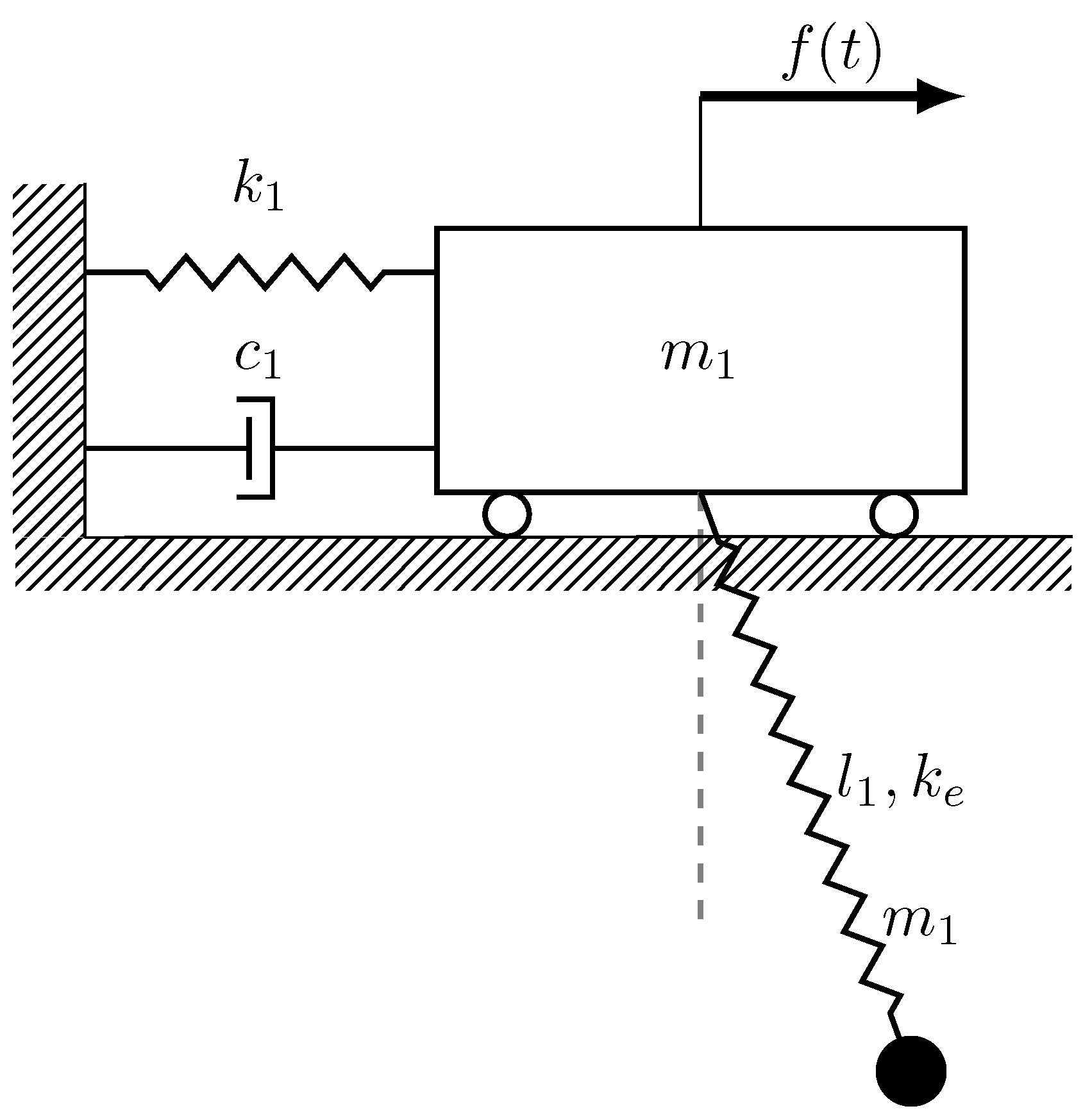
The model of vibration eliminator consists of a trolley attached to the wall by a spring to which an elastic pendulum is connected. A time-varying horizontal force externally forces the trolley. It was assumed that in the initial phase, all the liquid is inside the trolley. Activation of the damping will be initiated by transporting liquid into the pendulum.

A diagram explaining the selected concept is presented in Figure 2.

To analyse the dynamic behaviour of the proposed system, the equations of motion were derived using the Lagrangian formulation, which is expressed in general form as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L=E_k-E_p\end{array}\end{array}$$

(1)

where

• $E_p$—system’s potential energy;
• $E_k$—system’s kinetic energy.

The specific expressions for the potential and kinetic energies are as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill E_p={\displaystyle \frac{k{x}^2}{2}}+{\displaystyle \frac{k_l{u}^2}{2}}--g{m}_p\left(-{\displaystyle \frac{g{m}_p}{k_l}}-l-u\right)cos\left(\phi \right)\end{array}\end{array}$$

(2)

$$\begin{array}{cc}\hfill E_k=& {\displaystyle \frac{m_p{\dot{u}}^2}{2}}+{\displaystyle \frac{m_p{\dot{x}}^2}{2}}+{\displaystyle \frac{m_t{\dot{x}}^2}{2}}+{\displaystyle \frac{l^2{m}_p{\dot{\phi }}^2}{2}}+{\displaystyle \frac{m_p{u}^2{\dot{\phi }}^2}{2}}+l{m}_{p}u{\dot{\phi }}^2+m_{p}sin\left(\phi \right)\dot{u}\dot{x}+{\displaystyle \frac{g^2{m}_p^3{\dot{\phi }}^2}{2k_l^2}}+{\displaystyle \frac{gl{m}_p^2{\dot{\phi }}^2}{k_l}}+{\displaystyle \frac{g{m}_p^{2}u{\dot{\phi }}^2}{k_l}}\hfill \\ & +l{m}_{p}cos\left(\phi \right)\dot{\phi }\dot{x}+m_{p}ucos\left(\phi \right)\dot{\phi }\dot{x}+{\displaystyle \frac{g{m}_p^{2}cos\left(\phi \right)\dot{\phi }\dot{x}}{k_l}}\hfill \end{array}$$

(3)

where

• $k_l$—pendulum’s stiffness;
• x—trolley’s displacement;
• g—gravity constant;
• l—pendulum’s length;
• k—spring’s stiffness;
• $m_p$—the mass of the pendulum;
• t— time;
• u—pendulum’s elongation;
• $\phi$—pendulum’s swing angle;
• $\dot{\phi }$—pendulum’s swing angular velocity;
• $m_t$—the mass of the trolley;
• $\dot{x}$— trolley’s velocity;
• $\dot{u}$—pendulum’s elongation velocity.

From the Lagrangian function, the Euler–Lagrange equations are applied to derive the full set of equations of motion. These are given below:

$$\begin{array}{cc}\hfill L=& {\displaystyle \frac{m_p{\dot{u}}^2}{2}}+{\displaystyle \frac{m_p{\dot{x}}^2}{2}}+{\displaystyle \frac{m_t{\dot{x}}^2}{2}}-{\displaystyle \frac{k{x}^2}{2}}-{\displaystyle \frac{k_l{u}^2}{2}}+{\displaystyle \frac{l^2{m}_p{\dot{\phi }}^2}{2}}+{\displaystyle \frac{m_p{u}^2{\dot{\phi }}^2}{2}}+gl{m}_{p}cos\left(\phi \right)\\ & +g{m}_{p}ucos\left(\phi \right)+l{m}_{p}u{\dot{\phi }}^2+m_{p}sin\left(\phi \right)\dot{u}\dot{x}+{\displaystyle \frac{g^2{m}_p^{2}cos\left(\phi \right)}{k_l}}+{\displaystyle \frac{g^2{m}_p^3{\dot{\phi }}^2}{2k_l^2}}+{\displaystyle \frac{gl{m}_p^2{\dot{\phi }}^2}{k_l}}\hfill \\ & +{\displaystyle \frac{g{m}_p^{2}u{\dot{\phi }}^2}{k_l}}+l{m}_{p}cos\left(\phi \right)\dot{\phi }\dot{x}+m_{p}ucos\left(\phi \right)\dot{\phi }\dot{x}+{\displaystyle \frac{g{m}_p^{2}cos\left(\phi \right)\dot{\phi }\dot{x}}{k_l}}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill kx& +m_p\ddot{x}+m_t\ddot{x}-Fsin\left(\Omega t\right)+m_{p}sin\left(\phi \right)\ddot{u}+l{m}_{p}cos\left(\phi \right)\ddot{\phi }+m_{p}ucos\left(\phi \right)\ddot{\phi }-l{m}_{p}sin\left(\phi \right){\dot{\phi }}^2-m_{p}usin\left(\phi \right){\dot{\phi }}^2\hfill \\ & +2m_{p}cos\left(\phi \right)\dot{\phi }\dot{u}+{\displaystyle \frac{g{m}_p^{2}cos\left(\phi \right)\ddot{\phi }}{k_l}}-{\displaystyle \frac{g{m}_p^{2}sin\left(\phi \right){\dot{\phi }}^2}{k_l}}=0\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill gl{m}_{p}sin\left(\phi \right)& +g{m}_{p}usin\left(\phi \right)+l{m}_{p}cos\left(\phi \right)\ddot{x}+l^2{m}_p{cos}^2\left(\phi \right)\ddot{\phi }+l^2{m}_p{sin}^2\left(\phi \right)\ddot{\phi }+m_p{u}^2{cos}^2\left(\phi \right)\ddot{\phi }+m_p{u}^2{sin}^2\left(\phi \right)\ddot{\phi }\hfill \\ & +m_{p}ucos\left(\phi \right)\ddot{x}+{\displaystyle \frac{g^2{m}_p^{2}sin\left(\phi \right)}{k_l}}+{\displaystyle \frac{g{m}_p^{2}cos\left(\phi \right)\ddot{x}}{k_l}}+{\displaystyle \frac{g^2{m}_p^3{cos}^2\left(\phi \right)\ddot{\phi }}{k_l^2}}+{\displaystyle \frac{g^2{m}_p^3{sin}^2\left(\phi \right)\ddot{\phi }}{k_l^2}}+2l{m}_p{cos}^2\left(\phi \right)\dot{\phi }\dot{u}\hfill \\ & +2l{m}_{p}u{cos}^2\left(\phi \right)\ddot{\phi }+2l{m}_p{sin}^2\left(\phi \right)\dot{\phi }\dot{u}+2l{m}_{p}u{sin}^2\left(\phi \right)\ddot{\phi }+2m_{p}u{cos}^2\left(\phi \right)\dot{\phi }\dot{u}+2m_{p}u{sin}^2\left(\phi \right)\dot{\phi }\dot{u}\hfill \\ & +{\displaystyle \frac{2gl{m}_p^2{cos}^2\left(\phi \right)\ddot{\phi }}{k_l}}+{\displaystyle \frac{2gl{m}_p^2{sin}^2\left(\phi \right)\ddot{\phi }}{k_l}}+{\displaystyle \frac{2g{m}_p^2{cos}^2\left(\phi \right)\dot{\phi }\dot{u}}{k_l}}+{\displaystyle \frac{2g{m}_p^{2}u{cos}^2\left(\phi \right)\ddot{\phi }}{k_l}}+{\displaystyle \frac{2g{m}_p^2{sin}^2\left(\phi \right)\dot{\phi }\dot{u}}{k_l}}\hfill \\ & +{\displaystyle \frac{2g{m}_p^{2}u{sin}^2\left(\phi \right)\ddot{\phi }}{k_l}}=0\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill k_{l}u& +m_p{cos}^2\left(\phi \right)\ddot{u}+m_p{sin}^2\left(\phi \right)\ddot{u}+m_{p}sin\left(\phi \right)\ddot{x}-g{m}_{p}cos\left(\phi \right)-l{m}_p{cos}^2\left(\phi \right){\dot{\phi }}^2\hfill \\ & -l{m}_p{sin}^2\left(\phi \right){\dot{\phi }}^2-m_{p}u{cos}^2\left(\phi \right){\dot{\phi }}^2-m_{p}u{sin}^2\left(\phi \right){\dot{\phi }}^2-{\displaystyle \frac{g{m}_p^2{cos}^2\left(\phi \right){\dot{\phi }}^2}{k_l}}\hfill \\ & -{\displaystyle \frac{g{m}_p^2{sin}^2\left(\phi \right){\dot{\phi }}^2}{k_l}}=0\hfill \end{array}$$

(7)

where

• $\ddot{u}$—pendulum’s elongation acceleration;
• $\ddot{\phi }$—pendulum’s swing angular acceleration;
• F—excitation force;
• $\Omega$—excitation frequency;
• $\ddot{x}$—trolley’s acceleration.

Equations (5)–(7) together form a system of nonlinear, coupled differential equations that comprehensively describe the dynamics of the investigated object. Due to their complexity and nonlinear nature, analytical solutions in the general case are not feasible. Therefore, to facilitate further analysis and enable efficient simulation, the system was linearised around a selected operating point.

The linearised undamped model describes the dynamics in the neighbourhood of this equilibrium and is given by the following equations:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill kx+\left(m_p+m_t\right)\ddot{x}-Fsin\left(\Omega t\right)+m_p\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)\ddot{\phi }=0\end{array}\end{array}$$

(8)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill m_p{\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)}^2\ddot{\phi }+m_p\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)\ddot{x}+g{m}_p\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)\phi =0\end{array}\end{array}$$

(9)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill k_{l}u+m_p\ddot{u}-g{m}_p=0\end{array}\end{array}$$

(10)

These linearised differential Equations (8)–(10) describe the system’s response under small perturbations around the equilibrium state. The resulting system is linear with constant coefficients.

The structure of the equations also reveals partial coupling: Equations (8) and (9) form a coupled subsystem that must be solved simultaneously, whereas Equation (10) is decoupled and can be treated independently as a parametric input for the remaining system.

This decomposition significantly simplifies further analysis. The linear model enables the use of analytical methods to find closed-form solutions, allowing for a precise interpretation of the system’s dynamic behaviour and facilitating parametric studies under varied excitation conditions.

The system is excited by the kinematic force, acting on the trolley, in the form of a harmonic function (11):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill F_u=-Fsin\left(\Omega t\right)\end{array}\end{array}$$

(11)

After substituting individual parameters into the linearised equations of motion, matrices of inertia (12), stiffness (13), and damping (14) were determined.

$$M=\left[\begin{array}{ccc}{m}_p+m_t& m_p\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)& 0\\ m_p\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)& m_p{\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)}^2& 0\\ 0& 0& m_p\end{array}\right]$$

(12)

$$K=\left[\begin{array}{ccc}k& 0& 0\\ 0& g{m}_p\left({\displaystyle \frac{g{m}_p}{k_l}}+l\right)& 0\\ 0& 0& k_l\end{array}\right]$$

(13)

$$C=\left[\begin{array}{ccc}c& cl& 0\\ cl& {\widehat{c}}_{\phi }+c{l}^2& 0\\ 0& 0& c_l\end{array}\right]$$

(14)

The presented analysis describes the proposed model and the methodology used to determine the system’s equations of motion for both the non-linear and linear dynamics of the trolley and pendulum dynamic system. Based on this, the numerical solutions were divided and presented in the subsequent part of the paper. It is assumed that the pendulum’s movement does not affect the flow of the liquid through the pipe. The equation describing it, including previous assumption, has the following form (15):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f_t={\displaystyle \frac{1}{2}}-{\displaystyle \frac{atan\left(\lambda \left(t-t_0\right)\right)}{\pi }}\end{array}\end{array}$$

(15)

where

• $t_0$—activation time;
• $\lambda$—flow coefficient;
• $f_t$—flow function.

Based on Equation (15) above, we can derive time-varying mass functions for both parts of the system. These equations are given by (16) and (17):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill m_t={\displaystyle \frac{m_f}{2}}-{\displaystyle \frac{m_{f}atan\left(\lambda t-\lambda t_0\right)}{\pi }}\end{array}\end{array}$$

(16)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill m_p={\displaystyle \frac{m_f}{2}}+{\displaystyle \frac{m_{f}atan\left(\lambda t-\lambda t_0\right)}{\pi }}\end{array}\end{array}$$

(17)

where

• $m_f$—the mass of the fluid.

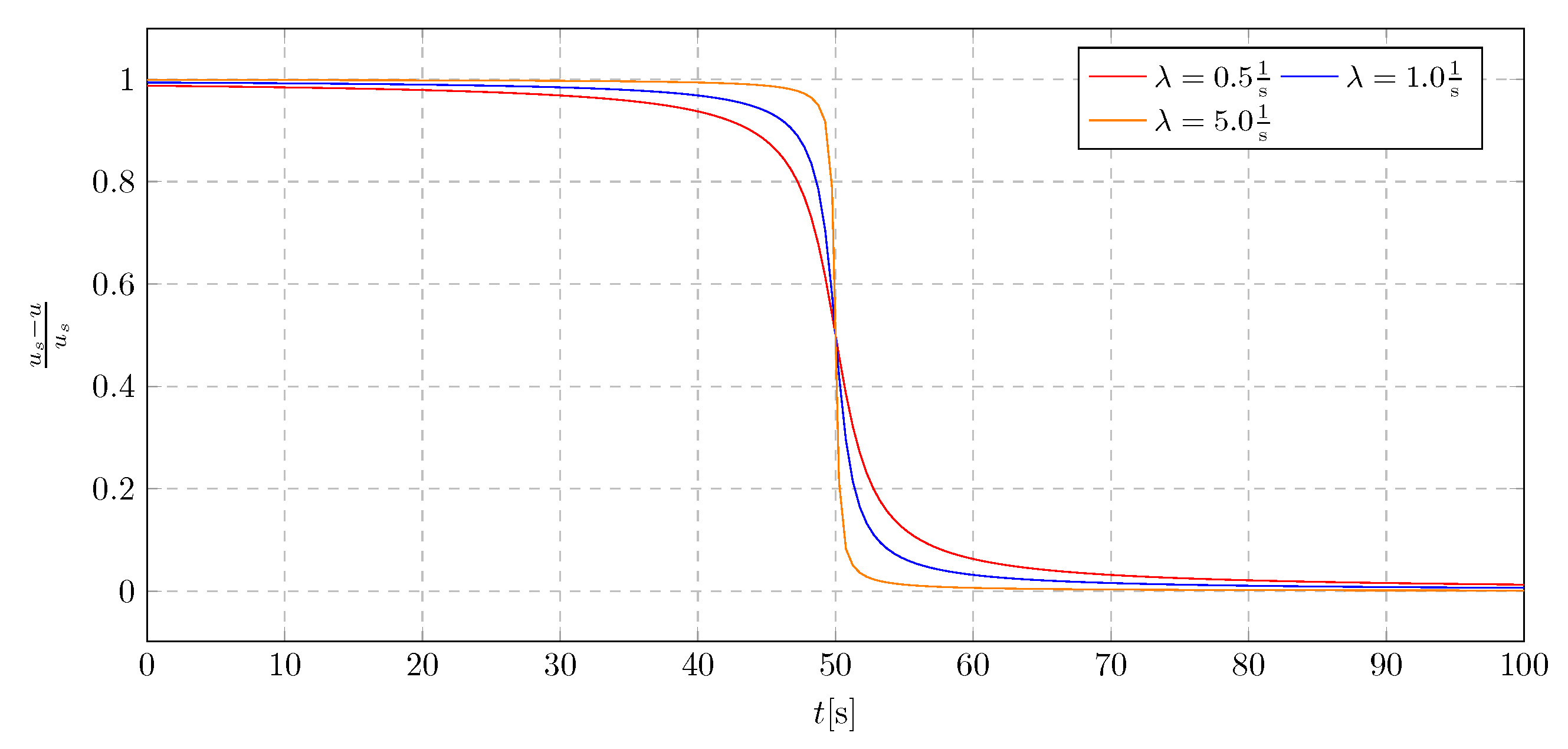
Liquid flow charts obtained using Formula (15) for different values of $t_0$ and $\lambda$ are presented in Figure 3 and Figure 4.

Figure 3 and Figure 4 demonstrate the universality of the developed function as it is possible to adjust the parameters for the damping control system.

3. Simulation Results—Investigation of Initial Frequency Influence

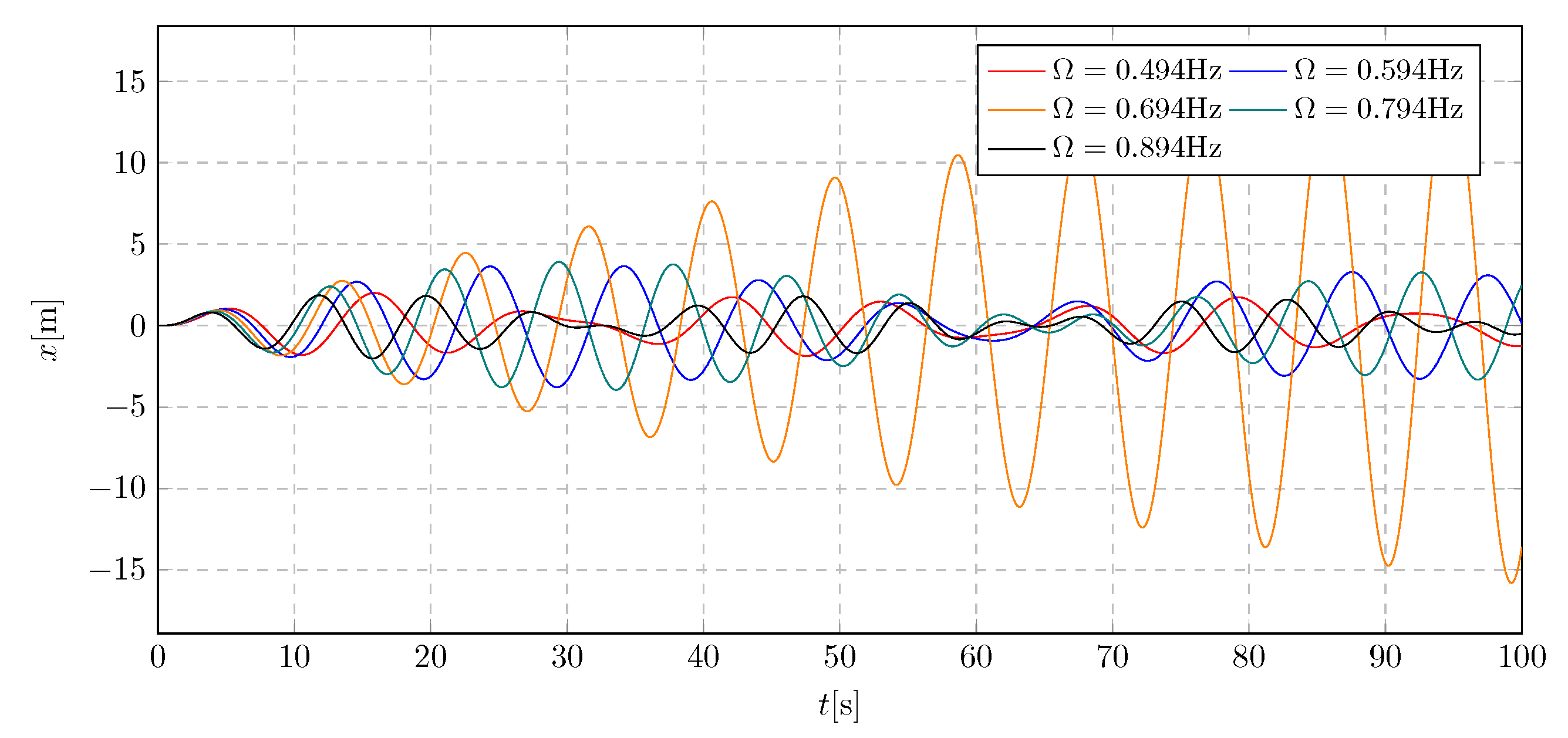
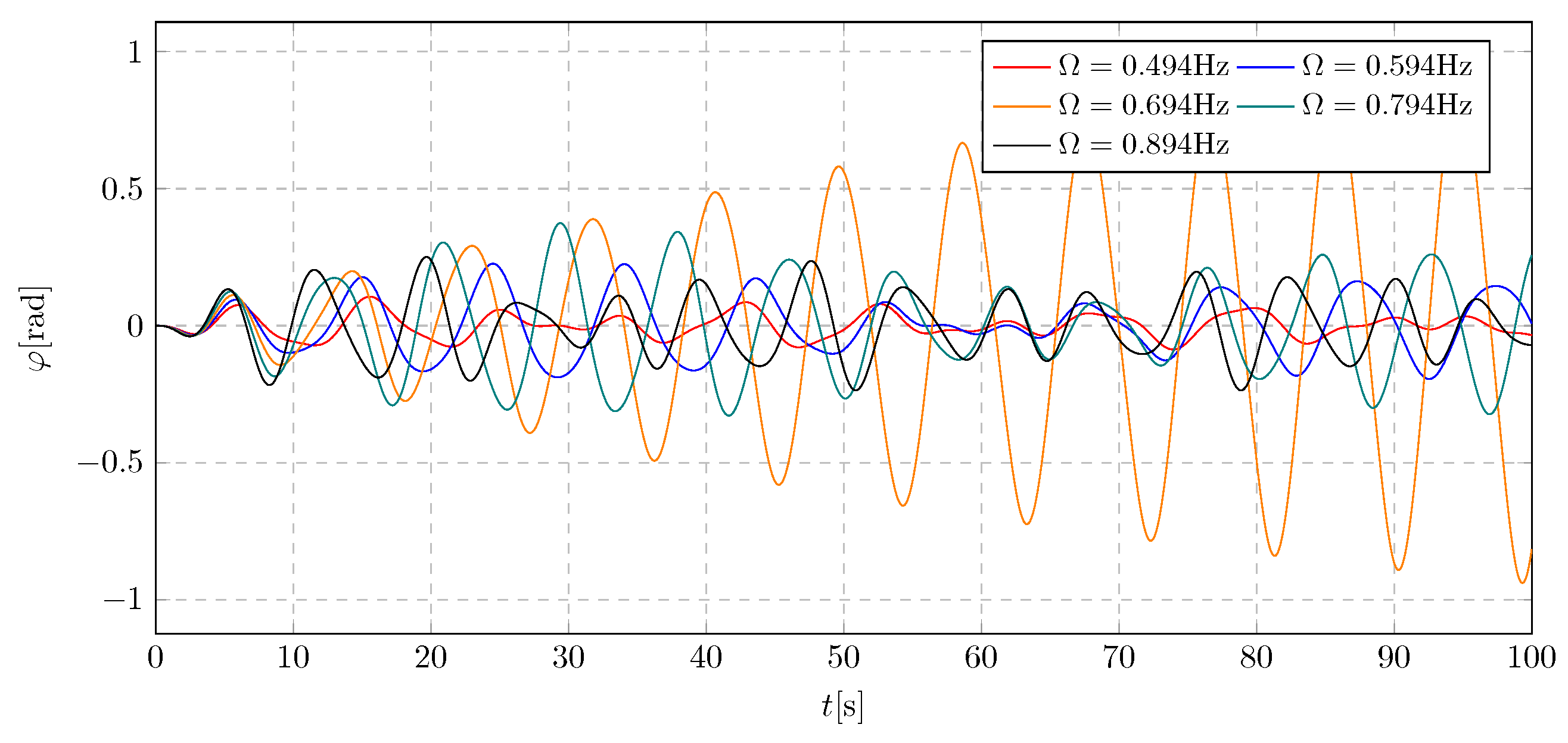
The excitation frequency value was verified through simulation. The analysis was conducted using parameters in the vicinity of the calculated natural frequency of the trolley, as required for the system to operate under resonance conditions. Simulation data was selected within the range of 0.494 to 0.894 Hz. The results are presented in Figure 5 and Figure 6. Based on these plots, the optimal excitation frequency was determined and will be used in subsequent simulations.

The simulations revealed a significant increase in amplitude for the excitation frequency $\Omega$ = 0.694 Hz. The observed growth in amplitude suggests that the system is operating within the resonance zone. For the remaining excitation frequencies, the amplitudes exhibit periodic variations within the allowable deflection range for large structures.

The graph of the pendulum’s angular displacement within the excitation frequency range of 0.494 to 0.894 Hz shows a similar amplitude pattern to that of the trolley. Again, a critical increase in amplitude was observed at $\Omega$ = 0.694 Hz. Based on these results, this value was identified as the fundamental excitation frequency and will be employed in further simulations.

4. Simulation Results—Investigation of Damping Coefficient Influence

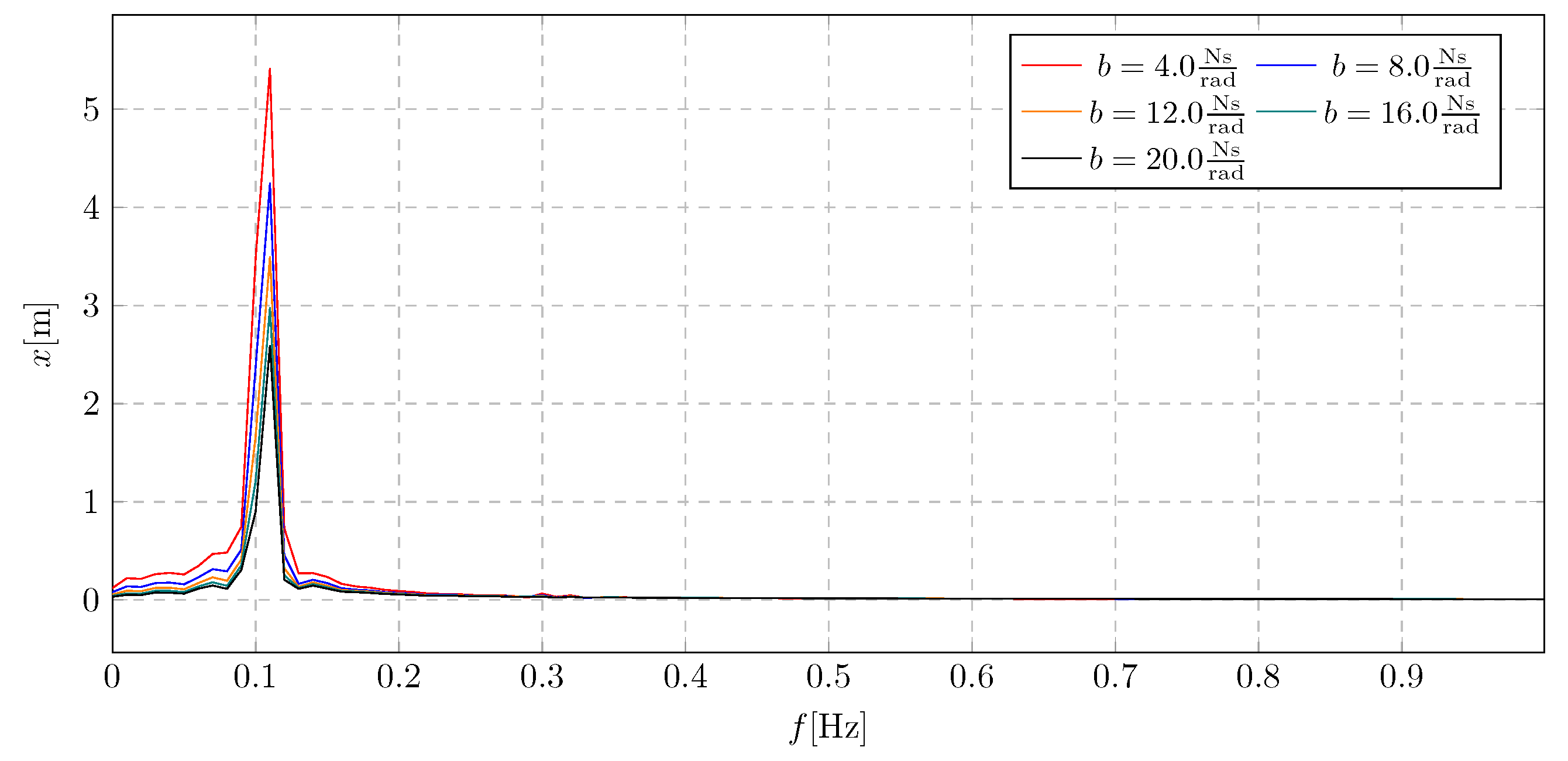
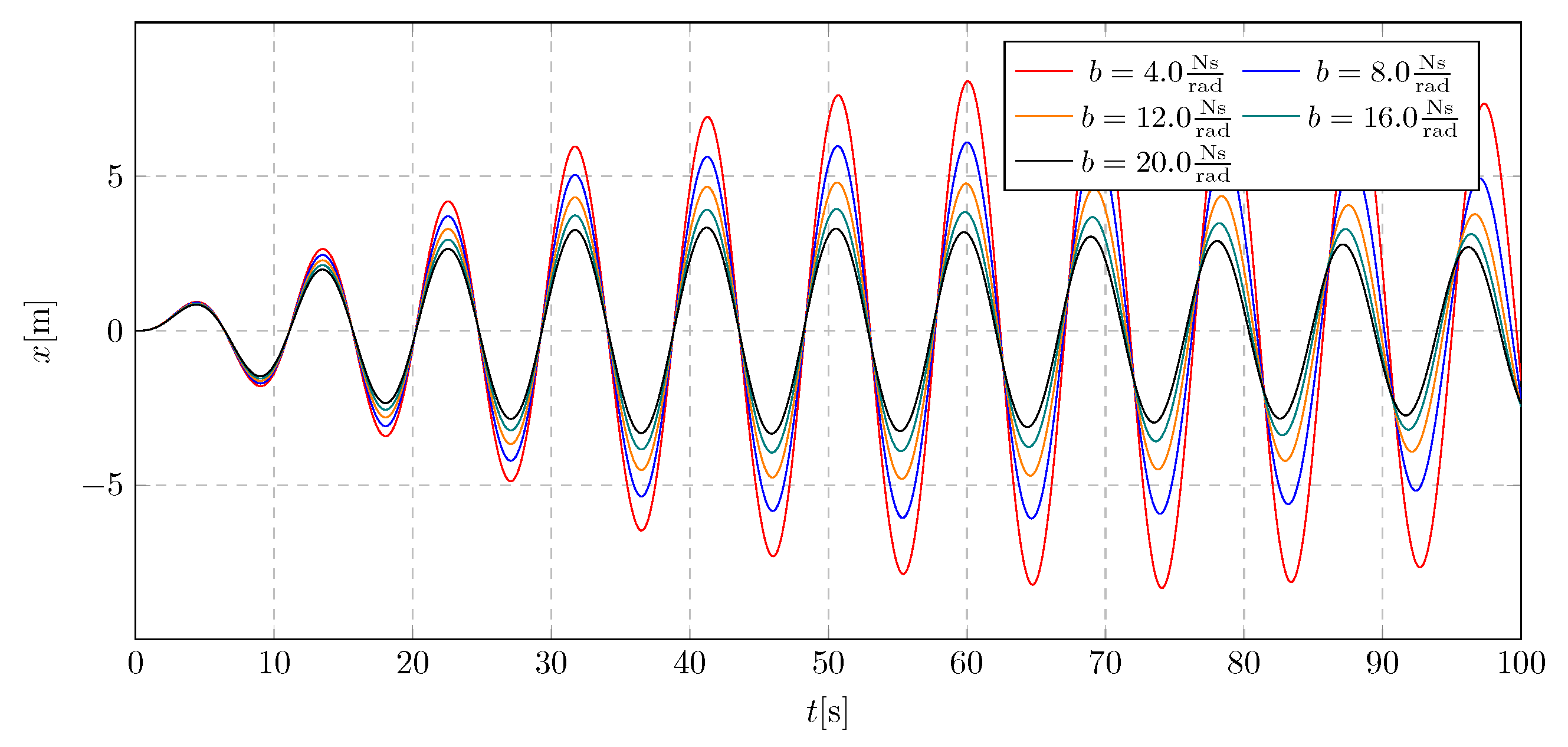
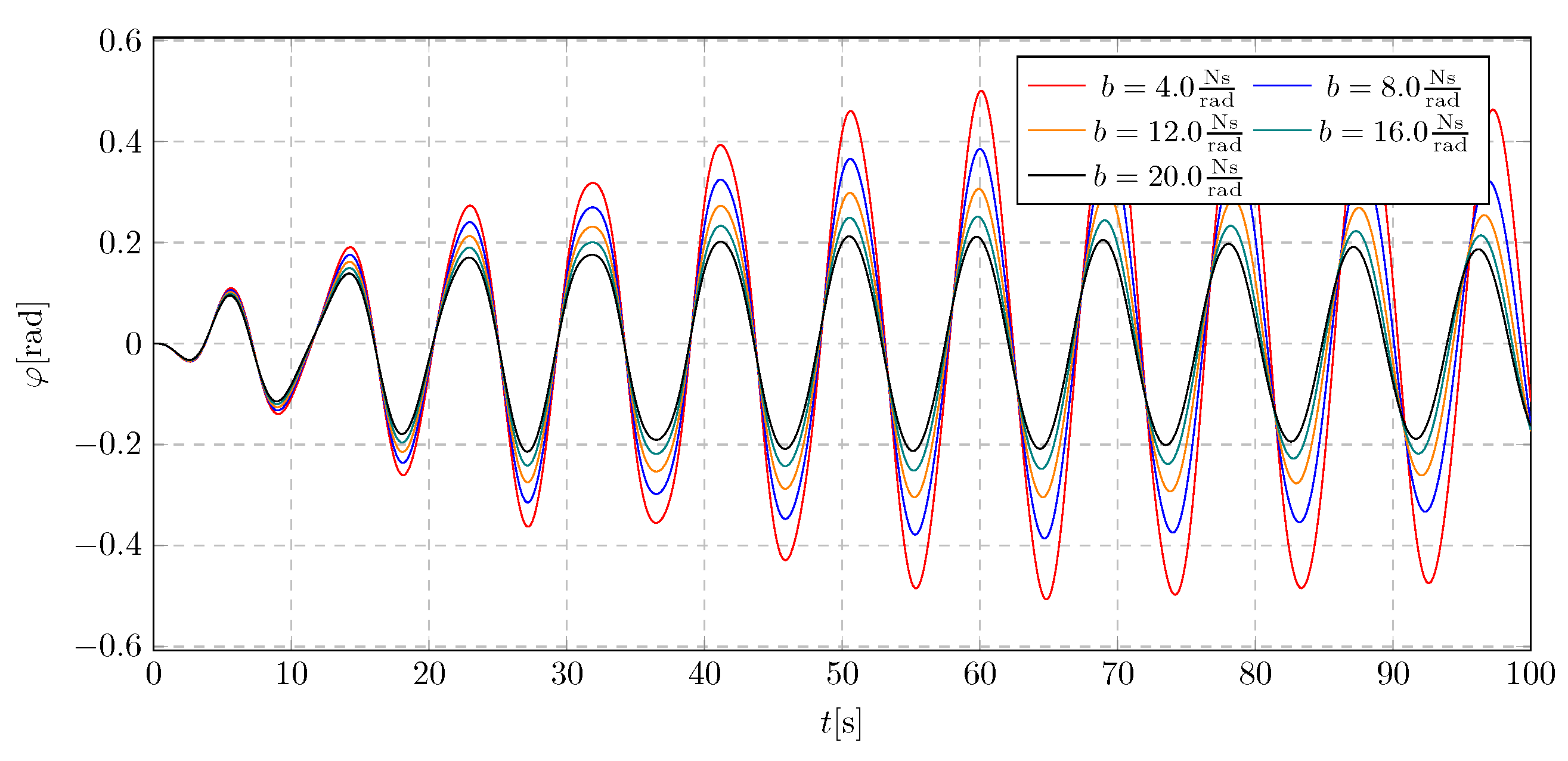
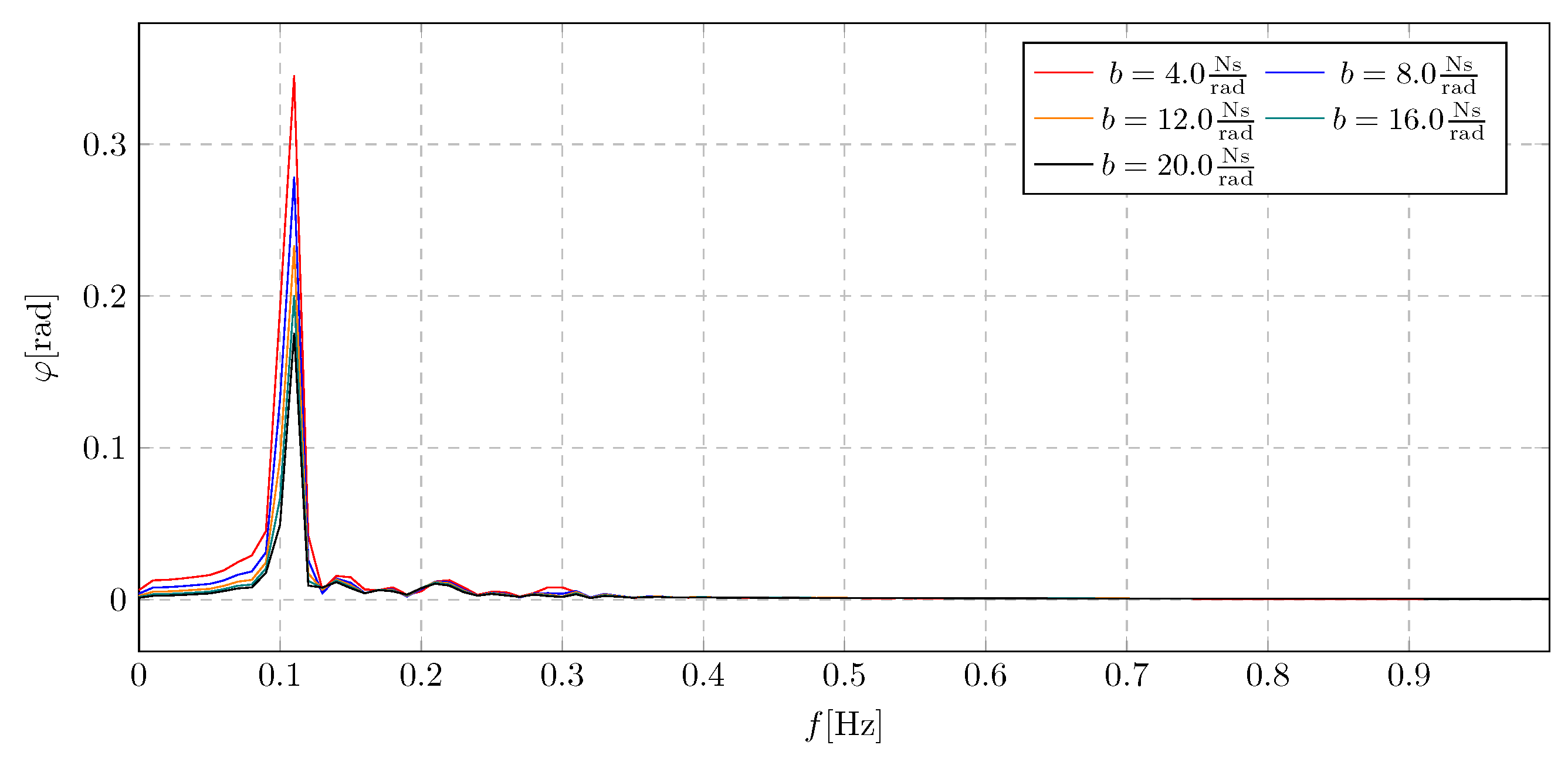
The influence of the damping coefficient on the system response under harmonic excitation is shown in Figure 7 and Figure 9 (displacement graphs), as well as in Figure 8 and Figure 10 (frequency spectra). The analysis considered damping coefficient values selected from the range of 80.0 to 120.0 s. This analysis allows the selection of the optimum damping coefficient value, ensuring system stability within the range of actual amplitude values.

Based on the performed simulations, a significant influence of the tested parameter on the range of amplitudes was observed. It was observed that for a damping coefficient value of $t_0$ equal to 80.0 s, the system experiences vibrations characteristic of the beating phenomenon after starting the liquid transport. When analysing the waveforms for subsequent parameters, no sudden changes in amplitudes and gradual stabilisation were observed. The extreme values of the amplitudes range from −8.33 m to 8.3 m.

Figure 8. Frequency spectra of trolley displacement for various damping coefficients.

Figure 8. Frequency spectra of trolley displacement for various damping coefficients.

The obtained frequency spectra are presented in Figure 8 to show the influence of the damping coefficient for $t_0$ on the overall amplitude range of the system. The frequency spectra in Figure 8 show that as the damping coefficient increases, the influence of individual dominant amplitudes decreases. In addition, the decrease in the amplitude values is smaller for higher values of the $t_0$ coefficient, which is associated with a decrease in the system’s sensitivity to mass changes at higher damping values. The maximum amplitude value is 5.42 m.

Figure 9. Pendulum angular displacement for various damping coefficients.

Figure 9. Pendulum angular displacement for various damping coefficients.

Analysing the influence of the damping coefficient $t_0$ on changes of the angle of the pendulum deflection, a short-term jump in amplitudes was observed at the moment of activation of the transport of liquid from the upper to the lower reservoir. This jump is due to a sharp change in the pendulum dynamics. It was observed that the amplitude jump at low values of the damping coefficient destabilised the system, causing the pendulum to oscillate in a dangerous range (above 15–20^∘). The minimum and maximum values range from −0.51 rad to 0.5 rad.

Figure 10. Frequency spectra of pendulum angular displacement for various damping coefficients.

Figure 10. Frequency spectra of pendulum angular displacement for various damping coefficients.

The frequency spectra shown in Figure 10 represent the overall amplitude range during the investigation of the effect of the damping coefficient $t_0$. From these spectra, the appearance of two components was observed. The former corresponds to the harmonic resulting from the applied excitation, and the latter to the activation of the liquid flow. It can then be seen that a higher value of the damping coefficient significantly reduces the increase in amplitudes in the transition phase. The maximum value of the component shown in the frequency spectrum is 0.35 rad.

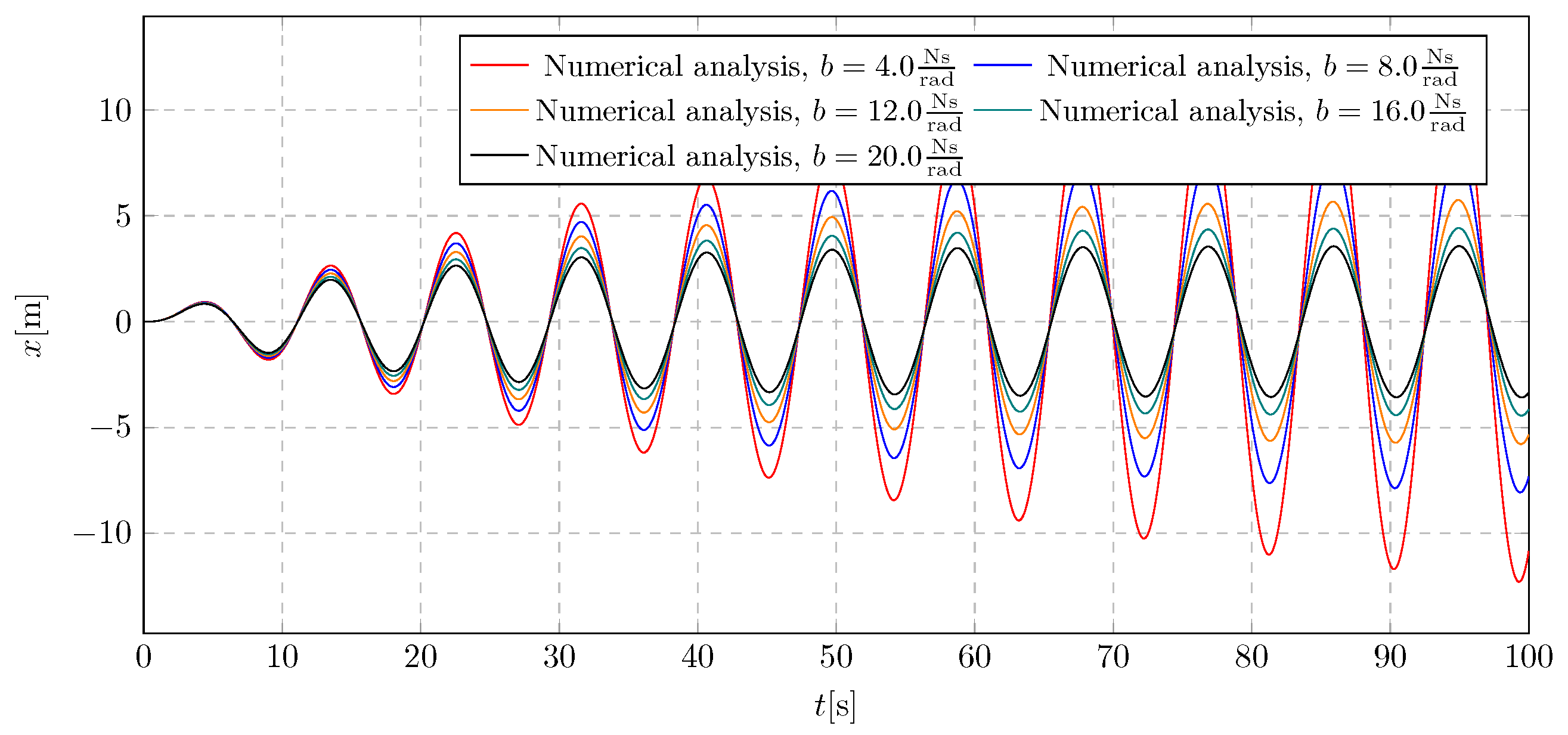
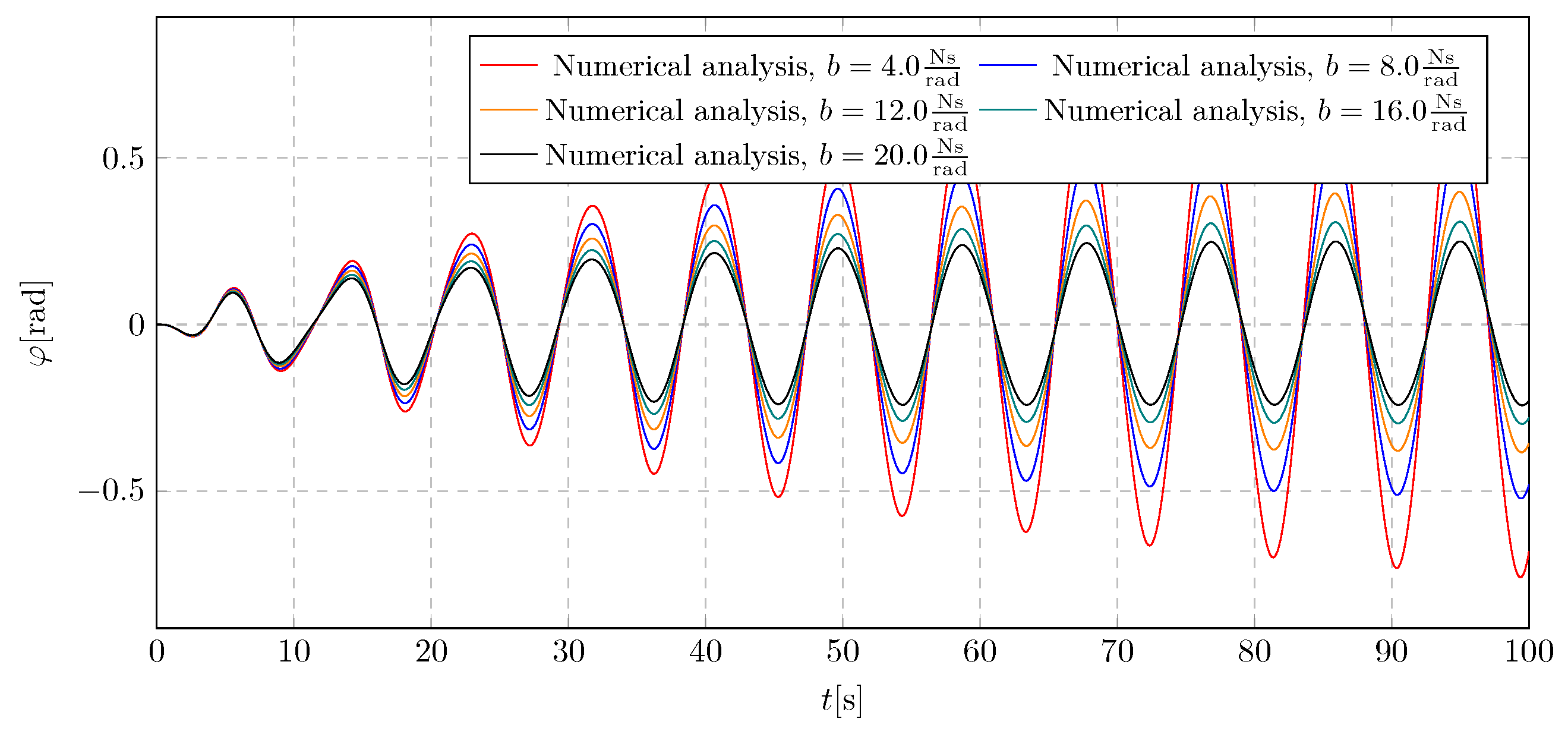
To analyse the selection of the damping coefficient, a simulation was performed without activating the liquid flow to isolate the influence of the damping coefficient on the system dynamics. The analysis was carried out for the damping coefficient b, within the range of 4 to $20{\displaystyle \frac{\mathrm{N}\mathrm{s}}{\mathrm{rad}}}$.

In Figure 11, it can be observed that the first three values of the parameter b—specifically 4, 8, and $12{\displaystyle \frac{\mathrm{N}\mathrm{s}}{\mathrm{rad}}}$—are insufficient to suppress the amplitude growth. Stabilisation is evident only for higher values of the damping coefficient. A similar trend is observed in the pendulum’s angular displacement in Figure 12.

Based on these results, and considering the simulations for both active and inactive dampers with variable mass, it was concluded that the damping coefficient b should be selected from the middle of the tested range. This choice ensures sufficiently high additional damping to mitigate pendulum amplitudes during active mass transport while avoiding excessive damping that could adversely affect system behaviour.

5. Simulation Results—Investigation of Damping Activation Time Influence

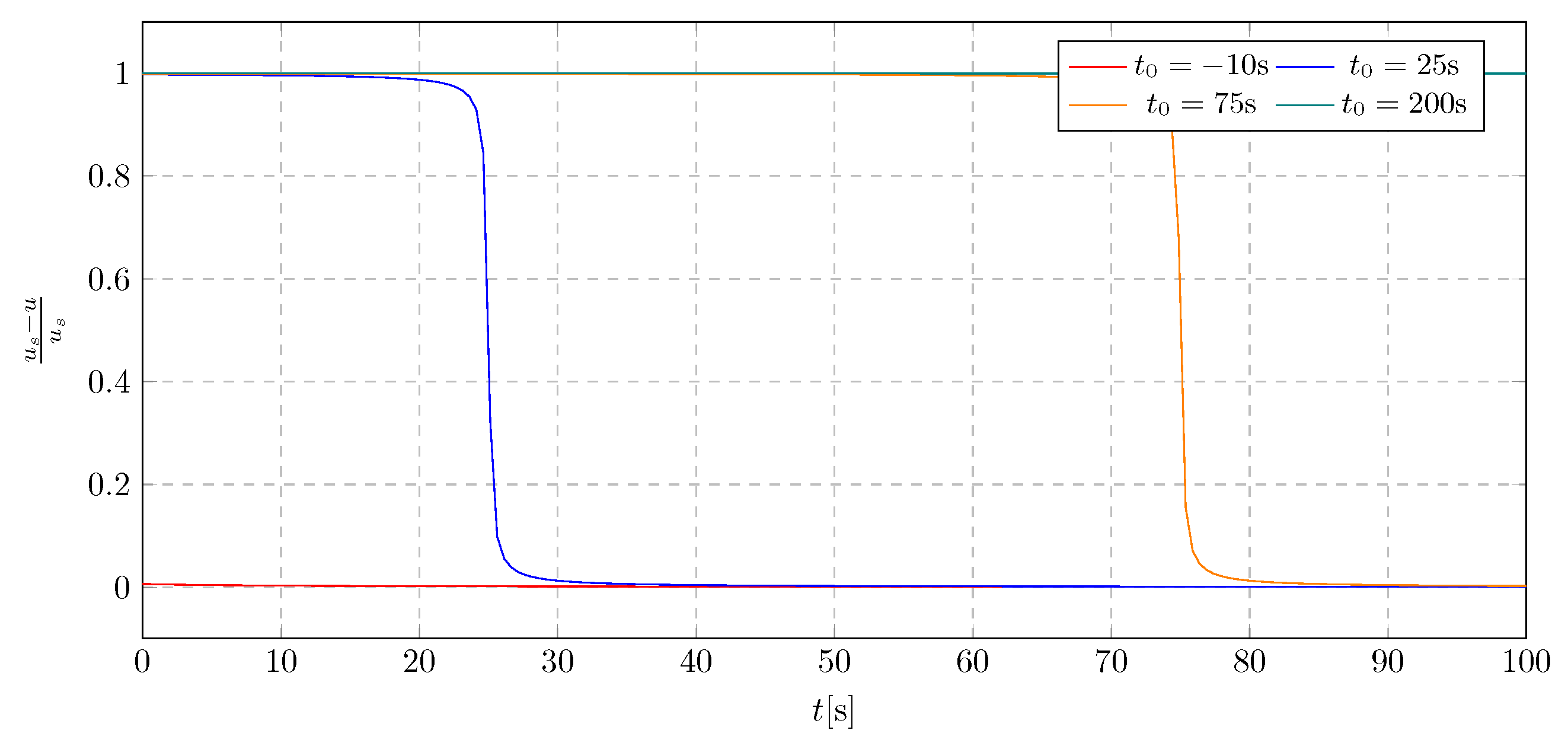
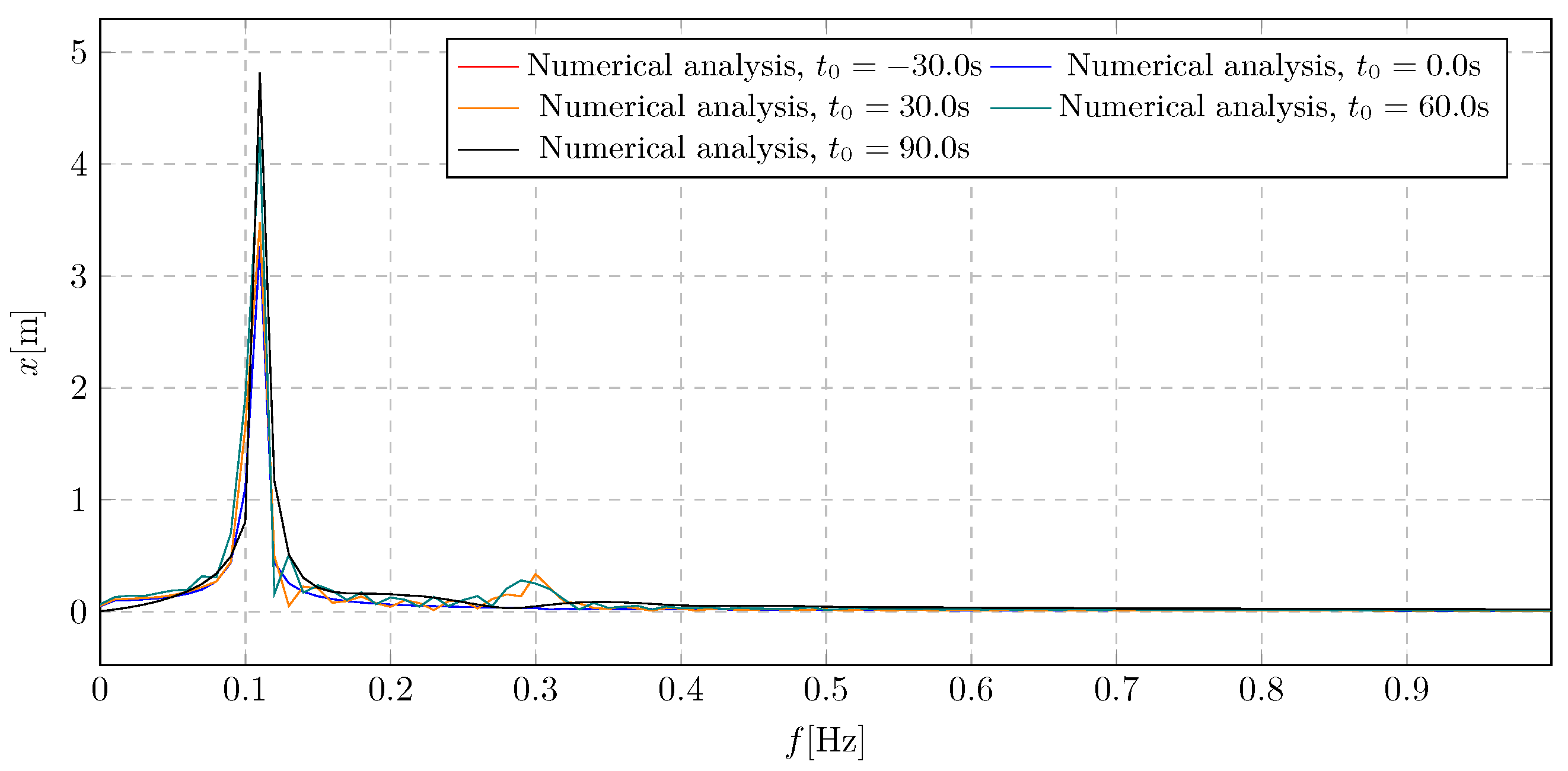
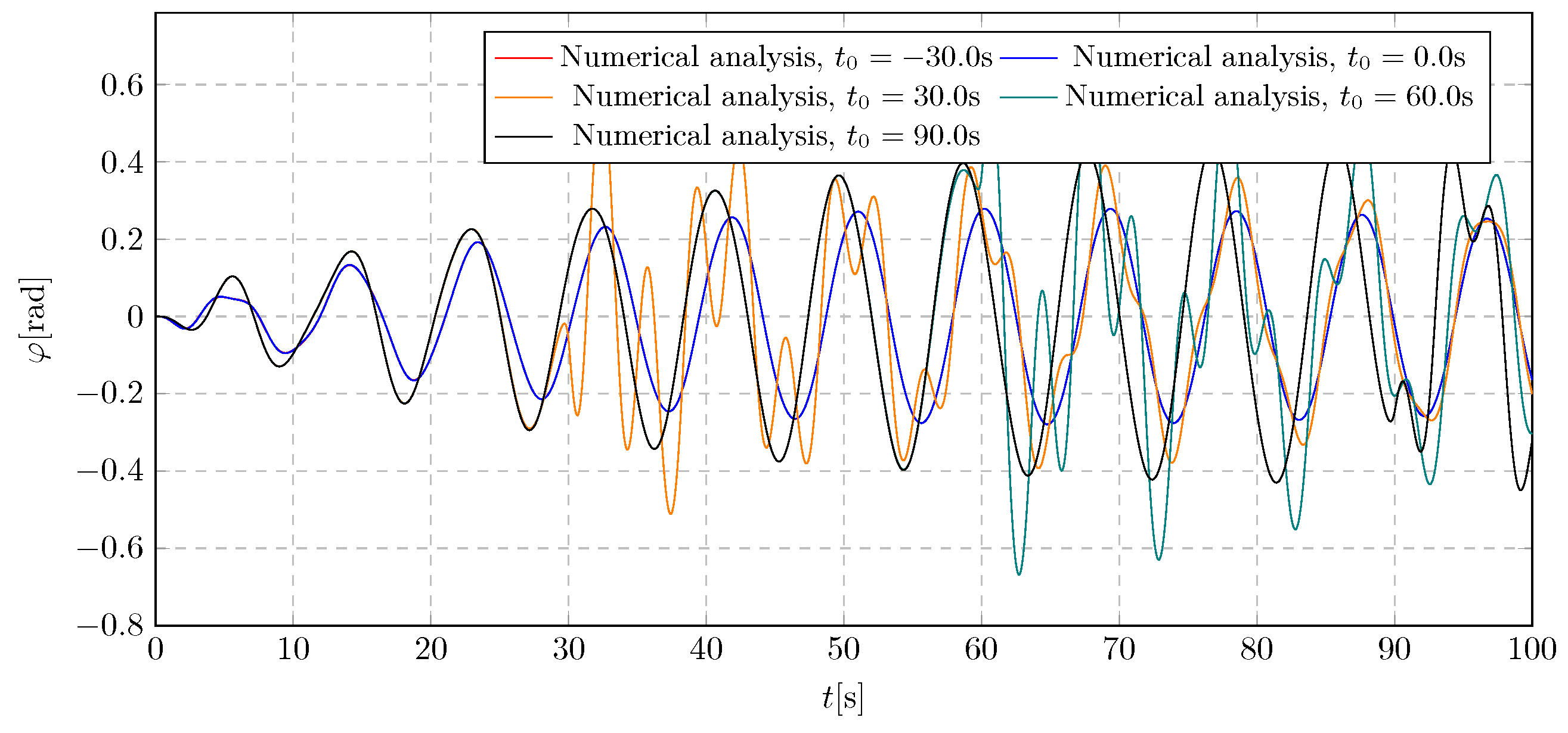
The analysis of the damping activation time was performed using a new damping coefficient value, determined based on the results from the previous section. The simulation outcomes are presented as displacement graphs in Figure 13 and Figure 15 as well as frequency spectra in Figure 14 and Figure 16. The approach to selecting the appropriate activation time was consistent with the methodology used in the damping coefficient analysis. Simulations were performed for activation times ranging from −30 s to 90 s. The objective was to investigate the impact of activation time on system dynamics, with a focus on both transient amplitudes during damping mass flow and steady-state behaviour.

Based on the simulation results shown in Figure 13, the influence of the activation time $t_0$ on the overall vibration characteristics of the system can be assessed. Initially, the activation of mass flow had a minimal effect on the trolley displacement; however, a stabilising behaviour was observed shortly afterwards. It was noted that earlier activation of the damping mechanism effectively limits the propagation of rapid resonance. The extreme displacement values recorded during the simulation were −6.86 m and 6.79 m.

Figure 13. Trolley displacement for various damping activation time.

Figure 13. Trolley displacement for various damping activation time.

Figure 14. Frequency spectra of trolley displacement for various damping activation time.

Figure 14. Frequency spectra of trolley displacement for various damping activation time.

The frequency characteristics shown in Figure 14 were used to evaluate the influence of the activation time $t_0$ on the generalised amplitude levels, with maximum values indicated for each spectrum. The spectra reveal that the excitation frequency primarily induces the dominant amplitudes Furthermore, it was observed that early or immediate activation of damping yielded identical results. In contrast, delayed activation led to higher overall amplitude levels. The maximum amplitude value recorded for the latest activation time of 90 s was 4.82 m.

Figure 15. Pendulum angular displacement for various damping activation time.

Figure 15. Pendulum angular displacement for various damping activation time.

Simulation results illustrating the pendulum’s angular displacement for various damping activation times are presented in Figure 15. In this case, a faster stabilisation of vibrations was observed compared to the trolley displacement results in Figure 13. Additionally, it was noted that regardless of the damping activation time, the system successfully eliminated resonance. Temporary amplitude growth was observed upon activation of the damping mass flow. The minimum and maximum angular displacement values were −0.67 rad and 0.65 rad, respectively.

Figure 16. Frequency spectra of pendulum angular displacement for various damping activation times.

Figure 16. Frequency spectra of pendulum angular displacement for various damping activation times.

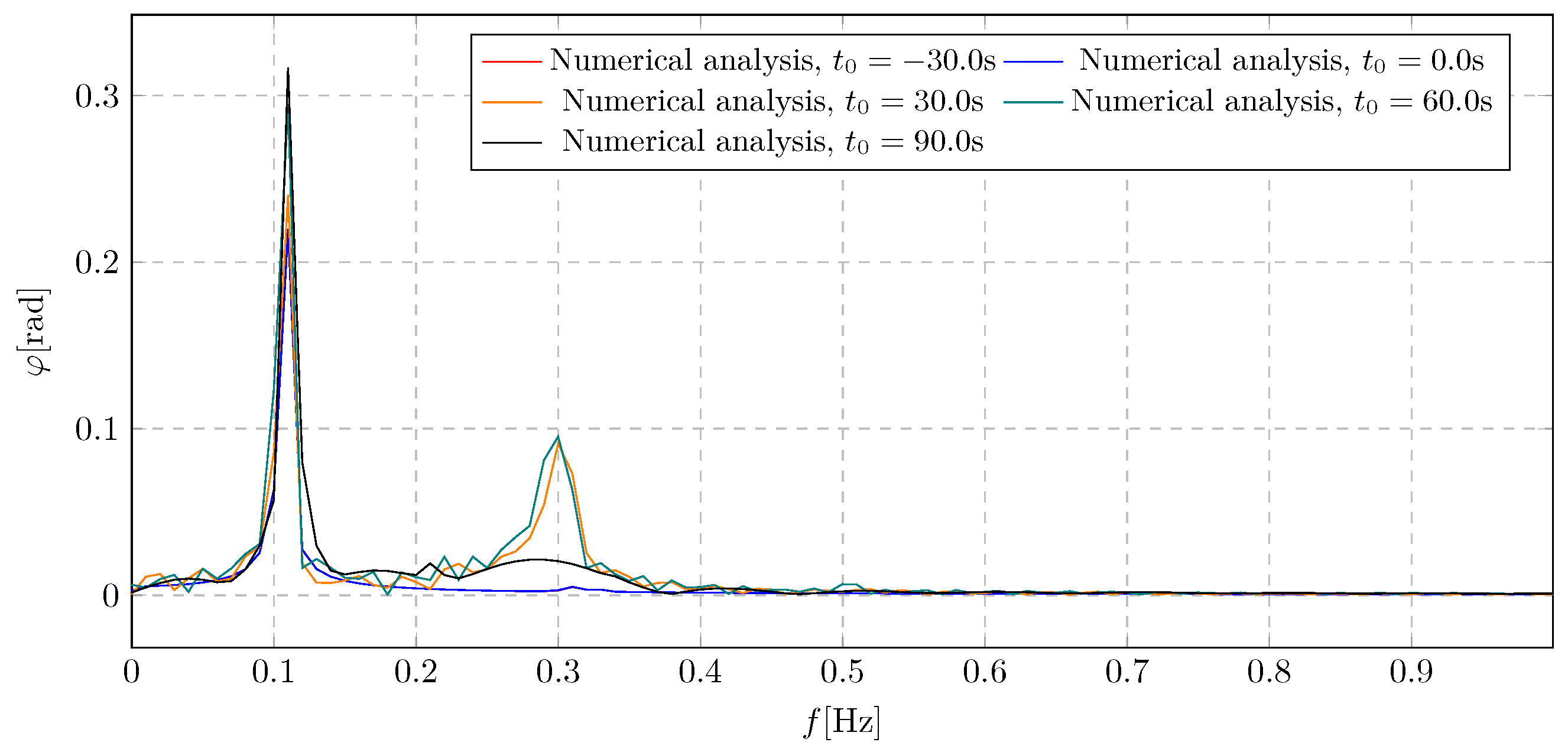
The frequency spectra presented in Figure 16 illustrate the amplitude distribution of the pendulum’s angular displacement across various damping activation times. Two distinct amplitude components were identified. The first corresponds directly to the excitation frequency and confirms that early damping activation significantly reduces the overall amplitude level. The second harmonic arises from the initiation of the damping mass flow. Notably, delayed activation results in a high transient amplitude, which could adversely affect system performance due to excessive temporary deflections. The maximum average amplitude value recorded was 0.32 rad.

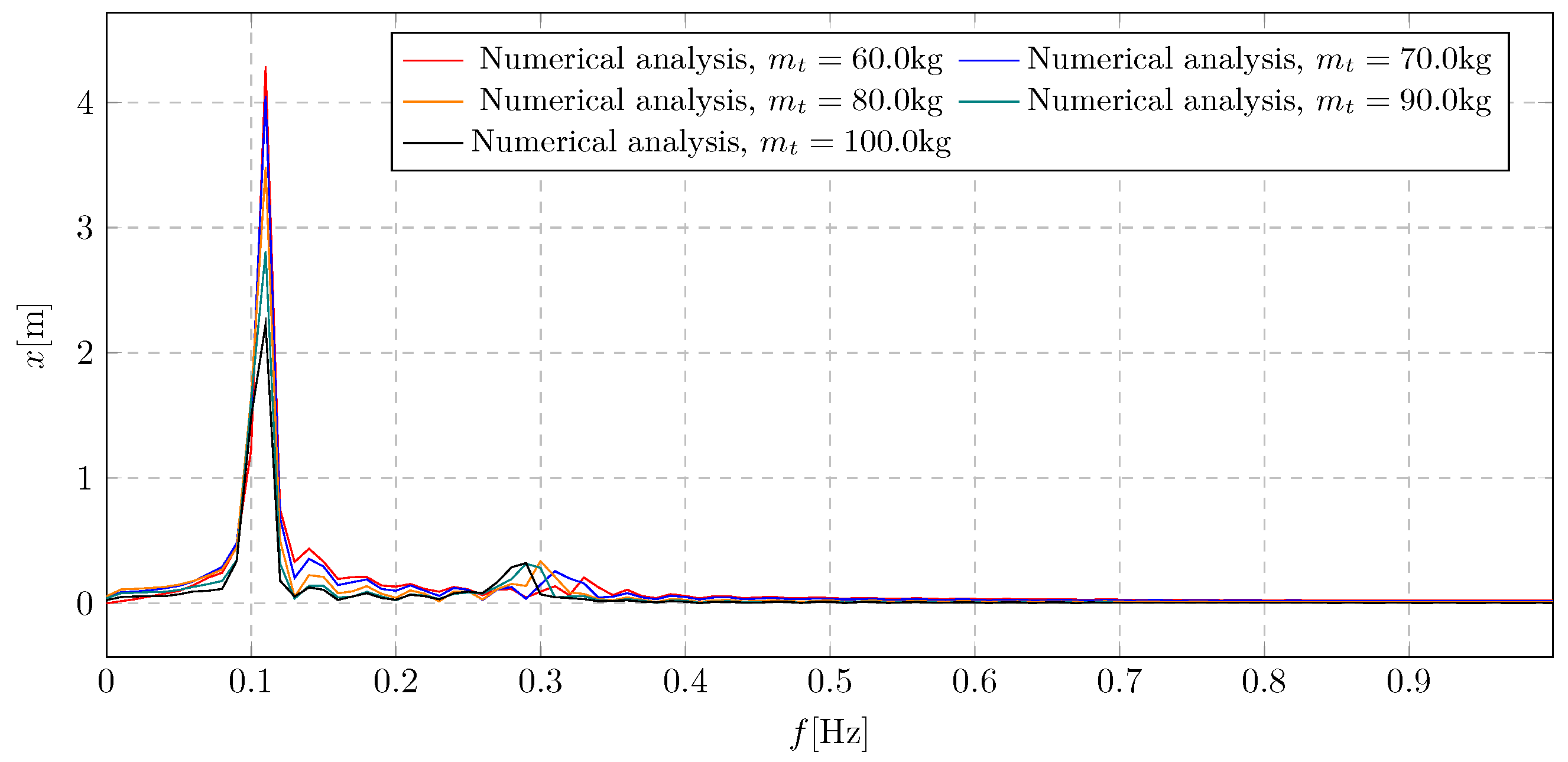
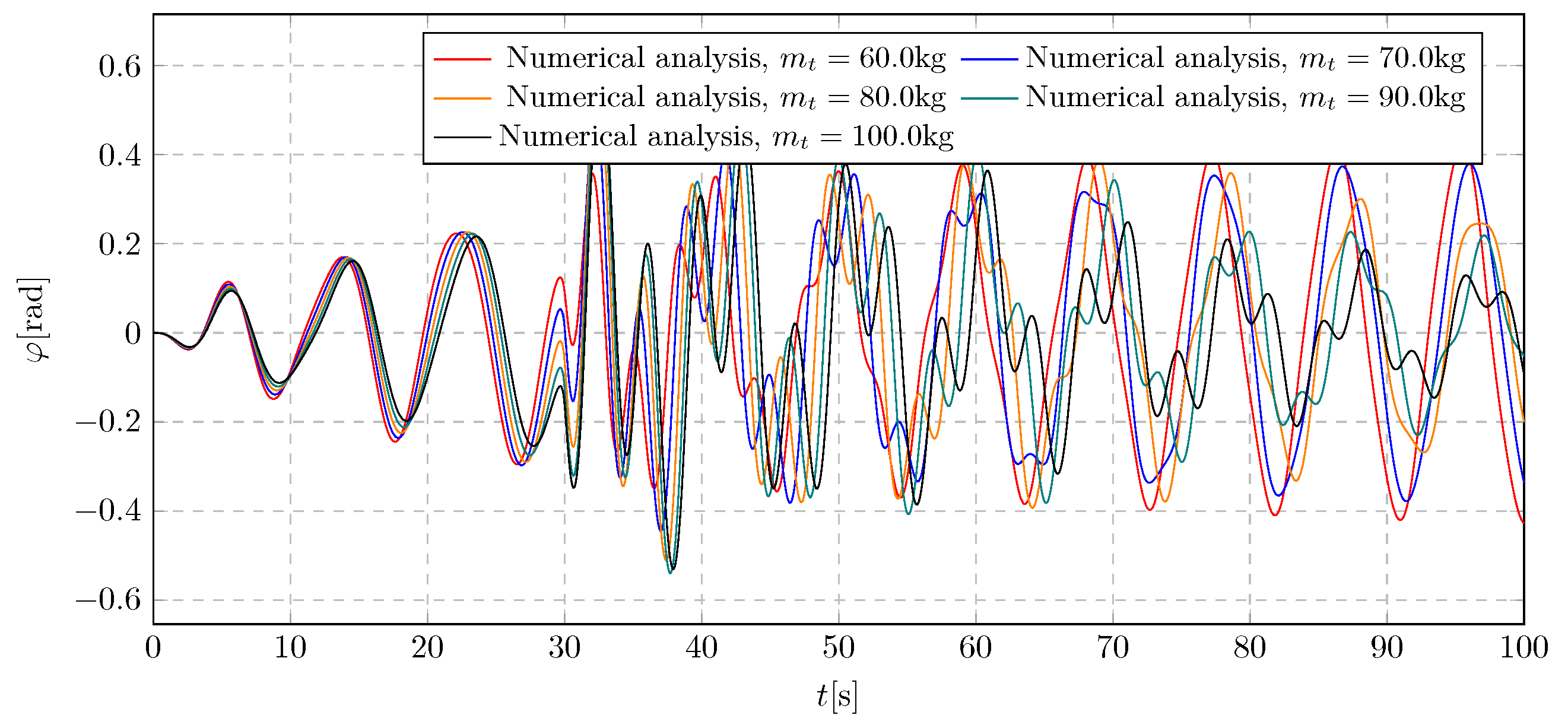
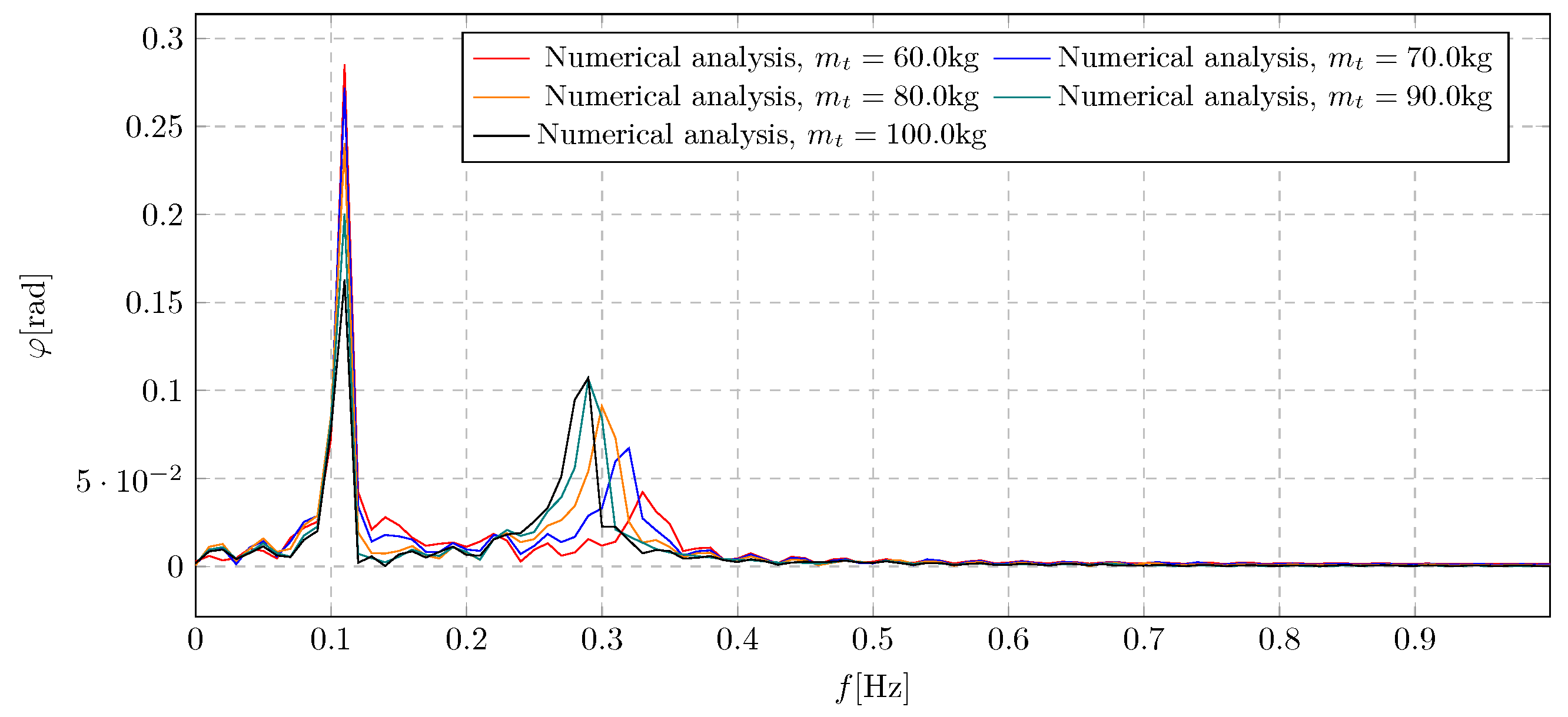
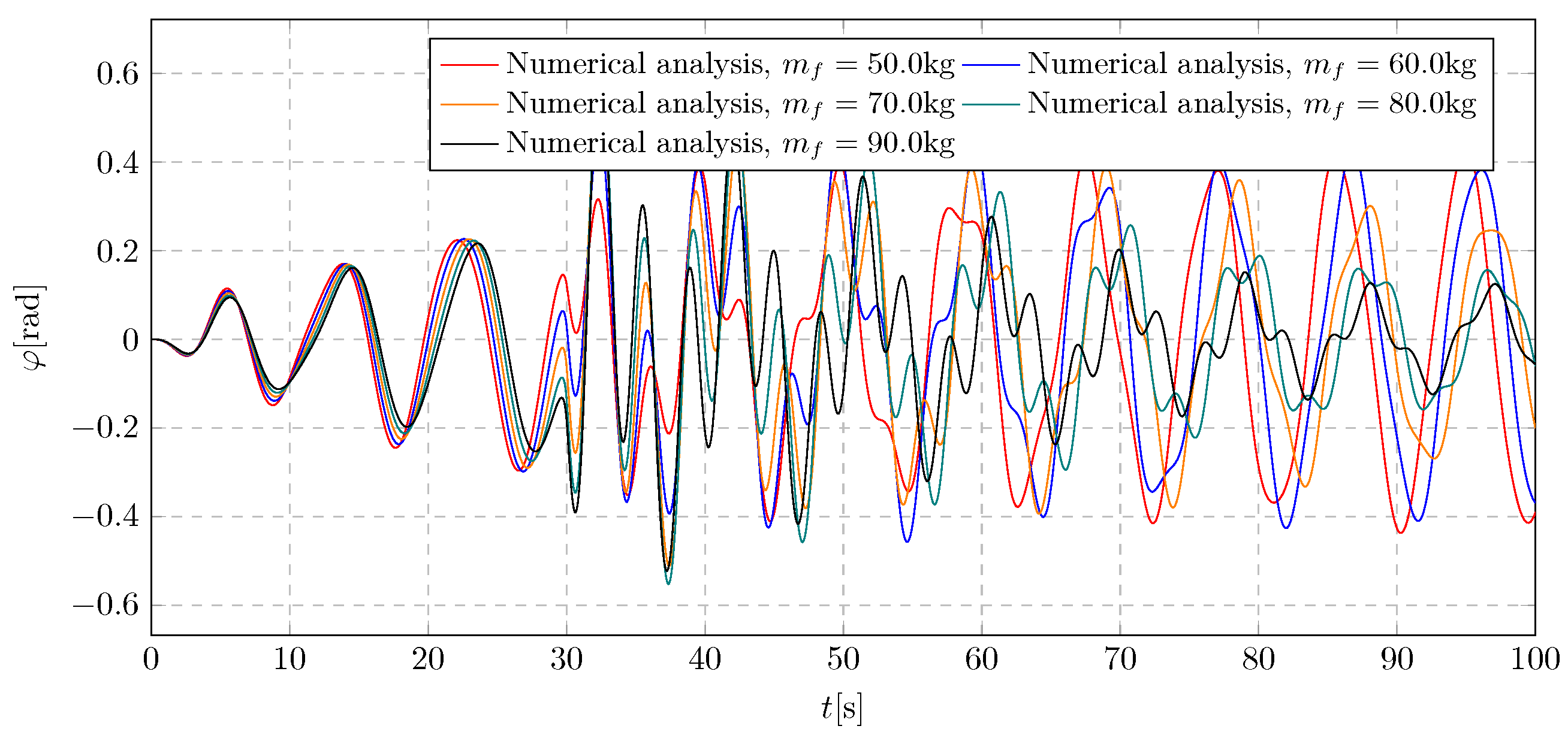
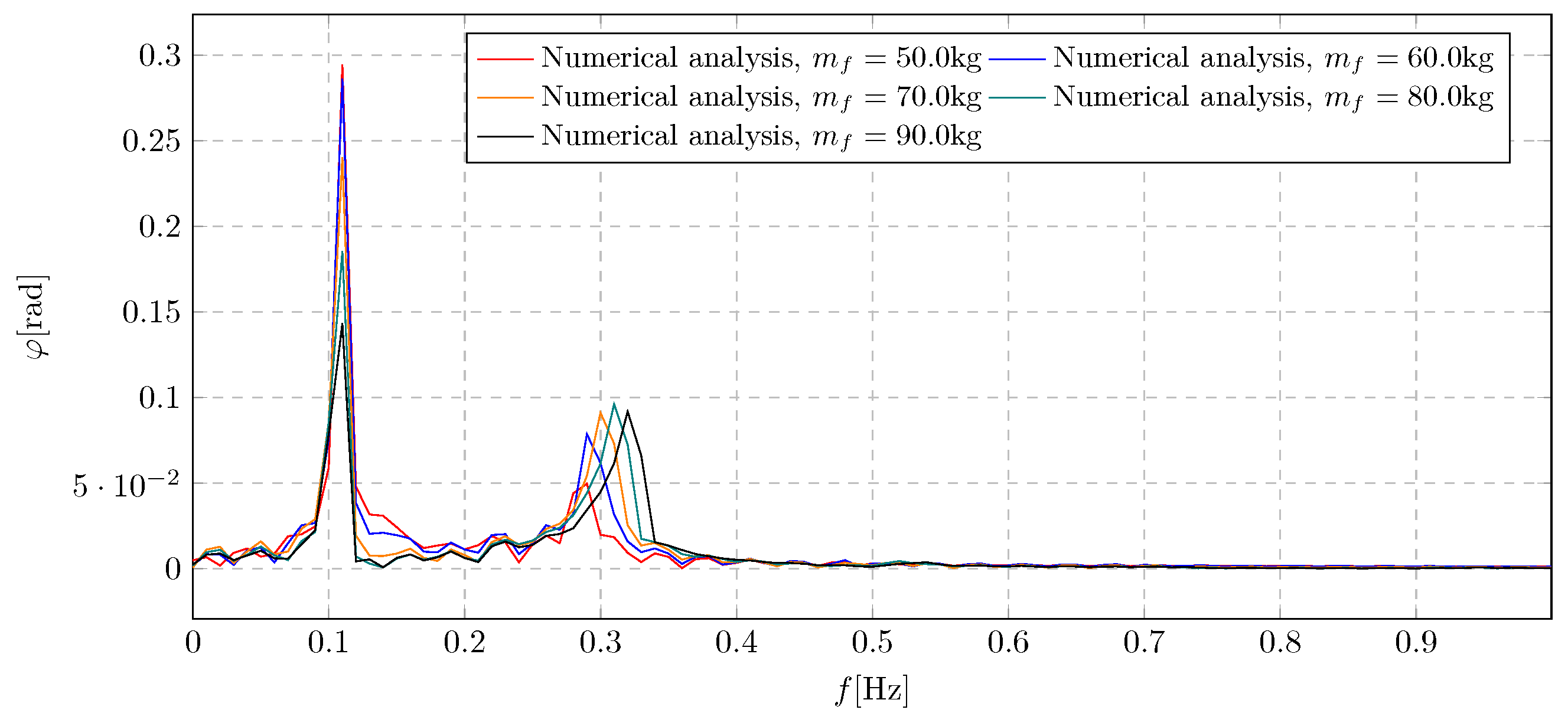
6. Simulation Results—Investigation of Trolley Mass Influence

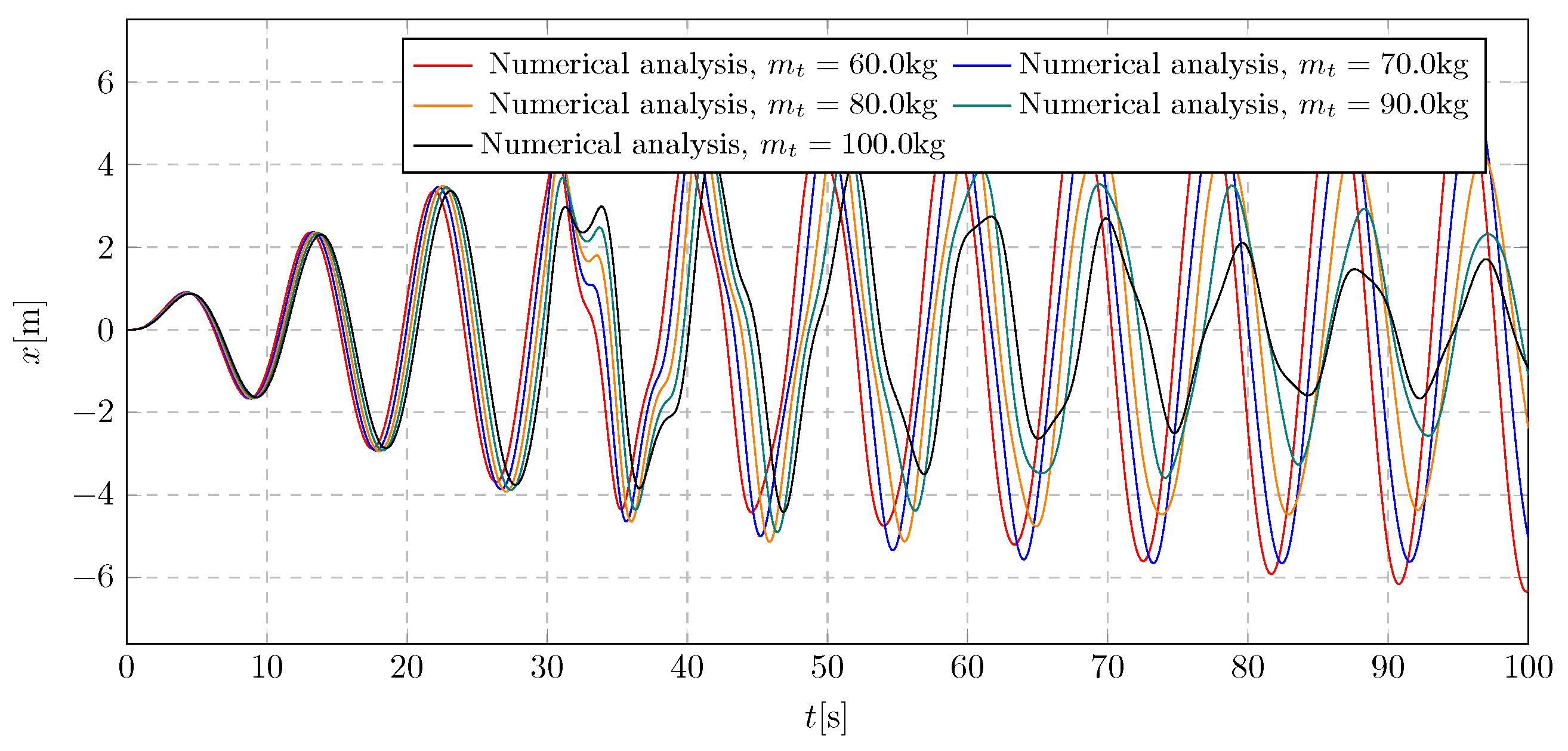
This section investigates the influence of the trolley mass on the general characteristics of the system’s amplitudes. The simulation outcomes are presented as displacement graphs in Figure 17 and Figure 19, along with the corresponding frequency spectra in Figure 18 and Figure 20. The considered values of the trolley mass range from 60 kg to 100 kg. Within this range, five representative values were selected for simulation purposes.

Figure 17. Trolley displacement for various trolley initial masses.

Figure 17. Trolley displacement for various trolley initial masses.

Figure 17 illustrates the impact of the b parameter on the trolley displacement. It can be observed that an insufficient initial mass of the trolley reduces the damping effectiveness of the vibration eliminator once the liquid flow is initiated. Extreme displacement amplitude values range from −6.34 m to 6.26 m.

Figure 18. Frequency spectra of trolley displacement for various trolley initial masses.

Figure 18. Frequency spectra of trolley displacement for various trolley initial masses.

In the frequency domain plot (Figure 18), a significant influence of the $m_t$ parameter on the system vibrations is evident. Specifically, the overall level of trolley vibration amplitudes diminishes for increasing trolley mass values, while the contribution of the frequency component associated with damping activation becomes more pronounced. The highest amplitude level was recorded for the lowest considered trolley mass of 60 kg, with a value of 4.29 m.

Figure 19. Pendulum angular displacement for various trolley initial masses.

Figure 19. Pendulum angular displacement for various trolley initial masses.

Figure 19 shows the pendulum’s angular displacement under harmonic excitation for different mass ratios of the trolley and pendulum. It is evident that as the trolley mass increases, the instantaneous amplitude surge (peak) due to damping activation also becomes more prominent. Moreover, it was observed that achieving a specific final pendulum mass does not guarantee the suppression of trolley resonance. The pendulum deflections range from −0.54 rad to 0.6 rad.

Figure 20. Frequency spectra of pendulum angular displacement for various initial trolley masses.

Figure 20. Frequency spectra of pendulum angular displacement for various initial trolley masses.

The frequency spectra in Figure 20 show the shift in harmonic components resulting from the activation of the damping mass flow, which depends on the initial trolley mass, $m_t$. A lower trolley mass results in vibrations with lower amplitude and higher frequency during damping activation. Additionally, a threshold was identified beyond which further increases in the trolley’s initial mass no longer contribute to elevated amplitude levels induced by damping activation. The maximum generalised amplitude of the pendulum oscillations reached 0.29 rad.

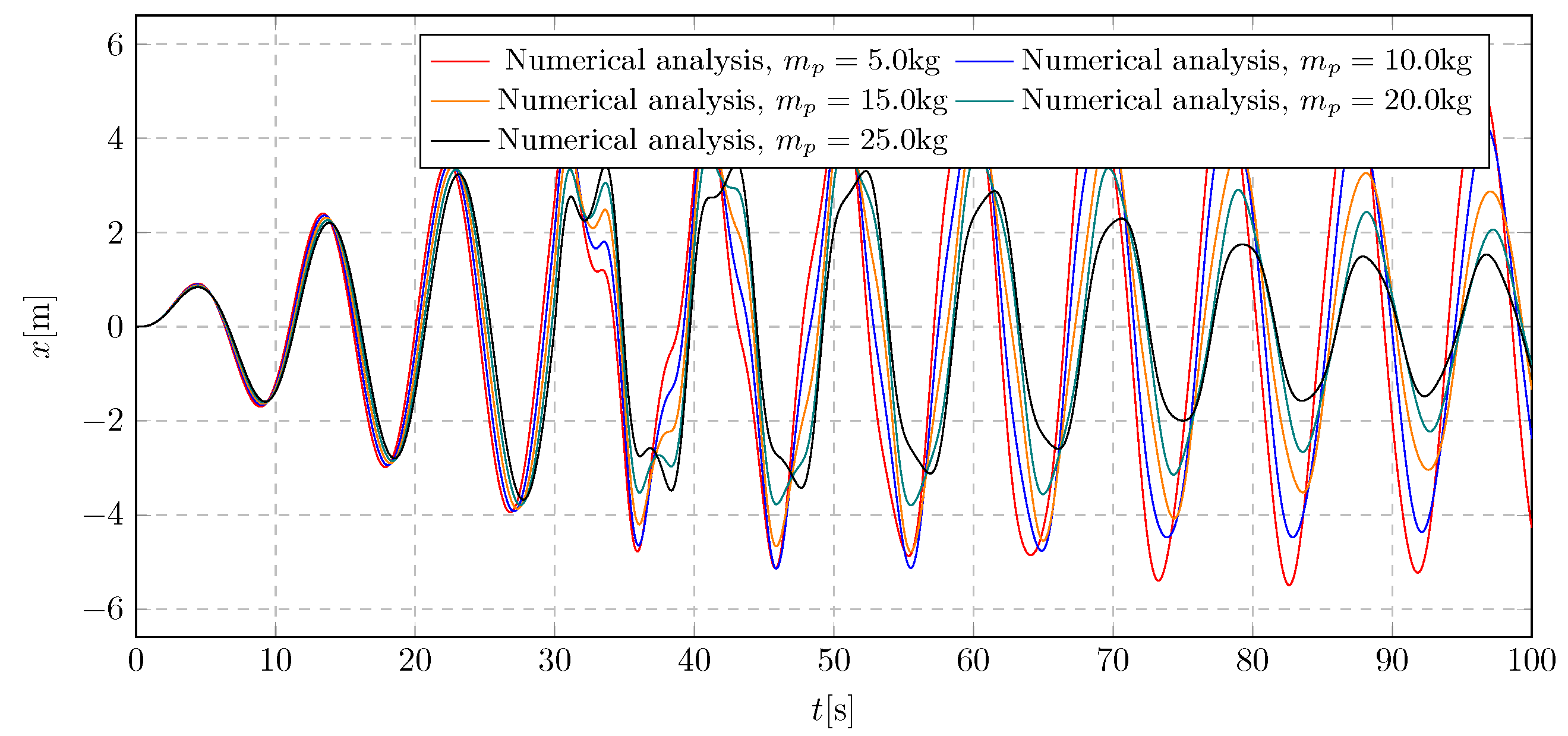
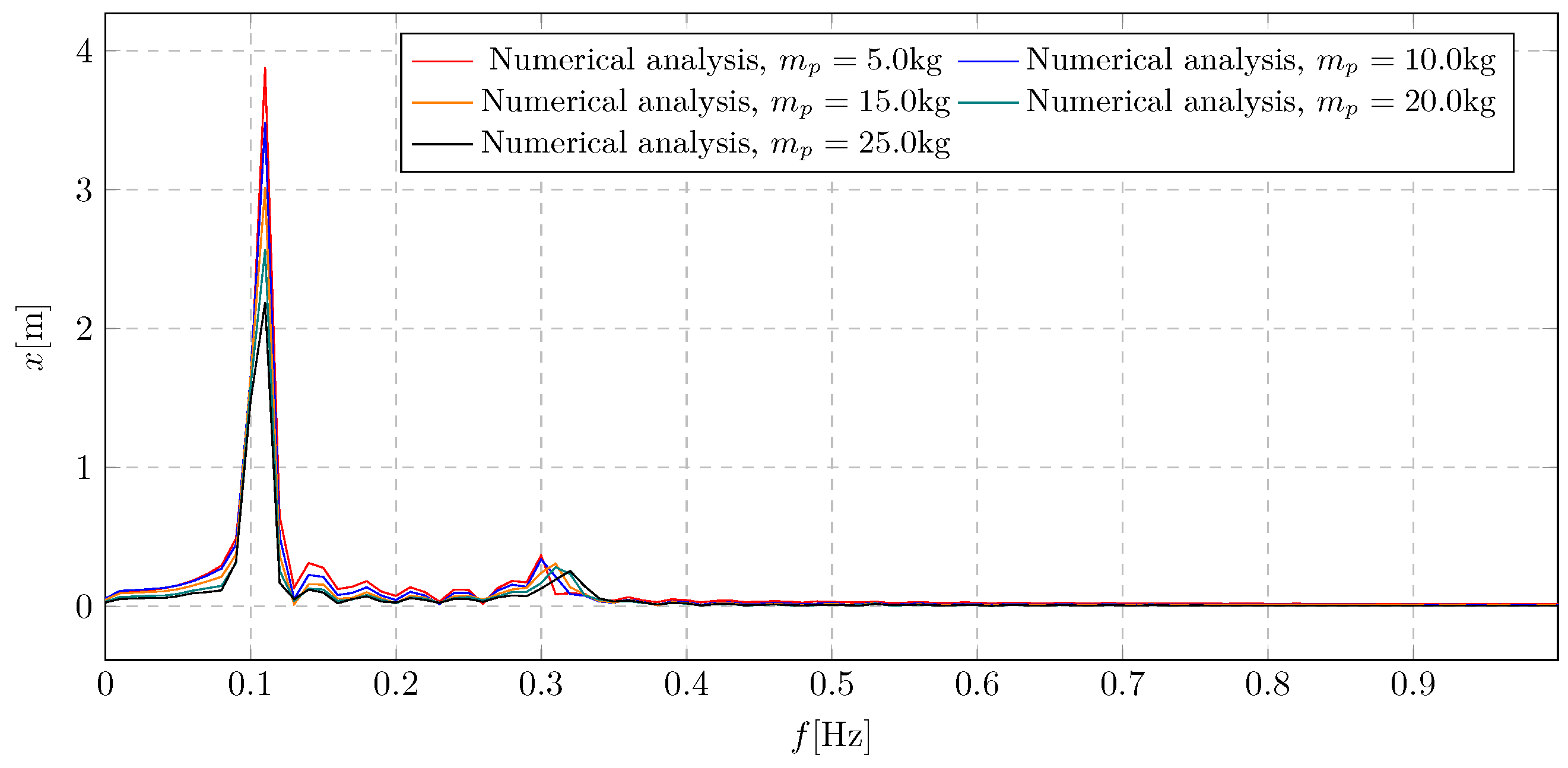
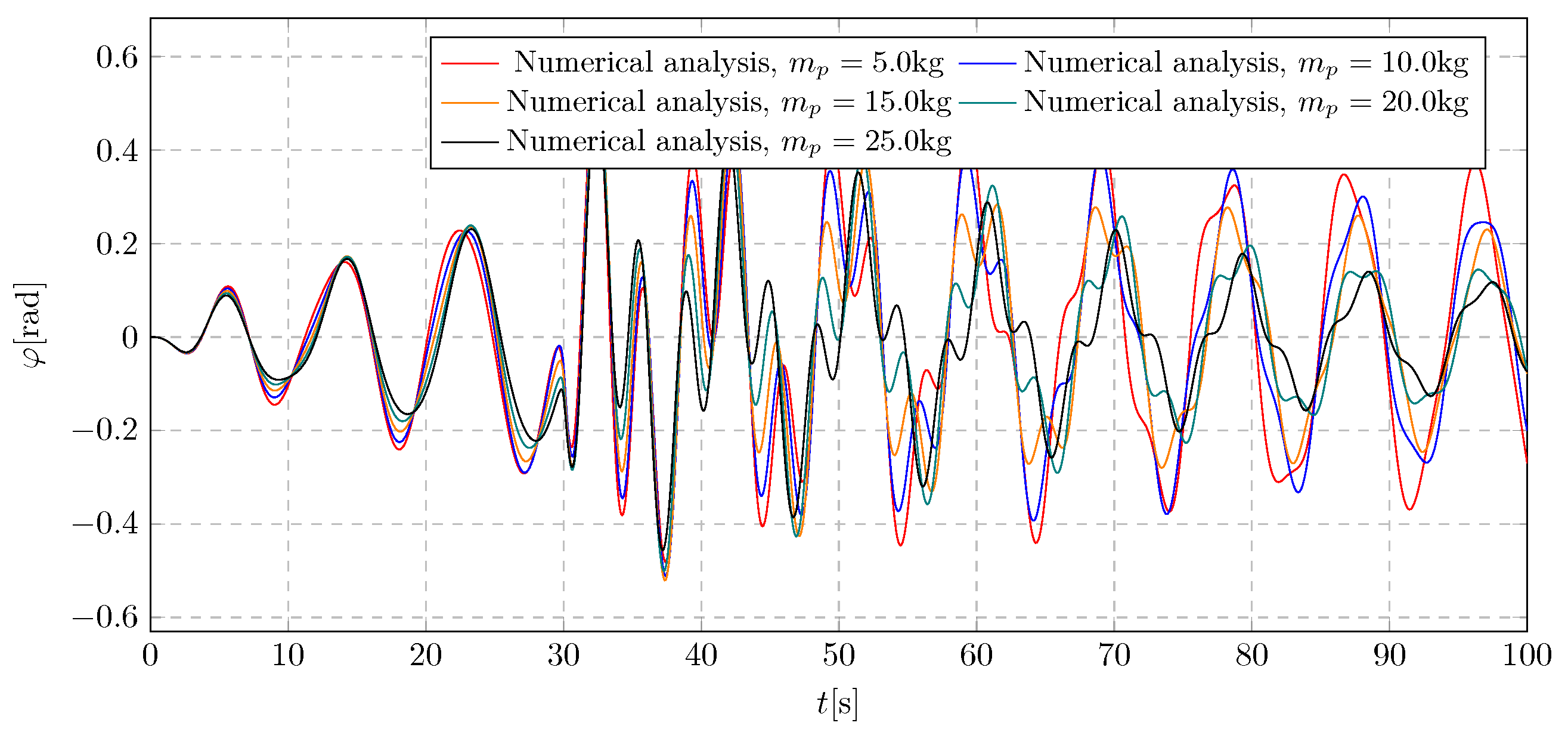
7. Simulation Results—Investigation of Pendulum Mass Influence

The results of the analysis of the pendulum’s initial mass on the system’s dynamics are presented as displacement graphs in Figure 21 and Figure 23, as well as frequency spectra in Figure 22 and Figure 24. Simulations were performed for values ranging from 5 kg to 25 kg. The primary purpose of the simulation was to determine the appropriate mass of the pendulum to eliminate potential rotation due to high harmonic excitation.

Figure 21. Trolley displacement for various pendulum initial masses.

Figure 21. Trolley displacement for various pendulum initial masses.

The graph showing the changes in the trolley’s position in relation to the pendulum’s initial mass is shown in Figure 21. Analysis of this graph allows for the observation of the limit value of the tested parameter at which the tested vibration eliminator is unable to compensate for the increase in amplitude, causing vibration modulation. The maximum amplitudes achieved range from m to 5.51 m.

Figure 22. Frequency spectra of trolley displacement for various pendulum initial masses.

Figure 22. Frequency spectra of trolley displacement for various pendulum initial masses.

The frequency spectra of the trolley displacement for different values of the initial mass of the pendulum are shown in Figure 22. The figure presents one dominant component resulting from the applied harmonic excitation and a small additional component resulting from the activation of the liquid flow. The graph illustrates a proportional decrease in the overall amplitude level as the initial mass of the pendulum increases. The maximum overall displacement amplitude of the trolley is 3.88 m.

Figure 23. Pendulum angular displacement for various pendulum initial masses.

Figure 23. Pendulum angular displacement for various pendulum initial masses.

An analysis of graphs in Figure 23, which shows the nature of changes in the pendulum’s angular displacement depending on the pendulum mass, reveals a characteristic increase in amplitude during the activation of the liquid flow. At first, the rise in amplitude is comparable for all tested initial pendulum masses. The difference in amplitude is visible only at the next swing deflection, where the heavier-mass pendulum achieves lower amplitudes, as expected. The extreme values of the obtained amplitudes range from −0.52 rad to 0.57 rad.

Figure 24. Frequency spectra of pendulum angular displacement for various pendulum initial masses.

Figure 24. Frequency spectra of pendulum angular displacement for various pendulum initial masses.

The obtained frequency spectra are presented in Figure 24. They can be used to read the inverse characteristics of amplitude and frequency changes in vibrations resulting from the activation of mass flow in the case of testing the influence of the trolley’s weight. In this case, it can be observed that as the pendulum mass increases, the amplitude decreases, and the frequency of vibrations resulting from the damper’s activation increases. Additionally, it was noted that there is a limit value for the pendulum mass below which the overall amplitude resulting from the damper’s mass flow does not change (remains constant). The maximum observed amplitude level is 0.26 rad.

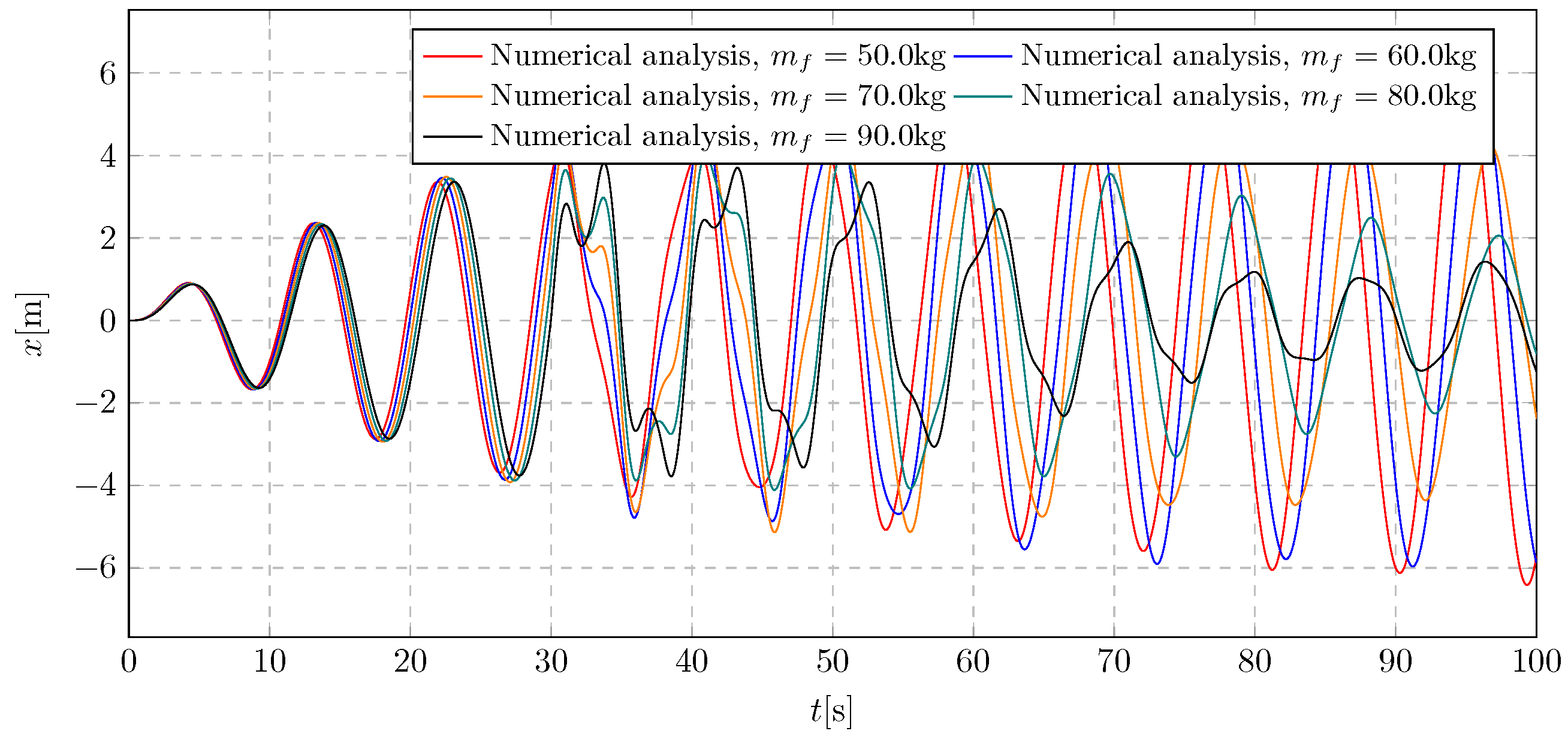
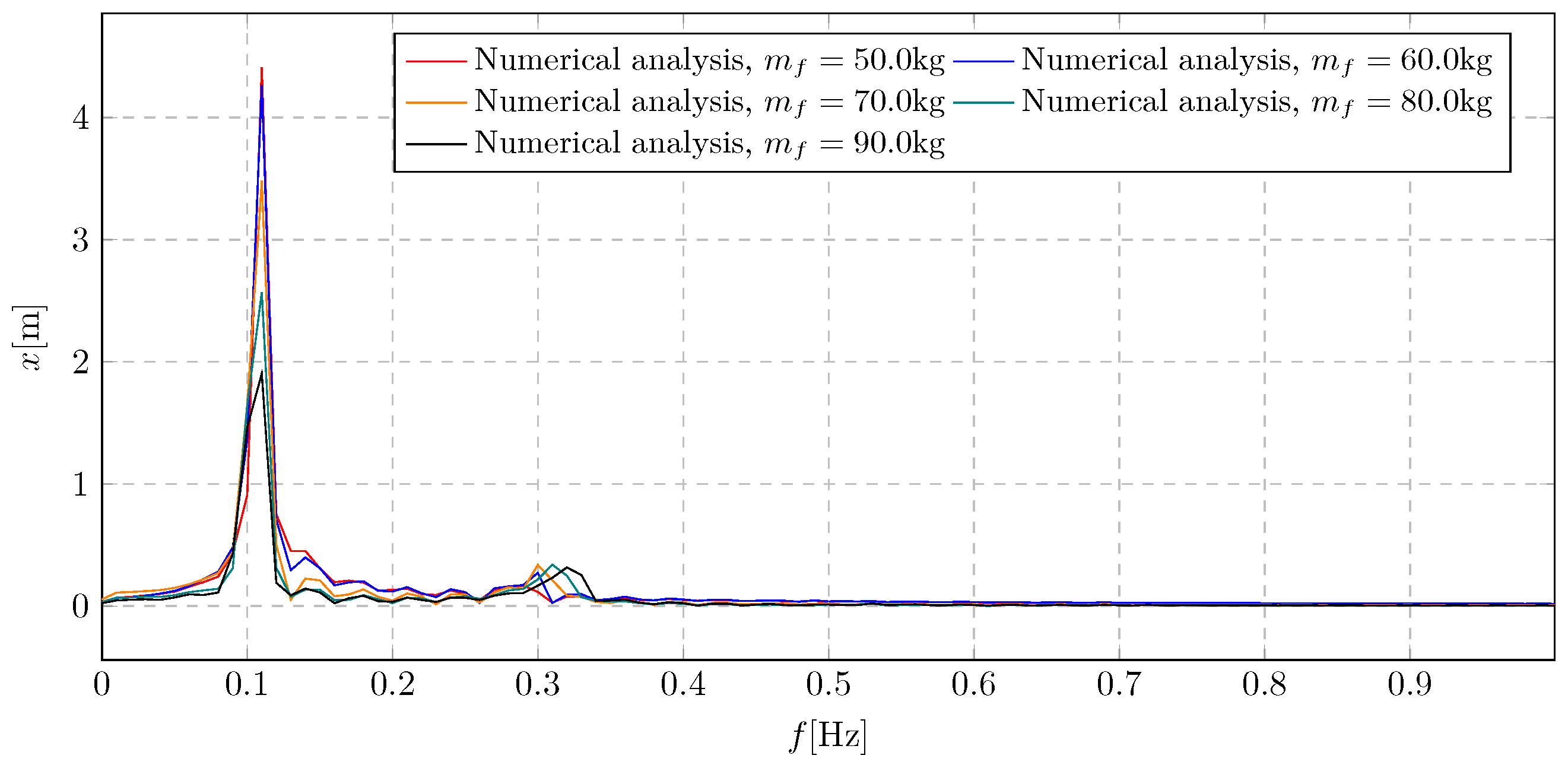
8. Simulation Results—Investigation of Transferred Fluid Mass Influence

The results of the research on the influence of the mass of the transported liquid on the overall dynamics of the system are presented in both the time domain (displacements in Figure 25 and Figure 27) and the frequency domain (spectra in Figure 26 and Figure 28). The presented results were obtained during the simulation for the parameter ranging from 50 kg to 90 kg. The primary purpose of the simulation was to investigate the impact of the amount of liquid poured on damping efficiency, specifically examining the amplitude values during both transient and steady-state vibrations.

Figure 25. Trolley displacement for various amounts of transferred fluid mass.

Figure 25. Trolley displacement for various amounts of transferred fluid mass.

The simulations carried out present the influence of the mass of the transferred liquid $m_f$ on the general level of trolley displacement amplitudes. Based on the presented results, it can be concluded that the appropriately selected mass of transferred water prevents the development of resonant vibrations of the tested pendulum system. Figure 25 shows the immediate response of the system upon the initiation of water transfer. Furthermore, it can be observed that the predetermined amount of transferred liquid adequately dampens the vibrations, without significant disturbances during the activation of the damper. The maximum and minimum values of the trolley amplitudes are in the range −6.41 m to 6.26 m.

Figure 26. Frequency spectra of trolley displacement for various amount of transferred fluid mass.

Figure 26. Frequency spectra of trolley displacement for various amount of transferred fluid mass.

The frequency spectra presented in Figure 26 show the influence of the transported mass $m_f$ on the overall vibration amplitude level of the system. The results of the spectral analysis are shown in the form of comparative graphs in the frequency domain. It can then be seen that there is a boundary value of the transferred mass below which no significant decrease in amplitudes is observed during resonance. In addition, a negligible effect of liquid transport on the overall level of system amplitudes was observed, as represented by a minor second component in the spectrum. In this case, the maximum overall amplitude level is 4.41 m.

Figure 27. Pendulum angular displacement for various amount of transferred fluid mass.

Figure 27. Pendulum angular displacement for various amount of transferred fluid mass.

Figure 27 shows the influence of the mass of the transferred liquid $m_f$ on changes in the angular displacement of the pendulum. The time courses show a significant impact of the investigated parameter on the pendulum’s dynamics. A limit value was observed at which the deflection at the moment of damping activation reaches its highest value. Additionally, a significant component was observed at higher values of the transferred mass. The extreme values of the trolley amplitudes range from −0.55 rad to 0.61 rad.

Figure 28. Frequency spectra of pendulum angular displacement for various amounts of transferred fluid mass.

Figure 28. Frequency spectra of pendulum angular displacement for various amounts of transferred fluid mass.

The analysis of the frequency spectrum shown in Figure 28 reveals a twofold decrease in the overall amplitude of the pendulum for cases with extreme values of the transferred liquid. Furthermore, by analysing the second amplitude component, it was observed that the amount of transferred mass must be carefully selected due to the non-linear relationship between the amount.

9. Simulation Results—Model Validation

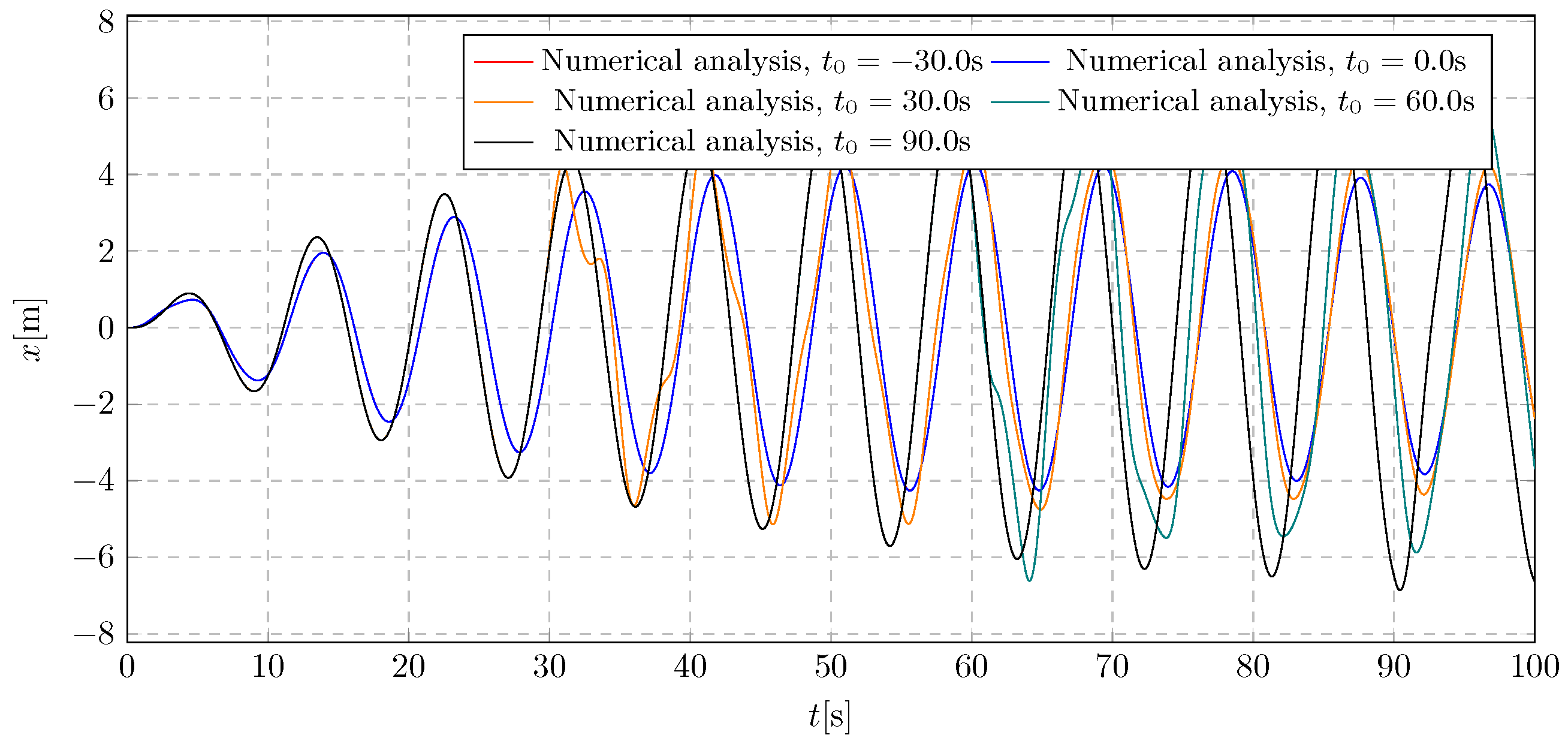
The mathematical model representing the trolley and pendulum system, as well as the variable mass model, has been parameterised. Parameter values were selected empirically based on the results of preliminary calculations. Furthermore, the applied load was estimated according to the inputs acting on real structures. To verify the correct operation of the proposed mathematical model, tests were conducted with parameters adopted for excitation frequencies close to, beyond, and exceeding the trolley’s natural frequency, as well as for damping activation times greater than the simulation duration. In addition, a system without a function simulating mass change with identical parameters was also tested. This system is widely recognised in the literature, which means it can serve as a basis for verifying the correct operation of more complex concepts. The results of both simulations were compared and presented in Figure 29 and Figure 30.

These simulations were performed for the two models considered:

• Basic model, which is a simple pendulum trolley with fixed masses.
• Advanced mode, which considers variable mass and adjustable-length cable.

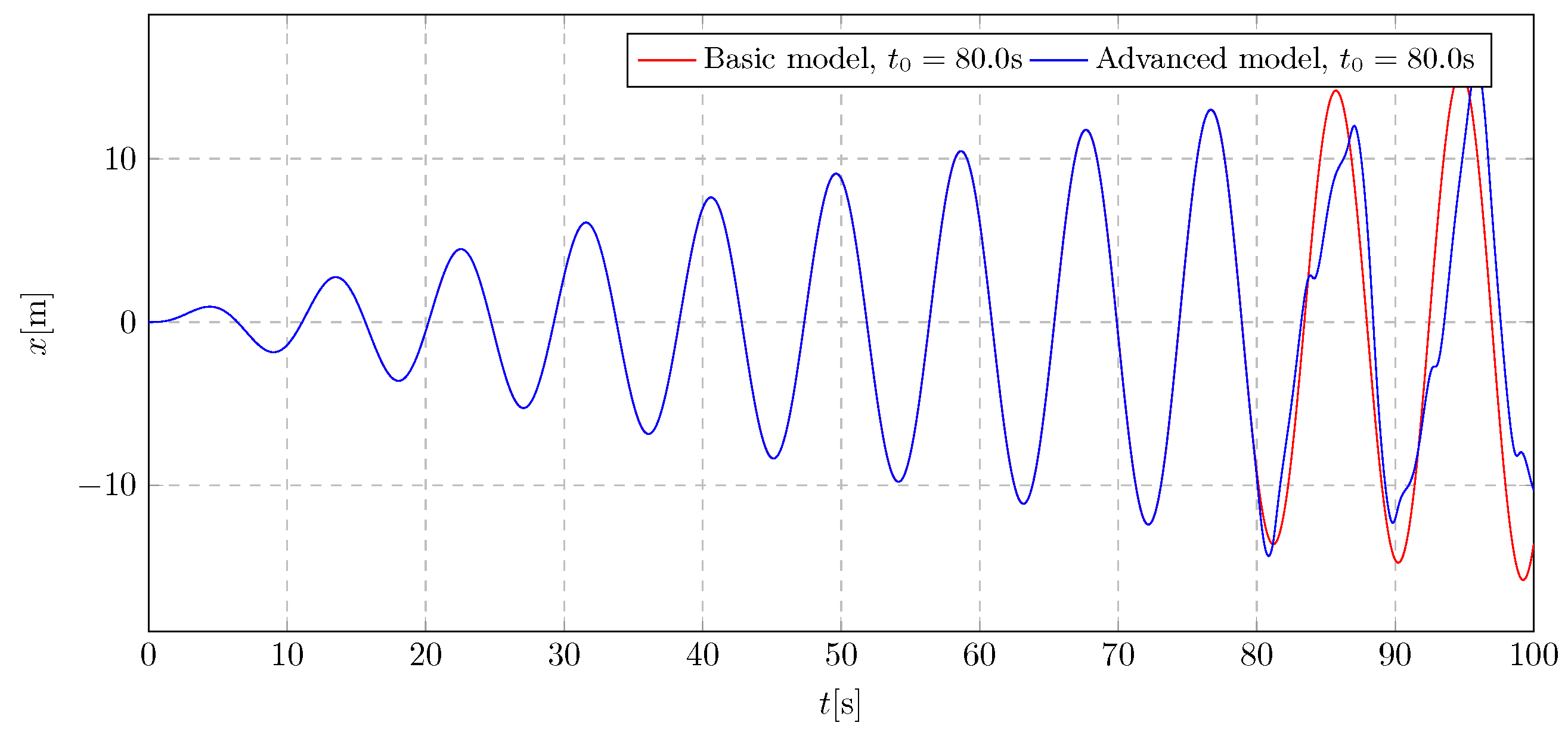
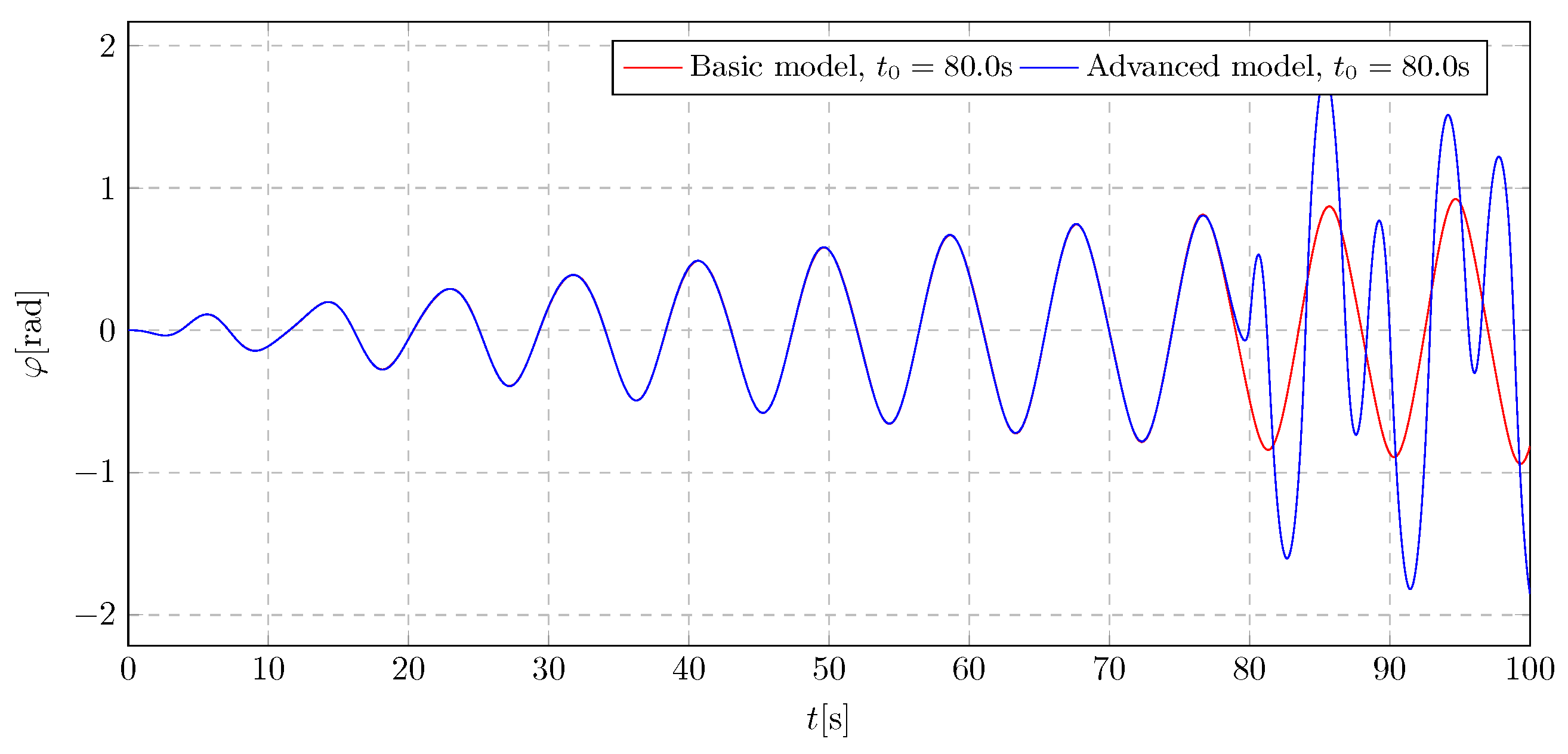
The simulation parameters were selected so that the proposed advanced model physically corresponded to the basic model with fixed parameters. The test results presented in Figure 29 and Figure 30 show full compliance for two different types of excitation. Both models were physically identical up to 80 s (activation time). This consistency was achieved by not activating the damping so that the system behaved as if the vibration eliminator had not been installed. Full compliance was found up to 80 s. Then, after 80 s, the parameters of the advanced model have changed, and differences became apparent, as expected. On this basis, the validity of the proposed methodology was preliminarily assessed before conducting experimental tests. These results confirm the correct operation of the system, enabling further investigation to be conducted and allowing for reliable conclusions to be drawn.

10. Test Stand

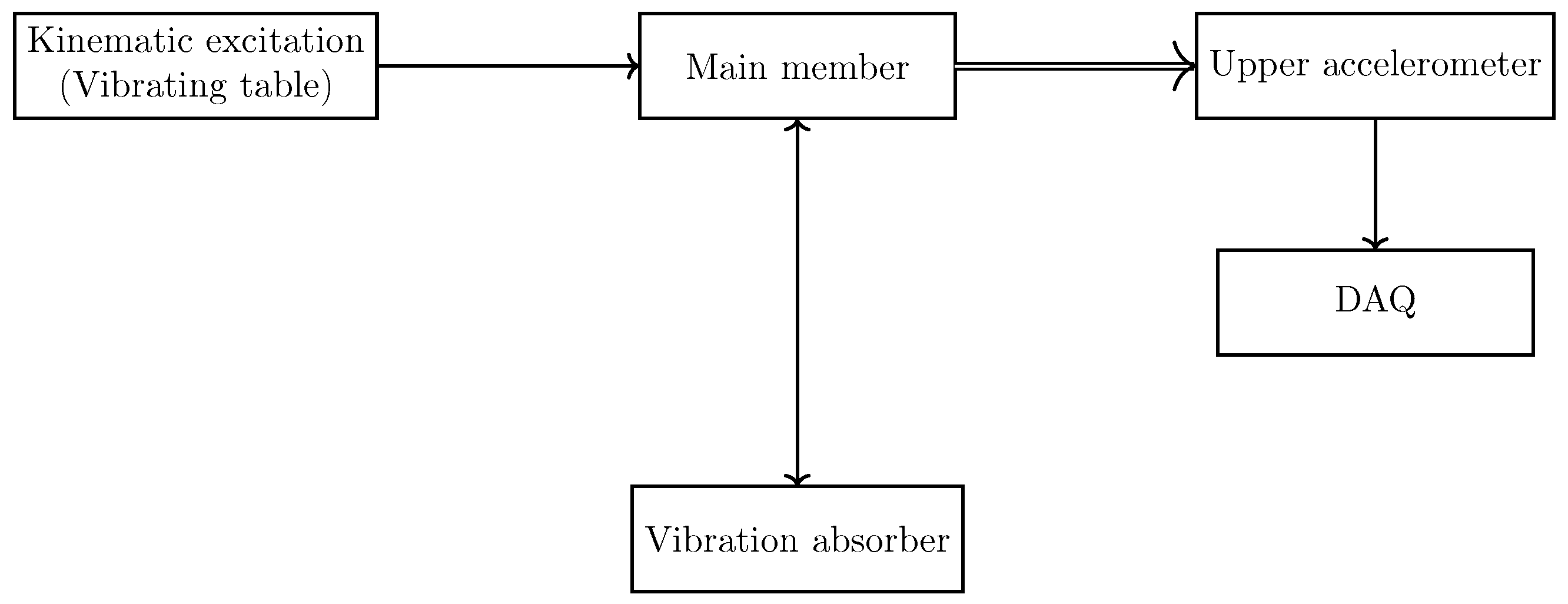
A test stand must be set up to verify the research concept and the results of the computer-simulation-based research. A block diagram of the test stand and the DAQ system is shown in Figure 31.

The test system being tested is located in a movable reference system. The forcing should be considered (treated) as kinematic. A laboratory stand (Figure 32) available at the Faculty of Automotive and Construction Machinery Engineering of the Warsaw University of Technology was used for experimental research. This stand’s principle is based on oscillatory movement. The tested object is connected to a forcing system.

Figure 31. Block diagram of the test stand and the DAQ system.

Figure 31. Block diagram of the test stand and the DAQ system.

Figure 32. Test stand based on oscillatory motion.

Figure 32. Test stand based on oscillatory motion.

The test stand consists of several key elements:

• Induction electric motor—source of mechanical energy.
• Inverter—allows the regulation of the motor’s rotational speed, which translates into the frequency of the applied force.
• Crank shaft enabling the conversion of rotary motion into reciprocating motion.
• Connecting rod—connecting the crank with the carriage.
• Carriage on which the tested object is fixed and moves along linear guides.
• Test stand frame—stable supporting structure on which all elements are fixed, ensuring proper working conditions and safety.
• A flexible frame with a weight attached to a thread is the test object; the weight is attached to the thread, which makes it possible to tune the resonance frequencies.
• The measuring system consists of two accelerometers for measuring vibrations and a signal acquisition conditioning unit.

The test stand’s operation principle is as follows: An electric motor drives the test setup via a drive train. The motor’s rotational speed can be adjusted using an inverter. During operation, vibrations are generated, which are transferred to the pendulum frame. Due to these vibrations, the oscillations of the pendulum inside the frame begin. The pendulum can be lengthened or shortened, which translates into the resonance frequencies of the system under test. The test stand enables the analysis of a vibrating system’s dynamics, including the investigation of the influence of external forces on the oscillations of a pendulum system and the vibration diagnosis of a structure, such as a test object, which consists of a frame and a pendulum attached to it. The vibration level of the frame and pendulum is recorded by accelerometers, which are mounted at appropriate points on the frame. A data recording system processes the signals from the accelerometers. This makes it possible to analyse the intensity and characteristics of the vibrations. The operating parameters of the test object on the test stand can be adjusted. This involves controlling the engine via an inverter, which sets the appropriate rotational speed. This way, the influence of different rotational speeds on the generated vibrations and the pendulum’s behaviour can be examined.

11. Empirical Study on a Physical Model

A total of 25 tests were conducted for five different cases. The free vibrations of the system were investigated, as well as those under forced conditions. The test procedure was as follows. First, the dynamic behaviour of the system was tested for two cases (1 and 2) of free vibrations while it was deflected from its equilibrium. Second, the dynamic behaviour of the system was tested for three cases (3, 4, and 5) under forced conditions.

• Free vibrations when the PTMD is inactive: PTMD was left to rest— lowered so that it rested on the frame, and the main system deflected from its equilibrium position. An initial displacement of 5 cm was applied, and free vibrations were recorded.
• Free vibrations during the adjustable-length cable of the PTMD: PTMD was lifted during free vibrations, while the main system was deflected from its equilibrium position. An initial displacement of 5 cm was applied, and free vibrations were recorded. Damping activation triggering conditions (time threshold): the damping was activated after 4 s of the main system vibration, and the adjustable-length cable of PTMD was shortened until the highest damping was achieved.
• Forced vibrations when the PTMD is inactive: PTMD was lowered so that it rested on the frame, and the main system was harmonically forced at a frequency of 2.065 Hz. Forced vibrations were then recorded.
• Forced vibrations during the adjustable-length cable of the PTMD: PTMD was raised during forced vibration, while the main system was harmonically forced at a frequency of 2.079 Hz. Forced vibrations were recorded. Damping activation triggering conditions (time threshold): the damping was activated after 4 s of the main system vibration, and the adjustable-length cable of PTMD was shortened to obtain the highest damping.
• System vibrations in resonance (the PTMD is inactive): PTMD was lowered so that it rested on the frame, and the main system was harmonically forced at a resonance frequency of 1.809 Hz. Forced vibrations were then recorded.

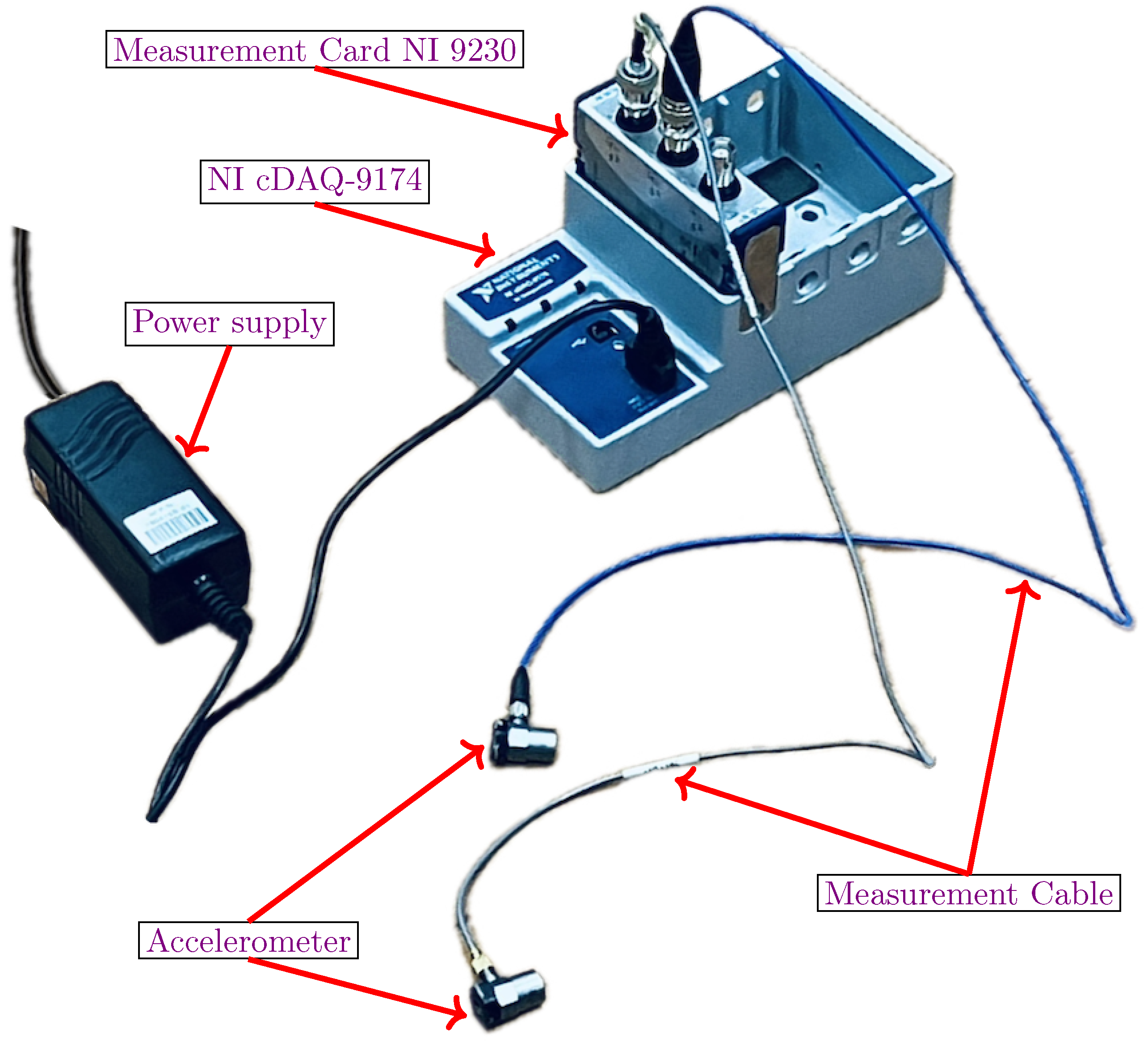
The measurement system was configured and set up as shown in Figure 33. The key acquisition components (Figure 34) are the data acquisition (NI cDAQ-9174) and the measurement card (NI 9230).

It was decided to use a system with an inertial mass based on two flat springs. In accordance with the analysis of linearised equations of motion, the flexible pendulum was replaced with a rope of variable length.

Three test scenarios were considered:

• Tests in which the pendulum length was constant (steady state).
• Tests in which the length of the rope was variable and the tension force (extortion) acted in a plane perpendicular to the direction of motion.
• Tests in which the tension force was applied in the vertical direction.

The influence of the tension force (extortion), the mass of the TMD, and the possibility of active vibration damping by changing the length of the rope in a quasi-static manner were evaluated.

The following results were obtained from the stand tests. The results were obtained during measurements on the physical model with the application of excitation by setting initial conditions. The excitation was introduced by imposing successive measured values of the initial displacement of the structure.

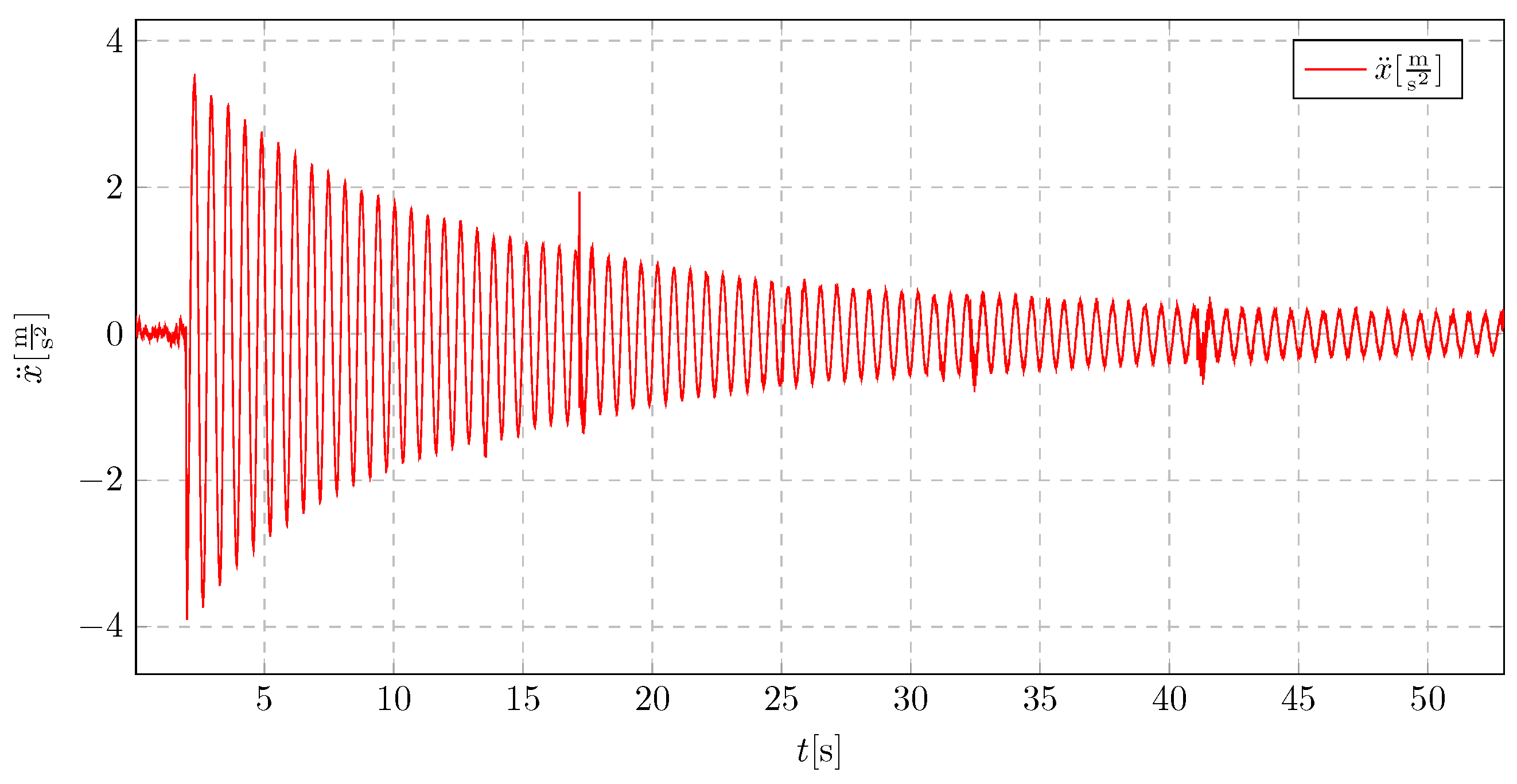
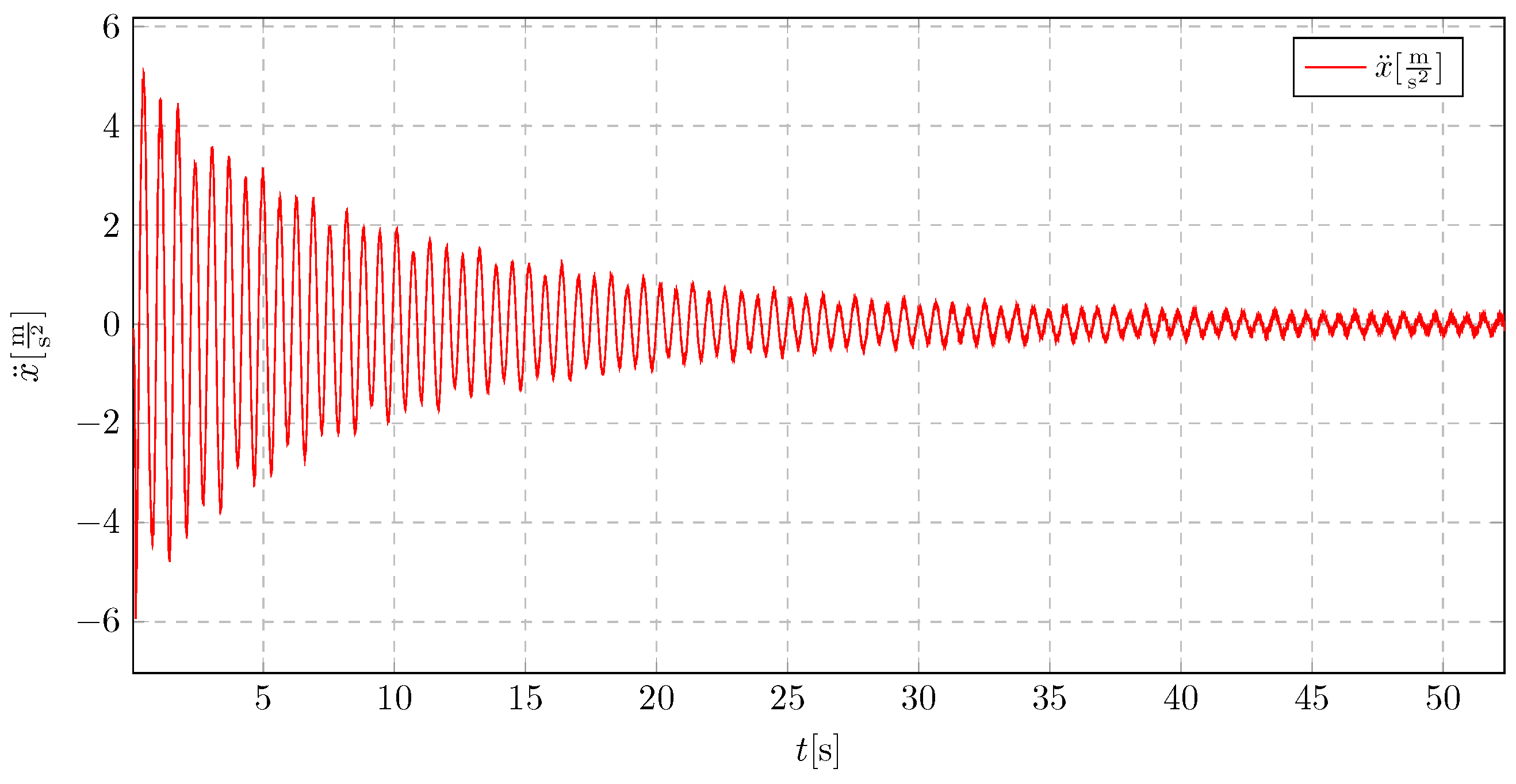
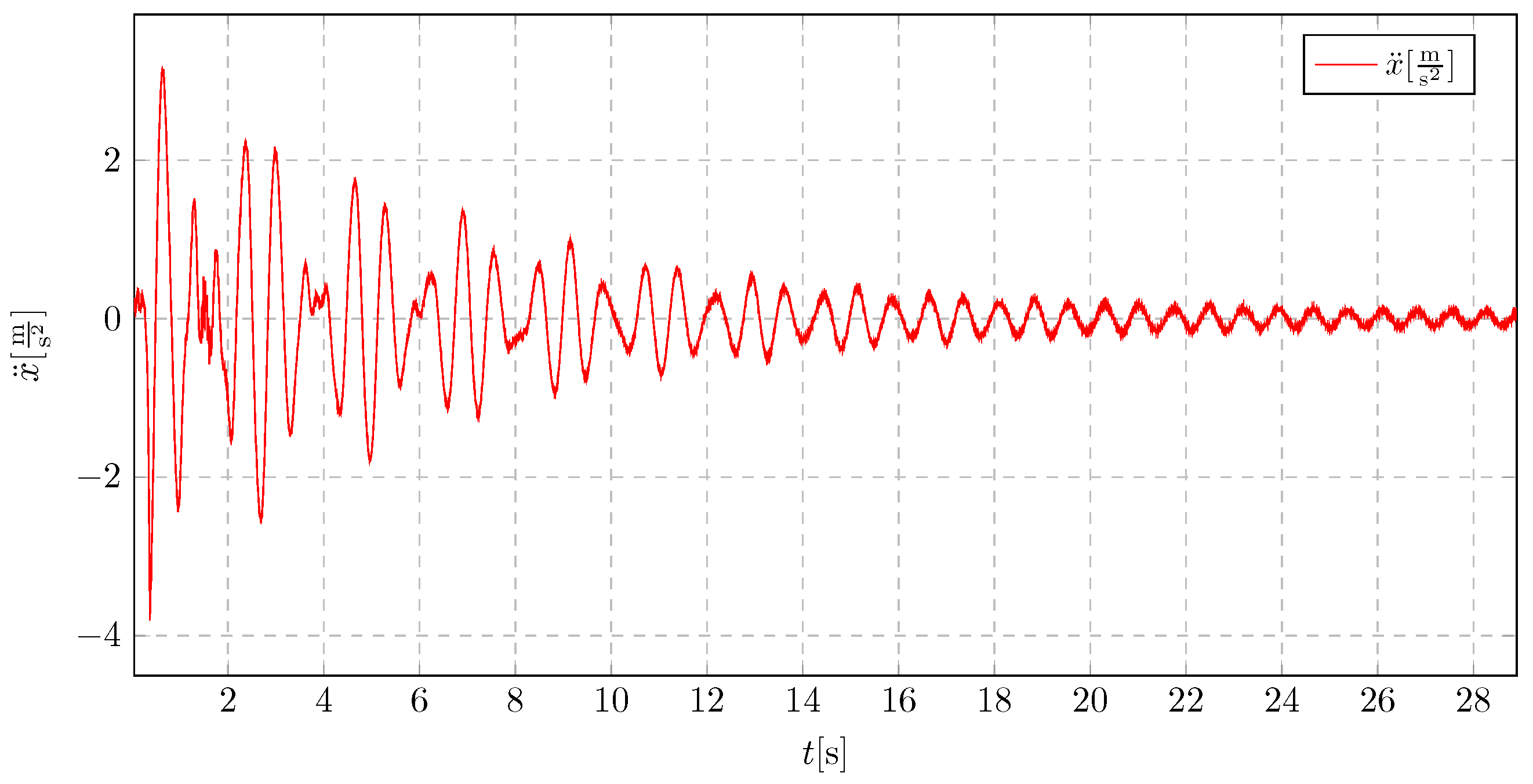
In the absence of a pendulum, the vibrations exhibit characteristics typical of underdamped oscillations, as seen in Figure 35. The acceleration amplitude decreases gradually, leading to prolonged exposure to vibration amplitudes that may be detrimental to the structural integrity.

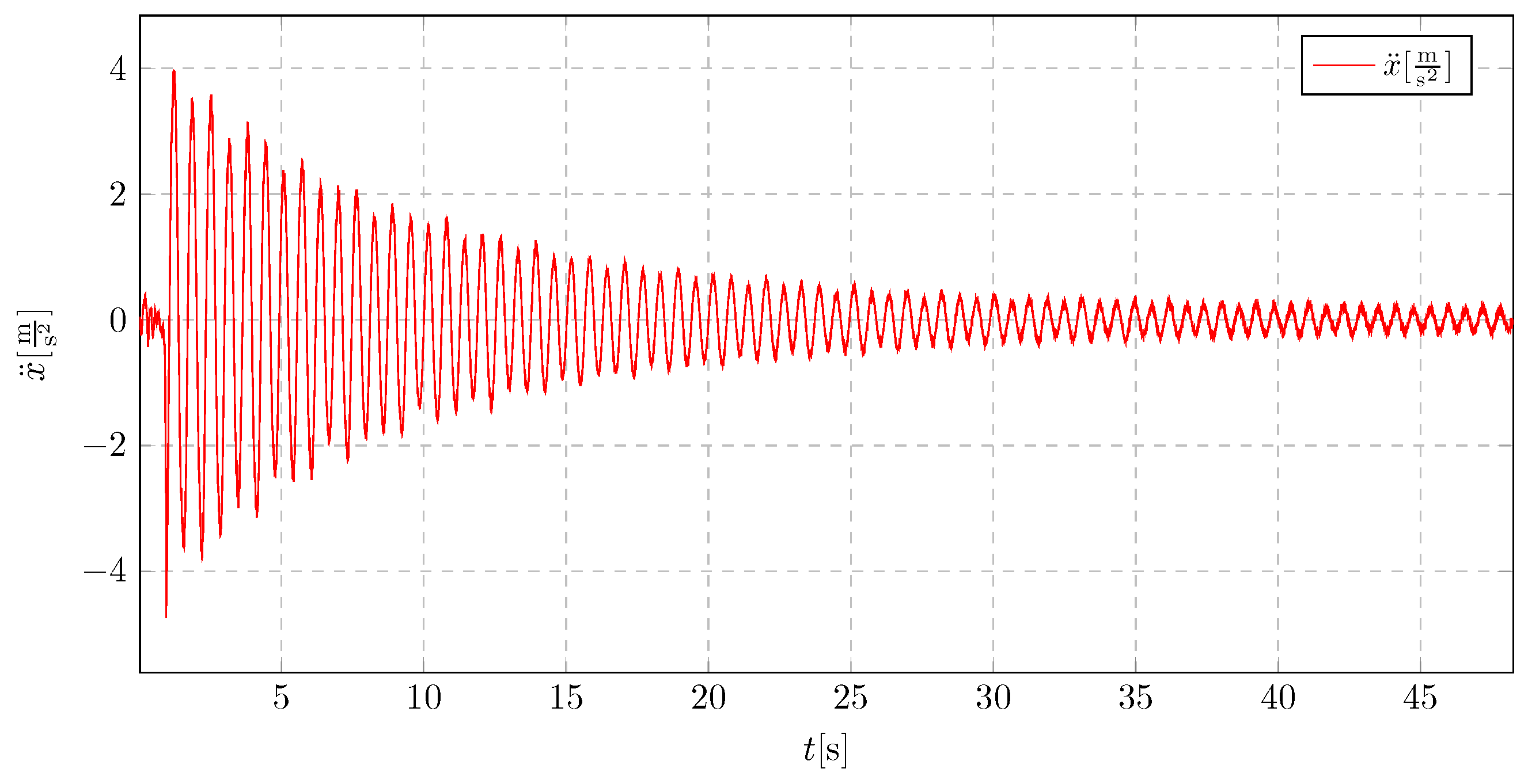
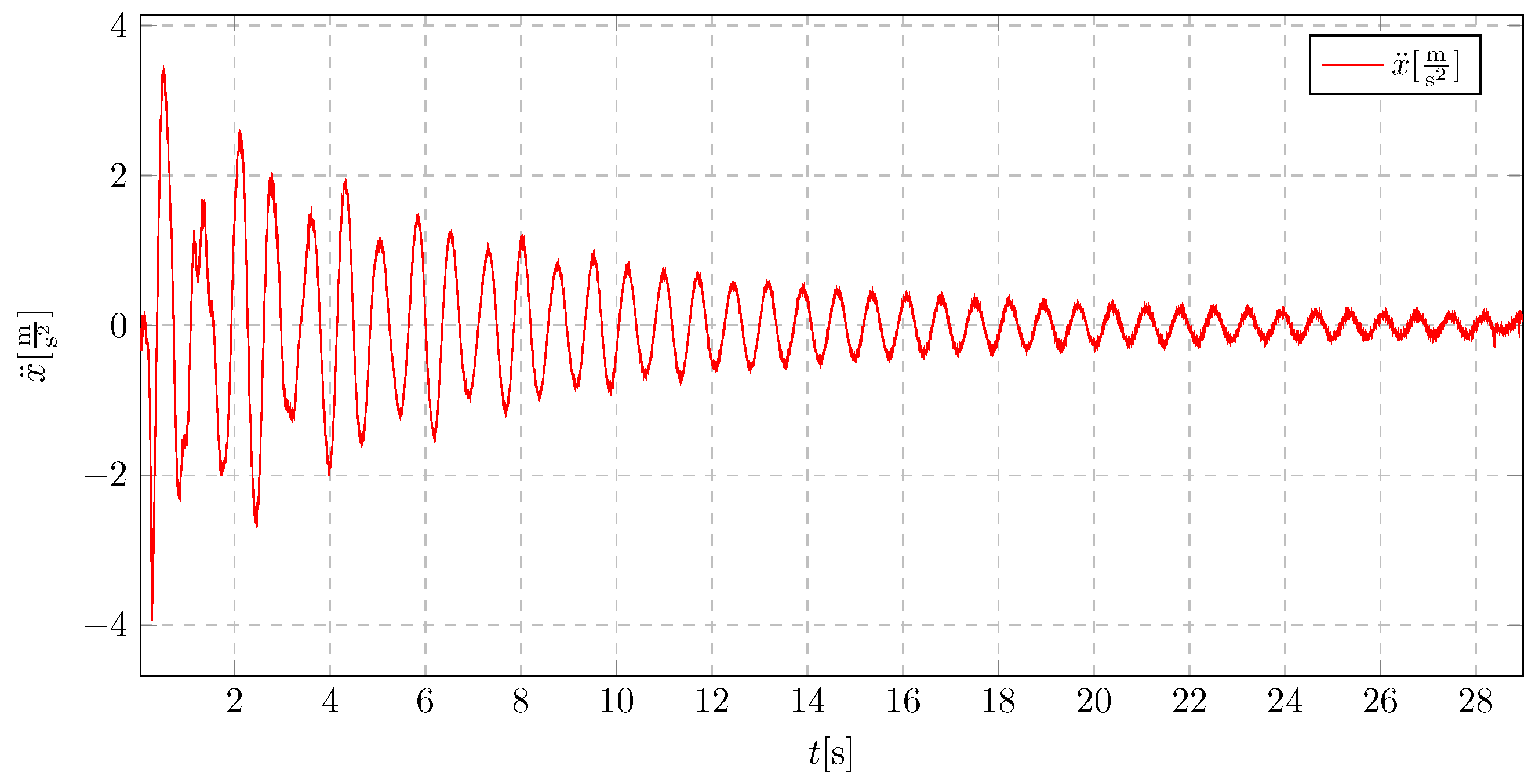
When a pendulum of 25 cm in length is implemented with an initial displacement of 8 cm, as presented in Figure 36, an increased initial acceleration amplitude is observed, which directly results from the initial conditions. Despite the higher initial amplitude, a significant improvement in vibration damping is evident. The damping effect occurs much faster compared to the model without a vibration absorber, even though the initial displacement is larger.

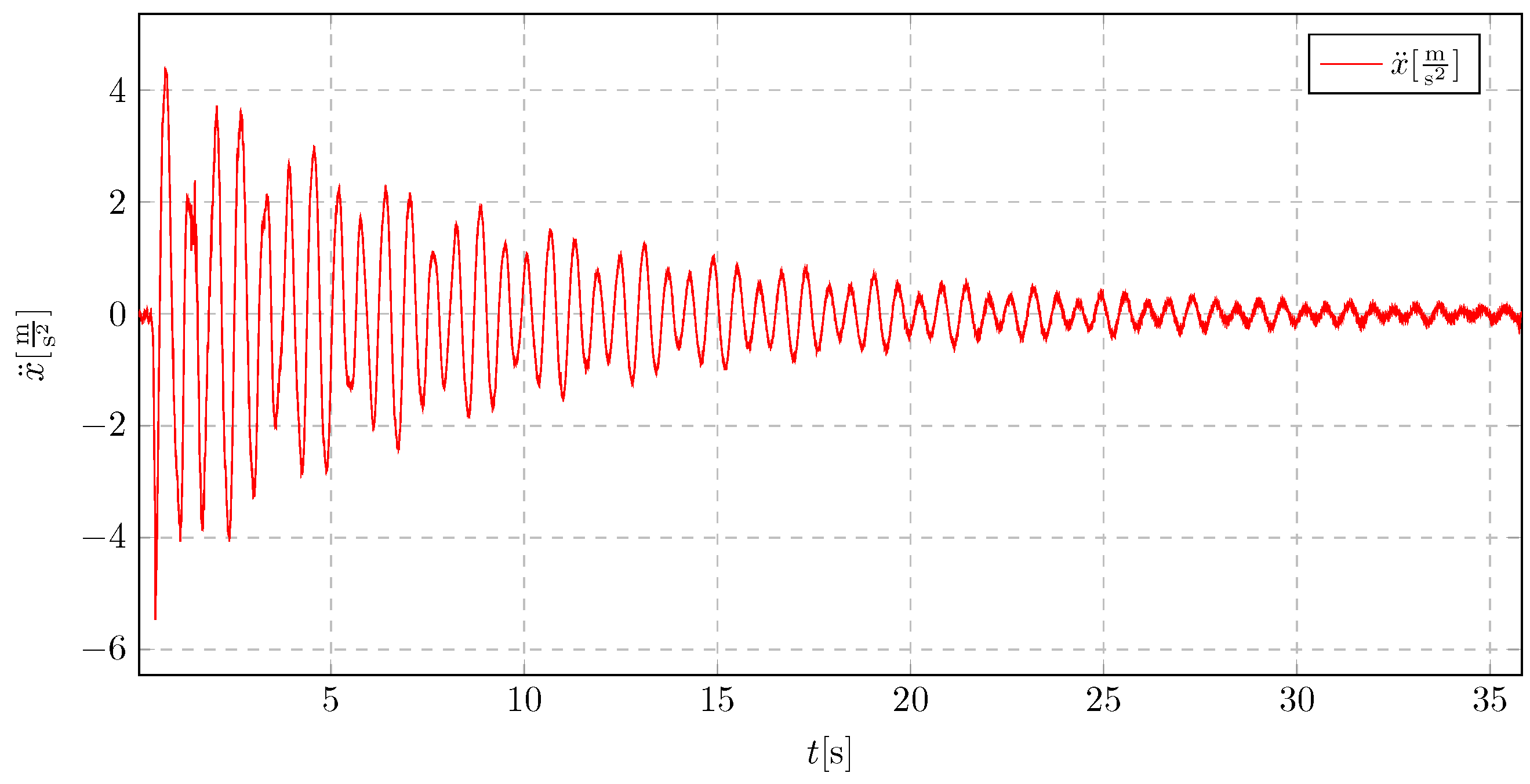
As shown, the vibration characteristics of a 5 cm initial displacement (Figure 37) are similar to those observed for an 8 cm displacement (Figure 36). A notable improvement is also evident compared to the structure without a vibration-damping system.

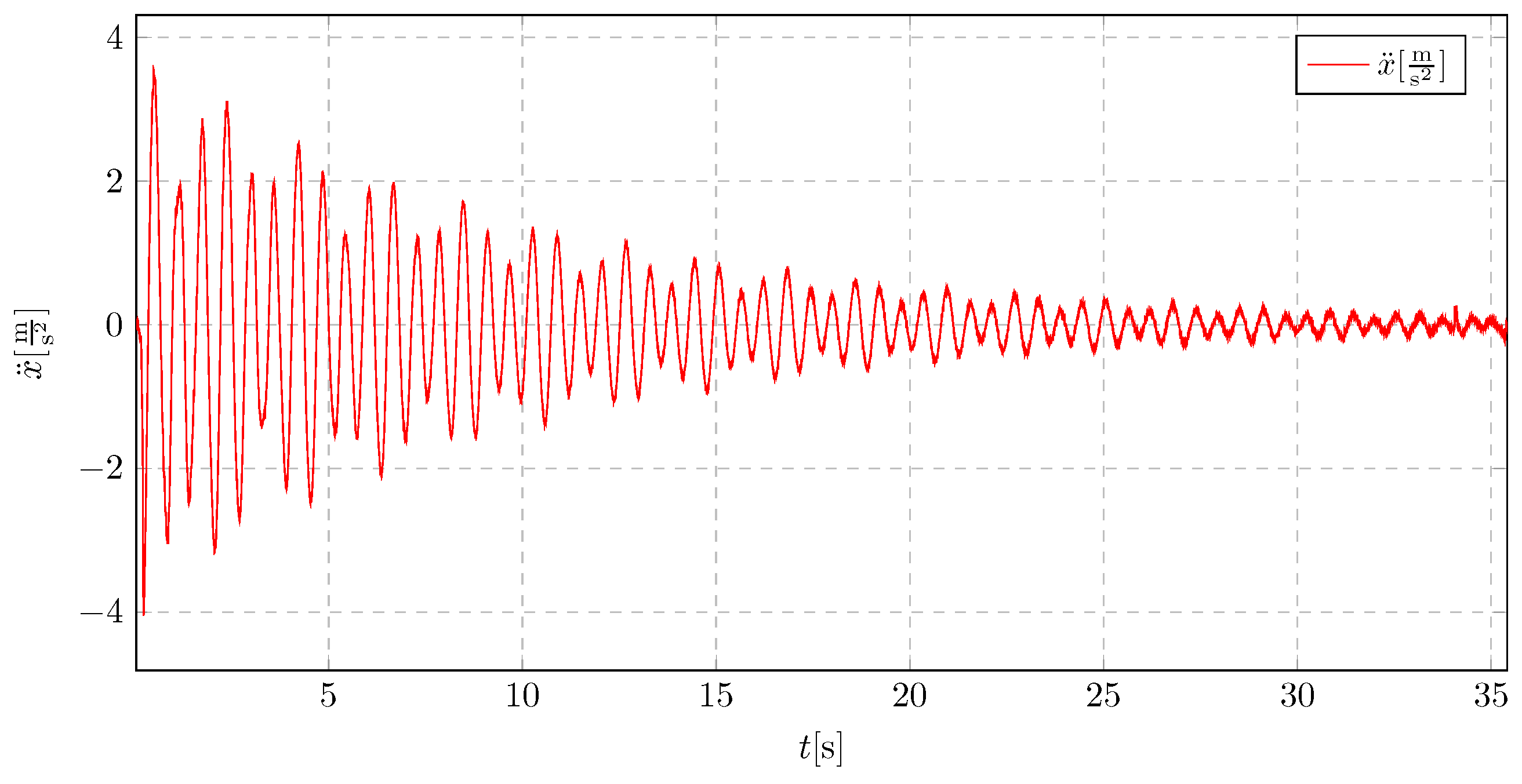
Reducing the pendulum length to 15 cm results in a considerable enhancement of the damping characteristics of the oscillations, Figure 38. The acceleration values exhibit irregular behaviour, with significant reductions occurring approximately every three oscillation periods. The natural period of the structure has also been reduced.

Reducing the initial displacement to 5 cm does not introduce significant changes in the acceleration characteristics, which are shown in Figure 39. The vibration absorber continues to operate similarly.

A pendulum length of 10 cm (Figure 40) proved to be the optimal solution for the presented skyscraper model. The acceleration characteristics indicate not only a substantial reduction in acceleration amplitude for approximately half of the oscillations but also a further increase in the oscillation period compared to the 15 cm pendulum length.

Further reduction in the pendulum length led to a decrease in the effectiveness of the vibration absorber, as seen in Figure 41. The shortening of the suspension cable was also constrained by the mounting method and the size of the attached pendulum mass. Further reduction in the pendulum length resulted in a decrease in the effectiveness of the vibration absorber, as shown in Figure 41. The shortening of the suspension cable was also constrained by the mounting method and the size of the attached pendulum mass. For further development of the measuring station, changing the attachment point to an optimal one can be applied. Additionally, there is an ongoing improvement aimed at exploring the possibility of dynamic changes in cable length during the current measurement series.

The measurement results for five cases (as described at the beginning of this section), in the form of statistical analysis, are presented in the

Table 1. Key values for subsequent series of measurements.

	Case	${\mathit{A}}_{\mathit{max}}$		${\mathit{f}}_{\mathit{main}}$
		Mean	Std	Mean	Std
var	1	0.003648	0.000453	1.865831	0.151370
free	2	0.005976	0.000206	1.846792	0.006595
forced	3	0.017255	0.001991	2.064675	0.019911
absorbed	4	0.022420	0.008824	2.079069	0.000000
resonance	5	0.028061	0.005428	1.808967	0.016286

.

The measurements were taken multiple times, and no disturbing observations were noted. Several additional tests were then conducted. On this basis, repeatability was checked.

12. Conclusions

To meet the challenge of damping vibrations in civil structures, an active damper model has been introduced, operating on the principle of tuned mass redistribution. The proposed system consists of upper and lower fluid reservoirs connected in a way that enables the transport of water between them. In response to the propagation of resonance, the system would start to transport the fluid. The change in system parameters impacts its nominal frequency, making it less susceptible to external excitations. The simplified scheme with three degrees of freedom (trolley–elastic pendulum) has been created. Its equations of motion were derived using Lagrange mechanics and served as the initial point for the primary analysis. The parameters of the system, which enhance its properties, were determined through simulations of its behaviour. This involves the nominal frequency of the system, the masses of the separate elements and the liquid, the activation time of the damping, and its value. The operation of the active vibration damper has been approximated using a fluid flow function based on actual measurements. In other words, the fluid flow function has been approximated to match the operation of an active vibration damper based on measurements. All the work was carried out in a Python-based environment developed in the object-oriented programming paradigm. The validation of all the research was carried out by building the physical model. Crucial outcomes of the work are as follows:

• There is a convergence between the displacement of a carriage and a pendulum under varying harmonic excitations.
• Selecting the correct value of the damping coefficient involves avoiding an overriding contribution from booster dampers, limiting pendulum swing angles, and maximising the damping rate of resonant vibrations.
• The activation time of fluid flow significantly affects the propagation of resonant vibrations. Early activation is essential to prevent damage to the structure. The system can resemble a classical dynamic vibration eliminator when fluid flow starts before resonance.
• There is a direct relationship between cart mass and pendulum response during liquid flow activation.
• An improper mass ratio between the cart and the pendulum can result in diagnostic limitations, excessive pendulum amplitudes, and damage to the structure.
• There exists a need for higher tare weights to limit amplitudes to a safe range, contrary to initial assumptions.
• Small pendulum masses can lead to the modulation of carriage vibrations due to inadequate damping.
• The analyses conducted allow us to conclude that the best suppression efficiency is achieved for a fluid mass of 90 kg.
• Appropriate selection of the activation time allows the amplitude to be reduced by up to 30–40% when the liquid is poured immediately after the onset of resonance excitation.
• The proposed test method ensures high repeatability of results. In the case of a forced test, the relative error in determining the amplitude is 5%, and the relative error in determining the frequency is 0.5%.

The proposed model of an active vibrations’ eliminator aims to answer the problem of vibration in civilian structures (e.g., skyscrapers) and expands the current state of knowledge in the field. However, the study was limited by a simplification in creating the model of the system, and the results show the opportunities of using the active liquid distribution in the structure as a way of changing its natural frequency and avoiding resonance phenomenon. To properly compare the data from the theory, the building of a more advanced physical model would be required. In conclusion, this study demonstrates the potential of precise, active control over the mass distribution in the system as a way of protecting the structure from dangers of external excitations.

In contrast to traditional TMDs with fixed mechanical properties, the proposed system allows dynamic modification of pendulum length, offering real-time resonance avoidance. This provides superior adaptability to time-varying excitation and enables energy-efficient operation by minimising active intervention. Unlike systems that require continuous control, the cable-adjustment approach acts only when necessary, thereby improving both responsiveness and sustainability.

In summary, this study demonstrates the potential of precise, active control over the mass distribution in the system as a way of protecting the structure from the dangers of external excitations.