Multidimensional Educational Inequality in Italy: A Stacking-Based Approach for Gender and Territorial Analysis

Abstract

This study investigates regional and gender disparities in educational attainment across Italy in 2021, drawing on the Fair and Sustainable Well-being (BES) dataset from ISTAT. By applying cluster analysis and composite indicators—including the Mazziotta–Pareto Index (MPI), geometric and arithmetic means, min-max normalization, and principal component analysis (PCA)—we assess the robustness and consistency of educational performance across regions. A key methodological innovation is the use of the stacking method to ensure comparability between genders. Results show persistent North–South educational divides and a consistent female advantage across all indicators. The paper contributes to Sustainable Development Goals by providing empirical insights into SDG 4 (Quality Education) through measurement of educational inequality and access; SDG 5 (Gender Equality) by highlighting structural advantages of women in educational outcomes; and SDG 10 (Reduced Inequalities) through a territorial analysis of disparities and policy implications. The findings offer both a methodological contribution—by testing multiple aggregation techniques—and a practical tool for policy evaluation, emphasizing the importance of multidimensional and gender-sensitive approaches in achieving educational sustainability.

1. Introduction

The level of education is a crucial indicator of a country’s social and economic development, directly influencing the quality of life, employment opportunities, and the competitiveness of the labor market. An efficient and accessible education system not only promotes individual growth but also contributes to collective progress, reducing social and territorial inequalities [1]. In Italy, educational inequalities between different geographical areas and between genders are a structural issue, with significant impacts on social cohesion and economic growth [2]. Empirical evidence has long documented a significant gap between the Northern and Southern regions of the country: the former has higher education rates, while the latter records higher levels of school dropout and more limited access to tertiary education [3,4]. This imbalance is also reflected in the labor market, generating differentials in terms of employment and remuneration. The causes of these disparities are multiple and attributable to economic, infrastructural, social, and cultural factors, which affect the quality of the training offered and educational opportunities [5]. In this context, the scientific literature has significantly deepened the analysis of educational inequalities, highlighting the importance of adopting methodological tools capable of synthesizing complex phenomena in a reliable manner. The complex and multidimensional nature of socioeconomic phenomena requires the adoption of different measures to analyze and understand them. The measurement process in the social sciences is associated with the construction of systems of indicators, which makes it possible to measure phenomena that would not otherwise be measurable [6]. In this study, we use non-compensatory aggregate indices that allow different aspects of the phenomenon investigated to be included in a single variable. Composite indicators for the measurement of multidimensional phenomena have become very popular in various social, economic, and political fields [7].

In line with the United Nations 2030 Agenda [8], education represents a foundational pillar for sustainable development. This study contributes directly to SDG 4 (Quality Education) by assessing the distribution and quality of educational outcomes; to SDG 5 (Gender Equality) by systematically comparing male and female educational performance; and to SDG 10 (Reduced Inequalities) by exploring territorial disparities in access and outcomes. Understanding these multidimensional gaps is essential for designing inclusive, effective, and evidence-based education policies that leave no one behind. Education is not only a right but also a driver of equity, economic resilience, and civic participation [9]. Reducing educational inequalities strengthens long-term social sustainability by empowering individuals, enhancing human capital, and fostering social mobility [10]. In contexts characterized by persistent territorial imbalances, such as Italy, promoting educational justice is crucial to mitigate systemic vulnerabilities and ensure sustainable regional development.

Despite a growing body of literature on educational disparities, there remains a lack of studies that apply advanced aggregation methods—such as the stacking technique—to explore multidimensional educational inequality with gender disaggregation. Most existing works focus either on single indicators (e.g., dropout rates or tertiary access) or rely on traditional composite measures, without addressing the internal heterogeneity of gender-based educational performance. This study seeks to fill this gap by offering an integrated approach that combines classical aggregation methods with the stacking procedure, allowing for a more robust comparison across population groups.

Moreover, although regional disparities in Italian education have been widely documented, fewer studies have contextualized these patterns in relation to international comparisons. Educational inequalities between regions—such as those observed in Spain [11], Germany [12], or the United States [13]—underscore the global relevance of spatial segmentation in education policy. By situating the Italian case within this broader framework, this study contributes to the global discourse on regional equity and educational justice.

Ivaldi and Ciacci [2] analyze the validity of the Gender Equality Index (GEI), proposed by the European Institute for Gender Equality, to measure gender inequalities in the Italian educational context, highlighting regional disparities in the period 2006–2014. These inequalities can be traced back to multiple factors, including economic conditions, infrastructure, and spatial factors [3].

From a methodological perspective, Montorsi and Gigliarano [5] propose spatial composite indicators built through Bayesian latent factor models in order to assess the territorial well-being of Italian provinces, also integrating the spatial dimension in the measurement. In line with this approach, Mazziotta and Pareto [7] introduce the non-compensatory indicator (MPI) of the same name, frequently adopted to summarize complex socioeconomic dimensions. This index has been applied in various contexts, such as the measurement of urban deprivation [14] and depopulation in Italian municipalities.

Numerous studies highlight how the choice of the summary index can significantly influence the results. For this reason, some authors have compared MPI with alternative methods, including principal component analysis (PCA), which is useful for the reduction of dimensionality [10] and the identification of latent patterns in educational variables [3].

However, an appropriate measurement model must support a PCA-based composite index to function properly [7]. Similarly, cluster analysis represents a widely used technique to segment the territory into homogeneous groups, allowing for highlighting the dichotomy between the North and South and to identify areas with atypical educational performances [14,15].

Studies such as Nardone et al. [4] have highlighted how the polarization between Northern and Southern Italy is not uniform but is articulated in sub-dynamics that also involve cultural, economic, and infrastructural factors. A particularly relevant contribution is provided by Alaimo [9], who uses an adapted version of the MPI, called AMPI, to classify Italian regions according to different areas of well-being, including education, confirming the validity of these tools also for comparative analyses on a national scale.

Finally, the coherence between different aggregation methods can be assessed through Spearman correlation analysis, a tool that allows us to verify the solidity of the results and the non-dependence of the conclusions on the synthesis technique adopted [1]. This comparative approach guarantees greater robustness in the interpretation of the data and contributes to the validation of the methodological choices in the field of measuring educational well-being.

This study aims to analyze the education levels of the Italian regions in the year 2021, distinguishing between men and women, through the use of the Fair and Sustainable Well-being (BES) data published by ISTAT. The analysis involves a segmentation of the regions using cluster analysis techniques applied to a set of educational variables, followed by the calculation of the Mazziotta–Pareto Indicator (MPI) through the application of the stacking method in order to make the index values comparable between the two genders. Furthermore, to test the robustness and consistency of the results obtained, additional aggregation methods were applied: arithmetic mean, geometric mean, min-max normalization, and principal component analysis (PCA) [7,10]. All techniques were adapted to the comparison between genders through stacking to ensure the methodological homogeneity of the approach. The consistency between the results obtained with the different methods was verified through Spearman correlation analysis [1].

The originality of this study lies precisely in the integration between classic aggregative approaches and the stacking technique applied systematically, to allow an accurate comparison between the education levels of the two genders. This approach, in addition to offering an innovative methodological contribution, can support the formulation of educational policies aimed at reducing territorial and gender inequalities in the Italian education system.

By employing multiple aggregation techniques and validating results across methods, this study offers a replicable framework for monitoring educational disparities. This methodological robustness enhances the policy relevance of the findings, supporting data-informed decision-making and the territorial targeting of educational interventions aligned with sustainable development principles.

2. Materials and Methods

The proposed analysis is based on the elaboration of a multidimensional set of educational indicators extracted from the ISTAT database of Fair and Sustainable Well-being (BES) for the year 2021 [16]. The selected variables represent different aspects of the regional education level: (a) population with at least a high school diploma (25–64 years), (b) transition to university, (c) early school dropout, (d) young people studying or working, (e) participation in continuing education, (f) tertiary qualifications in the STEM field, (g) cultural participation outside the home, (h) reading books/newspapers, (i) basic digital skills, and (j) graduates in the 25–34 age group.

Each of these ten variables was selected based on both theoretical relevance and empirical availability. For instance, “people with at least a high school diploma (25–64 years)” indicates the basic human capital and the minimum threshold for inclusion in skilled labor; a study related to the Chinese context uses this variable to analyze the state of the workforce and evaluate whether it is in line with the country’s sustainable development goals [17].

“Non-early school dropout” and “transition to university” capture the accessibility and continuity of the educational path. Asif and Searcy believe that evaluating the performance of higher education institutions can better guide the direction of funding in education [18]. While “STEM qualifications” and “basic digital skills” reflect the alignment of education with labor market demands, which is based on digitalization and innovations [19]. “Cultural participation” and “reading habits” represent broader cognitive and social capital dimensions [20]. “Participation in continuing education” is aligned with SDG4.3, which is the goal of lifelong and sustainable learning.

Table 1. Variables, descriptions, units of measure, statistical distributions, and sources (year 2021).

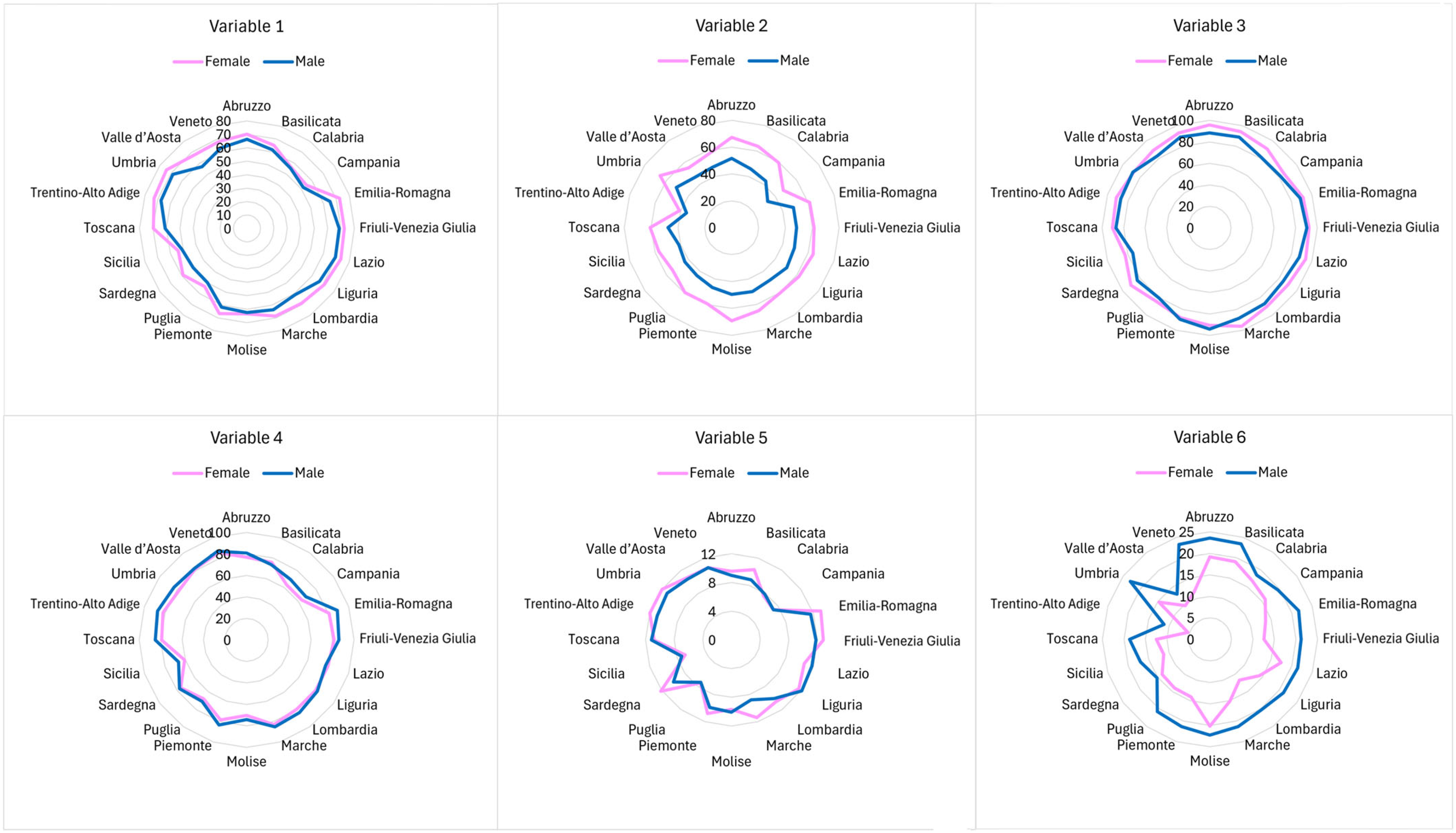
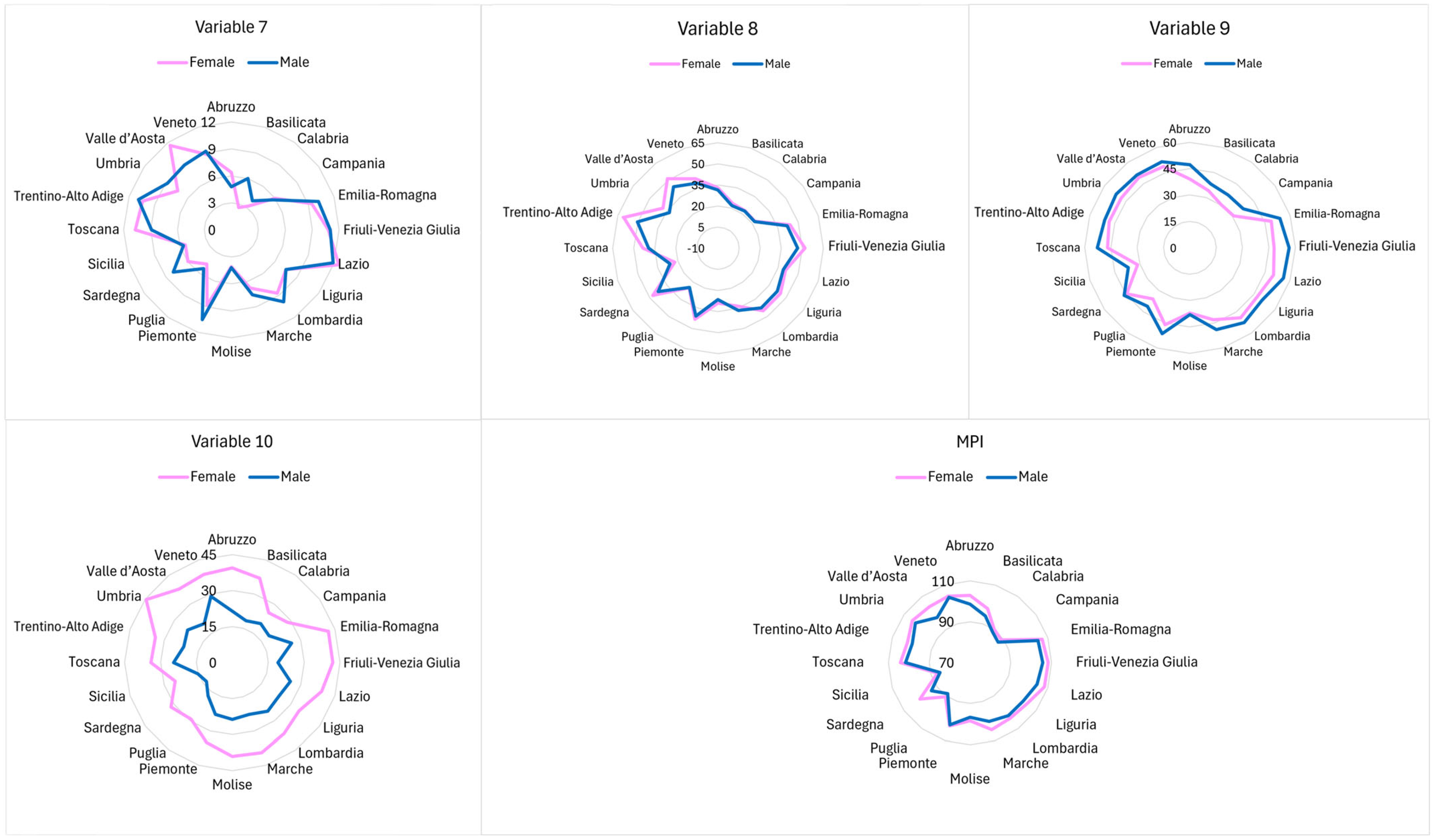
Variable	Description	Units of Measure	Statistical Distributions	Sources
1	People with at least a high school diploma (25–64 years)	Percentage values	Percentage of population aged 25–64	ISTAT—Labour Force Survey
2	Transition to university	Cohort-specific rate	Rate of high school graduates entering university	Ministry of Education; Ministry of University and Research
3	Not leaving education and training early	Percentage values	Percentage of 18- to 24-year-olds not in education/training	Re-elaborations on ISTAT data—Labour Force Survey
4	Young people in employment and education (NEET)	Percentage values	% of 15- to 29-year-olds not in employment, education, or training	Re-elaborations on ISTAT data—Labour Force Survey
5	Participation in continuing education	Percentage values	% of adults aged 25–64 in formal/non-formal education	ISTAT—Labour Force Survey
6	People who obtain a tertiary STEM qualification in the year	Per 1000 residents aged 20–29	Absolute rate per 1000 of the population 20–29	ISTAT—Ministry of University and Research data
7	Cultural participation outside the home	Percentage values	% of people participating in cultural activities	ISTAT—Survey Aspects of Daily Life
8	Reading books and newspapers	Percentage values	% of people who read at least one book or newspaper	ISTAT—Survey Aspects of Daily Life
9	At least basic digital skills	Percentage values	% of population with basic ICT skills	ISTAT—Survey Aspects of Daily Life
10	Graduates and other tertiary qualifications (25–34 years)	Percentage values	% of population aged 25–34 with a degree	ISTAT—Survey Aspects of Daily Life

summarizes the variables, descriptions, units of measure, statistical distributions, and data sources for each indicator during the year 2021. This detailed description ensures transparency in the construction of the composite index and allows for critical evaluation of its components.

First, a cluster analysis was carried out, using the K-means algorithm with k = 3, applied to the entire national sample (not distinguished by gender). The choice of k = 3 was guided by both statistical and substantive considerations. We tested several values of k and found that the Calinski–Harabasz and Silhouette coefficients reached optimal values at k = 3, indicating a well-defined clustering structure. Moreover, this solution aligns with the well-established North–Center–South tripartition commonly used in Italian territorial policy analysis, enhancing both interpretability and policy relevance.

The aim was to obtain a segmentation of the Italian regions into homogeneous groups based on the selected educational variables. This procedure made it possible to reduce the information complexity and identify recurring territorial patterns. The analysis was implemented using STATA 18 SE software.

The k-means algorithm minimizes the intra-cluster variance and maximizes the inter-cluster variance, optimizing the following objective function:

$$J=\sum _{i=1}^k\sum _{x_j\in C_i}{‖x_j-{\mu }_i‖}^2$$

where

-

$\mathit{k}$ is the default number of clusters;

-

${\mathit{C}}_{\mathit{i}}$ is the i-th cluster;

-

${\mathit{x}}_{\mathit{j}}$ is the feature vector of region j;

-

${\mathit{\mu }}_{\mathit{i}}$ is the centroid of the cluster ${\mathit{C}}_{\mathit{i}}$;

-

${‖{\mathit{x}}_{\mathit{j}}-{\mathit{\mu }}_{\mathit{i}}‖}^2$ is the Euclidean distance between a point and the cluster centroid.

This first investigation allows us to assign each region to the cluster with the closest centroid and obtain a regional breakdown based on the totality of the explanatory variables of the level of education.

Subsequently, for each cluster, the Mazziotta–Pareto Indicator (MPI) was calculated [21] in the decreasing version (MPI–) for the entire population and, separately, for each gender. In order to guarantee the comparability between male and female values, the stacking method was adopted [22,23,24] following the approach adapted by Bartimoro and Ivaldi [25,26], which allows comparative aggregation between distinct groups (males and females).

The formulation is as follows:

$${\mu }_j={\displaystyle \frac{\sum _{i=1}^n{x}_{i,j,F}+\sum _{i=1}^n{x}_{i,j,M} }{2n}}$$

$${\sigma }_j=\sqrt{{\displaystyle \frac{\sum _{i=1}^n{(x}_{i,j,F }-{\mu }_j)+\sum _{i=1}^n{(x}_{i,j,M }-{\mu }_j)}{2n}}}$$

where i = 1, 2, …, 20 are the Italian regions, j = 1, 2, …, 10 are the explanatory variables of education, and F and M are the two genders analyzed.

The MPI is a non-compensating composite index used to aggregate multiple variables into a single synthetic value, maintaining the structure of the original distributions. This method is particularly useful when you want to avoid extreme values of a variable compensate for low values of another. To calculate it, it is necessary to normalize the variables so that they have the same unit of measurement and can be compared with each other, after having performed a correction of their direction that makes them all positively oriented. Among the available aggregation techniques, the Mazziotta–Pareto Index (MPI) offers a non-compensatory approach particularly suited for sustainability analysis, as it penalizes unbalanced performance across dimensions and prevents compensation between poor and strong values. This characteristic is especially relevant when measuring environmental sustainability, where trade-offs may mask systemic weaknesses [21,27].

The synthetic index, for unit i at time t, is then calculated by applying the following formula:

$${MPI}_{it}^{+/-}={M_z}_{it}\pm {S_z}_{it}{cv}_{it}$$

where ${M_z}_{it}={\displaystyle \frac{\sum _{j=1}^m{z}_{ijt}}{m}}$; ${S_z}_{it}=\sqrt{{\displaystyle \frac{\sum _{j=1}^m{(z_{ijt}-{M_z}_{it})}^2}{m}}}$; ${cv}_{it}={\displaystyle \frac{{S_z}_{it}}{{M_z}_{it}}}$.

The aggregate MPI for each region was obtained by taking the arithmetic mean of the male and female values. The means of the aggregate values within each cluster were used to reorder the classes based on the overall level of education. The same ordering was repeated separately for the two genders, thus allowing direct comparison of the regional hierarchies within the same clustered structure.

A leave-one-out (jack-knife) sensitivity check was performed: the composite index was recalculated after sequentially removing each individual indicator to assess the influence of single variables on the overall result.

To ensure the robustness of the results, the procedure was replicated by adopting additional aggregation methods: arithmetic mean, geometric mean, min-max normalization, and PCA. In each case, the entire process was performed using the stacking methodology, thus ensuring analytical uniformity and comparability between genders. The simultaneous adoption of different techniques allows for the verification of the influence of the chosen methodology on the results obtained.

Finally, the Spearman correlation matrix was calculated between the indices obtained with the different aggregation methods in order to assess the degree of consistency between the measures and identify any discrepancies. A high degree of correlation would confirm the stability of the results and the validity of the conclusions, regardless of the aggregation approach used.

Similar studies investigate complex phenomena through a multidimensional approach. Hassan explores the multidimensional nature of DEI (Diversity, Equity, and Inclusion) with practical measurement tools for cultivating fair, respectful, and inclusive environments across workplaces, educational institutions, and communities [28]. Educational disparities have also been analyzed to improve student success and retention in educational context, considering different factors: clear student guidelines, integrating first-year transition coursework, intrusive academic advising to treat the nonacademic and personal factors, and traditional developmental education coursework and tutoring to address academic factors [29]. Also, in the Malaysian context, a comparison of gender enrolment across three dimensions has been studied to examine the gender disparity in higher education across different higher education institutions [30].

3. Results

This section presents the results obtained from the analysis of Italian regional educational data for the year 2021. The elaborations were carried out by distinguishing by gender and applying the stacking method to make the indicators comparable between the two components of the population.

First, Figure 1 and Figure 2 present the radar graphs for the ten educational variables and MPI in Italy by region, comparing them by gender. The pink lines indicate the values for females, while the blue lines indicate the values for males.

This visualization allows you to immediately grasp the territorial and gender differences in the variables.

The radar graphs also highlight the degree of homogeneity: more regular polygons indicate a more uniform distribution among the regions, while marked deformations suggest specific critical issues in the variable.

After that, the classification of the Italian regions into three homogeneous clusters is reported, obtained through the K-means algorithm and based on the set of educational variables considered. The ordering of the clusters was established on the basis of the average value of the Mazziotta–Pareto indicator (aggregate MPI), calculated as the arithmetic mean between the MPI of females and that of males (

Table 2. Total MPI and cluster.

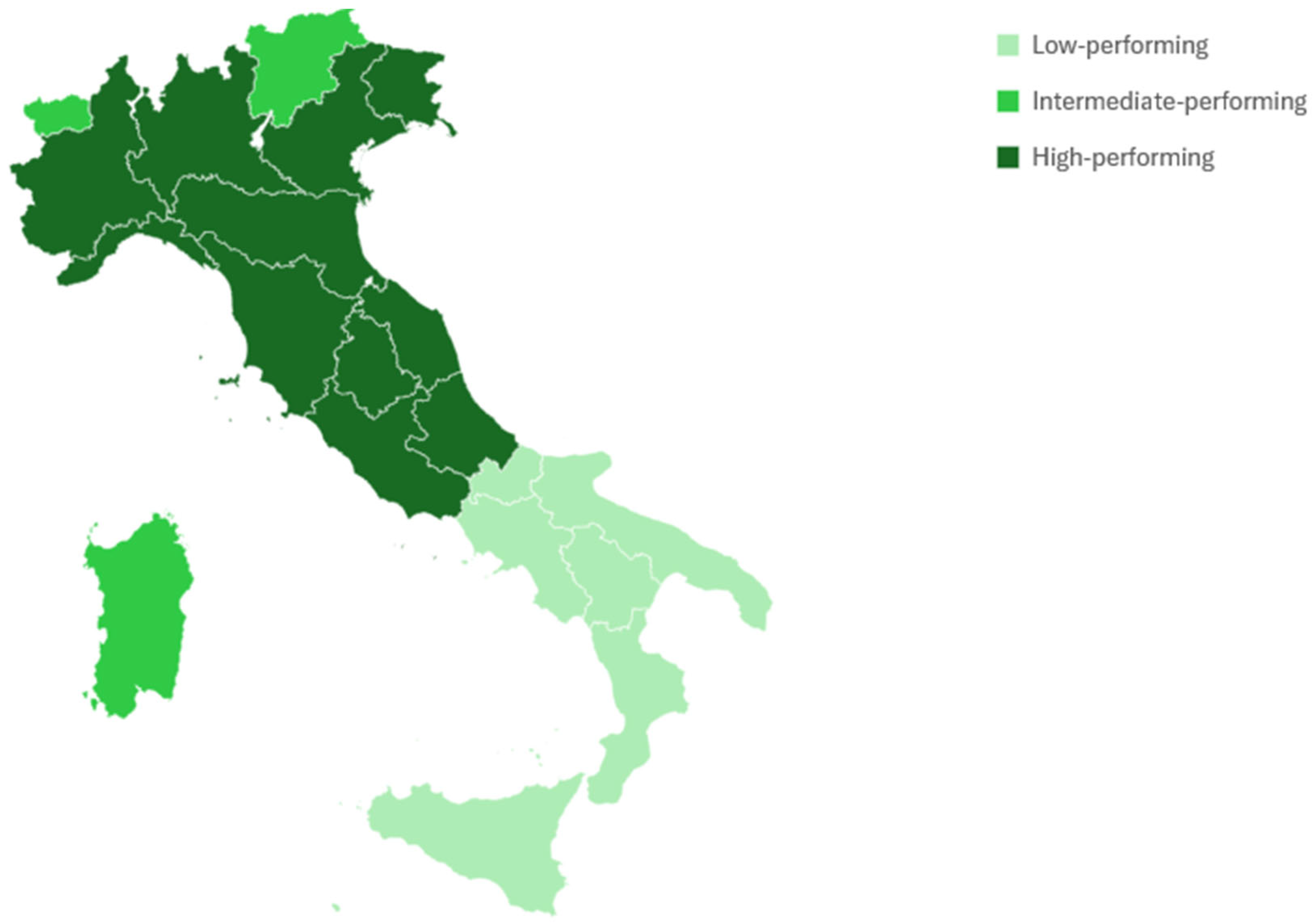
Region	Cluster	Aggregate MPI
Abruzzo	High-performing	100.79
Basilicata	Low-performing	95.92
Calabria	Low-performing	89.42
Campania	Low-performing	88.02
Emilia-Romagna	High-performing	106.16
Friuli-Venezia Giulia	High-performing	107.00
Lazio	High-performing	106.42
Liguria	High-performing	103.24
Lombardia	High-performing	102.84
Marche	High-performing	102.32
Molise	Low-performing	97.60
Piemonte	High-performing	102.31
Puglia	Low-performing	89.69
Sardegna	Intermediate-performing	96.90
Sicilia	Low-performing	86.07
Toscana	High-performing	102.90
Trentino-Alto Adige	Intermediate-performing	101.03
Umbria	High-performing	104.04
Valle d’Aosta	Intermediate-performing	100.64
Veneto	High-performing	103.97

).

We decided to label clusters in increasing order as follows: “Low-performing”, “Intermediate-performing”, and “High-performing”, based on the aggregate MPI values, so in cluster “Low-performing”, the aggregate MPI values vary between a minimum of 86.07 (Sicilia) and a maximum of 97.60 (Molise). In cluster “Intermediate-performing”, the range is between 96.90 (Sardegna) and 101.03 (Trentino-Alto Adige). Finally, cluster “High-performing” records the highest values, with a range from 102.31 (Piemonte) to 107.00 (Friuli-Venezia Giulia), as summarized in Table 2.

For visual support, a map of Italy is presented that graphically highlights the distribution of the regions in the three identified clusters (Figure 3).

Subsequently, all the indicators calculated with the stacking method are reported in

Table 3. Composite indicator values by gender: MPI, geometric and arithmetic means, min-max normalization, and PCA scores.

Region	MPI Female	MPI Male	Geometric Mean Female	Geometric Mean Male	Min-Max Female	Min-Max Male	Arithmetic Mean Female	Arithmetic Mean Male	PCA Female	PCA Male
Abruzzo	97.76	94.08	29.17	28.46	0.63	0.49	42.52	38.65	0.35	−1.10
Basilicata	90.11	88.73	26.08	25.82	0.27	0.23	37.69	35.91	−1.16	−2.08
Calabria	88.93	87.11	26.81	25.61	0.21	0.10	36.23	34.60	−1.68	−2.49
Campania	98.48	96.71	31.44	29.46	0.57	0.53	43.27	40.55	0.30	−0.38
Emilia-Romagna	90.64	88.75	27.32	26.54	0.16	0.02	38.15	36.12	−1.30	−2.27
Friuli-Venezia Giulia	86.72	85.43	25.39	25.24	0.18	0.05	35.62	34.16	−1.87	−2.80
Lazio	100.36	93.44	32.88	29.13	0.38	0.00	43.50	38.84	0.31	−1.42
Liguria	102.20	99.85	32.89	32.50	0.94	0.72	45.73	43.25	1.02	0.01
Lombardia	103.96	97.33	35.40	31.58	0.72	0.30	46.32	41.61	1.02	−0.62
Marche	102.94	98.64	34.02	30.87	0.84	0.68	45.68	42.43	1.10	−0.37
Molise	107.19	105.12	37.10	36.08	0.93	0.62	47.67	45.61	1.70	0.57
Piemonte	108.28	105.72	37.89	35.91	0.93	0.78	48.59	45.97	1.88	0.69
Puglia	108.35	104.49	38.15	36.20	0.97	0.80	48.13	44.89	1.72	0.53
Sardegna	104.37	102.11	35.16	34.36	0.88	0.70	46.29	44.10	1.08	0.12
Sicilia	103.66	102.03	34.81	34.59	0.78	0.47	46.09	44.07	1.01	0.01
Toscana	104.42	100.23	34.42	32.66	0.77	0.57	46.14	43.28	1.39	−0.20
Trentino-Alto Adige	102.54	102.07	34.71	34.34	0.69	0.49	45.00	43.79	0.64	0.03
Umbria	104.12	101.67	35.34	33.95	0.81	0.46	45.85	43.60	1.04	0.04
Valle d’Aosta	105.04	103.04	35.96	34.32	1.00	0.76	47.12	44.19	1.39	0.30
Veneto	104.34	103.60	34.84	35.30	0.74	0.55	46.33	44.82	1.17	0.30

, separately for gender. In particular, the following are presented: the Mazziotta–Pareto indicator (MPI), the geometric mean, the arithmetic mean, the normalized value through min-max scaling, and the score of the first principal component obtained by PCA.

The leave-one-out test confirmed the robustness of the index: omitting any single indicator changed the composite scores by less than 2% and did not alter the regional ranking.

In female MPI values, the range extends from 86.72 (Friuli-Venezia Giulia) to 108.35 (Puglia); for men, the corresponding range goes from 85.43 (Friuli-Venezia Giulia) to 105.72 (Piemonte). The female geometric mean varies between 25.39 (Friuli-Venezia Giulia) and 38.15 (Puglia), while the male mean varies between 25.24 (Friuli-Venezia Giulia) and 36.20 (Puglia). The min-max scaling values range from 0.16 to 1.00 for women and from 0.00 to 0.80 for men.

The female arithmetic mean values range from 35.62 (Friuli-Venezia Giulia) to 48.59 (Piemonte), while the male values range between 34.07 (Friuli-Venezia Giulia) and 45.97 (Piemonte). Finally, the PCA scores range between –1.87 and +1.88 for women and between –2.80 and +0.69 for men.

Table 4. Average values of composite indicators within each cluster, by gender.

Cluster	MPI Female	MPI Male	Geometric Mean Female	Geometric Mean Male	Min-Max Female	Min-Max Male	Arithmetic Mean Female	Arithmetic Mean Male	PCA Female	PCA Male
Low-performing	92.11	90.13	27.70	26.86	0.34	0.24	38.91	36.67	−0.89	−1.85
Intermediate-performing	102.17	96.87	33.72	31.07	0.68	0.34	45.18	41.23	0.79	−0.68
High-performing	105.02	102.61	35.67	34.42	0.85	0.63	46.63	44.25	1.28	0.18

shows the averages of each indicator within the clusters, again broken down by gender. This allows us to observe the average behavior of the indicators within each regional group and verify any systematic patterns between the clusters.

In the Low-performing cluster, the female MPI average is 92.11 against 90.13 for males; in the Intermediate-performing cluster, the averages are 102.17 (females) and 96.87 (males); finally, in the High-performing cluster, the values are 105.02 (females) and 102.61 (males). For the geometric average, the values vary from 27.70 to 35.67 (females) and from 26.86 to 34.42 (males). In the min-max, women range from 0.34 to 0.85 and men from 0.24 to 0.63. The female arithmetic mean grows from 38.91 to 46.63, while the male arithmetic mean grows from 36.67 to 44.25. Finally, the average PCA values rise from –0.89 to +1.28 for women and from –1.85 to +0.18 for men.

Table 5. Spearman correlation matrix among composite indicators for the female population.

	Geometric Mean Female	Min-Max Female	MPI Female	Arithmetic Mean Female	PCA Female
Geometric mean female	1.0000
Min-max female	0.8206	1.0000
MPI female	0.9504	0.8447	1.0000
Arithmetic mean female	0.9609	0.8394	0.9729	1.0000
PCA female	0.8977	0.8770	0.9684	0.9474	1.0000

and

Table 6. Spearman correlation matrix among composite indicators for the male population.

	Geometric Mean Male	Min-Max Male	MPI Male	Arithmetic Mean Male	PCA Male
Geometric mean male	1.0000
Min-max male	0.7248	1.0000
MPI male	0.9774	0.7925	1.0000
Arithmetic mean male	0.9820	0.7774	0.9970	1.0000
PCA male	0.9624	0.8045	0.9910	0.9880	1.0000

present the Spearman correlation matrix calculated between all the composite indicators considered. This matrix allows for evaluating the coherence and robustness of the measures adopted, providing an indication of the convergence between the different aggregation techniques applied.

For women, the highest correlations are between MPI and arithmetic mean (ρ = 0.9729) and between MPI and PCA (ρ = 0.9684). For men, the correlation between MPI and arithmetic mean is 0.9970, while that between MPI and PCA is 0.9910. These values indicate a high consistency between the different synthesis methods.

4. Discussion

The results of the analysis confirm the existence of significant territorial and gender disparities in education levels in Italy in 2021. The cluster analysis, conducted with the k-means algorithm, allowed us to group the Italian regions into three homogeneous clusters based on ten educational variables extracted from the BES database. The cluster with the highest scores of the aggregate Mazziotta–Pareto indicator (MPI)—above 102 points—mainly includes regions in the Centre-North, such as Emilia-Romagna (106.16), Friuli-Venezia Giulia (107.00), Lazio (106.42), and Marche (102.32). On the contrary, regions in the South, such as Campania (88.02), Calabria (89.42), and Sicilia (86.07), are placed in the cluster with the lowest values, highlighting a persistent North–South fracture in the distribution of educational opportunities. This result is consistent with the existing literature, including the studies of Nardone et al. [4], which emphasize that the educational gap between north and south is not only expressed in school dropout or access to tertiary education but also in the quality and inclusiveness of the educational offer. These disparities directly impact the acquisition of cognitive and digital skills, undermining equitable human capital development [31].

From the perspective of the United Nations 2030 Agenda [8], these findings raise critical concerns for achieving SDG 4 (Quality Education) and SDG 10 (Reduced Inequalities). Territorial inequalities in education hinder the creation of inclusive and sustainable societies, weakening social cohesion and economic resilience in less advantaged areas.

A second dimension of great importance is gender. The application of the stacking method made it possible to perform a direct and methodologically homogeneous comparison between men and women for each composite indicator. The results show that, across all methodologies used, women consistently score higher than men [32,33,34,35,36,37,38,39]. For example, in the High-performing cluster, the female MPI average reaches 105.02, compared to 102.61 for men. Even in clusters with lower overall performance—such as the Low-performing cluster—women maintain an advantage: 92.11 versus 90.13. Similar trends are observed in other indicators—in geometric mean, PCA scores, and min-max normalization. Even in disadvantaged regions such as Calabria, female scores outperform male ones. This trend supports the goals of SDG 5 (Gender Equality) by evidencing a structural and persistent female advantage in educational outcomes, even in socioeconomically fragile territories. These findings resonate with the conclusions of Ivaldi and Ciacci [2], who demonstrate a long-term improvement in female educational performance across Italian regions. The observed resilience of the female segment in education highlights a paradox when contrasted with the more precarious position that women continue to hold in the labor market, emphasizing the need for integrated, cross-sectoral policies [40,41,42,43,44,45,46,47].

Another relevant aspect concerns the consistency across the synthesis methods adopted. The Spearman correlation matrix, calculated separately by gender, reveals very high coefficients between indicators. For women, the correlation between MPI and arithmetic mean is 0.9729, and 0.9684 with PCA. Among men, the MPI correlates 0.9970 with the arithmetic mean and 0.9910 with PCA. These values confirm the robustness of the analytical framework. As Alaimo and Maggino [1] suggest, strong correlations between results obtained through different techniques enhance the empirical validity and policy relevance of composite indicators. The integration of PCA, a compensatory method, with non-compensatory indices such as MPI is particularly useful in validating latent structures, as also noted by Mazziotta and Pareto [7].

In the context of sustainability, these methodological choices offer a replicable and robust framework for monitoring progress toward inclusive and equitable education, aligned with SDG reporting and local policy needs. The hybridization of classical and innovative approaches—such as stacking—enables more sensitive detection of regional and gender-specific patterns, enriching the decision-making process. Overall, the integration between traditional aggregation approaches and newer methodologies such as stacking has proven particularly effective in producing a robust, comparable analysis of educational inequality in Italy. This work not only offers an accurate picture of existing disparities but also a valuable methodological contribution for future research and sustainable policy design. As highlighted by Montorsi and Gigliarano [5], conventional well-being models risk overlooking spatial dynamics and latent heterogeneity. The application of hybrid methods, such as stacked MPI and PCA, can address this limitation, enhancing both analytical sensitivity and territorial equity—core principles of sustainable development.

The policy implications of this study are closely aligned with the territorial clustering results. For low-performing Southern regions (Cluster Low-performing), policy makers should prioritize early intervention strategies, including investment in school infrastructure, expanded access to early childhood education, and targeted financial support for students at risk of dropout. For intermediate regions (Cluster Intermediate-performing), measures could focus on strengthening transitions from secondary to tertiary education and enhancing vocational pathways, especially in underdeveloped inland areas. In high-performing regions (Cluster High-performing), policy efforts may concentrate on consolidating existing strengths, such as promoting excellence programs, fostering lifelong learning, and addressing gender imbalances in STEM education.

Moreover, the consistent female advantage observed across all indicators calls for integrated gender-sensitive strategies [48]. These should not only recognize women’s educational achievements but also ensure that these are effectively translated into labor market opportunities. Gender mainstreaming in education policy, combined with labor-market reforms, is necessary to close the gap between educational performance and employment outcomes. While this study focuses on descriptive and comparative multidimensional analysis, future developments could incorporate inferential techniques to better understand the causal mechanisms behind regional and gender disparities in education. In particular, the use of regression models—both linear and multilevel—could allow researchers to test the impact of structural factors like household income [49,50,51,52], school infrastructure [30,53], and urban–rural location, as well as psychological or individual factors such as field of study (Wan, 2018), academic self-esteem, and intrinsic vs. extrinsic motivation [51,54,55], on composite educational outcomes. Additionally, structural equation modeling (SEM) could offer a more integrated framework to explore latent constructs and indirect effects among educational determinants. These analytical extensions, while beyond the scope of the present study, would further enrich the explanatory power of the multidimensional approach presented here.

5. Conclusions

This work has provided a detailed and methodologically robust analysis of educational inequalities in Italy, highlighting the disparities that persist between regions and between genders in the year 2021. The integration of cluster analysis and the Mazziotta–Pareto Indicator (MPI), enhanced by the systematic application of the stacking method, allowed for a solid and comparable classification of regional educational performance. The territorial segmentation of Italian regions into three clusters revealed a well-documented North–South divide, reinforcing the need for geographically differentiated policy interventions that can address structural deficiencies in the South and support excellence in the Center and North.

A particularly significant finding is the consistent educational advantage of women across all regions and all synthesis methods adopted. This result, often underemphasized in public discourse, emerges as a structural pattern and not as an isolated trend. It suggests that, at least from an educational perspective, female human capital in Italy is already stronger than male, raising important questions about the mismatch between educational attainment and labor market participation. Bridging this gap requires integrated and gender-sensitive policies, aimed not only at supporting education but also at ensuring the recognition and valorization of women’s skills in professional and societal contexts.

These conclusions speak directly to the objectives of SDG 4 (Quality Education), SDG 5 (Gender Equality), and SDG 10 (Reduced Inequalities). Ensuring equitable access to education, acknowledging the structural resilience of women in the educational sphere, and reducing territorial gaps are key priorities in the achievement of a sustainable, inclusive, and just society.

From a methodological standpoint, the study contributes to the growing literature on the use of composite indicators in educational research. By adopting and comparing multiple aggregation techniques—including arithmetic mean, geometric mean, min-max normalization, and principal component analysis—the analysis confirmed the internal consistency of the findings. The high Spearman correlations between indicators validated the reliability of the approach and its replicability across different territorial and temporal contexts. The application of the stacking method, originally employed in predictive modelling, proved effective in constructing composite indicators for non-overlapping population groups, reinforcing comparability and analytical clarity.

The contributions of Alaimo and Maggino [1] have been particularly valuable in reframing educational well-being as a multidimensional and interconnected system rather than as a sum of isolated indicators. The empirical validation of hybrid aggregative methods consolidates their role as effective tools for evaluating complex phenomena in line with sustainability assessment principles.

Despite its strengths, this study also presents some limitations. Composite indices, even when non-compensatory, may still mask internal imbalances between indicators. Although the use of Spearman correlations and multiple synthesis techniques improves robustness, a full sensitivity analysis of indicator weights could be implemented in future work. In addition, while stacking offers enhanced comparability, it does not address causality. The integration of regression models and SEM frameworks is recommended for future research to deepen the understanding of structural determinants and interactions within educational inequality. Finally, future developments could explore spatially aware composite indicators, such as those built on Bayesian latent factor models, to account for territorial contiguity and spillover effects.

In conclusion, the study not only offers a precise diagnosis of educational inequalities in Italy but also provides practical insights for developing fair and sustainable policy strategies. Reducing regional disparities requires targeted investment in infrastructure, accessibility, and quality of education in disadvantaged territories. Addressing the gender gap demands measures that ensure the full valorization of women’s educational assets, especially in the school-to-work transition.

Finally, the methodology proposed in this study represents a replicable and adaptable tool for monitoring educational equity over time and supporting evidence-based planning. Future research should further explore the integration of spatially sensitive composite indicators, such as those developed by Montorsi and Gigliarano [5], which leverage Bayesian latent factor models to capture territorial contiguity and diffusion dynamics. This line of inquiry holds promise for improving the predictive capacity and local policy relevance of educational sustainability metrics.