Abstract
With increasing attention to sustainability and energy efficiency in transportation systems, advanced intelligent algorithms provide promising solutions for optimizing urban rail transit operations. This study addresses the challenge of optimizing train operation plans for urban rail transit systems characterized by spatiotemporal passenger flow imbalance. By exploring a combined short-turning and unpaired train operation mode, a three-objective optimization model was established, aiming to minimize operational costs, reduce passenger waiting times, and enhance load balancing. To effectively solve this complex problem, an Improved GOOSE (IGOOSE) algorithm incorporating elite opposition-based learning, probabilistic exploration based on elite solutions, and golden-sine mutation strategies were developed, significantly enhancing global search capability and solution robustness. A case study based on real operational data adjusted for confidentiality was conducted, and comparative analyses with Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO) demonstrated the superiority of IGOOSE. Furthermore, an ablation study validated the effectiveness of each enhancement strategy within the IGOOSE algorithm. The optimized operation planning model reduced passenger waiting times by approximately 12.72%, improved load balancing by approximately 39.30%, and decreased the overall optimization objective by approximately 10.25%, highlighting its effectiveness. These findings provide valuable insights for urban rail transit operation management and indicate directions for future research, underscoring the significant potential for energy savings and emission reductions toward sustainable urban development.
1. Introduction
Rapid urbanization and accelerated population growth have intensified the imbalance between urban transportation demand and supply. This imbalance has led to widespread issues, including traffic safety concerns, excessive energy consumption, and environmental pollution, posing significant global challenges. Urban rail transit (URT), characterized by large capacity, high efficiency, low energy consumption, and minimal environmental impact, has increasingly gained global attention as a critical solution to mitigate urban sprawl and enhance transportation efficiency. Moreover, considering the diverse sociodemographic characteristics of urban populations, public transport supply needs to be carefully tailored to passenger profiles, which helps better match transport services with actual demand and effectively alleviates the demand–supply imbalance [1]. Consequently, urban rail transit plays an increasingly significant role in driving national economic growth and social development.
URT is undergoing accelerated expansion globally, significantly influencing ridership at existing stations [2]. This trend is particularly pronounced in densely populated countries like China. In the past year, China’s total urban rail transit ridership exceeded 32 billion passengers, an increase of 9.47% over the previous year. The average daily urban rail transit ridership across the country reached 88.13 million passengers, up 8.06% year-on-year. Additionally, passenger turnover volume reached 264.47 billion passenger-kilometers, representing a 7.92% increase compared to the same period in the previous year.
Urban rail transit not only effectively alleviates urban traffic pressure but also significantly contributes to the economic development of cities by promoting optimized industrial structures and enhancing residents’ living standards [3]. Additionally, the deployment of urban rail transit helps reduce pollution levels, improving air quality and thereby promoting sustainable urban and environmental operations [4,5].
Currently, urban rail transit faces considerable challenges, such as excessive passenger flows during peak hours, high operational costs, inefficient resource utilization, and uneven spatiotemporal passenger distribution. Consequently, developing targeted train operation plans is thus essential. Moreover, rapidly formulating effective response strategies for fluctuating and directionally imbalanced passenger demands imposes higher requirements on the computational efficiency of train operation optimization models. To address these challenges, this study proposes a combined short-turning operational model integrated with unpaired train dispatching strategies to manage tidal passenger flows and spatial passenger imbalances. A specialized algorithm was developed to efficiently find the scheduling solutions that best balance operational costs, passenger waiting times, and load distribution.
The remainder of this paper is organized as follows:
Section 2 provides a literature review on urban rail transit operation planning, passenger flow optimization under tidal conditions, and the related optimization algorithms.
In Section 3, the spatiotemporal characteristics of passenger flow and current operational modes in urban rail transit are analyzed, followed by the introduction of a combined operational mode integrating short-turning with unpaired train dispatching strategies.
Section 4 formulates a multi-objective optimization model aimed at minimizing operational costs, reducing passenger waiting times, and improving passenger load balance, along with practical operational constraints.
Section 5 proposes an Improved GOOSE algorithm enhanced through elite opposition-based learning, probabilistic exploration based on elite solutions, and golden-sine mutation strategies to effectively solve the optimization model.
Section 6 conducts a case study using data from Nanjing Metro Line 3 to validate the proposed model and algorithm, including comparative analyses against Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO), as well as sensitivity analysis and an ablation study.
Finally, Section 7 summarizes the main findings and outlines potential areas for future research.
2. Literature Review
2.1. Train Operation Plan
The train operation plan in urban rail transit is a complex and systematic problem encompassing four primary aspects: routing optimization, train frequency optimization, stop-skipping strategies, and train formation optimization.
Routing optimization refers to determining train routes and turn-back locations to efficiently match passenger demand with available operational resources.
Short turning and full-length train operations (short as short-turning or short-routing) represent the most common routing strategy. Canca et al. [6] developed a short-turning strategy to effectively handle demand disruptions, reducing passenger waiting times. Zhang et al. [7] optimized short-turning operations for Beijing Subway Line 4, significantly mitigating peak-hour congestion. He et al. [8] optimized short-turning schemes based on passenger demands, substantially enhancing passenger load balance. Zhang et al. [9] further integrated short-turning operations with express and local services, achieving notable improvements in overall service quality.
Meanwhile, the Y-shaped routing strategy has also received substantial attention from researchers. Yang et al. [10] introduced an integrated optimization approach for Y-shaped networks, coordinating train timetabling with rolling-stock circulation. Wang et al. [11] applied virtual coupling to real-time scheduling in Y-shaped networks, significantly improving operational efficiency.
Additionally, cross-line routing strategies have also been explored. Zhao et al. [12] optimized train operation plans considering balanced rolling-stock circulation across multiple lines, thus improving overall resource utilization.
Frequency optimization directly influences passenger waiting times and vehicle occupancy. Dou et al. [13] proposed a method focused on controlling load factors, significantly enhancing operational efficiency and reducing costs.
Stop-skipping strategies selectively skip stops at lower-demand stations to reduce travel times and improve operational efficiency. Hu et al. [14] integrated skip-stop patterns with passenger flow control, significantly reducing passenger waiting costs. Peftitsi et al. [15] evaluated skip-stop policies based on passenger travel costs, demonstrating substantial improvements. Sahachaiseree et al. [16] optimized a three-pattern skip-stop scheme, further reducing travel times. Bai and Zhang [17] studied skip-stop scheduling under virtual coupling conditions, enhancing operational efficiency.
Train formation optimization adjusts train compositions to match fluctuating passenger demands. Ren et al. [18] proposed a two-step optimization for train marshaling and real-time station control, effectively improving passenger transfer efficiency at major hubs.
In summary, routing and stop-skipping strategies remain primary research focuses in train operation plans. Recent studies increasingly integrate multiple operational modes rather than relying on single-mode optimizations.
2.2. Optimization Under Tidal Passenger Flows
Urban rail transit systems frequently face operational difficulties arising from tidal passenger flows, characterized by significant directional and temporal imbalances. To address these challenges, various operational strategies have been explored. Li et al. [19] proposed an asymmetric, demand-oriented skip-stop operational strategy, effectively alleviating directional passenger flow imbalances. Zhu et al. [20] developed an asymmetric rolling-stock repositioning method to optimize resource distribution during peak tidal periods. Chen et al. [21] combined real-time scheduling optimization with strategic stop-skipping adjustments, achieving substantial reductions in operational costs while effectively managing directional passenger flows. Xiao et al. [22] introduced a balanced timetable optimization approach utilizing queuing theory to minimize passenger flow density on metro platforms during tidal conditions, significantly alleviating platform congestion. Moreover, Tian et al. [23] investigated unpaired train dispatching strategies, highlighting their efficacy in handling imbalanced passenger distributions and providing flexible operational adjustments. Despite these advancements, research integrating short-turning and unpaired train dispatch strategies specifically to address tidal passenger flows remains limited, representing a critical research gap warranting further exploration.
2.3. Optimization Methods Overview
Efficient solutions for train operation optimization typically involve exact algorithms, heuristic algorithms, and alternative approaches.
Exact algorithms provide optimal solutions but are limited by computational complexity. Zhao et al. [24] presented a mixed-integer linear programming (MILP) model for scheduling under time-varying passenger demands, effectively demonstrating practical utility for precise train scheduling problems.
Heuristic algorithms, such as Genetic Algorithms and Particle Swarm Optimization, are extensively applied due to their computational efficiency and flexibility. Wei [25] employed PSO to optimize train scheduling for Y-shaped routes, achieving effective optimization results.
Recently, improved heuristic algorithms have emerged. Du et al. [26] proposed a surrogate-assisted multi-objective Grey Wolf Optimizer for empty-heavy train allocation, demonstrating superior performance as an emerging intelligent optimization algorithm, notably enhancing coordinated line utilization balance compared to traditional heuristic methods. El-Kenawy et al. [27] introduced the Greylag Goose Optimization, exhibiting higher efficiency and robustness compared to traditional heuristic methods. Hamad and Rashid [28] proposed the GOOSE algorithm inspired by the social behavior of geese, demonstrating superior convergence and local optima avoidance capabilities. Sun et al. [29] proposed an Improved Goose Optimization (IGO) algorithm inspired by the flocking behavior of geese, integrating dynamic inertia weight, chaotic mapping, and Lévy flight strategies to enhance global search performance in multi-objective optimization. This algorithm has primarily been applied in microgrid scheduling and environmental management but has yet to be explored in urban rail transit optimization, highlighting its research potential.
Alternative methodologies have also been explored. Wen et al. [30] proposed real-time scheduling optimization using Advantage Actor-Critic (A2C) deep reinforcement learning, showing significant operational improvements. Dong et al. [31] combined deep reinforcement learning with differential algorithms (DRLDA) for collaborative multi-train energy-saving control. Liu et al. [32] developed a comprehensive collaborative optimization framework integrating scheduling, transfer connections, and passenger flow control, significantly enhancing operational efficiency. Tian et al. [33,34] developed a surrogate-assisted bio-inspired algorithm, namely the Bioinspired Discrete Two-Stage Surrogate-Assisted Algorithm, for large-scale combinatorial problems, providing valuable insights for addressing complex optimization tasks.
Therefore, researchers continue to explore novel and advanced solution algorithms. Heuristic algorithms remain widely employed due to their computational efficiency and flexibility; however, there is still considerable scope for advancement. Developing newer and more intelligent heuristic algorithms remains critically important.
In summary, the existing research on urban rail transit operation planning has systematically addressed routing optimization, frequency adjustments, stop-skipping strategies, and train formation. However, studies specifically targeting directional passenger flow imbalances, particularly tidal passenger flows, remain relatively limited, and integrated analyses that simultaneously consider spatiotemporal characteristics and directional imbalances are even scarcer. Operational strategies such as combining short-turning and unpaired train dispatching—aiming to reduce passenger waiting times, balance passenger loads, and minimize operational costs—have not been thoroughly explored. Furthermore, advanced heuristic algorithms, especially recently developed intelligent optimization methods, still demonstrate considerable potential for effectively addressing complex multi-objective optimization problems. To address these identified research gaps, this study proposes a novel combined operational mode integrating short-turning with unpaired train dispatch strategy and develops an Improved GOOSE (IGOOSE) algorithm specifically designed to efficiently solve the resulting multi-objective optimization problem.
To validate the effectiveness of the proposed model and algorithm, a case study analysis is performed based on real-world operational scenarios of Nanjing Metro Line 3. Considering data confidentiality requirements, actual operational data are adjusted and processed before analysis. Results demonstrate that the proposed combined operational strategy effectively reduces passenger waiting times, improves load balancing, and significantly enhances overall operational efficiency. Consequently, this study provides novel theoretical insights and practical operational strategies for managing tidal passenger flows in urban rail transit systems.
3. Problem Description
3.1. Spatial–Temporal Distribution of Passenger Flow
In urban rail transit systems, developing an optimal train operation scheme is critical for effectively managing fluctuations in passenger flow, enhancing service quality, and optimizing operational costs. Given the substantial variability in passenger distribution over both time and space, operators can implement coordinated optimization strategies. These strategies not only cater to varying passenger demands during peak and off-peak periods but also effectively address tidal flows and directional imbalances, thus achieving balanced train operations and improved passenger service quality.
- (1)
- Temporal Distribution
In terms of temporal variation, significant differences can be observed. Passenger flow notably increases during morning and evening peak hours, whereas it markedly decreases during off-peak periods such as midday and nighttime. As illustrated in Figure 1, the morning peak typically occurs between 7:00 and 9:00, while the evening peak is concentrated around 17:00 to 19:00. Moreover, distinct passenger flow patterns are observed between weekdays and weekends; weekdays primarily feature commuting trips, whereas weekend travel often focuses on commercial and entertainment areas, exhibiting stronger variability.
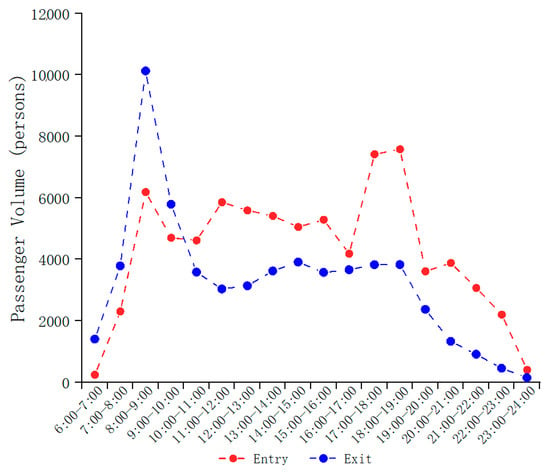
Figure 1.
Entry and exit passenger flow at Nanjing South Station on Nanjing Metro Line 1.
Typically, the periods between 7:00 and 10:00 and 16:00 and 19:00 are recognized as peak hours in urban rail transit systems, characterized by significantly higher passenger flows. Conversely, periods excluding the first and last hours of operation and peak hours are termed off-peak periods. Additionally, certain transit lines exhibit distinct tidal passenger flow phenomena. As shown in Figure 2, Nanjing Metro Line 3 exhibits a significant directional imbalance in passenger distribution during the morning peak hours, whereas such an imbalance is not observed during off-peak periods.
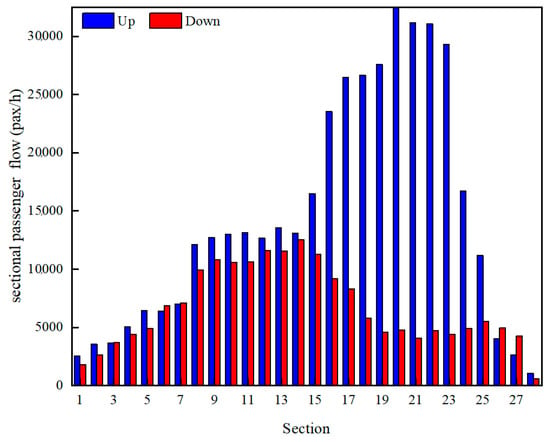
Figure 2.
Sectional passenger flow of Nanjing Metro Line 3 during morning peak hours.
Tidal passenger flow refers to a distinctively uneven distribution of passengers in urban public transportation systems (e.g., metros and buses) across different times or directions. This phenomenon is commonly observed during certain periods of the day, such as the morning and evening peaks, when passenger flow is predominantly concentrated in one direction, while during other periods, it appears relatively balanced or flows in the opposite direction. The direction imbalance coefficient D is expressed as follows:
Here, represents the total upstream sectional passenger flow, and denotes the total downstream cross-sectional passenger flow. In transportation planning and optimization, a directional imbalance coefficient D exceeding a specific threshold (e.g., 1.25) typically indicates a significant tidal flow phenomenon. Consequently, operational strategies such as deploying additional unidirectional services may be necessary to manage this passenger flow imbalance effectively.
- (2)
- Spatial Distribution
Spatially, passenger flow imbalance is reflected in disparities at station level and among different line sections. Stations near major transportation hubs, commercial centers, or educational institutions typically experience higher passenger volumes, while stations located in regular residential areas or suburban regions have relatively lower passenger volumes. Moreover, line sections within urban core areas or at intersections of critical transit lines tend to exhibit higher sectional passenger flows, resulting in heavily loaded segments. In contrast, passenger volumes in remote or less frequently utilized sections are typically lower.
As illustrated in Figure 3, significant spatial imbalances in passenger flow distribution are observed along Nanjing Metro Line 2 during peak hours. Certain sections, particularly around key stations, such as Xinjiekou Station, or densely populated urban areas, experience notably higher passenger volumes, forming heavily loaded segments. Conversely, passenger volumes substantially decrease in sections farther from the urban core or less frequently visited areas, highlighting the pronounced spatial disparity along the line.
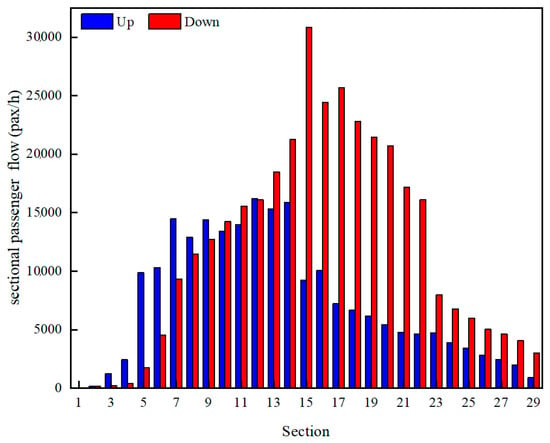
Figure 3.
Sectional passenger flow distribution of Nanjing Metro Line 2 during peak hours.
To decide whether mixed short-turn and full-length services should be implemented, it is necessary to examine the imbalance in passenger distribution across different sections. The sectional imbalance coefficient, a critical indicator quantifying this spatial disparity, is defined as the ratio between the maximum sectional passenger flow and the average sectional passenger flow across all sections in the same direction during a specific period:
where
: sectional imbalance coefficient
: passenger flow in section i
: section quantity
A higher sectional imbalance coefficient indicates greater variability in passenger flow among sections, suggesting greater suitability for implementing mixed short-turn and full-length train services. Conversely, a lower coefficient reflects more uniform passenger distribution across sections. Generally, when the sectional imbalance coefficient exceeds 1.5, adopting a mixed short-turn and full-length service strategy becomes appropriate.
3.2. Operation Modes
- (1)
- Mixed short-turn and full-length service
Mixed short-turn and full-length service (or short-route operation) is a commonly adopted and widely applied operational strategy in urban rail transit systems. Under this operation mode, the transit line simultaneously provides full-length services from the origin station to the terminal station (full-length service), and short-turn services between intermediate stations equipped with turn-back facilities. As illustrated in Figure 4, assuming a line consists of stations numbered from 1 to n, a short-turn service operates specifically between stations j and m, both of which have the capability for train turnaround. Typically, one of the short-turn endpoints can coincide with either the origin or terminal station of the line. Stations within the blue dashed line range constitute the set of short-route stations , while the full-length set includes all stations.
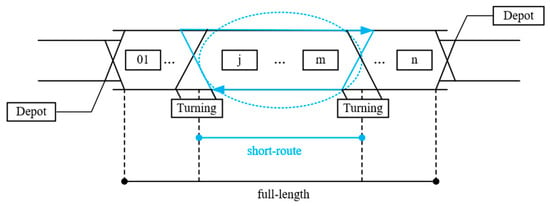
Figure 4.
Schematic diagram of mixed short-turn and full-length service.
Lines employing mixed short-turn and full-length services generally exhibit the following characteristics:
1. Existence of segments with notably high passenger flow: Such segments typically connect major nodes or significant transport hubs where passenger demand is concentrated.
2. Imbalanced passenger distribution: Passenger intensity varies significantly across different sections, with some segments having substantially higher volumes than others, resulting in distinct “peak” and “non-peak” segments.
3. Coexistence of short-distance and long-distance passenger demand: Short-distance passengers predominantly concentrate in core segments, while long-distance passengers travel across the entire route.
- (2)
- Unpaired Train Operation
Generally, metro trains operate in pairs. The unpaired train operation scheme involves dispatching unequal numbers of trains in the upstream and downstream directions within certain sections, without changing the original routing plans or station stopping patterns. The principle underlying the unpaired operation scheme is to adjust transport capacity in specified directions or sections by dispatching different numbers of trains in the upstream and downstream directions. The operational organization of the unpaired train scheme is illustrated in Figure 5. In the downstream direction, the dispatch frequency is higher than in the upstream direction. Typically, surplus trains in the higher-frequency direction are routed into nearby depots or stabling sidings. These trains subsequently re-enter service from the depot to continue the one-way operation scheme when reverse tidal passenger flows occur. The one-way operation path of these surplus trains is shown by the red arrows in the image, while the remaining trains, following the blue arrow path, perform a turning and continue to operate within the system.

Figure 5.
Schematic diagram of unpaired train operation.
The unpaired train operation scheme enhances or reduces transport capacity in specific local areas by adding or adjusting train services under existing infrastructure conditions. It provides transport capacity aligned with passenger demand in both directions, precisely addressing the characteristics of directional passenger flow imbalance without requiring hardware replacement or infrastructure upgrades. This operational approach effectively manages directional passenger flow imbalances resulting from tidal flow phenomena. Specifically, it allows for the adjustment of train dispatch frequencies during peak periods, enabling higher dispatch frequencies in the higher-demand direction and correspondingly lower frequencies in the opposite direction. Consequently, this scheme effectively addresses directional passenger flow imbalance and improves overall transport efficiency.
- (3)
- Combined Mode of Short Routing with Unpaired Train Operation
Although numerous studies have explored the combination of various train operation modes, research integrating short routing with unpaired train operations remains relatively limited. The unpaired train operation scheme effectively addresses issues of both spatial passenger flow imbalance and directional tidal flow. Meanwhile, short routing allows for flexible allocation of transport capacity along the line. Combining these two operational strategies can efficiently respond to complex spatial–temporal passenger demand patterns, highlighting significant research value and promising application potential, and thus warrants further in-depth exploration and practical implementation.
This combination has extensive application scenarios. Taking several lines of the Nanjing Metro as examples, Table 1 presents representative lines within the network, excluding lines with low passenger volumes or lines that were not fully operational during the statistical period. Apart from Line 1, nearly all the listed lines can potentially benefit from applying both short-turning and unpaired train operation optimization strategies.

Table 1.
Sectional and directional imbalance coefficients for selected lines of the Nanjing Metro.
In summary, this chapter analyzed the spatial–temporal imbalances of passenger flow distribution. Subsequently, the characteristics of short routing and unpaired train operation modes were elaborated. Furthermore, the potential benefits and feasibility of combining these two operational strategies were discussed. These analyses lay the necessary groundwork for the model formulation presented in the next section.
4. Modeling
4.1. Preparation for Modeling
- (1)
- Basic Assumptions
Considering the operational characteristics of urban rail transit and the necessity to simplify real-world factors for modeling, as well as the operational features of combined short routing and unpaired train operation, this chapter proposes the following assumptions:
1. Passenger arrivals are uniformly distributed at stations, and passengers always choose the earliest available train without considering capacity constraints. This simplifies the calculation of average waiting time and maintains a clear focus on train scheduling optimization.
2. Passenger demand in overlapping sections is proportionally distributed based on dispatch frequency of each route, reflecting realistic passenger behavior without distinct preference for short or full-length routes, simplifying load estimation.
3. Trains assigned to short and full-length routes are operated independently, without mutual interchange. The total number of operational trains is constrained by the maximum available fleet, ensuring feasibility in vehicle scheduling.
4. Train operations are unaffected by external factors such as infrastructure limitations or signal controls, and travel speeds are consistent in both directions without delays. This idealized assumption is suitable for strategic planning and optimization purposes.
5. Short-turning terminals must have turnaround facilities with fixed turnaround times, reflecting infrastructure constraints and simplifying operational cycle calculations.
6. All trains operate with a stop-at-all-stations policy, without overtaking in between stations, aligning with typical metro operation practices and reducing modeling complexity.
7. Both short-turning and full-length trains have identical train-set compositions, maintaining equal carrying capacities to facilitate objective comparative analyses between operation modes.
8. Combined short-turning and unpaired operations are implemented simultaneously, with surplus trains directly routed into depots, without considering subsequent reverse-direction empty runs.
- (2)
- Passenger Classification
The average waiting time for passengers is determined by train dispatch frequencies. Since the operational mode under consideration involves short routing, passengers’ average waiting times differ depending on the segments they utilize. As illustrated in Figure 6, passengers traveling in the up direction can be categorized into six types based on their origin and destination:
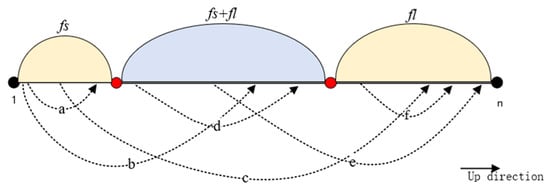
Figure 6.
Passenger classification based on origin-destination stations under short routing operation.
Passengers whose origin and destination stations are both on segments served exclusively by the full-length service (type a, c, f) are only serviced by the full-length train frequency ().
Passengers whose trips occur entirely within the overlapping section of short and full-length routes (type d) benefit from combined frequencies of both short and full-length services ().
The remaining passengers (type b and e), whose trips begin or end outside the short-turning segments, are still only serviced by the full-length frequency (, as they must initially or finally rely on full-length services.
4.2. Optimization Objectives
This study demonstrates the potential to enhance efficiency, cost-effectiveness, and sustainability in public transportation. Generally, the objective function of the optimization model comprises two main components: passenger travel cost and operational cost. Passenger travel cost reflects the impact of the train operation scheme on passenger service quality, primarily measuring passenger travel efficiency and travel experience. Operational cost, on the other hand, considers resource consumption and economic expenditures from the perspective of transit operators, associated with train operations.
- (1)
- Operational cost
This study addresses optimization problems under existing line conditions, and since the cost of acquiring new trains significantly differs from other operational costs, the scenario involving newly purchased vehicles is not considered here. Previous studies typically defined variable operational costs based on total train kilometers traveled, energy consumption costs, and operational time costs. Considering that this study incorporates the additional travel distance for surplus trains routed to depots in high-frequency directions as an operational cost indicator of unpaired train operation, total train travel distance is adopted consistently as the measure of operational cost.
The single-trip travel distances for full-length and short-turning trains are calculated as the summation of inter-station distances within their respective operational sections:
where
: distance from station to the next station
, : single-trip travel distances for full-length and short-turning trains
, : sets of stations served by the full-length and short-turning trains
Therefore, the total train travel distance is calculated as the product of train dispatch frequency and single-trip travel distance. Considering different dispatch frequencies in upstream and downstream directions, the dispatch frequencies for full-length and short-turning services (, ) are further subdivided into , , , , where subscript “1” denotes the upstream direction, and “2” denotes the downstream direction.
Therefore, the total train travel distance can be expressed as follows:
For the unpaired train operation scenario, it is necessary to consider the additional cost associated with surplus trains dispatched in the higher-frequency direction deadheading to stabling sidings or depots for standby.
The distance for trains to reach the nearest depot comprises two parts: the distance from the train’s current location to the station connected to depot k (denoted by ), and the entrance distance into depot k (denoted by ). Thus, the total depot-reaching distance () is expressed as follows:
Considering that the distances from the terminal stations of full-length and short-turning services to depots may differ, the total depot-reaching distances for full-length and short-turning trains are defined separately as , respectively.
The total deadhead distance to depots is expressed as follows:
where
, : Binary variables indicating whether the upstream and downstream directions have a higher dispatch frequency.
Thus, the objective function for operational cost optimization is formulated as follows:
This objective comprehensively reflects the constraints imposed by the model on operational costs, explicitly accounting for both actual train travel distances and additional deadhead distances resulting from unpaired train operations. By minimizing total train travel and deadhead distances, the proposed approach aims to significantly reduce operational costs while ensuring adequate transport capacity to meet passenger demands in urban rail transit systems. Moreover, reducing train deadhead mileage not only lowers energy consumption costs but also significantly decreases pollutant emissions, thus effectively supporting energy conservation, emission reduction, and the sustainable development of urban transportation systems.
- (2)
- Passenger cost
As mentioned previously, passenger travel costs include both passenger travel efficiency and travel experience. Regarding passenger travel efficiency, this study utilizes the total average passenger waiting time across different passenger types as the optimization objective. However, in terms of passenger travel experience, macro-level planning models typically cannot evaluate detailed passenger load rates as operational timetable optimization would. Therefore, this study employs the sectional loading rate as an indicator of passenger travel experience. This indicator also reflects the uneven distribution of passenger loads along the line, enabling an assessment of whether the optimization effectively mitigates passenger load imbalances.
1. Average Waiting Time
As described previously in passenger classification, passengers of type d are influenced simultaneously by the dispatch frequencies of both short-turning and full-length services, whereas the other passenger types are approximately considered to be influenced solely by the full-length service frequency. Passenger volumes can be obtained from OD data, and the expressions for the quantities of the two passenger categories are given below:
where
: the number of passengers traveling from station to station .
In contrast, full-length passengers () are those whose travel involves at least one station outside the short-turn section (i.e., either origin or destination lies beyond ). Their total passenger demand is represented as:
According to the previous assumption of uniform passenger arrivals, the average waiting time is equal to half the reciprocal of the train arrival frequency in the segment. Therefore, the total waiting times for passengers using full-length () and short-turning () services are expressed as follows:
Since the dispatch frequencies for short-turning and full-length services differ between upstream and downstream directions, the average passenger waiting times are correspondingly calculated separately for each direction (, ).
Therefore, the optimization objective is to minimize the overall total passenger waiting time across both directions:
This objective explicitly represents the comprehensive optimization of passenger travel efficiency and experience, emphasizing the reduction in average passenger waiting time at platforms to enhance overall urban rail transit service quality. By separately considering the upstream and downstream dispatch frequencies and distinguishing between short-turning and full-length services, the objective function accurately captures the diverse service demands of different passenger groups, enabling targeted optimization of service levels. Additionally, by minimizing passenger average waiting times, this optimization significantly enhances the attractiveness and service satisfaction of urban rail transit systems, helping to alleviate platform congestion during peak periods and considerably improving passenger comfort and convenience.
2. Sectional Load Balancing
The sectional loading rate is defined as the ratio of actual passenger volume to the provided transport capacity within a given section, which quantifies passenger load levels across different sections. This indicator effectively captures passenger travel experience while simultaneously enabling transit operators to enhance the overall load balancing along the line. Considering the differing dispatch frequencies in upstream and downstream directions under the unpaired train operation scenario, the sectional loading rates for each direction should be calculated separately.
For sections operated exclusively by full-length services, the sectional loading rates are calculated as follows:
where
, : sectional loading rates at section i for upstream and downstream directions
, : actual section passenger volumes at section i for upstream and downstream directions
C: carrying capacity per train
Similarly, the sectional loading rates for sections with short-turning services are calculated as follows:
Including as
The sectional load balancing indicator refers to the variance of the sectional loading rates along the line, used to measure the overall uniformity of passenger load distribution. Under the unpaired train operation scenario, dispatch frequencies differ between upstream and downstream directions, potentially resulting in significant differences in passenger load distributions. Therefore, to evaluate load balancing more accurately, this study separately calculates the sectional load balancing indicators for upstream and downstream directions. The specific formulas are as follows:
where
: variances of sectional loading rates in the upstream and downstream directions.
In summary, the sectional load balancing objective is formulated as
Combining all objectives, the final multi-objective function is formulated as
where
, , : weighting coefficients reflect the relative importance among operational cost, passenger waiting time, and load balancing objectives.
4.3. Constraints
To closely reflect the realistic operational context of urban rail transit and to ensure practical applicability of the proposed optimization model, this study enhances and extends the conventional constraints associated with short-turning and full-length service models, based on practical operational experience. The newly introduced and improved constraints explicitly account for infrastructure limitations, practical vehicle scheduling requirements, passenger service quality considerations, and operational efficiency objectives. These adjustments are intended to guarantee the feasibility of model solutions and the rationality of operational schemes.
Minimum dispatch interval constraint: To ensure that the train operation scheme adheres to the maximum line capacity constraints, a minimum dispatch interval constraint must be established. This ensures that the interval between consecutive trains satisfies safe train headway requirements. Considering that the dispatch frequencies in upstream and downstream directions differ under unpaired train operation, the minimum dispatch interval () constraints for both directions are expressed separately as follows:
Similarly, to further ensure dispatch safety within each operational route (short-turning and full-length service), the individual dispatch frequencies must also satisfy the minimum dispatch interval constraints:
Capacity Assurance Constraint: To prevent passenger overcrowding and ensure adequate transport capacity, passenger volumes in each section must not exceed the available transport capacity within the corresponding time period. The capacity assurance constraints for the two directions are expressed as follows:
Similarly, for sections exclusively served by full-length services, the capacity assurance constraints are expressed as follows:
Train Turnover Constraint: The total number of trains in operation must not exceed the available rolling stock. Therefore, the turnover constraint can be expressed as follows, where the turnover times for each type of train are calculated based on their respective cumulative travel times:
where
: round-trip time for a full-length train, calculated as:
: round-trip time for a short-turn train, calculated as:
Turnback station position constraint: To ensure operational feasibility, the starting and ending stations of short-turn services must be stations with turnback capabilities.
Short-turning Unpaired Passenger Flow Coverage Constraint: To guarantee a realistic passenger-demand basis for unpaired operations, the passenger flow ratio between upstream and downstream directions within the short-turning service segments must reflect clear tidal passenger flow characteristics, expressed as follows:
Short-routing Sectional Passenger Flow Coverage Constraint: To avoid selecting overly close origin–destination stations for short-turning services and ensure effective passenger load sharing, the cumulative passenger flow in sections covered by the short-turning service must constitute at least a certain proportion of the total sectional passenger flow when generating optimized solutions:
In this chapter, the fundamental assumptions necessary for model formulation were first defined, and passengers were classified according to the characteristics of short-turning and full-length operation modes, clearly identifying the service demands of different passenger groups. Subsequently, integrating the operational features of unpaired train operations, this study constructed a comprehensive mathematical model for combined operational scenarios. Three core optimization objectives—operational cost, passenger waiting time, and sectional load balancing—were established to achieve an optimal balance between operators’ economic efficiency and passengers’ service experience. Finally, based on practical operational regulations and accumulated experience, a set of constraints was proposed to guarantee the feasibility and practical applicability of optimization results. In the following chapter, an improved heuristic intelligent algorithm will be introduced and refined to efficiently solve the proposed combined-operation optimization model.
5. Improved GOOSE Algorithm
To effectively solve the multi-objective optimization model proposed in this study, an Improved GOOSE Algorithm (IGOOSE), based on the original GOOSE Algorithm, is introduced. Inspired by the characteristic behavior of geese maintaining balance while standing on one leg to protect other individuals within their group, the GOOSE Algorithm adaptively adjusts search resolution and speed within the search space, enabling rapid convergence and high accuracy.
The improvements made in this study include initializing the population using an elite opposition-based learning strategy, introducing probabilistic exploration based on specific elite solutions during the exploration phase, and employing a golden-sine-based mutation strategy to enhance individual solutions, thereby further improving the overall algorithm performance.
The improved algorithm primarily comprises the following phases: Population Initialization, Exploitation Phase, Exploration Phase, and Mutation Phase.
- (1)
- Population Initialization
Firstly, the initial population is generated. Let the optimization variable be denoted as vector , with lower and upper bounds represented by vectors and . Each individual in the population is initialized as follows:
where is a random vector with elements uniformly distributed between 0 and 1. Consequently, an initial population S composed of N goose individuals is generated.
Objective function values for each individual in the initial population are computed and stored in an array objs [1, 2, …, N]. Subsequently, the top N/2 individuals with the best objective values form the elite population E.
To enhance diversity and quality of the initial population, this study employs an elite opposition-based learning strategy, with the opposition-based individual calculated as:
where denotes the j-th dimension of the i-th elite individual in population E, and , denote the lower and upper bounds of the j-th dimension, respectively.
The generated opposition-based population is merged with the initial population S. After calculating their objective values, the top N individuals are selected to form the final initial population P.
During each iteration of the algorithm, each goose individual updates its position by randomly performing either an exploitation or an exploration operation, each with a probability of 0.5. After all individuals complete this probabilistic position update (exploitation or exploration), a mutation operation is uniformly performed on the entire population.
- (2)
- Exploitation phase and Exploration phase
1. Exploitation phase
After completing the initial population generation, the algorithm proceeds to the exploitation phase. For each goose individual , a random number pro is generated uniformly within the range [0, 1], and simultaneously, another random number within the range [5, 25] is generated, representing the stone weight associated with the individual goose.
In the exploitation phase, two position updating strategies are applied based on the random probability pro and the stone weight :
When pro > 0.2 and > 12:
Including
When pro ≤ 0.2:
where
: the free fall speed
: the distance between the two geese
is a 1 × dim vector consisting of random numbers uniformly distributed in [0, 1], representing the time needed for the sound from the stone hitting the ground to reach each dimension of the goose individual.
: the gravitational acceleration,
: the sound propagation speed (343 m/s),
, are the total and average sound propagation times, respectively,
is a random coefficient between 0 and 1.
2. Exploration phase
The exploration phase aims to enhance the global search capability of the population, preventing the algorithm from becoming trapped in local optima. Specifically, the updating rules for individual goose positions during exploration are as follows:
Initially, generate a random number in the range [0, 1]:
If > 0.5, the current global best individual position is selected directly as the exploration base position pos
If ≤ 0.5, compute the selection probability index for each goose individual using the following equation:
where are the objective function values for goose individuals and , respectively, denotes the Euclidean distance between individuals, and is a small constant to prevent division by zero. The individual goose with the largest value is selected as the exploration base position pos.
Subsequently, update the positions of goose individuals according to:
where
is the minimal average time required for the sound propagation to reach the goose individuals within the population up to the current iteration
denotes an adaptive factor defined as follows, dynamically adjusting the search scope of the algorithm:
is the current iteration number
represents the maximum number of iterations.
- (3)
- Mutation Phase
To further enhance the global search capability and avoid premature convergence to local optima, this study integrates a golden sine strategy into the GOOSE algorithm as a mutation operation. For each goose individual in the population, the mutation operation is performed as follows:
where
∈ [0, π], ∈ [0, 2π] are random numbers
denotes the historical best position of the i-th goose individual up to the current iteration t
are related to the golden ratio and are defined as
Here, is the golden ratio coefficient, specifically defined as: .
Then, the objective function value of the mutated individual is calculated. If the condition:
is satisfied, the original individual is replaced with the mutated individual , thus facilitating continuous improvement of the population.
In summary, the Improved GOOSE algorithm iteratively proceeds through four primary phases: Population Initialization, Exploitation, Exploration, and Mutation. Throughout these iterative phases, the positions and objective values of goose individuals are continuously updated and optimized. Upon reaching the maximum number of iterations or satisfying convergence criteria, the algorithm outputs the global optimal solution and the corresponding optimal objective value . By integrating elite opposition-based learning and golden-sine mutation strategies, the algorithm significantly enhances its global search capability, effectively avoids local optima, and ensures stability and reliability of the optimization results.
6. Case Study
Based on the combined operational mode optimization model and the Improved GOOSE (IGOOSE) algorithm presented in previous chapters, this chapter conducts a case study analysis using peak-hour passenger flow data and operational conditions of Nanjing Metro Line 3 as a template. To comply with data confidentiality requirements and to accentuate the optimization results, the actual operational data have been appropriately adjusted. Moreover, station names along the line have been anonymized and represented sequentially as “Station 1” through “Station n”.
Nanjing Metro Line 3 is an integral part of the urban rail transit network in Nanjing. The line extends over a total length of 44.87 km, employing both underground and elevated alignments, and consists of 29 stations. The line begins at Linchang station in the northern part of Nanjing and terminates at Mozhoudonglu station in the south, traversing major north–south transportation corridors of the city. It passes through several key administrative districts, including Pukou, Gulou, Xuanwu, Qinhuai, Yuhuatai, and Jiangning districts, effectively serving major residential, commercial, and business areas along its route.
The trains operating on Nanjing Metro Line 3 consist of six-car B-type trainsets with a maximum designed operating speed of 80 km/h, and the headway during peak hours ranges approximately from 3 to 5 min. The average daily ridership exceeds 600,000 passengers. Additionally, the line features two depots, situated at Linchang station in the northern terminal and Mozhoudonglu station in the southern terminal, providing essential facilities for train maintenance and stabling.
During weekday morning peak hours, Nanjing Metro Line 3 employs a short-turning strategy, featuring a significant directional passenger flow imbalance with a directional imbalance coefficient of up to 2.18. Such characteristics make it particularly suitable for analysis using the combined operational mode proposed in this paper. Due to confidentiality requirements and for ease of subsequent simulation analysis, the adjusted line data described below will be uniformly referred to as “Line X”.
The 44 rolling stock units employed in the optimization model reflect the realistic fleet size from the existing operational plan, rather than an arbitrary assignment. To ensure sufficient flexibility and loosen constraints in optimization, the total available fleet was set slightly higher at 50 trains. Ultimately, the optimization yielded a train usage number close to the original practical scenario, ensuring that the solution remains practically implementable and consistent with operational realities.
The values of model parameters and basic line conditions are presented in Table 2. Line X comprises 29 stations, with the turning station for short-turning services located at Station 11. The total length of the line is 44.87 km, and it is equipped with two depots and 50 trains for daily operations and maintenance. In the optimization model, parameters , β, and γ denote the optimization weights for passenger waiting time, train operational mileage, and passenger load balance, respectively, with assigned values of 20, 12, and 2000, reflecting a balanced consideration between passenger service quality and operational efficiency. The parameter ε, set at 60%, represents the proportion of the line covered by short-turning services, indicating coverage primarily over high-demand sections. Additionally, the maximum passenger capacity per train (C) is 1500 passengers, while the maximum and minimum dispatch intervals are set at 15 min and 2 min, respectively, ensuring moderate service frequency within operational constraints.

Table 2.
Line information and model parameters.
In real-world metro operations, short-turn and full-length trains are typically dispatched in integer frequency ratios (e.g., 1:1 or 2:1). This simplifies timetable scheduling and maintains operational stability, but also potentially limits optimization effectiveness. In this study, we consider two dispatching strategies: Integer-ratio dispatching, representing practical operational scenarios, and Flexible-frequency dispatching, where short-turn and full-length train frequencies are treated as continuous variables. By comparing the results from these two approaches, we aim to identify the gap between theoretical optimization potential and practical feasibility, offering insights to improve real-world scheduling practices.
To evaluate the efficiency and accuracy of the proposed IGOOSE algorithm, traditional GA and PSO methods are introduced for comparison. To clearly illustrate algorithmic performance differences, both comparative algorithms are applied under flexible-frequency dispatch scenarios, minimizing constraints from practical operations.
The optimization plans under different strategies are summarized in Table 3, where “(I)” indicates integer-ratio dispatching, “(F)” indicates flexible-frequency dispatching, and “F/S” abbreviates full-length and short-turn trains, respectively. As demonstrated, the proposed IGOOSE algorithm achieves superior frequency allocation compared to GA and PSO, reflecting its effectiveness in optimizing plan. In actual operational practice, train dispatch frequencies obtained from optimization (often expressed in decimals) are rounded to the nearest integer values for implementation. This rounding introduces minor deviations from theoretical optimal, but these differences typically have limited practical impact on operational efficiency.

Table 3.
Comparison of optimization plan for target models.
The optimization outcomes under different strategies are summarized in Table 4. Compared with the unoptimized scenario, all optimized strategies significantly reduce passenger waiting time and enhance load balance. Specifically, the flexible-frequency dispatch strategy optimized by the IGOOSE algorithm, under approximately constant operating costs, achieves the lowest optimal objective value (62,436.68), resulting in roughly a 12.72% reduction in passenger waiting time, a 39.30% improvement in load balance, and an overall 10.25% improvement in the objective value. Although the GA method obtained slightly lower passenger waiting times, it resulted in significantly higher operational costs and marginally improved load balancing. Hence, the comprehensive objective function value obtained by GA was inferior to that of the IGOOSE algorithm, demonstrating that GA could not achieve a comparatively optimal balance among the three objectives. These results clearly highlight the practical advantage of employing the flexible-frequency dispatching strategy, as it provides greater precision and adaptability.

Table 4.
Comparison of optimization results for target models.
However, due to real-world operational constraints, integer-ratio dispatching strategies inherently limit the potential to achieve the theoretically optimal solutions realized under flexible-frequency dispatching.
To comprehensively evaluate the performance of the proposed Improved GOOSE algorithm, traditional heuristic optimization algorithms including GA and PSO, alongside the Grey Wolf Optimizer—an intelligent optimization algorithm known for strong global search capabilities—were used as benchmarks. Figure 7 illustrates the convergence behaviors of these algorithms under a population size of 50 over 200 iterations. The comparative results demonstrate distinctive characteristics for each algorithm: PSO shows rapid initial convergence but tends to stagnate early, settling into local optima prematurely. GA, by contrast, converges relatively slowly but attains accuracy in later stages. GWO exhibited superior convergence performance compared to traditional heuristic methods (GA and PSO). Nevertheless, the proposed IGOOSE algorithm consistently outperforms all other algorithms, demonstrating not only faster convergence but also greater precision and robustness in continuously escaping local optima. This clearly highlights the superiority of the IGOOSE algorithm in addressing complex multi-objective optimization problems, such as urban rail transit operations.
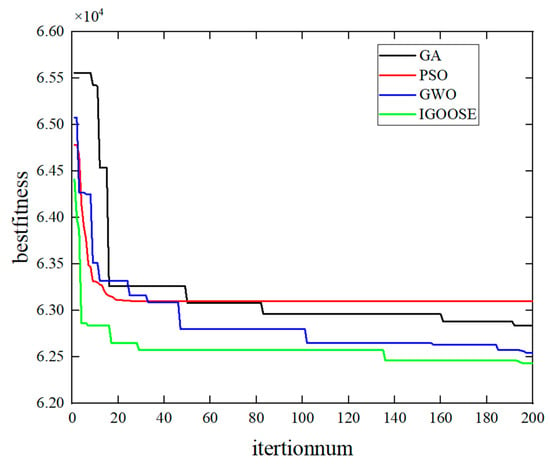
Figure 7.
Convergence curves of the four algorithms.
To evaluate the individual contributions of each improvement strategy integrated into the proposed IGOOSE algorithm, a comprehensive ablation study was conducted. Figure 8 illustrates the comparative convergence curves obtained from this ablation analysis. The original GOOSE algorithm serves as the baseline, while the variants “Improvement—1,” “Improvement—2,” and “Improvement—3” denote the algorithm with elite opposition-based learning, golden-sine mutation, and probabilistic exploration modules individually integrated, respectively. As depicted, the incorporation of each enhancement strategy demonstrates noticeable improvement in optimization performance compared to the baseline. Particularly, the golden-sine mutation strategy (“Improvement—2”) achieves the most substantial enhancement in convergence speed and optimal solution quality. This analysis explicitly confirms that each proposed modification contributes effectively to the overall algorithm performance, justifying the integration of these modules into the final improved algorithm.
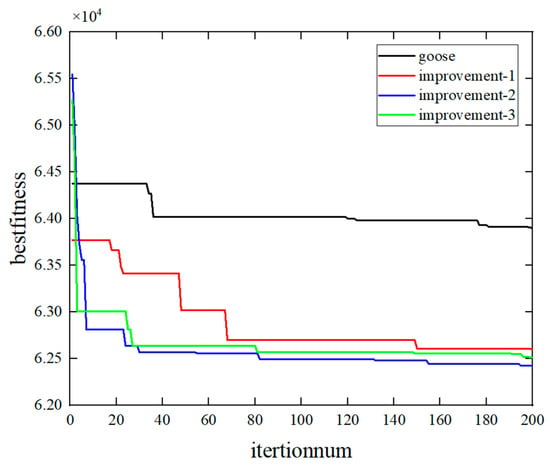
Figure 8.
Convergence curves of ablation study for the improved GOOSE algorithm.
A sensitivity analysis was conducted to assess the robustness of the proposed optimization model by altering key operational parameters, namely train capacity and minimum dispatch interval, as illustrated in Table 5. For the train capacity scenarios, capacities were varied to 90% and 110% of baseline levels to simulate decreased (90%) and increased (110%) carrying capacities. The results revealed a negative correlation between train capacity and the overall objective function value. Specifically, a 110% train capacity significantly improved load balance and effectively reduced the total objective function value, while a 90% capacity led to increased operational distances and elevated overall costs.

Table 5.
Sensitivity analysis results for train capacity and minimum dispatch interval scenarios.
In the scenarios examining minimum dispatch intervals, dispatch intervals of 3 min and 1 min were tested. Increasing the dispatch interval to 3 min notably increased passenger waiting times, deteriorated load balance, and substantially raised the overall objective function value, reflecting a positive correlation between dispatch interval duration and optimization performance deterioration. However, decreasing the dispatch interval to 1 min (despite being impractical in reality) resulted in negligible improvements in waiting time, and combined with increased operational distances, did not yield a notable improvement in the overall objective function, which remained largely consistent with the baseline. This finding underscores the diminishing marginal returns and potential inefficiencies associated with excessively short dispatch intervals, highlighting the necessity to carefully balance service frequency and operational practicality in real-world applications.
Figure 9 illustrates the comparison of sectional load factors on LineX before and after optimization. As demonstrated, the optimized strategy significantly alleviates passenger load pressures on the heavily utilized up-direction sections, effectively reducing overcrowding. Simultaneously, the optimization plan decreases resource wastage in the low-demand down-direction sections, thus achieving more balanced passenger load distribution and uniform load factors, enhancing the efficiency and practicality of the optimization model.
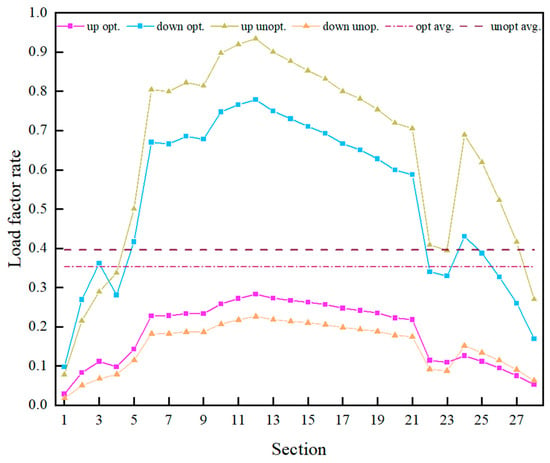
Figure 9.
Load factor distribution.
The proposed optimization approach effectively reduces passenger waiting times and significantly improves passenger load balancing across the metro line, thereby enhancing operational efficiency and service quality. Nevertheless, it may introduce increased operational complexity and slightly higher deadhead distances due to unpaired train dispatching strategies. The optimization is applied comprehensively to the entire line; however, the inherent nature of the combined short-turn and unpaired operations strategy means that some shorter segments receive customized operational plans and frequencies tailored to localized passenger demand.
7. Conclusions
This study analyzed the spatiotemporal imbalance characteristics of passenger flow in urban rail transit and discussed the promising potential for integrating mixed short-turn and full-length services with unpaired train operations. To address practical challenges, a comprehensive three-objective optimization model was established, focusing on minimizing operational costs, reducing passenger waiting times, and improving load balancing by synergistically combining these two operational strategies. To effectively solve the complex optimization problem, an Improved GOOSE algorithm (IGOOSE) was developed. The algorithm integrates elite opposition-based learning, probabilistic exploration based on elite solutions, and golden-sine mutation strategies, substantially enhancing its global exploration capability, effectively preventing local convergence issues, and ensuring robust and reliable optimization results.
A detailed case study utilizing adjusted operational data from Nanjing Metro Line 3 demonstrated the practical efficacy of the proposed model. Comparative analyses with traditional GA, PSO, and GWO algorithms indicated that all algorithms achieved improvements over the unoptimized scenario, thereby validating the effectiveness of the optimization model. Among these algorithms, the proposed IGOOSE demonstrated superior performance, achieving approximately a 12.72% reduction in passenger waiting times, around 39.30% improvement in load balancing, and a 10.25% reduction in the overall objective function value compared to the baseline. These results highlight the practical advantages and application potential of the IGOOSE algorithm.
Sensitivity analysis revealed that increasing train capacity notably improved load balancing and reduced total costs, whereas decreasing capacity negatively impacted system performance. Adjusting the minimum dispatch interval indicated that excessively extending intervals adversely affected passenger waiting experiences, while excessively shortening intervals offered diminishing returns, underscoring the necessity of appropriately balancing service frequency with practical operational considerations. The ablation study further demonstrated the effectiveness of each improvement within the IGOOSE algorithm, particularly highlighting the golden-sine mutation strategy’s critical contribution to accelerating convergence and significantly enhancing solution quality, followed by the notable contributions of elite opposition-based learning and probabilistic exploration strategies.
While the current optimization model explicitly considers passenger waiting times, train mileage, and load balancing, factors such as connectivity with other transit lines, labor impacts, and energy consumption were not directly addressed. Improved connectivity might indirectly benefit from reduced waiting times and improved load distributions, though explicit synchronization was not modeled. Future studies should explicitly incorporate these factors into a more comprehensive optimization framework.
Additionally, the current model relies on static, adjusted passenger flow data and thus does not explicitly capture dynamic real-time conditions such as train delays or equipment failures. Future research should therefore explore integrating adaptive or real-time optimization methods capable of rapidly recalibrating operational plans in response to unforeseen events, thereby enhancing resilience and adaptability.
In addition to its demonstrated advantages and identified limitations, the developed IGOOSE algorithm shows strong potential for broader applications across transportation contexts, such as airport transit scheduling, bus system optimization, and regional railway management, owing to its robust multi-objective optimization capabilities. Ultimately, this approach significantly contributes to broader societal objectives by enhancing operational efficiency and passenger service quality, thereby improving the accessibility, attractiveness, and sustainability of urban transit networks.
Author Contributions
Conceptualization, W.H. and G.Z.; methodology, W.H.; Software, Z.S. and W.H.; validation, X.L., W.H. and Z.S.; formal analysis, X.L.; resources, G.Z.; data curation, W.H.; writing—original draft preparation, Z.S.; writing—review and editing, W.H., G.Z., Z.S. and X.L.; visualization, Z.S.; supervision, Z.S.; project administration, G.Z.; funding acquisition, G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article.
Acknowledgments
The authors would like to express their gratitude to all those who helped them during the writing of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Macioszek, E.; Świerk, P.; Granà, A.; Sobota, A. Application of a Logit Model to Identify Socio-Demographic Factors Influencing the Choice of Public Transport for Daily Trips—A Case Study Based on the Example of the Górnośląska-Zagłębiowska Metropolis (Poland). Transp. Probl. 2024, 19, 183–192. [Google Scholar] [CrossRef]
- Du, Q.; Huang, Y.; Zhou, Y.; Guo, X.; Bai, L. Impacts of a new urban rail transit line and its interactions with land use on the ridership of existing stations. Cities 2023, 141, 104506. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, P.; Ni, S. Assessment of the impacts of urban rail transit on metropolitan regions using system dynamics model. Transp. Res. Procedia. 2014, 4, 521–534. [Google Scholar] [CrossRef]
- Cai, M.; Cui, L.; Zhang, Y. Beyond metros, pollution mitigation and environmental benefits in diverse transit systems. Transportation 2025, 28, 1–21. [Google Scholar] [CrossRef]
- Tian, A.Q.; Wang, X.Y.; Xu, H.; Pan, J.-S.; Snášel, V.; Lv, H.X. Multi-objective optimization model for railway heavy-haul traffic, Addressing carbon emissions reduction and transport efficiency improvement. Energy 2024, 294, 130927. [Google Scholar] [CrossRef]
- Canca, D.; Barrena, E.; Laporte, G.; Ortega, F.A. A short-turning policy for the management of demand disruptions in rapid transit systems. Ann. Oper. Res. 2016, 246, 145–166. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.; Su, S.; Tang, T.; Ning, B. A short turning strategy for train scheduling optimization in an urban rail transit line, the case of Beijing subway line 4. J. Adv. Transp. 2018, 2018, 5367295. [Google Scholar] [CrossRef]
- He, D.; He, Y.; Zhang, L.; Chen, Y.; Sun, Z.; Miao, J. Train operation scheme of short-turning routing in urban rail transit based on passenger travel. Transp. Res. Rec. 2024, 2678, 2125–2139. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, M.; Zhang, M.; Li, H.; Peng, R. Train service replanning in urban rail transit system, An integrated operation mode that combines express/local and short-turning strategies. Comput. Ind. Eng. 2025, 203, 111018. [Google Scholar] [CrossRef]
- Yang, L.; Gao, Y.; D’aRiano, A.; Xu, S. Integrated optimization of train timetable and train unit circulation for a Y-type urban rail transit system with flexible train composition mode. Omega 2024, 122, 102968. [Google Scholar] [CrossRef]
- Wang, H.; Yang, L.; Zhang, J.; Luo, Q.; Fan, Z. Real-time train timetabling with virtual coupling operations on a Y-type metro line. Eur. J. Oper. Res. 2024, 319, 168–190. [Google Scholar] [CrossRef]
- Zhao, S.; Wu, J.; Li, Z.; Meng, G. Train operational plan optimization for urban rail transit lines considering circulation balance. Sustainability 2022, 14, 5226. [Google Scholar] [CrossRef]
- Dou, F.; Zhang, H.; Yin, H.; Wei, Y.; Ning, Y. An Optimization Method of Urban Rail Train Operation Scheme Based on the Control of Load Factor. Sustainability 2022, 14, 14235. [Google Scholar] [CrossRef]
- Hu, Y.; Li, S.; Wang, Y.; Zhang, H.; Wei, Y.; Yang, L. Robust metro train scheduling integrated with skip-stop pattern and passenger flow control strategy under uncertain passenger demands. Comput. Oper. Res. 2023, 151, 106116. [Google Scholar] [CrossRef]
- Peftitsi, S.; Jenelius, E.; Cats, O. Evaluating skip-stop policy in urban rail transit systems based on passenger cost. J. Public Transp. 2023, 25, 100064. [Google Scholar] [CrossRef]
- Sahachaiseree, S.; Sadrani, M.; Antoniou, C. Stop plan optimisation for three-pattern skip-stop schemes for urban rail transit systems. EURO J. Transp. Logist. 2025, 14, 100149. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, Q. Optimization of Skip-Stop Train Schedule in Urban Rail Transit Under Virtual Coupling. J. Adv. Transp. 2025, 2025, 7897020. [Google Scholar] [CrossRef]
- Ren, H.; Song, Y.; Li, S.; Dong, Z. Two-step optimization of urban rail transit marshalling and real-time station control at a comprehensive transportation hub. Urban Rail Transit. 2021, 7, 257–268. [Google Scholar] [CrossRef]
- Li, Z.; Bai, Y.; Chen, Y.; Mao, B. Asymmetric demand oriented train service design with skip-stop tactics for a metro line. Expert Syst. Appl. 2025, 271, 126496. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, Y.; Shang, P.; Zhu, X. Efficient asymmetric reposition strategy of rolling stock for urban rail transit systems. Transp. A Transp. Sci. 2023, 12, 2294267. [Google Scholar] [CrossRef]
- Chen, Z.; Li, S.; D’aRiano, A.; Yang, L. Real-time optimization for train regulation and stop-skipping adjustment strategy of urban rail transit lines. Omega 2022, 110, 102631. [Google Scholar] [CrossRef]
- Xiao, L.; Liang, Y.; Li, J.; Xiao, X.; Li, D.; Tan, J. A study on optimization of passenger flow density of rail transit platform based on balanced train diagram. Electr. Drive Locomot. 2023, 5, 150–157. [Google Scholar] [CrossRef]
- Tian, P.N.; Mao, B.H.; Zhou, Q. Research on unpaired train dispatching schemes for urban rail transit. J. Shenzhen Univ. Sci. Eng. 2023, 40, 521–528. [Google Scholar] [CrossRef]
- Zhao, X.; Hou, Z.; Chen, J.; Zhang, Y.; Sun, J. Urban Rail Transit Scheduling under Time-Varying Passenger Demand. J. Adv. Transp. 2018, 2018, 7285148. [Google Scholar] [CrossRef]
- Zi-wen, W.E.I. Particle swarm optimization for train schedule of Y-type train routing in urban rail transit. J. Meas. Sci. Instrum. 2020, 11, 87–101. [Google Scholar] [CrossRef]
- Du, Z.; Ni, S.; Pan, J.-S.; Chu, S. A surrogate-assisted multi-objective Grey Wolf Optimizer for empty-heavy train allocation considering coordinated line utilization balance. J. Bionic Eng. 2024, 21, 383–397. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Abdelhamid, A.A.; Eid, M.M.; Ibrahim, A. Greylag goose optimization, nature-inspired optimization algorithm. Expert Syst. Appl. 2024, 238, 122147. [Google Scholar] [CrossRef]
- Hamad, R.K.; Rashid, T.A. GOOSE algorithm, a powerful optimization tool for real-world engineering challenges and beyond. Evol. Syst. 2024, 15, 1249–1274. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Gao, L.; Yang, H.; Zhang, K.; Ji, B.; Zhang, H. Multi-objective optimal scheduling for microgrids—Improved goose algorithm. Energies 2024, 17, 6376. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, W.; Liu, J.; Ren, G.; Zhang, N. Real-Time Optimization of Urban Rail Transit Train Scheduling via Advantage Actor–Critic Deep Reinforcement Learning. J. Transp. Eng. Part A Syst. 2024, 150, 04024046. [Google Scholar] [CrossRef]
- Dong, L.; Qin, L.; Xie, X.; Zhang, L.; Qin, X. Collaborative optimization method for multi-train energy-saving control with urban rail transit based on DRLDA algorithm. Appl. Sci. 2023, 13, 2454. [Google Scholar] [CrossRef]
- Liu, R.; Li, S.; Yang, L. Collaborative optimization for metro train scheduling and train connections combined with passenger flow control strategy. Omega 2020, 90, 101990. [Google Scholar] [CrossRef]
- Tian, A.-Q.; Lv, H.-X.; Wang, X.-Y.; Pan, J.-S.; Snášel, V. Bioinspired Discrete Two-Stage Surrogate-Assisted Algorithm for Large-Scale Traveling Salesman Problem. J. Bionic Eng. 2025, 11, 1–14. [Google Scholar] [CrossRef]
- Zhan, D.; Tian, A.Q.; Ni, S.Q. Optimizing PID control for multi-model adaptive high-speed rail platform door systems with an improved metaheuristic approach. Int. J. Electr. Power Energy Syst. 2025, 169, 110738. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).