Abstract
Distribution systems’ vulnerability to power losses remains high, among other parts of the power system, due to the high currents and lower voltage ratio. Connecting distributed generation (DG) units can reduce power loss and improve the overall performance of the distribution networks if sized and located correctly. However, existing studies have usually assumed that DGs operate only at the unity power factor (i.e., type-I DGs) and ignored their dynamic capability to control reactive power, which is unrealistic when optimizing DG allocation in power distribution networks. In contrast, optimizing the allocation of DG units injecting reactive power (type-II), injecting both active and reactive powers (type-III), and injecting active power and dynamically adjusting (absorbing or injecting) reactive power (type-IV) is a more likely approach, which remains unexplored in the current literature. Additionally, various metaheuristic optimization techniques are employed in the literature to optimally allocate DGs in distribution networks. However, the no-free-lunch theorem emphasizes employing novel optimization approaches, as no method is best for all optimization problems. This study demonstrates the potential of optimally allocating different DG types simultaneously to improve power distribution network performance using a parameter-free Jaya optimization technique. The primary objective of optimally allocating DG units is minimizing the distribution network’s power losses. The simulation validation of this study is conducted using the IEEE 33-bus test system. The results revealed that optimally allocating a multiunit DG mix instead of a single DG type significantly reduces power losses. The highest reduction of 96.14% in active power loss was obtained by placing three type-II, two type-III, and three type-IV units simultaneously. In contrast, the minimum loss reduction of 87.26% was observed by jointly allocating one unit of the aforementioned three DG types.
1. Background
Electrical energy is the most useful since it is flexible, dispatchable, and controllable [1]. The International Energy Outlook Report, 2016, states that the global electricity demand was 22 trillion kWh in 2012 and would increase by an average of 1.9 percent annually between 2012 and 2040 [2]. As the demand for electricity keeps rising, the transmission lines are forced to work at the bottleneck, which raises power losses, degrades voltage, undermines reliability, and increases the power system’s operating costs [1]. Alternative solutions to this scenario include incorporating distributed generation (DG) units into power distribution networks or constructing additional transmission networks and traditional centrally run power plants. DG is defined by the International Energy Agency (IEA) as a source of energy directly connected to the distribution network to maintain the network and service a local consumer [3]. Furthermore, a study [4] reports ten distinct definitions of DG, reflecting this diversity, and outlines multiple potential criteria to classify the DGs. Figure 1 depicts the classification criteria for DG.
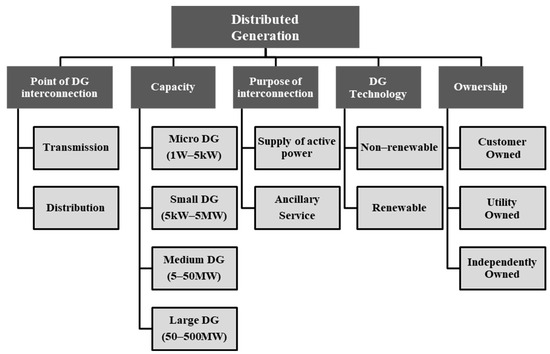
Figure 1.
Classification criteria for defining DG [4].
Since the distribution network generates the revenue needed to support the transmission and generating systems, the distribution system is the most crucial component of the power system. The distribution system has technical failures, which ultimately lead to financial damage. Therefore, these distribution network losses are of significant concern for the distribution companies (DISCOs). The distribution networks are passive by nature (i.e., devoid of power-generating units), and the grid far from the load center is the only power source that can meet the network’s overall demand. Consequently, power losses grow due to increased load demand because of the higher current flow. According to the states, about 70% of all power system losses occur in the distribution system [5]. It is noticeable that the losses of a particular system bus first drop when DG starts injecting power into it, but eventually, the losses increase. Put another way, integrating DG into the power system reduces system losses to a certain degree. Distribution networks’ performance starts to deteriorate rather than keep getting better after a certain DG penetration threshold. The DG outputs must be optimized before being integrated into the distribution networks to maximize their benefits in these situations. If the DG outputs are not optimized, there may be more power loss and voltage deterioration in the distribution network than if no DG is connected. This phenomenon is elaborated in Figure 2.
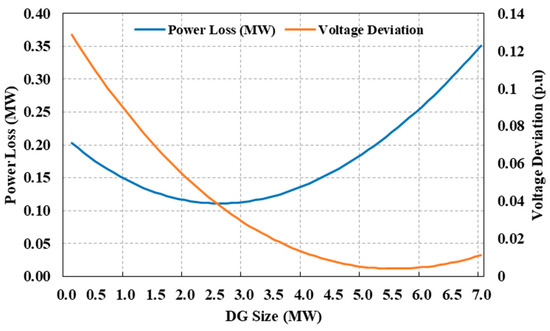
Figure 2.
Impact of DG allocation on distribution network’s power loss and voltage deviation [6].
The existing literature concerning the DGs’ optimal placement and sizing has made valuable contributions by adopting various metaheuristic optimization techniques. Employing a suitable metaheuristic algorithm for the DG allocation planning problem is vital. Nature-inspired intelligent metaheuristic algorithms have shown great potential for addressing issues in power systems. Wang, Li, and Golkar [7] developed an efficient approach that aggregates competitive search optimization (CSO) with fuzzy logic and chaotic theory to optimize capacitor banks (CBs), electric vehicle charging stations (EVCSs), and DG allocation. Basu et al. [8] addressed the issue of reactive power compensation in an island system by considering demand response programs. The authors employed several evolutionary methods, such as quasi-oppositional fast convergence evolutionary programming (QOFCEP), fast convergence evolutionary programming (FCEP), and evolutionary programming (EP). Kannemadugu et al. [9] eliminated voltage issues in the power distribution networks by optimizing DGs and FACTS-based DSTATCOM allocation. The method employed was the group teaching optimization (GTO) algorithm. Partap et al. [10] studied the optimal allocation of EVCSs, DG, and DSTATCOM using the cheetah optimization algorithm (COA) to minimize the ill effects of EVCSs in the power distribution networks. Rehman et al. [11] employed the reptile search algorithm (RSA) to allocate EVs in the IEEE 33- and 69-bus distribution networks along with the WTs to improve the voltage profile of the weakest bus in the system. The optimization process is subjected to the power flow, voltage, and DG capacity constraints.
Borousan and Hamidan [12] studied the DG allocation problem to improve the reliability of distribution networks using the chimp optimization algorithm (ChOA). The authors employed a 119-bus network to evaluate the ChoA’s performance against the GWO, ICA, SSA, and WOA. Selim et al. [13] used the wild horse optimization (WHO) technique to minimize power losses in IEEE 33- and 69-bus test systems by optimally placing and sizing DG units. The results concluded that adding three DGs resulted in a more reduced power loss than allocating one or two DG units. Ali et al. [14] proposed an improved WHO (IWHO) and performed a comparative study to evaluate its performance against the conventional WHO. Enhancing reliability indices and minimizing power losses in distribution networks were the study’s research objectives, which IWHO achieved in a superior way to WHO. Kawambwa et al. [15] proposed a new symbiotic organism search (SOS) variant for the DG allocation problem, the effectiveness of which was improved by adding the cloud theory. This improved SOS proves better in convergence speed and solution quality. The formulated fitness function includes the weighted sum of minimizing power losses, maximizing the voltage stability index, and improving the voltage profile. Salkuti [16] optimized the DSTATCOM and DG allocation in the IEEE 33- and 85-bus radial distributed systems using the evolutionary bat optimization algorithm (EBA) and came to the conclusion that their combined allocation can attain more loss reduction and improves the network bus voltages. Chakraborty et al. [17] integrated renewable-based solar DGs into the grid using Harris hawk optimization (HHO) to minimize power loss. The studied test systems were IEEE 33- and 69-bus systems. The study validated HHO’s findings against BA, BFOA, CTLBO, CTLBO ε-method, GA, I-DBEA, IMOEHO, IWO, MFO, PSO, QOTLBO, SA, and TLBO.
Fathy et al. [18] employed ChOA to optimally allocate DG units in 33-, 69-, and 119-bus radial distribution networks to minimize total active power loss. The ChOA significantly reduced active power loss against GA and PSO and performed better in convergence speed. Nguyen et al. [19] used the COA technique for allocating DGs and reconfiguring IEEE 69- and 119-bus test networks simultaneously. The formulated optimization problem consisted of several constraints while minimizing the real power loss. The results found that COA reduces power loss more than competitive methods. Chippagiri et al. [20] addressed the DG allocation and network reconfiguration problem by employing an improved elephant herding algorithm (IEHA) for IEEE 33- and 69-bus systems. Jalili and Taheri [21] optimized the allocation of different DG types in 33- and 69-bus distribution networks to reduce losses using firefly optimization (FO) inspired by fireflies’ mating patterns. The results proved FO’s efficient performance in addressing the proposed optimization problem. Ton et al. [22] located optimal-sized DGs in reconfigured radial networks to minimize losses. The algorithm and test system used were the coyote optimization algorithm (COA) and 33-bus system, respectively. The results concluded that the COA performed promisingly in achieving the required goal. Boukaroura et al. [23] optimized the allocation of multiple renewable DG units, considering load variations to reduce power loss in 33- and 69-bus test systems. The technique used for the aimed optimization problem was the dragonfly optimization algorithm (DOA). Zakaria et al. [24] employed two optimization techniques, genetic algorithm (GA) and ant colony optimization (ACO), to optimally allocate DGs in distribution networks. The effectiveness of both methods was tested on the IEEE 33- and 57-bus system. This study aimed to reduce total power loss in distribution systems. The findings of the study concluded ACO’s superiority over GA. Table 1 summarizes the reviewed studies.

Table 1.
Summary of reviewed studies.
Literature shows that various metaheuristic and evolutionary optimization techniques have frequently been developed and applied to address the complex optimization problem of DG allocation in distribution networks. However, each algorithm shows some limitations and they are not deemed perfect. Additionally, employing many nature-inspired metaheuristic optimization methods entails adjusting particular algorithm-specific parameters or determining the number of phases. Researchers must adjust these special parameters appropriately to improve such algorithms’ performance and achieve a global solution. Hence, there is a need to adopt simple and effective optimization techniques that do not involve algorithm-specified parameters to produce unbiased results.
Furthermore, while optimizing DG allocation in distribution networks, the literature has categorized DGs into four types based on their capability to inject or absorb the real and reactive powers. Type-I DGs inject only active power into the power distribution networks, such as solar photovoltaic (PV), fuel cells (FCs), and battery energy storage systems (BESSs) assumed to operate at unity power. Type-II DGs inject only reactive power into the system, such as capacitor banks (CBs) and synchronous condensers. Type-III DGs, such as synchronous generators (SGs), adjust both active and reactive power injections in the distribution networks. Type-IV DGs, such as fixed-speed induction generator (FSIG)-based wind turbines (WTs), inject active power and absorb reactive power. The DGs’ categorization per the literature is shown in Figure 3.
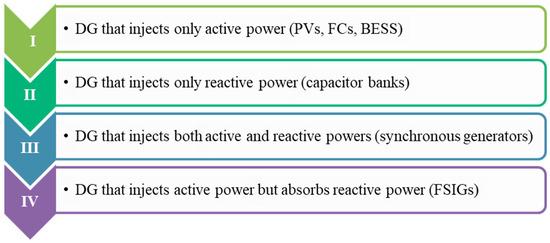
Figure 3.
DG types presented in the literature.
From these proposed four DG types, type-I DGs, such as solar PVs and BESSs, are extensively used in existing studies and are typically assumed to operate at a unity power factor that generates only active power. However, AC distribution networks are still extensively used worldwide. Therefore, modern PV systems integrate into the electric grid via advanced inverters that can supply active and reactive powers and do not necessarily operate at a unity power factor. On the other hand, type-IV DGs in existing studies are supposed to inject active power and absorb reactive power, as in the case of FSIGs. However, advanced variable-speed doubly fed induction generator (DFIG)-based WTs are commonly adopted in real power systems. They can regulate the reactive power as needed, thus supplying or absorbing reactive power per the grid requirements. Therefore, assuming the DGs’ operation only at the unity power factor and ignoring their dynamic capability to control the reactive power is unrealistic when optimizing DG allocation in the power distribution networks. In contrast, optimizing the allocation of DG units injecting reactive power (type-II), injecting both active and reactive powers (type-III), and injecting active power and dynamically adjusting (absorbing or injecting) reactive power (type-IV) is a more likely approach, whose combined allocation remains unexplored in the current literature. Therefore, the considered DG types for this study based on the inherent power-generating capabilities are categorized into three types, as shown in Figure 4.

Figure 4.
Proposed DG types.
Not attaining the optimal combination of these DGs may cause inefficient utilization of the mounted active and reactive power sources, leading to higher-than-expected power losses. An unoptimized mix of DG types may further deteriorate the network performance and thus fail to achieve the desired benefits of DG integration. Therefore, optimizing the DG allocation strategy is essential to maximize the techno-economic benefits while maintaining grid stability. This study aims to attain the optimal mix of the proposed three DG types, applying algorithm-specific parameter-free optimization techniques to optimize the sizing, placing, and operating power factors for certain DG types to improve the distribution network’s performance by minimizing losses.
Hence, this study contributions are:
- i.
- A new, realistic DG type with active power injecting and dynamically adjusting (absorbing or injecting) reactive power capabilities has been introduced.
- ii.
- The existing four DG types in the literature have been limited to three proposed types, i.e., type-II DG injecting reactive power, type-III DG injecting both active and reactive powers, and type-IV DGs injecting active power and dynamically adjusting (absorbing or injecting) reactive power.
- iii.
- The optimal combination of the proposed three DG types has been determined using the algorithm-specific parameter-free Jaya optimization (JO) technique. Although JO is already a well-established technique, its exclusive application to the proposed optimization problem to attain the optimal mix of the proposed three DG types has been explored.
- iv.
- The effectiveness of the proposed approach of simultaneously allocating the suggested three DG types against the existing DG types available in the literature has been examined.
The primary steps of the research methodology involved in executing this study are presented in Figure 5.
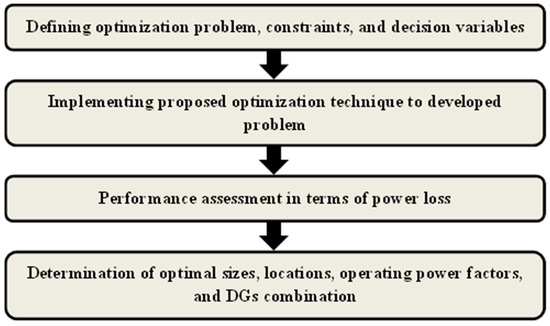
Figure 5.
Research methodology for the proposed study.
2. Significance of the Research
Distribution networks are more complex than transmission systems due to the high resistance-to-reactance ratio and higher power losses. Reducing such power loss is of severe concern for DISCOs as, in turn, it improves the distribution networks’ voltage profiles and overall performance. Integrating DG units is a significant standpoint in reducing power losses in distribution networks. For this reason, the optimal DG allocation in the distribution networks has become a renowned research area in the last few years. If appropriately positioned with optimum size, incorporating DG units in the distribution networks can play a vital role in reducing power losses and improving the overall performance of distribution networks. Practical implications of DGs can include technical, economic, and environmental dimensions such as:
- i.
- Regulate the voltage of weak, distant buses.
- ii.
- Prevent against the over- and under-voltages.
- iii.
- Reduce power losses, both active and reactive, by supplying power close to the load centers.
- iv.
- Act as a backup source in case of grid failure. Thus, it allows the distribution networks to operate in islanded mode, such as in rooftop solar photovoltaic systems.
- v.
- Enhance the reliability of power systems by acting as a backup source.
- vi.
- Allow consumers to use net metering, thus lowering their electricity bills.
- vii.
- Lower utilities’ operational costs, thus enhancing their revenue.
- viii.
- Defer or avoid the upgradation of power system infrastructure.
- ix.
- Renewable-based DGs (RE-DGs), like solar, wind, etc., can reduce greenhouse gas (GHG) emissions and carbon footprints.
- x.
- Reduce fossil-fuel dependence by enhancing the RE-DG penetration in the electric grid.
3. Problem Formulation
The problem formulation primarily involves specifying the fitness function and setting constraints as follows.
3.1. Fitness Function
The opted fitness function for the studied optimization problem is to minimize total active power losses (Ptotal_losses) in the power distribution lines, whose mathematical expression is given as Equation (1).
3.2. Constraints
Constraints are the limits posed on an optimization problem [1], which are essential to consider as real-world problems are complex and cannot be defined without introducing some constraints. This study considers four constraints to the DG allocation optimization problem in distribution networks, which are discussed below.
Power balance constraint
The active and reactive power balance constraint expressions are expressed as Equations (2) and (3).
where PSS, QSS are the active and reactive powers supply from the electrical grid, PDG, QDG are the active and reactive powers supply from optimally allocated DGs in the distribution networks, Pload, Qload are the load’s active and reactive power demands, and Ptotal_losses, Qtotal_losses are the total active and reactive power losses occurring in the distribution network. This constraint ensures optimal resource utilization by matching the load; otherwise, the over- or under-loading can affect the lifespan and reliability of devices. In addition, the voltage levels in the power distribution networks are directly affected by the reactive power flows; hence, balancing reactive power ensures voltage stability in the distribution networks.
Voltage magnitude limits
The bus voltages (Vb) are limited within ±10% of the rated voltage in order to maintain the voltage stability in power distribution networks, as given in Equation (4).
DG size constraint
The DG size limit is mathematically expressed as Equation (5).
PDG is the incorporated DG size in the grid, PDG,min is the minimum DG size allocated to a distribution network and PDG,max is the maximum DG size permitted to connect to a distribution network. This constraint limits the DG size to prevent system overloading, which could also lead to avoiding over-voltages in the distribution networks.
DG location limit constraint
The limitations posed for DG location are mathematically defined as Equation (6).
nbuses is the number of distribution network buses, which avoids DGs’ allocation at the bus1 (slack bus) as it is fixed only for the substation.
DG’s power factor limit constraint
Operating power factor limits for a type-III DG, i.e., DGpowerfactor, are set as Equation (7).
The power factor limit set for type-IV DG is given in Equation (8).
4. Jaya Optimization Algorithm
Nature-inspired optimization algorithms have two major categories: evolutionary and swarm intelligence (SI) algorithms. Additionally, some algorithm working phenomena adopt different natural mechanisms, e.g., biogeography-based optimization (BBO), gravitational search (GS), harmony search (HS), etc. The evolutionary and SI algorithms need controlling parameters such as agent population, iteration numbers, etc. In addition to the control parameters, some algorithms require algorithm-specific control parameters. The GA requires mutation, crossover, and selection probability operators; PSO requires inertia weight and social and cognitive parameters; ABC involves the on-looker, employed, and scout bee numbers. Properly tuning the algorithm-specific parameters is a crucial factor affecting the performance of the abovementioned algorithms. Improper algorithm-specific parameter tuning increases the computational effort or yields the local optimal solution.
Considering this fact, Rao et al. [25] introduced the teaching–learning-based optimization (TLBO) algorithm in 2011, which does not require any algorithm-specific parameters. The TLBO algorithm requires only standard controlling parameters like population size and number of generations. Keeping in view the success of the TLBO algorithm, another algorithm-specific parameter-less JO algorithm was proposed by Rao et al. [26] in 2016. However, unlike the two phases (i.e., teacher and learner phases) of the TLBO algorithm, the JO has only one phase and is comparatively uncomplicated to apply, which reduces computational cost and improves robustness in achieving global optima.
Let a fitness function f(x) be minimized or maximized. At any iteration i, assume that there are m design variables and n candidate solutions (i.e., population size, k = 1, 2,…, n). Let the best and worst candidate solutions, i.e., f(x)best and f(x)worst, in the whole candidate solutions set. Xj,k,i is the jth variable for the kth candidate during the ith iteration, which is modified as per Equation (9).
The term “” indicates the tendency of the solution to move closer to the best solution. The term “” indicates the tendency of the solution to avoid the worst solution. is accepted if it gives a better value to the fitness function. All the accepted function values at the end of the iteration are maintained and inputted into the next iteration. Rao and Waghmare [27] tested the performance of the proposed algorithm on 21 design benchmark functions and four constrained design problems. The computational results of this study have revealed that the JO is competitive with or superior to the other optimization algorithms for the considered problems.
Implementing JO in Proposed Problem
The steps involved in implementing JO in the proposed optimization problem are defined as follows:
- i.
- Setting the JO parameters, such as agent population and iteration count, is the starting step of the proposed optimization problem.
- ii.
- Initializing candidate solutions is the second step.
- iii.
- Initializing the iteration count is the third step.
- iv.
- The fourth phase analyzes the load flow to compute the initial values of the fitness function.
- v.
- The fifth step checks the iteration count.
- vi.
- The sixth step is to update the solutions using JO’s updating equation.
- vii.
- The seventh phase re-performs the load flow to compute each iteration’s candidate solutions’ fitness values.
- viii.
- The eighth step loops or ends the iterations for solution updating, after which the algorithm stops.
5. Results and Discussion
For the proposed optimization study, to evaluate the effect of allocating DG units in the radial distribution networks (RDNs), the IEEE 33-bus test system is selected, as shown in Figure 6. Because of its moderate structure, the IEEE 33-bus RDN has widely been used in the literature to test DG installations’ impact on the distribution networks’ performance. The performance of the JO algorithm for optimally allocating proposed DG types was evaluated using the MATLAB software R2016a Version 9.0 program, Intel Core i3-4030U CPU with 1.90 GHz and 4 GB of RAM. The JO’s input parameters of population size and maximum number of iterations are set as 50 and 100, respectively. The best optimal sizes, locations, and power factors for proposed DGs are reported after the 30 independent runs of JO, i.e., JO is run 30 times, starting with the randomly generated populations in each studied case.
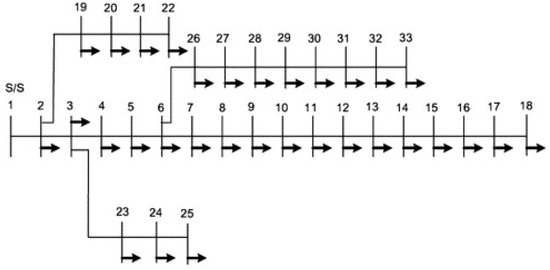
Figure 6.
IEEE 33-bus test system.
The total active and reactive power losses for the 33-bus RDN without any compensation (i.e., without DG installation) are obtained as 211 kW and 143.03 kVAR, respectively, which are high. Out of 33 buses, the minimum voltage of 0.90377 p.u. is observed at bus # 18.
5.1. Results for Type-II DG (Supply Active Power)
First, the impact of optimally allocating single and multiple type-II DG units capable of injecting only reactive power in the power distribution networks is evaluated. The mathematical formulation to model type-II DG is presented in Equation (10).
| DG Type | PDG Active power output | QDG Reactive power output | |
| Type-II | PDG = 0 | QDG = SDG | (10) |
The maximum number of DG units allocated to the IEEE 33-bus test system is limited to three. Hence, a total of three cases are studied, which are as follows:
Case A1: Optimal allocation of single type-II DG unit.
Case A2: Optimal allocation of two type-II DG units.
Case A3: Optimal allocation of three type-II DG units.
The key findings for the type-II DGs from the obtained results are as follows:
- i.
- Optimally allocating a single type-II DG unit reduces the power losses by 28.275% compared to the base case (when no DG is connected) and improves the voltage profile by 0.0127 p.u.
- ii.
- Including a second type-II DG unit optimally enhances power loss reduction by 4.517% and improves the voltage profile by 0.0138 p.u. compared to the first case.
- iii.
- Optimally incorporating three type-II DG units achieves a maximum loss reduction of 34.441% and a voltage profile improvement of 0.0273 p.u. compared to the base case. The graphical representation of obtained power losses and loss reductions are presented in Figure 7.
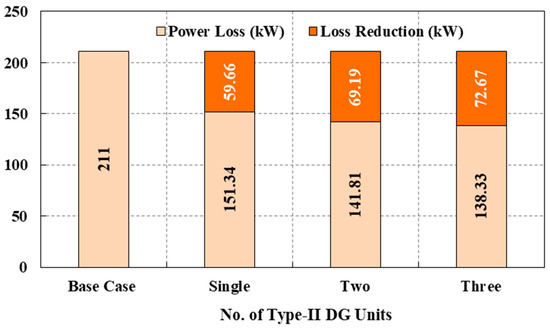 Figure 7. Power losses and loss reductions achieved by the type-II DG.
Figure 7. Power losses and loss reductions achieved by the type-II DG. - iv.
- Adding more DG units indicates a diminishing return effect, as the improvement margin for both power losses and voltage profile continues to reduce. It is also evident from Figure 8b,c, which appear nearly identical; however, a close examination reveals that case A2 exhibits a slight dominance in voltages for buses 30–33. For case A2, voltages on these buses lie close to 0.95 p.u., compared to approximately 0.94 p.u. in case A3. While case A3 attained a marginally higher minimum bus voltage, case A2 proved more beneficial overall on average, as more buses experienced significant voltage improvement.
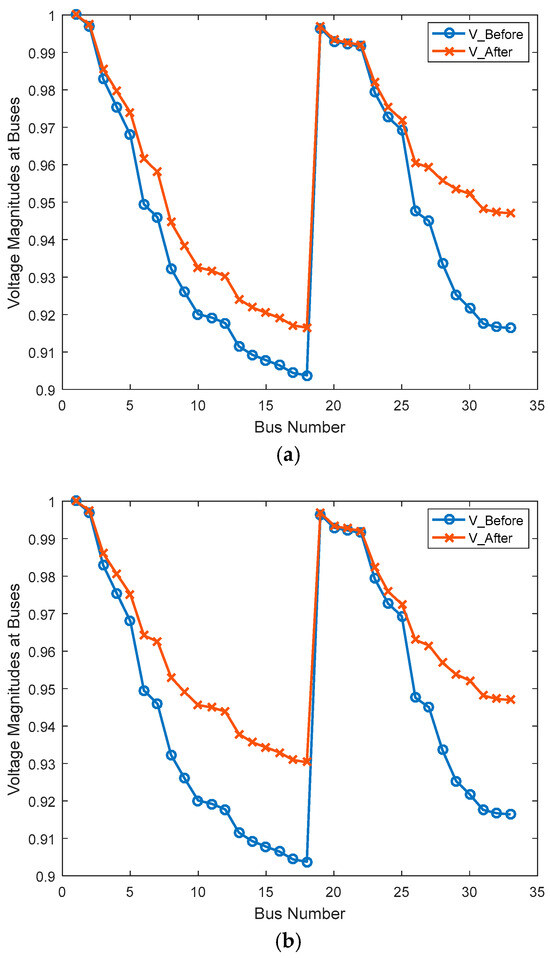
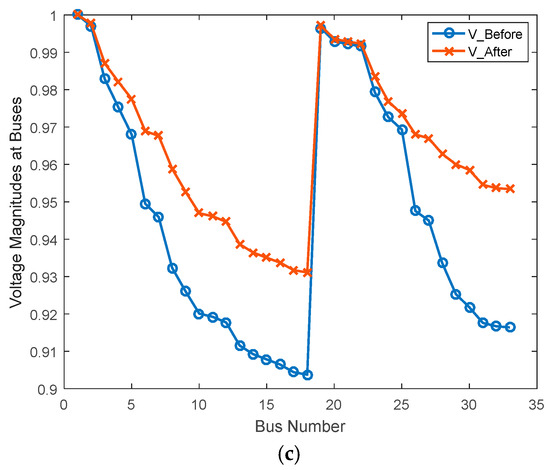 Figure 8. Obtained voltage profiles for (a) Case A1, (b) Case A2, (c) Case A3.
Figure 8. Obtained voltage profiles for (a) Case A1, (b) Case A2, (c) Case A3. - v.
- Before and after optimally allocating type-II DGs in the IEEE 33-bus test system, bus # 18 remains the weakest bus in the IEEE 33-bus test system, maybe because of its distant location from the grid station.
The results obtained in this case are summarized in Table 2.

Table 2.
Summary of obtained results for optimal allocation of single and multiple units of type-II DGs.
In addition, the network voltage profiles obtained in the above cases are presented in Figure 8.
5.2. Results for Type-III DG (Supply Active and Reactive Powers)
Next, the impact of optimally allocating single and multiple units of type-III DGs capable of injecting both active and reactive powers in the power distribution networks is illustrated. The mathematical formulation to model type-III DG is presented in Equation (11).
| DG Type | PDG Active power output | QDG Reactive power output | |
| Type-III | (11) |
Since type-III DGs can inject active and reactive powers, unlike type-II DGs, alongside DG size and location, an additional decision variable of operating power factor of DGs is also optimized to achieve the minimized power loss values. It increases the search space for the optimization technique, enhancing the overall complexity of the studied optimization problem. The operating power factors for type-III DGs are limited not to be less than 0.8. As type-III DGs can fulfill the reactive power demand of inductive load, their operating power factors are lagging. Similar to the previous case, a maximum of three type-III DG units can be allocated in the IEEE 33-bus test system. Hence, the three cases for type-III DG units are as follows:
Case B1: Optimal allocation of single type-III DG unit.
Case B2: Optimal allocation of two type-III DG units.
Case B3: Optimal allocation of three type-III DG units.
The key findings for the type-III DGs from the obtained results are as follows:
- i.
- Optimally allocating a single type-III DG unit reduces the power losses by 67.862% compared to the base case (when no DG is connected) and improves the voltage profile by 0.0545 p.u.
- ii.
- Including a second type-III DG unit optimally enhances the power loss reduction by 18.271% and improves the voltage profile by 0.0221 p.u. compared to the first case.
- iii.
- Optimally incorporating three type-III DG units achieves the maximum loss reduction of 93.948% and voltage profile improvement of 9.792% compared to the base case.
- iv.
- Similar to type-II DGs, adding more type-III DGs diminishes the return effect as the improvement margin for both power losses and voltage profile keeps reducing.
- v.
- Before allocating type-III DGs, bus # 18 was the weakest bus in the IEEE 33-bus test system, which switches between buses 8, 18, and 25 after optimally allocating the single and multiple units of type-III DGs.
- vi.
- Optimally allocating two type-III DG units enhances power loss reduction compared to a single DG unit allocation while requiring less active and reactive power from DGs. It signifies the impact of selecting proper locations for DGs’ placement. Choosing the proper DG location can significantly drop the DG’s power output, thus achieving better techno-economic performance of the distribution network.
The results obtained in this case are summarized in Table 3, whereas the graphical representations of obtained power losses and loss reductions are presented in Figure 9.

Table 3.
Summary of obtained results for optimal allocation of single and multiple units of type-III DGs.
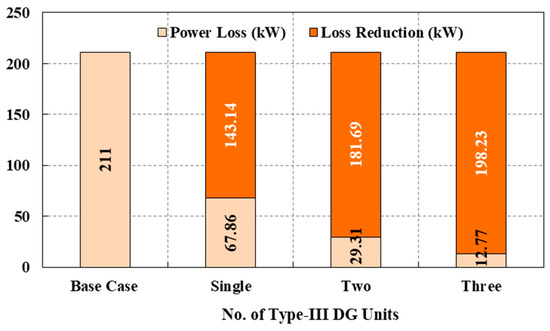
Figure 9.
Power losses and loss reductions achieved by the type-III DG.
The network voltage profiles obtained while allocating single, dual, and triple type-III DG units are presented in Figure 10.
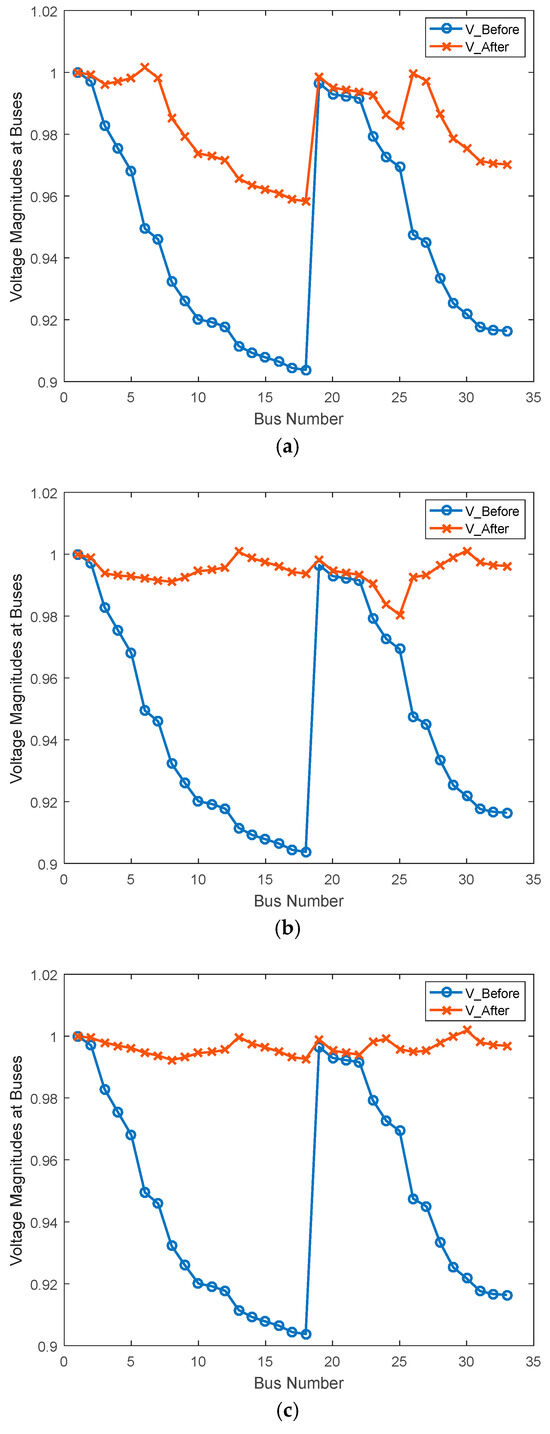
Figure 10.
Obtained voltage profiles for (a) Case B1, (b) Case B2, (c) Case B3.
5.3. Results for Type-IV DG (Supply Active Power and Dynamically Adjust Reactive Power)
Lastly, the impact of optimally allocating single and multiple units of type-IV DGs capable of injecting active power and dynamically adjusting the reactive power per the distribution network requirement is illustrated. The mathematical formulation to model type-IV DG is presented in Equation (12).
| DG Type | PDG Active power output | QDG Reactive power output | |
| Type-IV | (12) |
Unlike type-III DGs, which can only inject reactive power, type-IV DGs are set to adjust reactive power, i.e., inject or absorb VARs. Hence, it further increases the search space for the optimization technique as it has to select the optimal power factor value from a wide available range. The three studied cases for type-IV DG units are as follows:
Case C1: Optimal allocation of single type-IV DG unit.
Case C2: Optimal allocation of two type-IV DG units.
Case C3: Optimal allocation of three type-IV DG units.
The key findings for the type-IV DGs are presented in Table 4 and Figure 11. Comparing it with Table 3 shows that the improvements in power loss reduction and voltage profiles for cases C1, C2, and C3 are very close but slightly less than those obtained in cases B1, B2, and B3. This is because both DG types can adjust power factors. However, the broad operating power factor range for type-IV DGs increases the optimization problem’s overall complexity. For this reason, the proposed optimization technique, JO, shows a slight lag in attaining equal loss reductions in both cases. More findings for the type-IV DGs are listed as follows:

Table 4.
Summary of obtained results for optimal allocation of single and multiple units of type-IV DGs.
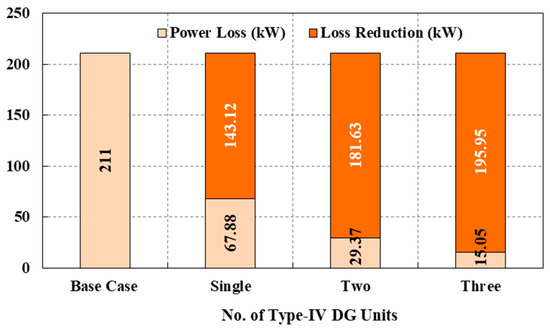
Figure 11.
Power losses and loss reductions achieved by the type-IV DG.
- i.
- Optimally allocating three type-IV DG units achieves the maximum loss reduction of 92.866% compared to the base case.
- ii.
- Similar to the two DG types previously studied, adding more type-IV DGs diminishes the improvement margin for power losses and voltage profile.
- iii.
- Before allocating type-IV DGs, bus # 18 was the weakest bus in the IEEE 33-bus test system, which switches between buses 18 and 25 after optimally allocating type-IV DGs.
- iv.
- Injecting active power is more effective than reactive power in enhancing the distribution network performance.
The voltage profiles of the distribution network obtained for studied type-IV DG cases are shown in Figure 12.
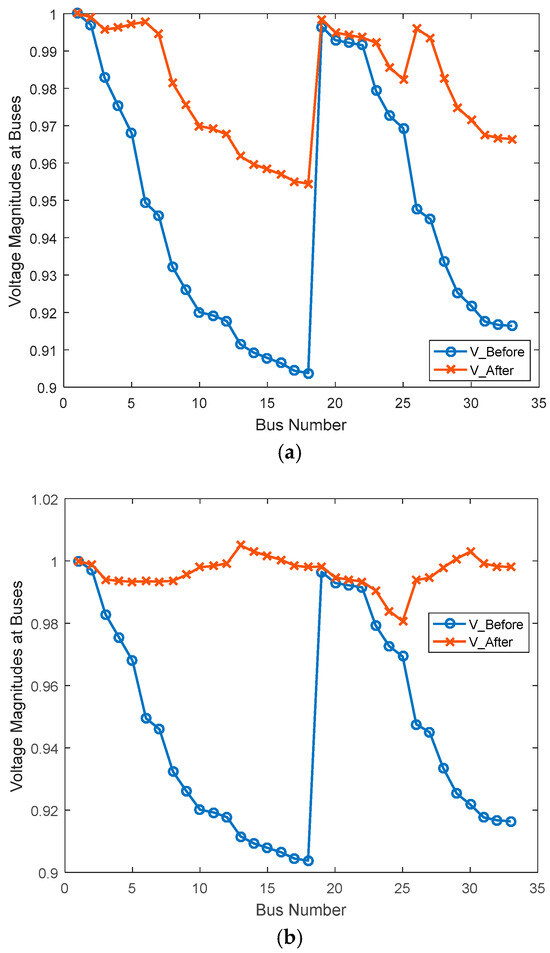
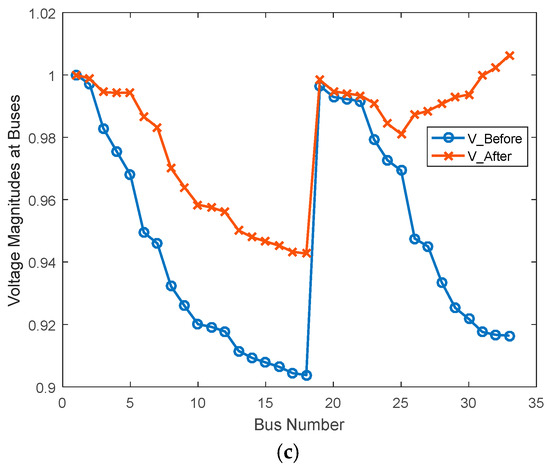
Figure 12.
Obtained voltage profiles for (a) Case C1, (b) Case C2, (c) Case C3.
The graphical performance comparison of optimal individual allocation of single and multiple units of type-II, type-III, and type-IV DG has been carried out in Figure 13, which shows the power loss reductions in kW and the percentage achieved by each DG type. The key observations analyzed from this comparative analysis are:
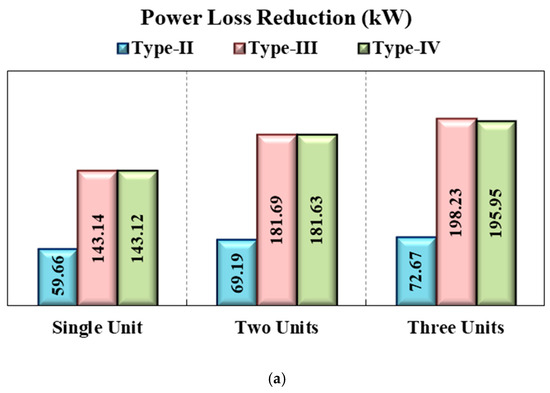
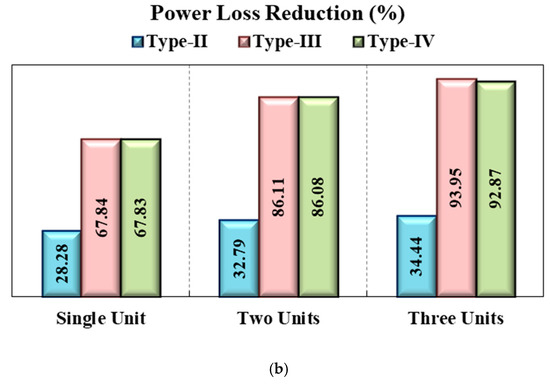
Figure 13.
Performance comparison of optimally allocating studied DG types individually in terms of power loss reduction (a) in kW, (b) in percentage.
- i.
- Type-III and type-IV DGs are more effective in enhancing the performance of power distribution networks as both DGs can adjust power factors.
- ii.
- Type-IV DGs slightly lag behind type-III DGs in attaining the same level of loss reduction despite both being capable of adjusting power factors. However, this lag stems from type-IV DG’s broader operating power factor range, which adds complexity to reaching equivalent performance.
- iii.
- Type-II DG, capable of injecting only reactive power, is the least effective among the four studied DG types in improving the distribution network performance.
- iv.
- One common observation for all DG types is that the optimal allocation of two units of each DG type is most effective in the obtained loss reduction to DGs’ power injection ratio.
5.4. Results for Combined DG Allocation
This section illustrates the impact of jointly allocating single and multiple units of proposed DG types (i.e., type-II, type-III, and type-IV) with three maximum allowable units to be allocated for each DG type. It makes twenty-seven (27) combinations of these DGs. The details of these cases in terms of the number of DGs for each type are provided below.
| Case 1 (A1B1C1): | Type-II DGs = 1, | Type-III DGs = 1, | Type-IV DGs = 1 |
| Case 2 (A1B1C2): | Type-II DGs = 1, | Type-III DGs = 1, | Type-IV DGs = 2 |
| Case 3 (A1B1C3): | Type-II DGs = 1, | Type-III DGs = 1, | Type-IV DGs = 3 |
| Case 4 (A1B2C1): | Type-II DGs = 1, | Type-III DGs = 2, | Type-IV DGs = 1 |
| Case 5 (A1B2C2): | Type-II DGs = 1, | Type-III DGs = 2, | Type-IV DGs = 2 |
| Case 6 (A1B2C3): | Type-II DGs = 1, | Type-III DGs = 2, | Type-IV DGs = 3 |
| Case 7 (A1B3C1): | Type-II DGs = 1, | Type-III DGs = 3, | Type-IV DGs = 1 |
| Case 8 (A1B3C2): | Type-II DGs = 1, | Type-III DGs = 3, | Type-IV DGs = 2 |
| Case 9 (A1B3C3): | Type-II DGs = 1, | Type-III DGs = 3, | Type-IV DGs = 3 |
| Case 10 (A2B1C1): | Type-II DGs = 2, | Type-III DGs = 1, | Type-IV DGs = 1 |
| Case 11 (A2B1C2): | Type-II DGs = 2, | Type-III DGs = 1, | Type-IV DGs = 2 |
| Case 12 (A2B1C3): | Type-II DGs = 2, | Type-III DGs = 1, | Type-IV DGs = 3 |
| Case 13 (A2B2C1): | Type-II DGs = 2, | Type-III DGs = 2, | Type-IV DGs = 1 |
| Case 14 (A2B2C2): | Type-II DGs = 2, | Type-III DGs = 2, | Type-IV DGs = 2 |
| Case 15 (A2B2C3): | Type-II DGs = 2, | Type-III DGs = 2, | Type-IV DGs = 3 |
| Case 16 (A2B3C1): | Type-II DGs = 2, | Type-III DGs = 3, | Type-IV DGs = 1 |
| Case 17 (A2B3C2): | Type-II DGs = 2, | Type-III DGs = 3, | Type-IV DGs = 2 |
| Case 18 (A2B3C3): | Type-II DGs = 2, | Type-III DGs = 3, | Type-IV DGs = 3 |
| Case 19 (A3B1C1): | Type-II DGs = 3, | Type-III DGs = 1, | Type-IV DGs = 1 |
| Case 20 (A3B1C2): | Type-II DGs = 3, | Type-III DGs = 1, | Type-IV DGs = 2 |
| Case 21 (A3B1C3): | Type-II DGs = 3, | Type-III DGs = 1, | Type-IV DGs = 3 |
| Case 22 (A3B2C1): | Type-II DGs = 3, | Type-III DGs = 2, | Type-IV DGs = 1 |
| Case 23 (A3B2C2): | Type-II DGs = 3, | Type-III DGs = 2, | Type-IV DGs = 2 |
| Case 24 (A3B2C3): | Type-II DGs = 3, | Type-III DGs = 2, | Type-IV DGs = 3 |
| Case 25 (A3B3C1): | Type-II DGs = 3, | Type-III DGs = 3, | Type-IV DGs = 1 |
| Case 26 (A3B3C2): | Type-II DGs = 3, | Type-III DGs = 3, | Type-IV DGs = 2 |
| Case 27 (A3B3C3): | Type-II DGs = 3, | Type-III DGs = 3, | Type-IV DGs = 3 |
The results obtained for each of the above cases are presented in Table 5. The graphical performance comparison of these twenty-seven (27) is presented in Figure 14. The key findings from the obtained results are as follows:

Table 5.
Summary of obtained results for optimal combined allocation of proposed three DG types.
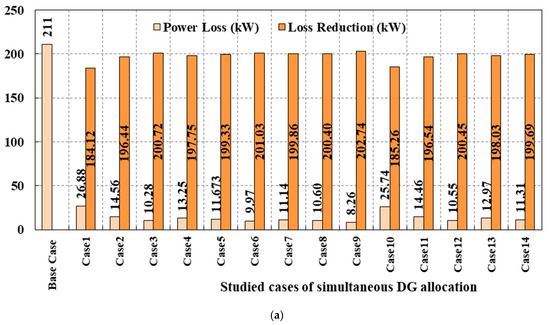
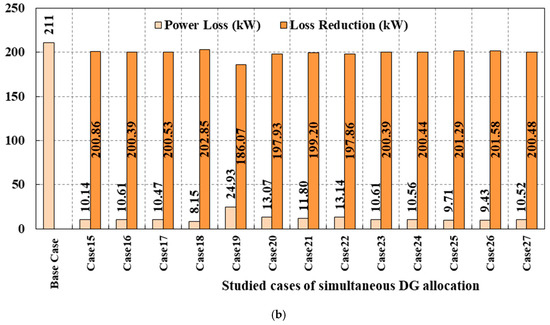
Figure 14.
Performance comparison of twenty-seven cases of optimally allocating proposed DG types simultaneously: (a) Cases 1–14, (b) Cases 15–27.
- i.
- The minimum power loss reduction of 87.262% is obtained by jointly allocating a single unit of each DG type, i.e., Case 1 (A1B1C1).
- ii.
- The highest power loss reduction of 96.139% is obtained by allocating two type-II DGs and three units of type-III and type-IV DGs, i.e., Case 18.
- iii.
- Case 14 is the worst regarding the power loss reduction to the DGs’ active power injection ratio, with a value of 0.059.
- iv.
- Case 19 is the best regarding the power loss reduction to the DGs’ active power injection ratio, with a value of 0.097.
- v.
- Adding more DG units is not always practical, as it may diminish the return effect of DG investment. It is evident from Cases 12 (B2C1D3) and 24 (A3B2C3) as both achieve the same level of loss reduction. However, Case 24 requires two additional DG units (one type-II DG and one type-III DG), which do not contribute to further improving the overall performance of the distribution network.
- vi.
- Adding type-III DGs with a corresponding decrement in the number of type-IV DGs does not significantly impact power losses. This phenomenon can be observed in Cases 12 and 16.
- vii.
- Integrating additional type-II DGs alongside type-III and IV DGs may be detrimental as the excessive reactive power injection can degrade network performance rather than improve it.
- viii.
- Bus # 18 is the commonly observed weakest bus in the IEEE 33-bus test system, sometimes switching to buses 25, 30, and 32. However, buses 18 and 25 are the commonly observed weakest buses after optimally allocating the DG units.
- ix.
- Among individual allocation of type-II to type-IV DG types, the highest loss reduction of 93.948% was observed while deploying three type-III units. In contrast, when the proposed DG types are allocated simultaneously, 18 out of 27 cases (Cases 3, 5–9, 12, 14–18, 21, 23–27) outperformed this best case of individual allocation by significant margins, thus highlighting the effectiveness of jointly allocating proposed DG types.
- x.
- Among the 18 best cases of simultaneous allocation of DG units that outperformed the best case of individual allocation, three cases (Cases 3, 7, and 8) attain more reductions in power losses by employing lower total active and reactive power capacities.
Table 6 summarizes the power loss reductions attained in each case, ranging from a minimum of 184.123 kW (Case 1) to a maximum of 202.854 kW (Case 18). The highlighted red value in the table indicates the lowest loss reduction, whereas the green value shows the highest achieved loss reduction value. On average, the studied cases demonstrate power loss reductions of approximately 94 to 95 percent. The graphical representation of this comparative analysis in terms of the obtained power loss reductions in percentages is presented in Figure 15.

Table 6.
Obtained percentage loss reductions for the studied cases of optimal combined allocation of three proposed DG types.
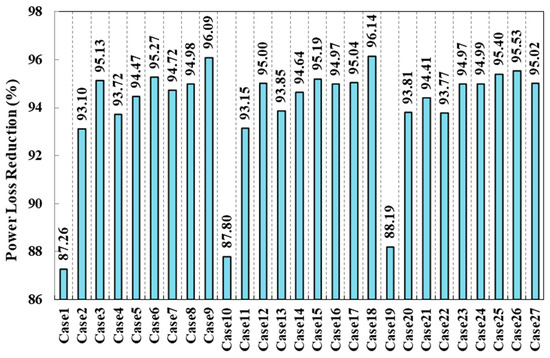
Figure 15.
Performance comparison of twenty-seven cases in terms of the percentage reduction in power losses.
5.5. Effectiveness of Proposed Approach Against Existing Studies
This section illustrates the effectiveness of the proposed optimization approach of simultaneously allocating the suggested three DG types against the existing DG types available in the literature. A summary of the comparative analysis of studied cases of simultaneous allocation of the three suggested DG types against existing studies is presented in Table 7. This comparative analysis demonstrates the superiority of allocating the proposed DG types against existing ones in the literature. The first part of the table suggests that using fewer proposed DG units may yield superior or comparable results. Case 1 achieves nearly the same loss reduction as WCA despite reducing total active and reactive power capacities and having half the number of DG units. Although it shows a slight shortfall in achieving the same loss reduction compared to WCA, the number of proposed DG units and their combined active–reactive power capacities are significantly lower than that of the WCA, demonstrating a more efficient allocation strategy. A similar phenomenon can also be observed in the second part of the table where Case 7 produces a 2.20% higher reduction in power losses compared to EGWO-PSO using less capacity and a lower number of units. The last part of the table demonstrates that the same number of proposed DG types can significantly boost the distribution network performance with lower active and reactive power injection capacities.

Table 7.
Comparative analysis of studied cases against existing studies.
6. Conclusions
This study overcomes the drawbacks of existing studies by using a more realistic modeling approach for DGs, considering their dynamic reactive power generation and absorption capabilities. In contrast to existing studies that assume DGs operate at unity power factor and inject active power while consuming reactive power, this study individually and simultaneously optimizes the allocation of DGs that inject only reactive power (type-II), inject both active and reactive powers (type-III), and inject active power while dynamically adjusting reactive power (type-IV). The proposed optimization approach improved the distribution network performance by significantly reducing power losses. The allocation of proposed DG types is optimized using the Jaya optimization algorithm to minimize power losses in the distribution network. The effectiveness of the proposed optimization framework is evaluated on a standard IEEE 33-bus test system. This study considers several cases that differ by the number, type, and simultaneous or individual allocation of suggested DGs. The results revealed that the simultaneous allocation of multiple units of DGs instead of a single DG type significantly reduces power losses. The findings illustrate that, among individual allocations of type-II to type-IV DGs, the highest loss reduction of 93.95% was observed while deploying three type-III units. In contrast, when the proposed DG types are allocated simultaneously, 18 out of 27 cases (Cases 3, 5–9, 12, 14–18, 21, 23–27) outperformed this best case of individual allocation by significant margins, thus highlighting the effectiveness of jointly allocating proposed DG types. The highest reduction of 96.14% in active power loss can be obtained by optimally simultaneously allocating two, three, and three units of type-II (that inject only reactive power), type-III (inject both active and reactive powers), and type-IV (inject active power while dynamically adjusting reactive power) DGs, respectively. On the other hand, the minimum loss reduction of 87.26% is obtained by jointly allocating a single unit of each DG type. In addition, a comparative performance analysis of the proposed optimization approach against existing studies demonstrates a promising improvement in loss reduction, which justifies its effectiveness.
7. Limitations and Future Research Directions
This study presents valuable contributions to optimally allocating different DG types, individually and simultaneously, in power distribution networks to minimize losses using the Jaya algorithm. However, the limitations of this study are also acknowledged, highlighting areas for future research directions. The limitations of this study are: a constant (static) load demand equal to 100 percent rated load capacity is assumed for the distribution network to simplify the analysis. The daily load demand profile is deterministic, i.e., time-dependent, and varies seasonally. Additionally, the uncertain intermittent nature of DGs’ output, such as type-III solar DGs with advanced converters and type-IV wind-based DFIGs, is also avoided. Thus, ignoring the dynamic loading and power generation capabilities may not fully capture the effectiveness of optimally allocating DG units in real-world dynamic scenarios. However, this study provides a basis for executing real-time and dynamic scenarios, which has a strong potential to extend to real-world applications as it supports improving power system performance by optimally allocating DG units. Researchers interested in extending this research work toward a more robust and uncertainty-aware DG allocation framework can incorporate the conditional value-at-risk (CVaR) energy management approach, as presented in [31], and adopt a stochastic bi-level optimization framework incorporating scenario-based uncertainty modeling and clustering techniques, as discussed in [32].
This optimization study is limited to a single objective of power loss minimization. The reason behind this approach is the significant impact, direct or indirect, of minimizing losses on improving the critical performance indices of the power distribution networks. Power losses can congest the network lines, causing overloading and diminishing the network components’ power-carrying capacity [33]. Thus, loss reduction can enhance the distribution network efficiency and improve the power system’s voltage profile, stability, and power quality [34]. All these benefits will finally translate into economic and environmental benefits. Future studies can adopt the holistic multiobjective optimization approach considering techno-economic–environmental parameters, whose potency can be evaluated against this single-objective approach.
The economic feasibility of allocating DGs is not considered, including DG capital (installation) and operational (running) costs, return on investment, and payback period analyses. Additionally, environmental impacts such as GHG emissions reduction and Sustainable Development Goal (SDG) achievement are not analyzed since these areas require separate detailed research. Similarly, the fault scenarios and their impact on reliability and protection schemes are excluded from this study’s intended objectives. These exclusions maintain a manageable and focused scope.
Furthermore, future studies can incorporate dynamic simulations involving power quality, control strategies, and communication frameworks to ensure the compatibility and manageability of mixed DG types.
Author Contributions
Conceptualization, M.I.B., F.F., and M.K.; methodology, M.I.B., F.F., M.K., and Z.H.L.; software, M.I.B. and Z.H.L.; validation, M.I.B., F.F., M.K., and Z.H.L.; formal analysis, M.I.B., T.A.J., and Z.A.M.; investigation, M.I.B., T.A.J., and Z.A.M.; resources, T.A.J. and M.I.M.; data curation, M.I.B., Z.H.L., and M.I.M.; writing—original draft preparation, M.I.B., F.F., M.K., and Z.H.L.; writing—review and editing, M.I.B., Z.H.L., and Z.A.M.; visualization, F.F., M.K., and M.I.M.; supervision, F.F. and M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Leghari, Z.H.; Hassan, M.Y.; Said, D.M.; Memon, Z.A.; Hussain, S. An efficient framework for integrating distributed generation and capacitor units for simultaneous grid-connected and islanded network operations. Int. J. Energy Res. 2021, 45, 1–39. [Google Scholar] [CrossRef]
- US Energy Information Administration. World Energy Demand and Economic Outlook. In International Energy Outlook; US Energy Information Administration: Washington, DC, USA, 2016; Volume 484, pp. 7–18. [Google Scholar]
- IEA. Distributed Generation in Liberalised Electricity Markets; IEA: Paris, France, 2002. [Google Scholar]
- Pesaran, H.A.M.; Huy, P.D.; Ramachandaramurthy, V.K. A review of the optimal allocation of distributed generation: Objectives, constraints, methods, and algorithms. Renew. Sustain. Energy Rev. 2017, 75, 293–312. [Google Scholar] [CrossRef]
- Sulaima, M.F.; Mohamad, M.F.; Jali, M.H.; Bukhari, W.M.; Baharom, M.F. A comparative study of optimization methods for 33kV distribution network feeder reconfiguration. Int. J. Appl. Eng. Res. 2014, 9, 1169–1182. [Google Scholar]
- Leghari, Z.H.; Kumar, M.; Shaikh, P.H.; Kumar, L.; Tran, Q.T. A critical review of optimization strategies for simultaneous integration of distributed generation and capacitor banks in power distribution networks. Energies 2022, 15, 8258. [Google Scholar] [CrossRef]
- Wang, S.; Li, Z.; Golkar, M.J. Optimum placement of distributed generation resources, capacitors and charging stations with a developed competitive algorithm. Heliyon 2024, 10, e26194. [Google Scholar] [CrossRef]
- Basu, M.; Jena, C.; Khan, B.; Ali, A.; Khurshaid, T. Optimal sizing and placement of capacitors in the isolated microgrid throughout the day considering the demand response program. Front. Energy Res. 2024, 12, 1346330. [Google Scholar] [CrossRef]
- Kannemadugu, R.P.; Adhimoorthy, V.; Devi, A.L.; Asokan, K. Optimal allocation of combined DG and DSTATCOM for improving voltage stability and economical benefits of distribution system. Int. Res. J. Adv. Eng. Hub 2024, 2, 18–25. [Google Scholar] [CrossRef]
- Pratap, A.; Tiwari, P.; Maurya, R.; Singh, B. Cheetah optimization algorithm for simultaneous optimal network reconfiguration and allocation of DG and DSTATCOM with electric vehicle charging station. Serbian J. Electr. Eng. 2024, 21, 1–37. [Google Scholar] [CrossRef]
- Rehman, N.; Mufti, M.D.; Gupta, N. Optimal location of electric vehicles in a wind integrated distribution system using reptile search algorithm. Distrib. Gener. Altern. Energy J. 2023, 38, 141–168. [Google Scholar] [CrossRef]
- Borousan, F.; Hamidan, M.A. Distributed power generation planning for distribution network using chimp optimization algorithm in order to reliability improvement. Electr. Power Syst. Res. 2023, 217, 109109. [Google Scholar] [CrossRef]
- Selim, S.O.; Selim, A.; Kamel, S. Power Loss Minimization Using Optimal Allocation of DGs Based on Wild Horse Optimizer. In Proceedings of the 23rd International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 13–15 December 2022. [Google Scholar]
- Ali, M.H.; Kamel, S.; Hassan, M.H.; Tostado-Véliz, M.; Zawbaa, H.M. An improved wild horse optimization algorithm for reliability based optimal DG planning of radial distribution networks. Energy Rep. 2022, 8, 582–604. [Google Scholar] [CrossRef]
- Kawambwa, S.; Hamisi, N.; Mafole, P.; Kundaeli, H. A cloud model based symbiotic organism search algorithm for DG allocation in radial distribution network. Evol. Intell. 2022, 15, 545–562. [Google Scholar] [CrossRef]
- Salkuti, S.R. Optimal allocation of DG D-STATCOM in a distribution system using evolutionary based Bat algorithm. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 4. [Google Scholar] [CrossRef]
- Chakraborty, S.; Verma, S.; Salgotra, A.; Elavarasan, R.M.; Elangovan, D.; Mihet-Popa, L. Solar-based DG allocation using Harris Hawks Optimization while considering practical aspects. Energies 2021, 14, 5206. [Google Scholar] [CrossRef]
- Fathy, A.; Yousri, D.; Abdelaziz, A.Y.; Ramadan, H.S. Robust approach based chimp optimization algorithm for minimizing power loss of electrical distribution networks via allocating distributed generators. Sustain. Energy Technol. Assess. 2021, 47, 101359. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Nguyen, N.A.; Duong, T.L. A novel method based on coyote algorithm for simultaneous network reconfiguration and distribution generation placement. Ain Shams Eng. J. 2021, 12, 665–676. [Google Scholar] [CrossRef]
- Chippagiri, S.S.; Pemmada, S.; Patne, N. Distribution network reconfiguration and distributed generation injection using improved Elephant Herding Optimization. In Proceedings of the IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25–26 September 2020. [Google Scholar]
- Jalili, A.; Taheri, B. Optimal sizing and sitting of distributed generations in power distribution networks using firefly algorithm. Technol. Econ. Smart Grids Sustain. Energy 2020, 5, 1–14. [Google Scholar] [CrossRef]
- Ton, T.N.; Nguyen, T.; Truong, A.; Vu, T.P. Optimal location and size of distributed generators in an electric distribution system based on a novel metaheuristic algorithm. Eng. Technol. Appl. Sci. Res. 2020, 10, 5325–5329. [Google Scholar] [CrossRef]
- Boukaroura, A.; Slimani, L.; Bouktir, T. Optimal placement and sizing of multiple renewable distributed generation units considering load variations via dragonfly optimization algorithm. Iran. J. Electr. Electron. Eng. 2020, 16, 353–362. [Google Scholar]
- Zakaria, Y.Y.; Swief, R.; El-Amary, N.H.; Ibrahim, A.M. Optimal distributed generation allocation and sizing using genetic and ant colony algorithms. J. Phys. Conf. Ser. 2020, 1447, 012023. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Balic, J. Teaching-learning-based optimization algorithm for unconstrained and constrained real-parameter optimization problems. Eng. Optim. 2012, 44, 1447–1462. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Rao, R.V.; Waghmare, G.G. A new optimization algorithm for solving complex constrained design optimization problems. Eng. Optim. 2017, 49, 60–83. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal placement and sizing of distributed generation and capacitor banks in distribution systems using Water Cycle Algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Saonerkar, A.K.; Bagde, B.Y. Optimized DG placement in radial distribution system with reconfiguration and capacitor placement using genetic algorithm. In Proceedings of the 2014 IEEE International Conference on Advanced Communications, Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 1077–1083. [Google Scholar]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.H.; Kim, M.K.; Nebhen, J. A novel multiobjective hybrid technique for siting and sizing of distributed generation and capacitor banks in radial distribution systems. Sustainability 2021, 13, 3308. [Google Scholar] [CrossRef]
- Zhai, X.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Wang, P.; Sun, H. Risk-averse energy management for integrated electricity and heat systems considering building heating vertical imbalance: An asynchronous decentralized approach. Appl. Energy 2025, 383, 125271. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Wang, P.; Guo, Q.; Su, H. A Stochastic Bi-level Optimal Allocation Approach of Intelligent Buildings Considering Energy Storage Sharing Services. IEEE Trans. Consum. Electron. 2024, 70, 5142–5153. [Google Scholar] [CrossRef]
- Gupta, B. Power System; S. Chand Publishing: Noida, India, 2008. [Google Scholar]
- Dixon, J.; Moran, L.; Rodriguez, J.; Domke, R. Reactive power compensation technologies: State-of-the-art review. Proc. IEEE 2005, 93, 2144–2164. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).