Optimization of NACA 6412 Using Taguchi Method and Computational Fluid Dynamics Analysis
Abstract
1. Introduction
2. Materials and Methods
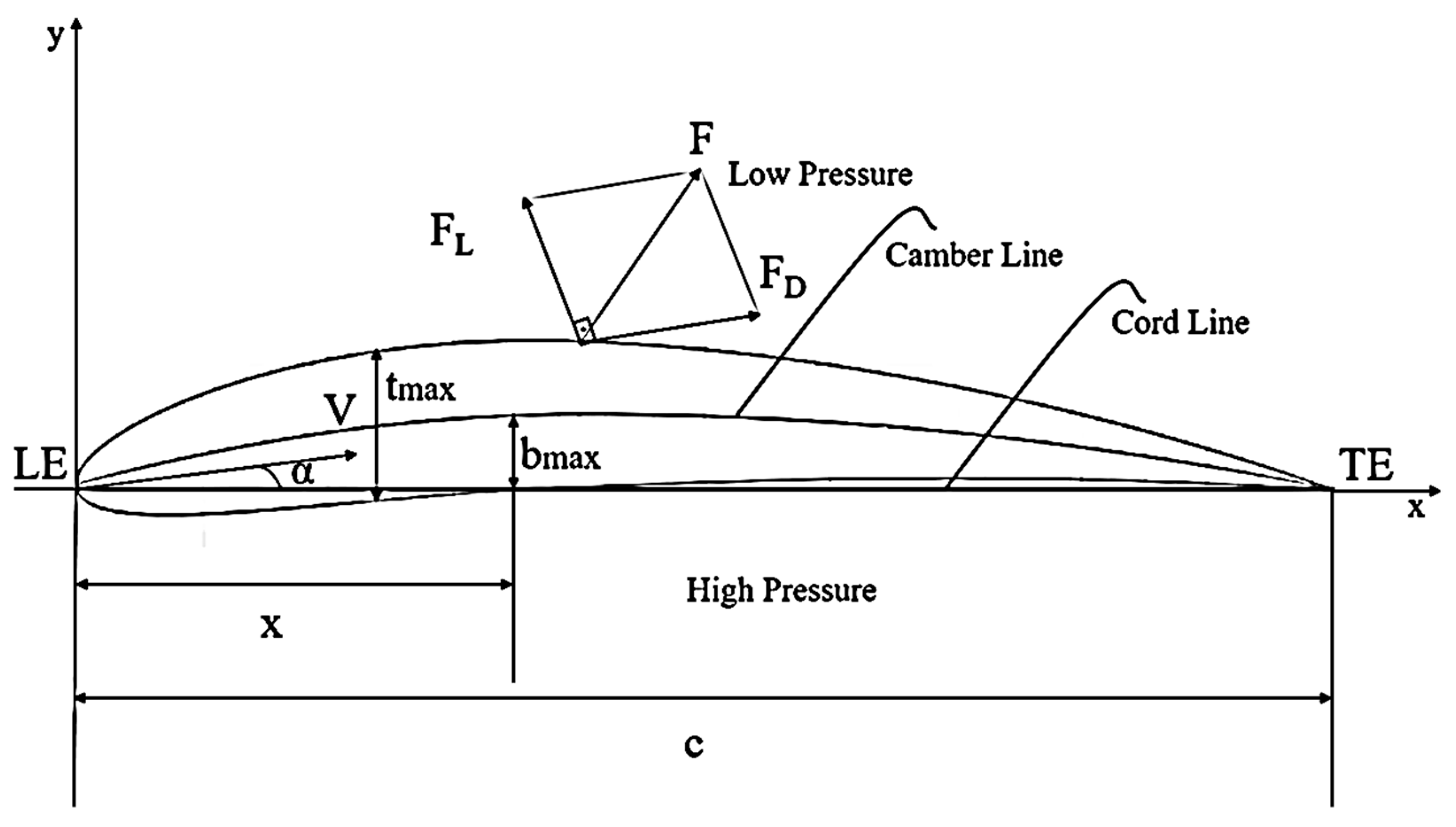
2.1. Analytical Approach
2.2. Taguchi Method
2.2.1. Optimization
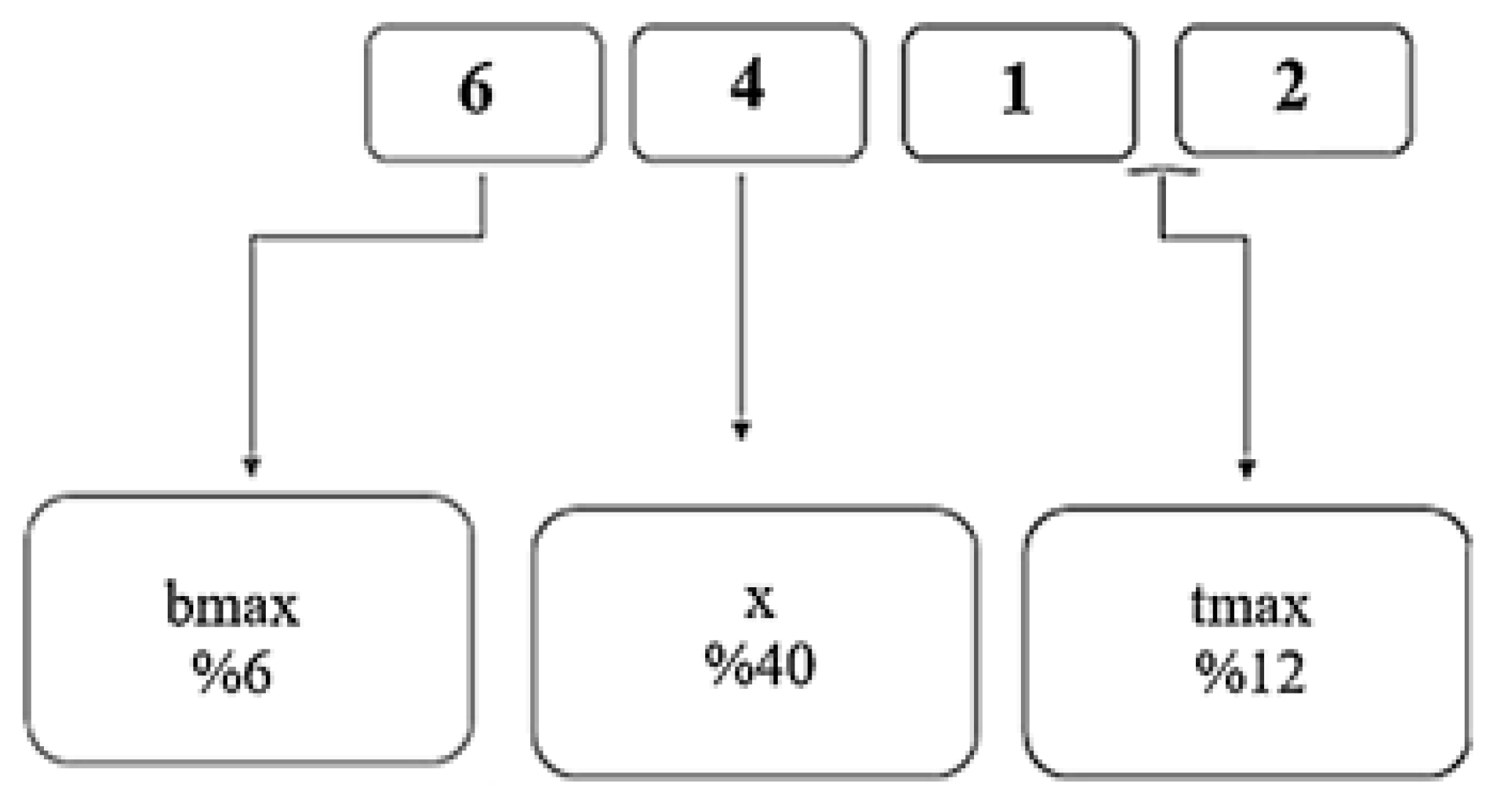
2.2.2. Parameters
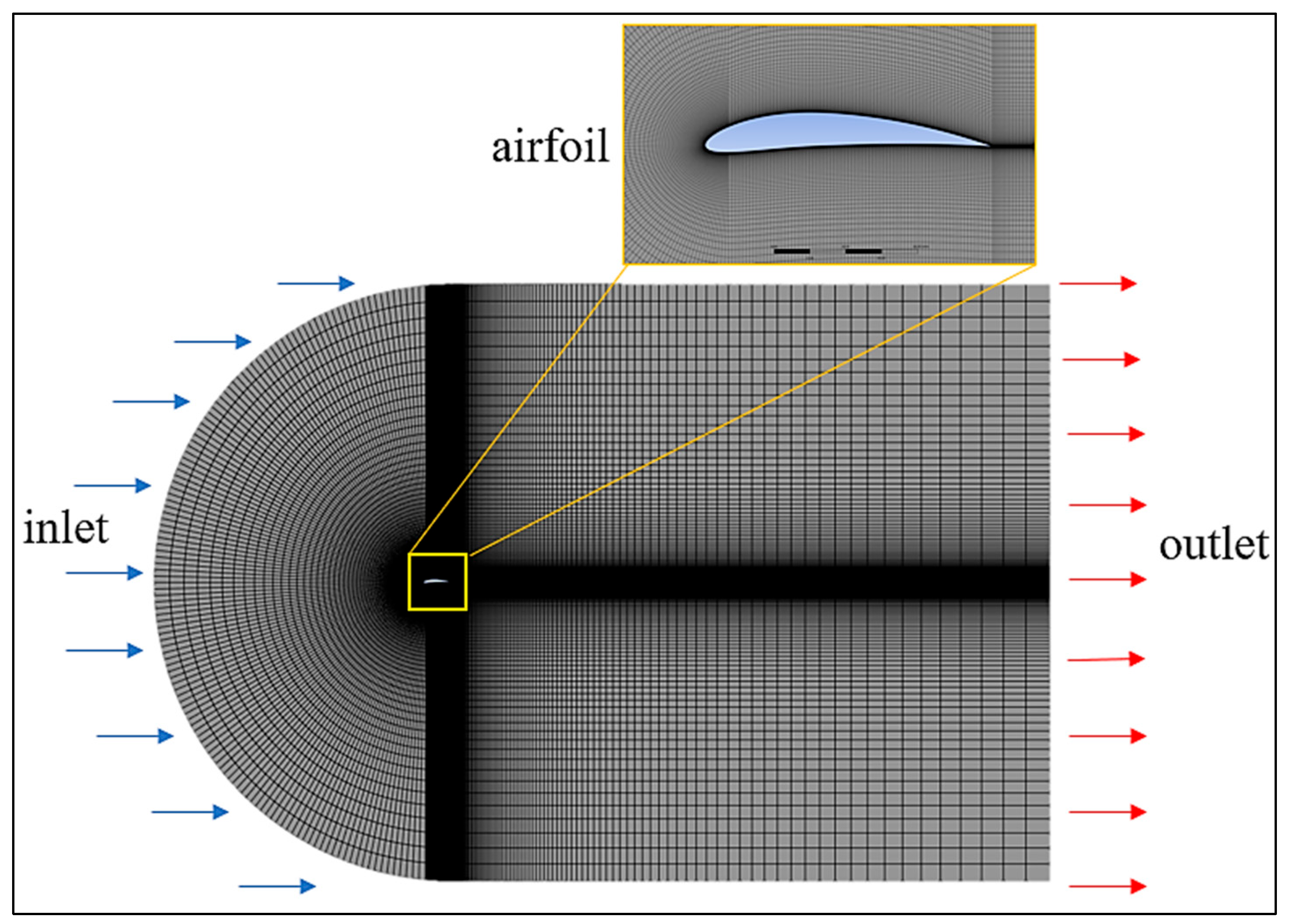
2.3. Numerical Modeling
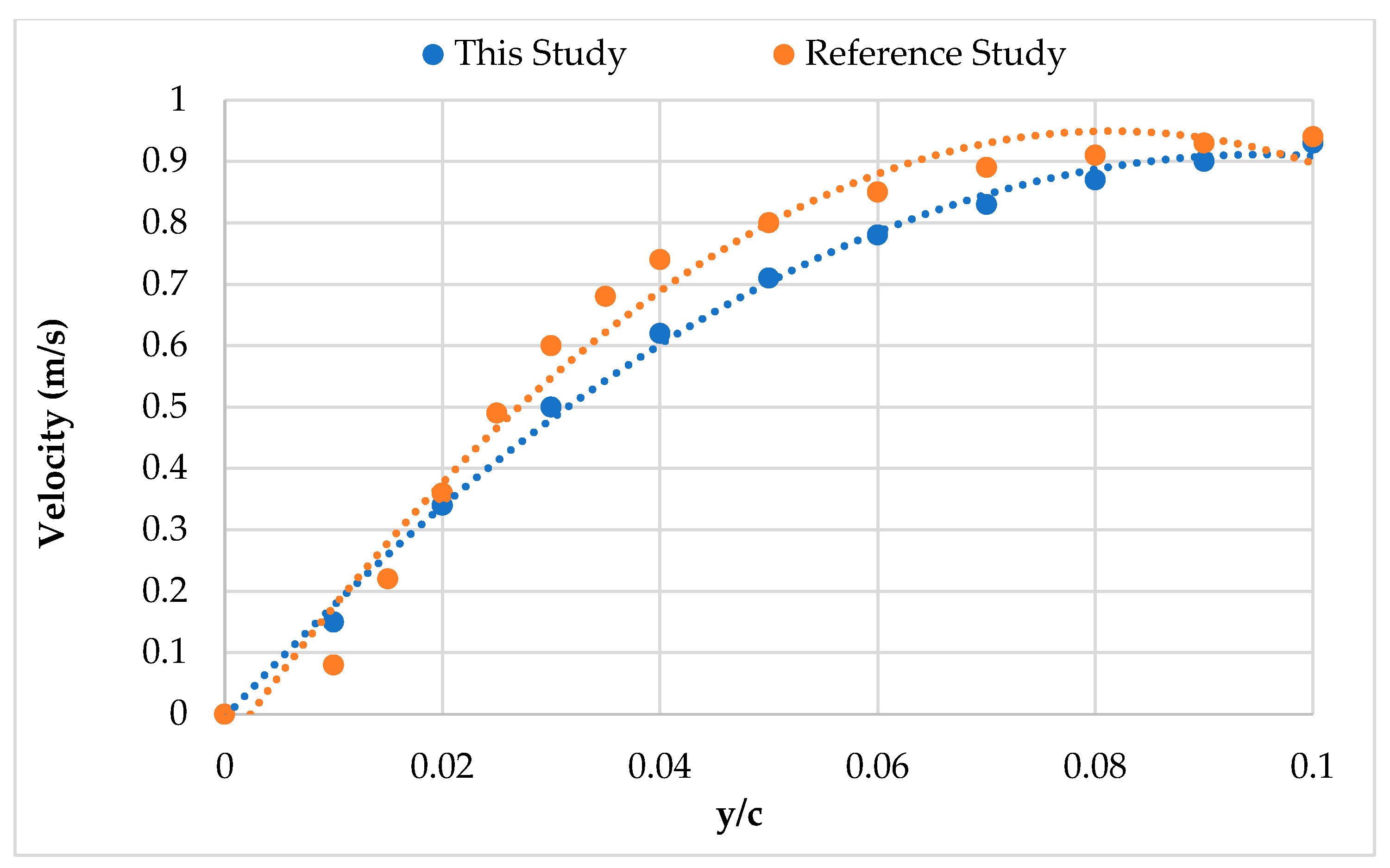
2.3.1. Validation
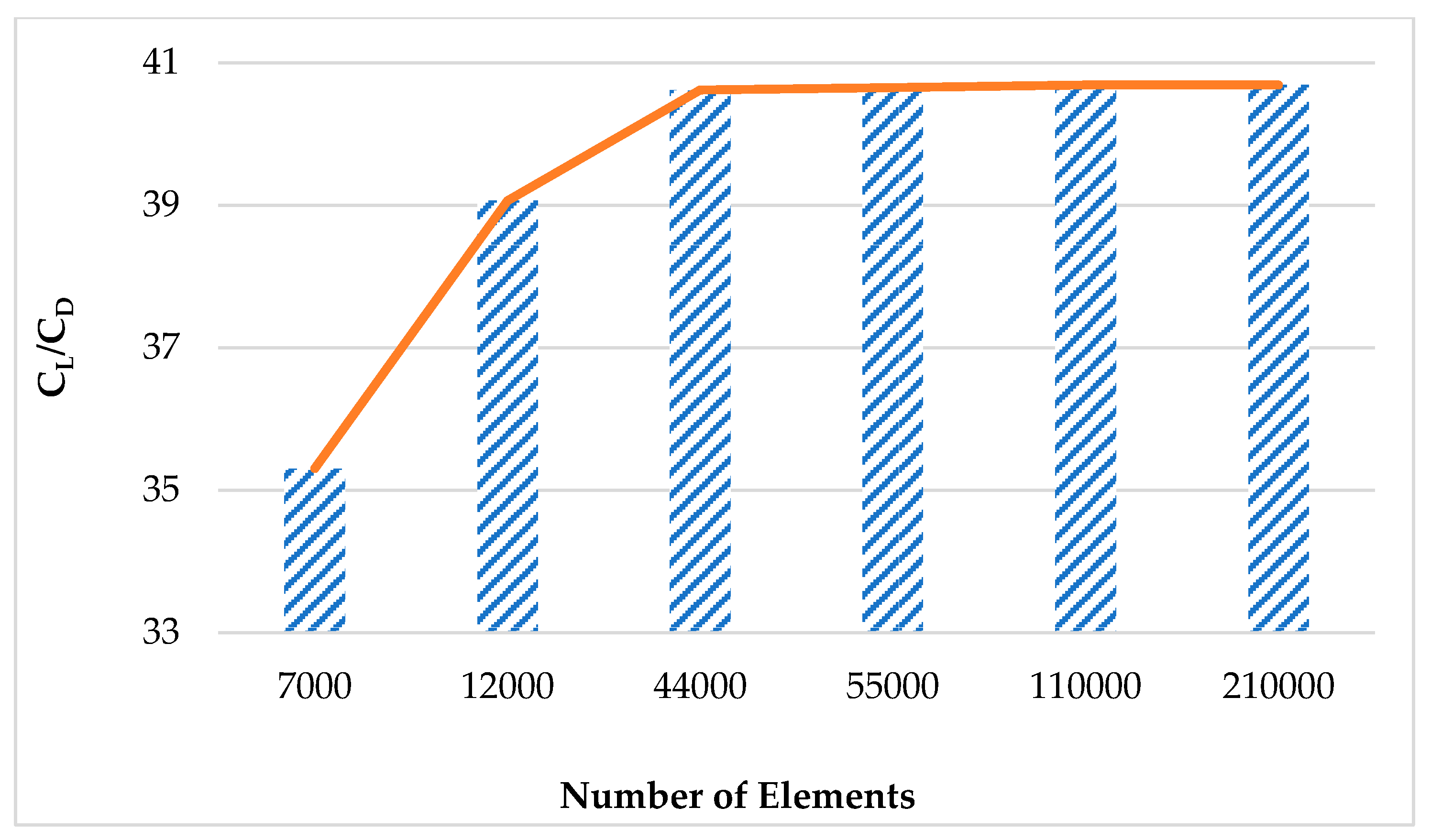
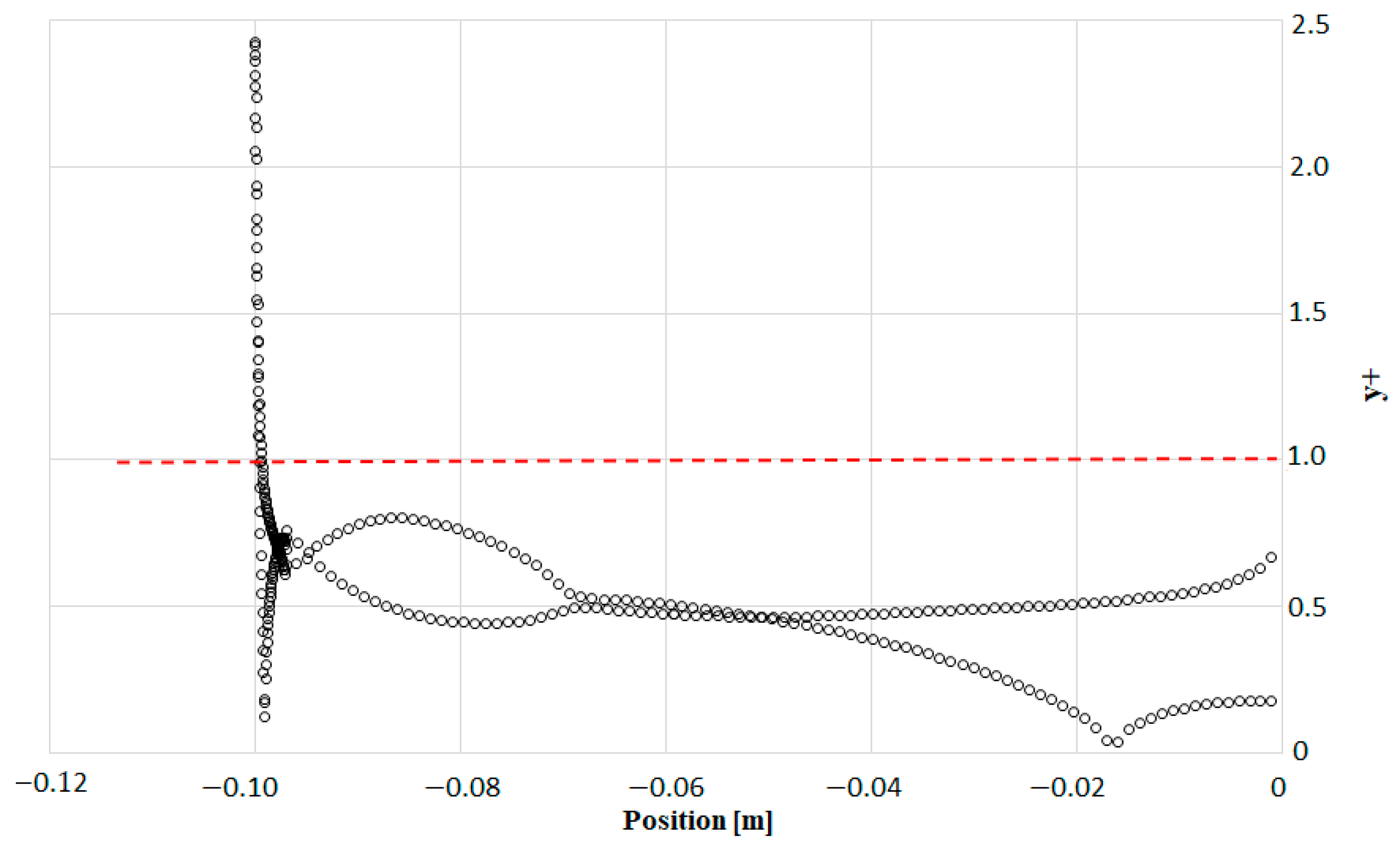
2.3.2. Mesh Independence and Solution
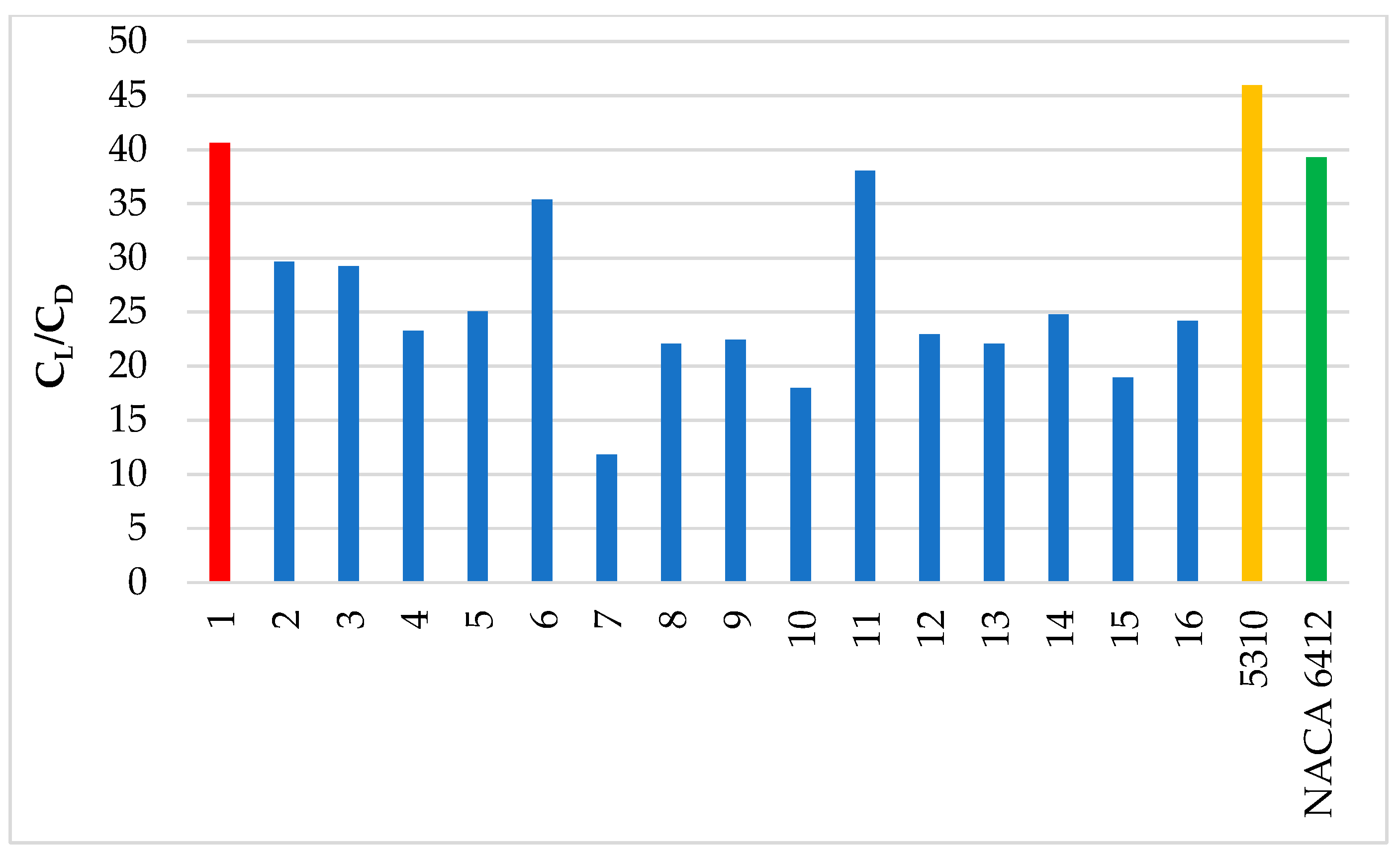
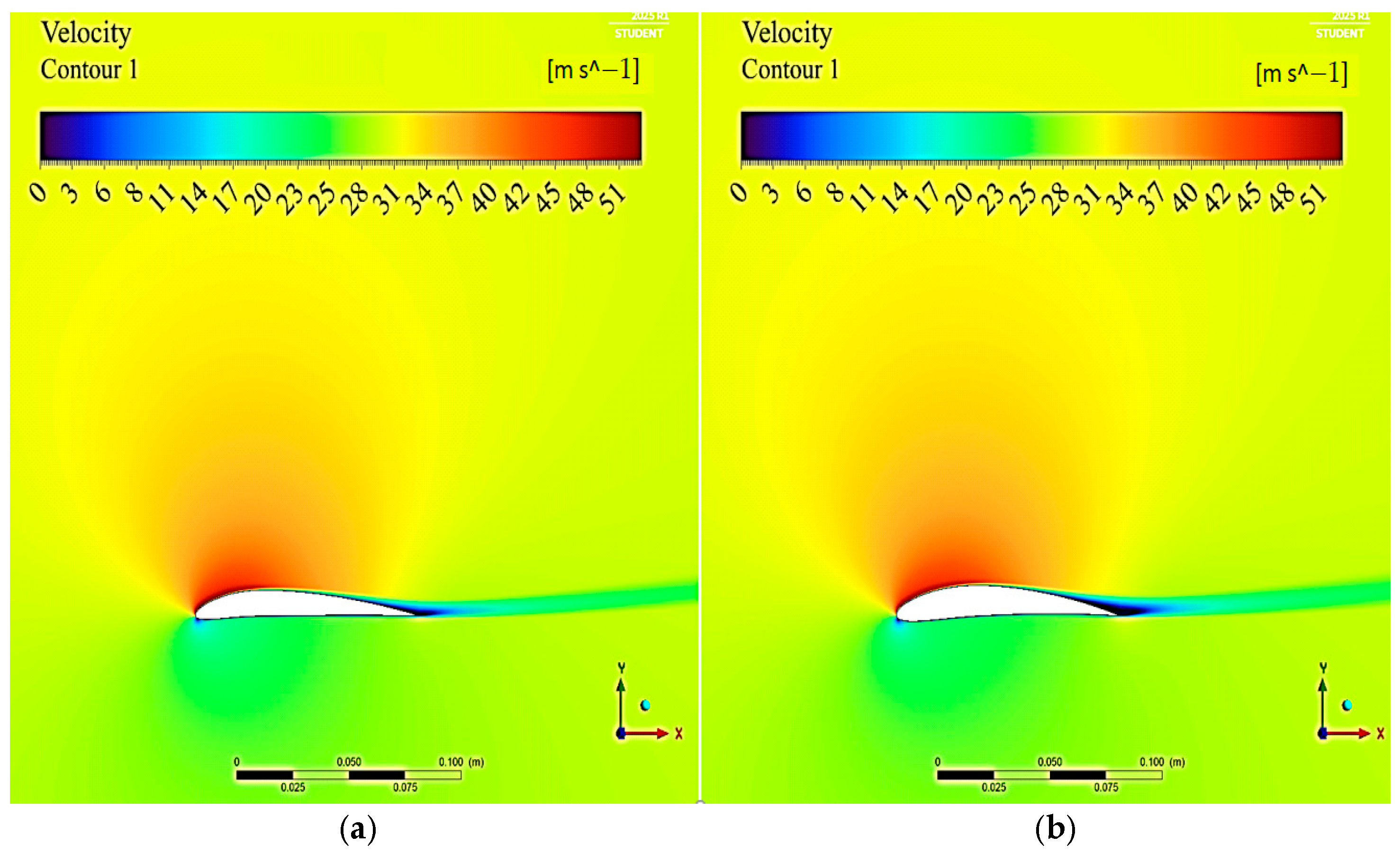
3. Results and Discussion
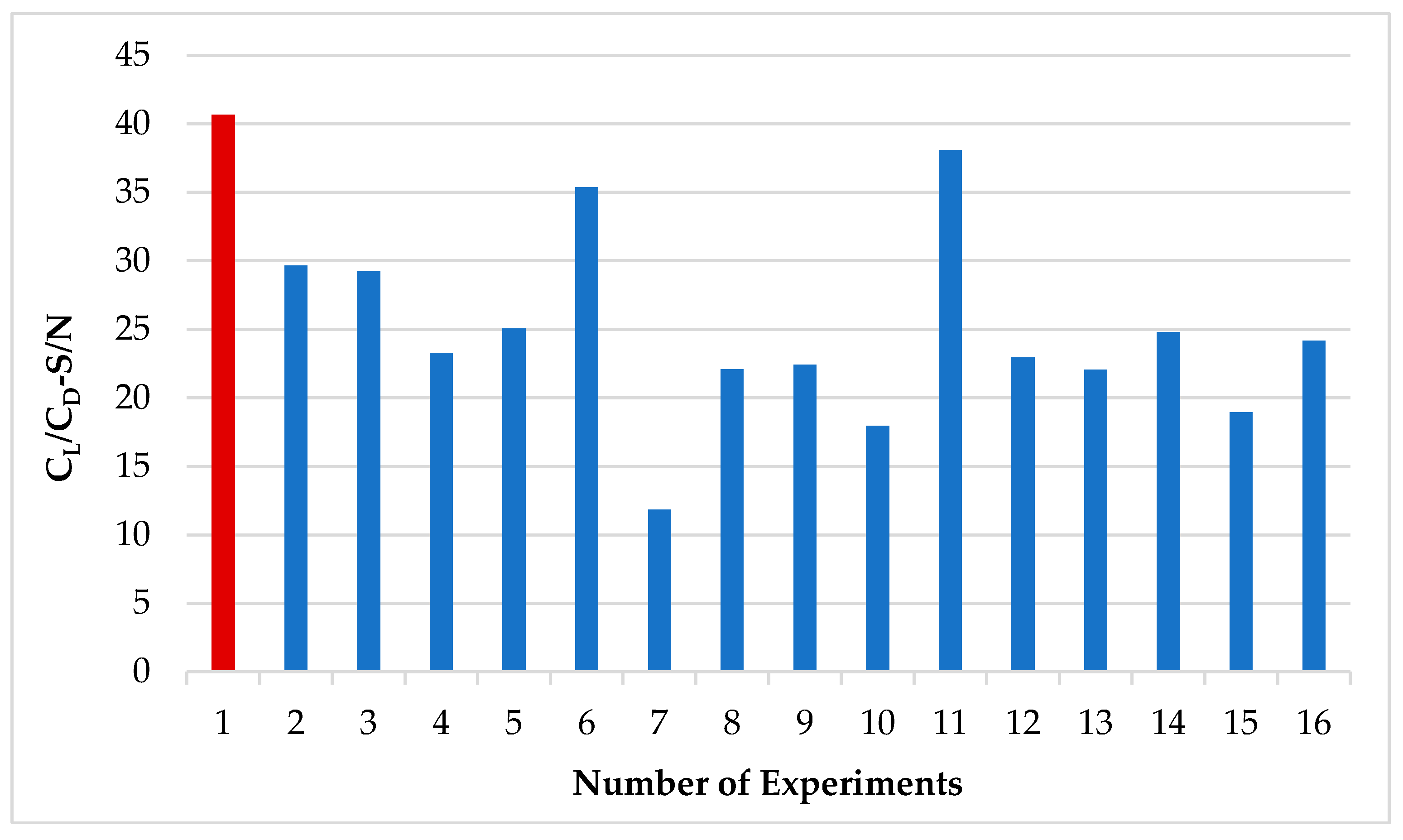
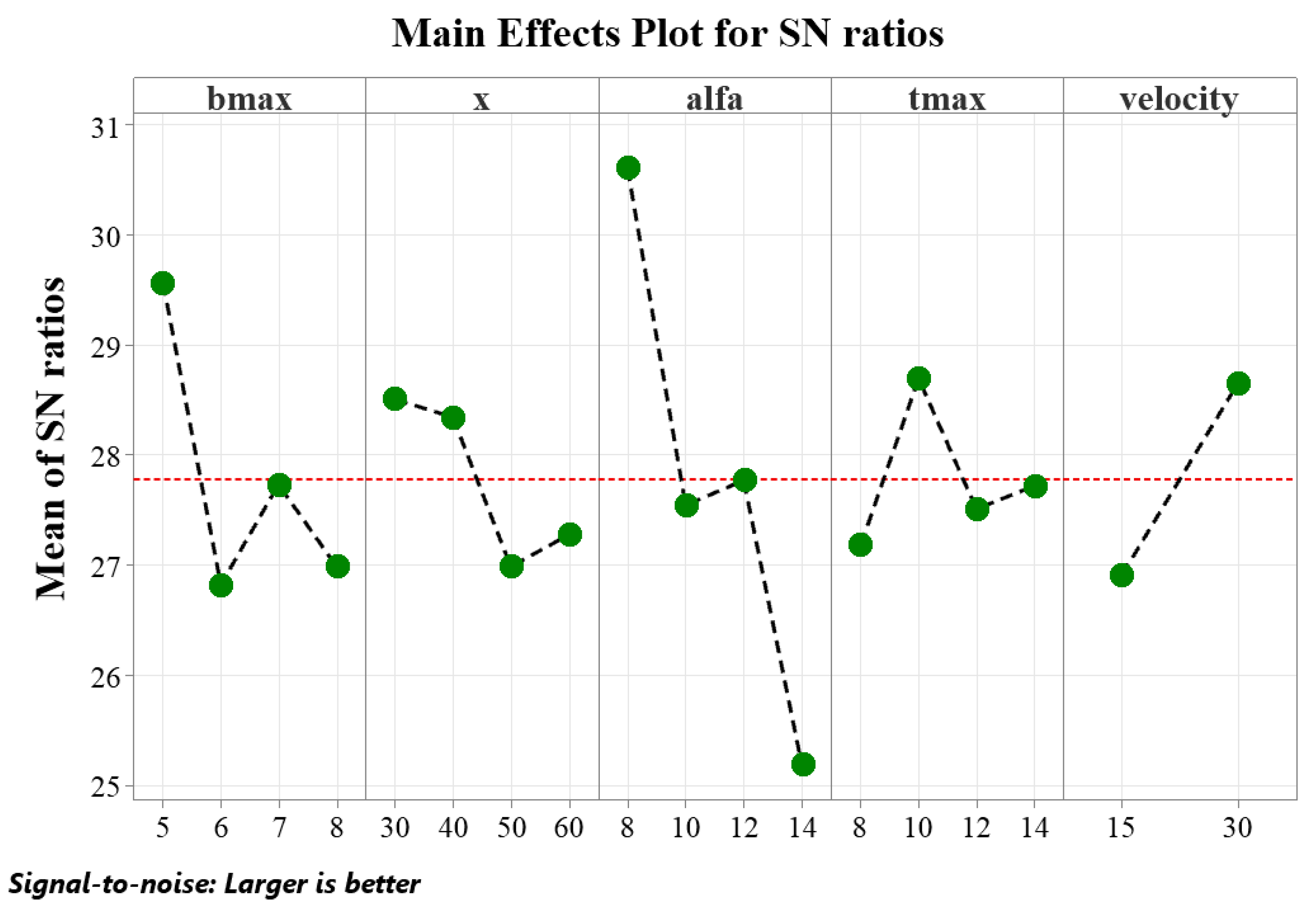
Results of the Taguchi Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FL | Lift Force (N) |
| FD | Drag Force (N) |
| CL | Lift Coefficient |
| CD | Drag Coefficient |
| CL/CD | Performance Ratio |
| bmax | Maximum Camber (%) |
| x | Position of Maximum Camber (%) |
| α | Attack of Angle (°) |
| tmax | Maximum Thickness (%) |
| V | Velocity (m/s) |
| c | Chord Length (m) |
References
- Drwiga, A.; Szelka, M.; Turewicz, A. Improvement of auxiliary ventilation efficiency in underground workings. IOP Conf. Ser. Earth Environ. Sci. 2019, 261, 012007. [Google Scholar] [CrossRef]
- Hassen, A.E. Flow characterization in mine ventilation fan blade design using CFD. J. Sustain. Min. 2021, 20, 144–156. [Google Scholar] [CrossRef]
- Taşkaya, G.; Erdogan, B. Investigation of a New Blade Design to Improve the Efficiency of an Axial Fan Used in an Underground Mine. Karaelmas J. Sci. Eng. 2024, 14, 144–162. [Google Scholar]
- Moralar, A.; Ekim, S. Application of NACA 6412 airfoil for noise and vibration reduction in evaporator fan blades. Processes 2024, 12, 2377. [Google Scholar] [CrossRef]
- Chen, W.-H.; Wang, J.-S.; Chang, M.-H.; Mutuku, J.K.; Hoàng, A.T. Efficiency improvement of a vertical-axis wind turbine using a deflector optimized by Taguchi approach with modified additive method. Energy Convers. Manag. 2021, 245, 114609. [Google Scholar] [CrossRef]
- Ouyang, K.; Chen, T.-Y.; You, J.-J. Utilizing the Taguchi Method to Optimize Rotor Blade Geometry for Improved Power Output in Ducted Micro Horizontal-Axis Wind Turbines. Sustainability 2024, 16, 4692. [Google Scholar] [CrossRef]
- Al-Hinai, A.H.; Karu, C.V.; Kumar, V.V. Performance optimization of a horizontal axis wind turbine simulator under the effects of blade’s pitch angle variation. Res. Eng. Struct. Mater. 2024, 10, 15–27. [Google Scholar] [CrossRef]
- Çakıroğlu, R.; Tanürün, H.E.; Acır, A.; Üçgül, F.; Olkun, S. Optimization of NACA 4412 augmented with a gurney flap by using grey relational analysis. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 167. [Google Scholar] [CrossRef]
- Suprayitno; Yu, J.C.; Aminnudin; Wulandari, R. Airfoil aerodynamics optimization under uncertain operating conditions. J. Phys. Conf. Ser. 2020, 1446, 012014. [Google Scholar] [CrossRef]
- Hwas, A.M.; Hatab, A.M. Effects of design parameters of wind turbine on airfoil coefficients using grey-based Taguchi method. J. Multidiscip. Eng. Sci. Technol. (JMEST) 2020, 7, 13103. [Google Scholar]
- Kaushik, V.; Shankar, R.N.; Rashid, N.I.H.; Khope, P.B. Implementation of Taguchi method for designing a robust wind energy system—A wind turbine. J. Eng. Sci. 2022, 13, 165–185. [Google Scholar] [CrossRef]
- Evran, S.; Yıldır, S.Z. Numerical and statistical aerodynamic performance analysis of NACA0009 and NACA4415 airfoils. Politek. Derg. 2024, 27, 849–856. [Google Scholar] [CrossRef]
- Sanaye, S.; Farvizi, A. Optimizing a vertical axis wind turbine with helical blades: Application of 3D CFD and Taguchi method. Energy Rep. 2024, 12, 2527–2547. [Google Scholar] [CrossRef]
- Yetis, Y.; Tehrani, K.; Jamshidi, M. Wind Speed Forecasting using Machine Learning Approach based on Meteorological Data-A case study. Energy Environ. Res. 2022, 12, 11–25. [Google Scholar] [CrossRef]
- Dey, S.; Saha, R. CFD study on aerodynamic effects of NACA 2412 airfoil as rear blade on a sports car. In Proceedings of the International Conference on Mechanical Engineering and Renewable Energy (ICMERE), Khulna, Bangladesh, 23–24 December 2018. [Google Scholar]
- Durmuş, S. Aerodynamic performance comparison of airfoils in flying blade UAV. Int. J. Innov. Eng. Appl. 2023, 7, 123–127. [Google Scholar] [CrossRef]
- Durmuş, S. Impact of airfoil type and placement on aerodynamic performance of blended blade body aircraft. Fırat Üniversitesi Mühendislik Bilim. Derg. 2025, 37, 351–361. [Google Scholar] [CrossRef]
- Fernando, V.N.; Mudunkotuwa, D.Y. Bio-Inspired Aircraft Blade Modification Analysis in ANSYS Fluent. In Proceedings of the 10th International Conference on Information and Automation for Sustainability, Negambo, Sri Lanka, 11–13 August 2021. [Google Scholar] [CrossRef]
- Kulkarni, S.; Malasane, P.; Zanje, N.; Metkari, Y.; Ghadge, N.; Athawale, S.; Kothmire, P. CFD analysis of drag reduction system (DRS) in cars. In Lecture Notes in Mechanical Engineering: Fluid Mechanics and Fluid Power; Springer Nature: Singapore, 2024; Volume 3, pp. 415–426. [Google Scholar] [CrossRef]
- Tehrani, K.; Beikbabaei, M.; Mehrizi-Sani, A.; Jamshidi, M. A smart multiphysics approach for wind turbines design in Industry 5.0. J. Ind. Inf. Integr. 2024, 42, 100704. [Google Scholar] [CrossRef]
- He, C.; Zhong, P.; Li, M.; Jie, L.; Li, Z. An evolutionary many-objective algorithm based on a novel tournament selection strategy. J. Comput. Commun. 2021, 9, 238–248. [Google Scholar] [CrossRef]
- Coello Coello, C.A. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chen, W.; Chiu, K.; Fuge, M.D. Airfoil design parameterization and optimization using Bézier generative adversarial networks. AIAA J. 2020, 58, 4723–4735. [Google Scholar] [CrossRef]
- Yılmaz, M.; Koten, H.; Çetinkaya, E.; Coşar, Z. A comparative CFD analysis of NACA0012 and NACA4412 airfoils. J. Energy Syst. 2018, 2, 145–154. [Google Scholar] [CrossRef]
- NACA 4 Digit Airfoil Generator (NACA 2412 AIRFOIL). Available online: http://airfoiltools.com/airfoil/details?airfoil=naca6412-il (accessed on 22 June 2025).
- Zengin, İ.; Erdoğan, B.; Benim, A.C. CFD and Taguchi based optimization of air driven single stage partial admission axial turbine blade profiles. Energy 2024, 290, 130333. [Google Scholar] [CrossRef]
- Fayyad, S.M.; Al Alawin, A.; Shabi, O.A.; Abulghanam, Z.; Abu-Ein, S.; Alsabagh, A.S.; Abu-Rahmeh, T.; Rawashdeh, M.O.; Momani, M.; Momani, W.; et al. Aerodynamics analysis comparison between NACA 4412 and Falco airfoils. J. Harbin Eng. Univ. 2024, 45. Available online: https://harbinengineeringjournal.com/index.php/journal/article/view/2526 (accessed on 22 June 2025).
- Berger, M.; Raffeiner, P.; Senfter, T.; Pillei, M. A comparison between 2D DeepCFD, 2D CFD simulations and 2D/2C PIV measurements of NACA 0012 and NACA 6412 airfoils. Eng. Sci. Technol. Int. J. 2024, 45, 101794. [Google Scholar] [CrossRef]

| Factors | Variable Parameters | Values | Units |
|---|---|---|---|
| A | Maximum Camber Ratio, (bmax) | 5; 6; 7; 8 | (%) |
| B | Maximum Camber Position, (x) | 30; 40; 50; 60 | (%) |
| C | Angle of Attack, (α) | 8; 10; 12; 14 | (°) |
| D | Blade’s Maximum Thickness Ratio, (tmax) | 8; 10; 12; 14 | (%) |
| E | Free Stream Velocity (V) | 15; 30 | (m/s) |
| No | Factors | Factors | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E |  | bmax | x | α | tmax | V | |
| 1 | 1 | 1 | 1 | 1 | 1 | 5 | 30 | 8° | 8 | 15 | |
| 2 | 1 | 2 | 2 | 2 | 1 | 5 | 40 | 10° | 10 | 15 | |
| 3 | 1 | 3 | 3 | 3 | 2 | 5 | 50 | 12° | 12 | 30 | |
| 4 | 1 | 4 | 4 | 4 | 2 | 5 | 60 | 14° | 14 | 30 | |
| 5 | 2 | 1 | 2 | 3 | 2 | 6 | 30 | 10° | 12 | 30 | |
| 6 | 2 | 2 | 1 | 4 | 2 | 6 | 40 | 8° | 14 | 30 | |
| 7 | 2 | 3 | 3 | 1 | 1 | 6 | 50 | 14° | 8 | 15 | |
| 8 | 2 | 4 | 3 | 2 | 1 | 6 | 60 | 12° | 10 | 15 | |
| 9 | 3 | 1 | 3 | 4 | 1 | 7 | 30 | 12° | 14 | 15 | |
| 10 | 3 | 2 | 4 | 3 | 1 | 7 | 40 | 14° | 12 | 15 | |
| 11 | 3 | 3 | 1 | 2 | 2 | 7 | 50 | 8° | 10 | 30 | |
| 12 | 3 | 4 | 2 | 1 | 2 | 7 | 60 | 10° | 8 | 30 | |
| 13 | 4 | 1 | 4 | 2 | 2 | 8 | 30 | 14° | 10 | 30 | |
| 14 | 4 | 2 | 3 | 1 | 2 | 8 | 40 | 12° | 8 | 30 | |
| 15 | 4 | 3 | 2 | 4 | 1 | 8 | 50 | 10° | 14 | 15 | |
| 16 | 4 | 4 | 1 | 3 | 1 | 8 | 60 | 8° | 12 | 15 | |
| Analysis Conditions | |
|---|---|
| Angle of Attack (α) | 0° |
| Air Velocity | 10 m/s |
| Air Density | 1.225 kg/s |
| Air Dynamic Viscosity | 1.7894 × 10−5 Pa·s |
| Reynolds Number | 82,000 |
| Reference Study [29] | Current Study | Error (%) | ||||
|---|---|---|---|---|---|---|
| α | CL | CD | CL | CD | CL | CD |
| 0° | 0.624 | 0.030 | 0.653 | 0.029 | 4.65 | 3.33 |
| Number of Elements | Max. Skewn. | Min. Orth. Quality | Lift Coefficient CL | Drag Coefficient CD | Performance Ratio CL/CD | Difference (%) |
|---|---|---|---|---|---|---|
| 7000 | 0.53 | 0.69 | 1.165 | 0.033 | 35.30 | 10.66 |
| 12,000 | 0.50 | 0.72 | 1.172 | 0.030 | 39.07 | 3.98 |
| 44,000 | 0.49 | 0.73 | 1.178 | 0.029 | 40.62 | 0.08 |
| 55,000 | 0.49 | 0.73 | 1.179 | 0.029 | 40.66 | 0.08 |
| 110,000 | 0.48 | 0.72 | 1.180 | 0.029 | 40.69 | * |
| Source | DF | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|
| A. Camber | 3 | 18.16% | 18.950 | 6317 | 5.89 | 0.148 |
| B. Position of Camber | 3 | 6.66% | 6.943 | 2.314 | 2.16 | 0.332 |
| C. Attack Angle | 3 | 56.66% | 59.110 | 19.703 | 18.39 | 0.052 |
| D. Thickness | 3 | 4.89% | 5.105 | 1.702 | 1.59 | 0.409 |
| E. Velocity | 1 | 11.57% | 12.070 | 12.070 | 11.26 | 0.078 |
| Error | 2 | 0.78% | 2.143 | 1.072 | - | - |
| Total | 15 | 100.00% | 104.322 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erdoğan, B.; Taşkaya, G. Optimization of NACA 6412 Using Taguchi Method and Computational Fluid Dynamics Analysis. Sustainability 2025, 17, 5861. https://doi.org/10.3390/su17135861
Erdoğan B, Taşkaya G. Optimization of NACA 6412 Using Taguchi Method and Computational Fluid Dynamics Analysis. Sustainability. 2025; 17(13):5861. https://doi.org/10.3390/su17135861
Chicago/Turabian StyleErdoğan, Beytullah, and Güneyhan Taşkaya. 2025. "Optimization of NACA 6412 Using Taguchi Method and Computational Fluid Dynamics Analysis" Sustainability 17, no. 13: 5861. https://doi.org/10.3390/su17135861
APA StyleErdoğan, B., & Taşkaya, G. (2025). Optimization of NACA 6412 Using Taguchi Method and Computational Fluid Dynamics Analysis. Sustainability, 17(13), 5861. https://doi.org/10.3390/su17135861






