Abstract
Nowadays, when battery-powered electric vehicles (EVs) travel along motorways, their drivers decide where to recharge their cars’ batteries with no or scarce information on the occupancy status of the next charging stations. While this may still be acceptable in most countries, due to the limited number of EVs on motorways, long queues may build-up in the coming years with increased electric mobility, unless smart allocation strategies are designed and implemented. For instance, as we shall investigate in this manuscript, a centralised coordination of the charging strategies of individual EVs has the potential to significantly reduce the queuing time at charging stations. In particular, in this paper we explain how the charging problem on motorways can be modelled as an optimisation problem, we propose some strategies based on dynamic optimisation to solve it, and we explain how this may be implemented in practice using a centralised charge manager that exchanges information with the EVs and solves the optimisation problems. Finally, we compare in a realistic scenario the current decentralised recharging strategies with a centralised one, and we show that, under simplifying assumptions, queueing times can be reduced by more than 50%. Such a significant reduction allows one to greatly improve vehicular flows and general journey durations without requiring building new infrastructure. Reducing queuing times has a positive impact on traffic congestion and emissions, and the more geographically balanced energy demand of the proposed methodology mitigates energy consumption peaks.
1. Introduction
1.1. Motivation
Decarbonization of the transport sector is moving forward and the new goal set by the European Commission is to reach 100% of newly registered cars and vans that are zero-CO2 emission by 2035 [1]. This agreement is expected to further accelerate the spread of battery-electric vehicles (EVs), and it is foreseen that global electric light-duty vehicle sales are set to reach almost 55% in 2035 [2]. Accordingly, the standards for the EV charging infrastructure have been updated to accommodate the growing demand. In particular, the Alternative Fuels Infrastructure Regulation (AFIR) states that by 2035 main European roads must have charging stations (CS’s) every 60 km and each Charging Station (CS) must offer “a power output of at least 600 kW and include at least two recharging points with an individual power output of at least 150 kW” [3].
However, despite a significant improvement in CS availability in Europe [4], the forecasted increase for the coming years in the number of EVs on the roads and their relatively long charging time (compared to conventional gas vehicles), raises concerns about queueing and waiting times, especially on roads with heavy traffic. In this context, to accommodate the growing charging demand of EVs, it will be pivotal to develop schemes and procedures that conveniently exploit the existing infrastructure before resorting to building new charging stations, which would imply large investment costs. In particular, coordinated charging of EVs may help to redistribute the charging demand among the available CS’s, thus reducing the burden on the busiest ones.
In a previous study [5], authors evaluated the impact of different penetration levels of EVs on the most important Italian motorway. In that research, it was assumed that EV drivers would select the CS where to recharge, if needed, depending only on local information (e.g., the state-of-charge SOC of their battery and their personal trip), or on a minimum amount of information of CSs (e.g., the availability of a free plug at the nearest CS). In the present manuscript, we want to investigate what improvement could be obtained—in terms of waiting times at CSs—if a centralised agent solves an optimisation problem to optimally assign each vehicle at CSs along its route. In particular, by knowing SOCs and trips of all vehicles, a centralised agent may orchestrate where EVs should be charged in order to avoid—or minimise—queues at CSs.
While a plethora of algorithms have already been investigated for this purpose in previous studies, most of them have been designed for urban settings, which are significantly different from motorways, and that are characterised by limited possibilities of re-routing and tighter constraints regarding charging times. The following section is dedicated to reviewing such existing algorithms.
1.2. State of the Art
The optimal use of the EV charging infrastructure has been studied from different perspectives, depending on the point of view of interest, such as the technical capabilities (e.g., vehicle-to-grid connection), and operational settings (microgrids, local markets, conventional urban settings, etc.). For example, a coordinated charging strategy may be used to shift the load demand and mitigate peak energy consumption [6] or to charge EVs during renewable energy sources generation [7]; it may also support the distribution system operator (DSO) operation by providing additional flexibility to power systems [2] or support microgrids (MGs) and local energy markets operation [6,7]. In [8], the authors show, in a small example, the performance of CSs with a limited number of charging slots in the uncontrolled charging case and the optimal charging scheduling, using different prices to lower the charging peak.
In addition to the rescheduling, rerouting of EVs may also be considered to avoid queues on the CSs [9]. For example, in [10] the authors compute an optimal route for delivery companies that are using an EV fleet. A secure way to reserve charging slots is suggested in [11], where the authors rely on blockchain technology to allow EVs to make reservations without sharing their information. Distributed ledger technologies are also used in [12] to optimally assign EVs at CSs based on personalised cost functions, to simultaneously take into account price, time, and battery constraints. In [13], the authors study charging schedules of EVs using a semi-decentralised real-time method, which considers charging urgency factor and a discount factor. The proposed method deals with EV uncertainties and meets charging demands with a given confidence level. In [14], in an urban setting again, EVs are optimally assigned to charging stations based on personalised cost functions that take into account distance, time, and cost of charging.
Among the coordinated strategies, a particular scenario is the coordination of EVs that are driving along a motorway. In this case, the vehicle’s batteries discharge faster due to the much higher air drag than in urban contexts [14], rerouting possibilities are quite limited, and drivers are willing to charge as soon as possible to continue their trips, thus rescheduling or reducing charging power is usually not considered. Since motorway trips are still a relatively novel option for EVs, which due to their limited range have been initially mostly deployed in urban settings, studies related to EVs on motorways are still mainly focused on the construction and allocation of the CS infrastructure. For example, Ref. [15] suggests a two-stage method for CS allocation and sizing on motorway networks, where the first stage extracts the optimal sites for CSs based on the traffic data and EV data, while the second stage optimises the capacities of photovoltaic panels and storage units in each charging station. Another bi-level planning model is suggested in [16], where the authors split the motorway charging problem into two stages: first, they determine CS construction plans and, secondly, they describe the user equilibrium-based traffic assignment model of the traffic network and the operation model of power distribution networks. The allocation of CS’s on motorways is also optimised in [17], where the authors also evaluate the possibility of using portable energy storage devices to support EV charging and relocate them to different CSs, to reduce queueing. The authors model both traffic and use of CSs by considering different flows and different optimisation goals for working days (peak-load mitigation) and holidays (reduce traffic congestions). The resulting mixed integer and nonlinear problem is then solved using a genetic algorithm methodology. Other works also address the same CS location problem, such as [18,19,20,21]. In particular [18] compares modelling and solution methods for locating EV charging stations on intercity highways, considering both uncongested and congested networks. It presents two frameworks and applies branch-and-bound algorithms with different strategies to analyse routing behaviour, efficiency, and implementation on the Sichuan Basin highway using real-world data. The study in [19] explores EV intercity travel in a time-sharing rental model, considering user behaviour, charging rates, and battery degradation. It proposes a mixed-integer model for charging station placement and introduces the KIGALNS heuristic, which outperforms existing methods in tests and a real case in Hubei, China. The authors in [20] propose a bilevel model to optimise charging station locations and capacities on expressways, balancing construction and EV travel costs. Using a genetic algorithm and traffic assignment, the model is tested in Shandong, China. Ref. [21] analyses real-time power demand data from EV charging station on a U.S. interstate in the Northern High Plains, examining usage patterns and solar energy potential. It offers insights for sustainable operation to integrate EV charging stations location with photo voltaic generation.
Conversely, in the current manuscript we investigate the problem of assigning EV charging to CSs in an already existing and operating charging infrastructure. Thus, we are interested in maximising the efficiency of the infrastructure, e.g., in terms of minimum queues at CSs. This problem has been more rarely investigated, and there are only a few works that have addressed it along highways. In [22], the authors suggest an enhanced A* shortest path search algorithm that also accounts for the constraints related to available state-of-charge of the EVs. Despite using a motorway setting, the authors consider several possible paths and rerouting for EVs, in case of long queues at CSs. In [23], the authors develop a coordination strategy to deal with queues using average flows of EVs and to uniformly use all available CSs along the motorway by applying a consensus-based distributed scheduling algorithm. To maximise the efficiency of motorway CSs, [24] proposes a pricing methodology that considers both the traffic flow and renewable energy generation, using hour-by-hour traffic flow and renewable generation forecasts. In [25], the authors propose a multi-objective scheduling of the motorway charging stations. They model charging behaviour of drivers by applying traffic flow prediction (Convolutional neural network—BiLSTM) and a load modelling method (M/M/Nsum/C queuing theory). The charging scheduling is planned by considering the day-ahead scheduling that is set based on price incentives and intra-day scheduling that involves flexibility resources to compensate uncertainties.
1.3. Contribution
The main contributions of this paper are as follows:
- We discuss and analyse how a centralised strategy to manage EV charge on motorways can be arranged and how this system can be formulated as a standard optimisation problem;
- We compare classic decentralised strategies from other papers in the literature with the proposed centralised strategy in a realistic case study, and show that improvements of queuing times greater than 50% may be achieved with centralised solutions.
2. Centralised Optimal Charging Strategy
2.1. General Approach
This strategy relies on a centralised scheme that allocates EVs to CSs in order to minimise their queuing time according to an optimal control strategy. It requires the presence of a Centralised Charging Manager (CCM), that must have bidirectional communication capabilities with EVs, as depicted in Figure 1. This is not an unrealistic assumption, since modern vehicles are already equipped with communication capabilities, or a connected device could be used for this purpose anyway, such as a car navigator or a smartphone.

Figure 1.
General scheme of a centralised recharging scheme.
With reference to Figure 1 we assume that whenever a vehicle enters the motorway, it will send the CCM the relevant initial data which are required to compute where to charge along the route. These include the following:
- Trip details (i.e., motorway entry and motorway exit);
- Current battery state-of-charge (SOC);
- Battery capacity;
- Expected driving speed;
- Expected specific energy consumption (i.e., the expected Wh/km);
- Charging curve (the maximum charging power as a function of SOC that the vehicle can accept);
- The maximum SOC at the end of charging process (this is typically 80% because going further is disadvantageous, since charging near full-charge condition is very slow).
While the first three points are strictly required, the other information may be easily predicted or estimated (e.g., by knowing the model of the vehicle, or traffic conditions). Additional data may be provided as well, if desired, e.g., the desired level of SOC when reaching the motorway destination.
Using this info, the CCM solves the optimisation problem and evaluates where this vehicle should stop to charge, and how much it should charge, taking into account information of other vehicles as well, as the following for instance:
- The current occupancy status of all the charging stations (as inferred from the vehicles already charging);
- The programmed future charging operations (as recommended to the vehicles that are already travelling);
- The state (position, SOC, etc.) of all the other vehicles already inside the motorway.
As soon as the optimisation problem is solved, indications on where and how much to recharge is sent by the CCM to the EVs. EV drivers may, in general, comply with the received recommendations or not. In principle, if the CCM recommends the optimal solution, it may be expected that most drivers will follow the received recommendation, as it is the most convenient one, and any other personalised choice is expected to be subject to an increased waiting time. However, a monetary incentive may be required in practice to further encourage the compliance of EV drivers (e.g., as a discount for the charging or reserving service).
In addition to sending drivers the charging plan along with the motorway, the CCM also reserves plugs for EVs to charge, at the time they are expected to reach the recommended CS. To do this, it uses the expected driving speed communicated by the EV upon entering the motorway, adding some safety margin to allow for unavoidable deviations, possibly caused by traffic conditions or other scenarios.
To conveniently handle the uncertainty of traffic conditions, which also influence the specific consumption (Wh/km), it is advisable that EVs periodically update their initial communication. Obviously, the most important updated quantity is SOC, but also the actual position and speed may be different from initially expected. In general, however, a total reprogramming may be required as well, for instance because an accident has occurred on the motorway, or for any other reason (e.g., the driver has changed the destination). Such updates allow for reducing the margin of time taking when reserving plugs for charge, thus improving the charging station’s utilisation.
2.2. Mathematical Formulation
In the following, we shall describe all the components of the optimisation problem, and, in particular, the variables of the optimisation, the cost function, the constraints, and the outcome of the optimisation. For simplicity, we shall not consider now the uncertainty of traffic and the need for reassigning the reservations of the CSs based on real-time traffic conditions. In practice, this corresponds to assuming that traffic is regular and it is not needed to make real-time updates on CSs assignments. We now see in detail the components of the optimisation problem.
2.2.1. Cost Function
We consider a cost function that consists of two components that are minimised as follows:
where the first term is required to take queuing times into account, while the second term can be used to take other aspects into account (for instance, some drivers perceive travelling with a SOC lower than, say, 50% as less comfortable). Parameters and are required to coherently combine the two terms and to give more importance to one or another. For instance, when is set equal to zero, an EV only intends to minimise queuing times at CSs, while when is set equal to zero, EVs will not travel with a SOC lower than 50%, and are not interested in queuing time.
When both components are present simultaneously, queuing times are minimised while avoiding travelling with a low SOC.
More specifically, we model in Equation (1) as follows:
where is valued 1 if at time step k the vehicle is queuing at a CS and zero otherwise, and likewise is valued 1 if at time step the vehicle is charging and zero otherwise. In Equation (2), is the time step (5 min in simulations proposed in the case study section). The rationale of including charging times in the queuing time is that drivers may use fast charging stations along motorways to reach their final destination, possibly with a final desired SOC, but should not charge more than necessary, as domestic charging plugs may be used for the latter case without giving rise to congestion along motorways. In addition, not considering charging times in the cost function may give rise to multiple optimal solutions, where EVs leave the motorway with different levels of SOC (all of them above a desired minimum value). As mentioned, the term in Equation (1) can be used to avoid, for instance, travelling with low SOCs. Accordingly, may be designed as a generic function of the SOC, as in the following for instance:
so that driving with low SOC is penalised, while does not affect when the SOC is larger than the desired value. In Equation (3), is a fixed parameter that may be used to shape the penalty function, if desired. In our simulations, we set = 1 and = 30%. The sum index in the previous equations goes from 1 until the moment the vehicle leaves the motorway. While this value is not known in advance (as it may depend on the specific strategy), it may simply set equal to a large enough value (e.g., 288 in the case study discussed below, as it corresponds to one day, being = 5 min).
2.2.2. Dynamics of EVs
We model EVs as dynamic systems characterised by a discrete state for the mode (i.e., travelling, queuing, or charging), and by a continuous state for the SOC, that is updated as follows:
positive value of depends on the charge rate of the vehicle (which, in general, varies as a function of SOC, even though in the case study proposed later we did not consider this dependence; see Table 1). The negative value of depends mainly on vehicle speed but also on vehicle characteristics (tyre rolling coefficient, aerodynamic drag coefficient, cross-sectional vehicle area). To simplify things, average values of vehicle parameters can be assumed, and a direct correlation between vehicle speed and specific consumption (Wh/km) may be assumed [26].

Table 1.
Case study input information.
When queuing, we consider zero SOC variations because we assume that the discharge of the battery of a vehicle is negligible during the wait for an available plug. This may not necessarily be true, especially if auxiliary services, such as radio or heating, are used during the wait. An EV passes from the “travelling” mode to the “queuing” mode when it stops for charging, from the ”queuing” mode to the ”charging” mode when it starts charging, and back to the “travelling” mode when it resumes its trip. We assume that the passage to the “queuing” mode is mandatory and lasts at least 5 min, even in the absence of actual queues, to account for all the overhead time spent for actually leaving the motorway and reaching the plug, connecting the plug in the socket, and handshaking with the charge provider.
2.2.3. SOC Constrains
In addition to the soft SOC constraint considered in Equation (1), to penalise driving in low-SOC conditions, it is important to consider a strong constraint on the minimum value that the SOC can achieve (here, we consider 15%). In this way, no EVs will ever travel with a SOC lower than 15%, and we penalise values of the SOC around 15% anyway. Also, we assume that the maximum value of the SOC during a charging event cannot exceed 80%. This second constraint is dictated by the fact that it usually takes a longer time to charge batteries above this threshold.
2.2.4. Optimisation Output
The CCM solves the optimisation problem and recommends to the driver where to stop for charging, if needed, and how much energy should be charged. In particular, the CCM reserves a plug for the EV at the expected time in the recommended CS.
In practice, there are several strategies that the CCM may decide to follow. For instance, it may opt to reserve for a longer time than strictly required to leave some margin to handle possible inaccuracies in arrival predictions not covered by the data updates shown in Figure 1. Alternatively, the CCM may opt for a safer strategy and only reserve a subset of the available plugs for the centralised strategy. In this way, the extra plugs may be used to compensate for uncertainties of travel, and, in general, for the EVs that are not compliant with the recommendations from CCM. In the case study investigated below, we do not consider such situations, which are beyond the scope of this paper, and leave them to future investigation.
2.3. Simplifying Assumptions for a Realistic Evaluation
In this manuscript, we want to evaluate the actual advantage that may be gained by adopting centralised strategies, with respect to classic decentralised decisions, where EV drivers decide where to stop based on local partial information. For the purpose of this comparison, we make the following simplifying assumptions:
- 1.
- All drivers accept the CCM recommendations;
- 2.
- No unforeseen events occur, and therefore optimisation is performed only when a new vehicle enters the motorway without the need for updates.
3. Case Study
3.1. Decentralised Reference Strategies
To evaluate the effectiveness of the proposed centralised optimal allocation algorithm, a comparison can be made with simpler decentralised strategies, based just on the local information available to drivers, i.e., just the local value of the SOC and, possibly, the state of occupancy of the nearest CS. Two decentralised strategies are here considered, which were presented in detail in paper [5] and tested on the simulator of [27].
3.1.1. Decentralised Strategy 1
This strategy considers that an EV chooses to charge at a given CS if, without stopping, the SOC would drop below a safety threshold of 30%. It is very simple to implement this strategy in practice, as a driver simply has to know the value of the SOC of the EV. Also, this strategy prevents a SOC from ever going below a given threshold. Its value has been set to 30%, but other choices are possible depending on how cautious the driver is, without affecting the spirit of the charging methodology.
3.1.2. Smart Decentralised Strategy 2
This strategy assumes that an EV may decide not to stop at the next CS if this is completely full and queuing is required, even if this implies going below the threshold of 30%. In this case, a second lower safety threshold is set, and the battery may temporarily go below 30%, but never below, say, 15%. This second strategy may help an EV to avoid a full CS, waiting until the next one in the hope that the following one has no queues.
This strategy is again simple to implement but requires that the occupancy of CSs is communicated to all drivers.
3.2. Structure of the Motorway
Simulations are performed based on the A1 motorway (also known as “Autostrada del Sole”), which is the main Italian motorway branch that crosses almost the whole country and connects Milan to Naples, connecting some of the most important Italian cities, such as Bologna, Florence, and Rome, as depicted in Figure 2. Considering that the flows in the two directions (i.e., North–South and South–North) are independent (they do not interact with each other and each direction has its own charging stations), we only consider the direction flow from Milan to Naples. The motorway is 760 km long and there are 55 exits/entries along its way.
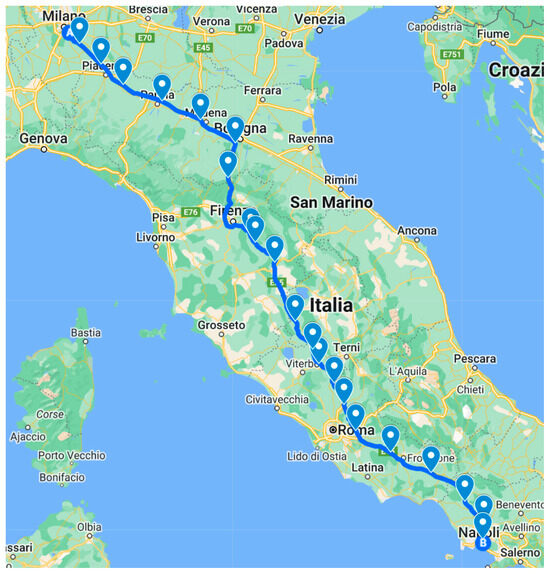
Figure 2.
A1 motorway and sequence of charging stations.
Twenty-four CSs are available along the motorway (see Figure 1), and each station is equipped with at least two high-power charges whose total maximum power is 300 kW (either for a single charger, or divided between two connected vehicles), and with a fast charger, which reaches 64 kW. Following [5], the charging infrastructure is simplified to five independent plugs, where each one may reach a charging power of 150 kW (considering future increase in output power).
3.3. Vehicular Flows
We exploit the daily periodic patterns of traffic, and consider a horizon of time of 24 h, with a time step of 5 min. The entrance and exit of EVs are modelled based on a realistic Origin/Destination (O/D) matrix, taken from average measured data, corresponding to vehicular flows along the A1 motorway on working days (see Figure 3a). Data were recorded based on toll booth tickets and collected and provided by the highway manager. In Figure 3a, whiter cells refer to trips with low probability, meaning that those routes are not chosen by any driver. Conversely, darker cells correspond to higher traffic volumes and can reasonably be associated with areas near larger cities along the highway. Moreover, the sub-diagonal of the matrix is made of zeros, as for simplicity our study considers only trips in the north-to-south direction.
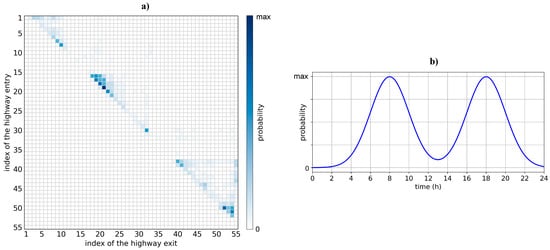
Figure 3.
(a): Origin/destination matrix adopted in our work shown in terms of probability of routes; (b) time distribution probability of vehicle entry time in the highway.
The entry time of EVs is then modelled considering two peaks of traffic in the morning and in the late afternoon hours, again according to average measured data (see Figure 3b). As shown in Figure 3, the peaks of the highest entry probability occur at 8 a.m. and 6 p.m., which can be reasonably associated with typical commuting times to and from working places. The total number of vehicles on the motorway is 500,000, including both EVs and conventional vehicles. Finally, we consider different penetration levels of EVs to assess and evaluate the effect of different number of EV on the motorway, also for future scenarios.
3.4. EV Characteristics
We considered a fleet of EVs with different characteristics, as summarised in Table 1. In particular, EVs of different brands have been grouped together based on the general vehicle’s characteristics, such as battery size and charging power, with a full description of these groups provided in [1]. The initial (at the time of entering motorway) values of the SOCs of EVs are randomly chosen within the range of 70–80%, where such high values are justified by the assumptions that EVs usually enter motorways with relatively well charged batteries. Other parameters related to the SOC are provided in Table 1 again: (here, 30%) represents the minimum threshold that car drivers want to avoid, if possible. In the smart decentralised strategy and in the centralised strategy, drivers may temporarily travel with lower SOCs, but they cannot go below (here, 15%). Also, we consider that the maximum level of the SOC is 80%, as it usually takes a particularly long time to charge from 80% to 100%, and we assume here that drivers stop charging at 80%. Finally, we assume that travel speeds range between 100 km/h, when drivers travel at a speed that prolongs the duration of the battery, and 130 km/h, which is the maximum allowed speed.
For convenience, all the parameters of the case study are summarised in Table 1. It should be noted that all parameters have been selected according to classic assumptions and are consistent with those used in other case studies (e.g., Ref. [5]), but other parameters may be selected instead without affecting the outcome of the comparison.
4. Simulation Results
We now compare the three different CS assignment schemes, to evaluate what can be achieved through the smart autonomous decisions of drivers, and most importantly by imposing a centralised assignment scheme. All simulations were carried out by developing the system model in Python using the Gurobi optimisation solver, version 10.0.0. The model is formulated as a Mixed-Integer Quadratically Constrained Program (MIQCP), consisting of 30,504 quadratic constraints, with 36,953 continuous variables and 13,392 integer variables. Gurobi solved the continuous relaxation at the root node using the Simplex method, with 849 iterations and a total runtime of 0.53 s on a PC equipped with a 12th Gen Intel(R) Core(TM) i7-12700 CPU, featuring 6 physical cores and 12 logical processors, utilising up to 12 threads during computation.
4.1. Penetration Level of 3%
While the current penetration level of EVs in Italy is rather low—around 0.7%—and queuing phenomena at CSs are hardly visible, we are interested in investigating what would happen with more significant penetration levels. For instance, a penetration level of 3% would imply a number of about 15,000 passenger electric cars.
Figure 4 summarises the occupancy levels of all the CSs along the motorway—in terms of minutes that EVs spend charging—according to the three different assignment schemes. The sum of the heights of all the bars of the same colour in the figure is the same, as we consider the same trips in all the cases, and thus the vehicles charge by approximately the same amount in all cases.
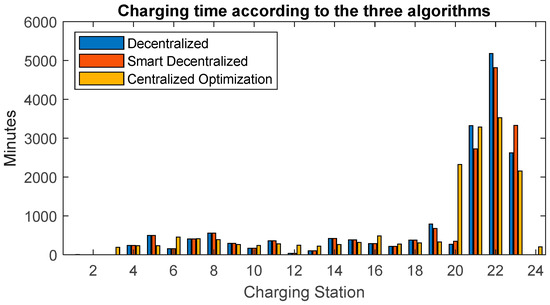
Figure 4.
Occupancy of charging stations with penetration level of 3%.
Two main things can be observed: first, not all CSs are equally deployed, but the CSs in the last part of the motorway (i.e., between Rome and Napoli) exhibit a much greater occupation. This is partly due to the intense traffic in that part of the motorway, and also due to the fact that CSs are less dense in that stretch of the motorway than in the rest of the motorway. A second thing that can be observed is that the centralised solution strongly deploys CS 20, which is otherwise poorly utilised according to the other two schemes, to decrease the utilisation of CSs 21–23 that are the three busiest CSs otherwise.
Figure 5 depicts the queuing times at the CSs. As could be expected as a consequence of Figure 4, queues only occur at the busiest CSs.
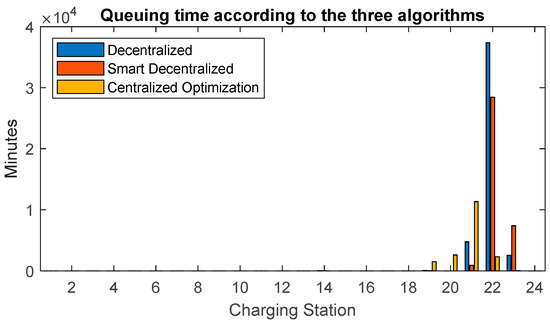
Figure 5.
Queuing Time at charging stations with a penetration level of 3%.
The centralised strategy gives rise to some queues at CSs 19 and 20, which did not exist with the other two strategies, and increases the queue length of CS 21. However, it dramatically reduces the duration of the queues at CSs 22 and 23. In particular, the average queuing time (calculated among all the EVs that had to recharge) decreases from 54 min (Strategy 1: decentralised solution) to 44 min (Strategy 2: smart decentralised solution), down to 21 min (Strategy 3: centralised solution).
4.2. Penetration Level of 5%
If we further increase the penetration level of EVs to 5%, which corresponds to 25,000 EVs along the motorways, similar results may be noticed. In this case the occupancy of all the CSs is depicted in Figure 6. Again, the centralised algorithm manages to better balance vehicles at CSs and exploits more at CS 20, which is under-utilised by decentralised algorithms, to shave the peak at CSs 21–23. Figure 7 shows the corresponding queuing times and, as before, longer queues appear at CSs 19–21, that do not exist (or are much smaller) in the decentralised case, but such queues are instrumental to dramatically reduce the queues at CSs 22 and 23. In addition, it is possible to observe that, due to the large penetration level of EVs, small queues also start building up at other CSs with the decentralised algorithms (i.e., 5, 8, and 17), but such queues are avoided thanks to the balancing effort of the centralised algorithm. With such a high penetration level, the average waiting time decreases from 122 min (Strategy 1: decentralised solution) to 114 min (Strategy 2: smart decentralised solution), down to 54 min (Strategy 3: centralised solution). Accordingly, the waiting time when the penetration level is 5% and a centralised solution is adopted is the same time, on average, of when the penetration level is 3% and drivers decide autonomously where to stop for charging.
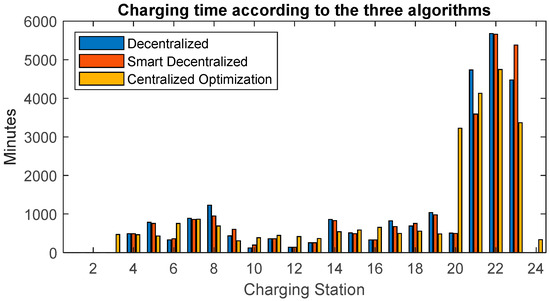
Figure 6.
Occupancy of charging stations with penetration level of 5%.
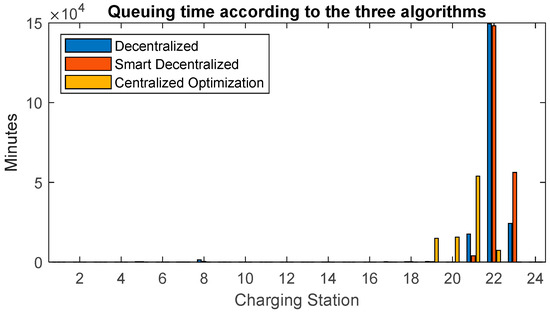
Figure 7.
Queuing Time at charging stations with a penetration level of 5%.
Thus, by adopting a centralised scheme, it is possible to increase the number of EVs and maintain the same charging infrastructure without sacrificing the quality of service (in terms of waiting time).
We have run extensive Monte Carlo simulation to filter out the stochastic effects of different fleets of EVs, different average cruising speeds, different initial SOCs, and different trips (yet, extracted from the same probability distribution of actual trips, as measured at toll booths), and improvements of centralised solutions are always within the range of 50–60% of waiting times.
5. Conclusions
Most motorways worldwide are nowadays witnessing a massive electrification effort to support the increasing penetration of EVs. This includes the construction of new charging points, with higher charging rates to keep up with the improved performance of recent batteries.
This manuscript discusses and evaluates the possibility of introducing centralised schemes for charging EVs in motorways, to better handle the vehicles and orchestrate their charging requirements in a balanced fashion. As can be easily expected, shorter queues are observed when vehicles are managed all together than when decentralised decisions are taken on the basis of only local and partial information. In particular, we show that when the centralised charging strategy is implemented in an ideal case, improvements of the order of 50 to 60% in reductions in queuing times can be experienced. This implies that the actual infrastructure may be used to handle a greater number of EVs without compromising the quality of service. Our findings demonstrate that the more balanced assignment of vehicles at charging stations of our methodology can significantly reduce queues and waiting times. This improvement not only contributes to greater traffic sustainability by mitigating congestion and associated emissions but also supports energy sustainability by promoting a more geographically balanced distribution of energy demand, thereby helping to reduce peak consumption levels.
In this paper, we also discuss the new challenges that would arise if the proposed centralised approach were to be adopted in practice. While technologies are available for a centralised management (e.g., in terms of bidirectional communication between CSs and EVs), other significant challenges include the following:
- (i)
- The need for cooperative utilisation of CSs: indeed, we have tacitly assumed that the CSs accept cooperating in receiving EVs in order to minimise the overall waiting times. However, if the CSs are owned by different utilities, they may not be willing to accept a centralised scheme and may rather compete with each other to attract as many EVs as possible. It is not, however, utopian to imagine that CSs may be forced to adhere to centralised strategies, as those investigated in this paper, with the common goal of improving the sustainability of motorway mobility.
- (ii)
- Compliance of drivers: as we have already mentioned, we assumed that all EV drivers accept the recommendations received by the CCM, and in no case do they decide to discard the indications and stop at other CSs (or charge by a different quantity than recommended). Although this may not occur in reality, it could, however, be possible to design pricing mechanisms to convince drivers to actually follow the prescribed recommendations (or similarly, increase the cost of the charging service of non-compliant EVs);
- (iii)
- Uncertainty of driving times: we have also assumed that the error of the time of arrival of EVs at the reserved CSs is not greater than a single time step (i.e., 5 min). Of course, this may not be realistic in many cases where unpredictable events (e.g., car accidents or changed traffic conditions) may occur. In addition to continuous exchange of information to improve the accuracy of estimated arrival times, one way to handle this uncertainty may be to reserve some plugs in CSs for EVs adhering to centralised schemes and the other plugs to EVs that unexpectedly arrive at the CSs, either due to delays or to non-compliance with the centralised scheme.
While this manuscript mainly focuses on introducing, discussing, and comparing a centralised strategy against the most popular decentralised approaches, this work can be easily extended to address in detail the previous aspects.
Author Contributions
Conceptualization, E.C. and M.C.; methodology, E.C. and M.C.; software, E.D.; data curation, E.D. and V.A.; writing—original draft preparation, E.D., M.C. and E.C.; writing—review and editing, E.D., C.S., V.A., M.C. and E.C.; supervision, V.A., M.C. and E.C.; funding acquisition, V.A. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by MOST—Sustainable Mobility Center through European Union Next-GenerationEU (Piano Nazionale di Ripresa e Resilienza (PNRR)—MISSIONE 4, COMPONENTE 2, INVESTIMENTO 1.4—D.D.1033 17/06/2022) under Grant CN00000023.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Valerio Apicella was employed by the company Movyon SpA. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EV | Electric vehicle |
| AFIR | Alternative Fuels Infrastructure Regulation |
| CS | Charging Station |
| SOC | State-of-Charge |
| CCM | Centralised Charge Manager |
References
- European Commission. EU Deal to End Sale of New CO2 Emitting Cars by 2035. Available online: https://ec.europa.eu/commission/presscorner/detail/en/ip_22_6462 (accessed on 4 December 2024).
- IEA. Trends in Electric Cars–Global EV Outlook 2024–Analysis. Available online: https://www.iea.org/reports/global-ev-outlook-2024/trends-in-electric-cars (accessed on 4 December 2024).
- Regulation (EU) 2023/1804 of the European Parliament and of the Council of 13 September 2023 on the Deployment of Alternative Fuels Infrastructure, and Repealing Directive 2014/94/EU (Text with EEA Relevance), Volume 234. 2023. Available online: http://data.europa.eu/eli/reg/2023/1804/oj/eng (accessed on 2 December 2024).
- ACEA. Charging Ahead: Accelerating the Roll-Out of EU Electric Vehicle Charging Infrastructure; ACEA: Brussels, Belgium, 2024. [Google Scholar]
- Scarpelli, C.; Ceraolo, M.; Crisostomi, E.; Apicella, V.; Pellegrini, G. Charging Electric Vehicles on Highways: Challenges and Opportunities. IEEE Access 2024, 12, 55814–55823. [Google Scholar] [CrossRef]
- Zhou, K.; Cheng, L.; Wen, L.; Lu, X.; Ding, T. A coordinated charging scheduling method for electric vehicles considering different charging demands. Energy 2020, 213, 118882. [Google Scholar] [CrossRef]
- Lezama, F.; Soares, J.; Hernandez-Leal, P.; Kaisers, M.; Pinto, T.; Vale, Z. Local Energy Markets: Paving the Path Toward Fully Transactive Energy Systems. IEEE Trans. Power Syst. 2019, 34, 4081–4088. [Google Scholar] [CrossRef]
- Liu, J.; Lin, G.; Huang, S.; Zhou, Y.; Li, Y.; Rehtanz, C. Optimal EV Charging Scheduling by Considering the Limited Number of Chargers. IEEE Trans. Transp. Electrif. 2021, 7, 1112–1122. [Google Scholar] [CrossRef]
- Jia, Y.-H.; Mei, Y.; Zhang, M. A Bilevel Ant Colony Optimization Algorithm for Capacitated Electric Vehicle Routing Problem. IEEE Trans. Cybern. 2022, 52, 10855–10868. [Google Scholar] [CrossRef]
- Cerna, F.V.; Pourakbari-Kasmaei, M.; Romero, R.A.; Rider, M.J. Optimal Delivery Scheduling and Charging of EVs in the Navigation of a City Map. IEEE Trans. Smart Grid 2018, 9, 4815–4827. [Google Scholar] [CrossRef]
- Danish, S.M.; Zhang, K.; Jacobsen, H.-A.; Ashraf, N.; Qureshi, H.K. BlockEV: Efficient and Secure Charging Station Selection for Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4194–4211. [Google Scholar] [CrossRef]
- Moschella, M.; Ferraro, P.; Crisostomi, E.; Shorten, R. Decentralized assignment of electric vehicles at charging stations based on personalized cost functions and distributed ledger technologies. IEEE Trans. Internet Things 2021, 14, 11112. [Google Scholar] [CrossRef]
- Wang, W.; Wu, L. A Semi-Decentralized Real-Time Charging Scheduling Scheme for Large EV Parking Lots Considering Uncertain EV Arrival and Departure. IEEE Trans. Smart Grid 2024, 15, 5871–5884. [Google Scholar] [CrossRef]
- Wager, G.; Whale, J.; Braunl, T. Driving electric vehicles at highway speeds: The effect of higher driving speeds on energy consumption and driving range for electric vehicles in Australia. Renew. Sustain. Energy Rev. 2016, 63, 158–165. [Google Scholar] [CrossRef]
- Xie, R.; Wei, W.; Khodayar, M.E.; Wang, J.; Mei, S. Planning Fully Renewable Powered Charging Stations on Highways: A Data-Driven Robust Optimization Approach. IEEE Trans. Transp. Electrif. 2018, 4, 817–830. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Wei, W.; Wu, L. A Bilevel EV Charging Station and DC Fast Charger Planning Model for Highway Network Considering Dynamic Traffic Demand and User Equilibrium. IEEE Trans. Smart Grid 2024, 15, 714–728. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Xiao, H.; Luo, F. Coordinated Planning of EV Charging Stations and Mobile Energy Storage Vehicles in Highways With Traffic Flow Modeling. IEEE Trans. Intell. Transp. Syst. 2024, 25, 21572–21584. [Google Scholar] [CrossRef]
- Zeng, X.; Xie, C. A comparative analysis of modeling and solution methods for the en-route charging station location problems within uncongested and congested highway networks. Multimodal Transp. 2024, 3, 100150. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, B.; Xu, P.; Guo, F. Electric vehicle charging strategy for intercity travel: Impact of user perception and battery degradation. Comput. Ind. Eng. 2024, 193, 110266. [Google Scholar] [CrossRef]
- Zhang, T.-Y.; Yang, Y.; Zhu, Y.-T.; Yao, E.-J.; Wu, K.-Q. Deploying Public Charging Stations for Battery Electric Vehicles on the Expressway Network Based on Dynamic Charging Demand. IEEE Trans. Transp. Electrif. 2022, 8, 2531–2548. [Google Scholar] [CrossRef]
- Stenstadvolden, A.; Hansen, L.; Zhao, L.; Kapourchali, M.H.; Lee, W.-J. Demand and Sustainability Analysis for A Level-3 Charging Station on the U.S. Highway Based on Actual Smart Meter Data. IEEE Trans. Ind. Appl. 2024, 60, 1310–1321. [Google Scholar] [CrossRef]
- Del Razo, V.; Jacobsen, H.-A. Smart Charging Schedules for Highway Travel with Electric Vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 160–173. [Google Scholar] [CrossRef]
- Gusrialdi, A.; Qu, Z.; Simaan, M.A. Distributed Scheduling and Cooperative Control for Charging of Electric Vehicles at Highway Service Stations. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2713–2727. [Google Scholar] [CrossRef]
- Zhou, S.; Qiu, Y.; Zou, F.; He, D.; Yu, P.; Du, J.; Luo, X.; Wang, C.; Wu, Z.; Gu, W.; et al. Dynamic EV Charging Pricing Methodology for Facilitating Renewable Energy With Consideration of Highway Traffic Flow. IEEE Access 2020, 8, 13161–13178. [Google Scholar] [CrossRef]
- Zhou, J.; Xiang, Y.; Zhang, X.; Sun, Z.; Liu, X.; Liu, J. Optimal self-consumption scheduling of highway electric vehicle charging station based on multi-agent deep reinforcement learning. Renew. Energy 2025, 238, 121982. [Google Scholar] [CrossRef]
- Bertucci, E.; Bucchi, F.; Ceraolo, M.; Frendo, F.; Lutzemberger, G. Battery Electric Vehicles: How Many Gears? A Technical–Economic Analysis. Vehicles 2024, 6, 71–92. [Google Scholar] [CrossRef]
- Dudkina, E.; Scarpelli, C. HELVES: A Python-based simulator to model circulation of electric vehicles on a highway. Softw. Impacts 2024, 21, 100658. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).