Multi-Objective Optimization for Intermodal Freight Transportation Planning: A Sustainable Service Network Design Approach
Abstract
1. Introduction
2. Literature Review
3. Model Construction
3.1. Sets
3.2. Parameters
3.3. Decision Variables
3.4. Objective Functions
- Transportation cost minimization:
- Delivery time minimization:
3.5. Objective Functions
- Flow conservation:
- Time update constraints:
- Capacity constraints (if applicable):
- Binary decision variables:
4. Applied Research
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaack, L.H.; Vaishnav, P.; Morgan, M.G.; Azevedo, I.L.; Rai, S. Decarbonizing intraregional freight systems with a focus on modal shift. Environ. Res. Lett. 2018, 13, 083001. [Google Scholar] [CrossRef]
- Janic, M. Modelling the full costs of an intermodal and road freight transport network. Transp. Res. Part D Transp. Environ. 2007, 12, 33–44. [Google Scholar] [CrossRef]
- Meyer, T. Decarbonizing road freight transportation—A bibliometric and network analysis. Transp. Res. Part D Transp. Environ. 2020, 89, 102619. [Google Scholar] [CrossRef]
- Yamahaki, C.; Breviglieri, G.V.; von Lüpke, H. Explaining the absence of climate change integration in low-carbon sectoral policies: An analysis of Brazil’s maritime cabotage policy. Case Stud. Transp. Policy 2024, 16, 101183. [Google Scholar] [CrossRef]
- Barlogis, R.; Montarnal, A.; Ouedraogo, C.; Gourc, D. Predicting container intermodal transport arrival times: An approach based on IoT data. Internet Things 2025, 29, 101460. [Google Scholar] [CrossRef]
- Balsalobre-Lorente, D.; Shah, S.A.R. Stay circular economy, empowerment, and natural resource utilization factual factors for SDG 12? The principal role of digital technologies. J. Environ. Manag. 2024, 370, 122459. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hossain, M.E. Green technology, policy and sustainable finance nexus with SDG-12: Moderating effects of stakeholder awareness. Sustain. Futures 2024, 8, 100405. [Google Scholar] [CrossRef]
- Aziz, K.M.A.; Daoud, A.O.; Singh, A.K.; Alhusban, M. Integrating digital mapping technologies in urban development: Advancing sustainable and resilient infrastructure for SDG 9 achievement—A systematic review. Alex. Eng. J. 2025, 116, 512–524. [Google Scholar] [CrossRef]
- Reyes-Menéndez, A.; Mediavilla, J.C.; García, N.V. Understanding STI and SDG with artificial intelligence: A review and research agenda for entrepreneurial action. Technol. Forecast. Soc. Change 2023, 196, 122785. [Google Scholar] [CrossRef]
- Simionescu, M.; Radulescu, M.; Cifuentes-Faura, J. The role of natural resources rents and e-government in achieving sustainable development in the European Union. Resour. Policy 2024, 97, 105278. [Google Scholar] [CrossRef]
- Baldassarre, B. Circular economy for resource security in the European Union (EU): Case study, research framework, and future directions. Ecol. Econ. 2025, 227, 108345. [Google Scholar] [CrossRef]
- Tatar, V.; Ayvaz, B.; Pamucar, D. Analysis of Renewable Energy Investments in China’s BRI Middle Corridor Using Spherical Fuzzy Decision-Making Framework. Renew. Energy 2025, 244, 122631. [Google Scholar] [CrossRef]
- Gandhi, N.; Kant, R.; Thakkar, J.J. Evaluation of benefits due to adoption of enablers of unimodal road to intermodal railroad freight transportation. Transp. Policy 2024, 146, 295–311. [Google Scholar] [CrossRef]
- Hu, Q.; Gu, W.; Wang, S. Optimal subsidy scheme design for promoting intermodal freight transport. Transp. Res. Part E Logist. Transp. Rev. 2022, 157, 102561. [Google Scholar] [CrossRef]
- Al-lami, A.; Török, Á. Assessing sustainability indicators of public transportation using PAHP. Sustain. Futures 2025, 9, 100500. [Google Scholar] [CrossRef]
- Kine, H.Z.; Gebresenbet, G.; Tavasszy, L.; Ljungberg, D. Digitalization and Automation in Intermodal Freight Transport and Their Potential Application for Low-Income Countries. 2022. Available online: https://www.semanticscholar.org/paper/Digitalization-and-Automation-in-Intermodal-Freight-Kine-Gebresenbet/011b316f7e0b6aa4379ffaa53d5c7f77a5f7f129 (accessed on 24 March 2025).
- Agamez-Arias, A.-M.; Moyano-Fuentes, J. Intermodal transport in freight distribution: A literature review. Transp. Rev. 2017, 37, 782–807. [Google Scholar] [CrossRef]
- Goyal, A.; Rani, Y. A Study on Advancement in Intermodal and Multimodal Transportation. Int. J. Res. Publ. Rev. 2024, 5, 5511–5540. [Google Scholar] [CrossRef]
- Verdeș, C.; Mironescu, A.A. The Future of Logistics: A Literature Review of Digitalization Trends. Commun. Int. Proc. 2023, 2023, 4126623. [Google Scholar] [CrossRef]
- Temizceri, F.T.; Kara, S.S. Towards sustainable logistics in Turkey: A bi-objective approach to green intermodal freight transportation enhanced by machine learning. Res. Transp. Bus. Manag. 2024, 55, 101145. [Google Scholar] [CrossRef]
- Wei, X.; Wang, M.; Meng, Q. Vulnerability Assessment and Reduction for Intermodal Freight Transportation Networks. Reliab. Eng. Syst. Saf. 2024, 245, 109969. [Google Scholar] [CrossRef]
- Sina Mohri, S.; Thompson, R. Designing sustainable intermodal freight transportation networks using a controlled rail tariff discounting policy—The Iranian case. Transp. Res. Part A Policy Pract. 2022, 157, 59–77. [Google Scholar] [CrossRef]
- Bei, H.; Yu, M.; Yang, T.; Murcio, R. Optimization of intermodal transportation routes for perishable goods considering customer satisfaction. Res. Transp. Bus. Manag. 2025, 59, 101261. [Google Scholar] [CrossRef]
- Meyer-Hollatz, T.; Kaiser, M.; Keller, R.; Schober, M. Understanding information needs for seamless intermodal transportation: Evidence from Germany. Transp. Res. Part D Transp. Environ. 2024, 130, 104161. [Google Scholar] [CrossRef]
- Weng, Y.; Zhang, J.; Yang, C.; Ramzan, M. Intermodal travel planning and decision support integrated with transportation and energy systems. Heliyon 2024, 10, e31577. [Google Scholar] [CrossRef]
- Klapita, V. Analysis of Operational Performance of Intermodal Transport Terminals in Slovakia in the Context of Intermodal Transport Infrastructure Development in EU Countries. Transp. Res. Procedia 2024, 77, 201–209. [Google Scholar] [CrossRef]
- Ballantyne, P.; Filomena, G.; Rowe, F.; Singleton, A. Developing two-dimensional indicators of transport demand and supply to promote sustainable transportation equity. Comput. Environ. Urban Syst. 2024, 113, 102179. [Google Scholar] [CrossRef]
- Thompson, E.A.; Alimo, P.K.; Abudu, R.; Lu, P. Towards sustainable freight transportation in Africa: Complementarity of the fuzzy Delphi and best-worst Methods. Sustain. Futures 2024, 8, 100371. [Google Scholar] [CrossRef]
- Vida, L.; Illés, B.; Bányainé-Tóth, Á. Logistics 4.0 in intermodal freight transport. Procedia Comput. Sci. 2023, 217, 31–40. [Google Scholar] [CrossRef]
- Hrušovský, M.; Demir, E.; Jammernegg, W.; Van Woensel, T. Real-time disruption management approach for intermodal freight transportation. J. Clean. Prod. 2021, 280, 124826. [Google Scholar] [CrossRef]
- Michela Le Pira Carla Giuffrida, N.; Tapia, R.J.; Pilla, F.; Tavasszy, L.A. Innovations in last mile logistics: Towards inclusivity, resilience and sustainability. Res. Transp. Econ. 2024, 105, 101446. [Google Scholar] [CrossRef]
- Hosseini, S.; Al Khaled, A. Freight flow optimization to evaluate the criticality of intermodal surface transportation system infrastructures. Comput. Ind. Eng. 2021, 159, 107522. [Google Scholar] [CrossRef]
- Li, L.; Wang, J.; Wang, H.; Jin, X.; Du, L. Intermodal transportation hub location optimization with governments subsidies under the Belt and Road Initiative. Ocean Coast. Manag. 2023, 231, 106414. [Google Scholar] [CrossRef] [PubMed]
- Mashayekhi, Z.; Verma, M. An Analytical Approach to Rail-Truck Intermodal Network Design. Transp. Res. Procedia 2025, 82, 356–366. [Google Scholar] [CrossRef]
- Braekers, K.; Caris, A.; Janssens, G.K. Optimal shipping routes and vessel size for intermodal barge transport with empty container repositioning. Comput. Ind. 2013, 64, 155–164. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, Y.H.; Chew, E.P.; Tan, K.C. Intermodal container terminal location and capacity design with decentralized flow estimation. Transp. Res. Part B Methodol. 2024, 190, 103092. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, Q.; Zheng, S.; Zhang, Q. Impact of subsidy strategies on the optimization of container intermodal transport route selection. Reg. Stud. Mar. Sci. 2025, 84, 104115. [Google Scholar] [CrossRef]
- Zhen, L.; Wu, J.; Wang, S.; Li, S.; Wang, M. Optimizing automotive maritime transportation in Ro-Ro and container shipping. Transp. Res. Part B Methodol. 2025, 194, 103175. [Google Scholar] [CrossRef]
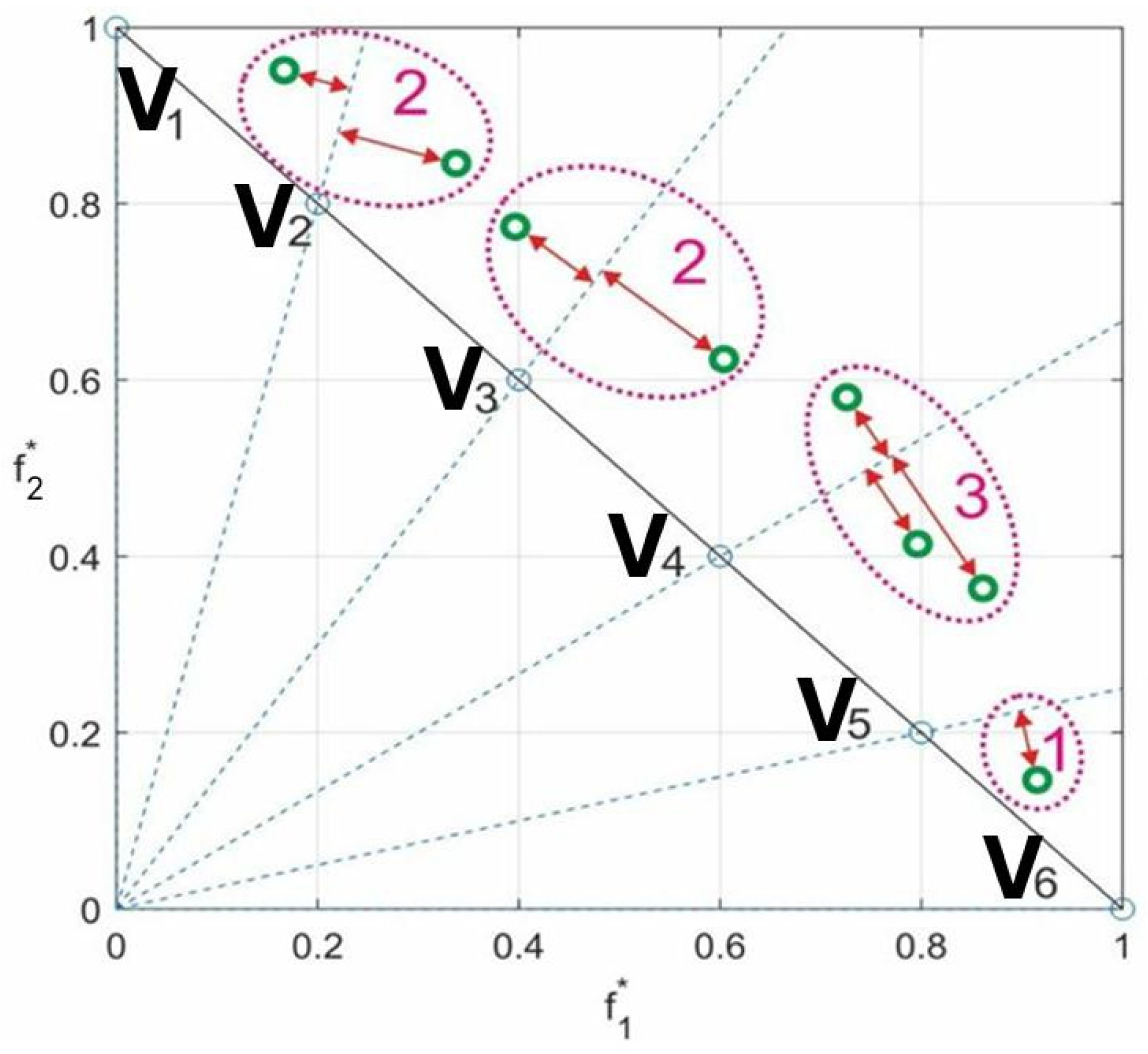
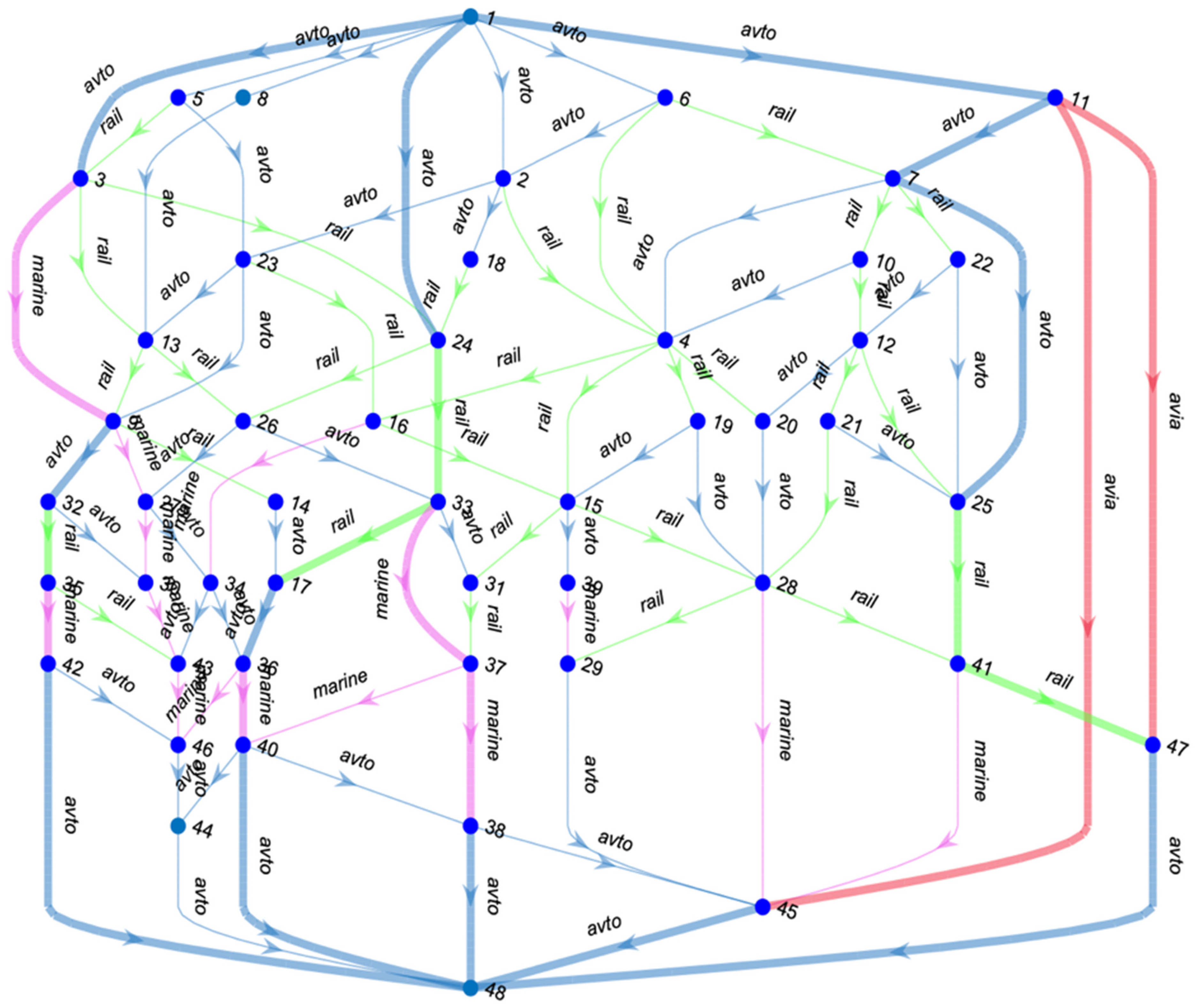
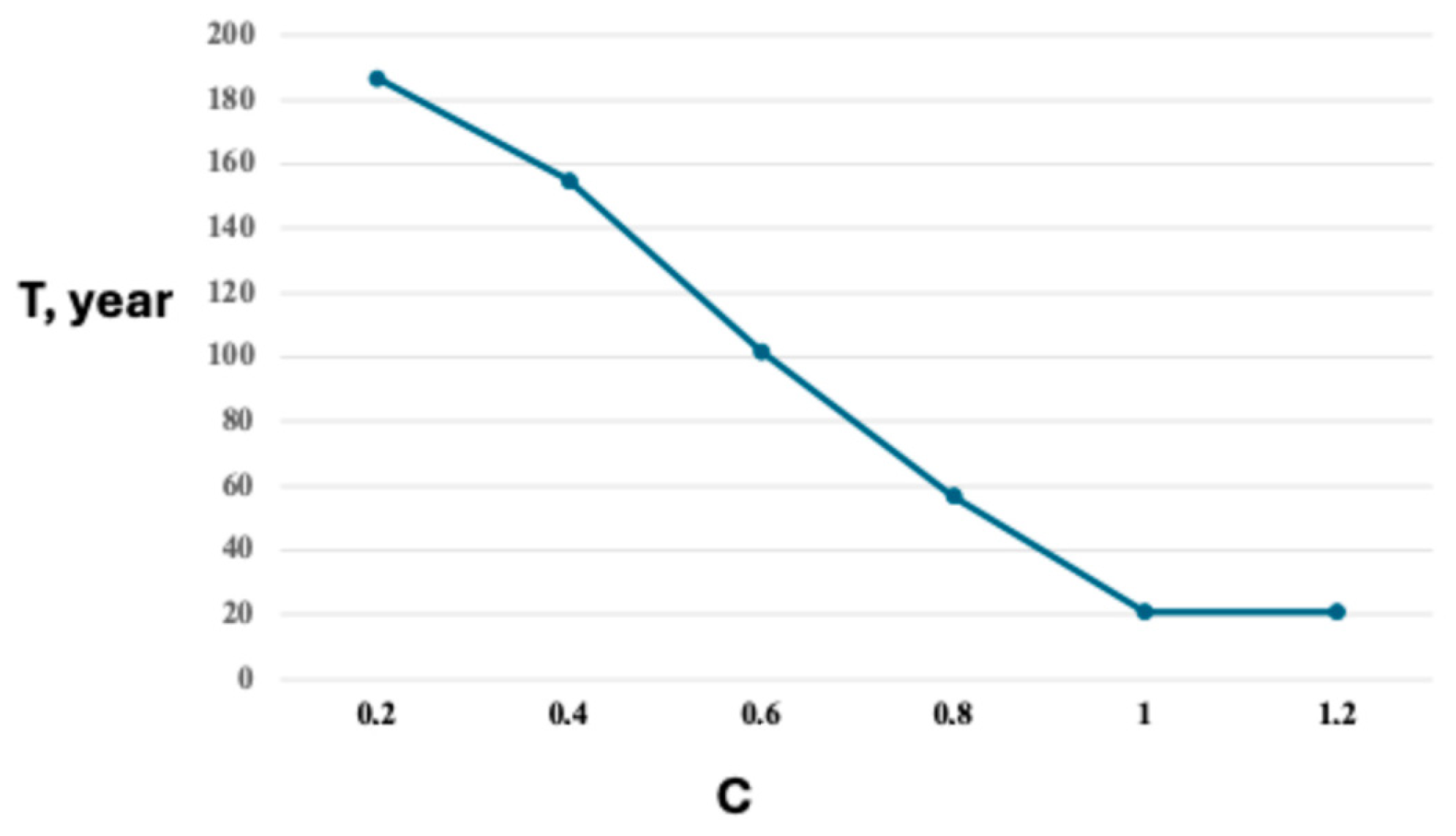
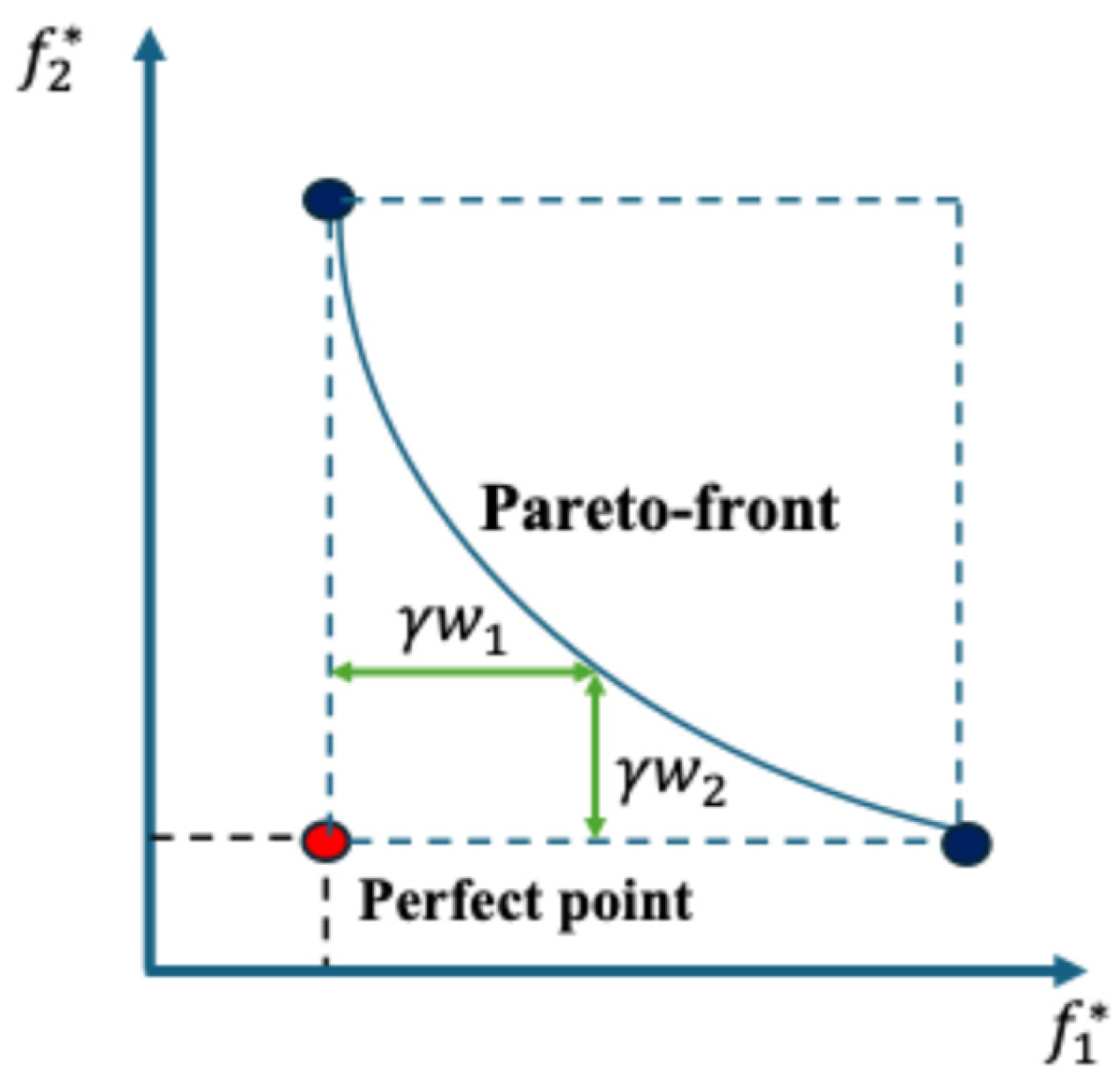
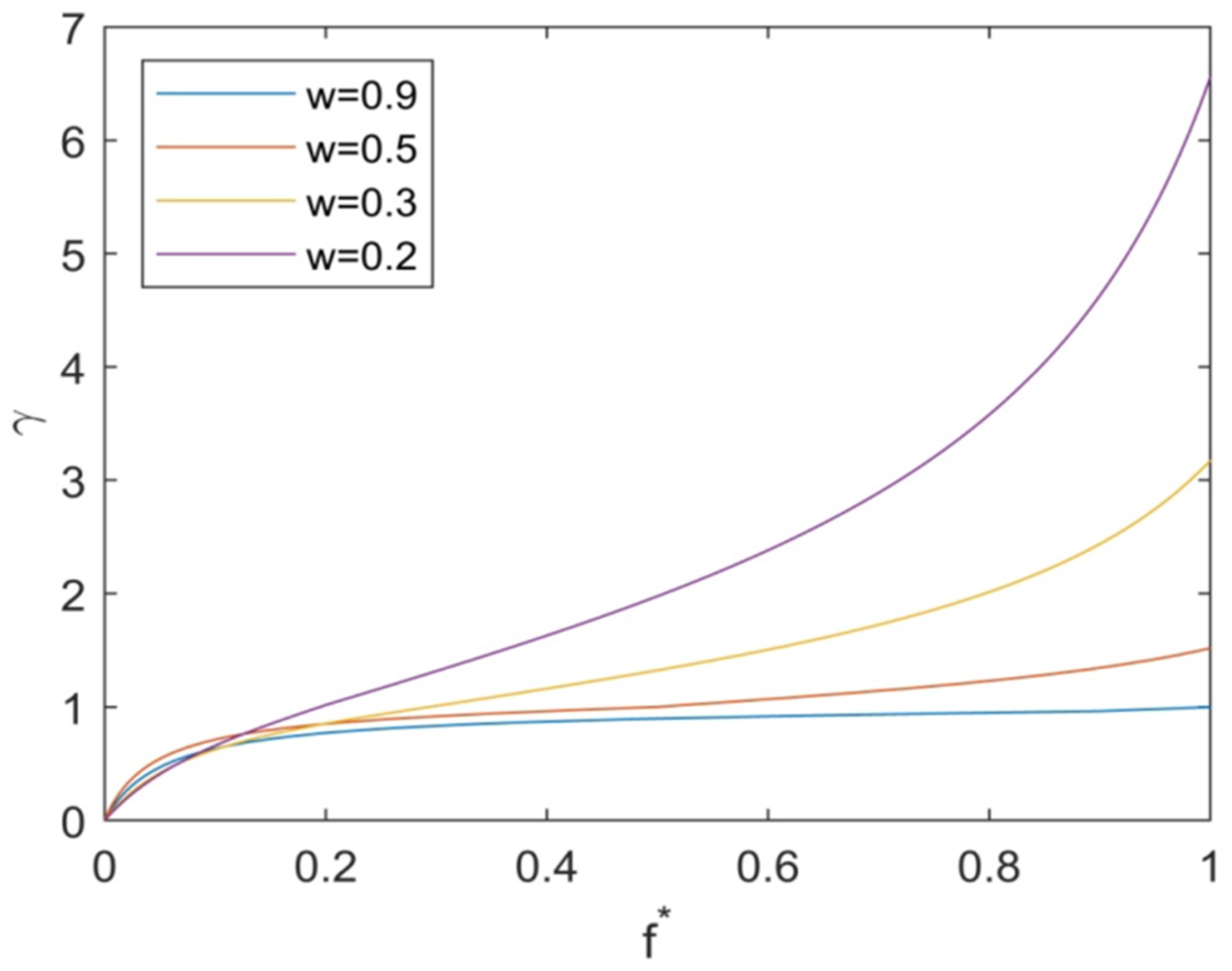

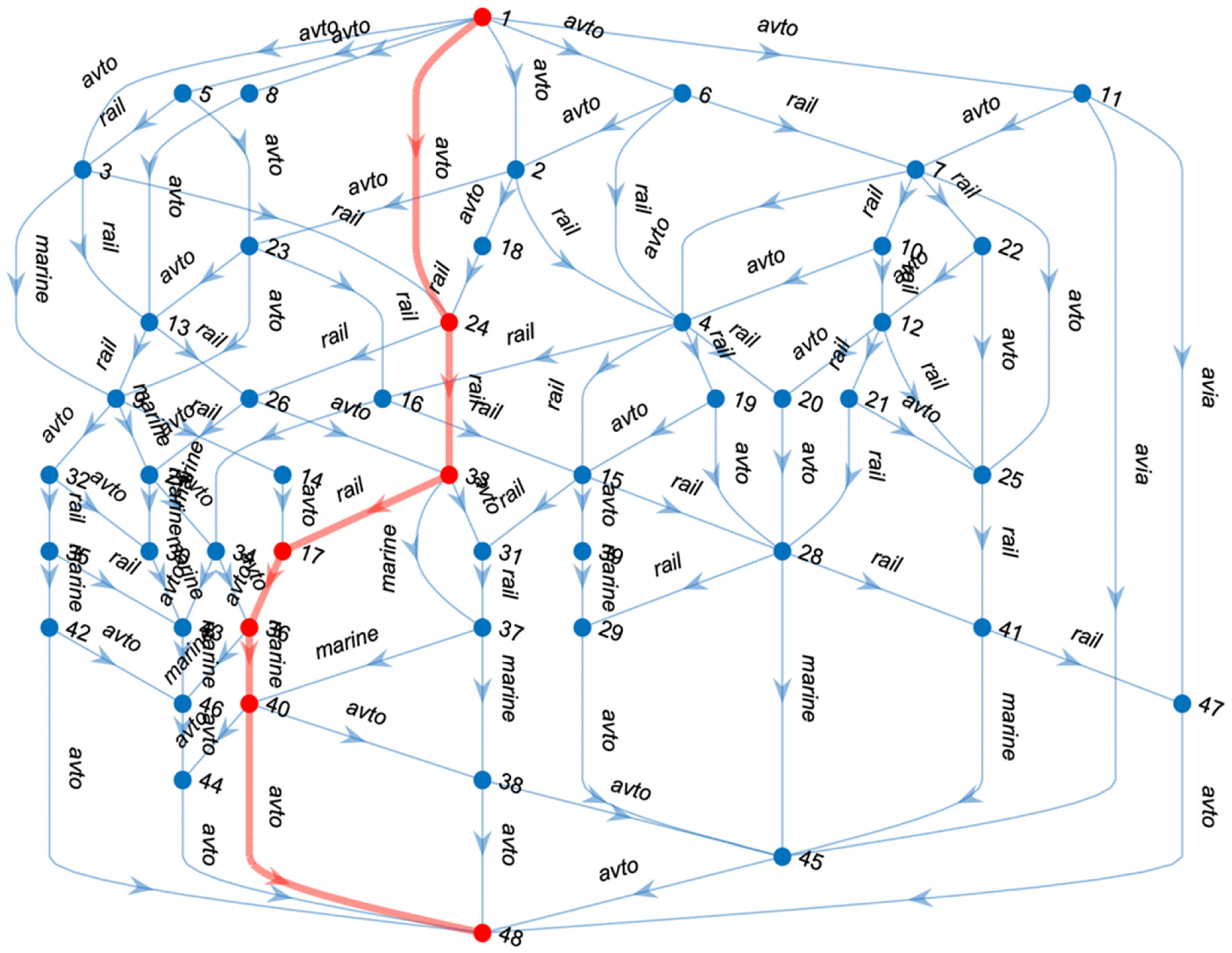
| № | Itinerary | Total Distance | | Year | |||
|---|---|---|---|---|---|---|---|
| 1 | 1,24,33,37,38,48 | 4604 | 4036.36 | 169.57 | 0 | 1 | 0.981615 |
| 2 | 1,3,9,32,35,42,48 | 4116 | 4492.69 | 153.88 | 0.0376 | 0.8967 | 0.430953 |
| 3 | 1,24,33,17,36,40,48 | 2964 | 4818.74 | 100.81 | 0.0645 | 0.5476 | 0.395761 |
| 4 | 1,11,7,25,41,47,48 | 2407 | 5203.52 | 57.86 | 0.0962 | 0.265 | 6.906039 |
| 5 | 1,11,47,48 | 4147 | 12,099.70 | 17.84 | 0.6648 | 0.0018 | 1.534167 |
| 6 | 1,11,45,48 | 4458 | 16,166.13 | 17.57 | 1 | 0 | 17.35612 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chupin, A.; Ragas, A.A.M.A.; Bolsunovskaya, M.; Leksashov, A.; Shirokova, S. Multi-Objective Optimization for Intermodal Freight Transportation Planning: A Sustainable Service Network Design Approach. Sustainability 2025, 17, 5541. https://doi.org/10.3390/su17125541
Chupin A, Ragas AAMA, Bolsunovskaya M, Leksashov A, Shirokova S. Multi-Objective Optimization for Intermodal Freight Transportation Planning: A Sustainable Service Network Design Approach. Sustainability. 2025; 17(12):5541. https://doi.org/10.3390/su17125541
Chicago/Turabian StyleChupin, Alexander, Abdelaal Ahmed Mostafa Ahmed Ragas, Marina Bolsunovskaya, Alexander Leksashov, and Svetlana Shirokova. 2025. "Multi-Objective Optimization for Intermodal Freight Transportation Planning: A Sustainable Service Network Design Approach" Sustainability 17, no. 12: 5541. https://doi.org/10.3390/su17125541
APA StyleChupin, A., Ragas, A. A. M. A., Bolsunovskaya, M., Leksashov, A., & Shirokova, S. (2025). Multi-Objective Optimization for Intermodal Freight Transportation Planning: A Sustainable Service Network Design Approach. Sustainability, 17(12), 5541. https://doi.org/10.3390/su17125541









