Robust Optimization of Multimodal Transportation Route Selection Based on Multiple Uncertainties from the Perspective of Sustainable Transportation
Abstract
1. Introduction
2. Literature Review
- (1)
- We take into account three uncertain factors, namely demand, transportation time and carbon trading price, simultaneously.
- (2)
- The decision-making objective is used to minimize the total cost including transportation cost, transshipment cost, time penalty cost and carbon emission cost.
- (3)
- We construct a multimodal transportation route optimization model based on hybrid robust stochastic optimization.
3. Model Construction
3.1. Problem Description
3.2. Symbol Explanation
3.3. Model Assumptions
- (1)
- During transportation, the goods must remain as a whole and cannot be split or transported in batches.
- (2)
- Suppose that each transfer node and the available transportation mode all have sufficient processing and transportation capacity, and the supply constraints caused by insufficient capacity are not considered.
- (3)
- At the node, the goods are allowed to change the mode of transportation at most once, thereby reducing the additional costs and complexities caused by excessive transshipment.
- (4)
- This study focuses on multimodal transportation routes and transportation processes, without considering the site selection, construction or operation costs of warehousing facilities. It is assumed that all the transfer nodes have the necessary loading, unloading and turnover conditions.
- (5)
- Considering the complexity of the model, serious delays or force majeure factors caused by external emergencies such as weather, equipment failure or goods damage during transportation are not taken into account. However, by setting uncertainty sets or scenario sets for the fluctuations of key parameters such as demand, transportation time, and carbon trading price, the influence of random disturbances in reality can be reflected to a certain extent.
- (6)
- Goods have a certain sensitivity to transportation time, so a minimum time limit and a soft time limit are set. When the total transportation time exceeds , the corresponding time penalty cost will be incurred. If the delay continues to exceed , the penalty cost will increase further.
- (7)
- The demand for goods will fluctuate, and the extent of the fluctuation is limited by the uncertain budget . The transportation time may vary within a certain range due to reasons such as traffic conditions and scheduling, and is controlled by the uncertain budget . Fluctuations in carbon trading price caused by changes in the market or policies are restricted by .
- (8)
- Suppose the carbon emission factor (the emission coefficient per unit distance) is closely related to the specific mode of transportation, but for the same mode of transportation, this factor is fixed at the same distance. The cost of carbon emissions is also affected by the carbon trading price, represented by , and is constrained by the uncertainty budget .
- (9)
- Suppose the occurrence probability of all scenarios is known and satisfies . In a multiple uncertain environment, various fluctuation situations in actual operation are characterized by applying the Box uncertain set and its corresponding budget , , and to the uncertain parameter .
3.4. Model Formulation
3.4.1. Objective Analysis
3.4.2. Analysis of Model Constraints
- (1)
- In the transportation network, the transportation of goods from any node to its next node is only allowed to adopt a single mode. This constraint is intended to simplify mode selection, reduce operational complexity, and enhance the controllability of the transportation process.
- (2)
- For each node in the network, the total input of goods must be equal to the total output. This constraint ensures that there is no unexplained increase or decrease in goods at the nodes, maintaining the consistency and integrity of the flow in the transportation system.
- (3)
- The disturbance of uncertain parameters during the transportation process needs to be limited by the budget parameters , and . By setting corresponding constraint conditions in the model and controlling the fluctuation amplitude of parameters, extreme deviations of the model solution caused by excessive perturbation can be avoided.
- (4)
- The total time of the entire transportation process shall not be lower than a reasonable minimum value. This constraint is set based on actual operational needs to ensure that the transportation timeliness meets the basic requirements while avoiding potential risks caused by excessively short durations.
- (5)
- The model characterizes the randomness of external disturbances through scenario probability and uncertainty budgeting. In multi-scenario analysis, the sum of the occurrence probabilities of each scenario must be equal to 1. This constraint follows the basic principles of probability theory to ensure the completeness and consistency of the scenario set.
3.4.3. Hybrid Robust–Stochastic Optimization Model for Multimodal Transportation Route Under Multiple Uncertainties
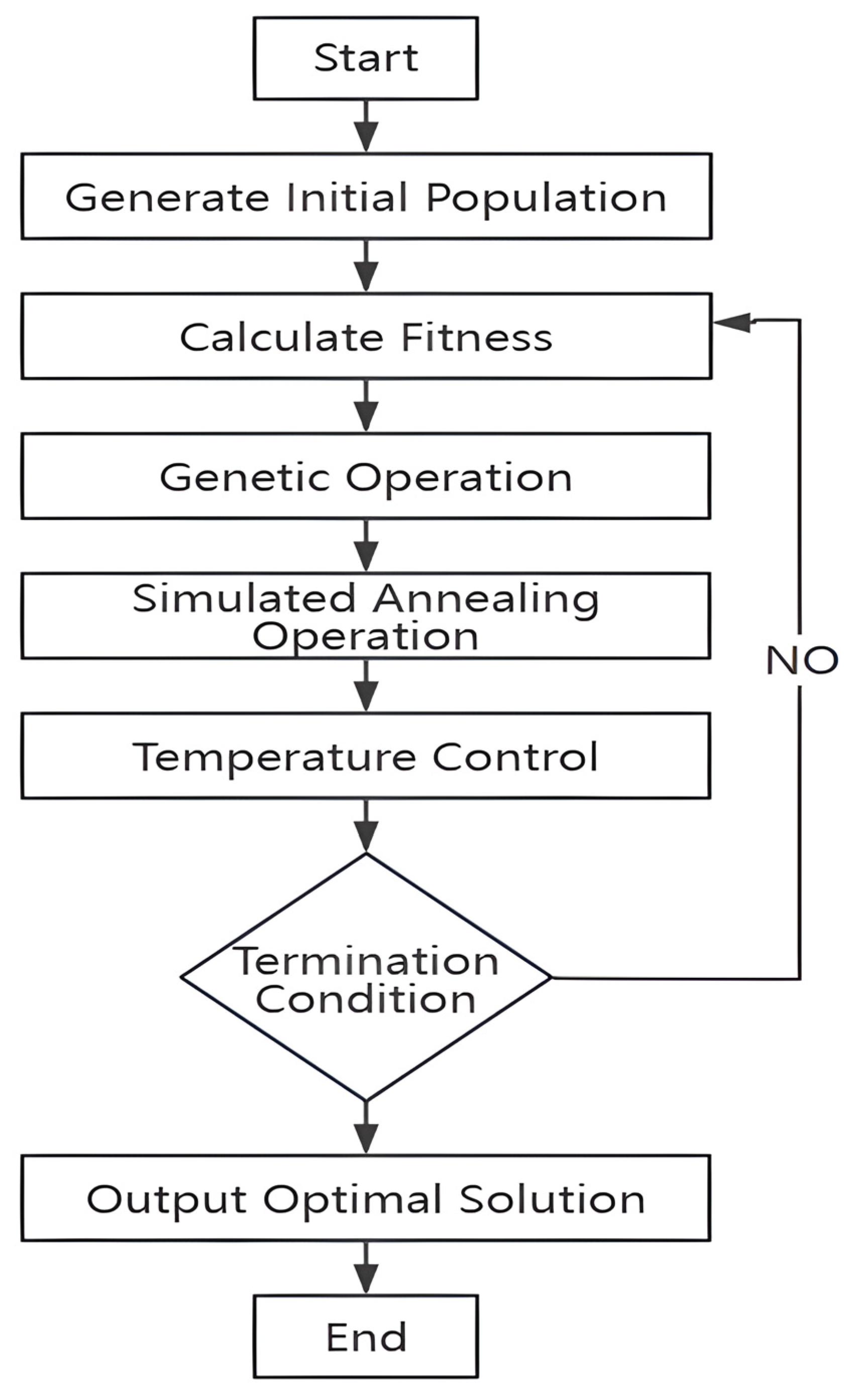
4. Algorithm Design
5. Example Analysis
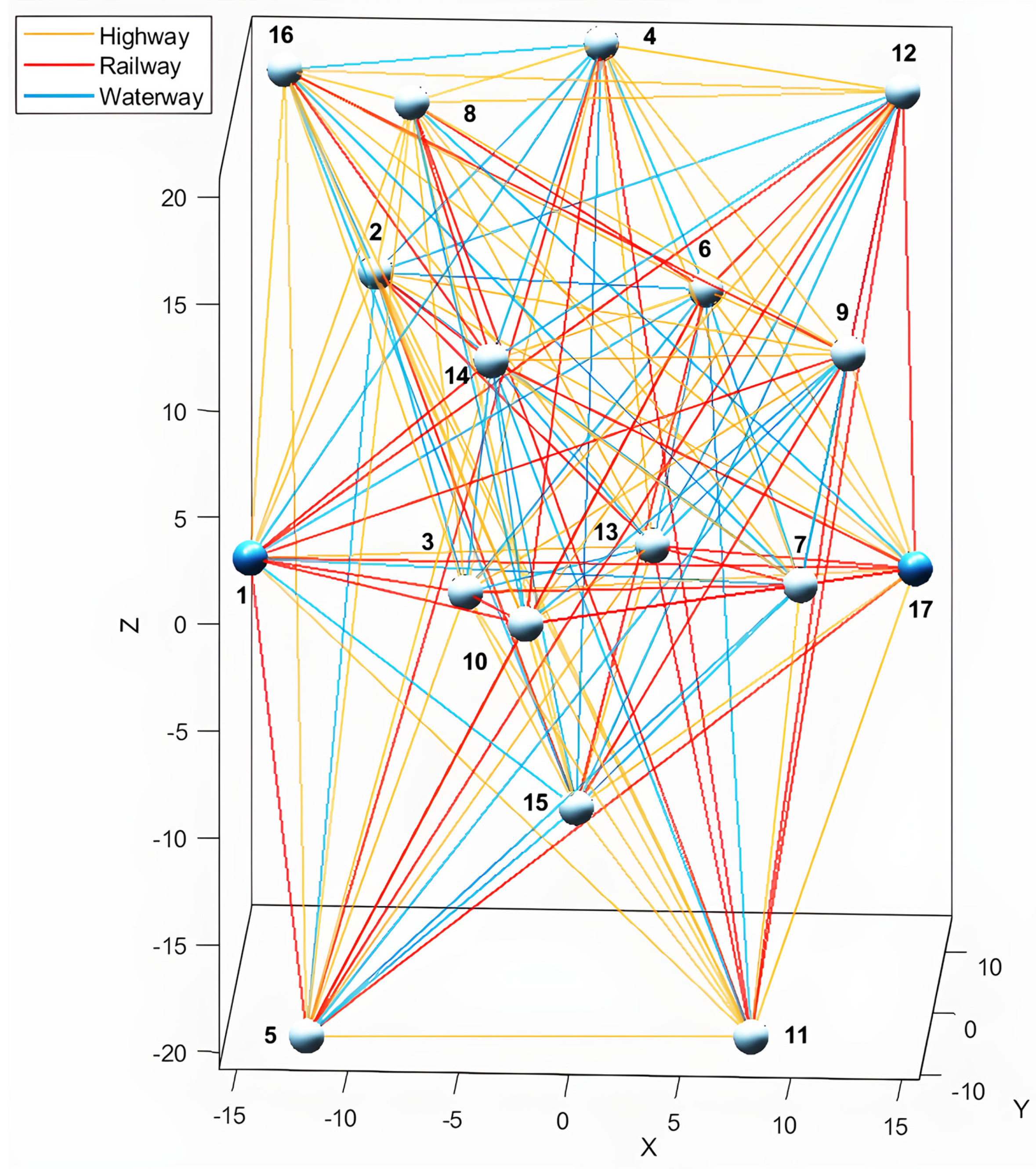
5.1. Case Information
5.2. Research Results and Analysis
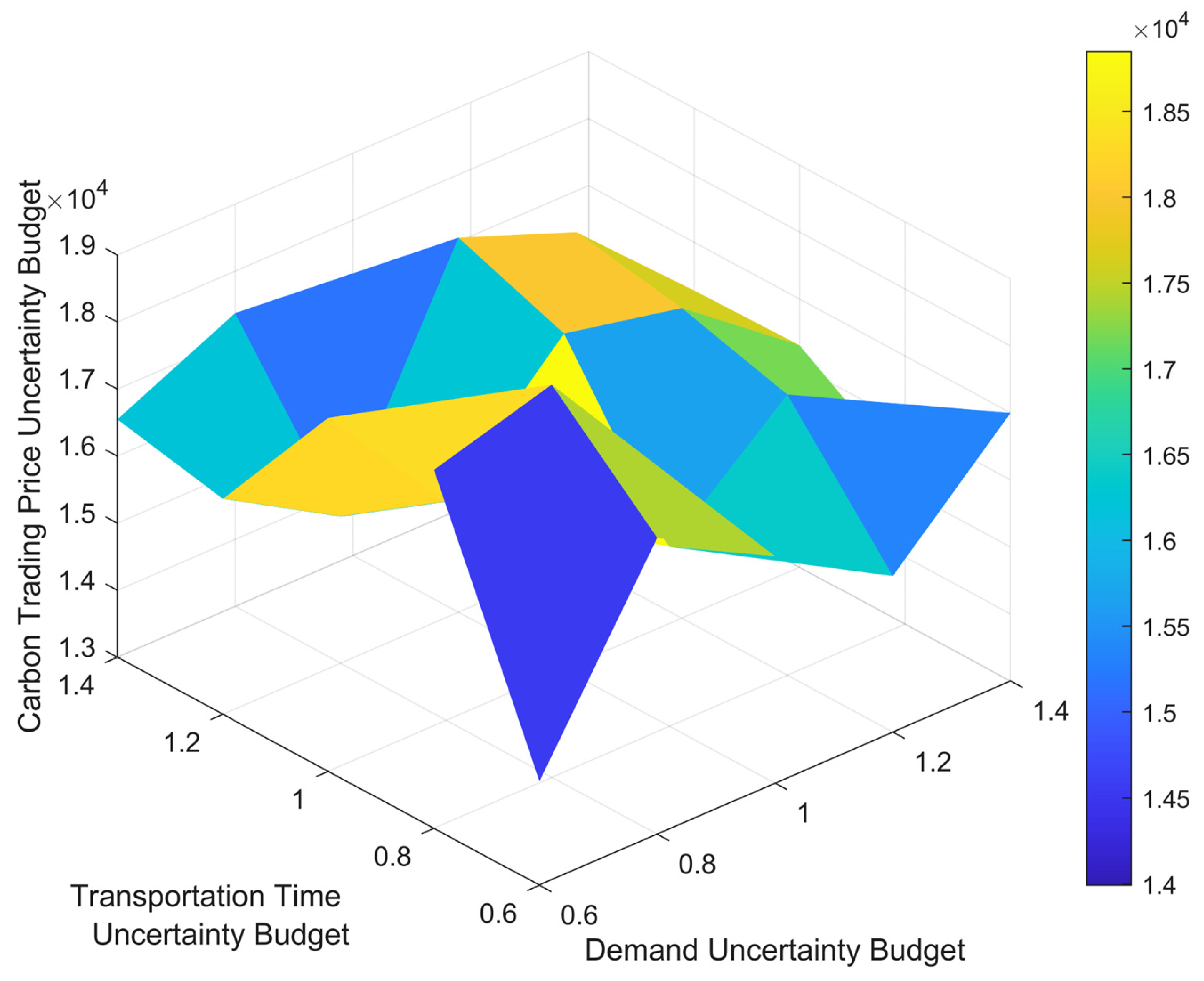
5.2.1. Analysis of the Impact of Uncertainty Budget Parameters
5.2.2. Comparative Analysis of Typical and Extreme Scenarios
5.2.3. Route Robustness Analysis
5.2.4. Algorithm Comparative Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Node i | Node j | Highway Distance | Railway Distance | Waterway Distance | Node i | Node j | Highway Distance | Railway Distance | Waterway Distance |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 9 | 1 | 1700 | 1900 | 10,000 |
| 1 | 2 | 1200 | 1463 | 1600 | 9 | 2 | 1600 | 1800 | 1900 |
| 1 | 3 | 2100 | 2294 | 2300 | 9 | 3 | 1000 | 1200 | 1300 |
| 1 | 4 | 2200 | 2372 | 2400 | 9 | 4 | 1100 | 1300 | 1400 |
| 1 | 5 | 1100 | 1300 | 1400 | 9 | 5 | 1400 | 1600 | 1700 |
| 1 | 6 | 1000 | 1162 | 1300 | 9 | 6 | 1300 | 1500 | 1600 |
| 1 | 7 | 1050 | 1150 | 1300 | 9 | 7 | 700 | 800 | 900 |
| 1 | 8 | 1600 | 1800 | 10,000 | 9 | 8 | 800 | 1000 | 1100 |
| 1 | 9 | 1700 | 1900 | 10,000 | 9 | 9 | 0 | 0 | 0 |
| 1 | 10 | 1050 | 1200 | 10,000 | 9 | 10 | 600 | 700 | 800 |
| 1 | 11 | 650 | 700 | 10,000 | 9 | 11 | 900 | 1000 | 10,000 |
| 1 | 12 | 600 | 660 | 700 | 9 | 12 | 1600 | 1800 | 1900 |
| 1 | 13 | 850 | 900 | 1000 | 9 | 13 | 1900 | 2100 | 2200 |
| 1 | 14 | 1800 | 2050 | 2100 | 9 | 14 | 1700 | 1900 | 2000 |
| 1 | 15 | 1700 | 1900 | 2000 | 9 | 15 | 1400 | 1600 | 1700 |
| 1 | 16 | 1300 | 1500 | 10,000 | 9 | 16 | 1500 | 1700 | 1800 |
| 1 | 17 | 2300 | 2600 | 10,000 | 9 | 17 | 800 | 900 | 1000 |
| 2 | 1 | 1200 | 1463 | 1600 | 10 | 1 | 1050 | 1200 | 10,000 |
| 2 | 2 | 0 | 0 | 0 | 10 | 2 | 1300 | 1500 | 10,000 |
| 2 | 3 | 1300 | 1400 | 1500 | 10 | 3 | 1900 | 2100 | 10,000 |
| 2 | 4 | 1500 | 1600 | 1700 | 10 | 4 | 2000 | 2200 | 10,000 |
| 2 | 5 | 150 | 180 | 200 | 10 | 5 | 1100 | 1300 | 10,000 |
| 2 | 6 | 250 | 300 | 350 | 10 | 6 | 1000 | 1200 | 10,000 |
| 2 | 7 | 750 | 800 | 900 | 10 | 7 | 900 | 1000 | 10,000 |
| 2 | 8 | 1800 | 2000 | 10,000 | 10 | 8 | 700 | 800 | 900 |
| 2 | 9 | 1600 | 1800 | 1900 | 10 | 9 | 600 | 700 | 800 |
| 2 | 10 | 1300 | 1500 | 10,000 | 10 | 10 | 0 | 0 | 0 |
| 2 | 11 | 900 | 1000 | 1100 | 10 | 11 | 400 | 500 | 10,000 |
| 2 | 12 | 600 | 700 | 800 | 10 | 12 | 900 | 1000 | 10,000 |
| 2 | 13 | 900 | 1000 | 1100 | 10 | 13 | 1200 | 1300 | 1400 |
| 2 | 14 | 800 | 900 | 1000 | 10 | 14 | 1300 | 1500 | 1600 |
| 2 | 15 | 500 | 600 | 700 | 10 | 15 | 1000 | 1200 | 1300 |
| 2 | 16 | 700 | 800 | 900 | 10 | 16 | 1100 | 1300 | 1400 |
| 2 | 17 | 1700 | 1900 | 10,000 | 10 | 17 | 700 | 800 | 10,000 |
| 3 | 1 | 2100 | 2294 | 2300 | 11 | 1 | 650 | 700 | 10,000 |
| 3 | 2 | 1300 | 1400 | 1500 | 11 | 2 | 900 | 1000 | 1100 |
| 3 | 3 | 0 | 0 | 0 | 11 | 3 | 1500 | 1600 | 1700 |
| 3 | 4 | 120 | 140 | 150 | 11 | 4 | 1600 | 1700 | 1800 |
| 3 | 5 | 700 | 800 | 900 | 11 | 5 | 700 | 800 | 900 |
| 3 | 6 | 1200 | 1300 | 1400 | 11 | 6 | 600 | 700 | 800 |
| 3 | 7 | 900 | 1000 | 1100 | 11 | 7 | 400 | 500 | 600 |
| 3 | 8 | 2100 | 2300 | 10,000 | 11 | 8 | 1000 | 1200 | 10,000 |
| 3 | 9 | 1000 | 1200 | 1300 | 11 | 9 | 900 | 1000 | 10,000 |
| 3 | 10 | 1900 | 2100 | 10,000 | 11 | 10 | 400 | 500 | 10,000 |
| 3 | 11 | 1500 | 1600 | 1700 | 11 | 11 | 0 | 0 | 0 |
| 3 | 12 | 1600 | 1800 | 1900 | 11 | 12 | 500 | 600 | 700 |
| 3 | 13 | 2300 | 2500 | 2600 | 11 | 13 | 800 | 900 | 1000 |
| 3 | 14 | 1500 | 1700 | 1800 | 11 | 14 | 900 | 1100 | 1200 |
| 3 | 15 | 200 | 300 | 400 | 11 | 15 | 700 | 800 | 900 |
| 3 | 16 | 300 | 400 | 500 | 11 | 16 | 800 | 900 | 1000 |
| 3 | 17 | 600 | 700 | 800 | 11 | 17 | 400 | 500 | 10,000 |
| 4 | 1 | 2200 | 2372 | 2400 | 12 | 1 | 600 | 660 | 700 |
| 4 | 2 | 1500 | 1600 | 1700 | 12 | 2 | 600 | 700 | 800 |
| 4 | 3 | 120 | 140 | 150 | 12 | 3 | 1600 | 1800 | 1900 |
| 4 | 4 | 0 | 0 | 0 | 12 | 4 | 1700 | 1900 | 2000 |
| 4 | 5 | 800 | 900 | 1000 | 12 | 5 | 400 | 500 | 600 |
| 4 | 6 | 1300 | 1400 | 1500 | 12 | 6 | 300 | 400 | 500 |
| 4 | 7 | 1000 | 1100 | 1200 | 12 | 7 | 700 | 800 | 900 |
| 4 | 8 | 2200 | 2400 | 10,000 | 12 | 8 | 1800 | 2000 | 10,000 |
| 4 | 9 | 1100 | 1300 | 1400 | 12 | 9 | 1600 | 1800 | 1900 |
| 4 | 10 | 2000 | 2200 | 10,000 | 12 | 10 | 900 | 1000 | 10,000 |
| 4 | 11 | 1600 | 1700 | 1800 | 12 | 11 | 500 | 600 | 700 |
| 4 | 12 | 1700 | 1900 | 2000 | 12 | 12 | 0 | 0 | 0 |
| 4 | 13 | 2400 | 2600 | 2700 | 12 | 13 | 300 | 400 | 400 |
| 4 | 14 | 1600 | 1800 | 1900 | 12 | 14 | 600 | 700 | 700 |
| 4 | 15 | 300 | 400 | 500 | 12 | 15 | 200 | 300 | 300 |
| 4 | 16 | 400 | 500 | 600 | 12 | 16 | 300 | 400 | 400 |
| 4 | 17 | 700 | 800 | 900 | 12 | 17 | 900 | 1000 | 10,000 |
| 5 | 1 | 1100 | 1300 | 1400 | 13 | 1 | 850 | 900 | 1000 |
| 5 | 2 | 150 | 180 | 200 | 13 | 2 | 900 | 1000 | 1100 |
| 5 | 3 | 700 | 800 | 900 | 13 | 3 | 2300 | 2500 | 2600 |
| 5 | 4 | 800 | 900 | 1000 | 13 | 4 | 2400 | 2600 | 2700 |
| 5 | 5 | 0 | 0 | 0 | 13 | 5 | 700 | 800 | 900 |
| 5 | 6 | 200 | 250 | 300 | 13 | 6 | 600 | 700 | 800 |
| 5 | 7 | 450 | 500 | 600 | 13 | 7 | 1000 | 1100 | 1200 |
| 5 | 8 | 1500 | 1700 | 10,000 | 13 | 8 | 2100 | 2300 | 10,000 |
| 5 | 9 | 1400 | 1600 | 1700 | 13 | 9 | 1900 | 2100 | 2200 |
| 5 | 10 | 1100 | 1300 | 10,000 | 13 | 10 | 1200 | 1300 | 1400 |
| 5 | 11 | 700 | 800 | 900 | 13 | 11 | 800 | 900 | 1000 |
| 5 | 12 | 400 | 500 | 600 | 13 | 12 | 300 | 400 | 400 |
| 5 | 13 | 700 | 800 | 900 | 13 | 13 | 0 | 0 | 0 |
| 5 | 14 | 1000 | 1200 | 1300 | 13 | 14 | 900 | 1000 | 1000 |
| 5 | 15 | 200 | 300 | 400 | 13 | 15 | 500 | 600 | 600 |
| 5 | 16 | 300 | 400 | 500 | 13 | 16 | 600 | 700 | 700 |
| 5 | 17 | 800 | 900 | 10,000 | 13 | 17 | 1100 | 1200 | 10,000 |
| 6 | 1 | 1000 | 1162 | 1300 | 14 | 1 | 1800 | 2050 | 2100 |
| 6 | 2 | 250 | 300 | 350 | 14 | 2 | 800 | 900 | 1000 |
| 6 | 3 | 1200 | 1300 | 1400 | 14 | 3 | 1500 | 1700 | 1800 |
| 6 | 4 | 1300 | 1400 | 1500 | 14 | 4 | 1600 | 1800 | 1900 |
| 6 | 5 | 200 | 250 | 300 | 14 | 5 | 1000 | 1200 | 1300 |
| 6 | 6 | 0 | 0 | 0 | 14 | 6 | 900 | 1000 | 1100 |
| 6 | 7 | 350 | 400 | 500 | 14 | 7 | 1100 | 1300 | 1400 |
| 6 | 8 | 1400 | 1600 | 10,000 | 14 | 8 | 2000 | 2000 | 10,000 |
| 6 | 9 | 1300 | 1500 | 1600 | 14 | 9 | 1700 | 1900 | 2000 |
| 6 | 10 | 1000 | 1200 | 10,000 | 14 | 10 | 1300 | 1500 | 1600 |
| 6 | 11 | 600 | 700 | 800 | 14 | 11 | 900 | 1100 | 1200 |
| 6 | 12 | 300 | 400 | 500 | 14 | 12 | 600 | 700 | 700 |
| 6 | 13 | 600 | 700 | 800 | 14 | 13 | 900 | 1000 | 1000 |
| 6 | 14 | 900 | 1000 | 1100 | 14 | 14 | 0 | 0 | 0 |
| 6 | 15 | 400 | 500 | 600 | 14 | 15 | 200 | 300 | 300 |
| 6 | 16 | 500 | 600 | 700 | 14 | 16 | 300 | 400 | 400 |
| 6 | 17 | 700 | 800 | 10,000 | 14 | 17 | 1200 | 1400 | 10,000 |
| 7 | 1 | 1050 | 1150 | 1300 | 15 | 1 | 1700 | 1900 | 2000 |
| 7 | 2 | 750 | 800 | 900 | 15 | 2 | 500 | 600 | 700 |
| 7 | 3 | 900 | 1000 | 1100 | 15 | 3 | 200 | 300 | 400 |
| 7 | 4 | 1000 | 1100 | 1200 | 15 | 4 | 300 | 400 | 500 |
| 7 | 5 | 450 | 500 | 600 | 15 | 5 | 200 | 300 | 400 |
| 7 | 6 | 350 | 400 | 500 | 15 | 6 | 400 | 500 | 600 |
| 7 | 7 | 0 | 0 | 0 | 15 | 7 | 600 | 700 | 800 |
| 7 | 8 | 1200 | 1400 | 10,000 | 15 | 8 | 1900 | 2100 | 10,000 |
| 7 | 9 | 700 | 800 | 900 | 15 | 9 | 1400 | 1600 | 1700 |
| 7 | 10 | 900 | 1000 | 10,000 | 15 | 10 | 1000 | 1200 | 1300 |
| 7 | 11 | 400 | 500 | 600 | 15 | 11 | 700 | 800 | 900 |
| 7 | 12 | 700 | 800 | 900 | 15 | 12 | 200 | 300 | 300 |
| 7 | 13 | 1000 | 1100 | 1200 | 15 | 13 | 500 | 600 | 600 |
| 7 | 14 | 1100 | 1300 | 1400 | 15 | 14 | 200 | 300 | 300 |
| 7 | 15 | 600 | 700 | 800 | 15 | 15 | 0 | 0 | 0 |
| 7 | 16 | 700 | 800 | 900 | 15 | 16 | 100 | 200 | 100 |
| 7 | 17 | 300 | 400 | 10,000 | 15 | 17 | 600 | 700 | 10,000 |
| 8 | 1 | 1600 | 1800 | 10,000 | 16 | 1 | 1300 | 1500 | 10,000 |
| 8 | 2 | 1800 | 2000 | 10,000 | 16 | 2 | 700 | 800 | 900 |
| 8 | 3 | 2100 | 2300 | 10,000 | 16 | 3 | 600 | 700 | 500 |
| 8 | 4 | 2200 | 2400 | 10,000 | 16 | 4 | 700 | 800 | 600 |
| 8 | 5 | 1500 | 1700 | 10,000 | 16 | 5 | 800 | 900 | 500 |
| 8 | 6 | 1400 | 1600 | 10,000 | 16 | 6 | 700 | 800 | 700 |
| 8 | 7 | 1200 | 1400 | 10,000 | 16 | 7 | 300 | 400 | 900 |
| 8 | 8 | 0 | 0 | 0 | 16 | 8 | 1000 | 1200 | 10,000 |
| 8 | 9 | 800 | 1000 | 1100 | 16 | 9 | 800 | 900 | 1800 |
| 8 | 10 | 700 | 800 | 900 | 16 | 10 | 800 | 800 | 1400 |
| 8 | 11 | 1000 | 1200 | 10,000 | 16 | 11 | 400 | 500 | 1000 |
| 8 | 12 | 1800 | 2000 | 10,000 | 16 | 12 | 900 | 1000 | 400 |
| 8 | 13 | 2100 | 2300 | 10,000 | 16 | 13 | 1100 | 1200 | 700 |
| 8 | 14 | 2300 | 2500 | 10,000 | 16 | 14 | 1200 | 1400 | 400 |
| 8 | 15 | 1800 | 2000 | 10,000 | 16 | 15 | 600 | 700 | 100 |
| 8 | 16 | 1900 | 2100 | 10,000 | 16 | 16 | 0 | 0 | 0 |
| 8 | 17 | 1000 | 1200 | 1300 | 16 | 17 | 200 | 300 | 10,000 |
| 17 | 8 | 600 | 800 | 1300 | 17 | 1 | 2300 | 2600 | 10,000 |
| 17 | 9 | 400 | 600 | 1000 | 17 | 2 | 1700 | 1900 | 10000 |
| 17 | 10 | 1200 | 1400 | 10,000 | 17 | 3 | 1200 | 1400 | 800 |
| 17 | 11 | 1300 | 1500 | 10,000 | 17 | 4 | 1300 | 1500 | 900 |
| 17 | 12 | 2000 | 2200 | 10,000 | 17 | 5 | 1800 | 2000 | 10,000 |
| 17 | 13 | 2300 | 2500 | 10,000 | 17 | 6 | 1700 | 1900 | 10,000 |
| 17 | 14 | 2100 | 2300 | 10,000 | 17 | 7 | 1500 | 1700 | 10,000 |
| 17 | 15 | 1400 | 1600 | 10,000 | 17 | 16 | 1100 | 1300 | 10,000 |
| 17 | 17 | 0 | 0 | 0 |
References
- Macioszek, E. Cargo transport on the example of a selected mode of transport in Poland. Sci. J. Sil. Univ. Technol. Series Transp. 2024, 122, 181–197. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Q.; Chen, D. Route selection of multimodal transport based on China railway transportation. J. Adv. Transp. 2021, 2021, 9984659. [Google Scholar] [CrossRef]
- Rouky, N.; Boukachour, J.; Boudebous, D.; Alaoui, A.E.H. Optimization under uncertainty: Generality and application to multimodal transport. Int. J. Supply Oper. Manag. 2023, 10, 223–244. [Google Scholar]
- Wu, C.; Zhang, Y.; Xiao, Y.; Mo, W.; Xiao, Y.; Wang, J. Optimization of multimodal paths for oversize and heavyweight cargo under different carbon pricing policies. Sustainability 2024, 16, 6588. [Google Scholar] [CrossRef]
- Sun, J.Q.; Wang, S.N.; Yan, S.X. Path selection of multimodal transport for refrigerated containers considering carbon emission. J. Dalian Marit. Univ. 2022, 48, 57–65. (In Chinese) [Google Scholar]
- Li, H.F.; Hu, D.W.; Chen, X.Q.; Wang, Y. Expand hub location-routing problem for hybrid hub-and-spoke multimodal transport network considering carbon emissions. J. Traffic Transp. Eng. 2022, 22, 306–321. (In Chinese) [Google Scholar]
- Laurent, A.B.V.S.V.D. CarbonRoadMap: A multicriteria decision tool for multimodal transportation. Int. J. Sustain. Transp. 2020, 14, 205–214. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, C.; Wu, X. Multi-objective path optimization of highway-railway multimodal transport considering carbon emissions. Appl. Sci. 2023, 13, 4731. [Google Scholar] [CrossRef]
- Li, M.; Sun, X. Path optimization of low-carbon container multimodal transport under uncertain conditions. Sustainability 2022, 14, 14098. [Google Scholar] [CrossRef]
- Peng, Y. Research on green multimodal transportation path optimization based on distributionally robust chance constraints with uncertain demand. In Proceedings of the Eighth International Conference on Traffic Engineering and Transportation System (ICTETS 2024), Dalian, China, 20–22 September 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13421, pp. 1666–1676. [Google Scholar]
- Liu, Z.; Zhou, S.; Liu, S. Optimization of multimodal transport paths considering a low-carbon economy under uncertain demand. Algorithms 2025, 18, 92. [Google Scholar] [CrossRef]
- Peng, Y.; Yong, P.; Luo, Y. The route problem of multimodal transportation with timetable under uncertainty: Multi-objective robust optimization model and heuristic approach. RAIRO Oper. Res. 2021, 55, S3035–S3050. [Google Scholar] [CrossRef]
- Wang, T.; Dai, C.; Li, H.; Wu, R. Multimodal Transportation Routing Optimization Considering Schedule Constraints and Uncertain Time. IAENG Int. J. Appl. Math. 2024, 54, 2656–2668. [Google Scholar]
- Guo, J.; Liu, T.; Song, G.; Guo, B. Solving the robust shortest path problem with multimodal transportation. Mathematics 2024, 12, 2978. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, F.Y.; Yuan, X.M.; Zhang, H.Y. Low-carbon multimodal transportation path optimization under dual uncertainty of demand and time. Sustainability 2021, 13, 8180. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Zhang, T.; Zou, Y.; Zhao, X. Optimum route and transport mode selection of multimodal transport with time window under uncertain conditions. Mathematics 2023, 11, 3244. [Google Scholar] [CrossRef]
- Peng, X.; Heng, Z.; Xi, C. Optimization of intermodal routes for reefer containers under double uncertainty. In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2024; Volume 512, p. 03015. [Google Scholar]
- Li, X.; Sun, Y.; Qi, J.; Wang, D. Chance-constrained optimization for a green multimodal routing problem with soft time window under twofold uncertainty. Axioms 2024, 13, 200. [Google Scholar] [CrossRef]
- Hou, D.N.; Liu, S.C. Optimization of cold chain multimodal transportation routes considering carbon emissions under hybrid uncertainties. Artif. Intell. 2024, 32, 2243–2256. [Google Scholar] [CrossRef]
- Sun, Y. Green and reliable freight routing problem in the road-rail intermodal transportation network with uncertain parameters: A fuzzy goal programming approach. J. Adv. Transp. 2020, 2020, 7570686. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, C.; Zheng, S.; Ma, G.; Chen, Z. Multimodal transportation route optimization of emergency supplies under uncertain conditions. Sustainability 2024, 16, 10905. [Google Scholar] [CrossRef]
- Han, W.; Chai, H.; Zhang, J.; Li, Y. Research on path optimization for multimodal transportation of hazardous materials under uncertain demand. Arch. Transp. 2023, 67, 91–104. [Google Scholar] [CrossRef]
- Zhu, C.; Zhu, X. Multi-objective path-decision model of multimodal transport considering uncertain conditions and carbon emission policies. Symmetry 2022, 14, 221. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Han, W.; Li, Y. Research on optimization of multimodal hub-and-spoke transport network under uncertain demand. Arch. Transp. 2024, 70, 137–157. [Google Scholar] [CrossRef]
- Gao, X.; Yao, J.; Liu, H. Path Optimization of Multimodal Transport Models under Carbon Tax Policy. In Proceedings of the International Conference on Traffic and Transportation Studies, Singapore, 10–12 July 2024; Springer Nature: Singapore, 2024; pp. 427–434. [Google Scholar]
- Reşat, H.G.; Türkay, M. Design and operation of intermodal transportation network in the Marmara region of Turkey. Transp. Res. Part E Logist. Transp. Rev. 2015, 83, 16–33. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, J.; Zou, Y. Multimodal transportation routing optimization based on multi-objective Q-learning under time uncertainty. Complex Intell. Syst. 2024, 10, 3133–3152. [Google Scholar] [CrossRef]
- Cao, Q.K.; Qin, M.N.; Ren, X.Y. Bi-level programming model and genetic simulated annealing algorithm for inland collection and distribution system optimization under uncertain demand. Adv. Prod. Eng. Manag. 2018, 13, 147–157. [Google Scholar] [CrossRef]
- Shao, Y.; Han, X.L.; Cao, L.J. Optimization of multimodal transport path considering carbon policy. In Proceedings of the Sixth International Conference on Traffic Engineering and Transportation System (ICTETS 2022), Chengdu, China, 22–24 July 2022; Edited by SPIE. SPIE: Bellingham, WA, USA, 2023; pp. 728–736. [Google Scholar]
- Zhao, F.; Zeng, X. Optimization of transit network layout and headway with a combined genetic algorithm and simulated annealing method. Eng. Optim. 2006, 38, 701–722. [Google Scholar] [CrossRef]
- Cheng, X.; Jin, C.; Yao, Q.; Wang, C. Robust optimization study on multimodal transportation route selection under carbon trading policy. Chin. Manag. Sci. 2021, 29, 82–90. [Google Scholar]


| Category | Uncertainty | Objective Function | Model | |||||
|---|---|---|---|---|---|---|---|---|
| Factor | Demand | Transportation Time | Carbon Trading Price | Transportation Cost | Transshipment Cost | Time Penalty Cost | Carbon Emission Cost | Robust Optimization |
| Reference | ||||||||
| Li and Sun (2022) [9] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Peng (2024) [10] | ✓ | Mixed Integer Programming | ||||||
| Liu et al. (2025) [11] | ✓ | ✓ | ✓ | ✓ | ||||
| Peng et al. (2021) [12] | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Wang et al. (2024) [13] | ✓ | ✓ | ✓ | Integer Programming | ||||
| Guo et al. (2024) [14] | ✓ | Mixed Integer Programming | ||||||
| Zhang et al. (2021) [15] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Li et al. (2023) [16] | ✓ | ✓ | ✓ | Fuzzy Optimization | ||||
| Peng et al. (2024) [17] | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Li et al. (2024) [18] | ✓ | ✓ | ✓ | ✓ | Fuzzy Optimization | |||
| Hou et al. (2024) [19] | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Sun (2020) [20] | ✓ | ✓ | ✓ | ✓ | ✓ | Fuzzy Optimization | ||
| Xu et al. (2024) [21] | ✓ | ✓ | ✓ | ✓ | ||||
| Han et al. (2023) [22] | ✓ | ✓ | ✓ | Fuzzy Optimization | ||||
| Zhu (2022) [23] | ✓ | Mixed Integer Programming | ||||||
| Zhang et al. (2024) [24] | ✓ | ✓ | ✓ | ✓ | Fuzzy Optimization | |||
| Gao et al. (2024) [25] | ✓ | ✓ | Integer Programming | |||||
| Reşat and Türkay (2015) [26] | ✓ | ✓ | Mixed Integer Programming | |||||
| Category | Symbol | Implication |
|---|---|---|
| Set/Indices | Scenario index. | |
| Node indices. | ||
| Transportation mode index. | ||
| Transshipment mode index. | ||
| Parameters | Demand quantity. | |
| Distance from node to node , using transportation mode . | ||
| Unit transportation cost of using transportation mode . | ||
| Transshipment cost at node from mode to mode . | ||
| Processing time at node . | ||
| Lower bound of the flexible time window. | ||
| Range of the flexible time window. | ||
| Time penalty cost coefficient. | ||
| Carbon emissions of transportation mode . | ||
| Carbon trading price. | ||
| Average demand. | ||
| Uncertainty coefficient of demand. | ||
| Average carbon trading price. | ||
| Uncertainty coefficient of carbon trading price. | ||
| Uncertainty coefficient of transportation time. | ||
| Decision Variables | Decision variable of transportation route from node to node using mode . | |
| Auxiliary Variables | Random variable of demand. | |
| Uncertainty variable of transportation time. | ||
| Random variable of carbon trading price. | ||
| Demand uncertainty budget. | ||
| Transportation time uncertainty budget. | ||
| Carbon trading price uncertainty budget. | ||
| Set of all uncertainty scenarios. | ||
| Probability of scenario occurring. |
| Parameter Symbol | Highway | Railway | Waterway |
|---|---|---|---|
| 9.39 | 4.14 | 2.34 | |
| 0.1 | 0.05 | 0.02 | |
| 70 | 60 | 15 | |
| 0.01386 | 0.00264 | 0.00544 |
| Parameter Symbol | Highway–Railway | Highway–Waterway | Railway–Highway | Railway–Waterway | Waterway–Highway | Waterway–Railway |
|---|---|---|---|---|---|---|
| 150 | 200 | 150 | 250 | 200 | 250 | |
| 0.5 | 0.5 | 0.5 | 1 | 0.5 | 1 |
| Optimal Route | Min. Cost (CNY) | |||
|---|---|---|---|---|
| 0.6 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 14,545.76 |
| 0.8 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 17,411.26 |
| 1.0 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 16,378.70 |
| 1.2 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 15,324.08 |
| 1.4 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 16,998.73 |
| Optimal Route | Min. Cost (CNY) | |||
|---|---|---|---|---|
| 1.0 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 16,378.70 |
| 1.0 | 0.8 | 0.6 | 1-Waterway-12-Waterway-16-Railway-17 | 15,671.16 |
| 1.0 | 1.0 | 0.6 | 1-Waterway-7-Railway-17 | 18,004.49 |
| 1.0 | 1.2 | 0.6 | 1-Waterway-7-Railway-17 | 18,587.72 |
| 1.0 | 1.4 | 0.6 | 1-Waterway-7-Railway-17 | 14,222.07 |
| Optimal Route | Min. Cost (CNY) | |||
|---|---|---|---|---|
| 1.2 | 1.0 | 0.6 | 1-Waterway-7-Railway-17 | 17,625.40 |
| 1.2 | 1.0 | 0.8 | 1-Waterway-12-Waterway-16-Railway-17 | 17,488.58 |
| 1.2 | 1.0 | 1.0 | 1-Waterway-7-Railway-17 | 16,666.34 |
| 1.2 | 1.0 | 1.2 | 1-Waterway-12-Waterway-16-Railway-17 | 16,877.21 |
| 1.2 | 1.0 | 1.4 | 1-Waterway-7-Railway-17 | 16,909.49 |
| No. | Scenario | Optimal Route | Min. Cost (CNY) | |||
|---|---|---|---|---|---|---|
| 1 | Low Uncertainty | 0.6 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 14,545.76 |
| 2 | High Uncertainty | 1.4 | 1.4 | 1.4 | 1-Waterway-7-Railway-17 | 18,070.30 |
| 3 | High Demand Uncertainty | 1.4 | 0.6 | 0.6 | 1-Waterway-7-Railway-17 | 16,998.73 |
| 4 | High Time Uncertainty | 0.6 | 1.4 | 0.6 | 1-Waterway-12-Waterway-16-Railway-17 | 17,373.90 |
| 5 | High Carbon Trading Price Uncertainty | 0.6 | 0.6 | 1.4 | 1-Waterway-12-Waterway-16-Railway-17 | 16,080.56 |
| 6 | High Demand and High Time Uncertainty | 1.4 | 1.4 | 0.6 | 1-Waterway-7-Railway-17 | 16,282.30 |
| 7 | High Time and High Carbon Price Uncertainty | 0.6 | 1.4 | 1.4 | 1-Waterway-12-Waterway-16-Railway-17 | 17,022.51 |
| 8 | High Demand and High Carbon Price Uncertainty | 1.4 | 0.6 | 1.4 | 1-Waterway-7-Railway-17 | 17,771.81 |
| Optimal Route | Frequency | Proportion (%) |
|---|---|---|
| 1-Waterway-7-Railway-17 | 91 | 72.8 |
| 1-Waterway-12-Waterway-16-Railway-17 | 14 | 11.2 |
| 1-Waterway-12-Railway-16-Railway-17 | 12 | 9.6 |
| 1-Railway-11-Railway-17 | 5 | 4.0 |
| 1-Waterway-12-Waterway-16-Highway-17 | 2 | 1.6 |
| 1-Waterway-12-Waterway-15-Waterway-16-Railway-17 | 1 | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, X.; Pan, S.; Zheng, G. Robust Optimization of Multimodal Transportation Route Selection Based on Multiple Uncertainties from the Perspective of Sustainable Transportation. Sustainability 2025, 17, 5508. https://doi.org/10.3390/su17125508
Ren X, Pan S, Zheng G. Robust Optimization of Multimodal Transportation Route Selection Based on Multiple Uncertainties from the Perspective of Sustainable Transportation. Sustainability. 2025; 17(12):5508. https://doi.org/10.3390/su17125508
Chicago/Turabian StyleRen, Xiaoxue, Shuangli Pan, and Guijun Zheng. 2025. "Robust Optimization of Multimodal Transportation Route Selection Based on Multiple Uncertainties from the Perspective of Sustainable Transportation" Sustainability 17, no. 12: 5508. https://doi.org/10.3390/su17125508
APA StyleRen, X., Pan, S., & Zheng, G. (2025). Robust Optimization of Multimodal Transportation Route Selection Based on Multiple Uncertainties from the Perspective of Sustainable Transportation. Sustainability, 17(12), 5508. https://doi.org/10.3390/su17125508




