Toward Sustainable Solar Energy: Predicting Recombination Losses in Perovskite Solar Cells with Deep Learning
Abstract
1. Introduction
- We propose a novel LSTM-MLP hybrid deep learning framework that dynamically predicts dominant recombination losses (band-to-band, grain boundary, and interface) in perovskite solar cells using light intensity-dependent J–V characteristics.
- We conduct extensive ablation and comparative studies, demonstrating the model’s superiority over traditional ML methods (e.g., Random Forest and XGBoost) in terms of accuracy and generalizability.
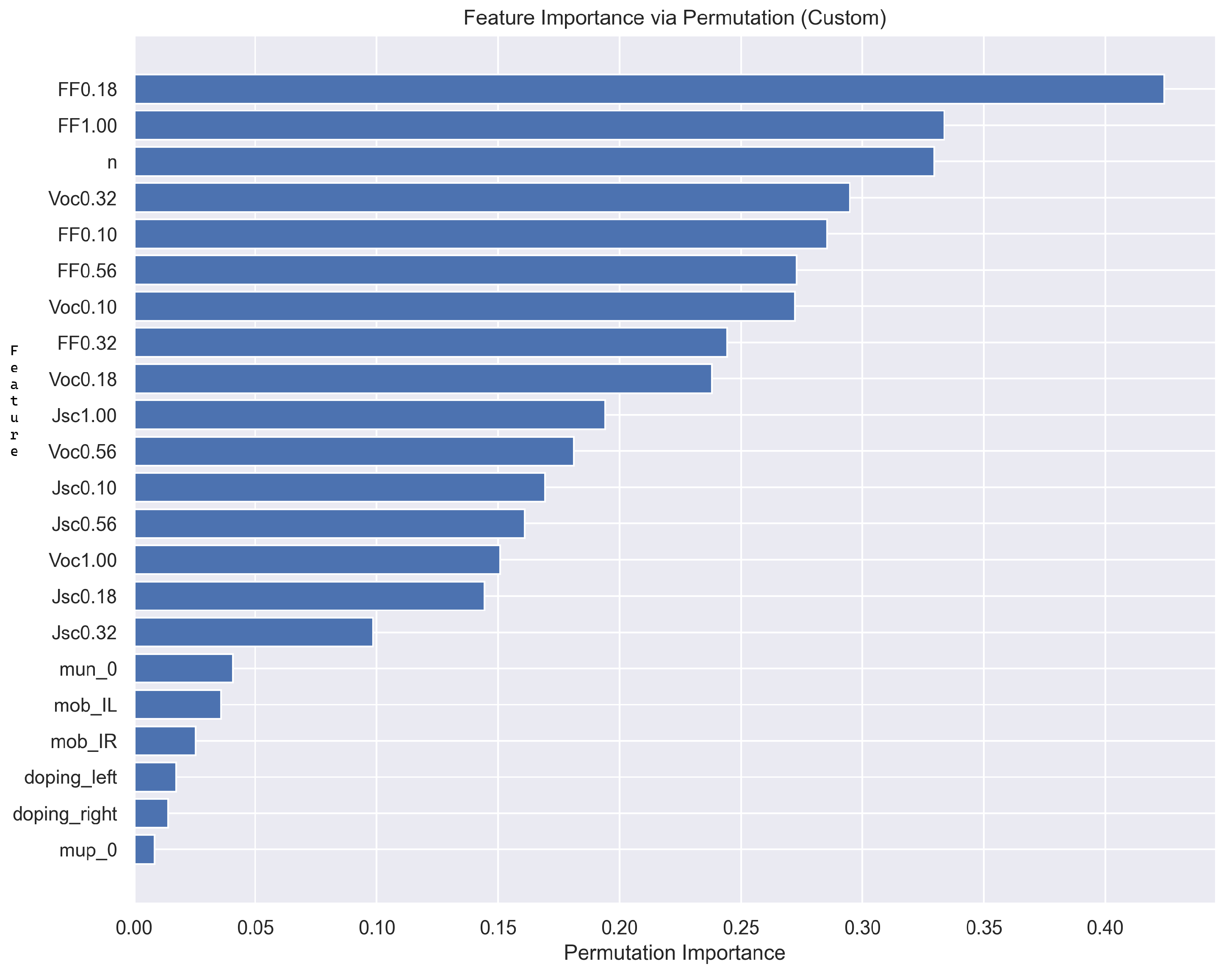
- We perform interpretability analysis using permutation importance and ROC curves to validate the physical relevance and diagnostic capabilities of the model.
- Our framework contributes toward automated, scalable recombination diagnostics in PSCs, aligning with global goals for clean and efficient solar energy technologies.
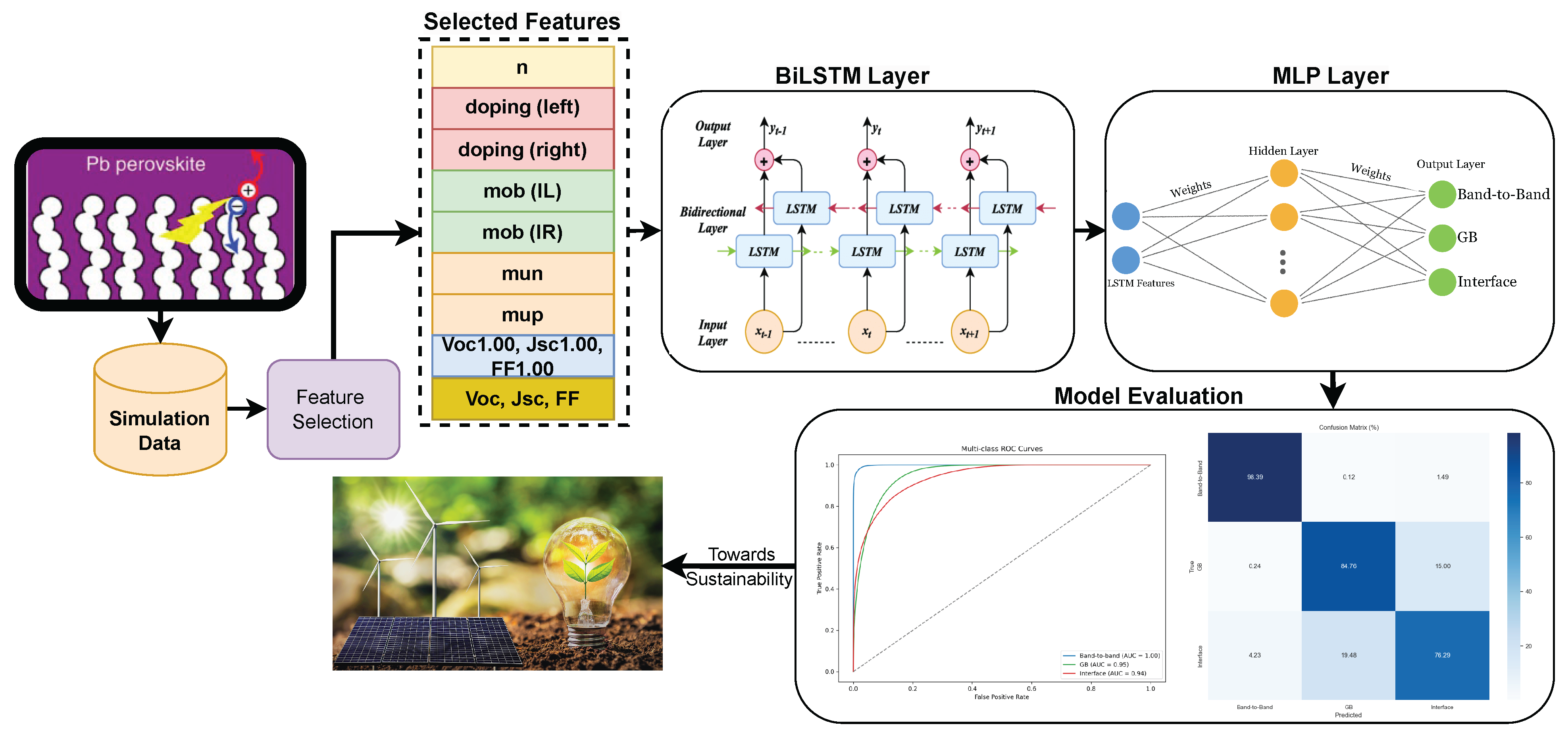
2. Methodology
2.1. Dataset and Feature Engineering
2.1.1. Feature Selection
2.1.2. Data Scaling
2.1.3. Data Splitting
2.2. Model Architecture
2.2.1. Long Short-Term Memory (LSTM)
- -
- is the input vector at time step t;
- -
- is the hidden state from the previous time step;
- -
- is the cell state at time step t;
- -
- and tanh are activation functions.
2.2.2. Bidirectional LSTM
2.2.3. Multi-Layer Perceptron (MLP)
2.3. Training Procedure
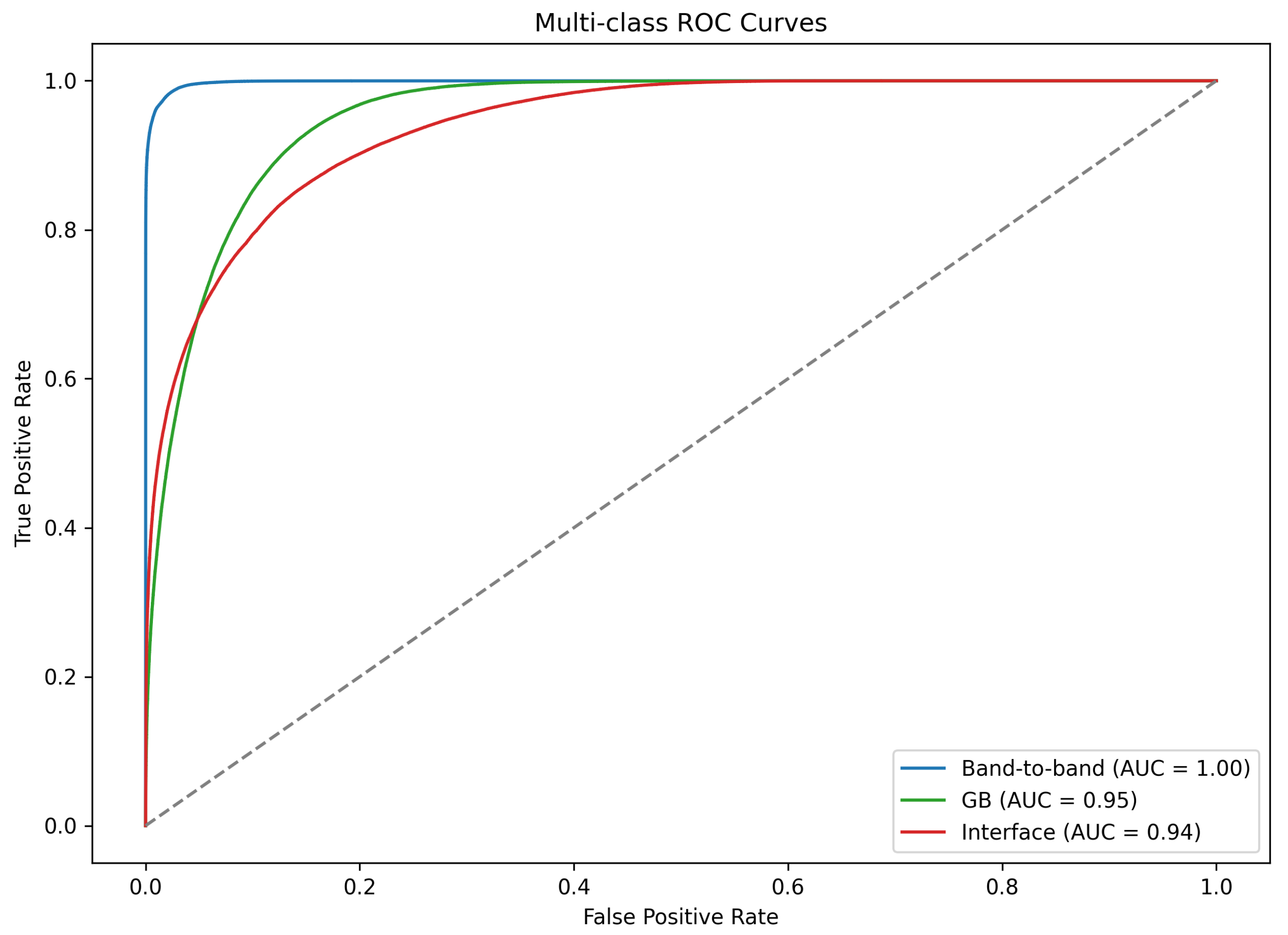
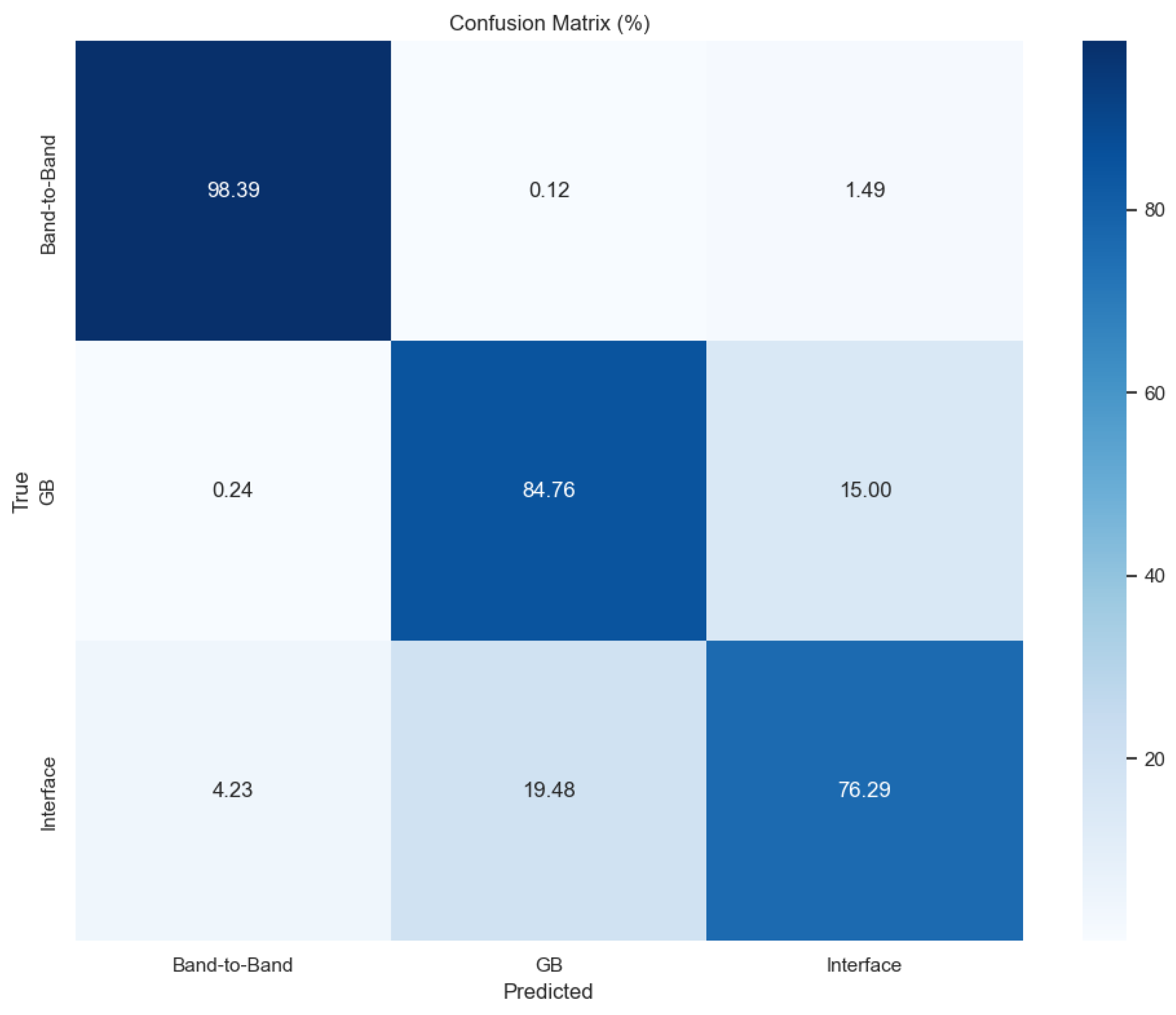
2.4. Evaluation Metrics
2.5. Suitability of the Approach for the Problem
- PSCs’ current–voltage characteristics exhibit temporal dependencies, especially under varying light intensities. LSTM is well suited to capture these dependencies, allowing the model to account for the dynamic nature of the solar cell’s performance.
- The recombination losses in PSCs are governed by multiple physical processes, such as grain boundaries, interfaces, and band-to-band recombination. The model’s ability to handle multi-dimensional data with multiple features, including light intensity and voltage characteristics, makes it ideal for differentiating between these loss mechanisms.
- The bidirectional LSTM allows the model to capture information from both past and future time steps, enriching its ability to predict the recombination loss mechanism more accurately. Furthermore, the integration of MLP ensures that the output is a clear classification of the dominant recombination loss.
3. Results
3.1. Ablation Study
3.2. Comparison with Previously Reported Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Zuo, Y.; Sun, R.; Zhou, L. Research on the conversion efficiency and preparation technology of monocrystalline silicon cells based on statistical distribution. Sustain. Energy Technol. Assess. 2021, 47, 101482. [Google Scholar] [CrossRef]
- Maldonado, S. The importance of new “sand-to-silicon” processes for the rapid future increase of photovoltaics. ACS Energy Lett. 2020, 5, 3628–3632. [Google Scholar] [CrossRef]
- Niu, X.; Ma, N.; Bu, Z.; Hong, W.; Li, H. Thermodynamic analysis of supercritical Brayton cycles using CO2-based binary mixtures for solar power tower system application. Energy 2022, 254, 124286. [Google Scholar] [CrossRef]
- Du, Y.; Xue, Y.; Wu, W.; Shahidehpour, M.; Shen, X.; Wang, B.; Sun, H. Coordinated planning of integrated electric and heating system considering the optimal reconfiguration of district heating network. IEEE Trans. Power Syst. 2023, 39, 794–808. [Google Scholar] [CrossRef]
- Roy, P.; Ghosh, A.; Barclay, F.; Khare, A.; Cuce, E. Perovskite solar cells: A review of the recent advances. Coatings 2022, 12, 1089. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X.; Liu, Z.; Zhu, Y.; Lu, J.; Chen, Z.; Li, C.; Wang, J.; Xue, Q.; He, F.; et al. Annual research review of perovskite solar cells in 2023. Mater. Futur. 2024, 3, 022102. [Google Scholar] [CrossRef]
- Ouedraogo, N.A.N.; Ouyang, Y.; Guo, B.; Xiao, Z.; Zuo, C.; Chen, K.; He, Z.; Odunmbaku, G.O.; Ma, Z.; Long, W.; et al. Printing Perovskite Solar Cells in Ambient Air: A Review. Adv. Energy Mater. 2024, 14, 2401463. [Google Scholar] [CrossRef]
- Yu, M.; Qin, T.; Gao, G.; Zu, K.; Zhang, D.; Chen, N.; Wang, D.; Hua, Y.; Zhang, H.; Zhao, Y.B.; et al. Multiple defects renovation and phase reconstruction of reduced-dimensional perovskites via in situ chlorination for efficient deep-blue (454 nm) light-emitting diodes. Light. Sci. Appl. 2025, 14, 102. [Google Scholar] [CrossRef]
- Li, K.; Zhu, Y.; Chang, X.; Zhou, M.; Yu, X.; Zhao, X.; Wang, T.; Cai, Z.; Zhu, X.; Wang, H.; et al. Self-induced bi-interfacial modification via fluoropyridinic acid for high-performance inverted perovskite solar cells. Adv. Energy Mater. 2025, 15, 2404335. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, S.; Chen, L. Can Pb-Free Halide Perovskites be Realized by Incorporating the Neutral or Anionic Molecule? Adv. Theory Simul. 2025, 2401546. [Google Scholar] [CrossRef]
- Ngiam, K.Y.; Khor, W. Big data and machine learning algorithms for health-care delivery. Lancet Oncol. 2019, 20, e262–e273. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]
- Eesaar, H.; Joe, S.; Rehman, M.U.; Jang, Y.; Chong, K.T. SEiPV-Net: An efficient deep learning framework for autonomous multi-defect segmentation in electroluminescence images of solar photovoltaic modules. Energies 2023, 16, 7726. [Google Scholar] [CrossRef]
- Cao, B.; Adutwum, L.A.; Oliynyk, A.O.; Luber, E.J.; Olsen, B.C.; Mar, A.; Buriak, J.M. How to optimize materials and devices via design of experiments and machine learning: Demonstration using organic photovoltaics. ACS Nano 2018, 12, 7434–7444. [Google Scholar] [CrossRef]
- Ahmed, S.; Alshater, M.M.; El Ammari, A.; Hammami, H. Artificial intelligence and machine learning in finance: A bibliometric review. Res. Int. Bus. Financ. 2022, 61, 101646. [Google Scholar] [CrossRef]
- Bhavsar, P.; Safro, I.; Bouaynaya, N.; Polikar, R.; Dera, D. Machine learning in transportation data analytics. In Data Analytics for Intelligent Transportation Systems; Elsevier: Amsterdam, The Netherlands, 2017; pp. 283–307. [Google Scholar]
- Häse, F.; Roch, L.M.; Aspuru-Guzik, A. Next-generation experimentation with self-driving laboratories. Trends Chem. 2019, 1, 282–291. [Google Scholar] [CrossRef]
- Xia, R.; Brabec, C.J.; Yip, H.L.; Cao, Y. High-throughput optical screening for efficient semitransparent organic solar cells. Joule 2019, 3, 2241–2254. [Google Scholar] [CrossRef]
- Wilbraham, L.; Sprick, R.S.; Jelfs, K.E.; Zwijnenburg, M.A. Mapping binary copolymer property space with neural networks. Chem. Sci. 2019, 10, 4973–4984. [Google Scholar] [CrossRef]
- Lampe, C.; Kouroudis, I.; Harth, M.; Martin, S.; Gagliardi, A.; Urban, A.S. Rapid Data-Efficient Optimization of Perovskite Nanocrystal Syntheses through Machine Learning Algorithm Fusion. Adv. Mater. 2023, 35, 2208772. [Google Scholar] [CrossRef]
- Yuqi, J.; An, A.; Lu, Z.; Ping, H.; Xiaomei, L. Short-term load forecasting based on temporal importance analysis and feature extraction. Electr. Power Syst. Res. 2025, 244, 111551. [Google Scholar] [CrossRef]
- Fang, C.; Song, K.; Yan, Z.; Liu, G. Monitoring phycocyanin in global inland waters by remote sensing: Progress and future developments. Water Res. 2025, 275, 123176. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, L.; Zhang, J.; Wu, Q.; Jiang, L.; Shi, Y.; Lyu, L.; Cai, G. Fault diagnosis of energy storage batteries based on dual driving of data and models. J. Energy Storage 2025, 112, 115485. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H. EEG Signal Recognition of VR Education Game Players Based on Hybrid Improved Wavelet Threshold and LSTM. Int. Arab J. Inf. Technol. (IAJIT) 2025, 22, 170–181. [Google Scholar] [CrossRef]
- Wang, T.; Li, J.; Wu, H.N.; Li, C.; Snoussi, H.; Wu, Y. ResLNet: Deep residual LSTM network with longer input for action recognition. Front. Comput. Sci. 2022, 16, 166334. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Bao, H.; Xia, D.; Zhang, Q.; Wang, G. Cost-Sensitive Neighborhood Granularity Selection for Hierarchical Classification. IEEE Trans. Knowl. Data Eng. 2025. [Google Scholar] [CrossRef]
- Edri, E.; Kirmayer, S.; Mukhopadhyay, S.; Gartsman, K.; Hodes, G.; Cahen, D. Elucidating the charge carrier separation and working mechanism of CH3NH3PbI3- x Cl x perovskite solar cells. Nat. Commun. 2014, 5, 3461. [Google Scholar] [CrossRef]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef]
- Stolterfoht, M.; Wolff, C.M.; Márquez, J.A.; Zhang, S.; Hages, C.J.; Rothhardt, D.; Albrecht, S.; Burn, P.L.; Meredith, P.; Unold, T.; et al. Visualization and suppression of interfacial recombination for high-efficiency large-area pin perovskite solar cells. Nat. Energy 2018, 3, 847–854. [Google Scholar] [CrossRef]
- Fang, R.; Wu, S.; Chen, W.; Liu, Z.; Zhang, S.; Chen, R.; Yue, Y.; Deng, L.; Cheng, Y.B.; Han, L.; et al. [6, 6]-Phenyl-C61-butyric acid methyl ester/cerium oxide bilayer structure as efficient and stable electron transport layer for inverted perovskite solar cells. ACS Nano 2018, 12, 2403–2414. [Google Scholar] [CrossRef]
- Yang, G.; Chen, C.; Yao, F.; Chen, Z.; Zhang, Q.; Zheng, X.; Ma, J.; Lei, H.; Qin, P.; Xiong, L.; et al. Effective carrier-concentration tuning of SnO2 quantum dot electron-selective layers for high-performance planar perovskite solar cells. Adv. Mater. 2018, 30, 1706023. [Google Scholar] [CrossRef]
- Sherkar, T.S.; Momblona, C.; Gil-Escrig, L.; Bolink, H.J.; Koster, L.J.A. Improving perovskite solar cells: Insights from a validated device model. Adv. Energy Mater. 2017, 7, 1602432. [Google Scholar] [CrossRef]
- Momblona, C.; Gil-Escrig, L.; Bandiello, E.; Hutter, E.M.; Sessolo, M.; Lederer, K.; Blochwitz-Nimoth, J.; Bolink, H.J. Efficient vacuum deposited pin and nip perovskite solar cells employing doped charge transport layers. Energy Environ. Sci. 2016, 9, 3456–3463. [Google Scholar] [CrossRef]
- Leijtens, T.; Eperon, G.E.; Barker, A.J.; Grancini, G.; Zhang, W.; Ball, J.M.; Kandada, A.R.S.; Snaith, H.J.; Petrozza, A. Carrier trapping and recombination: The role of defect physics in enhancing the open circuit voltage of metal halide perovskite solar cells. Energy Environ. Sci. 2016, 9, 3472–3481. [Google Scholar] [CrossRef]
- Shao, S.; Abdu-Aguye, M.; Qiu, L.; Lai, L.H.; Liu, J.; Adjokatse, S.; Jahani, F.; Kamminga, M.E.; ten Brink, G.H.; Palstra, T.T.; et al. Elimination of the light soaking effect and performance enhancement in perovskite solar cells using a fullerene derivative. Energy Environ. Sci. 2016, 9, 2444–2452. [Google Scholar] [CrossRef]
- DeQuilettes, D.W.; Zhang, W.; Burlakov, V.M.; Graham, D.J.; Leijtens, T.; Osherov, A.; Bulović, V.; Snaith, H.J.; Ginger, D.S.; Stranks, S.D. Photo-induced halide redistribution in organic–inorganic perovskite films. Nat. Commun. 2016, 7, 11683. [Google Scholar] [CrossRef]
- Liao, G.; Sun, E.; Kana, E.G.; Huang, H.; Sanusi, I.A.; Qu, P.; Jin, H.; Liu, J.; Shuai, L. Renewable hemicellulose-based materials for value-added applications. Carbohydr. Polym. 2024, 341, 122351. [Google Scholar] [CrossRef]
- Li, T.; Sun, W.; Qian, D.; Wang, P.; Liu, X.; He, C.; Chang, T.; Liao, G.; Zhang, J. Plant-derived biomass-based hydrogels for biomedical applications. Trends Biotechnol. 2024, 43, 802–811. [Google Scholar] [CrossRef]
- Liao, G.; Zhang, L.; Li, C.; Liu, S.Y.; Fang, B.; Yang, H. Emerging carbon-supported single-atom catalysts for biomedical applications. Matter 2022, 5, 3341–3374. [Google Scholar] [CrossRef]
- Le Corre, V.M.; Sherkar, T.S.; Koopmans, M.; Koster, L.J.A. Identification of the dominant recombination process for perovskite solar cells based on machine learning. Cell Rep. Phys. Sci. 2021, 2, 100346. [Google Scholar] [CrossRef]
- Akbar, B.; Tayara, H.; Chong, K.T. Unveiling dominant recombination loss in perovskite solar cells with a XGBoost-based machine learning approach. Iscience 2024, 27, 109200. [Google Scholar] [CrossRef]
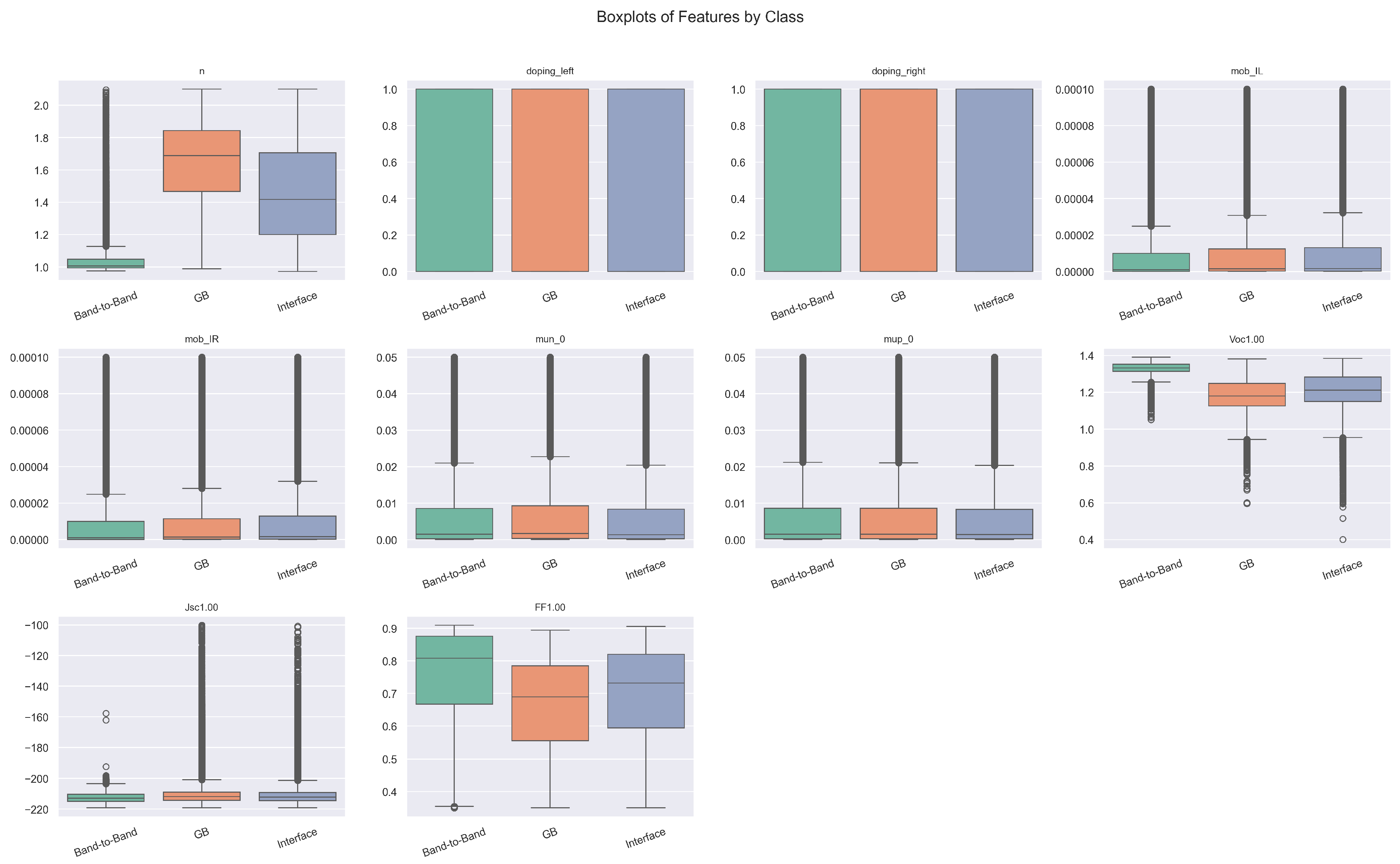
| Feature | Description |
|---|---|
| n | Ideal exponential factor for the diode equation |
| doping_left | Doping concentration in the left region (HTL) |
| doping_right | Doping concentration in the right region (ETL) |
| mob_IL | Charge carrier mobility at the left interface |
| mob_IR | Charge carrier mobility at the right interface |
| mun_0 | Initial electron mobility in the bulk |
| mup_0 | Initial hole mobility in the bulk |
| Voc1.00, Jsc1.00, and FF1.00 | Standard photovoltaic metrics at full light intensity |
| Voc_i, Jsc_i, and FF_i | Metrics computed at reduced light intensities |
| where and |
| Layer No. | Description |
|---|---|
| 1 | Linear: |
| 2 | ReLU Activation |
| 3 | Batch Normalization |
| 4 | Dropout (rate = 0.1) |
| 5 | Linear: |
| 6 | ReLU Activation |
| 7 | Dropout (rate = 0.1) |
| 8 | Linear: |
| 9 | ReLU Activation |
| 10 | Output: |
| Metric | Band-to-Band | GB | Interface | |
|---|---|---|---|---|
| Without LSTM | Precision | 0.9640 | 0.7449 | 0.8148 |
| Recall | 0.9725 | 0.8712 | 0.6697 | |
| F1-Score | 0.9683 | 0.8031 | 0.7352 | |
| Class Accuracy | 0.9788 | 0.8577 | 0.8390 | |
| MCC | 0.9523 | 0.6980 | 0.6272 | |
| With LSTM | Precision | 0.9566 | 0.8122 | 0.8222 |
| Recall | 0.9839 | 0.8476 | 0.7629 | |
| F1-Score | 0.9700 | 0.8295 | 0.7915 | |
| Class Accuracy | 0.9797 | 0.8839 | 0.8660 | |
| MCC | 0.9549 | 0.7419 | 0.6940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, S.R.; Mir, B.A.; Ryu, J.; Lee, S.W. Toward Sustainable Solar Energy: Predicting Recombination Losses in Perovskite Solar Cells with Deep Learning. Sustainability 2025, 17, 5287. https://doi.org/10.3390/su17125287
Abbas SR, Mir BA, Ryu J, Lee SW. Toward Sustainable Solar Energy: Predicting Recombination Losses in Perovskite Solar Cells with Deep Learning. Sustainability. 2025; 17(12):5287. https://doi.org/10.3390/su17125287
Chicago/Turabian StyleAbbas, Syed Raza, Bilal Ahmad Mir, Jihyoung Ryu, and Seung Won Lee. 2025. "Toward Sustainable Solar Energy: Predicting Recombination Losses in Perovskite Solar Cells with Deep Learning" Sustainability 17, no. 12: 5287. https://doi.org/10.3390/su17125287
APA StyleAbbas, S. R., Mir, B. A., Ryu, J., & Lee, S. W. (2025). Toward Sustainable Solar Energy: Predicting Recombination Losses in Perovskite Solar Cells with Deep Learning. Sustainability, 17(12), 5287. https://doi.org/10.3390/su17125287







