A Comparative Modeling Framework for Forecasting Distributed Energy Resource Adoption Under Trend-Based and Goal-Oriented Scenarios
Abstract
:1. Introduction
- Compare the logistic growth and Bass diffusion models for three DERs, EVs, HPs, and PV, using data for a region in Denmark;
- Demonstrate how these models can function effectively with limited historical data, highlighting the significance of social interaction parameters (Bass) versus simpler S-curve assumptions (logistic);
- Integrate goal-based calibration, where policy targets (e.g., 80% adoption) are incorporated as additional constraints in model fitting, thereby enabling scenario analyses that align historical trends with future objectives.
2. Literature Review
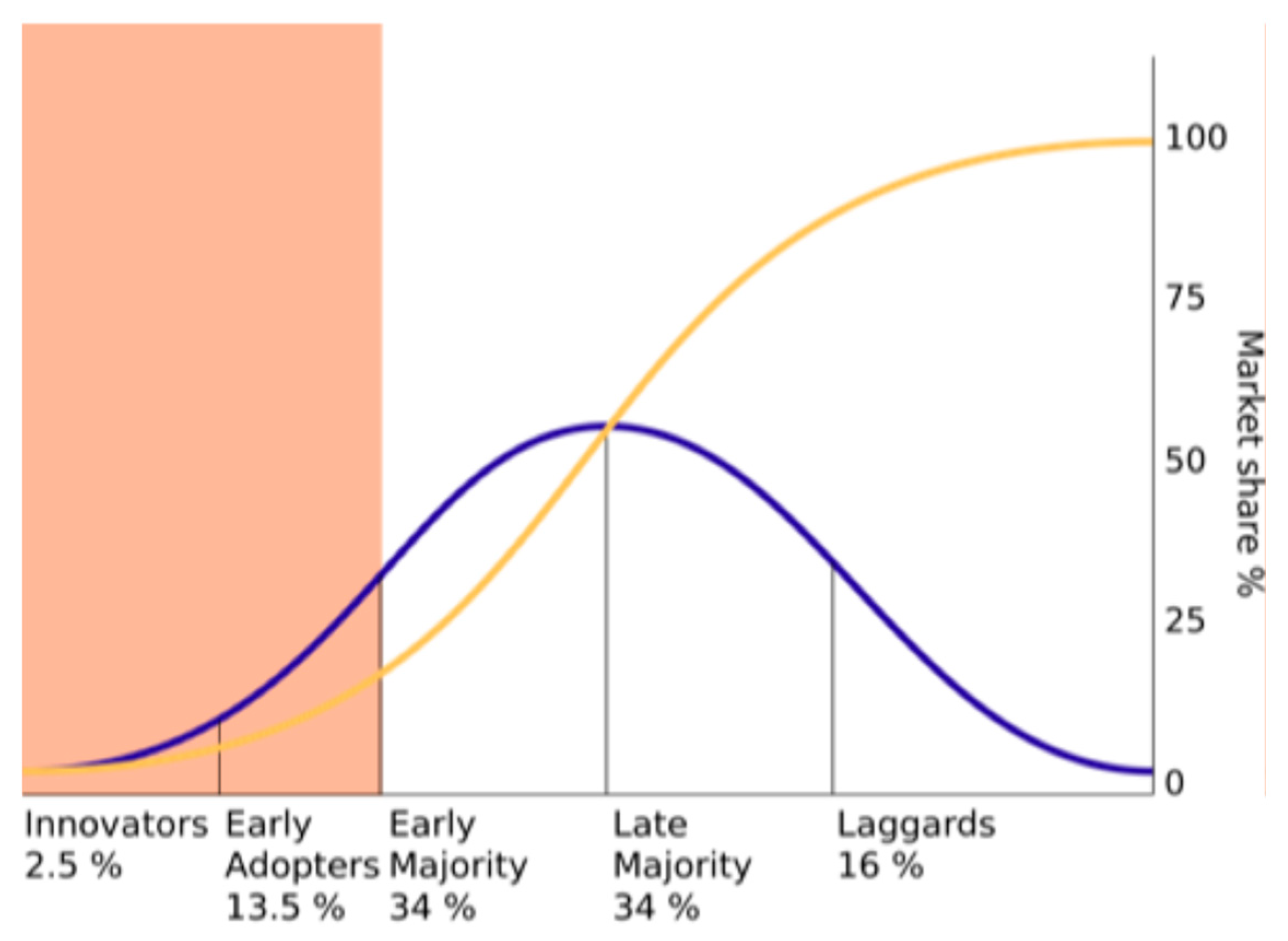
2.1. Theories of Technology Adoption and Diffusion
2.2. DER Adoption
2.2.1. Electric Vehicles
2.2.2. Heat Pumps
2.2.3. Photovoltaics
2.3. Technology Diffusion Methods
2.3.1. Bass Diffusion Model
2.3.2. Logistic Growth Model
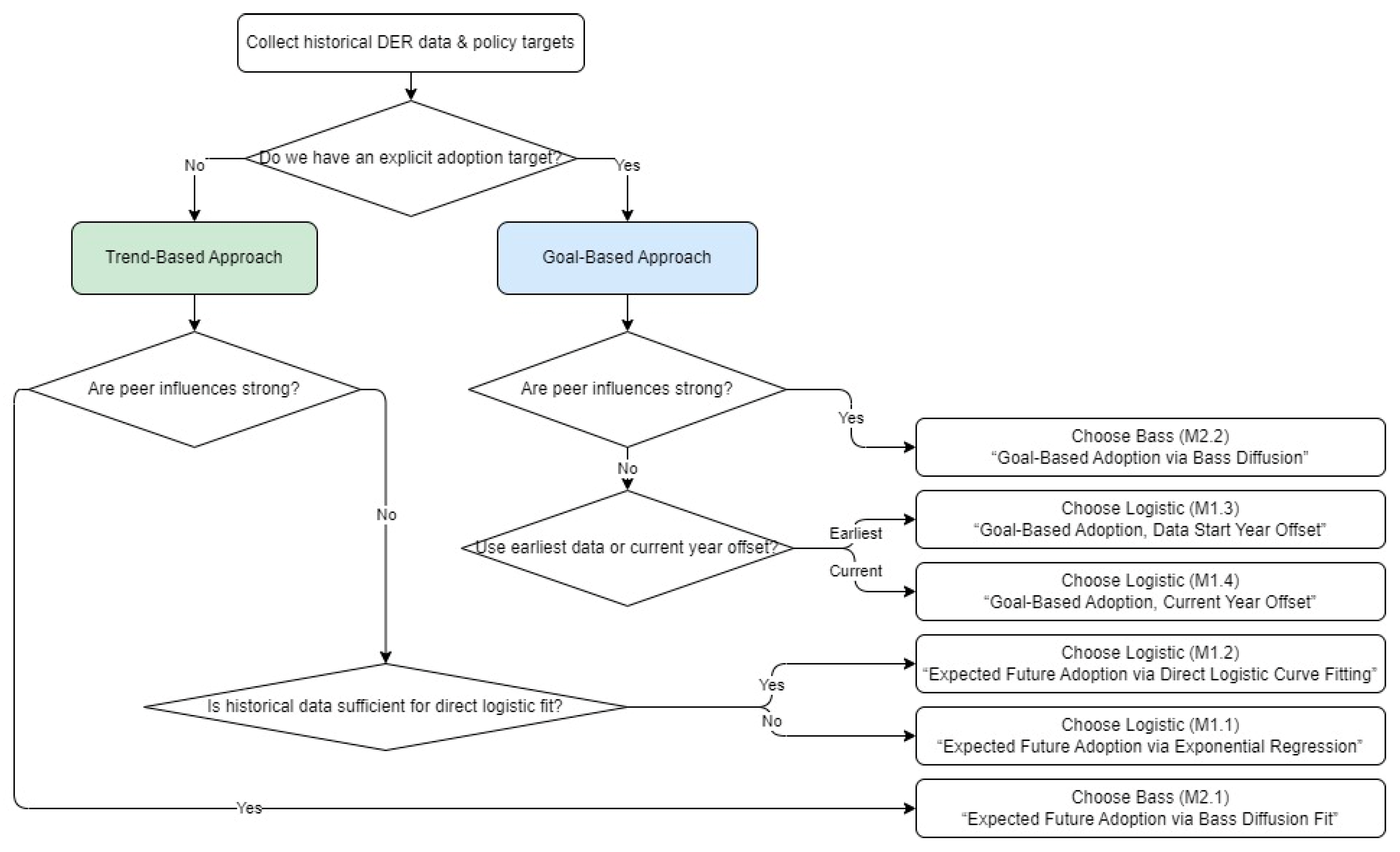
3. Model Selection and Curve-Fitting Framework for DER Adoption
3.1. Logistic Growth Model Approaches
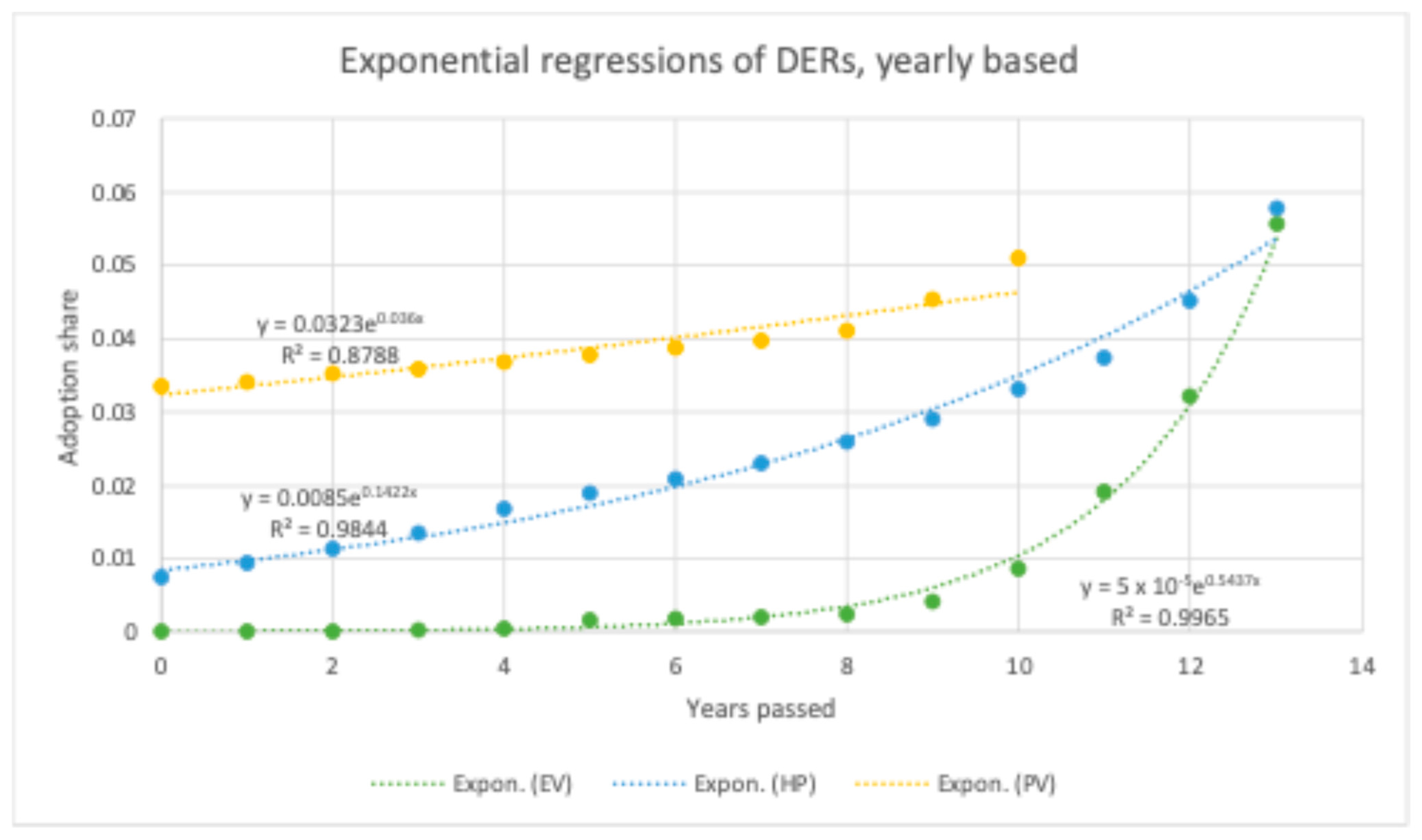
3.1.1. M1.1: Expected Future Adoption via Exponential Regression
3.1.2. M1.2: Expected Future Adoption via Logistic Fit
3.1.3. M1.3: Goal-Based Adoption (Data Start Year Offset)
3.1.4. M1.4: Goal-Based Adoption (Current Year Offset)
3.2. Bass Diffusion Model Approaches
3.2.1. M2.1: Expected Future Adoption via Bass Diffusion Fit
3.2.2. M2.2: Goal-Based Adoption via Bass Diffusion Fit
4. Empirical Application: Distributed Energy Resource Adoption in Denmark
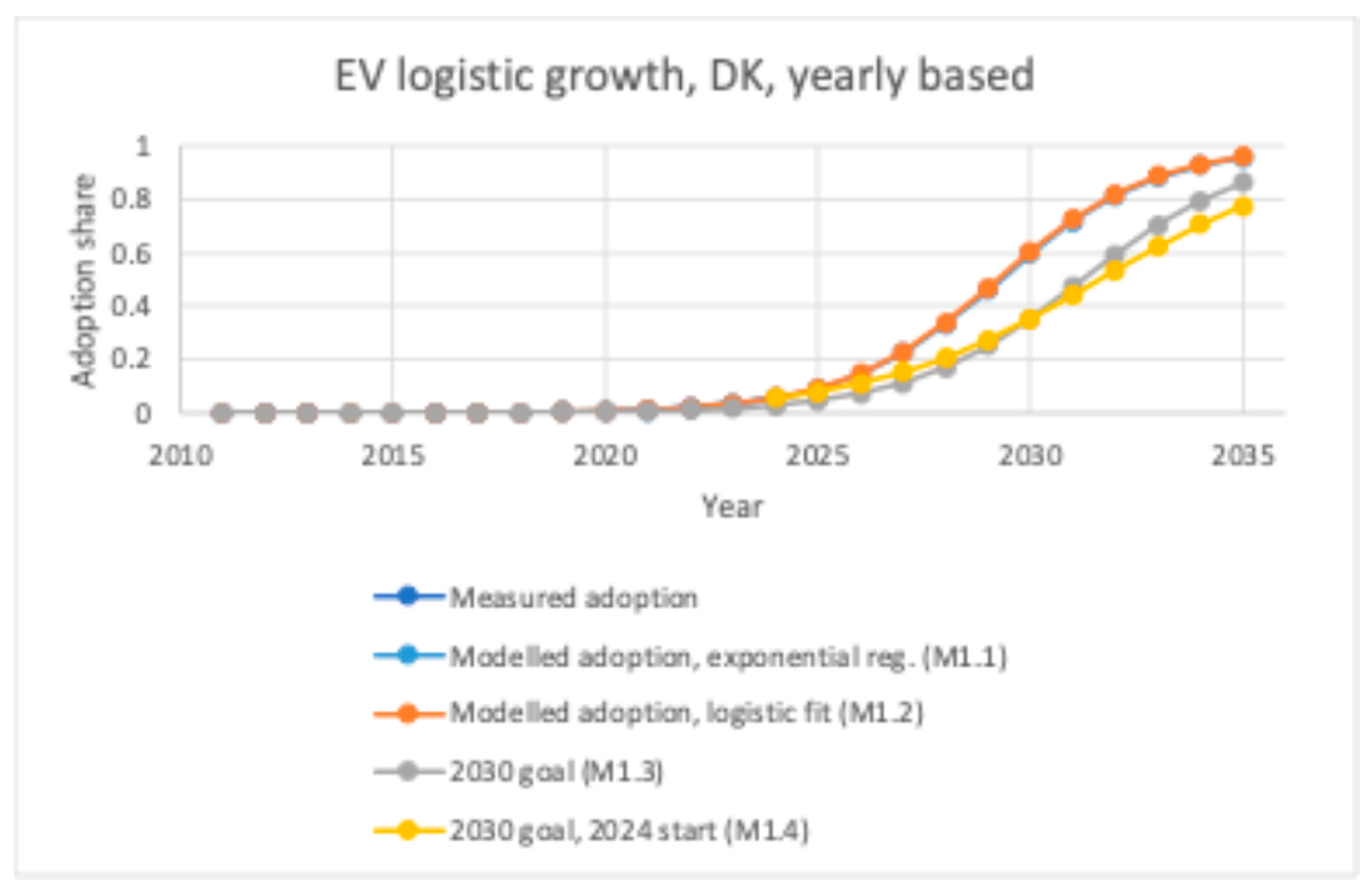
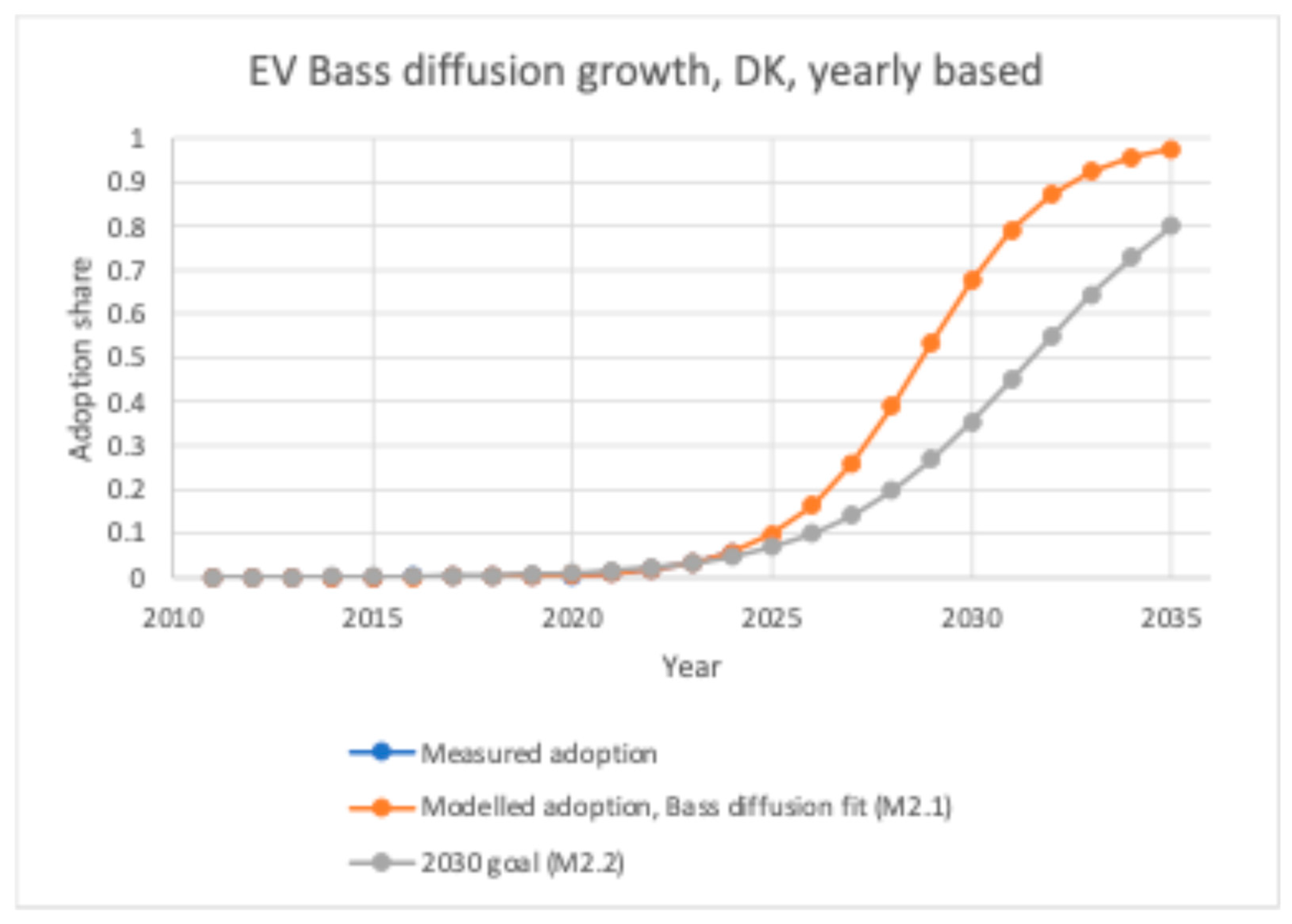
4.1. Electric Vehicle Adoption
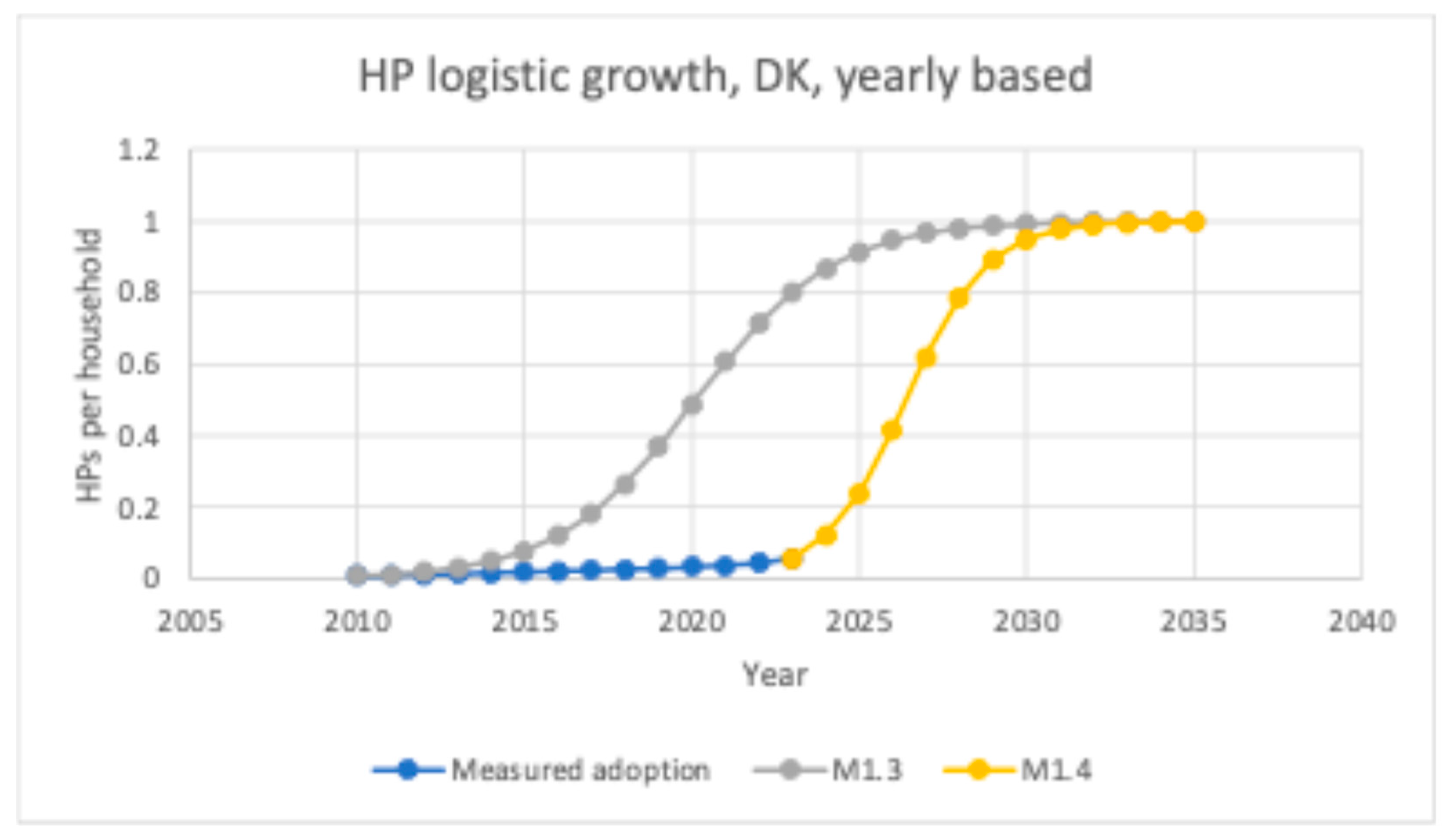
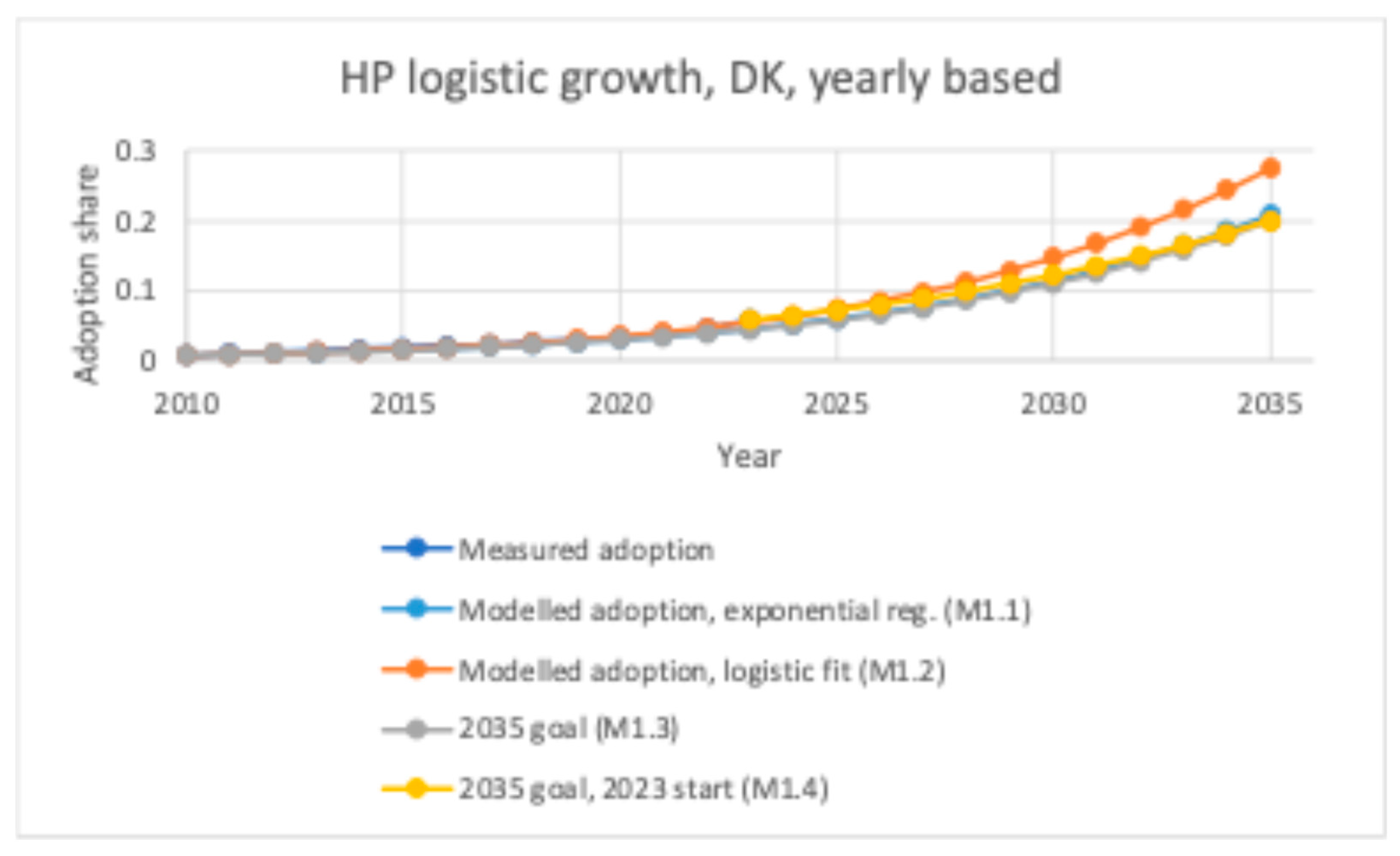
4.2. Heat Pump Adoption
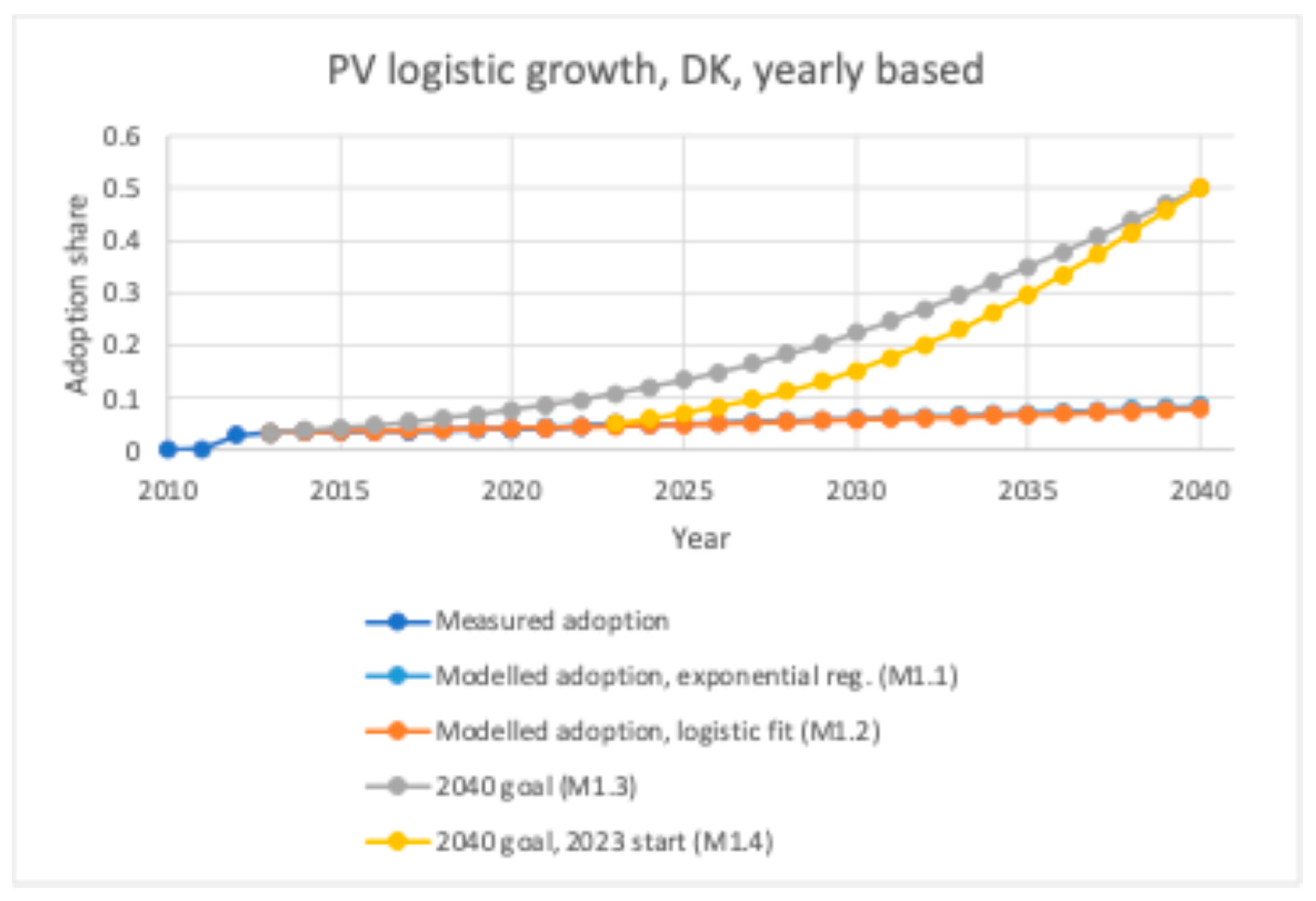
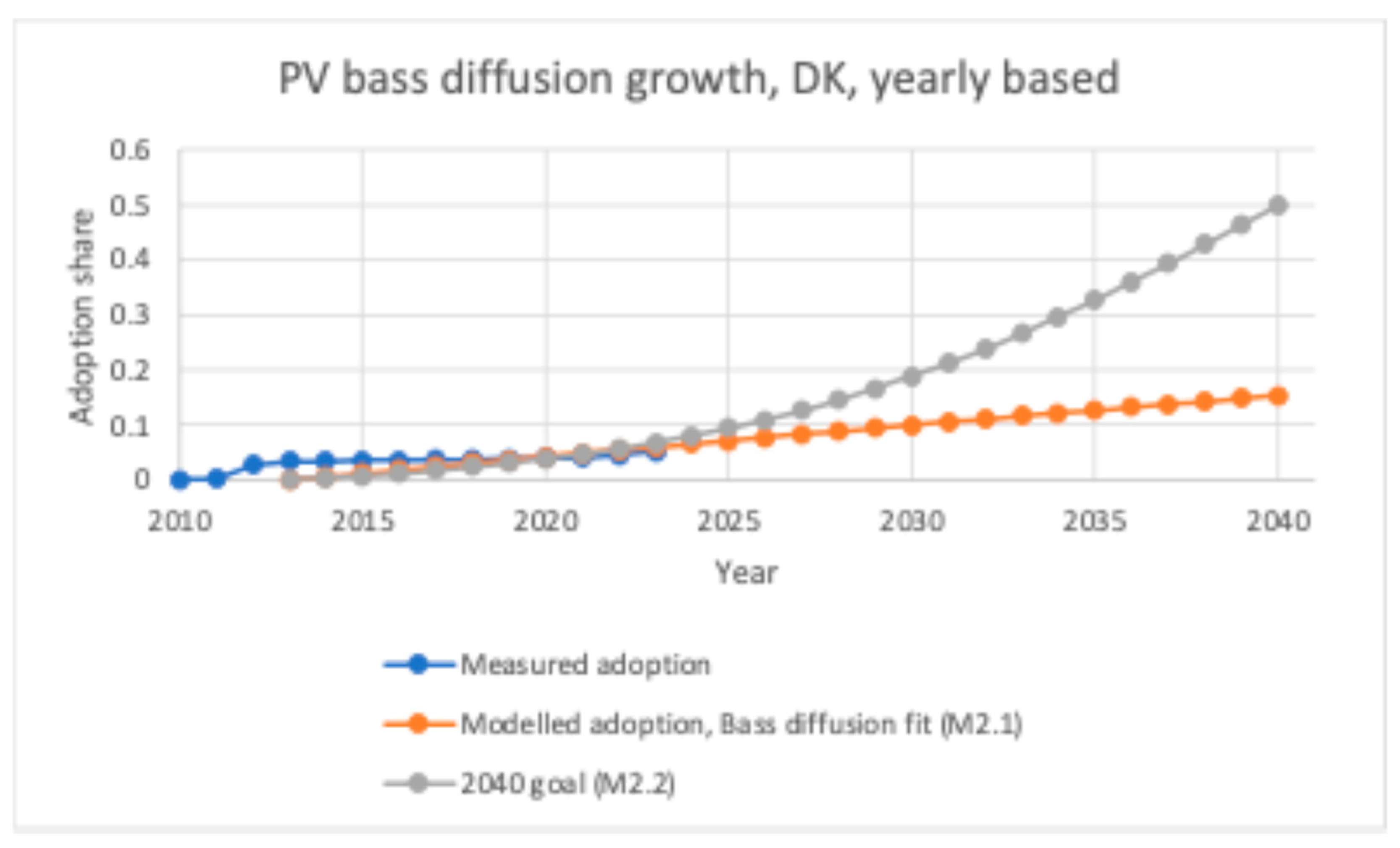
4.3. Photovoltaic Adoption
5. Discussion
5.1. Evaluation of Results
5.2. Limitations and Future Perspectives
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DERs | Distributed Energy Resources |
| EVs | Electric Vehicles |
| HPs | Heat Pumps |
| PVs | Photovoltaics |
| DOI | Diffusion of Innovations |
| TAM | Technology Acceptance Model |
| MLP | Multi-Level Perspective |
| ABM | Agent-based model |
| RET | Renewable Energy Technology |
| LDES | Long-Duration Energy Storage |
| NEV | New Energy Vehicle |
| SEM | Structural Equation Modeling |
| WTP | Willingness To Pay |
| SHT | Smart Home Technology |
| LRT | Loss-Reduction Technology |
| GIS | Geographic Information System |
| GRG | Generalized Reduced Gradient |
| kWp | Kilowatt peak (solar power rating) |
References
- Liu, W.; Guo, C.; Gui, X.; Li, D.; Chen, X. Exploring preferences for household energy technology adoption from a spatiotemporal perspective: Evidence from demographics, the economy, and the environment. Energy 2025, 319, 134957. [Google Scholar] [CrossRef]
- Baumgartner, N.; Sloot, D.; Guenther, A.; Hahnel, U.J.J. Development and test of a dual-pathway model of personal and community factors driving new energy technology adoption—The case of V2G in three European countries. Ecol. Econ. 2025, 230, 108514. [Google Scholar] [CrossRef]
- Galster, H.S.; van der Wal, A.J.; Batenburg, A.E.; Koning, V.; Faaij, A.P.C. A comprehensive review of integrating behavioral drivers of technology adoption and energy service use in energy system models. Renew. Sustain. Energy Rev. 2025, 214, 115520. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, S.; Chen, L. Analysis of Rapid Demand Variation in Electric Vehicle Industry based on Innovation Diffusion Theory: Internet technology adoption and firm energy efficiency: Evidence from China. Technol. Forecast. Soc. Change 2024, 201, 123214. [Google Scholar] [CrossRef]
- Feng, X.; Li, Y.; Huang, B. Research on manufacturer’s investment strategy and green credit policy for new energy vehicles based on consumers’ preferences and technology adoption. Technol. Forecast. Soc. Change 2023, 191, 122476. [Google Scholar] [CrossRef]
- Selanniemi, A.; Hellstrom, M.; Bjorklund-Sankiaho, M. Socio-technical energy transitions: Modelling innovation diffusion through markets with heterogeneous boundedly rational agents: Long-duration energy storage technology adoption: Insights from U.S. energy industry experts. Energy Rep. 2025, 13, 378–396. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Z. Assessment of North Delhi People’s Electric Vehicle Purchase Intent through Consumer Behavior and Technology Adoption Theory: Game Analysis of Electric Vehicle Innovation Diffusion Based on Complex Network. Complex Syst. Complex. Sci. 2024, 21, 45–51. [Google Scholar] [CrossRef]
- Antonopoulos, C.A.; Fuentes, T.L.; McCord, K.H.; Rackley, A.L.S.; Biswas, S. Regional assessment of household energy decision-making and technology adoption in the United States. Energy Policy 2024, 185, 113940. [Google Scholar] [CrossRef]
- Geels, F.W. Demand-side emission reduction through behavior change or technology adoption? Empirical evidence from UK heating, mobility, and electricity use. One Earth 2023, 6, 337–340. [Google Scholar] [CrossRef]
- Chanda, H.; Mohareb, E.; Peters, M.; Harty, C. Community-led solar energy technology adoption in rural Zambia: The role of observational learning and neighbor influence. Energy Res. Soc. Sci. 2025, 122, 103972. [Google Scholar] [CrossRef]
- Chekol, F.; Giera, M.; Alemu, B.; Dessie, M.; Alemayehu, Y.; Ewuinetu, Y. Rural Households’ Behaviour towards Modern Energy Technology Adoption Choices in East Gojjam Zone of Ethiopia: A Multivariate Probit Regression Analysis. Cogent Eng. 2023, 10, 2178107. [Google Scholar] [CrossRef]
- Vimal, K.E.K.; Kandasamy, J.; Vezhavendhan, R.; Bose, B.; Menon, A.K.; Sivakumar, K. Digital technology adoption model for electric vehicle battery recycling supply chain—An influential relationship mapping. Oper. Manag. Res. 2024, 17, 1469–1508. [Google Scholar] [CrossRef]
- Hansen, A.R.; Trotta, G.; Gram-Hanssen, K. Smart home technology adoption in Denmark: Diffusion, social differences, and energy consumption. Energy Effic. 2024, 17, 16. [Google Scholar] [CrossRef]
- Ullah, N.; Alnumay, W.S.; Al-Rahmi, W.M.; Alzahrani, A.I.; Al-Samarraie, H. Modeling cost saving and innovativeness for blockchain technology adoption by energy management. Energies 2020, 13, 4783. [Google Scholar] [CrossRef]
- Esposito, L.; Brahmi, M.; Joshi, M. The importance of innovation diffusion in the renewable energy sector. In Exploring Business Ecosystems and Innovation Capacity Building in Global Economics; IGI Global: Hershey, PA, USA, 2023; pp. 283–302. [Google Scholar]
- He, P.; Lovo, S.; Veronesi, M. Social networks and renewable energy technology adoption: Empirical evidence from biogas adoption in China. Energy Econ. 2022, 106, 105789. [Google Scholar] [CrossRef]
- Jabeen, G.; Wang, D.; Ahmad, M.; Isik, C.; Pinzon, S.; Rehman, A.; Ongan, S. Transitioning to sustainable energy: Multidimensional factors guiding solar power technology adoption. Energy 2024, 312, 133468. [Google Scholar] [CrossRef]
- Saraji, M.K.; Aliasgari, E.; Streimikiene, D. Assessment of the challenges to renewable energy technologies adoption in rural areas: A Fermatean CRITIC-VIKOR approach. Technol. Forecast. Soc. Change 2023, 189, 122399. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Z. Promoting electric vehicle cell innovation diffusion considering patent licensing strategy: A combination of evolutionary game and optimization algorithm approach. World Electr. Veh. J. 2021, 12, 95. [Google Scholar] [CrossRef]
- Qamar, S.; Ahmad, M.; Oryani, B.; Zhang, Q. Solar energy technology adoption and diffusion by micro, small, and medium enterprises: Sustainable energy for climate change mitigation. Environ. Sci. Pollut. Res. 2022, 29, 49385–49403. [Google Scholar] [CrossRef]
- Bilgili, F.; Onderol, S.; Kuskaya, S.; Alnour, M.; Hoque, M.E.; Balsalobre-Lorente, D. Renewable energy and technology adoption: Mitigating CO2 emissions through implementation strategies. Nat. Resour. Forum 2024, 49, 1478–1535. [Google Scholar] [CrossRef]
- Dhirasasna, N.; Sahin, O. A system dynamics model for renewable energy technology adoption of the hotel sector. Renew. Energy 2021, 163, 1994–2007. [Google Scholar] [CrossRef]
- Dhirasasna, N.; Becken, S.; Sahin, O. A systems approach to examining the drivers and barriers of renewable energy technology adoption in the hotel sector in Queensland, Australia. J. Hosp. Tour. Manag. 2020, 42, 153–172. [Google Scholar] [CrossRef]
- van Dijk, J.; Delacretaz, N.; Lanz, B. Technology Adoption and Early Network Infrastructure Provision in the Market for Electric Vehicles. Environ. Resour. Econ. 2022, 83, 631–679. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Luo, N.; Shalpegin, T.; Cui, H. The influence of carbon emission reduction instruments on blockchain technology adoption in recycling batteries of the new energy vehicles. Int. J. Prod. Res. 2024, 62, 891–908. [Google Scholar] [CrossRef]
- Roberts, S.; Roland, T.; Amarasekara, A.S. Factors affecting renewable energy technology adoption policies of 50 states and district of Columbia in the USA. Clean Technol. Environ. Policy 2023, 25, 211–219. [Google Scholar] [CrossRef]
- Barnes, J.; Silvonen, T.; Taylor, M. ‘No Courage at the Heart of Government’: What Are the Most Important Changes Needed to Accelerate Heat Pump Deployment in the UK? SSRN: Rochester, NY, USA, 2023. [Google Scholar]
- Mulugeta, S.; Leta, A. Determinants of Renewable Energy Technologies Adoption and Energy Source Choice of Households in Boset District, Ethiopia. Sarhad J. Agric. 2022, 38, 422–429. [Google Scholar] [CrossRef]
- Jacobson, M.G. Chapter 15—Water–energy–food nexus approaches to facilitate smallholder agricultural technology adoption in Africa. In Water-Energy-Food Nexus Narratives and Resource Securities; Mabhaudhi, T., Senzanje, A., Modi, A., Jewitt, G., Massawe, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 279–297. [Google Scholar]
- Nelson, H.; Chen, C.-F.; Li, J. Equity in Renewable Energy Technology Adoption in China: A Review of the Social-Psychological and Demographic Barriers. Curr. Sustain./Renew. Energy Rep. 2021, 8, 91–100. [Google Scholar] [CrossRef]
- Bhatt, B.; Singh, A. Stakeholders’ role in distribution loss reduction technology adoption in the Indian electricity sector: An actor-oriented approach. Energy Policy 2020, 137, 111064. [Google Scholar] [CrossRef]
- Ke, J.; Khanna, N.; Zhou, N. Indirect estimation of willingness to pay for energy technology adoption. Appl. Energy 2022, 312, 118701. [Google Scholar] [CrossRef]
- Heymann, F.; Duenas, P.; Soares, F.J.; Miranda, V.; Rüdisüli, M. Simulating spatiotemporal energy technology adoption patterns under different policy designs. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar]
- Fatima, N.; Li, Y.; Li, X.; Abbas, W.; Jabeen, G.; Zahra, T.; Isik, C.; Ahmed, N.; Ahmad, M.; Yasir, A. Households’ Perception and Environmentally Friendly Technology Adoption: Implications for Energy Efficiency. Front. Energy Res. 2022, 10, 830286. [Google Scholar] [CrossRef]
- Mishra, R.; Raut, R.D.; Kumar, M.; Naik, B.K.R.; Luthra, S. Renewable energy technology adoption in building a sustainable circular supply chain and managing renewable energy-related risk. Ann. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Wang, L.; Morabito, M.; Payne, C.T.; Robinson, G. Identifying institutional barriers and policy implications for sustainable energy technology adoption among large organizations in California. Energy Policy 2020, 146, 111768. [Google Scholar] [CrossRef]
- Liang, J.; Liu, P.; Qiu, Y.; Wang, Y.D.; Xing, B. Indonesia State Electricity Company’s Self-Service Technology Adoption: New PLN Mobile: Time-of-Use Electricity Pricing and Residential Low-carbon Energy Technology Adoption. Energy J. 2020, 41, 1–38. [Google Scholar] [CrossRef]
- Cairns, I.; Hannon, M.; Braunholtz-Speight, T.; McLachlan, C.; Mander, S.; Hardy, J.; Sharmina, M.; Manderson, E. Financing grassroots innovation diffusion pathways: The case of UK community energy. Environ. Innov. Soc. Transit. 2023, 46, 100679. [Google Scholar] [CrossRef]
- Denmark, S. Statistikbanken. Available online: https://www.statistikbanken.dk (accessed on 24 February 2025).
- Ministry of Transport. “A Greener Transport System in Denmark”, Frederiksholms Kanal 27 DK-1220 København K. Available online: https://www.trm.dk/media/0eudwtac/a-greener-transport-system-netversion-1.pdf (accessed on 27 February 2025).
- Hohmeyer, O.; Møller-K, A. Final Report of the Electricity Grid and Potentials for Energy Flexibility in Southeastern Denmark and Northern Germany; Gate21: Sarajevo, Bosnia and Herzegovina, 2023; Available online: https://gate21.dk/wp-content/uploads/2023/10/DG-STORE-Final-Report-DK.pdf (accessed on 3 March 2025).
- Danish Energy Agency. Energistatistik 2023; Danish Energy Agency: Copenhagen, Denmark, 2023; Available online: https://ens.dk/media/6308/download (accessed on 3 March 2025).
- Energinet. Long-Term Development Needs in the Power Grid; Energinet: Fredericia, Denmark, 2025; Available online: https://en.energinet.dk/media/mvyg5kxn/long-term-development-needs-in-the-danish-power-grid.pdf (accessed on 4 February 2025).
- Steffen, B.; Karplus, V.; Schmidt, T.S. State ownership and technology adoption: The case of electric utilities and renewable energy. Res. Policy 2022, 51, 104534. [Google Scholar] [CrossRef]

| Ref. | DER Aspect | Method | Key Results/Insights |
|---|---|---|---|
| [1] | Household heating/cooling technology adoption | Econometric analysis, GIS-based spatial study | Identifies strong spatial disparities in heating/cooling technology adoption, with air conditioning dominating; highlights cost/environmental drivers. |
| [2] | Renewable energy technology diffusion (RET) | Network analysis, threshold modeling | Shows that both personal norms and community influences shape technology adoption; underscores social network effects in driving RET diffusion. |
| [3] | Behavioral realism in Energy System Models | Structured literature review, expert interviews | Emphasizes that current energy system models underrepresent non-economic drivers; recommends stronger empirical grounding for behavioral factors. |
| [6] | Long-duration energy storage (LDES) adoption | Agent-based modeling (ABM), interviews | Demonstrates that LDES uptake depends on integrated policy, social acceptance, and market considerations; interviews reveal critical investor concerns. |
| [4] | Electric vehicle (EV) market growth (S-curve) | Historical trend analysis | Highlights government policies as key impetus for early EV adoption; indicates that cost reductions and incentives accelerate the S-shaped diffusion. |
| [7] | EV purchase intention | Survey-based, structural modeling | Finds that EV adoption is strongly influenced by subjective norms, range anxiety, and cost expectations; concludes EVs remain in early diffusion stage. |
| [13] | Smart home technology (SHT) uptake | Survey data, regression analysis | Reveals that SHT adoption is more common among younger households; links adoption to mixed energy outcomes (e.g., some higher energy use). |
| [5] | New energy vehicle (NEV) investment strategy | Mathematical tri-level modeling, scenarios | Shows that green credit can significantly incentivize NEV manufacturers’ R&D investment; indicates interplay between financial tools and innovation. |
| [35] | Renewables adoption in logistics and supply chains | Survey (451 experts), structural equation modeling (SEM) | Identifies core constructs influencing renewable energy technology adoption for a sustainable and circular supply chain; highlights managerial implications. |
| [9] | Demand-side emission reductions | Policy analysis | Argues that technology adoption has contributed more to emission cuts than behavior change; calls for integrated socio-technical strategies. |
| [24] | EV charging infrastructure and adoption | Econometric modeling, synthetic control | Demonstrates early charging infrastructure is crucial for EV uptake; documents non-linear stock effects and range anxiety as pivotal adoption barriers. |
| [32] | Willingness to pay (WTP) for energy technology | Optimization-based methodological approach | Proposes an indirect method to estimate WTP using constrained optimization; valuable for incomplete or aggregated data in energy markets. |
| [33] | Spatiotemporal patterns of DER uptake | Simulation, policy scenario analysis | Finds that DER adoption tends to cluster in both space and time; policy incentives can alter the geographic concentration of adoption. |
| [36] | Institutional barriers to sustainable technology | Survey, interviews | Shows that large organizations often prioritize lowest first cost over life-cycle benefits, impeding technology adoption; proposes organizational reforms. |
| [31] | Loss-reduction technology (LRT) in electricity distribution | Actor-oriented/stakeholder analysis | Concludes that slow LRT diffusion is linked to weak consumer engagement and fragmented utility-level governance; suggests enhanced stakeholder coordination. |
| Model | Key References | Advantages | Limitations |
|---|---|---|---|
| Bass Diffusion | [2,5,6,19,20] | Accounts for imitation and innovation effects; well-known S-curve patterns | Assumes homogenous population or constant p/q across subgroups |
| Logistic Growth | [1,3,9,17,33] | Simple S-curve, often robust with limited data | Ignores network effects and word-of-mouth influences |
| Gompertz | [3,18,21] | Captures asymmetric S-curve, good for certain biological or social processes | May overfit with short data series or misrepresent early-stage growth |
| Agent-Based Models | [6,9,22,23] | Rich representation of heterogeneous agents and interactions | Data-intensive, complex calibration, often scenario-based |
| Econometric/SEM | [1,13,24,34,37] | Good for cross-sectional or panel data analysis of adoption | Often limited in capturing feedback effects or dynamic processes |
| Method | ID | Model | Parameter Estimation | Future Goal? |
|---|---|---|---|---|
| Expected future adoption, exponential regression | M1.1 | Logistic growth | Exponential regression | No |
| Expected future adoption, logistic fit | M1.2 | Data fit (optimization) | No | |
| Goal-based adoption, data start year offset | M1.3 | Goal-based optimization | Yes | |
| Goal-based adoption, current year offset | M1.4 | Yes | ||
| Expected future adoption, bass diffusion fit | M2.1 | Bass diffusion | Data fit (optimization) | No |
| Goal-based adoption, bass diffusion fit | M2.2 | Yes |
| Method | Start Year | Key Parameters | Goal Year | Adoption Goal | |
|---|---|---|---|---|---|
| P0 | r | ||||
| M1.1 | 2011 | 4.7979 × 10−5 | 0.54372 | N/A | N/A |
| M1.2 | 2011 | 4.7979 × 10−5 | 0.54599 | N/A | N/A |
| M1.3 | 2011 | 4.7979 × 10−5 | 0.49147 | 2030 | 35.3% |
| M1.4 | 2024 | 0.055729 | 0.37053 | 2030 | 35.3% |
| M2.1 | 2011 | 1.5830 × 10−5 | 0.59279 | N/A | N/A |
| M2.2 | 2011 | 1.1238 × 10−4 | 0.39830 | 2030 | 35.3% |
| Method | Start Year | Key Parameters | Goal Year | Adoption Goal | |
|---|---|---|---|---|---|
| P0 | r | ||||
| M1.1 | 2010 | 0.0074741 | 0.14217 | N/A | N/A |
| M1.2 | 2010 | 0.0074741 | 0.48378 | N/A | N/A |
| M1.3 | 2010 | 0.0074741 | 0.13999 | 2035 | 20% |
| M1.4 | 2023 | 0.057804 | 0.11703 | 2035 | 20% |
| M2.1 | 2010 | 0.0030149 | 0.042528 | N/A | N/A |
| M2.2 | 2010 | 0.0022956 | 0.097793 | 2030, 2035 | 14%, 20% |
| Method | Start Year | Key Parameters | Goal Year | Adoption Goal | |
|---|---|---|---|---|---|
| P0 | r | ||||
| M1.1 | 2013 | 0.033435 | 0.036014 | N/A | N/A |
| M1.2 | 2013 | 0.033435 | 0.033544 | N/A | N/A |
| M1.3 | 2013 | 0.033435 | 0.12463 | 2040 | 50% |
| M1.4 | 2023 | 0.050900 | 0.17211 | 2040 | 50% |
| M2.1 | 2013 | 0.0061566 | 0 | N/A | N/A |
| M2.2 | 2013 | 0.0033684 | 0.13489 | 2040 | 50% |
| M1.1 Expected Future Adoption via Exponential Regression | M1.2 Expected Future Adoption via Logistic Fit | M2.1 Expected Future Adoption via Bass Diffusion Fit | M2.2 Goal-Based Adoption via Bass Diffusion Fit | |
|---|---|---|---|---|
| Electric Vehicle | 1.9430 × 10−5 | 1.6195 × 10−5 | 8.4579 × 10−6 | 1.6823 × 10−4 |
| Heat Pump | 2.6373 × 10−4 | 5.1593 × 10−5 | 2.5367 × 10−4 | 5.0361 × 10−4 |
| PV | 4.5165 × 10−5 | 4.1117 × 10−5 | 3.1616 × 10−3 | 4.4467 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.G.; Værbak, M.; Jørgensen, B.N. A Comparative Modeling Framework for Forecasting Distributed Energy Resource Adoption Under Trend-Based and Goal-Oriented Scenarios. Sustainability 2025, 17, 5283. https://doi.org/10.3390/su17125283
Ma ZG, Værbak M, Jørgensen BN. A Comparative Modeling Framework for Forecasting Distributed Energy Resource Adoption Under Trend-Based and Goal-Oriented Scenarios. Sustainability. 2025; 17(12):5283. https://doi.org/10.3390/su17125283
Chicago/Turabian StyleMa, Zheng Grace, Magnus Værbak, and Bo Nørregaard Jørgensen. 2025. "A Comparative Modeling Framework for Forecasting Distributed Energy Resource Adoption Under Trend-Based and Goal-Oriented Scenarios" Sustainability 17, no. 12: 5283. https://doi.org/10.3390/su17125283
APA StyleMa, Z. G., Værbak, M., & Jørgensen, B. N. (2025). A Comparative Modeling Framework for Forecasting Distributed Energy Resource Adoption Under Trend-Based and Goal-Oriented Scenarios. Sustainability, 17(12), 5283. https://doi.org/10.3390/su17125283









