Optimal Multi-Period Manufacturing–Remanufacturing–Transport Planning in Carbon Conscious Supply Chain: An Approach Based on Prediction and Optimization
Abstract
1. Introduction
2. Literature Review
3. Targeted Contributions
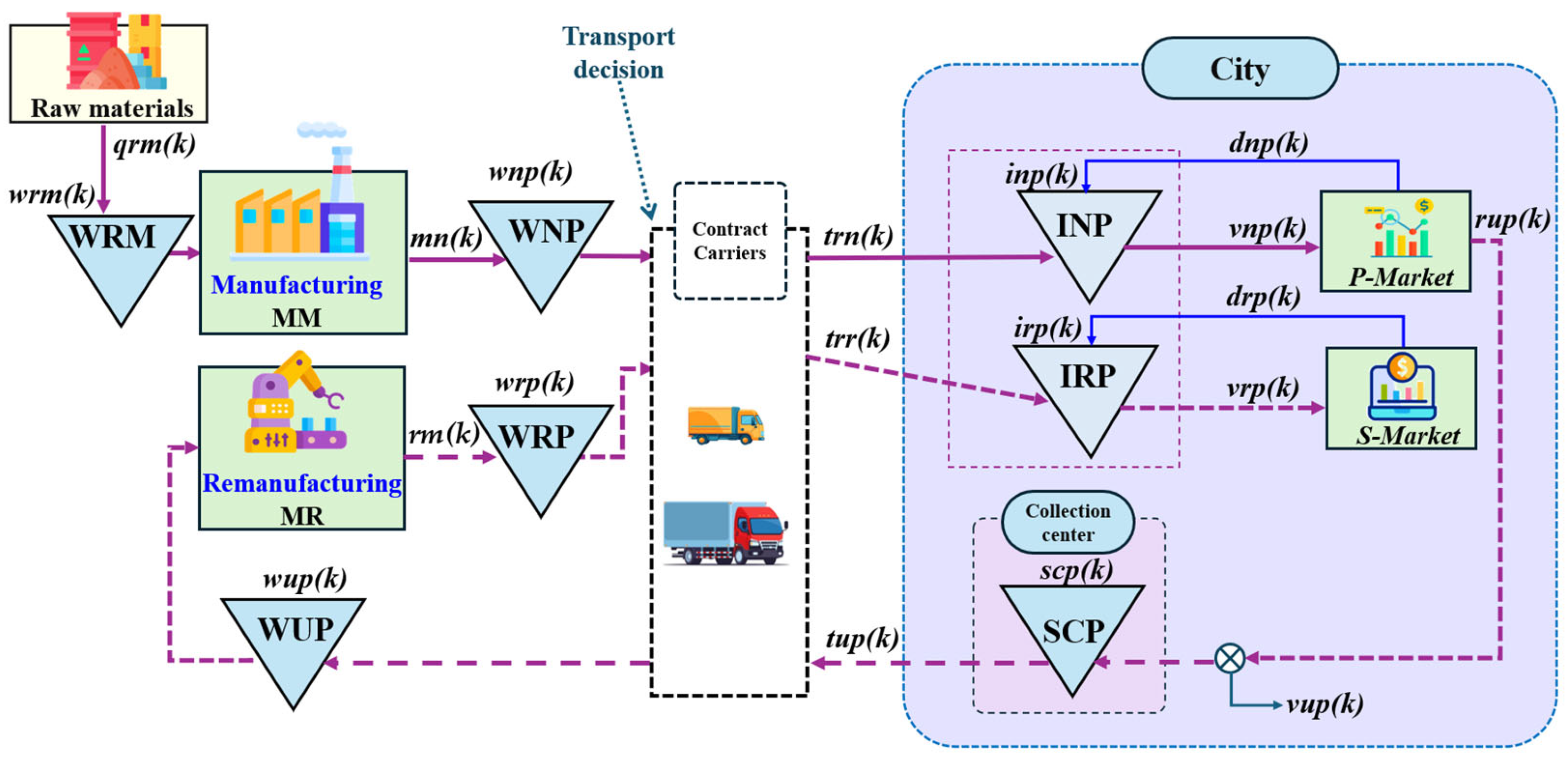
4. Problem Statement
5. Analytical Study
5.1. Notations
5.1.1. Parameters
| λ | Length of the production period |
| Z | Number of production periods in the planning horizon |
| Z. λ | Length of the finite planning horizon |
| PRCX(Z) | Total profit considering carbon tax strategy |
| qrm(k) | Quantity of raw materials to order during period k |
| qrm0 | Quantity of raw materials to order at the start of period 1 |
| mn(k) | Produced quantity of machine MM during period k |
| mn0 | Produced quantity of machine MM at the start of period 1 |
| rm(k) | Produced quantity of machine MR during period k |
| rm0 | Produced quantity of machine MR at the start of period 1 |
| trn(k) | Transported quantities of new products at period k |
| trn0 | Transported quantities of new products at the start of period 1 |
| trr(k) | Transported quantities of remanufactured products at period k |
| trr0 | Transported quantities of remanufactured products at the start of period 1 |
| tup(k) | Transported used products from SCP to WUP at period k |
| tup0 | Transported used products from SCP to WUP at the start of period 1 |
| rup(k) | Quantity of collected used products from the primary market at period k |
| rup0 | Quantity of collected used products from the primary market at the start of period 1 |
| vup(k) | Quantity sold of collected products at the end of period k |
| vup0 | Quantity sold of collected products at the start of period 1 |
| wrm(k) | Warehouse level of raw materials at the end of period k |
| wrm0 | Warehouse level of raw materials at the start of period 1 |
| wnp(k) | Warehouse level of new products at the end of period k |
| wnp0 | Warehouse level of new products at the start of period 1 |
| wrp(k) | Warehouse level of remanufactured products at the end of period k |
| wrp0 | Warehouse level of remanufactured products at the start of period 1 |
| wup(k) | Warehouse level of used products at the end of period k |
| wup0 | Warehouse level of used products at the start of period 1 |
| inp(k) | Sales inventory level of new products at the end of period k |
| inp0 | Sales inventory level of new products at the start of period 1 |
| irp(k) | Sale inventory level of remanufactured products at the end of period k |
| irp0 | Sale inventory level of remanufactured products at the start of period 1 |
| scp(k) | Storage level of collected used products in SCP at the end of period k |
| scp0 | Storage level of collected used products in SCP at the start of period 1 |
| dnp(k) | Demand in the primary market (new product) at the period k |
| drp(k) | Demand in the secondary market (remanufactured product) at the period k |
| lnp (k) | Unsatisfied demand quantity of new products at the period k |
| lnp0 | Unsatisfied demand for new products at the start of period 1 |
| lrp (k) | Unsatisfied demand quantity of remanufactured products at the period k |
| lrp0 | Unsatisfied demand quantity of remanufactured products at the start of period 1 |
| x | Cost acquisition of one raw materials unit |
| a | Unit production cost of new products |
| b | Unit production cost of remanufactured products |
| wx | Warehousing cost of one raw materials unit in WRM |
| wa | Warehousing cost of one new product in WNP |
| wb | Warehousing cost of one remanufactured product in WRP |
| wc | Warehousing cost of one remanufactured product in WUP |
| ct | Transport cost of new product |
| ca | Inventory holding cost of one new product in INP |
| cb | Inventory holding cost of one remanufactured product in IRP |
| cs | Storage cost of one collected item unit in SCP |
| y | Cost of one returned product |
| sn | Shortage cost of one new product |
| sr | Shortage cost of one remanufactured product |
| FT1 | Fixed round trip cost for vehicle V1 |
| FT2 | Fixed round trip cost for vehicle V2 |
| TCX (Z) | Total carbon tax cost over the horizon |
| vnp(k) | Quantity of new products sold at period k |
| vnp0 | Quantity of new products sold at the start of period 1 |
| vrp(k) | Quantity of remanufactured products sold at period k |
| vrp0 | Quantity of remanufactured products sold at the start of period 1 |
| pn | Unit selling price for a new product |
| pr | Unit selling price for remanufactured product |
| pv | Unit selling price for collected product |
| ucp | Unit carbon tax price |
| CF(Z) | Carbon footprint over Z |
| CF0 | Carbon footprint at the start of period 1 |
| RM | Maximum capacity of WRM |
| NP | Maximum capacity of WNP |
| RP | Maximum capacity of WRP |
| N | Maximum capacity of INP |
| R | Maximum capacity of IRP |
| SP | Maximum capacity of SCP |
| TRV1 | Capacity of the transport vehicle V1 |
| TRV2 | Capacity of the transport vehicle V2 |
| γ1(k) | Transport decision variable for the vehicle 1 |
| γ2(k) | Transport decision variable for the vehicle 2 |
| BN | Big number for the linearization |
| GM | Maximum quantity produced by MM during period k |
| GR | Maximum quantity produced by MR during period k |
| em | Unit carbon emissions from acquisition of raw materials |
| en | Unit carbon emissions from manufacturing new product |
| er | Unit carbon emissions from remanufacturing product |
| erm | Unit carbon emissions from holding raw materials in WRM |
| ewn | Unit carbon emissions from holding new product in WNP |
| ewr | Unit carbon emissions from holding remanufactured in WRP |
| esc | Unit carbon emissions from holding one collected product in SCP |
| ecu | Unit carbon emissions from holding one used product in WUP |
| enp | Unit carbon emissions from holding new product in INP |
| erp | Unit carbon emissions from holding remanufactured products in IRP |
| etr | Unit carbon emissions from transporting new, remanufactured, or returned products |
| efrt1 | Fixed quantity of carbon emitted by vehicle V1 |
| efrt2 | Fixed quantity of carbon emitted by vehicle V2 |
| MC(Z) | Manufacturing cost over Z |
| RC(Z) | Remanufacturing cost over Z |
| NSC(Z) | Shortage cost of new products over horizon Z |
| RSC(Z) | Shortage cost of remanufactured products over horizon Z |
| HRM(Z) | Inventory holding cost of raw material stock over horizon Z |
| HNP(Z) | Inventory holding cost of new products stock over horizon Z |
| HRP(Z) | Inventory holding cost of remanufactured products stock over horizon Z |
| HUP(Z) | Inventory holding cost of returned products stock over horizon Z |
| HIN(Z) | Inventory holding cost of sales inventory stock of new products over horizon Z |
| HIR(Z) | Inventory holding cost of sales inventory stock of remanufactured products over horizon Z |
| HCP(Z) | Inventory holding cost of stock of collected products over horizon Z |
| TC(Z) | Transportation cost over horizon Z |
| ARM(Z) | Acquisition of raw material cost over horizon Z |
| RPC(Z) | Returned products cost over horizon Z |
| R(Z) | Revenue over the horizon Z |
5.1.2. Decision Variables
| QRM | raw materials quantity order plan |
| MN | manufacturing plan of the machine MM |
| RM | remanufacturing plan of the machine MR |
| TRN | transport plan of new products |
| TRR | transport plan of remanufactured products |
| TUP | transported returned quantity plan of used products from SCP |
5.2. Working Assumptions
- We assume that after their useful lives are over, the remanufactured products sold in Market 2 will be destroyed;
- We assumed that the demands dnp(k), drp(k), and rup(k) are predicted using best prediction model;
- To meet the demands dnp(k) and drp(k), the quantities mn(k) and rm(k) produced during period k are added to the stock at the end of the period;
- There are no backorders, and a shortage cost is incurred because the units are lost;
- Considering that the remanufactured products were the same size as the new ones but were of lower quality and price;
- It is assumed that stocks WRM, WNP, WRP, INP, IRP, and SCP have limited capacities;
- We consider the period of time between the making of an order and the reception of raw materials. It means that the decided quantity of raw materials is ordered at period k and received at time k+ 1 in order to have a realistic approach to our system.
5.3. Formulation of the Total Expected Profit
5.3.1. Balance Inventory
5.3.2. Quantities Sold of New and Remanufacturing Products at Period k
5.3.3. Manufacturing and Remanufacturing Costs
5.3.4. Shortage Costs
5.3.5. Inventory Holding Costs
5.3.6. Transport Cost
5.3.7. Raw Material Acquisition Cost
5.3.8. Returned Products Cost
5.3.9. Carbon Reduction Strategy: Carbon Tax
5.3.10. Revenue
5.3.11. Model Constraints
- Production capacity:
- Capacity of transportation:
- Linearization constraints:
- Inventories capacities constraints
5.3.12. Objective Function
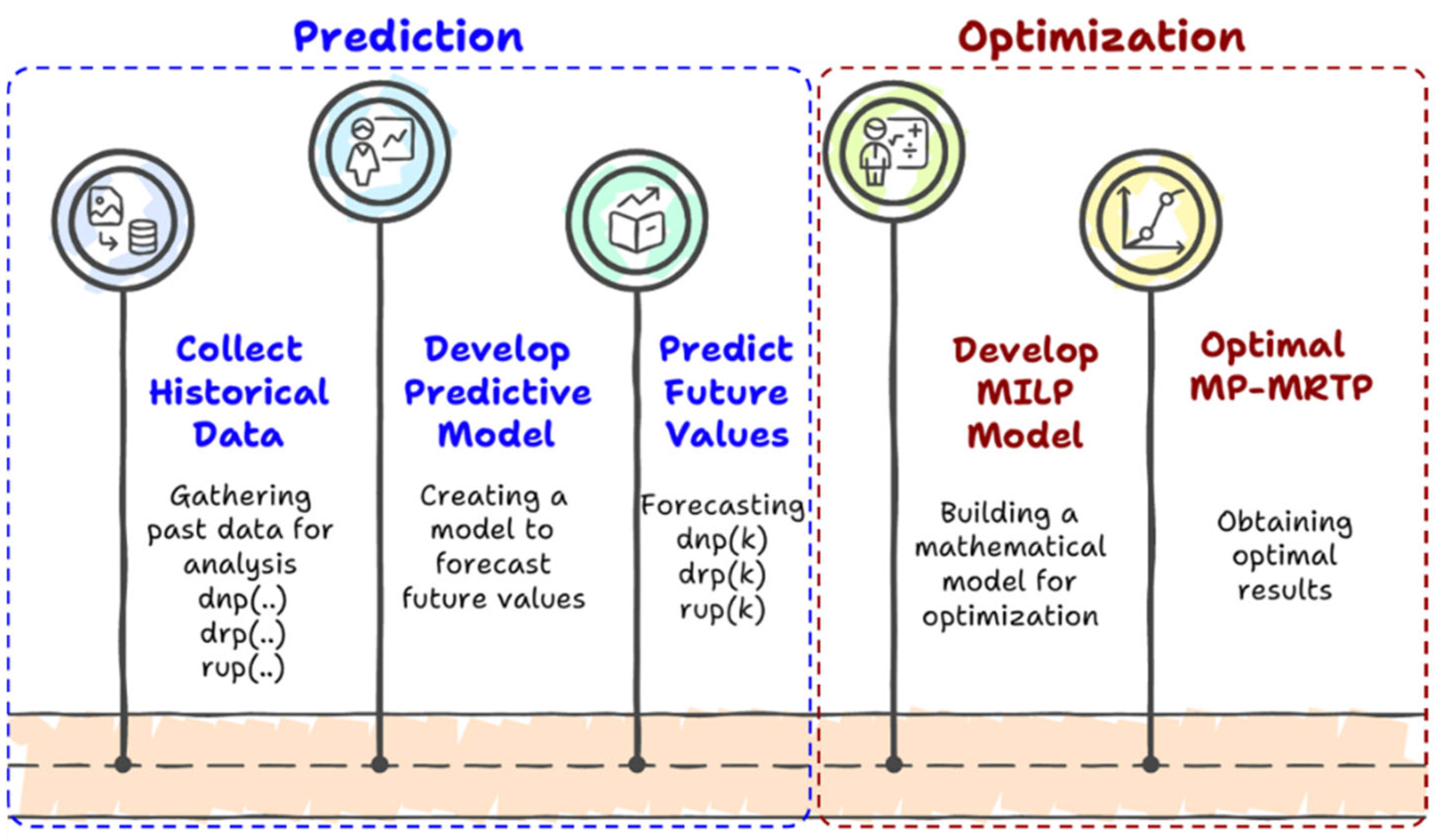
6. Prediction and Optimization Approach
6.1. Two-Stage Framework Approach
6.2. Case Study and Prediction Results
6.2.1. Case Study of an MRTSC
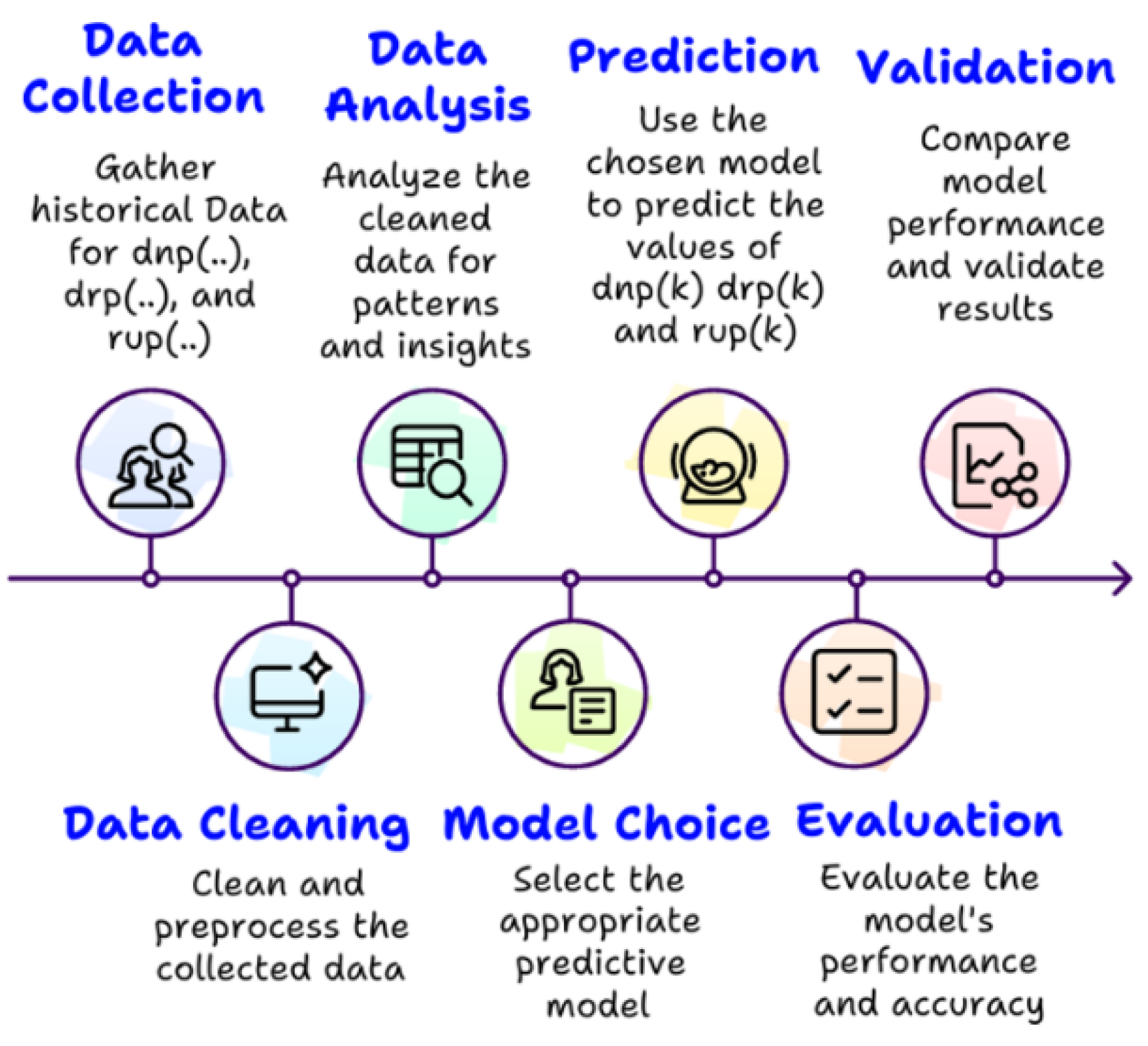
6.2.2. Prediction Results
Prediction-Based Machine Learning of Future Values of dnp(k), drp(k), and rup(k)
Data Analysis and Selection of Candidate Models
Prediction and Choice of the Best Model
- VAR algorithm
- SARIMA algorithm
- SARIMA/VAR Hybrid algorithm
- LSTM algorithm
- HWES algorithm
- -
- Level = True\None, means the model includes\not a level component.
- -
- Trend = True\None, means the model includes\not a trend component.
- -
- Seasonal = mul\add, means that her seasonality is multiplicative\additive.
- Conclusion and choice of the best model
7. Numerical Results
7.1. The System’s Performance
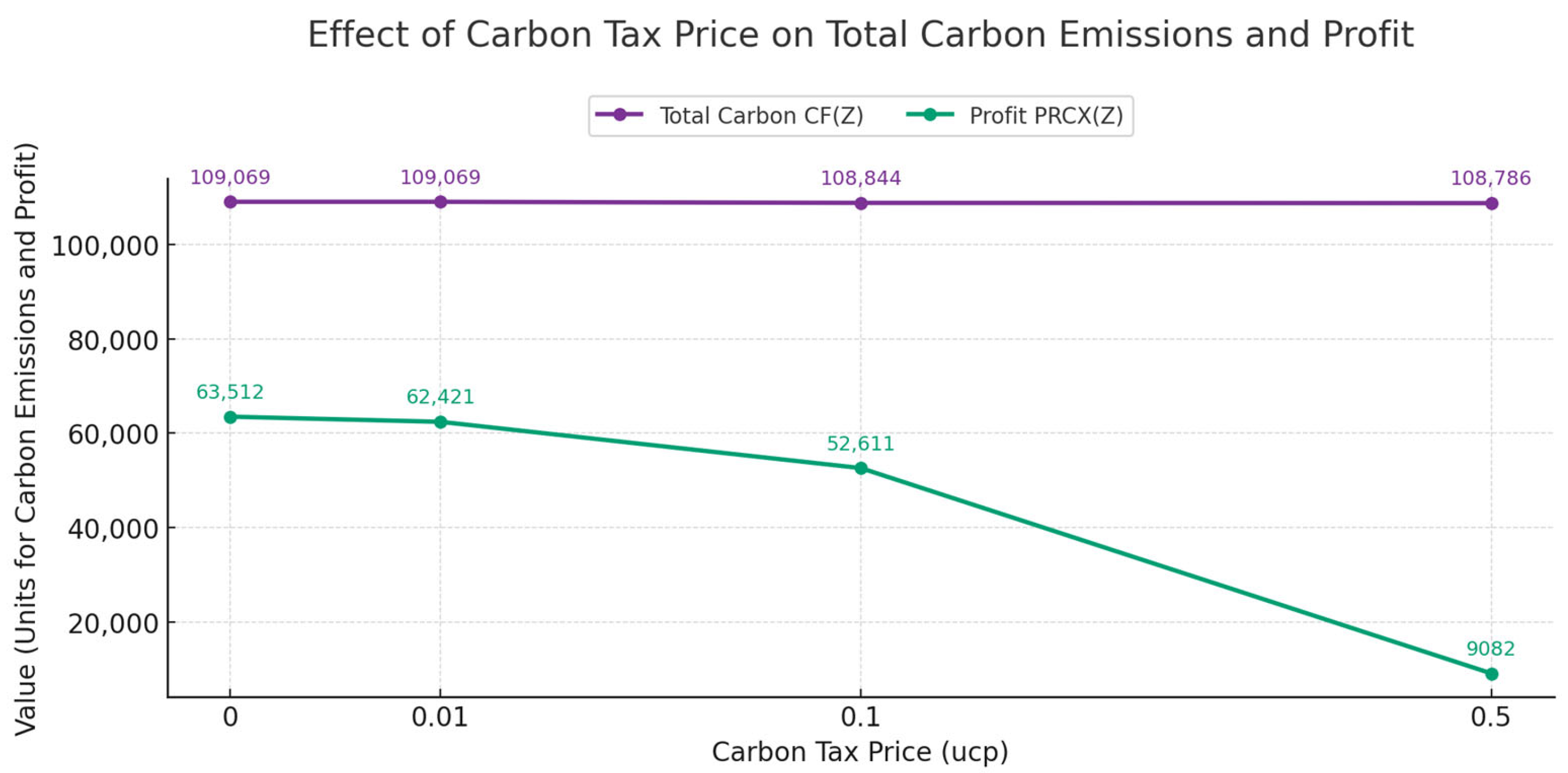
7.2. Results Based on Carbon Tax Price
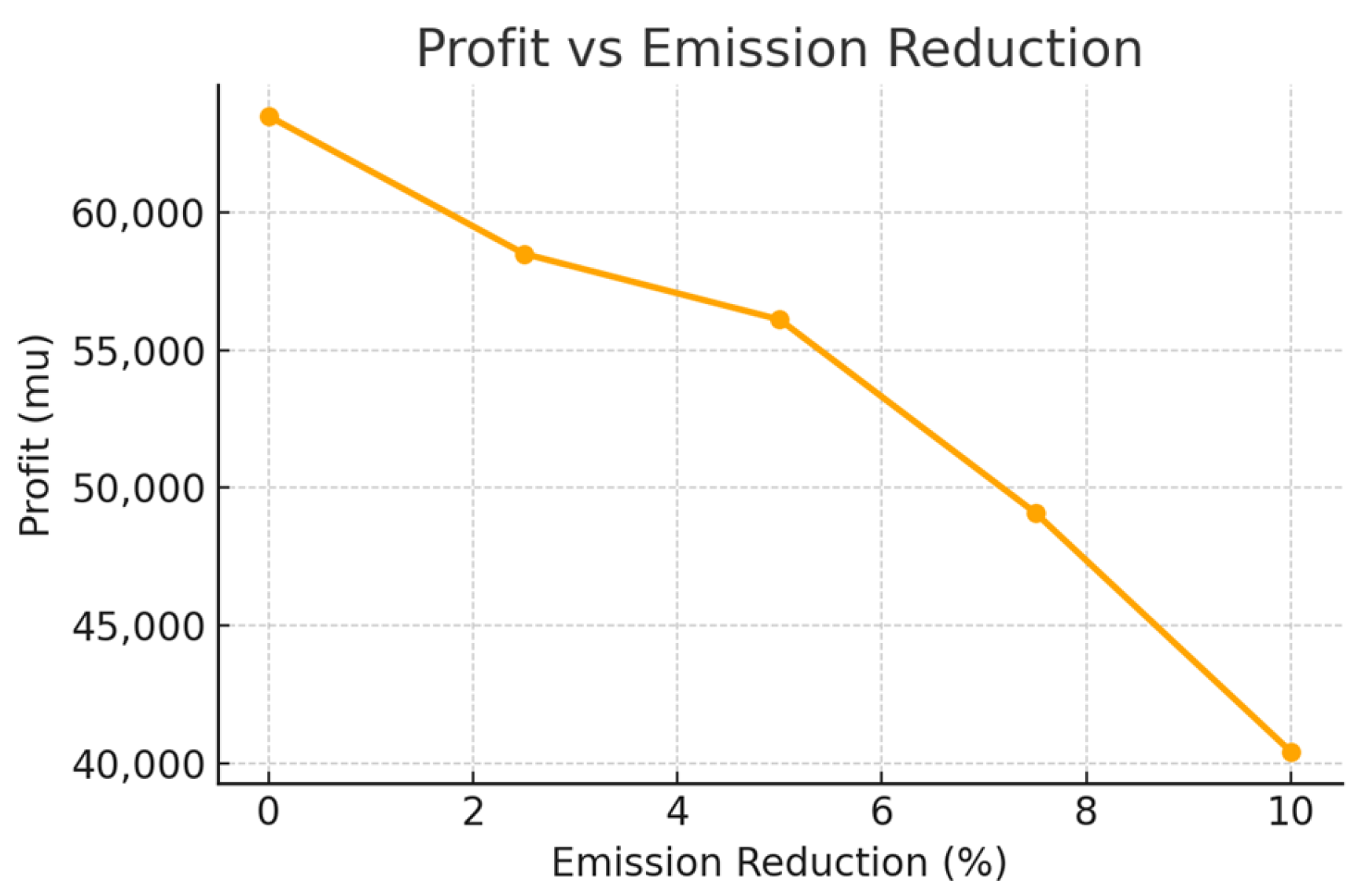
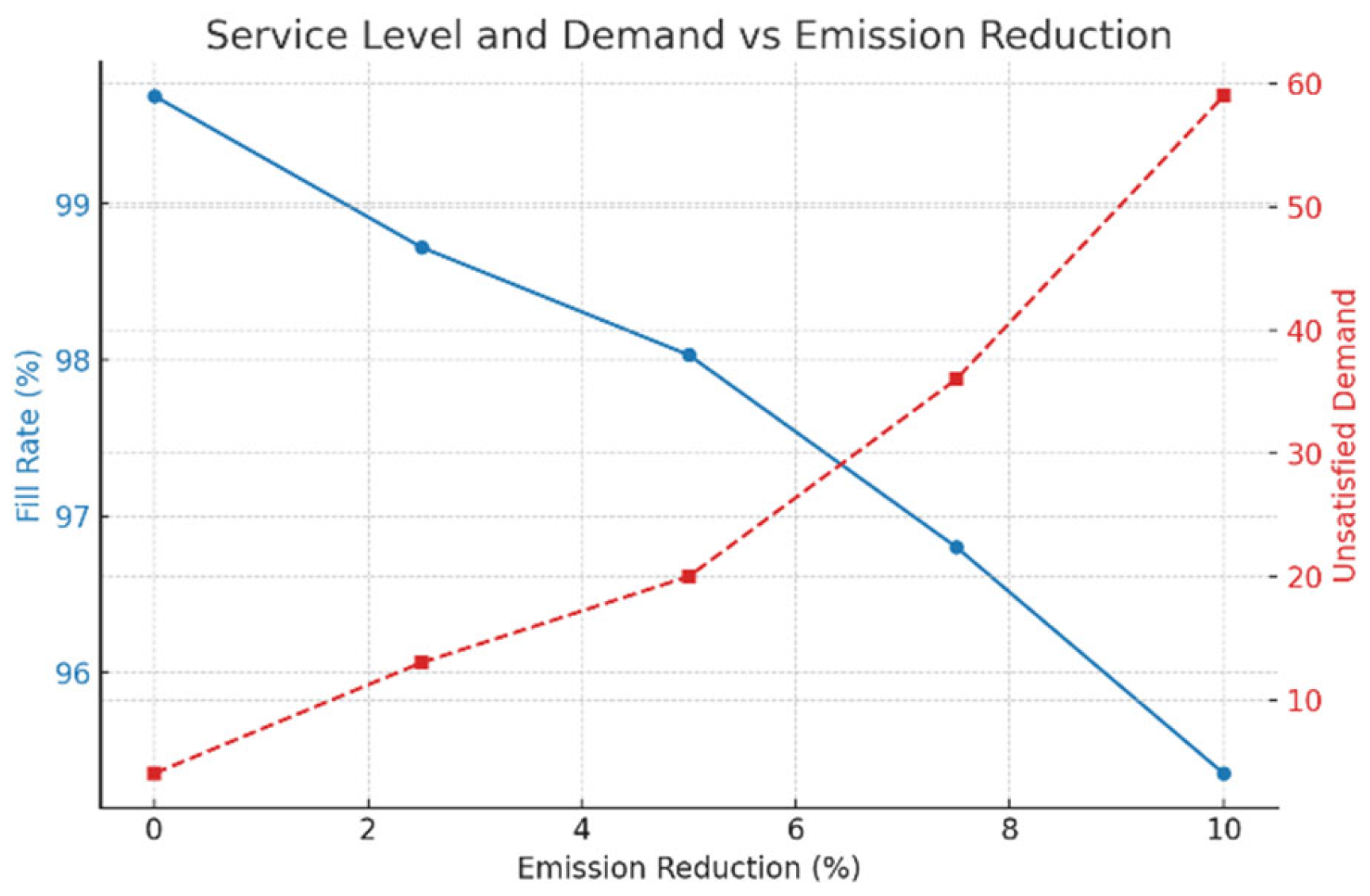
7.3. Based on Paris Agreement Limitation
7.4. Theoretical and Managerial Implications of the Model
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Additional Data and Tables
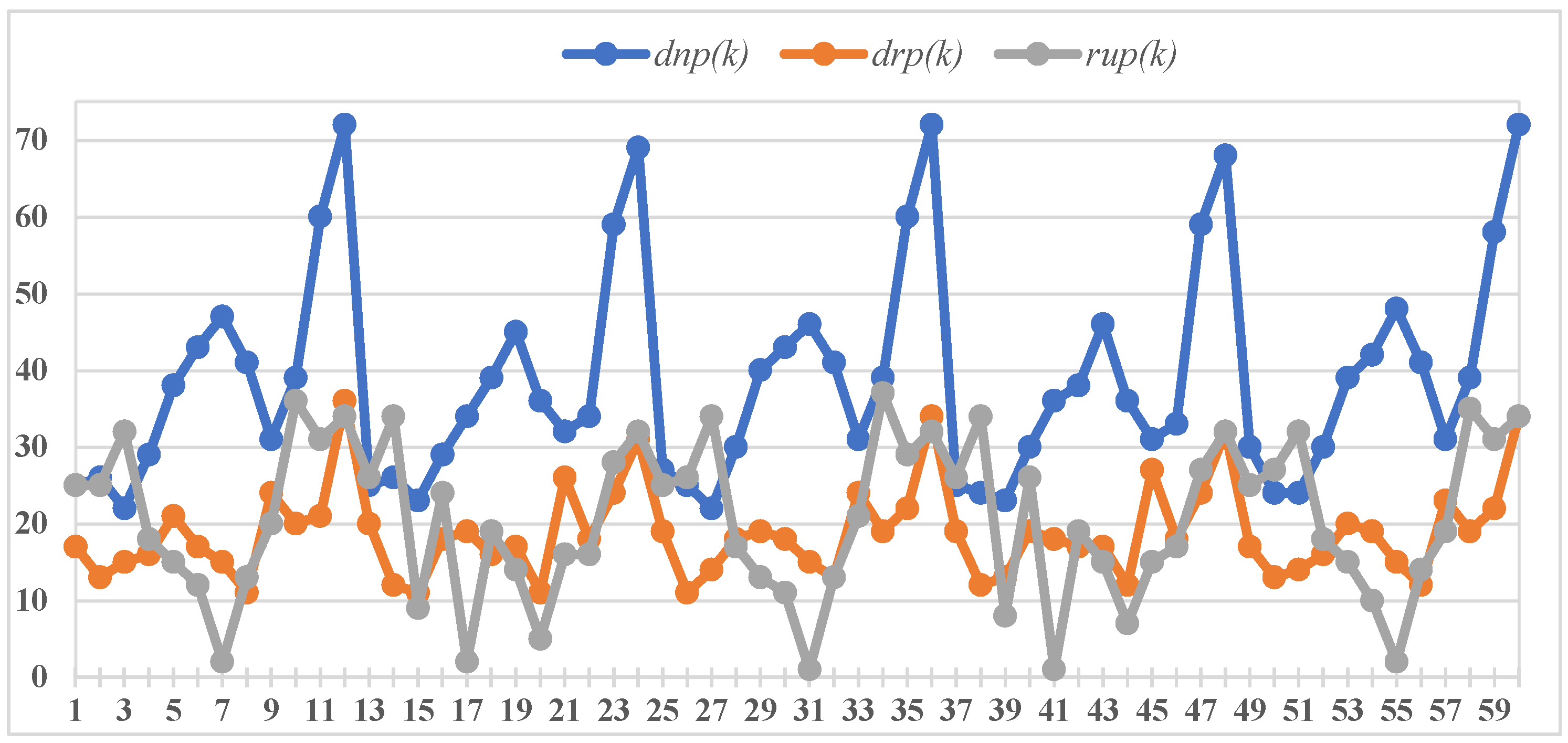
| Period | dnp(k) | drp(k) | rup(k) | Period | dnp(k) | drp(k) | rup(k) | Period | dnp(k) | drp(k) | rup(k) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 17 | 25 | 21 | 32 | 26 | 16 | 41 | 36 | 18 | 1 |
| 2 | 26 | 13 | 25 | 22 | 34 | 18 | 16 | 42 | 38 | 17 | 19 |
| 3 | 22 | 15 | 32 | 23 | 59 | 24 | 28 | 43 | 46 | 17 | 15 |
| 4 | 29 | 16 | 18 | 24 | 69 | 31 | 32 | 44 | 36 | 12 | 7 |
| 5 | 38 | 21 | 15 | 25 | 27 | 19 | 25 | 45 | 31 | 27 | 15 |
| 6 | 43 | 17 | 12 | 26 | 25 | 11 | 26 | 46 | 33 | 18 | 17 |
| 7 | 47 | 15 | 2 | 27 | 22 | 14 | 34 | 47 | 59 | 24 | 27 |
| 8 | 41 | 11 | 13 | 28 | 30 | 18 | 17 | 48 | 68 | 32 | 32 |
| 9 | 31 | 24 | 20 | 29 | 40 | 19 | 13 | 49 | 30 | 17 | 25 |
| 10 | 39 | 20 | 36 | 30 | 43 | 18 | 11 | 50 | 24 | 13 | 27 |
| 11 | 60 | 21 | 31 | 31 | 46 | 15 | 1 | 51 | 24 | 14 | 32 |
| 12 | 72 | 36 | 34 | 32 | 41 | 13 | 13 | 52 | 30 | 16 | 18 |
| 13 | 25 | 20 | 26 | 33 | 31 | 24 | 21 | 53 | 39 | 20 | 15 |
| 14 | 26 | 12 | 34 | 34 | 39 | 19 | 37 | 54 | 42 | 19 | 10 |
| 15 | 23 | 11 | 9 | 35 | 60 | 22 | 29 | 55 | 48 | 15 | 2 |
| 16 | 29 | 18 | 24 | 36 | 72 | 34 | 32 | 56 | 41 | 12 | 14 |
| 17 | 34 | 19 | 2 | 37 | 25 | 19 | 26 | 57 | 31 | 23 | 19 |
| 18 | 39 | 16 | 19 | 38 | 24 | 12 | 34 | 58 | 39 | 19 | 35 |
| 19 | 45 | 17 | 14 | 39 | 23 | 13 | 8 | 59 | 58 | 22 | 31 |
| 20 | 36 | 11 | 5 | 40 | 30 | 19 | 26 | 60 | 72 | 34 | 34 |
| Parameter Symbol | Value | Parameter Symbol | Value |
|---|---|---|---|
| Z | 24 | NP | 220 |
| Z. λ | 24 | RP | 200 |
| x | 18 | N | 160 |
| a | 75 | R | 110 |
| b | 20 | SP | 150 |
| wx | 0.1 | TRV1 | 70 |
| wa | 0.5 | TRV2 | 100 |
| wb | 0.4 | GM | 80 |
| ct | 1 | GR | 60 |
| ca | 3.5 | em | 5 carbon units |
| cb | 3 | en | 60 carbon units |
| cs | 1 | er | 10 carbon units |
| y | 15 | erm | 1 carbon units |
| sn | 400 | ewn | 2 carbon units |
| sr | 320 | ewr | 2 carbon units |
| FT1 | 500 | esc | 1 carbon units |
| FT2 | 600 | ecu | 1 carbon units |
| pn | 145 | enp | 3 carbon units |
| pr | 110 | erp | 3 carbon units |
| pv | 17 | etr | 1 carbon units |
| ucp | 0.01 | efrt1 | 2500 carbon units |
| RM | 150 | efrt2 | 2800 carbon units |
| Parameter Symbol | Value | Parameter Symbol | Value |
|---|---|---|---|
| dnp0 | 50 | wup0 | 10 |
| drp0 | 40 | scp0 | 10 |
| rup0 | 10 | inp0 | 30 |
| qrm0 | 30 | irp0 | 20 |
| mn0 | 30 | vnp0 | 50 |
| rm0 | 20 | vrp0 | 40 |
| trn0 | 30 | lnp0 | 0 |
| trr0 | 20 | lrp0 | 0 |
| tup0 | 10 | γ1(k) | 1 |
| wrm0 | 30 | γ2(k) | 0 |
| wnp0 | 20 | vup0 | 0 |
| wrp0 | 30 | CF0 | 0 |
Appendix B. Additional Results
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mn(k) | 16 | 26 | 74 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 | 0 |
| rm(k) | 0 | 15 | 26 | 0 | 15 | 33 | 0 | 34 | 6 | 32 | 32 | 0 | 25 | 0 | 34 | 0 | 26 | 0 | 43 | 0 | 23 | 31 | 0 | 0 |
| qrm(k) | 56 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 | 0 | 0 | 0 |
| trn(k) | 17 | 19 | 26 | 74 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 |
| trr(k) | 8 | 13 | 24 | 26 | 0 | 15 | 33 | 0 | 34 | 6 | 32 | 32 | 0 | 25 | 0 | 34 | 0 | 26 | 0 | 43 | 0 | 23 | 31 | 0 |
| tup(k) | 23 | 25 | 32 | 16 | 0 | 23 | 0 | 0 | 32 | 35 | 29 | 32 | 0 | 57 | 0 | 32 | 0 | 17 | 0 | 19 | 0 | 29 | 0 | 0 |
| wnp(k) | 19 | 26 | 74 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 | 0 |
| wrp(k) | 22 | 24 | 26 | 0 | 15 | 33 | 0 | 34 | 6 | 32 | 32 | 0 | 25 | 0 | 34 | 0 | 26 | 0 | 43 | 0 | 23 | 31 | 0 | 0 |
| wrm(k) | 44 | 74 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 | 0 | 0 |
| wup(k) | 33 | 43 | 49 | 65 | 50 | 40 | 40 | 6 | 32 | 35 | 32 | 64 | 39 | 96 | 62 | 94 | 68 | 85 | 42 | 61 | 38 | 36 | 36 | 36 |
| scp(k) | 23 | 25 | 32 | 16 | 13 | 23 | 0 | 13 | 32 | 35 | 29 | 32 | 25 | 57 | 8 | 32 | 0 | 17 | 14 | 19 | 14 | 29 | 27 | 57 |
| vnp(k) | 26 | 21 | 19 | 26 | 35 | 39 | 43 | 36 | 28 | 35 | 55 | 69 | 24 | 22 | 20 | 25 | 31 | 35 | 41 | 33 | 27 | 30 | 56 | 65 |
| vrp(k) | 17 | 11 | 13 | 16 | 19 | 15 | 15 | 11 | 22 | 19 | 21 | 32 | 18 | 10 | 11 | 18 | 17 | 16 | 17 | 10 | 25 | 18 | 23 | 31 |
| inp(k) | 21 | 19 | 26 | 74 | 39 | 43 | 64 | 28 | 35 | 64 | 77 | 46 | 22 | 45 | 25 | 66 | 35 | 74 | 33 | 57 | 30 | 56 | 65 | 0 |
| irp(k) | 11 | 13 | 24 | 34 | 15 | 15 | 33 | 22 | 34 | 21 | 32 | 32 | 14 | 29 | 18 | 34 | 17 | 27 | 10 | 43 | 18 | 23 | 31 | 0 |
| lnp(k) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| lrp(k) | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vup(k) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| γ1(k) | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| γ2(k) | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mn(k) | 16 | 26 | 74 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 | 0 |
| rm(k) | 0 | 15 | 26 | 0 | 15 | 33 | 0 | 34 | 6 | 32 | 32 | 0 | 25 | 0 | 34 | 0 | 26 | 0 | 43 | 0 | 23 | 31 | 0 | 0 |
| qrm(k) | 56 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 | 0 | 0 | 0 |
| trn(k) | 17 | 19 | 26 | 74 | 0 | 43 | 64 | 0 | 35 | 64 | 68 | 38 | 0 | 45 | 0 | 66 | 0 | 74 | 0 | 57 | 0 | 56 | 65 | 0 |
| trr(k) | 8 | 13 | 24 | 26 | 0 | 15 | 33 | 0 | 34 | 6 | 32 | 32 | 0 | 25 | 0 | 34 | 0 | 26 | 0 | 43 | 0 | 23 | 31 | 0 |
| tup(k) | 23 | 25 | 32 | 16 | 0 | 23 | 0 | 0 | 32 | 35 | 29 | 32 | 0 | 57 | 0 | 32 | 0 | 17 | 0 | 19 | 0 | 29 | 0 | 0 |
References
- Karim, R.; Roshid, M.M.; Waaje, A. Circular Economy and Supply Chain Sustainability. In Strategic Innovations for Dynamic Supply Chains; IGI Global: Hershey, PA, USA, 2024; pp. 1–30. [Google Scholar]
- Hajipour, V.; Kaveh, S.H.; Yiğit, F.; Gharaei, A. A multi-objective supply chain optimization model for reliable remanufacturing problems with M/M/m/k queues. Supply Chain. Anal. 2025, 10, 100118. [Google Scholar] [CrossRef]
- Cheng, F.; Jia, S.; Gao, W. Low-Carbon Logistics Distribution Vehicle Routing Optimization Based on INNC-GA. Appl. Sci. 2024, 14, 3061. [Google Scholar] [CrossRef]
- Salas-Navarro, K.; Castro-García, L.; Assan-Barrios, K.; Vergara-Bujato, K.; Zamora-Musa, R. Reverse Logistics and Sustainability: A Bibliometric Analysis. Sustainability 2024, 16, 5279. [Google Scholar] [CrossRef]
- Alkahtani, M.; Ziout, A.; Salah, B.; Alatefi, M.; Abd Elgawad, A.E.E.; Badwelan, A.; Syarif, U. An Insight into Reverse Logistics with a Focus on Collection Systems. Sustainability 2021, 13, 548. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, B.; Feng, Z.; Wang, Y.; Yan, W. A Review on Remanufacturing Reverse Logistics Network Design and Model Optimization. Processes 2021, 10, 84. [Google Scholar] [CrossRef]
- Dam, S.; Bakker, C. Between a Rock and a Hard Place. A Case Study on Simplifying the Reverse Logistics of Car Parts to Enable Remanufacturing. J. Circ. Econ. 2024, 2, 1–23. [Google Scholar]
- Mbago, M.; Ntayi, J.M.; Mkansi, M.; Namagembe, S.; Tukamuhabwa, B.R.; Mwelu, N. Implementing reverse logistics practices in the supply chain: A case study analysis of recycling firms. Mod. Supply Chain Res. Appl. 2025. ahead of print. [Google Scholar] [CrossRef]
- Muchenje, K. Green Logistics and Supply Chain Management. In Contemporary Solutions for Sustainable Transportation Practices; IGI Global: Hershey, PA, USA, 2024; pp. 33–61. [Google Scholar]
- Yin, C.; Zhang, Z.A.; Fu, X.; Ge, Y.E. A low-carbon transportation network: Collaborative effects of a rail freight subsidy and carbon trading mechanism. Transp. Res. Part A Policy Pract. 2024, 184, 104066. [Google Scholar] [CrossRef]
- Sifaoui, T.; Aïder, M. Beyond green borders: An innovative model for sustainable transportation in supply chains. RAIRO Oper. Res. 2024, 58, 2185–2237. [Google Scholar] [CrossRef]
- Abassi, B.; Turki, S.; Dellagi, S.; Bellamine, I. Low-carbon manufacturing-remanufacturing supply chain: Systematic review and bibliometric analysis. Supply Chain Forum Int. J. 2025, 204, 160–173. [Google Scholar] [CrossRef]
- Metcalf, G.E.; Stock, J.H. The Macroeconomic Impact of Europe’s Carbon Taxes. Am. Econ. J. Macroecon. 2023, 15, 265–286. [Google Scholar] [CrossRef]
- Stechemesser, A.; Koch, N.; Mark, E.; Dilger, E.; Klösel, P.; Menicacci, L.; Nachtigall, D.; Pretis, F.; Ritter, N.; Schwarz, M.; et al. Climate policies that achieved major emission reductions: Global evidence from two decades. Science 2024, 385, 884–892. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Li, H.; Shi, J. Collaborative innovation in low-carbon supply chain under cap-and-trade: Dual perspective of contracts and regulations. J. Clean. Prod. 2025, 499, 145223. [Google Scholar] [CrossRef]
- Ding, J. Design of a low carbon economy model by carbon cycle optimization in supply chain. Front. Ecol. Evol. 2023, 11, 1122682. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Yuan, Y. Research on low-carbon closed-loop supply chain strategy based on differential games-dynamic optimization analysis of new and remanufactured products. AIMS Math. 2024, 9, 32076–32101. [Google Scholar] [CrossRef]
- Mirzaee, H.; Samarghandi, H.; Willoughby, K. A robust optimization model for green supplier selection and order allocation in a closed-loop supply chain considering cap-and-trade mechanism. Expert Syst. Appl. 2022, 228, 120423. [Google Scholar] [CrossRef]
- Turki, S.; Jemmali, M.; Hidri, L. Optimal control for unreliable manufacturing and remanufacturing system under environmental subsidy and overrun penalty mechanism. IEEE Trans. Eng. Manag. 2025, 72, 1983–2002. [Google Scholar] [CrossRef]
- Mecheter, A.; Pokharel, S.; Tarlochan, F.; Tsumori, F. A multi-period multiple parts mixed integer linear programming model for AM adoption in the spare parts supply Chain. Int. J. Comput. Integr. Manuf. 2024, 37, 550–571. [Google Scholar] [CrossRef]
- Hamzaoui, A.F.; Malek, M.; Zied, H.; Sadok, T. Optimal production and non-periodic maintenance plan for a degrading serial production system with uncertain demand. Int. J. Syst. Sci. Oper. Logist. 2023, 10, 2235808. [Google Scholar] [CrossRef]
- Wang, J.; Rickman, D.; Yu, Y. Dynamics between global value chain participation, CO2 emissions, and economic growth: Evidence from a panel vector autoregression model. Energy Econ. 2022, 109, 105965. [Google Scholar] [CrossRef]
- Brucke, K.; Schmitz, S.; Köglmayr, D.; Baur, S.; Räth, C.; Ansari, E.; Klement, P. Benchmarking reservoir computing for residential energy demand forecasting. Energy Build. 2024, 314, 114236. [Google Scholar] [CrossRef]
- Wolny, M.; Kmiecik, M. Unveiling Patterns in Forecasting Errors: A Case Study of 3PL Logistics in Pharmaceutical and Appliance Sectors. Sustainability 2025, 17, 214. [Google Scholar] [CrossRef]
- Zhao, Y. E-Commerce Demand Forecasting Using SARIMA Model and K-means Clustering Analysis. J. Innov. Dev. 2024, 7, 1–6. [Google Scholar] [CrossRef]
- Falatouri, T.; Darbanian, F.; Brandtner, P.; Udokwu, C. Predictive Analytics for Demand Forecasting—A Comparison of SARIMA and LSTM in Retail SCM. Procedia Comput. Sci. 2022, 200, 993–1003. [Google Scholar] [CrossRef]
- Koohikeradeh, E.; Gumiere, S.; Bonakdari, H. NDMI-Derived Field-Scale Soil Moisture Prediction Using ERA5 and LSTM for Precision Agriculture. Sustainability 2025, 17, 2399. [Google Scholar] [CrossRef]
- Fuqua, D.; Hespeler, S. Commodity demand forecasting using modulated rank reduction for humanitarian logistics planning. Expert Syst. Appl. 2022, 206, 117753. [Google Scholar] [CrossRef]
- Ahlaqqach, M.; Elkourchi, A.; Ali Moulay, E.O. Demand Forecast of Pharmaceutical Products During COVID-19 Using Holt-Winters Exponential Smoothing. In International Conference on Artificial Intelligence & Industrial Applications; Springer Nature: Cham, Switerland, 2023; Volume 772, pp. 427–437. [Google Scholar]
- Tsigler, A.; Bartlett, P.L. Benign overfitting in ridge regression. J. Mach. Learn. Res. 2023, 24, 1–76. [Google Scholar]
- Chiquier, S.; Fajardy, M.; Dowell, N. CO2 removal and 1.5 °C: What, where, when, and how? Energy Adv. 2022, 1, 524–561. [Google Scholar] [CrossRef]
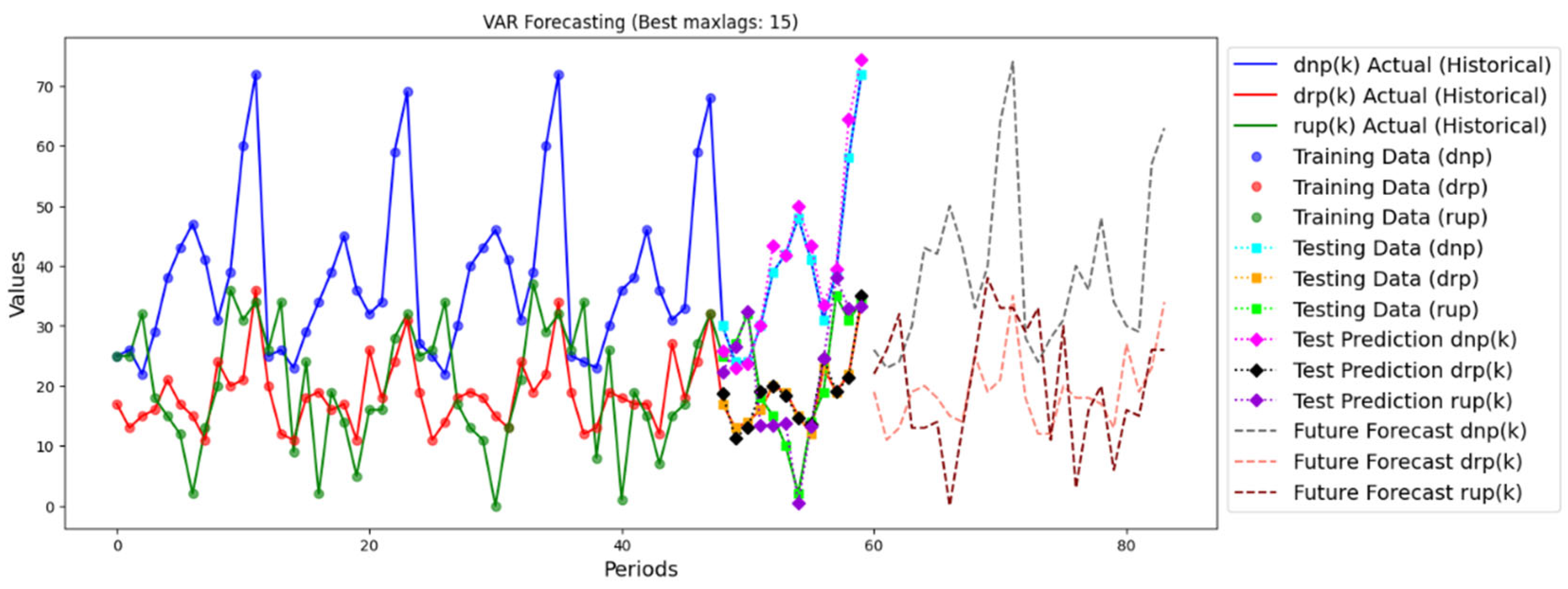
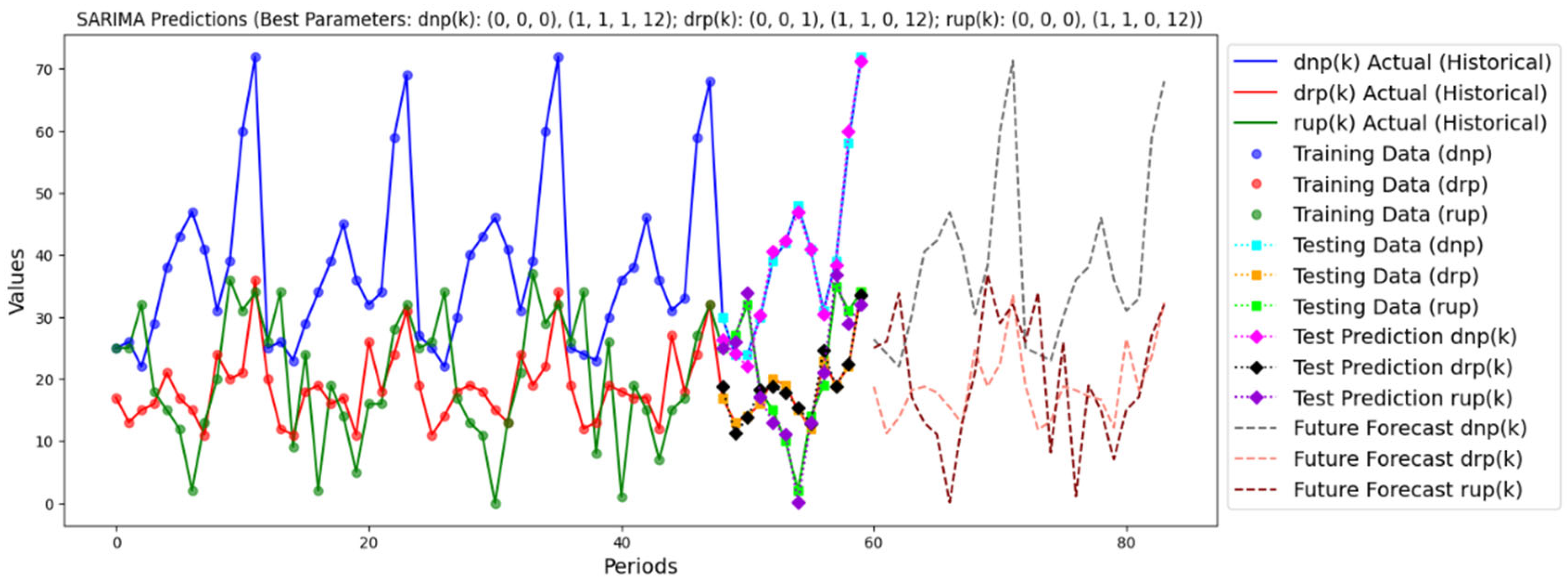
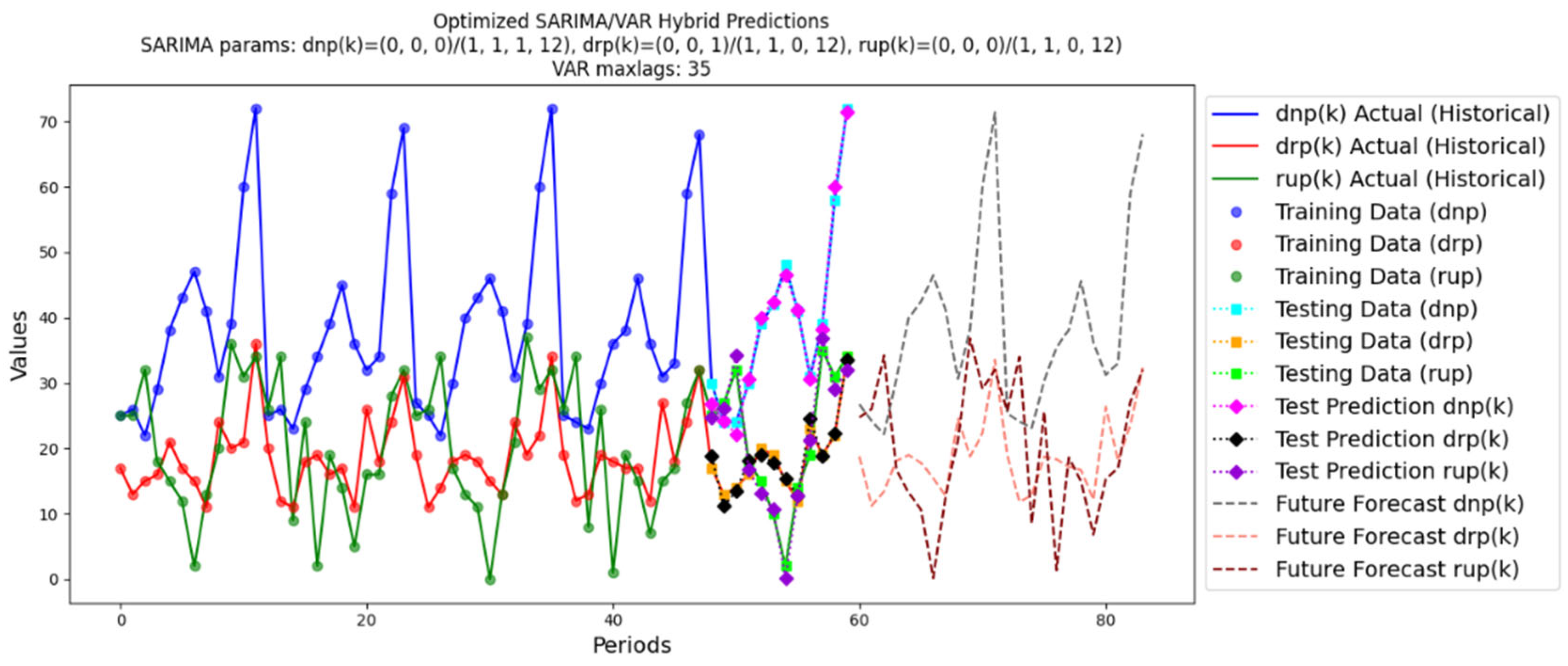
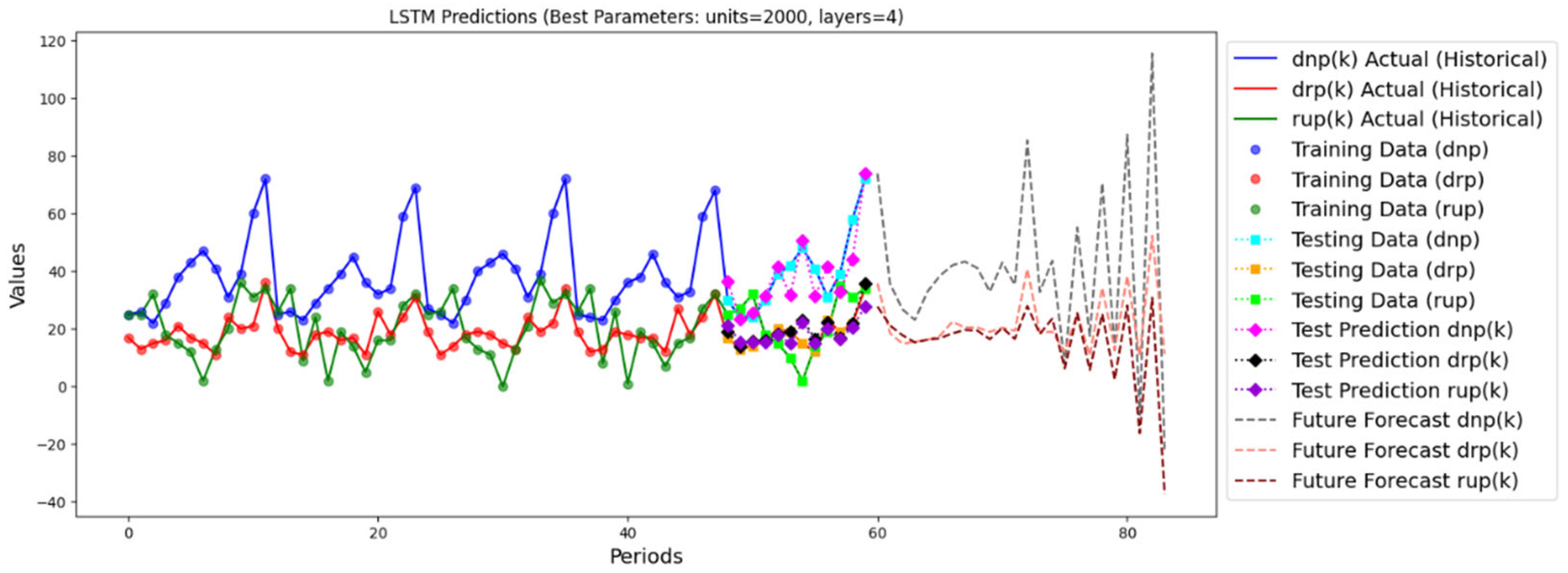
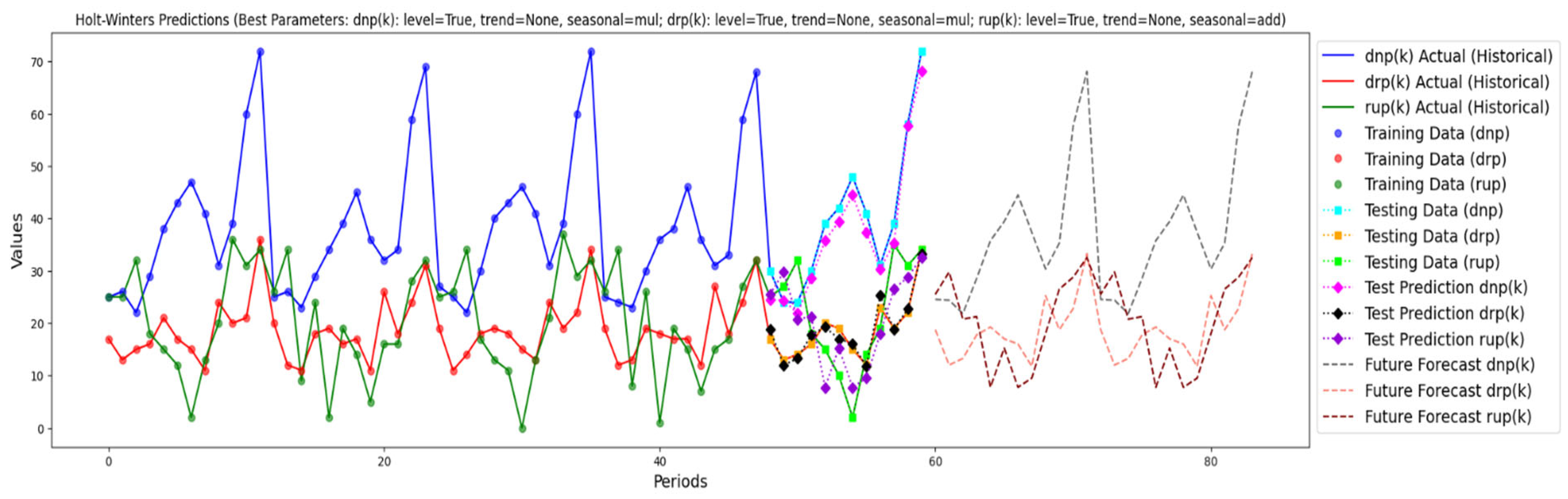
| Algorithm | MAE a | MSE b | R2 c | MAPE d |
|---|---|---|---|---|
| VAR | 1.86 | 6.01 | 0.94 | 10.08% |
| SARIMA | 1.19 | 2.07 | 0.98 | 7.76% |
| SARIMA/VAR | 1.19 | 1.99 | 0.98 | 7.61% |
| LSTM | 5.75 | 60.51 | 0.68 | 38.68% |
| HWES | 2.71 | 13.55 | 0.92 | 18.98% |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| dnp(k) a | 26 | 21 | 19 | 26 | 35 | 39 | 43 | 36 | 28 | 35 | 55 | 69 | 24 | 22 | 20 | 25 | 31 | 35 | 41 | 33 | 27 | 30 | 56 | 65 |
| drp(k) b | 17 | 11 | 13 | 16 | 19 | 17 | 15 | 11 | 22 | 19 | 21 | 34 | 18 | 10 | 11 | 18 | 17 | 16 | 17 | 10 | 25 | 18 | 23 | 31 |
| rup(k) c | 23 | 25 | 32 | 16 | 13 | 10 | 0 | 13 | 19 | 35 | 29 | 32 | 25 | 32 | 8 | 24 | 0 | 17 | 14 | 5 | 14 | 15 | 27 | 30 |
| Case | Profit PRCX(Z) | Total Carbon CF(Z) | Loss of Earnings | Total of lnp(k) a | Total of lrp(k) b | Total of lnp(k) and lrp(k) | Global Service Level (Order Fill Rate) |
|---|---|---|---|---|---|---|---|
| Without limitation | 63,512.1 | 109,069 | 0 | 0 | 4 | 4 | 99.69% |
| 2.5% reduction compared to emissions without limitation | 58,510.1 | 106,336 | 5002 | 12 | 4 | 16 | 98.74% |
| 5% reduction compared to emissions without limitation | 56,118 | 103,615 | 7394.1 | 17 | 4 | 21 | 98.35% |
| 7.5% reduction compared to emissions without limitation | 49,098.3 | 100,888 | 14,413.8 | 29 | 8 | 37 | 97.09% |
| 10% reduction compared to emission without limitation | 40,413.2 | 98,162 | 23,098.9 | 35 | 24 | 59 | 95.35% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abassi, B.; Turki, S.; Dellagi, S. Optimal Multi-Period Manufacturing–Remanufacturing–Transport Planning in Carbon Conscious Supply Chain: An Approach Based on Prediction and Optimization. Sustainability 2025, 17, 5218. https://doi.org/10.3390/su17115218
Abassi B, Turki S, Dellagi S. Optimal Multi-Period Manufacturing–Remanufacturing–Transport Planning in Carbon Conscious Supply Chain: An Approach Based on Prediction and Optimization. Sustainability. 2025; 17(11):5218. https://doi.org/10.3390/su17115218
Chicago/Turabian StyleAbassi, Basma, Sadok Turki, and Sofiene Dellagi. 2025. "Optimal Multi-Period Manufacturing–Remanufacturing–Transport Planning in Carbon Conscious Supply Chain: An Approach Based on Prediction and Optimization" Sustainability 17, no. 11: 5218. https://doi.org/10.3390/su17115218
APA StyleAbassi, B., Turki, S., & Dellagi, S. (2025). Optimal Multi-Period Manufacturing–Remanufacturing–Transport Planning in Carbon Conscious Supply Chain: An Approach Based on Prediction and Optimization. Sustainability, 17(11), 5218. https://doi.org/10.3390/su17115218







