Abstract
Limited surface energy and mass flux data hinder the understanding of glacier retreat mechanisms on the Qinghai–Tibet Plateau (QTP). Glaciers in the west Nyainqentanglha Range (WNR) supply meltwater to the densely populated Lhasa River basin (LRB) and Nam Co, the QTP’s second-largest endorheic lake. In this study, we used a glacier mass balance model based on the degree-day method (GMB-DDM) to understand the response of glacier changes to climate warming. The spatiotemporal variation in degree-day factors for ice (DDFice; plural form: DDFsice) was assessed to characterize the sensitivity of glacier melt to warming over 44 years in the WNR. Our results demonstrate that the GMB_DDM effectively captured the accelerated mass loss and regional heterogeneity of WNR glaciers from 2000 to 2020, particularly the intensified negative balance after 2014. Moreover, glacier ablation was more sensitive to warming in the WNR during 2000–2020 than 1976–2000, with DDFice increases of 21% ± 8% in the LRB and 31% ± 10% in the Nam Co basin (NCB). Increased precipitation during the ablation season and reduced glacier surface albedo can explain the increased sensitivity to warming during 2000–2020. These findings could support sustainable water resource management in the LRB, NCB, and the surrounding areas of the QTP.
1. Introduction
Known as solid reservoirs, glaciers on the Qinghai–Tibet Plateau (QTP) are melting at an accelerated rate as the climate warms [1,2]. This poses challenges to society and policymakers in dealing with changing glacier runoff contributions to downstream water supply [3]. Glacier melt contributions to runoff have increased by 12–43% in the Yarlung Zangbo River tributaries since 1997 [4]. It is therefore important to understand the sensitivity of glacier ablation to a warming climate.
The temporal heterogeneity in glacier mass balance (MB) on the QTP has become increasingly apparent. The average mass loss of Himalayan glaciers was found to have doubled between the periods of 1976–2000 and 2000–2016, using KH-9 Hexagon images and ASTER digital elevation models (DEMs) [2]. Similarly, glacier mass losses in the Kangri Karpo Mountains accelerated in the period of 1980–2015, based on DEMs derived from the 1980 topographic maps, the Shuttle Radar Topography Mission (SRTM) and the TerraSAR-X/Tandem-X [1]. In the west Nyainqentanglha Range (WNR), glacier thinning rates doubled between 2000–2013 and 2013–2020, based on the Ziyuan-3 and the SRTM DEMs [5]. And the glacier areal retreat rate has more than doubled between the two periods of 1976–2000 and 2000–2020, and surface lowering also accelerated with particularly intense melting after 2014 [6]. The possible causes include increased summer air temperatures over these decades, a potential decrease in solid precipitation (largely snowfall) on glaciers [1,7], or a change in the sensitivity of glacier melting to warming, for example, through changes in albedo, net short- and long-wave radiation, or the relative flux of sensible and latent heat fluxes [8,9].
Glacier ablation models based on empirical/statistical relationships and physical mechanisms can help explain the impact of climate warming on glacier ablation [8,10]. Physical models can reveal the process of glacier ablation in detail but also require lots of input data, usually due to higher complexity [8,11]. The statistical degree-day model employs empirical relationships between air temperature and melt rate, which are relatively simple to describe and calculate [8]. Additionally, air temperature data, compared to other meteorological parameters, are relatively easy to obtain and predict. For catchment-scale studies employing daily time steps, it was found that the degree-day model with fewer variables and less complexity could obtain similar results to those of a physical energy-balance model [8,10,12,13].
As the core parameter in the degree-day model, the degree-day factor (DDF), characterizing the sensitivity of glacier melt to warming, is a simple summation of the complex process of energy transfer and transformation on the glacier surface and its near-surface layer, and it closely links glacier change with accumulated positive air temperature (APT) [8]. The DDF varies significantly due to spatiotemporal variations in the components of the glacier energy balance [8,14]. Mihalcea et al. showed that DDFs are related to the surface topography (e.g., elevation, slope, and aspect) using observation data on the Baltoro Glacier from June to July 2004 [15]. Several studies have indicated that elevation is positively correlated with the DDF [14,15,16,17]. A positive relationship between the DDF and the thickness of the surface debris layer was found on the Khumbu Glacier from 21 May to 1 June in 1999 [18] and on the Koxkar Glacier (KG) from 2005 to 2010 [14]. Seasonal variations in DDFs for ice (DDFice; plural form: DDFsice) are less pronounced due to relatively low seasonal variation in ice surface albedo [14,16,19]. DDFice showed an increasing trend with inter-annual variation on the Sachen, Gharko, and Barpu glaciers from 2014 to 2016 [20]. Zhang et al. found that the DDFsice of glaciers in the eastern QTP were higher than those in the west, based on 15 and 40 measured glaciers from different periods, respectively [16,17]. Moreover, the DDFs for snow are considerably lower than those for ice, due to the higher albedo of snow [10,16]. Some studies about DDF assume that ice begins to melt after snow on the glacier has melted first [21,22]. Sometimes, only the total mass balance (MB) of glaciers is available, which represents the overall loss of ice and snow. Since it is difficult to distinguish between accumulation and ablation processes corresponding to snow versus ice on glaciers, the degree-day factor (DDF) is assumed to apply to a mixture of snow and ice [21]. Qiao et al. showed that the variation trend of DDFs for the mixture of ice and snow with altitude is similar to that of ice DDFs with altitude [21]. Now that net glacier MB can be measured from remote sensing data [2,6], we have an alternative approach to estimating DDFs over large regions and spanning several decades. A more detailed quantification of DDF variations is conducted to evaluate the sensitivity of glacier ablation to climate warming in high-elevation regions where detailed measurements of surface energy and mass flux are scarce.
Glacier ablation in the WNR has contributed to significant increases in water discharge to the densely populated Lhasa River basin (LRB) and the Nam Co, the second largest endorheic lake on the QTP (Figure 1) [6,23]. Due to the absence of detailed measurements of surface energy and mass flux in the WNR, a glacier mass balance model based on the degree-day model (GMB_DDM) was adopted. This model relates the observed mass changes to variations in air temperature (APT) and solid precipitation (SP) to study the response of past glacier ablation to climate warming in the WNR. We simulated the inter-and intra-annual glacier MB of the LRB and Nam Co basin (NCB) from 1976 to 2020 using GMB_DDM to explain the spatiotemporal heterogeneity of glacier MB in the WNR. In addition, the changes in the DDF for ice were obtained to quantify the sensitivity of glacier melt to warming based on the observed glacier net MBs from the 1976–2000 and 2000–2020 periods, and glacier outlines from 1976, 2000 and 2020, respectively.
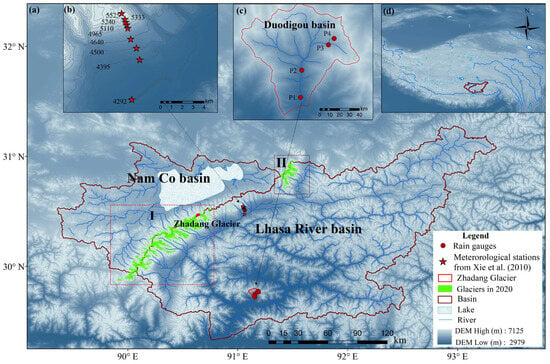
Figure 1.
The location of the study area. (a) The distribution of glaciers in the WNR. (b) The distribution of meteorological stations from [24]. (c) The distribution of rain gauges. (d) The overview map of the study area on the QTP. Label I in the large, red rectangle represents the SW section of the WNR, and Label II in the small, dark red rectangle represents the NE section. Note that DDFsice of glaciers in section II (NE WNR) for 1976–2000 are not available due to a lack of high-quality remote sensing data to extract their MB values. Therefore, only the DDFsice of glaciers in section I during 1976–2000 and 2000–2020 were studied comparatively in this study.
2. Materials and Methods
2.1. Study Area
The study area is in the WNR with an average altitude of 4930 m (Figure 1). The main ridge is 230 km from southwest to northeast, rising from 4000 m to 7162 m, with the NCB in the northwest and the LRB in the southeast [25]. The Nam Co Lake is the second largest saline lake on the QTP, and its water storage increased by 2.67 × 108 m3 a−1 during 1976–2009 [26]. The LRB, a major branch of the Yarlung Zangbo River, is one of the most densely populated areas on the QTP [27]. The region is dominated by the Indian monsoon in summer and westerlies in winter, with annual precipitation and air temperature ranging from 37 mm to 500 mm and −0.6 °C to 2.8 °C, respectively [28].
The WNR glaciers are located in the transition zone between maritime and continental mountain climates [29]. There are a total of 1022 glaciers covering 713.51 km2 (RGI 7.0) [30], and glacier melt water is an important water source for the NCB and the LRB. It was found that glaciers in the WNR experienced a more than doubling of the areal retreat rate between the two periods 1976–2000 and 2000–2020 (from −0.54 ± 0.21% a−1 to −1.17 ± 0.30% a−1), and glacier mass loss also accelerated (from −0.26 ± 0.09 to −0.37 ± 0.15 m w.e a−1), with particularly intense melting occurring after 2014. In addition, the glacier mass loss in the NCB (−0.31 ± 0.15m w.e a−1 during 1976–2000 and −0.44 ± 0.16 m w.e a−1 during 2000–2020) was more significant than in the LRB (−0.25 ± 0.10 m w.e a−1 during 1976–2000 and −0.34 ± 0.14 m w.e a−1 during 2000–2020) during the period from 1976 to 2020 [6].
2.2. Data and Methods
2.2.1. Data
- (1)
- Glacier mass balance and glacier area data
The glacier MB in the WNR during 1976–2000 and 2000–2020 and glacier area in the WNR in 1976, 2000, and 2020 were used from [6]. The glacier MB during 1976–2000 was estimated based on the declassified KH-9 images and the Shuttle Radar Topography Mission DEM (2000), and glacier MB during 2000–2020 was estimated based on the ASTER DEMs. The uncertainty of glacier MB was larger at lower and higher altitudes due to small glacier areas and lower valid image coverage. We calculated glacier MB by focusing on altitude changes in glaciers within the range of 5600–6000 m, where 75% of the total glacier area in the WNR is distributed and glacier MB has a small uncertainty range. The results, which have lower uncertainty, were close to that from all glacier altitude bins with available data in [6] (Table 1). The glacier area data in vector polygons for 1976, 2000, and 2020 were mapped from Landsat MSS/ETM+/OLI. Detailed data processing steps for glacier MB and area are presented in [6].

Table 1.
Glacier MB over the WNR from 1976 to 2020.
- (2)
- Meteorological data
We used the daily precipitation product of the Final Run V06B IMERG (IMERGV06) for 2001–2020 at a resolution of 0.1°. The IMERG products, particularly for IMERG final run product, outperform ERA5-Land precipitation in estimating precipitation amount on the QTP [31]. The IMERGV06 data are corrected by gauge data to provide research-level products with an improved ability to detect light precipitation and solid precipitation [32,33,34]. In the LRB, IMERG showed high accuracy at a monthly scale (CC = 0.92, bias = 10%) compared with dense rain gauges [35]. The IMERG data can correctly identify non-rainy days and capture the precipitation on the Gangotri Glacier in the Indian Himalayas well [36]. To extend precipitation coverage to 1976–2020, we used the ERA5-Land precipitation product (https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=form, last access: 20 March 2025) with a resolution of 0.1° [37]. We found the correlation between IMERG and ERA5-Land, for their overlapping period of 2001–2020, to be good, with a CC of 0.98, but with a bias of 48.05% (Figure 2). To correct for this bias, we calculated the difference in monthly mean precipitation at each grid cell for 2001–2020 over the study area and then used this to calibrate daily precipitation according to the amount of daily precipitation in the corresponding month.
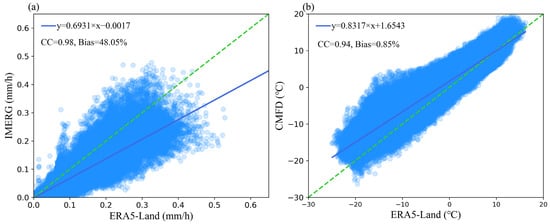
Figure 2.
Scatterplots of monthly (a) precipitation from IMERG and ERA5-Land during 2001–2020, and (b) temperature from CMFD and ERA5-Land during 1979–2018. The diagonal reference line was indicated by green dash line, and the fitting line (determined via the least- squares method) was indicated by a blue solid line.
For temperature data, China Meteorological Forcing Data at a spatial resolution of 0.1° × 0.1° and 3 h time interval for 1979–2018 were used (http://data.tpdc.ac.cn, last access: 20 March 2025) [38]. This dataset is derived from the fusion of conventional meteorological station observations of the China Meteorological Administration, Princeton reanalysis GLDAS data, and GEWEX-SRB radiation data [38,39]. We also used the 2 m temperature of ERA5-Land data with a resolution of 0.1° during 1976–1979 and 2019–2020 to extend the temperature to the period of 1976–2020. The correlation between the temperature data of ERA5-Land and China Meteorological Forcing Data has a high CC of 0.94, and a low bias of only 0.85% (Figure 2b). Hence, in this study, the slight bias was not corrected.
The area-weighted mean APT and SP of each 50 m elevation bin in the glacier region were used. We interpolated temperature into the glacier elevation zones in each 0.1° grid, based on the lapse rates of temperature with altitude. The mean monthly and annual temperature altitude lapse rates were calculated from the measured data of nine meteorological stations, with elevations ranging from 4292 m to 5525 m, during 2006–2008 and Dangxiong meteorological station during 1963–2008 at the southeast slope of the central part of the WNR (Figure 1) [24]. The monthly temperature lapse rates in summer are higher than those in winter, and the annual temperature lapse is close to the common lapse of 0.65 °C/100 m (Figure 3).
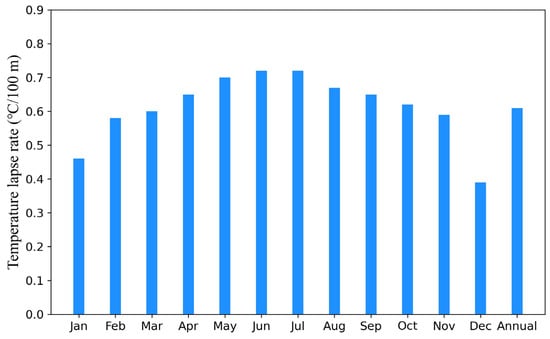
Figure 3.
The lapse rate (°C/100 m) of monthly temperature with altitude (between 4300 and 5500 m) at the southern slope of the WNR [24].
Precipitation on the QTP is more complex, although some studies have adjusted precipitation on glaciers with altitude [40]. However, we found contradictions and inconsistencies in existing observations of varying precipitation with elevation in the WNR region (see Supplementary Materials for more details). As glaciers in the WNR are mainly concentrated in the range of 5600 m to 6000 m, where precipitation measurements are rare, we chose to directly interpolate the gridded IMERGV06/ERA5 precipitation field to elevation bins of 50 m without altitude corrections to avoid the potential introduction of error.
In addition, wind speed data were from China Meteorological Forcing Data, at a spatial resolution of 0.1° × 0.1° and 3 h time interval, for 1979–2018 (http://data.tpdc.ac.cn, last access: 25 March 2025) [38] The product dataset of daily snow albedo in China from 2000 to 2020 with a spatial resolution of 0.005° was from the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn, last access: 25 March 2025) [41].
2.2.2. Methods
The Mass Balance Model Based on Degree-Day Model (GMB_DDM)
The calculation of glacier MB includes the melting of ice/snow and the accumulation of snow. The ice/snow melt is calculated using the classical degree-day model, employing Equations (1) and (2), and the mass accumulation is calculated employing Equation (3) [42]. Glacier MB is described by Equation (4) with inputs of only air temperature and precipitation.
where A is glacial accumulation (mm d−1); M is glacial ablation (mm d−1); DDFice/snow is the degree-day factor (mm d−1 °C−1) for ice/snow; APT is accumulative positive air temperature (°C); T is daily air temperature (°C); P is daily precipitation (mm d−1); and MB is mass balance (mm w.e. d−1). T0 is critical air temperature to differentiate between solid and liquid precipitation. The single critical air temperature method is widely accepted for high Asian mountains [43]. Thus, a single critical air temperature, i.e., T0 = 2 °C, was adopted, which was derived from observations of the multi-layer comprehensive observation and research station [44]. The APT corresponding to ice melting (APTice) is the total APT minus the APT corresponding to snow melting (APTsnow) [42]. In addition, DDFs for snow and ice are assumed to be related to one another to reduce the number of model parameters [12,40]. The DDF of snow is assumed to be 58% of the DDF of ice (DDFice) in the WNR [16]. During the period of 1976–2020, the glacier MB of the WNR is negative; that is, the MB equals the MB of ice (MBice). The APTice can be calculated using Equations (5) and (6).
M = DDFice/snow × APT
APT = ∑T, T > 0 °C
A = ∑P, T < T0
MB = A − M
Combining Equations (5) and (6), DDFice can be calculated as follows:
A schematic overview of the research workflow is presented in Figure 4. The monthly APT and SP of glaciers in the LRB and the NCB during 1979–2020 and MB during 1976–2000 and 2000–2020 were used to invert for the DDF. Then, we simulated the annual glacier MB using the GMB_DDM. In this study, we calculated the area-weighted mean APT and SP of each 50 m elevation bin in the LRB and the NCB. The extent of the glacier was limited, respectively, by the glacier outline in the first and last years of the corresponding period. The DDF was calculated from the mean of the area-weighted average SP and APT in the glacier area of the first and last years of the study period.
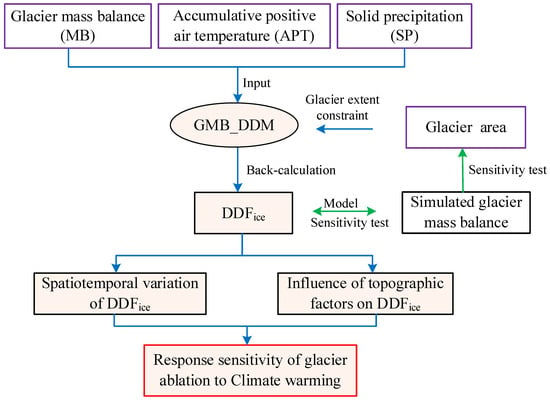
Figure 4.
Flowchart of the methodology used in this study.
For the DDF of individual glaciers, the DDF values for glaciers larger than 2 km2 were calculated. This threshold was adopted because the uncertainty associated with remotely sensed glacier mass balance (MB) estimates increases significantly as glacier size decreases. For glaciers smaller than 2 km2, the uncertainties often exceed the magnitude of the actual mass changes, which can lead to unreliable estimations of glacier mass balance [2,6]. In contrast, in the calculation of the regional DDF, the glacier mass balance was derived from elevation changes using an area-weighted approach across elevation bands, which inherently includes contributions from small glaciers [2,6]. Therefore, this threshold does not affect the overall assessment of mass changes for all glaciers in the region.
We examined the sensitivity of glacier MB to the DDFs by exchanging them between different time periods and regions. Specifically, DDFs during 2000–2020 were used to model the glacier MB during 1976–2000 in the LRB and the NCB, and vice versa. Additionally, the DDFs from the NCB were used to simulate the glacier MB in the LRB, and vice versa. The sensitivity of glacier MB to DDFs was then evaluated based on the discrepancies between the simulated MB after exchanging the DDFs and the original values.
Furthermore, it is essential to use glacier boundaries to delineate the glacier extent when extracting the DDFs for calculating APT and SP. In this study, the area-weighted mean APT and SP were extracted based on glacier boundaries from the first and last years of a specific period. The DDFs and the accumulative MB were then calculated and compared with those obtained by using the average values of APT and SP extracted with the glacier boundaries from the first and last years of the same period. This comparison was conducted to assess the sensitivity of the DDFs and the accumulative MB to changes in glacier area.
In addition, the study adopted the method of linear regression to analyze the influence of topographic features on DDFs. We set the significance level at 0.05 and considered whether DDFs changed statistically significantly with topographic features [45]. Furthermore, the Theil–Sen linear regression in robust linear regressions was used to test the possible influence of outliers [46].
Calculation of uncertainty. The uncertainty of the DDF was calculated as follows:
where δA is the uncertainty of glacial accumulation (mm d−1); δMB is the uncertainty of glacial mass balance; δAPT is the uncertainty of accumulative positive air temperature. The δMB was derived from [6]. The IMERG root mean square error (RMSE) was 6 mm, and the bias was 10% at a daily scale compared to 67 independent gauges during 2014–2017 over high mountainous tributaries in the LRB [35]. The uncertainty of daily IMERG was calculated as 0.03 mm (around 1.5% of the mean) according to Equation (9), with the RMSE and number of observations (n) [47]. The uncertainty of ERA5-Land precipitation data was 4.2%, calculated by Equation (9). Terrain had a certain influence on the accuracy of precipitation products, with lower accuracy the higher the altitude [35]. Although the accuracy of IMERG was higher than that of ERA5-Land precipitation data, and the ERA5-Land precipitation data were corrected using IMERG for system bias, we still conservatively took the uncertainty of ERA5-Land precipitation data as the uncertainty of precipitation data. For δAPT, He et al. reported that the CMFD air temperature data had good precision, with a bias of 0 °C, correlation coefficient of 0.99, and RMSE of 1 °C, compared to 40 stations during 2001–2010 [38]. The uncertainty of CMFD air temperature data was calculated as 0.16 °C according to Equation (9), which was approximately 2.4% of the average of absolute temperature values. The air temperature data of ERA5-Land was also in good agreement with CMFD in the WNR (Figure 2b). However, the assumption of a constant temperature lapse rate from 4292 m to 5525 m may not hold at very high elevations. Hence, the value of δAPT was conservatively determined as 4%.
The DDF change (ΔDDF, %) between 1976–2000 and 2000–2020 was obtained as follows:
The uncertainty of DDF change (δΔDDF, %) between 1976–2000 and 2000–2020 was obtained as follows:
3. Results
3.1. The Inverted DDFsice and GMB_DDM Simulations at Basin Scale
The inverted glacier DDFsice in the LRB were 7.15 ± 0.55 mm d−1 °C−1 during 1976–2000 and 8.62 ± 0.62 mm d−1 °C−1 during 2000–2020, respectively. Both were higher than the DDFsice in the NCB in the same period (6.02 ± 0.58 mm d−1 °C−1 during 1976–2000 and 7.88 ± 0.71 mm d−1 °C−1 during 2000–2020). However, the change rate of DDFice in the NCB (21% ± 8%) was higher than that in the LRB (31% ± 10%) (Table 2).

Table 2.
The DDFsice of glaciers in the LRB and NCB during 1976–2000 and 2000–2020 using different glacier boundaries.
The APTs in the LRB and the NCB showed an overall upward trend from 1976 to 2020, with a sharp jump in 2015, and maintained higher values from 2016 to 2020, while the SP showed a downward trend from 1976 to 2020 with lower values during 2016–2020 (Figure 5a,b). The APT in the NCB was higher than that in the LRB, and the SP in the NCB was smaller than that in the LRB. The annual glacier MBs in the LRB and the NCB fluctuated from 1976 to 2014 but were predominantly and increasingly negative in the period of 2015–2020, which corresponded to the variations in APT and SP (Figure 5).
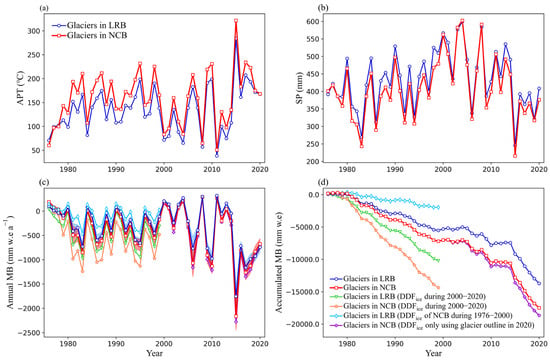
Figure 5.
The interannual variations in (a) accumulated positive air temperature (APT), (b) solid precipitation (SP), (c) mass balance (MB), and (d) accumulated MB modeled using the GMB_DDM of glaciers in the LRB and the NCB. The blue and red shadows in (c) represent the uncertainty range of the annual mass balance (MB) of glaciers in the LRB and the NCB, respectively.
Because the glacier MB data available to invert DDFice are relatively rare, the sensitivity of glacier MB to DDFice was examined (Table 3 and Figure 5). The DDFsice determined for the 2000–2020 period in the LRB and the NCB were used to retrospectively model the glacier MB for 1976–2000 in these areas. We found that the mass loss (10,215 mm w.e.) modeled in this way for the LRB glaciers was 85% greater than the observed loss (5520 mm w.e.), and that of the NCB was even 99% greater (Table 3). These discrepancies between the modeled and observed mass loss are larger than the changes in DDFsice in the LRB and NCB, i.e., ΔDDFsice of 21% and 31%, respectively. We found similar discrepancies when we used DDFsice calculated for 1976–2000 to estimate the glacier mass losses for 2000–2020. For instance, the mass loss was underestimated by 59% in the NCB (Table 3). In addition, the DDFsice of NCB and LRB were used to cross-simulate the glacier mass balance of LRB and NCB basins in the same period, and the maximum deviation reached 65%. These tests demonstrate the importance of accounting for temporal and spatial changes of DDFsice when modeling glacier mass losses.

Table 3.
The sensitivity of calculated glacier MB to the DDFice used and the sensitivity of calculated DDFsice to the glacier outline used.
Our DDFice calculations were also sensitive to the availability and accuracy of glacier outlines, which we used to limit the extent of glaciers when extracting APT and SP, but most glaciers on the QTP typically have only two sets of glacier area observations, i.e., Chinese Glacier Inventory (CGI) I and CGI II, and glacier area data of small regions in some years. To determine the error in accumulative MB estimations introduced when only one year’s glacier outline data were used to limit the extent of glaciers over the preceding 20 years, we tested the sensitivity of DDFice and accumulated MB to glacier area. The DDFice calculated with only one-year glacier extent deviated slightly (less than 4%) from the value of DDFice calculated with two-year (both the first and last years of the study period) outlines, which resulted in an accumulated MB bias lower than 11%.
3.2. The DDFsice for >2 km2 Glaciers
The DDFsice for glaciers with an area larger than 2 km2 were inverted for the periods of 1976–2000 and 2000–2020. During 1976–2000 and 2000–2020, the changes in DDFsice of all glaciers were spatially similar, with the northeast being the highest, followed by the central part, and then the southwest (Figure 6). The DDFice during 2000–2020 was significantly higher than that during 1976–2000, especially for glaciers in the red rectangle in Figure 6. The DDFice values varied greatly among different glaciers, e.g., 2.61–21.23 mm d−1 °C−1 during 1976–2000 and 3.06–19.38 mm d−1 °C−1 during 2000–2020. The maximum DDFsice were almost eight times and six times greater than the minimum values, with variation coefficients of 0.39 and 0.31, respectively, during 1976–2000 and 2000–2020. Compared with the period of 1976–2000, the spatial heterogeneity of DDFsice was smaller during 2000–2020.

Figure 6.
The distribution of DDFsice for glaciers (>2 km2) in the WNR from (a) 1976 to 2000 and (b) 2000 to 2020. The red box indicates the region with larger DDFsice.
Moreover, the relationship between DDFsice and the topographical attributes, e.g., elevation, slope, aspect, area, longitude, and latitude, were examined (Figure 7). During the periods of 1976–2000 and 2000–2020, we found that the DDFsice were significantly positively correlated with mean longitude and latitude (p < 0.01). DDFsice increased significantly with elevation during 1976–2000, but not significantly during 2000–2020. While DDFsice decreased significantly with the increase in slope in 2000–2020, this relationship was not significant in 1976–2000. There were no significant correlations between DDFsice and the glacier mean aspect and area. To test the possible influence of outliers, the robust Theil–Sen linear regression was adopted, and it was found that the linear change trends of DDFsice with altitude, slope, longitude, and latitude were consistent with the trend of least-squares linear regression.
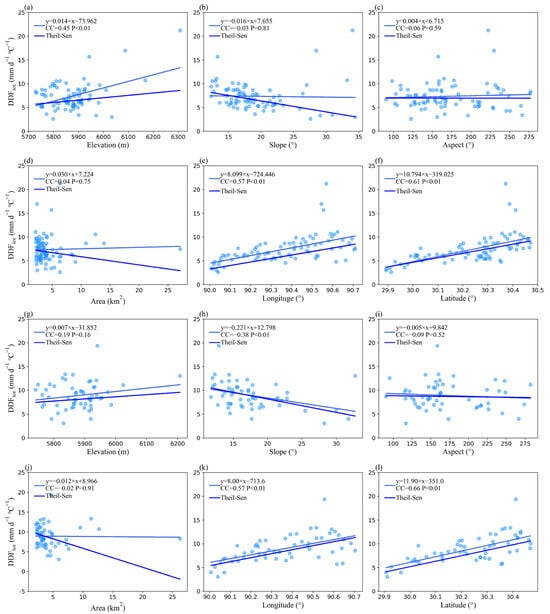
Figure 7.
The scatterplot of DDFsice (a–f) during 1976–2000, and (g–l) during 2000–2020, versus mean elevation, slope, aspect, area, longitude, and latitude.
4. Discussion
4.1. Uncertainty
In this study, DDFice uncertainty was calculated mainly from three aspects, including glacier MB, precipitation, and temperature data. Among these, the large uncertainty in geodetic glacier MB data significantly affected the uncertainty of DDFice. As shown in Equation (8), the uncertainty contributed by glacier mass balance was explicitly included in the calculation. Without considering the uncertainty associated with precipitation and temperature data, this component accounts for approximately 68–89% of the total uncertainty. The accuracy of these data needs significant improvement, although an increasing amount of geodetic glacier MB data can help calibrate the spatial variability of glacier DDFsice [40,48].
We selected IMERG precipitation and CMFD temperature data with higher accuracy in the study area and extended the data series with ERA5-Land data (see Section 2.2.2 for details). The ERA5-Land precipitation data were corrected for systematic bias when extending the data series, which may have also introduced further errors. In addition, terrain has a certain influence on the accuracy of precipitation products, with lower accuracy at higher altitudes [35,49]. Additionally, using air temperature gradients calculated from a small amount of observed temperature data in mid- to high-altitude areas to interpolate temperature data in high-altitude regions could also introduce errors. At present, this part of error is inevitable due to the scarcity of observations in high-altitude areas [48,50,51].
In addition, determining the critical air temperature for distinguishing between rain and snow might introduce errors. This study adopts a critical air temperature of 2 °C from the observation station near the glacier area [44]. In addition, the primary focus of this paper is on the relative changes in DDFsice over the 20 years around the year 2000, which are less dependent on the threshold temperature.
Although the GMB_DDM is an empirical approach, it remains widely used in glacier melt studies due to its simplicity, computational efficiency, and relatively low data requirements [8]. It has proven particularly valuable in data-scarce regions, such as high mountain areas, where detailed energy balance measurements are often lacking or impractical to obtain [12,13]. In this context, the model provides a practical means of estimating glacier ablation and assessing its response to climate change over long time scales. However, we acknowledge that empirical models like the degree-day method have limitations in capturing the full complexity of physical processes driving glacier ablation [8]. More sophisticated, physically based energy-balance models could offer deeper insights into these mechanisms by explicitly accounting for factors such as radiation, turbulent heat fluxes, and subsurface ice melt [11]. We therefore suggest that future research should aim to incorporate energy-balance modeling approaches when improved observational datasets become available.
4.2. Response of Glacier Ablation in the WNR to Climate Warming
The broad patterns of glacier MB on the QTP are controlled by regional atmospheric circulation [52], but the changes in precipitation and air temperature within this region cannot always fully explain observed glacier changes on this scale [1,29]. The simulated results presented here offer a good explanation for the spatiotemporal heterogeneity of glacier change in the WNR from 1976 to 2020, through the effects of APT and SP. The results of the GMB_DDM also show that glaciers’ APT in the LRB and NCB had a sharp jump in 2015 and maintains higher values from 2016 to 2020, while SP maintains lower values during 2016–2020. These changes combined to cause strongly negative annual glacier MB values in 2015, which remains strongly negative from 2016 to 2020. This supports a suggestion by [6] of particularly intense melting in the WNR after 2014. Within the WNR, it showed slightly greater warming over glaciers in the LRB than in the NCB and a slightly greater precipitation increase in the NCB than in the LRB. Weather stations on the north and south sides show a similar warming trend in the ablation season and accumulation season, but an unremarkable variation trend of precipitation. This suggests that it is difficult to explain a more negative glacier MB in the NCB than that in the LRB [6]. However, The APT in the NCB is higher than that in the LRB and the SP in the NCB is lower than that in the LRB, which could clearly explain that the more negative glacier MB in the NCB than that in the LRB.
4.3. The Influences Topographic Factors on DDFsice
We found a spatial diversity of glacier DDFsice during both 1976–2000 and 2000–2020 in the WNR. The main reason for the variation of DDFsice is the differences in relative importance of individual components providing energy for melt, since energy balance characteristics vary considerably in space and time [10]. DDFsice increase with altitude and solar radiation, and as surface albedo declines [8,10]. In the regions where solar radiation plays a dominant role in glacier ablation, topographic factors have a significant controlling effect on DDFsice. We found that DDFsice are positively correlated with altitude, longitude, and latitude but are uncorrelated with aspect and glacier area (Figure 7).
The DDFice and glacier melt rates typically increase as incident solar radiation increases [53]. Many studies have shown that the value of DDFsice increases with elevation on the QTP [11,14,16], which is similar to our findings. This correlation may be explained by solar radiation increasing with elevation as atmospheric absorption decreases. Typically, the southern aspect of a mountain also receives the most direct solar radiation, as do glaciers at lower latitudes. And hence, in radiation-dominant ablation regimes, more southernly aspects and lower latitudes correlate positively with DDFsice, while longitude shows a weak correlation. However, DDFsice in the WNR show no correlations with aspect, and a positive correlation with both increased latitude and longitude. A similar correlation with latitude and longitude has been reported more broadly for High Mountain Asia by [17]. This may be explained because variations in ablation with latitude and longitude (as well as aspect) are often strongly affected by related local variables such as cloud cover, surface albedo, altitude, air temperature, precipitation, and wind speed [53,54]. Figure 8 shows that there is less precipitation in ablation season in the southwest WNR compared with the northeast WNR, which means less sensible and latent heat released by rainfall. This could explain why the DDFsice showed a positive correlation with both increased latitude and longitude.
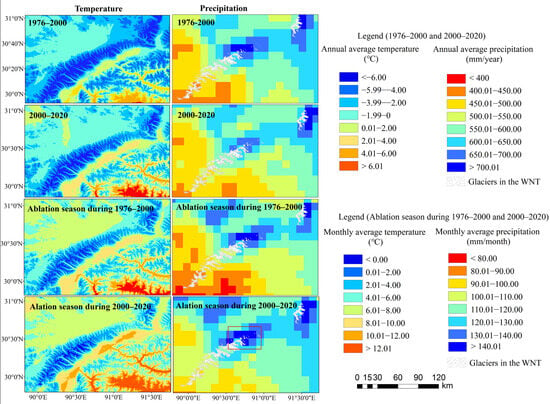
Figure 8.
Annual mean air temperature and precipitation and monthly mean air temperature and precipitation during ablation season (June to September) in the WNR during 1976–2000 and 2000–2020. The red box indicates the region with significantly higher precipitation.
During 1976–2000 and 2000–2020, the glacier DDFsice in the LRB are higher than those in the NCB (Table 2). Average altitude in the NCB is lower than that in the LRB [6]. As mentioned above, the DDFsice are small when the altitude is lower. Moreover, high air temperature and speed lead to high sensible heat flux, and high shares of sensible heat flux density to the heat of melt are related to low DDFsice [55]. APT and wind speed in the NCB are higher than that in the LRB (Figure 5 and Figure 9), which shows higher sensible heat flux in the NCB than that in the LRB. The higher shares of sensible heat flux density to the heat of melt could explain the lower DDFsice in the NCB. Qiao et al. also showed that the lower DDFsice are related to higher air temperatures and lower altitudes [21].
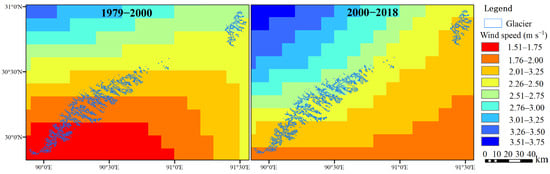
Figure 9.
Annual mean surface wind speed in the WNR during 1976–2000 and 2000–2020.
4.4. Increasing Sensitivity of Glaciers Ablation to APT
Based on observations of the Zhadang Glacier on the southeast slope of the WNR from June to September 2007 and July to September 2008, Wu et al. reported that the DDFs of the Zhadang Glacier for ice and snow were 9.2 mm d−1 °C−1 and 5.3 mm d−1 °C−1, respectively [44]. In this study, the DDFice and DDFsnow for the Zhadang Glacier were 8.28 mm d−1 °C−1 and 4.80 mm d−1 °C−1 respectively, which are lower than that reported by [44]. This might be caused by the difference in time scales. Furthermore, the mean DDFsice in the LRB and the NCB were 7.15 ± 0.55 mm d−1 °C−1 and 6.02 ± 0.58 mm d−1 °C−1 during 1976–2000, increasing to 8.62 ± 0.62 mm d−1 °C−1 and 7.88 ± 0.71 mm d−1 °C−1, respectively, during 2000–2020 (Table 2). These values are within the range (from 5.94 to 16.9 mm d−1 °C−1) of ten measured glaciers in the Yarlung Zangbo River basin [56], indicating that our results are consistent with observational data from similar regions.
The DDFsice of glaciers in the NCB and LRB become higher between 2000 and 2020 compared to that during 1976–2000, which means the sensitivity of glacier ablation in the WNR to APT has increased. A similar phenomenon was reported by Wu et al. based on the Sachen, Gharko, and Barpu glaciers from 2014 to 2016 [20]. Glacier melting is determined by the energy balance at the glacier–atmosphere interface, which is controlled by the physical properties of the glacier itself and the meteorological conditions above it [8].
The possible reason for increasing sensitivity of glaciers ablation to APT is that the characteristics of the ice surface change due to the increasing black carbon and dust [57,58]. By processing the snow albedo data (white sky albedo and black sky albedo) during 2000–2020 in the study area, it was found that both white sky albedo and black sky albedo tend to decrease at high altitudes and increase at low altitudes (Figure 10). The white sky albedo and black sky albedo in the study area decreased at average rates of 0.00036 and 0.00039 per year, respectively, during 2000–2020. Although the average annual decrease in albedo is small, the cumulative effect over long time scales may be large. In addition, Qu et al. also showed that an increase in black carbon and dust led to a decrease in albedo for the Zhadang Glacier (in the NCB) during 2001–2012 [58].
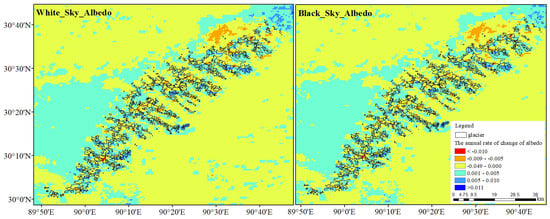
Figure 10.
The change in albedo in the study area during 2000–2020.
Another possible reason may be the increase in ablation season precipitation in the 2000–2020 period (Figure 8), because glacier melting can be particularly intense under warm and wet conditions [59,60]. The increased precipitation depicted in the red rectangle in Figure 8 (Ablation season during 2000–2020) corresponds geographically to the higher DDFsice in the WNR highlighted in the red rectangle in Figure 6. Sensible and latent heat released by rainfall increases snow and ice ablation; however, the empirical GMB_DDM cannot simulate this process. Rainfall also makes the snow on the surface of the glacier wetter and the snow grains bigger, reducing surface albedo and driving an increase in absorption of downwelling shortwave radiation, further promoting melting [61,62]. In addition, decreasing wind would increase the glacier melt in the whole of eastern and southern TP [63]. However, we found that in the WNR region, the average surface wind speeds during the 2000–2020 period are slightly larger than that during the 1976–2000 period (Figure 8 and Figure 9). The increased sensitivity of glaciers to APT had little to do with surface wind speed in the WNR. Due to the lack of data, it is difficult to analyze changes in the net downward solar radiation, net longwave radiation, cloud cover, humidity, and resultant turbulent heat fluxes over the period of 1976–2020, which needs further study.
4.5. Implications of Glacier Ablation Changes for Water Resource Sustainability
Miles et al. reported that around 40 ± 11% of glacier ablation across High Mountain Asia is currently unsustainable, indicating that glacier-fed basins such as the Ganges–Brahmaputra system will face growing water stress in dry months in the coming decades [64]. Glacier melt in the WNR contributes approximately 8.5 ± 4.6% of the annual runoff in the upper Yangbajain Basin—a headwater region highly dependent on glacial sources. This contribution, although smaller at the basin scale (1.6 ± 1.0% for the entire LRB), remains significant during dry or pre-monsoon seasons when other water sources are limited [6,65]. These results emphasize the seasonal importance of glacier meltwater in maintaining streamflow, especially under increasing climatic variability. In the Nam Co Basin, glacier runoff accounts for about 30.9 ± 15.4% of the observed lake level rise during 1976–2014 [6], underscoring its influence on regional hydrology and lake ecosystem stability.
We found that glacier ablation has become more sensitive to warming during 2000–2020 compared to the earlier period (1976–2000), as evidence by a 21~31% increase in the DDFice. This increased sensitivity implies that future warming may further intensify seasonal water availability while reducing long-term reliability. This has direct implications for sustainable development, particularly in agricultural and urban areas reliant on predictable water supply.
Our findings highlight the critical role of glacier meltwater in sustaining water availability in high-altitude regions, particularly in the LRB and NCB, which support both ecological systems and human communities [3,6]. Under ongoing climate change, glaciers are retreating at an accelerated pace, altering hydrological regimes and posing long-term risks to water security [6]. These findings call for integrated basin-scale monitoring systems and adaptive water governance strategies that can account for changing cryospheric inputs and manage trade-offs between upstream and downstream users.
5. Conclusions
Based on the glacier MB over the periods 1976–2000 and 2000–2020 and glacier outlines from 1976, 2000 and 2020 in the WNR, we modeled retrospectively the interannual glacier MB during 1976–2020 to explain the spatial and temporal heterogeneity of glacier MB in the WNR with SP and APT. In addition, we analyzed spatial and temporal variations in DDFsice of glaciers at the basin scale and for the population of individual glaciers to analyze the sensitivity of glacier ablation to warming. Our main conclusions are as folows:
- (1)
- The temporal and spatial heterogeneity of WNR glacier changes, particularly the intensified negative MB after 2014 revealed using remote sensing data, can be well explained by the GMB_DDM model through the effects of ablation season warming (APT) and reductions in snowfall (SP).
- (2)
- DDFsice of glaciers in both the LRB and NCB during 2000–2020 are higher than that during 1976–2000, and the change rate of DDFice in the NCB (31% ± 10%) is higher than that in the LRB (21% ± 8%) from 1976–2000 to 2000–2020. Glacier ablation in the WNR is more sensitive to climate warming during 2000–2020 than 1976–2000, which may be caused by the increase in precipitation during ablation season and the decrease in glacier surface albedo. DDFsice in the LRB are higher than that in the NCB during both 1976–2000 and 2000–2020. We find that substantial errors in modeled regional MB could arise if DDFsice are held constant through time, without allowing for the changes that we observe.
- (3)
- The spatial pattern of DDFsice of individual glaciers remains similar between 1976–2000 and 2000–2020, but the DDFsice vary greatly within this population, with maximum values eight and six times greater than minimum values for the 1976–2000 and 2000–2020 periods, respectively. DDFsice are positively correlated with elevation, longitude, and latitude in the same region during 1976–2000 and 2000–2020, but uncorrelated with aspect and glacier area.
- (4)
- Glacier meltwater plays a vital role in sustaining water resources in high-altitude regions such as the LRB and NCB, which are essential for both ecological stability and human livelihoods. The accelerated rapid glacier retreat under ongoing climate change is altering hydrological patterns and threatening long-term water security. These changes highlight the urgent need for integrated, basin-scale monitoring systems and adaptive water governance frameworks that can account for changing cryospheric inputs and manage trade-offs between upstream and downstream users.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su17115143/s1, Table S1. Measured precipitation at four rainfall stations distributed with increasing altitude in 2019 and 2020 in the southern LRB. References [66,67] are cited in the Supplementary Materials.
Author Contributions
Conceptualization, S.W. and J.L.; methodology, S.W., H.D.P. and W.Q.; software, S.W., X.S. and X.Q.; validation, H.D.P. and J.L.; formal analysis, S.W.; data curation, S.W.; writing—original draft preparation, S.W.; writing—review and editing, H.D.P. and J.L.; visualization, S.W. and J.Z.; supervision, J.L. and H.D.P.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Second Tibetan Plateau Scientific Expedition and Research Program (STEP, Ministry of Science and Technology, MOST, grant number 2019QZKK0207-2), the National Natural Science Foundation of China (NSFC, grant number 92047301), the Science and Technology Program of Gansu Province, grant number 25JRRA200, Youth Science Foundation of Lanzhou Jiaotong University, grant number 202435, and the Science and Technology Program of Gansu Province, grant number 22JR11RA143.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wu, K.; Liu, S.; Jiang, Z.; Xu, J.; Wei, J.; Guo, W. Recent Glacier Mass Balance and Area Changes in the Kangri Karpo Mountains from DEMs and Glacier Inventories. Cryosphere 2018, 12, 103–121. [Google Scholar] [CrossRef]
- Maurer, J.M.; Schaefer, J.M.; Rupper, S.; Corley, A. Acceleration of Ice Loss across the Himalayas over the Past 40 Years. Sci. Adv. 2019, 5, eaav7266. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Gao, M.; Liu, J.; Wang, J.; Wang, S.; Chen, X.; Liu, H. Understanding the Effects of Climate Warming on Streamflow and Active Groundwater Storage in an Alpine Catchment: The Upper Lhasa River. Hydrol. Earth Syst. Sci. 2020, 24, 1145–1157. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Liu, J.; Hu, Q. Changes of Precipitation-Runoff Relationship Induced by Climate Variation in a Large Glaciated Basin of the Tibetan Plateau. J. Geophys. Res. Atmos. 2021, 126, e2020JD034367. [Google Scholar] [CrossRef]
- Ren, S.; Menenti, M.; Jia, L.; Zhang, J.; Zhang, J.; Li, X. Glacier Mass Balance in the Nyainqentanglha Mountains between 2000 and 2017 Retrieved from ZiYuan-3 Stereo Images and the SRTM DEM. Remote Sens. 2020, 12, 864. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J.; Pritchard, H.D.; Ke, L.; Qiao, X. Characterizing Four Decades of Accelerated Glacial Mass Loss in the West Nyainqentanglha Range of the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2023, 27, 933–952. [Google Scholar] [CrossRef]
- Ke, L.; Song, C.; Yong, B.; Lei, Y.; Ding, X. Which Heterogeneous Glacier Melting Patterns Can Be Robustly Observed from Space? A Multi-Scale Assessment in Southeastern Tibetan Plateau. Remote Sens. Environ. 2020, 242, 111777. [Google Scholar] [CrossRef]
- Hock, R. Glacier Melt: A Review of Processes and Their Modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W.; Xia, J.; Shen, Y.; Kang, S. Study of Degree-Day Model from 2000 to 2016: The Main Progress and Key Issues. J. Glaciol. Geocryol. 2017, 39, 801–810. (In Chinese) [Google Scholar]
- Hock, R. Temperature Index Melt Modelling in Mountain Areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Li, H. Spatial and Temporal Transferability of Degree-Day Model and Simplified Energy Balance Model: A Case Study. Sci. Cold Arid. Reg. 2020, 12, 95–103. [Google Scholar]
- Huss, M.; Hock, R. A New Model for Global Glacier Change and Sea-Level Rise. Front. Earth Sci. 2015, 3, 1–22. [Google Scholar] [CrossRef]
- Kraaijenbrink, P.D.A.; Bierkens, M.F.P.; Lutz, A.F.; Immerzeel, W.W. Impact of a Global Temperature Rise of 1.5 Degrees Celsius on Asia’s Glaciers. Nature 2017, 549, 257–260. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Han, H.; Kang, S. The Temporal and Spatial Variation of Positive Degree-Day Factors on the Koxkar Glacier over the South Slope of the Tianshan Mountains, China, from 2005 to 2010. Sci. Cold Arid. Reg. 2017, 9, 425–431. [Google Scholar]
- Mihalcea, C.; Mayer, C.; Diolaiuti, G.; Lambrecht, A.; Smiraglia, C.; Tartari, G. Ice Ablation and Meteorological Conditions on the Debris-Covered Area of Baltoro Glacier, Karakoram, Pakistan. Ann. Glaciol. 2006, 43, 292–300. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Ding, Y. Observed Degree-Day Factors and Their Spatial Variation on Glaciers in Western China. Ann. Glaciol. 2006, 43, 301–306. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Wang, X. A Dataset of Spatial Distribution of Degree-Day Factors for Glaciers in High Mountain Asia. China Sci. Data 2019, 4, 1–10. [Google Scholar] [CrossRef]
- Kayastha, R.B.; Takeuchi, Y.; Nakawo, M.; Ageta, Y. Practical Prediction of Ice Melting beneath Various Thickness of Debris Cover on Khumbu Glacier, Nepal, Using a Positive Degree-Day Factor. In Symposium at Seattle 2000–Debris-Covered Glaciers; IAHS Publication: Wallingford, UK, 2000; Volume 264, pp. 71–81. [Google Scholar]
- Braithwaite, R.J.; Olesen, O.B. Seasonal Variation of Ice Ablation at the Margin of the Greenland Ice Sheet and Its Sensitivity to Climate Change, Qamanarssup Sermia, West Greenland. J. Glaciol. 1993, 39, 267–274. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Gao, H.; Zou, X.; Wazir, M.A. Variation of Degree-Day Factors and Its Affecting Factorsin the Upper Indus Basin. Arid. Zone Res. 2020, 37, 264–274. [Google Scholar] [CrossRef]
- Qiao, C.; He, X.; Ye, B. Study of the Degree-Day Factors for Snow and Ice on the Dongkemadi Glacier, Tanggula Range. J. Glaciol. Geocryol. 2010, 32, 257–264. (In Chinese) [Google Scholar]
- Laumann, T.; Reeh, N. Sensitivity to Climate Change of the Mass Balance of Glaciers in Southern Norway. J. Glaciol. 1993, 39, 656–665. [Google Scholar] [CrossRef]
- Zhu, L.P.; Xie, M.P.; Wu, Y.H. Quantitative Analysis of Lake Area Variations and the Influence Factors from 1971 to 2004 in the Nam Co Basin of the Tibetan Plateau. Chinese Sci. Bull. 2010, 55, 1294–1303. [Google Scholar] [CrossRef]
- Xie, J.; Liu, J.; Mingyuan, D.; Kang, S.; Wang, K. Analysis of the Observation Results of Temperature and Precipitation over an Alpine Mountain, the Lhasa River Basin. Progress. Geogr. 2009, 28, 223–230. (In Chinese) [Google Scholar]
- Yao, T.D.; Li, Z.G.; Yang, W.; Guo, X.J.; Zhu, L.P.; Kang, S.C.; Wu, Y.H.; Yu, W.S. Glacial Distribution and Mass Balance in the Yarlung Zangbo River and Its Influence on Lakes. Chinese Sci. Bull. 2010, 55, 2072–2078. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhu, L.; Wang, J.; Li, J.; Chen, D. Estimation and Trend Detection of Water Storage at Nam Co Lake, Central Tibetan Plateau. J. Hydrol. 2011, 405, 161–170. [Google Scholar] [CrossRef]
- Luo, W.; Zhang, G.; Chen, W.; Xu, F. Response of Glacial Lakes to Glacier and Climate Changes in the Western Nyainqentanglha Range. Sci. Total Environ. 2020, 735, 139607. [Google Scholar] [CrossRef]
- Yu, W.; Yao, T.; Kang, S.; Pu, J.; Yang, W.; Gao, T.; Zhao, H.; Zhou, H.; Li, S.; Wang, W.; et al. Different Region Climate Regimes and Topography Affect the Changes in Area and Mass Balance of Glaciers on the North and South Slopes of the Same Glacierized Massif (the West Nyainqentanglha Range, Tibetan Plateau). J. Hydrol. 2013, 495, 64–73. [Google Scholar] [CrossRef]
- Li, G.; Lin, H. Recent Decadal Glacier Mass Balances over the Western Nyainqentanglha Mountains and the Increase in Their Melting Contribution to Nam Co Lake Measured by Differential Bistatic SAR Interferometry. Glob. Planet. Change 2017, 149, 177–190. [Google Scholar] [CrossRef]
- Consortium R 7.0 Randolph Glacier Inventory—A Dataset of Global Glacier Outlines, Version 7.0; NSIDC National Snow and Ice Data Center: Boulder, CO, USA, 2023.
- Wu, X.; Su, J.; Ren, W.; Lü, H.; Yuan, F. Statistical Comparison and Hydrological Utility Evaluation of ERA5-Land and IMERG Precipitation Products on the Tibetan Plateau. J. Hydrol. 2023, 620, 129384. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Le, M. Evaluation of Profile Classification Module of GPM-DPR Algorithm after Launch. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5174–5177. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, D.; Qin, Z.; Zheng, Y.; Guo, J. Assessment of the GPM and TRMM Precipitation Products Using the Rain Gauge Network over the Tibetan Plateau. J. Meteorol. Res. 2018, 32, 324–336. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Wang, S.; Liu, J.; Wang, J.; Qiao, X.; Zhang, J. Evaluation of GPM IMERG V05B and TRMM 3B42V7 Precipitation Products over High Mountainous Tributaries in Lhasa with Dense Rain Gauges. Remote Sens. 2019, 11, 2080. [Google Scholar] [CrossRef]
- Verma, P.; Ghosh, S.K. Study of GPM-Imerg Rainfall Data Product for Gangotri Glacier. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2018, 42, 383–388. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1950 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2019. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-land?tab=overview (accessed on 20 March 2025).
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The First High-Resolution Meteorological Forcing Dataset for Land Process Studies over China. Sci. Data 2020, 7, 1–11. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C.K. On Downward Shortwave and Longwave Radiations over High Altitude Regions: Observation and Modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Rounce, D.R.; Hock, R.; Shean, D.E. Glacier Mass Change in High Mountain Asia Through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 2020, 7, 1–20. [Google Scholar] [CrossRef]
- Xiao, P.; Hu, R.; Zhang, Z.; Qin, S. China Daily Snow Albedo Product Data Set (2000–2020); National Tibetan Plateau Data Center: Lanzhou, China, 2022. [Google Scholar]
- Braithwaite, R.J.; Zhang, Y. Sensitivity of Mass Balance of Five Swiss Glaciers to Temperature Changes Assessed by Tuning a Degree-Day Model. J. Glaciol. 2000, 46, 7–14. [Google Scholar] [CrossRef]
- Chen, R.S.; Liu, J.F.; Song, Y.X. Precipitation Type Estimation and Validation in China. J. Mt. Sci. 2014, 11, 917–925. [Google Scholar] [CrossRef]
- Wu, Q.; Shichang, K.; Yongjun, Z.; Gao, T. The Characteristics of the Positive Degree-Day Factors of the Zhadang Glacieron the Nyaingentanglha Range of Tibetan Plateau, and Its Application. J. Glaciol. Geocryol. 2010, 32, 891–897. (In Chinese) [Google Scholar]
- Uyanık, G.K.; Güler, N. A Study on Multiple Linear Regression Analysis. Procedia Soc. Behav. Sci. 2013, 106, 234–240. [Google Scholar] [CrossRef]
- Idochi, O.; Jude, O.; Amarachi, O.; Uwabunkonye, B. Parametric Versus Non-Parametric Simple Linear Regression on Data with and Without Outliers. Int. J. Innov. Sci. Math. 2016, 4, 175–180. [Google Scholar]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling High-Altitude Precipitation in the Upper Indus Basin with Glacier Mass Balances and Runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shrestha, A.B.; Bierkens, M.F.P. Climate Change Impacts on the Upper Indus Hydrology: Sources, Shifts and Extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Tang, G.; Long, D.; Yong, B.; Zhong, L.; Wan, W.; Hong, Y. Similarity and Error Intercomparison of the GPM and Its Predecessor-TRMM Multisatellite Precipitation Analysis Using the Best Available Hourly Gauge Network over the Tibetan Plateau. Remote Sens. 2016, 8, 569. [Google Scholar] [CrossRef]
- Li, D.; Yang, K.; Tang, W.; Li, X.; Zhou, X.; Guo, D. Characterizing Precipitation in High Altitudes of the Western Tibetan Plateau with a Focus on Major Glacier Areas. Int. J. Climatol. 2020, 40, 5114–5127. [Google Scholar] [CrossRef]
- Liu, L.; Gu, H.; Xie, J.; Xu, Y.P. How Well Do the ERA-Interim, ERA-5, GLDAS-2.1 and NCEP-R2 Reanalysis Datasets Represent Daily Air Temperature over the Tibetan Plateau? Int. J. Climatol. 2021, 41, 1484–1505. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different Glacier Status with Atmospheric Circulations in Tibetan Plateau and Surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Pokhrel, P. The Study of Temporal and Spatail Variability of Degree Day Factor of Snowmelt in Colorado. Master’s Thesis, University of North Texas, Denton, TX, USA, 2016. [Google Scholar]
- Han, H.; WangJ, I.; Wang, X.; Zhang, P. Study of the Positive Degree-Day Factor of Ice Cliff Ablation in Debris-Covered Area of the Koxkar Glacier. J. Glaciol. Geocryol. 2009, 31, 620–627. (In Chinese) [Google Scholar]
- Ambach, W. Interpretation of the Positive-Degree-Days Factor by Heat Balance Characteristics—West Greenland. Nord. Hydrol. 1988, 19, 217–224. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, W. Spatial Variability in Degree-Day Factors in Yarlung Zangbo River Basin in China. J. Univ. Chin. Acad. Sci. 2018, 35, 704–711. (In Chinese) [Google Scholar]
- Ming, J.; Cachier, H.; Xiao, C.; Qin, D.; Kang, S.; Hou, S.; Xu, J. Black Carbon Record Based on a Shallow Himalayan Ice Core and Its Climatic Implications. Atmos. Chem. Phys. 2008, 8, 1343–1352. [Google Scholar] [CrossRef]
- Qu, B.; Ming, J.; Kang, S.C.; Zhang, G.S.; Li, Y.W.; Li, C.D.; Zhao, S.Y.; Ji, Z.M.; Cao, J.J. The Decreasing Albedo of the Zhadang Glacier on Western Nyainqentanglha and the Role of Light-Absorbing Impurities. Atmos. Chem. Phys. 2014, 14, 11117–11128. [Google Scholar] [CrossRef]
- Li, Y.; Ding, Y.; Shangguan, D.; Wang, R. ScienceDirect Regional Differences in Global Glacier Retreat from 1980 to 2015. Adv. Clim. Change Res. 2020, 10, 203–213. [Google Scholar] [CrossRef]
- Oerlemans, J.; Fortuin, J.P.F. Sensitivity of Glaciers and Small Ice Caps to Greenhouse Warming. Science 1992, 258, 115–117. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Nakawo, M.; Hashimoto, S.; Sakai, A. Preferential Exchange Rate Effect of Isotopic Fractionation in a Melting Snowpack. Hydrol. Process 2008, 22, 3734–3740. [Google Scholar] [CrossRef]
- Zhou, S.; Nakawo, M.; Hashimoto, S.; Sakai, A. The Effect of Refreezing on the Isotopic Composition of Melting Snowpack. Hydrol. Process 2008, 22, 873–882. [Google Scholar] [CrossRef]
- Qi, W.; Feng, L.; Kuang, X.; Zheng, C.; Liu, J.; Chen, D.; Tian, Y.; Yao, Y. Divergent and Changing Importance of Glaciers and Snow as Natural Water Reservoirs in the Eastern and Southern Tibetan Plateau. J. Geophys. Res. Atmos. 2022, 127, 1–20. [Google Scholar] [CrossRef]
- Miles, E.; McCarthy, M.; Dehecq, A.; Kneib, M.; Fugger, S.; Pellicciotti, F. Health and Sustainability of Glaciers in High Mountain Asia. Nat. Commun. 2021, 12, 2868. [Google Scholar] [CrossRef]
- Pritchard, H.D. Asia’s Shrinking Glaciers Protect Large Populations from Drought Stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef]
- Xie, J. Distribution of Water and Heat in Lhasa River Basin and Its Hydrological Effects. Doctoral Dissertation, Graduate School of Chinese Academy of Sciences, Beijing, China, 2010. [Google Scholar]
- Zhou, S.; Kang, S.; Chen, F.; Joswiak, D.R. Water Balance Observations Reveal Significant Subsurface Water Seepage from Lake Nam Co, South-Central Tibetan Plateau. J. Hydrol. 2013, 491, 89–99. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).