Research on Composite Robot Scheduling and Task Allocation for Warehouse Logistics Systems

Abstract

With the rapid development of e-commerce, warehousing and logistics systems are facing the dual challenges of increasing order processing demand and green and low-carbon transformation. Traditional manual and single-robot scheduling methods are not only limited in efficiency, but will also make it difficult to meet the strategic needs of sustainable development due to their high energy consumption and resource redundancy. Therefore, in order to respond to the sustainable development goals of green logistics and resource optimization, this paper replaces the traditional mobile handling robot in warehousing and logistics with a composite robot composed of a mobile chassis and a robotic arm, which reduces energy consumption and labor costs by reducing manual intervention and improving the level of automation. Based on the traditional contract net protocol framework, a distributed task allocation strategy optimization method based on an improved genetic algorithm is proposed. This framework achieves real-time optimization of the robot task list and enhances the rationality of the task allocation strategy. By combining the improved genetic algorithm with the contract net protocol, multi-robot multi-task allocation is realized. The experimental results show that the improvement strategy can effectively support the transformation of the warehousing and logistics system to a low-carbon and intelligent sustainable development mode while improving the rationality of task allocation.

1. Introduction

With the advancement of technology and the enhancement of global environmental awareness, robotic technology in the warehousing and logistics field has achieved significant accomplishments, enhancing operational efficiency and transforming traditional logistics operation models, and has also provided technical support for the realization of green supply chain management [1]. However, as global freight volumes increase and market demands become more complex, early robots have gradually revealed functional limitations, and they have difficulty meeting the ever-growing demands [2], which has gradually become a bottleneck restricting the sustainable development of the logistics industry. To address this challenge, researchers have developed advanced automated guided vehicles (AGVs) that navigate precisely using electromagnetic or optical technologies and efficiently transport items after receiving instructions [3]. When they encounter obstacles, AGVs can intelligently identify and navigate around them, ensuring that operations are efficient and safe, thereby reducing the labor intensity for workers and improving the efficiency of logistics processes [4], reducing resource waste and reducing carbon emissions. Wurman [5] and others developed the KIVA SYSTEM warehouse management system, which addresses the logistics needs of small civilian goods. This system consists of over 500 autonomous mobile robots, significantly improving warehouse efficiency, reducing the reliance on human labor, and enhancing the convenience and efficiency of warehouse management [6].

1.1. Introduction to Composite Robots

As warehousing scenarios transition to “small batch, multiple batches, and high timeliness”, the limitations of traditional AGVs are becoming more apparent. Traditional AGVs only support standardized pallet handling, unable to meet flexible demands such as piece picking and sorting of irregular packages [7]. When humans and AGVs work together, waiting time accounts for more than 30% (e.g., human picking delays AGV return). The annual growth rate of labor costs is 8–12%, while AGVs can only replace manual labor in the transport segment. Composite robots, composed of robotic arms, AGVs, and vision systems, can break through these bottlenecks with their integrated “perception–decision–execution” capabilities [8].

There are significant differences in hardware architecture and function implementation between traditional AGVs and composite robots (which integrate AGVs and robotic arms). Traditional AGVs typically consist of navigation modules, chassis drive systems, and batteries, with the core function of transporting standardized goods (such as pallets and full boxes) along preset paths. However, their operation process relies on humans to complete actions like grabbing and placing goods, forming a “transport–human sorting–transport” broken process [9]. Composite robots achieve full-process automation of “perception–grabbing–transport–placing” by integrating high-degree-of-freedom robotic arms, vision sensors, or force control sensors with AGV chassis. The robotic arm can identify irregular goods through the vision system [10] and use force control technology to achieve flexible grabbing, overcoming the limitation of traditional AGVs that can only transport fixed carriers.

In terms of efficiency, for example, a traditional AGV warehousing system with three operators and three traditional AGVs working together requires humans to handle shelf picking (20 s per pick) and sorting operations, while AGVs only execute shelf transport tasks. The speed of human operations is limited by proficiency and requires coordination with AGVs (e.g., waiting for human operations after AGVs are in place), resulting in a comprehensive efficiency of 80–100 pieces per hour, with efficiency further decreasing due to human fatigue. If three composite robots and one supervisor are deployed, robots autonomously complete shelf positioning, grabbing (5–8 s per piece), transport, and sorting processes through visual recognition, with humans only intervening in grabbing exceptions. The efficiency advantage is reflected in parallel operations (simultaneous robotic arm grabbing and AGV transport, eliminating waiting time) and 24 h continuous operation capability, increasing comprehensive efficiency to 300–400 pieces per hour, with robotic arm grabbing speed reaching 4–6 times that of humans, completely breaking through human–machine collaboration bottlenecks.

Composite robots enhance warehousing operation efficiency to 3–4 times that of traditional AGV systems through mechatronics and intelligent perception technologies, reducing labor demand by over 60%. Their advantages in flexibility and multi-task compatibility provide an efficient and sustainable solution for the unmanned upgrade of high-complexity warehousing scenarios [11], helping the logistics industry transform to a green supply chain management model.

1.2. Research Content

The functions of AGVs are relatively limited, primarily focusing on the transportation and handling of goods. They lack adaptability to complex environments and the flexibility for multitasking. With the increasing complexity of logistics demands, composite robots have emerged. These composite robots not only possess the basic handling functions of AGVs but also integrate various advanced technologies, such as visual recognition, artificial intelligence, and deep learning, enabling them to make autonomous decisions and perform intelligent operations in dynamic and complex environments. With their flexibility, multifunctionality, and efficiency, composite robots bring significant improvements and advantages to warehouse logistics systems [12]. The composite robot used in this article consists of a CR5 robotic arm (produced by Dobot Robotics in Shenzhen, China) and a P4M21 mobile chassis (produced by SLAMTEC in Shanghai, China).

Multi-robot systems have greater flexibility and complexity in task allocation, and researchers have extensively discussed the cooperative control of multi-robot systems, which aims to improve the performance and efficiency of multi-robot systems to cope with complex tasks and environmental requirements. The market-based approach is inspired by market transactions and provides a functional solution to the problem of multi-robot task allocation (MRTA) [13]. The auction algorithm [14,15] is a market-based approach that is widely used in the MRTA literature. This method assigns tasks to the robot with the highest bid, similar to how goods are sold in the market to the highest bidder [16]. In MRTA, the bot bids on tasks based on specific criteria, while a central agent (server or bot) is responsible for receiving bids and assigning tasks to the bot. Robots can communicate with each other to resolve conflicts and assign tasks, so these methods rely on a strong communication network. Distributed auction algorithms have been used to solve multi-robot task assignment problems with task duration constraints [17,18]. The objective function is to maximize the total return on the tasks assigned to the bot, while respecting deadlines and the limited number of tasks that each bot can perform.

Liu et al. [19] introduced a distributed market algorithm with a polynomial time complexity that is better than that of classical auction algorithms. Choi et al. [20] developed a consensus-based bundle algorithm (CBBA) based on the auction algorithm, which combined auction and consensus to establish conflict-free allocation. CBBA can provide near-optimal or suboptimal solutions based on some optimization methods, and this work has stimulated the interest of other researchers to propose more efficient CBBA algorithms [21,22,23,24,25]. In addition, Nayak et al. [26] extended CBBA to deal with communication issues. There are some other algorithms, such as that by Wang et al. [27], who proposed a YOLOv5-PPO model based on A3C optimization, which cleverly combines YOLOv5’s object detection capabilities and a PPO reinforcement learning algorithm to improve the efficiency and accuracy of collaborative work between logistics and warehousing robot groups. Li [28] leveraged the powerful AI paradigm of reinforcement learning (RL) and soft computing to improve warehouse automation processes while considering market needs.

Distributed task allocation based on contract networks is a collaborative approach that relies on negotiation mechanisms. These algorithms simulate the tendering–bidding–awarding process found in human commercial activities, facilitating task allocation through a bidding mechanism among nodes, with the aim of enabling the system to complete distributed tasks at a lower cost and with higher quality. The innovation of this study is to replace the traditional AGVs used in warehouse logistics systems with composite robots, and to study the scheduling and task allocation of multi-composite robots in warehouse logistics systems. The shortcomings of the distributed task allocation method based on the contract network were analyzed, including the inability of robots to handle multiple tasks and the task allocation strategies obtained not achieving global optimality. Based on the contract net framework, an elite genetic algorithm was implemented to sort the robots’ individual task lists, making it easier to achieve a globally optimal strategy for each task during allocation. Finally, experiments were conducted to validate the proposed approach. This technology path can not only meet the needs of high-complexity warehousing scenarios, but also meet the sustainable development goals of the global logistics industry for low-carbon and automated transformation [29].

2. Task Allocation Model

2.1. Problem Analysis

The capabilities of robots are described as follows. A multi-robot set consisting of n robots is defined as $R=\left\{R_i\right|i=1,2,\cdots ,n\}$. The capability matrix of each robot can be represented as $B_{R_i}=diag\{b_{i_1},b_{i_2},\cdots ,b_{i_k}\}$, with $b_{i_k}$ representing the quantified value of the k-th type of capability of that robot. If the robot does not possess a particular type of capability, the value is defined as 0. The set of capability attributes possessed by the robot is defined as $C={[c_1,c_2,\cdots ,c_k]}^T$, where $c_k$ represents a specific attribute label that the robot possesses. These include various intrinsic attributes and behavioral capabilities, such as the remaining battery, movement, grasping, food preparation, and computation. If a robot does not possess a certain type of capability, the corresponding element in the set is valued at 0; otherwise, it is assigned a value of 1. The overall capability value of each robot can be represented as $A(R_i)=B_{R_i}\times C=diag\{b_{i_1}{c}_1,b_{i_2}{c}_2,\cdots ,b_{i_k}{c}_k\}$.

Description of task information. The total task set consisting of m tasks is defined as $T=\left\{T_j\right|j=1,2,\cdots ,m\}$, and the ability value required for each task is represented as $B_{T_k}=diag\{q_{j_1},q_{j_2},\cdots ,q_{j_k}\}$. The ability requirement for task $T_j$ for an individual robot can be represented as $A(T_j)=B_{T_j}\times C=diag\{q_{j_1}{c}_1,q_{j_2}{c}_2,\cdots ,q_{j_k}{c}_k\}$. For the i-th robot and the j-th task, if robot i is to be able to perform task j, the requirement is $A(T_j)\le A(R_i)$.

Description of the costs incurred by robots. During the execution of tasks, robots incur various costs, such as energy consumption and travel distance. To clearly establish the process of task allocation and execution by the robots, we assume that all robots have the ability to move and are assigned movement tasks within the robot group. We further assume that all robots do not consume energy when not performing tasks [30]. When executing tasks, they have the same energy consumption rate, and all robots maintain a consistent movement speed. The consumption for robot i executing various tasks is represented by the vector $Ct(R_i)={[C{t}_{i1},C{t}_{i2},\cdots ,C{t}_{im}]}^T$. $C{t}_{ij}$ represents the consumption required for robot i to perform task j. If robot i does not have the capability for task j, this value is −1.

2.2. Task Allocation Method

In order to improve the robustness of the system, a distributed algorithm can be used to solve the task allocation of multi-robot systems. Distributed algorithms help balance the computational burden of the entire system and improve the stability of the system. Methods of distributed task distribution include behavior-based methods, swarm intelligence methods, and contract net methods. The selection of the appropriate distributed algorithm depends on the specific requirements and environmental conditions of the system.

The contract net protocol [31] is a typical market mechanism method, which completes task allocation through negotiation. In this method, robots bid, tender, and negotiate, and the contract is ultimately awarded to the robot with the highest bid. Each robot plays the role of either a buyer or a seller in the contract net, communicating information with other robots as nodes. Tasks are allocated through a bidding–tendering–awarding mechanism, effectively dispersing the computational complexity of tasks [32].

In the contract net protocol, the tenderer creates a task bid document and sends it to the bidders, evaluates the bid values, selects a winner, and establishes a contract. In addition, it is responsible for supervising the execution of the task. Bidders analyze the bid document, decide whether to accept it, and provide a bid value. If they win the bid, they execute the task according to the contract and provide feedback on the results. The core of task allocation is achieved through bidding and tendering. Market mechanisms are used to efficiently distribute tasks and balance the computational load [33].

In the scheduling system, after orders are mapped to tasks, the system selects a robot or allows a device to act as the tenderer based on the robot’s status, initiating the collaboration process. The task is published by the tenderer broadcasting the task information. Bidders evaluate the task and submit bids. The tenderer evaluates the bids and selects the best bidder, and the winning bidder executes the task and provides feedback on the results. The contract ends after the task is completed. The negotiation process in the contract net is illustrated in Figure 1.

Although traditional contract net protocols can achieve task allocation through negotiation, they also have many drawbacks that reduce the efficiency of the task distribution [34]. For example, the capabilities and loads of bidders can vary greatly. Furthermore, robots lack an understanding of the overall task and of the other robots, which increases the coordination difficulties and leads to challenges in task allocation. Therefore, in practical applications, it is necessary to adjust and supplement algorithms based on this situation, such as the extended contract net protocol proposed by Saxena et al. [35].

2.3. Research on the Impact of MSR on Port Efficiency

The task allocation problem describes the relationship between robots and tasks, establishes variables for robots and tasks, and represents them using a mathematical model:

$${\mathrm{x}}_{ij}=\left\{\begin{array}{c}\begin{array}{cc}1& \mathrm{Robot}\mathrm{i}\mathrm{performs}\mathrm{task}\mathrm{j}\end{array}\hfill \\ \begin{array}{cc}0& \mathrm{Unexecuted}\mathrm{task}\end{array}\hfill \end{array}\right.,y_{ij}=\left\{\begin{array}{c}\begin{array}{cc}1& \mathrm{Robot}\mathrm{i}\mathrm{receives}\mathrm{task}\mathrm{j}\end{array}\hfill \\ \begin{array}{cc}0& \mathrm{Others}\end{array}\hfill \end{array}\right.,$$

(1)

The optimization goal of multi-robot task allocation algorithms is to minimize the total cost of the entire system while ensuring that all tasks are successfully executed. Therefore, the objective function is defined as follows:

$$\min Z={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m}C{t}_{ij}\times y_{ij}}},$$

(2)

This formula represents the minimum cost incurred by a multi-robot system to complete all tasks under ideal conditions. The following are the constraints for Formula (3):

$$\left\{\begin{array}{ll}{\displaystyle \sum _{i}A(R_i)\ge {\displaystyle \sum _{j}A(T_j)\times y_{ij},}}\begin{array}{c}i=1,2,\dots ,n\begin{array}{c}j=1,2,\dots ,m\end{array}\end{array}\hfill & \hfill (a)\\ {\displaystyle \sum _j{y}_{ij}}=1,\begin{array}{c}i=1,2,\dots ,n\end{array}& \hfill (b)\\ {\displaystyle \sum _j{\mathrm{x}}_{ij}}\le 1,\begin{array}{c}i=1,2,\dots ,n\end{array}& \hfill (c)\end{array}\right.$$

(3)

In the above formula, the purpose of Formula (3)(a) is to ensure that the sum of the capabilities of all robots in the whole system is sufficient to meet the needs of all tasks, where $A(R_i)$ represents the ability attribute value possessed by robot i, and $A(T_j)$ represents the ability value of the robot required by task j. Formula (3)(b) ensures that each task will only be assigned to one robot, while Formula (3)(c) specifies that the robot can handle a maximum of one task in a single execution.

3. Algorithm Design

3.1. Improving Traditional Algorithms

The performance of the traditional contract net algorithm is improved in this article by introducing a bidder’s initial selection and a credit mechanism. The initial selection of bidders reduces the communication frequency and enhances the task bidding efficiency by introducing a robot capability table [36]. The capability table filters certain robots for communication, thereby avoiding the need to communicate with all robots for every task. Each robot maintains a capability table that includes capability values, and when new members are added, it broadcasts and updates the capability values, thereby helping the capability distribution of the robot group to be understood and achieving intelligent task allocation.

In the bidding process, the robot’s capability value is used for the first round of screening to assess the execution ability. Additionally, a credit score indicator is introduced, and the robot maintains a credit table that reflects its performance on different tasks. The initial credit score is relatively low, and the tenderer adjusts the credit score based on task execution feedback (CrV(i, j)). These improvements make the contract net protocol more systematic and reasonable. As a result, it is suitable for the entire process of task negotiation and allocation.

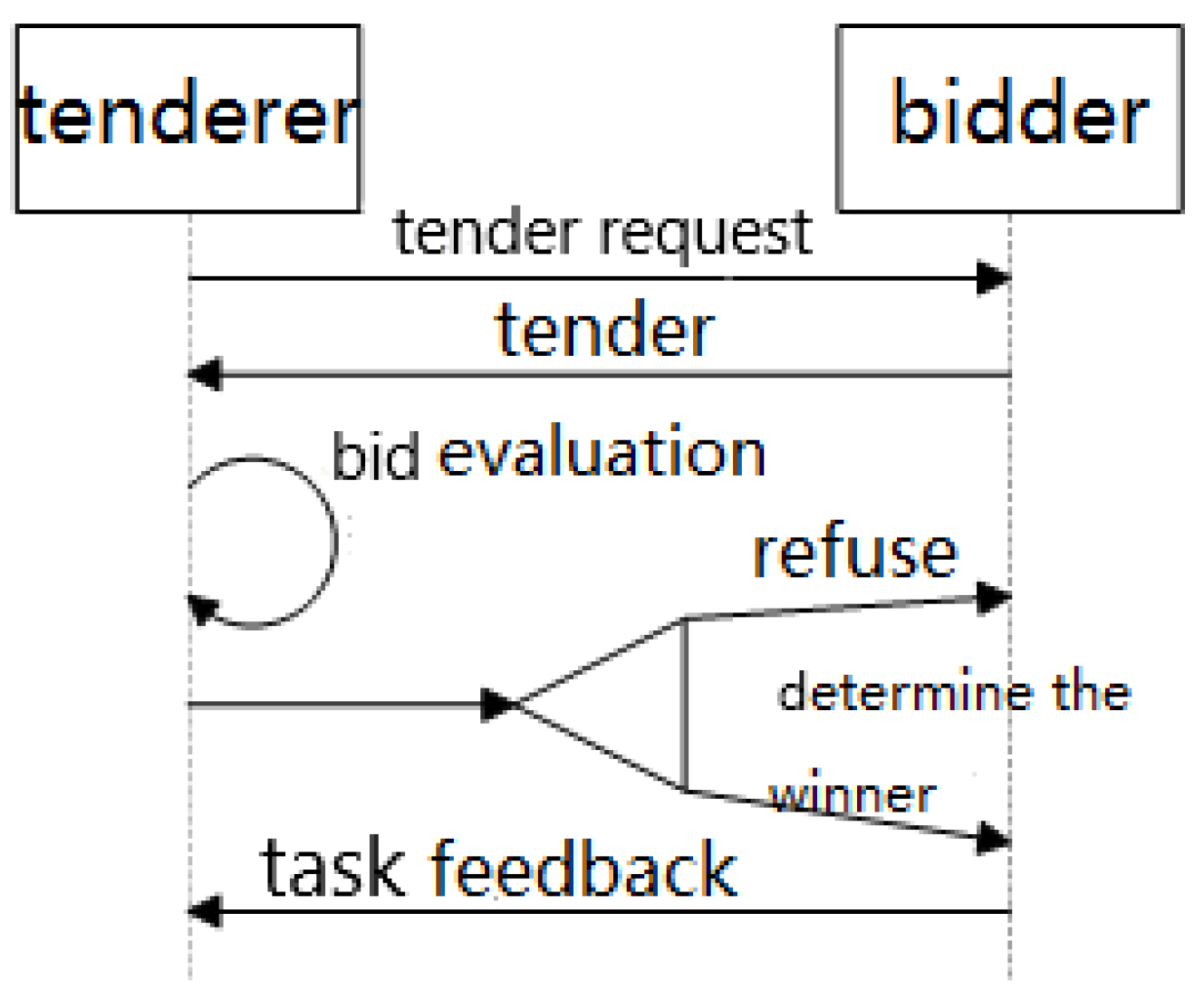
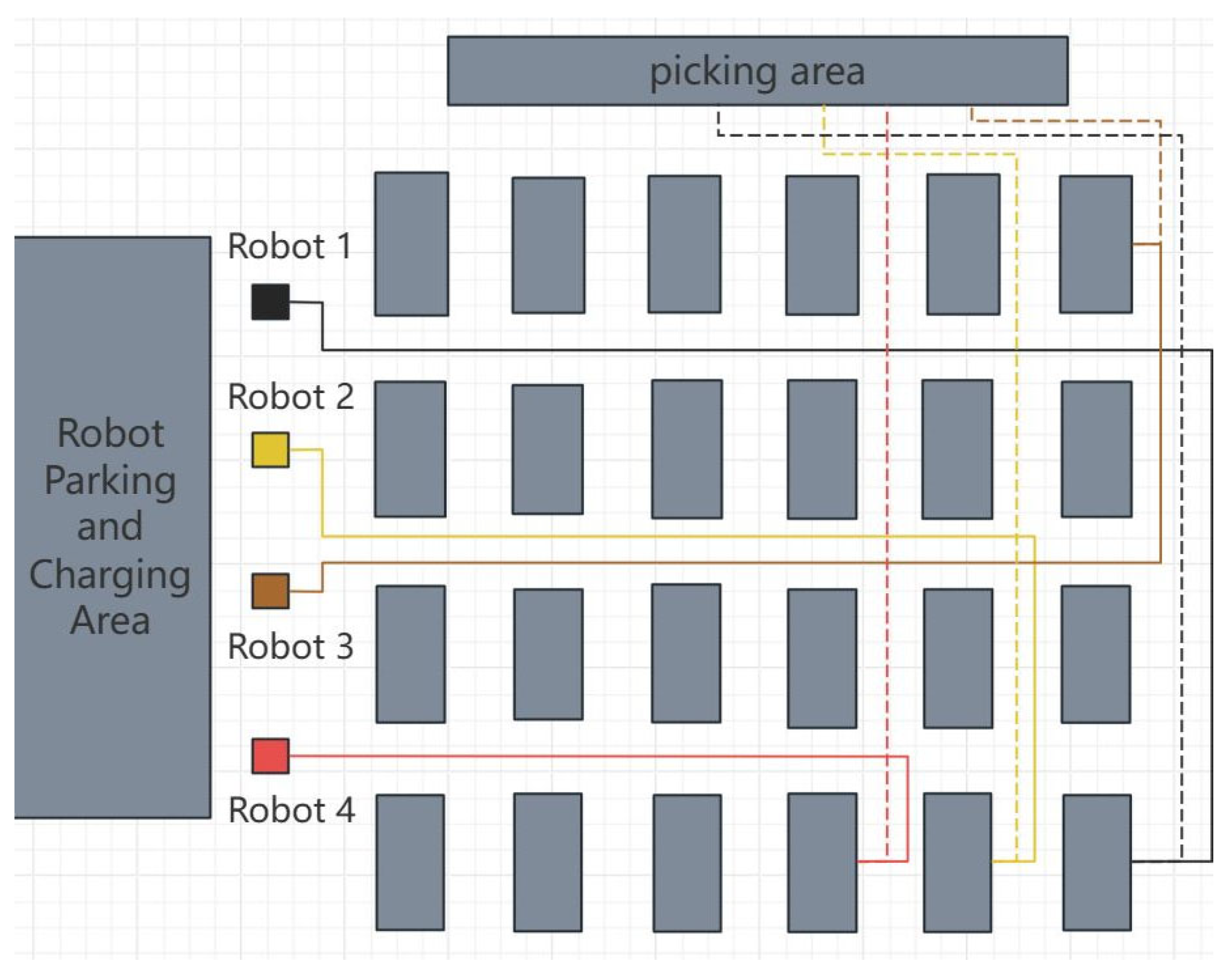
Step 1: Select the bidding target. First, the task parser of the tenderer analyzes the task. The task format is Job = {JobID, OrderID, Manager, JobDescription, JobRequirement}. JobID represents the task number and is used to uniquely identify the task. OrderID represents the order number, which the robot needs to read from the central control order pool. Manager represents the ID of the robot that parses the task, that is, the ID of the tenderer; JobDescription indicates the specific description of the task by the tenderer, including the task type information, the special description of the task, the composition of the task, and additional requirements, etc.; JobRequirement represents the competency requirements for that task, generated based on the type of task and additional requirements, for the initial screening of bidders.

Assuming there are k capability indicators for the task and the type of this task is j, the capability value $\{q_{j_1}{c}_1,q_{j_2}{c}_2,\cdots ,q_{j_k}{c}_k\}$ required for this type of task is obtained. Then, the robot capability table is queried to sequentially obtain the capability values $\{b_{i_1}{c}_1,b_{i_2}{c}_2,\cdots ,b_{i_k}{c}_k\}$ of all the robots. When the capability value of a certain robot meets the following criterion, that robot is included in the list of bidding robots:

$$b_{i_z}\ge q_{j_z}\begin{array}{c}\forall z\in \end{array}k,$$

(4)

where $b_{i_z}$ represents the ability value of the z-th capability attribute of robot i, and $q_{j_z}$ represents the required value of the z-th capability attribute of the robot by task type j.

Step 2: Issue the bid. The tenderer sends the bid document to the bidding robot. If the robot’s list is empty, the task is deleted and reported. If it is not empty, the bidder will receive the bid document when free; otherwise, it will be rejected. If all bidders are busy, the tenderer will wait and retry later. The proposed format for the bid document is Contract = {JobID, OrderID, Manager, JobDescription}. JobID refers to the task number, which is used to uniquely identify the task. OrderID refers to the order number, which the robot needs to read from the central control order pool. Manager refers to the bidder ID of the task; JobDescription refers to the specific description of the task, including the task type, the special description of the task, the composition of the task, and the additional requirements.

Step 3: Bidding. After the bidder receives the bid document, they confirm their capabilities and read the JobDescription (including the destination). The Manhattan distance [37] is used to define the distance between two points. Let $(x_i,y_i)$ be the position of the robot and $(x_j,y_j)$ be the position of the task target point. The cost for the robot to move to the target point can be calculated using the following formula:

$$C(t_j)=\left|x_i-x_j\right|+\left|y_i-y_j\right|,$$

(5)

After obtaining the path consumption, the bidder will refer to the credit table based on the task type in the JobDescription to find the corresponding credit score. Then, by combining the path consumption and the credit score, the bidding value will be provided:

$$Bid(i,j)=C(t_j)(1-\alpha Cr{V}^{*}(i,j)),Cr{V}^{*}(i,j)=CrV(i,j)/\beta ,$$

(6)

where $Cr{V}^{*}(i,j)$ represents the creditworthiness of the current robot i corresponding to the task of type j after normalization. In the formula on the left side of Formula (6), $\mathsf{\alpha }$ is the weight of the creditworthiness, less than 1 and greater than 0. Once the bidder calculates the bid value, it is fed back to the tenderer. In the formula to the right of Formula (6), $\mathsf{\beta }$ represents the upper limit of the credit value.

Step 4: Bid evaluation. The tenderer evaluates all bids and selects the one with the lowest bid value as the winner.

Step 5: Bid announcement. The tenderer notifies the winning bidder, and after receiving confirmation from the winner, a contract is established with the tenderer, making them the task executor.

Step 6: Task supervision and feedback. The tenderer supervises the winner’s task execution and updates their credit rating based on their performance. The following formula is used in the credit rating update process:

$$CrV(i,j)=\left\{\begin{array}{cc}\begin{array}{c}CrV(i,j)+\mathsf{\xi }\end{array}\hfill & \mathrm{Complete}\mathrm{the}\mathrm{tasks}\mathrm{of}\mathrm{the}\mathrm{bidder}\hfill \\ \begin{array}{c}CrV(i,j)/2\end{array}\hfill & \mathrm{Incomplete}\hfill \end{array}\right.,$$

(7)

In Formula (7), $\mathsf{\xi }$ represents the increased creditworthiness of the tenderer after completing the task. For bots that successfully complete tasks, their credit value increases; robots that fail to successfully complete the task will be severely punished, and their credit value will be significantly reduced. Through such a mechanism, the probability of suitable robots performing the same type of tasks can be improved, and the robots can also be avoided from bidding indiscriminately when their actual capabilities are not suitable for completing the task, resulting in a decrease in the efficiency of task allocation.

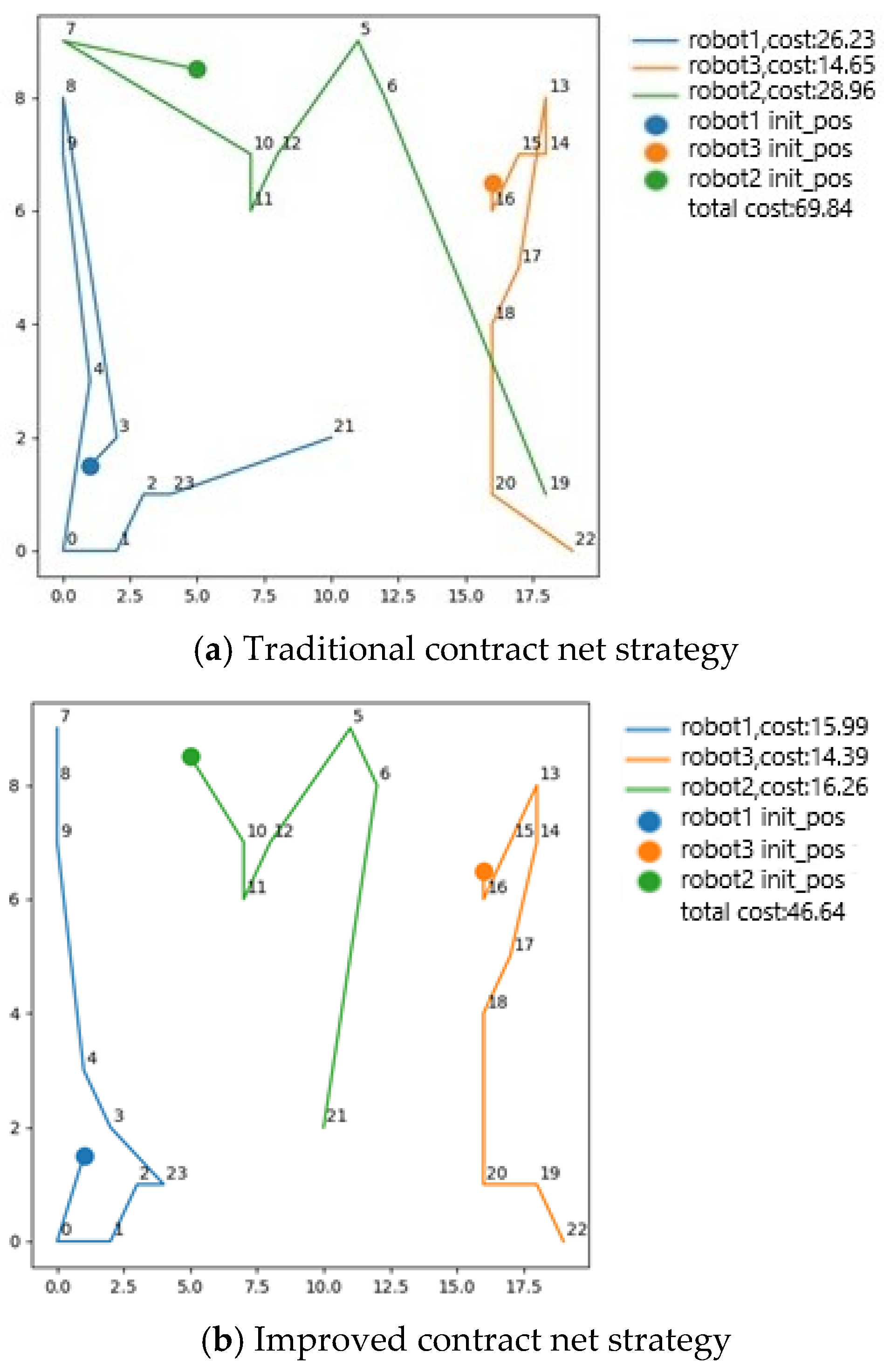
The core of the contract network algorithm is the tendering–bidding–winning mechanism, and the minimization of the total cost objective function (Equation (2)) is directly reflected in the bidding process through the design of the bidding value function (Equation (6)), and in the task allocation process of the contract network algorithm; the total cost target is embedded in the bidding value calculation, and the system indirectly realizes the minimization of the total cost by minimizing the bid value.

3.2. Combination with Genetic Algorithm

There are some limitations of traditional contract network protocols, such as the allocation of a single task, and the fact that global optimization cannot be achieved. The robot can only receive tasks when it is idle, and cannot consider multiple tasks and order its own multiple tasks, meaning that the task execution order cannot be optimized. In order to solve these problems, the algorithm needs to be improved.

Specifically, the following improvements can be made: in the link where the bidder sends the bid, the bidder will give a reasonable bid value to the new task, which not only takes into account factors such as its own power and distance to the task point, but also takes into account the type of task, its own pressure, and other factors. In addition, bidders will sort their task lists appropriately to ensure that the tasks are executed in the best order. In the process of selecting the winner, the tenderer not only considers the bid value of each bidder, but also considers the loss of each task strategy to the robot team to complete the assigned tasks.

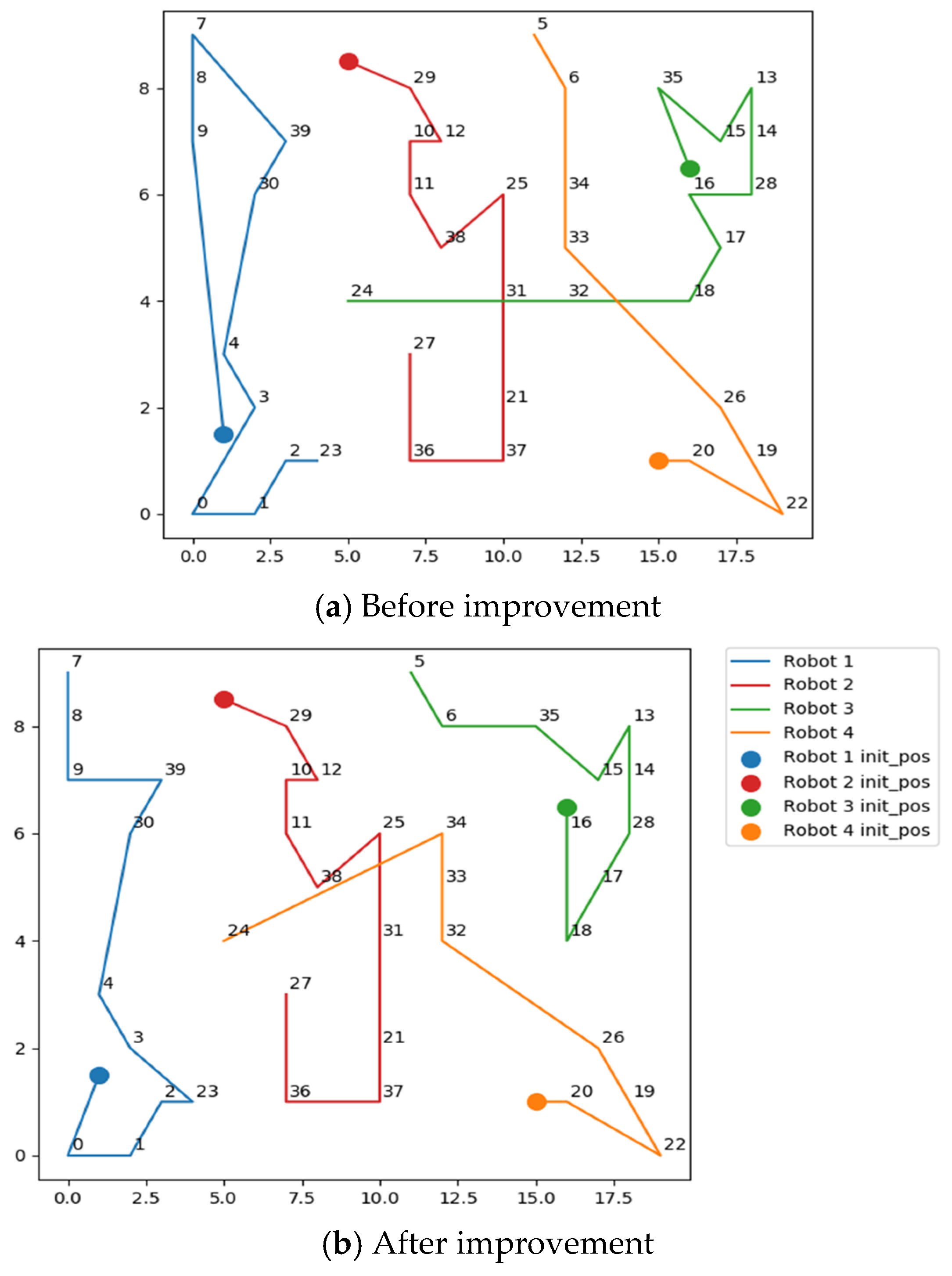
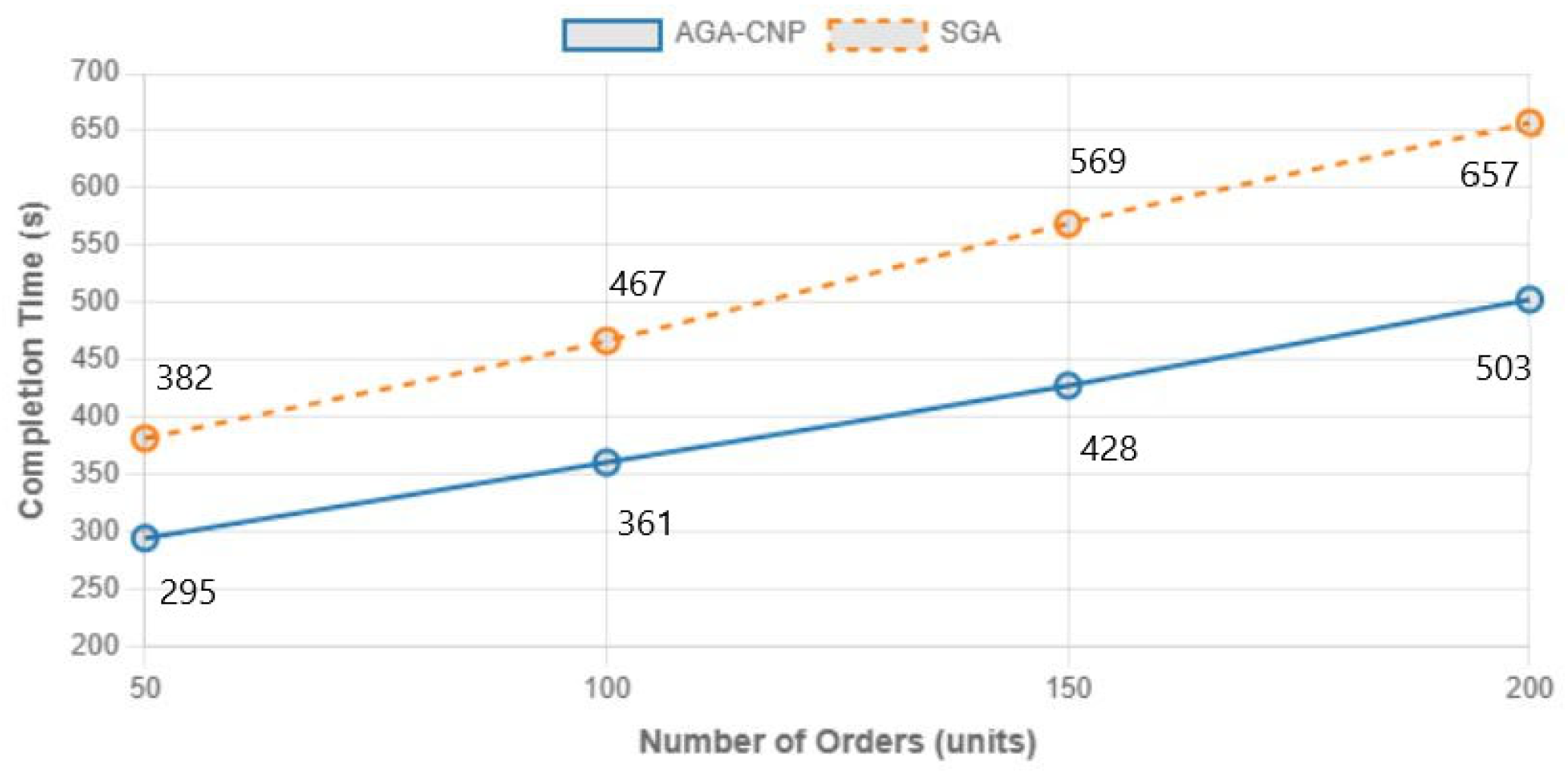
In order to achieve the above improvement, a new mathematical model and algorithm are introduced here. Regarding loss, the loss caused by distance is mainly considered, so the algorithm needs to sort the task points so that the bidder can achieve the shortest task execution distance, and the bidder needs to constantly update their task list to achieve the shortest path. After adding a new task, it is necessary to consider how to avoid the task sequence falling into the local optimum. In the genetic algorithm, in order to avoid the phenomenon of precocious convergence, this can be achieved by increasing the diversity of the population, changing the selection operator or cross-operator, and modifying the evolving population through the Metropolis acceptance criterion to increase the randomness and diversity of the algorithm to make it more likely to obtain the global optimum, combined with the above characteristics. The genetic algorithm is used to optimize task allocation and update the task list. Combined with the market mechanism, it is possible to reasonably allocate a set of tasks to the robot group. Finally, the experimental results verify that the algorithm can effectively solve the problem of multi-task allocation in the real-time task allocation scenario.

3.2.1. Objective Optimization

In warehousing logistics, task scheduling faces challenges of real-time performance and task density. The real-time performance requires new tasks to not be delayed, while a high task density demands quick and efficient task allocation [38]. Therefore, the improved contract net protocol introduces optimization algorithms aimed at optimizing task sequences. The order pool works in conjunction with the task generator to ensure the timely processing and assignment of tasks, thereby improving efficiency and customer satisfaction [39].

To better evaluate the performance of the optimization algorithm, the optimization objective has been improved. Suppose there are n identical robots, and each robot can perform move-type tasks. Each robot $R_i$ has a task list $S_i$, which contains multiple tasks $S_i=\left\{t_j\right|j=1,2,\cdots ,m\}$ arranged in order. The task set of the robot team is $\{S_1,S_2,S_3,\cdots ,S_n\}$, and the cost for the robot to complete the task list is $C(i,S)$. The cost for the robot to move from the current position to the first task point is $Dis(i,t_1)$, and the cost to move from one task point a to another task point b is $Dis(t_a,t_b)$. The cost of the tasks is represented by calculating the Manhattan distance between task points, and the cost of the task list is the total Manhattan distance between the coordinate points. The starting point of the robot $R_i$ is denoted as $(x_i,y_i)$, and there are m tasks in the task list, sorted by index. The total cost for robot $R_i$ to complete the task list $S_i$ is

$$C(i,S)=Dis(i,t_1)+Dis(t_1,t_2)+\dots +Dis(t_{m-1},t_m)$$

(8)

Therefore, the total consumption of tasks for all robots in the warehouse can be expressed as ${\displaystyle \sum _{i=1}^{n}C(r_i,S_i)}$. First, the total distance traveled by the robot team to complete all tasks is selected as the optimization objective. Therefore, the optimization objective is

$$\min {\displaystyle \sum _{i=1}^{n}C(R_i,S_i)}$$

(9)

Second, the optimization objective is the time required for the robot team to complete all tasks. Since all robots have the same transfer speed and the computation time is not considered during task allocation, the time required for the robot team to complete the tasks is equivalent to the time required by the robot that needs to move the longest distance. Therefore, the optimization objective is $\min (\max C(r_i,S_i))$.

3.2.2. Task Order Optimization

The process of improving the genetic algorithm [40] for task sequence optimization is as follows:

(1) Population initialization: The robot’s position is fixed at the starting point, and the task list is converted into coordinate points and arranged in order. The initial population combines a neighborhood search and a random generation to ensure diversity, improve the population quality, and reduce the risk of local optima.

(2) Fitness function design: In the genetic algorithm, the optimization goal is to minimize the distance required for new tasks. A higher fitness value indicates a shorter distance traveled by the robot, making the individual superior and more likely to enter the next generation.

$$f=1/(D(i,S\cup t_j)-D(i,S)+\epsilon )$$

(10)

This function represents the extra distance that the robot moves after task $t_j$ is assigned to the current robot $R_i$, and takes the reciprocal of it as a fitness function, where $D(i,S\cup {\mathrm{t}}_j)$ is the total distance of the robot after adding the new task $t_j$ to its task set, $D(i,S)$ is the total distance of the task set before the robot adds a new task $t_j$, and $\mathsf{\epsilon }$ represents the smaller number close to 0.

(3) Selection: To eliminate individuals with low fitness values and retain those with high fitness values, the “roulette wheel method” is used to ensure that superior solutions are prioritized for the next generation, enhancing the quality of the solutions.

$$P_s(i)={\displaystyle \frac{f(i)}{{\displaystyle \sum _{i=1}^{n}f(i)}}}$$

(11)

where $f(i)$ represents the fitness of the i-th individual and n represents the total number of individuals.

(4) Adaptive crossover and mutation: Adaptive crossover and mutation probabilities are introduced that are automatically adjusted based on the current population’s fitness to avoid the loss of excellent individuals due to fixed probabilities. The crossover probability $P_c$ and mutation probability $P_m$ are defined as follows:

$$P_c(i)=\left\{\begin{array}{c}{k}_1\sin ({\displaystyle \frac{f_{\max }-f^{\prime }}{f_{\max }-f_{\min }}})\begin{array}{cc},& f^{\prime }\ne f_{\max },f_{\min }\end{array}\hfill \\ k_2\begin{array}{cc},& f^{\prime }=f_{\min }\end{array}\hfill \\ k_3\begin{array}{cc},& f^{\prime }=f_{\max }\end{array}\hfill \end{array}\right.,P_m(i)=\left\{\begin{array}{c}{k}_4\sin ({\displaystyle \frac{f_{\max }-f^{\prime }}{f_{\max }-f_{\min }}})\begin{array}{cc},& f^{\prime }\ne f_{\max },f_{\min }\end{array}\hfill \\ k_5\begin{array}{cc},& f^{\prime }=f_{\min }\end{array}\hfill \\ k_6\begin{array}{cc},& f^{\prime }=f_{\max }\end{array}\hfill \end{array}\right.,$$

(12)

In Formula (12), $f^{\prime }$ is the one with the higher fitness in the first two parents of the crossover and mutation operation, $f_{\max },f_{\min }$ are the maximum and minimum values of fitness in the population, and $k_1,k_2,k_3,k_4,k_5,k_6$ is a constant between 0~1. When $f_{\max }-f^{\prime }$ becomes small, it means that the maximum value of the fitness value of the individuals in the population is close to the average value of the fitness of the individuals in the population, and the algorithm may be close to the global optimal solution, but it may also fall into the local optimal solution. In order to increase the diversity of the population, crossover probability $P_c$ and mutation probability $P_m$ should be increased. When $f_{\max }-f^{\prime }$ becomes larger, the opposite is true. In a certain generation of population, different individuals should have different crossover probabilities and mutation probabilities to retain high-quality individuals and eliminate low-quality individuals as much as possible. To achieve this, their $P_c$ and $P_m$ are adjusted according to the fitness values of the individuals. When the fitness value of the individual is high, the corresponding $P_c$ and $P_m$ are reduced; when the fitness value of the individual is low, the corresponding $P_c$ and $P_m$ are increased. This nonlinear change is achieved by introducing trigonometric functions to adjust the crossover probability and mutation probability, which helps the algorithm jump out of the local optimal solution.

(5) Incorporating the Metropolis criterion: Solutions with low performances are accepted based on probability principles, helping the algorithm escape local optima and improve global optimization capabilities, preventing premature convergence. The standard is implemented by comparing the fitness of each individual in the new generation with the fitness of the corresponding individual in the previous generation after each new generation of population. If the new generation of individuals has a higher degree of adaptability than the previous generation, they are retained; otherwise, the instance still has a chance to be retained. The probability of the Metropolis criterion retention is:

$$P_{Metropolis}=\left\{\begin{array}{ccc}{e}^{-{\displaystyle \frac{\mathsf{\Delta }f}{k}}}\hfill & ,& \hfill \mathsf{\Delta }f<0\\ 1\hfill & ,& \hfill \mathsf{\Delta }f>0\end{array}\right.$$

(13)

In Formula (13), $\mathsf{\Delta }f$ represents the difference between the fitness of an individual in a new population and the optimal fitness in an old population, and k is a parameter that assists in calculating the probability of retaining an individual if the current individual is below the optimal fitness of the old population.

(6) End process: If the evolution conditions are not met, for example, if the maximum number of evolution iterations is reached and the best individual does not change for 10 consecutive generations, the evolution ends, and the best path and corresponding distance are output.

3.2.3. Overall Process of Task Scheduling

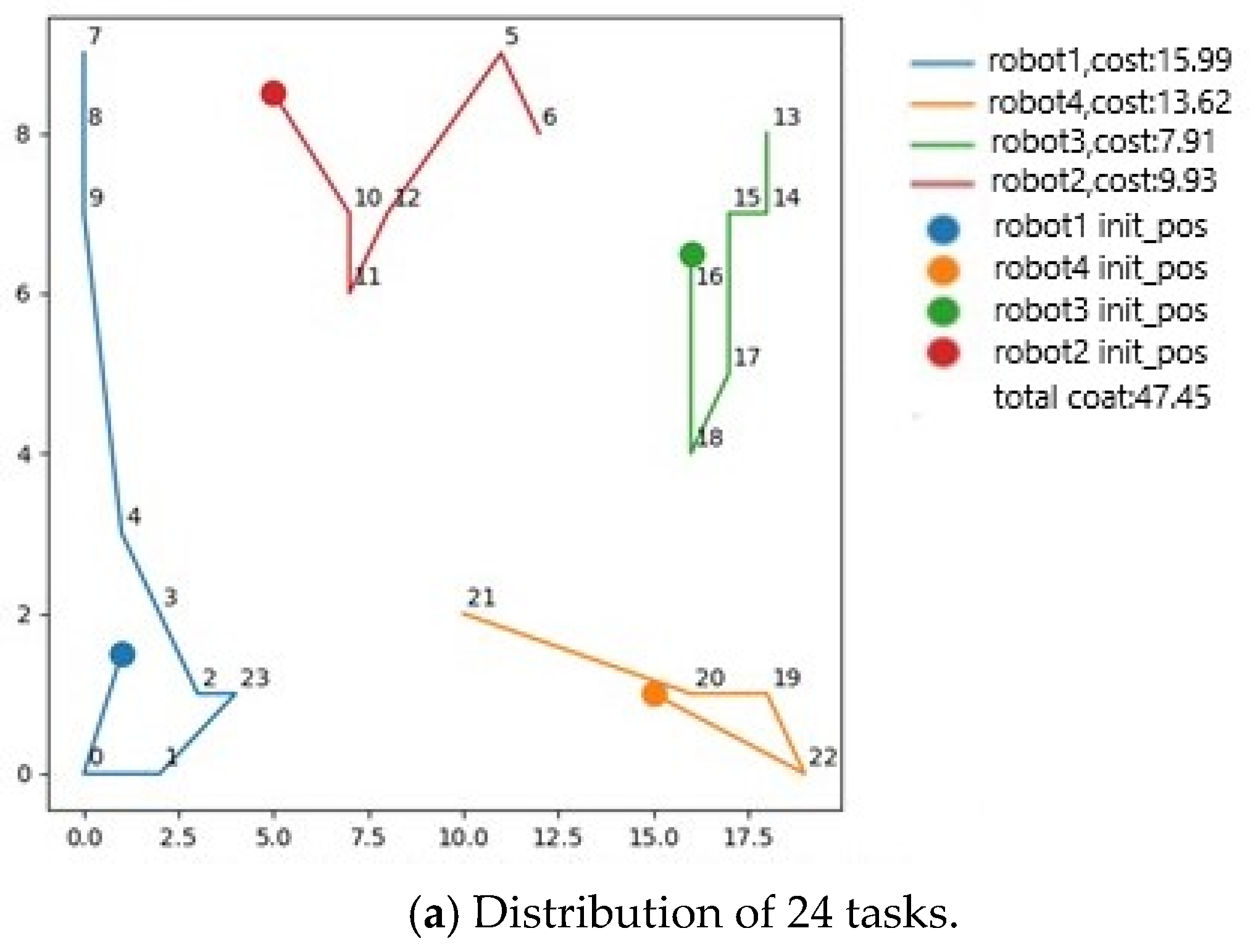
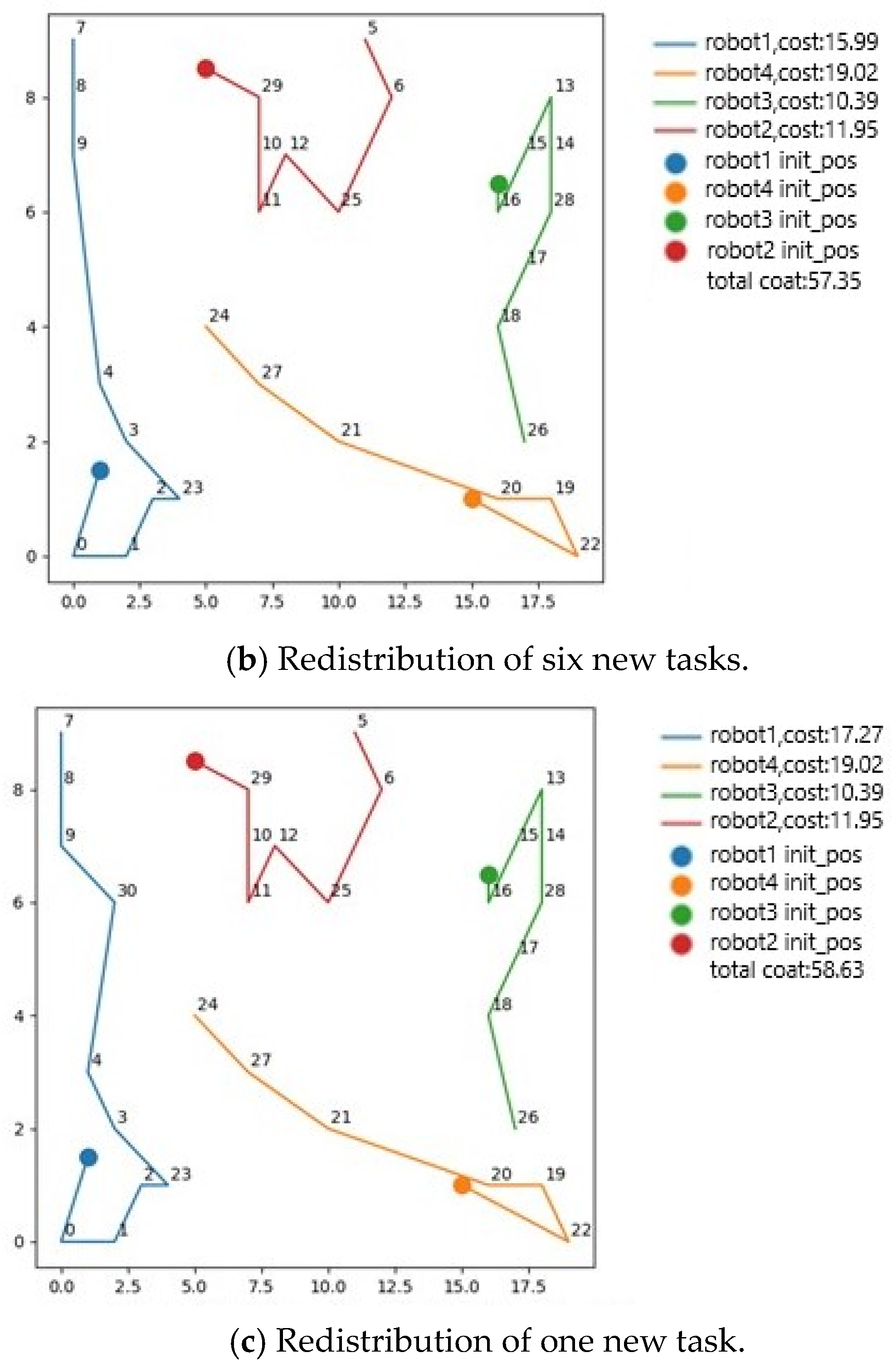
Task assignment is a highly dynamic process, with customer orders constantly being generated as the system runs, and the types of tasks and requirements corresponding to these orders are constantly changing. Task buffers can effectively respond to this changing demand for tasks, not only by centralizing tasks, but also by providing an opportunity for tenderers to evaluate and bid on these tasks. Each bidder needs to provide a bid value for each task in the task pool, which represents the price or value they are willing to pay to perform the task. In order to effectively manage these bid values, a bid pool is introduced, which acts as a hub for storing the bid values for each task to ensure a transparent task assignment process. Through the introduction of task pools and bid pools, the challenges of dynamic task assignment can be better addressed, ensuring that tasks flow and are distributed efficiently throughout the system, while providing a fair competition opportunity for tenderers. This design helps maintain the timeliness, efficiency, and fairness of the system.

When assigning tasks, in order to ensure load balancing among the robot swarm and reduce the number of situations in which some robots become overloaded, a bidding evaluation method is designed:

$$Bid(i,j)=\alpha {\displaystyle \frac{C(i,S\cup t_j)}{n}}+\beta (C(i,S\cup t_j)-C(i,S))(1-\gamma Cr{V}^{*}(i,j)),$$

(14)

In Formula (14), $C(i,S\cup t_j)$ is the cost of the new scheme formed by the bidder after incorporating $t_j$ into its task list, $C(i,S)$ is the cost of the task list when the tenderer does not add a new task, $Cr{V}^{*}(i,j)$ is the normalized trust degree corresponding to the related task, n is the number of tasks in the task list after the robot adds a new task, and $\mathsf{\alpha }$, $\mathsf{\beta }$, and $\mathsf{\gamma }$ are, respectively, the robot’s own stress, the additional loss to the robot due to the new task, and the weights of the corresponding task trustworthiness.

The tenderer obtains the bid values corresponding to all tasks in the task pool through Formula (11) and stores them in its own bidding pool. The bidder takes the smallest bid value from the bidding pool to compete with the bid values selected by other robots. This bid value represents the bidder’s consideration of its own capabilities and the challenges of the new tasks. These two key factors are taken into account to determine the most suitable task for each individual bidder. The formula for bidder i to select the bid value is

$$Bi{d}_i=\min (Bid(1),Bid(2),\cdots ,Bid(m)),$$

(15)

In Formula (15), $Bi{d}_i$ represents the value of the bid issued by Robot $R_i$, and m represents the total number of tasks received by Robot $R_i$. After the robot submits the bid, the tenderer compares the bid value of each robot, combines the global information mastered by the tenderer, and selects the most suitable bidder as the winner through the tenderer formula.

For the optimization goal of minimizing the completion time of all tasks in the task pool, the system increment after assigning new tasks t_k to robot R_i is

$$f_t(r_i,t_k)=\left\{\begin{array}{c}D(r_i,S_i\cup t_k)-D^{\prime }(r,S)\begin{array}{cc},& D(r_i,S_i\cup t_k)-D^{\prime }(r,S)>0\end{array}\hfill \\ \begin{array}{ccc}0& ,& D(r_i,S_i\cup t_k)-D^{\prime }(r,S)\le 0\end{array}\hfill \end{array}\right.,$$

(16)

This increment represents the time taken by the system after $t_k$ is assigned to robot $R_i$, where $D^{\prime }(r,S)$ represents the longest time taken to complete its own task in the robot group that has not yet added a new task. $D(r_i,S_i\cup t_k)$ is the time taken by a robot to complete all its tasks after assigning $t_k$ to $R_i$.

The bidders’ assessments of the tasks and the tenderer’s objective of minimizing the total completion time of all tasks in the task pool are considered as a dual optimization objective. When using an auction method for task allocation, the robots $R_i$ calculate the final score for the tasks $r_k$ using a weighted approach, as follows:

$$Cor{e}_i=v\times Bi{d}_i+(1-v)f_t(r_i,t_k),$$

(17)

In Equation (17), $Bi{d}_i$ represents the value of the bid issued by robot $R_i$, $f_t(r_i,t_k)$ is the time increment of the system after $t_k$ is assigned to robot $R_i$, and $v$ is the weight factor. The lower the value of $Cor{e}_i$, the better the strategy.

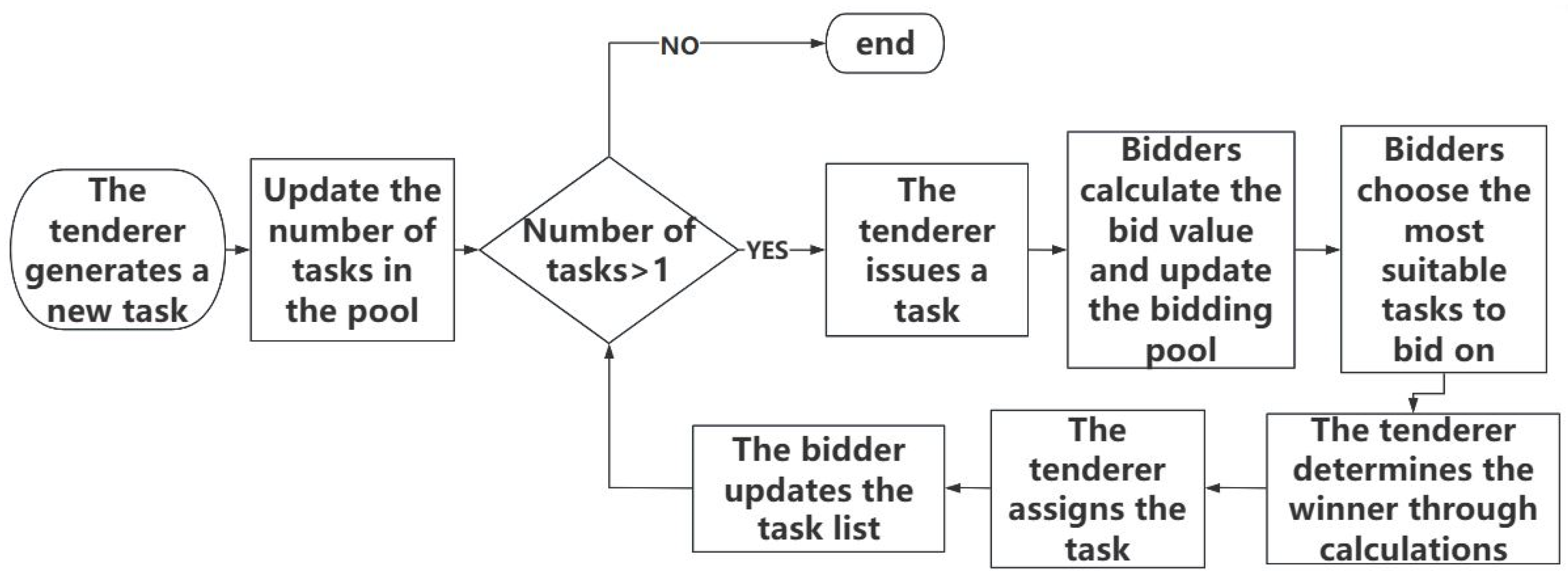
Subsequently, the tenderer removes the allocated orders from the order list and sends notifications to all bidders. After receiving the notification, the bidders update their bidding pools by clearing the bid values corresponding to the allocated orders. Furthermore, in subsequent order bidding, the already-allocated orders are no longer included in the bidding pool. Figure 2 illustrates the overall process of the auction method for task scheduling combined with the genetic algorithm.

In order to address the limitations of the contract network algorithm, the genetic algorithm is used to optimize task allocation, update the task list, and combine the market mechanism to realize the reasonable allocation of a group of tasks to the robot group. The adaptive genetic algorithm is embedded in the decision-making process of the contract network and acts as a global optimizer. When a robot completes initial task bidding through the contract network, the system encodes all the current bidding schemes into a population of “chromosomes” of the genetic algorithm, where each chromosome represents a potential task assignment scheme. The objective function (i.e., the total cost Formula (2)) is directly used as the fitness function (Formula (10)) of the genetic algorithm to evaluate the advantages and disadvantages of each allocation scheme. Through selection, crossover, and mutation operations, the algorithm evolves a better allocation strategy in parallel in the robot population. At the same time, the adaptive characteristics of the algorithm avoid the defect that traditional genetic algorithms fall easily into local optimum. The objective function of minimizing the total cost (Formula (2)) drives the deep integration of the adaptive genetic algorithm and the distributed contract network algorithm. The objective function provides a clear optimization direction for the algorithm, the contract network realizes flexible negotiation under the distributed framework, and the genetic algorithm continuously approaches the lower limit of cost through global search.

The process steps are described in detail as follows:

(1)

The tenderer receives the order, generates tasks, and updates the task pool.

(2)

Task allocation for the new task pool is performed using an auction method:

• Bidders extract tasks from the task pool and use a genetic algorithm for each task to obtain the execution order, distance, and bid value after integrating the new tasks. These tasks are then saved in their own bidding pool. When calculating the execution order, the tasks currently being executed by the bidder are not considered.
• Each bidder selects the minimum bid value from their bidding pool to place a bid.
• After receiving all bid values, the tenderer combines them with the bidding algorithm to score each bid value and designates the robot with the lowest score as the winner. The corresponding task is assigned to the winner.
• The tenderer removes the task from the task pool and notifies all bidders.
• The winner updates their task list based on the optimization results.
• This process is repeated until all tasks in the task pool are removed.

(3)

The robots execute all tasks in their task list sequentially based on the optimal task order.

(4)

The process then waits for new tasks to arrive.

4. Experimental Analysis

4.1. Analysis of Improved Traditional Algorithms

4.1.1. Scene Setup

To test the performance of the algorithm in multi-robot task allocation, Robot Operating System (ROS) and Gazebo were used to build the experimental environment. The experimental environment was set up in Gazebo, where two types of robots were imported, totaling five robots. This scenario provided a realistic and controllable context, which helped to observe and analyze the behaviors of robots under different positions and task requirements, evaluate the accuracy and efficiency of the task allocation algorithm, and provide directions for improving the task execution of the robot team. The constructed experimental environment is shown in Figure 3. The basic information of the robots, such as type, name, and location, is shown in

Table 1. Basic information of robots in the simulation environment.

id	Type	Executable Task Type	Location/m
qim01	qim	Move, Load	(0.5, −8.0)
qim02	qim	Move, Load	(4.0, −2.0)
qim03	qim	Move, Load	(−6.0, 0.0)
qiz01	qiz	Move, Unload	(−6.5, 9.5)
qiz02	qiz	Move, Unload	(5.0, 6.0)

, and all robots had a speed of 0.5 m/s. In Figure 3, the qim-type robots can perform Move and Load tasks, while the qiz-type robots can perform Move and Unload tasks.

4.1.2. Result Analysis

This section illustrates the multi-robot scheduling system and task allocation process through the constructed experimental scenario and analyzes the improved contract net protocol. The dimensions of the experimental scenario were 24 m × 14 m, with task allocation conducted in two rounds. An order containing eight tasks was assigned to an additional robot, which became a tenderer and allocated the tasks to five robots. The small icons in Figure 4 represent different task types: the red triangle represents Move tasks, the yellow square represents Load tasks, and the purple circle represents Unload tasks. Due to environmental obstacles, the task allocation algorithm could not use the Manhattan distance, so the open-source basic A* algorithm in ROS was used to calculate the costs between nodes. Due to space limitations, the costs between nodes are not detailed here. In Figure 4, job01 represents task 1.

The initial credit value of all robots for all types of tasks was set to 5, to ensure that the credit value was not less than 0, and the algorithm parameters were configured as shown in

Table 2. Experimental parameter table of the algorithm part.

Parameter Name	Description	Parameter Value
α	Weight of creditworthiness	0.3
β	Credit limit	10
ξ	Reward creditworthiness	2

. The two types of robots had different capabilities, and when the tenderer conducted the bidding, it was necessary to selectively bid according to each robot’s ability table. The ability values of the two types of robots are shown in

Table 3. Robot capability values.

Robot Type	Compute	Move	Crawl	Unloading	Pick Up	Steer	Talk
qim	3	1	2	0	0	0	2
qiz	2	1	0	2	0	0	0

.

The tasks were assigned, and the robot team distributed them in order of priority. Here, all tasks were set to the same priority, so the robot team allocated them according to the order of the task IDs. Among the eight tasks released in the first round, there were three different types of tasks.

Table 4. Basic information of the first-round tasks.

Id	Type	Location	Id	Type	Location
job01	Move	(−5.0, −9.0)	job05	Load	(3.0, 0.5)
job02	Move	(−6.0, 7.0)	job06	Load	(−1.5, 6.0)
job03	Move	(4.0, 9.0)	job07	Unload	(2.5, −6.5)
job04	Move	(−4.0, 1.5)	job08	Unload	(1.5, −9.0)

presents the basic information of these tasks.

Figure 5 shows the allocation results of the first round of tasks, the execution process, and the Gantt chart. The colors in the Gantt chart represent the path color of the robot, and the numbers represent the task ID. For example, the first row in the diagram represents the qim01 robot executing the job01 task, and the path is the red line segment of the qim01 robot walking in the first round of the task chart. In the initial phase, all robots were in an idle state, so Move-type tasks that all robots could perform were assigned first, given to the nearest robot. After completing the Move-type tasks, only qim02 remained idle, as it could only perform Move and Load tasks, so the Load task was assigned to qim02. At this point, all robots were assigned tasks and had begun execution. When qiz01 completed job02, it was the only one in an idle state. Since the qiz-type robots could only perform Move-type and Unload-type tasks, job06 was skipped during task allocation, and job07 was assigned to qiz02. Similarly, the Load-type task job06 and the Unload-type task job08 were assigned to qim03 and qiz02, respectively. It was verified that tasks were allocated based on the capabilities and status of the robots.

After the robot team had completed the first round of tasks, the robot’s position remained unchanged, and the second round of tasks was immediately assigned. There was a total of 10 tasks, divided into three types.

Table 5. Basic information of the second-round tasks.

Id	Type	Location	Id	Type	Location
job09	Move	(0, 2.0)	job14	Load	(−5.0, −3.5)
job10	Move	(0, 10.0)	job15	Load	(−2.0, 11.0)
job11	Move	(−1.0, −3.0)	job16	Load	(2.0, 11.0)
job12	Move	(4.0, −4.0)	job17	Load	(−6.0, −3.0)
job13	Move	(−4.0, −6.0)	job18	Unload	(3.5, 5.0)

presents the basic information of these tasks.

Figure 6 shows the results of the task allocation and execution process, and the Gantt chart for the second round of tasks. It can be observed that when allocating the task for job09, the position of qim02 was closer to the task point compared to that of qim03. However, in the first round of task allocation, qim03 completed more Move-type tasks, which gave it a higher credibility. Therefore, the algorithm chose to assign the task to qim03. Additionally, based on the execution results of the task allocation, when executing job10 and job16 on qim02, if job16 were executed first followed by job10, it would result in a lower cost for qim02 and the entire robot team. This indicated that the algorithm had a problem where the robots were unable to optimize the order of assigned tasks on their own.

Due to the limitations of traditional contract net algorithms, which allocate tasks sequentially, it is not possible to achieve better task distribution from a global perspective. During the execution of job13 and job14 by qim01, if it were simultaneously assigned to job17, it would not only have little impact on the completion of the entire round of tasks but would also significantly reduce the burden on qim03, thereby greatly improving the overall execution efficiency of the robot team.

The experiments showed that the task allocation algorithm classified based on the task requirements and the robot capabilities, accurately targeting communication goals during the initial selection of bidders to reduce the communication frequency. As tasks were executed, the algorithm assigned tasks to robots with higher trust levels. After introducing capability values and credit mechanisms, the contract net algorithm reduced the communication frequency and improved the allocation accuracy as the number of tasks completed by the robots increased, optimizing the performance of the multi-robot system. However, the traditional contract net protocol could not optimize the order of the assigned tasks. This issue will be addressed below.

4.2. Analysis of Adaptive Genetic Algorithm

In order to verify the improvement effect of the algorithm in multi-robot task allocation, a series of experiments are carried out in this section to verify the effectiveness of the algorithm. In these experiments, all robot types and task types were uniformly set to the Move type, the simulation environment of the experiment was programmed in Python (Version:3.10.11), and the more intuitive Matplotlib (Version:3.7.1) tool was used to create the experimental scene. By drawing a roadmap for the robot to perform the task, the performance of the algorithm can be analyzed and evaluated. By setting the task type to the Move type, the movement path and execution efficiency of the robot under different task allocation algorithms can be investigated in the experiment. A setup like this helps to more visually observe and compare the performance of the algorithm, and to obtain information about the robot’s movement and task execution from the roadmap.

4.2.1. Performance Analysis of Improved Genetic Algorithm

To study the impact of population size in the genetic algorithm on the task allocation results, an experiment was conducted. In this experiment, four robots were used to allocate a total of 40 tasks in one round. First, the same number of iterations and other parameters were set. Then, several groups of experiments were conducted before and after the improvement of the genetic algorithm with population size set at 5, 10, 20, 30, 40, 50, 60, 100, 200, 250, and 300. Experimental results with larger errors were excluded, and the average of the distance loss was taken for comprehensive analysis.

According to Figure 7, population size was negatively correlated with the total loss of task completion; the total loss decreased as population size increased, with the greatest rate of decrease in the range of 0–50 individuals. A smaller number of individuals limited the algorithm’s search capability, resulting in a larger total loss. Although the total loss slightly increased after population size exceeded 50, it continued to decrease thereafter. This was because a larger number of individuals helped to better explore the solution space and find more optimal solutions. This result emphasizes the importance of selecting an appropriate number of individuals, as both too few and too many can affect performance. Therefore, it is necessary to comprehensively consider population size to optimize the task allocation. The relationship between population size and the total loss is shown in Figure 7.

By comparing the loss curves of the genetic algorithm before and after improvement, it can be seen that when the population size was less than 50, the improved algorithm exhibited stronger stability and a lower loss. The improved algorithm, through adaptability and the Metropolis criterion, not only preserved the inheritance of elite genes but also ensured higher crossover and mutation rates, thereby reducing the probability of getting trapped in local optima. If the population size exceeds 50, attention should be paid to fine-tuning the genes of elite individuals to further reduce the loss. Overall, the improved algorithm not only approached the global optimal solution faster but also had a lower loss at each stage.

Figure 8 shows the task allocation results when population size was 30. In Figure 8a, the total loss was 107.8, and in Figure 8b, the total loss was 89.32. It can be seen that when population size was small, the task allocation performance of the genetic algorithm was limited due to a small selection population and low diversity in the task sequences, making it easy to fall into local optima. By comparing the allocation routes in Figure 8a,b, the improved genetic algorithm, due to its higher mutation rate, is shown to be less likely to become trapped in local optima. By comparing the total losses, it was concluded that the allocation results after the improvement showed a significant overall improvement compared to those before the improvement.

When population size exceeded 50, the results of each algorithm did not show a significant improvement with the increase in population size. Figure 9 shows the task allocation results obtained with a population size of 300. The total loss in Figure 9a was 84.08, and the total loss in Figure 9b was 75.62.

From the comparison of experimental results before and after the algorithm improvement, it can be concluded that there is still significant room for reducing the losses in the allocation results before the improvement. For example, Robot1 in Figure 9a could further optimize its task list to avoid large round trips. Additionally, the improved task allocation results led to a more balanced load among the robots, making their task distribution better than that before the improvement.

When population size was large, the genetic algorithm performed better in task allocation, and the solutions were closer to the global optimal solution. This was because increasing population size expanded the search space of the genetic algorithm, increased the diversity of the task sequences, and thus enhanced the likelihood of finding the global optimal solution.

4.2.2. Performance Analysis of Multi-Robot Multi-Task Allocation

To verify the advantages of the improved auction method compared to the traditional auction method, a comparison of the total distances of the robot paths and the task allocation results was conducted. The experimental scene and results were plotted using the Matplotlib library, with the experimental scene set to a length of 20 and a width of 10. Initially, 24 task points were set, labeled from 0 to 23, with the following coordinates: (0, 0.5), (2, 0.5), (3, 1.5), (2.5, 2), (1, 3), (11, 9.5), (12, 8.5), (0.5, 9.5), (0.5, 8), (0.8, 7), (7, 7), (7, 6.5), (8, 7), (18, 8.5), (18, 7), (17, 7), (16, 6.5), (17, 5.5), (16, 4), (18, 1), (16, 1), (10, 2), (19, 0.2), and (4, 1), respectively. Three tenderers, Robot1, Robot2, and Robot3, were set with initial positions at (1, 1.5), (5, 8.5), and (16, 6.5), respectively, and their average travel speed was 0.5 units/s. The bidding methods used were the traditional auction method and the improved auction method. Some parameters of the algorithm are shown in

Table 6. Experimental parameters.

Parameter Name	Description	Parameter Value	Parameter Name	Description	Parameter Value
job09	robot pressure weight	0.5	pop	individual quantity	100
job11	additional task loss weight	0.5	mut	mutation rate	0.5
job12	task trust weight	0.5	gen	number of iterations	50
job13	bid value weight	0.5	tourn	elite quantity	50

.

The allocation results are shown in Figure 10. The consumption of each robot represented the distance the robot needed to travel to complete the tasks in its task list, while the total distance represented the sum of the distances traveled by the robot to complete all tasks. In addition, the improved auction method took into account the pressure on the tenderers when seeking bid values and the weight of additional losses from new tasks, represented by the parameters α and β, respectively, which were set to 0.5 in the experiments. The weights of Bid_i and $f_t(r_i,t_k)$ when the tenderer calculated the score of the bidders, represented by parameter V, were also set to 0.5 in the experiments. By comparing the allocation results in Figure 10a,b under the same experimental conditions, significant differences can be observed. The variance of the allocation results in Figure 10a was approximately 38.58, while the variance in Figure 10b was only about 0.683, significantly lower than that of Figure 10a. This indicated that the improved auction method distributed tasks to robots more evenly compared to the traditional auction method, achieving a more balanced load distribution.

The total distance for the improved auction method was 46.64, while that for the traditional method was 69.84, clearly indicating that the improved method performed better in terms of the total distance. From the perspective of the robots executing tasks, as shown in Figure 10a, Robot1’s path was repetitive, resulting in a significant unnecessary distance. In contrast, as shown in Figure 10b, Robot1 efficiently completed the task in a straight line, minimizing the movement distance. Robot2 and Robot3 also showed similar effects. In summary, the improved auction method not only performed excellently in terms of load balancing for task allocation but also achieved significant improvements in the total distance and execution efficiency. The numbers in Figure 10 represent the tasks; for example, “1” represents task point 1.

4.2.3. Performance Analysis of Multi-Task Real-Time Allocation

To verify the real-time performance and effectiveness of the improved auction method for task allocation in a dynamic environment, an additional robot, Robot4, was added with an initial position of (15, 1). The parameters and foundation were the same as in the previous experiment. The task points remained consistent with those in experiment 4.2.2. Figure 11a shows the results of assigning 24 tasks to four robots. On this basis, six new task points are added to the task pool, 24~29, respectively; the corresponding coordinates are (5,4), (10,6), (17.5,2), (7.5,3), (18,6), (7.5,8); and the four robots are allocated to the six tasks by auction again under the condition that the tasks have been allocated. Figure 11b shows the distribution result of six new tasks. Subsequently, a new task point, numbered 30, was added to the task pool, with coordinates of (2.5, 6). Figure 11c shows the task allocation results after adding this new task to the task pool.

As shown in Figure 11a, after the task allocation was completed, the four robots successfully acquired the tasks and optimized the execution order. In Figure 11b, with the addition of six new tasks, Robot3’s task route underwent significant changes, indicating that the algorithm could comprehensively reorder tasks based on new situations rather than just making minor adjustments, thereby optimizing the path. In Figure 11c, although the new task was far from Robot1’s endpoint, it was close to its route, while it was closer to Robot4 but deviated from its route. Ultimately, Robot1 successfully acquired and integrated the task.

The experimental results indicated that the algorithm could effectively allocate single and multiple tasks, balance the robot’s load, and avoid overload or idleness. Ultimately, the task allocation scheme was optimized, achieving efficient real-time task distribution.

4.3. Comparison of Efficiency in Warehousing Scenarios

In this experiment, four composite robots were deployed in the warehousing and logistics system, the warehouse plane size was 54 m × 45 m, the warehouse layout was composed of 24 shelf units, and the configuration parameters of the composite robots are shown in

Table 7. Composite robot configuration parameters.

Parameter Category	Metric Values	Parameter Category	Metric Values
Mobile Chassis	Omnidirectional wheel drive	Positioning accuracy	≤±40 mm, 2°
No-load speed	1.5 m/s ±0.1 m/s	Battery life	16.5 h (no load), 9.5 (full load)
Load speed	1.0 m/s ±0.05 m/s	Maximum load	300 kg (including robotic arm)

. The goods stored in the experimental scenario are Omron industrial electrical components, covering six categories such as relays, sensors, switches, controllers, etc., with a total of 52 specific models (such as G3PE series relays, E2E-X5ME1 proximity sensors, MY4N-GS relay modules, etc.), with a single product size ranging from 60 mm × 40 mm × 30 mm to 150 mm × 100 mm × 80 mm, and a weight distribution of 0.1–3.5 kg. The shelves adopt a classified storage strategy, components of the same type are stored in adjacent shelf units, and the safety redundancy spacing (≥50 mm) is set to prevent mechanical interference during handling. The composite robot starts from the parking and charging area, goes to the shelf to pick up the goods (solid line) according to the content of the assigned order, and puts the goods in the picking area (dotted line) after taking the goods, as shown in Figure 12.

The simulation platform is used to generate uniformly distributed random order data (5–15 individual goods in a single order), and the probability distribution of the types of goods in the order is consistent with the actual production requirements: 38% relays, 27% sensors, 15% controllers, and the rest comprising switches and auxiliary components. There are two task allocation algorithms used for the experiment: one is the method studied in this paper (an algorithm that combines the Adaptive Genetic Algorithm (AGA) with the Contract Network Protocol (CNP)), and the other is the Simple Genetic Algorithm (SGA). The optimal algorithm is derived by comparing the time it takes both algorithms to complete the task.

In order to analyze the adaptability of the algorithm to the expansion of the order size, Figure 13 compares the task completion time of the two algorithms under different order quantities. The AGA-CNP algorithm (solid blue line) increases the completion time linearly from 295 s to 503 s when the order volume increases from 50 to 200 orders, while the SGA algorithm (orange dotted line) shows a significant non-linear increase. When the order volume reaches 200 orders, the time difference between the two algorithms expands to 154 s, which is due to the fact that the dynamic task bidding mechanism of AGA-CNP can effectively allocate multiple robots to work together. Therefore, the research method in this paper is better in terms of efficiency and can shorten the time to complete the task.

5. Conclusions

This paper focuses on the sustainable development needs of intelligent warehousing and logistics systems. The shortcomings of traditional manual and single-robot scheduling methods were analyzed, and the use of composite robots to replace traditional AGVs to solve task allocation issues in multi-robot scheduling was proposed. In response to the frequent communication required by traditional contract net protocols when selecting bidders, which cannot adapt to changes in the robot capabilities, an improved method is proposed that introduces initial bidder selection and a credit mechanism. This approach was validated through experiments to show its effectiveness. Furthermore, the shortcomings of traditional auction methods in warehouse environments were analyzed, such as poor dynamism, uneven load distribution, and the inability to handle multi-task sequencing. To address these issues, new concepts of task pools and bidding pools were introduced, aiming to minimize bidding values and system time, thereby improving task efficiency and balancing robot loads. Additionally, an improved genetic algorithm was designed to optimize the task execution order. Ultimately, by combining the genetic algorithm with the contract net protocol, a new task allocation method was established. Finally, the efficiency of task completion is compared in a logistics scenario using the research method of this paper and the SGA algorithm, and the experiments illustrate that the method of this paper is more efficient and further improves the reliability. Experimental results indicated that this algorithm effectively enhances the system’s efficiency, alleviates the computational pressure on tenderers, brings the allocation results closer to the optimal solution, reduces the overall energy consumption and equipment loss, and provides a technical guarantee for the sustainable development of the warehousing and logistics system. This technology path provides a scalable low-carbon solution for the warehousing and logistics industry, which not only reduces human resource consumption, but also promotes the transformation of the warehousing system into an environment-friendly smart hub through algorithm-driven equipment energy efficiency optimization, and responds to the needs of the global carbon neutrality strategy.

In the current social environment, intelligent robots are the main stream of research in the future information age, and the use of robots to replace manpower to complete certain tasks is the trend of social development. In future research, this study could be carried out from the following perspectives: (1) improvement of the task allocation algorithm through the adaptive adjustment of the genetic algorithm parameters could tailor the task allocation algorithm to different scenarios, and ensure that the task allocation algorithm can be efficiently carried out so as to meet the energy efficiency optimization requirements of different scenarios; (2) the dispatching system has only been tested in a warehouse environment, and whether it would perform well in other scenarios such as restaurants and hospitals needs further research.