Predicting Soil Organic Carbon Stocks Under Native Forests and Grasslands in the Dry Chaco Region of Argentina
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Sites and Description of Datasets
- where,
- SOCi = soil organic carbon stock (in Mg C ha−1) of the depth increment i,OCi = organic carbon content (Mg C g soil−1) of the fine soil fraction (<2 mm) in the depth increment i,
- BDfinei = the mass of the fine earth per volume of fine earth of the depth increment i (g fine earth cm−3 fine earth = dry soil mass [g] − coarse mineral fragment mass [g])/(soil sample volume [cm3] − coarse mineral fragment volume [cm3]),
- vGi = the volumetric coarse fragment content of the depth increment i,
- ti = thickness (depth, in cm) of the depth increment i,
- 0.1 = conversion factor for converting Mg C cm−2 to Mg C ha−1.
2.2. Simulation Model
2.3. Calculation of C Inputs
2.4. Evaluation of the Model’s Performance
3. Results and Discussion
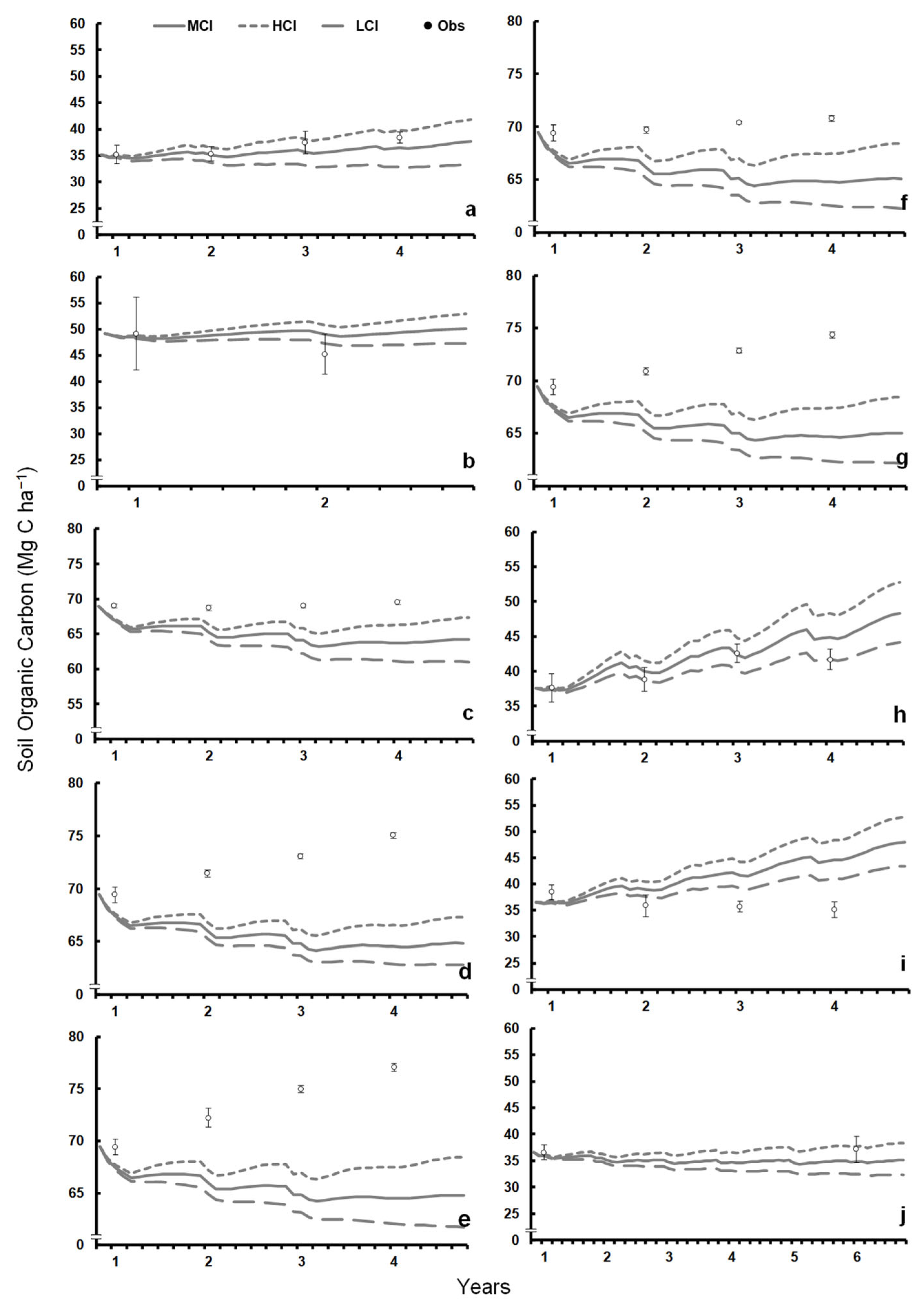
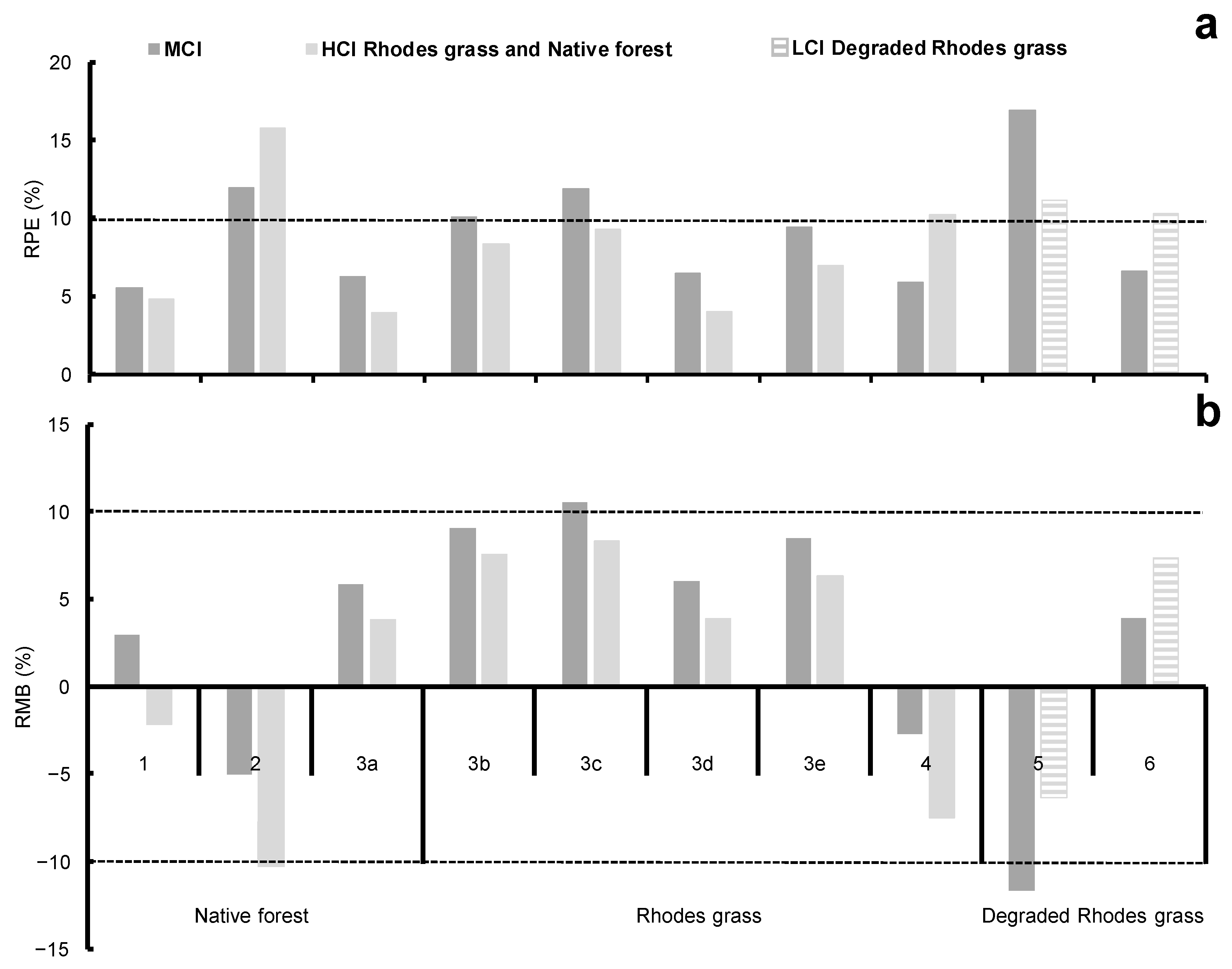
3.1. Model Performance by Land Cover Type
3.2. Model Performance by Experiment
3.3. Uncertainties and Limitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tifafi, M.; Guenet, B.; Hatté, C. Large Differences in Global and Regional Total Soil Carbon Stock Estimates Based on SoilGrids, HWSD, and NCSCD: Intercomparison and Evaluation Based on Field Data From USA, England, Wales, and France. Glob. Biogeochem. Cycles 2018, 32, 42–56. [Google Scholar] [CrossRef]
- Smith, P. Soils and climate change. Curr. Opin. Environ. Sustain. 2012, 4, 539–544. [Google Scholar] [CrossRef]
- Lal, R.; Smith, P.; Jungkunst, H.F.; Mitsch, W.J.; Lehmann, J.; Ramachandran Nair, P.K.; McBratney, A.B.; De Moraes Sá, J.C.; Schneider, J.; Zinn, Y.L.; et al. The carbon sequestration potential of terrestrial ecosystems. J. Soil Water Conserv. 2018, 73, 145A–152A. [Google Scholar] [CrossRef]
- Scharlemann, J.P.W.; Tanner, E.V.J.; Hiederer, R.; Kapos, V. Global soil carbon: Understanding and managing the largest terrestrial carbon pool. Carbon Manag. 2014, 5, 81–91. [Google Scholar] [CrossRef]
- Villarino, S.H.; Studdert, G.A.; Baldassini, P.; Cendoya, M.G.; Ciuffoli, L.; Mastrángelo, M.; Piñeiro, G. Deforestation impacts on soil organic carbon stocks in the Semiarid Chaco Region, Argentina. Sci. Total Environ. 2017, 575, 1056–1065. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Calvo Buendia, E., Tanabe, K., Kranjc, A., Baasansuren, J., Fukuda, M., Ngarize, S., Osako, A., Pyrozhenko, Y., Shermanau, P., Federici, S., Eds.; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Portillo-Quintero, C.A.; Sánchez-Azofeifa, G.A. Extent and conservation of tropical dry forests in the Americas. Biol. Conserv. 2010, 143, 144–155. [Google Scholar] [CrossRef]
- Sarmiento, G. Ecological and floristic convergences between seasonal plant formations of tropical and subtropical South America. J. Ecol. 1972, 60, 367–410. [Google Scholar] [CrossRef]
- Fernández, P.D.; Baumann, M.; Baldi, G.; Banegas, R.N.; Bravo, S.; Gasparri, N.I.; Lucherini, M.; Marinaro, S.; Nanni, A.S.; Nasca, J.S.; et al. Grasslands and Open Savannas of the Dry Chaco. In Encyclopedia of the World’s Biomes; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Baumann, M.; Gasparri, I.; Piquer-Rodríguez, M.; Gavier Pizarro, G.; Griffiths, P.; Hostert, P.; Kuemmerle, T. Carbon emissions from agricultural expansion and intensification in the Chaco. Glob. Change Biol. 2016, 23, 1902–1916. [Google Scholar] [CrossRef]
- Conti, G.; Pérez-Harguindeguy, N.; Quètier, F.; Gorné, L.D.; Jaureguiberry, P.; Bertone, G.A.; Enrico, L.; Cuchietti, A.; Díaz, S. Large changes in carbon storage under different land-use regimes in subtropical seasonally dry forests of southern South America. Agric. Ecosyst. Environ. 2014, 197, 68–76. [Google Scholar] [CrossRef]
- Lambin, E.F.; Gibbs, H.K.; Ferreira, L.; Grau, R.; Mayaux, P.; Meyfroidt, P.; Morton, D.C.; Rudel, T.K.; Gasparri, I.; Munger, J. Estimating the world’s potentially available cropland using a bottom-up approach. Glob. Environ. Change 2013, 23, 892–901. [Google Scholar] [CrossRef]
- Torrella, S.A.; Adámoli, J. Situación ambiental de la ecorregión del Chaco Seco. La Situación Ambient. Argentina 2005, 2005, 73–75. [Google Scholar]
- Kunst, C.; Ledesma, R.; Castañares, M.; Cornacchione, M.; van Meer, H.; Godoy, J. Yield and growth features of Panicum maximum (Jacq.) var Trichoglume cv Petrie (Green Panic) under woody cover, Chaco region, Argentina. Agroforest Syst. 2014, 88, 157–171. [Google Scholar] [CrossRef]
- Nasca, J.A.; Berone, G.; Arroquy, J.I.; Feldkamp, C.; Colombatto, D. Evaluación de un modelo de producción de pasturas mediante pruebas empíricas. Rev. Investig. Agropecu. 2020, 46, 88–95. [Google Scholar]
- Fernández, P.D.; de Waroux, Y.P.; Jobbágy, E.G.; Loto, D.E.; Gasparri, N.I. A hard-to-keep promise: Vegetation use and aboveground carbon storage in silvopastures of the Dry Chaco. Agric. Ecosyst. Environ. 2020, 303, 107117. [Google Scholar] [CrossRef]
- Instituto Nacional de Tecnología Agropecuaria (INTA); Ministerio de Agricultura Ganadería y Pesca (MAGyP). Reporte Nacional: Estimación de las Reservas de Carbono Orgánico del Suelo con Plantaciones Forestales y Otros Usos de la Tierra, en Distintas Regiones de Argentina; MAGyP: Buenos Aires, Argentina, 2022; p. 80. [Google Scholar]
- Smith, P.; Smith, J.U.; Powlson, D.S.; McGill, W.B.; Arah, J.R.M.; Chertov, O.G.; Coleman, K.; Franko, U.; Frolking, S.; Jenkinson, D.S.; et al. A comparison of the performance of nine soil organic matter models using datasets from seven long-term experiments. Geoderma 1997, 81, 153–225. [Google Scholar] [CrossRef]
- Campbell, E.E.; Paustian, K. Current developments in soil organic matter modeling and the expansion of model applications: A review. Environ. Res. Lett. 2015, 10, 123004. [Google Scholar] [CrossRef]
- Jørgensen, S.E. Overview of the model types available for development of ecological models. Ecol. Modell. 2018, 215, 3–9. [Google Scholar] [CrossRef]
- Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- Coleman, K.; Jenkinson, D.S.; Crocker, G.J.; Grace, P.R.; Klír, J.; Körschens, M.; Poulton, P.R.; Richter, D.D. Simulating trends in soil organic carbon in long-term experiments using RothC-26.3. Geoderma 1997, 81, 109–120. [Google Scholar] [CrossRef]
- Nieto, O.M.; Castro, J.; Fernández, E.; Smith, P. Simulation of soil organic carbon stocks in a Mediterranean olive grove under different soil-management systems using the RothC model. Soil Use Manag. 2010, 26, 118–125. [Google Scholar] [CrossRef]
- Falloon, P.; Smith, P. Simulating SOC changes in long-term experiments with rothC and CENTURY: Model evaluation for a regional scale application. Soil Use Manag. 2002, 18, 101–111. [Google Scholar] [CrossRef]
- Farina, R.; Coleman, K.; Whitmore, A.P. Modification of the RothC model for simulations of soil organic C dynamics in dryland regions. Geoderma 2013, 200–201, 18–30. [Google Scholar] [CrossRef]
- Siyum, Z.G. Tropical dry forest dynamics in the context of climate change: Syntheses of drivers, gaps, and management perspectives. Ecol. Process. 2020, 9, 25. [Google Scholar] [CrossRef]
- Yao, J.; Liu, H.; Huang, J.; Gao, Z.; Wang, G.; Li, D.; Yu, H.; Chen, X. Accelerated dryland expansion regulates future variability in dryland gross primary production. Nat. Commun. 2020, 11, 1665. [Google Scholar] [CrossRef]
- Schlesinger, W.H. An evaluation of abiotic carbon sinks in deserts. Glob. Change Biol. 2017, 23, 25–27. [Google Scholar] [CrossRef]
- Sierra, C.A.; Müller, M.; Trumbore, S.E. Modeling radiocarbon dynamics in soils: SoilR version 1.1. Geosci. Model Dev. 2014, 7, 1919–1931. [Google Scholar] [CrossRef]
- Nasca, J.A.; Feldkamp, C.R.; Arroquy, J.I.; Colombatto, D. Efficiency and stability in subtropical beef cattle grazing systems in the northwest of Argentina. Agric. Syst. 2015, 133, 85–96. [Google Scholar] [CrossRef]
- Studdert, G.A.; Monterubbianesi, M.G.; Domínguez, G.F. Use of RothC to simulate changes of organic carbon stock in the arable layer of a Mollisol of the southeastern Pampas under continuous cropping. Soil Tillage Res. 2011, 117, 191–200. [Google Scholar] [CrossRef]
- Villarino, S.H.; Studdert, G.A.; Laterra, P. Greenhouse gas inventories: Deriving soil organic carbon change factors and assessing soil depth relevance in Argentinean Semiarid Chaco. Catena 2018, 169, 164–174. [Google Scholar] [CrossRef]
- Baldassini, P.; Paruelo, J.M. Deforestation and current management practices reduce soil organic carbon in the semi-arid Chaco, Argentina. Agric. Syst. 2020, 178, 102749. [Google Scholar] [CrossRef]
- Banegas, N.; Albanesi, A.S.; Pedraza, R.O.; Dos Santos, D.A. Non-linear dynamics of litter decomposition under different grazing management regimes. Plant Soil 2015, 393, 47–56. [Google Scholar] [CrossRef]
- Cruzate, G.A.; Morras, H.J.M.; Pizarro, M.J.; Gómez, L.A. Argentina Físico-Natural: Suelos. ANIDA. Atlas Nacional Interactivo de Argentina; Instituto Geográfico Nacional: Buenos Aires, Argentina, 2023; p. 61. [Google Scholar]
- Secretaria de Recursos Naturales y Desarrollo sustenable (SRNyDS). Eco-Regiones de la Argentina; Secretaria de Recursos Naturales y Desarrollo sustenable (SRNyDS): Buenos Aires, Argentina, 1999; p. 43. [Google Scholar]
- Nasca, J.A.; Banegas, N.; García Posse, F.; Martín, A.; Della Rosa, M.; Molina, A.; Fernández, P. Evaluación productiva y emisiones de gases de efecto invernadero en dos sistemas de cría bovina contrastante del Chaco Seco argentino. Rev. Agronómica Del. Noroeste Argent. 2020, 40, 13–22. [Google Scholar]
- Nelson, D.W.; Sommers, L.E. Total carbon, organic carbon, and organic matter. In Methods of Soil Analysis. Part 2, 2nd ed; Agron. Monogr. 9. ASA and SSSA; American Society of Agronomy, Soil Science Society of America: Madison, WI, USA, 1982; pp. 539–579. [Google Scholar]
- RRes, 2007. Rothamsted Carbon Model (RothC). Rothamsted Research, Harpenden, Hertfordshire, United Kingdom. Available online: http://www.rothamsted.ac.uk/rothamsted-carbon-model-rothc (accessed on 5 July 2024).
- Coleman, K.; Jenkinson, D.S. RothC-26.3-A Model for the Turnover of Carbon in Soil. Evaluation of Soil Organic Matter Models. In Evaluation of Soil Organic Matter Models Using Existing Long-Term Datasets; Powlson, D.S., Smith, P., Smith, J.U., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 237–246. [Google Scholar]
- Smith, P.F.; Holzworth, D.P.; Robertson, M.J. Linking icon-based models to code-based models: A case study with the agricultural production systems simulator. Agric. Syst. 2005, 83, 135–151. [Google Scholar] [CrossRef]
- Bala, B.K.; Arshad, F.M.; Noh, K.M. System Dynamics: Modelling and Simulation; Springer: Singapore, 2017; p. 278. [Google Scholar] [CrossRef]
- Rezende, C.P.; Cantarutti, R.B.; Braga, J.M.; Gomide, J.A.; Pereira, J.M.; Ferreira, E.; Tarré, R.; Macedo, R.; Alves, B.J.R.; Urquiaga, S.; et al. Litter deposition and disappearance in Brachiaria pastures in the Atlantic forest region of the South of Bahia, Brazil. Nutr. Cycl. Agroecosyst. 1999, 54, 99–112. [Google Scholar] [CrossRef]
- Villarino, S.H.; Pinto, P.; Jackson, R.B.; Piñeiro, G. Plant rhizodeposition: A key factor for soil organic matter formation in stable fractions. Sci. Adv. 2021, 7, eabd3176. [Google Scholar] [CrossRef]
- Ye, J.; Yue, C.; Hu, Y.; Ma, H. Spatial patterns of global-scale forest root-shoot ratio and their controlling factors. Sci. Total Environ. 2021, 800, 149251. [Google Scholar] [CrossRef]
- Jackson, R.B.; Canadell, J.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. A global analysis of root distributions for terrestrial biomes. Oecologia 1996, 108, 389–411. [Google Scholar] [CrossRef]
- Holl, K.D. Effects of above- and below-ground competition of shrubs and grass on Calophyllum brasiliense (Camb.) seedling growth in abandoned tropical pasture. For. Ecol. Manag. 1998, 109, 187–195. [Google Scholar] [CrossRef]
- Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 89, 225–247. [Google Scholar] [CrossRef]
- Bryant, J.R.; Lopez Villalobos, N. Choice of the most appropriate models and estimation procedures of lactation curves for grazing dairy cattle. Proc. N. Z. Soc. Anim. Prod. 2007, 67, 209–214. [Google Scholar]
- Lin, L.I.K. A concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Poeplau, C. Estimating root: Shoot ratio and soil carbon inputs in temperate grasslands with the RothC model. Plant Soil 2016, 407, 293–305. [Google Scholar] [CrossRef]
- Fernández, P.D.; Gasparri, N.I.; Rojas, T.N.; Banegas, N.R.; Nasca, J.A.; Jobbágy, E.G.; Kuemmerle, T. Silvopastoral management for lowering trade-offs between beef production and carbon storage in tropical dry woodlands. Sci. Total Environ. 2024, 912, 168973. [Google Scholar] [CrossRef]
- Singh, L.; Singh, J.S. Storage and flux of nutrients in a dry tropical forest in India. Ann. Bot. 1991, 68, 275–284. [Google Scholar] [CrossRef]
- Eclesia, R.P.; Jobbagy, E.G.; Jackson, R.B.; Rizzotto, M.; Piñeiro, G. Stabilization of new carbon inputs rather than old carbon decomposition determines soil organic carbon shifts following woody or herbaceous vegetation transitions. Plant Soil 2016, 409, 99–116. [Google Scholar] [CrossRef]
- Barcella, M.; Filipponi, F.; Assini, S. A simple model to support grazing management by direct field observation. Agric. Ecosyst. Environ. 2016, 234, 107–117. [Google Scholar] [CrossRef]
- Shirato, Y.; Yokozawa, M. Applying the Rothamsted Carbon Model for Long-Term Experiments on Japanese Paddy Soils and Modifying It by Simple Tuning of the Decomposition Rate. Soil Sci. Plant Nutr. 2005, 51, 405–415. [Google Scholar] [CrossRef]
- Liu, D.L.; Chan, K.Y.; Conyers, M.K. Simulation of soil organic carbon under different tillage and stubble management practices using the Rothamsted carbon model. Soil Tillage Res. 2009, 104, 65–73. [Google Scholar] [CrossRef]
- FAO. Measuring and Modelling Soil Carbon Stocks and Stock Changes in Livestock Production Systems: Guidelines for Assessment (Version 1). Livestock Environmental Assessment and Performance (LEAP) Partnership; FAO: Rome, Italy, 2019; p. 170. [Google Scholar]
- Schrumpf, M.; Schulze, E.D.; Kaiser, K.; Schumacher, J. How accurately can soil organic carbon stocks and stock changes be quantified by soil inventories? Biogeosciences 2011, 8, 1193–1212. [Google Scholar] [CrossRef]
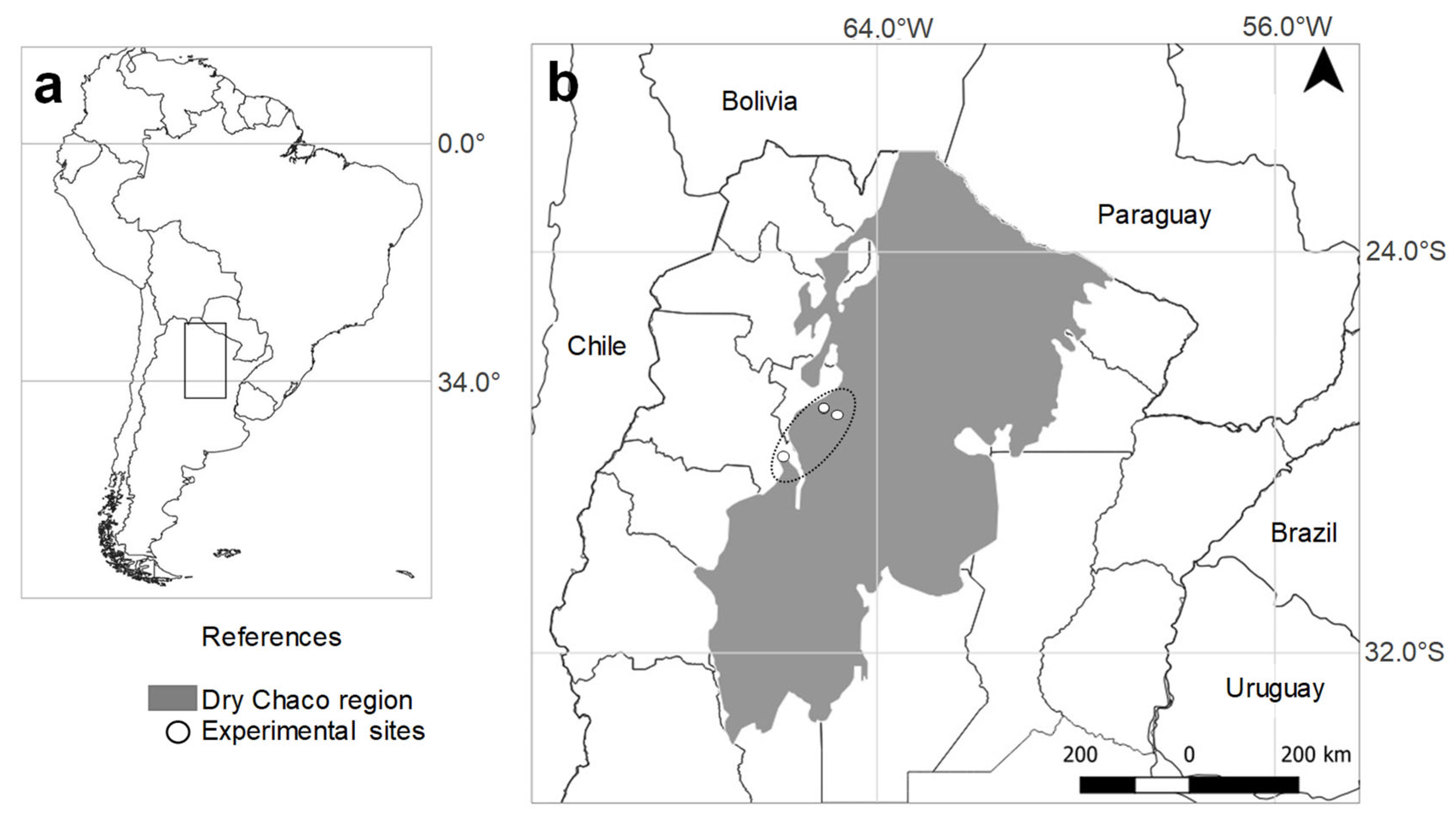

| Exp. No. | Initial SOC Stocks (Mg ha−1) 1 | Annual Mean Air Temp (°C) | Annual Rainfall (mm) | Annual Potential ET (mm) 2 | Soil Characteristics | Duration of Experiment (Years) | Aim of Experiment | Land Cover and Management | Reference |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 35.2 | 19.8 | 889 | 1356 | Clay: 13.0%, soil pH: 6.8, EC 3: 6.2 | 4 | Evaluate native vegetation (secondary ecological succession) | Native forests (Zizyphus mistol, Geoffroea decorticans, Sideroxylon obtusifolium, Ruprechtia laxiflora) | Animal Research Institute of Semiarid Chaco (IIACS) |
| 2 | 49.1 | 20.1 | 694 | 1367 | Clay: 12.0%, soil pH: 7.5, EC: 2.0 | 2 | |||
| 3a | 69.0 | 19.6 | 903 | 1481 | Clay: 12.0%, soil pH: 7.2, EC: 5.5 | 4 | [34] | ||
| 3b | 69.4 | 19.6 | 903 | 1481 | Clay: 13.2%, soil pH: 6.5, EC: 0.5 | 4 | Understand and model the dynamics of litter decomposition with varying pasture management. | Rhodes grass without N applied on grazed plots. | [34] |
| 3c | Clay: 14.0%, soil pH: 6.8, EC: 0.6 | 4 | Rhodes grass with N (100 kg N ha−1) on grazed plots. | ||||||
| 3d | Clay: 13.5%, soil pH: 6.6, EC: 0.7 | 4 | Rhodes grass for hay making without N. | ||||||
| 3e | Clay: 14.3%, soil pH: 6.5, EC: 0.5 | 4 | Rhodes grass for hay with N (100 kg N ha−1). | ||||||
| 4 | 37.6 | 19.8 | 889 | 1356 | Clay: 15.7%, soil pH: 5.9, EC: 0.3 | 4 | Evaluate intensification of cow–calf systems. | Corn/Rhodes grass | [37] |
| 5 | 38.4 | 19.8 | 889 | 1356 | Clay: 17.0%, soil pH: 6.0, EC: 0.6 | 4 | Evaluate intensification of cow–calf systems. | Degraded Rhodes grass with annual yields of ~4 Mg DM ha−1 (vs. 8 Mg DM ha−1 in experiments 3 & 4) | Unpublished data. IIACS. |
| 6 | 36.5 | 19.7 | 853 | 1345 | Clay: 11.0%, soil pH: 7.5, EC: 2.0 | 2 |
| Items | MCI | HCI | LCI |
|---|---|---|---|
| Aboveground OM formation efficiency factor (%) 1 | 7 | 10 | 4 |
| Belowground OM formation efficiency factor (%) 1 | |||
| Native forest | 49 | 60 | 38 |
| Rhodes grass and degraded Rhodes grass | 50 | 56 | 44 |
| Root/aboveground ratio (%) | |||
| Native forest 2 | 29 | 32 | 26 |
| Rhodes grass 3 | 92 | 93 | 91 |
| Rhodes grass and degraded Rhodes grass 4 | 81 | 88 | 74 |
| Items | Land Cover | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Native Forests (N = 57) | Rhodes Grass (N = 104) | Degraded Rhodes Grass (N = 48) | |||||||
| 1 MCI | 2 HCI | 3 LCI | MCI | HCI | LCI | MCI | HCI | LCI | |
| Mean observed (O) | 48.2 | 59.7 | 36.7 | ||||||
| Mean predicted (P) | 46.8 | 48.5 | 44.9 | 56.3 | 57.9 | 54.9 | 39.6 | 41.6 | 37.8 |
| Mean bias (O–P) | 1.41 | −0.3 | 3.2 | 3.3 | 1.7 | 4.7 | −3.3 | −5.2 | −1.5 |
| 4 RMSEP | 3.6 | 3.5 | 4.8 | 5.6 | 4.9 | 6.6 | 5.7 | 7.9 | 4.0 |
| 5 RPE, % | 7.5 | 7.3 | 10.0 | 9.5 | 8.2 | 11.1 | 15.6 | 21.4 | 11.0 |
| Decomposition of error | |||||||||
| % bias | 14.8 | 1.0 | 45.2 | 35.0 | 12.4 | 51.3 | 55.5 | 64.6 | 28.0 |
| % slope | 23.4 | 29.9 | 10.9 | 45.6 | 63.7 | 30.0 | 0.3 | 0.3 | 9.6 |
| % random | 61.7 | 69.1 | 43.9 | 19.4 | 23.9 | 18.7 | 44.1 | 35.1 | 62.3 |
| 6 CCC | 0.96 | 0.97 | 0.94 | 0.92 | 0.94 | 0.89 | −0.25 | −0.17 | −0.34 |
| 7 R2 | 0.95 | 0.95 | 0.94 | 0.95 | 0.96 | 0.94 | 0.23 | 0.24 | 0.17 |
| 8 MEF | 0.92 | 0.92 | 0.87 | 0.77 | 0.82 | 0.71 | −1.84 | −1.98 | −1.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filip, I.D.; Peri, P.L.; Banegas, N.; Nasca, J.; Sacido, M.; Faverin, C.; Vibart, R. Predicting Soil Organic Carbon Stocks Under Native Forests and Grasslands in the Dry Chaco Region of Argentina. Sustainability 2025, 17, 5012. https://doi.org/10.3390/su17115012
Filip ID, Peri PL, Banegas N, Nasca J, Sacido M, Faverin C, Vibart R. Predicting Soil Organic Carbon Stocks Under Native Forests and Grasslands in the Dry Chaco Region of Argentina. Sustainability. 2025; 17(11):5012. https://doi.org/10.3390/su17115012
Chicago/Turabian StyleFilip, Iván Daniel, Pablo Luis Peri, Natalia Banegas, José Nasca, Mónica Sacido, Claudia Faverin, and Ronaldo Vibart. 2025. "Predicting Soil Organic Carbon Stocks Under Native Forests and Grasslands in the Dry Chaco Region of Argentina" Sustainability 17, no. 11: 5012. https://doi.org/10.3390/su17115012
APA StyleFilip, I. D., Peri, P. L., Banegas, N., Nasca, J., Sacido, M., Faverin, C., & Vibart, R. (2025). Predicting Soil Organic Carbon Stocks Under Native Forests and Grasslands in the Dry Chaco Region of Argentina. Sustainability, 17(11), 5012. https://doi.org/10.3390/su17115012







