Quantum-Inspired Spatio-Temporal Inference Network for Sustainable Car-Sharing Demand Prediction
Abstract
1. Introduction
2. Literature Review
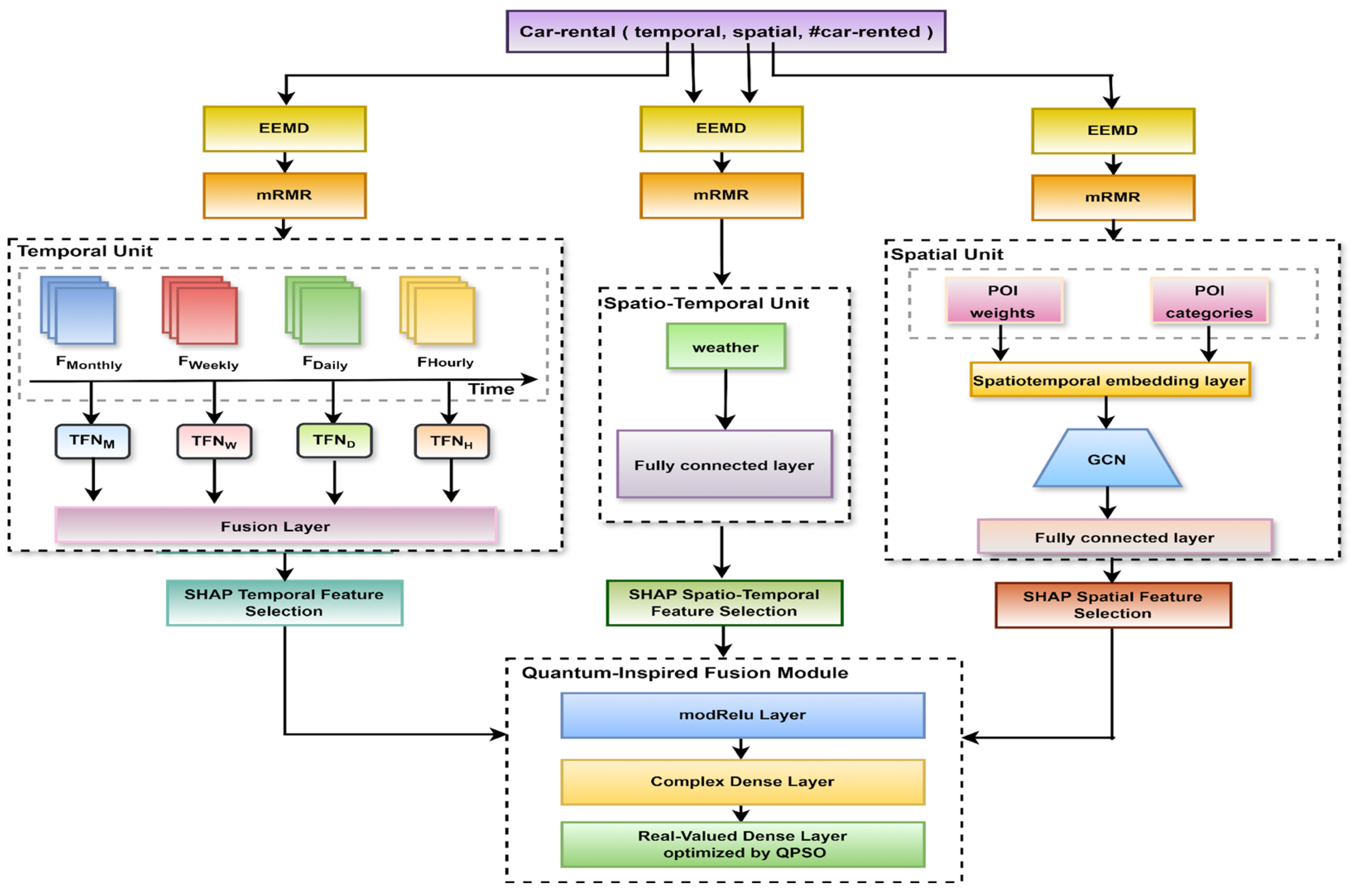
3. Methodology
3.1. Feature Extraction
3.2. Feature Selection
3.3. Predictive Model
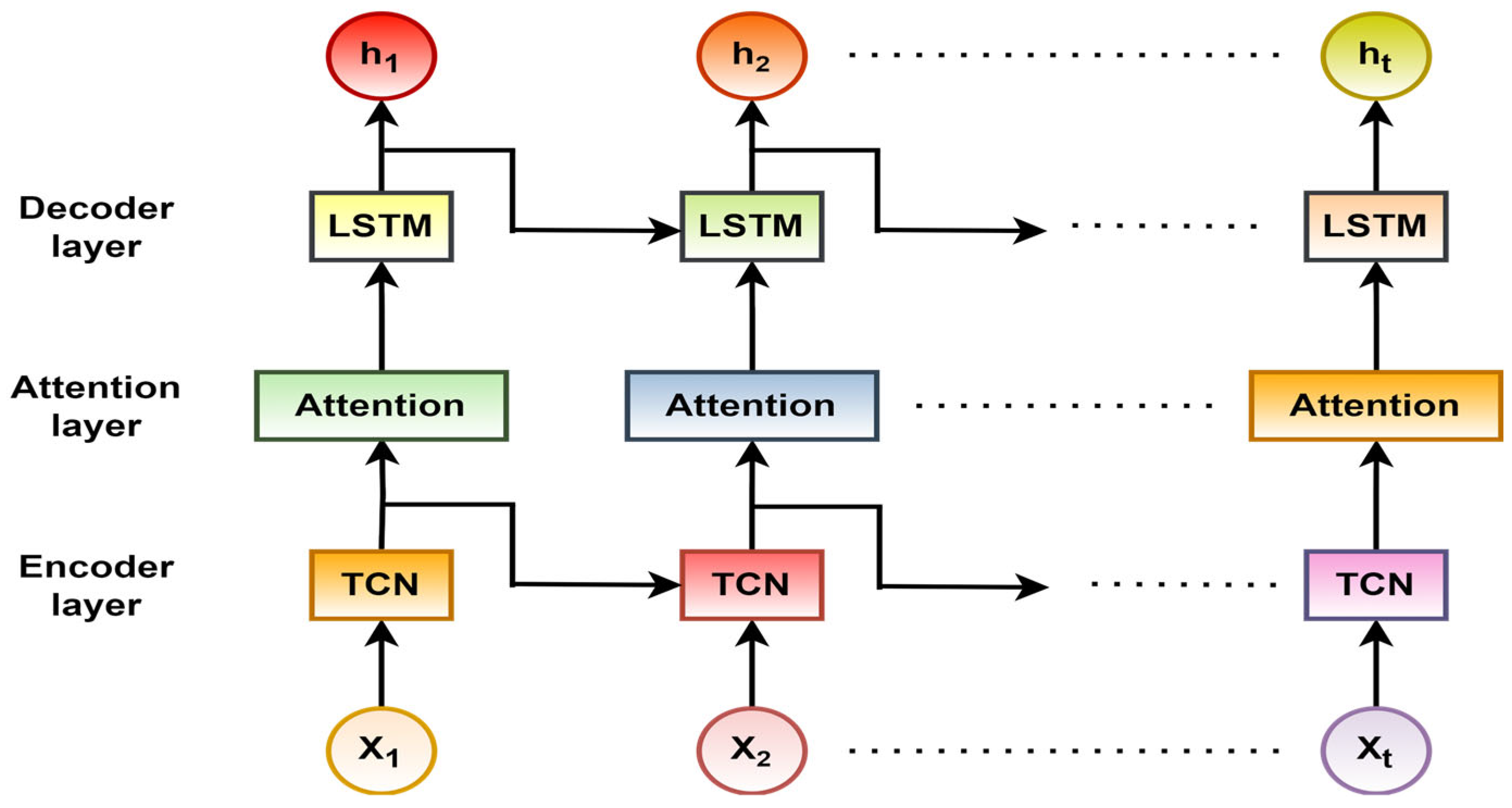
3.3.1. Temporal Feature Unit
- 1.
- Encoder: temporal convolutional network (TCN)
- 2.
- Attention mechanism layer
- 3.
- Decoder: long short-term memory layer (LSTM)
3.3.2. Spatial Feature Unit
- 1.
- Spatial density calculation
- 2.
- Regression model
- 3.
- Spatiotemporal embedding layer
- 4.
- Graph convolutional network layer (GCN)
- 5.
- Fully connected layer
3.3.3. Spatio-Temporal Feature Unit
3.3.4. Quantum Inspired Fusion Module
- 1.
- Encoding multimodal features in the complex domain
- 2.
- Nonlinear activation in the complex domain
- 3.
- Complex-valued representation through dense transformation
- 4.
- Real-Valued Output Regression Layer
- 5.
- Optimization with Quantum Particle Swarm Optimization (QPSO)
- 6.
- Final Demand Prediction Output
4. Experiment
4.1. Data Description
4.2. Baseline Models Configuration
4.3. Model Configuration
4.4. Evaluation Metrics
4.4.1. Mean Absolute Error (MAE)
4.4.2. Mean Square Error (MSE)
4.4.3. Root Mean Square Error (RMSE)
4.4.4. Mean Absolute Percentage Error (MAPE)
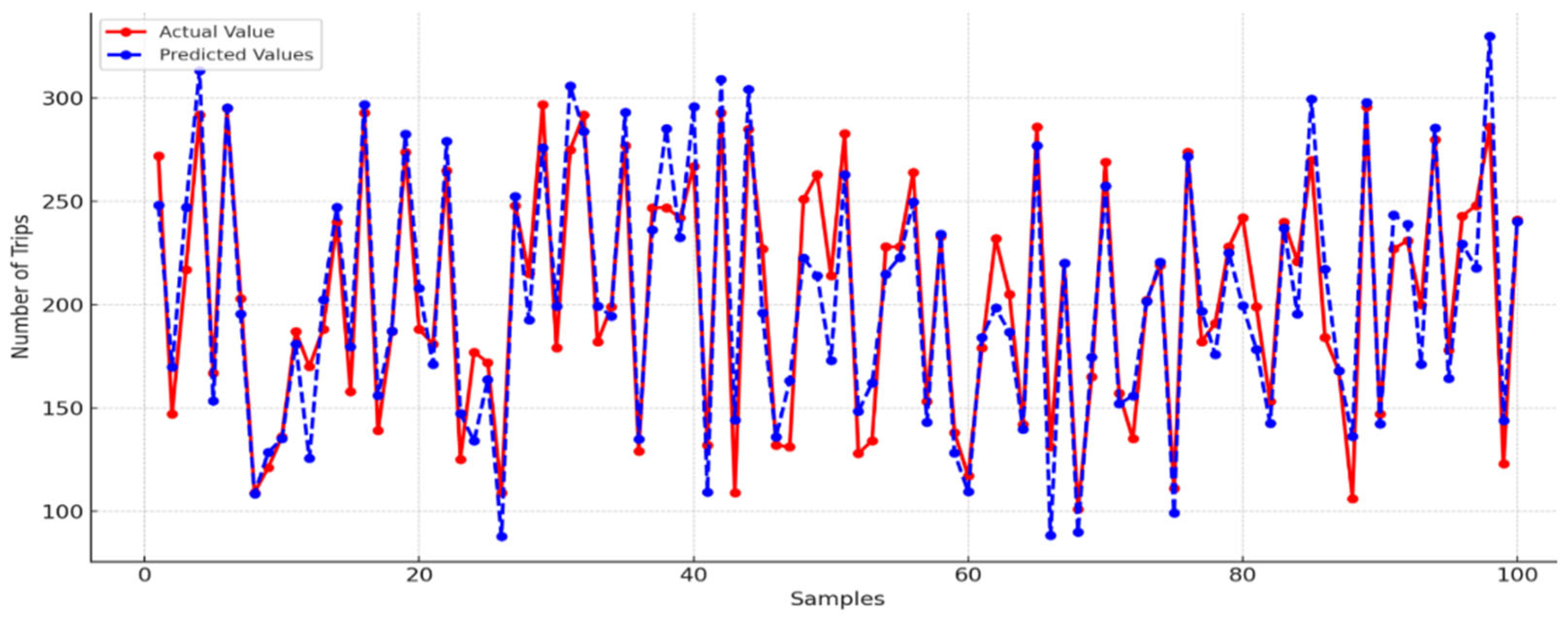
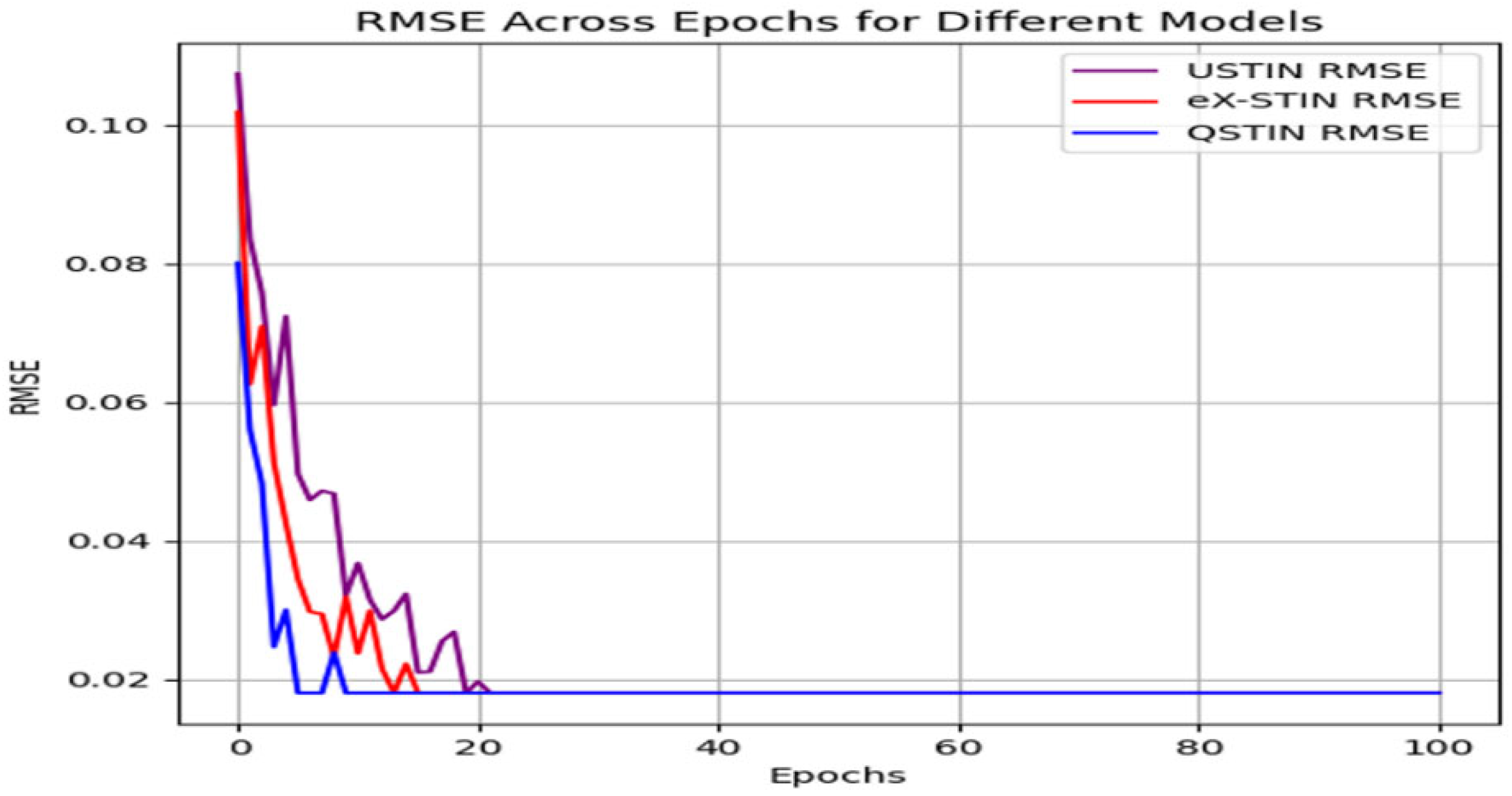
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, Y.; You, J.; Wang, R.; Qin, B.; Han, S. Urban Transportation Data Research Overview: A Bibliometric Analysis Based on CiteSpace. Sustainability 2024, 16, 9615. [Google Scholar] [CrossRef]
- Brahimi, N.; Zhang, H.; Razzaq, Z. Explainable Spatio-Temporal Inference Network for Car-Sharing Demand Prediction. ISPRS Int. J. Geo-Inf. 2025, 14, 163. [Google Scholar] [CrossRef]
- Schuld, M.; Sinayskiy, I.; Petruccione, F. The quest for a Quantum Neural Network. Quantum Inf. Process. 2014, 13, 2567–2586. [Google Scholar] [CrossRef]
- Beer, K.; Bondarenko, D.; Farrelly, T.; Osborne, T.J.; Salzmann, R.; Scheiermann, D.; Wolf, R. Training deep quantum neural networks. Nat. Commun. 2020, 11, 808. [Google Scholar] [CrossRef]
- Sun, J.; Xu, W.; Feng, B. A global search strategy of Quantum-behaved Particle Swarm Optimization. In Proceedings of the 2004 IEEE Conference Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; pp. 111–116. [Google Scholar] [CrossRef]
- Zouache, D.; Nouioua, F.; Moussaoui, A. Quantum-inspired firefly algorithm with particle swarm optimization for discrete optimization problems. Soft Comput. 2016, 20, 2781–2799. [Google Scholar] [CrossRef]
- Brahimi, N.; Zhang, H.; Zaidi, S.D.A.; Dai, L. A Unified Spatio-Temporal Inference Network for Car-Sharing Serial Prediction. Sensors 2024, 24, 1266. [Google Scholar] [CrossRef]
- Brahimi, N.; Zhang, H.; Dai, L.; Zhang, J. Modelling on Car-Sharing Serial Prediction Based on Machine Learning and Deep Learning. Complexity 2022, 8843000. [Google Scholar] [CrossRef]
- Chen, L.; Chen, H. Joint distribution route optimization of vehicle and drone based on NSGA II. In Proceedings of the International Conference on Smart Transportation and City Engineering (STCE 2023), Chongqing, China, 16–18 December 2023; p. 109. [Google Scholar] [CrossRef]
- Chai, X.; Zhang, Y.; Du, D.; Sun, Y. Bi-level optimization scheduling of electric vehicle-distribution network considering demand response and carbon quota. J. Phys. Conf. Ser. 2024, 2849, 012075. [Google Scholar] [CrossRef]
- Luan, R. Logistics distribution route optimization of electric vehicles based on distributed intelligent system. Int. J. Emerg. Electr. Power Syst. 2024, 25, 629–639. [Google Scholar] [CrossRef]
- Petri, M.; Kniess, J.; Parpinelli, R.S. Resource scheduling for mobility scenarios with time constraints. In Proceedings of the 2018 44th Latin American Computer Conference (CLEI 2018), Sao Paulo, Brazil, 1–5 October 2018; pp. 184–191. [Google Scholar] [CrossRef]
- Hsieh, C.; Sani, A.; Dutt, N. The case for exploiting underutilized resources in heterogeneous mobile architectures. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019. [Google Scholar] [CrossRef]
- Feng, S.; Ke, J.; Yang, H.; Ye, J. A Multi-Task Matrix Factorized Graph Neural Network for Co-Prediction of Zone-Based and OD-Based Ride-Hailing Demand. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5704–5716. [Google Scholar] [CrossRef]
- Wang, C.; Deng, Z. Multi-perspective Spatiotemporal Context-aware Neural Networks for Human Mobility Prediction. In Proceedings of the HuMob 2023—1st International Workshop on the Human Mobility Prediction Challenge, Hamburg, Germany, 13 November 2023; pp. 32–36. [Google Scholar] [CrossRef]
- He, M.; Li, X.; Zhao, H.; Yao, Y.; Zhou, T. A Topology-Enhanced Graph Convolutional Network for Urban Traffic Prediction. In Proceedings of the 2024 7th International Conference on Electronics Technology, Chengdu, China, 17–20 May 2024; pp. 1093–1097. [Google Scholar] [CrossRef]
- Yuan, G.; Fan, X.; Huang, Y.; Xuesong, J. Research on Urban Traffic Flow Prediction Model Utilizing Heterogeneous Data Fusion. In Proceedings of the 2024 10th IEEE International Conference on Intelligent Data and Security (IDS), New York City, NY, USA, 10–12 May 2024; pp. 32–36. [Google Scholar] [CrossRef]
- Pan, Z.; Liang, Y.; Wang, W.; Yu, Y.; Zheng, Y.; Zhang, J. Urban traffic prediction from spatio-temporal data using deep meta learning. In Proceedings of the 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1720–1730. [Google Scholar] [CrossRef]
- Yu, B.; Li, M.; Zhang, J.; Zhu, Z. 3D Graph Convolutional Networks with Temporal Graphs: A Spatial Information Free Framework for Traffic Forecasting. arXiv 2019, arXiv:1903.00919. [Google Scholar] [CrossRef]
- Ou, J.; Sun, J.; Zhu, Y.; Jin, H.; Liu, Y.; Zhang, F.; Huang, J.; Wang, X. STP-TrellisNets+: Spatial-Temporal Parallel TrellisNets for Multi-Step Metro Station Passenger Flow Prediction. IEEE Trans. Knowl. Data Eng. 2023, 35, 7526–7540. [Google Scholar] [CrossRef]
- Kardashin, A.; Balkybek, Y.; Palyulin, V.V.; Antipin, K. Predicting properties of quantum systems by regression on a quantum computer. Phys. Rev. Res. 2025, 7, 013201. [Google Scholar] [CrossRef]
- Huerga, A.; Aguilera, U.; Almeida, A.; Lago, A.B. A Quantum Computing Approach to Human Behavior Prediction. In Proceedings of the 2022 7th International Conference on Smart and Sustainable Technologies, Bol, Croatia, 5–8 July 2022. [Google Scholar] [CrossRef]
- Surendiran, B.; Dhanasekaran, K.; Tamizhselvi, A. A Study on Quantum Machine Learning for Accurate and Efficient Weather Prediction. In Proceedings of the 2022 Sixth International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Dharan, Nepal, 10–12 November 2022; pp. 534–537. [Google Scholar] [CrossRef]
- Li, Q.; Huang, Z.; Jiang, W.; Tang, Z.; Song, M. Quantum Algorithms Using Infeasible Solution Constraints for Collision-Avoidance Route Planning. IEEE Trans. Consum. Electron. 2024. [Google Scholar] [CrossRef]
- Zhuang, Y.; Azfar, T.; Wang, Y.; Sun, W.; Wang, X.; Guo, Q.; Ke, R. Quantum Computing in Intelligent Transportation Systems: A Survey. CHAIN 2024, 1, 138–149. [Google Scholar] [CrossRef]
- Qu, Z.; Liu, X.; Zheng, M. Temporal-Spatial Quantum Graph Convolutional Neural Network Based on Schrödinger Approach for Traffic Congestion Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8677–8686. [Google Scholar] [CrossRef]
- Pandurangan, K.; Priyadharshini, A.; Taseen, R.; Galebathullah, B.; Yaseen, H.; Ravichandran, P. Quantum-Inspired Algorithms for AI and Machine Learning. In Integration of AI, Quantum Computing, and Semiconductor Technology; IGI Global: Hershey, PA, USA, 2024; pp. 79–92. [Google Scholar] [CrossRef]
- Zhang, B. Quantum Neural Networks: A New Frontier. Theor. Nat. Sci. 2024, 41, 122–128. [Google Scholar] [CrossRef]
- Tomal, S.M.Y.I.; Al Shafin, A.; Afaf, A.; Bhattacharjee, D. Quantum Convolutional Neural Network: A Hybrid Quantum-Classical Approach for Iris Dataset Classification. J. Future Artif. Intell. Technol. 2024, 1, 284–295. [Google Scholar] [CrossRef]
- Thakkar, S.; Kazdaghli, S.; Mathur, N.; Kerenidis, I.; Ferreira–Martins, A.J.; Brito, S. Improved financial forecasting via quantum machine learning. Quantum Mach. Intell. 2024, 6, 27. [Google Scholar] [CrossRef]
- Dong, Y.; Xie, J.; Hu, W.; Liu, C.; Luo, Y. Variational algorithm of quantum neural network based on quantum particle swarm. J. Appl. Phys. 2022, 132, 104401. [Google Scholar] [CrossRef]
- Alvarez-Alvarado, M.S.; Alban-Chacón, F.E.; Lamilla-Rubio, E.A.; Rodríguez-Gallegos, C.D.; Velásquez, W. Three novel quantum-inspired swarm optimization algorithms using different bounded potential fields. Sci. Rep. 2021, 11, 11655. [Google Scholar] [CrossRef] [PubMed]
- Fallahi, S.; Taghadosi, M. Quantum-behaved particle swarm optimization based on solitons. Sci. Rep. 2022, 12, 13977. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Wang, J.; Fan, H.; Zhang, T.; Gao, J.; Yang, P. New method of traffic flow forecasting based on quantum particle swarm optimization strategy for intelligent transportation system. Int. J. Commun. Syst. 2021, 34, e4647. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Data Clustering using a Hybrid of Fuzzy C-Means and Quantum-behaved Particle Swarm Optimization. In Proceedings of the 2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 8–10 January 2018; pp. 137–142. [Google Scholar] [CrossRef]
- Mao, X.; Yang, A.C.; Peng, C.K.; Shang, P. Analysis of economic growth fluctuations based on EEMD and causal decomposition. Phys. A Stat. Mech. Its Appl. 2020, 553, 124661. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Hu, C.; Peng, Z. Recent progress on decoupling diagnosis of hybrid failures in gear transmission systems using vibration sensor signal: A review. Measurement 2016, 90, 4–19. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, C.; Li, T. Gene selection algorithm by combining reliefF and mRMR. BMC Genom. 2008, 9 (Suppl. S2), S27. [Google Scholar] [CrossRef]
- Ardiles, L.G.; Tadano, Y.S.; Costa, S.; Urbina, V.; Capucim, M.N.; da Silva, I.; Braga, A.; Martins, J.A.; Martins, L.D. Negative Binomial regression model for analysis of the relationship between hospitalization and air pollution. Atmos. Pollut. Res. 2018, 9, 333–341. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Wang, M. A Unified Approach to Interpreting Model Predictions Scott. Nips 2012, 16, 426–430. [Google Scholar]
- Ahmed, S.F.; Bin Alam, S.; Hassan, M.; Rozbu, M.R.; Ishtiak, T.; Rafa, N.; Mofijur, M.; Ali, A.B.M.S.; Gandomi, A.H. Deep learning modelling techniques: Current progress, applications, advantages, and challenges. Artif. Intell. Rev. 2023, 56, 13521–13617. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A survey of methods for explaining black box models. ACM Comput. Surv. 2018, 51, 93. [Google Scholar] [CrossRef]
- Zhao, Q.; Hou, C.; Xu, R. Quantum-inspired complex-valued language models for aspect-based sentiment classification. Entropy 2022, 24, 621. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Wang, Z.; Cui, G.; Wang, S.; Shang, R.; Li, W.; Wei, Z.; Gu, Y. Quantum-inspired complex convolutional neural networks. Appl. Intell. 2022, 52, 17912–17921. [Google Scholar] [CrossRef]
- Caragea, A.; Lee, D.G.; Maly, J.; Pfander, G.; Voigtlaender, F. Quantitative Approximation Results for Complex-Valued Neural Networks. SIAM J. Math. Data Sci. 2022, 4, 553–580. [Google Scholar] [CrossRef]
- Liu, L.; Fan, X. An Improved Quantum Particle Swarm Optimization Algorithm for Target Tracking Deployment in Spatial Sensor Networks. J. Internet Technol. 2024, 25, 709–721. [Google Scholar] [CrossRef]
- Zamani Joharestani, M.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef]
- Chen, C.; Twycross, J.; Garibaldi, J.M. A new accuracy measure based on bounded relative error for time series forecasting. PLOS ONE 2017, 12, e0174202. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Hosamo, H.; Mazzetto, S. Performance Evaluation of Machine Learning Models for Predicting Energy Consumption and Occupant Dissatisfaction in Buildings. Buildings 2024, 15, 39. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Y.; Yang, C.; Wu, C. A new improved quantum-behaved particle swarm optimization model. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications (ICIEA 2009), Xi’an, China, 25–27 May 2009; pp. 1560–1564. [Google Scholar] [CrossRef]
- AlBaity, H.; Meshoul, S.; Kaban, A. On extending quantum behaved particle swarm optimization to multiobjective context. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation (CEC 2012), Brisbane, QLD, Australia, 10–15 June 2012. [Google Scholar] [CrossRef]
| Feature Category | Indicators |
|---|---|
| Usage Feature | number_of_rented_cars |
| Temporal Features | workday (binary: 1 = yes, 0 = no), rush_hour (binary) |
| Weather Conditions | temperature (℃), precipitation (binary), air_quality_index (AQI) |
| Building Environment (POIs) | hotel, domestic_services, gyms, shopping, beauty, leisure_entertainment, education, culture_media, tourist_attractions, medical, car_services, transport_facilities, finance, corporate, real_estate, government_agency, natural_features, landmarks, access_points, address_markers, etc. |
| Model | Hyperparameters | Values |
|---|---|---|
| MLP | layers | 2 |
| hidden_units | 2 layers (20, 15 neurons) | |
| XGBoost | num_estimators | 25 |
| max_depth | 5 | |
| KNN | num_neighbours | 5 |
| weights | uniform | |
| RF | num_estimators | 100 |
| max_depth | 5 | |
| min_samples_split | 15 | |
| LSTM | hidden_units | 2 layers (25, 15 neurons) |
| learning rate | 0.01 | |
| dropout | 0.5 | |
| optimizer | Adam | |
| epochs | 80 | |
| CNN-LSTM | CNN layers | 2 |
| LSTM layers | 2 | |
| filters | 64 | |
| kernel size | 3 | |
| LSTM units | 50 | |
| dropout | 0.3 | |
| optimizer | Adam | |
| Att-LSTM | layers | 5 |
| units | 50 | |
| attention type | Bahdanau | |
| dropout | 0.4 | |
| optimizer | Adam | |
| ConvLSTM | layers | 2 |
| filters | 64 | |
| kernel_size | 3 × 3 | |
| dropout | 0.3 | |
| optimizer | Adam | |
| GATs | attention heads | 4 |
| hidden units | 20 | |
| learning rate | 0.01 | |
| dropout | 0.6 | |
| optimizer | Adam | |
| Transformer | heads | 4 |
| layers | 3 | |
| size | 128 | |
| feedforward_size | 512 | |
| dropout | 0.1 | |
| optimizer | Adam | |
| ST-GCN | spatial GCN layers | 3 |
| hidden units | 64 | |
| kernel size | 5 | |
| dropout | 0.2 | |
| optimizer | Adam | |
| DCN | cross layers | 3 |
| deep layers | 2 | |
| hidden units deep layer | 32 | |
| dropout | 0.2 | |
| optimizer | Adam |
| Model | Hyperparameters | Values |
|---|---|---|
| TCN | hidden layers | 3 |
| kernel size | 3 | |
| dilations | [1, 2, 4, 8, 16, 32, 64] | |
| number of filters | 64 | |
| learning rate | 0.01 | |
| drop out | 0.2 | |
| optimizer | Adam | |
| epochs | 80 | |
| LSTM | hidden layers | 2 |
| hidden units | 2 layers (25, 15 neurons) | |
| learning rate | 0.01 | |
| drop out | 0.3 | |
| optimizer | Adam | |
| epochs | 100 | |
| GCN | hidden Layers | 2 layers (32, 64 neurons) |
| learning rate | 0.01 | |
| epochs | 80 | |
| QINN | 0.001 | |
| num particles (QPSO) | 30 | |
| 0.75 | ||
| 0.0001 | ||
| dropout | 0.2 | |
| complex dense layer size | 64 | |
| output neurons | 1 | |
| activation function | modReLU |
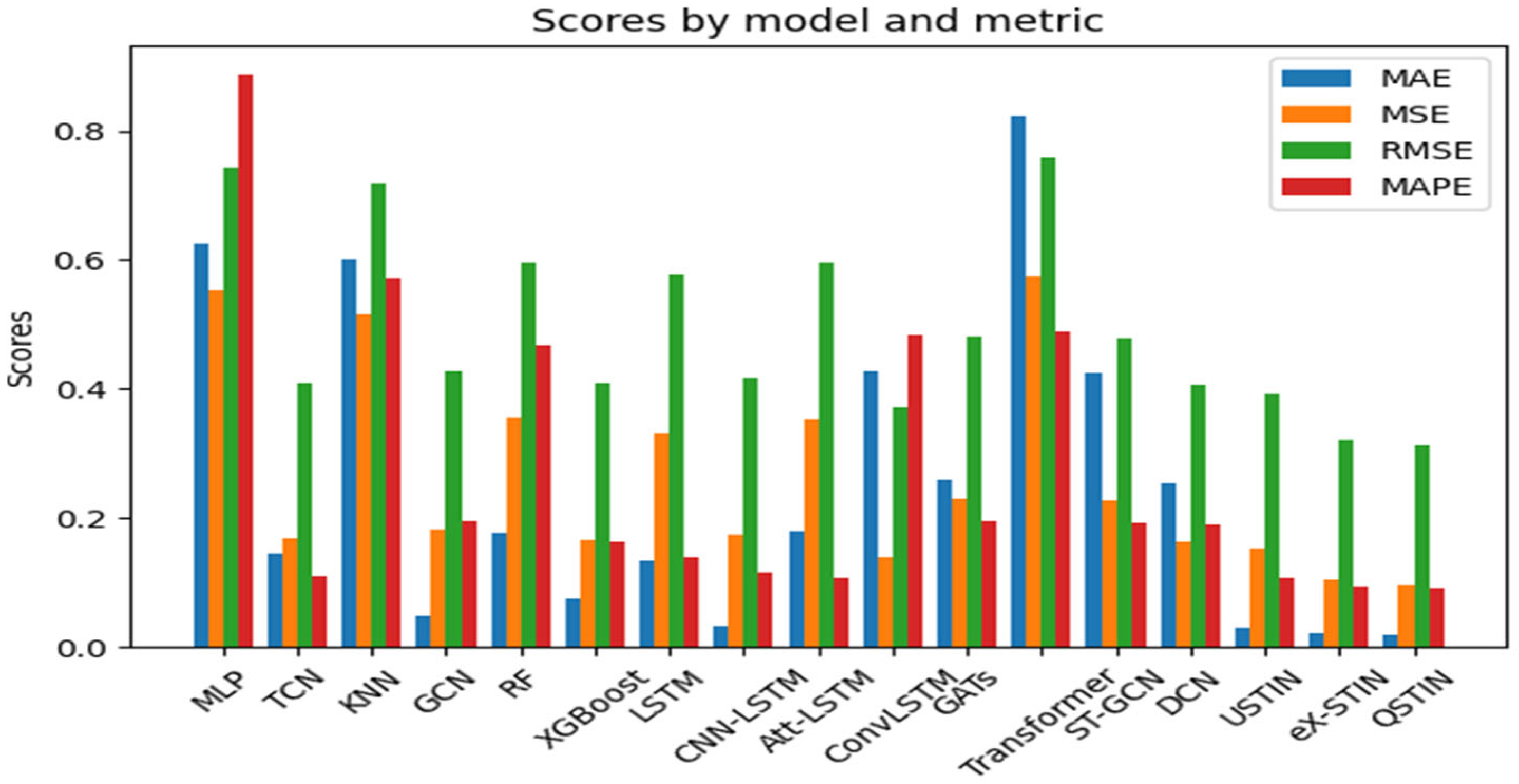
| MAE | MSE | RMSE | MAPE | |
|---|---|---|---|---|
| MLP | 0.626 | 0.554 | 0.744 | 0.887 |
| TCN | 0.145 | 0.168 | 0.410 | 0.109 |
| KNN | 0.601 | 0.515 | 0.718 | 0.571 |
| GCN | 0.048 | 0.182 | 0.427 | 0.195 |
| RF | 0.177 | 0.356 | 0.597 | 0.469 |
| XGBoost | 0.076 | 0.167 | 0.409 | 0.164 |
| LSTM | 0.135 | 0.333 | 0.577 | 0.139 |
| CNN-LSTM | 0.033 | 0.175 | 0.418 | 0.115 |
| Att-LSTM | 0.181 | 0.354 | 0.595 | 0.108 |
| ConvLSTM | 0.428 | 0.139 | 0.373 | 0.484 |
| GATs | 0.259 | 0.230 | 0.480 | 0.195 |
| Transformer | 0.824 | 0.575 | 0.758 | 0.488 |
| ST-GCN | 0.426 | 0.229 | 0.479 | 0.192 |
| DCN | 0.255 | 0.165 | 0.406 | 0.191 |
| USTIN | 0.031 | 0.154 | 0.392 | 0.108 |
| eX-STIN | 0.022 | 0.104 | 0.322 | 0.094 |
| Proposed (QSTIN) | 0.020 | 0.098 | 0.313 | 0.078 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brahimi, N.; Zhang, H.; Razzaq, Z. Quantum-Inspired Spatio-Temporal Inference Network for Sustainable Car-Sharing Demand Prediction. Sustainability 2025, 17, 4987. https://doi.org/10.3390/su17114987
Brahimi N, Zhang H, Razzaq Z. Quantum-Inspired Spatio-Temporal Inference Network for Sustainable Car-Sharing Demand Prediction. Sustainability. 2025; 17(11):4987. https://doi.org/10.3390/su17114987
Chicago/Turabian StyleBrahimi, Nihad, Huaping Zhang, and Zahid Razzaq. 2025. "Quantum-Inspired Spatio-Temporal Inference Network for Sustainable Car-Sharing Demand Prediction" Sustainability 17, no. 11: 4987. https://doi.org/10.3390/su17114987
APA StyleBrahimi, N., Zhang, H., & Razzaq, Z. (2025). Quantum-Inspired Spatio-Temporal Inference Network for Sustainable Car-Sharing Demand Prediction. Sustainability, 17(11), 4987. https://doi.org/10.3390/su17114987






