Numerical Modeling of Biofilm–Flow Dynamics in Gravel-Bed Rivers: A Framework for Sustainable Restoration
Abstract
1. Introduction
2. Materials and Methods
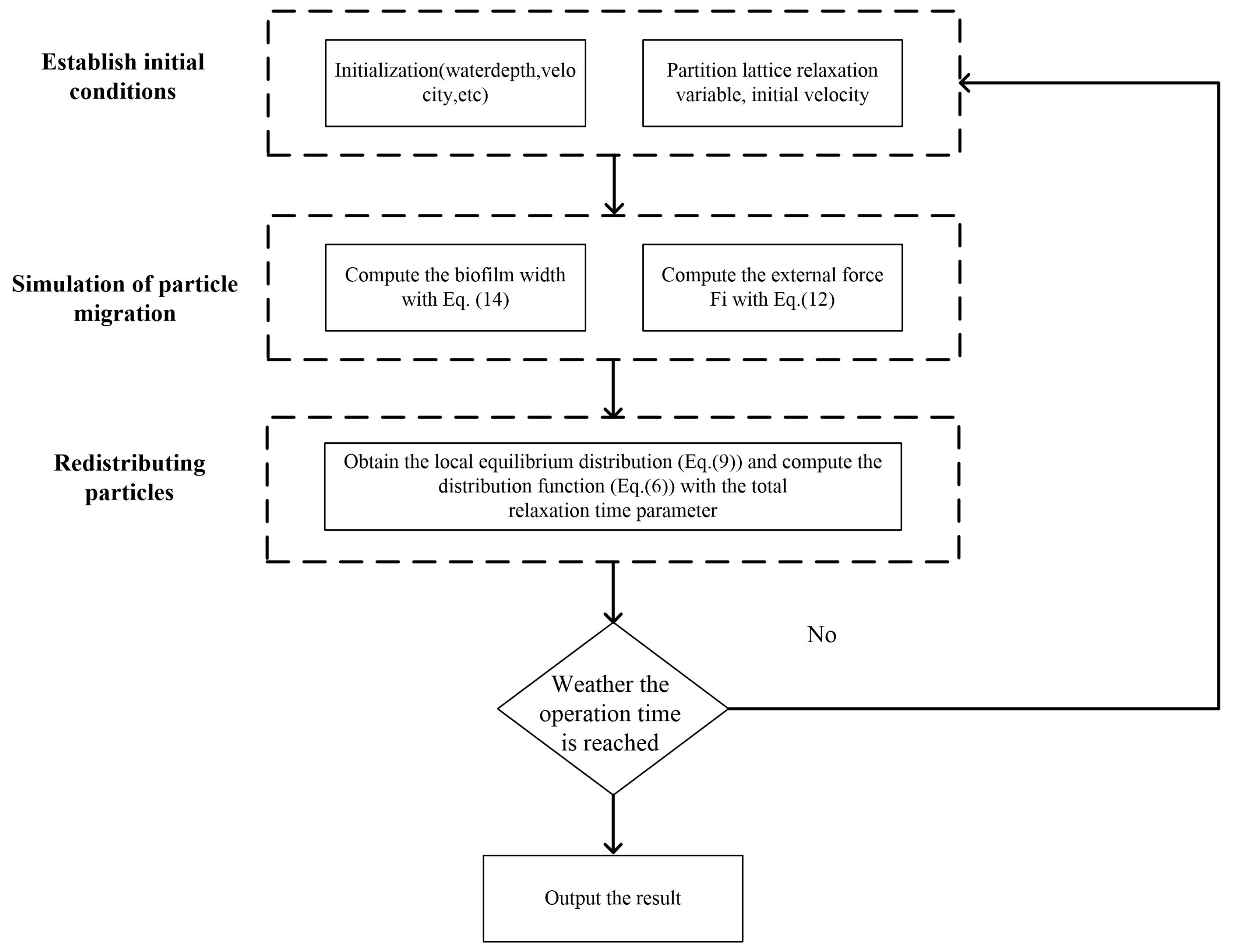
2.1. Numerical Model
2.1.1. Hydraulic Model
2.1.2. Biofilm Growth and Detachment Model
2.1.3. Error Analysis
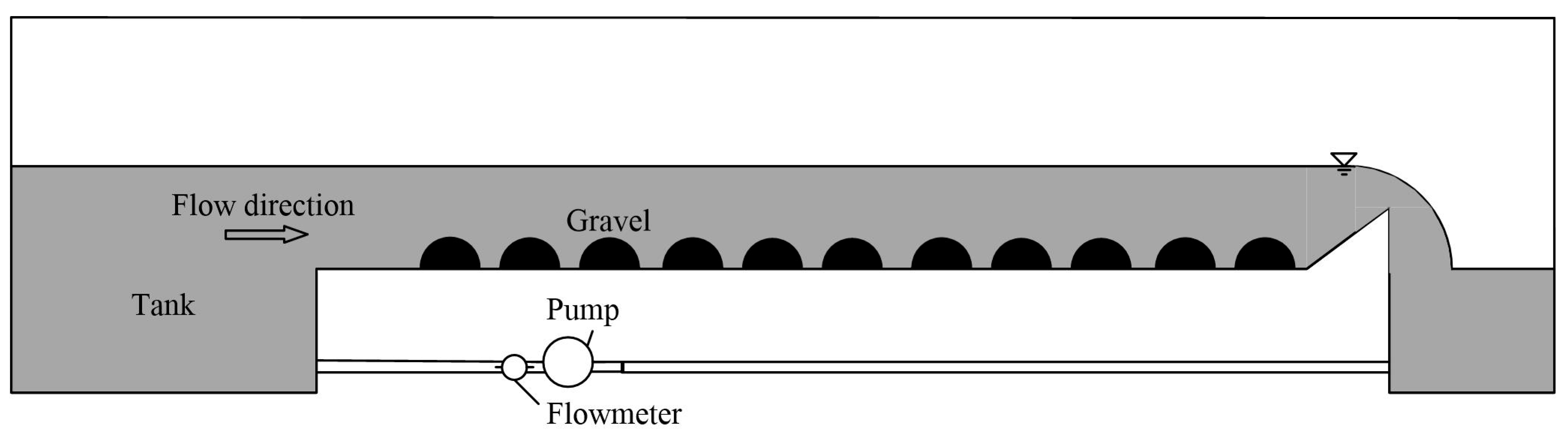
2.2. Validation Data
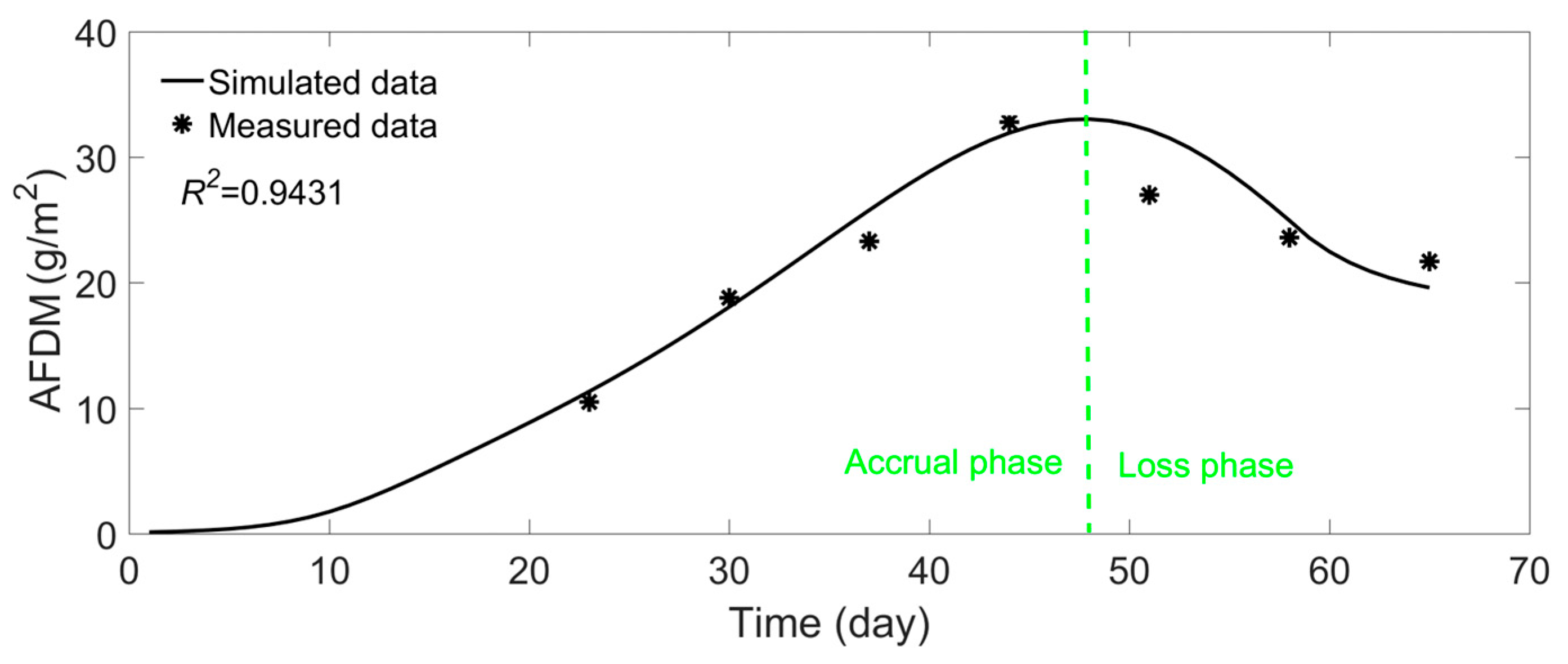
3. Results
4. Discussion
4.1. Velocity Analysis
4.2. Pollution Transport Analysis
4.3. Limitation of This Study
4.3.1. Limited Field Data
4.3.2. Homogeneous Growth Model
4.4. Future Work
5. Conclusions
- (1)
- Nonlinear Modulation of Hydraulic Roughness by Biofilm: Biofilm growth exhibits a dual-phase regulatory mechanism. Moderate colonization reduces equivalent roughness by smoothing interstitial gravel pores, while excessive accumulation forms emergent biological structures, significantly increasing flow resistance. This highlights the dynamic equilibrium role of biofilm in modulating hydraulic characteristics.
- (2)
- Model Validation and Applicability: Validation against laboratory flume data (65-day biofilm growth cycle) demonstrated the model’s accuracy in simulating biomass trends (ash-free dry mass) and velocity distribution patterns, confirming its reliability under short-term, homogeneous substrate conditions.
- (3)
- Theoretical Innovation and Engineering Value: By establishing a dynamic correlation model between biofilm thickness and roughness parameters, this study addresses the limitations of conventional models that neglect biofilm–flow coupling effects. It provides a numerical platform for optimizing ecological river restoration strategies, such as balancing pollutant removal efficiency with hydraulic resistance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, J.; Rao, M.; Zhang, H.; Wang, Q.; Shen, Y.; Ye, J.; Zhang, S. Evolution of Interspecific Interactions Underlying the Nonlinear Relationship Between Active Biomass and Pollutant Degradation Capacity in Bioelectrochemical Systems. Water Res. 2025, 274, 123071. [Google Scholar] [CrossRef] [PubMed]
- Anlanger, C.; Risse-Buhl, U.; von Schiller, D.; Noss, C.; Weitere, M.; Lorke, A. Hydraulic and Biological Controls of Biofilm Nitrogen Uptake in Gravel-Bed Streams. Limnol. Oceanogr. 2021, 66, 3887–3900. [Google Scholar] [CrossRef]
- Zhang, L.; Luo, W. Reach-Averaged Flow Resistance in Gravel-Bed Streams. J. Water Clim. Chang. 2021, 12, 1580–1597. [Google Scholar] [CrossRef]
- Nikora, V.; Goring, D.; McEwan, I.; Griffiths, G. Spatially Averaged Open-Channel Flow over Rough Bed. J. Hydraul. Eng. 2001, 127, 123–133. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Maddahi, M.R.; Sui, J. Bedform Characteristics in a Gravel-Bed River. J. Hydrol. Hydromech. 2017, 65, 366. [Google Scholar] [CrossRef]
- Bertin, S.; Groom, J.; Friedrich, H. Isolating Roughness Scales of Gravel-Bed Patches. Water Resour. Res. 2017, 53, 6841–6856. [Google Scholar] [CrossRef]
- Dey, S. Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena; Springer: Berlin, Germany, 2014. [Google Scholar]
- Hardy, R.J.; Best, J.L.; Lane, S.N.; Carbonneau, P.E. Coherent Flow Structures in a Depth-Limited Flow over a Gravel Surface: The Role of Near-Bed Turbulence and Influence of Reynolds Number. J. Geophys. Res. Earth Surf. 2009, 114, F01003. [Google Scholar] [CrossRef]
- van der Mark, C.F.; Blom, A.; Hulscher, S.J.M.H. Quantification of Variability in Bedform Geometry. J. Geophys. Res. Earth Surf. 2008, 113, F03020. [Google Scholar] [CrossRef]
- Dreszer, C.; Vrouwenvelder, J.S.; Paulitsch-Fuchs, A.H.; Zwijnenburg, A.; Kruithof, J.C.; Flemming, H.C. Hydraulic Resistance of Biofilms. J. Membr. Sci. 2013, 429, 436–447. [Google Scholar] [CrossRef]
- Battin, T.J.; Kaplan, L.A.; Newbold, J.D.; Cheng, X.; Hansen, C. Effects of Current Velocity on the Nascent Architecture of Stream Microbial Biofilms. Appl. Environ. Microbiol. 2003, 69, 5443–5452. [Google Scholar] [CrossRef]
- Bilgili, E.; Bomers, A.; van Lente, G.J.W.; Huthoff, F.; Hulscher, S.J. The Effect of a Local Mesh Refinement on Hydraulic Modelling of River Meanders. River Res. Appl. 2023, 39, 832–846. [Google Scholar] [CrossRef]
- Grimaldi, S.; Li, Y.; Walker, J.P.; Pauwels, V.R.N. Effective Representation of River Geometry in Hydraulic Flood Forecast Models. Water Resour. Res. 2018, 54, 1031–1057. [Google Scholar] [CrossRef]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-Dimensional Numerical Model for Flow and Bed Deformation around River Hydraulic Structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Ahn, J.; Na, Y.; Park, S.W. Development of Two-Dimensional Inundation Modelling Process Using MIKE21 Model. KSCE J. Civ. Eng. 2019, 23, 3968–3977. [Google Scholar] [CrossRef]
- Xu, C.; Tian, J.; Liu, Z.; Wang, R.; Wang, G. Three-Dimensional Reverse Modeling and Hydraulic Analysis of the Intake Structure of Pumping Stations on Sediment-Laden Rivers. Water Res. Manag. 2023, 37, 537–555. [Google Scholar] [CrossRef]
- Tassi, P.; Benson, T.; Delinares, M.; Fontaine, J.; Huybrechts, N.; Kopmann, R.; Walther, R. GAIA—A Unified Framework for Sediment Transport and Bed Evolution in Rivers, Coastal Seas and Transitional Waters in the TELEMAC-MASCARET Modelling System. Environ. Model. Softw. 2023, 159, 105544. [Google Scholar] [CrossRef]
- Darijani, Z.; Ghaeini-Hessaroeyeh, M.; Fadaei-Kermani, E. Flood Inundation and Hazard Mapping Using the HEC-RAS 2D Model: A Case Study of Adoori River, Iran. Model. Earth Syst. Environ. 2025, 11, 78. [Google Scholar] [CrossRef]
- Haddach, A.; Smaoui, H.; Radi, B. The Study of Coastal Flows Based on Lattice Boltzmann Method: Application Oualidia Lagoon. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 225. [Google Scholar] [CrossRef]
- Biscarini, C.; Di Francesco, S.; Mencattini, M. Application of the Lattice Boltzmann Method for Large-Scale Hydraulic Problems. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 584–601. [Google Scholar] [CrossRef]
- Delavar, M.A.; Wang, J. Lattice Boltzmann Method in Modeling Biofilm Formation, Growth and Detachment. Sustainability 2021, 13, 7968. [Google Scholar] [CrossRef]
- Bray, D.I. Estimating Average Velocity in Gravel-Bed Rivers. J. Hydraul. Div. 1979, 105, 1103–1122. [Google Scholar] [CrossRef]
- Huai, W.; Hu, Y.; Zeng, Y.; Han, J. Velocity Distribution for Open Channel Flows with Suspended Vegetation. Adv. Water Resour. 2012, 49, 56–61. [Google Scholar] [CrossRef]
- Wu, F.C.; Shen, H.W.; Chou, Y.J. Variation of Roughness Coefficients for Unsubmerged and Submerged Vegetation. J. Hydraul. Eng. 1999, 125, 934–942. [Google Scholar] [CrossRef]
- Ding, Y.; Liu, H.; Peng, Y.; Xing, L. Lattice Boltzmann Method for Rain-Induced Overland Flow. J. Hydrol. 2018, 562, 789–795. [Google Scholar] [CrossRef]
- Zhao, F.; Huai, W.; Li, D. Numerical Modeling of Open Channel Flow with Suspended Canopy. Adv. Water Resour. 2017, 105, 132–143. [Google Scholar] [CrossRef]
- Ilseven, E.; Mendoza, M. Lattice Boltzmann Model for Numerical Relativity. Phys. Rev. E 2016, 93, 023303. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, J.G.; Burrows, R. Lattice Boltzmann Simulations of the Transient Shallow Water Flows. Adv. Water Resour. 2010, 33, 387–396. [Google Scholar] [CrossRef]
- Enouy, R.W.; Walton, K.M.; Malton, I.I. A Mechanistic Derivation of the Monod Bioreaction Equation for a Limiting Nutrient. J. Math. Biol. 2022, 84, 62. [Google Scholar] [CrossRef]
- Graba, M.; Moulin, F.Y.; Boulêtreau, S.; Garabétian, F.; Kettab, A.; Eiff, O.; Sauvage, S. Effect of Near-Bed Turbulence on Chronic Detachment of Epilithic Biofilm: Experimental and Modeling Approaches. Water Resour. Res. 2010, 46, W11531. [Google Scholar] [CrossRef]
- Uehlinger, U.R.S.; Bührer, H.; Reichert, P. Periphyton Dynamics in a Floodprone Prealpine River: Evaluation of Significant Processes by Modelling. Freshwater Biol. 1996, 36, 249–263. [Google Scholar] [CrossRef]
- Fothi, A. Effets Induits de la Turbulence Benthique sur les Mécanismes de Croissance du Périphyton. Ph.D. Dissertation, Toulouse INPT, Toulouse, France, 2002. [Google Scholar]
- Labiod, C.; Godillot, R.; Caussade, B. The Relationship Between Stream Periphyton Dynamics and Near-Bed Turbulence in Rough Open-Channel Flow. Ecol. Model. 2007, 209, 78–96. [Google Scholar] [CrossRef]
- Marquis, G.A.; Roy, A.G. Effect of Flow Depth and Velocity on the Scales of Macroturbulent Structures in Gravel-Bed Rivers. Geophys. Res. Lett. 2006, 33, L24406. [Google Scholar] [CrossRef]
- Milan, D.J. Virtual Velocity of Tracers in a Gravel-Bed River Using Size-Based Competence Duration. Geomorphology 2013, 198, 107–114. [Google Scholar] [CrossRef]
- Brenna, A.; Surian, N.; Mao, L. Virtual Velocity Approach for Estimating Bed Material Transport in Gravel-Bed Rivers: Key Factors and Significance. Water Resour. Res. 2019, 55, 1651–1674. [Google Scholar] [CrossRef]
- Franca, M.J.; Ferreira, R.M.; Lemmin, U. Parameterization of the Logarithmic Layer of Double-Averaged Streamwise Velocity Profiles in Gravel-Bed River Flows. Adv. Water Resour. 2008, 31, 915–925. [Google Scholar] [CrossRef]
- Luo, M.; Ye, C.; Wang, X.; Huang, E.; Yan, X. Analytical Model of Flow Velocity in Gravel-Bed Streams under the Effect of Gravel Array with Different Densities. J. Hydrol. 2022, 608, 127581. [Google Scholar] [CrossRef]
- Meier, C.I.; Reid, B.L.; Sandoval, O. Effects of the Invasive Plant Lupinus polyphyllus on Vertical Accretion of Fine Sediment and Nutrient Availability in Bars of the Gravel-Bed Paloma River. Limnologica 2013, 43, 381–387. [Google Scholar] [CrossRef]
- Taube, N.; Ryan, M.C.; He, J.; Valeo, C. Phosphorus and Nitrogen Storage, Partitioning, and Export in a Large Gravel Bed River. Sci. Total Environ. 2019, 657, 717–730. [Google Scholar] [CrossRef]
- Quinn, J.M.; Rutherford, J.C.; Schiff, S.J. Nutrient Attenuation in a Shallow, Gravel-Bed River. I. In-Situ Chamber Experiments. N. Z. J. Mar. Freshwater Res. 2020, 54, 393–409. [Google Scholar] [CrossRef]
- Tsuchiya, Y.; Eda, S.; Kiriyama, C.; Asada, T.; Morisaki, H. Analysis of Dissolved Organic Nutrients in the Interstitial Water of Natural Biofilms. Microb. Ecol. 2016, 72, 85–95. [Google Scholar] [CrossRef]
- Paudel, S.; Singh, U.; Crosato, A.; Franca, M.J. Effects of Initial and Boundary Conditions on Gravel-Bed River Morphology. Adv. Water Resour. 2022, 166, 104256. [Google Scholar] [CrossRef]




| Parameters | Value | According to | References |
|---|---|---|---|
| 1.1 d−1 | Refer to the typical range of laboratory and field research (0.5–1.2 d−1), and optimize experimental data through model fitting. | Uehlinger et al. [31] | |
| 0.085 g−1·m2 | The self-inhibitory effect of biomass on growth rate was determined by fitting experimental data using the least squares method. | Graba et al. [30] | |
| 0.0014 d−1 | The effectiveness of using roughness Reynolds number as a driving factor for separation was verified through calibration of its correlation with the separation process. | Fothi [32]; Labiod et al. [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Wang, H.; Wu, M. Numerical Modeling of Biofilm–Flow Dynamics in Gravel-Bed Rivers: A Framework for Sustainable Restoration. Sustainability 2025, 17, 4905. https://doi.org/10.3390/su17114905
Bai Y, Wang H, Wu M. Numerical Modeling of Biofilm–Flow Dynamics in Gravel-Bed Rivers: A Framework for Sustainable Restoration. Sustainability. 2025; 17(11):4905. https://doi.org/10.3390/su17114905
Chicago/Turabian StyleBai, Yu, Hui Wang, and Muhong Wu. 2025. "Numerical Modeling of Biofilm–Flow Dynamics in Gravel-Bed Rivers: A Framework for Sustainable Restoration" Sustainability 17, no. 11: 4905. https://doi.org/10.3390/su17114905
APA StyleBai, Y., Wang, H., & Wu, M. (2025). Numerical Modeling of Biofilm–Flow Dynamics in Gravel-Bed Rivers: A Framework for Sustainable Restoration. Sustainability, 17(11), 4905. https://doi.org/10.3390/su17114905








