Abstract
This paper proposes a distributed cloud–edge collaborative scheduling method to address the oversight of network transmission delay in traditional task scheduling, a critical factor that frequently leads to degraded execution efficiency. A holistic framework is introduced that dynamically models transmission delays, designs a decentralized scheduling algorithm, and optimizes resource competition through a two-dimensional matching mechanism. The framework integrates real-time network status monitoring to adjust task allocation, enabling edge nodes to independently optimize local queues and avoid single-point failures. A delay-aware scheduling algorithm is developed to balance task computing requirements and network latency, transforming three-dimensional resource matching into a two-dimensional problem to resolve conflicts in shared resource allocation. Simulation results verify that the method significantly reduces task execution time and queue backlogs compared with benchmark algorithms, demonstrating improved adaptability in dynamic network environments. This study offers a novel approach to enhancing resource utilization and system efficiency in distributed cloud–edge systems.
1. Introduction
With the rapid advancement of mobile Internet and IoT technologies, traditional centralized cloud computing architectures have struggled to meet the low-latency demands for real-time services, often causing core network congestion and privacy vulnerabilities [1]. This challenge has catalyzed the emergence of cloud–edge collaborative computing architectures that synergize cloud-scale data processing with edge nodes’ localized responsiveness, thus forming a “cloud–edge–end” triad that optimizes resource utilization and service quality [2,3]. As illustrated in Figure 1, the Network Collaborative Open Control Architecture (NCOCA) epitomizes this paradigm through distributed autonomous decision-making and entity-level coordination, which contrasts sharply with legacy centralized systems prone to single-point failures and scalability constraints [4]. By decentralizing management functions to network entities, NCOCA enhances operational efficiency while enabling mission-critical applications such as millisecond-response power grid inspections and the distributed vehicular network processing of dynamic road conditions [5].
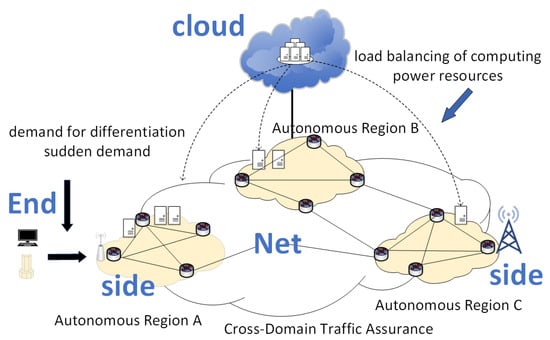
Figure 1.
Cloud-side network architecture diagram.
However, existing architectures still face serious challenges in coordinating heterogeneous device capabilities and meeting real-time mission requirements. Heterogeneous devices, varying widely in computational, storage, and network capabilities (e.g., grid sensors, IoT terminals, industrial park energy devices, fog computing nodes, and industrial IoT equipment), present significant challenges in resource integration, interoperability, and dynamic access stability. For example, it is necessary to resolve data transmission and task offloading strategies among cameras, edge controllers, and cloud servers due to the computational disparities among these devices [6]. Ren et al. [7] and Deng et al. [8] highlight how the fragmented capabilities of IoT terminals, photovoltaic nodes, and energy storage devices give rise to cross-domain collaboration and dynamic resource scheduling issues. Liu et al. [9] proposed an edge-cloud collaborative information interaction mechanism and distributed iterative optimization algorithm for industrial park integrated energy systems, which can effectively improve multi-energy synergy efficiency. In smart factories and energy systems, fog computing nodes and industrial sensors face reliability challenges during dynamic access owing to the complexities of heterogeneous resource management [10,11]. Dynamic tasks further complicate this landscape with strict real-time requirements—the use of real-time traffic processing in telematics, UAV target tracking, and analogous tasks demand millisecond-level responses to handle load fluctuations and tight time windows—thereby avoiding decision-making errors [7,8,12]. Smart logistics scenarios experience amplified scheduling complexity stemming from environmental uncertainties such as abrupt path changes or equipment failures [13,14]. Additionally, grid video surveillance and fog computing tasks are constrained by the need for latency-sensitive real-time data processing [10,15]. The main contributions of this paper to address the “fragmented” capabilities of heterogeneous devices and the “real-time” requirements of dynamic tasks are as follows:
- (1)
- Delay-driven dynamic scheduling mechanism: the real-time monitoring of network status (channel quality, node load), the dynamic adjustment of task allocation strategy, and the resolution of resource competition conflicts;
- (2)
- Decentralized collaborative decision-making framework: design distributed algorithms that allow edge nodes to autonomously optimize local queues, avoiding the single-point failure inherent in centralized architectures;
- (3)
- Lightweight 2D matching mechanism: Optimize resource allocation for high-priority tasks by incorporating latency and queue backlog perception and downgrading 3D resource matching to a 2D problem. Through comparisons with traditional algorithms (PDPRA, CSA, simple neural networks) in NS-3 simulations, the proposed approach demonstrates excellent adaptability and robustness in large-scale dynamic network environments.
The rest of this paper is as follows: Section 2 provides a comprehensive overview of related works. Section 3 elaborates on the distributed cloud–edge collaborative control modeling with consideration of network transmission delay. Section 4 introduces the cloud–edge collaborative data processing optimization algorithm based on processing delay and backlog perception matching. In Section 5, the effectiveness of the proposed distributed cloud–edge collaborative scheduling algorithm (with network transmission delay constraints) is validated through simulation experiments and compared against three other algorithms. Section 6 concludes the entire work. The overall research content framework is shown in Figure 2.
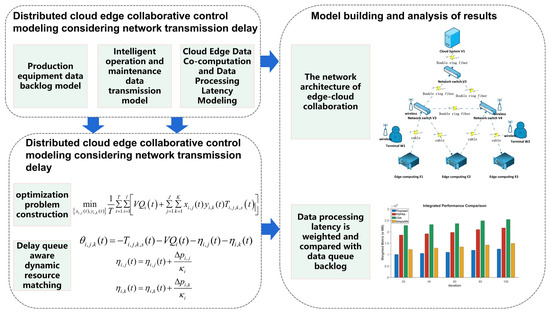
Figure 2.
Cloud–edge network architecture diagram.
2. Related Work
The development of cloud–edge collaborative architectures aims to optimize latency and energy consumption through distributed resource management, while existing research focuses on task offloading strategies, resource allocation optimization, and algorithm design to balance multiple objectives such as latency, energy consumption, and quality of service (QoS).
Earlier studies assumed task independence or only considered simple dependencies, a limitation that makes models insufficient for complex workflows. Karimi et al. [16] proposed a deep reinforcement learning (DRL)-based task offloading framework to jointly optimize the resource allocation between edge and cloud nodes, thereby reducing response time and improving task acceptance rates. However, this framework fails to account for the impact of network bandwidth fluctuations. Li et al. [17] designed an edge–cloud cooperative algorithm based on Lyapunov stability theory to balance queue delay and energy consumption, but it overlooked inter-task dependencies, leading to limited scheduling efficiency for complex workflows.
To address the task dependency problem, Tang et al. [18] introduced a directed acyclic graph (DAG) to describe task dependency and proposed a deep reinforcement learning algorithm based on task prioritization (TPDRTO), improving the scheduling efficiency of the dependent tasks. Notably, its high deep neural network training complexity in large-scale scenarios and real-time performance are insufficient. Wang et al. [19] combined blockchain technology and incentive mechanism to facilitate edge node collaboration via smart contracts, but this approach increased system communication overhead, potentially degrading overall performance. Chen et al. [20] proposed the concept of computational task contouring for complex workflows in the medical and industrial domains, designed a DRL task scheduling algorithm to optimize resource usage and computational cost, and verified that it outperformed the baseline approach through NS-3 simulation. However, the algorithm did not address the coupling effect of bandwidth allocation. Collectively, these studies highlight that modeling task dependencies and achieving efficient scheduling remain outstanding challenges.
Heuristic and meta-heuristic algorithms are widely used in energy and performance optimization. Hussain et al. [21,22] proposed Energy and Performance Efficient Task Scheduling Algorithms (EPETS), which dynamically adjust resource allocation to reduce the overuse of high-speed resources via task slack time. However, this approach is only applicable to standalone tasks. The multi-quantum-inspired genetic algorithm (MQGA) proposed by the authors’ team addresses medical workflow scheduling to optimize Makespan and energy consumption, but it suffers from limitations imposed by quantum computing hardware environments and lacks universal applicability.
Data-driven heuristics are gradually becoming mainstream. Bao et al. [23] proposed a gated recurrent unit (GRU)-based edge–cloud cooperative prediction model (TP-ECC), which dynamically adjusts resource allocation by integrating traffic prediction to enhance system foresight, but it is confined to single-edge-node scenarios. Liu et al. [24] combined CNN, LSTM, and attention mechanism to achieve efficient decision-making in dynamic environments with 30–50% computational efficiency improvements, but this approach relied on large amounts of labeled data and exhibited limited generalization ability. The MoDEMS system used the sequential greedy algorithm to generate migration plans, applying a Markovian mobility prediction model to reduce the user latency, but it overlooked global suboptimality arising from resource competition among multiple users [25]. To address the Pareto-optimality challenge in multi-objective optimization, Pang et al. [26] proposed a dynamic weight adjustment algorithm, which balances latency and energy consumption optimization objectives in real time via reinforcement learning and mitigates the insufficient adaptability of traditional static weight allocation strategies in dynamic telematics environments. However, it fails to account for the compatibility issues of heterogeneous devices.
Exact optimization methods based on mathematical planning, such as Integer Linear Programming (ILP) or Mixed-Integer Programming (MIP), theoretically approximate the optimal solution, but the computational complexity grows exponentially with the task size. The DEWS algorithm produced by Hussain et al. [27] constructs an optimization model, which is solved by the Variable Neighborhood Descent (VND) algorithm, to minimize the energy cost under deadline constraints, yet its time complexity renders it ill-suited for large-scale real-time scenarios. The subsequent EPEE algorithm integrates electricity price fluctuation and data transmission time to achieve energy efficiency and cost co-optimization, but it still assumes static data center resource allocation and neglects real-time load variations [28].
The time-varying nature of edge node resources and network bandwidth in dynamic environments thus causes traditional static scheduling strategies to fail. Although algorithms such as DRL try to handle dynamic states, real-time performance and convergence in large-scale scenarios still need to be optimized. For example, CTOCLA introduces an attention mechanism to handle task weights, but fails to model the additional delay induced by cross-domain data transmission security and privacy protection [24]. MoDEMS exhibits limited dynamic adaptability, as abrupt changes in user mobility patterns increase migration plan failure probability by approximately 20% [25]. To tackle dynamic resource fluctuations, Jiang et al. [29] proposed a deep reinforcement learning (DRL)-based cloud–edge cooperative multilevel dynamic reconfiguration method for the real-time optimization of urban distribution networks (UDNs). The method is divided into three levels (feeder, transformer, and substation), combining a multi-intelligent system (MAS) with a cloud–edge architecture, and adopting a “centralized training-decentralized execution” (CTDE) model. Meanwhile, Li et al. [30] proposed a cloud–edge cooperative approach based on MADDPG for the integrated electric–gas system (IEGS) scheduling problem. The electricity and gas systems are computed independently at the edge, and the cloud optimizes globally based on the boundary information. However, it overlooks the parallelism limitation stemming from the cloud’s reliance on edge parameter transfers.
There are three systemic deficiencies. Firstly, there is a lack of dynamic delay modeling, ignoring the impact of network fluctuations and interference on task offloading. This results in delay estimation bias. Secondly, there is insufficient decentralized scheduling, and the centralized architecture suffers from lagging state synchronization and privacy risks. Thirdly, there is an imbalance in multi-objective optimization, lacking a joint optimization framework for multiple objectives such as latency and energy consumption, making it difficult to meet the demands of complex scenarios. This paper systematically addresses these gaps through dynamic latency modeling, distributed collaborative decision-making, and lightweight resource matching:
- (1)
- Dynamic adaptability: avoiding static model bias by the real-time sensing of network state.
- (2)
- Privacy and reliability: decentralized architecture circumvents a single point of failure.
- (3)
- Multi-objective synergy: balancing delay, energy consumption, and resource fragmentation through a two-dimensional matching mechanism.
3. Distributed Cloud–Edge Collaborative Control Modeling Considering Network Transmission Delay
A distributed cloud–edge collaborative data processing architecture is a system that combines computational power from both cloud and edge devices while accounting for network transmission latency. This architecture optimizes data processing to improve efficiency, reduce latency, and alleviate reliance on network bandwidth. Data generated or collected at edge devices can be transmitted to either the cloud or other edge nodes for processing. To mitigate the impact of transmission latency on performance, designers employ strategies such as edge-side preprocessing and adaptive task partitioning.
To address the dynamic interaction between network transmission and task processing, this section introduces a distributed cloud–edge collaborative control model. We first model the data backlog dynamics at terminals (Section 3.1), subsequently presenting a transmission model that integrates channel characteristics and resource allocation (Section 3.2). Finally, we systematically derive a comprehensive latency model (Section 3.3) that combines computational delays at servers with network transmission delays across the cloud–edge continuum, serving as the foundation for the optimization algorithm in Section 4. The nomenclature used throughout the paper is systematically presented and explained in Table 1.

Table 1.
Relevant symbol.
3.1. Production Equipment Data Backlog Model
Assume that there is I data acquisition terminal, represented by . T data processing iterations are considered, expressed as . In each iteration, according to the available communication and computing resources, the terminal will offload the locally cached data to the edge layer or cloud layer for collaborative data processing. The locally cached data of the terminal can be simulated using the cache queue, and the queue backlog updates can be represented by the following formula:
where and are the amounts of data collected and transmitted in the t iteration, representing the input and output of the queue, respectively.
Equation (1) describes the dynamic balance of terminal cache: the current backlog equals the previous backlog plus new data minus transmitted data. This captures the accumulation of data that requires offloading, directly influencing subsequent transmission and processing decisions.
3.2. Intelligent Operation and Maintenance Data Transmission Model
Assume that there are a total of K servers that form the set , where represents the cloud server and represents the edge server. Considering the end–edge channel, the end–cloud channel, and the cloud–edge load profile, the available communication and computation resources are partitioned into J resource blocks, denoted as . In the tth iteration, the signal-to-noise ratio of the terminal transmitting the captured data to the server through the resource block is expressed as follows:
We define the matching indicator variable between the terminal and the resource block as . shows that the terminal matches with the resource block at the tth iteration; otherwise, . We define the matching indicator variable between the terminal and the server as . shows that the terminal offloads the data to the server at the tth iteration; otherwise, . Based on Equation (2), the transmission rate for the transfer of data to the server from the terminal is calculated as follows:
The amount of data transmitted in the tth iteration is expressed as follows:
where denotes the iterative transmission length.
The data transmission delay for transferring data from to is expressed as follows:
Consider T data processing iterations, denoted as . In each iteration, the terminal offloads the locally cached collection data to the edge layer or the cloud layer for collaborative data processing, depending on the available communication and computation resources. The locally cached data is modeled by the cache queue shown in Equation (1).
Equations (2)–(5) link channel quality (SNR) to transmission efficiency: higher SNR (better channel) enables higher rates and lower delays. This forms the basis of resource block allocation, as terminals prefer resource blocks with higher to minimize transmission latency.
3.3. Cloud–Edge Data Co-Computation and Data Processing Latency Modeling
The edge server or cloud server can process the data from the endpoints only after it has processed its own computational load. The latency to process the collected data from is expressed as follows:
where is the delay when waiting to complete its computational load, is the computational resources required to process the unit data, i.e., computational complexity, and is the computational resources provided by the resource block .
The total latency incurred during task offloading consists of two main components. The first part is the CPU cycle consumed by the execution of the task on the server and this is termed execution latency. The other part is the time taken by the task to transfer between different servers during the offloading process. The execution latency further comprises the task execution latency on the server can be subdivided into the processing latency of the task and the queuing latency waiting for the previous task to finish processing. The task processing latency is usually related to the server performance and the computational resources required by the task. Let the total offloading latency of the system be T, where the execution latency is , the queuing latency is , the processing latency is , the offloading latency for transmitting the task to other servers is , and the transmission latency for the task to be transmitted from one edge server to another edge server is . The execution delay of task is expressed in Equation (7).
Let K be the set of offloaded yet incomplete tasks on the ECS; the queuing latency of is shown in Equation (8).
The offload latency of a task can be decomposed into six parts, including the offload latency, the transmission latency between edge servers, the offload latency from the edge servers to the macro base station, the offload latency from the edge servers to the central cloud server, and the offload latency from the macro base station to the central cloud server. The offload delay of the task transmission to another server depends on the size of the task and the transmission power of the terminal. The offload delay of the task can be formulated using Equation (9).
The binary variable indicates whether the transmission uses the cross-edge server mode, and indicates that the transmission is performed in cross-edge server mode. , the transmission delay between edge servers, is determined using Equation (10).
When a task cannot be offloaded on the local terminal, the cloud server will assign a more reasonable transmission mode to the task—that is, the wireless transmission mode—and set the transmission delay to , as shown in Equation (11).
indicates the task transmission mode selected by the cloud server, represents the task transmission times, and indicates the task transmission rate of the terminal.
Due to the limited storage and computing resources of the edge server, when the edge server cannot handle task offloading, it will offload the task to the central cloud server. However, due to the long distance between the edge server and the central cloud server, frequent tasks will generate large energy consumption, which reduces the utilization rate of system resources. In this architecture, macro base stations with large computing resources and storage resources are placed reasonably near to edge server farms to greatly reduce the probability of requests to the central cloud server, thereby reducing delay and system energy consumption and effectively improving resource utilization. Then, the transmission delay of from the edge server to the macro base station is , as shown in Equation (12).
where and are the amounts of data collected and transmitted in the t iteration, representing the input and output of the queue, respectively.
We set the transmission delay of offloaded data to the central cloud server through the macro base station , as shown in Equation (14).
The tasks generated by the terminal can be executed on four types of servers: terminal-local, edge server, macro-base station, and central cloud server. The total offloading delay of is , as shown in Equation (15).
The total offloading delay of the system is shown in Equation (16).
4. Cloud–Edge Collaborative Data Processing Optimization Algorithm Based on Processing Delay and Backlog Sensing Matching
In this section, a cloud–edge collaborative data processing optimization algorithm based on processing delay and backlog perception matching is proposed to solve the above optimization problems. The algorithm’s principles and implementation process are described as follows.
4.1. Cloud–Edge Collaborative Data Processing Optimization Problem Construction
The goal of cloud–edge collaborative data processing is to achieve optimal matching among terminals, resource blocks, and servers while minimizing latency and reducing endpoint data queue backlogs. The optimization problem is formulated in Equation (17).
where V is the weight used to weigh the optimization of processing latency and data queue backlog, and is the quota of the server. When V tends towards 1, the algorithm gives priority to minimizing latency, which is suitable for real-time tasks; when V tends to 0, the algorithm gives priority to alleviating queue backlog, which is suitable for data throughput-sensitive scenarios. and are constraints on terminals matching resource blocks, indicating that each terminal can match at most one resource block and that each resource block can be used by at most one terminal to avoid transmission conflicts caused by multi-channel competition. and are constraints on terminals matching servers, indicating that each endpoint can be configured with at most one server to limit endpoint single-path offloads and server load ceilings to prevent steep latency increases in edge/cloud nodes due to task overload, and each server can serve a maximum of terminals.
The optimization problem is essentially a three-dimensional resource-matching problem (involving terminals, resource blocks, and servers), which is transformed into a two-dimensional matching problem by combining resource blocks and servers into combinatorial options. However, due to the inclusion of binary decision variables , and coupling constraints, the problem still falls into the category of NP-hard Integer Linear Programming (ILP), and traditional exact algorithms are unable to solve large-scale instances in polynomial time. The multi-objective optimization property (weighted summation processing delay with queue backlog) further increases the solution complexity and requires us to rely on heuristic algorithms for approximate optimization. The detailed proof procedure for the optimization problem is provided in Appendix A.
4.2. Delay Queue-Aware Dynamic Resource Matching
The principle of the algorithm is illustrated in Figure 3. By integrating resource blocks and servers into new matching units, the complexity of three-dimensional matching among terminals, resource blocks, and servers is reduced, transforming the issue into a two-dimensional matching problem between terminals and resource block–server combination units. Using this approach, the cloud–edge collaborative data processing matching preference of terminals is formulated by incorporating the processing delays of cloud/edge servers and the backlogs of terminal data queues. According to the matching preference list, matching is achieved among terminals, resource blocks, and servers. Finally, terminals selectively offload data to edge or cloud servers for collaborative processing based on the matching outcomes.
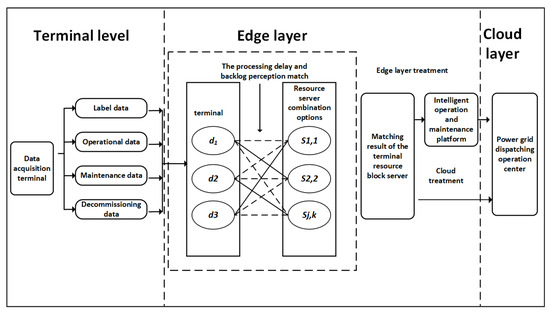
Figure 3.
Delay queue-aware dynamic matching algorithm process.
4.3. Implementation Process
The implementation process of the algorithm is shown below and it includes three steps: processing delay and backlog perception; cloud–edge data processing matching preference construction based on processing delay and backlog perception; and cloud–edge collaborative data processing matching iterative optimization considering resource competition. The details are elaborated as follows.
- Communication network service orchestration transmission delay model
The edge layer combines information such as the amount of data collected by the terminal, end-side channel status, end-cloud channel status, cloud-available computing resources, and edge–cloud load to determine the processing delay and backlog. Specifically, for the resource block–server combination option , Equation (6) is used to evaluate the processing delay of the server . For the terminal , the backlog of its data queue is evaluated according to Equation (1).
- 2.
- Cloud–edge data processing matching preference construction based on processing delay and backlog perception
Based on processing delay and backlog perception, cloud–edge data processing matching preferences are constructed. We define the terminal preference value for the resource block server combination option to be , denoted as follows:
where is the matching cost between and resource block , and is the matching cost between and server . This which is used to solve the resource competition problem between multiple terminals and the same combination option.
The algorithm has a time complexity of ( is the number of terminals, is the number of resource blocks, and is the number of servers), and achieves polynomial-level complexity by transforming 3D matching into 2D matching and by employing distributed iteration to optimize the cost of matching and finite subconvergence; the space complexity is , which can be optimized by sparse storage. The algorithm solves the exponential complexity problem of traditional 3D matching by balancing the computational efficiency and optimization effect in the dynamic network with the help of a distributed architecture of autonomous decision-making by edge nodes. The detailed procedure of the proposed algorithm is presented in Algorithm 1.
| Algorithm 1: Delay-Aware Dynamic Resource Matching Algorithm |
| Input: Terminal set
, Resource blocks
, Servers
, Iterations
, Priority weights
, Terminal priority weight
Output: total delay |
|
- 3.
- Cloud–edge collaborative data processing matching iterative optimization considering resource competition
By increasing the matching cost of or , the terminal’s preference for the combination option is reduced, thus reducing the number of terminals applied to match the same combination option and resolving resource competition conflicts. In the process of matching costs, the data processing priorities of different service terminals should be considered, and the matching cost for low-priority services should be increased. The matching cost update formula of the resource block and server is expressed as follows:
where and are the matching cost enhancement steps of and resource block and server , and is the priority weight of . The larger is, the higher the priority of .
5. Example Analysis
To verify the effectiveness of the proposed cloud–edge collaborative network architecture, the distributed cloud–edge collaborative control model, and the optimization algorithm based on processing delay and backlog perception, this section conducts experiments on the NS-3 simulation platform. The experimental objectives include verifying the adaptability of the network architecture, evaluating the effectiveness of the model and algorithm, and comparing its performance with the result of traditional methods. The experimental environment is configured with the NS-3 simulation platform (version 3.36), with hardware specifications of an Intel Core i5-4460 CPU, 3.8 GiB of memory, and a 64-bit Ubuntu 18.04.6 LTS operating system (running in a VMware virtualization environment with a 63.1 GB disk). The network topology is designed based on actual industrial operation and maintenance scenarios.
This paper builds a comprehensive network model, which includes a cloud system as the core hub. This is connected with three network switches, which are connected to build a high-availability internal network infrastructure. The model also includes three edge nodes, which are distributed in different geographical locations to provide services and data processing closer to users. In addition, two wireless nodes are integrated into the network to support the connection of mobile devices and sensors. The network architecture of edge–cloud collaboration is shown in Figure 4.
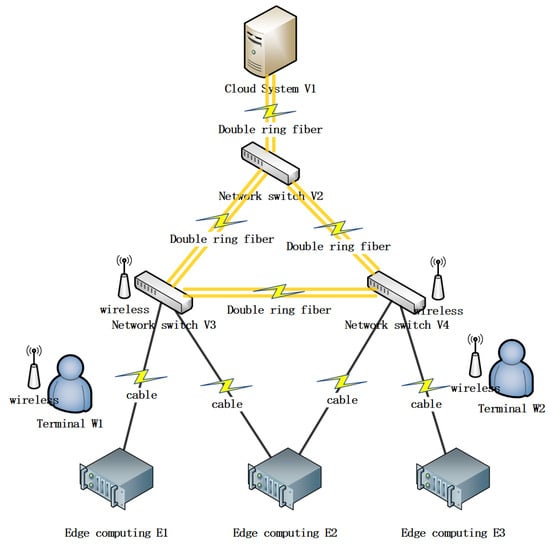
Figure 4.
Edge–cloud collaborative system.
Based on the intelligent operation and maintenance scenario of a company’s actual production equipment, this paper considers various data acquisition terminals such as label data, operation data, maintenance data, and decommissioning data; the simulation is conducted using NS-3. Two simulation scenarios are as follows:
- (1)
- In scenario 1, data is sent from the sensor at end 1 → switch 2 → edge device 1→ switch 2 → switch 1 → cloud-side complex operation → output results to switch 1 0→ switch 2 → edge device 1 → switch 2 → return to the actuator at end 1.
- (2)
- In, scenario 2 data is sent from the sensor at end 1→ switch 2→ edge device 1→ switch 2 → switch 3 → switch 1 → cloud-side complex operation → output the result to switch 1 → switch 3 → switch 2 → edge device 1 → switch 2 → return to the actuator at end 1.
Use NetAnim to visualize the architecture model built in ns-3, as shown in Figure 5.
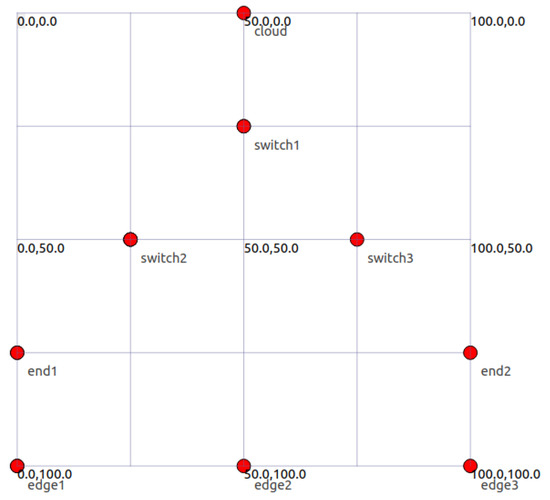
Figure 5.
Architecture model visualization.
The initial IP addresses of each point are shown in Table 2.

Table 2.
Initial IP addresses.
5.1. Simulation Parameter
The initial values of the parameters and the initial coordinate settings for each node are shown in Table 3 and Table 4.

Table 3.
Initial value of the parameter.

Table 4.
Initial coordinates of each node (m).
5.2. Contrast Algorithm Setting
In this paper, the performance of the proposed algorithm is verified, and three different cloud–edge collaborative data processing algorithms are used for comparison. The first algorithm is based on processing-delay-first resource block allocation (PDPRA), which is characterized by the transfer of all data to edge servers for processing. The second algorithm is the computing-resource-based algorithm (CSA), in which the terminal prefers the computing resources of the server but does not consider the quality of the channel or the backlog of the terminal data queue. The third algorithm, simple neural network-based resource allocation (Simple NN), employs real-time channel status and node load to generate resource allocation strategies. Although Simple NN offers basic online reasoning, it lacks dynamic adaptability and integration. Moreover, none of these three comparison algorithms can solve the problem of resource competition.
As illustrated in Figure 6, the proposed algorithm demonstrates superior performance over PDPRA, CSA, and Simple NN, with its task execution time curve consistently occupying the lowest region. The algorithm achieves an average execution time reduction of 28–35% compared to the benchmark methods. This can be mainly attributed to its multi-objective dynamic optimization framework, which integrates real-time channel quality monitoring, node load balancing, and queue backlog awareness. Through a conflict-aware weighted resource-matching strategy, the algorithm dynamically optimizes the trade-off between transmission and computation during iterative updates.
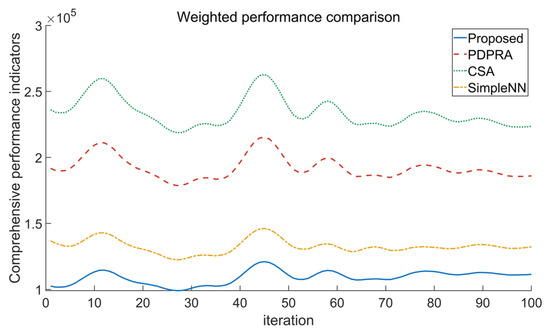
Figure 6.
Algorithm performance comparison.
The performance comparison in Figure 7 shows that the proposed algorithm reduces data processing latency by 11.05%, 12.18%, and 18.4%; decreases data queue backlog by 13.35%, 15.2%, and 22.7%; and outperforms PDPRA, CSA, and Simple NN, respectively. These improvements can be attributed to the new algorithm’s consideration of the differences in processing delay caused by resource blocks and the differences in terminal data queue backlog caused by server selection, which are weighted according to different choices. In addition, the new algorithm can better solve the matching conflict, and updating the matching cost ensures a smaller delay and data queue backlog for high-priority terminals. In contrast, the PDPRA algorithm only optimizes processing latency while ignoring server resource competition and matching conflicts, resulting in suboptimal performance. The CSA algorithm neglects communication resource contention, whereas the Simple NN algorithm, constrained by its static neural network architecture, exhibits increased latency and worsened queue backlog in dynamic scenarios.
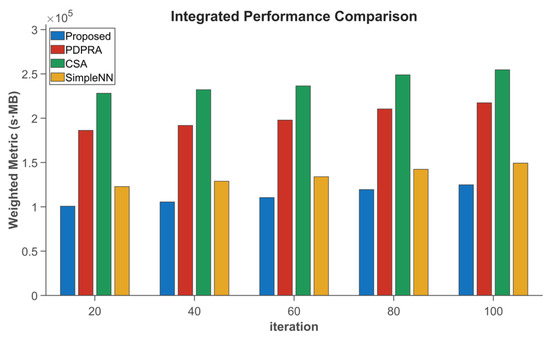
Figure 7.
Data processing latency is weighted and compared with data queue backlog.
As demonstrated in Figure 8 and Figure 9, the proposed algorithm significantly outperforms PDPRA, CSA, and Simple NN, achieving 6.26%, 13.18%, and 19.2% reductions in data processing latency, and 13.57%, 16.16%, and 22.5% improvements in queue backlog mitigation, respectively. This improvement is due to the new algorithm’s integration of the communication and computing resources of the cloud and edge layers, which are organized into resource blocks and combined with cloud–edge servers through the Cartesian product. This approach allows terminals to better select servers and resource blocks and transfer data to edge or cloud servers for computation, significantly reducing data processing delays and data queue backlogs.
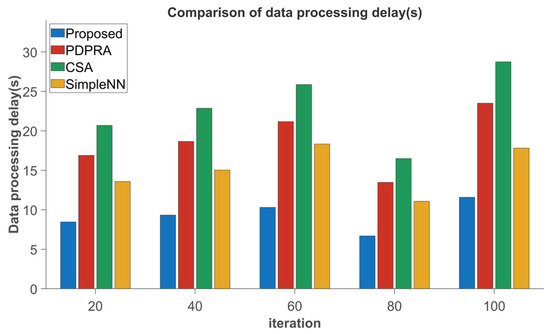
Figure 8.
Comparison of data processing delay.
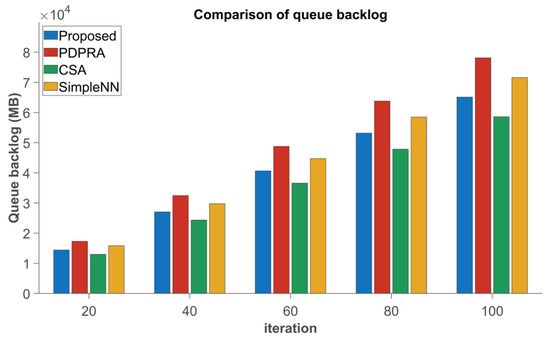
Figure 9.
Data queue backlog comparison.
Figure 10 shows the weighted sum comparison of data processing delay and data queue backlog when the number of terminals increases in a large-scale device access scenario. As the number of terminals grows, the number of resource blocks that can be occupied by terminals decreases accordingly, resulting in an upward trend in the weighted sums of the three comparison algorithms, namely, PDPRA, CSA, and Simple NN. When the number of terminals exceeds 200, the number of terminals choosing the same server increases significantly, the processing capacity of communication and computation resource blocks decreases significantly, and the competition between terminals and servers for high-processing-capacity resource blocks intensifies, resulting in a steep increase in the weighted sum of the three comparison algorithms. In contrast, the proposed algorithm effectively mitigates the resource competition conflict by guiding terminals to preferentially match resource blocks with better processing capacity with server combinations through the matching cost iterative optimization mechanism in the case of declining resource processing capacity, and its weighting and growth are significantly smaller than those of the comparison algorithms.
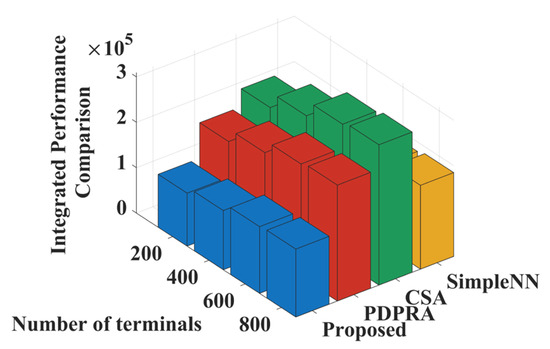
Figure 10.
Weighting functions and comparisons as the number of terminals increases.
Figure 11 shows the weighted sum comparison of data processing delay and data queue backlog when the number of edge servers increases in the large-scale device access scenario. When the number of edge servers increases, the total number of high-performance servers in the system rises, and the overall processing capacity of the edge layer increases significantly. Since the PDPRA, CSA, and Simple NN algorithms also achieve some processing capacity increase when server resources are sufficient, the weighted sums of all three algorithms show a decreasing trend. The proposed algorithm further dynamically selects the optimal servers through a delay- and backlog-aware mechanism to reduce the queue backlog while lowering the data processing delay when there is a surplus of server resources. As a result, its weighted sum performance decreases in a more pronounced fashion and is consistently superior to the values of the comparison algorithms.
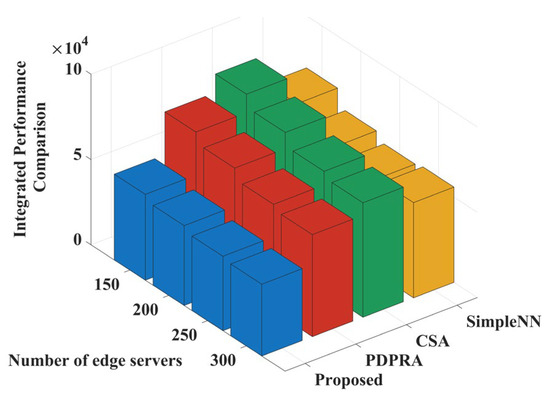
Figure 11.
Weighting functions and comparisons as edge servers increases.
At the same time, if there is a data queue backlog at the terminal of the current iteration, according to Equation (1), the backlog data will be transferred to the edge or cloud server for processing in the next iteration. Through the rational selection of resource blocks and servers by the new algorithm, the data queue backlog is kept at a low level, and the system performance is further optimized.
5.3. Simulation Result
The comparison of latency performance between Path 1 and Path 2 is shown in Figure 12.
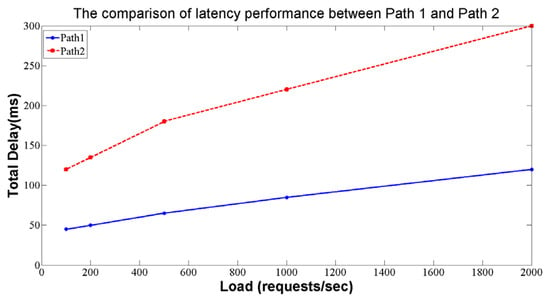
Figure 12.
The comparison of latency performance between Path 1 and Path 2.
The delay in Path 2 is significant due to the following reasons:
- (1)
- Additional Path Switching: In Path 2, the data needs to pass through three distinct network switches. The presence of multiple-path switching results in a longer transmission path, thereby increasing overall latency.
- (2)
- Increased Network Devices: Path 2 contains a relatively large number of network devices. Each time data is transferred from one switch to another, packets need to be processed and forwarded, which introduces delays in communication and coordination between different devices.
- (3)
- Potential Congestion: The involvement of additional network devices and path switching in Path 2 heightens the potential risk of network congestion. This congestion can lead to packet queuing during transmission, which further exacerbates latency.
Taking these factors into account, the latency of Path 2 is relatively high due to the introduction of additional network switches and path switching, as well as more complex data transmission routes. High latency can adversely affect applications and real-time settings that require low latency. Therefore, designing a network architecture requires a careful balance between performance requirements and network topology to select the most appropriate transmission path.
The selection of transmission media directly influences the delay characteristics of the system, and the reasonable selection can balance performance and cost factors while satisfying application requirements, making it a crucial decision in network design and optimization.
As verified by simulation, the proposed delay-aware distributed cloud-edge scheduling framework exhibits significant performance improvements in dynamic network environments. As shown in Figure 8 and Figure 9, the algorithm outperforms the traditional approaches (PDPRA, CSA, Simple NN) by reducing the data processing latency by 6.26–19.2%, and improving the queue backlog alleviation rate by 13.57–22.5%. This superiority stems from its unique integration of the following components:
- (1)
- Dynamic Network Modeling: Real-time monitoring of channel quality and node load, enabling adaptive task allocation and reducing transmission delays caused by outdated network state information.
- (2)
- Distributed 2D Matching: By transforming 3D resource matching (endpoint-resource block–server) into a 2D problem, the algorithm efficiently resolves shared resource conflicts and reduces overall task execution time.
- (3)
- Priority-Aware Resource Competition Solution: An iterative matching cost adjustment mechanism ensures that high-priority tasks are given priority for resource allocation, thus minimizing latency for latency-sensitive applications.
These results highlight the effectiveness of the framework in balancing computational requirements and network latency, addressing the central challenge facing traditional approaches that ignore dynamic transmission delays.
Although the proposed method shows good performance in simulation, its practical application still faces the following challenges. First, when an edge node fails suddenly (e.g., power interruption of industrial sensors or malfunctions in computation units), the existing architecture lacks real-time fault sensing and dynamic rescheduling mechanisms, and tasks relying on the node face the risk of timeout due to delayed migration to redundant nodes, potentially increasing task failure rates. Second, the movement of the equipment (such as AGVs, inspection drones) triggers channel fading, and the algorithm’s delay prediction model fails to track channel parameter changes in real time, potentially increasing task assignment error rates.
To further validate the algorithm’s universality in dynamic abnormal scenarios, the following experiments will be carried out in the future research. First, we will inject high-frequency random node failure events and sudden traffic congestion models into the NS-3 simulation environment, simulate extreme scenarios such as sensor node cluster failures in smart factories or sudden reductions in the bandwidth of industrial buses, and test the algorithm’s failure-aware delay and task rescheduling success rate. Second, we will develop a “mobile trajectory prediction” model to address the challenges of equipment mobility, and develop a “mobile trajectory prediction” model to address the challenges of equipment mobility. Further, to address the challenges of device mobility, we develop a joint mechanism of “mobile trajectory prediction and task pre-migration” to train LSTM prediction models with historical mobile data. The above experiments will systematically verify the robustness of the algorithm in dynamic disruption and mobile scenarios, and provide theoretical support for industrial-scale deployment.
6. Conclusions
In this paper, we present a novel cloud–edge collaborative scheduling method that explicitly accounts for network transmission delay, a critical factor often overlooked in task execution. Traditional methods neglect the influence of network transmission delay on task execution efficiency. To bridge this gap, we propose a distributed cloud–edge collaborative scheduling method that explicitly considers network transmission delay to optimize task allocation and execution order. Experiments show that this method can significantly boost task execution efficiency and enhance the overall performance of the system. This work offers a novel optimization solution for task scheduling in distributed cloud–edge systems, significantly contributing to the promotion of green computing and advancing sustainable development objectives. Future research will aim to develop scheduling strategies that incorporate dynamic network disruptions (e.g., node failures, traffic congestion) and equipment mobility. By integrating probabilistic models or adaptive learning mechanisms, such as reinforcement learning, these strategies aim to enhance the algorithm’s resilience in uncertain environments, ensuring stable performance under volatile conditions. Such advancements are expected to further propel the field toward more efficient, robust, and sustainable distributed computing systems, aligning with the growing demands for reliability and adaptability in emerging networked applications.
Author Contributions
Conceptualization and methodology, W.Z. and C.W.; writing, W.X.; supervision, Y.L.; data curation and validation, W.X. and G.S.; investigation and visualization, W.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number (62173082, U22B20115), and the National Key Research and Development Program of China, grant number (2022YFB4100802).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
The authors would like to appreciate the editors and the anonymous reviewers for their insightful suggestions to improve the quality of this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The objective of the optimization problem (Equation (17)) is to minimize the weighted sum of average processing delay and data queue backlog. Due to the inclusion of integer variables in the constraint conditions, it is difficult to solve directly. Therefore, introducing Lagrange multipliers , a Lagrange function is constructed:
The dual problem involves and . By solving the dual problem, the original problem is transformed into a state of unconstrained optimization.
Decompose the global problem into terminal-level sub-problems. The local optimization objective for each terminal is as follows:
The terminal selects the resource block server combination for maximizing the preference value, and the preference value is defined in Equation (18).
Next, we will prove the convergence of the algorithm.
Theorem A1 (Convergence).
The algorithm converges to a stable match after a finite number of iterations.
According to Equations (18) and (19), the preference values satisfy the following:
The preference value strictly decreases over time.
In each iteration, if terminal switches to a better match , the total cost will be reduced by at least the following value:
The number of resource blocks and server combinations is limited (set as ), so there is a lower bound for the total cost. The algorithm must terminate after a finite number of iterations , satisfying the following criterion:
Definition A1 (Nash equilibrium condition).
When the preference values of all terminals are stable, they satisfy the following:
The current match of each terminal is the local optimal selection. When the preference values of all terminals no longer change, it satisfies the following:
According to Equation (19), at this point, , which means there is no resource competition conflict. Combining Equations (A3)–(A5), the algorithm must converge to a stable state while satisfying monotonicity, boundedness, and limited resources.
Theorem A2 (Queue Stability).
If the system satisfies , then the queue backlog is bounded on average and satisfies the following:
where
is a constant and
is a weight parameter that balances delay and queue backlog.
Define the Lyapunov function as the sum of squares of the queue backlog:
Define the single time slot Lyapunov drift as follows:
By substituting the queue update Equation (6) and expanding it, we can obtain the following:
We assuming that the data arrival and transmission volume meet the following conditions:
Combined with the term in the optimization objective, the total drift and penalty term meet the following requirements:
From , we can obtain the following:
Through Lyapunov drift analysis, the average boundedness of the queue backlog is proved, and the upper bound is inversely proportional to the trade-off parameter V.
Theorem A3 (delay optimality).
Let the total cost of the global optimal solution be and the total cost of the algorithm solution be , then there is a constant such that the following prevails:
where
is the weight parameter to weigh the delay and queue backlog.
Defining the total cost as Equation (17), combined with Theorem A2, the total contribution of queue backlog terms can be obtained as follows:
Let the delay term of the global optimal solution be as follows:
The Equation (A17) satisfies:
where ε is the delay difference between the algorithm and the optimal solution.
According to Lyapunov drift theory, the total delay term satisfies the following:
Combining the results of queue backlog items, the total cost difference is shown in Equation (A17). The average value of the queue backlog is limited to , and increasing can further reduce the backlog. The difference between the delay term of the algorithm and the global optimal solution is , indicating that the algorithm has asymptotic optimality in delay optimization. By adjusting , the queue backlog and delay optimization can be balanced.
References
- Zheng, L.; Chen, J.; Liu, T.; Liu, B.; Yuan, J.; Zhang, G. A Cloud-Edge Collaboration Framework for Power Internet of Things Based on 5G networks. In Proceedings of the 2021 IEEE 9th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 25–28 November 2021; pp. 273–277. [Google Scholar]
- Mohiuddin, K.; Fatima, H.; Khan, M.A.; Khaleel, M.A.; Nasr, O.A.; Shahwar, S. Mobile learning evolution and emerging computing paradigms: An edge-based cloud architecture for reduced latencies and quick response time. Array 2022, 16, 100259. [Google Scholar] [CrossRef]
- Liu, G.; Dai, F.; Xu, X.; Fu, X.; Dou, W.; Kumar, N.; Bilal, M. An adaptive DNN inference acceleration framework with end–edge–cloud collaborative computing. Future Gener. Comput. Syst. 2023, 140, 422–435. [Google Scholar] [CrossRef]
- Zhou, J.; Kondo, M. An Edge-Cloud Collaboration Framework for Graph Processing in Smart Society. IEEE Trans. Emerg. Top. Comput. 2023, 11, 985–1001. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, K.; Wu, L.; Wu, J. Efficient Caching in Vehicular Edge Computing Based on Edge-Cloud Collaboration. IEEE Trans. Veh. Technol. 2023, 72, 2468–2481. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, K.; Fei, Z.; Luo, H. The Technical Architecture and Mechanism of Power Grid Mobile Security Inspection Cloud-Edge Collaboration Based on the 5G Network. In Proceedings of the 2023 3rd International Conference on New Energy and Power Engineering (ICNEPE), Huzhou, China, 24–26 November 2023; pp. 1036–1040. [Google Scholar]
- Ren, C.; Gong, C.; Liu, L. Task-Oriented Multimodal Communication Based on Cloud–Edge–UAV Collaboration. IEEE Internet Things J. 2024, 11, 125–136. [Google Scholar] [CrossRef]
- Deng, X.; Li, J.; Liu, E.; Zhang, H. Task allocation algorithm and optimization model on edge collaboration. J. Syst. Archit. 2020, 110, 101778. [Google Scholar] [CrossRef]
- Liu, G.; Song, X.; Xin, C.; Liang, T.; Li, Y.; Liu, K. Edge–Cloud Collaborative Optimization Scheduling of an Industrial Park Integrated Energy System. Sustainability 2024, 16, 1908. [Google Scholar] [CrossRef]
- Reyana, A.; Kautish, S.; Alnowibet, K.A.; Zawbaa, H.M.; Wagdy Mohamed, A. Opportunities of IoT in Fog Computing for High Fault Tolerance and Sustainable Energy Optimization. Sustainability 2023, 15, 8702. [Google Scholar] [CrossRef]
- Zhang, Z.; Qu, T.; Zhao, K.; Zhang, K.; Zhang, Y.; Liu, L.; Wang, J.; Huang, G.Q. Optimization Model and Strategy for Dynamic Material Distribution Scheduling Based on Digital Twin: A Step towards Sustainable Manufacturing. Sustainability 2023, 15, 16539. [Google Scholar] [CrossRef]
- Shao, S.; Su, L.; Zhang, Q.; Wu, S.; Guo, S.; Qi, F. Multi task dynamic edge–end computing collaboration for urban Internet of Vehicles. Comput. Netw. 2023, 227, 109690. [Google Scholar] [CrossRef]
- Ma, X.; Zhao, J.; Jia, L.; Chen, X.; Li, Z. Optimal edge-cloud collaboration based strategies for minimizing valid latency of railway environment monitoring system. High-Speed Railw. 2023, 1, 185–194. [Google Scholar] [CrossRef]
- Zhu, Q.; Yu, X.; Zhao, Y.; Nag, A.; Zhang, J. Resource Allocation in Quantum-Key-Distribution-Secured Datacenter Networks With Cloud–Edge Collaboration. IEEE Internet Things J. 2023, 10, 10916–10932. [Google Scholar] [CrossRef]
- Ou, Q.; Wang, Y.; Song, W.; Zhang, N.; Zhang, J.; Liu, H. Research on network performance optimization technology based on cloud-edge collaborative architecture. In Proceedings of the 2021 IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering (ICBAIE), Nanchang, China, 26–28 March 2021; pp. 274–278. [Google Scholar]
- Karimi, E.; Chen, Y.; Akbari, B. Task offloading in vehicular edge computing networks via deep reinforcement learning. Comput. Commun. 2022, 189, 193–204. [Google Scholar] [CrossRef]
- Li, Q.; Guo, M.; Peng, Z.; Cui, D.; He, J. Edge–Cloud Collaborative Computation Offloading for Mixed Traffic. IEEE Syst. J. 2023, 17, 5023–5034. [Google Scholar] [CrossRef]
- Tang, T.; Li, C.; Liu, F. Collaborative cloud-edge-end task offloading with task dependency based on deep reinforcement learning. Comput. Commun. 2023, 209, 78–90. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, S.; Wu, M. Incentive-Aware Blockchain-Assisted Intelligent Edge Caching and Computation Offloading for IoT. Engineering 2023, 31, 127–138. [Google Scholar] [CrossRef]
- Chen, Z.; Ren, Y.; Sun, Q.; Li, N.; Han, Y.; Huang, Y.; Li, H.; I, C.-L. Computing Task Orchestration in Communication and Computing Integrated Mobile Network. In Proceedings of the 2023 IEEE Globecom Workshops (GC Wkshps), Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 2073–2078. [Google Scholar]
- Hussain, M.; Wei, L.F.; Lakhan, A.; Wali, S.; Ali, S.; Hussain, A. Energy and Performance-Efficient Task Scheduling in Heterogeneous Virtualized Cloud Computing. Sustain. Comput. Inform. Syst. 2021, 30, 100517. [Google Scholar] [CrossRef]
- Hussain, M.; Wei, L.-F.; Abbas, F.; Rehman, A.; Ali, M.; Lakhan, A. A Multi-Objective Quantum-Inspired Genetic Algorithm for Workflow Healthcare Application Scheduling With Hard and Soft Deadline Constraints in Hybrid Clouds. Appl. Soft Comput. 2022, 128, 109440. [Google Scholar] [CrossRef]
- Bao, B.; Yang, H.; Yao, Q.; Guan, L.; Zhang, J.; Cheriet, M. Resource Allocation With Edge-Cloud Collaborative Traffic Prediction in Integrated Radio and Optical Networks. IEEE Access 2023, 11, 7067–7077. [Google Scholar] [CrossRef]
- Liu, S.; Qiao, B.; Han, D.; Wu, G. Task offloading method based on CNN-LSTM-attention for cloud–edge–end collaboration system. Internet Things 2024, 26, 101204. [Google Scholar] [CrossRef]
- Kim, T.; Sathyanarayana, S.D.; Chen, S.; Im, Y.; Zhang, X.; Ha, S.; Joe-Wong, C. MoDEMS: Optimizing Edge Computing Migrations for User Mobility. IEEE J. Sel. Areas Commun. 2023, 41, 675–689. [Google Scholar] [CrossRef]
- Pang, S.; Hou, L.; Gui, H.; He, X.; Wang, T.; Zhao, Y. Multi-mobile vehicles task offloading for vehicle-edge-cloud collaboration: A dependency-aware and deep reinforcement learning approach. Comput. Commun. 2024, 213, 359–371. [Google Scholar] [CrossRef]
- Hussain, M.; Wei, L.-F.; Rehman, A.; Abbas, F.; Hussain, A.; Ali, M. Deadline-Constrained Energy-Aware Workflow Scheduling in Geographically Distributed Cloud Data Centers. Future Gener. Comput. Syst. 2022, 132, 211–222. [Google Scholar] [CrossRef]
- Hussain, M.; Wei, L.-F.; Rehman, A.; Hussain, A.; Ali, M.; Javed, M.H. An Electricity Price and Energy-Efficient Workflow Scheduling in Geographically Distributed Cloud Data Centers. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102170. [Google Scholar] [CrossRef]
- Jiang, S.; Gao, H.; Wang, X.; Liu, J.; Zuo, K. Deep reinforcement learning based multi-level dynamic reconfiguration for urban distribution network: A cloud-edge collaboration architecture. Glob. Energy Interconnect. 2023, 6, 1–14. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z. A Cloud-Edge Computing Method for Integrated Electricity-Gas System Dispatch. Processes 2023, 11, 2299. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).