Assessing the Accuracy of 3D Modeling of Hydrotechnical Structures Using Bathymetric Drones: A Study of the Karatomara Reservoir
Abstract
1. Introduction
- firstly, what is the real situation with the Karatomar reservoir after 78 years of use (as well as other reservoirs of the cascade);
- secondly, how accurately do the bathymetric studies provide an assessment of the bottom relief of the reservoir after interpolation of bathymetric data;
- thirdly, with what step of bathymetric drone trajectory lines and with what required density of measurements should bathymetric assessment of plain reservoir bowls (cascade of reservoirs on the Tobol River) be carried out to achieve the required accuracy of 3D modeling.
2. Materials and Methods
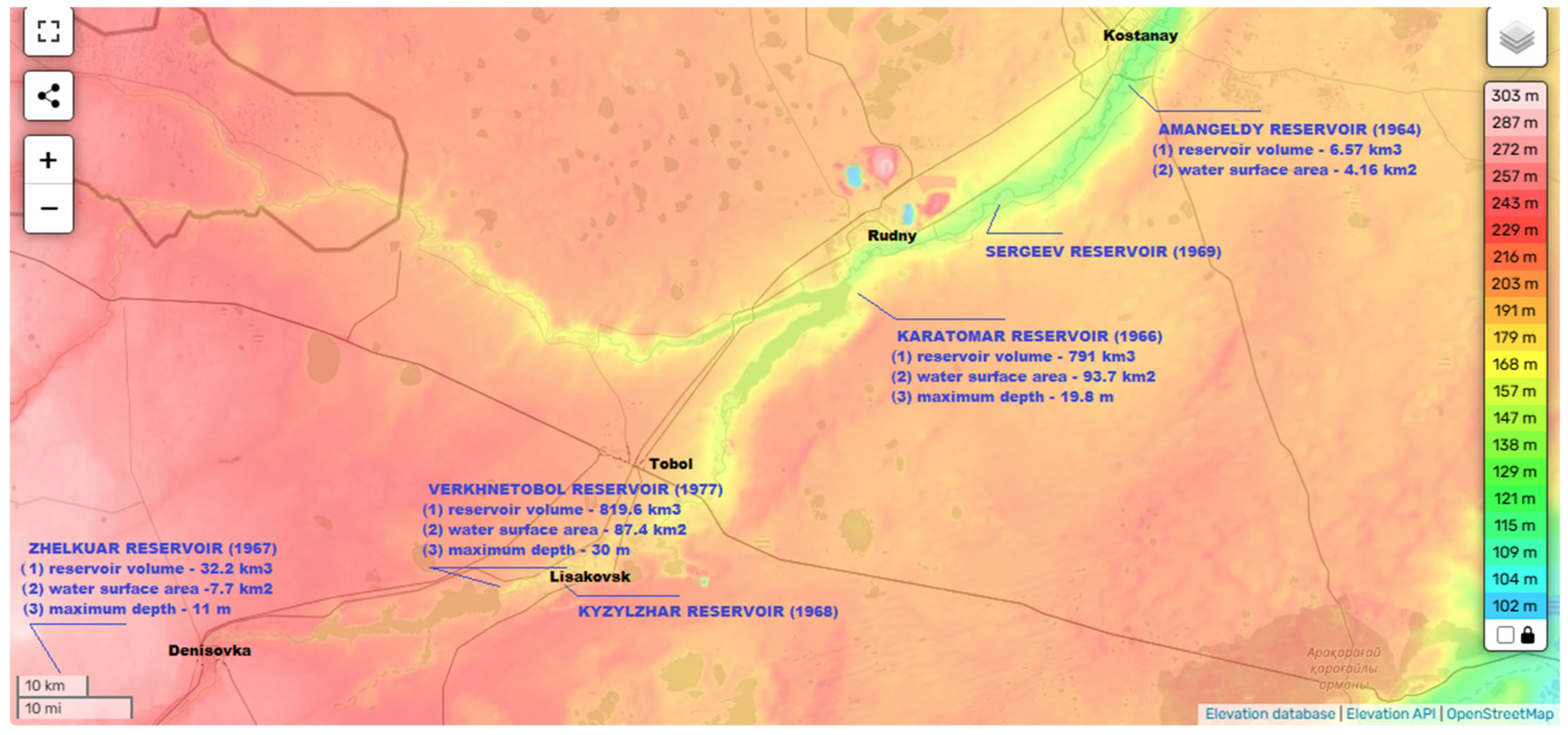
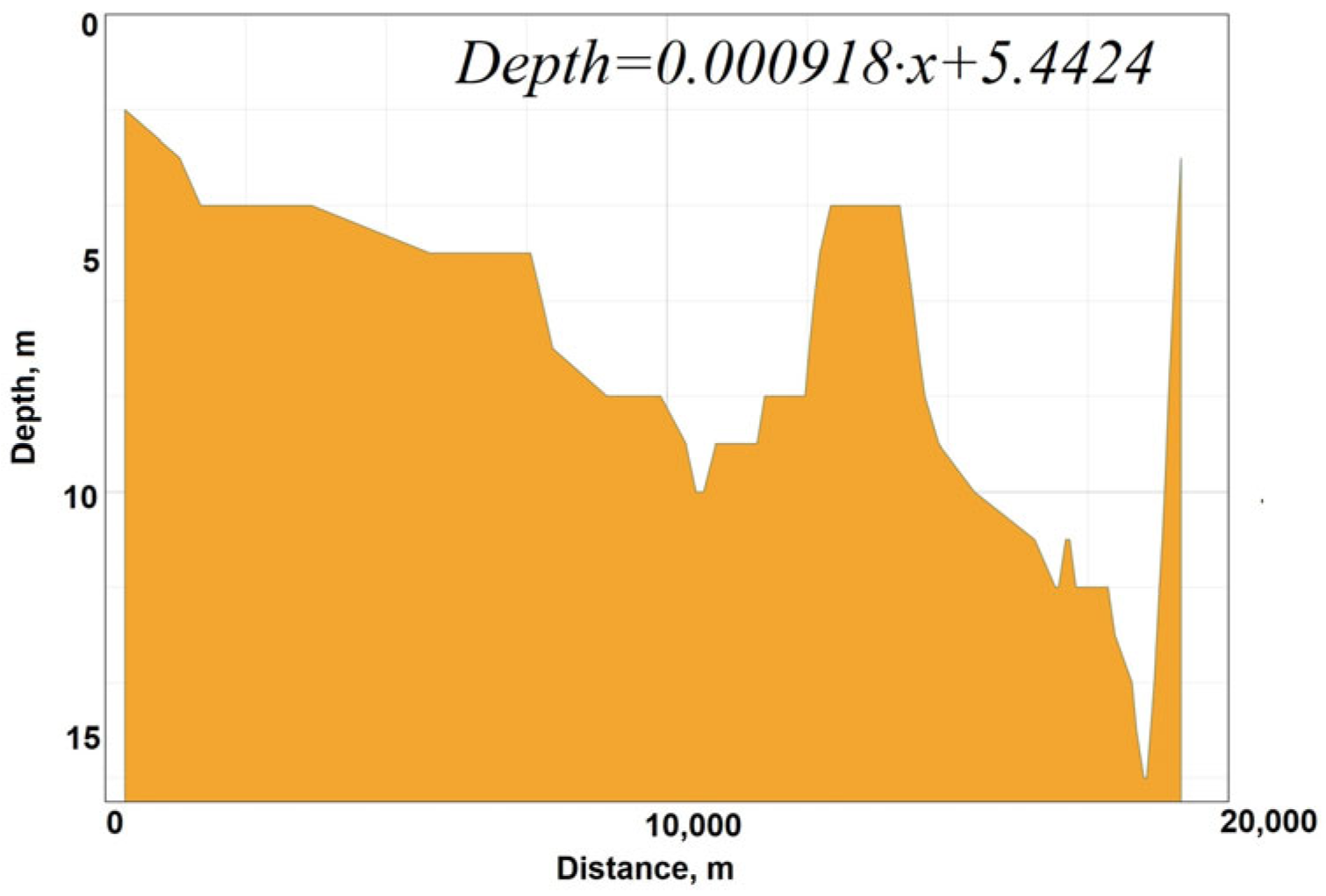
2.1. Object of Study
2.2. Obtaining Initial Data
2.3. Methods of Processing Initial Bathymetric Information
3. Results
3.1. Analysis of Potential Methods for Studying Reservoir Bowls
| Link | Name/Brief Description of the Method | Required Equipment | Advantages | Disadvantages |
|---|---|---|---|---|
| Manual methods of depth measurement and topographic survey of the relief of the coastal zone of the reservoir | ||||
| - | The method is based on measuring the length of the released lead line from the side of the vessel. | Hand lot, vessel | Affordability of single measurements | Low speed and accuracy of water body depth measurements |
| [28] | Theodolite survey | Theodolite, steel measuring tape (or optical rangefinder) | Affordability of single measurements | Low measurement speed, Limited sizes of theodolite traverses (polygons), Difficulty of carrying out work on hard-to-reach riverbed slopes |
| Tacheometric survey | Tacheometer | |||
| Tablet survey | Measuring plate | Difficulty of carrying out work on riverbed slopes | ||
| Surface leveling (vertical or altitude survey) | Level | High precision | Need for additional planning and reference work of reference points | |
| Phototheodolite survey of coastline relief (terrestrial) | Phototheodolite | |||
| Methods of automated bathymetry and topographic survey of the relief of the coastal zone of the reservoir | ||||
| [37] | Hydroacoustic sounding of the underwater part of the reservoir | Echo sounder, underwater measurement vessel/drone, attitude sensors | Possibility of capturing large volumes of data with high accuracy | Impossibility of taking measurements on overgrown areas of the reservoir |
| [38,39] | Phototheodolite survey of the coastline relief (aerial photography) | Aircraft, aerial camera | Possibility of obtaining plans of large areas. | Need for additional planning and reference work of reference points Sensitivity of measurement accuracy to the density of vegetation cover. |
| [40] | Laser scanning of the coastline relief | LiDAR, optional aerial survey aircraft + attitude sensors | Obtaining topographic plans of complex profiles. High accuracy. Measurement speed. | Sensitivity of measurement quality when working with reflective surfaces |
| Methods of remote satellite sensing and digital modeling of water bodies | ||||
| [33,35] | Group of space radar altimetry methods | Requires satellite LiDAR data and field survey data to determine depth | Obtaining topographic plans of complex profiles. High accuracy. Measurement speed | Dependent on cloudiness and weather conditions. The complexity of constructing a model of the underwater part of a water body with high accuracy |
| [5,36] | A group of methods for reconstructing and forecasting bathymetry using space data and global models. | Space photography data is required | Possibility of constructing the full relief of a reservoir bowl | Often does not take into account the complex bathymetry of a water body |
3.2. Analysis of Hydrogeology of the Tobol and Ayat Rivers in the Karatomar Reservoir Zone
- the hydromorphological situation is represented by alternating shallow riffles with shallow and medium-depth pools. The depth of the pools can reach up to 5 m, and in some cases up to 10 m or more;
- the river bottom is sandy-silty, rocky in places;
- the width of the channel varies from 50 to 400 m;
- the banks are mainly loamy, overgrown with small bushes, and slightly intersected by dry stream beds. The banks are steep, in places precipitous, 5–6 m high, and at the confluence with the slopes of the valley, they reach up to 30 m;
- snow waters are predominant in the river’s nutrition (70–90%). In winter, rivers are fed by underground waters, in summer—by underground waters, less often by rain;
- the water regime is characterized by a pronounced spring flood (up to 85–96% of the annual flow) and a long low water period;
- the mineralization of water during the spring flood period is 100–200 mg/L, and the hardness is 0.5–1.25 millimoles/L. In summer, the mineralization of water increases, and the water becomes sulfate or weakly hydrocarbonate.
- the soils of the basin are mainly sandy and loamy, sometimes salty. Alluvial channels are located in a well-defined river valley;
- the channel is gently winding, stretching, and located in a well-defined river valley;
- the bottom of the river is sandy-silty, and rocky in places;
- the width of the riverbed varies from 5 to 20 m;
- the maximum water depth is 2 m;
- the water regime is unstable, almost the entire annual flow occurs during the spring flood;
- due to large fluctuations in the water level, there are spits, islands-middens, and shoals on the river.
3.3. Evaluation of the Boat’s Tack Pitch to Ensure the Required Measurement Accuracy
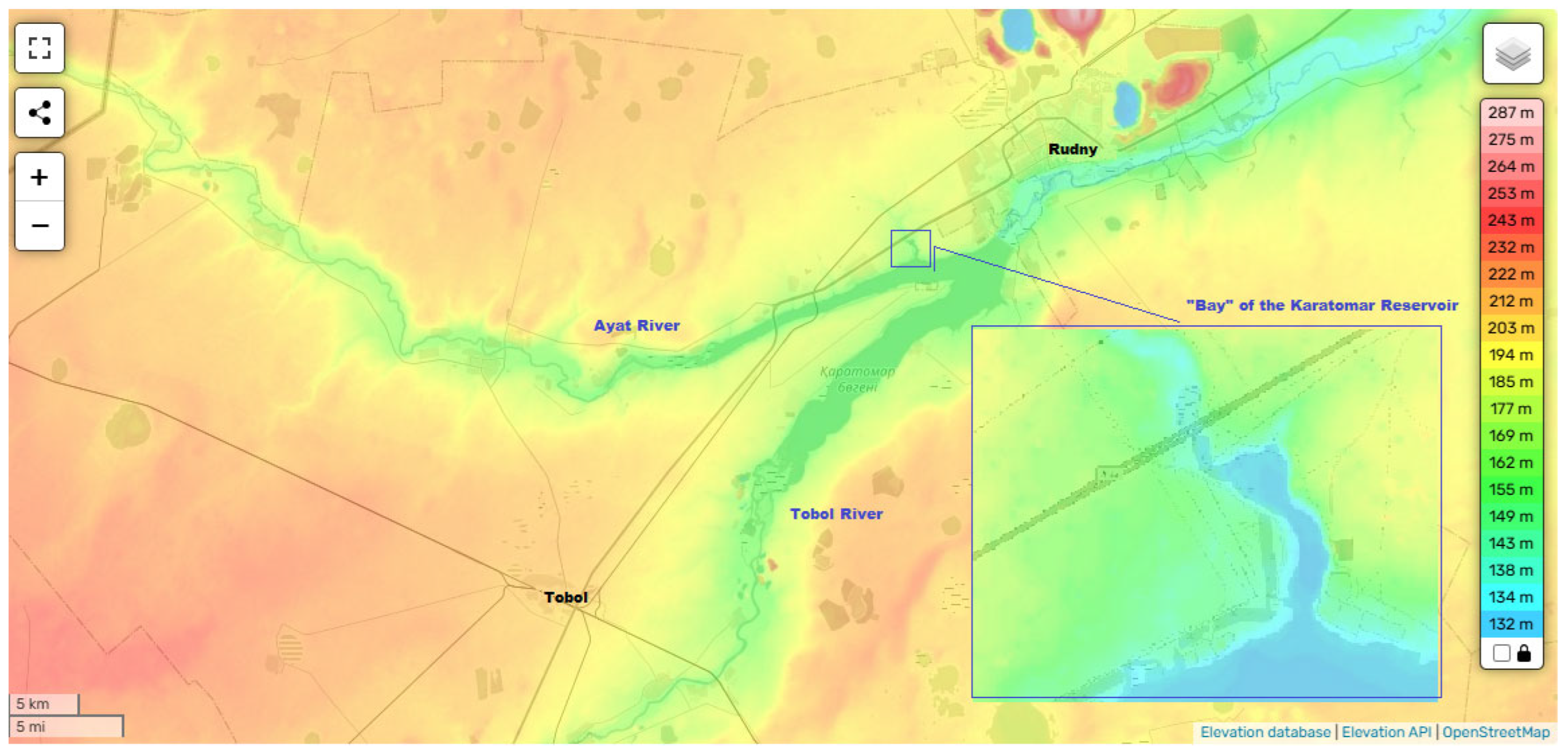
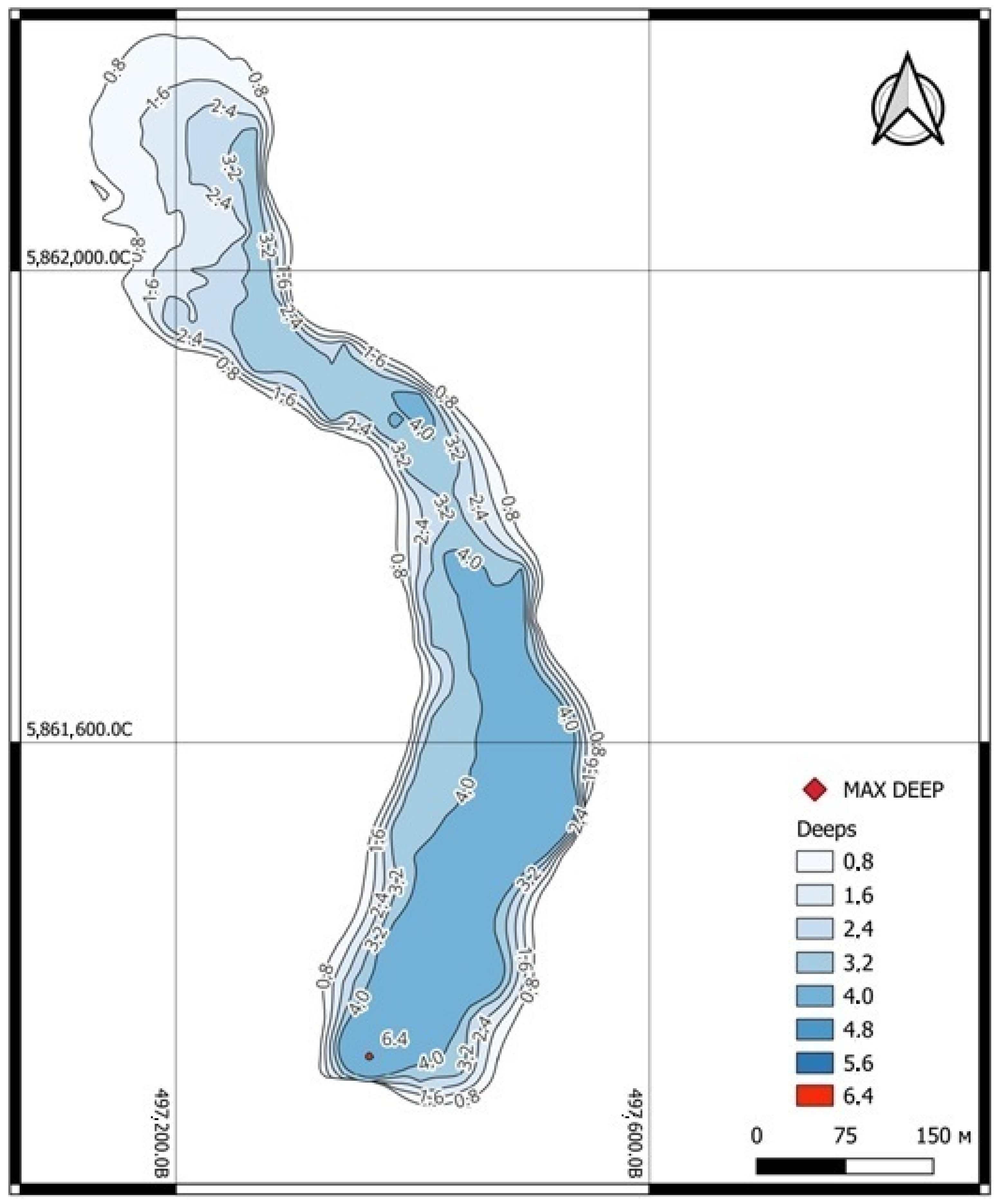
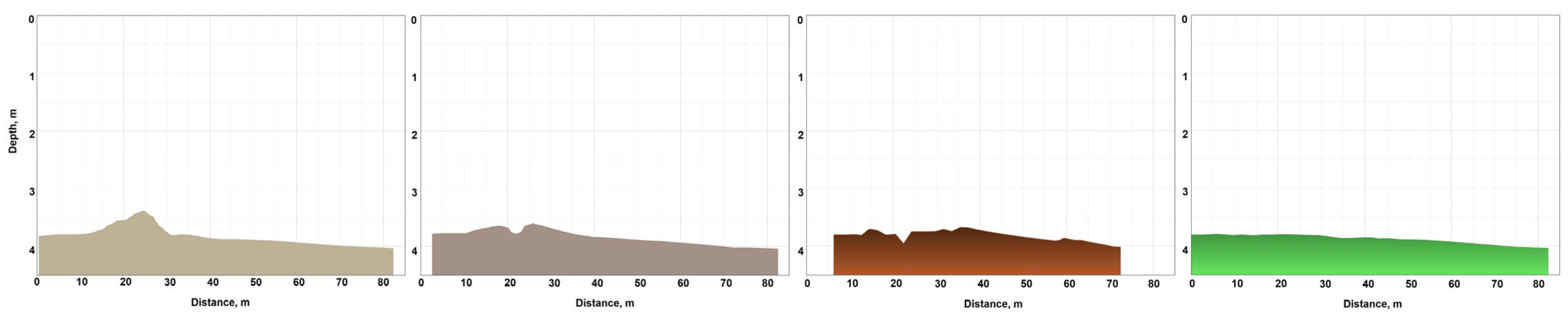
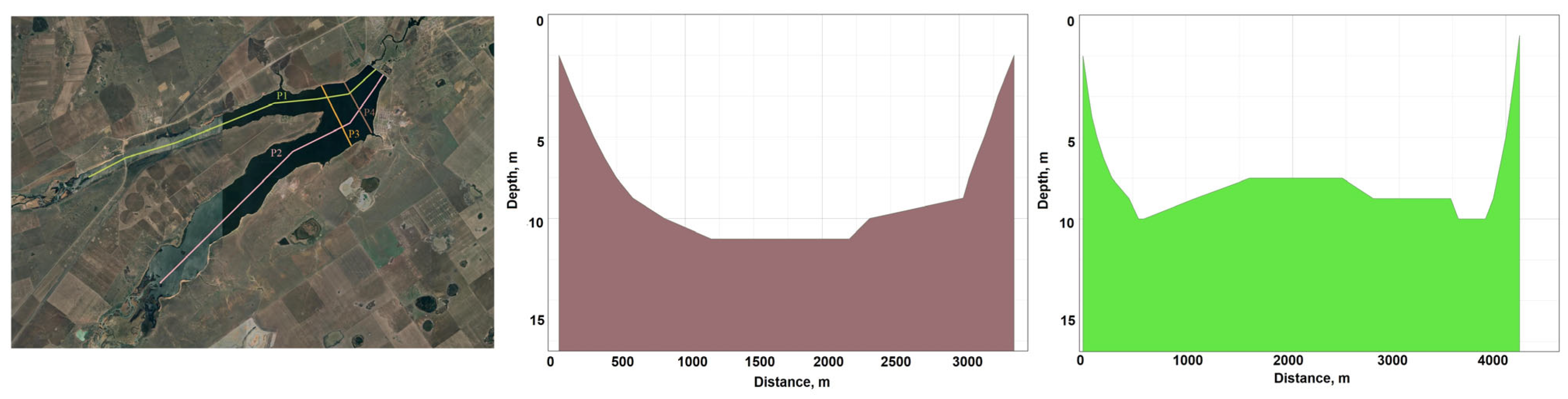
3.4. Evaluation of the Compliance of the Tobol River Bed with the Conditions Taken as the Standard “Bay”
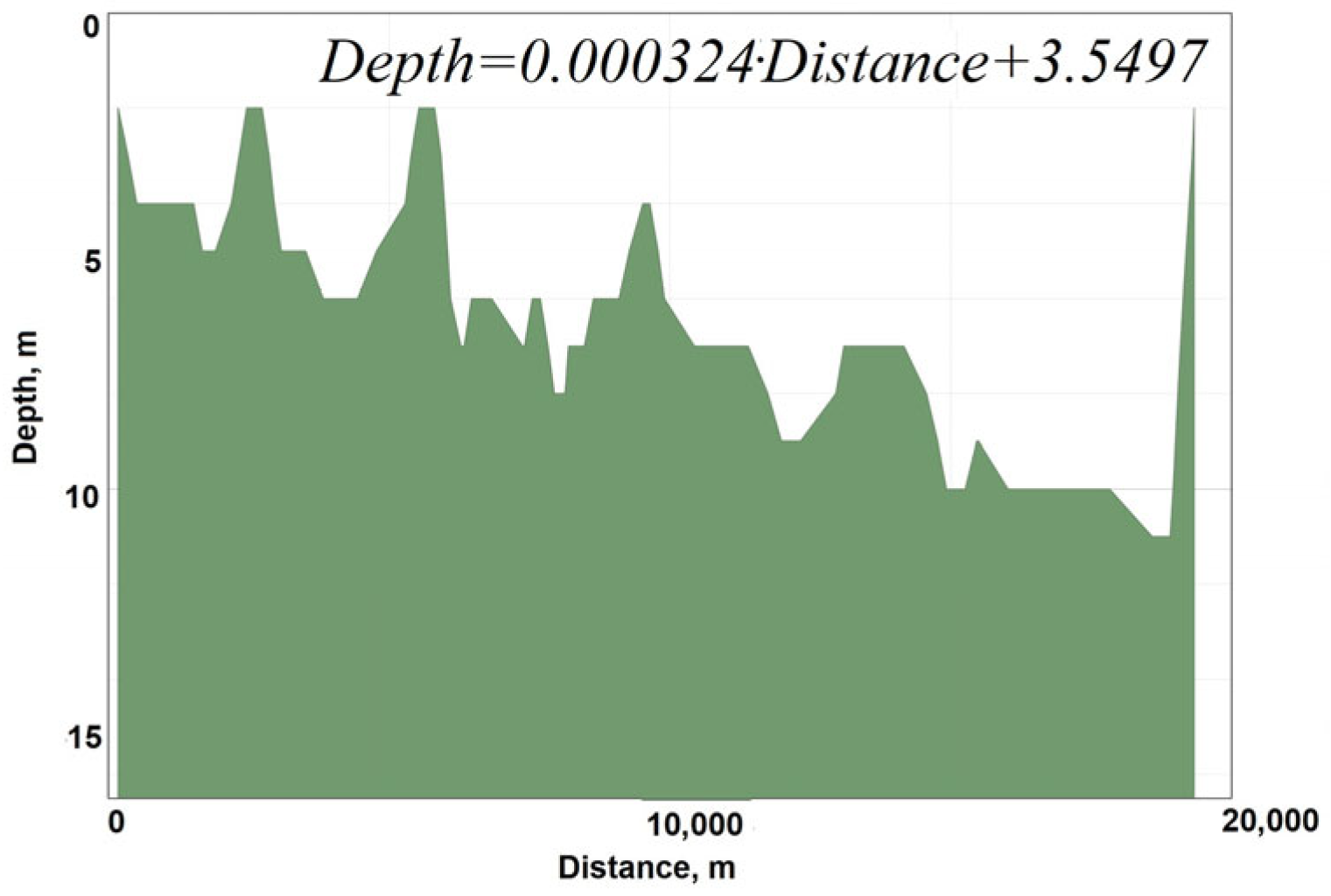
3.5. Modeling the State of the Kartomar Reservoir
4. Discussion
- 3.3 thousand affected families received a one-time social payment for a total of 1.1 billion tenge;
- 1149 houses were surveyed and assessed. More than 700 of them were recognized as unsuitable for habitation;
- more than 270 families received compensation for the repair and restoration of their houses for a total of 821.1 million tenge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LI | Interpolation method. Linear interpolation (midpoint method) |
| GPI | Interpolation method. Interpolation by the global polynomial method |
| LPI | Interpolation method. Interpolation by the local polynomial method |
| IDW | Interpolation method. Interpolation by the inverse distance weighted method |
| RBF | Interpolation method. Interpolation based on the application of radial basis functions |
| Kriging | Interpolation method. Ordinary, simple, universal, indicator, probabilistic, disjunctive and empirical Bayesian kriging. |
| RMSE | Root mean square error |
| SRTM | Shuttle Radar Topography Mission |
| MLP | Multilayer perceptron |
| RBFN | Radial basis function neural network |
| FNN | Back propagation neural network |
| DNN | Deep neural network |
| CapsNet | Capsule neural networks |
| MSE | Mean square error |
| MRD | Maximum relative deviation |
References
- Cooley, S.W.; Ryan, J.C.; Smith, L.C. Human alteration of global surface water storage vriability. Nature 2021, 591, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Chao, B.; Wu, Y.; Li, Y. Impact of artificial reservoir water impoundment on global sea level. Science 2008, 320, 212–214. [Google Scholar] [CrossRef] [PubMed]
- Williamson, C.E.; Saros, J.E.; Vincent, W.F.; Smol, J.P. Lakes and reservoirs as sentinels, integrators, and regulators of climate change. Limnol. Oceanogr. 2009, 54 Pt 2, 2273–2282. [Google Scholar] [CrossRef]
- On Approval of the Concept for the Development of the Water Resources Management System of the Republic of Kazakhstan for 2024–2030, Resolution of the Government of the Republic of Kazakhstan Dated 5 February 2024. No. 66. Available online: https://adilet.zan.kz/rus/docs/P2400000066 (accessed on 27 March 2025).
- Yigzaw, W.; Li, H.Y.; Demissie, Y.; Hejazi, M.I.; Leung, L.R.; Voisin, N.; Payn, R. A new global storage-area-depth data set for modeling reservoirs in land surface and earth system models. Water Resour. Res. 2018, 54, 386. [Google Scholar] [CrossRef]
- Bandini, F.; Olesen, D.; Jakobsen, J.; Kittel, C.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Bathymetry observations of inland water bodies using a tethered single-beam sonar controlled by an unmanned aerial vehicle. Hydrol. Earth Syst. Sci. 2018, 22, 4165–4181. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Jasinski, M.F.; Zhang, S.; Stoll, J.D. Deriving high-resolution reservoir bathymetry from ICESat-2 prototype photon-counting lidar and landsat imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7883–7893. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.; Belz, J.; Chapin, E.; Martin, J.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products; Technical Report JPL D-31639; Jet Propulsion Laboratory: Pasadena, CA, USA, 2005; 143p. [Google Scholar]
- Zhang, K.; Gann, D.; Ross, M.; Robertson, Q.; Sarmiento, J.; Santana, S.; Rhome, J.; Fritz, C. Accuracy assessment of ASTER, SRTM, ALOS, and TDX DEMs for Hispaniola and implications for mapping vulnerability to coastal flooding. Remote Sens. Environ. 2019, 225, 290–306. [Google Scholar] [CrossRef]
- Hao, Z.; Chen, F.; Jia, X.; Cai, X.; Yang, C.; Du, Y.; Ling, F. GRDL: A New Global Reservoir Area-Storage-Depth Data Set Derived Through Deep Learning-Based Bathymetry Reconstruction. Water Resour. Res. 2024, 1, e2023WR035781. [Google Scholar] [CrossRef]
- Pirani, F.; Modarres, R. Geostatistical and deterministic methods for rainfall interpolation in the Zayandeh. Hydrol. Sci. J. 2020, 65, 2678–2692. [Google Scholar] [CrossRef]
- Zarubin, M.; Zarubina, V.; Jamanbalin, K.; Akhmetov, D.; Yessenkulova, Z.; Salimbayeva, R. Digital Technologies as a Factor in Reducing the Impact of Quarries on the Environment. Environ. Clim. Technol. 2021, 25, 436–454. [Google Scholar] [CrossRef]
- Dovile, K.; Zenonas, N.; Raimondas, Č.; Minvydas, R. An extended Prony’s interpolation scheme on an equispaced grid. Open Math. 2015, 13, 000010151520150031. [Google Scholar] [CrossRef]
- Skorokhodov, I. Interpolating Points on a Non-Uniform Grid Using a Mixture of Gaussians. 2020. Available online: https://arxiv.org/pdf/2012.13257 (accessed on 27 March 2025).
- Gilewski, P. Impact of the Grid Resolution and Deterministic Interpolation of Precipitation on Rainfall-Runoff Modeling in a Sparsely Gauged Mountainous Catchment. Water 2021, 13, 230. [Google Scholar] [CrossRef]
- Ben-Or, M.; Tiwari, P. A deterministic algorithm for sparse multivariate polynomial interpolation. In Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing (STOC ’88), Chicago, IL, USA, 2–4 May 1988; pp. 301–309. [Google Scholar] [CrossRef]
- Biernacik, P.; Kazimierski, W.; Wlodarczyk-Sielicka, M. Comparative Analysis of Selected Geostatistical Methods for Bottom Surface Modeling. Sensors 2023, 23, 3941. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Parente, C. The Influence of Interpolated Point Location and Density on 3D Bathymetric Models Generated by Kriging Methods: An Application on the Giglio Island Seabed (Italy). Geosciences 2022, 12, 62. [Google Scholar] [CrossRef]
- Chowdhury, M.; Alouani, A.T.; Hossain, F. Comparison of Ordinary Kriging and Artificial Neural Network for Spatial Mapping of Arsenic Contamination of Groundwater. Stoch. Environ. Res. Risk Assess. 2008, 24, 1–7. [Google Scholar] [CrossRef]
- Janowicz, K.; Gao, S.; McKenzie, G.; Hu, Y.; Bhaduri, B. GeoAI: Spatially explicit artificial intelligence techniques for geographic knowledge discovery and beyond. Int. J. Geogr. Inf. Sci. 2019, 34, 625–636. [Google Scholar] [CrossRef]
- Zarubin, M.; Zarubina, V. Results of using neural networks for technological processes control of iron mill. J. Energy Procedia 2016, 95, 512–516. [Google Scholar] [CrossRef][Green Version]
- Huang, Y.-L.; Chang, R.F. MLP interpolation for digital image processing using wavelet transform. In Proceedings of the Acoustics, Speech, and Signal Processing, 06 (ICASSP ’99), Phoenix, AZ, USA, 15–19 March 1999; IEEE Computer Society: Washington, DC, USA, 1999; pp. 3217–3220. [Google Scholar]
- Nevtipilova, V.; Pastwa, J.; Boori, M.S.; Vozenilek, V. Testing Multilayer Perceptron (MLP) for Spatial Interpolation. Interexpo Geo-Siberia. 2014, pp. 33–51. Available online: https://cyberleninka.ru/article/n/testing-multilayer-perceptron-mlp-for-spatial-interpolation (accessed on 27 March 2025).
- Yeh, I.; Huang, K.-C.; Kuo, Y.-H. Spatial interpolation using MLP–RBFN hybrid networks. Int. J. Geogr. Inf. Sci. 2013, 27, 1884–1901. [Google Scholar] [CrossRef]
- Gotway, C.; Ferguson, R.; Hergert, G.; Peterson, T. Comparison of Kriging and Inverse-Distance Methods for Mapping Soil Parameters. Soil Sci. Soc. Am. J. SSSAJ 1996, 60, 1237–1247. [Google Scholar] [CrossRef]
- Qian, Y.; Ghorbanidehno, H.; Lee, J.H.; Farthing, M.; Hesser, T.; Kitanidis, P.K.; Darve, E.F. Applications of Deep Neural Network to Near-Shore Bathymetry with Sparse Measurements. American Geophysical Union, Fall Meeting 2019, Abstract #EP43C-04, 2019. Available online: https://ui.adsabs.harvard.edu/abs/2019AGUFMEP43C..04Q/abstract (accessed on 27 March 2025).
- Mazzia, V.; Salvetti, F.; Chiaberge, M. Efficient-CapsNet: Capsule network with self-attention routing. Sci. Rep. 2021, 11, 14634. [Google Scholar] [CrossRef]
- Nurpeisova, M.B.; Zharkimbaev, B.M. Geodesy; KazNTU: Almaty, Kazakstan, 2002; pp. 217–239. [Google Scholar]
- Neumann, J. Maximum depth and average depth of lakes. J. Fish. Board Can. 1959, 16, 923–927. [Google Scholar] [CrossRef]
- Anderson, D. A note on the morphology of the basins of the Great Lakes. J. Fish. Board Can. 1961, 18, 273–277. [Google Scholar] [CrossRef]
- Lehman, J.T. Reconstructing the rate of accumulation of lake sediment: The effect of sediment focusing. Quat. Res. 1975, 5, 541–550. [Google Scholar] [CrossRef]
- Carpenter, S.R. Lake geometry: Implications for production and sediment accretion rates. J. Theor. Biol. 1983, 105, 273–286. [Google Scholar] [CrossRef]
- Gao, H.; Birkett, C.; Lettenmaier, D. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res. 2012, 48, W09504. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, F.; Ling, F.; Du, Y. Monitoring surface water inundation of Poyang Lake and Dongting Lake in China using Sentinel-1 SAR images. Remote Sens. 2022, 14, 3473. [Google Scholar] [CrossRef]
- Yao, F.; Minear, J.T.; Rajagopalan, B.; Wang, C.; Yang, K.; Livneh, B. Estimating reservoir sedimentation rates and storage capacity losses using high-resolution Sentinel-2 satellite and water level data. Geophys. Res. Lett. 2023, 50, e2023GL103524. [Google Scholar] [CrossRef]
- Liu, K.; Song, C.; Wang, J.; Ke, L.; Zhu, Y.; Jingying, Z.; Luo, Z.L. Remote sensing-based modeling of the bathymetry and water storage for channel-type reservoirs worldwide. Water Resour. Res. 2020, 56, e2020WR027147. [Google Scholar] [CrossRef]
- Yun, H.-S.; Cho, J.-M. Hydroacoustic Application of Bathymetry and Geological Survey for Efficient Reservoir Management. J. Korean Soc. Surv. Geod. Photogramm. Cartogr. 2011, 29, 209–217. [Google Scholar] [CrossRef][Green Version]
- Madden, J.D. Coastline delineation by aerial photography. Aust. Surv. 1978, 29, 76–82. [Google Scholar] [CrossRef]
- Gonçalves, J.; Bastos, M.; Pinho, J.; Granja, H. Digital aerial photography to monitor changes in coastal areas based on direct georeferencing. In Proceedings of the 5th EARSeL Workshop on Remote Sensing of the Coastal ZoneAt, Prague, Czech Republic, 3 June 2011; Available online: https://www.researchgate.net/publication/360427485_DIGITAL_AERIAL_PHOTOGRAPHY_TO_MONITOR_CHANGES_IN_COASTAL_AREAS_BASED_ON_DIRECT_GEOREFERENCING (accessed on 27 March 2025).
- Tyszkowski, S.; Zbucki, Ł.; Kaczmarek, H.; Duszyński, F.; Strzelecki, M. Detection of Coastal Changes along Rauk Coasts of Gotland, Baltic Sea. Remote Sens. 2023, 15, 1667. [Google Scholar] [CrossRef]
- Lubczonek, J.; Kazimierski, W.; Zaniewicz, G.; Lacka, M. Methodology for Combining Data Acquired by Unmanned Surface and Aerial Vehicles to Create Digital Bathymetric Models in Shallow and Ultra-Shallow Waters. Remote Sens. 2022, 14, 105. [Google Scholar] [CrossRef]
- Lubczonek, J.; Wlodarczyk-Sielicka, M.; Lacka, M.; Zaniewicz, G. Methodology for Developing a Combined Bathymetric and Topographic Surface Model Using Interpolation and Geodata Reduction Techniques. Remote Sens. 2021, 13, 4427. [Google Scholar] [CrossRef]
- Han, D. Comparison of Commonly Used Image Interpolation Methods. In Proceedings of the ICCSEE 2013, Hangzhou, China, 22–24 March 2013. [Google Scholar]
- Jiao, Y.; Zhang, F.; Huang, Q.; Liu, X.; Li, L. Analysis of Interpolation Methods in the Validation of Backscattering Coefficient Products. Sensors 2023, 23, 469. [Google Scholar] [CrossRef]
- Zarubina, V.; Zarubin, M.; Yessenkulova, Z.; Gumarova, T.; Daulbayeva, A.; Meimankulova, Z.; Kurmangalieva, A. Sustainable Development of Small Business in Kazakhstan. Economies 2024, 12, 247. [Google Scholar] [CrossRef]
- Weather in Rudny in July 2024. Available online: https://belkraj.by/pogoda/kazakhstan/l1519843/rudnyy/july (accessed on 1 September 2024).
- Tobol. Ministry of Natural Resources of Russia; State Water Register: Moskow, Russia, 2009. [Google Scholar]
- Gui, R.; Song, W.; Lv, J.; Lu, Y.; Liu, H.; Feng, T.; Linghu, S. Digital Elevation Model-Driven River Channel Boundary Monitoring Using the Natural Breaks (Jenks) Method. Remote Sens. 2025, 17, 1092. [Google Scholar] [CrossRef]
- Skariah, M.; Suriyakala, C.D. Gauging of sedimentation in Idukki reservoir, Kerala (1974–2019), and the impact of 2018 Kerala floods on the reservoir. J. Indian Soc. Remote Sens. 2021, 49, 2103–2112. [Google Scholar] [CrossRef]
- Wagh, S.; Manekar, V. Assessment of reservoir sedimentation using satellite remote sensing technique (SRS). J. Inst. Eng. (India) Ser. A 2021, 102, 851–860. [Google Scholar] [CrossRef]



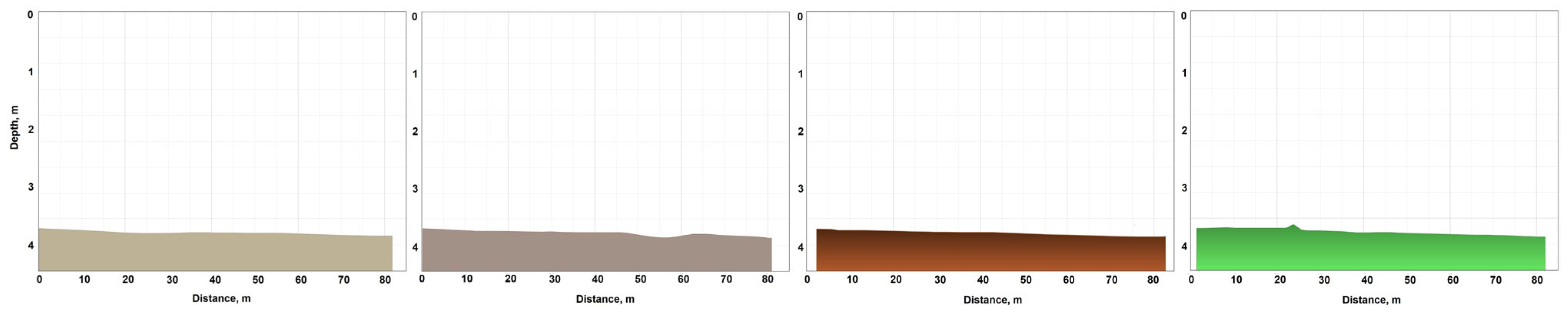

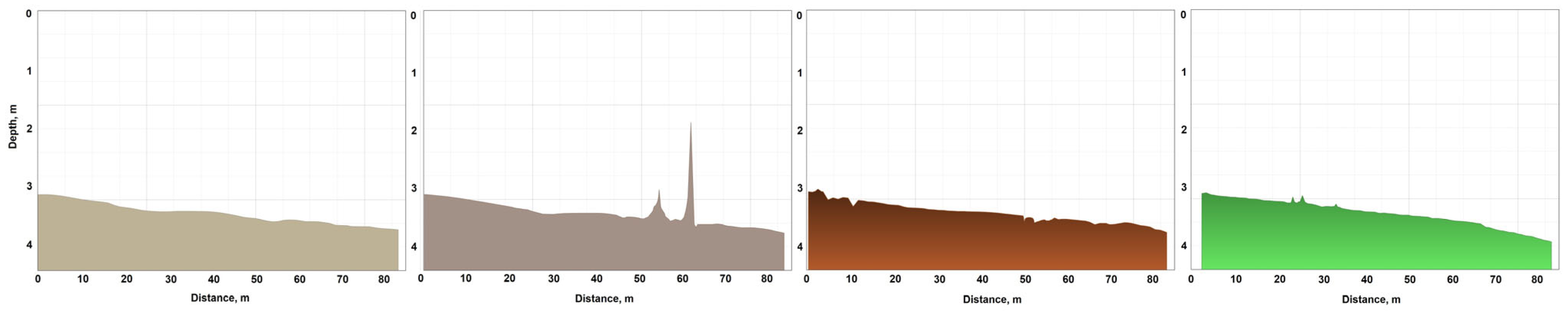


| Parameter Name | Value |
|---|---|
| Echo sounder | |
| Measured depth range, m | from 0.15 to 200 |
| Echo sounder operating frequency, kHz | 200 |
| Echo sounder resolution, m | 0.01 |
| Echo sounder beam width, ° | 6.5 ± 1 |
| Root mean square error (RMSE) of depth measurements, m | 0.01 + 0.001·H, where H is the measured depth in cm |
| Location | |
| Number of channels | 624 |
| GNSS | GPS NAVSTAR: L1C/A, L1C, L2C, L2P, L5 ΓЛOHACC: L1C/A, L1P, L2C/A, L2P BeiDou: B1, B2, B3 Galileo: E1, E5A, E5B SBAS: WAAS, EGNOS, MSAS, QZSS, GAGAN |
| RMSE | RTK in plan 8.0 mm + 1.0 mm/km |
| RMSE | RTK in height 15.0 mm + 1.0 mm/km |
| RMSE DGPS in plan | 0.25 m |
| RMSE DGPS in altitude | 0.5 m |
| Heading accuracy | 0.2° per 1 m baseline |
| Inertial navigation stability | 6° per hour |
| Parameter | Depth (Minimum) | Depth (Maximum) | ||||||
|---|---|---|---|---|---|---|---|---|
| Run step | 10 | 25 | 50 | 100 | 10 | 25 | 50 | 100 |
| Interpolation method | ||||||||
| Linear | 0.800 | 0.400 | 0.130 | 1.540 | 5.540 | 5.250 | 5.490 | 5.360 |
| Planar Regression: Z = AX + BY + C | 0.1353 | 0.009 | 0.016 | 0.001 | 3.054 | 1.073 | 1.096 | 0.707 |
| Kriging | 1.573 | 1.141 | 1.007 | 2.727 | 5.550 | 5.419 | 5.919 | 5.348 |
| Parameter | Depth (Mean) | MSE (Relative Mean Diff) | ||||||
|---|---|---|---|---|---|---|---|---|
| Run step | 10 | 25 | 50 | 100 | 10 | 25 | 50 | 100 |
| Interpolation method | ||||||||
| Linear | 4.225 | 4.216 | 4.274 | 4.301 | 0.112 | 0.106 | 0.105 | 0.161 |
| Planar Regression: Z = AX + BY + C | 2.245 | 0.313 | 0.320 | 0.288 | 0.164 | 0.359 | 0.301 | 0.342 |
| Kriging | 4.298 | 4.261 | 4.343 | 4.367 | 0.119 | 0.102 | 0.107 | 0.105 |
| Section P1 | Section P2 | Section P3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Run step | 10 | 25 | 50 | 100 | 10 | 25 | 50 | 100 | 10 | 25 | 50 | 100 |
| Point | Depth | |||||||||||
| 0 | 3.82 | 3.79 | 3.80 | 3.81 | 4.18 | 4.18 | 4.18 | 4.18 | 4.51 | 4.49 | 4.52 | 4.52 |
| 10 | 3.79 | 3.78 | 3.80 | 3.81 | 4.22 | 4.22 | 4.22 | 4.19 | 4.52 | 4.52 | 4.52 | 4.51 |
| 20 | 3.55 | 3.68 | 3.79 | 3.8 | 4.27 | 4.23 | 4.23 | 4.19 | 3.33 | 4.52 | 4.58 | 4.60 |
| 30 | 3.76 | 3.69 | 3.74 | 3.83 | 4.27 | 4.24 | 4.25 | 4.24 | 4.61 | 4.55 | 4.65 | 4.71 |
| 40 | 3.87 | 3.85 | 3.72 | 3.86 | 4.27 | 4.26 | 4.26 | 4.28 | 4.57 | 4.63 | 4.69 | 4.82 |
| 50 | 3.90 | 3.89 | 3.84 | 3.89 | 4.27 | 4.30 | 4.28 | 4.29 | 4.64 | 4.71 | 4.71 | 4.92 |
| 60 | 3.94 | 3.94 | 3.87 | 3.93 | 4.29 | 4.32 | 4.31 | 4.31 | 4.73 | 4.74 | 4.80 | 4.99 |
| 70 | 4.00 | 4.01 | 4.00 | 4.00 | 4.32 | 4.32 | 4.33 | 4.33 | 4.83 | 4.81 | 4.74 | 5.03 |
| 80 | 4.03 | 4.04 | 4.02 | 4.04 | 4.33 | 4.36 | 4.34 | 4.36 | 4.98 | 4.99 | 4.67 | 5.03 |
| Parameter | P1 | P2 | P3 | P4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Run step | 25 | 50 | 100 | 25 | 50 | 100 | 25 | 50 | 100 | 25 | 50 | 100 |
| MSE | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.00 | 0.16 | 0.19 | 0.21 | 0.00 | 0.00 | 0.01 |
| MRD | 0.02 | 0.04 | 0.00 | 0.01 | 0.01 | 0.02 | 0.01 | 0.06 | 0.00 | 0.00 | 0.01 | 0.04 |
| Pearson correlation coefficient | 0.93 | 0.69 | 0.85 | 0.90 | 0.94 | 0.87 | 0.60 | 0.44 | 0.57 | 1.00 | 0.99 | 0.96 |
| Similarity coefficient | 0.99 | 0.97 | 0.96 | 0.99 | 0.98 | 0.99 | 0.99 | 0.94 | 0.92 | 0.98 | 0.97 | 0.95 |
| Depth, m | Pirson Ayat | Pirson Tobol | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Distance, m | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |||
| r. Ayat | P1 | 3.55 | −3.55 | 3.56 | 3.56 | 3.56 | 3.57 | 3.57 | 3.57 | 3.58 | ||
| r. Tobol | P2 | 5.44 | 5.45 | 5.45 | 5.46 | 5.46 | 5.47 | 5.47 | 5.48 | 5.48 | ||
| “Bay” | P1 | 3.82 | 3.79 | 3.55 | 3.76 | 3.87 | 3.90 | 3.94 | 4.03 | 4.00 | 0.74 | 0.74 |
| P2 | 4.18 | 4.22 | 4.27 | 4.27 | 4.27 | 4.27 | 4.29 | 4.32 | 4.33 | 0.93 | 0.93 | |
| P3 | 4.51 | 4.52 | 3.33 | 4.61 | 4.57 | 4.64 | 4.73 | 4.83 | 4.98 | 0.54 | 0.54 | |
| Depth, m | Mirror Area by Depth | Bowl Volume by Depth | ||
|---|---|---|---|---|
| km2 | % of Maximum | km3 | % of Maximum | |
| 0 | 61.466 | 100.00 | 367.049 | 100.00 |
| 1 | 55.254 | 89.89 | 305.582 | 83.25 |
| 2 | 50.716 | 82.51 | 250.329 | 68.20 |
| 3 | 45.473 | 73.98 | 199.613 | 54.38 |
| 4 | 38.947 | 63.36 | 154.140 | 41.99 |
| 5 | 31.860 | 51.83 | 115.192 | 31.38 |
| 6 | 24.899 | 40.51 | 83.332 | 22.70 |
| 7 | 20.794 | 33.83 | 58.433 | 15.92 |
| 8 | 16.750 | 27.25 | 37.638 | 10.25 |
| 9 | 11.618 | 18.90 | 20.889 | 5.69 |
| 10 | 5.739 | 9.34 | 9.271 | 2.53 |
| 11 | 2.137 | 3.48 | 3.531 | 0.96 |
| 12 | 0.878 | 1.43 | 1.394 | 0.38 |
| 13 | 0.309 | 0.50 | 0.516 | 0.14 |
| 14 | 0.129 | 0.21 | 0.208 | 0.06 |
| 15 | 0.061 | 0.10 | 0.079 | 0.02 |
| 16 | 0.018 | 0.03 | 0.018 | 0.00 |
| Parameters | Data 1966 | Data 2024 | Deviation |
|---|---|---|---|
| Reservoir volume, | 791 mil. m3 (when the bowl is 100% full | 367 mil. m3 (at 98% bowl filling | −53.60% |
| Useful reservoir volume, | 562 mil. m3 | Not rated | - |
| Water surface area, | 93.7 km2 | 61.47 km2 (based on digitized polygon) ± 5.63 km2 | −34.44 ± 6.01% |
| Maximum depth, m | 19.8 | 16.0 | −18.99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarubin, M.; Kuanyshbayev, S.; Chashkov, V.; Yskak, A.; Nugmanov, A.; Salykova, O.; Bashev, A.; Nurpeisov, A. Assessing the Accuracy of 3D Modeling of Hydrotechnical Structures Using Bathymetric Drones: A Study of the Karatomara Reservoir. Sustainability 2025, 17, 4858. https://doi.org/10.3390/su17114858
Zarubin M, Kuanyshbayev S, Chashkov V, Yskak A, Nugmanov A, Salykova O, Bashev A, Nurpeisov A. Assessing the Accuracy of 3D Modeling of Hydrotechnical Structures Using Bathymetric Drones: A Study of the Karatomara Reservoir. Sustainability. 2025; 17(11):4858. https://doi.org/10.3390/su17114858
Chicago/Turabian StyleZarubin, Mikhail, Seitbek Kuanyshbayev, Vadim Chashkov, Aliya Yskak, Almabek Nugmanov, Olga Salykova, Artem Bashev, and Adil Nurpeisov. 2025. "Assessing the Accuracy of 3D Modeling of Hydrotechnical Structures Using Bathymetric Drones: A Study of the Karatomara Reservoir" Sustainability 17, no. 11: 4858. https://doi.org/10.3390/su17114858
APA StyleZarubin, M., Kuanyshbayev, S., Chashkov, V., Yskak, A., Nugmanov, A., Salykova, O., Bashev, A., & Nurpeisov, A. (2025). Assessing the Accuracy of 3D Modeling of Hydrotechnical Structures Using Bathymetric Drones: A Study of the Karatomara Reservoir. Sustainability, 17(11), 4858. https://doi.org/10.3390/su17114858







