An Innovative Framework for Forecasting the State of Health of Lithium-Ion Batteries Based on an Improved Signal Decomposition Method
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution
1.4. Organization of the Paper
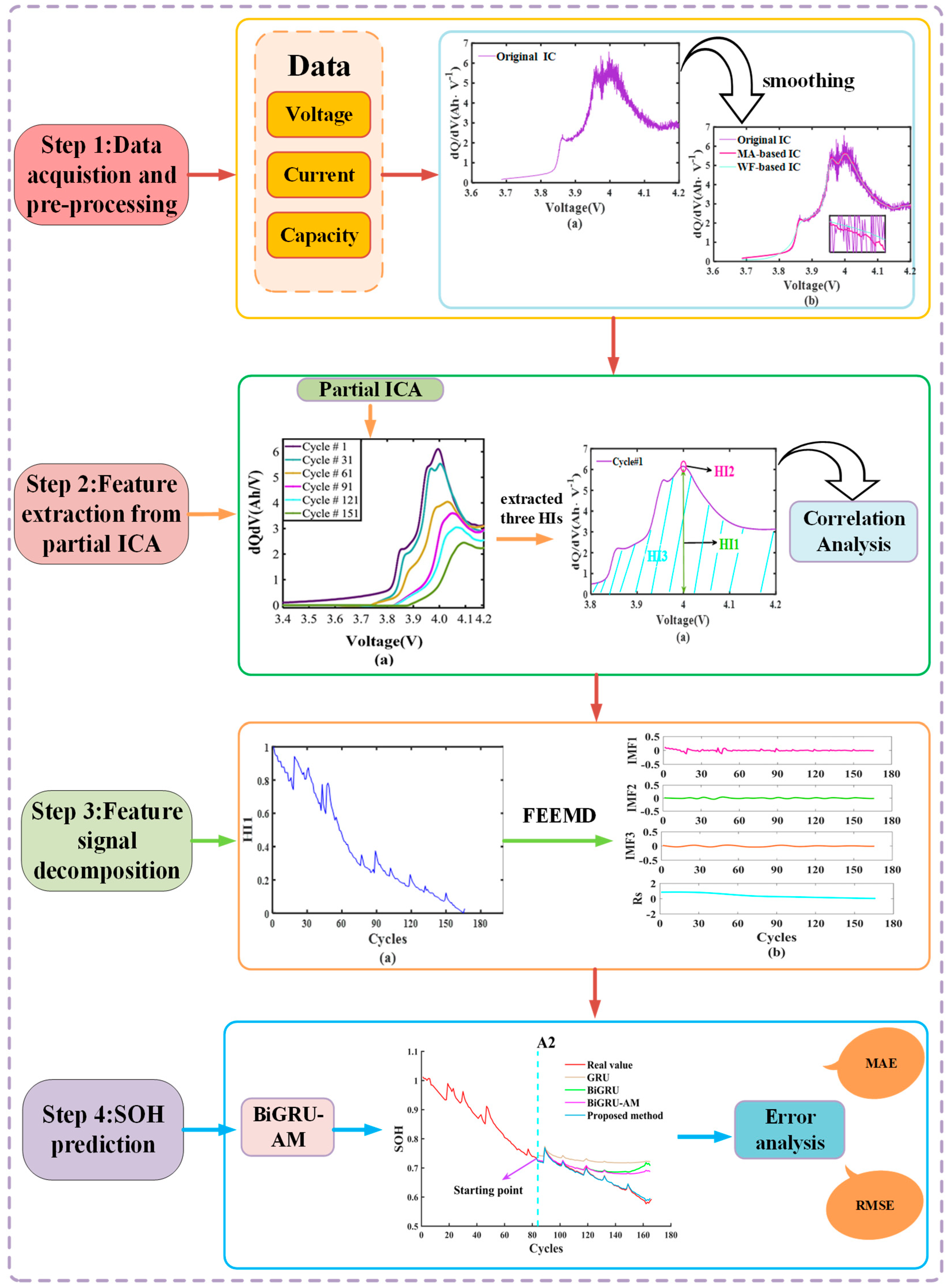
2. Methodology
2.1. Incremental Capacity Curve Analysis and Smoothing Technique
2.2. Feature Extraction
2.3. The Assessment of HIs
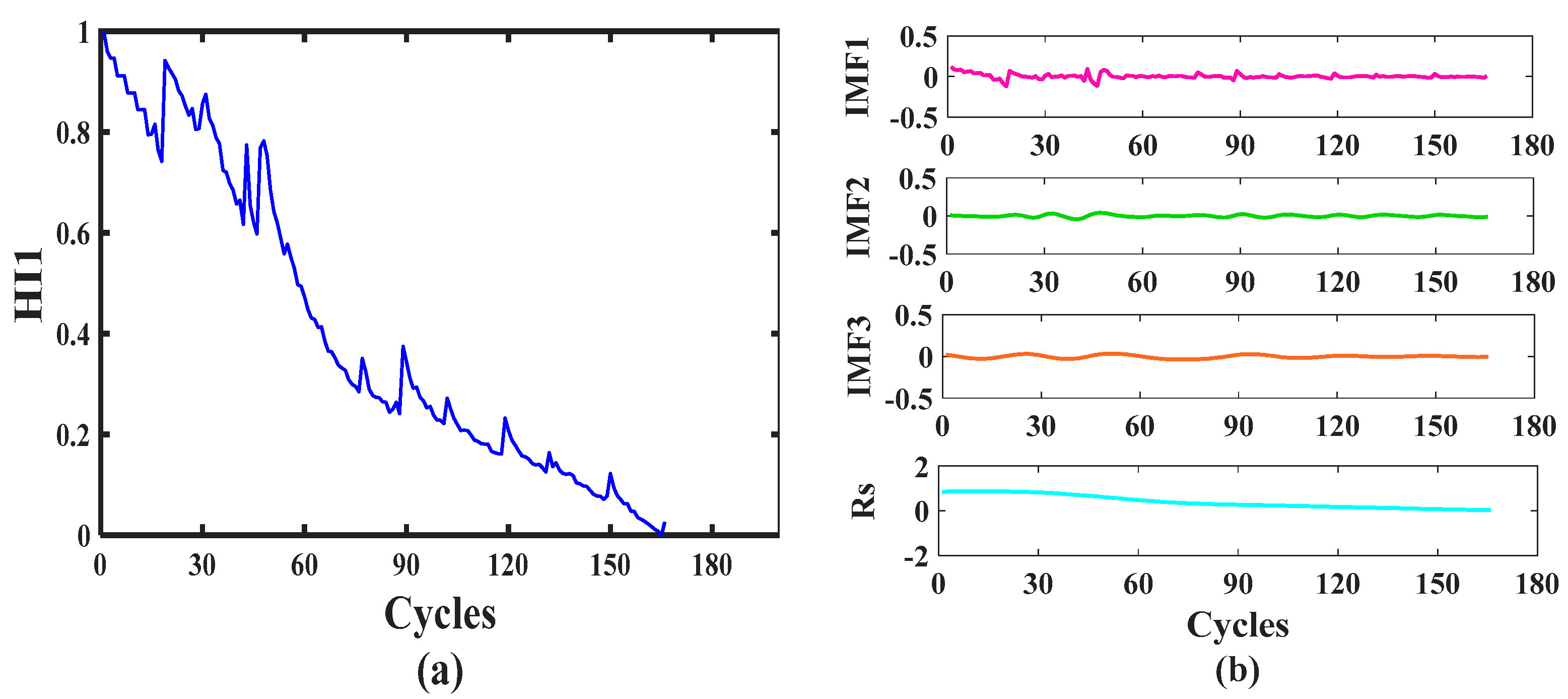
2.4. Feature Signal Decomposition
2.4.1. Box-Counting Dimension
2.4.2. The Principle of FEEMD Algorithm
2.4.3. Decomposition Performance of FEEMD
2.4.4. Feature Decomposition
2.5. Forecasting Method
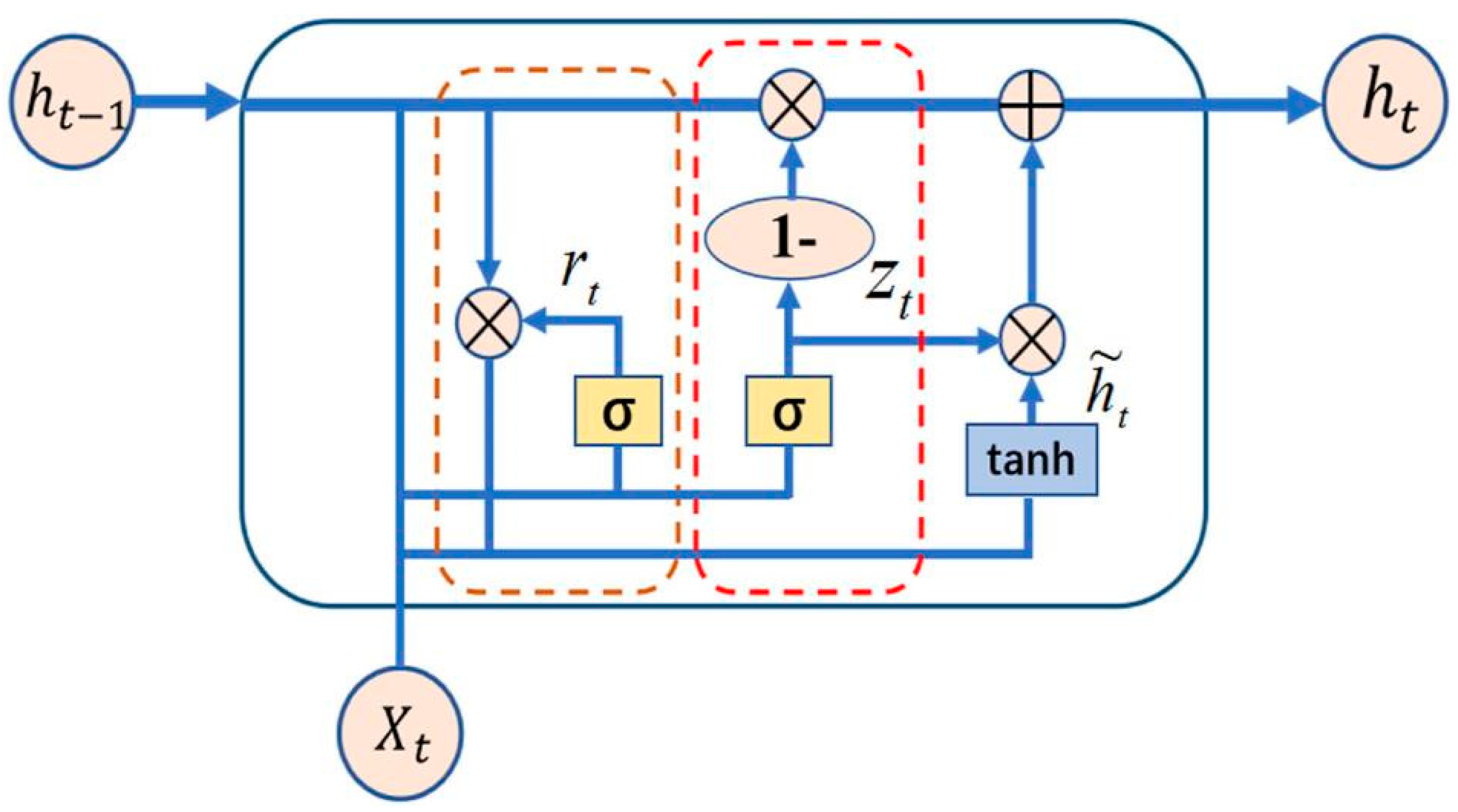
2.5.1. Bidirectional Gated Recurrent Unit (BiGRU)
2.5.2. Bidirectional Gated Recurrent Unit with Attention Mechanism (BiGRU-AM)
3. Architecture of the Proposed Framework
4. Experimental Results and Discussion
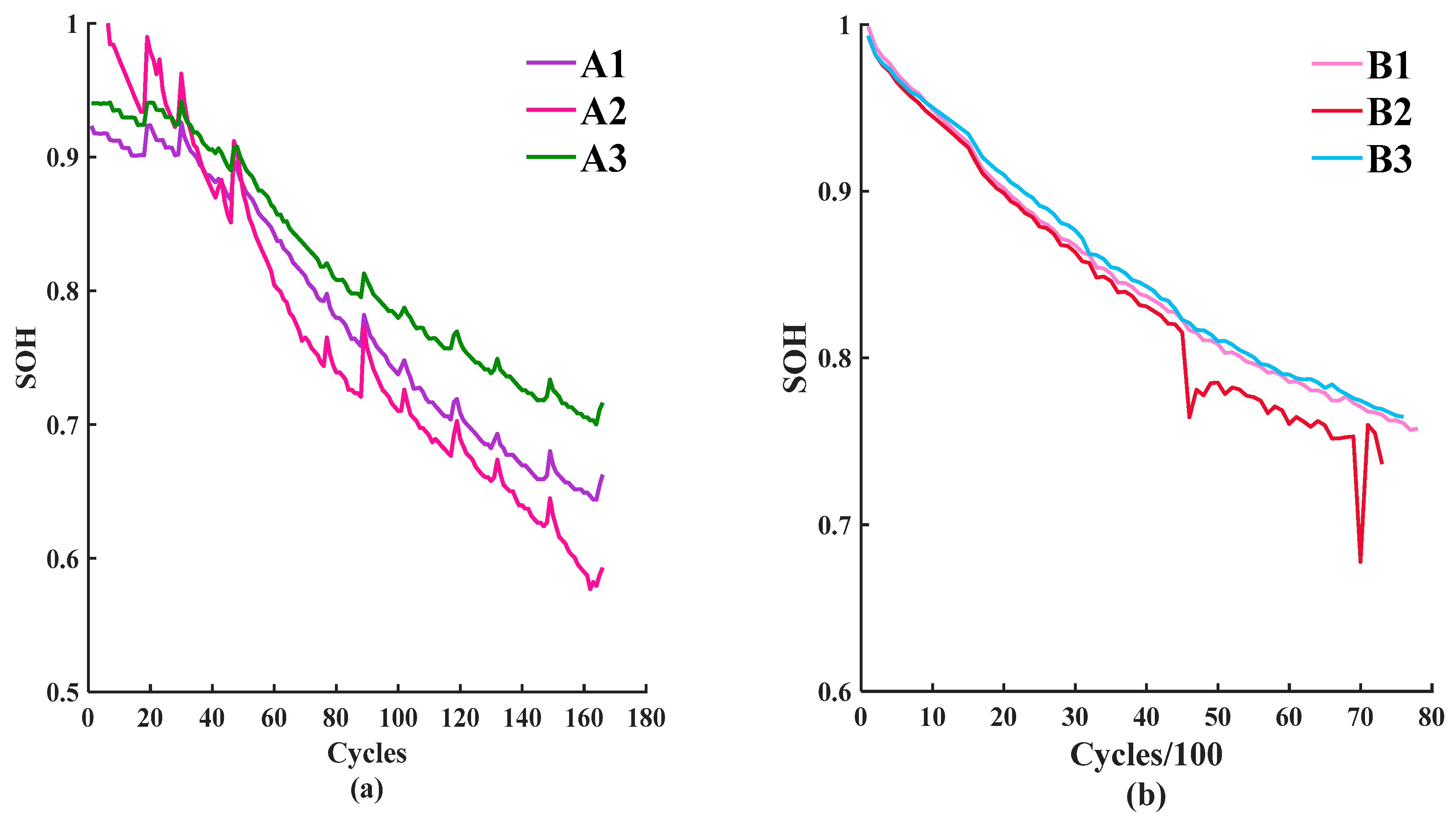
4.1. Datasets Description
4.2. Hyperparameters Setting
4.3. Evaluation Benchmarks
4.4. Comparative Experiments
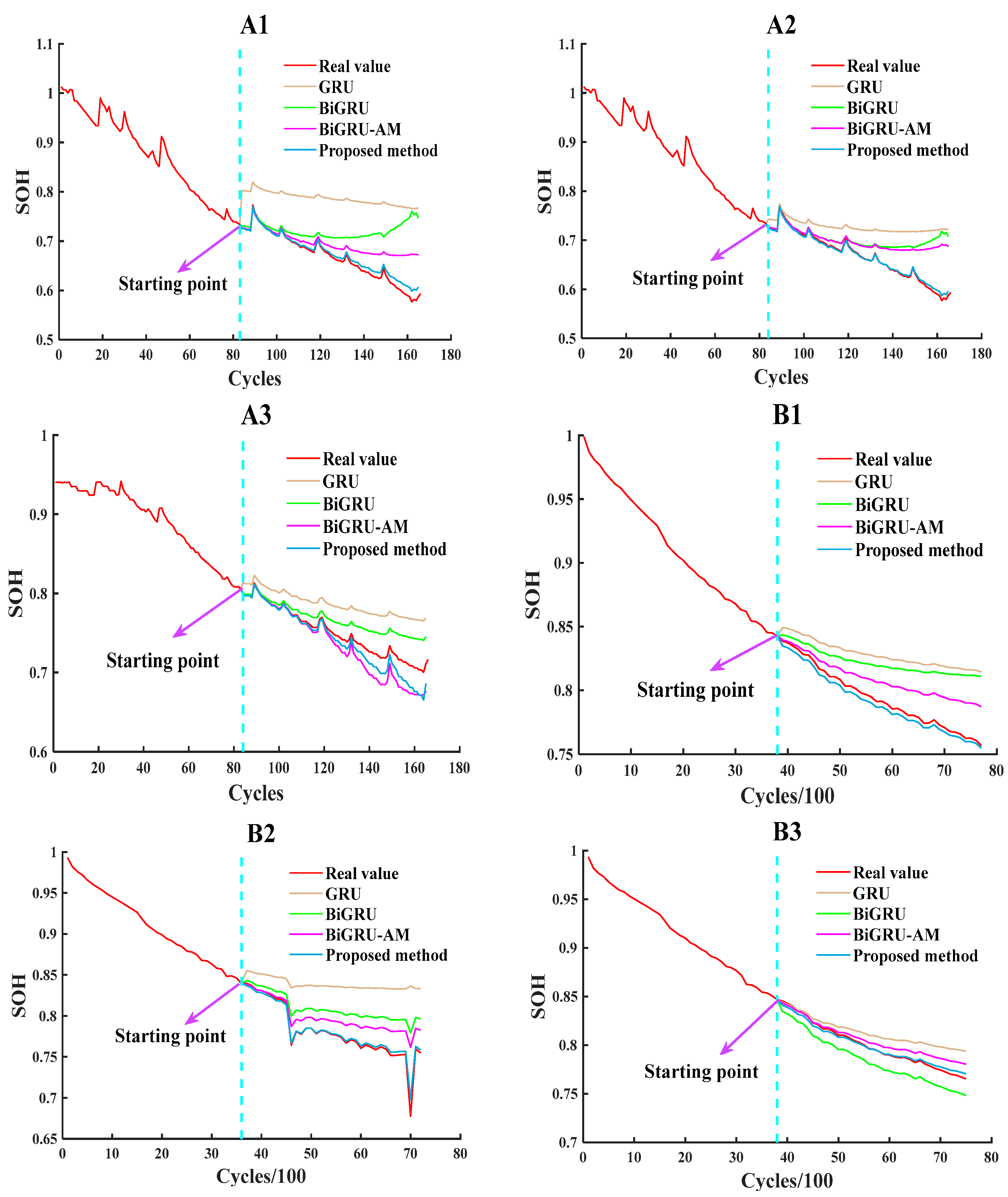
4.4.1. Comparative Experiments I
4.4.2. Comparative Experiments II
4.4.3. Comparative Experiments III
| Error | MAE (%) | RMSE (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| Battery ID | [37] | [38] | [39] | Proposed | [37] | [38] | [39] | Proposed |
| A1 | 0.279 | 0.3287 | 0.92 | 0.20 | 0.349 | 0.4077 | 1.27 | 0.31 |
| A2 | 0.400 | 0.7219 | 1.10 | 0.36 | 0.479 | 0.9587 | 1.53 | 0.39 |
| A3 | 0.357 | 0.4163 | 1.34 | 0.28 | 0.522 | 0.5338 | 1.62 | 0.48 |
| Error | MAE (%) | RMSE (%) | ||||
|---|---|---|---|---|---|---|
| Battery ID | [40] | [41] | Proposed | [40] | [41] | Proposed |
| B1 | 0.753 | 0.64 | 0.59 | 0.915 | 0.70 | 0.55 |
| B2 | 1.637 | 0.44 | 0.38 | 1.834 | 0.79 | 0.43 |
| B3 | 1.288 | 0.46 | 0.40 | 1.564 | 0.57 | 0.44 |
4.4.4. Error Source Analysis and Robustness Evaluation
5. Conclusions and Future Work
5.1. Conclusions
5.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lipu, M.H.; Hannan, M.; Hussain, A.; Hoque, M.; Ker, P.J.; Saad, M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Liu, K. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Von Buelow, F.; Meisen, T. A review on methods for state of health forecasting of lithium-ion batteries applicable in real-world operational conditions. J. Energy Storage 2023, 57, 105978. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Han, X.; Ouyang, M.; Sauer, D.U. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter. J. Power Sources 2020, 476, 228534. [Google Scholar] [CrossRef]
- Ouyang, T.; Xu, P.; Chen, J.; Lu, J.; Chen, N. An Online Prediction of Capacity and Remaining Useful Life of Lithium-Ion Batteries Based on Simultaneous Input and State Estimation Algorithm. IEEE Trans. Power Electron. 2020, 36, 8102–8113. [Google Scholar] [CrossRef]
- Sun, Q.; Zeng, G.; Xu, X.; Li, J.; Biendicho, J.J.; Wang, S.; Tian, Y.; Ci, L.; Cabot, A. Are Sulfide-Based Solid-State Electrolytes the Best Pair for Si Anodes in Li-Ion Batteries? Adv. Energy Mater. 2024, 14, 2402048. [Google Scholar] [CrossRef]
- Li, J.; Zeng, G.; Horta, S.; Martínez-Alanis, P.R.; Biendicho, J.J.; Ibáñez, M.; Xu, B.; Ci, L.; Cabot, A.; Sun, Q. Crystallographic Engineering in Micron-Sized SiOx Anode Material Toward Stable High-Energy-Density Lithium-Ion Batteries. ACS Nano 2025, 19, 16096–16109. [Google Scholar] [CrossRef]
- Liu, B.; Tang, X.; Gao, F. Joint estimation of battery state-of-charge and state-of-health based on a simplified pseudo-two-dimensional model. Electrochim. Acta 2020, 344, 136098. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Chen, Z. Degradation model and cycle life prediction for lithium-ion battery used in hybrid energy storage system. Energy 2019, 166, 796–806. [Google Scholar] [CrossRef]
- Shen, D.; Wu, L.; Kang, G.; Guan, Y.; Peng, Z. A novel online method for predicting the remaining useful life of lithium-ion batteries considering random variable discharge current. Energy 2021, 218, 119490. [Google Scholar] [CrossRef]
- Shi, E.; Xia, F.; Peng, D.; Li, L.; Wang, X.; Yu, B. State-of-health estimation for lithium battery in electric vehicles based on improved unscented particle filter. J. Renew. Sustain. Energy 2019, 11, 024101. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Lu, D.D.-C.; Wang, G.; He, T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Agudelo, B.O.; Zamboni, W.; Monmasson, E. Application domain extension of incremental capacity-based battery SoH indicators. Energy 2021, 234, 121224. [Google Scholar] [CrossRef]
- Chang, C.; Wu, Y.; Jiang, J.; Jiang, Y.; Tian, A.; Li, T.; Gao, Y. Prognostics of the state of health for lithium-ion battery packs in energy storage applications. Energy 2022, 239, 122189. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Gao, Y.; Guo, Q. Recognition of battery aging variations for LiFePO4 batteries in 2nd use applications combining incremental capacity analysis and statistical approaches. J. Power Sources 2017, 360, 180–188. [Google Scholar] [CrossRef]
- Fly, A.; Chen, R. Rate dependency of incremental capacity analysis (dQ/dV) as a diagnostic tool for lithium-ion batteries. J. Energy Storage 2020, 29, 101329. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. Multi-time-scale Framework for Prognostic Health Condition of Lithium Battery using Modified Gaussian Process Regression and Nonlinear Regression. J. Power Sources 2020, 467, 228358. [Google Scholar] [CrossRef]
- Zhang, Z.; Min, H.; Guo, H.; Yu, Y.; Sun, W.; Jiang, J.; Zhao, H. State of health estimation method for lithium-ion batteries using incremental capacity and long short-term memory network. J. Energy Storage 2023, 64, 107063. [Google Scholar] [CrossRef]
- Kaya, G.O. A Hybrid Method Based on Empirical Mode Decomposition and Random Forest Regression for Wind Power Forecasting. J. Mult.-Valued Log. Soft Comput. 2018, 31, 123–137. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary Ensemble Empirical Mode Decomposition: A Novel Noise Enhanced Data Analysis Method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Li, R.; Xu, S.; Li, S.; Zhou, Y.; Zhou, K.; Liu, X.; Yao, J. State of Charge Prediction Algorithm of Lithium-ion Battery Based on PSO-SVR Cross Validation. IEEE Access 2020, 8, 10234–10242. [Google Scholar] [CrossRef]
- Schulz, E.; Speekenbrink, M.; Krause, A. A tutorial on Gaussian process regression: Modelling, exploring, and exploiting functions. J. Math. Psychol. 2018, 85, 1–16. [Google Scholar] [CrossRef]
- Shi, J.Q.; Choi, T. Gaussian Process Regression Analysis for Functional Data; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar] [CrossRef]
- Wang, S.; Jin, S.; Deng, D.; Fernandez, C. A Critical Review of Online Battery Remaining Useful Lifetime Prediction Methods. Front. Mech. Eng. 2021, 7, 719718. [Google Scholar] [CrossRef]
- Nathans, L.L.; Oswald, F.L.; Nimon, K. Interpreting multiple linear regression: A guidebook of variable importance. Pract. Assess. Res. Eval. 2012, 17, n9. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, C.; Yang, L.; Chen, Y. DSTP-RNN: A dual-stage two-phase attention-based recurrent neural networks for long-term and multivariate time series prediction. Expert Syst. Appl. 2020, 143, 113082. [Google Scholar] [CrossRef]
- Faraji, M.; Nadi, S.; Ghaffarpasand, O.; Homayoni, S.; Downey, K. An integrated 3D CNN-GRU deep learning method for short-term prediction of PM25 concentration in urban environment. Sci. Total Environ. 2022, 834, 155324. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, W.; Yu, M. A novel hybrid scheme for remaining useful life prognostic based on secondary decomposition, BiGRU and error correction. Energy 2023, 276, 127565. [Google Scholar] [CrossRef]
- Niu, D.; Yu, M.; Sun, L.; Gao, T.; Wang, K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, W.; Yu, M. A novel blood glucose time series prediction framework based on a novel signal decomposition method. Chaos Solitons Fractal 2022, 164, 112673. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, W.; Yu, M. Short-Term Wind Speed Prediction Based on FEEMD-PE-SSA-BP. Environ. Sci. Pollut. Res. 2022, 29, 79288–79305. [Google Scholar] [CrossRef] [PubMed]
- Moein, M.J.A.; Valley, B.; Evans, K.F. Scaling of Fracture Patterns in Three Deep Boreholes and Implications for Constraining Fractal Discrete Fracture Network Models. Rock Mech. Rock Eng. 2019, 52, 3. [Google Scholar] [CrossRef]
- Jin, J.; Wang, B.; Yu, M.; Li, B. Short-term wind speed prediction based on fractal dimension-variational mode decomposition and general continued fraction. Chaos Solitons Fractals 2023, 173, 113704. [Google Scholar] [CrossRef]
- Yang, L.; Xu, H.; Zhang, X.; Li, S.; Ji, W. Study on Fractal Multistep Forecast for the Prediction of Driving Behavior. J. Adv. Transp. 2020, 2020, 9150583. [Google Scholar] [CrossRef]
- Goh, H.H.; Lan, Z.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C. New Findings on Machine Learning from Guangxi University Summarized [Estimation of the State of Health (Soh) of Batteries Using Discrete Curvature Feature Extraction. J. Energy Storage 2022, 50, 104646. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A novel method for state of health estimation of lithium-ion batteries based on improved LSTM and health indicators extraction. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Gong, Y.; Zhang, X.; Gao, D.; Li, H.; Yan, L.; Peng, J.; Huang, Z. State-of-health estimation of lithium-ion batteries based on improved long short-term memory algorithm. J. Energy Storage 2022, 53, 105046. [Google Scholar] [CrossRef]
- Lin, M.; Yan, C.; Meng, J.; Wang, W.; Wu, J. Lithium-ion batteries health prognosis via differential thermal capacity with simulated annealing and support vector regression. Energy 2022, 250, 123829. [Google Scholar] [CrossRef]
- Lin, M.; Wu, D.; Meng, J.; Wu, J.; Wu, H. A multi-feature-based multi-model fusion method for state of health estimation of lithium-ion batteries. J. Power Sources 2022, 518, 230774. [Google Scholar] [CrossRef]
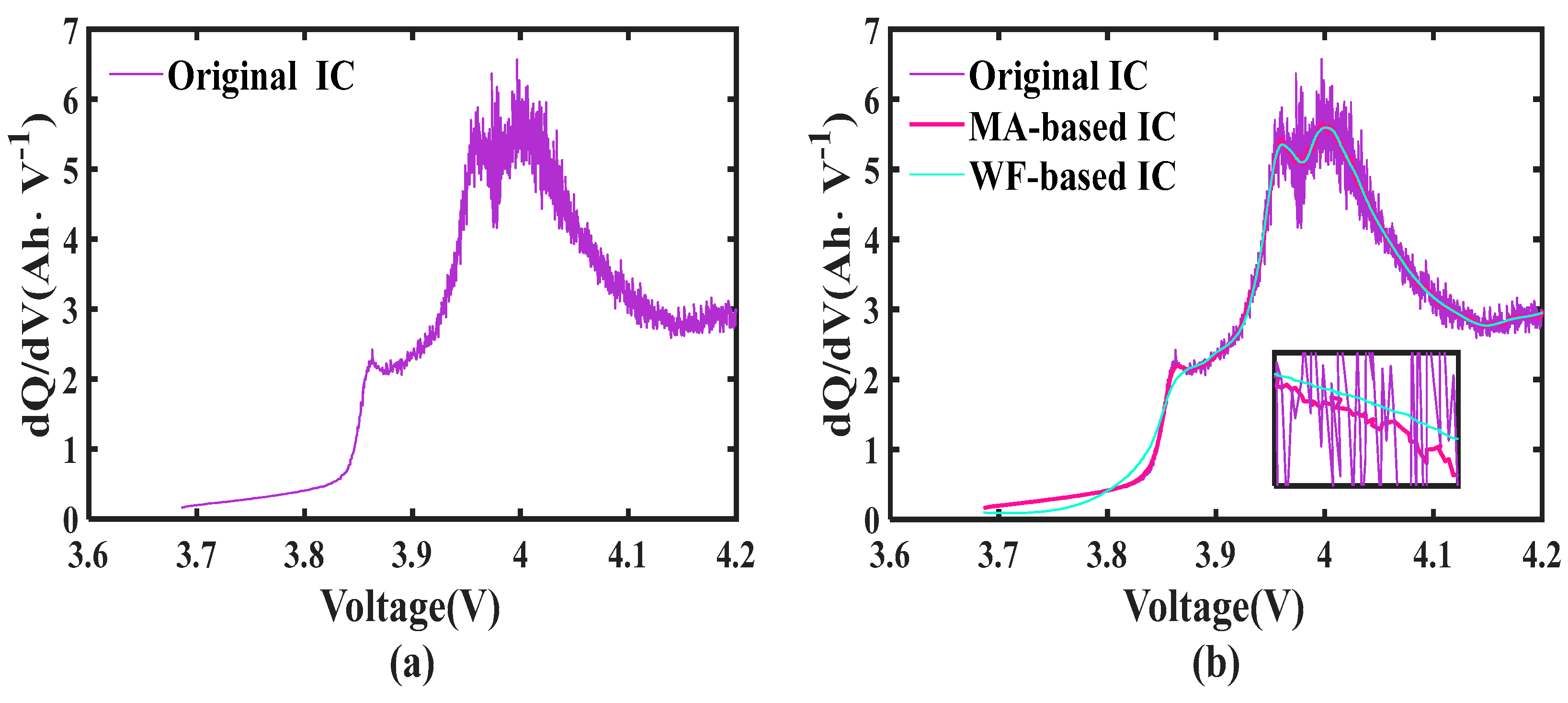
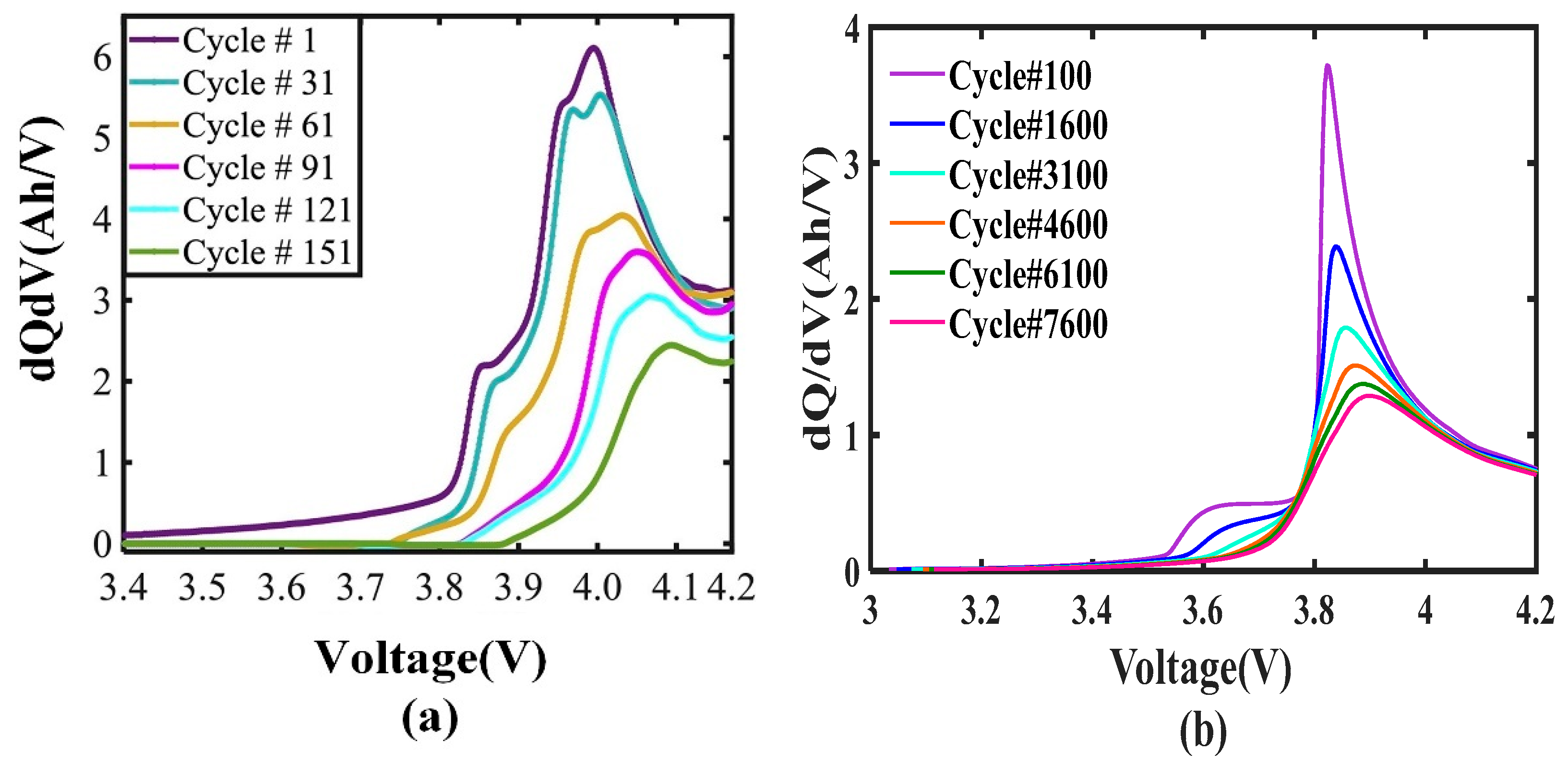
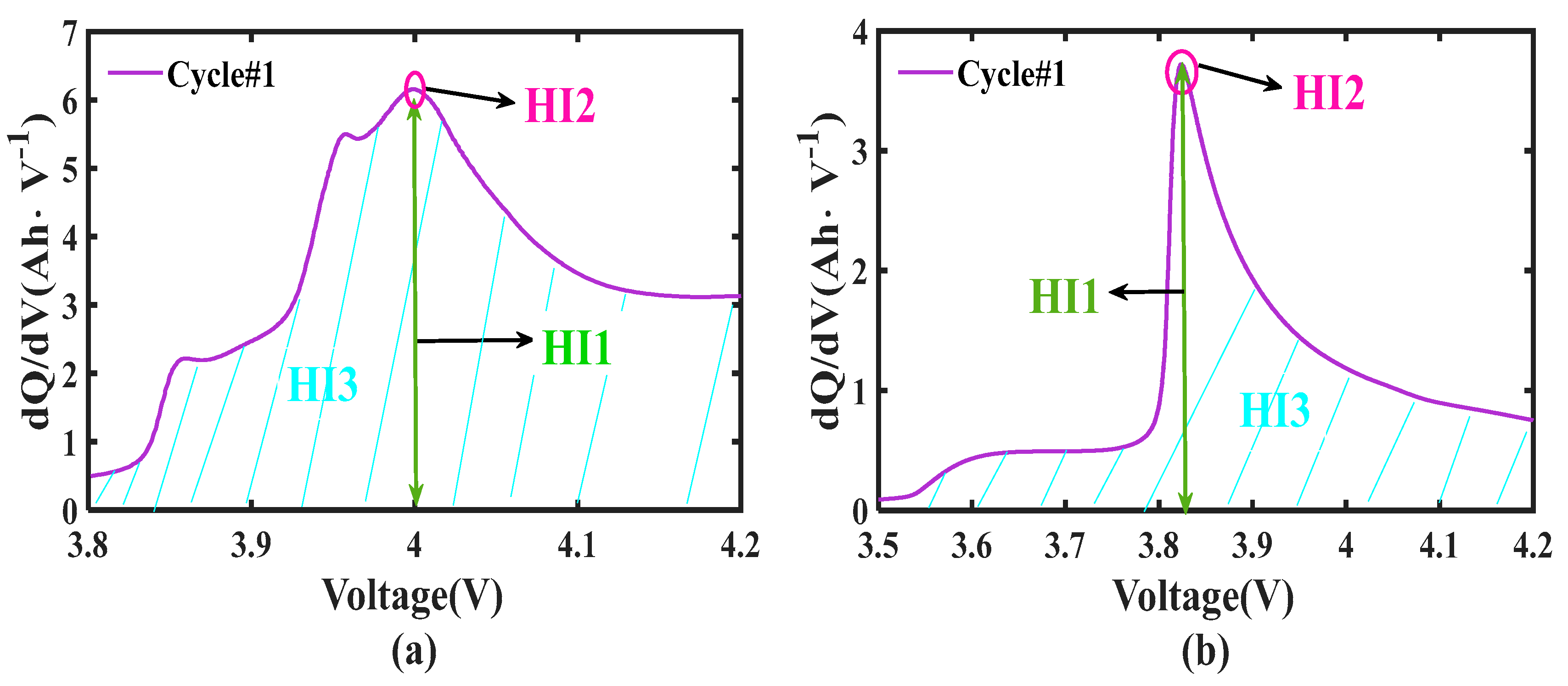



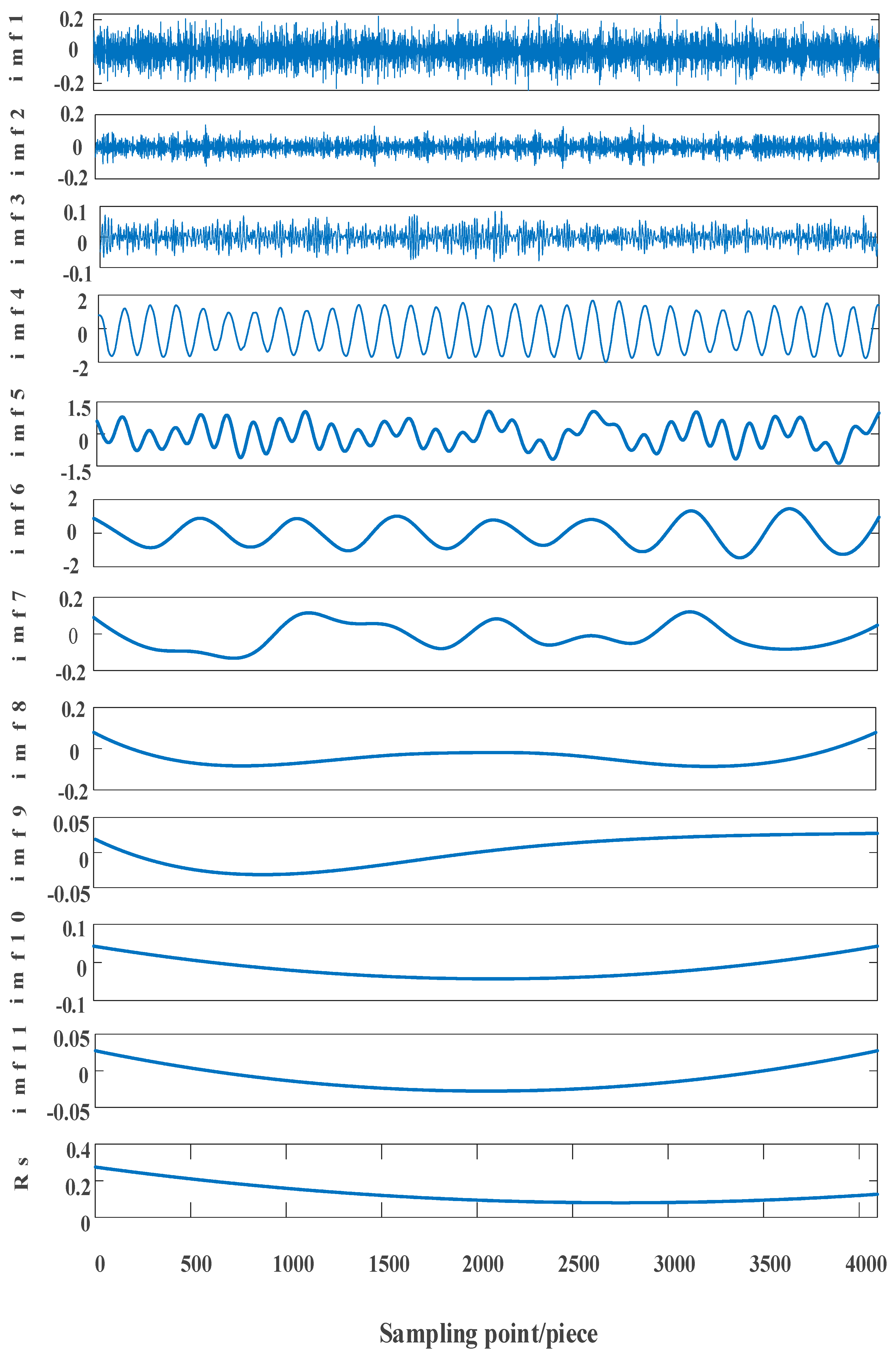




| Battery ID | Between HI1 and Capacity | Between HI2 and Capacity | Between HI3 and Capacity |
|---|---|---|---|
| A1 | 0.9906 | −0.9496 | 0.9981 |
| A2 | 0.9955 | −0.9606 | 0.9950 |
| A3 | 0.9748 | −0.9521 | 0.9871 |
| B1 | 0.9647 | −0.9776 | 0.9946 |
| B2 | 0.9541 | −0.9785 | 0.9948 |
| B3 | 0.9689 | −0.9842 | 0.9954 |
| Time-Frequency Algorithms | /s | |
|---|---|---|
| EMD | 0.2762 | 6.847 |
| CEEMD | 0.1377 | 19.288 |
| FEEMD | 0.0574 | 10.280 |
| Dataset | Form Factor | Cell Anode | Cell Cathode | Charge Conditions | Discharge Conditions | Nominal Capacity | Nominal Voltage | Upper Cut-Off Voltage | Lower Cut-Off Voltage |
|---|---|---|---|---|---|---|---|---|---|
| NASA | 18,650 | Graphite | LiCoO2/LiNiCoAlO2 | CC-CV | 1C | 2 Ah | - | 4.2 V | 2.7 V, 2.5 V, 2.2 V, 2.5 V |
| Oxford | Pouch | Graphite | LiCoO2/LiNiMnCoO2 | 2C | Artemis urban drive cycle | 0.74 Ah | 3.7 V | 4.2 V | 2.7 V |
| Battery ID | MAE (%) | RMSE (%) | ||||||
|---|---|---|---|---|---|---|---|---|
| GRU | BiGRU | BiGRU-AM | Proposed | GRU | BiGRU | BiGRU-AM | Proposed | |
| A1 | 4.67 | 3.18 | 2.70 | 0.20 | 6.97 | 4.88 | 3.31 | 0.31 |
| A2 | 3.59 | 2.62 | 1.97 | 0.36 | 5.73 | 3.84 | 2.35 | 0.39 |
| A3 | 6.96 | 4.84 | 3.66 | 0.28 | 9.39 | 6.34 | 3.89 | 0.48 |
| B1 | 1.27 | 0.83 | 0.66 | 0.59 | 1.83 | 1.14 | 0.86 | 0.55 |
| B2 | 1.16 | 0.75 | 0.53 | 0.38 | 1.77 | 1.05 | 0.73 | 0.43 |
| B3 | 0.94 | 0.80 | 0.66 | 0.40 | 1.53 | 1.25 | 0.94 | 0.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Wang, W.; Cao, Y.; Liu, X.; Lai, Z.; Lan, H. An Innovative Framework for Forecasting the State of Health of Lithium-Ion Batteries Based on an Improved Signal Decomposition Method. Sustainability 2025, 17, 4847. https://doi.org/10.3390/su17114847
Zhu T, Wang W, Cao Y, Liu X, Lai Z, Lan H. An Innovative Framework for Forecasting the State of Health of Lithium-Ion Batteries Based on an Improved Signal Decomposition Method. Sustainability. 2025; 17(11):4847. https://doi.org/10.3390/su17114847
Chicago/Turabian StyleZhu, Ting, Wenbo Wang, Yu Cao, Xia Liu, Zhongyuan Lai, and Hui Lan. 2025. "An Innovative Framework for Forecasting the State of Health of Lithium-Ion Batteries Based on an Improved Signal Decomposition Method" Sustainability 17, no. 11: 4847. https://doi.org/10.3390/su17114847
APA StyleZhu, T., Wang, W., Cao, Y., Liu, X., Lai, Z., & Lan, H. (2025). An Innovative Framework for Forecasting the State of Health of Lithium-Ion Batteries Based on an Improved Signal Decomposition Method. Sustainability, 17(11), 4847. https://doi.org/10.3390/su17114847






