Path Planning Method for Unmanned Vehicles in Complex Off-Road Environments Based on an Improved A* Algorithm

Abstract

In recent years, autonomous driving technology has made remarkable progress in urban transportation and logistics, while its application in complex off-road environments has gradually become a research hotspot. Compared to traditional manned vehicles, unmanned vehicles demonstrate higher safety and flexibility in scenarios such as rapid transportation, emergency rescue, and environmental reconnaissance. However, current research on path planning is predominantly focused on structured environments, with limited attention given to unstructured off-road conditions. This paper proposes an improved A* algorithm tailored to address the challenges of path planning in complex off-road environments. First, a grid map incorporating multi-dimensional information is constructed by integrating elevation data, risk zones, and surface attributes, significantly enhancing environmental perception accuracy. At the algorithm level, the heuristic function and search strategy of the A* algorithm are optimized to improve its efficiency and path smoothness in complex terrains. Furthermore, the method supports the flexible planning of three types of paths—minimizing time, minimizing risk, or optimizing smoothness—based on specific task requirements. Simulation results demonstrate that the improved A* algorithm effectively adapts to dynamic off-road environments, providing intelligent and efficient path planning solutions for unmanned vehicles. The proposed method holds significant value for advancing the application of autonomous driving technology in complex environments.

1. Introduction

In recent years, with the rapid development of autonomous driving technologies, their application has gradually expanded from urban transportation and logistics to more complex off-road environments. Unmanned vehicles, owing to their significant advantages in scenarios such as rapid transportation, emergency rescue, and environmental reconnaissance, have garnered widespread attention [1]. However, compared to structured environments like cities, off-road environments are often characterized by complexity and dynamism, such as variable terrain, irregular obstacle distribution, and unpredictable weather conditions, which pose new challenges to the path planning capabilities of autonomous vehicles [2]. As a core technology for autonomous vehicle navigation, path planning is critical to ensuring their safe and efficient operation. Therefore, research into path planning in complex off-road environments holds both significant theoretical value and practical application potential.

Currently, most studies on path planning for autonomous vehicles focus on fundamental factors such as path length, obstacle avoidance, and travel time, often relying on traditional grid maps for modeling. However, traditional grid maps have notable limitations in representing information, particularly in handling unstructured and dynamic environments, where they struggle to comprehensively reflect complex terrain features and environmental states. To address this issue, this paper proposes a multi-dimensional information overlay grid map method that integrates elevation data, risk zones, and surface attributes to construct a more comprehensive environmental model, thereby enhancing the perception capability of autonomous vehicles in complex environments.

Path planning plays a pivotal role in autonomous navigation systems, particularly in complex off-road environments characterized by unstructured terrain, dynamic obstacles, and real-time constraints. Current path planning methodologies are broadly categorized into global and local planning paradigms [3]. Classical global planners, such as the Dijkstra algorithm, guarantee path optimality through exhaustive node traversal. However, their O(n²) time complexity leads to computational inefficiency and limited adaptability to dynamic environmental changes [4]. Although geometric topology optimization-based enhancements improve path smoothness [5], they predominantly focus on path length while neglecting other influencing factors. The traditional A* algorithm excels in structured environments via heuristic search but suffers from degraded real-time obstacle avoidance capabilities in unstructured terrain due to the discretization limitations of grid-based modeling [6]. The bidirectional A* algorithm reduces path redundancy through dual-directional search [7], yet its O(b^d) complexity (where b denotes the branching factor and d the search depth) incurs significant planning latency in large-scale scenarios.

Probabilistic sampling approaches offer novel solutions for high-dimensional spaces. The Rapidly-exploring Random Tree (RRT) achieves probabilistic completeness through random sampling but generates suboptimal paths prone to local minima [8]. Enhanced RRT* variants incorporating Gaussian-biased sampling and adaptive step-size control accelerate convergence [9], though their asymptotic optimality remains constrained by strong assumptions regarding terrain continuity. The Probabilistic Roadmap (PRM) method relies on offline roadmap construction in static environments but exhibits increased path failure probabilities when dynamic obstacles are present [10]. Chen et al. proposed a modified PRM to enhance path smoothness and dynamic obstacle avoidance [11], yet its planning quality remains suboptimal. Local planners adopt reactive strategies to address dynamic uncertainties. The Dynamic Window Approach (DWA) samples velocity space under vehicular kinematic constraints but produces oscillatory trajectories in multi-obstacle scenarios [12]. Artificial Potential Field (APF) methods navigate via potential gradients but are susceptible to local optima [13]. The Timed Elastic Band (TEB) method improves trajectory smoothness through elastic topology optimization [14] but underperforms in highly dynamic environments with complex kinematic constraints.

Emerging hybrid methodologies integrate multi-paradigm advantages [15,16]. The A*-DWA fusion framework demonstrates efficacy in 2D grid environments by guiding local velocity sampling with global heuristics [17], though its adaptability to 3D terrain elevation data remains unverified. The improved RRT-Connect algorithm reduces redundant nodes via bidirectional growth strategies [18] but requires sensitive parameter tuning and yields non-optimal path quality. The Sigmoid-based Ant Colony Optimization algorithm excels in global optimization [19]; however, its O(n²k) complexity (where n represents the number of nodes and k iterations) results in exponentially increasing computation time with problem scale.

For complex off-road path planning, Wang et al. proposed a risk-aware A* algorithm to avoid hazardous regions [20], yet it provides only a single-path solution. Yin et al. developed a cost-optimal A* variant to minimize unmanned vehicle traversal costs [21], but the generated paths exhibit excessive redundancy and insufficient smoothness. Yao et al. introduced a visibility-based bidirectional A* algorithm to enhance search efficiency and path safety [22]; however, its environmental considerations lack comprehensiveness, particularly in risk zone incorporation.

To address the aforementioned challenges, this paper proposes an improved A* algorithm that combines a multi-dimensional information-overlay grid map with optimized heuristic functions and search strategies, significantly enhancing the efficiency and accuracy of path planning. To accommodate the diverse requirements for timeliness, safety, and smoothness in complex off-road environments, this study further designs three task/priority-based path planning schemes, offering options for the shortest time, lowest risk, or optimal smoothness. The main contributions of this paper are summarized as follows.

• Construction of a Grid Map and Evaluation Criteria: This paper employs an overlay-based grid map approach, constructing a foundational grid map using the grid method and overlaying it with elevation data, risk zones, and surface attributes to enhance the comprehensiveness of environmental perception. Additionally, a time/cost model for vehicle traversal is established based on various ground conditions. Furthermore, a path quality evaluation system based on safety and timeliness is developed according to actual environmental conditions.
• Obstacle Handling and Path Optimization: To improve the quality of path planning, this paper first performs obstacle expansion, treating obstacles occupying less than one grid as fully occupying the grid. It extends the four-directional or eight-directional search of the A* algorithm to a sixteen-directional 24-neighborhood search mechanism, resulting in smoother paths. Additionally, by integrating a path quality evaluation standard system, three heuristic algorithms are designed based on the shortest time, minimum risk, and optimal stability.
• Simulation Experiments and Validation: Simulation experiments on unmanned vehicle path planning in complex field environments were conducted. Through comparative experiments with other algorithms, it was demonstrated that the proposed algorithm can meet various path planning requirements, proving the advantages and effectiveness of the method.

The remaining manuscript structure is organized as follows. Section 2 presents the methodological framework for wilderness environment modeling. Section 3 details the enhanced A* algorithm specifically designed for unstructured field navigation. Section 4 demonstrates comparative experimental analysis between the proposed method and benchmark algorithms with comprehensive result visualization. The concluding section synthesizes the principal contributions and findings of this research endeavor.

2. Modeling of Complex Off-Road Environments

2.1. Environmental Map Modeling

In the research and application of autonomous vehicles, environmental map modeling is a critical component, particularly in complex off-road environments. A high-quality environmental map serves not only as the foundation for path planning but also as a prerequisite for achieving safe and efficient navigation. Complex off-road environments are typically characterized by variable terrains, dynamic obstacles, and potential hazards, all of which impose higher demands on the efficiency and accuracy of path planning for autonomous vehicles.

The grid map is a widely used and effective method for environmental modeling. By dividing the environment into uniform grid cells, this approach allows each cell to carry rich environmental information [23,24]. In this study, a multi-source information fusion-based grid map is designed, integrating essential attributes such as coordinates, elevation, slope, and other geographic and environmental parameters to effectively represent diverse environmental features. This enhanced grid map is not only applicable to the modeling of static scenes but can also incorporate a dynamic updating mechanism to meet the real-time path planning requirements of autonomous vehicles in complex environments [25]. Depending on the specific application scenario, this method can flexibly construct grid maps at varying levels of resolution, enabling adaptation to different operational demands. By leveraging this approach, the proposed grid map ensures a comprehensive, flexible, and adaptable representation of complex environments, laying a robust foundation for efficient and reliable autonomous vehicle navigation.

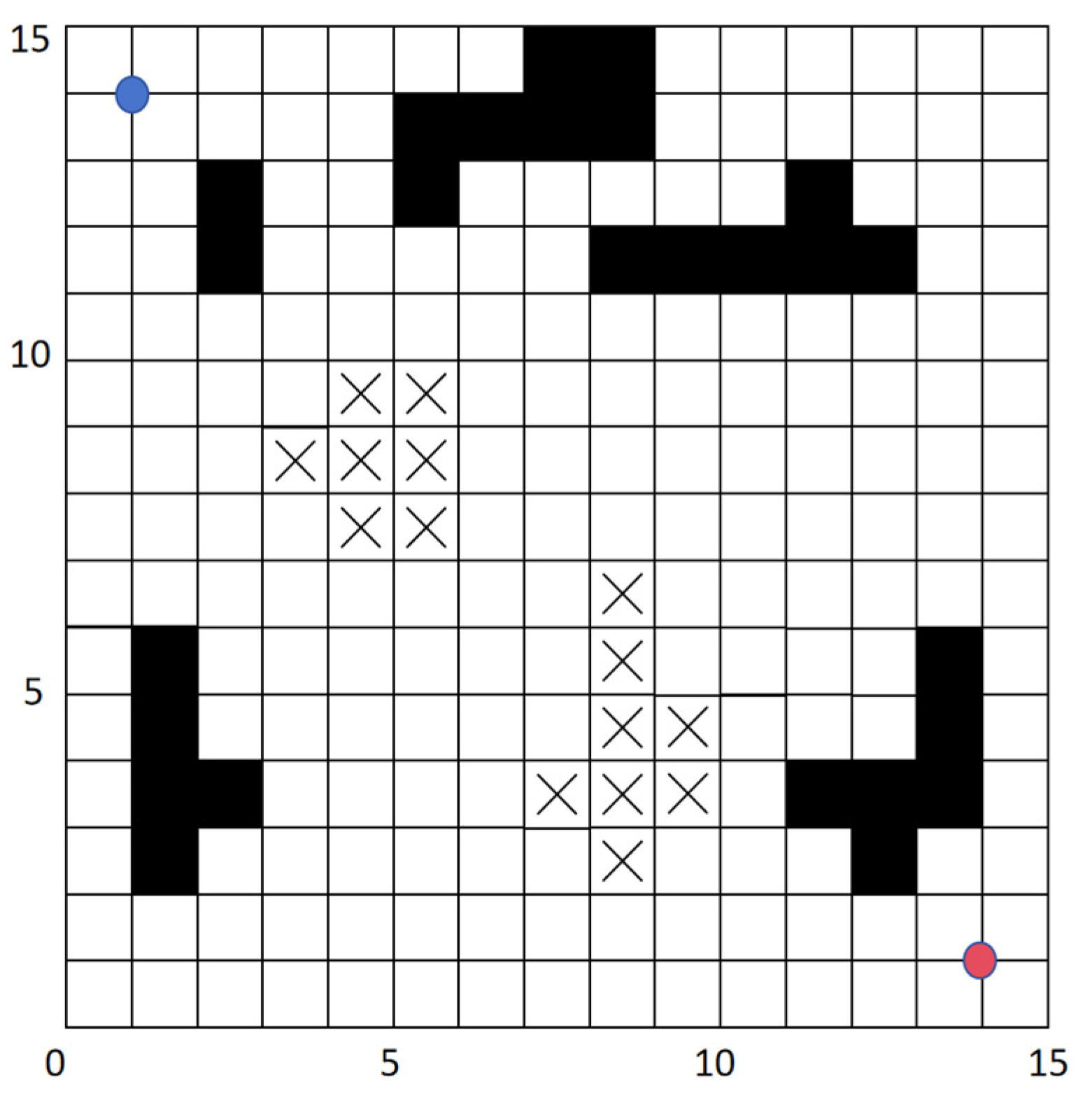
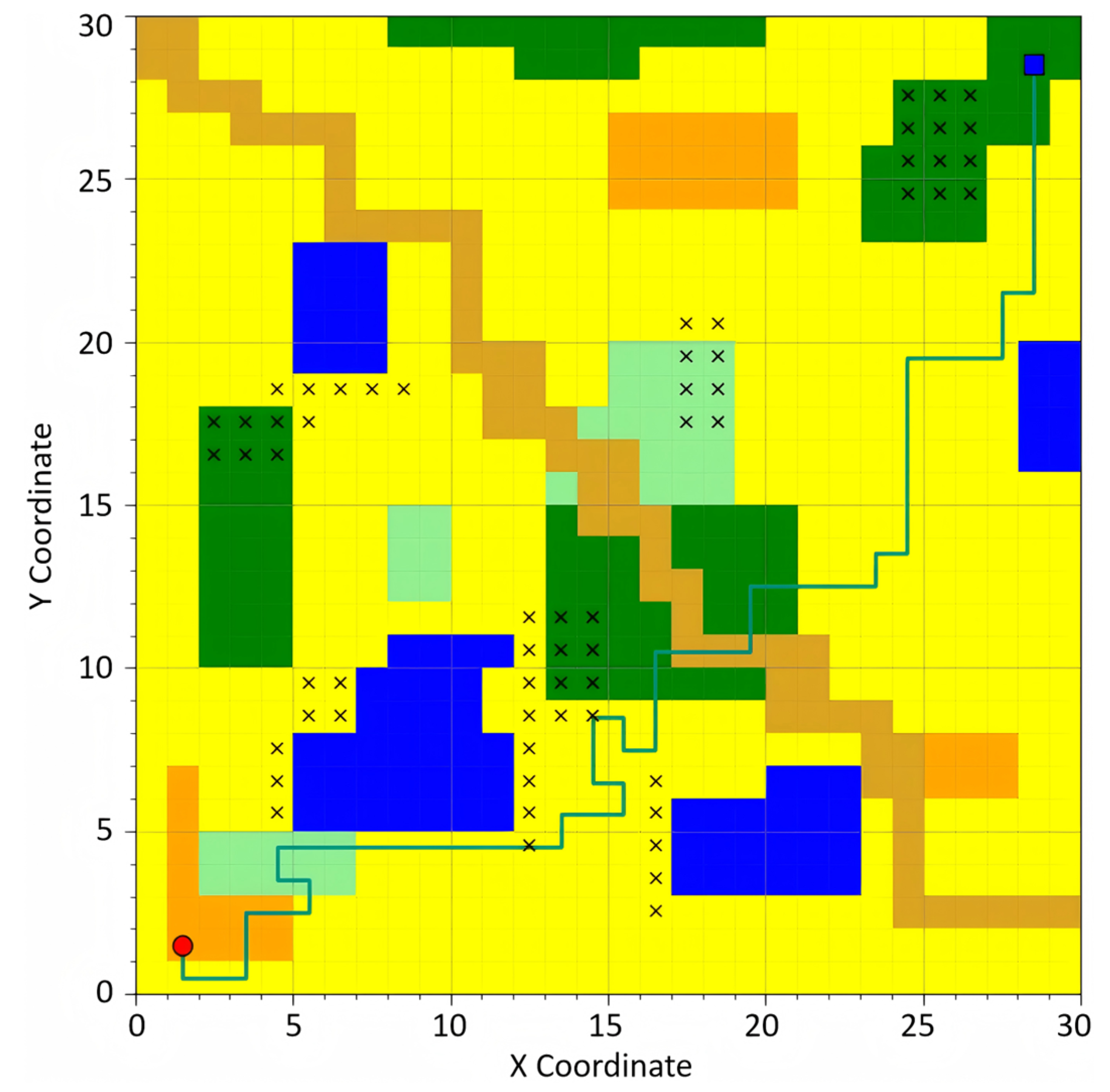
As shown in Figure 1, the grid map achieves the integration and visualization of multiple types of information by dividing the environment into discrete grid units.

• Black Grids: Represent impassable obstacle regions, such as buildings, rivers, or lakes. These areas are strictly excluded from path planning.
• Grids with “×” Symbols: Indicate areas with potential risks, such as geological hazards or muddy terrains. Autonomous vehicles face high risks when traversing these zones, and they are typically assigned higher traversal costs to discourage navigation through them.
• White Grids: Denote traversable areas, providing potential spaces for autonomous vehicles to choose paths. These regions serve as the primary focus for path planning algorithms to identify safe and efficient routes.
• The red dot and the blue dot represent the starting point and the ending point respectively.

This intuitive representation enables a clear understanding of the environment, supporting both static and dynamic path planning with enhanced situational awareness.

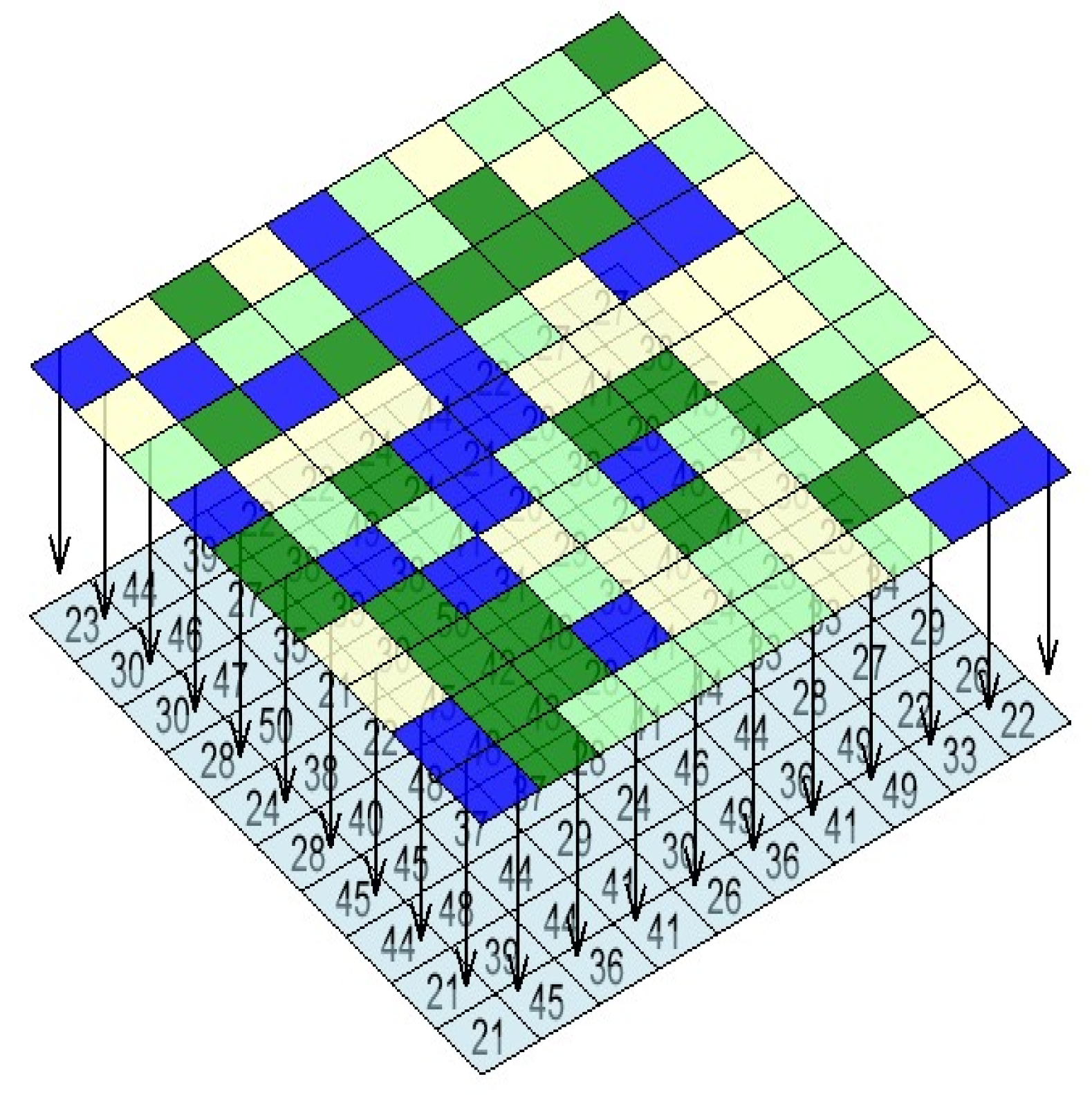
Based on the aforementioned modeling, this paper integrates different surface attributes and elevations in the environment into the grid, as shown in Figure 2, where different grid colors represent distinct surface attributes, and the numbers indicate the elevation of the grid.

2.2. Surface Information Modeling

Traditional grid maps typically represent only the distribution of simple obstacles. However, in complex off-road environments, surface attributes play a critical role in path planning. Different surface conditions can significantly affect the mobility and performance of autonomous vehicles. Therefore, it is essential to perform a quantitative analysis of ground features in traversable areas.

Building on the driving capabilities of autonomous vehicles in off-road environments and referencing methodologies from studies [26], this research conducts a quantitative evaluation of the traversability of various surface types. This evaluation helps to provide a more precise representation of the environment for effective navigation and decision-making.

To visually differentiate surface conditions, this study assigns color codes to various surface types, as shown in

Table 1. Surface Types, Characteristics, Traversability, and Color Codes.

Surface Type	Characteristics	Traversability	Color
Hard Surface	Relatively flat surface, allowing vehicles to maintain stability during movement.	1
Soil Road	Uneven surface with puddles and obstacles, leading to unstable movement.	0.8
Grassland	Flat terrain with good vegetation coverage, but may contain small obstacles.	0.6
Sandy Terrain	Loose and slippery surface; deep sand areas may cause difficulty for vehicle travel.	0.4
Forest	Dense trees with ground covered by leaves and weeds; limited visibility.	0.2
Water Bodies	Includes rivers, lakes, and wetlands; vehicles cannot traverse these areas.	0

. These color codes enhance the interpretability of the grid map by allowing quick identification of surface characteristics. It is important to note that in off-road environments, water bodies—including rivers, lakes, and wetlands—are regarded as completely impassable obstacles and are excluded from the set of traversable areas.

This approach ensures a detailed and intuitive representation of surface information, facilitating safer and more efficient path planning for autonomous vehicles in complex and challenging environments.

The traversability values range from 0.0 to 1.0, reflecting the ease or difficulty of vehicle navigation across different surface types. A higher value (1.0) indicates a surface that is highly suitable for vehicle travel. A lower value (0.0) corresponds to completely impassable surfaces, such as water bodies.

The color coding for each surface type will be assigned to visually represent the grid map, ensuring intuitive differentiation of terrain types in path planning. This detailed classification provides a robust foundation for improving the safety and efficiency of autonomous navigation in off-road environments.

This classification and quantification based on surface types provides a direct reference for path planning in unmanned vehicles. It enables unmanned vehicles to select the optimal route according to varying environmental scenarios, thereby enhancing their adaptability and navigation efficiency. By incorporating detailed surface information into the decision-making process, the system ensures that the vehicle can make informed choices to balance safety, efficiency, and performance in complex off-road environments.

2.3. Field Environment Modeling

In real-world off-road environments, to develop a computationally tractable path planning model, this study employs a grid-based approach to discretize the operational environment. Each grid cell is defined by its fundamental attributes, including x-coordinate, y-coordinate, elevation, and terrain characteristics, as formally presented in Equation (1).

$$Gx,y=[x,y,h,b]$$

(1)

where x represents the grid’s horizontal coordinate, y represents the grid’s vertical coordinate, h denotes the grid’s elevation, and b represents the grid’s surface attribute

Slope gradient serves as a simplified representation of actual terrain surfaces. Given that the precise terrain geometry remains undetermined, only elevation measurements at grid cell centroids are practically obtainable. To facilitate computational processing, this investigation approximates each grid-associated terrain patch as a planar surface, hereafter referred to as the slope plane. The orthogonal projection of this slope plane onto the horizontal datum plane coincides with the original grid cell, while preserving the elevation value at the grid centroid through first-order geometric approximation. The dihedral angle between the slope plane and horizontal datum plane quantifies the grid-specific slope gradient, which is numerically estimated using elevation differences from adjacent grid cells, as demonstrated in Figure 3 [27].

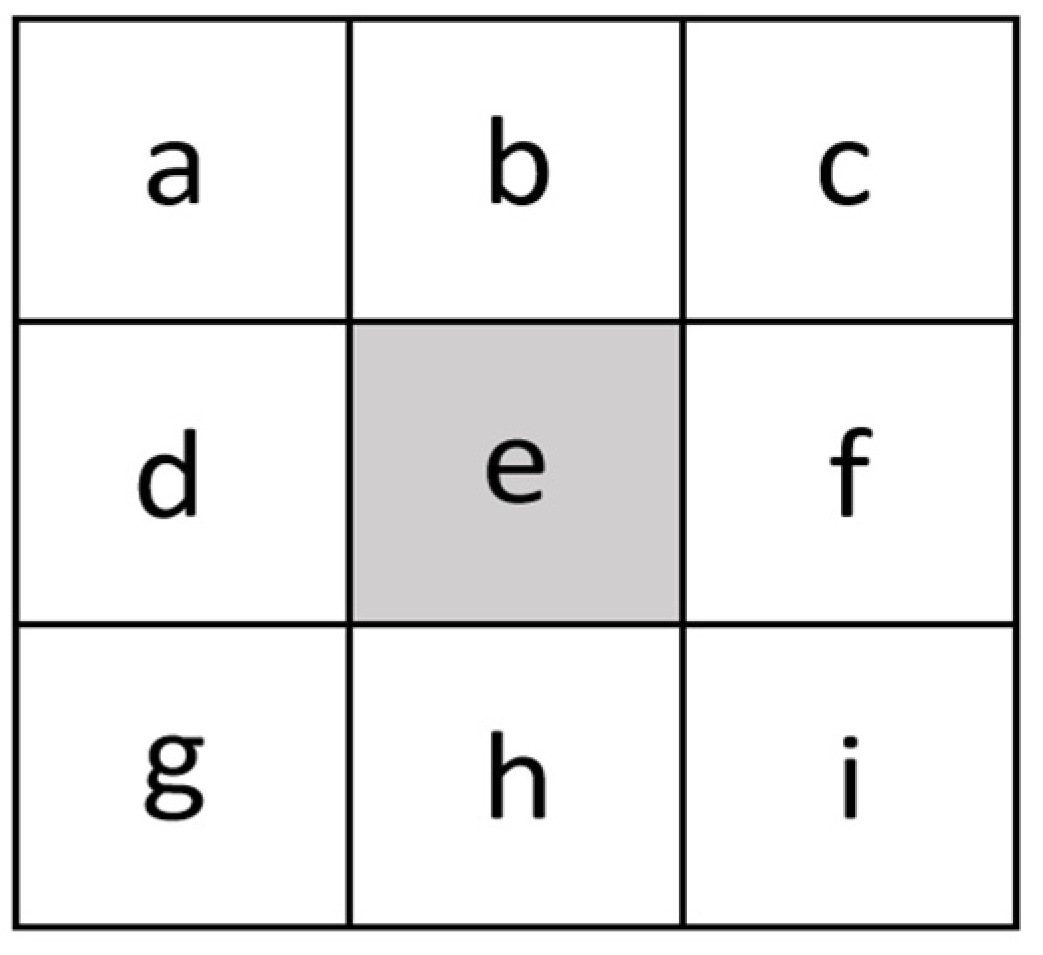
The white grid cells represent the eight neighboring grid cells surrounding the central gray grid cell. e represents the raster in the middle for which the slope needs to be calculated, while a, b, c, d, f, g, h, and i represent the adjacent rasters surrounding the central raster respectively. The slopes of the gray grid cell is approximately calculated using the following formula [28].

$$\left\{\begin{array}{c}{\displaystyle \frac{\Delta z}{\Delta x}}={\displaystyle \frac{[h(c)+2h(f)+h(i)]-[h(a)+2h(d)+h(g)]}{8\times size}}\\ {\displaystyle \frac{\Delta z}{\Delta y}}={\displaystyle \frac{[h(a)+2h(b)+h(c)]-[h(g)+2h(h)+h(i)]}{8\times size}}\end{array}\right.$$

(2)

$$s=\arctan (\sqrt{{({\displaystyle \frac{\Delta z}{\Delta x}})}^2+{({\displaystyle \frac{\Delta z}{\Delta y}})}^2})\times {\displaystyle \frac{180}{\pi }}$$

(3)

In the formula, h(a), h(b), h(c), h(d), h(f), h(g), h(h), h(i) denote the elevation values of the eight adjacent grid cells surrounding the central grid cell. Δz/Δx represents the slope change rate of the grid in the x-direction, Δz/Δy represents the slope change rate of the grid in the y-direction, and Size is the side length of the grid.

To evaluate the ride comfort of an autonomous vehicle during its path traversal, the smoothness indicator, e e, is calculated using the following formula.

$$e={\displaystyle \sum _{i=1}^{n-1}|s_{i+1}-s_i|}$$

(4)

In the formula, s_i represents the slope gradient of grid cell G_i, where s_i+1 − s_i denotes the slope gradient difference between two consecutive grid cells along the traversal path. The smoothness index is then operationally defined as the cumulative sum of slope gradient differences between all adjacent grid cell pairs along the unmanned ground vehicle’s navigation trajectory. For an autonomous vehicle, the lower the smoothness indicator e, the better the smoothness of the path.

The entire m × n grid region can be represented as a three-dimensional array G, where the grid structure captures the terrain information. Each element of the array corresponds to a specific grid cell and contains its elevation or derived properties, such as slope or smoothness.

$$G=\left(\begin{array}{ccc}{G}_{11}& \dots & G_{1n}\\ ⋮& \ddots & ⋮\\ G_{m1}& \dots & G_{mn}\end{array}\right)$$

(5)

Finally, the surface property layer information and elevation information are projected onto the grid map.

3. Improvements to the A* Algorithm

3.1. The Traditional A* Algorithm

The A* algorithm is a widely used heuristic search algorithm for path planning and graph search problems. It combines the global optimality of Dijkstra’s algorithm with the efficiency of greedy best-first search by utilizing a heuristic evaluation function to guide the search process. By balancing optimality and completeness, the A* algorithm effectively finds the shortest path from the start node to the target node. The core idea of A* lies in maintaining a priority queue to dynamically evaluate the “cost” of each node. At the heart of the algorithm is the definition of a composite evaluation function, f(n), which estimates the total cost from the start node to the current node, n. This function consists of two components.

$$f(n)=g(n)+h(n)$$

(6)

In the formula, g(n) represents the actual cost from the start node to the current node n, while h(n) denotes the estimated cost from node n to the target node, which is derived from the heuristic function.

This study incorporates the Euclidean distance calculation method and takes into account the influence of elevation, reflecting the conditions of real outdoor environments. The distance estimation formula is given as follows.

$$f(n)=g(n)+h(n)dn=\sqrt{{(xg-xn)}^2+{(yg-yn)}^2+{(zg-zn)}^2}$$

(7)

3.2. Improved Search Mechanism

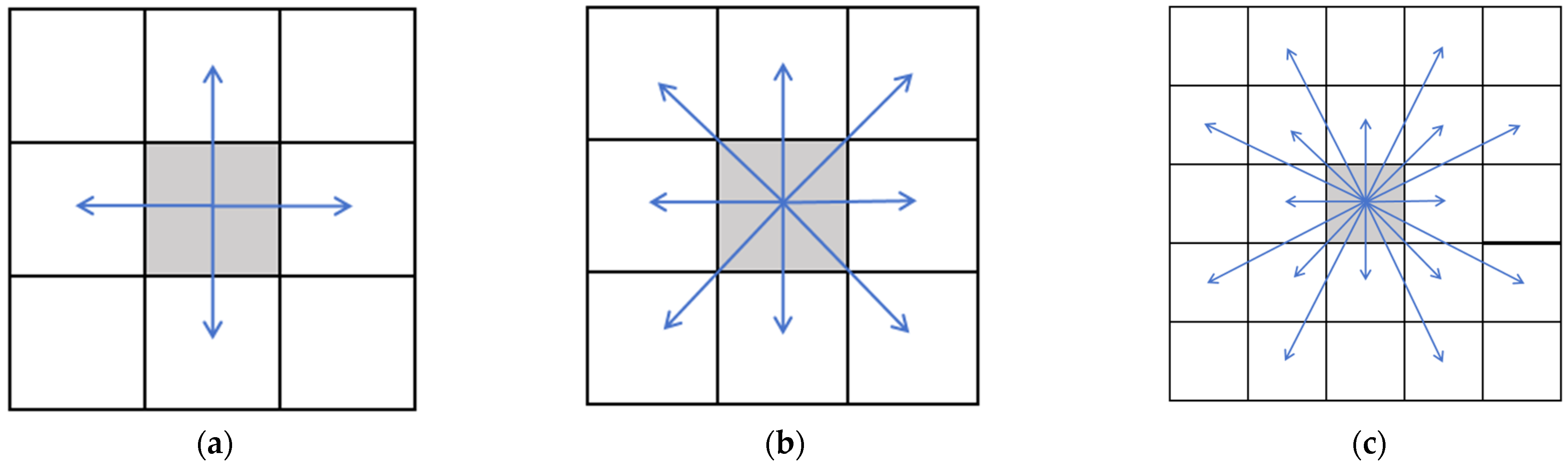
In the traditional A* algorithm, the search mechanism is typically restricted to 8 primary directions (up, down, left, right, and the four diagonal directions). This limitation leads to two main issues in path planning. First, due to the constrained search scope, the generated paths often exhibit a lack of smoothness, resulting in unnecessary sharp turns or unstable driving during practical operations of autonomous vehicles. Second, this restriction increases the likelihood of the algorithm becoming trapped in local optima, making it difficult to find the global optimal path, particularly in complex and dynamically changing environments.

To address these issues, this study proposes a dynamic adjacency mechanism based on the concept of a 24-neighbor system [29,30]. By enabling a broader range of search directions, this mechanism significantly enhances the flexibility and reliability of path planning. Specifically, the search neighborhood is expanded to 24 directions, allowing the path search to consider not only the directly adjacent grid cells around the current grid but also more distant neighboring nodes.

This approach introduces additional search directions, effectively reducing abrupt changes in the planned path and improving the overall continuity and smoothness of the trajectory. The expanded search mechanism mitigates the limitations of traditional 8-directional searches, enabling the algorithm to better adapt to the demands of real-world scenarios. The conceptual illustration of this method is shown in Figure 4. The gray square represents the current node’s position, the blue arrow indicates the direction of its next exploration, and the pointed grid denotes the location of the next node to be explored.

When conducting searches in outdoor environments, the complexity of the environmental information necessitates a more comprehensive approach. It is insufficient to simply prune search directions based on the relative position between the target point and the current point. The dynamic adjacency mechanism addresses this challenge by evaluating environmental changes in real time, such as obstacles, hazardous areas, and traversability, and adaptively adjusting the search neighborhood accordingly.

Under varying environmental conditions, the algorithm flexibly selects the most suitable adjacent grid for path exploration, based on the characteristics of the current grid and the surrounding resources. During the generation of neighboring nodes, two primary factors influence the traversability of a grid.

• Obstacle and Non-Traversable Area Detection: The algorithm evaluates whether the neighboring node is occupied by an obstacle or designated as a non-traversable area. If so, the node is excluded from the search space and deemed unavailable.
• Boundary Constraints: To ensure the validity of generated neighboring nodes, the algorithm verifies that all nodes remain within the boundaries of the grid map, avoiding access to invalid grid cells outside the map.

By dynamically accounting for environmental details and constraints, this approach enhances the robustness and adaptability of the path-planning process in outdoor scenarios, ensuring that the selected neighbors are both feasible and optimal for the given conditions.

3.3. Design of the Heuristic Function

Traditional heuristic functions predominantly focus on geometric distance, often neglecting the influence of surface attributes, path smoothness, and potential risks. To address these limitations and better accommodate real outdoor environments and the diverse requirements of unmanned vehicle tasks, this study proposes three distinct heuristic functions: the time-priority heuristic function ht(n), the safety-priority heuristic function hr(n), and the smoothness-priority heuristic function hs(n). These functions not only account for surface characteristics and the impacts of risk areas but also provide tailored path planning strategies for different scenarios, offering more flexibility than relying on a single heuristic approach.

In autonomous vehicle path planning, timeliness refers to minimizing the time cost required to complete the path planning task. It directly reflects the operational efficiency of the path and the speed of task completion. This aspect becomes particularly critical in complex outdoor environments, where timeliness imposes higher requirements on path planning for autonomous vehicles. Specifically, in high-urgency tasks such as disaster rescue missions or emergency supply delivery, the vehicle must select a path that minimizes travel time while maximizing task efficiency.

Moreover, due to the unique characteristics of outdoor environments, varying terrains—such as muddy roads, sandy paths, rocky trails, or smooth grasslands—have a significant impact on vehicle speed. This renders traditional path-planning strategies based solely on minimizing path length insufficient for real-world applications. To address these challenges, an improved A* algorithm is proposed, incorporating timeliness considerations. The revised formula is as follows.

$$gt(n)={\displaystyle \sum _{i=1}^{n}time(i)}$$

(8)

$$ht(n)={\displaystyle \frac{dn}{v\max }}$$

(9)

$$ft(n)=gt(n)+ht(n)$$

(10)

In the formula, time(i) represents the time required to traverse a specific grid cell i, d_n denotes the distance from the current grid cell to the target grid cell, and v_max is the maximum speed of the autonomous vehicle. The term d_n/v_max constitutes an admissible heuristic for the remaining travel time estimation. This formula rigorously guarantees that the heuristic function h_t(n) maintains the critical property of never overestimating the actual path cost, thereby ensuring the algorithmic optimality of A* search implementations.

In autonomous vehicle path planning, safety is a critical metric as it directly impacts the feasibility of the planned path and the ability to control risks during task execution. This is particularly significant in complex outdoor environments, where autonomous vehicles face highly dynamic and uncertain threats, such as irregular terrain variations and hidden obstacles (e.g., rocks or tree roots concealed in grass). Therefore, path planning must not only focus on task efficiency but also ensure that the vehicle avoids potential dangers throughout its journey, thereby maximizing operational safety. The improved A* algorithm is formulated as follows.

$$gr(n)={\displaystyle \sum _{i=1}^{n}risk(i)}$$

(11)

$$hr(n)=dn$$

(12)

$$fr(n)=gr(n)+hr(n)$$

(13)

In the formula, risk(i) represents the risk time associated with traversing a specific grid cell i. The aggregate path risk is computed through linear superposition of individual grid cell risks. The potential hazard escalates proportionally with temporal duration in risk zones.

In the path planning of autonomous vehicles, the smoothness metric is critical for evaluating the smoothness of a path and the vehicle’s stability when navigating complex terrains. This metric is directly related to the driving comfort, stability, and safety of the vehicle’s equipment. Particularly in challenging outdoor environments, an uneven path may lead to navigation system errors, accelerated wear and tear of hardware, and even significantly affect the success rate of task execution. To address the path planning requirements of autonomous vehicles in such environments, this study proposes a smoothness modeling method based on grid-based terrain data. By calculating the elevation of each grid cell and determining the slope differences between adjacent grid cells along the path, the method quantifies smoothness by summing the slope differences of all adjacent grid cells. This enables a comprehensive evaluation and optimization of path smoothness. The improved A* algorithm is formulated as follows.

$$gs(n)={\displaystyle \sum _{i=1}^{n}sl}$$

(14)

$$avg={\displaystyle \frac{gs(n)}{n}}$$

(15)

$$hs(n)=dn•avg$$

(16)

$$fs(n)=gs(n)+hs(n)$$

(17)

In the formula, g_s(n) represents its current smoothness cost, avg denotes the average gradient difference of the autonomous vehicle’s traveled path, and h_s(n) indicates the estimated smoothness cost to the destination.

4. Path Planning Experiments

4.1. Experimental Environment

To verify the effectiveness of the proposed A* algorithm in real outdoor environments, this study utilized remote sensing technology to sample surface data from actual outdoor terrains. The obtained surface information was processed using a spline interpolation method to fit the data points. Subsequently, surface attribute information was classified using the maximum likelihood classification algorithm. Finally, the data were rasterized and overlaid to generate a map for use in the simulation experiments. The performance of different algorithms was analyzed in terms of timeliness, smoothness, and risk assessment.

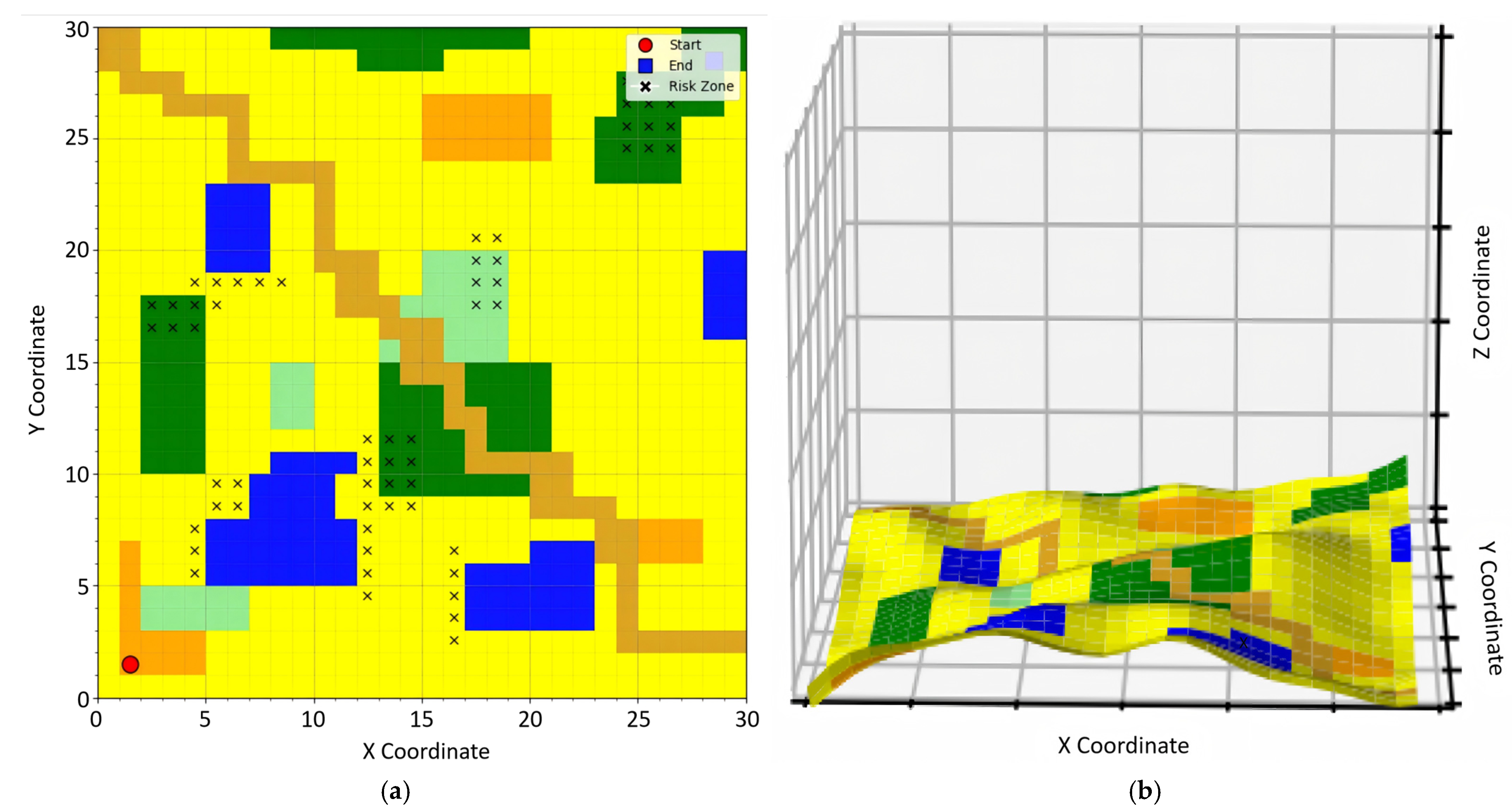
The experimental setup abstracts real-world off-road environments into a discretized grid model, constructing a 300 m × 300 m two-dimensional simulated scenario (Figure 5a) with corresponding three-dimensional topographic mapping (Figure 5b). Spatial discretization is implemented through a 30 × 30 grid matrix, where each grid cell maintains a resolution of 10 m × 10 m, encoding actual terrain elevation data and obstacle distribution characteristics. The unmanned ground vehicle kinematic model assumes constant velocity at 10 m/s. This experiment systematically evaluates the comprehensive performance of path planning algorithms under multi-constrained conditions, with particular emphasis on temporal efficiency, risk mitigation, and motion stability metrics. Environmental parametrization incorporates digital elevation models (DEMs) and probabilistic obstacle maps to simulate heterogeneous terrain configurations typically encountered in off-road navigation scenarios. The different grid colors in the figure represent different surface attributes, while the lines in various colors denote the planned paths of different algorithms.

The specific experimental environment is detailed in

Table 2. Experimental Environment.

Experimental Environment	Specific Configurations
Operating System	Windows11
CPU	13th Gen Intel(R) Core(TM) i9-13900HX
GPU	NVIDIA GeForce RTX 4080
Memory	32 G
Software	Visual Studio 2022
Language	Python 3.9.12

.

4.2. Comparative Experiment

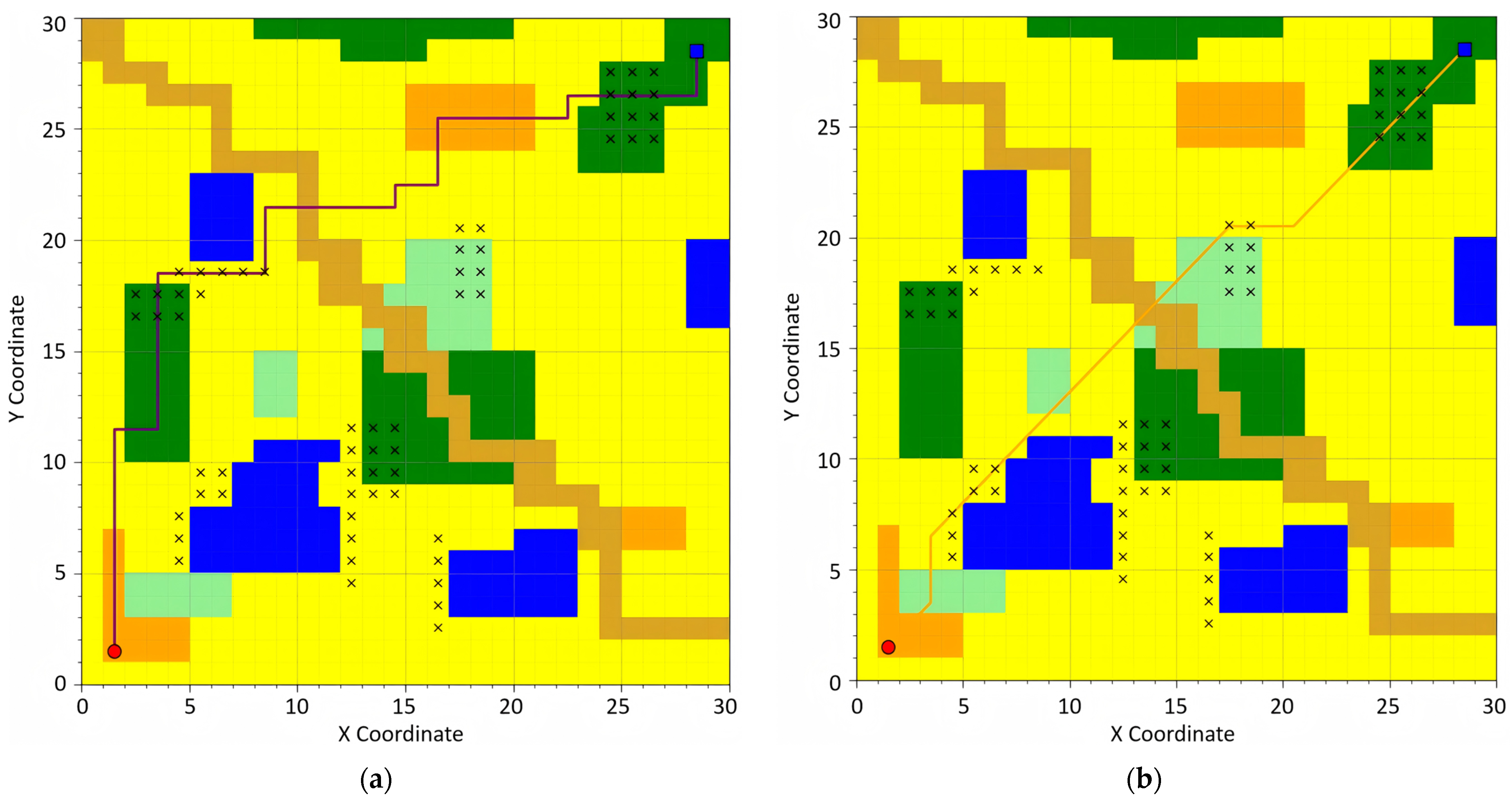
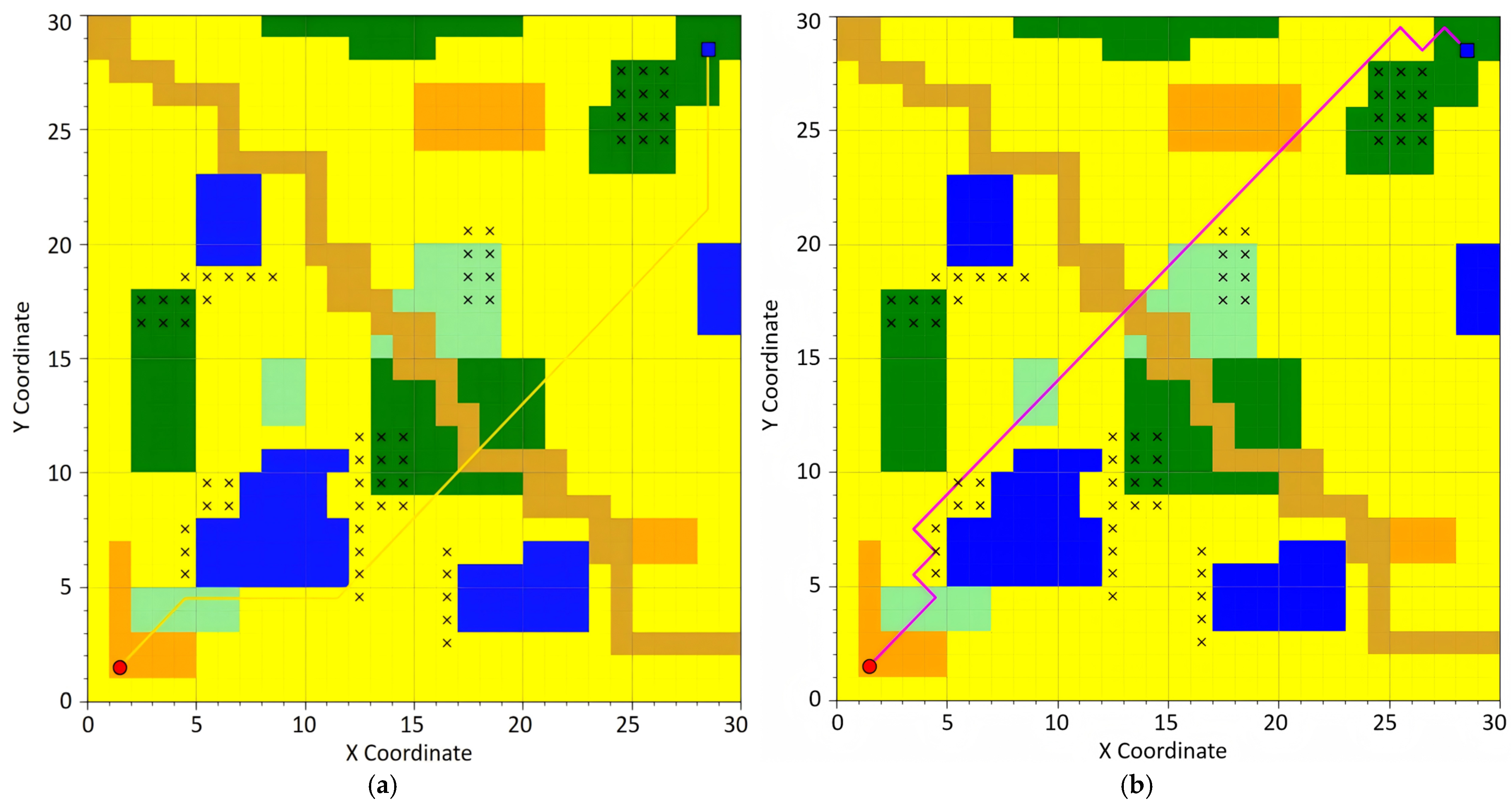
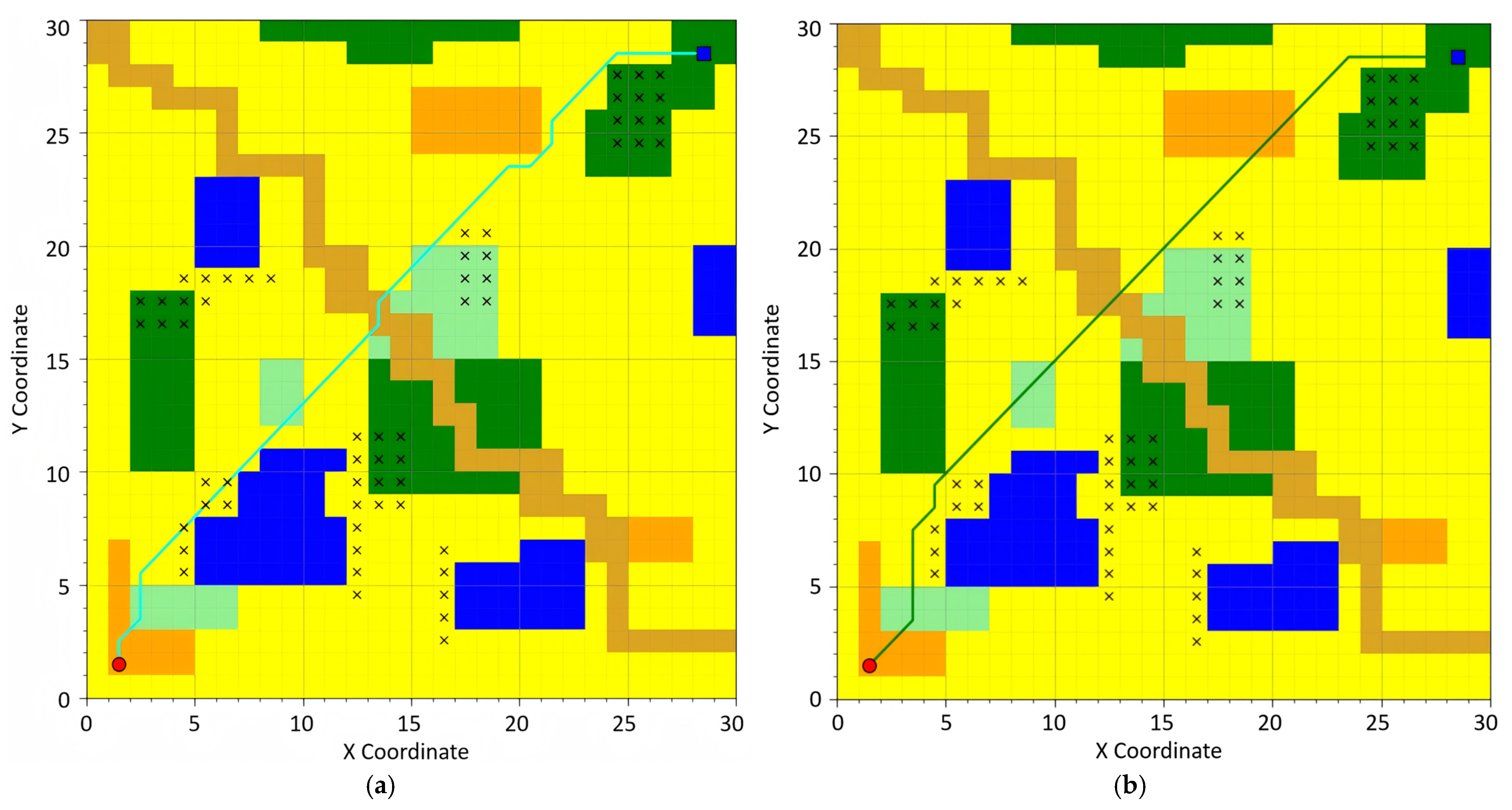
For the experiment, the following path planning algorithms were selected for evaluation: the traditional A* algorithm, the optimized A* algorithm based on 24-neighborhood search [27], Depth-First Search (DFS), Breadth-First Search (BFS), Dijkstra’s Algorithm, and Ant Colony Optimization. The planned paths generated by these algorithms are visually demonstrated in Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, providing a comparative analysis of their performance and efficiency.

Depth-First Search (DFS) constitutes a stack-based (or recursive) graph traversal algorithm that prioritizes maximal depth exploration along the current branch until reaching terminal nodes, followed by backtracking to the most recent unexplored node. The algorithm adheres to the Last-In-First-Out (LIFO) principle, typically implemented via either an implicit stack (recursion call stack) or explicit stack structure. Breadth-First Search (BFS) operates as a queue-driven graph traversal methodology, systematically expanding search coverage in a level-wise progression while prioritizing nodes with minimal distance from the origin. Its FIFO (First-In-First-Out) operational paradigm guarantees shortest-path discovery in unweighted graphs. Best-First Search constitutes a heuristic-driven exploration methodology that dynamically selects the most promising node for expansion through an evaluation function. This algorithmic framework essentially integrates the heuristic guidance characteristic of Depth-First Search with the systematic exploration paradigm inherent to Breadth-First Search, thus achieving balanced optimization between search efficiency and solution completeness. Dijkstra’s Algorithm represents a greedy approach for resolving single-source shortest path problems in graphs with non-negative edge weights. By maintaining a priority queue (typically structured as a min-heap), it iteratively selects the node possessing the current minimal tentative distance for relaxation operations. Ant Colony Optimization (ACO) emerges as a swarm intelligence-based metaheuristic that emulates the pheromone-mediated pathfinding behavior of ant colonies. Its core mechanisms encompass positive reinforcement (pheromone accumulation on optimal paths) and negative reinforcement through pheromone evaporation, collectively enabling emergent optimization capabilities.

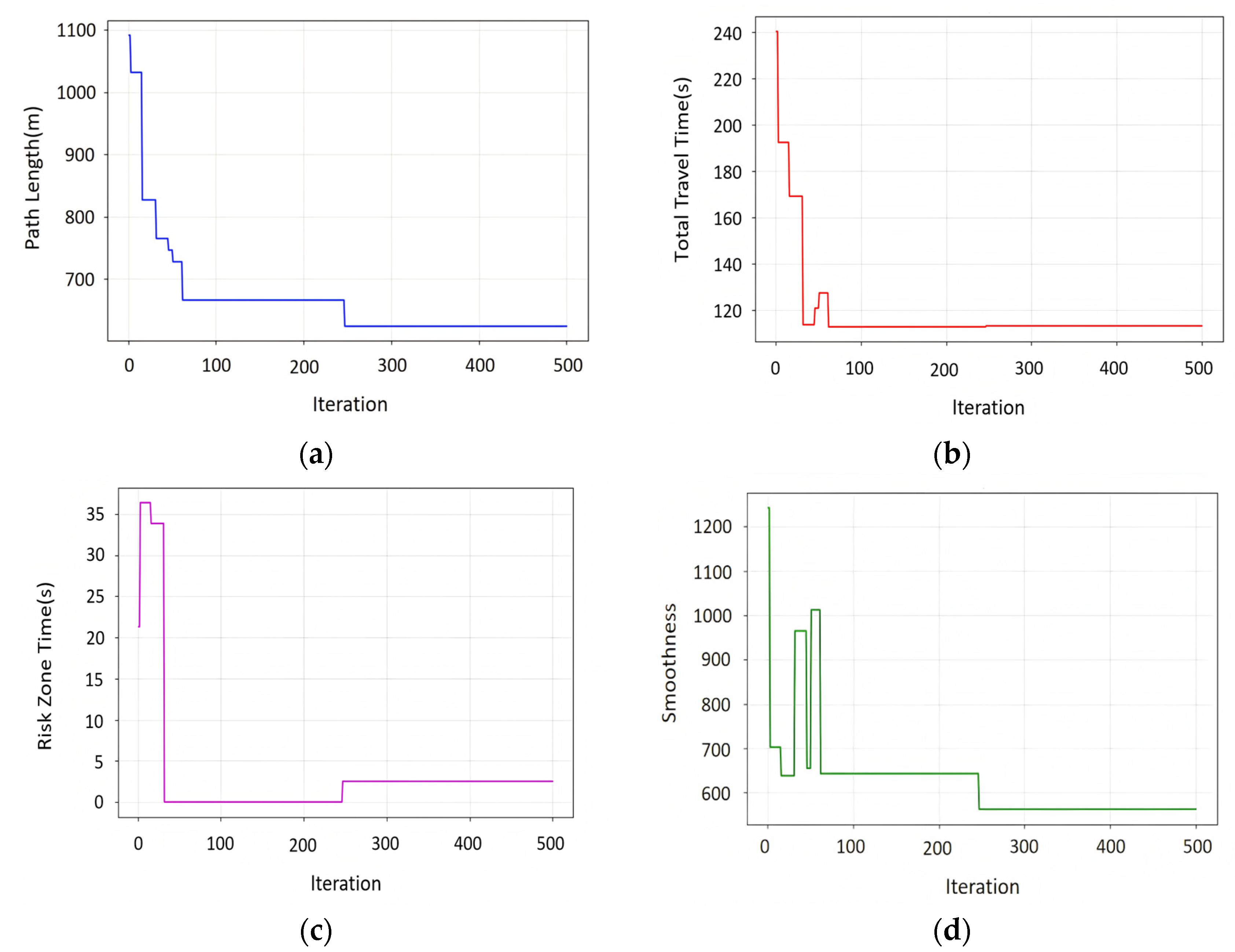
Figure 10 shows the variations in path length, path time, time spent traversing risk zones, and stability of the ACO algorithm as the number of iterations changes.

To ensure the universality and statistical significance of the experimental results, except for the ACO algorithm, the results of all other algorithms were averaged over 100 runs, while the ACO algorithm was set to iterate 500 times. A comparison was conducted on the path length, time, risk, stability, and the time required to run each algorithm, followed by a comprehensive analysis of the performance and complexity of the algorithms.

Due to the characteristics of the ACO algorithm, multiple iterations are required, so its runtime is the sum of all iteration times, while the runtime of other algorithms is the average of 100 execution counts. The experimental results are shown in

Table 3. Experimental results of different algorithms.

Algorithm	Path Length (m)	Time (s)	Risk (s)	Stationarity (Degrees)	Algorithm Time (s)
A*	541.50	137.66	31.33	397.25	0.135
24-neighbor A*	400.39	86.78	29.57	188.49	0.454
Depth-First Search	440.09	71.80	3.54	389.32	0.0025
Breadth-First Search	401.26	92.34	31.28	172.19	0.0553
Best-First Search	424.20	89.08	1.77	371.08	0.0071
Dijkstra	562.43	76.61	0.00	389.31	0.0756
ACO	623.93	113.28	2.51	562.39	22.050

.

The experimental results indicate that since the experiment was conducted through rasterization simulation in an actual field environment, it differs from conventional two-dimensional grid network diagrams. Grids of different colors exhibit varying traversal speeds for unmanned vehicles due to their distinct surface attributes. Moreover, as real terrain conditions were considered, three-dimensional distance calculations were employed instead of two-dimensional ones. Consequently, while different algorithms may yield similar routes on the path planning map, there can be notable differences in actual path distances and traversal times.

To evaluate the computational complexity of the implemented algorithms, we conducted 100 independent test runs using Python’s time module for precise time measurement, with averaged results ensuring statistical significance. Experimental data revealed that Depth-First Search (DFS) and Best-First Search demonstrated superior time efficiency, attributable to their streamlined search strategies. Dijkstra’s algorithm and Breadth-First Search (BFS) showed moderate computational demand, while the standard A* algorithm exhibited increased latency due to extended node expansion requirements and dual cost function maintenance. The 24-neighborhood A* variant incurred higher computational overhead than conventional A*, reflecting its enhanced path optimality through expanded search space. Ant Colony Optimization (ACO) displayed the highest time complexity, consistent with its iterative optimization process requiring pheromone matrix updates across 500+ iterations.

4.3. Comparative Experiment with A* Algorithm

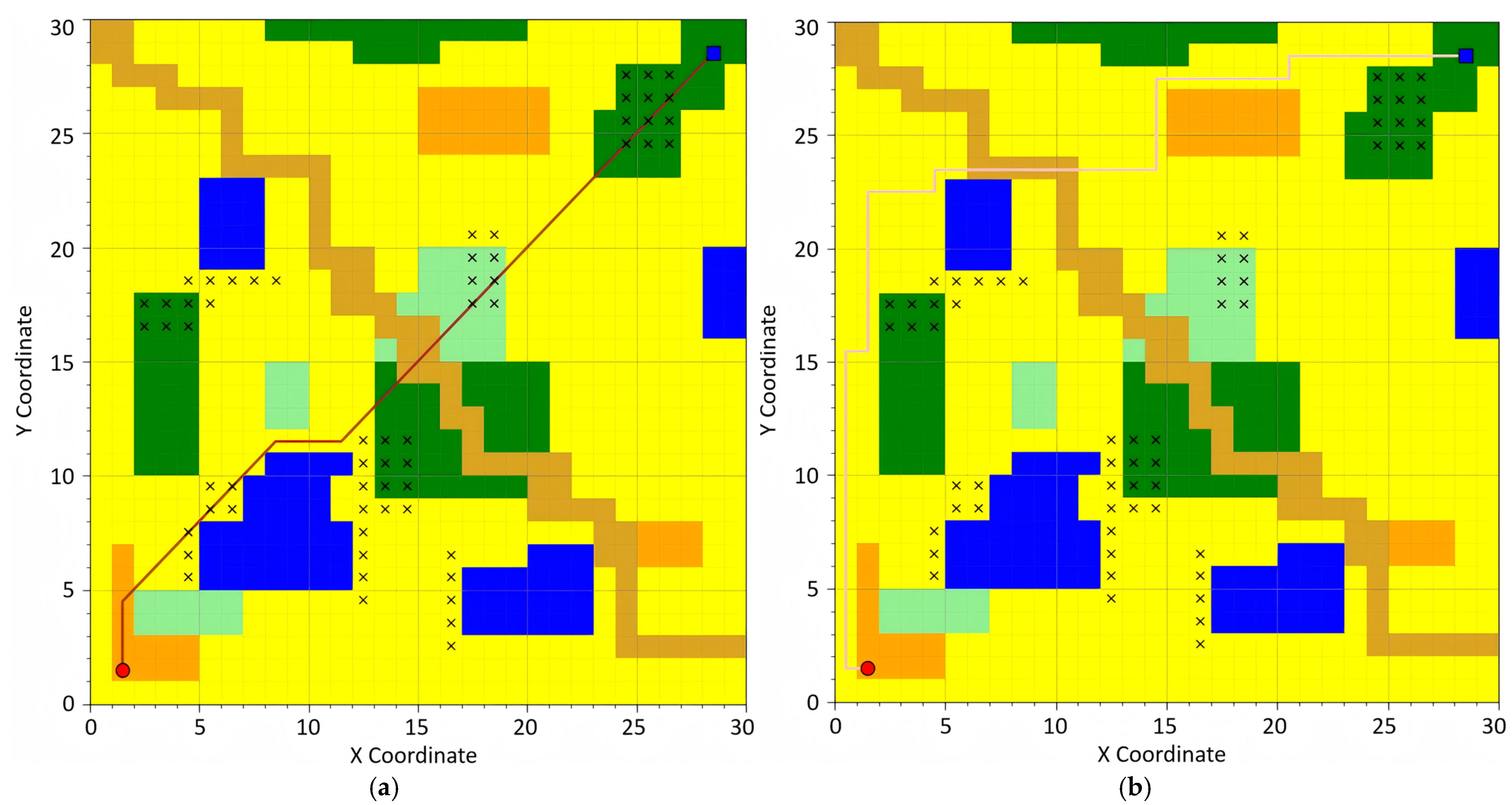
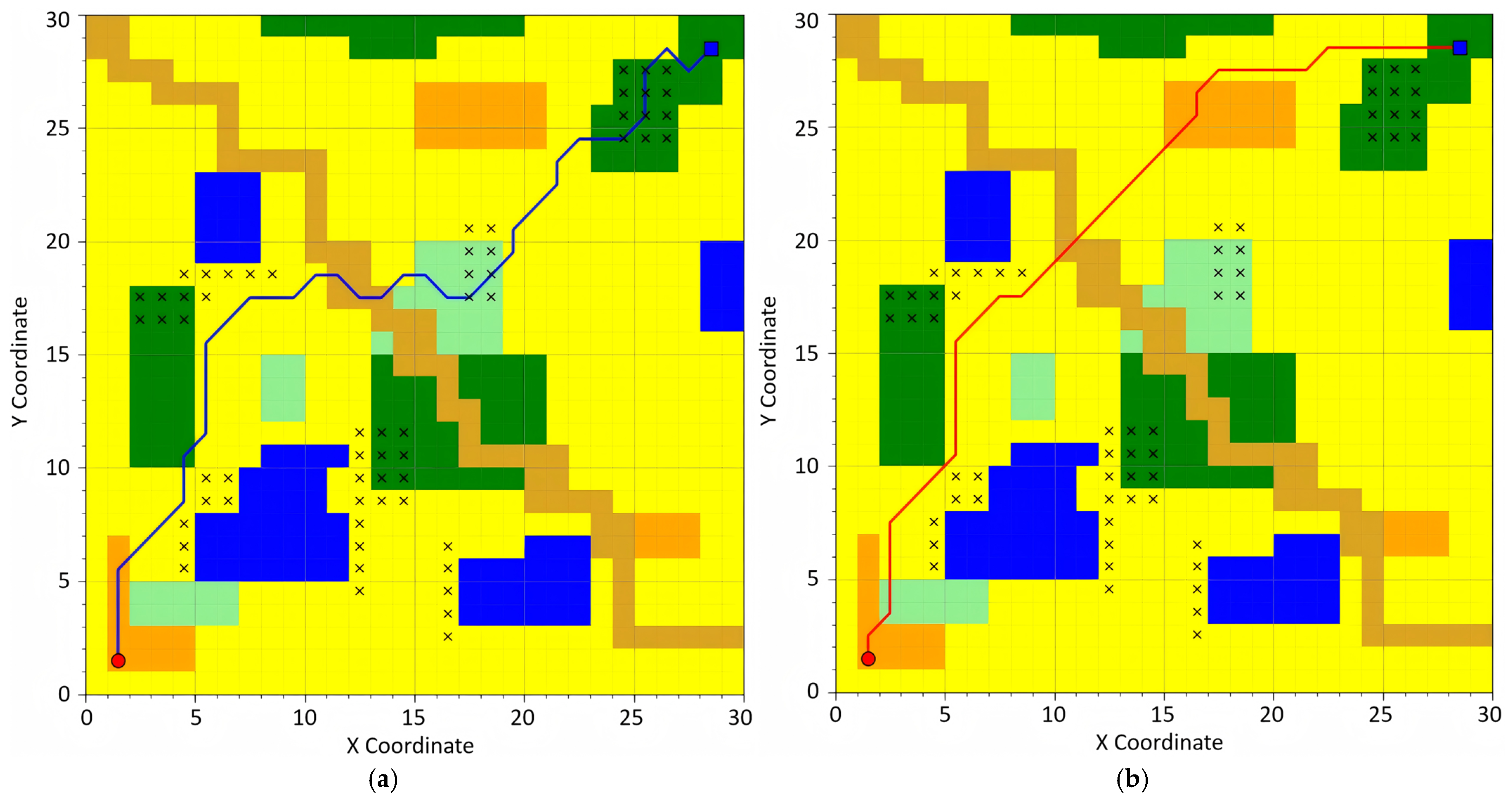
Afterward, path planning was conducted based on the proposed A* algorithm, which prioritizes timeliness, safety, and smoothness. Additionally, a comprehensive path planning process was carried out by considering all three path metrics simultaneously. The results are illustrated in Figure 11 and Figure 12.

The experimental design simplified field environment considerations by focusing on four key metrics: path distance, traversal time, risk assessment, and stability index. Path distance was computed based on three-dimensional measurements rather than conventional two-dimensional grid-based linear distance calculations. Traversal time estimation incorporated terrain-dependent speed parameters, where distinct velocity values were assigned based on surface characteristics, while recognizing that practical applications require more sophisticated speed modeling. Risk assessment evaluated potential hazards, including mudslides and wildlife activity, using uniform risk classification across zones, acknowledging that actual environments demand differentiated risk grading. The stability index was derived through slope gradient analysis of terrain surfaces.

Path planning strategies were adaptively selected based on mission requirements: time-optimal routing for urgent destination arrival, safety-critical navigation for vehicle protection, and stability-oriented trajectory planning to mitigate excessive vibration during cargo transportation. In this experimental framework, the cost function was configured with adjustable weight coefficients (time efficiency/safety assurance/stability maintenance = 1:2:1) to generate comprehensive routing solutions. Field implementations permit dynamic weight adjustments through parameter tuning interfaces to accommodate specific operational priorities.

Upon learning the mission area, it is feasible to conduct advance planning by sacrificing a certain amount of time in exchange for high-quality paths. Therefore, this experiment adopted a 24-neighborhood search strategy and considered metrics such as three-dimensional distance, surface attributes, risk level, and stability to ensure high-quality path planning in field environments. The experimental results are shown in

Table 4. Experimental Results of A* Algorithm.

Algorithm	Path Length (m)	Time (s)	Risk (s)	Stationarity (Degrees)	Algorithm Time (s)
A*	541.50	137.66	31.33	397.25	0.135
24-neighbor A*	400.39	86.78	29.57	188.49	0.454
A* (Time-Priority)	412.87	62.06	5.30	211.53	0.553
A* (Safety-Priority)	412.38	66.26	0.00	234.28	0.432
A* (Smoothness-Priority)	491.52	102.49	26.17	105.06	0.614
A* (Balanced-Priority)	447.89	70.31	0.00	134.90	0.584

.

In terms of path length, the standard A* algorithm produces the longest path, measuring 541.50 m, indicating its lack of optimization for smoothness and other complex factors. This is primarily due to its preference for directly connecting to the destination nodes. The improved A algorithm, however, achieves significant optimization with a path length of 400.39 m, representing a 26.05% reduction compared to the standard A* algorithm. This demonstrates the effectiveness of the adjustments made to its search strategy. Depth-First Search (DFS) and Breadth-First Search (BFS) yield shorter path lengths, measuring 400.09 m and 401.26 m, respectively, highlighting their strengths in simple distance-based optimization.

Regarding timeliness, the time-prioritized A* algorithm achieves the shortest execution time of 62.06 s, indicating its ability to identify the fastest path for autonomous vehicle navigation in outdoor environments. This represents a 54.91% reduction in computation time compared to the standard A* algorithm. Meanwhile, the comprehensive A* algorithm reduces execution time by 48.93% compared to the standard A* algorithm, while being 6.78% slower than the time-prioritized A* algorithm.

In terms of safety, both the safety-prioritized A* algorithm and the comprehensive A* algorithm exhibit a risk value of 0.00, indicating their complete avoidance of high-risk areas. This underscores their effectiveness in incorporating risk factors during path planning. In contrast, the other algorithms fail to consider safety, resulting in paths with varying levels of risk.

For smoothness, the smoothness-prioritized A* algorithm achieves a smoothness metric of 105.06 degrees, indicating that it significantly optimizes path smoothness by selecting gentler terrains. This represents a 73.54% reduction in smoothness value compared to the standard A* algorithm. The comprehensive A* algorithm achieves a smoothness metric of 134.9 degrees, which is a 66.05% reduction compared to the standard A* algorithm, but 28.37% higher than that of the smoothness-prioritized A* algorithm.

4.4. Experimental Limitations

The current simulation framework, derived from field environment modeling, was limited to six primary terrain types: hard surface, soil road, grassland, sandy terrain, forest, and water bodies. Whereas actual field conditions exhibit greater terrain diversity with varying vehicular traversal characteristics, enhanced simulation granularity would yield improved navigational accuracy and path planning quality.

Furthermore, the parametric selection of sampling resolution constitutes a critical implementation consideration. Hyperfine spatial resolution induces prohibitive computational complexity, while over-coarse resolution risks omitting critical terrain features. This necessitates context-dependent optimization of 3D grid mapping resolutions to balance computational tractability against environmental representational fidelity.

5. Conclusions

This study addresses the challenges of autonomous vehicle path planning in complex outdoor environments by proposing an improved A* algorithm. Through environmental modeling, algorithm optimization, and simulation experiments, the proposed method has been validated for its effectiveness and adaptability. The results demonstrate that the proposed approach achieves significant improvements in terms of timeliness, safety, and smoothness for path planning, showcasing its potential for practical applications in complex environments. Based on the improved A* algorithm, this study enables the dynamic selection of three path planning schemes: shortest time, lowest risk, and optimal smoothness. Simulation experiments reveal that the time-prioritized algorithm reduces planning time by 54.91%, the safety-prioritized algorithm completely avoids high-risk areas, and the smoothness-prioritized algorithm improves path smoothness by 73.54%. This multi-objective path planning capability significantly enhances the adaptability of autonomous vehicles in complex outdoor environments.

However, the methodology still exhibits notable limitations in three-dimensional field environments. The current implementation necessitates the pre-acquisition of terrain elevation profiles across operational areas to enable path planning. When confronted with dynamic field conditions, particularly transient obstructions, the algorithm predominantly relies on heuristic adjustments governed by deterministic rules. Future investigations will focus on integrating dynamic scenario reinforcement learning architectures. This enhancement aims to implement local obstacle avoidance based on existing global trajectories when encountering unexpected barriers, thereby enhancing algorithmic adaptability and generalization capacity.