A Framework for Optimal Parameter Selection in Electrocoagulation Wastewater Treatment Using Integrated Physics-Based and Machine Learning Models
Abstract
1. Introduction
2. Methodology
2.1. Development of Physics-Based Model
2.1.1. Governing Equations
- Electrode Reactions (Electrochemical Reaction)
- Chemical Reactions
- Mass Balance Equations
- Fluid Flow
- Saturation
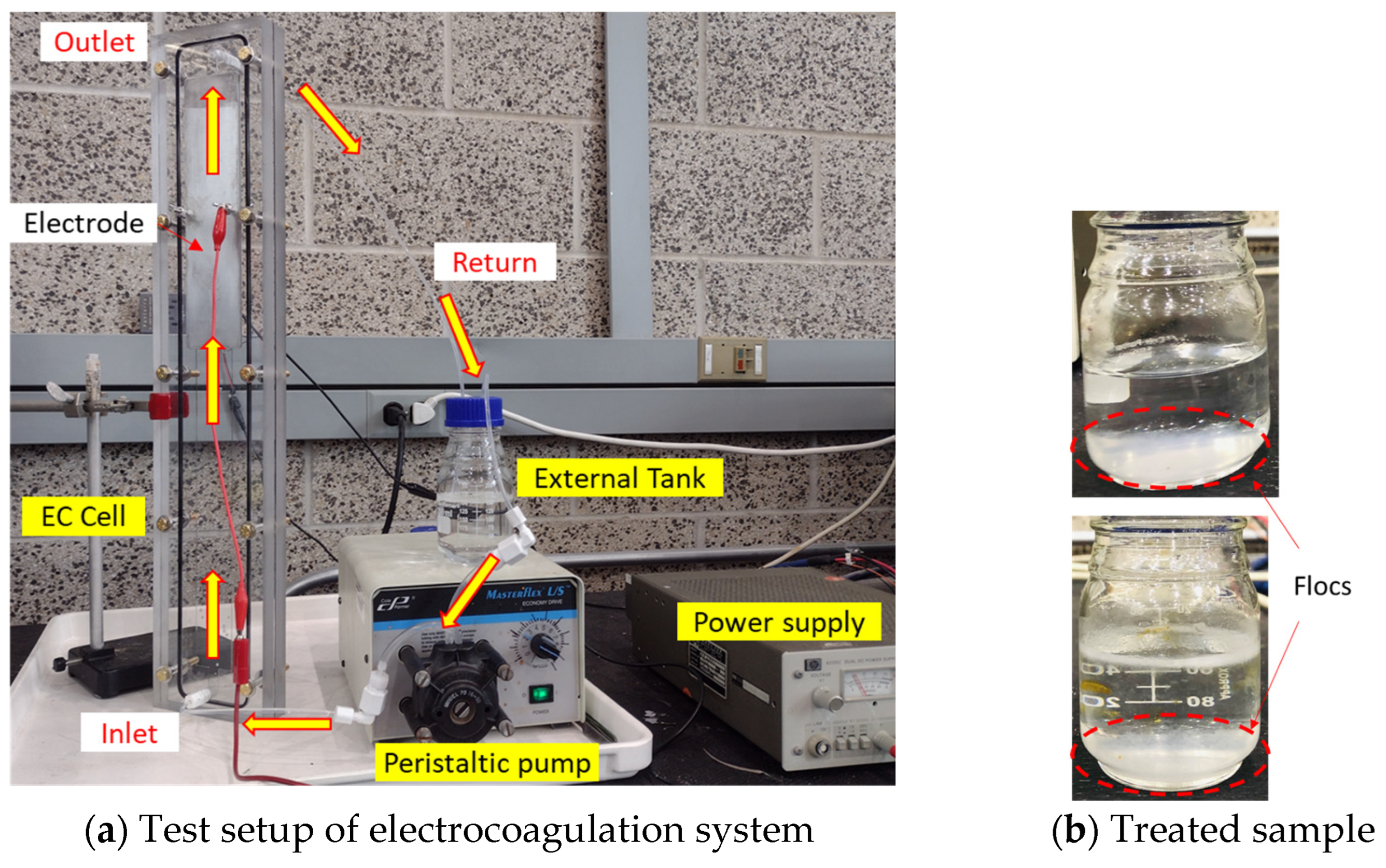
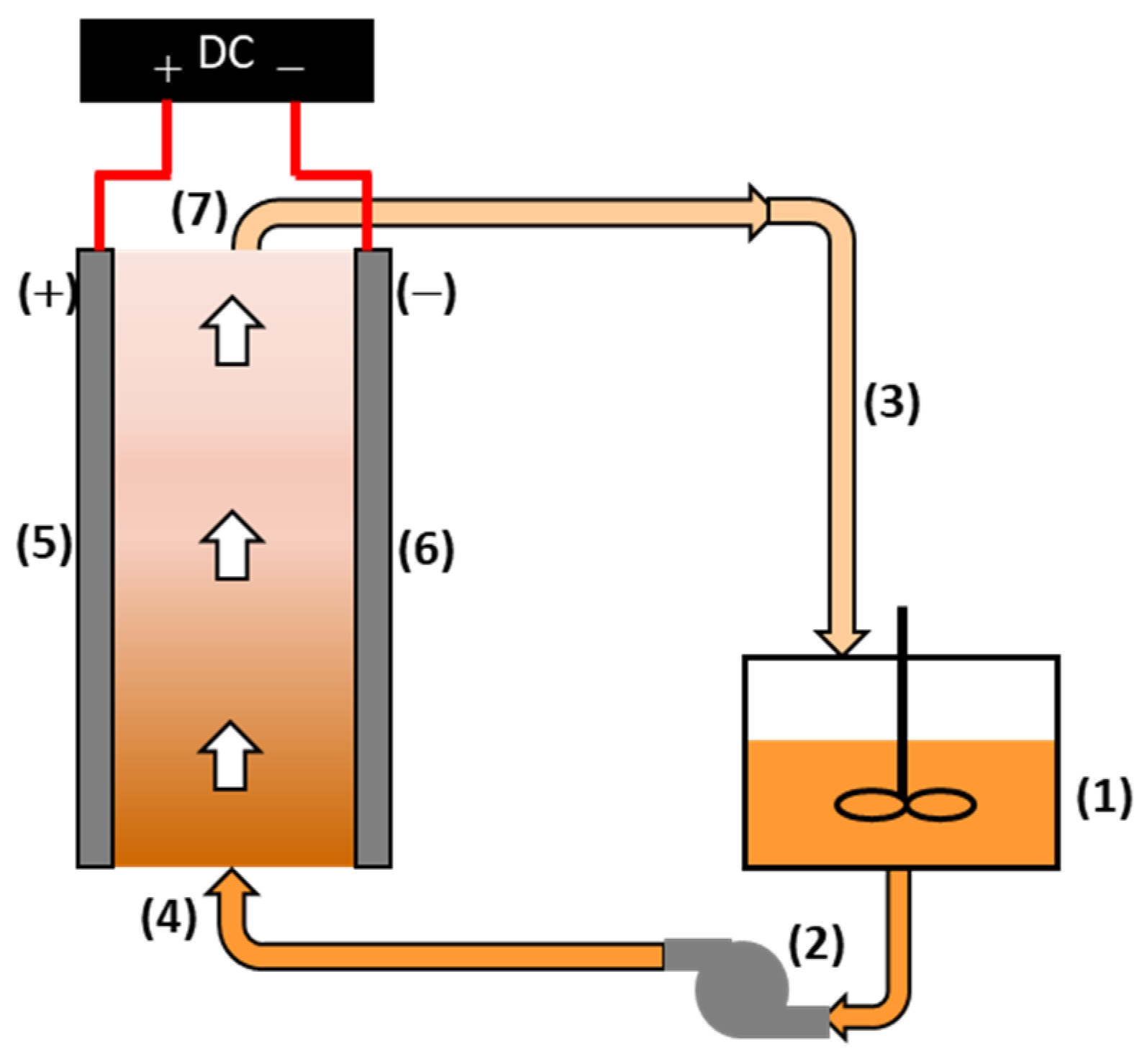
- External Tank
2.1.2. Boundary Conditions
2.1.3. Arsenic Removal
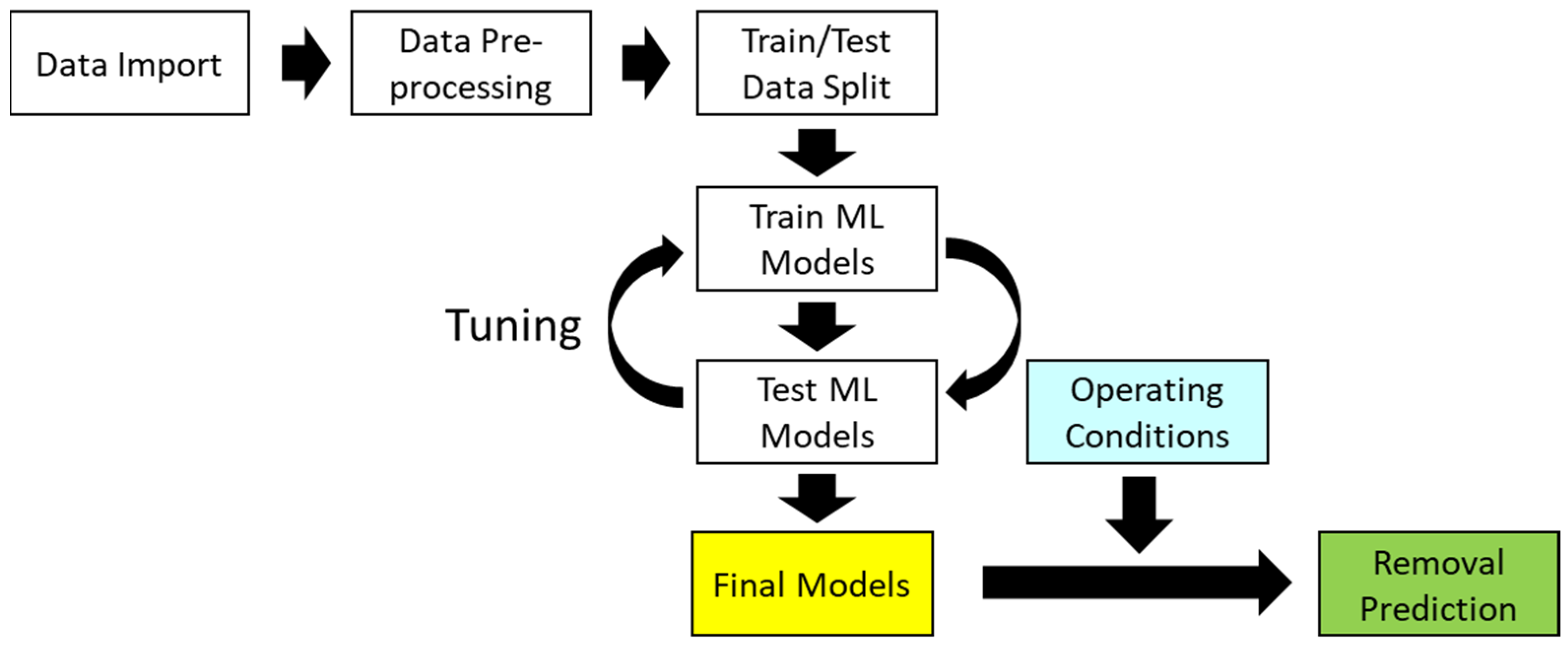
2.2. Development of Data-Based Model (Machine Learning Model)
2.2.1. Data Preprocessing
2.2.2. Machine Learning Algorithms
- K-Nearest Neighbors (KNN)
- Decision Tree and Random Forest
- Lasso and Ridge Regression
- Logistic Regression
- Voting Ensemble Method
2.2.3. Test Methods of Machine Learning Models
- Cross-Validation
- Classification
- Regression
3. Results and Discussion
3.1. Physics-Based Model
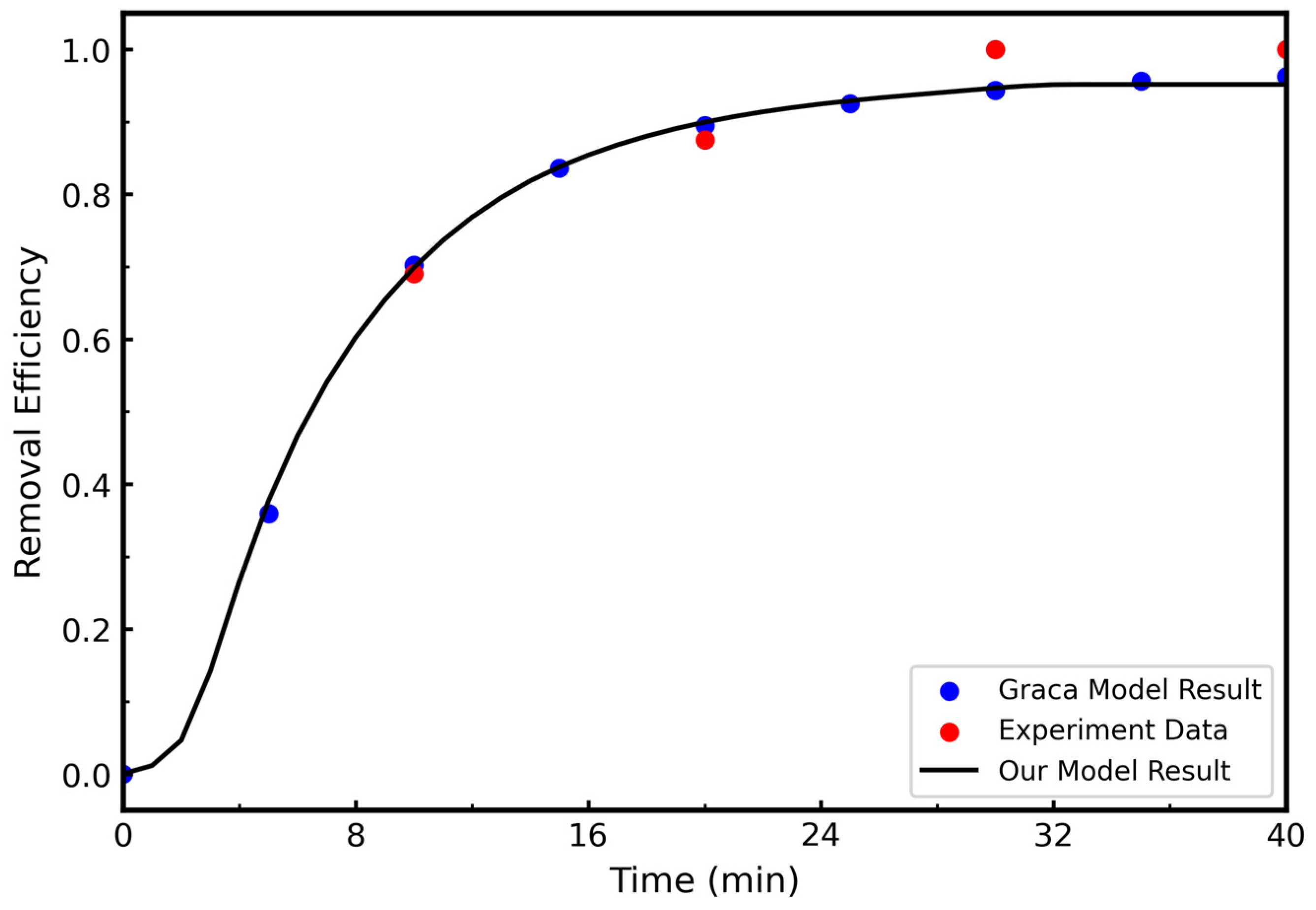
3.1.1. Model Validation
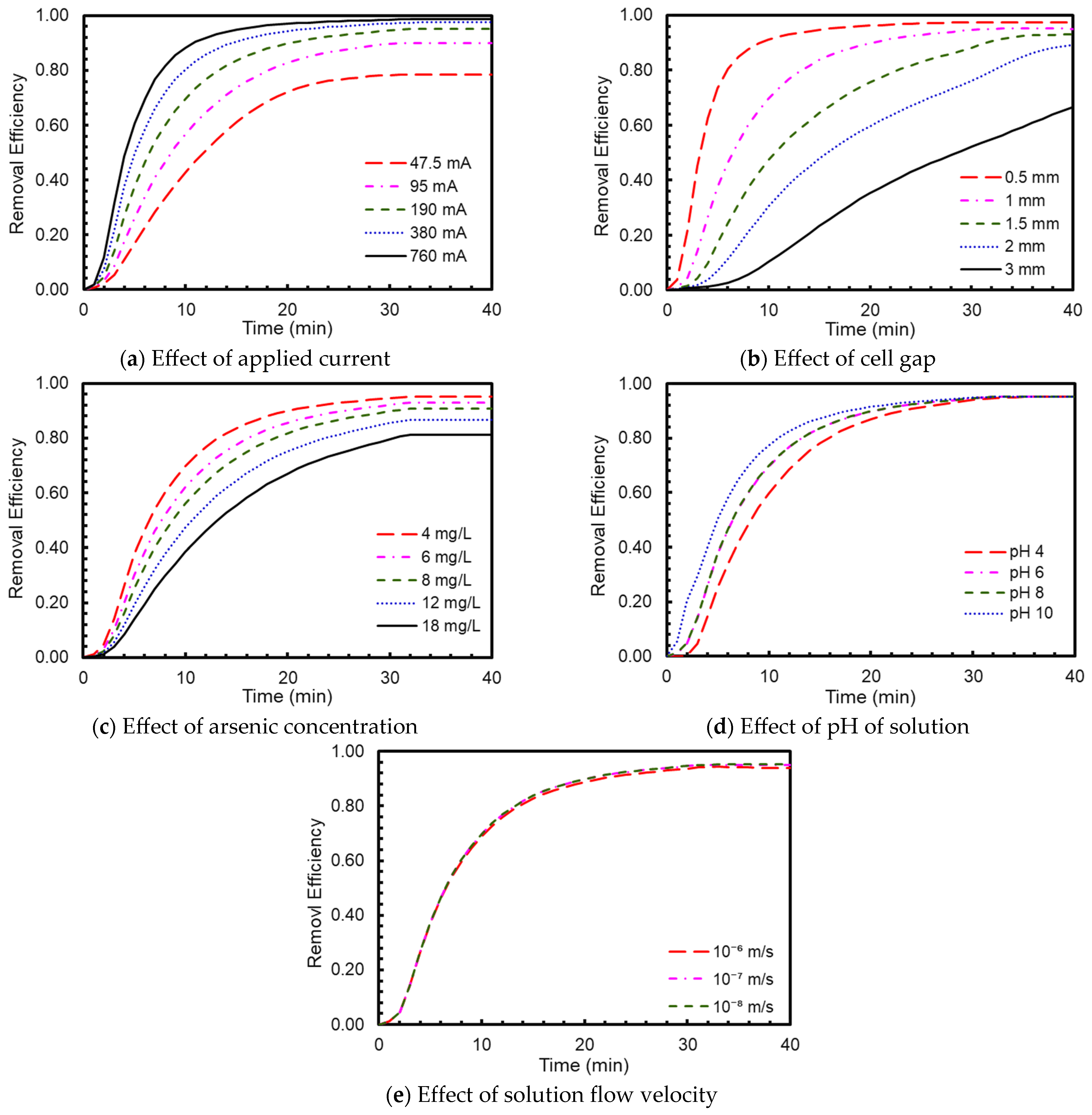
3.1.2. Parametric Study
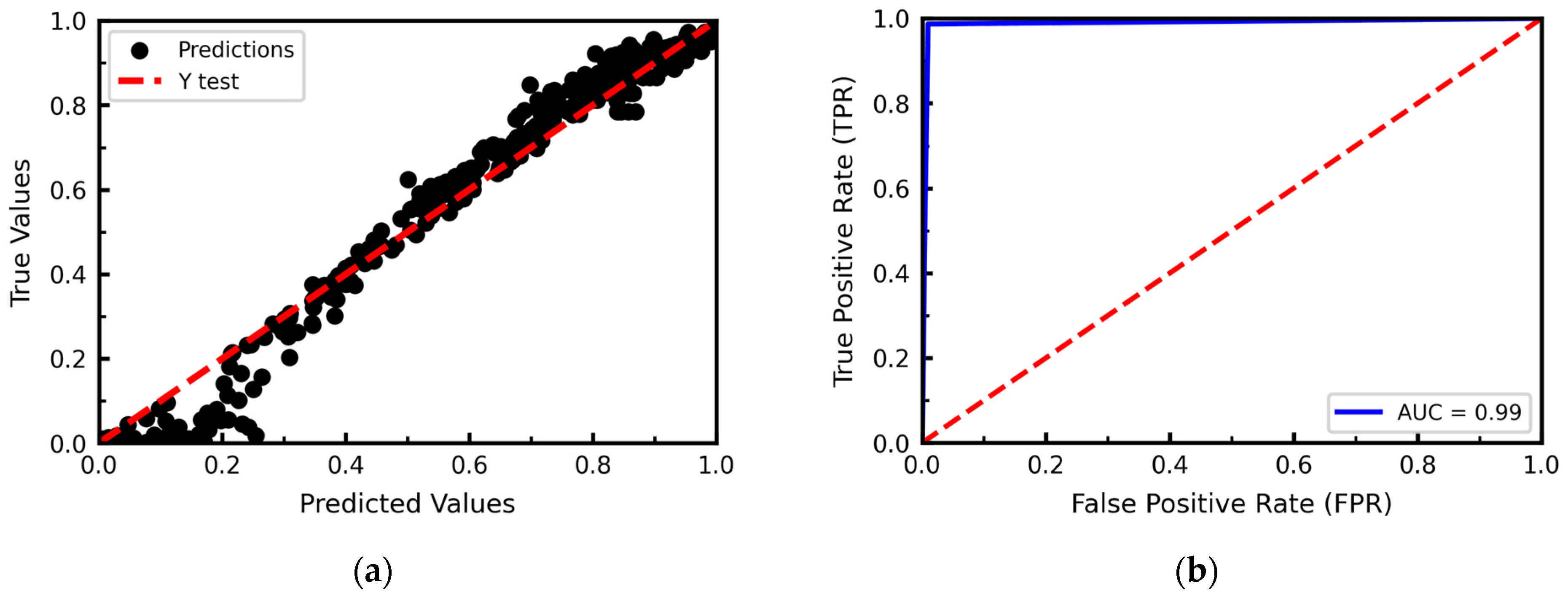
3.2. Data-Based Model
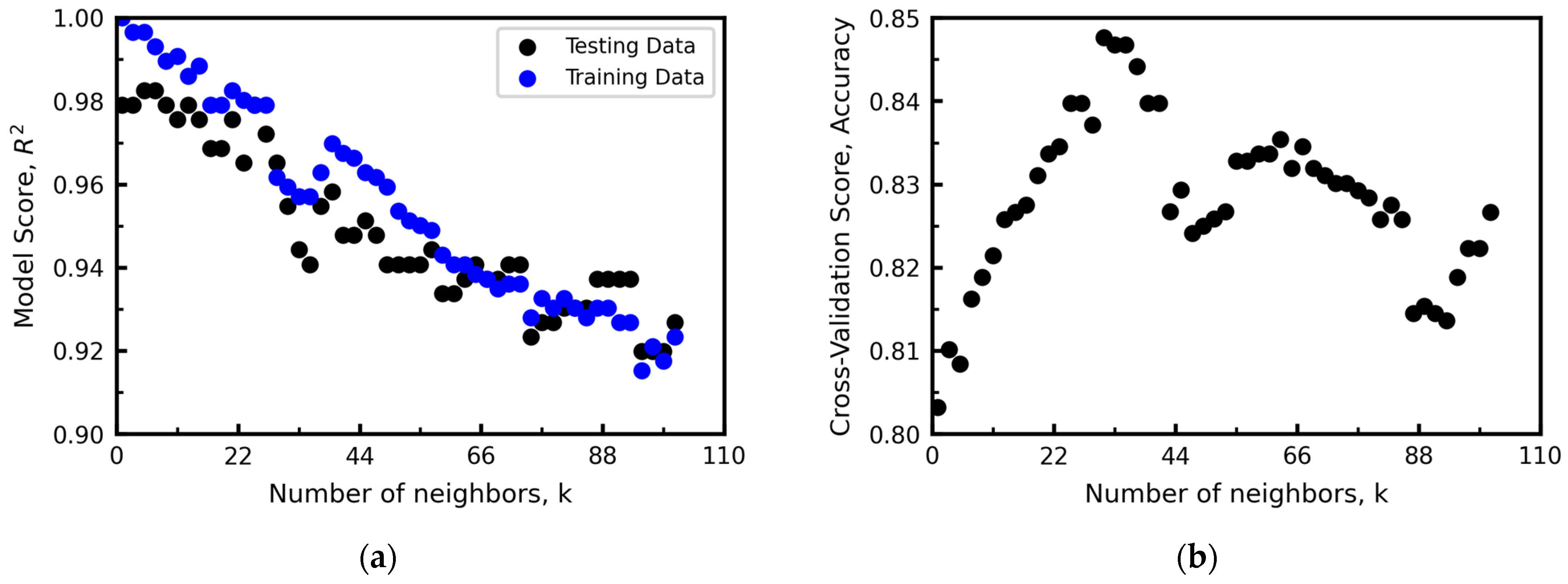
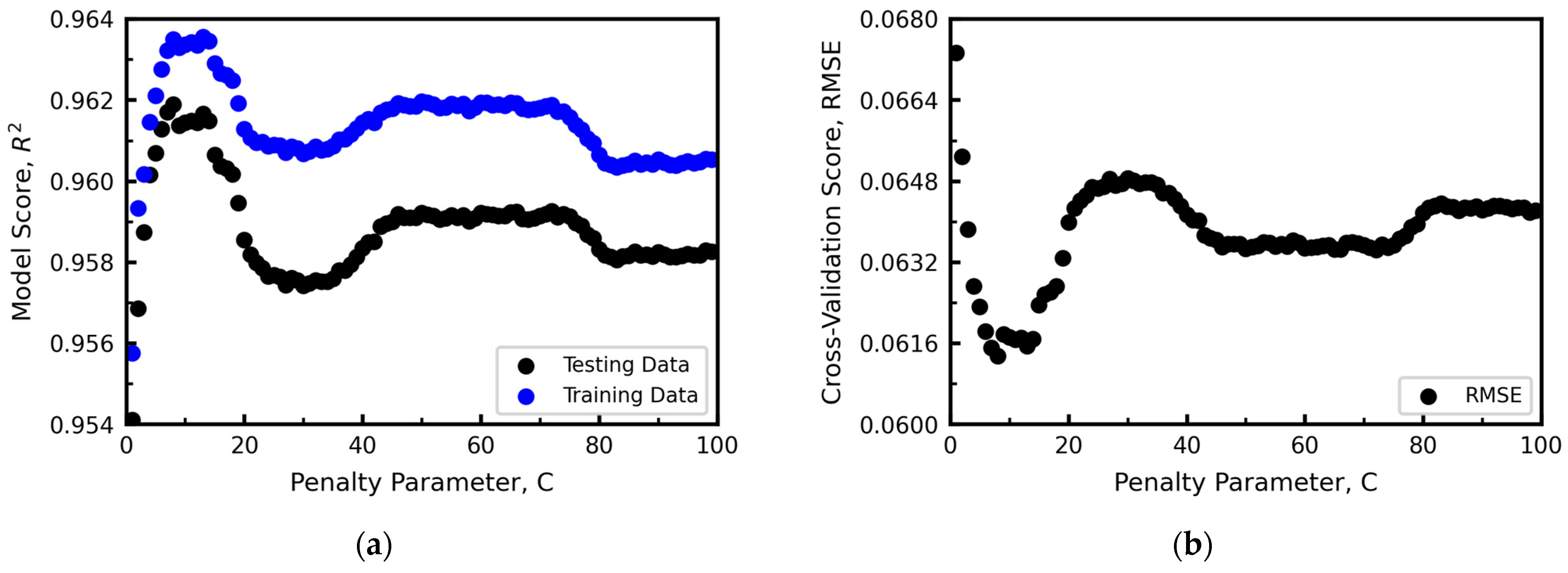
Hyperparameter Optimization
3.3. Generation of Processing Map
3.3.1. Processing Map: Effect of Cell Gap
3.3.2. Processing Map: Effect of Current
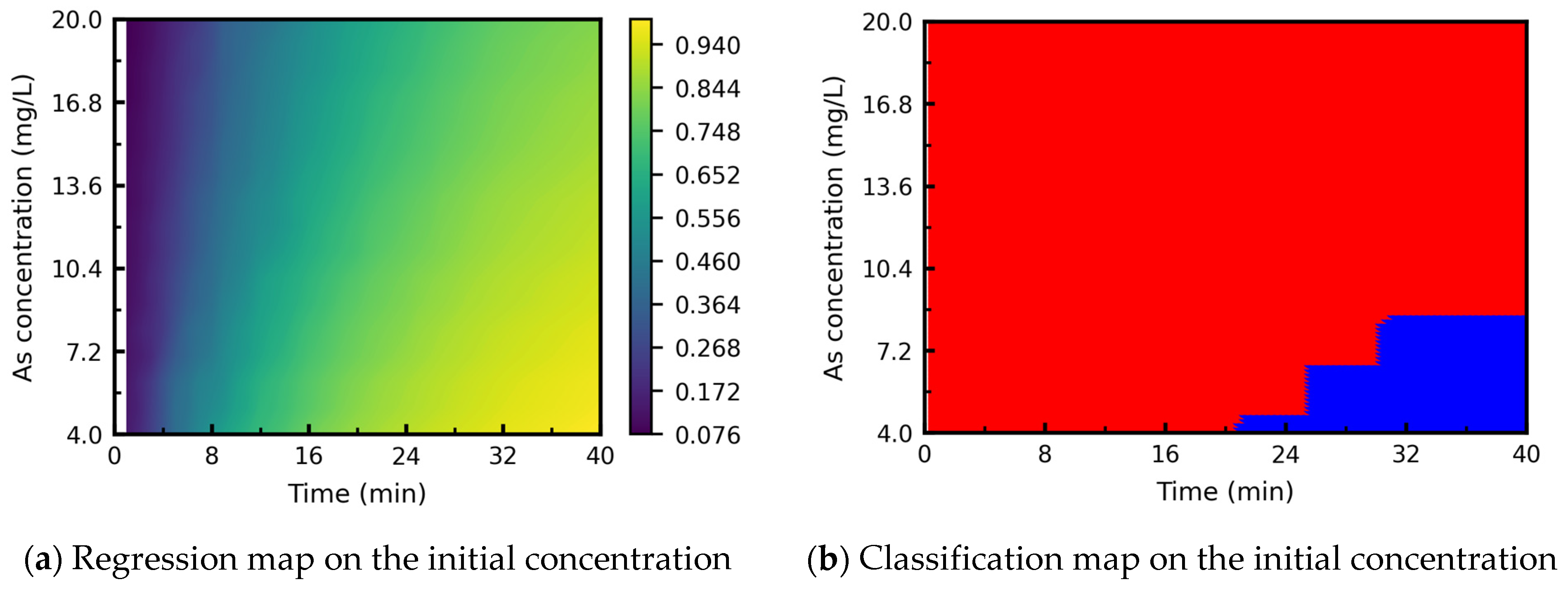
3.3.3. Processing Map: Effect of Initial Arsenic Concentration
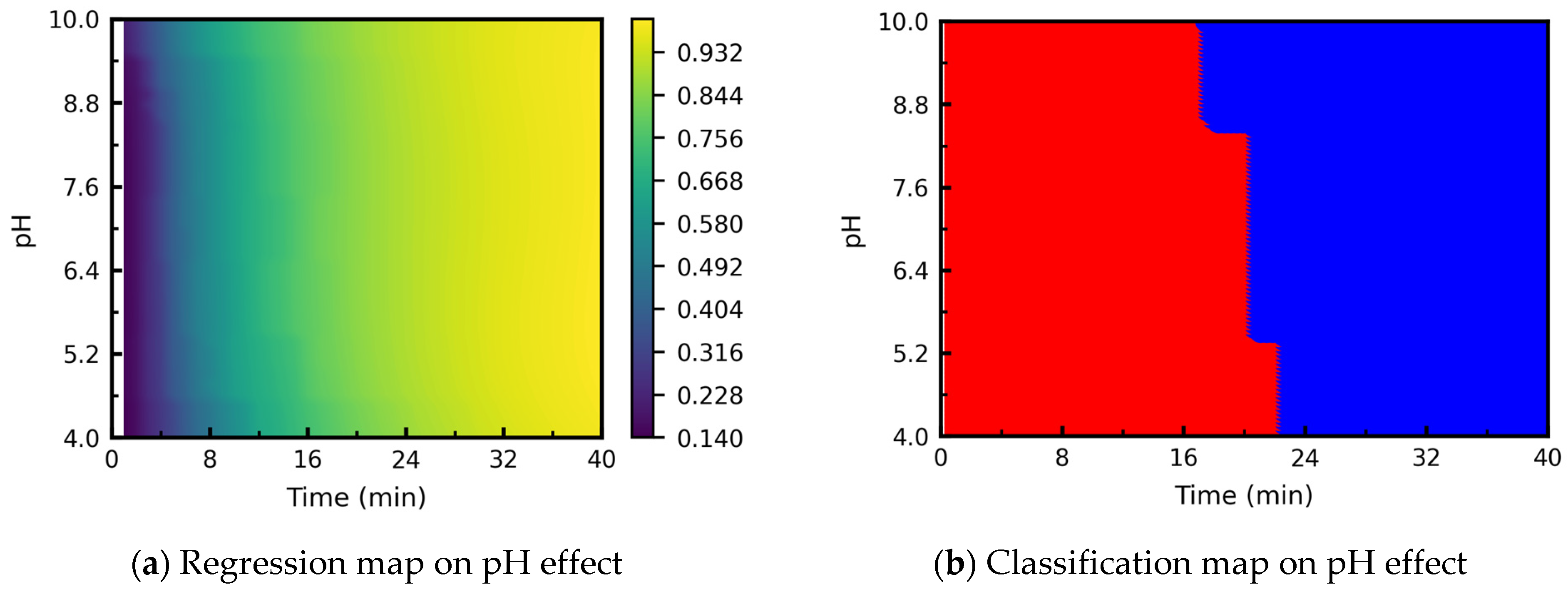
3.3.4. Processing Map: Effect of pH
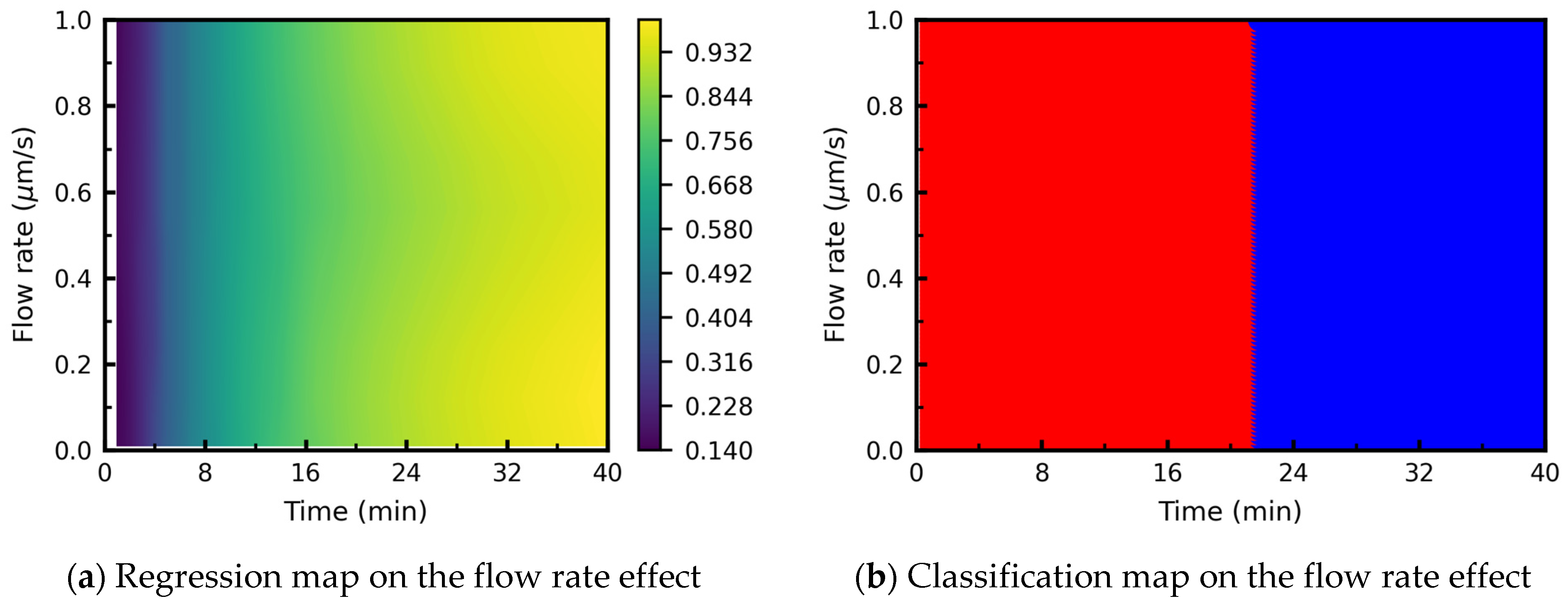
3.3.5. Processing Map: Effect of Flow Rate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AUC | Area under the ROC curve |
| BOD | Biochemical oxygen demand |
| CART | Classification and regression tree |
| COD | Chemical oxygen demand |
| EC | Electrocoagulation |
| FPR | False positive rate |
| KNN | K-nearest neighbors |
| MSE | Mean squared error |
| RBF | Radial basis function |
| ROC | Receiver operating characteristic curve |
| RSS | Residual sum of squares |
| SVM | Support vector machine |
| TPR | True positive rate |
| TSS | Total sum of squares |
Appendix A
Appendix A.1

Appendix A.2
References
- Patel, S.K.; Shukla, S.C.; Natarajan, B.R.; Asaithambi, P.; Dwivedi, H.K.; Sharma, A.; Singh, D.; Nasim, M.; Raghuvanshi, S.; Sharma, D.; et al. State of the art review for industrial wastewater treatment by electrocoagulation process: Mechanism, cost and sludge analysis. Desalination Water Treat. 2025, 321, 100915. [Google Scholar] [CrossRef]
- Jo, S.; Kadam, R.; Jang, H.; Seo, D.; Park, J. Recent Advances in Wastewater Electrocoagulation Technologies: Beyond Chemical Coagulation. Energies 2024, 17, 5863. [Google Scholar] [CrossRef]
- Mao, Y.; Zhao, Y.; Cotterill, S. Examining Current and Future Applications of Electrocoagulation in Wastewater Treatment. Water 2023, 15, 1455. [Google Scholar] [CrossRef]
- Silva, J.F.A.; Graça, N.S.; Ribeiro, A.M.; Rodrigues, A.E. Electrocoagulation process for the removal of co-existent fluoride, arsenic and iron from contaminated drinking water. Sep. Purif. Technol. 2018, 197, 237–243. [Google Scholar] [CrossRef]
- Fajardo, A.S.; Rodrigues, R.F.; Martins, R.C.; Castro, L.M.; Quinta-Ferreira, R.M. Phenolic wastewaters treatment by electrocoagulation process using Zn anode. Chem. Eng. J. 2015, 275, 331–341. [Google Scholar] [CrossRef]
- İrdemez, Ş.; Demircioğlu, N.; Yıldız, Y.Ş.; Bingül, Z. The effects of current density and phosphate concentration on phosphate removal from wastewater by electrocoagulation using aluminum and iron plate electrodes. Sep. Purif. Technol. 2006, 52, 218–223. [Google Scholar] [CrossRef]
- Grich, N.B.; Attour, A.; Mostefa, M.L.P.; Tlili, M.; Lapicque, F. Fluoride removal from water by electrocoagulation with aluminium electrodes: Effect of the water quality. Desalination Water Treat. 2019, 144, 145–155. [Google Scholar] [CrossRef]
- Nidheesh, P.V.; Singh, T.S.A. Arsenic removal by electrocoagulation process: Recent trends and removal mechanism. Chemosphere 2017, 181, 418–432. [Google Scholar] [CrossRef]
- Amrose, S.; Gadgil, A.; Srinivasan, V.; Kowolik, K.; Muller, M.; Huang, J.; Kostecki, R. Arsenic removal from groundwater using iron electrocoagulation: Effect of charge dosage rate. J. Environ. Sci. Health Part A 2013, 48, 1019–1030. [Google Scholar] [CrossRef]
- Gomes, J.A.G.; Daida, P.; Kesmez, M.; Weir, M.; Moreno, H.; Parga, J.R.; Irwin, G.; McWhinney, H.; Grady, T.; Peterson, E.; et al. Arsenic removal by electrocoagulation using combined Al–Fe electrode system and characterization of products. J. Hazard. Mater. 2007, 139, 220–231. [Google Scholar] [CrossRef]
- Lai, C.L.; Lin, S.H. Electrocoagulation of chemical mechanical polishing (CMP) wastewater from semiconductor fabrication. Chem. Eng. J. 2003, 95, 205–211. [Google Scholar] [CrossRef]
- Wang, C.-T.; Chou, W.-L.; Chen, L.-S.; Chang, S.-Y. Silica particles settling characteristics and removal performances of oxide chemical mechanical polishing wastewater treated by electrocoagulation technology. J. Hazard. Mater. 2009, 161, 344–350. [Google Scholar] [CrossRef] [PubMed]
- Chen, G. Electrochemical technologies in wastewater treatment. Sep. Purif. Technol. 2004, 38, 11–41. [Google Scholar] [CrossRef]
- Moussa, D.T.; El-Naas, M.H.; Nasser, M.; Al-Marri, M.J. A comprehensive review of electrocoagulation for water treatment: Potentials and challenges. J. Environ. Manag. 2017, 186, 24–41. [Google Scholar] [CrossRef]
- Magnisali, E.; Yan, Q.; Vayenas, D.V. Electrocoagulation as a revived wastewater treatment method-practical approaches: A review. J. Chem. Technol. Biotechnol. 2022, 97, 9–25. [Google Scholar] [CrossRef]
- Graça, N.S.; Ribeiro, A.M.; Rodrigues, A.E. Modeling the electrocoagulation process for the treatment of contaminated water. Chem. Eng. Sci. 2019, 197, 379–385. [Google Scholar] [CrossRef]
- Matteson, M.J.; Dobson, R.L.; Glenn, R.W.; Kukunoor, N.S.; Waits, W.H.; Clayfield, E.J. Electrocoagulation and separation of aqueous suspensions of ultrafine particles. Colloids Surf. A: Physicochem. Eng. Asp. 1995, 104, 101–109. [Google Scholar] [CrossRef]
- Khemis, M.; Leclerc, J.-P.; Tanguy, G.; Valentin, G.; Lapicque, F. Treatment of industrial liquid wastes by electrocoagulation: Experimental investigations and an overall interpretation model. Chem. Eng. Sci. 2006, 61, 3602–3609. [Google Scholar] [CrossRef]
- Lacasa, E.; Cañizares, P.; Sáez, C.; Martínez, F.; Rodrigo, M.A. Modelling and cost evaluation of electro-coagulation processes for the removal of anions from water. Sep. Purif. Technol. 2013, 107, 219–227. [Google Scholar] [CrossRef]
- Carmona, M.; Khemis, M.; Leclerc, J.-P.; Lapicque, F. A simple model to predict the removal of oil suspensions from water using the electrocoagulation technique. Chem. Eng. Sci. 2006, 61, 1237–1246. [Google Scholar] [CrossRef]
- Lu, J.; Li, Y.; Yin, M.; Ma, X.; Lin, S. Removing heavy metal ions with continuous aluminum electrocoagulation: A study on back mixing and utilization rate of electro-generated Al ions. Chem. Eng. J. 2015, 267, 86–92. [Google Scholar] [CrossRef]
- Song, P.; Song, Q.; Yang, Z.; Zeng, G.; Xu, H.; Li, X.; Xiong, W. Numerical simulation and exploration of electrocoagulation process for arsenic and antimony removal: Electric field, flow field, and mass transfer studies. J. Environ. Manag. 2018, 228, 336–345. [Google Scholar] [CrossRef]
- Dubrawski, K.L.; Du, C.; Mohseni, M. General Potential-Current Model and Validation for Electrocoagulation. Electrochim. Acta 2014, 129, 187–195. [Google Scholar] [CrossRef]
- Chen, X.; Chen, G.; Yue, P.L. Investigation on the electrolysis voltage of electrocoagulation. Chem. Eng. Sci. 2002, 57, 2449–2455. [Google Scholar] [CrossRef]
- Balasubramanian, N.; Kojima, T.; Srinivasakannan, C. Arsenic removal through electrocoagulation: Kinetic and statistical modeling. Chem. Eng. J. 2009, 155, 76–82. [Google Scholar] [CrossRef]
- Amani-Ghadim, A.R.; Aber, S.; Olad, A.; Ashassi-Sorkhabi, H. Optimization of electrocoagulation process for removal of an azo dye using response surface methodology and investigation on the occurrence of destructive side reactions. Chem. Eng. Process. Process Intensif. 2013, 64, 68–78. [Google Scholar] [CrossRef]
- Garg, K.K.; Prasad, B. Development of Box Behnken design for treatment of terephthalic acid wastewater by electrocoagulation process: Optimization of process and analysis of sludge. J. Environ. Chem. Eng. 2016, 4, 178–190. [Google Scholar] [CrossRef]
- Akoulih, M.; Tigani, S.; Byoud, F.; Rharib, M.E.; Saadane, R.; Pierre, S.; Chehri, A.; Ghachtouli, S.E. Electrocoagulation-based AZO DYE (P4R) Removal Rate Prediction Model using Deep Learning. Procedia Comput. Sci. 2024, 236, 51–58. [Google Scholar] [CrossRef]
- Bhagawati, P.B.; Kiran Kumar, H.S.; Lokeshappa, B.; Malekdar, F.; Sapote, S.; Adeogun, A.I.; Chapi, S.; Goswami, L.; Mirkhalafi, S.; Sillanpää, M. Prediction of electrocoagulation treatment of tannery wastewater using multiple linear regression based ANN: Comparative study on plane and punched electrodes. Desalination Water Treat. 2024, 319, 100530. [Google Scholar] [CrossRef]
- Shirkoohi, M.G.; Tyagi, R.D.; Vanrolleghem, P.A.; Drogui, P. A comparison of artificial intelligence models for predicting phosphate removal efficiency from wastewater using the electrocoagulation process. Digit. Chem. Eng. 2022, 4, 100043. [Google Scholar] [CrossRef]
- Dey, S.; Adejinle, A.; Cho, K.T. Modeling Study of Aluminum-Based Electrocoagulation System for Wastewater Treatment. J. Environ. Eng. 2024, 150, 04023099. [Google Scholar] [CrossRef]
- Newman, J.S.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; J. Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R.; Tryggvason, G. Fluid Mechanics, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Xiao, F.; Zhang, B.; Lee, C. Effects of low temperature on aluminum(III) hydrolysis: Theoretical and experimental studies. J. Environ. Sci. 2008, 20, 907–914. [Google Scholar] [CrossRef] [PubMed]
- Murphy, K.P. Machine Learning—A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bishop, C.M.; Bishop, H. Deep Learning: Foundations and Concepts; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Lee, W.-M. Python Machine Learning; John Wiley and Sons: Indianapolis, IN, USA, 2019. [Google Scholar]


| Kinetic Constants [16] | Equilibrium Constants [16] | Saturation Constants [34] |
|---|---|---|
| Variable | Value | Description |
|---|---|---|
| F | 96,485 [C/mol] | Faraday Constant |
| V | 100 [mL] | External Tank Volume |
| K | 1 | Separation Factor |
| Q | 2 [mgAs/mgAl] | Solid Capacity |
| D | Diffusion Coefficient | |
| L | 1 [cm] | Electrode Length |
| Parameter | Value | Units |
|---|---|---|
| pH | 7 | - |
| Current | 190 | mA |
| Cell Gap | 1 | mm |
| Initial Arsenic Concentration | 4 | mg/L |
| Flow Velocity | m/s |
| Test | Parameter and Range |
|---|---|
| Parametric Study 1 | pH: 4–10 |
| Parametric Study 2 | Current: 190 mA, ×0.5, ×0.25, ×2, ×4 |
| Parametric Study 3 | Cell gap: 0.5 mm–4mm |
| Parametric Study 4 | Arsenic concentration: 4–20 mg/L |
| Parametric Study 5 | Flow: |
| Time (min) | Current (mA) | pH | Flow (m/s) | Cell Gap (mm) | RR (%) | |
|---|---|---|---|---|---|---|
| 0 | 190 | 4 | 4 | 1 | 0 | |
| 5 | 190 | 4 | 4 | 1 | 25.3 | |
| 10 | 190 | 4 | 4 | 1 | 59.7 | |
| 20 | 190 | 4 | 4 | 1 | 87 | |
| 30 | 190 | 4 | 4 | 1 | 94 |
| Algorithm | Hyperparameter/Effect | Range Considered |
|---|---|---|
| Lasso | α: Strength of penalty | 0.01–1 |
| Ridge | α: Strength of penalty | 0.01–1 |
| KNN | K: Number of neighbors | 1–99 (odd number) |
| SVM | -Kernel: transform data into linear form -C: high C minimizes error low C maximizes hyperplane margin | RBF, poly, linear1–2000 |
| Decision Tree | -Max. depth: max layers in tree -Min. sample split: minimum points to split node | 2–no limit2–10 |
| Random Forest | Number of estimators | 1–1000 |
| Voting | Feature weights (regression) Hard/soft (classification) | - |
| Algorithm (Regression) | Hyperparameter | Result |
|---|---|---|
| Lasso | α | 0.01 |
| Ridge | α | 1 |
| KNN | K | 3 |
| SVM | Kernel, C | RBF, C = 8 |
| Decision Tree | Max. depth, min. sample split | Default (a) |
| Random Forest | Number of estimates | 100 |
| Voting | Feature weights | Equal |
| Algorithm (Classification) | Hyperparameter | Result |
|---|---|---|
| KNN | K | 31 |
| SVM | Kernel, C | RBF, C = 1100 |
| Decision Tree | Max. depth, min. sample split | Default (b) |
| Random Forest | Number of estimators | Default (c) |
| Voting | Hard/soft | Soft |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, K.T.; Cotton, A.; Shibata, T. A Framework for Optimal Parameter Selection in Electrocoagulation Wastewater Treatment Using Integrated Physics-Based and Machine Learning Models. Sustainability 2025, 17, 4604. https://doi.org/10.3390/su17104604
Cho KT, Cotton A, Shibata T. A Framework for Optimal Parameter Selection in Electrocoagulation Wastewater Treatment Using Integrated Physics-Based and Machine Learning Models. Sustainability. 2025; 17(10):4604. https://doi.org/10.3390/su17104604
Chicago/Turabian StyleCho, Kyu Taek, Adam Cotton, and Tomoyuki Shibata. 2025. "A Framework for Optimal Parameter Selection in Electrocoagulation Wastewater Treatment Using Integrated Physics-Based and Machine Learning Models" Sustainability 17, no. 10: 4604. https://doi.org/10.3390/su17104604
APA StyleCho, K. T., Cotton, A., & Shibata, T. (2025). A Framework for Optimal Parameter Selection in Electrocoagulation Wastewater Treatment Using Integrated Physics-Based and Machine Learning Models. Sustainability, 17(10), 4604. https://doi.org/10.3390/su17104604







