Max-Pressure Controller for Traffic Networks Considering the Phase Switching Loss

Abstract

Efficient traffic signal control plays a critical role in promoting sustainable mobility by reducing congestion and minimizing vehicle emissions. This paper proposes an enhanced max-pressure (MP) signal control strategy that explicitly accounts for phase switching time losses in grid road networks. While the traditional MP control strategy is recognized for its decentralized architecture and simplicity, it often neglects the delays introduced by frequent phase changes, limiting its real-world effectiveness. To address this issue, three key improvements are introduced in this study. First, a redefined phase pressure formulation is presented, which incorporates imbalances in traffic demand across multiple inlet roads within a single phase. Second, a dynamic green phase extension mechanism is developed, which adjusts phase durations in real time based on queue lengths to improve traffic flow responsiveness. Third, a current-phase protection mechanism is implemented by applying an amplification factor to the current-phase pressure calculations, thereby mitigating unnecessary phase switching. Simulation results using SUMO on a grid network demonstrate that the proposed strategy significantly reduces average vehicle delays and queue lengths compared with traditional MP, travel-time based MP, and fixed-time control strategies, leading to improved overall traffic efficiency. Specifically, the proposed method reduces total delay by 24.83%, 26.67%, and 47.11%, and average delay by approximately 16.18%, 18.91%, and 36.22%, respectively, while improving traffic throughput by 2.25%, 2.76%, and 5.84%. These improvements directly contribute to reducing traffic congestion, fuel consumption, and greenhouse gas emissions, thereby reinforcing the role of adaptive signal control in achieving smart and sustainable cities. The proposed approach can serve as a practical reference for improving real-world traffic signal control systems, particularly in regions seeking to improve sustainability and operational efficiency.

1. Introduction

In recent years, an increasing emphasis has been placed on integrating traffic and transportation engineering with energy-saving strategies to support the development of smart cities. Macioszek et al. [1] provided a comprehensive review of the key challenges and advancements in this field, emphasizing the roles of traffic calming measures, sustainable urban mobility, and intelligent transportation systems in improving energy efficiency and reducing environmental impacts. Motivated by this context, the present study investigates the optimization of traffic signal control as a practical and effective means to enhance intersection performance while minimizing energy consumption. As a cost-effective strategy to alleviate traffic congestion, traffic signal control enhances intersection access efficiency and capacity by allocating right-of-way to each inlet road during different periods, thereby and temporally separating vehicle flows into the intersections [2]. Well-designed signal control systems are critical to sustainable transportation management, as they can significantly reduce travel delays, vehicle idling, and stop-and-go conditions, all of which are major contributors to fuel consumption, greenhouse gas emissions, and local air pollution. Although well-designed traffic control strategies can effectively alleviate traffic congestion, poorly implemented systems may exacerbate it, contributing to energy waste and pollution [3]. Numerous studies have explored traffic signal control using methods such as optimal control and optimization [4,5,6] and reinforcement learning [7,8]. However, regional signal control remains a challenging area of research. The interdependence of traffic signal timings at intersections within a region leads to a dramatic increase in the computational burden for coordinated control as the area expands. In addition, the costs of infrastructure installation and maintenance further hinder scalability [9].

Methods of coordinated regional control can be divided into centralized and distributed control. Centralized control methods usually optimize the strategy with the objectives of overall regional throughput, delay, and average vehicle operating speed. However, computational burdens limit the scalability of centralized control to smaller regions, and optimizing overall metrics often comes at the expense of local performance [10,11]. For instance, some researchers have improved green wave bandwidth through the coordinated control of multiple intersections [12,13]. Others have reformulated the control strategy as a multi-objective optimization problem, integrating indicators such as delay, queue length, and environmental pollution for global optimization [14,15]. However, most models in this category rely on mixed-integer programming, whose computational complexity, solution time, and implementation difficulty increase substantially with the size of the control region. As a result, these methods perform well at small scales but become impractical for large-scale real road networks due to the exponentially growing computational demands [16].

Distributed control strategies are highly scalable. Among them, the distributed reinforcement learning framework achieves coordination through information sharing and cooperation among local agents [17,18]. Many researchers have formulated traffic signal control problems into reinforcement learning problems [19,20]. Since reinforcement learning typically selects the strategy with the highest reward value based on the current state, it requires the estimation of reward values for all possible actions for the subsequent step. To address this challenge, several researchers have combined reinforcement learning with neural networks to improve the learning efficiency and achieve better control results [16,21,22]. Moreover, under variable traffic conditions, this combined approach consistently yields robust and effective control results [23,24].

Another representative distributed control strategy is the maximum pressure (MP) algorithm. In the maximum pressure signal control algorithm, the pressure value is primarily used to quantify the traffic demand of each phase at an intersection. A higher traffic demand in a given phase corresponds to a higher pressure value. To effectively accommodate the phase with the greatest traffic demand, the control strategy prioritizes activating the phase with the maximum pressure, thereby improving the overall traffic flow efficiency. This algorithm was first applied to signalized intersection networks by Varaiya [25], who proposed a maximum pressure control model. The MP algorithm models the evolution of the traffic flow on each road section and determines the next signal phase at each intersection based on the queue lengths on the upstream and downstream sections. It calculates a pressure value by considering the difference between these queue lengths, incorporating turn rate information, and then summing the pressure values for all road sections associated with each phase, ultimately activating the phase with the highest total pressure. Furthermore, unlike classical control algorithms such as SCATS [26] and SCOOT [27], the MP algorithm ensures the stability of the regional traffic operations without requiring prior traffic demand information.

Although the traditional MP signal control strategy exhibits many ideal features, its reliance on strong assumptions, such as an unlimited link capacity and the absence of switching loss time, limits its applicability in real road networks. In addition, this strategy may not optimize key performance indicators such as delay, throughput, and travel time.

To overcome these limitations while preserving the excellent features of the MP control strategy, many scholars have proposed various improvement strategies. Kouvelas et al. [28] and Wei et al. [29] proposed a computational method that uses the ratio of the actual queue length and the section length, rather than the raw queue length, to address the assumption of unlimited queue capacity. Their results demonstrated that the proposed control strategy effectively improves throughout while accounting for capacity constraints. Xiao et al. [30] integrated a pressure release principle into the traditional MP control strategy to account for limited queue capacity constraints, demonstrating that the improved strategy maintains the stability of road network operations under these conditions. Gregoire et al. [31] normalized the pressure values while retaining the core concept and their simulations showed that this modification effectively reduces congestion probability. Li et al. [32] developed an MP control strategy based on a first-order continuous traffic model, demonstrating notable advantages in reducing delay, mitigating congestion propagation, and enhancing congestion recovery. To address regional congestion in urban traffic networks, Liu et al. [33] proposed the N-MP (network-state-based MP) algorithm, which integrates regional traffic states and perimeter control into the MP framework. Xu et al. [34] introduced the Smoothing-MP algorithm, which incorporates signal coordination into the MP control strategy to reduce delays while maintaining stability.

The traditional MP control strategy relies solely on pressure differences for phase switching. However, this approach may lead to the selection of phases with minimal traffic demand, resulting in excessive waiting times. To address this issue, Le et al. [35] used a cyclic phase structure. Similarly, Levin et al. [36] and others introduced signal cycle constraints, ensuring that each phase is activated at least once per cycle, and imposed a maximum signal duration limit. Experimental results confirmed the stability of these modifications. Furthermore, recognizing that obtaining accurate queue length data in real road networks is complex, researchers have proposed MP control strategies that compute the pressure value based on alternative traffic parameters, such as delays [37,38] and travel time [39,40].

Traffic signal phase switching loss time refers to the interval during which the signal transitions from one phase to another, an essential aspect of phase timing in real road networks. The strong assumption of zero switching loss time in the traditional MP control strategy limits its practical application and may prevent it from maximizing throughput. In response, Lioris et al. [41] proposed a control method that incorporates phase switching loss time, with simulation results verifying its effectiveness. Additionally, Levin et al. [36] developed an MP strategy based on fixed cyclic phases that accounts for switching losses and demonstrates maximum stability. Moreover, Wang et al. [42] introduced an MP control strategy based on a reinforcement learning algorithm that considers phase switching loss time. Simulations showed that this approach outperforms the traditional MP strategies proposed by other researchers. Figure 1 outlines the overall approaches to regional traffic signal control, and

Table 1. A summary of MP variants.

Title of Study	Pressure Calculation	Specificities	Inadequate
Original MP [25]	Instant queue length	Maximum stability	Infinite link capacity; Zero fixed phase sequence; Zero switching loss time
Improved MP [28]	Instant queue length	Link capacity limit	Zero switching loss time
Fixed cycle length [35]	Instant queue length	Maximum stability; fixed phase sequence	Infinite link capacity; Zero switching loss time
Based on travel time [39]	Normalized travel time during a cycle	Normalized travel time	Infinite link capacity
Based on delay [38]	Delay of stopped vehicle	Maximum stability	Zero switching loss time
Considering phase switching loss [42]	Real-time traffic density	Considering switching loss	No fixed phase sequence

summarizes these MP variants.

In this paper, we propose an enhanced MP control strategy that incorporates phase switching loss time and utilizes dynamic traffic state information to optimize traffic signal control. By accounting for phase switching loss time, a critical factor in real road network operations, we adopt an acyclic phase-switching sequence that significantly improves network throughput. We compare our proposed MP control strategy with both the traditional MP control strategy and fixed-time control strategy using simulation examples that evaluate key performance metrics, including average delay, throughput, and queue length. The simulation results demonstrate that our improved MP control strategy reduces wasting time, shortens queue lengths at inlets, and increases throughput compared with the traditional MP approach. The significance of this research lies in addressing the phase switching loss time, which cannot be overlooked in real road networks. Most existing MP control strategies fail to fully account for this loss time, which significantly impacts traffic flow. By incorporating phase switching loss time and dynamic traffic state information, the proposed improved strategy offers a more accurate reflection of road network conditions, enhancing the precision and applicability of traffic signal control. This study not only contributes to optimized traffic signal controls, delay reduction, and throughput improvement but also provides novel insights and methodologies for real-world traffic signal control, offering both theoretical and practical value. These improvements translate into lower fuel usage, reduced emissions, and enhanced overall system resilience, supporting environmental sustainability goals and improving long-term road network performance under growing traffic demand.

The rest of this paper is organized as follows. Section 2 describes the conventional MP control strategy and the proposed MP strategy with phase switching loss time. Section 3 and Section 4 present simulation results for road networks, while Section 5 presents results from real road networks. Finally, Section 5 summarizes current and future research directions.

2. Max-Pressure Controller Considering the Phase Switching Loss

The max-pressure (MP) strategy, first proposed by Varaiya [25], has been recognized as an optimal decentralized method for traffic signal control at intersections due to its stability under varying traffic conditions. Implementing the MP control strategy does not require prior knowledge of traffic demand but relies solely on real-time information regarding the number of queuing vehicles and the turning rates within each lane.

However, traditional MP approaches face challenges when applied to road networks with intersections characterized by uneven traffic demand across inlet lanes. To address this, this paper proposes an innovative maximum pressure control algorithm that explicitly accounts for the loss time associated with phase switching.

Firstly, an improved phase pressure calculation method is designed to explicitly accommodate the varied traffic demands across different inlet lanes. Traditional phase pressure approaches typically assign equal priority to lanes without fully considering the uneven traffic distribution. In contrast, the proposed improved method calculates phase pressure values by directly considering real-time queuing vehicle numbers and their specific turning proportions in each lane, allowing for a more responsive and lane-specific control strategy. Secondly, a phase protection mechanism is introduced to reduce unnecessary phase switching and minimize associated time losses. Specifically, if the pressure of an alternative phase is only marginally higher than that of the current phase, switching may not be beneficial due to the time cost incurred. In such cases, the phase protection mechanism temporarily amplifies the pressure value of the current phase, preventing frequent switches triggered by small pressure differences. This preserves operational stability and enhances control efficiency. Finally, to effectively implement the phase protection strategy, a dynamic phase extension calculation method is proposed. This approach dynamically determines the appropriate extension time for the current protected phase based on the real-time demand of upstream and downstream lanes. This adaptive mechanism ensures that green phase durations are flexibly adjusted to match actual traffic conditions, effectively reducing unnecessary switches while addressing lane-specific traffic demands. Consequently, the overall efficiency and reliability of the intersection signal control strategy are enhanced.

2.1. Traditional MP Model

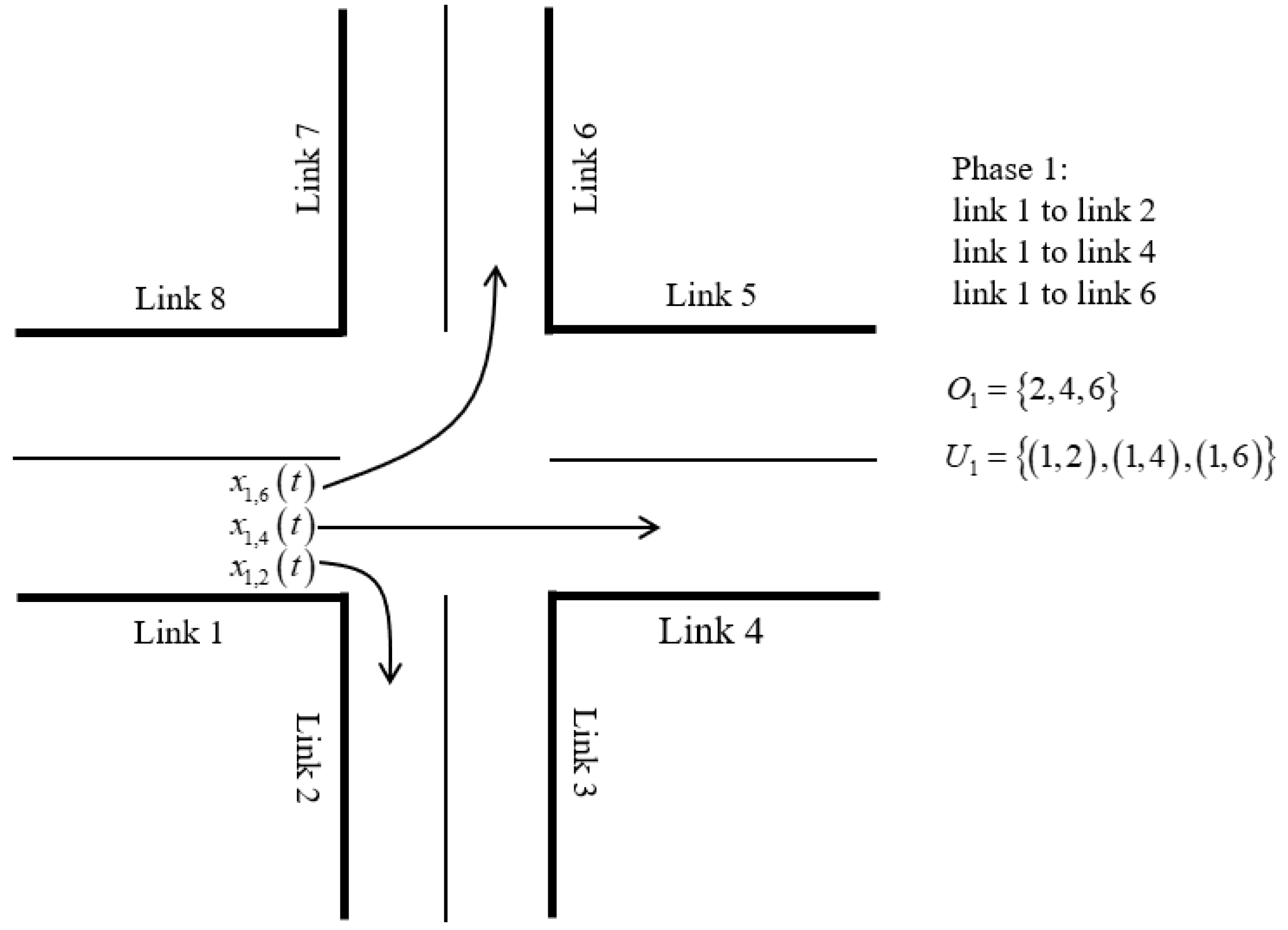
The traditional max-pressure (MP) control model, introduced by Varaiya [25], is a decentralized signal control method designed to optimize traffic flow at intersections within a road network. Its fundamental principle is to select the next activated phase by assessing the difference between the number of vehicles or queue lengths in the inlet and exit lanes. Specifically, this method aims to maximize the intersection throughput by activating the phase that has the largest potential to reduce congestion based on real-time queue conditions (Figure 2).

To formalize this concept, let the queue length at link $l$ with destination $m$ at time $t$ be represented by $x_{l,m}\left(t\right)$, which is used to calculate the weight of movement from link $l$ to link $m$. $C_{l,m}\left(t\right)$ denotes the saturation flow, which represents the maximum number of vehicles that can potentially depart from link $l$ to link $m$. The parameter $r_{l,m}\left(t\right)$ represents the turning ratio from link $l$ to link $m$. The set $O_l$ denotes all the downstream links of link $l$. $U_j$ denotes the set of all pairs of upstream and downstream links that have right of way during the phase $j$. The form of the weight value of movement from link $l$ to link $m$ at time $t$ $w_{l,m}\left(t\right)$ can be expressed as Equation (1). The form of the pressure of phase $j$ at time $t$ $p\left(S_j\right)\left(t\right)$ can be expressed as Equation (2).

$$w_{l,m}\left(t\right)=x_{l,m}\left(t\right)-{\displaystyle \sum _{n\in O_m}{x}_{l,m}\left(t\right)r_{m,n}\left(t\right)}$$

(1)

$$p\left(S_j\right)\left(t\right)={\displaystyle \sum _{\left(l,m\right)\in U_j}{C}_{l,m}\left(t\right)w_{l,m}\left(t\right)}$$

(2)

When the control algorithm determines the need for a phase switch at time $t$, the pressure values of all candidate phases at the intersection are compared. The control algorithm selects the phase $S^{*}\left(t\right)$ with the highest pressure. The form of the $S^{*}\left(t\right)$ can be expressed as Equation (3).

$$S^{*}\left(t\right)=\arg \underset{j}{\max }p\left(S_j\right)\left(t\right)$$

(3)

Ultimately, the decision to either extend the current phase or activate the next phase is made by directly comparing the pressure values between the currently active phase and the phase with the maximum calculated pressure. If the current phase has the maximum pressure, it will continue with an extension; otherwise, the intersection transitions to the new phase with higher priority, thus systematically optimizing intersection throughput and minimizing delays.

2.2. MP Model Considering Phase Switching Loss Time

The traditional MP signal control model determines whether to extend the current green phase or activate the next phase by calculating and comparing the pressure values of each phase within the intersection. However, this traditional MP control strategy does not account for phase switching loss time, which can limit its effectiveness in improving intersection traffic efficiency.

To address this limitation, this paper modifies the pressure calculation by selecting the maximum pressure from each inlet lane within a phase, ensuring that road sections experiencing high traffic demand are prioritized.

Additionally, the proposed strategy dynamically adjusts the phase extension time based on the pressure of the current phase rather than using a fixed extension period. These modifications specifically target intersections characterized by significant variations in traffic demand. Compared with the traditional MP approach, the proposed method effectively reduces the frequency of phase switching, thus minimizing the total loss time. An example of the loss time associated with phase switching is illustrated in Figure 3. In Figure 3, The green section represents the duration of the green light, the red section represents the duration of the red light, and the yellow section represents the duration of the yellow light.

The control process in this section is as follows. The form of the weight value of movement from link $l$ to link $m$ at time $t$ $w_{l,m}\left(t\right)$ can be expressed as Equation (4). The form of the pressure of phase $j$ at time $t$ $p\left(S_j\right)\left(t\right)$ can be expressed as Equation (5).

$$w_{l,m}\left(t\right)=x_{l,m}\left(t\right)-{\displaystyle \sum _{n\in O_m}{x}_{l,m}\left(t\right)r_{m,n}\left(t\right)}$$

(4)

$$p\left(S_j\right)\left(t\right)=\underset{\left(l,m\right)\in U_j}{\max }{C}_{l,m}\left(t\right)w_{l,m}\left(t\right)$$

(5)

When the control algorithm determines the need for a phase switch at time $t$, the pressure values of all candidate phases at the intersection are compared. The control algorithm selects the phase $S^{*}\left(t\right)$ with the highest pressure. The form of the $S^{*}\left(t\right)$ can be expressed as Equation (6).

$$S^{*}\left(t\right)=\arg \underset{j}{\max }p\left(S_j\right)\left(t\right)$$

(6)

To avoid the issue of frequent phase switching, this paper proposes a current-phase protection strategy. This strategy involves temporarily increasing the pressure value of the current phase, thus reducing unnecessary phase switching. Specifically, the current-phase pressure is multiplied by an amplification factor, enabling the current phase to have priority in maintaining a green signal if its amplified pressure exceeds that of other phases. The detailed control strategy $D$ is shown in Equation (7).

$$D=\left\{\begin{array}{l}\mathrm{extend}\mathrm{time}{t}_{extend},S^{*}\left(t\right)=S_{now}\left(t\right)\\ \mathrm{extend}\mathrm{time}{t}_{extend},S^{*}\left(t\right)\ne S_{now}\left(t\right),\left(1+k\right)p\left(S_{now}\left(t\right)\right)\ge \underset{j}{\max }p\left(S_j\right)\left(t\right)\\ \mathrm{activate}\mathrm{next}\mathrm{phase},S^{*}\left(t\right)\ne S_{now}\left(t\right),\left(1+k\right)p\left(S_{now}\left(t\right)\right)<\underset{j}{\max }p\left(S_j\right)\left(t\right)\end{array}\right.$$

(7)

where $S_{now}\left(t\right)$ denotes the current phase of intersection $S$ at time $t$, $k$ is the amplification factor, and $p\left(S_{now}\left(t\right)\right)$ denotes the pressure value of phase $S_{now}\left(t\right)$.

Under this strategy, if the current phase initially has the maximum pressure value, it continues to extend. If it does not, its pressure value is multiplied by an amplification factor. If the resulting amplified pressure surpasses the current maximum pressure, the current-phase duration is extended; otherwise, the intersection switches to the next phase.

In the traditional MP control strategy, the signal extension time is set to a fixed value. Selecting an excessively long extension time leads to wasted green light time during periods of low traffic demand, reducing overall efficiency. Conversely, if the extension time is too short, frequent phase switching may occur during periods of high traffic demand, increasing signal loss time and vehicle delays. Therefore, it is essential to adjust the green light extension time dynamically, allowing the signal timing to effectively match real-time traffic conditions and ensure efficient use of intersection capacity. Specifically, the extension should accommodate upstream vehicles entering downstream roadways, while preventing overflow in downstream queues.

The extension time is determined based on the maximum number of vehicles queued in the lane during the current phase $j$. The specific expression for calculating the control duration is as follows:

$$t_{extend}=\underset{\left(l,m\right)\in U_j}{\min }\left\{\underset{l}{\max }\left\{{\displaystyle \frac{N_l}{C_l}}+t_{loss}\right\},\underset{m}{\min }\left\{\left({\displaystyle \frac{L_m}{\left(L_v+d_v\right)}}-N_m\right)/C_m\right\}\right\}$$

where $N_l$ denotes the number of stops on the link $l$. $C_l$ denotes the saturation flow, which represents the maximum number of vehicles that can potentially depart from link $l$, the general value is 1800 veh/h, which is selected based on the characteristics of the simulated link in this study. $t_{loss}$ denotes the vehicles’ start-up loss time. $L_m$ denotes the length of link $m$. $L_v$ denotes the length of the vehicle, the general value is 5 m, which is based on the default configuration in SUMO 1.17.0. $d_v$ denotes the safe distance between two vehicles, with a general value of 1 m, representing the minimum spacing maintained to avoid collisions.

The first term represents the time required for all vehicles stopped in the inlet lane of the current phase to clear that lane, specifically indicating the duration needed for upstream vehicles to pass through the intersection. The second term accounts for the capacity limitations of the downstream roadway, ensuring that vehicles entering from upstream do not result in overflow downstream. Therefore, the complete equation accurately determines the minimum necessary time to allow all upstream queued vehicles to enter the downstream road segment while simultaneously preventing overflow in the downstream section.

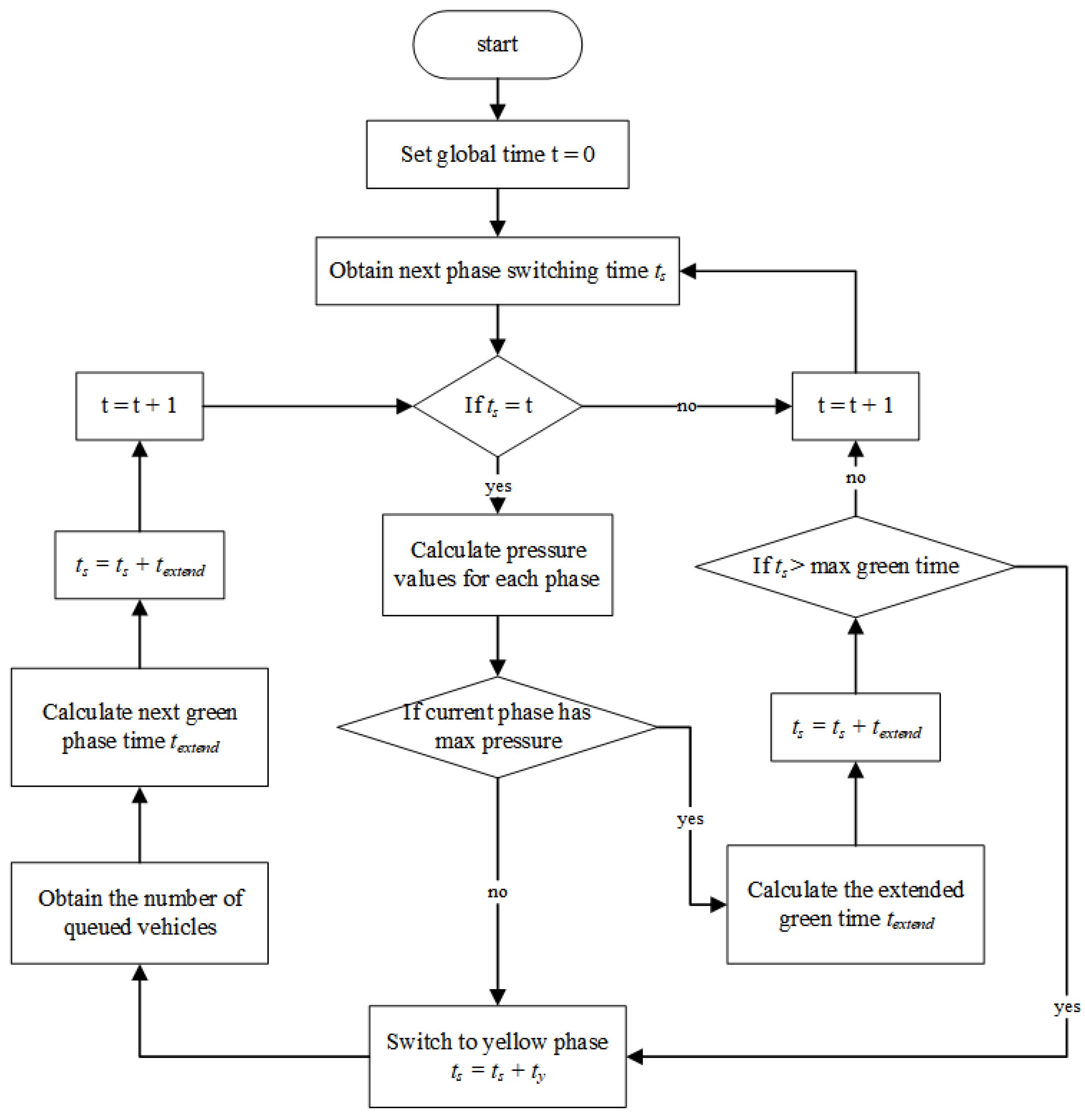
Figure 4 illustrates the flowchart of the proposed control strategy. In Figure 4, $t_y$ represents the duration of the yellow light phase, which corresponds to the lost time during phase switching; $t_s$ denotes the scheduled switching time of a specific phase; and $t$ refers to the current simulation time.

3. Simulation Experiment

In this paper, a 4 × 4 regional road network is simulated to represent typical urban traffic conditions. The network consists of 16 signalized intersections arranged in a grid layout, as illustrated in Figure 5. Each road segment within this network is uniformly designed with a length of 600 m to ensure consistency in travel distances across the grid. Additionally, each road segment comprises three lanes: one dedicated left-turn lane, one straight-only lane, and one lane that accommodates both straight and right-turn movements. This configuration is chosen to realistically reflect common lane distributions at urban intersections, where dedicated left-turn lanes help mitigate turning conflicts, and combined straight-right lanes facilitate traffic flow and reduce lane-changing behaviors. Moreover, the uniform length and structured arrangement simplify the comparison of traffic performance metrics across intersections and enable a clear analysis of network-wide traffic dynamics.

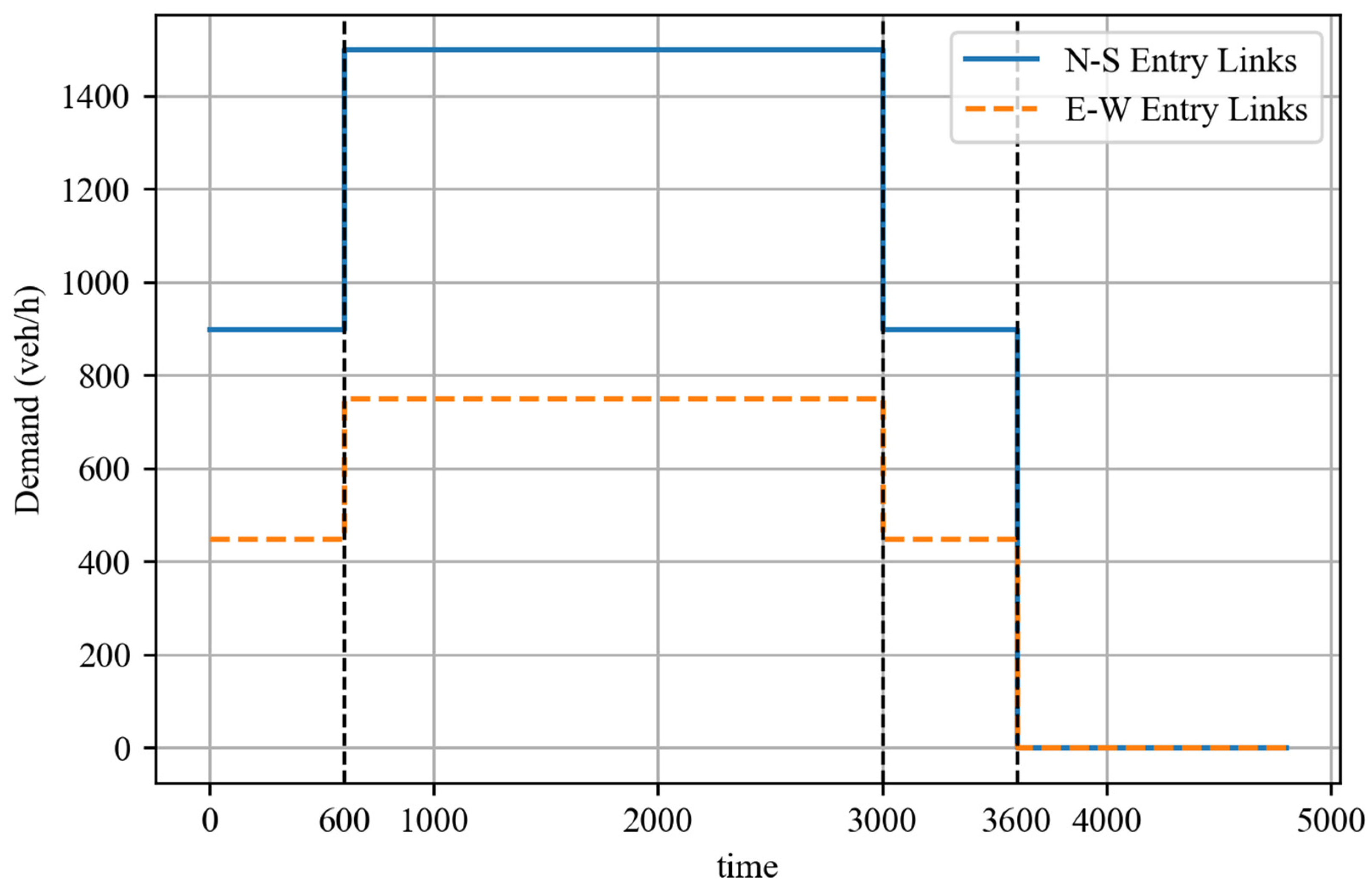
Where the turning rate of each internal road is 0.2 (left), 0.6 (straight), and 0.2 (right), the maximum speed of all roads is set to 20 m/s, and the IDM follow-the-leader model and MOBIL lane change model are used by default. The flow rate of the north and south inlet roads is twice that of the east and west inlet roads, where the flow rate inputs are shown in Figure 6. The average flow rate of the north and south inlet roads is 1300 veh/h, and the average flow rate of the east and west inlet roads is 650 veh/h. Two demand profiles are considered in the simulation period: the first 10 min and 50 to 60 min represent periods of lower traffic demand, 10 to 50 min represents a period of higher traffic demand, and finally, the flow inputs are stopped until the vehicles inside the road network are completely cleared from the road network. Ten different traffic demands were generated using random seeds for subsequent simulations to eliminate the effect of chance. The black dashed lines represent the time points of flow changes.

The turning proportions for each internal road segment are set at 0.2 for left turns, 0.6 for straight movements, and 0.2 for right turns. The maximum allowable speed for all road segments is uniformly set at 20 m/s. However, due to signal delays, vehicle interactions, and acceleration/deceleration, the actual operating speeds mostly fall within 14–16 m/s. Additionally, the Intelligent Driver Model (IDM) is adopted for longitudinal vehicle-following behavior, while the MOBIL model is employed for lateral lane-changing maneuvers.

Traffic flow at the network boundaries is differentiated by direction, as depicted in Figure 5. Specifically, the flow rates of the north and south inlet roads (average 1300 veh/h) are set to twice that of the east and west inlet roads (average 650 veh/h). For the east–west approaches, the flow rate was set to half that of the main north–south artery to reflect an imbalanced traffic demand scenario. This configuration enables a more meaningful evaluation of signal control strategies under uneven traffic loading conditions. To simulate varying traffic conditions, two distinct demand periods are defined within the simulation timeframe: a low-demand period spanning the first 10 min and the final 10 min (50–60 min), and a high-demand period lasting from 10 to 50 min. Following the final low-demand period, vehicle inflow is halted, and the simulation continues until all vehicles have exited the network entirely. To mitigate randomness and ensure robustness of the results, ten different traffic demand scenarios are generated using unique random seeds, which reduces the influence of stochastic variations on the simulation outcomes.

In this study, all data were derived from simulation experiments and are not based on real-world field data. Specifically, the traffic flow, signal control schemes, and other parameters used in the simulation were developed based on the traffic characteristics of typical urban arterials, with reference to the relevant literature. Therefore, the results reflect the traffic flow and control effects under simulated conditions and do not represent actual field data or real-world traffic scenarios. The traffic flow input and road network configuration were primarily developed with reference to the work of Liu and Gayah [38], which provides a representative model of urban arterial traffic characteristics.

Based on the left-turn, straight, and right-turn flows into the intersection, the duration of the green light allocation for each phase is calculated with the help of Webster’s signal timing method. In this case, a 3 s yellow light phase is used when the two phases are switched.

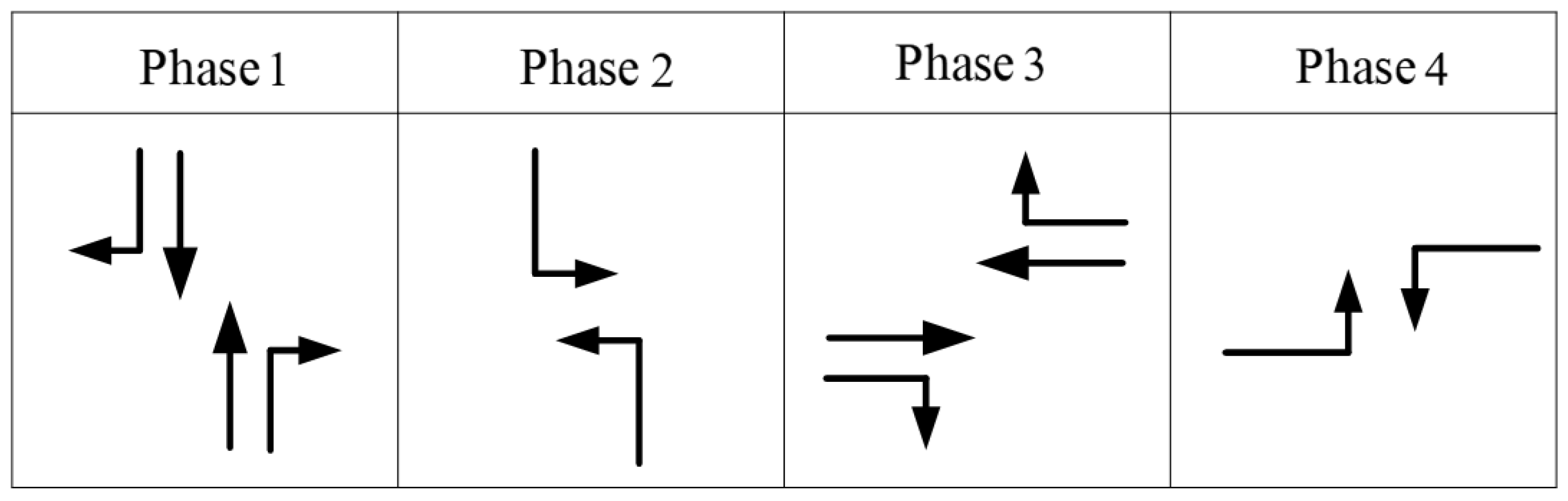
In traffic signal control, a phase refers to a period during which a specific set of non-conflicting traffic movements at an intersection is given the right-of-way. The division of intersection phases applied in this study is illustrated in Figure 7. The intersection adopts a four-phase signal control scheme. Phase 1 serves North–South through and right-turn movements; phase 2 serves North–South left-turn movements; phase 3 serves East–West through and right-turn movements; and phase 4 serves East–West left-turn movements.

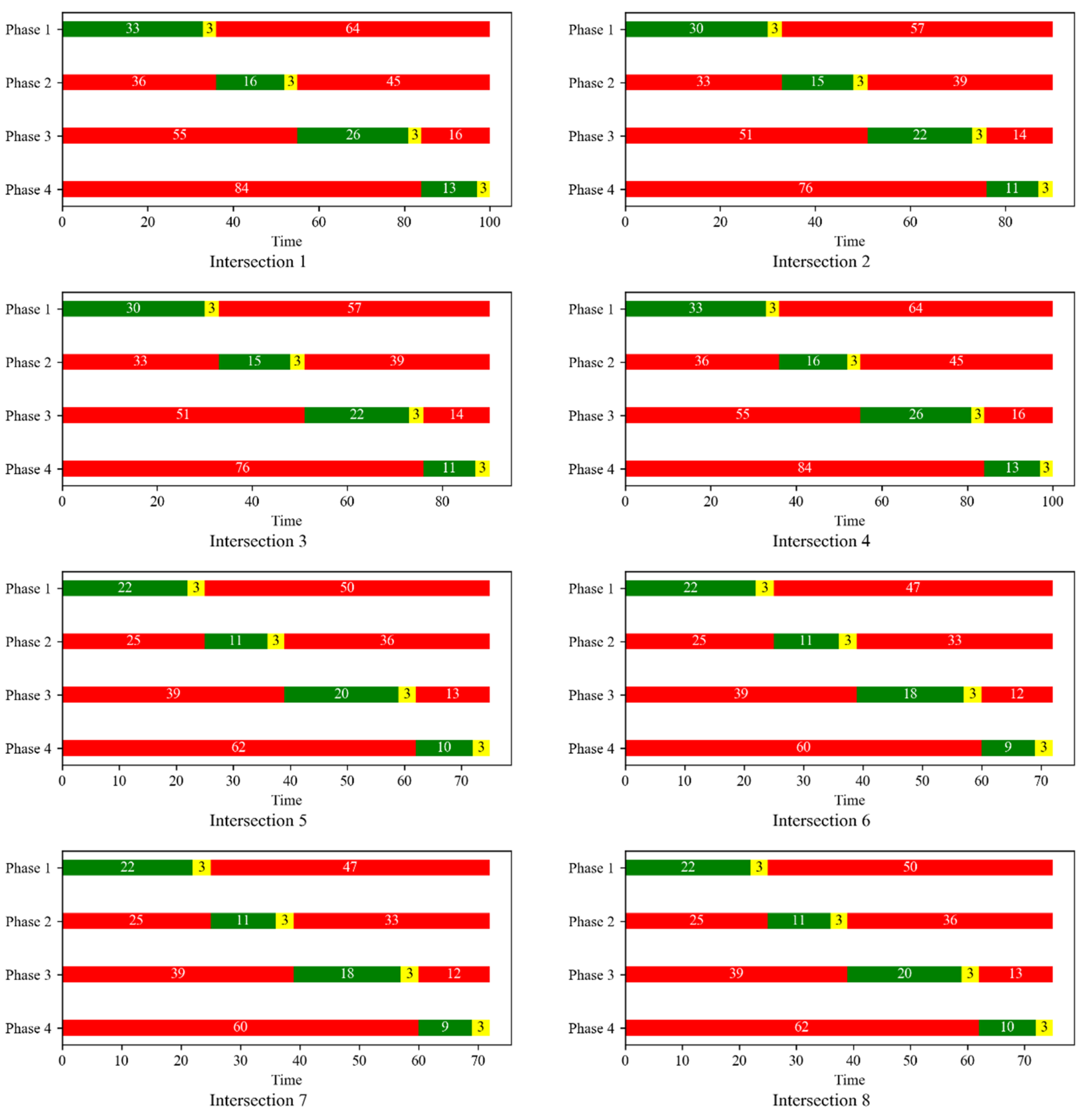
The phase distribution time at each intersection is shown in Figure 8.

In Figure 8, the phase distribution for each intersection is presented based on simulation data. All timing is referenced to the starting point of the first green phase at intersection 1, which also marks the beginning of the simulation. The phase sequences at all intersections follow a fixed cycle, beginning simultaneously at the simulation start time. This ensures consistent temporal alignment across intersections during the first and subsequent cycles. Additionally, the intersection labels in the subplots of Figure 8 correspond to the intersection nodes in Figure 5. In Figure 8, Red, green, and yellow represent the duration of the red, green, and yellow light phases, respectively.

To ensure the reproducibility of the simulation results, the following key simulation parameters are summarized: The simulation was conducted using SUMO, with a network consisting of 16 signalized intersections, spaced 600 m apart along the main arterial road. All vehicles are set as passenger cars, which is the default setting in SUMO. The maximum speed was set to 20 m/s. The simulation duration was 5400 s, and the traffic demand was set at 1300 veh/h for the main arterial road and 650 veh/h for the secondary roads, reflecting an imbalanced demand scenario. All intersections were equipped with three-lane approaches, consisting of left-turn, through, and through and right-turn lanes.

Regarding signal control strategies, the Webster timing plan was used for the timed control strategy to calculate signal timings. In the MP signal control scheme, the minimum green signal time was set to 20 s, the maximum green signal time to 70 s, and the control step size was set to 10 s. Vehicle routes were randomly assigned based on the turning rates at each intersection.

4. Results

Using the road network and traffic conditions described above, this study compares the performance of four signal control strategies: timed control, traditional MP signal control, travel time-based MP signal control, and the signal control method proposed in this paper. The travel time-based time MP signal control method improves upon the traditional MP control approach by modifying the pressure calculation mechanism. Specifically, it utilizes the travel time on each link as a measure of link pressure, rather than relying on the traditional pressure calculation. The evaluation criteria include internal delays, the number of vehicles experiencing congestion, and network throughput. The results of 10 simulation runs are plotted and analyzed, focusing on the maximum, minimum, and average values obtained.

The simulation duration is 90 min, divided into four distinct stages reflecting varying traffic demands. Traffic demand is low during the first and third stages, while it peaks during the second stage. In the final (fourth) stage, vehicle entry into the network ceases completely, allowing sufficient time for all vehicles already in the system to exit the road network. This staged approach ensures a clear evaluation of each signal control strategy’s effectiveness under fluctuating demand scenarios.

4.1. Delays on Internal Road Sections at Various Times

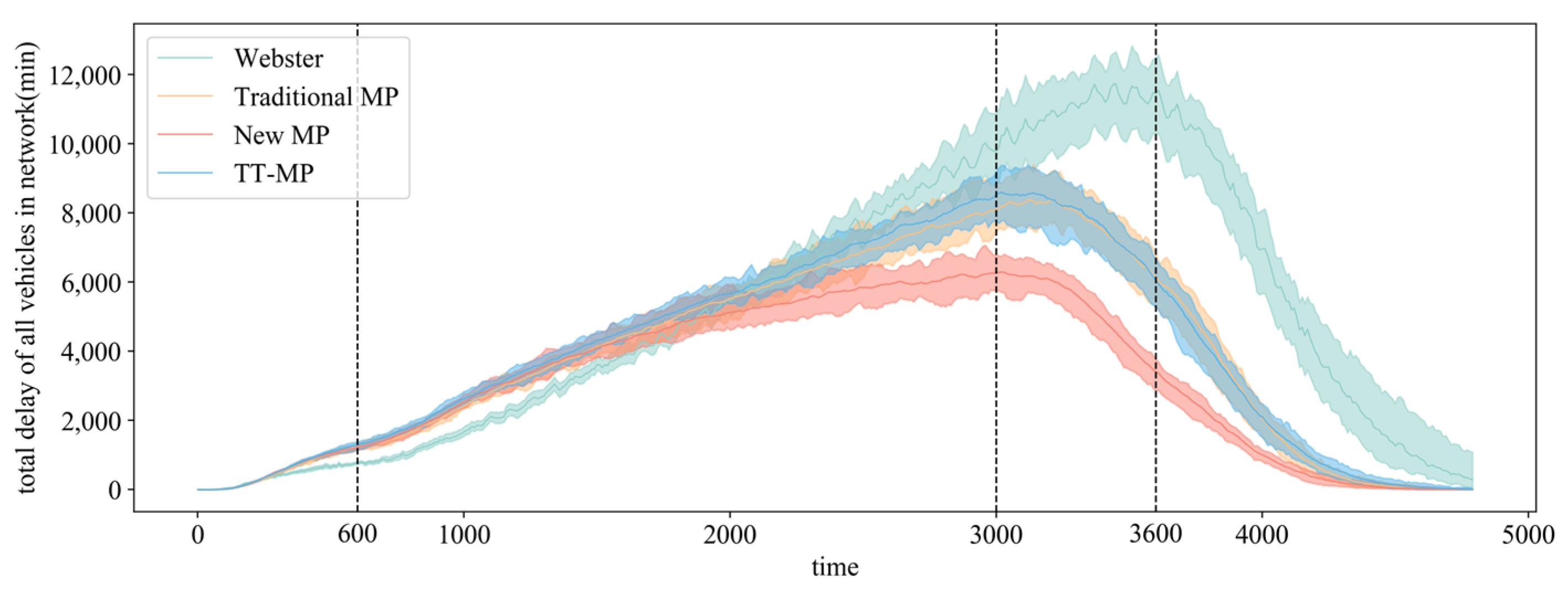
Figure 9 compares the total internal delays experienced by vehicles under the four different signal control strategies. Internal network delay is defined as the cumulative delay vehicles experience after entering the road network. The black dashed lines represent the time points of flow changes.

The results indicate that under the conditions of low traffic volume, the timed control strategy results in relatively small delays. However, as the number of vehicles entering the road network increases, the MP control strategy proposed in this study becomes more effective at reducing internal network delays. The control performance of travel time MP (TT-MP) is relatively close to that of the traditional MP, mainly because the TT on the link is primarily determined by the flow and capacity of the link. It is important to note that the comparatively low total delay observed across all strategies during periods of lower traffic demand may primarily result from the smaller number of vehicles present within the network. This suggests that the MP signal control strategy proposed in this paper is better suited to handling scenarios with higher traffic volumes within the road network.

When the total internal delay within the road network is high, specifically during the 3000–3600 s period of the simulation, the MP signal control method proposed in this study is more effective than other control methods in reducing internal delays, keeping the maximum total internal delay within the road network at a relatively low level.

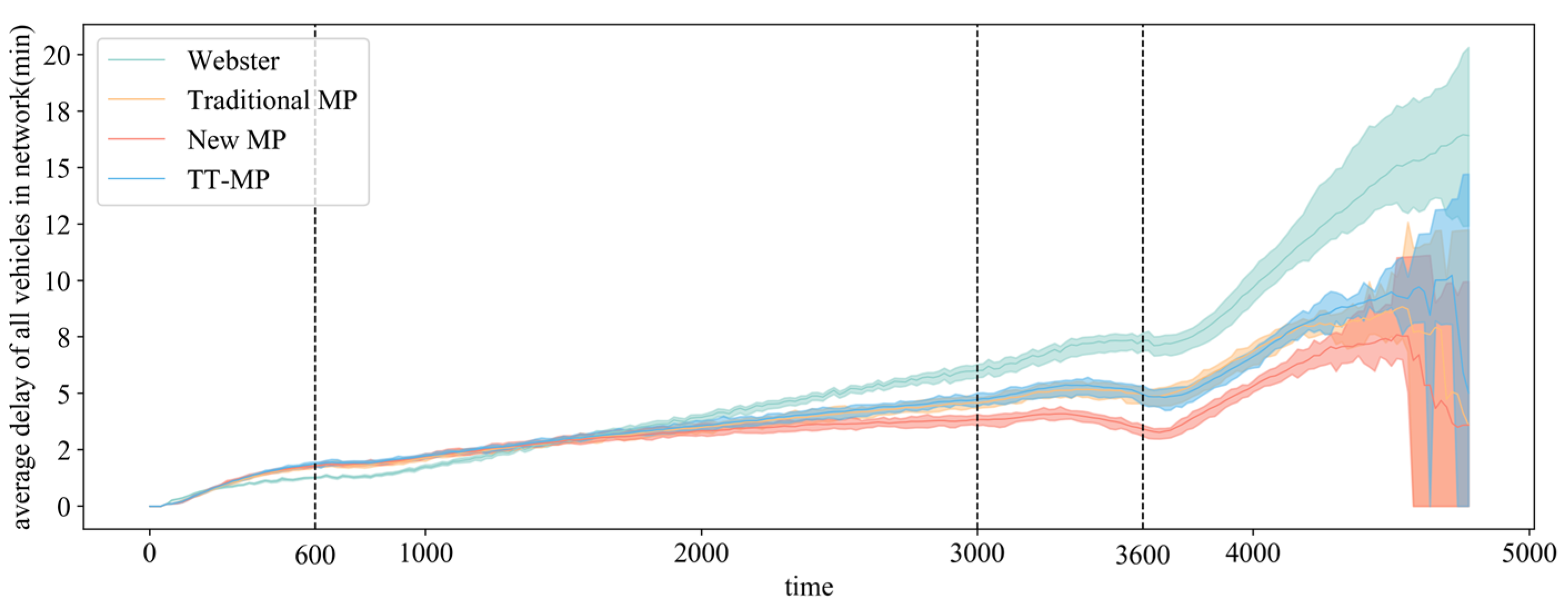
To eliminate the influence of variations in vehicle volumes on total delay, the average delay per vehicle within the road network is further analyzed. The calculated average delays under the different signal control strategies are presented in Figure 10. The black dashed lines represent the time points of flow changes.

The results show that when vehicle volumes are low, the proposed MP control strategy performs slightly worse than the timed control strategy in terms of average vehicle delay. However, as traffic volume increases, the MP control strategy proposed in this paper becomes more effective in reducing average delays within the road network.

As shown in Figure 10, during the 3000–3600 s period of the simulation, the MP signal control method proposed in this study maintains a lower average vehicle delay within the road network compared with other control methods. After the 4000 s mark of the simulation, the average delay increases across all control methods, which may be attributed to the decrease in the number of vehicles within the network. As the number of vehicles decreases, the average delay becomes more influenced by the delay of individual vehicles. When only a few vehicles remain in the network, the average delay is determined by the total delay of those individual vehicles, leading to an apparent increase in the average delay value.

4.2. Entry and Exit Flows of the Road Network

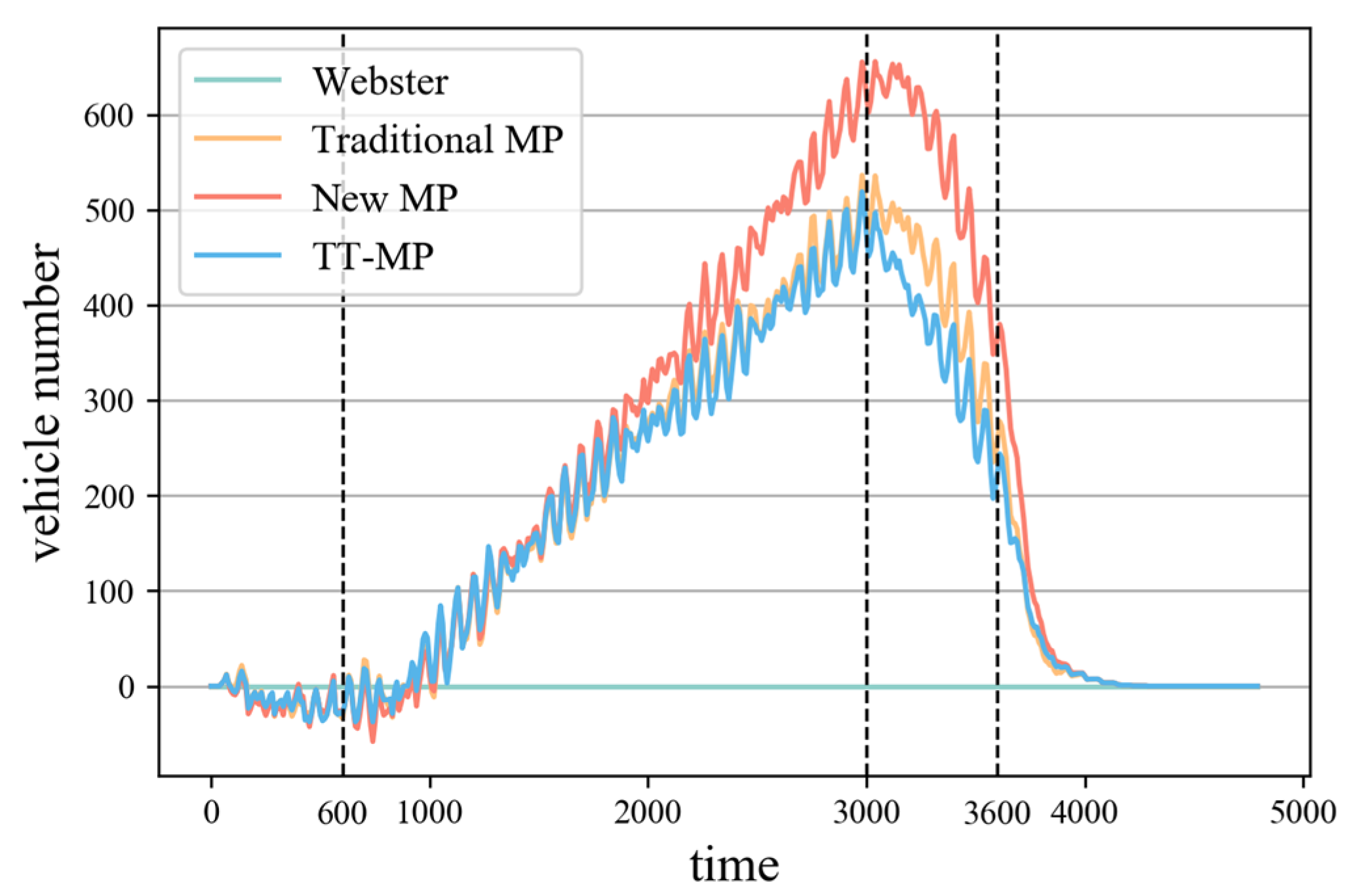
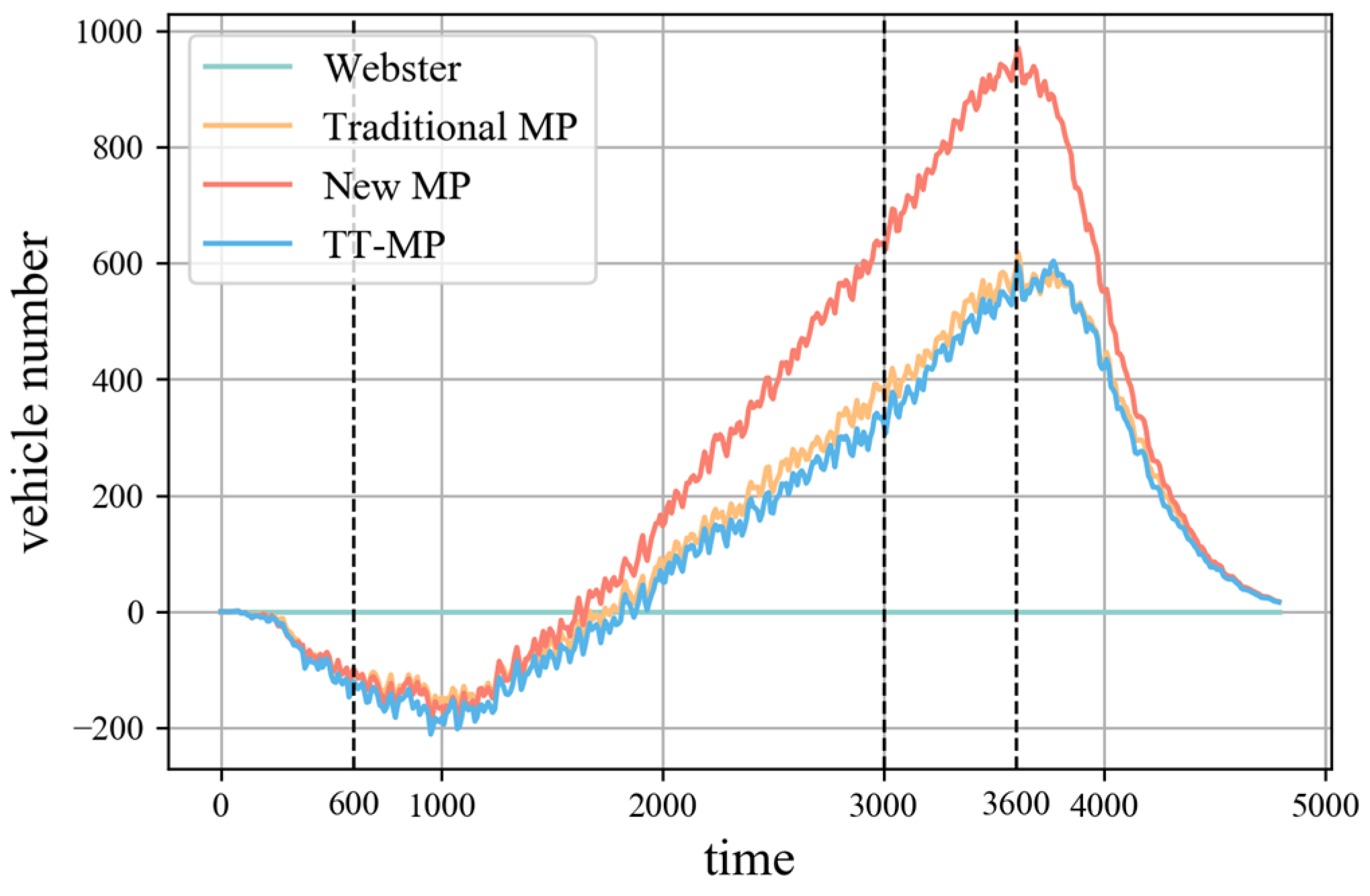
Figure 11 and Figure 12 represent the traffic flow into and out of the road network at each moment, respectively, based on the traffic flow into and out of the road network under timed control. The result is the differences in traffic inflow and outflow volumes across the entire road network under various control strategies, relative to those observed under Webster-timed control. The results show that when the traffic demand is low, the original maximum pressure signal control leads to lower control accuracy if the phase extension time is too long due to the setting of the phase extension time, which in turn makes the drive-in and drive-out traffic flow of the road network lower. Additionally, if the phase extension time is too short, it leads to frequent phase switching, and the ratio of the yellow light duration to the total cycle increases, which in turn makes the delay increase. The control performance of TT-MP is similar to that of the traditional MP strategy, and it also faces issues related to phase extension time. When the traffic demand is high, the traditional maximum pressure signal control and travel time-based maximum pressure signal control can better meet the current traffic demand, so the outbound flow increases accordingly. The maximum pressure signal control proposed in this paper outperforms the timed control during the remaining periods, except that the inbound and outbound flow does not perform as well as the timed control at the beginning of the simulation. The black dashed lines represent the time points of flow changes.

Figure 11 and Figure 12 illustrate the traffic flow entering and exiting the road network at each moment under different control strategies. The results indicate that when traffic demand is low, the traditional MP signal control strategy and travel time-based MP signal control strategy encounter challenges in maintaining optimal traffic flow. Specifically, if the phase extension time is set too long, the control precision is reduced, resulting in decreased inbound and outbound traffic flow within the network. Conversely, if the phase extension time is too short, the control strategy leads to frequent phase switching, increasing the proportion of yellow light durations within each cycle and subsequently increasing delays.

Under high traffic demand, the traditional MP signal control strategy and travel time-based MP signal control strategy better adapts to prevailing traffic conditions, effectively increasing the outbound flow. Compared with timed control, the MP signal control strategy proposed in this paper achieves superior overall performance in terms of both inbound and outbound traffic flow throughout most of the simulation period. However, during the initial stage of simulation, its performance regarding inbound and outbound traffic flow is slightly lower than that of the timed control strategy.

5. Conclusions

The MP control strategy proposed in this paper introduces several key improvements. First, a new definition of phase pressure is proposed, accounting for significant disparities in traffic demand among different inlet roads within the same phase. Second, a novel green phase extension strategy is introduced, dynamically adjusting the duration of the green phase extension based on the real-time vehicle queue lengths at road intersections. Additionally, a current-phase protection mechanism is implemented by introducing an amplification factor into the calculation of current-phase pressure, effectively reducing unnecessary phase switching. Simulations conducted using SUMO demonstrate that the proposed MP control strategy outperforms both traditional MP control and fixed-time control strategies. Specifically, the proposed approach significantly reduces vehicle delays, enhances traffic throughput, and decreases congestion, particularly when accounting for time lost due to frequent phase switching. The main contribution of this paper is the proposal of a novel MP signal control method that explicitly accounts for phase switching lost time and aims to enhance the practical applicability of MP control strategies in real-world traffic networks. By optimizing traffic signal timing and reducing fuel-consuming delays, the proposed method also contributes to energy conservation and emissions reduction, aligning with the principles of sustainable urban mobility.

One limitation of the proposed MP control strategy is its variable phase-switching sequence. Although this flexibility can enhance overall network throughput, Levin et al. [36] highlighted that the variability in signal phases may lead to confusion among drivers, pedestrians, and other traffic participants. This issue significantly contributes to the limited real-world adoption of MP control strategies in urban road networks. Furthermore, the proposed strategy primarily aims to improve throughput within the internal network and does not fully address the management of traffic flow in external bottleneck areas, such as entrance nodes or upstream intersections, which can significantly influence overall network performance.

Additionally, the current study relies exclusively on simulation data from SUMO, which, despite its robustness, may differ from real-world conditions due to assumptions inherent in simulation modeling, such as the variability in driver behavior, vehicle composition, and real-time incidents. Therefore, the practical applicability of the proposed method should be validated through empirical testing in field conditions. Moreover, the effectiveness of the proposed control strategy varies with traffic demand levels. Under low-demand conditions, its performance is comparable to that of fixed-time control strategies; however, in high-demand scenarios, it significantly enhances traffic efficiency, making it more suitable for road networks characterized by heavy traffic demand. It is also important to note that with the advancement of autonomous vehicle technologies, where precise vehicle control and communication are achievable, the phase switching loss time may become negligible. In such a future context, the relevance and applicability of the proposed control strategy could be fundamentally reduced.

Future research should explore methods to reduce driver confusion caused by varying phase sequences, potentially by integrating driver assistance technologies or adaptive signage systems. In addition, the impact of intersection spacing on the effectiveness of control strategies should be further examined to enable more scientifically designed signal control schemes. Furthermore, incorporating the proposed MP control strategy with coordinated external traffic management measures, such as adaptive ramp metering, queue management at network entrances, and upstream intersection coordination, could comprehensively improve network efficiency. Lastly, comparative evaluations using real-world experimental data would provide more robust evidence to support the practical implementation of the proposed strategy.