Research on the Evolutionary Game of Rural River Governance Under the River Chief System

Abstract

The river chief system (RCS) has been progressively integrated into rural river governance, resulting in notable improvements in river environments. However, the governance involves multiple stakeholders with conflicting interests and challenges, including low efficiency in collaborative governance. Based on evolutionary game theory, this paper explores the strategy evolution mechanism of multiple stakeholders in rural river governance under the RCS. A four-party evolutionary game model is constructed, involving the government, rural river chiefs, functional organizations, and villagers. By employing phase diagrams, Jacobian matrices, and Lyapunov’s first method, we investigate the evolutionary process of the four-party game and analyze its asymptotic stability. The study identifies the following two evolutionary stable strategies: lenient supervision, no patrol, governance, and participation and lenient supervision, no patrol, governance, and non-participation. Then, numerical simulation analysis is conducted using MATLAB 2024b to validate the scientific rigor and effectiveness of the evolutionary game model and analyze the impact of key parameters’ changes on the strategy choices of each stakeholder. The findings provide guidance for improving the efficiency of multi-stakeholder collaboration in rural river governance and the smooth implementation of the RCS in rural areas.

1. Introduction

Rural environmental governance in developing countries constitutes a strategic imperative to break the self-reinforcing cycle of environmental degradation and entrenched poverty, where resource-dependent livelihoods amplify ecological vulnerabilities [1,2,3]. As the largest developing nation, China’s environmental governance challenges during its urban–rural transition exemplify systemic dilemmas faced by similar economies [4]. Notably, accelerating the integration of urban and rural systems has intensified pollution pressures in rural rivers, predominantly driven by agricultural runoff, domestic sewage, and industrial effluents [5,6,7,8]. Mitigating these multi-source pollutants has emerged as the foremost challenge in advancing rural habitat sustainability, requiring a balance between ecological conservation and developmental priorities.

Triggered by the 2007 cyanobacterial crisis in Lake Taihu, China has progressively established a river chief system (RCS) characterized by administrative–technical synergy, marking a paradigm shift in rural river governance [9]. This institutional framework designates local party government leaders as river chiefs, empowering them to coordinate water resource conservation, pollution control, and ecological remediation through territorially embedded management protocols [10]. The system has undergone technological metamorphosis, with the integration of IoT sensor networks, satellite remote sensing, and artificial intelligence catalyzing the emergence of “Smart River Chief” platforms. Such innovation has revolutionized monitoring capabilities, transitioning from manual sampling to AI-powered precision systems capable of multi-parameter, real-time surveillance. Empirical evidence demonstrates enhanced cross-departmental coordination efficiency and pollutant incident resolution accuracy through dynamic accountability mechanisms driven by real-time water quality analytics [11,12,13]. Legal institutionalization has progressed in tandem. The 2017 Water Pollution Prevention and Control Law marked the RCS’s first formal legal recognition, followed by cross-jurisdictional coordination frameworks established through the 2020 Yangtze River Protection Law and 2023 Yellow River Protection Law. However, critical legislative gaps persist; the current Water Law fails to clarify authority demarcation between basin management agencies and local river chiefs, while the River Channel Management Regulations lack specific provisions for small rural rivers. These legislative lags have effectively exacerbated rural governance fragmentation.

Globally, river governance systems exhibit diverse institutional trajectories. The European Union’s Water Framework Directive (WFD), a transboundary integrated management mechanism, has redefined multinational river governance regimes, such as the Rhine, by implementing binding ecological targets, six-year cyclical management plans, and legally mandated public consultation processes [14,15]. In contrast, China’s RCS operationalizes a vertically integrated party–state accountability model, combining grid-based spatial governance units with cadre performance evaluations to address rural river governance deficits. The divergence in governance paradigms highlights institutional path dependencies, with the WFD coordinating multi-stakeholder engagement through supranational legal frameworks and the RCS achieving policy penetration by embedding itself within existing bureaucratic hierarchies. Although the RCS enhances top–down enforcement efficacy, operational challenges persist. These include interagency coordination inefficiencies, insufficient legal grounding, and a lack of transparent oversight mechanisms, all of which reflect fragmented governance and misaligned stakeholder incentives [16,17,18,19,20,21,22,23]. Scholars have proposed multifaceted optimization strategies for the RCS, such as strengthening public participation, instituting scientific evaluation protocols, enhancing supervisory frameworks, and improving interdepartmental collaboration. To address legislative gaps, statutory reforms, such as clarifying jurisdictional boundaries, developing region-specific regulations, and codifying RCS protocols into local legislation are prioritized [24,25,26]. Additionally, current research revealed that the implementation effectiveness of the RCS varies significantly across regions, primarily attributed to uneven regional economic development and institutional environments. A notable contrast emerges between policy practices in northwestern China and the Yangtze River Delta region. In the northwest, policy diffusion followed a temporal pattern characterized by “slow development followed by rapid intensification”, with a spatial trajectory progressing from south to north [27]. In contrast, the Yangtze River Delta demonstrated sustained policy implementation effectiveness, driven by stronger economic capacity, robust cross-regional coordination mechanisms, and a well-established governance technology framework [28].

Evolutionary game theory has emerged as a pivotal analytical framework for investigating multi-agent dynamic interactions in river basin governance. Early research on cross-regional river coordination primarily focused on modeling the strategic interactions between upstream and downstream governments, systematically developing ecological compensation mechanisms [29,30,31,32,33,34,35,36,37,38,39,40]. These studies revealed that, in the absence of external constraints, both parties tend to adopt passive ecological governance strategies [41]. The finding underscores the need for central government intervention to establish incentive-compatible regulatory mechanisms that guide both parties toward optimal behavioral evolution. As governance systems have evolved toward greater stakeholder diversity, research perspectives have expanded to incorporate tripartite game theoretic models, involving government, enterprises, and the public. Numerical simulations have identified key determinants of effective river governance [42,43]. These studies have empirically validated both the dominant role of government regulation [44] and the synergistic effects of public participation [45,46] in river governance. However, a few researchers have turned their attention to rural river governance. Xu et al. developed a tripartite game model involving local governments, enterprises, and villagers, showing that compensation mechanisms protecting villagers’ rights can significantly improve rural river treatment efficiency [47]. Luo’s subsequent research confirmed these findings, demonstrating that reducing participation costs while compensating for ecological losses effectively activates endogenous drivers in rural river governance [48]. These results establish the public as key stakeholders in river governance, whose monitoring and advocacy activities significantly enhance governance effectiveness [49,50,51,52]. Yang constructed a more complex quadrilateral evolutionary game model involving two regional governments, central authorities, and the public. This work systematically elucidated the intricate relationships in transboundary river governance through cross-regional coordination mechanisms [53]. However, current research faces two major limitations. First, existing models primarily focus on urban or interprovincial basins, neglecting the complexity of governance levels for rural rivers. Second, the failure to incorporate river chiefs as independent decision makers in these models obscures their crucial bridging role in policy implementation.

The RCS has restructured the responsibility framework for rural river governance, as follows: the government, as the policy-making body, sets the strategic direction; river chiefs, as administrative leaders, oversee local supervision; and villagers participate in the governance process through daily supervision. Additionally, functional organizations are directly coordinated by river chiefs and handle specific tasks like pollution investigation and river dredging. While this multi-layered governance system strengthens administrative mobilization, divergent objectives and misaligned responsibilities among diverse stakeholders can trigger systemic conflicts. For instance, the government’s long-term ecological goals may conflict with villagers’ short-term production needs, river chiefs’ assessment pressure may not align with the executive capacity of functional organizations, and insufficient legal empowerment leads to high coordination costs across entities. Studying the evolutionary dynamics among these stakeholders is a critical breakthrough for enhancing the effectiveness of rural river governance. To address these challenges, this paper constructs a four-party evolutionary game model to examine the stable strategies among governments, rural river chiefs, functional organizations, and villagers. This analysis provides important insights for optimizing rural river governance structures, enhancing governance efficiency, and achieving sustainable development.

2. Materials and Methods

In analyzing the multi-stakeholder interest relationships in rural river governance, this study is grounded in the theoretical framework of Jiangsu Province’s RCS. As China’s institutional pioneer in implementing the RCS, Jiangsu Province exhibits a complete policy evolution trajectory, a high village-level river governance coverage rate, and a well-developed institutional system, collectively providing a robust foundation for identifying critical interest dynamics. While rooted in this context, the developed evolutionary game model abstracts core governance mechanisms through the following four key stakeholder interactions: government regulation, enforcement, organizational coordination, and villager participation. This ensures analytical validity for rural regions with hierarchical governance frameworks when locally calibrated.

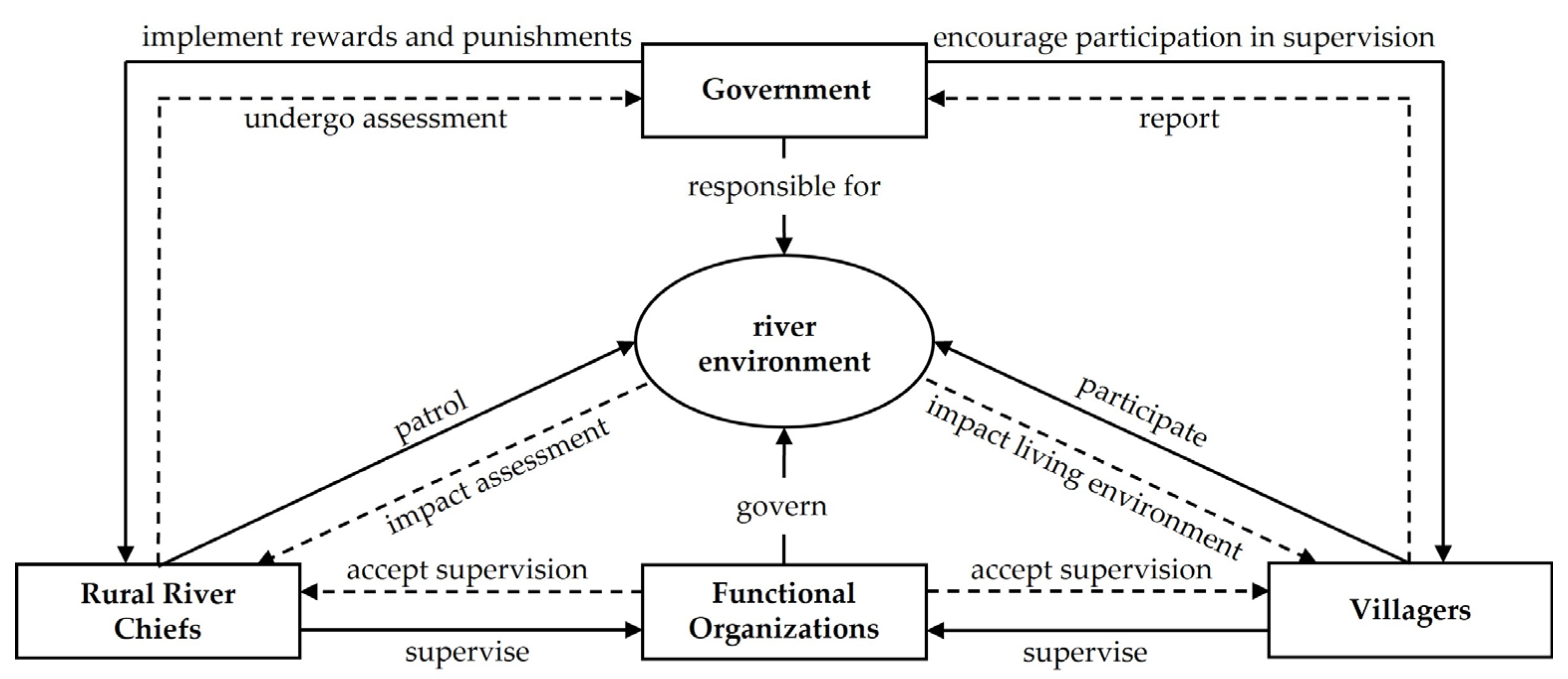
2.1. Stakeholders and Strategies

2.1.1. Government

The government plays the central role in coordinating rural river governance, with its decision making primarily driven by the objective of building an ecologically harmonious society. This distinctive public service orientation sets the government apart from other stakeholders focused exclusively on profit maximization. In practice, the government operates both as a regulatory manager and an active participant, ensuring the smooth implementation of governance efforts. To oversee river chiefs, the government conducts performance evaluations based on environmental criteria assessed through regular inspections. Top-performing river chiefs receive rewards; whereas, those failing to meet standards face penalties. Under Jiangsu Province’s RCS assessment protocol, each village is required to deposit CNY 2000 as a performance bond for river chief responsibilities. In the annual evaluation, the top three ranked villages receive full bond refunds along with additional awards of CNY 10,000, CNY 8000, and CNY 5000, respectively, while the two lowest-ranked villages that fail to meet performance standards have their entire bond forfeited. The system also engages villagers by encouraging pollution reporting through official channels. When verified, reported cases trigger accountability measures against responsible parties, with reporters receiving formal recognition or material incentives.

In practice, the government may resort to lenient supervision when facing high regulatory costs or supervisory neglect, effectively lowering oversight expenses. Consequently, the strategy set for the government is strict supervision/lenient supervision.

2.1.2. Rural River Chiefs

Given resource constraints and limited administrative capacity, the government appoints rural river chiefs to conduct pollution patrols and oversee subordinate functional organizations responsible for river governance. Within the framework, rural river chiefs serve as field supervisors under direct government authority. They implement monitoring and feedback systems to rapidly detect issues and enforce corrective measures. When patrols identify river pollution, rural river chiefs directly mandate response actions by relevant agencies. Should agencies neglect their duties, river chiefs escalate violations to the government, triggering penalties against non-compliant organizations through established accountability frameworks.

In practice, river chiefs often face pressures and conflicting interests from various stakeholders, making it difficult to fulfill their duties effectively. In such situations, they may avoid conducting patrols. Consequently, the strategy set for rural river chiefs is patrol/no patrol.

2.1.3. Functional Organizations

Functional organizations are the specific entities responsible for rural river governance and serve as the primary actors in the overall river governance system. They employ advanced river governance technologies and dedicate personnel to pollutant containment and river cleanup operations. Their effectiveness faces dual oversight, one of which is the river chief, who will evaluate their performance as the basis for rewards or penalties, and the other is the villager, who can report poor governance outcomes to higher authorities.

In practice, governing rural rivers demands substantial effort and resources, which may lead functional organizations to avoid undertaking such responsibilities. Consequently, the strategy set for functional organizations is governance/non-governance.

2.1.4. Villagers

Villagers are the direct beneficiaries of river governance. In previous governance systems, villagers were often overlooked and not considered for inclusion. Contemporary research underscores the critical role of public participation, which not only strengthens the democratic legitimacy of governance but also cultivates civic responsibility, enhancing overall governance efficiency. Villagers can participate in rural river governance in the following two ways: first, by regulating their own behavior to minimize harmful substances into rivers; second, by reporting misconduct or inefficiencies of functional organizations and river chiefs to higher authorities. The 2021 Jiangsu Provincial Regulations on Protecting and Rewarding Environmental Whistleblowers categorize reward criteria into five tiers, with maximum financial incentives reaching CNY 500,000 for substantiated reports of ecological violations.

In practice, the public awareness of participation is still to be improved, particularly among rural residents. Villagers’ environmental consciousness determines whether they will engage in river governance. Consequently, the strategy set for villagers is participation/non-participation.

Combined with the above analysis, the relationship of interests between the various subjects is shown in Figure 1.

2.2. Basic Assumptions and Parameter Settings

Assumption 1.

The four parties involved in the game are the government, rural river chiefs, functional organizations, and villagers, all of whom often exhibit bounded rationality, making decisions based on limited information and resources.

Assumption 2.

The probability that the government chooses strict supervision is $x$, and the probability of choosing lenient supervision is $1-x$; the probability that the rural river chief chooses to patrol the river is $y$, and the probability of choosing not to patrol is $1-y$; the probability that the functional organization chooses to govern the rural river is $z$, and the probability of choosing not to govern is $1-z$; the probability that villagers choose to participate in the rural river governance is $w$, and the probability of choosing not to participate is $1-w$. Here, $x,y,z,w\in [0,1]$.

Assumption 3.

The government assumes social responsibility for the for rural river governance, establishes, and supervises rural river chiefs to carry out the work, with a supervision intensity of $r$$(0<r\le 1)$. When $r=1$, the government is in a state of strict supervision, with a supervision cost of $C_1$; when $0<r<1$, the government is in a state of lenient supervision, with the supervision cost at $r{C}_1$. If the river governance is effective, the government can enjoy environmental benefits $E_1$.

Assumption 4.

The cost of rural river chiefs patrolling the river is $C_2$. Regardless of whether the river chief conducts patrol, if the functional organization actively governs the river and maintains a healthy river environment, the rural river chief in charge will receive material rewards or promotion opportunities from the government, denoted as $R_1$. Conversely, if the functional organization fails to govern the river promptly and the river chief also neglects patrols, leading to severe river pollution, the river chief in charge will face penalties $F_1$.

Assumption 5.

The cost of functional organizations governing the river is $C_3$. When these organizations do govern the river, villagers’ participation will save them a certain governance cost, denoted as $E_2$$(E_2<C_3)$, and at the same time, the villagers will receive a reward $R_2$. If the functional organization fails to govern, and the government adopts lenient supervision while the river chief does not conduct patrols, the government suffers a loss $S_1$ in credibility and influence upon public reporting. As functional organizations are directly supervised by river chiefs, patrol-detected governance failures will result in a penalty $F_2$ imposed by them. Conversely, proactive governance by the functional organization earns trust from the government and society, thereby gaining reputational benefits $R_3$.

Assumption 6.

The daily life of rural residents is closely related to the river environment. Villagers’ participation in river governance is manifested in many aspects, such as not throwing used pesticides into the river, using phosphorus-free laundry detergent when washing clothes, etc. The cost paid for this behavior is $C_4$. The villagers can also participate in rural governance through personal reporting. If the report is verified, they receive a reward $R_4$. Specifically, when the river chief conducts patrols but the functional organization fails to act, the reward is issued by the functional organization. Conversely, if the river chief does not patrol and the functional organization does not act, the reward is issued by the river chief. Furthermore, a poor river environment negatively impacts the growth of vegetation and crops, resulting in losses for villagers, denoted as $S_2$.

The specific parameters and their description are shown in

Table 1. Parameters in the evolutionary game.

Stakeholder	Parameter	Description
Government	$x$	Probability of the government choosing strict supervision
	$r$	Intensity of government supervision
	$C_1$	Costs of strict government supervision
	$r{C}_1$	Costs of lenient government supervision
	$E_1$	Environmental benefits enjoyed by the government
	$S_1$	Reputational damage caused by lenient government supervision
Rural river chiefs	$y$	Probability of rural river chiefs choosing to patrol rivers
	$C_2$	Costs of river patrol by rural river chiefs
	$R_1$	Rewards granted to rural river chiefs by the government
	$F_1$	Punishments imposed on river chiefs by the government
Functional organizations	$z$	Probability of functional organizations choosing to govern
	$C_3$	Costs of river governance by functional organizations
	$E_2$	Cost savings achieved by functional organizations
	$R_2$	Rewards given to villagers by functional organizations
	$F_2$	Punishments for functional organizations
	$R_3$	Reputation gains for functional organizations
Villagers	$w$	Probability of villagers choosing to participate in governance
	$C_4$	Costs of villagers participating in governance
	$R_4$	Rewards obtained by villagers for reporting
	$S_2$	Environmental damage suffered by villagers

.

Based on the above assumptions, the payoff matrix for the four-party evolutionary game involving the government, rural river chiefs, functional organizations, and villagers is set, as shown in

Table 2. Payoff matrix of the four-party evolutionary game.

Government	Rural River Chief	Functional Organization
		Governance (z)		Non-Governance (1−z)
		Villager		Villager
		Participation (w)		Non-Participation (1−w)
Strict supervision (x)	Patrol (y)	$-C_1+E_1-R_1$ $-C_2+R_1$ $-C_3+E_2-R_2+R_3$ $-C_4+R_2$	$-C_1+E_1-R_1$ $-C_2+R_1$ $-C_3+R_3$ $0$	$-C_1$ $-C_2+F_2$ $-F_2-R_4$ $-C_4+R_4-S_2$	$-C_1$ $-C_2+F_2$ $-F_2$ $-S_2$
	No patrol (1−y)	$-C_1+E_1-R_1$ $R_1$ $-C_3+E_2-R_2+R_3$ $-C_4+R_2$	$-C_1+E_1-R_1$ $R_1$ $-C_3+R_3$ $0$	$-C_1+F_1$ $-F_1-R_4$ $0$ $-C_4+R_4-S_2$	$-C_1+F_1$ $-F_1$ $0$ $-S_2$
Lenient supervision (1−x)	Patrol (y)	$-r{C}_1+E_1$ $-C_2$ $-C_3+E_2-R_2+R_3$ $-C_4+R_2$	$-r{C}_1+E_1$ $-C_2$ $-C_3+R_3$ $0$	$-r{C}_1$ $-C_2+F_2$ $-F_2-R_4$ $-C_4+R_4-S_2$	$-r{C}_1$ $-C_2+F_2$ $-F_2$ $-S_2$
	No patrol (1−y)	$-r{C}_1+E_1$ $0$ $-C_3+E_2-R_2+R_3$ $-C_4+R_2$	$-r{C}_1+E_1$ $0$ $-C_3+R_3$ $0$	$-r{C}_1-S_1$ $-R_4$ $0$ $-C_4+R_4-S_2$	$-r{C}_1$ $0$ $0$ $-S_2$

.

3. Results

3.1. Stability Analysis of Strategies

3.1.1. Stability Strategy Analysis of the Government

When the government chooses the strategy of strict supervision, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{11}& =yzw\left(-C_1+E_1-R_1\right)+yz(1-w)\left(-C_1+E_1-R_1\right)+y(1-z)w\left(-C_1\right)+\hfill \\ & \hspace{1em}y(1-z)(1-w)\left(-C_1\right)+(1-y)zw\left(-C_1+E_1-R_1\right)+\hfill \\ & \hspace{1em}(1-y)zw\left(-C_1+E_1-R_1\right)+(1-y)z(1-w)\left(-C_1+E_1-R_1\right)+\hfill \\ & \hspace{1em}(1-y)(1-z)w\left(-C_1+F_1\right)+(1-y)(1-z)(1-w)\left(-C_1+F_1\right)\hfill \\ & =z\left(E_1-R_1\right)+(1-y)(1-z)F_1-C_1\hfill \end{array}$$

(1)

When the government chooses the strategy of lenient supervision, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{12}& =yzw\left(-r{C}_1+E_1\right)+yz(1-w)\left(-r{C}_1+E_1\right)+\hfill \\ & \hspace{1em}y(1-z)w\left(-r{C}_1\right)+y(1-z)(1-w)\left(-r{C}_1\right)+\hfill \\ & \hspace{1em}(1-y)zw\left(-r{C}_1+E_1\right)+(1-y)z(1-w)\left(-r{C}_1+E_1\right)+\hfill \\ & \hspace{1em}(1-y)(1-z)w\left(-r{C}_1-S_1\right)+(1-y)(1-z)(1-w)\left(-r{C}_1\right)\hfill \\ & =z{E}_1-r{C}_1-(1-y)(1-z)w{S}_1\hfill \end{array}$$

(2)

The government’s average expected return is as follows:

$$U_1=x{U}_{11}+(1-x)U_{12}$$

(3)

The replication dynamic equation [54] of the government is as follows:

$$\begin{array}{l}F(x)=dx/dt=x\left(U_{11}-U_1\right)=x(1-x)\left(U_{11}-U_{12}\right)\\ \hspace{1em}\hspace{1em}=x(1-x)\left[(1-y)(1-z)F_1+(1-y)(1-z)w{S}_1-(1-r)C_1-z{R}_1\right]\end{array}$$

(4)

The replication dynamic equation that calculates the partial derivation of x is as follows:

$$\begin{array}{l}{F}^{\prime }(x)=dF(x)/dx\\ \hspace{1em}\hspace{1em} =(1-2x)\left[(1-y)(1-z)F_1+(1-y)(1-z)w{S}_1-(1-r)C_1-z{R}_1\right]\end{array}$$

(5)

According to the stability theorem of differential equations [55], the strategy of the government must satisfy the conditions for a stable state $F(x)=0$ and $F^{\prime }(x)<0$.

Proposition 1.

When $w>w^{\prime }$, the government’s stable strategy is strict supervision; when $w<w^{\prime }$, the government’s stable strategy is lenient supervision; when $w=w^{\prime }$, the government’s stable strategy cannot be determined, and the threshold is $w^{\prime }=\left[z{R}_1+(1-r)C_1-(1-y)(1-z)F_1\right]{\left[(1-y)(1-z)S_1\right]}^{-1}$.

Proof. 

Let $G(w)=(1-y)(1-z)F_1+(1-y)(1-z)w{S}_1-(1-r)C_1-z{R}_1$, $𝜕G(w)/𝜕w>0$; therefore, $G(w)$ is an increasing function with respect to $w$. When $w>w^{\prime }$, $G(w)>0$, ${\left.F(x)\right|}_{x=1}=0$ and ${\left.F^{\prime }(x)\right|}_{x=1}<0$, then $x=1$ is stable; when $w<w^{\prime }$, $G(w)<0$, ${\left.F(x)\right|}_{x=0}=0$ and ${\left.F^{\prime }(x)\right|}_{x=0}<0$, then $x=0$ is stable; when $w=w^{\prime }$, $G(w)=0$, $F(x)=0$ and $F^{\prime }(x)=0$, then $x\in [0,1]$ all are in a stable state, and the stable strategy cannot be determined. □

It is necessary to point out that the implications of Proposition 1. In rural river governance, if villagers actively participate in river governance and report untreated river pollution, and the reported situation is verified as true, it will negatively impact the government’s reputation and credibility. Consequently, the government’s strategy may shift from lenient supervision to strict supervision. Conversely, if villagers are not highly motivated to participate, and no reputational loss occurs regardless of whether the government opts for lenient or strict supervision, the government is more likely to choose lenient supervision to minimize costs.

The phase diagram of the government strategy choice is determined by relevant parameters. By Proposition 1, we can see that

$$y_1=1-\left[z{R}_1+(1-r)C_1\right]{\left[(1-z)F_1\right]}^{-1}\mathrm{when}{w}^{\prime }=0,$$

and

$$y_2=1-\left[z{R}_1+(1-r)C_1\right]{\left[(1-z)\left(S_1+F_1\right)\right]}^{-1}\mathrm{when}{w}^{\prime }=1.$$

Based on the relationship of magnitudes, it is known that $0<y_1<y_2<1$, then the phase diagram of the government strategy choice is as shown in Figure 2.

From Figure 2, it is known that the volume of $V_{x0}$ represents the probability of the government adopting a strict supervision strategy, and the volume of $V_{x1}$ represents the probability of adopting a lenient supervision strategy. After calculation, it can be obtained that

$$\left\{\begin{array}{l}{V}_{x0}={\displaystyle {\int }_0^1{\displaystyle {\int }_{y_1}^{y_2}{w}^{\prime }dydx+{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{y_1}dydx}}=}}1-\left[z{R}_1+(1-r)C_1\right]{\left[(1-z)B{S}_1{F}_1\right]}^{-1}\left\{-S_1^2-B{F}_1\ln \left(F_1/B\right)\right\}\\ V_{x1}=1-V_{x0}=\left[z{R}_1+(1-r)C_1\right]{\left[(1-z)B{S}_1{F}_1\right]}^{-1}\left\{-S_1^2-B{F}_1\ln \left(F_1/B\right)\right\}\end{array}\right.$$

(6)

where $B=S_1+F_1$.

Inference 1.

The government’s likelihood of implementing strict supervision is inversely related to the associated supervision costs. As these costs increase, the government tends to favor a more lenient approach to minimize expenditure. Additionally, when functional organizations are more likely to involved in river governance, the probability of timely pollution control increase. Consequently, the intensity of government supervision diminishes, leaning to a more lenient stance.

3.1.2. Stability Strategy Analysis of Rural River Chiefs

When the river chief chooses the strategy of river patrol, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{21}& =xzw\left(-C_2+R_1\right)+xz(1-w)\left(-C_2+R_1\right)+x(1-z)w\left(-C_2+F_2\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}x(1-z)(1-w)\left(-C_2+F_2\right)+(1-x)zw\left(-C_2\right)+(1-x)z(1-w)\left(-C_2\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)(1-z)w\left(-C_2+F_2\right)+(1-x)(1-z)(1-w)\left(-C_2+F_2\right)\hfill \\ & =(1-z)F_2+xz{R}_1-C_2\hfill \end{array}$$

(7)

When the river chief chooses the strategy of not patrol, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{22}& =xzw{R}_1+xz(1-w)R_1+x(1-z)w\left(-F_1-R_2\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}x(1-z)(1-w)\left(-F_1\right)+(1-x)(1-z)w\left(-R_2\right)\hfill \\ & =-x(1-z)F_1+xz{R}_1-(1-z)w{R}_2\hfill \end{array}$$

(8)

The rural river chief’s average expected return is as follows:

$$U_2=y{U}_{21}+(1-y)U_{22}$$

(9)

The replication dynamic equation of the rural river chief is as follows:

$$\begin{array}{l}F(y)=dy/dt=y\left(U_{21}-U_2\right)=y(1-y)\left(U_{21}-U_{22}\right)\\ \hspace{1em}\hspace{1em}=y(1-y)\left[(1-z)F_2+x(1-z)F_1+(1-z)w{R}_2-C_2\right]\end{array}$$

(10)

The replication dynamic equation that calculates the partial derivation of y is as follows:

$$F^{\prime }(y)=dF(y)/dy=(1-2y)\left[(1-z)F_2+x(1-z)F_1+(1-z)w{R}_2-C_2\right]$$

(11)

According to the stability theorem of differential equations, the strategy of the rural river chief must satisfy the conditions for a stable state $F(y)=0$ and $F^{\prime }(y)<0$.

Proposition 2.

When $x>x^{\prime }$, the stable strategy of rural river chiefs is to patrol rivers; when $x<x^{\prime }$, the stable strategy of rural river chiefs is not to patrol rivers; when $x=x^{\prime }$, the stable strategy of rural river chiefs cannot be determined, and the threshold is $x^{\prime }=\left[C_2-(1-z)w{R}_2-(1-z)F_2\right]{\left[(1-z)F_1\right]}^{-1}$.

Proof. 

Let $L(x)=(1-z)F_2+x(1-z)F_1+(1-z)w{R}_2-C_2$, $𝜕L(x)/𝜕x>0$; therefore, $L(x)$ is an increasing function with respect to $x$. When $x>x^{\prime }$, $L(x)>0$, ${\left.F(y)\right|}_{y=1}=0$ and ${\left.F^{\prime }(y)\right|}_{y=1}<0$, then $y=1$ is stable; when $x<x^{\prime }$, $L(x)<0$, ${\left.F(y)\right|}_{y=0}=0$ and ${\left.F^{\prime }(y)\right|}_{y=0}<0$, then $y=0$ is stable; when $x=x^{\prime }$, $L(x)=0$, $F(y)=0$ and $F^{\prime }(y)=0$, then $y\in [0,1]$ all are in a stable state, and the stable strategy cannot be determined. □

It is easy to draw out the implications of Proposition 2, as follows. The higher the probability of the government choosing strict supervision, the greater the likelihood that rural river chiefs will choose to patrol rivers. Rural river chiefs undergo performance evaluations by higher-level governments, with their interests closely tied to the government. When the government adopts a strict supervision strategy, the evaluation mechanism for rural river chiefs becomes more stringent as well. At this point, rural river chiefs are less likely to slack off in their duties and tend to opt for patrolling rivers.

The phase diagram of the rural river chief strategy choice is determined by relevant parameters. By Proposition 2, we can see that

$$w_1=\left[C_2-(1-z)F_2\right]{\left[(1-z)R_2\right]}^{-1}\mathrm{when}{x}^{\prime }=0,$$

and

$$w_2=\left[C_2-(1-z)\left(F_1+F_2\right)\right]{\left[(1-z)R_2\right]}^{-1}\mathrm{when}{x}^{\prime }=1.$$

Based on the relationship of magnitudes, this paper only discusses that $0<w_2<w_1<1$, then the phase diagram of the rural river chief strategy choice is as shown in Figure 3.

From Figure 3, it is known that the volume of $V_{y0}$ is the probability that rural river chiefs adopt the strategy of not patrolling, and the volume of $V_{y1}$ is the probability that rural river chiefs adopt the strategy of patrolling the river. After calculation, it can be obtained that

$$\left\{\begin{array}{l}{V}_{y0}={\displaystyle {\int }_0^1{\displaystyle {\int }_{w_2}^{w_1}{x}^{\prime }}dwdy+}{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{w_2}dwdy}=\left[C_2-(1-z)F_2\right]{\left[2(1-z)R_2\right]}^{-1}}\\ V_{y1}=1-V_{y0}=1-\left[C_2-(1-z)F_2\right]{\left[2(1-z)R_2\right]}^{-1}\end{array}\right.$$

(12)

Inference 2.

The probability of rural river chiefs adopting the strategy of river patrol is inversely proportional to their patrol costs. Higher patrol costs make them more inclined to avoid patrols. However, if the punishment for not patrolling is severe, their decision shifts from not patrolling to patrolling. Therefore, when river chiefs fail to act, the government must enforce strict reward and punishment systems to regulate and standardize their behavior.

3.1.3. Stability Strategy Analysis of Functional Organizations

When the functional organization chooses the strategy of governing the river, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{31}& =xyw\left(-C_3+E_2-R_2+R_3\right)+xy(1-w)\left(-C_3+R_3\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}x(1-y)w\left(-C_3+E_2-R_2+R_3\right)+x(1-y)(1-w)\left(-C_3+R_3\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)yw\left(-C_3+E_2-R_2+R_3\right)+(1-x)y(1-w)\left(-C_3+R_3\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)(1-y)w\left(-C_3+E_2-R_2+R_3\right)+(1-x)(1-y)(1-w)\left(-C_3+R_3\right)\hfill \\ & =w\left(E_2-R_2\right)-C_3+R_3\hfill \end{array}$$

(13)

When the functional organization chooses the strategy of not governing the river, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{32}& =xyw\left(-F_2-R_4\right)+xy(1-w)\left(-F_2\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)yw\left(-F_2-R_4\right)+(1-x)y(1-w)\left(-F_2\right)\hfill \\ & =-y{F}_2-yw{R}_4\hfill \end{array}$$

(14)

The functional organization’s average expected return is as follows:

$$U_3=z{U}_{31}+(1-z)U_{32}$$

(15)

The replication dynamic equation of the functional organization is as follows:

$$\begin{array}{l}F(z)=dz/dt=z\left(U_{31}-U_3\right)=z(1-z)\left(U_{31}-U_{32}\right)\\ \hspace{1em}\hspace{1em}=z(1-z)\left(yw{R}_4+y{F}_2+w{E}_2-w{R}_2-C_3+R_3\right)\end{array}$$

(16)

The replication dynamic equation that calculates the partial derivation of z is as follows:

$$F^{\prime }(z)=dF(z)/dz=(1-2z)\left(yw{R}_4+y{F}_2+w{E}_2-w{R}_2-C_3+R_3\right)$$

(17)

According to the stability theorem of differential equations, the strategy of the functional organization must satisfy the conditions for a stable state $F(z)=0$ and $F^{\prime }(z)<0$.

Proposition 3.

When $y>y^{\prime }$, the stable strategy of functional organizations is to govern the river; when $y<y^{\prime }$, the stable strategy of functional organizations is not to govern the river; when $y=y^{\prime }$, the stable strategy of functional organizations cannot be determined, and the threshold is $y^{\prime }=\left(C_3-R_3-w{E}_2+w{R}_2\right){\left[F_2+w{R}_4\right]}^{-1}$.

Proof. 

Let $N(y)=yw{R}_4+y{F}_2+w{E}_2-w{R}_2-C_3+R_3$, $𝜕N(y)/𝜕y>0$; therefore, $N(y)$ is an increasing function with respect to $x$. When $y>y^{\prime }$, $N(y)>0$, ${\left.F(z)\right|}_{z=1}=0$ and ${\left.F^{\prime }(z)\right|}_{z=1}<0$, then $z=1$ is stable; when $y<y^{\prime }$, $N(y)<0$, ${\left.F(z)\right|}_{z=0}=0$ and ${\left.F^{\prime }(z)\right|}_{z=0}<0$, then $z=0$ is stable; when $y=y^{\prime }$, $N(y)=0$, $F(z)=0$ and $F^{\prime }(y)=0$, then $z\in [0,1]$ all are in a stable state, and the stable strategy cannot be determined. □

We are now in a position to offer a few insights from Proposition 3. In river governance, increased patrols by rural river chiefs can prompt functional organizations to shift from non-governance to governance. This indicates that regular river patrols can effectively encourage functional organizations to govern rivers, preventing issues like neglect and dereliction of duty. Therefore, rural river chiefs should actively conduct patrols and intensify supervision over the effectiveness of functional organization governance.

The phase diagram of the functional organization strategy choice is determined by relevant parameters. By Proposition 3, we can see that

$$w_1=\left(C_3-R_3\right){\left(E_2-R_2\right)}^{-1}\mathrm{when}{y}^{\prime }=0,$$

and

$$w_2=\left(F_2-C_3+R_3\right){\left(R_2-E_2+R_4\right)}^{-1}\mathrm{when}{y}^{\prime }=1.$$

Based on the relationship of magnitudes, it is known that $0<w_1<1$ and $0<w_2<1$, then the phase diagram of the functional organization strategy choice is as shown in Figure 4.

From Figure 4, it is known that the volume of $V_{z0}$ is the probability that functional organizations adopt the strategy of not governing the river, and the volume of $V_{z1}$ is the probability that functional organizations adopt the strategy of governing the river. After calculation, it can be obtained that

$$\left\{\begin{array}{l}{V}_{z0}={\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{y}^{\prime }}dwdz=\left[R_4\left(C_3-R_3\right)+F_2(E_2-R_2)\right]\ln \left(1+R_4{\left(F_2\right)}^{-1}\right){\left(R_4\right)}^{-2}-1}\\ V_{z1}=1-V_{z0}=2-\left[R_4\left(C_3-R_3\right)+F_2\left(E_2-R_2\right)\right]\ln \left(1+R_4{\left(F_2\right)}^{-1}\right){\left(R_4\right)}^{-2}\end{array}\right.$$

(18)

Inference 3.

When the cost of functional organizations in river governance increases, the probability of these organizations choosing to govern the river decreases significantly, leading them to opt for no governance at all. The governance costs for functional organizations encompass both human resource costs and technical costs, with the latter being particularly high. Therefore, reducing technical costs substantially would enhance the probability of functional organizations participating in river governance.

3.1.4. Stability Strategy Analysis of Villagers

When the villager chooses the strategy of participating in the governance, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{41}& =xyz\left(-C_4+R_3\right)+xy(1-z)\left(-C_4+R_2-S_2\right)+x(1-y)z\left(-C_4+R_3\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}x(1-y)(1-z)\left(-C_4+R_2-S_2\right)+(1-x)yz\left(-C_4+R_3\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)y(1-z)\left(-C_4+R_2-S_2\right)+(1-x)(1-y)z\left(-C_4+R_3\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)(1-y)(1-z)\left(-C_4+R_2-S_2\right)\hfill \\ & =(1-z)\left(R_2-S_2\right)-C_4+z{R}_3\hfill \end{array}$$

(19)

When the villager chooses the strategy of not participating in the governance, the expected return is as follows:

$$\begin{array}{cc}\hfill U_{42}& =xy(1-z)\left(-S_2\right)+x(1-y)(1-z)\left(-S_2\right)+\hfill \\ & \hspace{0.17em}\hspace{0.17em}(1-x)y(1-z)\left(-S_2\right)+(1-x)(1-y)(1-z)\left(-S_2\right)\hfill \\ & =-(1-z)S_2\hfill \end{array}$$

(20)

The villager’s average expected return is as follows:

$$U_4=w{U}_{41}+(1-w)U_{42}$$

(21)

The replication dynamic equation of the villager is as follows:

$$\begin{array}{l}F(w)=dw/dt=w\left(U_{41}-U_4\right)=w(1-w)\left(U_{41}-U_{42}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}=w(1-w)\left[(1-z)R_4-C_4+z{R}_2\right]\end{array}$$

(22)

The replication dynamic equation that calculates the partial derivation of w is as follows:

$$F^{\prime }(w)=dF(w)/dw=(1-2w)\left[(1-z)R_4-C_4+z{R}_2\right]$$

(23)

According to the stability theorem of differential equations, the strategy of the villager must satisfy the conditions for a stable state $F(w)=0$ and $F^{\prime }(w)<0$.

Proposition 4.

When $z<z^{\prime }$, the stable strategy of villagers is to participate in the governance; when $z<z^{\prime }$, the stable strategy of functional organizations is not to participate in the governance; when $z=z^{\prime }$, the stable strategy of villagers cannot be determined, and the threshold is $z^{\prime }=(C_4-R_4){(R_2-R_4)}^{-1}$.

Proof. 

Let $H(z)=(1-z)R_4-C_4+z{R}_2$, $𝜕H(z)/𝜕z<0$; therefore, $H(z)$ is an decreasing function with respect to $z$. When $z<z^{\prime }$, $H(z)>0$, ${\left.F(w)\right|}_{w=1}=0$ and ${\left.F^{\prime }(w)\right|}_{w=1}<0$, then $w=1$ is stable; when $z>z^{\prime }$, $H(z)<0$, ${\left.F(w)\right|}_{w=0}=0$ and ${\left.F^{\prime }(w)\right|}_{w=0}<0$, then $w=0$ is stable; when $z=z^{\prime }$, $H(z)=0$, $F(w)=0$ and $F^{\prime }(w)=0$, then $z\in [0,1]$ all are in a stable state, and the stable strategy cannot be determined. □

Now, we are ready to explain the implications of Proposition 4. The higher the probability that functional organizations fail to govern rivers, the more likely villagers will shift from non-participation to participation in governance. When functional organizations opt out of governance, river pollution worsens. Villagers then participate by reporting the pollution. If their reports are verified, they receive rewards from higher authorities. This, in turn, boosts villagers’ voluntary participation enthusiasm.

The phase diagram of the villager strategy choice is determined by relevant parameters. According to Proposition 4, the phase diagram of the villager strategy choice is as shown in Figure 5.

From Figure 5, it is known that the volume of $V_{w0}$ is the probability that villagers adopt the strategy of participating in the governance, and the volume of $V_{w1}$ is the probability that villagers adopt the strategy of participating in the governance. After calculation, it can be obtained that

$$\left\{\begin{array}{l}{V}_{w1}={\displaystyle {\int }_0^1{\displaystyle {\int }_0^1{z}^{\prime }}dxdw=z^{\prime }=\left(C_4-R_4\right){\left(R_2-R_4\right)}^{-1}}\\ V_{w0}=1-V_{w1}=1-z^{\prime }=1-\left(C_4-R_4\right){\left(R_2-R_4\right)}^{-1}\end{array}\right.$$

(24)

Inference 4.

When the cost of villagers’ participation is greater, the probability of villagers choosing to participate in river governance will decrease accordingly. At the same time, under the influence of government incentive mechanisms, villagers tend to choose to participate in governance and report the inaction of functional organizations and rural river chiefs.

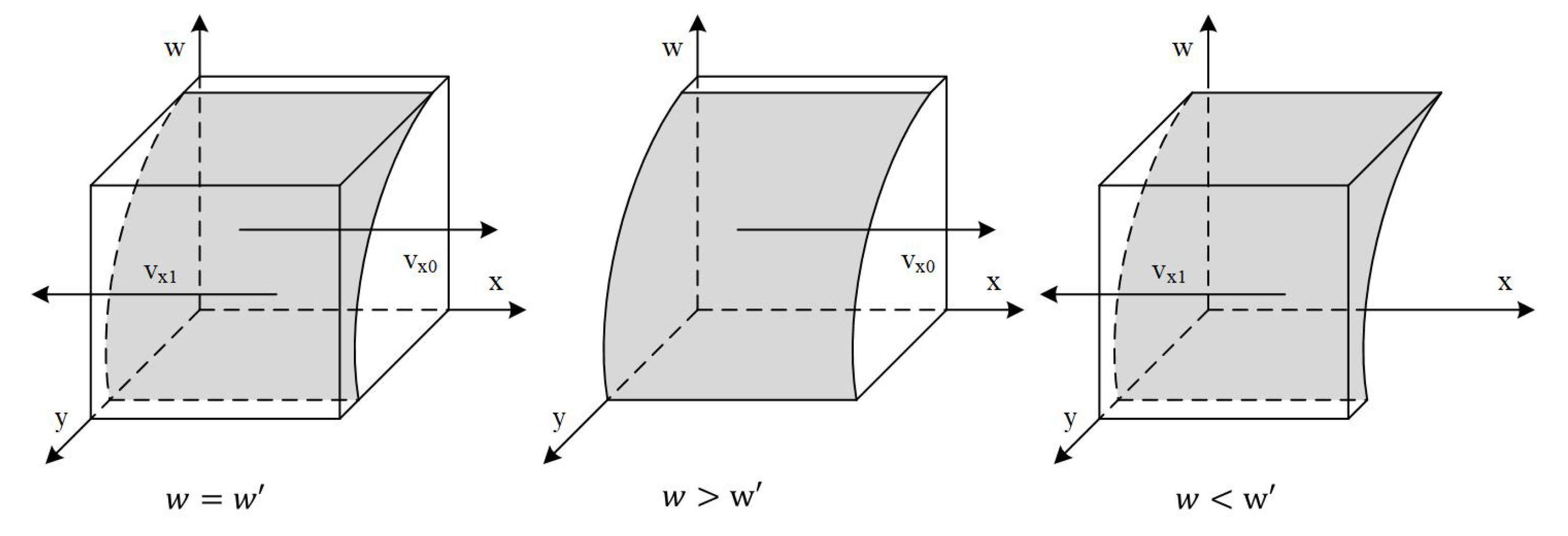
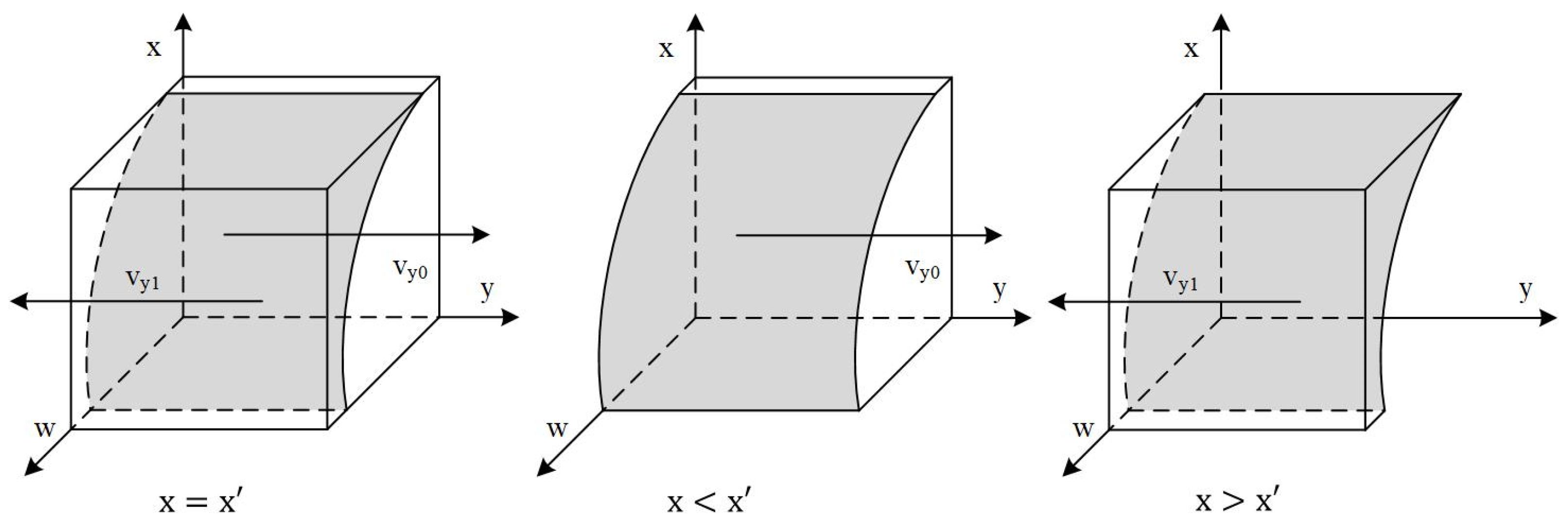
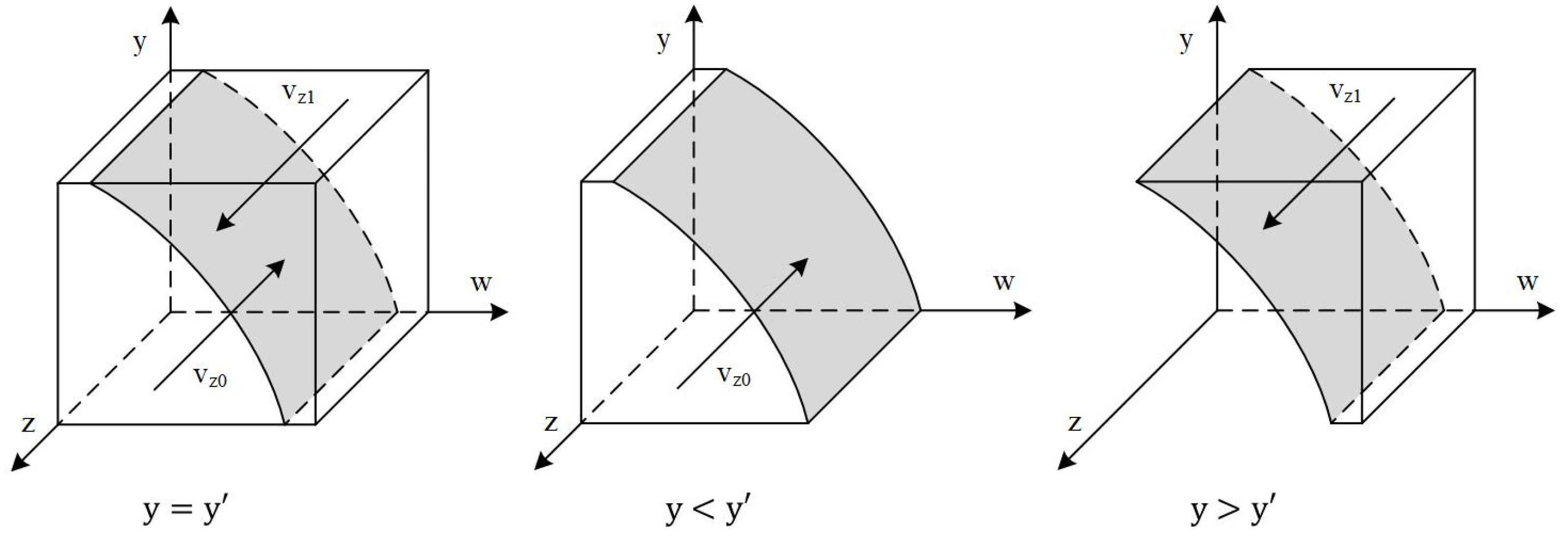
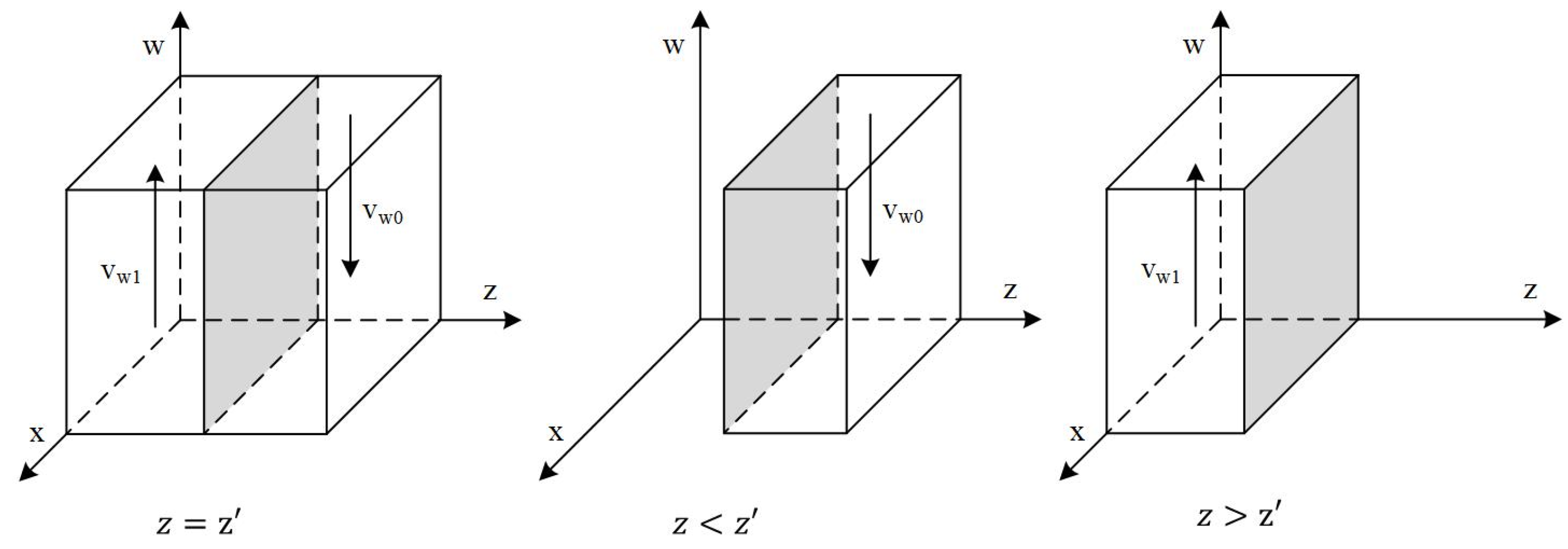
3.2. Local Stability Analysis of the Evolutionary Game System

To reveal the formation process of stable strategies in the evolution game of rural river governance, this paper constructs and solves the replication dynamic equations for the game among the government, rural river chiefs, functional organizations, and villagers. By setting $F(x)=0$, $F(y)=0$, $F(z)=0$, $F(w)=0$, multiple solutions are derived, all of which are strict Nash equilibria [56]. Therefore, this paper only needs to analyze pure strategies. The equilibrium points are substituted into the Jacobian matrix and judged according to Lyapunov’s first method as follows: when all eigenvalues of the matrix are less than 0, then the equilibrium point is asymptotically stable; when at least one eigenvalue is positive, then the equilibrium point is unstable. This paper will conduct stability analysis on 16 pure strategy equilibrium points.

According to the replication dynamic equations [57] of the four-party evolutionary game subjects, Jacobian matrix can be obtained.

$$J=\left[\begin{array}{cccc}𝜕F(x)/𝜕x& 𝜕F(x)/𝜕y& 𝜕F(x)/𝜕z& 𝜕F(x)/𝜕w\\ 𝜕F(y)/𝜕x& 𝜕F(y)/𝜕y& 𝜕F(y)/𝜕z& 𝜕F(y)/𝜕w\\ 𝜕F(z)/𝜕x& 𝜕F(z)/𝜕y& 𝜕F(z)/𝜕z& 𝜕F(z)/𝜕w\\ 𝜕F(w)/𝜕x& 𝜕F(w)/𝜕y& 𝜕F(w)/𝜕z& 𝜕F(w)/𝜕w\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]$$

(25)

where

• $a_{11}=(1-2x)\left[(1-y)(1-z)F_1+(1-y)(1-z)w{S}_1-(1-r)C_1-z{R}_1\right]$;
• $a_{12}=x(1-x)\left[-(1-z)\left(F_1+w{S}_1\right)\right]$, $a_{13}=x(1-x)\left[-(1-y)\left(F_1+w{S}_1\right)-R_1\right]$;
• $a_{14}=x(1-x)(1-y)(1-z)S_1$, $a_{21}=y(1-y)(1-z)F_1$;
• $a_{22}=(1-2y)\left[(1-z)F_2+x(1-z)F_1+(1-z)w{R}_4-C_2\right]$, $a_{23}=y(1-y)\left(-F_2-x{F}_1-w{R}_4\right)$;
• $a_{24}=y(1-y)(1-z)R_4$, $a_{31}=0$, $a_{32}=z(1-z)\left(w{R}_4+F_2\right)$;
• $a_{33}=(1-2z)\left(yw{R}_4+w{E}_2+y{F}_2-C_3-w{R}_2+R_3\right)$, $a_{34}=z(1-z)\left(y{R}_2+E_2-R_2\right)$;
• $a_{41}=0$, $a_{42}=0$, $a_{43}=w(1-w)\left(R_2-R_4\right)$, $a_{44}=(1-2w)\left[(1-z)R_4-C_4+z{R}_2\right]$.

3.2.1. Stability Strategy Analysis Under Lenient Government Supervision

When the stable strategy of the government is lenient supervision, that is, condition ① $(1-y)(1-z)F_1+(1-y)(1-z)w{S}_1-(1-r)C_1-z{R}_1<0$ is satisfied, the stability of the equilibrium points under this condition is as shown in

Table 3. Stability analysis of equilibrium points under lenient government supervision.

Equilibrium Point	Eigenvalue	Sign	Stability
$E_1(0,0,0,0)$	$F_1-(1-r)C_1,F_2-C_2,R_3-C_3,R_4-C_4$	$\times -\times +$	Instability
$E_2(0,1,0,0)$	$-(1-r)C_1,C_2-F_2,F_2+R_3-C_3,R_2-C_4$	$-+\times \times$	Instability
$E_3(0,0,1,0)$	$-(1-r)C_1-R_1,-C_2,C_3-R_3,R_2-C_4$	$--\times \times$	ESS when (a) and (c) are satisfied
$E_4(0,0,0,1)$	$F_1+S_1-(1-r)C_1,F_2+R_4-C_2,E_2-C_3-R_2+R_3,C_4-R_4$	$+-\times -$	Instability
$E_5(0,1,1,0)$	$-(1-r)C_1-R_1,C_2,C_3-F_2-R_3,R_2-C_4$	$-+\times \times$	Instability
$E_6(0,1,0,1)$	$-(1-r)C_1,C_2-F_2-R_4,R_4+E_2+F_2-C_3-R_2+R_3,C_4-R_4$	$-+\times -$	Instability
$E_7(0,0,1,1)$	$-(1-r)C_1-R_1,-C_2,C_3-E_2+R_2-R_3,C_4-R_2$	$--\times \times$	ESS when (b) and (d) are satisfied
$E_8(0,1,1,1)$	$-(1-r)C_1-R_1,C_2,C_3-R_4-E_2-F_2+R_2-R_3,C_4-R_2$	$-+\times \times$	Instability

Note: $\times$ indicates that the sign is uncertain. Condition (a): $C_3-R_3<0$, condition (b): $C_3-E_2+R_2-R_3<0$, condition (c): $R_2-C_4<0$, condition (d): $C_4-R_2<0$.

.

From Table 3, it can be observed that, under lenient government supervision, the possible equilibrium points are $E_3(0,0,1,0)$ and $E_7(0,0,1,1)$. Since condition (c) and condition (d) cannot be satisfied simultaneously, only one evolutionarily stable strategy (ESS) point can ultimately exist. Therefore, the analysis focuses on this single potential ESS point.

Between the two possible equilibrium points, the most ideal one is $E_7(0,0,1,1)$, where, under the lenient supervision, functional organizations actively govern rivers without the need for rural river chiefs to patrol and supervise their governance. Villagers can also voluntarily participate in river governance, regulating personal behavior to protect the ecological environment. However, a comparison with previous analyses reveals that $E_7(0,0,1,1)$ does not align with earlier findings; villagers’ participation in governance has not prompted the government to adopt a strict supervision strategy. Further analysis shows that, under the joint participation of functional organizations and villagers, the benefits $E_2+R_3$ gained by functional organizations outweigh their governance costs $C_3+R_2$. The rewards $R_2$ given by functional organizations to villagers for regulating their own behavior exceed the costs $C_4$ they incur. If the $R_2$ is less than $C_4$, villagers would not choose to participate in governance. In this case, the cost $C_3$ of river governance by functional organizations would be lower than the reputation benefits $R_3$ derived from their governance, leading the four-party game participants to evolve toward $(0,0,1,0)$ and eventually stabilize.

In the case where only functional organizations are involved in rural river governance, lenient supervision by the government is not conducive to improving the efficiency of river governance. To prevent low efficiency in this process, the government can establish incentive mechanisms to encourage villager participation. As villagers’ participation enthusiasm and environmental awareness rise, they can oversee functional organizations, helping reduce governance costs. This makes governance a more stable strategy for functional organizations.

3.2.2. Stability Strategy Analysis Under Strict Government Supervision

When the stable strategy of the government is strict supervision, that is, condition ② $(1-y)(1-z)F_1+(1-y)(1-z)w{S}_1-(1-r)C_1-z{R}_1>0$ is satisfied, the stability of the equilibrium point under this condition is as

Table 4. Stability analysis of equilibrium points under strict government supervision.

Equilibrium Point	Eigenvalue	Sign	Stability
$E_9(1,0,0,0)$	$(1-r)C_1-F_1,F_1+F_2-C_2,R_3-C_3,R_4-C_4$	$\times \times \times +$	Instability
$E_{10}(1,1,0,0)$	$(1-r)C_1,C_2-F_1-F_2,F_2-C_3+R_3,R_4-C_4$	$+\times \times +$	Instability
$E_{11}(1,0,1,0)$	$(1-r)C_1+R_1,-C_2,C_3-R_3,R_2-C_4$	$+-\times \times$	Instability
$E_{12}(1,0,0,1)$	$(1-r)C_1-F_1-S_1,F_1+F_2+R_4-C_2,E_2-C_3-R_2+R_3,C_4-R_4$	$-+\times -$	Instability
$E_{13}(1,1,1,0)$	$(1-r)C_1+R_1,C_2,C_3-F_2-R_3,R_2-C_4$	$++\times \times$	Instability
$E_{14}(1,1,0,1)$	$(1-r)C_1,C_2-F_1-F_2-R_4,R_4+E_2+F_2-C_3-R_2+R_3,C_4-R_4$	$+-\times -$	Instability
$E_{15}(1,0,1,1)$	$(1-r)C_1+R_1,-C_2,C_3-E_2-R_2+R_3,C_4-R_2$	$+-+\times$	Instability
$E_{16}(1,1,1,1)$	$(1-r)C_1+R_1,C_2,C_3-R_4-E_2-F_2-R_2+R_3,C_4-R_2$	$++\times \times$	Instability

as shown.

From Table 4, it can be observed that, under strict government supervision, there are no pure strategy equilibrium points. By examining the stability of the equilibrium point $E_{11}(1,0,1,0)$, it is evident that, if the government enforces strict supervision and functional organizations govern rivers, the rural river chiefs and villagers will choose the strategies of “no patrol” and “non-participation”, respectively. However, the government strategy choice is unstable. As the voluntary efforts of functional organizations in river governance increase, and the river environment improves, the government will opt for lenient supervision rather than costly strict supervision. Therefore, this equilibrium point is unstable, aligning with the earlier analysis of the stability of government supervision strategies.

3.3. Numerical Simulation Analysis

To more intuitively observe the evolutionary trajectories of the four-party game participants under different constraints and to further investigate the impact of key parameters on the evolutionary stable strategies, this paper employs MATLAB to conduct a numerical simulation analysis of the evolutionary paths of the government, rural river chiefs, functional organizations, and villagers.

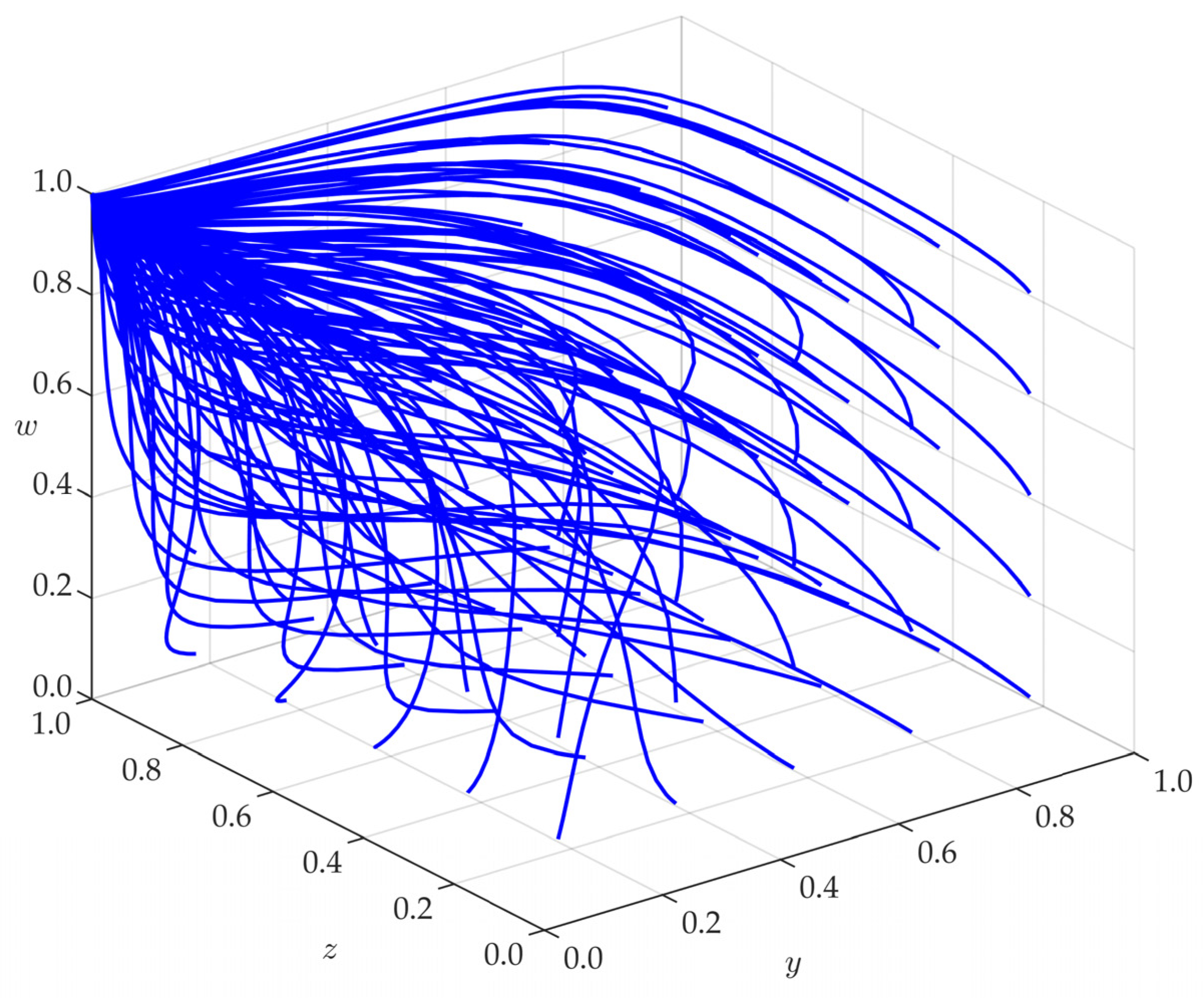
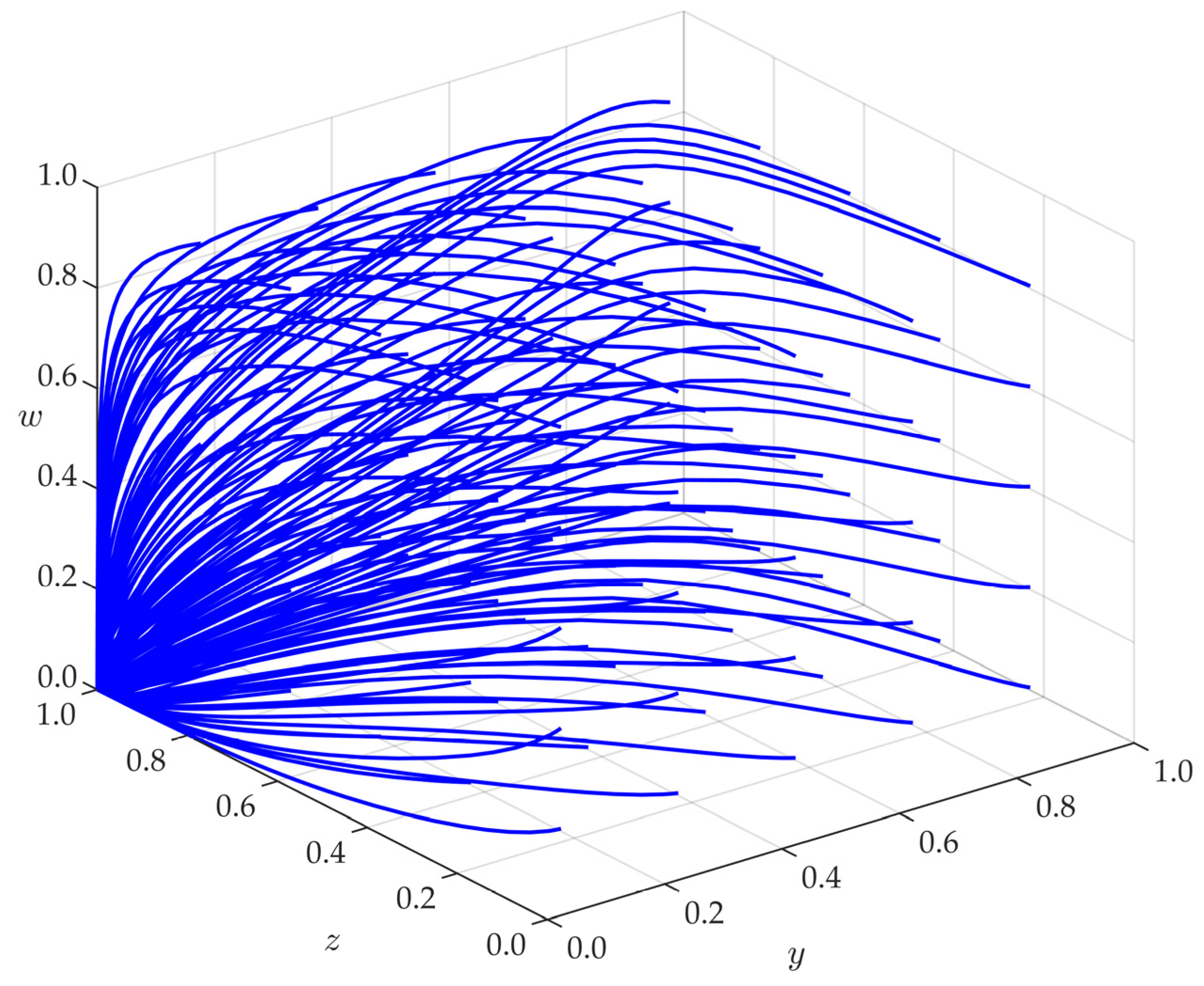
3.3.1. Verification of Equilibrium Stable Strategies

Based on the above analysis, it can be concluded that two equilibrium points may exist in this game model, denoted as $(0,0,1,1)$ and $(0,0,1,0)$, where $(0,0,1,1)$ represents the ideal state. To validate the effectiveness of the preceding analysis, this paper establishes two sets of initial parameter values by synthesizing Jiangsu Province’s RCS implementation context and respective constraints, as shown in

Table 5. Parameter assignment table.

Parameter	$\mathit{r}$	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{R}}_1$	${\mathit{F}}_1$	${\mathit{S}}_1$	${\mathit{C}}_3$	${\mathit{E}}_2$	${\mathit{F}}_2$	${\mathit{C}}_4$	${\mathit{R}}_2$	${\mathit{S}}_2$	${\mathit{R}}_3$	${\mathit{R}}_4$
Array 1	0.5	20	16	5	8	30	30	20	15	6	12	15	25	10
Array 2	0.5	20	16	5	8	30	20	20	15	15	6	15	25	10

. Select parameters are rigorously grounded in empirical data from provincial policy documents, including but not limited to river chief performance rewards aligned with the 2019 Jiangsu River Chief System Assessment Guidelines, and resident reporting incentives quantified through the 2021 Jiangsu Regulations on Protecting and Rewarding Environmental Violation Whistleblowers. The constraint conditions for the equilibrium points are as follows: (1) equilibrium point $(0,0,1,1)$: $C_3-E_2+R_2-R_3<0$, $C_4-R_2<0$; (2) equilibrium point $(0,0,1,0)$: $C_3-R_3<0$, $R_2-C_4<0$.Additionally, the initial decision probabilities for each stakeholder are set to $(0.4,0.4,0.5,0.3)$.

By substituting the two sets of numerical values into the model, the simulation results of the replication dynamic equations evolving over 50 iterations are shown in Figure 6 and Figure 7, respectively.

From the two figures, it can be observed that, under lenient government supervision, the system exhibits two evolutionarily stable points as follows: $(0,0,1,1)$ and $(0,0,1,0)$. These correspond to the stable strategy combinations of (lenient supervision, no patrol, governance, participation) and (lenient supervision, no patrol, governance, non-participation) for the government, rural river chiefs, functional organizations, and villagers, respectively. This indicates that the simulation results of the two datasets are consistent with the earlier stability strategy, thereby validating the analysis.

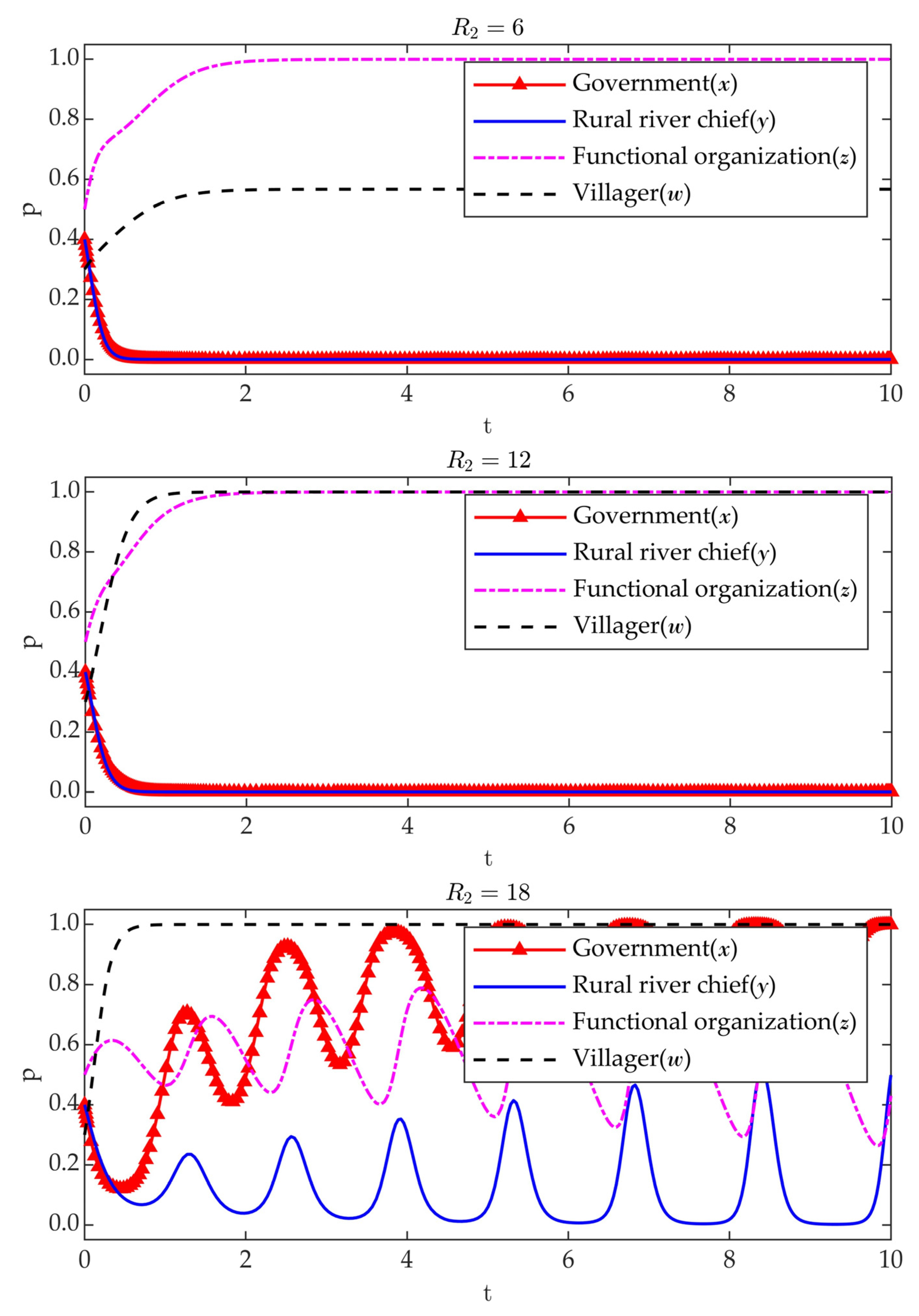
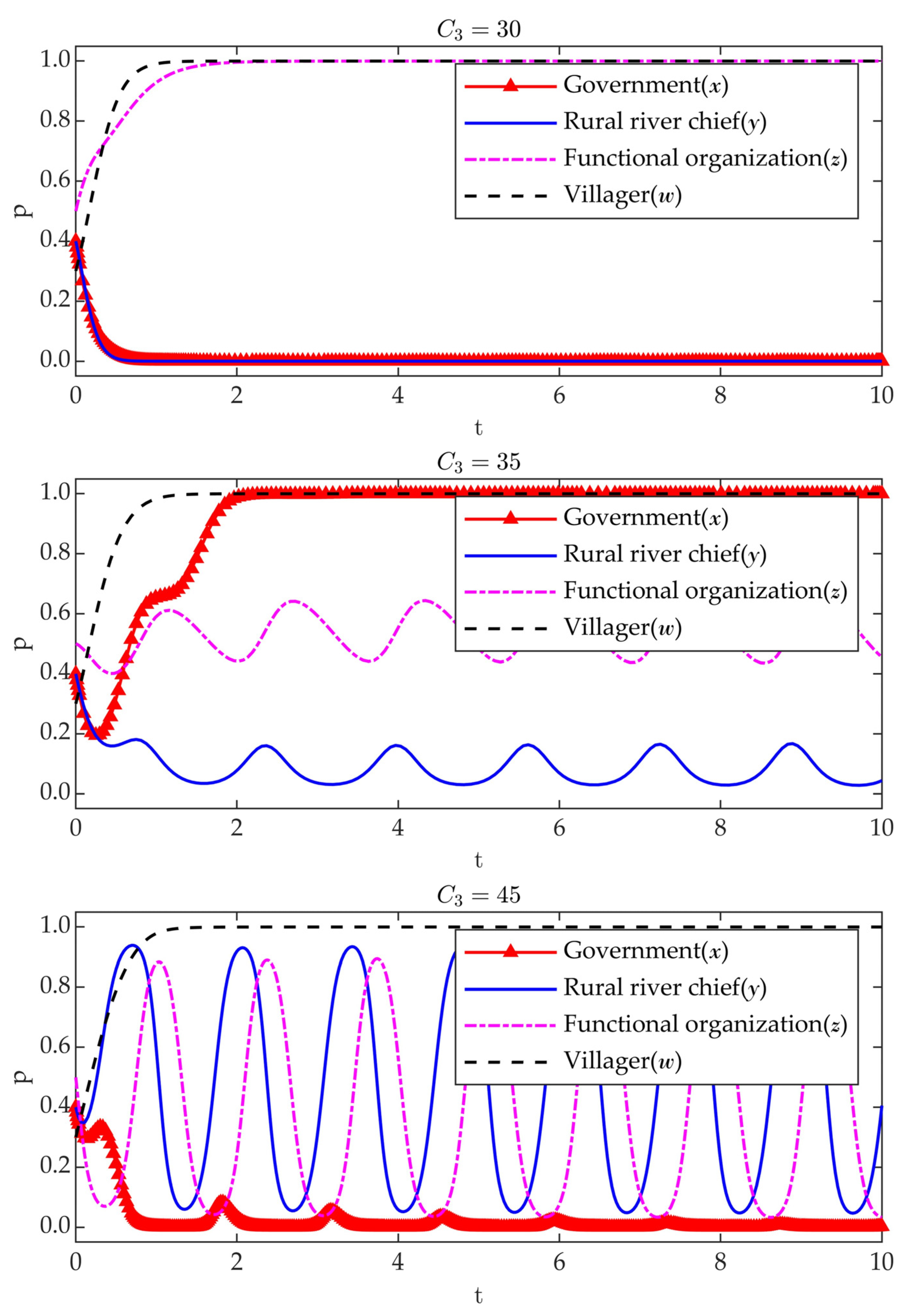
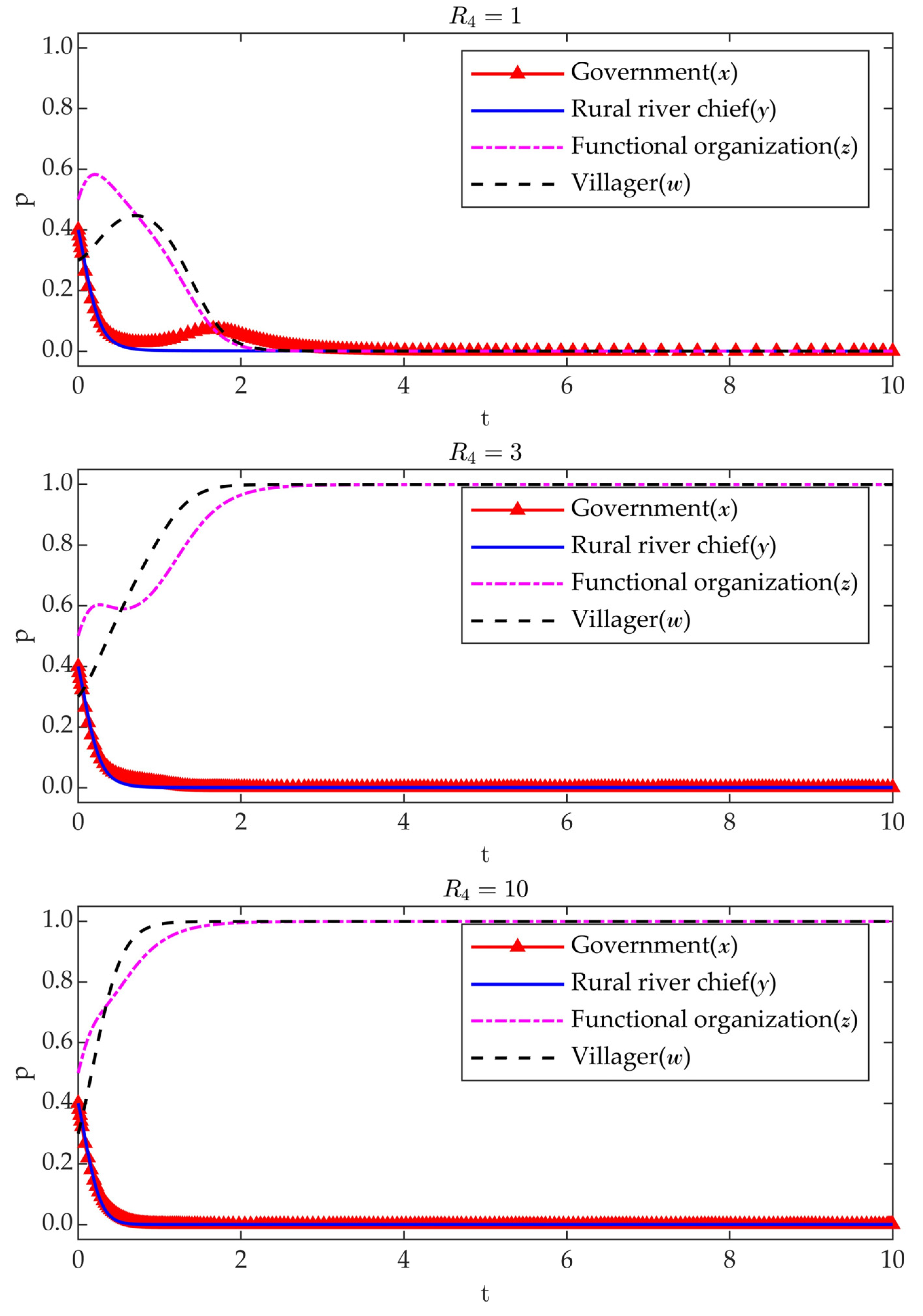
3.3.2. Sensitivity Analysis of Parameters

Based on the above analysis, it is evident that the key stakeholders in the evolutionary process are functional organizations and villagers. Therefore, this paper focuses on the payoff parameters related to these stakeholders. By assigning different values to these parameters, we can observe changes in the strategic choices of each game participant. The aim is to provide theoretical guidance for rural river governance efforts.

(1)

Impacts of $R_2$ on Evolutionary Results.

Let $R_2=\left\{6,12,18\right\}$. The evolutionary process of the four parties’ strategies is illustrated in Figure 8.

$R_2$ represents the rewards that villagers receive for actively participating in river governance when functional organizations are governing the rivers. This parameter directly impacts both functional organizations and villagers, creating a potential conflict of interest between them. Initially, $R_2$ is set to 12. When $R_2$ increases to 18, indicating that functional organizations provide higher rewards to villagers, villagers’ strategies remain stable in participating in governance. However, the strategic choices of the other three parties undergo change. As the increased reward reduces the functional organizations’ benefits, their strategy no longer stabilizes at river governance. Instead, the probability of choosing an active strategy fluctuates around 0.5, with the fluctuation amplitude increasing over time. This indicates significant uncertainty regarding whether functional organizations will choose to govern the river. Consequently, the government and rural river chiefs no longer stabilize at lenient supervision and not patrolling strategies, respectively. Instead, they tend to adopt more active strategies. Specifically, the probability of the government choosing strict supervision gradually converges to 1. When $R_2$ is reduced from its initial value of 12 to 6, the stable strategies of the government and rural river chiefs remain unchanged. However, due to the decrease in villagers’ rewards, their enthusiasm for participating in governance diminishes, and the probability of their participation stabilizes around 0.6. At the same time, the convergence of the functional organizations’ strategy toward governance slows down significantly. This phenomenon can be explained by the fact that the reduced villagers’ participation lowers the benefits functional organizations derive from their efforts, while the workload for river governance remains unchanged. Therefore, the strategic choice of the functional organization in the early stage does not directly tend to governance.

Based on the above analysis, the rewards given by functional organizations to villagers should be moderate. A low amount could dampen villagers’ enthusiasm for participating in governance, while a high amount might result in losses to their own interests. However, as bounded rational entities, functional organizations often set actual reward amounts below the optimal level. Therefore, functional organizations should also pay attention to incentive measures for villagers in river governance.

(2)

Impacts of $R_3$ on Evolutionary Results.

Let $R_3=\left\{20,22,25\right\}$. The evolutionary process of the four parties’ strategies is illustrated in Figure 9.

$R_3$ represents reputation benefits functional organizations gain from river governance. This parameter is closely related to the functional organizations’ incentives and does not directly impact other stakeholders. Initially, $R_3$ is set to 25. As this parameter decreases gradually, the stable strategies of other stakeholders also change. When it drops to 22, there is a significant shift in the stable strategies of both functional organizations and the government. The probability of functional organizations governing the river decreases significantly, stabilizing around 0.6, without fully transitioning to governance. With active participation from villagers, they report negative governance practices of functional organizations, leading the government’s strategy to stabilize at strict supervision. When it further decreases to 20, both the government and rural river chiefs opt for active strategies. The probability of the functional organization choosing to govern the river no longer stabilizes at 0.6 but fluctuates around 0.5, indicating some uncertainty. At this point, as direct supervisors of functional organizations, rural river chiefs, under strict supervision, decide not to patrol rivers with high probability but instead choose to patrol them with lower probability.

Based on the above analysis, reputation benefits directly and significantly impact functional organizations. To enhance the effectiveness of these benefits, the government should consider the social reputation of each functional organization when assigning river governance tasks. Organizations with higher reputations can gain access to more business resources, and appropriate reward measures should be implemented to incentivize their continued participation.

(3)

Impacts of $C_3$ on Evolutionary Results.

Let $C_3=\left\{30,35,45\right\}$. The evolutionary process of the four parties’ strategies is illustrated in Figure 10.

$C_3$ represents the governance costs of functional organizations, a parameter that significantly impacts their benefits. When $C_3$ is at its initial value of 30, the strategy choices of all parties reach an ideal state. However, as the value gradually increases, the strategy choices of the government, rural river chiefs, and functional organizations change, while only villagers maintain consistent participation in governance. When $C_3$ is set to 35, the probability of functional organizations governing fluctuates around 0.5, indicating uncertainty in their commitment. At the same time, both the government and rural river chiefs shift from passive to more active strategies. Specifically, rural river chiefs choose to patrol rivers with a relatively low probability, while the government’s strategy stabilizes at strict supervision. This shift occurs because, despite the villagers’ active participation, functional organizations do not fully fulfill their responsibilities, prompting the government and rural river chiefs to enforce supervision. Additionally, since villagers report issues directly to the government, the government takes the lead in implementing strict supervision to ensure accountability and effective governance. When $C_3$ is set to 45, the governance costs for functional organizations become even higher, and the probability of their choosing to govern fluctuates more significantly around 0.5, indicating heightened uncertainty in their commitment to river governance. At this stage, the rural river chiefs assume a more prominent supervisory role. According to the evolutionary trends, the probability of functional organizations choosing to govern correlates with the probability of rural river chiefs patrolling the river. Simultaneously, the government gradually transitions toward a more lenient supervision strategy, delegating the primary supervision responsibilities to the rural river chiefs.

Based on the above analysis, it can be known that the governance costs of functional organizations have the greatest impact on their benefits. The higher the governance costs, the harder it becomes for stakeholders to reach the ideal state of evolution strategy, which corresponds to Inference 3 in the previous article. Therefore, reducing the river governance costs is also an urgent problem to be solved.

(4)

Impacts of $R_4$ on Evolutionary Results.

Let $R_4=\left\{1,3,10\right\}$. The evolution process of the strategy of the four parties is shown in Figure 11.

$R_4$ represents the rewards that villagers receive for reporting the inaction of rural river chiefs or functional organizations under strict government supervision. Initially set at 10, a decrease in the value of $R_4$ leads to changes in the stable strategies of functional organizations and villagers. When $R_4$ drops to 3, the evolutionary stable strategies of the four parties in the rural river governance system remain unchanged and still converge to the ideal state. However, in the early stages, it is evident that the convergence of functional organizations’ and villagers’ strategies toward governance and participation slows down significantly. As the rewards given by the government to villagers decrease, villagers directly suffer a loss of benefits, which reduces their enthusiasm for participating in governance but does not impact their stable strategies. When the parameter is set to 1, villagers converge on the strategy of non-participation in governance, mainly due to the low reward amount, making it difficult for the government’s incentive mechanism to influence villagers’ enthusiasm for participating in governance. Therefore, with the other three parties adopting passive strategies in rural river governance and no supervisory body overseeing the functional organizations’ governance efforts, functional organizations ultimately choose not to govern the river.

According to the above analysis, the government’s incentive mechanism for villagers is indispensable. Even when the reward is at a low level, it can still motivate villagers to participate in governance. The Several Provisions on Protecting and Rewarding Informants of Ecological and Environmental Violations issued by Jiangsu Province in 2021 divides the reward categories into five levels, with the highest prize reaching up to CNY 500,000. Although the reward is already secured, the government’s incentive mechanism for villagers needs to be more transparent, with effective publicity to ensure that villagers are aware. Only then can their enthusiasm be effectively mobilized.

4. Discussion

This study develops a four-party evolutionary game model for rural river governance under the institutional framework of RCS. Behavioral strategies and underlying factors were analyzed and are discussed separately below.

4.1. Analysis of Evolutionary Stable Strategies in Rural River Governance

Through the stability analysis of an evolutionary game system, this study identifies the long-term equilibrium strategy combination for rural river governance as lenient supervision, no patrol, governance, and participation. Specifically, both the government and rural river chiefs initially drive governance efforts through strict supervision and proactive patrols. However, over time, their strategies shift toward passive states characterized by lenient supervision and non-patrol, ultimately stabilizing at this equilibrium. This evolutionary trajectory aligns with findings from Qu et al. and Chen et al., collectively underscoring a common characteristic of diminishing motivation among governance entities over time [42,46].

This study further elucidates two critical mechanisms underlying the evolutionary dynamics of rural river governance. Firstly, during the short-term governance phase, the government’s strategic choices play a decisive role. Through high-intensity supervision and policy guidance, the government effectively transitions villagers from non-participation to active engagement in governance. For instance, initial regulatory measures, such as reward–punishment mechanisms, directly enhance villagers’ motivation, as validated by Chen et al. in their proposed “government-led incentive effect”. Secondly, rural river chiefs, as an innovative governance entity, fulfill a role insufficiently explored in existing literature. The findings reveal that river chiefs act as intermediaries between functional organizations and villagers. Their proactive patrols in early stages not only reinforce the authority of government regulation but also indirectly incentivize villager participation through demonstration effects. However, the synchronized evolution of strategies between river chiefs and the government suggests a feedback-driven mechanism; once functional organizations and villagers achieve proactive governance through early-stage policy interventions, regulatory entities (the government and river chiefs) tend to reduce oversight intensity, ultimately stabilizing in a passive equilibrium.

4.2. Sensitivity Analysis of Key Parameters

Through the sensitivity analysis of the payoff parameters related to functional organizations and villagers, this study reveals three critical findings. (1) Providing villagers with moderate monetary rewards significantly enhances their participation in governance, validating Luo et al.’s conclusion that compensation and incentives for villagers are pivotal to activating endogenous governance dynamics [48]. However, a threshold constraint exists; excessively high rewards undermine the direct benefits of functional organizations, such as diverting funds from core governance tasks, ultimately reducing their operational efficiency. (2) The reputation benefits of functional organizations positively correlate with their governance proactivity, yet high operational costs hinder their transition to active governance strategies. This aligns with Li et al., who demonstrated that corporate reputation drives pollution control but is constrained by cost affordability, indicating a universal principle that the efficacy of reputation mechanisms hinges on cost sustainability across governance contexts [45]. (3) While incentive mechanisms, like subsidies, promote villager engagement, their lack of transparency in rural areas, due to information asymmetry and cultural–cognitive disparities, creates implementation barriers. For instance, unclear reward criteria may suppress participation, despite high compensation, contrasting with urban models where institutional rigidity often masks transparency gaps.

5. Conclusions

5.1. Findings

According to the above analysis, this paper draws the following conclusions:

(1)

When functional organizations and villagers jointly participate in rural river governance, the following ideal evolutionary outcome can be achieved: lenient supervision, no patrol, governance, and participation. In this case, the government and rural river chiefs initially drive the governance efforts but gradually shift toward a more passive role, eventually reaching a stable state.

(2)

Functional organizations and villagers are the key entities in the evolutionary game process, and the payoff parameters associated with them significantly influence the strategic choices of all parties. If the reward amount given by functional organizations to villagers is too small, it reduces villagers’ enthusiasm for participation; if it is too large, it harms the functional organizations’ own interests and lowers the efficiency of river governance. Reputation benefits have a direct and practical impact on functional organizations; the greater the reputational benefits, the more inclined they are to choose river governance. The cost of governance for functional organizations is a critical factor affecting their willingness to participate; excessively high costs make it difficult to evolve toward a scenario where functional organizations and villagers co-govern the river. While incentive mechanisms encourage villagers to participate in rural river governance, the lack of transparency in these mechanisms creates difficulties for villagers in understanding and engaging with them effectively.

5.2. Recommendations

Based on the conclusions, this paper proposes the following recommendations to address the identified challenges and improve the effectiveness of rural river governance under the RCS.

(1)

Improve the assessment and accountability mechanism for river chiefs to enhance their sense of responsibility. On one hand, local governments should formulate detailed rural river chief evaluation methods and criteria based on the actual operation of the RCS in their regions, clearly defining all evaluation indicators to demonstrate the fairness and seriousness of government evaluations of rural river chiefs’ work. On the other hand, based on the evolution results, rewards and penalties should be strictly enforced according to the evolution criteria. Specialized training should be provided to underperforming rural river chiefs, with a focus on improving the quality of their river patrols.

(2)

Empower the RCS through digital means to enhance its information management level. The government should establish a platform with diverse functions, including data collection and the monitoring of rivers, river patrol management, public feedback, data analysis, and decision making, to improve the efficiency and level of RCS management and facilitate public participation in river governance.

(3)

Promote collaborative development between functional organizations and other stakeholders. The reward amount given by functional organizations to villagers should follow the principle of moderation and remain within a reasonable range to foster a collaborative governance relationship between the two parties. Attention should be paid to the conversion rate of reputational benefits to enhance the motivation of functional organizations. The government should prioritize the technical capabilities and reputation of functional organizations, providing more business resources to those with higher reputational benefits. Efforts should be made to develop river pollution control technologies to reduce the governance costs of functional organizations. The government can encourage investment in technology research and development by offering subsidies to functional organizations and professional R&D teams or institutions.

(4)

Improve and publicize incentive mechanisms to enhance villagers’ participation in river governance. On one hand, reward measures should be implemented for villager involvement in governance, encouraging them to actively monitor rivers and regulate personal behavior to minimize the discharge of harmful substances. On the other hand, it must be ensured that incentive measures specified by local authorities are transparent and well-publicized among villagers, fully enhancing the effectiveness of this mechanism.

(5)

Providing employment opportunities serves to amplify villagers’ engagement enthusiasm. Local governments could establish “Village-Level River Conservation Officer” positions within the RCS, prioritizing the recruitment of low-income villagers and returning youth. These officers would be responsible for daily patrols, waste removal, and environmental education initiatives. By empowering villagers with direct governance responsibilities and complementing these roles with digital tools, such positions can significantly improve the efficiency of environmental issue response, while fostering a stronger sense of community ownership. This approach not only institutionalizes grassroots participation but also aligns with sustainable governance frameworks that emphasize accountability and technological integration.

(6)

Strengthening legal–institutional coordination within the RCS is essential for effective rural river governance [58]. This can be achieved by incorporating villagers’ supervisory rights into local water protection regulations and integrating community monitoring data into the RCS evaluation framework through digital platforms, thereby establishing legally mandated participatory mechanisms. Simultaneously, the regular disclosure of river governance outcomes and violation resolutions via village-level public disclosure mechanisms is essential for aligning governance incentives with regulatory obligations.

5.3. Limitations and Future Research

(1)

While existing research predominantly examines governmental and community stakeholders in rural river governance, it inadequately addresses industrial enterprises as major pollution sources due to uncontrolled wastewater discharge. The complex interactions between corporations and key stakeholders create governance challenges that transcend traditional regulatory methods. Future studies should simplify regulatory systems and integrate enterprises into game theory models to better analyze multi-stakeholder dynamics. This approach would improve understanding of how industries, authorities, and communities make environmental decisions under changing ecological pressures.

(2)

The deterministic assumptions of our evolutionary game model, while effective for identifying stable equilibria, may oversimplify real decision-making processes. In practice, stakeholders frequently exhibit stochastic behavioral shifts driven by external uncertainties or imperfect information. To address this gap, follow-up research could develop evolutionary game frameworks incorporating random disturbance factors, thereby enhancing the model’s capacity to simulate emergent strategies in dynamic environmental governance scenarios.

(3)

The theoretical framework of this study employs numerical simulations due to challenges in obtaining reliable empirical parameters. Future research can systematically integrate multi-source data from certified environmental monitoring systems and governmental records to establish an empirical validation framework. Comparative analyses between simulation outcomes and case-specific datasets, particularly those documenting pollution control processes in similar rural watersheds, can help re-searchers develop evidence-based validation protocols. This approach not only strengthens the empirical foundation of the study but also enhances the model’s decision support capabilities through parameter calibration.