2D Model of a Biomass Single Particle Pyrolysis—Analysis of the Influence of Fiber Orientation on the Thermal Decomposition Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Governing Equations
| Parameter, Unit | Value/Function | Reference |
|---|---|---|
| 0.38 | [28] 1 | |
| 0.15 | [28] 1 | |
| [45] 1 | ||
| 360 | [46] | |
| 299 | [46] | |
| [47] | ||
| [28] | ||
| [48] 1 | ||
| 0.966 | [49] 1 | |
| [50] 1 | ||
| , % | 60 | [51] |
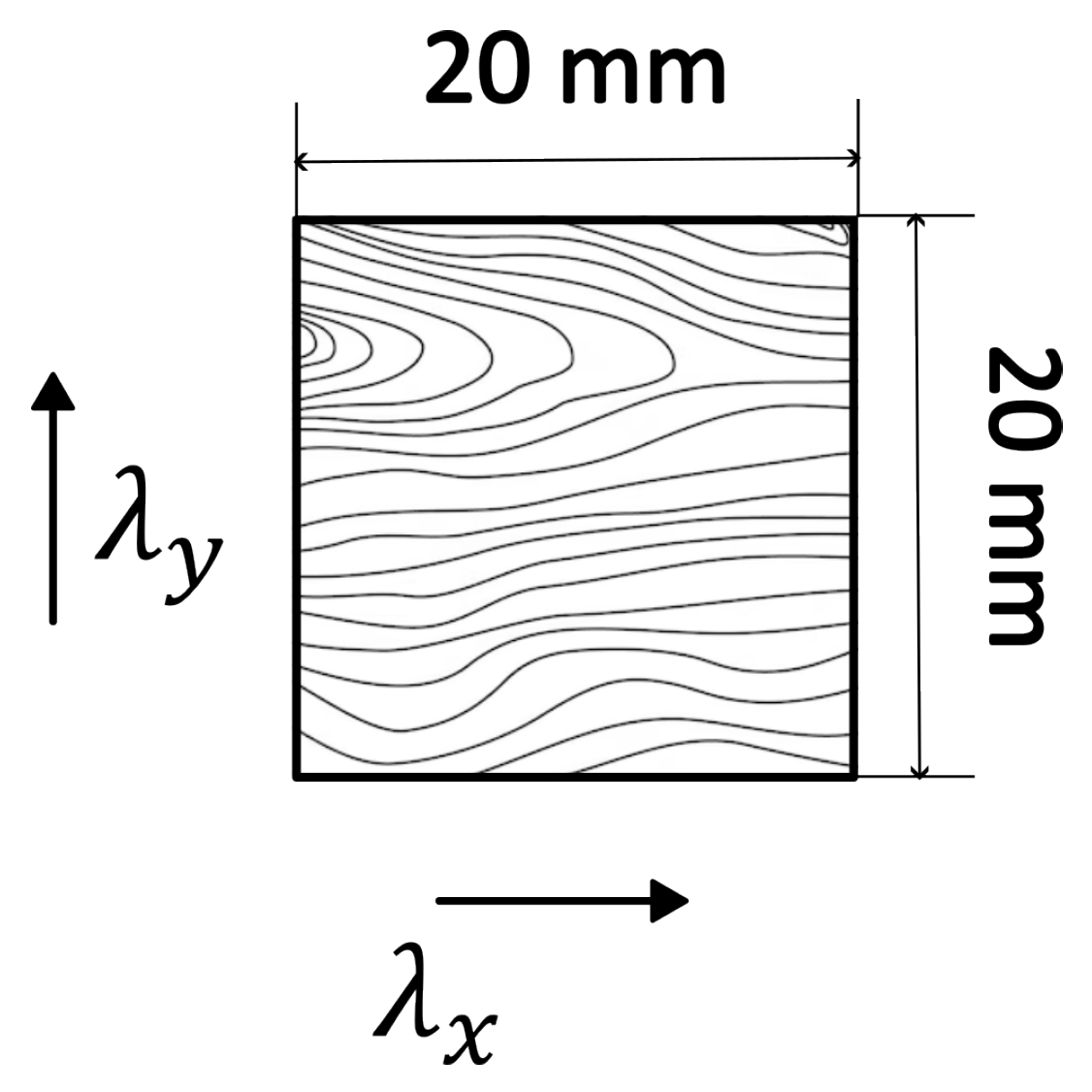
2.2. Geometry and Mesh
2.3. Initial and Boundary Conditions
2.4. Computational Approach
3. Results and Discussion
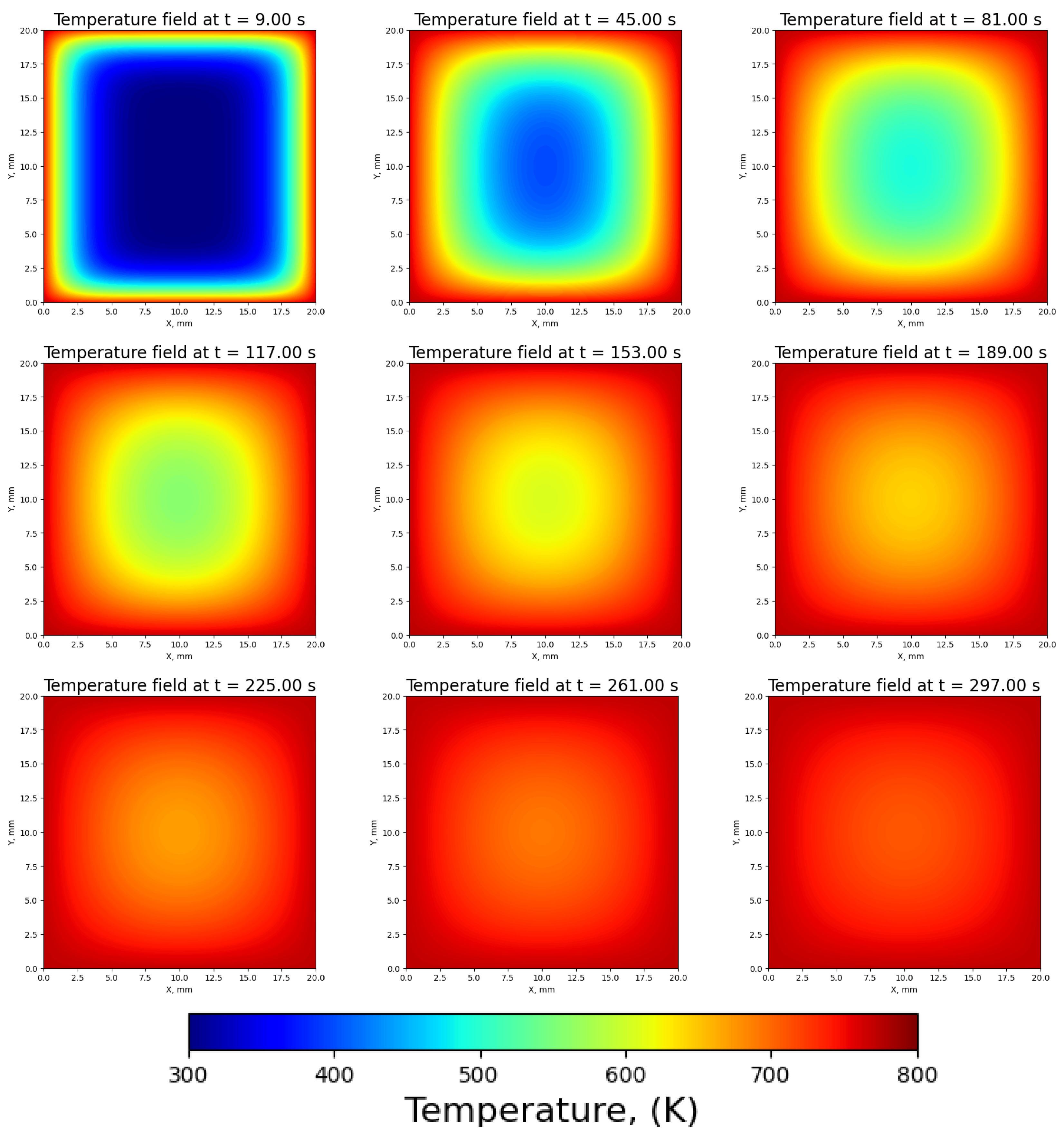
3.1. Temperature Distribution
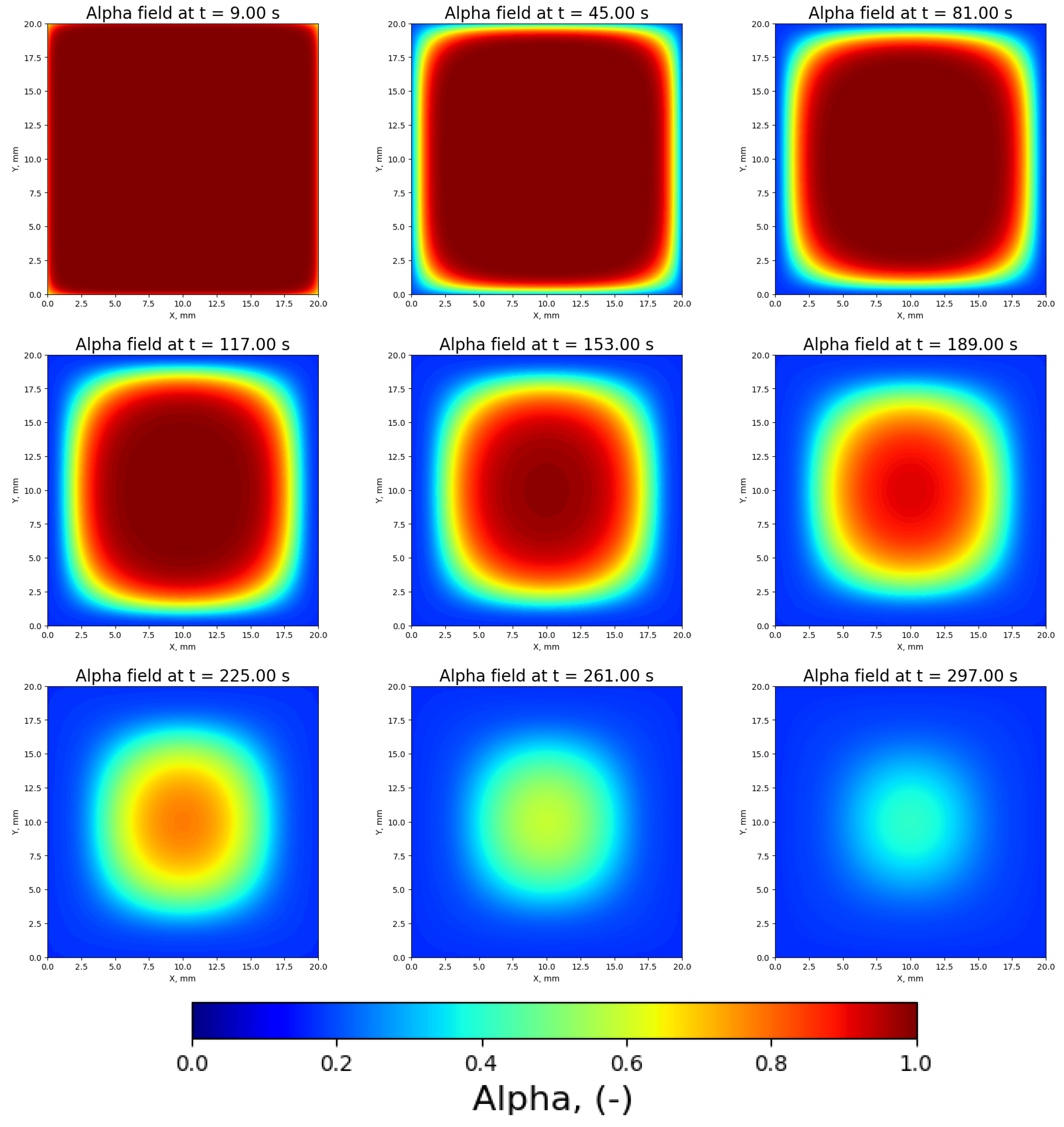
3.2. Normalized Mass Coefficient
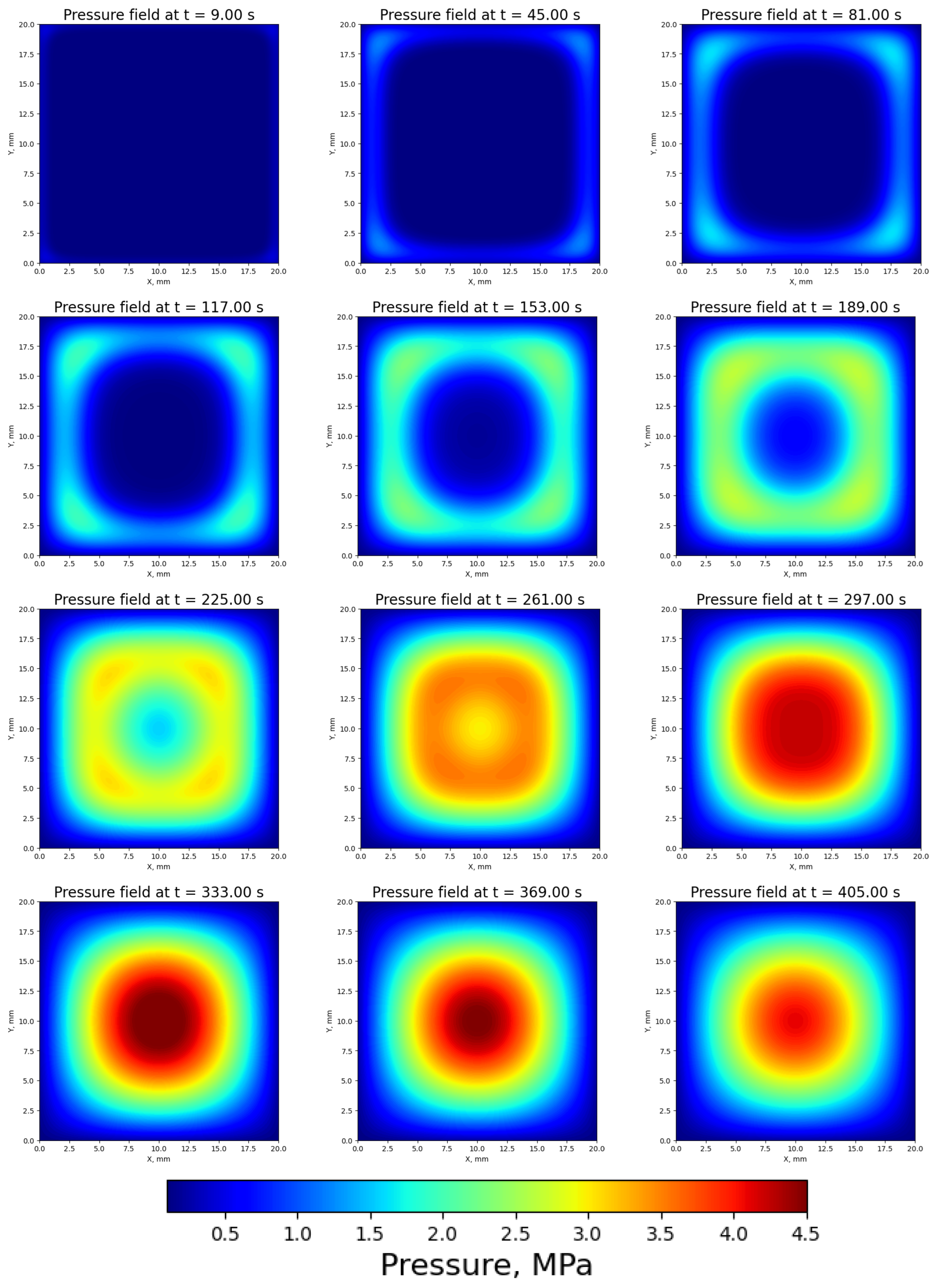
3.3. Pressure Distribution
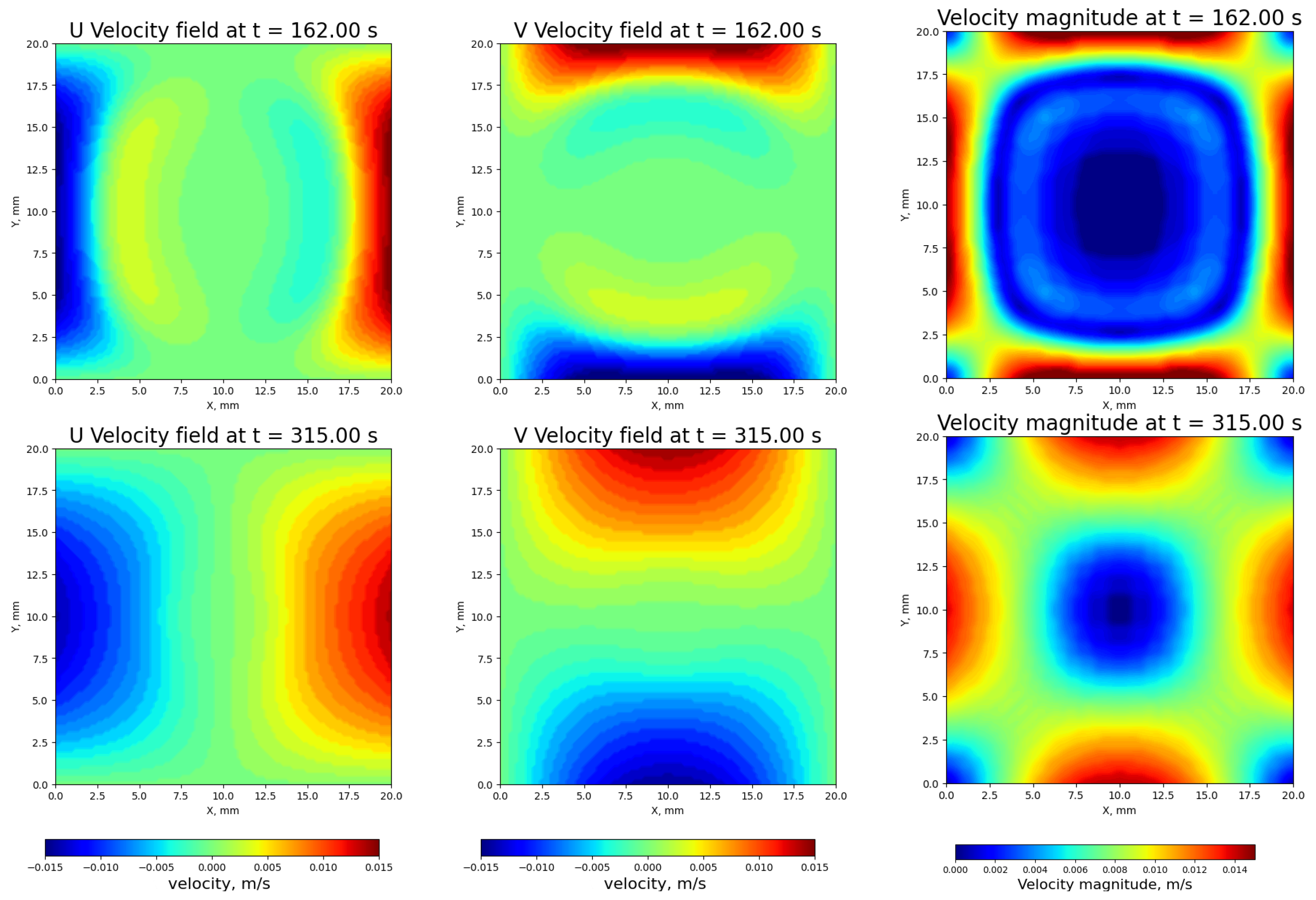
3.4. Velocity Distributions
3.5. Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Azeta, O.; Ayeni, A.O.; Agboola, O.; Elehinafe, F.B. A review on the sustainable energy generation from the pyrolysis of coconut biomass. Sci. Afr. 2021, 13, e00909. [Google Scholar] [CrossRef]
- Elfaki, H.; Hemachandra, N.; Stockinger, G.; Al-Sharshani, A.; Solim, S.; Al-Mohannadi, D.M. Sustainable Valorization of Oil and Gas Industry Biosolids: Optimal Reuse Pathways. Sustainability 2024, 16, 9738. [Google Scholar] [CrossRef]
- The European Green Deal—Commission.Europa.eu. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en (accessed on 29 October 2024).
- Lenz, V.; Szarka, N.; Jordan, M.; Thrän, D. Status and perspectives of biomass use for industrial process heat for industrialized countries. Chem. Eng. Technol. 2020, 43, 1469–1484. [Google Scholar] [CrossRef]
- Ganesh, A.; Banerjee, R. Biomass pyrolysis for power generation—A potential technology. Renew. Energy 2001, 22, 9–14. [Google Scholar] [CrossRef]
- Mousa, E.; Wang, C.; Riesbeck, J.; Larsson, M. Biomass applications in iron and steel industry: An overview of challenges and opportunities. Renew. Sustain. Energy Rev. 2016, 65, 1247–1266. [Google Scholar] [CrossRef]
- Kusuma, R.T.; Hiremath, R.B.; Rajesh, P.; Kumar, B.; Renukappa, S. Sustainable transition towards biomass-based cement industry: A review. Renew. Sustain. Energy Rev. 2022, 163, 112503. [Google Scholar] [CrossRef]
- Prasanth, S.; Kumar, P.S.; Harish, S.; Rishikesh, M.; Nanda, S.; Vo, D.V.N. Application of biomass derived products in mid-size automotive industries: A review. Chemosphere 2021, 280, 130723. [Google Scholar] [CrossRef] [PubMed]
- Ireson, R.; Stewart, B.; García, P.G.; Isaac, D.; Backhouse, D.; Toperesu, M.; Ledger, J.; Fuller, A. Renewable Waste-Derived Fuels for Glass and Ceramics Manufacturing: Feasibility Study Final Report; Technical Report; Glass Futures: Saint Helens, UK, 2023. [Google Scholar]
- Punnarapong, P.; Promwungkwa, A.; Tippayawong, N. Development and performance evaluation of a biomass gasification system for ceramic firing process. Energy Procedia 2017, 110, 53–58. [Google Scholar] [CrossRef]
- Basu, P. Biomass Gasification and Pyrolysis: Practical Design and Theory; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Igliński, B.; Kujawski, W.; Kiełkowska, U. Pyrolysis of Waste Biomass: Technical and Process Achievements, and Future Development—A Review. Energies 2023, 16, 1829. [Google Scholar] [CrossRef]
- Gupta, G.K.; Mondal, M.K. Chapter 14 - Pyrolysis: An alternative approach for utilization of biomass into bioenergy generation. In Biofuels and Bioenergy; Gurunathan, B., Sahadevan, R., Zakaria, Z.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 279–300. [Google Scholar] [CrossRef]
- Zhu, J.; Guo, Y.; Chen, N.; Chen, B. A Review of the Efficient and Thermal Utilization of Biomass Waste. Sustainability 2024, 16, 9506. [Google Scholar] [CrossRef]
- Jahirul, M.I.; Rasul, M.G.; Chowdhury, A.A.; Ashwath, N. Biofuels Production through Biomass Pyrolysis—A Technological Review. Energies 2012, 5, 4952–5001. [Google Scholar] [CrossRef]
- Mohanty, A.; Ajmera, S.; Chinnam, S.; Kumar, V.; Mishra, R.K.; Acharya, B. Pyrolysis of waste oils for biofuel production: An economic and life cycle assessment. Fuel Commun. 2024, 18, 100108. [Google Scholar] [CrossRef]
- Yu, J.; Liu, X.; Millan, M. A study on pyrolysis of wood of different sizes at various temperatures and pressures. Fuel 2023, 342, 127846. [Google Scholar] [CrossRef]
- Banagiri, S.; Parameswaran, M.; Khadakkar, I.; Meadows, J.; Lattimer, B.Y. A reduced wood pyrolysis mechanism for evaluating solid and gas phase parameters. Fuel 2025, 381, 133416. [Google Scholar] [CrossRef]
- Dhaundiyal, A.; Singh, S.B. Optimisation of the performance of a pyrolysis reactor for G50 chips. Arch. Thermodyn. 2020, 41, 245–263. [Google Scholar] [CrossRef]
- Plavniece, A.; Dobele, G.; Volperts, A.; Zhurinsh, A. Hydrothermal carbonization vs. Pyrolysis: Effect on the porosity of the activated carbon materials. Sustainability 2022, 14, 15982. [Google Scholar] [CrossRef]
- Kumar Mishra, R.; Singh, B.; Acharya, B. A comprehensive review on activated carbon from pyrolysis of lignocellulosic biomass: An application for energy and the environment. Carbon Resour. Convers. 2024, 7, 100228. [Google Scholar] [CrossRef]
- Rodier, L.; Bilba, K.; Onésippe, C.; Arsène, M.A. Utilization of bio-chars from sugarcane bagasse pyrolysis in cement-based composites. Ind. Crop. Prod. 2019, 141, 111731. [Google Scholar] [CrossRef]
- Kizinievic, O.; Kizinievic, V. Utilisation of wood ash from biomass for the production of ceramic products. Constr. Build. Mater. 2016, 127, 264–273. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, F.; An, X.; Wu, Z.; Li, T.; Yang, Q. Microwave co-pyrolysis of biomass, phosphorus, and magnesium for the preparation of biochar-based fertilizer: Fast synthesis, regulable structure, and graded-release. J. Environ. Chem. Eng. 2021, 9, 106456. [Google Scholar] [CrossRef]
- Gokelma, M.; Diaz, F.; Çapkın, I.Y.; Friedrich, B. A Viability Study of Thermal Pre-Treatment for Recycling of Pharmaceutical Blisters. Sustainability 2024, 16, 8968. [Google Scholar] [CrossRef]
- Niu, Y.; Pan, F.; Shen, K.; Yang, X.; Niu, S.; Xu, X.; Zhou, H.; Fu, Q.; Li, X. Status and Enhancement Techniques of Plastic Waste Degradation in the Environment: A Review. Sustainability 2024, 16, 9395. [Google Scholar] [CrossRef]
- Rodríguez-Grau, G.; Cordonnier, P.L.; Navarrete, B.; Montero, C.; Alvarado, C.; Pommier, R.; Rosales, V.; Galarce, C. The adhesion performance in green-glued finger joints using different wood ring orientations. Sustainability 2024, 16, 7158. [Google Scholar] [CrossRef]
- Grønli, M. Theoretical and Experimental Study of the Thermal Degradation of Biomass. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1996. [Google Scholar]
- Hameed, S.; Sharma, A.; Pareek, V.; Wu, H.; Yu, Y. A review on biomass pyrolysis models: Kinetic, network and mechanistic models. Biomass Bioenergy 2019, 123, 104–122. [Google Scholar] [CrossRef]
- Vikram, S.; Rosha, P.; Kumar, S. Recent Modeling Approaches to Biomass Pyrolysis: A Review. Energy Fuels 2021, 35, 7406–7433. [Google Scholar] [CrossRef]
- Xia, C.; Cai, L.; Zhang, H.; Zuo, L.; Shi, S.Q.; Lam, S.S. A review on the modeling and validation of biomass pyrolysis with a focus on product yield and composition. Biofuel Res. J. 2021, 8, 1296–1315. [Google Scholar] [CrossRef]
- Seo, D.K.; Park, S.S.; Hwang, J.; Yu, T.U. Study of the pyrolysis of biomass using thermo-gravimetric analysis (TGA) and concentration measurements of the evolved species. J. Anal. Appl. Pyrolysis 2010, 89, 66–73. [Google Scholar] [CrossRef]
- Fischer, O.; Lemaire, R.; Bensakhria, A. Thermogravimetric analysis and kinetic modeling of the pyrolysis of different biomass types by means of model-fitting, model-free and network modeling approaches. J. Therm. Anal. Calorim. 2024, 149, 10941–10963. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Lemaire, R.; Bensakhria, A.; Luart, D. Thermogravimetric analysis and kinetic modeling of the co-pyrolysis of a bituminous coal and poplar wood. Chin. J. Chem. Eng. 2023, 58, 53–68. [Google Scholar] [CrossRef]
- Lin, Y.; Cho, J.; Davis, J.M.; Huber, G.W. Reaction-transport model for the pyrolysis of shrinking cellulose particles. Chem. Eng. Sci. 2012, 74, 160–171. [Google Scholar] [CrossRef]
- Bates, R.B.; Ghoniem, A.F. Modeling kinetics-transport interactions during biomass torrefaction: The effects of temperature, particle size, and moisture content. Fuel 2014, 137, 216–229. [Google Scholar] [CrossRef]
- Kardaś, D.; Hercel, P.; Wardach-Święcicka, I.; Polesek-Karczewska, S. On the kinetic rate of biomass particle decomposition - Experimental and numerical analysis. Energy 2021, 219, 119575. [Google Scholar] [CrossRef]
- Assoumani, N.; Simo-Tagne, M.; Kifani-Sahban, F.; Tagne Tagne, A.; El Marouani, M.; Obounou Akong, M.B.; Rogaume, Y.; Girods, P.; Zoulalian, A. Numerical study of cylindrical tropical woods pyrolysis using Python tool. Sustainability 2021, 13, 13892. [Google Scholar] [CrossRef]
- Wardach-Święcicka, I.; Kardaś, D. Modeling of heat and mass transfer during thermal decomposition of a single solid fuel particle. Arch. Thermodyn. 2013, 34, 53–71. [Google Scholar] [CrossRef]
- Wardach-Święcicka, I.; Kardaś, D. Modelling thermal behaviour of a single solid particle pyrolysing in a hot gas flow. Energy 2021, 221, 119802. [Google Scholar] [CrossRef]
- Postrzednik, S. Heat of solid fuel pyrolysis—Determination method, basic properties, in Polish. Karbo-Energochemia-Ekologia 1994, 9, 220. [Google Scholar]
- Wardach-Świȩcicka, I. Modelling of Physico-Chemical Processes in a Single Solid Fuel Particle in a Stream of Hot Gases. Ph.D. Thesis, Institute of Fluid-Flow Machinery, Polish Academy of Sciences, Gdańsk, Poland, 2016. (In Polish). [Google Scholar]
- Wagenaar, B.; Prins, W.; van Swaaij, W. Flash pyrolysis kinetics of pine wood. Fuel Process. Technol. 1993, 36, 291–298. [Google Scholar] [CrossRef]
- Muvhiiwa, R.F.; Sempuga, B.; Hildebrandt, D.; Van Der Walt, J. Study of the effects of temperature on syngas composition from pyrolysis of wood pellets using a nitrogen plasma torch reactor. J. Anal. Appl. Pyrolysis 2018, 130, 159–168. [Google Scholar] [CrossRef]
- Park, J.S.; Lee, J.J. Fire resistance of light-framed wood floors exposed to real and standard fire. J. Fire Sci. 2004, 22, 449–471. [Google Scholar] [CrossRef]
- Gupta, M. Density of softwood bark and softwood char: Procedural calibration and measurement by water soaking and kerosene immersion method. Fuel 2002, 81, 1379–1384. [Google Scholar] [CrossRef]
- Gupta, M.; Yang, J.; Roy, C. Specific heat and thermal conductivity of softwood bark and softwood char particles. Fuel 2003, 82, 919–927. [Google Scholar] [CrossRef]
- Ronewicz, K.; Kardaś, D. Experimental and Theoretical Investigation over the Wood Permeability to Air as a Function of Pyrolysis Temperature. Appl. Mech. Mater. 2016, 831, 295–305. [Google Scholar] [CrossRef]
- Gases—Densities—Engineeringtoolbox.com. Available online: https://www.engineeringtoolbox.com/gas-density-d_158.html (accessed on 14 November 2024).
- Gases—Dynamic Viscosities—engineeringtoolbox.com. Available online: https://www.engineeringtoolbox.com/gases-absolute-dynamic-viscosity-d_1888.html (accessed on 13 November 2024).
- Plötze, M.; Niemz, P. Porosity and pore size distribution of different wood types as determined by mercury intrusion porosimetry. Eur. J. Wood Wood Prod. 2011, 69, 649–657. [Google Scholar] [CrossRef]
- Sadhukhan, A.K.; Gupta, P.; Saha, R.K. Modelling of pyrolysis of large wood particles. Bioresour. Technol. 2009, 100, 3134–3139. [Google Scholar] [CrossRef] [PubMed]
- Kazimierski, P.; Januszewicz, K.; Hercel, P.; Kardaś, D. Experimental and numerical analysis of the pyrolysis dynamics of a single wood particle: Presentation of the radiographic technique. Wood Sci. Technol. 2023, 57, 1157–1173. [Google Scholar] [CrossRef]
- Handiso, B.; Pääkkönen, T.; Wilson, B.P. Effect of pyrolysis temperature on the physical and chemical characteristics of pine wood biochar. Waste Manag. Bull. 2024, 2, 281–287. [Google Scholar] [CrossRef]
- Soria-Verdugo, A.; Cano-Pleite, E.; Passalacqua, A.; Fox, R.O. Effect of particle shape on biomass pyrolysis in a bubbling fluidized bed. Fuel 2023, 339, 127365. [Google Scholar] [CrossRef]
- Kazimierski, P.; Wardach-Święcicka, I.; Tiutiurski, P.; Kardaś, D. Pyrolysis analysis of a single wood particle. Inżynieria Apar. Chem. 2017, 6, 202–204. (In Polish) [Google Scholar]
- Hoang, N.Q.; Vanierschot, M.; Croymans, T.; Pittoors, R.; Van Caneghem, J. A two-dimensional pyrolysis model for thermally thick particles. In Proceedings of the 12th European Conference on Industrial Furnaces and Boilers, INFUB, Porto, Portugal, 14–17 April 2021. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hercel, P.; Orhon, A.; Jóźwik, M.; Kardaś, D. 2D Model of a Biomass Single Particle Pyrolysis—Analysis of the Influence of Fiber Orientation on the Thermal Decomposition Process. Sustainability 2025, 17, 279. https://doi.org/10.3390/su17010279
Hercel P, Orhon A, Jóźwik M, Kardaś D. 2D Model of a Biomass Single Particle Pyrolysis—Analysis of the Influence of Fiber Orientation on the Thermal Decomposition Process. Sustainability. 2025; 17(1):279. https://doi.org/10.3390/su17010279
Chicago/Turabian StyleHercel, Paulina, Atahan Orhon, Michał Jóźwik, and Dariusz Kardaś. 2025. "2D Model of a Biomass Single Particle Pyrolysis—Analysis of the Influence of Fiber Orientation on the Thermal Decomposition Process" Sustainability 17, no. 1: 279. https://doi.org/10.3390/su17010279
APA StyleHercel, P., Orhon, A., Jóźwik, M., & Kardaś, D. (2025). 2D Model of a Biomass Single Particle Pyrolysis—Analysis of the Influence of Fiber Orientation on the Thermal Decomposition Process. Sustainability, 17(1), 279. https://doi.org/10.3390/su17010279







